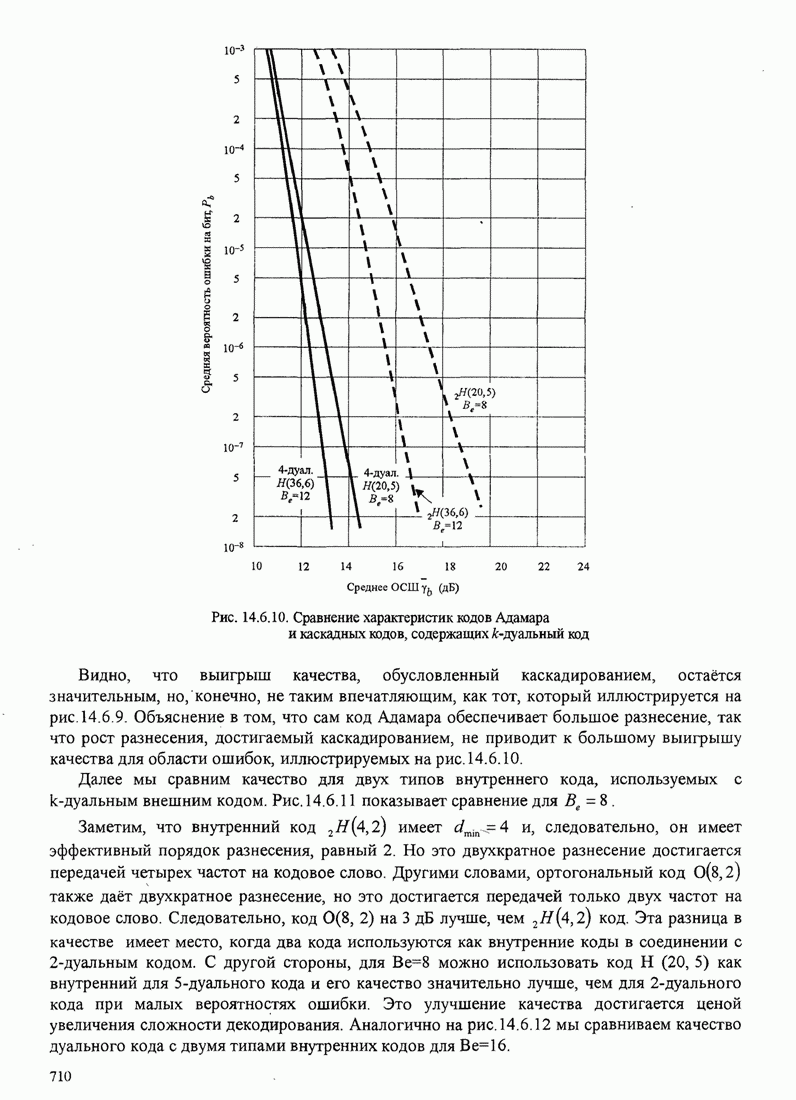
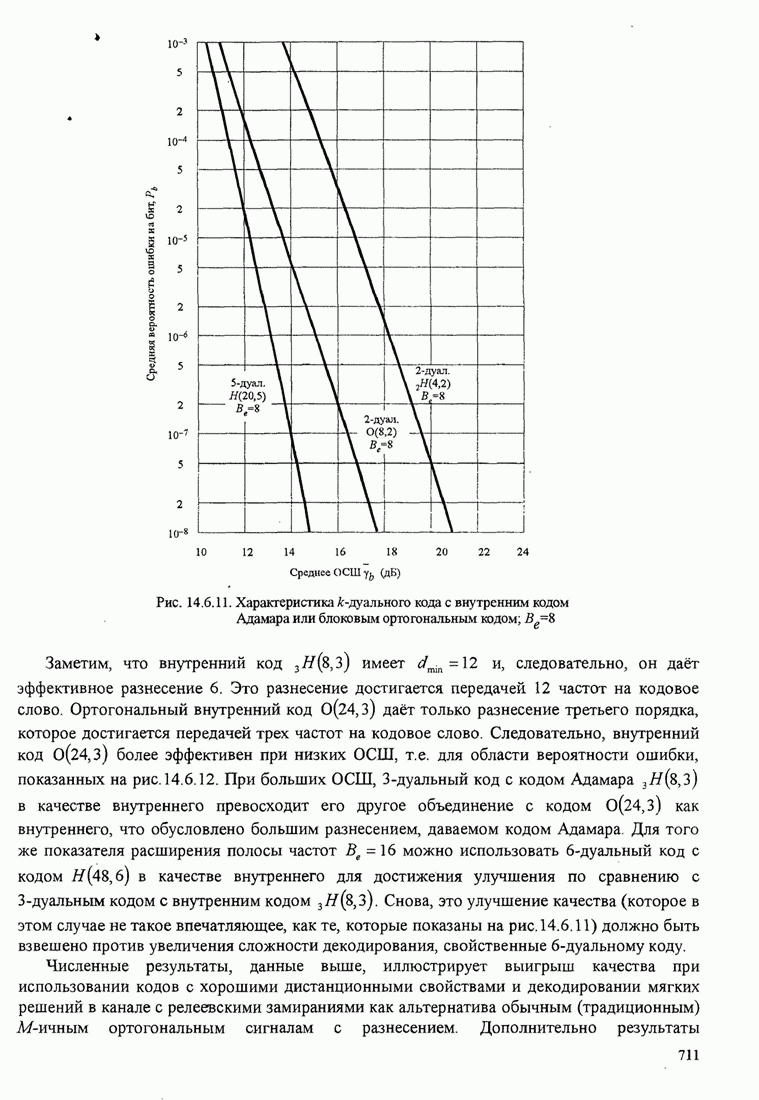
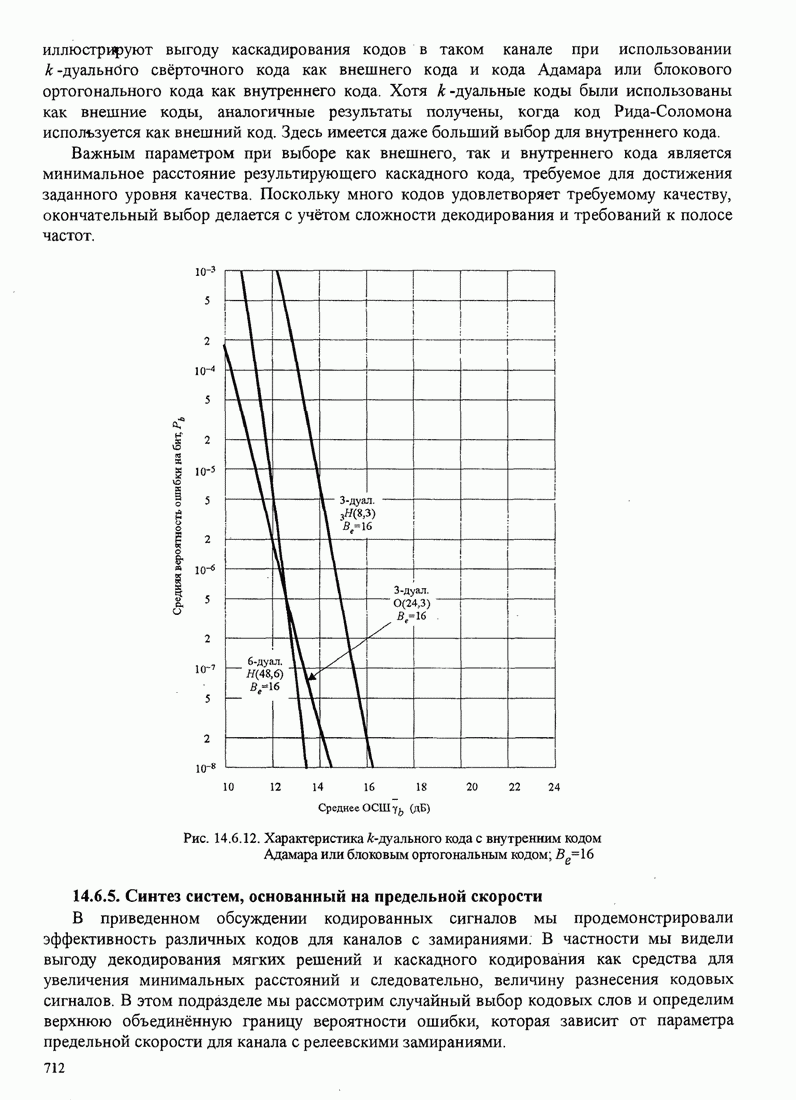
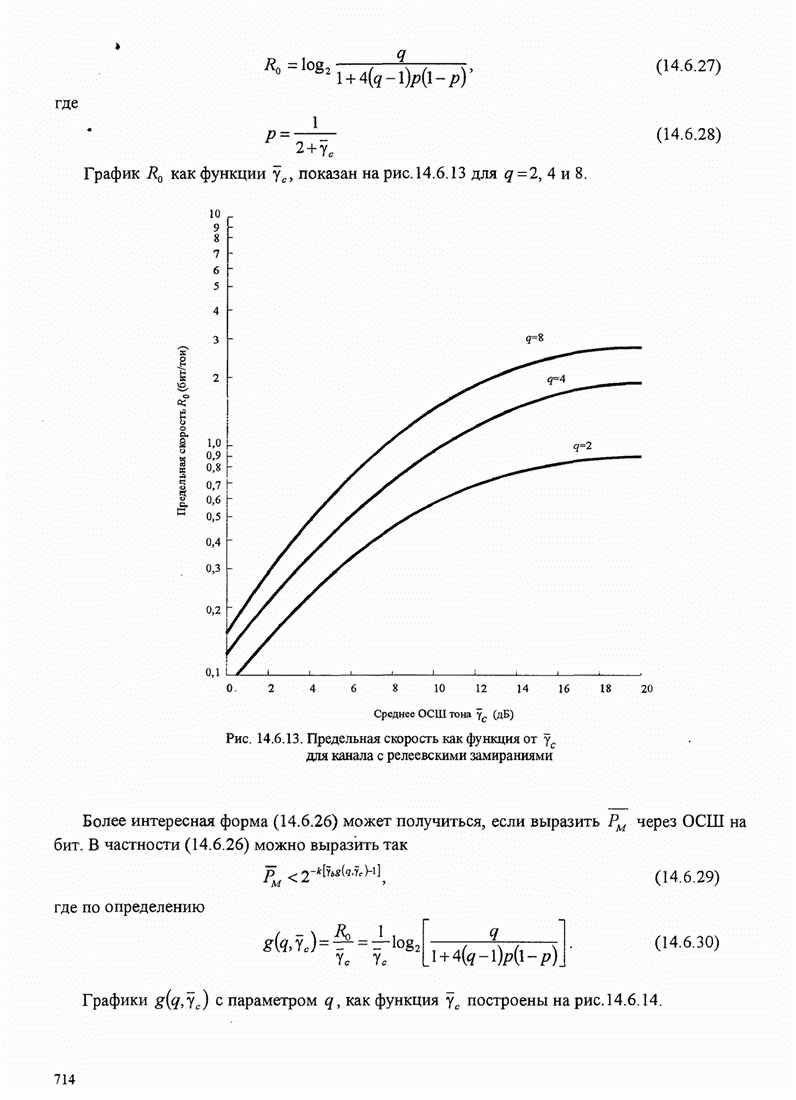
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
При декодировании
блокового кода в канале без памяти, мы вычисляем расстояние (расстояние
Хемминга при декодировании жёстких решений и расстояние Евклида при
декодировании мягких решений) между принимаемым кодовыми словами и ![]() возможными
к передаче кодовыми словами. Затем мы выбираем кодовое слово, которое наиболее
близко по расстоянию к принятому кодовому слову. Это правило решения, которое
требует вычисления
возможными
к передаче кодовыми словами. Затем мы выбираем кодовое слово, которое наиболее
близко по расстоянию к принятому кодовому слову. Это правило решения, которое
требует вычисления ![]() метрик, оптимально в том смысле, что
оно приводит к минимуму средней вероятности ошибки в двоичном симметричном
канале с АБГШ и
метрик, оптимально в том смысле, что
оно приводит к минимуму средней вероятности ошибки в двоичном симметричном
канале с АБГШ и ![]() .
.
В отличие от блокового
кода, который имеет фиксированную длину ![]() , свёрточный код порождается
устройством с ограниченным числом состояний. Как следствие, оптимальный декодер
является максимально правдоподобным последовательным оценивателем (МППО) вида,
описанного в разделе 5.1.4 для сигналов с памятью, таких как ДБНП и МНФ. Поэтому
оптимальное декодирование свёрточных кодов включает поиск по решётке наиболее
правдоподобной последовательности. В зависимости от того, формирует ли
детектор, за которым следует декодер, жёсткие или мягкие решения,
соответствующие метрики при поиске по решётке могут быть или метриками Хемминга
или метриками Евклида, соответственно. Более подробно мы это рассмотрим ниже,
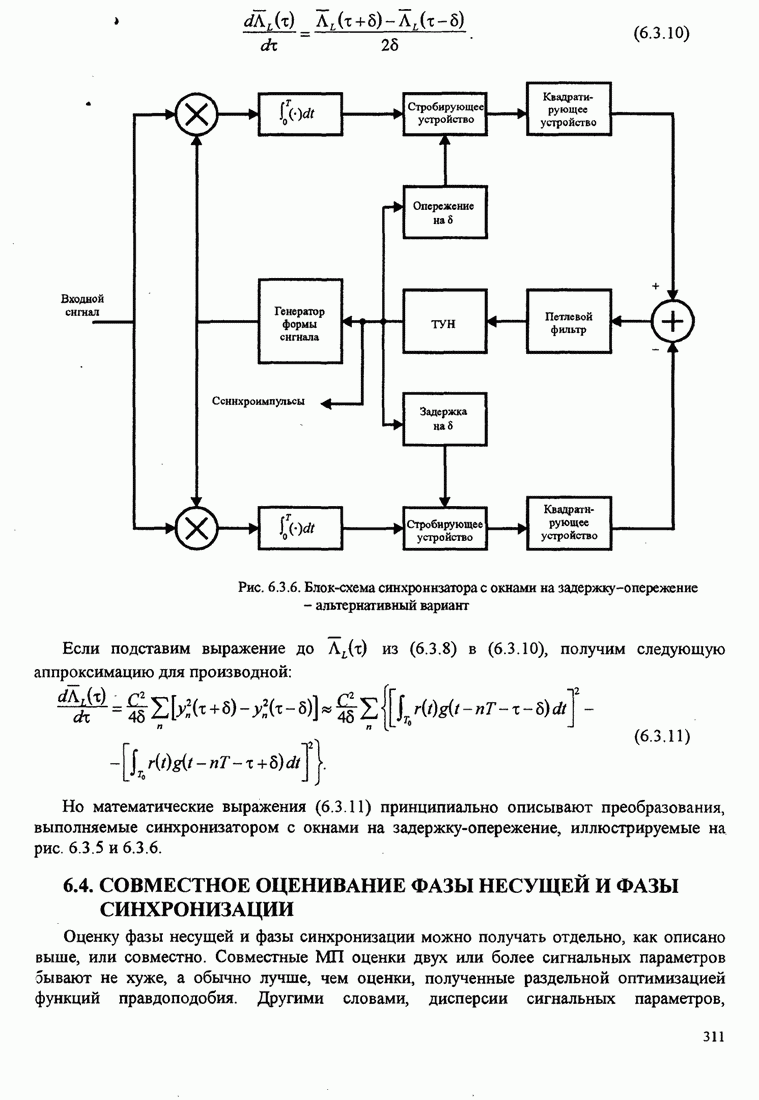
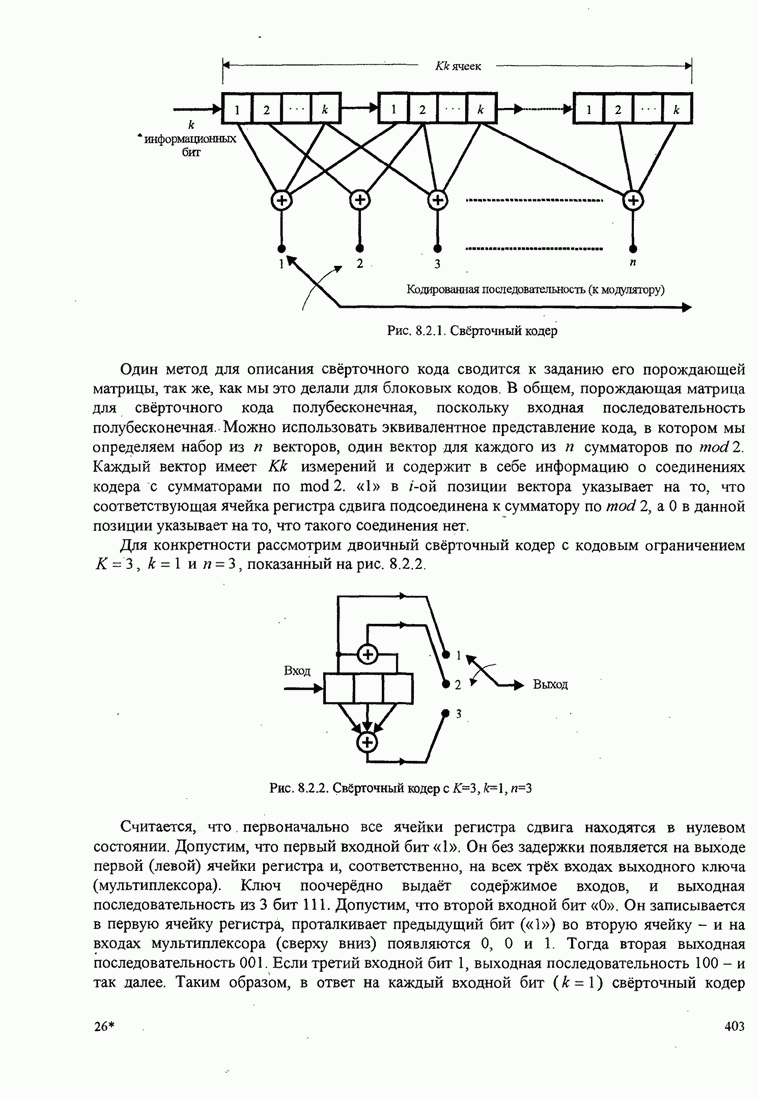
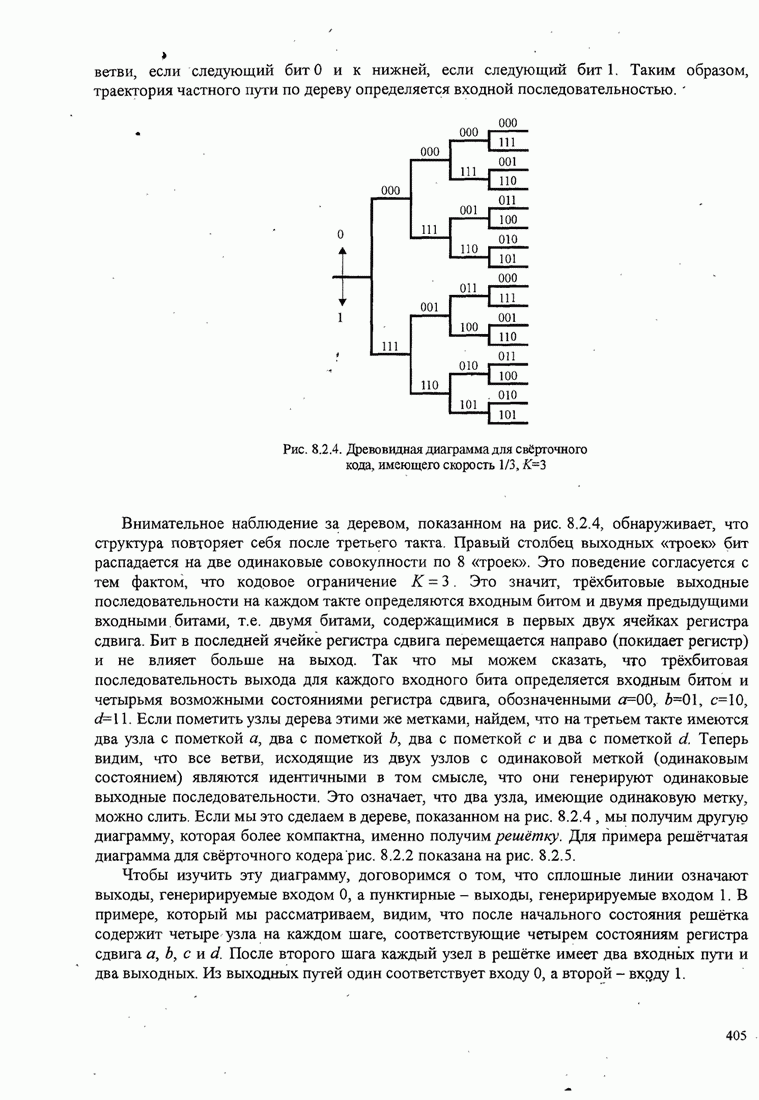
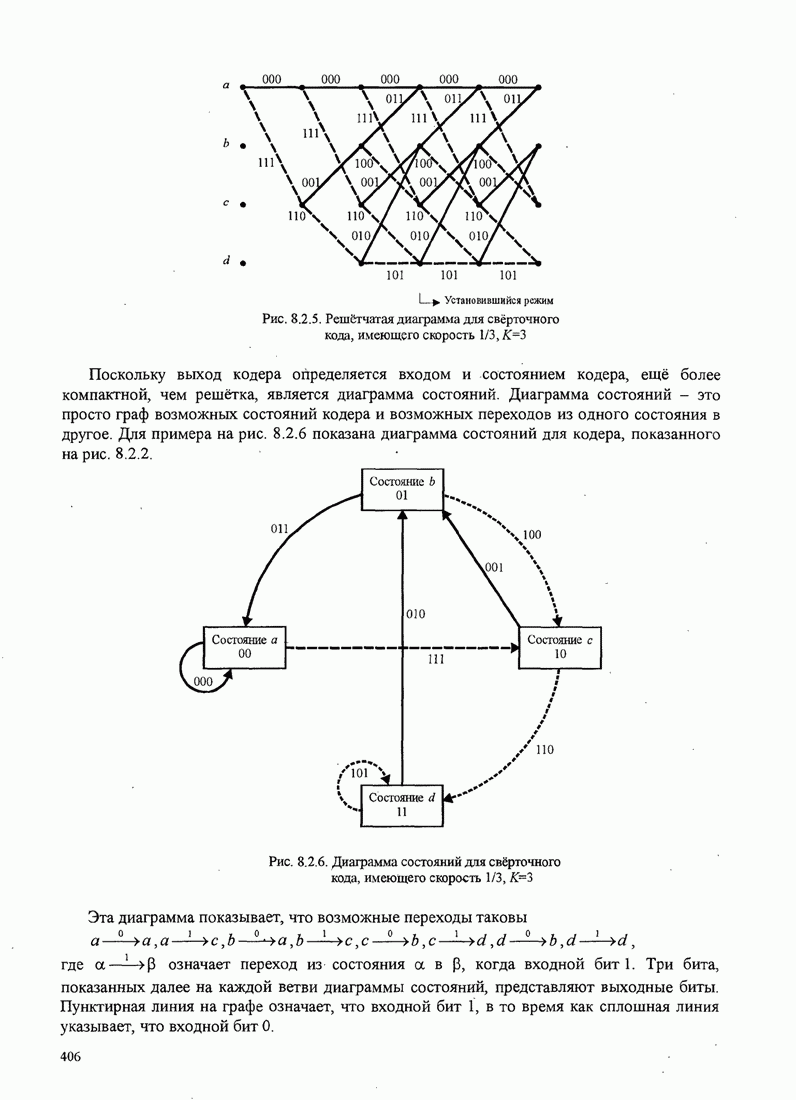
используя решётку рис. 8.2.5 для свёрточного кода, показанного на рис. 8.2.2.
, свёрточный код порождается
устройством с ограниченным числом состояний. Как следствие, оптимальный декодер
является максимально правдоподобным последовательным оценивателем (МППО) вида,
описанного в разделе 5.1.4 для сигналов с памятью, таких как ДБНП и МНФ. Поэтому
оптимальное декодирование свёрточных кодов включает поиск по решётке наиболее
правдоподобной последовательности. В зависимости от того, формирует ли
детектор, за которым следует декодер, жёсткие или мягкие решения,
соответствующие метрики при поиске по решётке могут быть или метриками Хемминга
или метриками Евклида, соответственно. Более подробно мы это рассмотрим ниже,
используя решётку рис. 8.2.5 для свёрточного кода, показанного на рис. 8.2.2.
Рассмотрим два пути на
решётке, которые начинаются в начальном состоянии ![]() и сливаются в состоянии
и сливаются в состоянии ![]() после трёх
переходов (трёх ветвей), которые соответствуют двум информационным последовательностям
000 и 100 и передаваемым последовательностям 000 000 000 и 111 001 011 соответственно.
Обозначим переданные биты через
после трёх
переходов (трёх ветвей), которые соответствуют двум информационным последовательностям
000 и 100 и передаваемым последовательностям 000 000 000 и 111 001 011 соответственно.
Обозначим переданные биты через ![]() , где индекс
, где индекс ![]() указывает на
указывает на ![]() -ю ветвь, а индекс
-ю ветвь, а индекс ![]() указывает на
указывает на ![]() -й бит в этой
ветви. Соответственно определим
-й бит в этой
ветви. Соответственно определим ![]() как выход демодулятора. Если детектор
формирует жёсткие решения, его выходом для каждого переданного бита является
или 0, или 1. С другой стороны, если используется декодирование мягких решений,
а кодированная последовательность передаётся двоичной когерентной ФМ, то
входные величины для декодера определяются так:
как выход демодулятора. Если детектор
формирует жёсткие решения, его выходом для каждого переданного бита является
или 0, или 1. С другой стороны, если используется декодирование мягких решений,
а кодированная последовательность передаётся двоичной когерентной ФМ, то
входные величины для декодера определяются так:
![]() , (8.2.9)
, (8.2.9)
где ![]() представляет собственный шум,
а
представляет собственный шум,
а ![]() - энергия,
сигнала каждого переданного кодового символа (бита).
- энергия,
сигнала каждого переданного кодового символа (бита).
Для ![]() -й ветви и
-й ветви и ![]() -го пути по решётке
метрики определяются как логарифм совместной плотности вероятности
последовательности
-го пути по решётке
метрики определяются как логарифм совместной плотности вероятности
последовательности ![]() при условии передачи
последовательности
при условии передачи
последовательности ![]() для
для ![]() -го пути.
-го пути.
То есть
![]() (8.2.10)
(8.2.10)
Далее, метрика ![]() -го пути решётки,
содержащего
-го пути решётки,
содержащего ![]() ветвей,
определяется так:
ветвей,
определяется так:
 . (8.2.11)
. (8.2.11)
Правило для решения между
двумя путями по решетке сводится к выбору того, у которого больше метрика. Это
правило максимизирует вероятность правильного решения или, что эквивалентно,
минимизирует вероятность ошибки в информационной последовательности. Например,
предположим, что демодулятором формируются жёсткие решения при принимаемой
последовательности ![]() . Пусть
. Пусть ![]() означает путь с тремя ветвями из
одних нулей, а
означает путь с тремя ветвями из
одних нулей, а ![]() означает
второй путь с тремя ветвями, который начинается в начальном состоянии
означает
второй путь с тремя ветвями, который начинается в начальном состоянии ![]() и сливается с
путём из одних нулей в состоянии
и сливается с
путём из одних нулей в состоянии ![]() после трёх переходов. Метрики для
этих двух путей таковы
после трёх переходов. Метрики для
этих двух путей таковы
 (8.2.12)
(8.2.12)
где ![]() — вероятность ошибочного
приёма бита. Предположив, что
— вероятность ошибочного
приёма бита. Предположив, что ![]() , находим, что метрика
, находим, что метрика ![]() больше, чем
метрика
больше, чем
метрика ![]() .
Этот результат согласуется с наблюдением, что путь из одних нулей
.
Этот результат согласуется с наблюдением, что путь из одних нулей ![]() имеет расстояние
Хемминга
имеет расстояние
Хемминга ![]() от
принимаемой последовательности, в то время как путь с
от
принимаемой последовательности, в то время как путь с ![]() имеет расстояние Хемминга
имеет расстояние Хемминга ![]() от принимаемого
пути. Таким образом, расстояние Хемминга является эквивалентной метрикой
для декодирования с жёстким решением.
от принимаемого
пути. Таким образом, расстояние Хемминга является эквивалентной метрикой
для декодирования с жёстким решением.
Аналогично предположим, что используется декодирование мягких решений, а канал прибавляет к сигналу АБГШ. Тогда выход демодулятора описывается статистически через условную ФПВ
 , (8.2.13)
, (8.2.13)
где ![]() - дисперсия
аддитивного гауссовского шума. Если мы пренебрегаем слагаемыми, общими для
всех метрик ветвей, метрику
- дисперсия
аддитивного гауссовского шума. Если мы пренебрегаем слагаемыми, общими для
всех метрик ветвей, метрику ![]() -й ветви
-й ветви ![]() -го пути можно выразить так:
-го пути можно выразить так:
![]() , (8.2.14)
, (8.2.14)
где в нашем примере ![]() . Таким образом,
корреляционные метрики для двух путей при оговоренных условиях
. Таким образом,
корреляционные метрики для двух путей при оговоренных условиях
 (8.2.15)
(8.2.15)
Имея метрики ветвей и
метрики путей, рассчитанные декодером, мы теперь рассмотрим использование
алгоритма Витсрби для оптимального декодирования информационной
последовательности при свёрточном кодировании. Мы рассмотрим два пути,
описанные выше, которые сливаются в состоянии ![]() после трёх переходов. Заметим, что
какой-либо частный путь по решётке, который ответвляется от этого узла, будет
суммировать идентичные слагаемые в метриках путей
после трёх переходов. Заметим, что
какой-либо частный путь по решётке, который ответвляется от этого узла, будет
суммировать идентичные слагаемые в метриках путей ![]() и
и ![]() . Как следствие, если
. Как следствие, если ![]() , у сливающегося
узла
, у сливающегося
узла ![]() после
трёх переходов,
после
трёх переходов, ![]() будет
продолжать быть больше
будет
продолжать быть больше ![]() для любого пути, который ответвляется
от узла
для любого пути, который ответвляется
от узла ![]() .
Это значит, что путь, соответствующий
.
Это значит, что путь, соответствующий ![]() , можно исключить из дальнейшего
решения. Путь, соответствующий метрике
, можно исключить из дальнейшего
решения. Путь, соответствующий метрике ![]() , является выжившим. Аналогично,
один из двух путей, которые сливаются в состоянии
, является выжившим. Аналогично,
один из двух путей, которые сливаются в состоянии ![]() , может быть исключен на основе двух
соответствующих метрик. Эта процедура повторяется в состоянии
, может быть исключен на основе двух
соответствующих метрик. Эта процедура повторяется в состоянии ![]() и состоянии
и состоянии ![]() . Как результат,
после трёх первых переходов имеются четыре выживших пути, один кончающийся на
каждом состоянии, и соответствующие метрики для каждого выжившего пути. Эта
процедура повторяется на каждом шаге решетки по мере того, как принимаются новые
сигналы в последующих временных интервалах.
. Как результат,
после трёх первых переходов имеются четыре выживших пути, один кончающийся на
каждом состоянии, и соответствующие метрики для каждого выжившего пути. Эта
процедура повторяется на каждом шаге решетки по мере того, как принимаются новые
сигналы в последующих временных интервалах.
В общем, когда
декодируется двоичный свёрточный код с ![]() и кодовым ограничением
и кодовым ограничением ![]() посредством
алгоритма Витерби, имеются
посредством
алгоритма Витерби, имеются ![]() состояний. Следовательно, имеются
состояний. Следовательно, имеются ![]() выживших путей на
каждом шаге и
выживших путей на
каждом шаге и ![]() метрик,
по одной для каждого выжившего пути. Далее, двоичный свёрточный код с
метрик,
по одной для каждого выжившего пути. Далее, двоичный свёрточный код с ![]() входными битами,
которые сдвигаются по кодеру, содержащему
входными битами,
которые сдвигаются по кодеру, содержащему ![]() (
(![]() -битовых) ячеек регистров сдвига,
генерирует решётку, которая имеет
-битовых) ячеек регистров сдвига,
генерирует решётку, которая имеет ![]() состояний. Следовательно,
декодирование такого кода посредством алгоритма Витерби требует сохранить следы
состояний. Следовательно,
декодирование такого кода посредством алгоритма Витерби требует сохранить следы
![]() выживших
путей и
выживших
путей и ![]() метрик.
На каждом шаге решётки имеются
метрик.
На каждом шаге решётки имеются ![]() путей, которые сливаются в каждый
узел. Поскольку каждый путь, который сходится в общей узел, требует вычисления
метрик, имеются
путей, которые сливаются в каждый
узел. Поскольку каждый путь, который сходится в общей узел, требует вычисления
метрик, имеются ![]() метрик,
вычисленных на каждом узле. Из
метрик,
вычисленных на каждом узле. Из ![]() путей, которые сливаются в каждом
узле, только один выживет, и это наиболее вероятный (с минимальным расстоянием)
путь. Таким образом, число вычислений при декодировании, выполняемых на каждом
шаге, возрастает экспоненциально с
путей, которые сливаются в каждом
узле, только один выживет, и это наиболее вероятный (с минимальным расстоянием)
путь. Таким образом, число вычислений при декодировании, выполняемых на каждом
шаге, возрастает экспоненциально с ![]() и
и ![]() . Экспоненциальный рост вычислительных
затрат ограничивает использование алгоритма Витерби только для относительно
малых значений
. Экспоненциальный рост вычислительных
затрат ограничивает использование алгоритма Витерби только для относительно
малых значений ![]() и
и
![]() .
.
Задержка при
декодировании при декодировании длинных информационных последовательностей,
которые были кодированы свёрточным кодом, обычно слишком велика для большинства
практических применений. Более того, память, требуемая для хранения всей длины
выживших последовательностей, велика и дорогая. Как указано в разделе 5.1.4,
решение этой проблемы заключается в модификации алгоритма Витерби таким
образом, чтобы установить фиксированную задержку декодирования без существенной
потери качества оптимальности алгоритма. Напомним, что модификация сводится к
тому, чтобы удержать в заданное время ![]() только самые последние
только самые последние ![]() декодированных
информационных бит (символов) в каждой выжившей последовательности. По мере
приёма новых информационных битов (символов) оптимальное решение принимается
относительно бита (символа), принятого на
декодированных
информационных бит (символов) в каждой выжившей последовательности. По мере
приёма новых информационных битов (символов) оптимальное решение принимается
относительно бита (символа), принятого на ![]() ветвей раньше по решётке, путём
сравнения метрик выживших последовательностей и принятия решение о бите в
последовательности, имеющей наибольшую метрику. Если
ветвей раньше по решётке, путём
сравнения метрик выживших последовательностей и принятия решение о бите в
последовательности, имеющей наибольшую метрику. Если ![]() выбран достаточно большим,
все выжившие пути будут содержать одинаковый декодируемый бит (символ),
принятый на
выбран достаточно большим,
все выжившие пути будут содержать одинаковый декодируемый бит (символ),
принятый на ![]() ветвей
раньше. Это значит, что с большой вероятностью, все выжившие последовательности
к моменту
ветвей
раньше. Это значит, что с большой вероятностью, все выжившие последовательности
к моменту ![]() выходят
из одного и того же узла в момент времени
выходят
из одного и того же узла в момент времени ![]() . Экспериментально показано
(компьютерное моделирование), что задержка
. Экспериментально показано
(компьютерное моделирование), что задержка ![]() обеспечивает пренебрежимо малое
ухудшение качества относительно оптимального алгоритма Витерби.
обеспечивает пренебрежимо малое
ухудшение качества относительно оптимального алгоритма Витерби.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- СПИСОК СОКРАЩЕНИЙ
- 1. ВВЕДЕНИЕ
- 1.1. ЭЛЕМЕНТЫ СИСТЕМ ЦИФРОВОЙ СВЯЗИ
- 1.2. КАНАЛЫ СВЯЗИ И ИХ ХАРАКТЕРИСТИКИ
- 1.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 1.4. ИСТОРИЧЕСКИЙ ОБЗОР РАЗВИТИЯ ЦИФРОВОЙ СВЯЗИ
- 1.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- 2. ВЕРОЯТНОСТЬ И СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. ВЕРОЯТНОСТЬ
- 2.1.1. Случайные величины, распределение вероятностей и плотности вероятностей
- 2.1.2. Функции от случайных величин
- 2.1.3. Статистическое усреднение случайных величин
- 2.1.4. Некоторые часто используемые распределения
- 2.1.5. Верхняя граница для вероятностей «хвостов»
- 2.1.6. Суммы случайных величин и центральная предельная теорема
- 2.2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.2.1. Статистические средние
- 2.2.2. Спектральная плотность мощности
- 2.2.3. Отклик линейной стационарной системы на случайный входной сигнал
- 2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов
- 2.2.5. Случайные сигналы и системы с дискретным временем
- 2.2.6. Процессы с циклической стационарностью
- 2.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 3. КОДИРОВАНИЕ ИСТОЧНИКА
- 3.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ИСТОЧНИКОВ ИНФОРМАЦИИ
- 3.2. ЛОГАРИФМИЧЕСКАЯ МЕРА ИНФОРМАЦИИ
- 3.2.1. Средняя взаимная информация и энтропия
- 3.2.2. Измерение информации для непрерывных случайных величин
- 3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ
- 3.3.1. Кодирование для дискретных источников без памяти
- 3.3.2. Дискретные стационарные источники
- 3.3.3. Алгоритм Лемпела-Зива
- 3.4. КОДИРОВАНИЕ ДЛЯ АНАЛОГОВЫХ ИСТОЧНИКОВ — ОПТИМАЛЬНОЕ КВАНТОВАНИЕ
- 3.4.1. Функция скорость-искажение R(D)
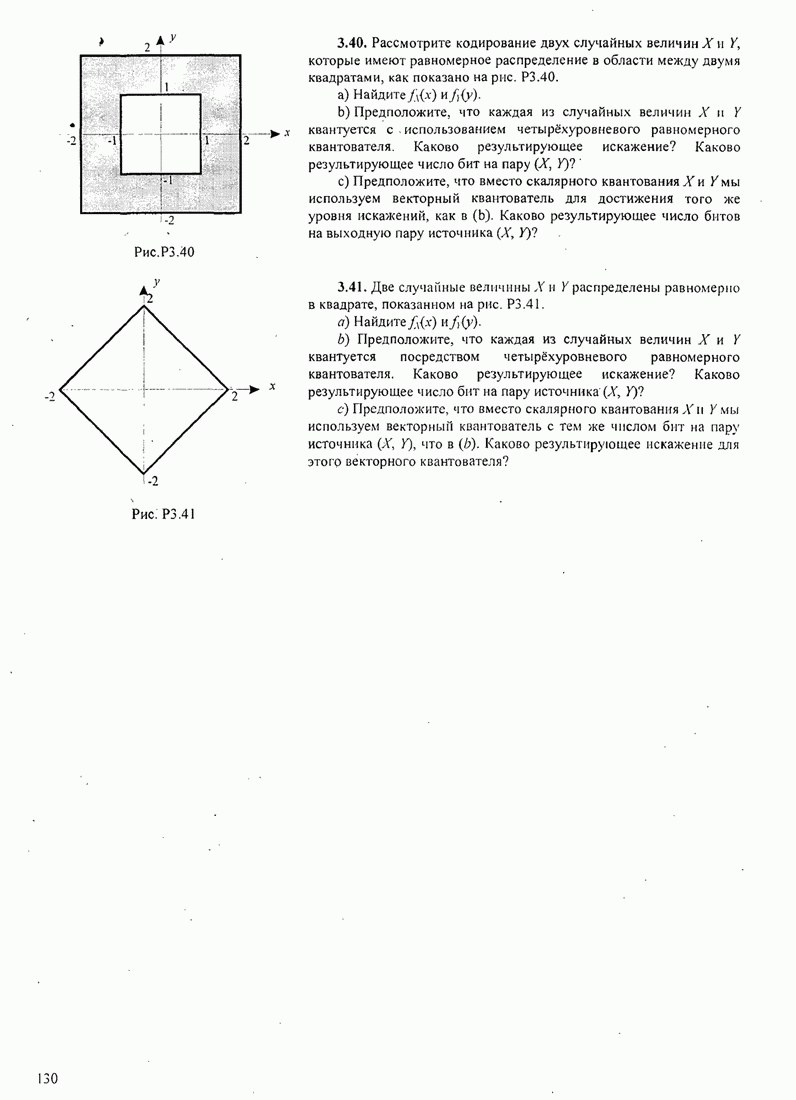
- 3.4.2. Скалярное квантование
- 3.4.3. Векторное квантование
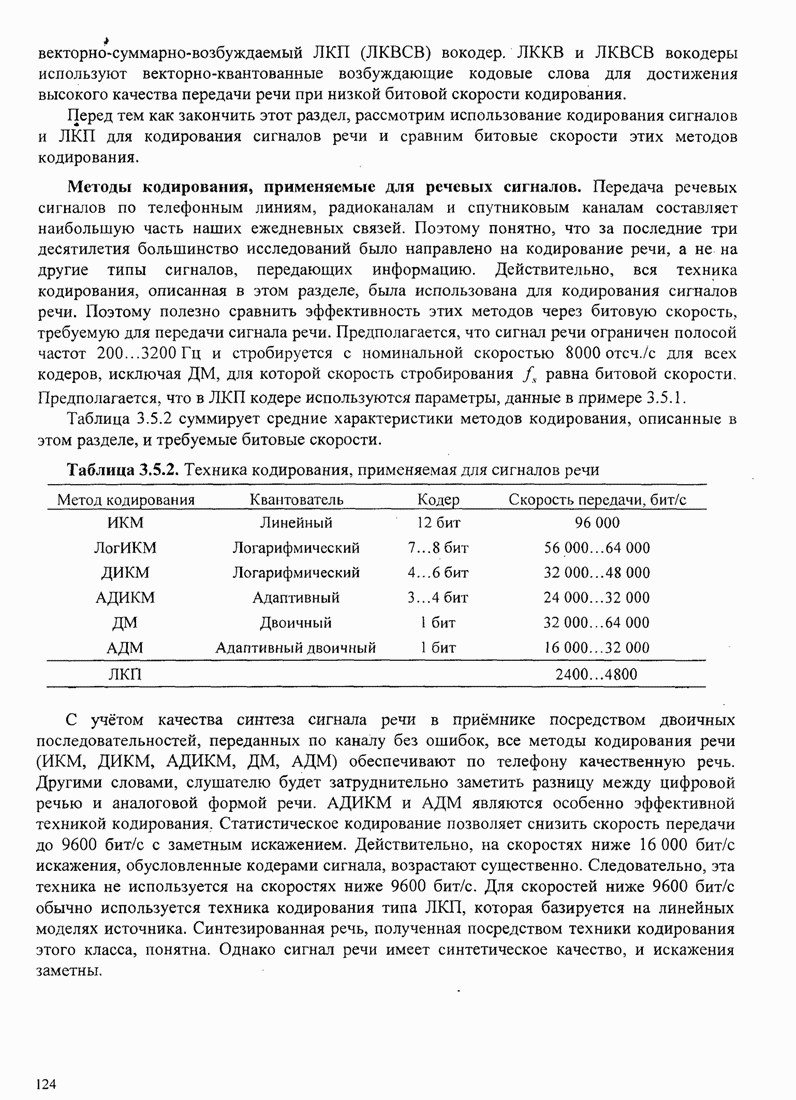
- 3.5. ТЕХНИКА КОДИРОВАНИЯ АНАЛОГОВЫХ ИСТОЧНИКОВ
- 3.5.1. Временное сигнальное кодирование
- 3.5.2. Спектральное кодирование сигнала
- 3.5.3. Модельное кодирование источника
- 3.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 4. ХАРАКТЕРИСТИКИ СИГНАЛОВ И СИСТЕМ СВЯЗИ
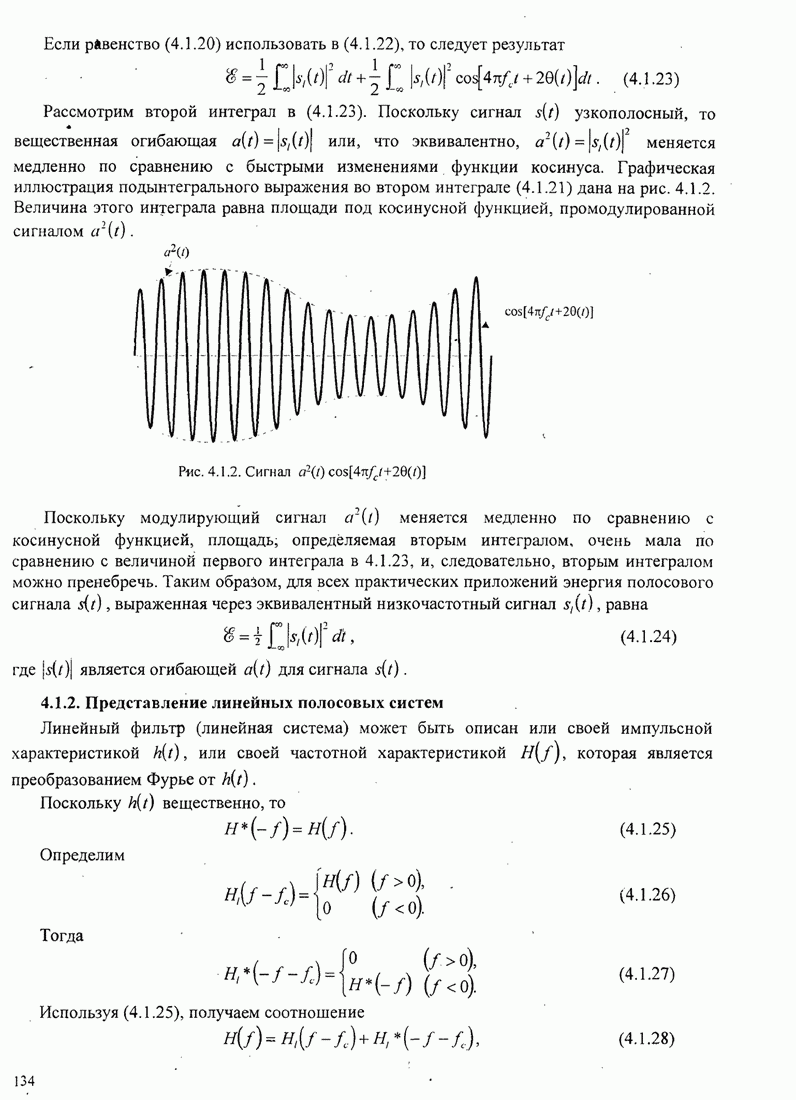
- 4.1. ПРЕДСТАВЛЕНИЕ ПОЛОСОВЫХ СИГНАЛОВ И СИСТЕМ
- 4.1.1. Представление полосовых сигналов
- 4.1.2. Представление линейных полосовых систем
- 4.1.3. Отклик полосовой системы на полосовой сигнал
- 4.1.4. Представление полосовых случайных процессов
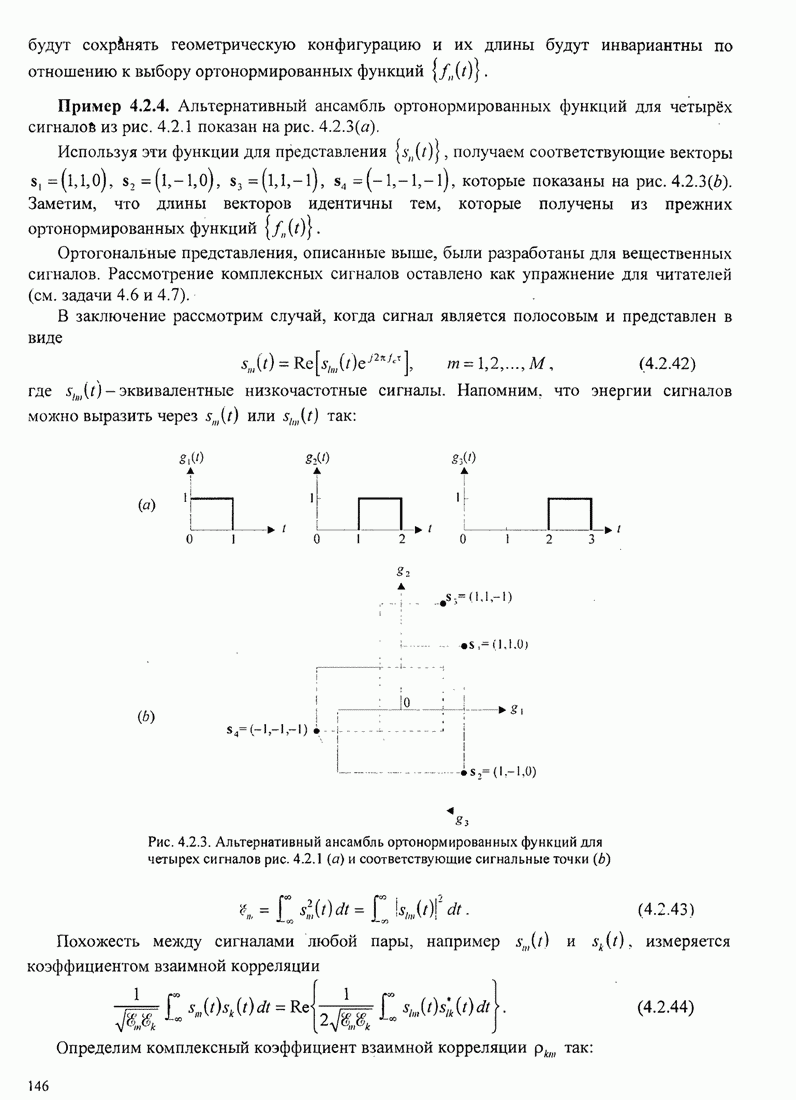
- 4.2. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
- 4.2.1. Концепция векторного пространства
- 4.2.2. Концепции пространства сигналов
- 4.2.3. Ортогональное разложение сигналов
- 4.3. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.3.1. Методы модуляции без памяти
- 4.3.2. Линейная модуляция с памятью
- 4.3.3. Нелинейные методы модуляции с памятью
- 4.4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СИГНАЛОВ ЦИФРОВОЙ МОДУЛЯЦИИ
- 4.4.1. Спектр мощности сигналов линейной модуляции
- 4.4.2. Спектр мощности для сигналов ЧМНФ и МНФ
- 4.4.3. Спектр мощности для модулированных сигналов с памятью
- 4.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 5. ОПТИМАЛЬНЫЕ ПРИЁМНИКИ ДЛЯ КАНАЛА С АДДИТИВНЫМ БЕЛЫМ ГАУССОВСКИМ ШУМОМ
- 5.1. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ, ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ АДДИТИВНОГО БЕЛОГО ГАУССОВСКОГО ШУМА
- 5.1.1. Корреляционный демодулятор
- 5.1.2. Согласованный фильтр как демодулятор
- 5.1.3. Оптимальный детектор
- 5.1.4. Последовательный детектор максимального правдоподобия. Алгоритм Витерби
- 5.1.5. Посимвольное детектирование для сигналов с памятью
- 5.2. ХАРАКТЕРИСТИКИ КАЧЕСТВА ОПТИМАЛЬНОГО ПРИЁМНИКА ДЛЯ МОДУЛЯЦИИ БЕЗ ПАМЯТИ
- 5.2.1. Вероятность ошибки при двоичной модуляции
- 5.2.2. Вероятность ошибки для M-позиционных ортогональных сигналов
- 5.2.3. Вероятность ошибки для М-позиционной биортогональной системы сигналов
- 5.2.4. Вероятность ошибки для симплексных сигналов
- 5.2.5. Вероятность ошибки для M-позиционной системы с двоичными кодовыми сигналами
- 5.2.6. Вероятность ошибки для М-позиционной AM
- 5.2.7. Вероятность ошибки для М-позиционной ФМ
- 5.2.8. Дифференциальная ФМ (ДФМ) и её характеристики качества
- 5.2.9. Вероятность ошибки для КАМ
- 5.2.10. Сравнение цифровых методов модуляции
- 5.3. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ МНФ
- 5.3.1 Оптимальные демодуляция и детектирование для МНФ
- 5.3.2. Характеристики качества сигналов МНФ
- 5.3.3. Посимвольные детектирование сигналов МНФ
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК ДЛЯ СИГНАЛОВ СО СЛУЧАЙНОЙ ФАЗОЙ В КАНАЛЕ С АБГШ
- 5.4.1. Оптимальный приёмник двоичных сигналов
- 5.4.2. Оптимальный приёмник для М-позиционных ортогональных сигналов
- 5.4.3. Вероятность ошибки при детектировании огибающей для М-позиционных ортогональных сигналов
- 5.4.4. Вероятность ошибки для коррелированных двоичных сигналов при детектировании огибающей
- 5.5. РЕГЕНЕРАТИВНЫЕ ПОВТОРИТЕЛИ И АНАЛИЗ РЕСУРСОВ ЛИНИЙ СВЯЗИ
- 5.5.1. Регенеративные повторители
- 5.5.2. Анализ ресурсов линий связи
- 5.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 6. СИНХРОНИЗАЦИЯ НЕСУЩЕЙ И ТАКТОВАЯ СИНХРОНИЗАЦИЯ
- 6.1. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СИГНАЛА
- 6.1.1. Функция правдоподобия
- 6.1.2. Восстановление несущей и тактовая синхронизация при демодуляции сигнала
- 6.2. ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ
- 6.2.1. МП оценка фазы несущей
- 6.2.2. Модели замкнутой ФАП
- 6.2.3. Влияние аддитивного шума на оценку фазы
- 6.2.4. Петли, управляемые решениями
- 6.2.5. Петли, не управляемые решениями
- 6.3. ОЦЕНИВАНИЕ ПРИ СИНХРОНИЗАЦИИ СИМВОЛОВ
- 6.3.1. Максимально правдоподобная оценка параметра задержки
- 6.3.2 Оценивание параметра задержки, не управляемое решениями
- 6.4. СОВМЕСТНОЕ ОЦЕНИВАНИЕ ФАЗЫ НЕСУЩЕЙ И ФАЗЫ СИНХРОНИЗАЦИИ
- 6.5. ХАРАКТЕРИСТИКИ КАЧЕСТВА МП ОЦЕНИВАТЕЛЕЙ
- 6.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 7. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА И КОДИРОВАНИЕ
- 7.1. МОДЕЛИ КАНАЛОВ И ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ
- 7.1.1. Модели канала
- 7.1.2. Пропускная способность канала
- 7.1.3. Пропускная способность канала, достигаемая при помощи ортогональных сигналов
- 7.1.4. Функции надёжности канала
- 7.2. СЛУЧАЙНЫЙ ВЫБОР КОДОВ
- 7.2.1. Случайное кодирование, основанное на использовании ансамбля из М двоичных кодовых слов
- 7.2.2. Случайное кодирование, основанное на использовании М кодовых слов с многоуровневыми сигналами
- 7.2.3. Сравнение предельной скорости с пропускной способностью канала с АБГШ
- 7.3. СИНТЕЗ СИСТЕМЫ СВЯЗИ, ОСНОВАННЫЙ НА ПРЕДЕЛЬНОЙ СКОРОСТИ
- 7.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 8. БЛОКОВЫЕ И СВЁРТОЧНЫЕ КОДЫ
- 8.1. ЛИНЕЙНЫЕ БЛОКОВЫЕ КОДЫ
- 8.1.1. Порождающая и проверочная матрицы
- 8.1.2. Некоторые известные линейные блоковые коды
- 8.1.3. Циклические коды
- 8.1.4. Оптимальное декодирование мягких решений для линейных блоковых кодов
- 8.1.5. Декодирование жёстких решений
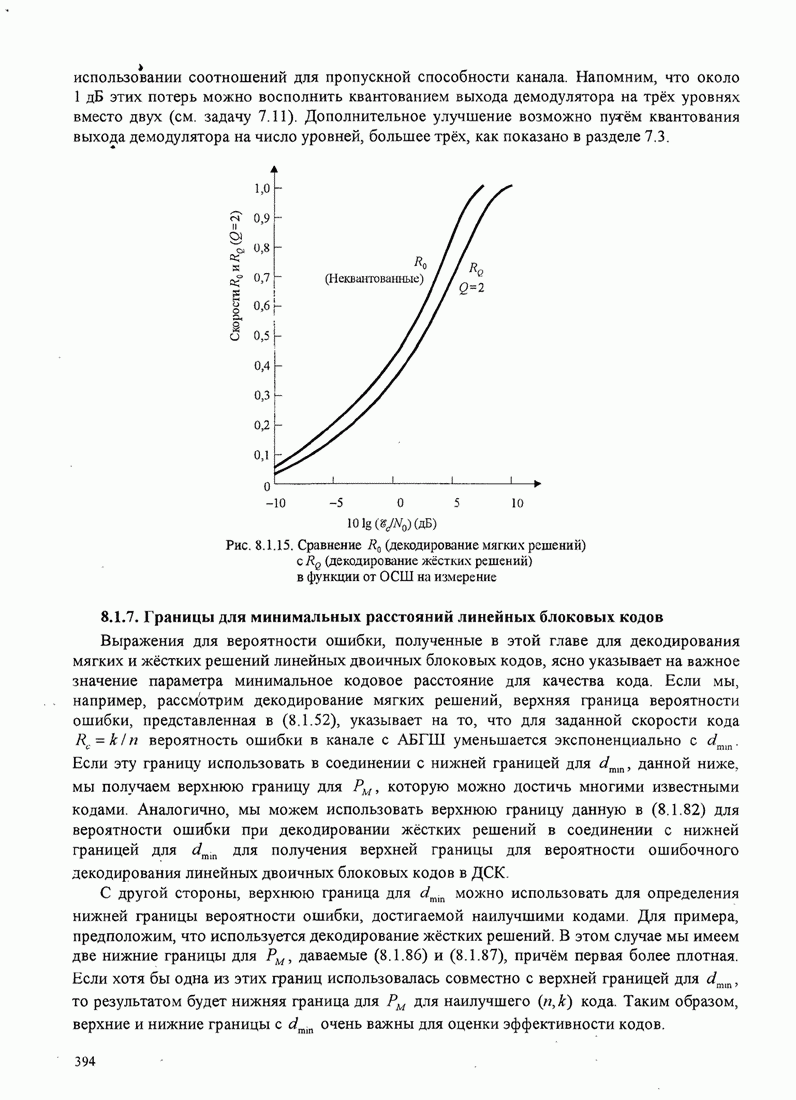
- 8.1.6. Сравнение качества декодирования жёстких и мягких решений
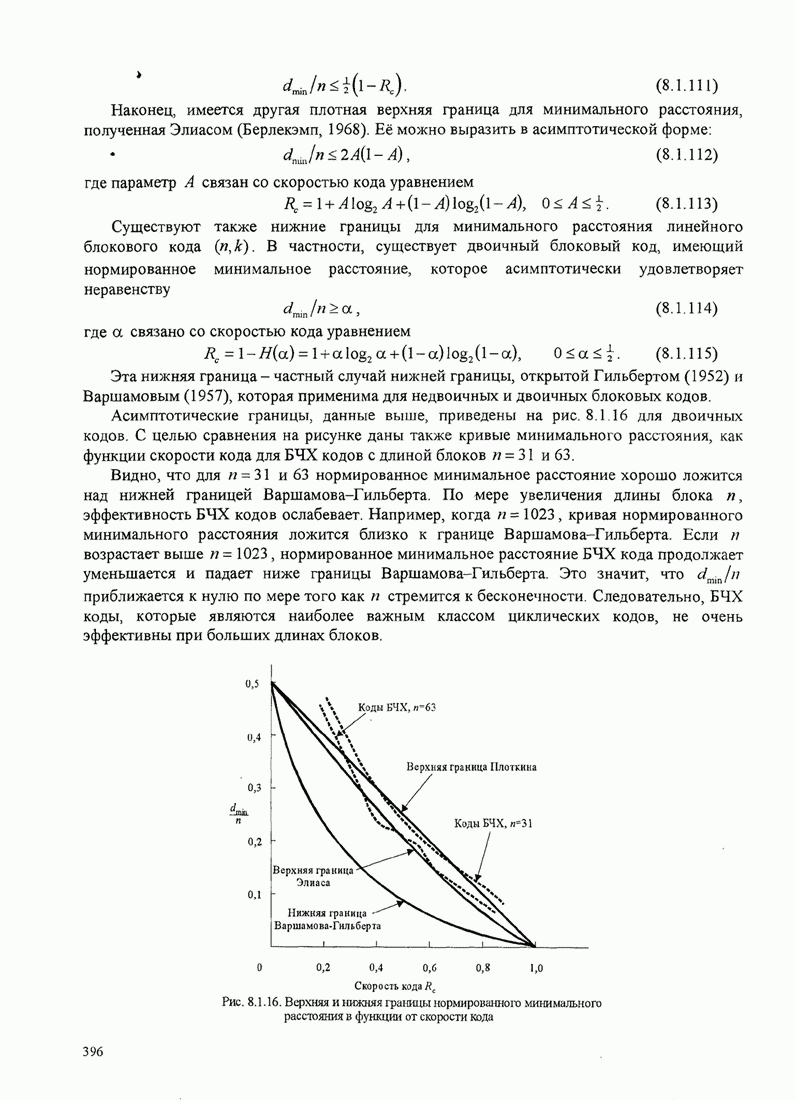
- 8.1.7. Границы для минимальных расстояний линейных блоковых кодов
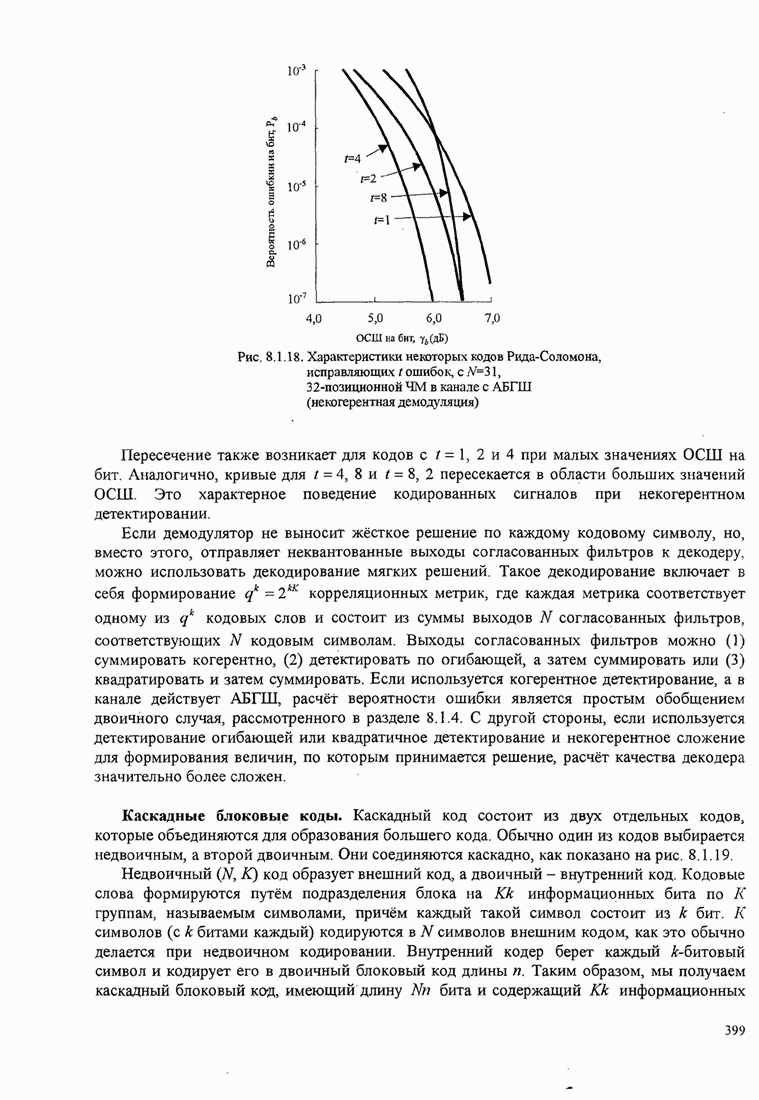
- 8.1.8. Недвоичные блоковые коды и каскадные блоковые коды
- 8.1.9. Перемежение кодовых символов в каналах с пакетами ошибок
- 8.2. СВЁРТОЧНЫЕ КОДЫ
- 8.2.1. Передаточная функция свёрточного кода
- 8.2.2. Оптимальное декодирование для свёрточных кодов — алгоритм Витерби
- 8.2.3. Вероятность ошибки при декодирования мягких решений
- 8.2.4. Вероятность ошибки при декодировании жёстких решений
- 8.2.5. Дистанционные характеристики двоичных свёрточных кодов
- 8.2.6. Недвоичные k-дуальные коды и каскадные коды
- 8.2.7. Другие алгоритмы декодирования свёрточных кодов
- 8.2.8. Практические соображения по применению свёрточных кодов
- 8.3. КОДИРОВАННАЯ МОДУЛЯЦИЯ ДЛЯ ЧАСТОТНО-ОГРАНИЧЕННЫХ КАНАЛОВ
- 8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 9. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.1. ХАРАКТЕРИСТИКА ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2. СИНТЕЗ СИГНАЛОВ ДЛЯ ОГРАНИЧЕННЫХ ПО ПОЛОСЕ КАНАЛОВ
- 9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции — критерий Найквиста
- 9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ — сигналы с парциальным откликом
- 9.2.3. Детектирование данных при контролируемой МСИ
- 9.2.4. Синтез сигналов для каналов с искажениями
- 9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM
- 9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ
- 9.3.2. Вероятность ошибки при детектировании сигналов с парциальным откликом
- 9.3.3. Вероятность ошибки для оптимальных сигналов в канале с искажением
- 9.4. МОДУЛЯЦИОННЫЕ КОДЫ ДЛЯ ФОРМИРОВАНИЯ СПЕКТРА
- 9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 10. СВЯЗЬ В ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ
- 10.1. ОПТИМАЛЬНЫЙ ПРИЕМНИК ДЛЯ КАНАЛА С МСИ И АБГШ
- 10.1.1. Оптимальный приёмник максимального правдоподобия
- 10.1.2. Модель канала с МСИ с дискретным временем
- 10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом
- 10.1.4. Качество алгоритма МППО для каналов с МСИ
- 10.2. ЛИНЕЙНОЕ ВЫРАВНИВАНИЕ
- 10.2.1. Критерий пикового скажения
- 10.2.2. Критерий минимума среднеквадратичной ошибки (СКО)
- 10.2.3. Характеристики качества эквалайзера по минимуму СКО
- 10.2.4. Дробные эквалайзеры
- 10.3. ВЫРАВНИВАНИЕ С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 10.3.1. Оптимизация коэффициентов
- 10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР
- 10.3.3. Эквалайзер с обратной связью по решению и предсказаниям
- 10.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 11. АДАПТИВНЫЕ ЭКВАЛАЙЗЕРЫ
- 11.1. АДАПТИВНЫЙ ЛИНЕЙНЫЙ ЭКВАЛАЙЗЕР
- 11.1.1. Алгоритм сведения к нулю
- 11.1.2. Алгоритм наименьших квадратов (НК)
- 11.1.3. Свойство сходимости алгоритма НК
- 11.1.4. Излишек СКО, обусловленный зашумлёнными оценками градиентов
- 11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов
- 11.2. АДАПТИВНЫЙ ЭКВАЛАЙЗЕР С ОБРАТНОЙ СВЯЗЬЮ ПО РЕШЕНИЮ
- 11.2.1. Адаптивное выравнивание для решётчато-кодированных сигналов
- 11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ
- 11.4. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ МИНИМАЛЬНЫХ КВАДРАТОВ ДЛЯ АДАПТИВНОГО ВЫРАВНИВАНИЯ
- 11.4.1. Рекуррентный алгоритм (Калмана) наименьших квадратов
- 11.4.2. Линейное предсказание и лестничные фильтры
- 11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ
- 11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия
- 11.5.2. Стохастический градиентный алгоритм
- 11.5.3. Алгоритмы слепого выравнивания, основанные на статистике сигнала второго и более высокого порядка
- 11.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 12. МНОГОКАНАЛЬНЫЕ СИСТЕМЫ И СИСТЕМЫ С МНОГИМИ НЕСУЩИМИ
- 12.1. МНОГОКАНАЛЬНАЯ ЦИФРОВАЯ СВЯЗЬ В КАНАЛАХ С АБГШ
- 12.1.1. Двоичные сигналы
- 12.1.2. M-ичные ортогональные сигналы
- 12.2. СВЯЗЬ СО МНОГИМИ НЕСУЩИМИ
- 12.2.1. Пропускная способность неидеального линейного фиксированного канала
- 12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье
- 12.3. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 13. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ ДЛЯ ЦИФРОВОЙ СВЯЗИ (СИГНАЛЫ С РАССЕЯННЫМ СПЕКТРОМ)
- 13.1. МОДЕЛЬ ЦИФРОВЫХ СИСТЕМ СВЯЗИ С ШИРОКОПОЛОСНЫМИ СИГНАЛАМИ
- 13.2. ШИРОКОПОЛОСНЫЕ СИГНАЛЫ С ПРЯМЫМИ ПСЕВДОШУМОВЫМИ (ПШ) ПОСЛЕДОВАТЕЛЬНОСТЯМИ
- 13.2.1. Качество декодера
- 13.2.2.Некоторые приложения широкополосных сигналов с ПП
- 13.2.3. Влияние импульсной интерференции на широкополосные ПП системы
- 13.2.4. Генерирование ПШ последовательностей
- 13.3. ШИРОКОПЛОСНЫЕ СИГНАЛЫ СО СКАЧКАМИ ЧАСТОТЫ
- 13.3.1. Качество широкополосных сигналов со скачками частоты (СЧ) в канале с АБГШ
- 13.3.2. Качество широкополосных сигналов с СЧ при парционально-полосовой интерференции
- 13.3.3. CDMA система, основанная на широкополосных сигналах с СЧ
- 13.4. ДРУГИЕ ТИПЫ ШИРОКОПОЛОСНЫХ СИГНАЛОВ
- 13.5. СИНХРОНИЗАЦИЯ ШИРОКОПОЛОСНЫХ СИСТЕМ
- 13.6. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 14. ЦИФРОВАЯ СВЯЗЬ ЧЕРЕЗ МНОГОПУТЕВЫЕ КАНАЛЫ С ЗАМИРАНИЯМИ
- 14.1. ХАРАКТЕРИСТИКИ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.1.1. Корреляционная функция канала и спектр мощности
- 14.1.2. Статистические модели для каналов с замираниями
- 14.2. ВЛИЯНИЕ ХАРАКТЕРИСТИК СИГНАЛА НА ВЫБОР МОДЕЛИ КАНАЛА
- 14.3. КАНАЛ, НЕСЕЛЕКТИВНЫЙ ПО ЧАСТОТЕ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.4. ТЕХНИКА РАЗНЕСЕНИЯ ДЛЯ МНОГОПУТЕВЫХ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.4.1. Двоичные сигналы
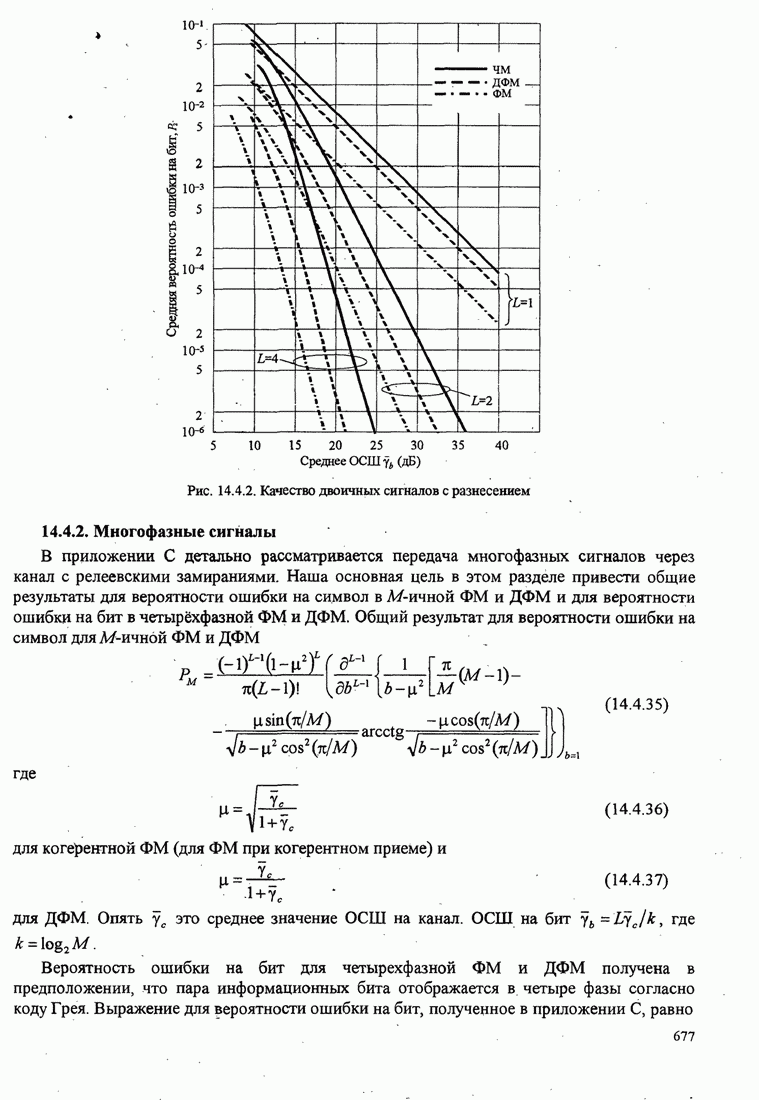
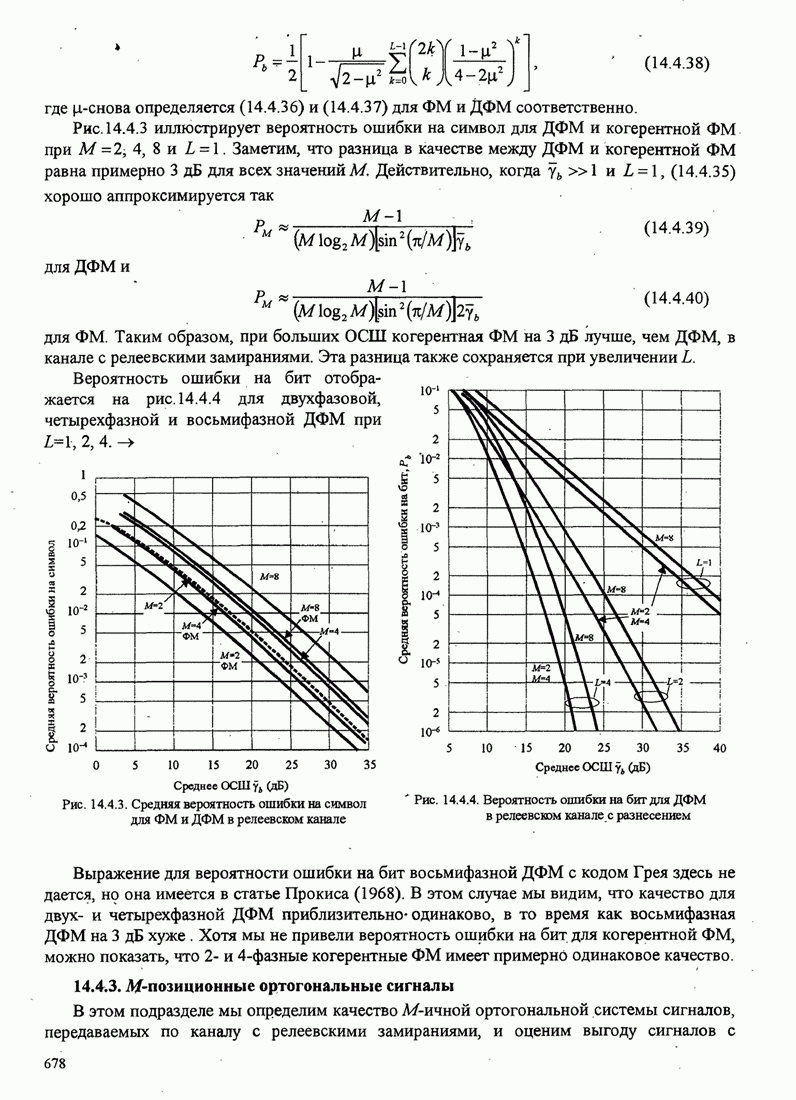
- 14.4.2. Многофазные сигналы
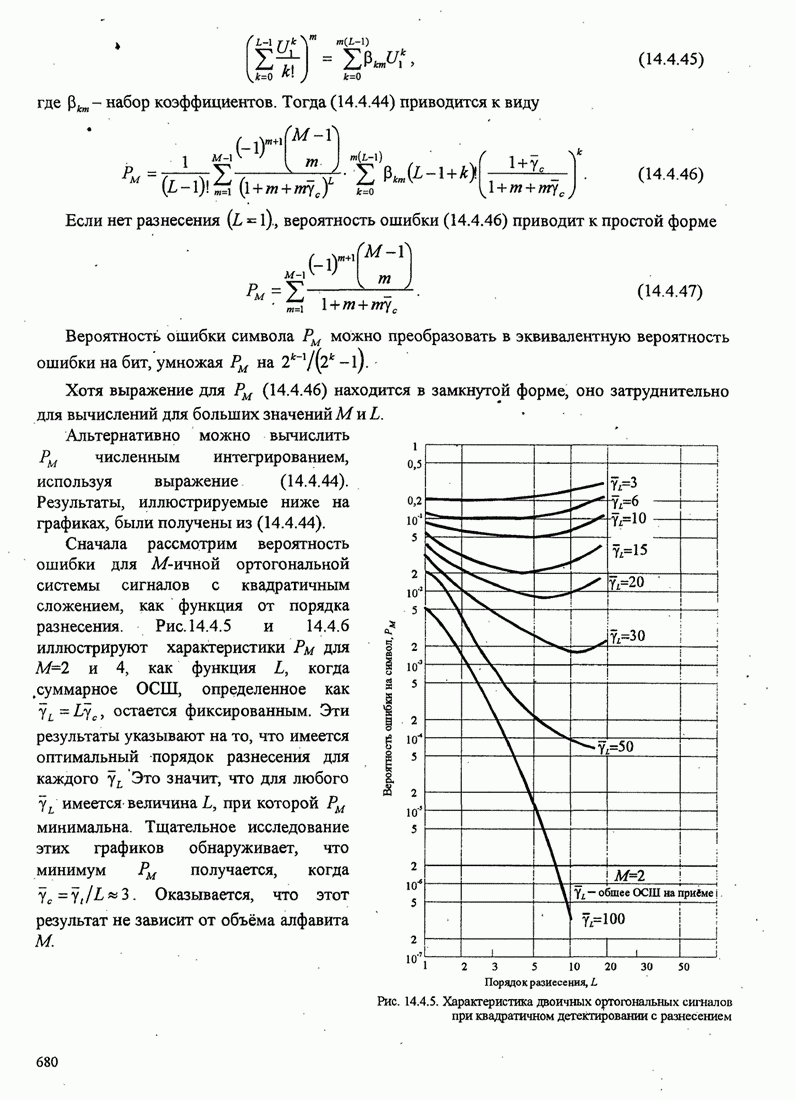
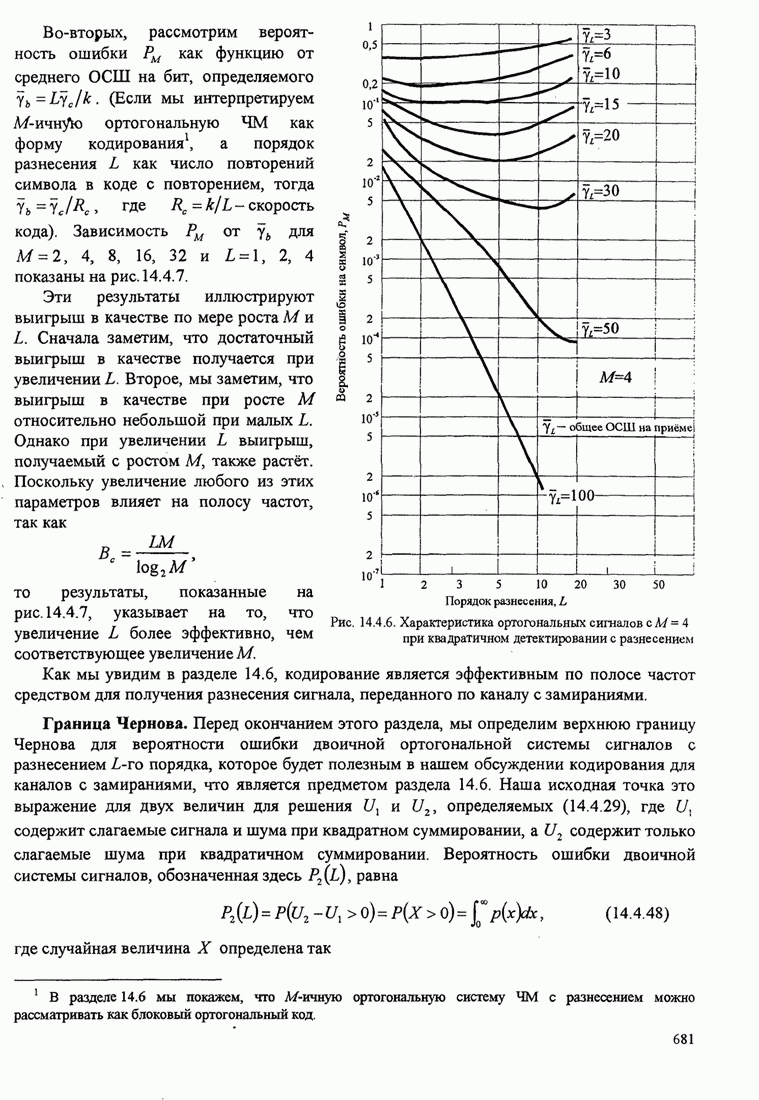
- 14.4.3. М-позиционные ортогональные сигналы
- 14.5. ЦИФРОВАЯ ПЕРЕДАЧА ПО ЧАСТОТНО-СЕЛЕКТИВНОМУ КАНАЛУ С МЕДЛЕННЫМИ ЗАМИРАНИЯМИ
- 14.5.1. Модель канала в виде линии задержки с отводами
- 14.5.2. RAKE демодулятор
- 14.5.3. Качество RAKE приемника
- 14.6. КОДИРОВАННЫЕ СИГНАЛЫ ДЛЯ КАНАЛОВ С ЗАМИРАНИЯМИ
- 14.6.1. Вероятность ошибки при декодировании мягких решений и использовании двоичного блокового кода
- 14.6.2. Вероятность ошибки при декодировании жёстких решений и использовании линейных двоичных блоковых кодов
- 14.6.3. Верхние границы качества свёрточных кодов в канале с релеевскими замираниями
- 14.6.4. Использование кодов с постоянным весом и каскадных кодов для канала с замираниями
- 14.6.5. Синтез систем, основанный на предельной скорости
- 14.6.6. Решётчато-кодовая модуляция
- 14.7. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- 15. СИСТЕМЫ СВЯЗИ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- 15.1. ВВЕДЕНИЕ В ТЕХНИКУ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.2. ПРОПУСКНАЯ СПОСОБНОСТЬ МЕТОДОВ МНОЖЕСТВЕННОГО ДОСТУПА
- 15.3. МНОЖЕСТВЕННЫЙ ДОСТУП С КОДОВЫМ РАЗДЕЛЕНИЕМ
- 15.3.1. Сигналы CDMA и модели канала
- 15.3.2. Оптимальный приёмник
- 15.3.3. Субоптимальные детекторы
- 15.3.4. Характеристики качества детекторов
- 15.4. Методы случайного доступа
- 15.4.1. АЛОХА. Системы и протоколы
- 15.4.2. Системы, которые обнаруживают несущую, и протоколы
- 15.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ
- ЗАДАЧИ
- ПРИЛОЖЕНИЕ А. АЛГОРИТМ ЛЕВИНСОНА-ДУРБИНА
- ПРИЛОЖЕНИЕ B. ВЕРОЯТНОСТЬ ОШИБКИ ДЛЯ МНОГОКАНАЛЬНЫХ ДВОИЧНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ C. ВЕРОЯТНОСТИ ОШИБКИ ДЛЯ АДАПТИВНОГО ПРИЁМА М-ФАЗНЫХ СИГНАЛОВ
- ПРИЛОЖЕНИЕ D. ФАКТОРИЗАЦИЯ МАТРИЦЫ (ПРИ РЕШЕНИИ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ)