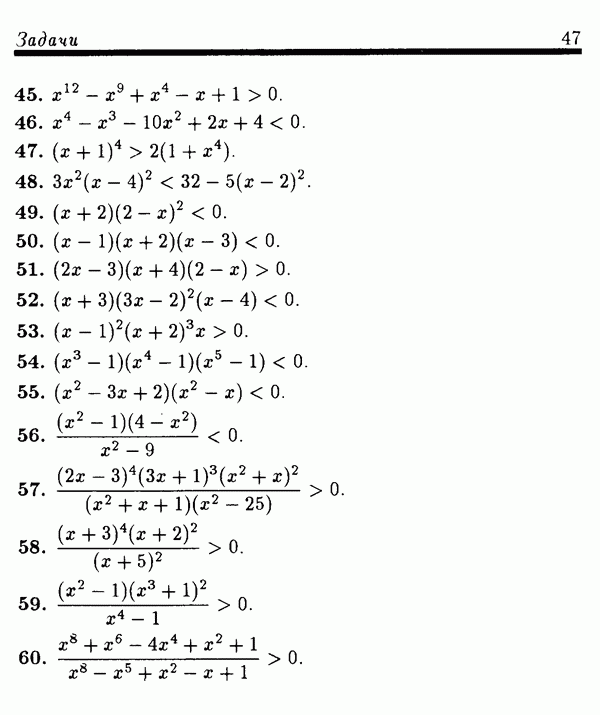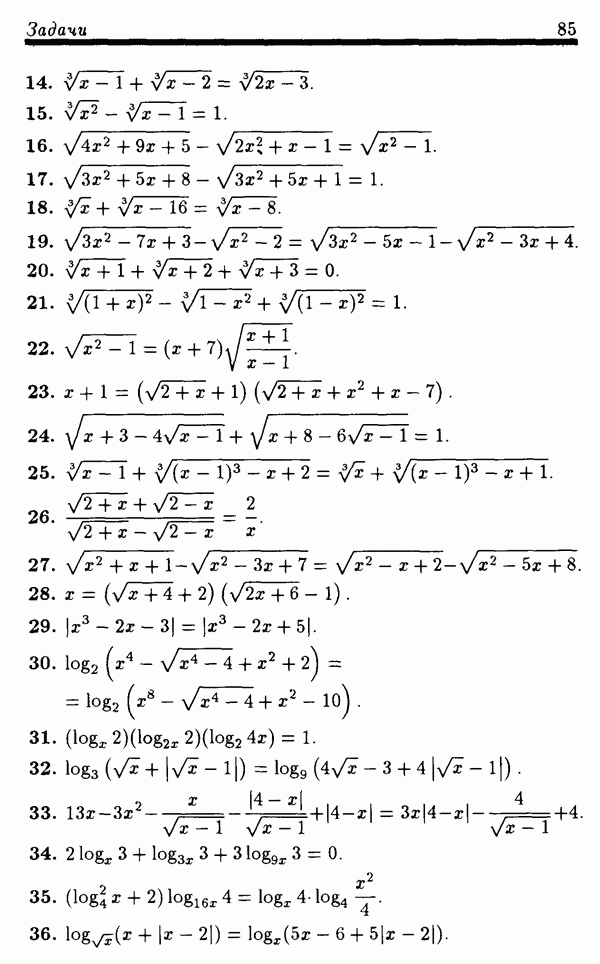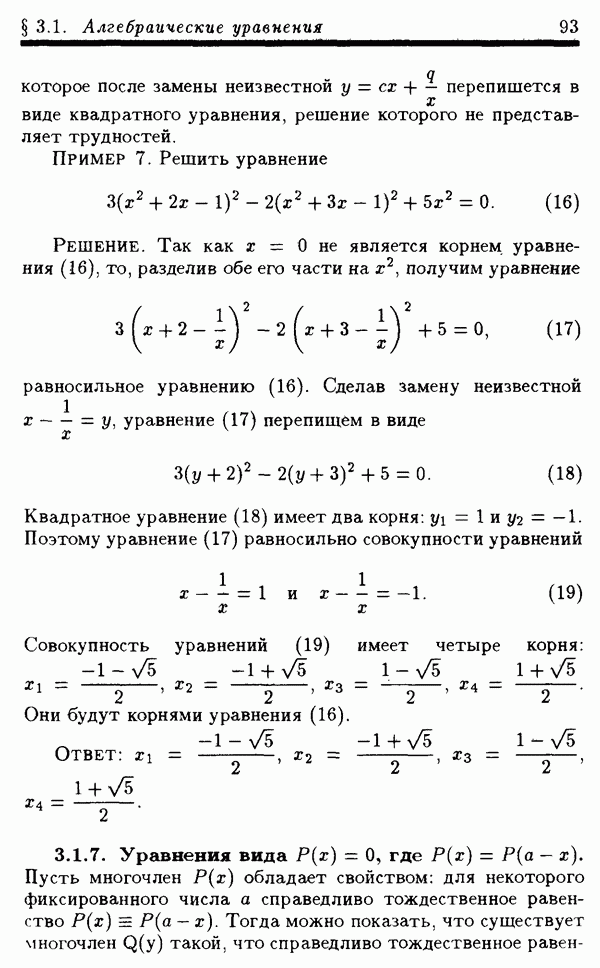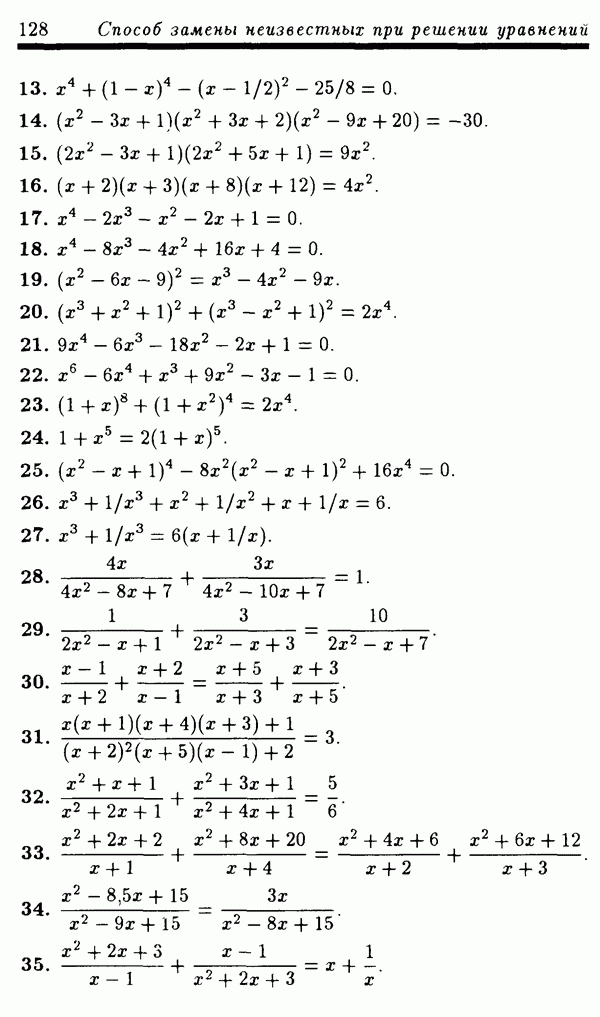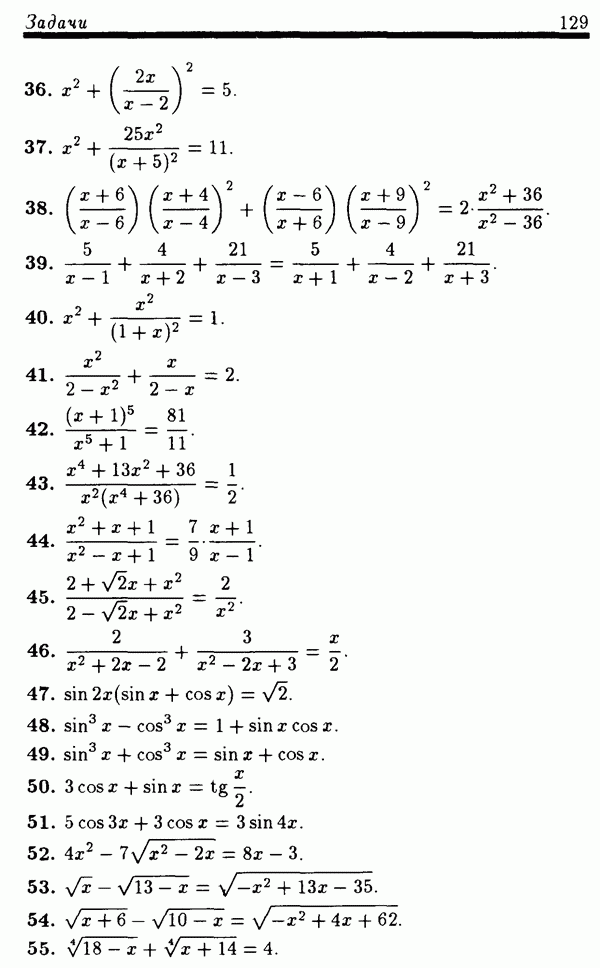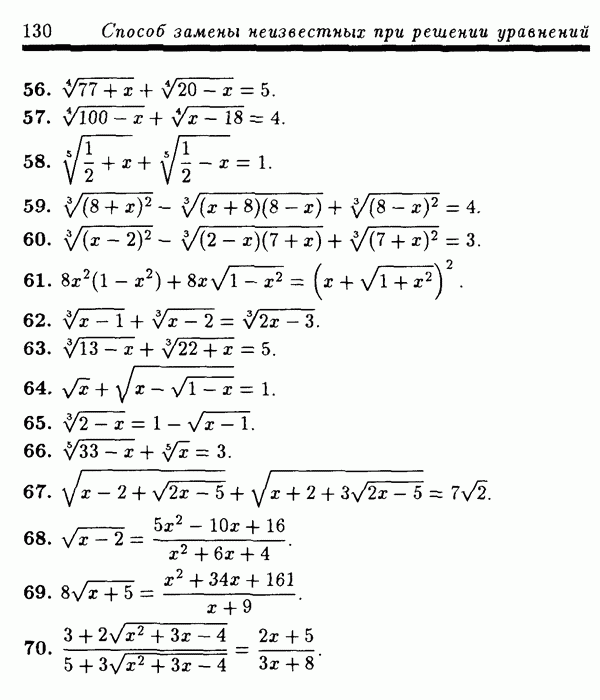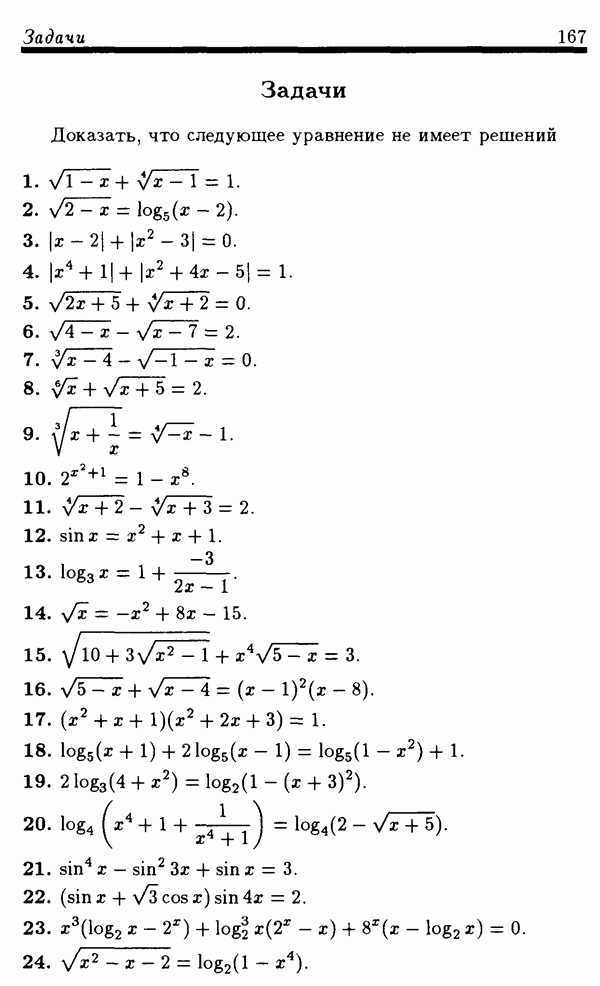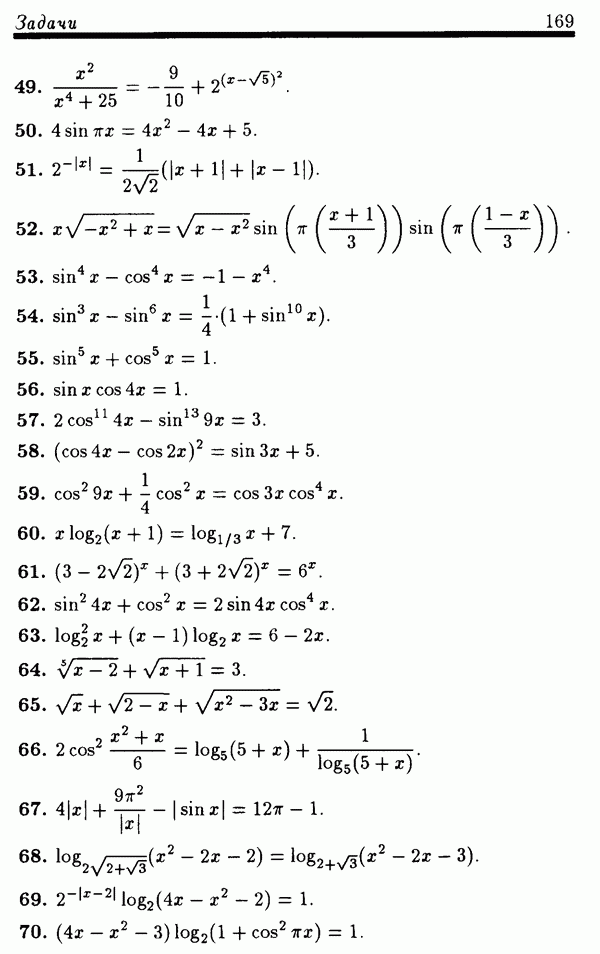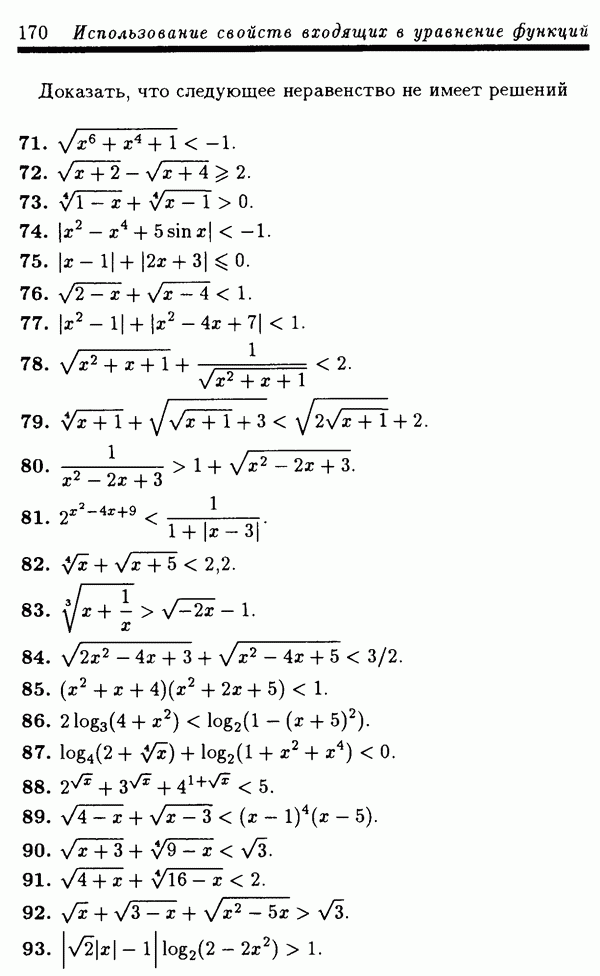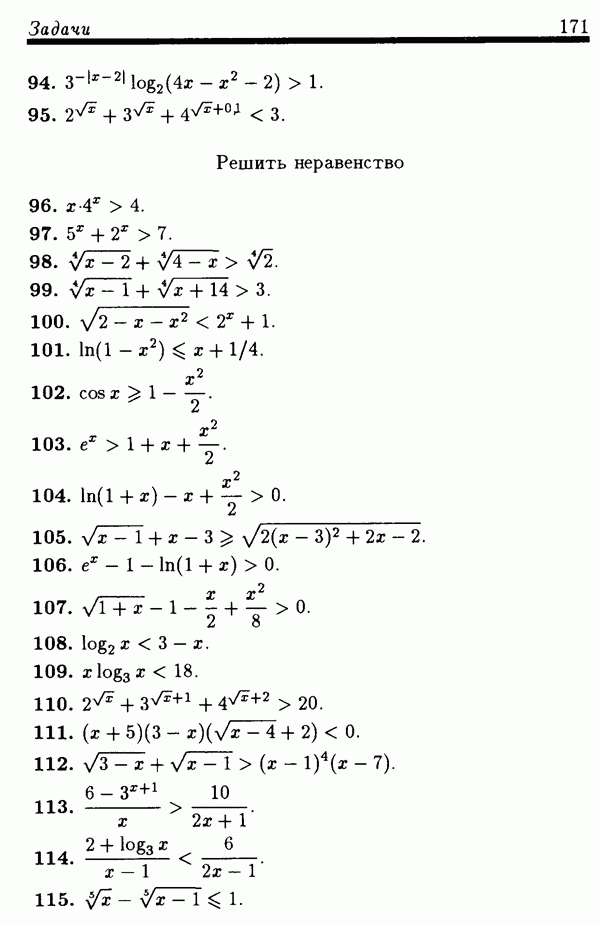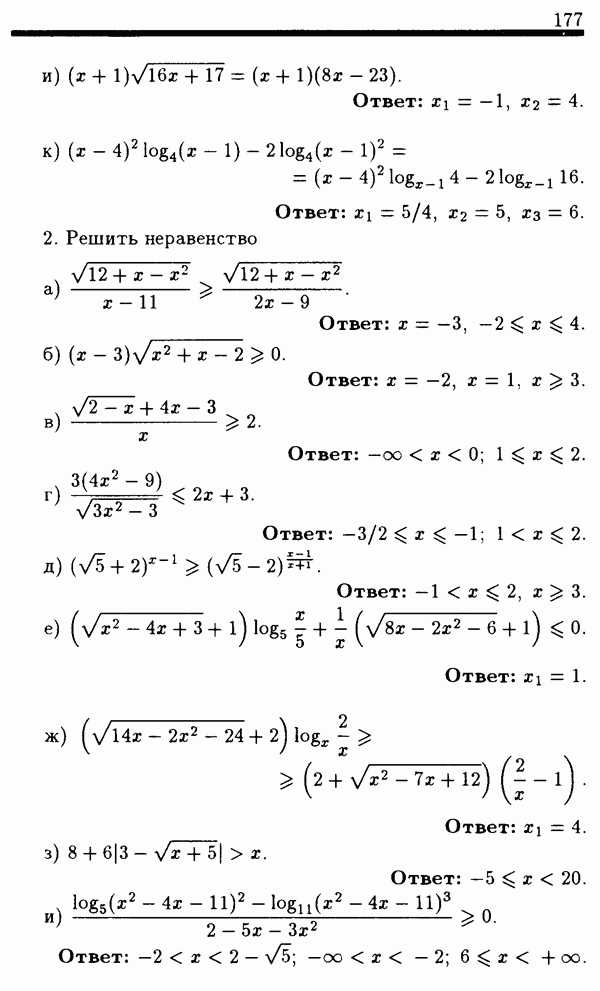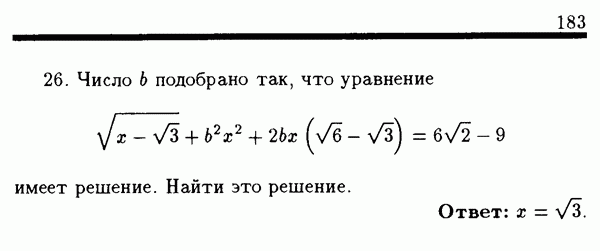| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5.3. Обобщенный метод интервалов.
Иногда алгебраические неравенства степеней более высоких, чем два, путем равносильных преобразований приводятся к виду

где  целые положительные числа;
целые положительные числа;  действительные числа, среди которых нет равных, такие, что
действительные числа, среди которых нет равных, такие, что 
Такие неравенства могут быть решены с помощью так называемого обобщенного метода интервалов.
В основе его лежит следующее свойство двучлена  точка а делит числовую ось на две части, причем:
точка а делит числовую ось на две части, причем:
а) если  четное, то выражение
четное, то выражение  справа и слева от точки
справа и слева от точки  сохраняет положительный знак,
сохраняет положительный знак,
б) если  нечетное, то выражение
нечетное, то выражение  справа от точки
справа от точки  положительно, а слева от точки
положительно, а слева от точки  отрицательно.
отрицательно.
Рассмотрим многочлен

где  .
.
Для любого числа  такого, что
такого, что  соответствующее значение любого сомножителя в (18) положительно, поэтому числовое значение
соответствующее значение любого сомножителя в (18) положительно, поэтому числовое значение  также положительно.
также положительно.
Для любого  взятого из интервала
взятого из интервала  соответствующее значение любого сомножителя в (18), кроме последнего, положительно, а соответствующее значение последнего сомножителя положительно, если
соответствующее значение любого сомножителя в (18), кроме последнего, положительно, а соответствующее значение последнего сомножителя положительно, если  четное число, и отрицательно, если
четное число, и отрицательно, если  нечетное число. Поэтому число
нечетное число. Поэтому число  положительно, если
положительно, если  четное число, и
четное число, и  отрицательно, если
отрицательно, если  нечетное число.
нечетное число.
Аналогично показывается, что если известен знак  на интервале
на интервале  то на промежутке
то на промежутке  знак
знак  определяется по следующему правилу. Многочлен
определяется по следующему правилу. Многочлен  при переходе через точку
при переходе через точку 
а) меняет знак на противоположный знаку  на
на  если
если  нечетное число;
нечетное число;
б) не меняет знака (тот же знак, что  на
на  если к, — четное число.
если к, — четное число.
На этом рассуждении и основан обобщенный метод интервалов: на числовую ось наносят числа  в промежутке справа от наибольшего из корней многочлена ставят знак плюс, а затем, двигаясь справа налево, при переходе через очередной корень а, меняют знак, если
в промежутке справа от наибольшего из корней многочлена ставят знак плюс, а затем, двигаясь справа налево, при переходе через очередной корень а, меняют знак, если  нечетное число, и сохраняют знак, если
нечетное число, и сохраняют знак, если  четное число.
четное число.
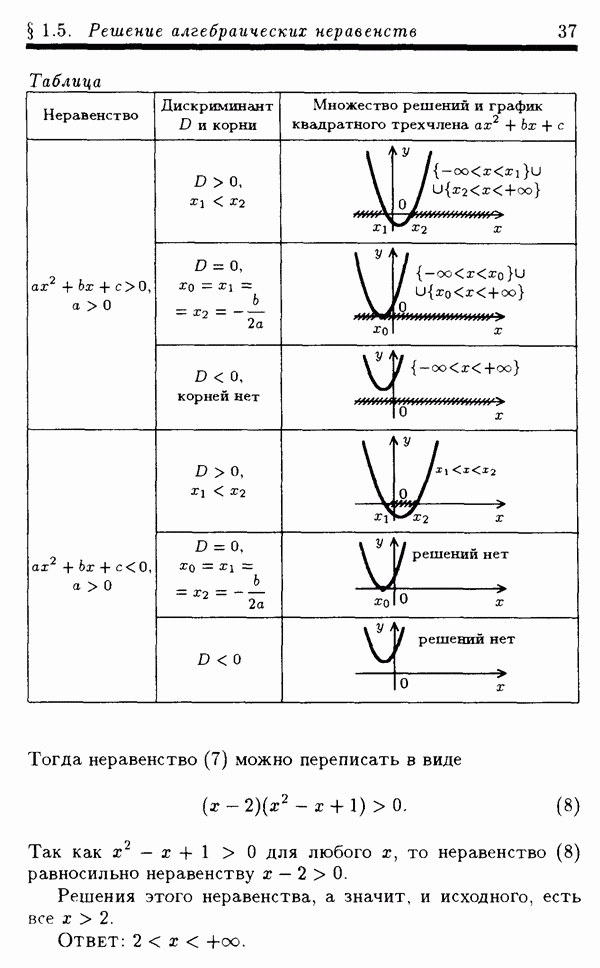
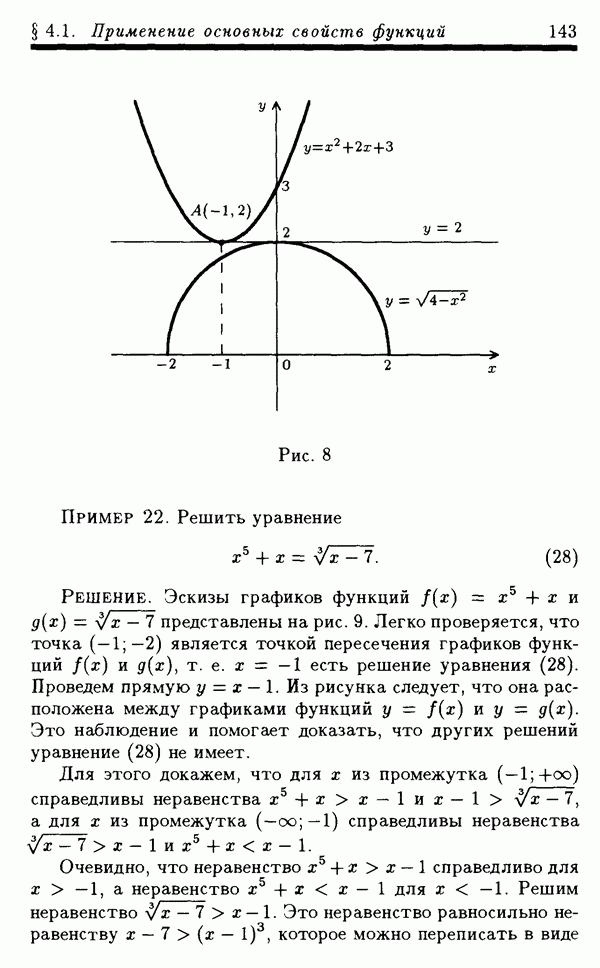
Пример 5. Решить неравенство

Решение. Перепишем неравенство в равносильном виде

Для решения этого неравенства применим обобщенный метод интервалов. На числовой оси отметим числа —7, —10/3, 5/2, 6 (рис. 4). Справа от наибольшего числа (числа 6) ставим знак плюс.

Рис. 4
При переходе через точку  многочлен
многочлен

меняет знак, так как двучлен  содержится в нечетной степени, поэтому в промежутке
содержится в нечетной степени, поэтому в промежутке  ставим знак минус. При переходе через точку
ставим знак минус. При переходе через точку  многочлен
многочлен  меняет знак, так как двучлен
меняет знак, так как двучлен  содержится в произведении (21) в нечетной степени, поэтому в промежутке
содержится в произведении (21) в нечетной степени, поэтому в промежутке  ставим знак плюс. При переходе через точку
ставим знак плюс. При переходе через точку  многочлен
многочлен  не меняет знака, так как двучлен
не меняет знака, так как двучлен  содержится в произведении (21) в четной степени, поэтому в
содержится в произведении (21) в четной степени, поэтому в
промежутке  ставим знак плюс. Наконец, при переходе через точку
ставим знак плюс. Наконец, при переходе через точку  многочлен
многочлен  меняет знак, так как двучлен
меняет знак, так как двучлен  содержится в произведении (21) в первой степени, поэтому в промежутке
содержится в произведении (21) в первой степени, поэтому в промежутке  ставим знак минус. Решением неравенства (20), а значит, и равносильного ему исходного неравенства будет совокупность промежутков, где стоит знак плюс, т. е. объединение множеств
ставим знак минус. Решением неравенства (20), а значит, и равносильного ему исходного неравенства будет совокупность промежутков, где стоит знак плюс, т. е. объединение множеств 
Ответ:  Замечание 1. Обобщенный метод интервалов можно применять и при решении неравенств
Замечание 1. Обобщенный метод интервалов можно применять и при решении неравенств

где  многочлены, если заметить, что на множестве всех действительных чисел неравенство (22) равносильно неравенству
многочлены, если заметить, что на множестве всех действительных чисел неравенство (22) равносильно неравенству

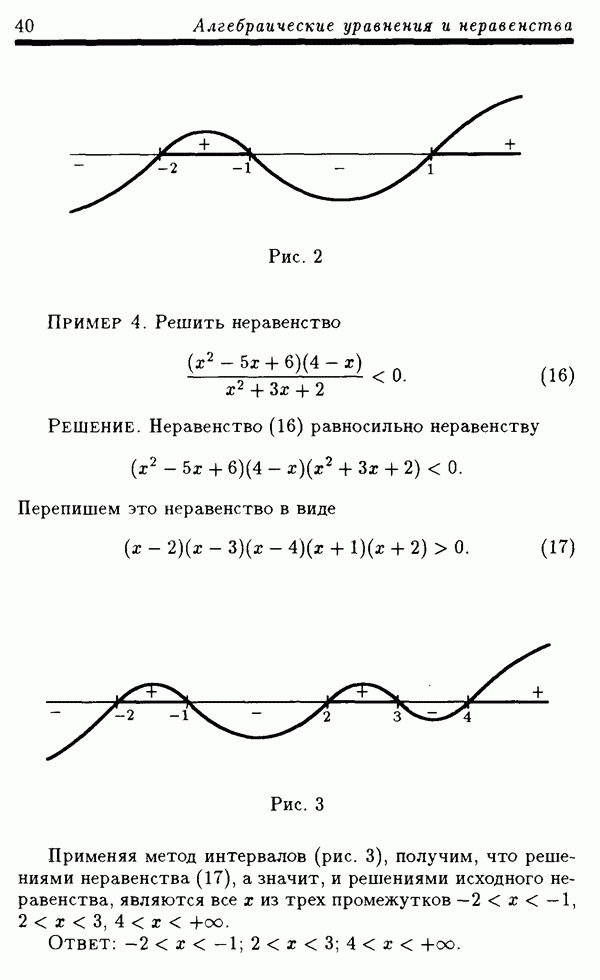
Пример 6. Решить неравенство

Решение. Неравенство (23) равносильно неравенству

Поскольку  при любом х, то последнее неравенство равносильно неравенству
при любом х, то последнее неравенство равносильно неравенству

Применим обобщенный метод интервалов. На числовой оси отметим точки —2, —1, 1, 3/2 и 3 и расставим знаки, как указано на рис. 5. Те промежутки, где стоит знак минус, и дадут все решения неравенства (23).
Ответ: 

Рис. 5
Замечание 2. Обобщенный метод интервалов можно применять и так:
1) найти все различные корни  многочлена
многочлена 
2) выяснить знак многочлена  на каждом из интервалов
на каждом из интервалов  подставляя в
подставляя в  вместо х любое число из этого интервала.
вместо х любое число из этого интервала.
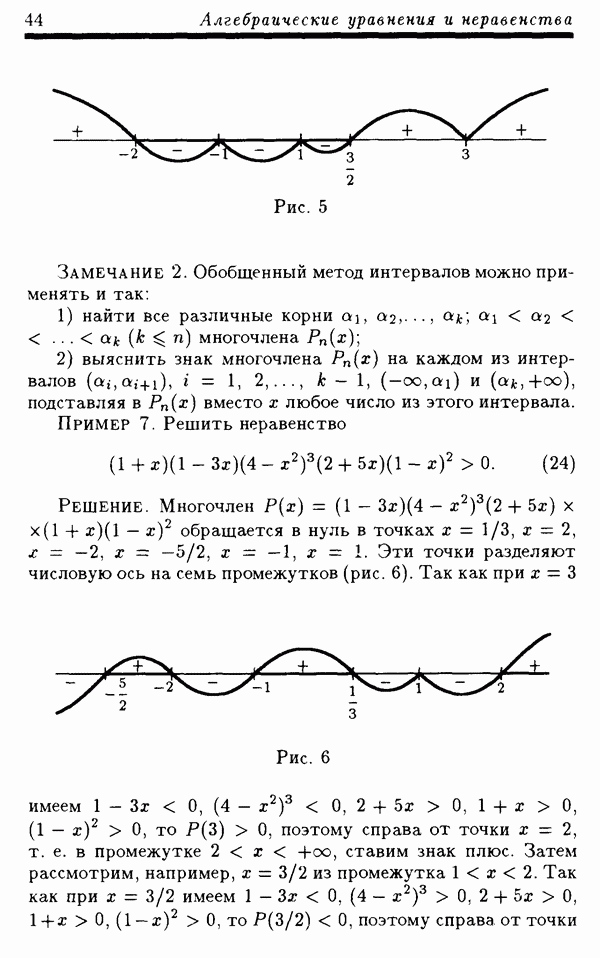
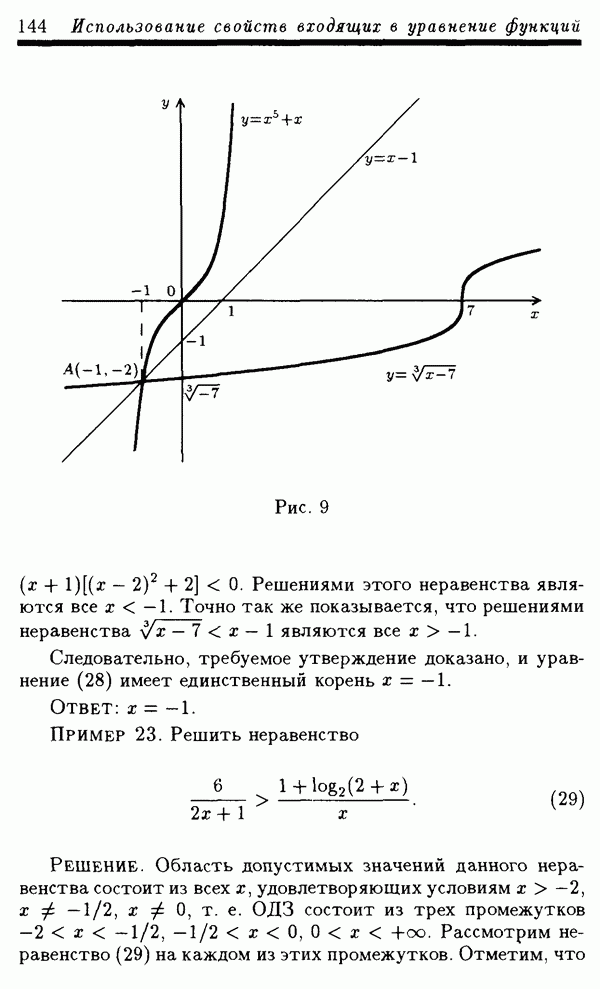
Пример 7. Решить неравенство

Решение. Многочлен  обращается в нуль в точках
обращается в нуль в точках  Эти точки разделяют числовую ось на семь промежутков (рис. 6).
Эти точки разделяют числовую ось на семь промежутков (рис. 6).

Рис. 6
Так как при  имеем
имеем  то
то  поэтому справа от точки
поэтому справа от точки  е. в промежутке
е. в промежутке  ставим знак плюс. Затем рассмотрим, например,
ставим знак плюс. Затем рассмотрим, например,  из промежутка
из промежутка  Так как при
Так как при  имеем
имеем  то
то  поэтому справа от точки
поэтому справа от точки
 в промежутке
в промежутке  ставим знак минус. Поступая аналогично, расставим знаки плюс или минус, как указано на рис. 6.
ставим знак минус. Поступая аналогично, расставим знаки плюс или минус, как указано на рис. 6.
Решением неравенства (24) будет объединение всех тех промежутков, в которых поставлен знак плюс, т. е. это будет объединение промежутков 
Ответ: 
Задачи
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. Алгебраические уравнения и неравенства
- § 1.1. Разложение многочлена на множители
- 1.1.2. Применение формул сокращенного умножения.
- 1.1.3. Выделение полного квадрата.
- 1.1.4. Группировка.
- 1.1.5. Метод неопределенных коэффициентов.
- 1.1.6. Подбор корня многочлена по его старшему и свободному коэффициентам.
- 1.1.7. Метод введения параметра.
- 1.1.8. Метод введения новой неизвестной.
- 1.1.9. Комбинирование различных методов.
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- 1.3.2. Симметрические уравнения четвертой степени.
- 1.3.3. Возвратные уравнения.
- 1.3.4. Уравнения четвертой степени с дополнительными условиями на коэффициенты.
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- 1.4.2. Угадывание корня уравнения.
- 1.4.3. Использование симметричности уравнения.
- 1.4.4. Использование суперпозиции функций.
- 1.4.5. Исследование уравнения на промежутках действительной оси.
- § 1.5. Решение алгебраических неравенств
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. Уравнения и неравенства, содержащие радикалы, степени, логарифмы и модули
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком корня
- 2.1.4. Умножение уравнения или неравенства на функцию.
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- 2.2.2. Переход к основанию, содержащему неизвестную.
- 2.2.3. Уравнения вида …
- 2.2.5. Неравенства вида …
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- 2.4.6. Использование свойств абсолютной величины.
- Глава III. Способ замены неизвестных при решении уравнений
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- 3.3.3. Сведение решения иррационального уравнения к решению тригонометрического уравнения.
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнений сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. Решение уравнений и неравенств с использованием свойств входящих в них функций
- § 4.1. Применение основных свойств функций
- 4.1.2. Использование ограниченности функций.
- 4.1.3. Использование монотонности.
- 4.1.4. Использование графиков.
- 4.1.5. Метод интервалов для непрерывных функций.
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- 4.2.3. Использование ограниченности функций.
- 4.2.4. Использование свойств синуса и косинуса.
- 4.2.5. Использование числовых неравенств.
- § 4.3. Применение производной
- 4.3.2. Использование наибольшего и наименьшего значений функции.
- 4.3.3. Применение теоремы Лагранжа.
- Дополнения