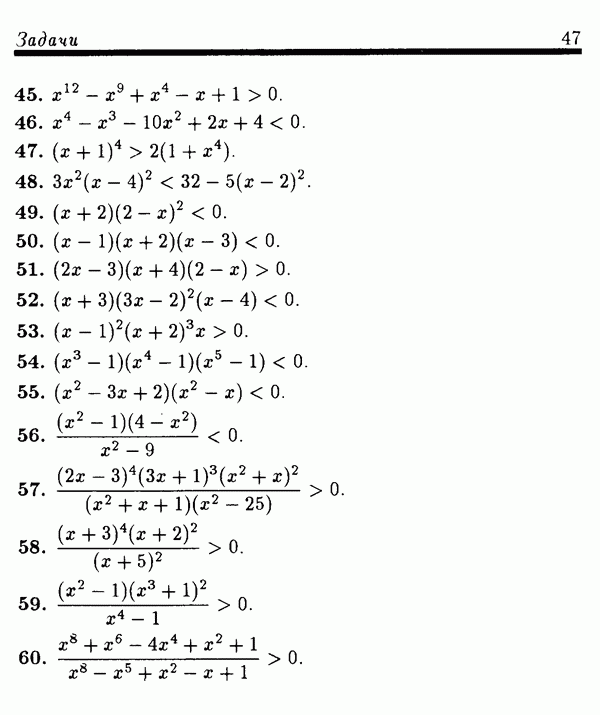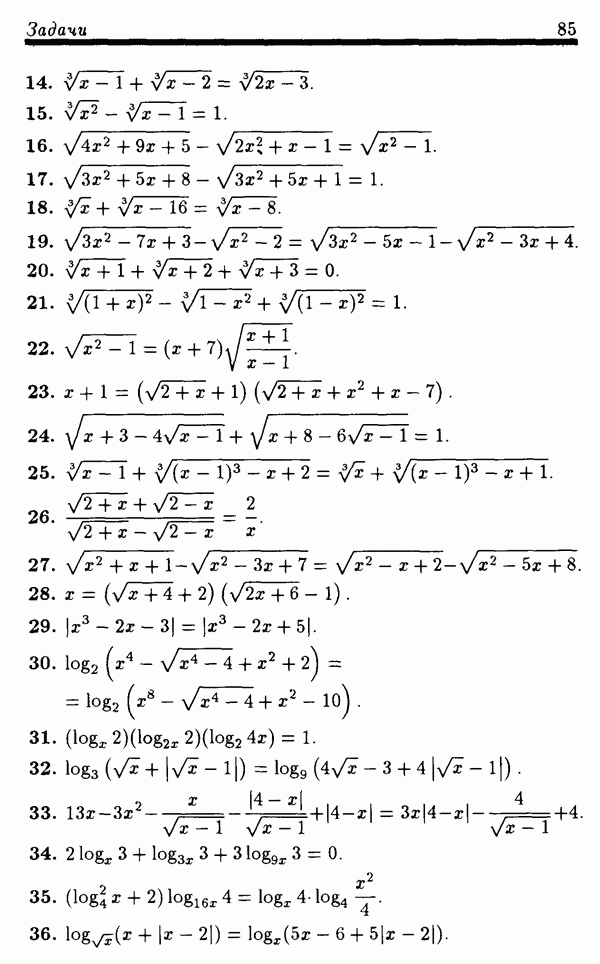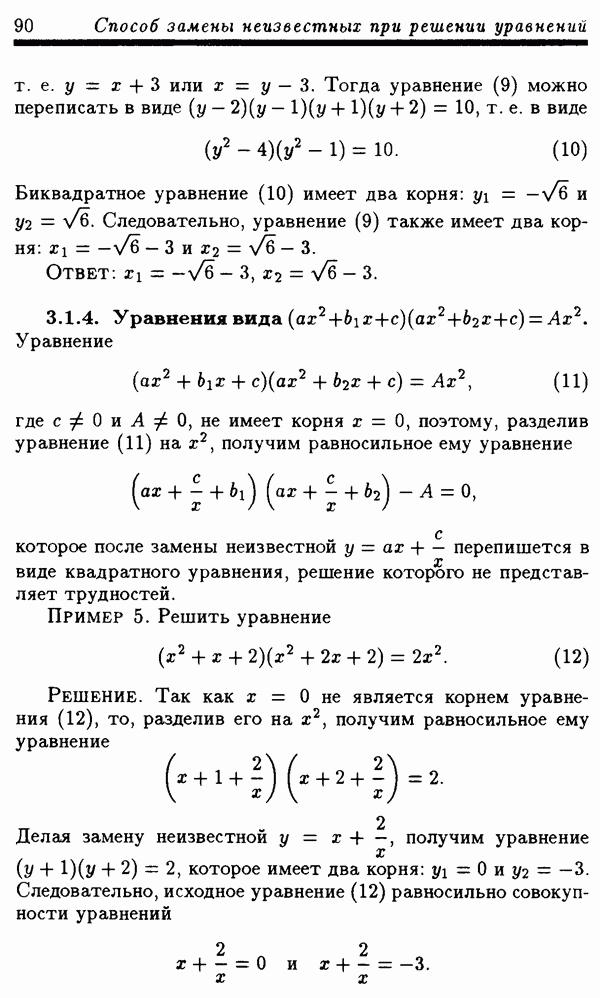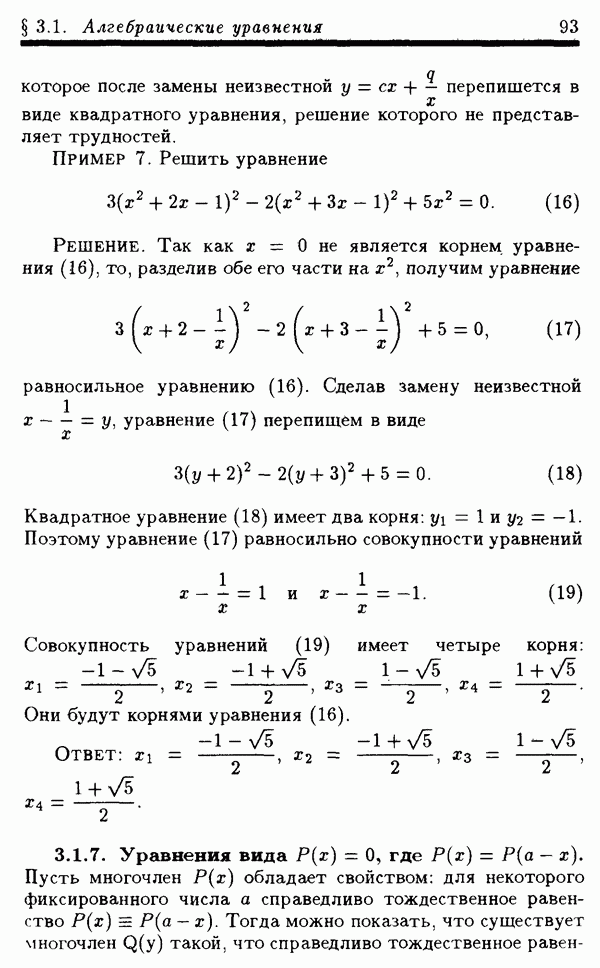| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.1.4. Умножение уравнения или неравенства на функцию.
В некоторых случаях полезно умножение обеих частей уравнения или неравенства, содержащих радикалы, на некоторую функцию  имеющую смысл на их ОДЗ.
имеющую смысл на их ОДЗ.
При решении уравнения этим способом надо либо следить за равносильностью преобразований на ОДЗ исходного уравнения, либо в конце решения надо делать проверку, так как могут появиться посторонние корни.
При решении неравенства надо следить за равносильностью преобразований неравенства на его ОДЗ, и поэтому можно умножать обе части неравенства на функцию, принимающую на ОДЗ неравенства только значения одного знака либо разбивать ОДЗ на промежутки, на которых функция знакопостоянна, и делать равносильные преобразования на этих промежутках.
Пример 7. Решить уравнение

Решение. Умножив обе части уравнения на функцию  получим уравнение
получим уравнение

являющееся следствием уравнения (40). Перепишем уравнение (41) в виде

Следствием уравнения (42) является уравнение

Решениями уравнения (43) являются  Проверка показывает, что
Проверка показывает, что  является корнем исходного уравнения,
является корнем исходного уравнения,  являются его корнями.
являются его корнями.
Ответ: 
Пример 8. Решить уравнение

Решение. ОДЗ уравнения состоит из всех х, удовлетворяющих одновременно условиям  е. ОДЗ есть все
е. ОДЗ есть все  На ОДЗ уравнение (44) можно переписать в виде
На ОДЗ уравнение (44) можно переписать в виде

или в виде

После умножения обеих частей уравнения (45) на функцию  принимающую на ОДЗ уравнения (44) только положительные значения, получим уравнение
принимающую на ОДЗ уравнения (44) только положительные значения, получим уравнение

равносильное исходному на его ОДЗ. Поскольку выражение  обращается в нуль при
обращается в нуль при  то разобьем множество
то разобьем множество  на два множества:
на два множества:  Для любого
Для любого  [1/2; 5] левая часть уравнения (46) неположительна, а правая положительна. Значит, ни одно из этих х не может быть решением уравнения (46), а значит, и исходного уравнения.
[1/2; 5] левая часть уравнения (46) неположительна, а правая положительна. Значит, ни одно из этих х не может быть решением уравнения (46), а значит, и исходного уравнения.
Для любого  обе части уравнения (46) положительны, и оно на этом множестве равносильно уравнению
обе части уравнения (46) положительны, и оно на этом множестве равносильно уравнению

т. е. уравнению

Уравнение (47) на множестве  равносильно уравнению
равносильно уравнению

т. е. уравнению

Решения уравнения (48) есть  Из этих значений х условию
Из этих значений х условию  удовлетворяет только
удовлетворяет только  оно и является решением исходного уравнения.
оно и является решением исходного уравнения.
Ответ: 
Пример 9. Решить неравенство

Решение. ОДЗ неравенства (49) состоит из всех х, для которых  Поскольку на
Поскольку на  то, умножив неравенство (49) на функцию
то, умножив неравенство (49) на функцию  получим неравенство
получим неравенство

равносильное исходному на множестве 
При  имеем
имеем  и неравенство (50) перепишется в виде
и неравенство (50) перепишется в виде

Решения неравенства (51) составляют промежуток 
Поэтому для этих  решения неравенства (50) составляют промежуток
решения неравенства (50) составляют промежуток 
При  неравенство (50) перепишется в виде
неравенство (50) перепишется в виде

Решения неравенства (52) составляют промежуток  Поэтому для этих х решения неравенства (50) составляют промежуток
Поэтому для этих х решения неравенства (50) составляют промежуток  Следовательно,
Следовательно,
множеством решений неравенства (49) является объединение промежутков

т. е. интервал

Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. Алгебраические уравнения и неравенства
- § 1.1. Разложение многочлена на множители
- 1.1.2. Применение формул сокращенного умножения.
- 1.1.3. Выделение полного квадрата.
- 1.1.4. Группировка.
- 1.1.5. Метод неопределенных коэффициентов.
- 1.1.6. Подбор корня многочлена по его старшему и свободному коэффициентам.
- 1.1.7. Метод введения параметра.
- 1.1.8. Метод введения новой неизвестной.
- 1.1.9. Комбинирование различных методов.
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- 1.3.2. Симметрические уравнения четвертой степени.
- 1.3.3. Возвратные уравнения.
- 1.3.4. Уравнения четвертой степени с дополнительными условиями на коэффициенты.
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- 1.4.2. Угадывание корня уравнения.
- 1.4.3. Использование симметричности уравнения.
- 1.4.4. Использование суперпозиции функций.
- 1.4.5. Исследование уравнения на промежутках действительной оси.
- § 1.5. Решение алгебраических неравенств
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. Уравнения и неравенства, содержащие радикалы, степени, логарифмы и модули
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком корня
- 2.1.4. Умножение уравнения или неравенства на функцию.
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- 2.2.2. Переход к основанию, содержащему неизвестную.
- 2.2.3. Уравнения вида …
- 2.2.5. Неравенства вида …
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- 2.4.6. Использование свойств абсолютной величины.
- Глава III. Способ замены неизвестных при решении уравнений
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- 3.3.3. Сведение решения иррационального уравнения к решению тригонометрического уравнения.
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнений сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. Решение уравнений и неравенств с использованием свойств входящих в них функций
- § 4.1. Применение основных свойств функций
- 4.1.2. Использование ограниченности функций.
- 4.1.3. Использование монотонности.
- 4.1.4. Использование графиков.
- 4.1.5. Метод интервалов для непрерывных функций.
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- 4.2.3. Использование ограниченности функций.
- 4.2.4. Использование свойств синуса и косинуса.
- 4.2.5. Использование числовых неравенств.
- § 4.3. Применение производной
- 4.3.2. Использование наибольшего и наименьшего значений функции.
- 4.3.3. Применение теоремы Лагранжа.
- Дополнения