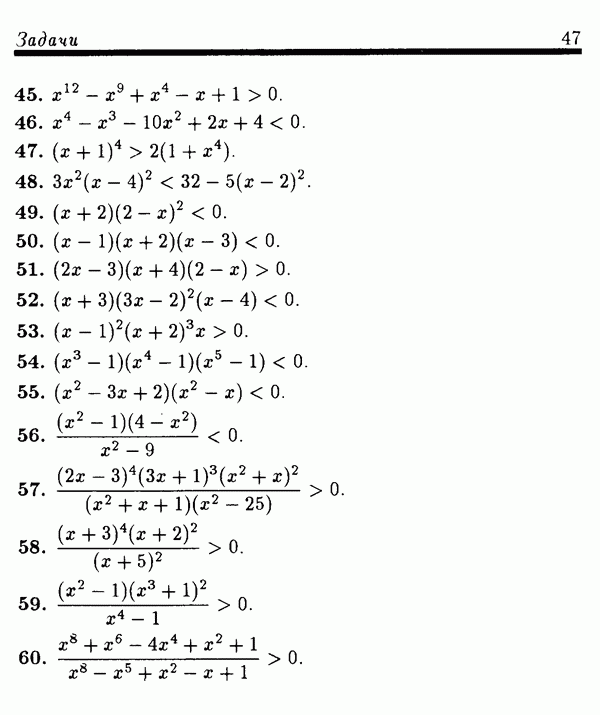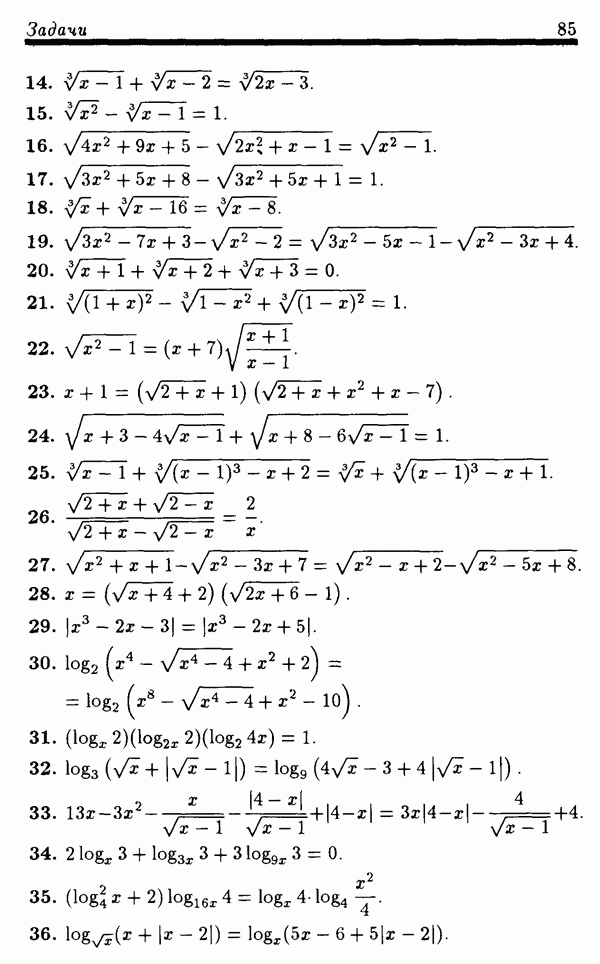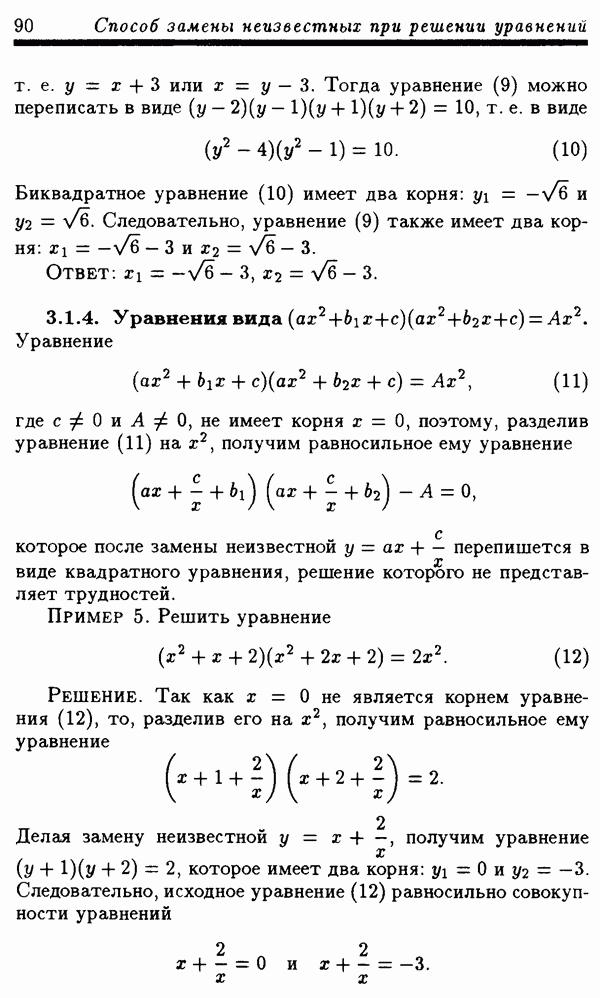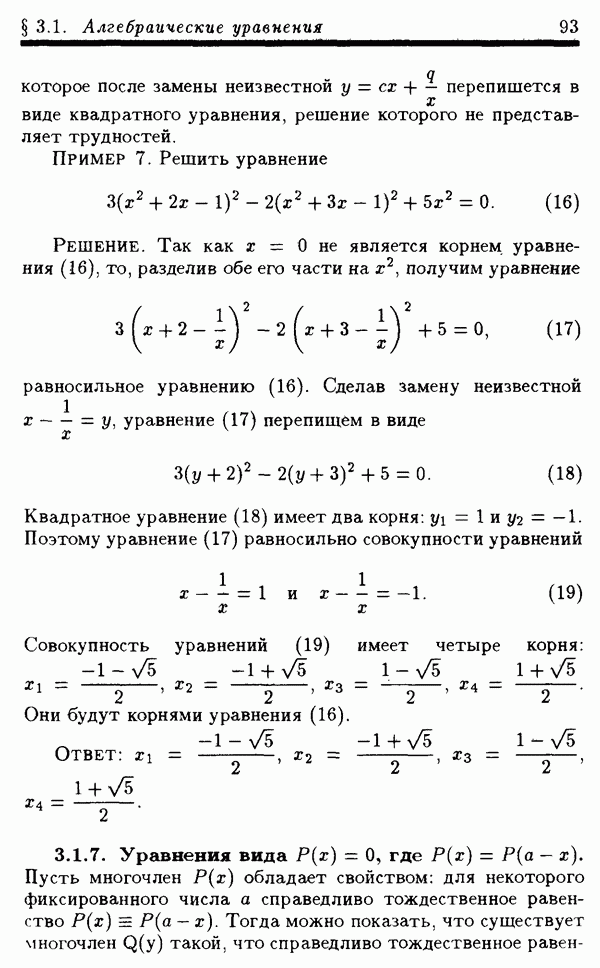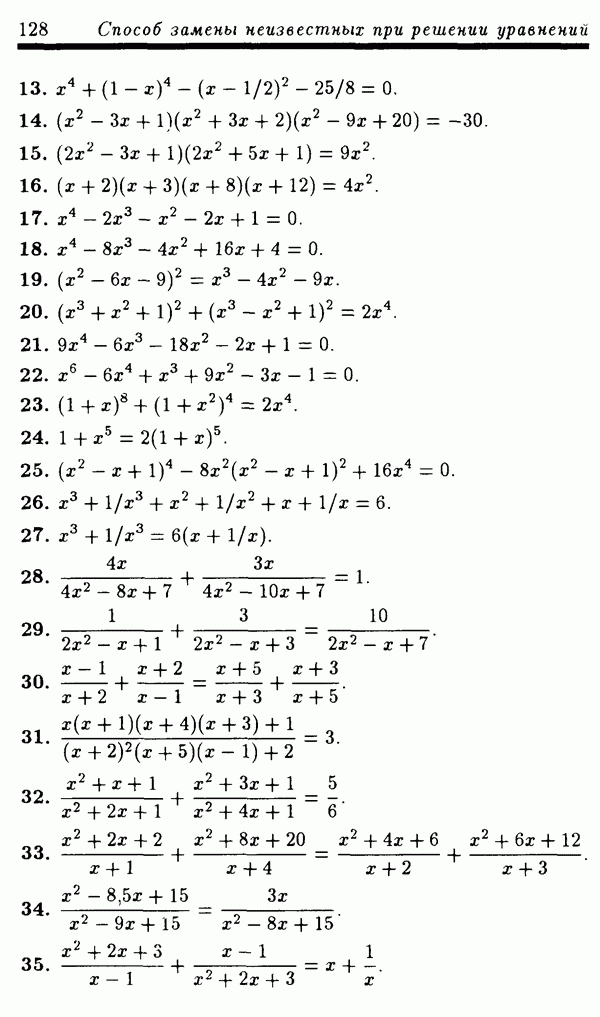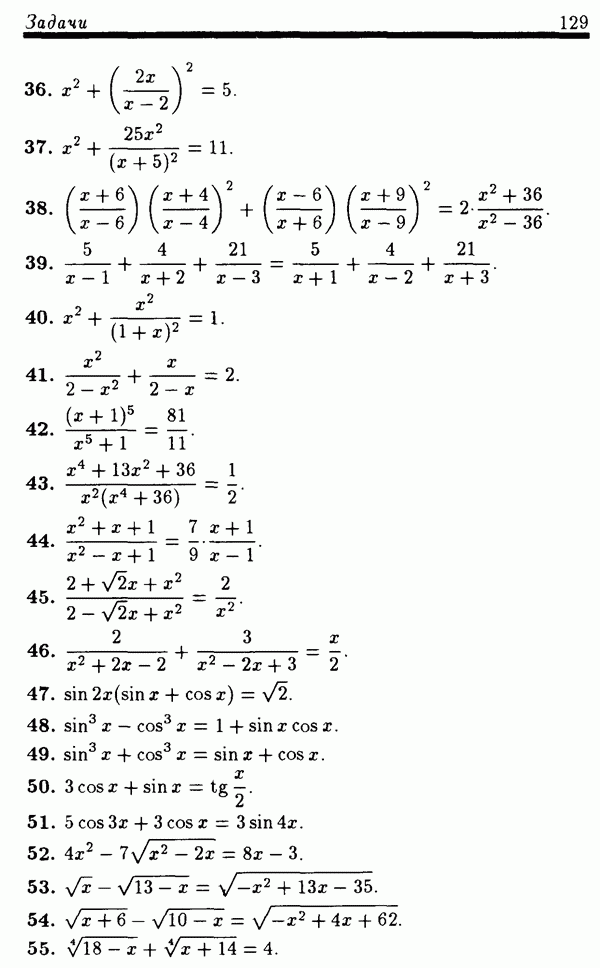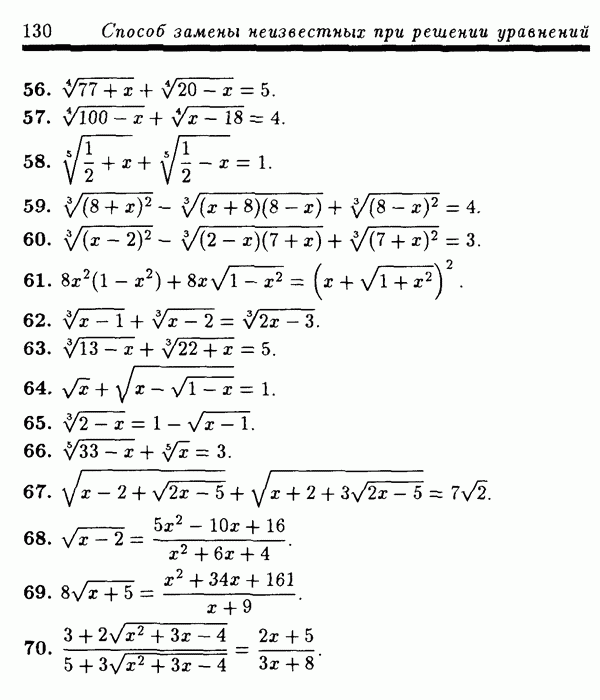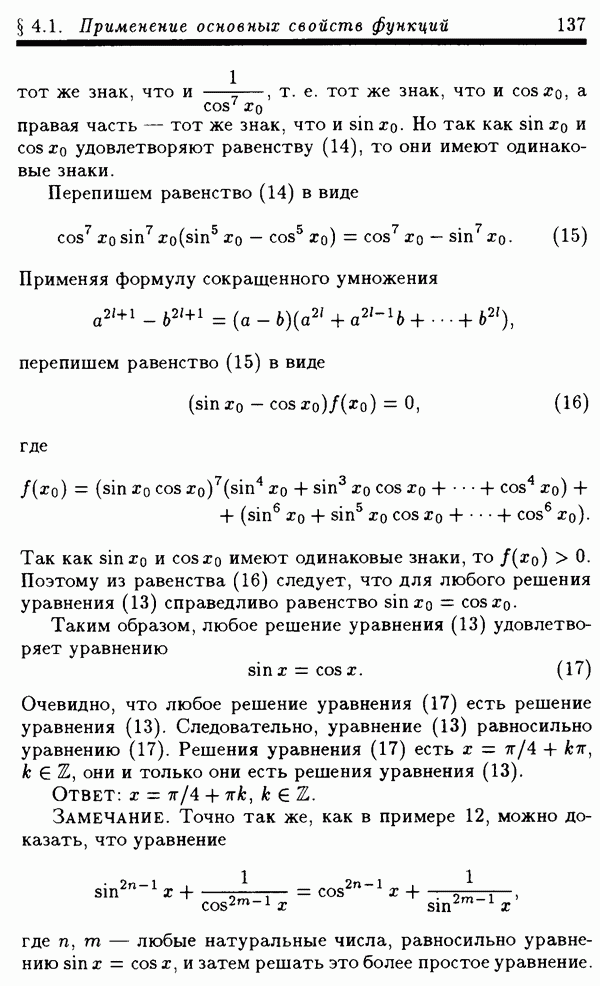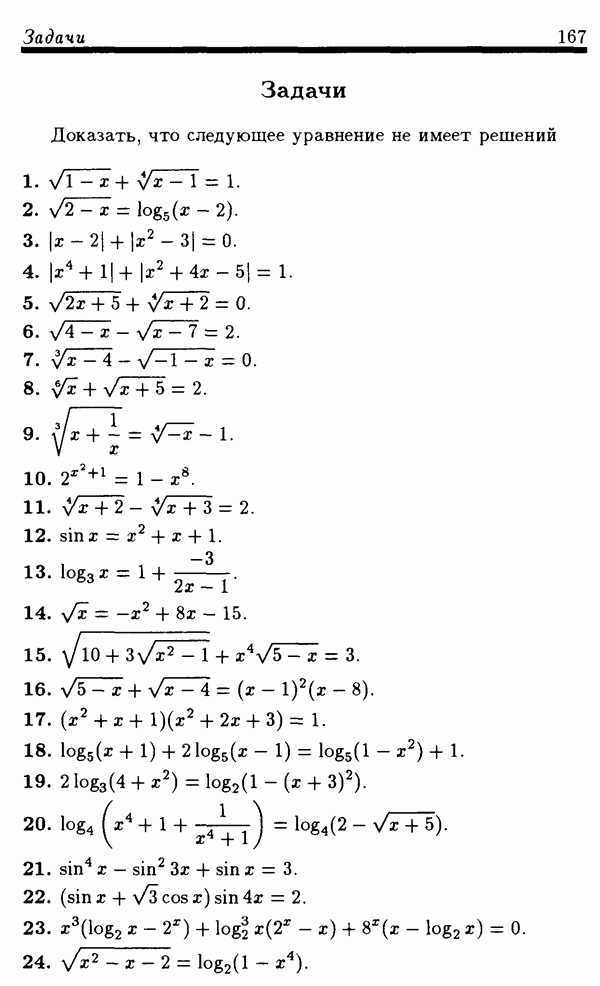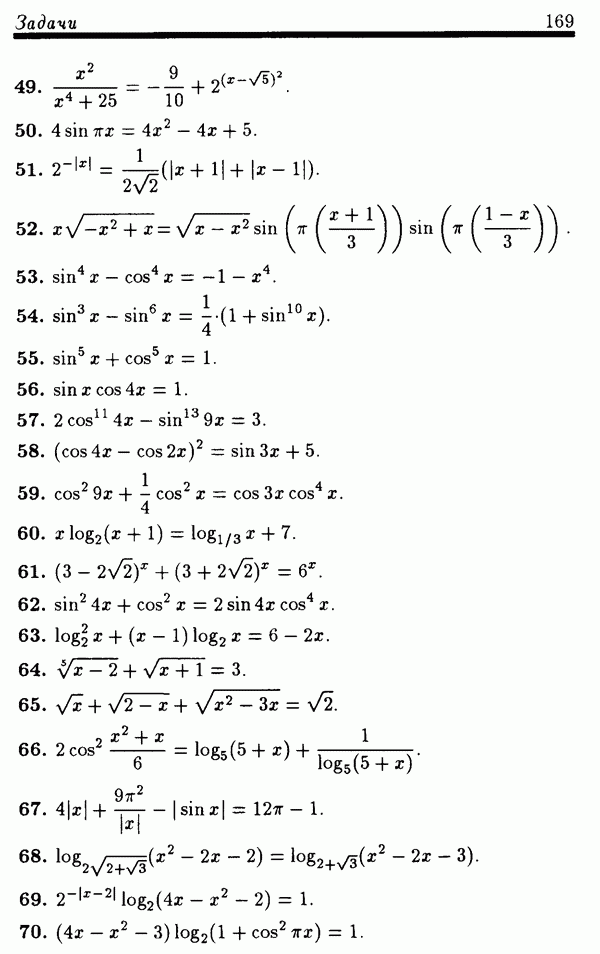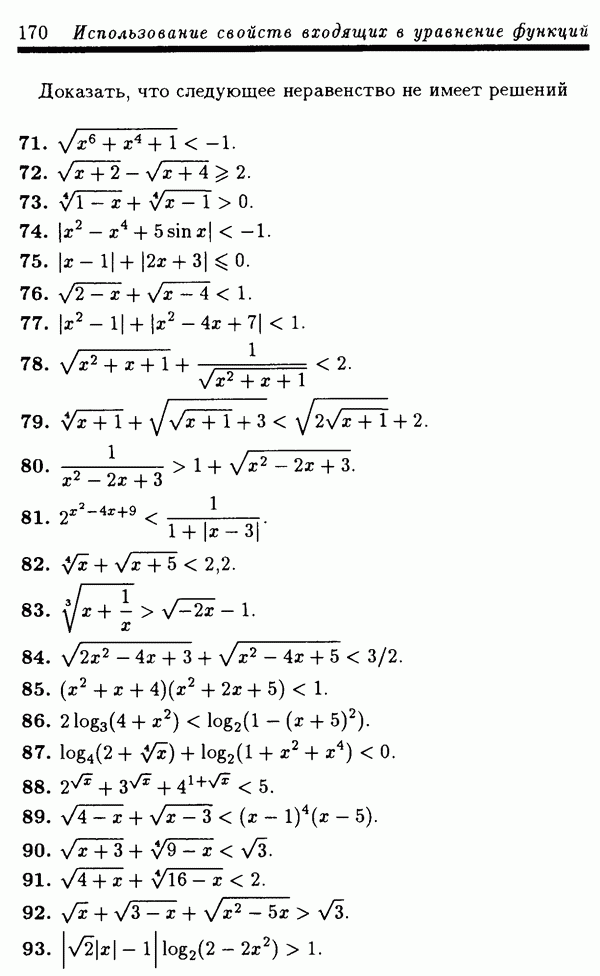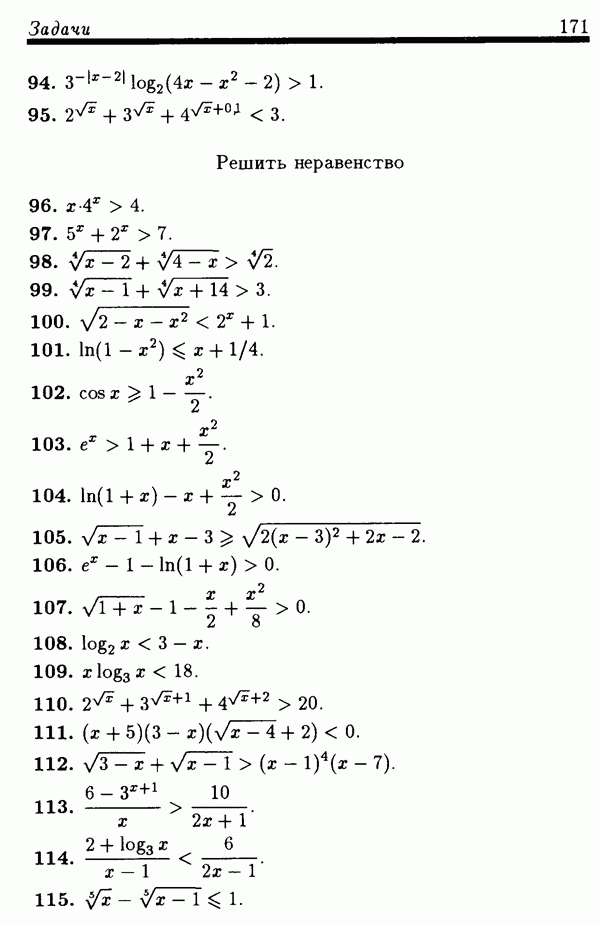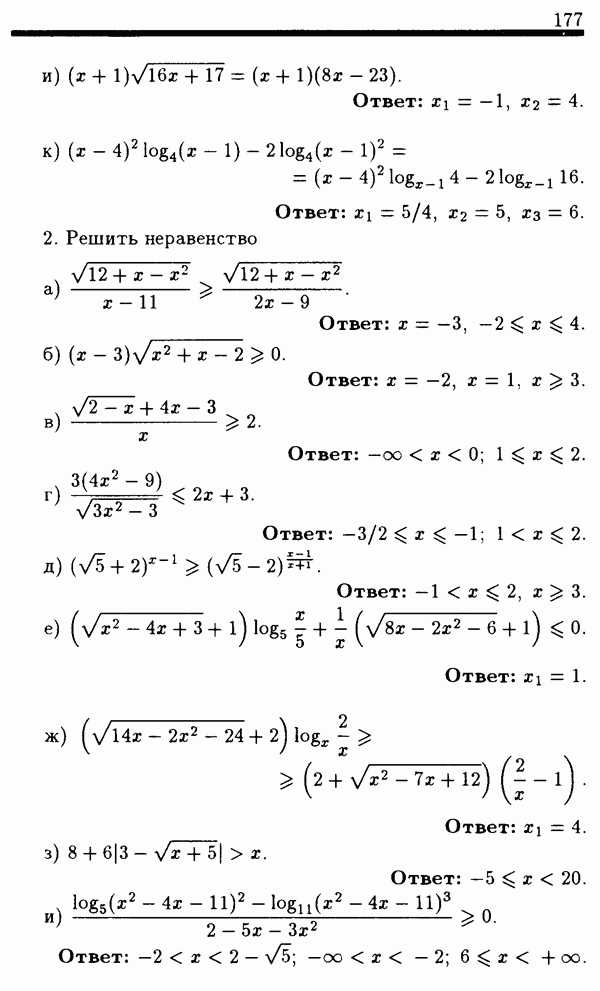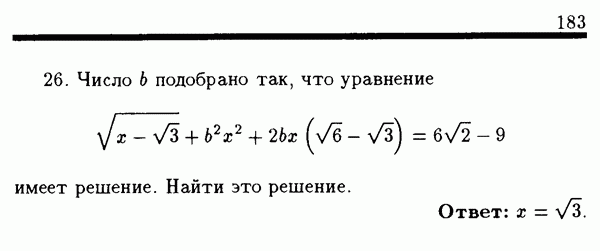| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3.3. Сведение решения иррационального уравнения к решению тригонометрического уравнения.
Заменой неизвестной решение иррациональных уравнений иногда можно свести к решению тригонометрических уравнений. При этом полезными могут оказаться следующие замены неизвестной. 
1. Если в уравнение входит радикал  то можно сделать замену
то можно сделать замену  или
или 
2. Если в уравнение входит радикал  то можно сделать замену
то можно сделать замену 
3. Если в уравнение входит радикал  то можно сделать замену
то можно сделать замену 
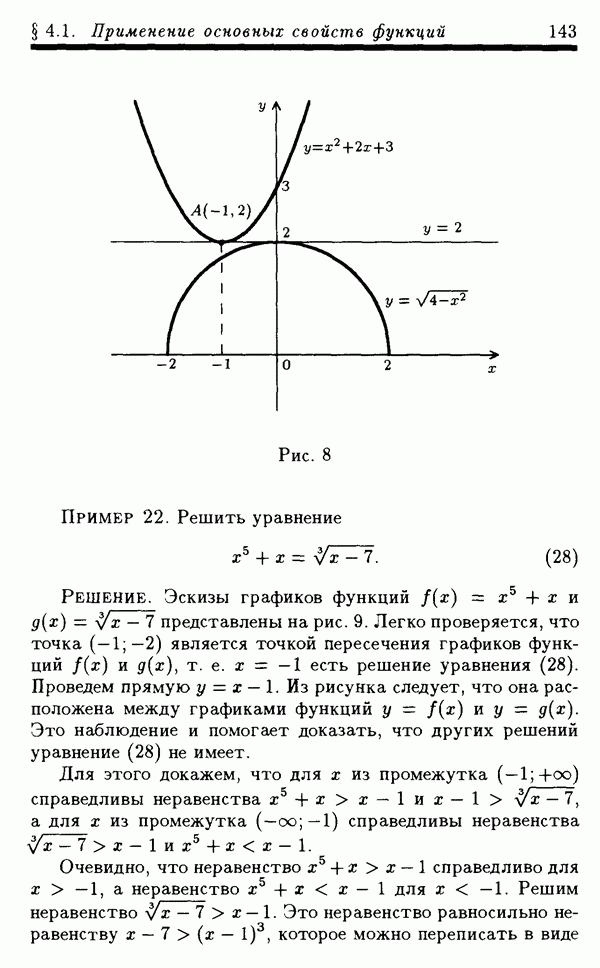
Пример 5. Решить уравнение

Решение. ОДЗ уравнения (30) есть все действительные х. Сделаем замену неизвестной  где можно считать, что
где можно считать, что  Тогда уравнение (30) запишется в виде
Тогда уравнение (30) запишется в виде

Поскольку  для рассматриваемых
для рассматриваемых  то уравнение (31) для этих
то уравнение (31) для этих  равносильно уравнению
равносильно уравнению

Уравнение (32) равносильно совокупности уравнений

Из решений этих уравнений промежутку  принадлежит только
принадлежит только  Поэтому соответствующее х есть
Поэтому соответствующее х есть

Ответ:  .
.
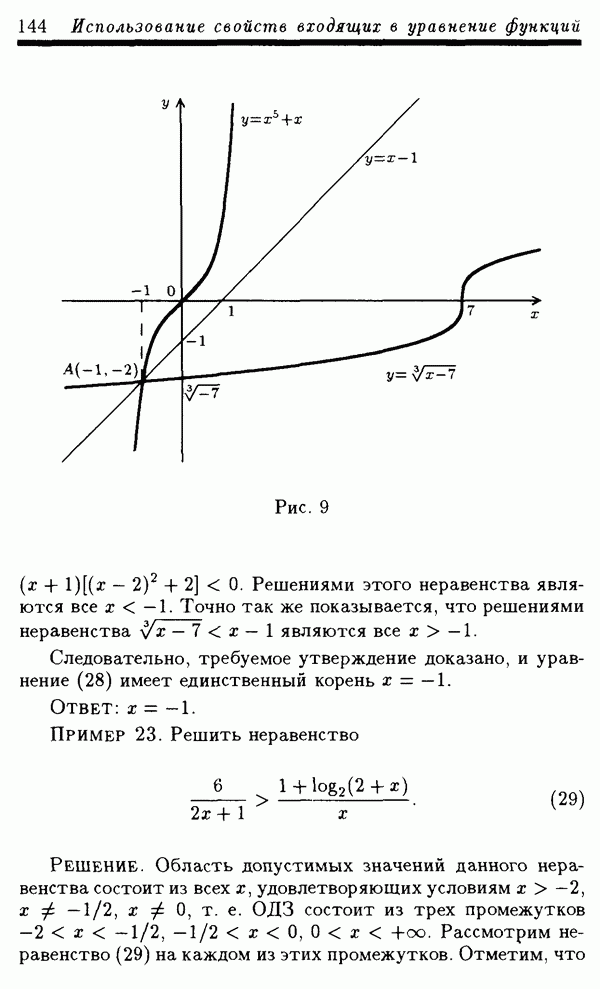
ПРИМЕР 6. Решить уравнение

РЕШЕНИЕ. ОДЗ уравнения (34) состоит из всех х, удовлетворяющих условию  Ясно, что никакое отрицательное х из ОДЗ не может быть решением уравнения (34). Следовательно, все решения уравнения (34) лежат в области
Ясно, что никакое отрицательное х из ОДЗ не может быть решением уравнения (34). Следовательно, все решения уравнения (34) лежат в области  . Сделаем замену неизвестной
. Сделаем замену неизвестной  , где можно считать, что
, где можно считать, что  Тогда уравнение (34) можно переписать в виде
Тогда уравнение (34) можно переписать в виде

Это уравнение для рассматриваемых  равносильно уравнению
равносильно уравнению

которое для этих  равносильно уравнению
равносильно уравнению

Делая замену неизвестной  уравнение (37) можно переписать в виде
уравнение (37) можно переписать в виде

Уравнение (38) имеет корни  Поэтому уравнение (37) равносильно совокупности уравнений
Поэтому уравнение (37) равносильно совокупности уравнений

Первое уравнение совокупности (39) не имеет решений из промежутка  так как для любого 10 из этого промежутка
так как для любого 10 из этого промежутка  Следовательно, все решения уравнения (35), удовлетворяющие условию
Следовательно, все решения уравнения (35), удовлетворяющие условию  содержатся среди решений второго уравнения совокупности (39). Обозначая
содержатся среди решений второго уравнения совокупности (39). Обозначая  это уравнение для рассматриваемых
это уравнение для рассматриваемых  можно записать в виде
можно записать в виде

Уравнение (40) имеет два корня:  Поэтому уравнение (35) на промежутке
Поэтому уравнение (35) на промежутке  имеет два решения:
имеет два решения:  а это означает, что уравнение (34) имеет два корня:
а это означает, что уравнение (34) имеет два корня: 
Ответ: 
ПРИМЕР 7. Сколько корней на отрезке [0; 1] имеет уравнение

Решение. Так как искомые корни удовлетворяют условию  то делаем замену неизвестной
то делаем замену неизвестной  Тогда каждому корню
Тогда каждому корню  исходного уравнения будет соответствовать ровно один корень
исходного уравнения будет соответствовать ровно один корень  где
где  уравнения
уравнения

и, наоборот, каждому корню  уравнения (42) соответствует ровно один корень
уравнения (42) соответствует ровно один корень  [0; 1] уравнения (41). Таким образом, задача может быть переформулирована так: сколько корней на промежутке
[0; 1] уравнения (41). Таким образом, задача может быть переформулирована так: сколько корней на промежутке  имеет уравнение
имеет уравнение 
Поскольку  то перепишем уравнение (42) в виде
то перепишем уравнение (42) в виде

Так как  не есть корень уравнения (43), то оно равносильно на промежутке
не есть корень уравнения (43), то оно равносильно на промежутке  уравнению
уравнению

или уравнению  или, наконец, уравнению
или, наконец, уравнению

Решения уравнения (44) есть

Из этих чисел условию  удовлетворяют только три числа
удовлетворяют только три числа  Следовательно, исходное уравнение (41) имеет на отрезке [0; 1] три корня.
Следовательно, исходное уравнение (41) имеет на отрезке [0; 1] три корня.
Ответ: три корня.
| << Предыдущий параграф | Следующий параграф >> |
- От авторов
- Глава I. Алгебраические уравнения и неравенства
- § 1.1. Разложение многочлена на множители
- 1.1.2. Применение формул сокращенного умножения.
- 1.1.3. Выделение полного квадрата.
- 1.1.4. Группировка.
- 1.1.5. Метод неопределенных коэффициентов.
- 1.1.6. Подбор корня многочлена по его старшему и свободному коэффициентам.
- 1.1.7. Метод введения параметра.
- 1.1.8. Метод введения новой неизвестной.
- 1.1.9. Комбинирование различных методов.
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- 1.3.2. Симметрические уравнения четвертой степени.
- 1.3.3. Возвратные уравнения.
- 1.3.4. Уравнения четвертой степени с дополнительными условиями на коэффициенты.
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- 1.4.2. Угадывание корня уравнения.
- 1.4.3. Использование симметричности уравнения.
- 1.4.4. Использование суперпозиции функций.
- 1.4.5. Исследование уравнения на промежутках действительной оси.
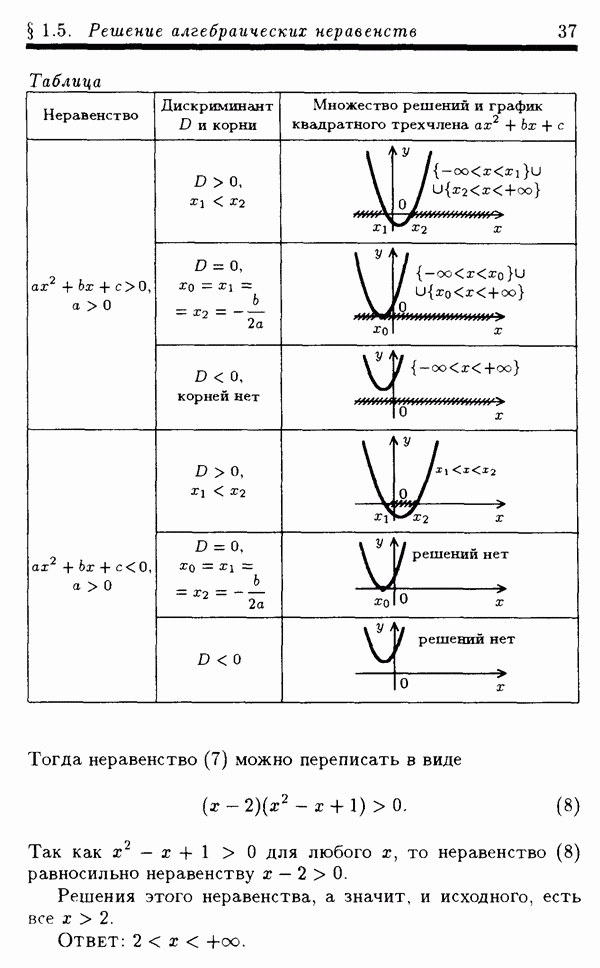
- § 1.5. Решение алгебраических неравенств
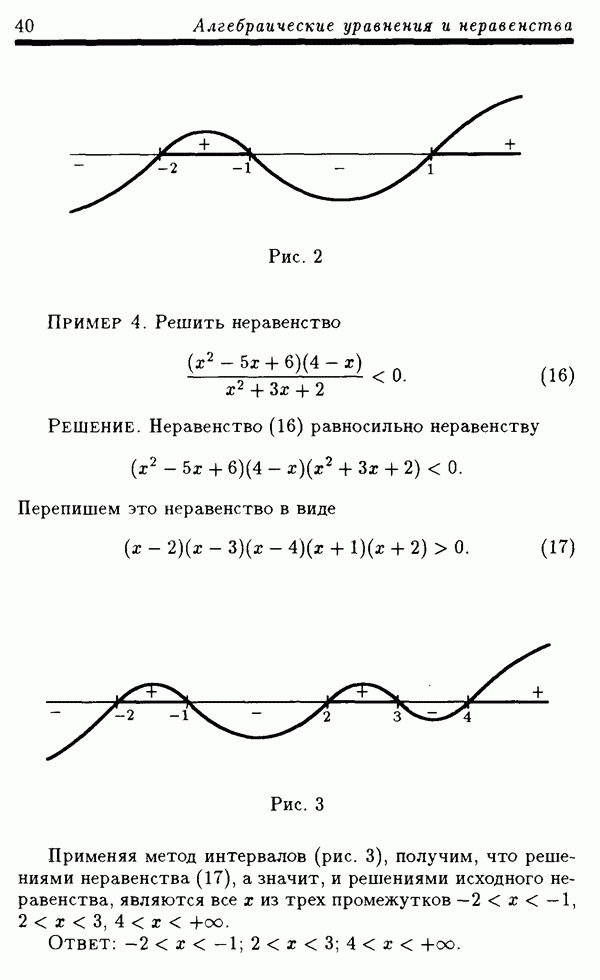
- 1.5.2. Метод интервалов.
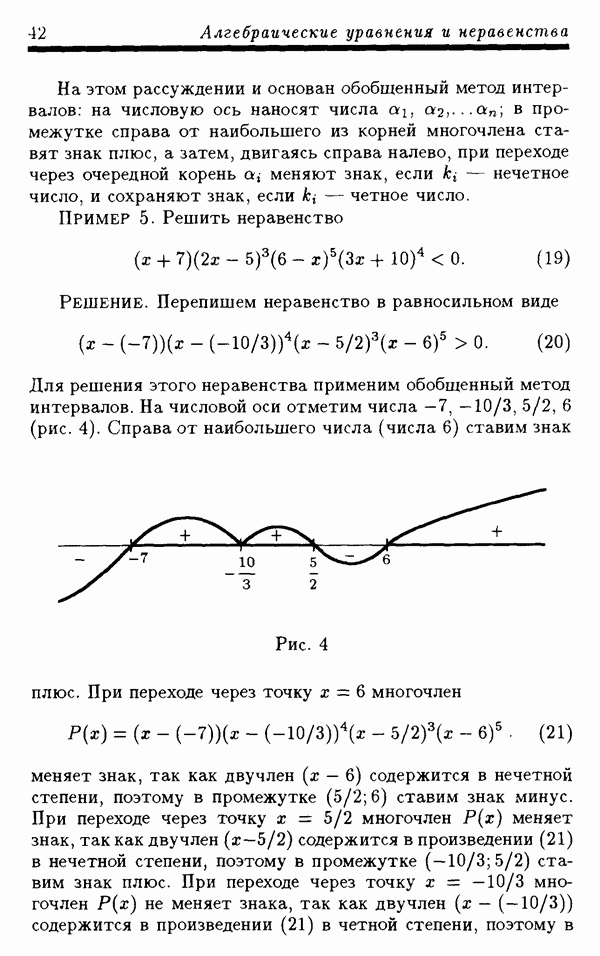
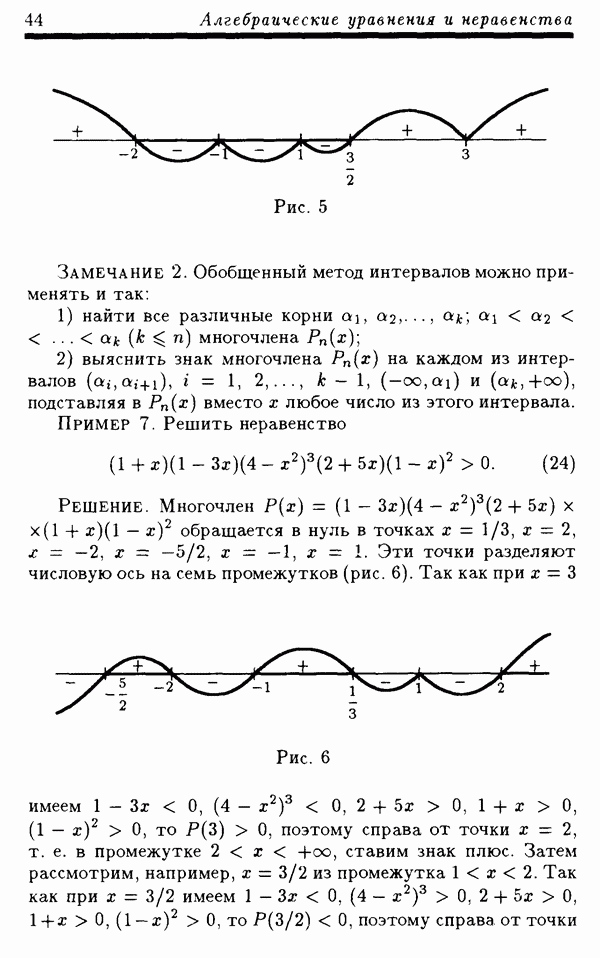
- 1.5.3. Обобщенный метод интервалов.
- Глава II. Уравнения и неравенства, содержащие радикалы, степени, логарифмы и модули
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком корня
- 2.1.4. Умножение уравнения или неравенства на функцию.
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- 2.2.2. Переход к основанию, содержащему неизвестную.
- 2.2.3. Уравнения вида …
- 2.2.5. Неравенства вида …
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- 2.4.6. Использование свойств абсолютной величины.
- Глава III. Способ замены неизвестных при решении уравнений
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- 3.3.3. Сведение решения иррационального уравнения к решению тригонометрического уравнения.
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнений сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. Решение уравнений и неравенств с использованием свойств входящих в них функций
- § 4.1. Применение основных свойств функций
- 4.1.2. Использование ограниченности функций.
- 4.1.3. Использование монотонности.
- 4.1.4. Использование графиков.
- 4.1.5. Метод интервалов для непрерывных функций.
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- 4.2.3. Использование ограниченности функций.
- 4.2.4. Использование свойств синуса и косинуса.
- 4.2.5. Использование числовых неравенств.
- § 4.3. Применение производной
- 4.3.2. Использование наибольшего и наименьшего значений функции.
- 4.3.3. Применение теоремы Лагранжа.
- Дополнения