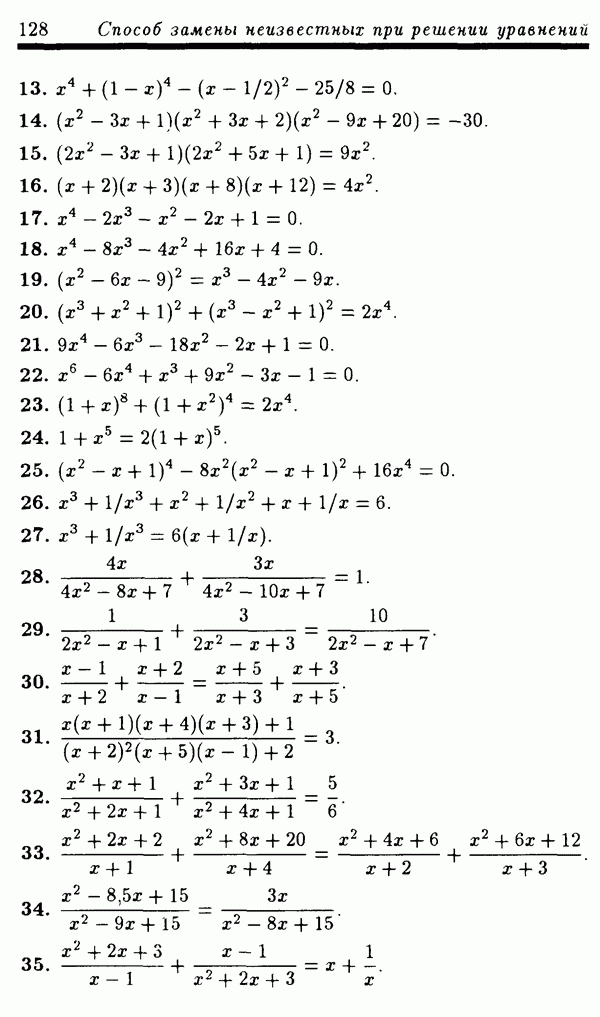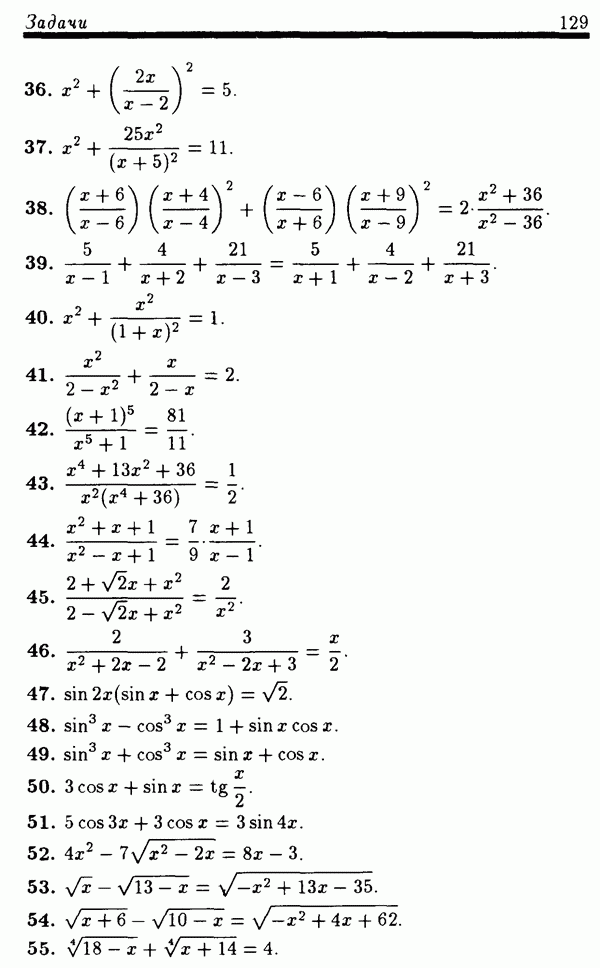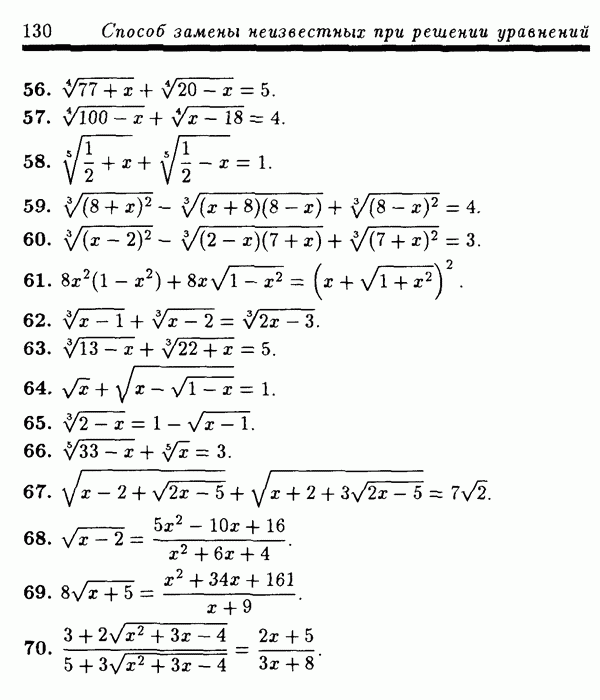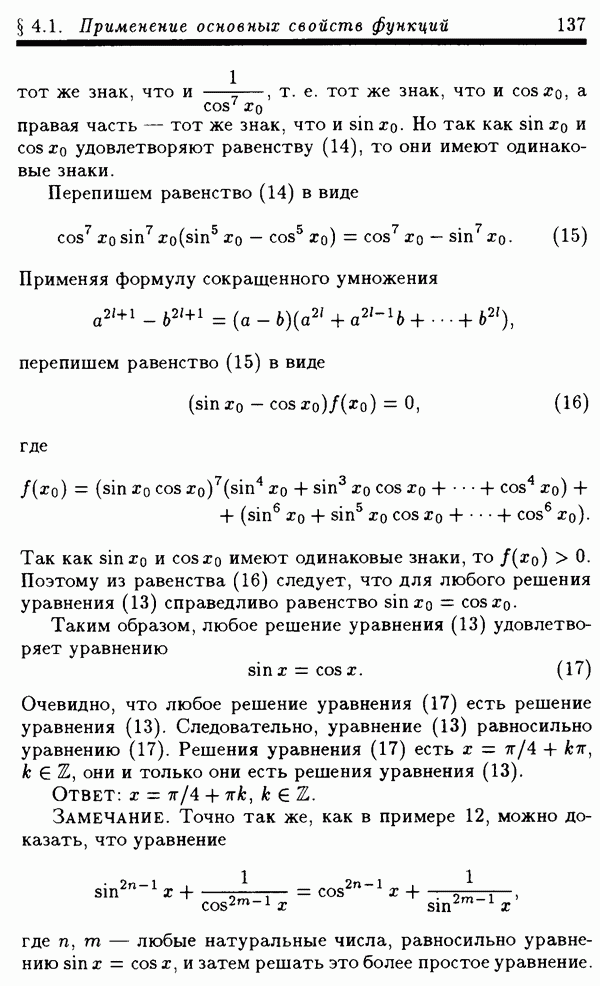| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.2.5. Использование числовых неравенств.
Иногда, применяя то или иное числовое неравенство к одной из частей уравнения (неравенства), его можно заменить равносильной ему системой уравнений. Примером такого неравенства является неравенство между средним арифметическим и средним геометрическим —  где а и
где а и  — положительные числа, причем равенство здесь возможно лишь при
— положительные числа, причем равенство здесь возможно лишь при 
Часто бывает полезно пользоваться следствиями из этих неравенств, например, а  при
при  причем
причем  тогда и только тогда, когда
тогда и только тогда, когда  при
при  причем а
причем а  тогда и только тогда, когда
тогда и только тогда, когда 
Пример 13. Решить уравнение

Решение. ОДЗ этого уравнения есть все действительные числа. Переписав левую часть уравнения (35) в виде

замечаем, что она не меньше четырех, как сумма двух взаимно обратных положительных величин, и только при  она равна четырем. В то же время правая часть при
она равна четырем. В то же время правая часть при  также равна четырем, а для всех
также равна четырем, а для всех  меньше четырех. Следовательно,
меньше четырех. Следовательно,  есть единственное решение уравнения (35). Ответ:
есть единственное решение уравнения (35). Ответ: 
Пример 14. Решить уравнение

Решение. Докажем, что для любых положительных чисел а и 6 справедливо неравенство

В самом деле, применяя неравенство о среднем арифметическом и среднем геометрическом сначала к числам  затем к числам а и
затем к числам а и  , имеем
, имеем

откуда

Поскольку на ОДЗ уравнения (36) имеем  то, применяя неравенство (37), получаем, что для любого такого х левая часть уравнения (36) не меньше 4. В то же время на ОДЗ уравнения
то, применяя неравенство (37), получаем, что для любого такого х левая часть уравнения (36) не меньше 4. В то же время на ОДЗ уравнения  Следовательно, уравнение (36) равносильно системе уравнений
Следовательно, уравнение (36) равносильно системе уравнений

Из последнего уравнения системы (38) находим его решения  Подставляя эти значения в первое уравнение системы (38), получаем, что они являются его решениями. Следовательно,
Подставляя эти значения в первое уравнение системы (38), получаем, что они являются его решениями. Следовательно,  являются решениями исходного уравнения (36).
являются решениями исходного уравнения (36).
Ответ: 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- От авторов
- Глава I. Алгебраические уравнения и неравенства
- § 1.1. Разложение многочлена на множители
- 1.1.2. Применение формул сокращенного умножения.
- 1.1.3. Выделение полного квадрата.
- 1.1.4. Группировка.
- 1.1.5. Метод неопределенных коэффициентов.
- 1.1.6. Подбор корня многочлена по его старшему и свободному коэффициентам.
- 1.1.7. Метод введения параметра.
- 1.1.8. Метод введения новой неизвестной.
- 1.1.9. Комбинирование различных методов.
- § 1.2. Простейшие способы решения алгебраических уравнений
- § 1.3. Симметрические и возвратные уравнения
- 1.3.2. Симметрические уравнения четвертой степени.
- 1.3.3. Возвратные уравнения.
- 1.3.4. Уравнения четвертой степени с дополнительными условиями на коэффициенты.
- § 1.4. Некоторые искусственные способы решения алгебраических уравнений
- 1.4.2. Угадывание корня уравнения.
- 1.4.3. Использование симметричности уравнения.
- 1.4.4. Использование суперпозиции функций.
- 1.4.5. Исследование уравнения на промежутках действительной оси.
- § 1.5. Решение алгебраических неравенств
- 1.5.2. Метод интервалов.
- 1.5.3. Обобщенный метод интервалов.
- Глава II. Уравнения и неравенства, содержащие радикалы, степени, логарифмы и модули
- § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком корня
- 2.1.4. Умножение уравнения или неравенства на функцию.
- § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов
- 2.2.2. Переход к основанию, содержащему неизвестную.
- 2.2.3. Уравнения вида …
- 2.2.5. Неравенства вида …
- § 2.3. Уравнения и неравенства, содержащие неизвестную в основании и показателе степени
- § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины
- 2.4.6. Использование свойств абсолютной величины.
- Глава III. Способ замены неизвестных при решении уравнений
- § 3.1. Алгебраические уравнения
- § 3.2. Рациональные уравнения
- § 3.3. Иррациональные уравнения
- 3.3.3. Сведение решения иррационального уравнения к решению тригонометрического уравнения.
- § 3.4. Уравнения вида
- § 3.5. Решение некоторых уравнений сведением их к решению систем уравнений относительно новых неизвестных
- Глава IV. Решение уравнений и неравенств с использованием свойств входящих в них функций
- § 4.1. Применение основных свойств функций
- 4.1.2. Использование ограниченности функций.
- 4.1.3. Использование монотонности.
- 4.1.4. Использование графиков.
- 4.1.5. Метод интервалов для непрерывных функций.
- § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной
- 4.2.3. Использование ограниченности функций.
- 4.2.4. Использование свойств синуса и косинуса.
- 4.2.5. Использование числовых неравенств.
- § 4.3. Применение производной
- 4.3.2. Использование наибольшего и наименьшего значений функции.
- 4.3.3. Применение теоремы Лагранжа.
- Дополнения