| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 21. О СОБСТВЕННЫХ ВЕКТОРАХ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ С СИММЕТРИЧЕСКОЙ МАТРИЦЕЙ
В § 18—20 мы рассмотрели основные предложения о собственных векторах и собственных значениях. Среди линейных преобразований часто встречаются такие, матрицы которых в некотором базисе симметричны. Для таких преобразований справедливы специфические теоремы о собственных значениях и собственных векторах.
Напомним некоторые свойства комплексных чисел. Если  есть комплексное число, сопряженное числу
есть комплексное число, сопряженное числу  модуль числа
модуль числа  то
то

Для произвольной матрицы А с комплексными элементами через А обозначают матрицу, получающуюся из А заменой всех ее элементов на сопряженные. Из (1) следует, что для произвольных матриц  справедливо:
справедливо:


где а — комплексное число.
Условие вещественности комплексного числа  и матрицы А запишется так:
и матрицы А запишется так: 
Теорема 22. Все собственные значения линейного преобразования  с вещественной симметрической матрицей А вещественны.
с вещественной симметрической матрицей А вещественны.
Доказательство. Пусть  есть линейное пространство над полем комплексных чисел и
есть линейное пространство над полем комплексных чисел и  линейное преобразование в
линейное преобразование в  Пусть, далее, в некотором базисе матрица А преобразования
Пусть, далее, в некотором базисе матрица А преобразования  является симметрической матрицей с вещественными элементами. Рассмотрим любое собственное значение X преобразованияф (X — комплексное число) и соответствующий ему собственный вектор
является симметрической матрицей с вещественными элементами. Рассмотрим любое собственное значение X преобразованияф (X — комплексное число) и соответствующий ему собственный вектор 

Обозначим через

матрицу-столбец комплексных координат вектора х в рассматриваемом базисе. Тогда равенство (4) запишется в виде

Обозначим через  строку координат векторах. Тогда имеет смысл произведение матриц
строку координат векторах. Тогда имеет смысл произведение матриц  Это произведение будет матрицей с одним элементом.
Это произведение будет матрицей с одним элементом.
Используя симметричность матрицы А и соотношение (4), получаем:

Используя вещественность матрицы А и соотношения (2), (3), (4), имеем:

Но  а потому получаем матричное равенство:
а потому получаем матричное равенство:

где  есть матрица из одного числа. Именно:
есть матрица из одного числа. Именно:

причем матрица  не нулевая, поскольку
не нулевая, поскольку 
Перейдя от матричного равенства (5) к числовому и сократив на число  не равное нулю, получим:
не равное нулю, получим:

Значит, к вещественно.
Теорема 23. Пусть линейное преобразование  в некотором базисе задается симметрической матрицей А. Если х и у — два собственных вектора преобразования
в некотором базисе задается симметрической матрицей А. Если х и у — два собственных вектора преобразования  отвечающие различным собственным значениям к и
отвечающие различным собственным значениям к и  координаты этих векторов в рассматриваемом базисе, то
координаты этих векторов в рассматриваемом базисе, то

Доказательство. Сохраняем обозначения:  матрицы-столбцы,
матрицы-столбцы,  матрицы-строки координат. По условию
матрицы-строки координат. По условию  значит,
значит,

Произведение  имеет смысл. Используя симметричность матрицы А, имеем:
имеет смысл. Используя симметричность матрицы А, имеем:

С другой стороны,

Но  а потому
а потому

где  Отсюда
Отсюда

Так как  то из (6) следует
то из (6) следует  Теорема доказана.
Теорема доказана.
Векторы  координаты которых удовлетворяют соотношению
координаты которых удовлетворяют соотношению  впредь будем называть ортогональными. Тогда теорему 23 можно сформулировать так: собственные векторы линейного преобразования с симметрической матрицей, соответствующие различным собственным значениям, ортогональны между собой.
впредь будем называть ортогональными. Тогда теорему 23 можно сформулировать так: собственные векторы линейного преобразования с симметрической матрицей, соответствующие различным собственным значениям, ортогональны между собой.
Пример. Матрицу А линейного преобразования привести, если это возможно, к диагональному виду:

Решение. Замечаем, что матрица А симметрическая. Находим сначала собственные значения, а затем соответствующие им собственные векторы:

Собственные значения:  кратности
кратности  кратности 1.
кратности 1.
Для  отыскание собственных векторов сводится к решению уравнения
отыскание собственных векторов сводится к решению уравнения

Система (7) имеет три линейно независимых решения, например:

Находим собственный вектор для 

Система векторов  линейно независима (свойство 3, § 18); ее можно принять за базис пространства Тк. Так как
линейно независима (свойство 3, § 18); ее можно принять за базис пространства Тк. Так как

то матрица данного линейного преобразования  в базисе
в базисе  принимает диагональную форму:
принимает диагональную форму:

Замечание. Вектор  ортогонален к векторам
ортогонален к векторам  (согласно теореме 23). Но векторы
(согласно теореме 23). Но векторы  вообще говоря, не обязаны получаться попарно ортогональными: они соответствуют одному собственному значению 2. Однако и для 2 можно найти попарно ортогональные собственные векторы
вообще говоря, не обязаны получаться попарно ортогональными: они соответствуют одному собственному значению 2. Однако и для 2 можно найти попарно ортогональные собственные векторы

Действительно, собственные векторы, соответствующие  находятся из уравнения (7). В качестве первого собственного вектора
находятся из уравнения (7). В качестве первого собственного вектора  возьмем, например,
возьмем, например,

Второй собственный вектор  найдем из условия ортогональности
найдем из условия ортогональности  Для этого, кроме (7), должно быть
Для этого, кроме (7), должно быть 

Из системы уравнений (7) и (8) находим:

Для отыскания третьего собственного вектора  добавляем к уравнению (7) условия ортогональности вектора
добавляем к уравнению (7) условия ортогональности вектора  к векторам
к векторам  т. е. уравнения
т. е. уравнения

Из системы уравнений (7), (8), (9) находим:

Таким образом, попарно ортогональными собственными векторами данного преобразования  являются:
являются:

Упражнения
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Глава I. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- § 2. ПРОСТЕЙШИЕ СВОЙСТВА ЛИНЕЙНЫХ ПРОСТРАНСТВ
- § 3. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- § 4. БАЗИС ЛИНЕЙНОГО ПРОСТРАНСТВА. КООРДИНАТЫ ВЕКТОРА ОТНОСИТЕЛЬНО БАЗИСА
- § 5. РАЗМЕРНОСТЬ ЛИНЕЙНОГО ПРОСТРАНСТВА
- § 6. ИЗОМОРФИЗМ ЛИНЕЙНЫХ ПРОСТРАНСТВ
- § 7. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ВЕКТОРА ПРИ ИЗМЕНЕНИИ БАЗИСА
- § 8. ПОДПРОСТРАНСТВА ЛИНЕЙНОГО ПРОСТРАНСТВА
- § 9. ЛИНЕЙНАЯ ОБОЛОЧКА ИЛИ ПОДПРОСТРАНСТВО, НАТЯНУТОЕ НА ДАННУЮ СИСТЕМУ ВЕКТОРОВ
- § 10. ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ ОДНОРОДНОЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 11. ЛИНЕЙНОЕ МНОГООБРАЗИЕ. ЛИНЕЙНОЕ МНОГООБРАЗИЕ РЕШЕНИЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- Глава II. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
- § 12. ПОНЯТИЕ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ МАТРИЦЕЙ
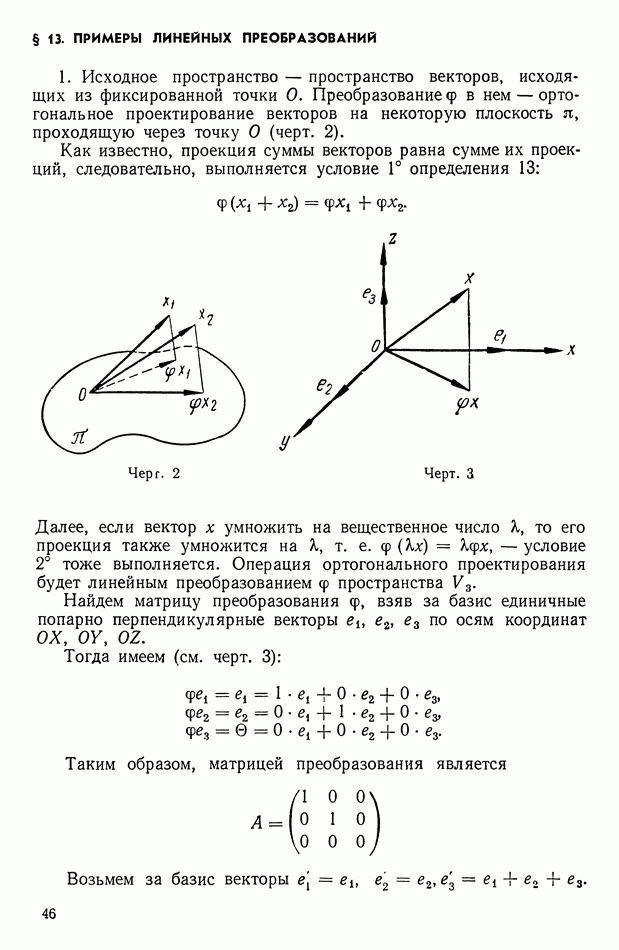
- § 13. ПРИМЕРЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ
- § 14. СВЯЗЬ МЕЖДУ МАТРИЦАМИ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ В РАЗЛИЧНЫХ БАЗИСАХ
- § 15. ДЕЙСТВИЯ НАД ЛИНЕЙНЫМИ ПРЕОБРАЗОВАНИЯМИ И МАТРИЦАМИ. КОЛЬЦО ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ И КОЛЬЦО МАТРИЦ
- § 16. ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ. ВЫРОЖДЕННЫЕ И НЕВЫРОЖДЕННЫЕ ПРЕОБРАЗОВАНИЯ. РАНГ И ЯДРО ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- § 17. ОБ ИНВАРИАНТНЫХ ПОДПРОСТРАНСТВАХ И ИНДУЦИРОВАННЫХ ПРЕОБРАЗОВАНИЯХ
- § 18. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- § 19. ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН МАТРИЦЫ И ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. СУЩЕСТВОВАНИЕ СОБСТВЕННЫХ ВЕКТОРОВ
- § 20. О ПРИВЕДЕНИИ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ К ДИАГОНАЛЬНОЙ ФОРМЕ
- § 21. О СОБСТВЕННЫХ ВЕКТОРАХ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ С СИММЕТРИЧЕСКОЙ МАТРИЦЕЙ
- Глава III. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- § 22. ПОНЯТИЕ ЕВКЛИДОВА ПРОСТРАНСТВА. ПРИМЕРЫ
- § 23. ДЛИНА ВЕКТОРА. УГОЛ МЕЖДУ ВЕКТОРАМИ. НЕРАВЕНСТВО КОШИ—БУНЯКОВСКОГО
- § 24. ПОНЯТИЕ МЕТРИЧЕСКОГО ПРОСТРАНСТВА
- § 25. ОРТОГОНАЛЬНОСТЬ ВЕКТОРОВ. ОРТОНОРМИРОВАННЫЙ БАЗИС. ОРТОГОНАЛЬНО-ДОПОЛНИТЕЛЬНОЕ ПОДПРОСТРАНСТВО
- § 26. ИЗОМОРФИЗМ ЕВКЛИДОВЫХ ПРОСТРАНСТВ
- § 27. ОРТОГОНАЛЬНЫЕ МАТРИЦЫ
- § 28. ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА
- § 29. СИММЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА
- § 30. ПРЕДСТАВЛЕНИЕ НЕВЫРОЖДЕННОГО ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА В ВИДЕ ПРОИЗВЕДЕНИЯ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ НА СИММЕТРИЧЕСКОЕ
- § 31. ТЕОРЕМА О ТРАНСФОРМИРОВАНИИ СИММЕТРИЧЕСКОЙ МАТРИЦЫ В ДИАГОНАЛЬНУЮ МАТРИЦУ С ПОМОЩЬЮ ОРТОГОНАЛЬНОЙ
- Глава IV. КВАДРАТИЧНЫЕ ФОРМЫ
- § 32. ПОНЯТИЕ КВАДРАТИЧНОЙ ФОРМЫ
- § 33. ПРЕОБРАЗОВАНИЕ МАТРИЦЫ КВАДРАТИЧНОЙ ФОРМЫ ПРИ ЛИНЕЙНОЙ ЗАМЕНЕ ПЕРЕМЕННЫХ. КАНОНИЧЕСКИЙ ВИД КВАДРАТИЧНОЙ ФОРМЫ
- § 34. ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ
- § 35. НАХОЖДЕНИЕ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ, ПРИВОДЯЩЕГО ВЕЩЕСТВЕННУЮ КВАДРАТИЧНУЮ ФОРМУ К КАНОНИЧЕСКОМУ ВИДУ
- § 36. МЕТОД ЛАГРАНЖА ПРИВЕДЕНИЯ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ
- § 37. ЗАКОН ИНЕРЦИИ КВАДРАТИЧНЫХ ФОРМ
- § 38. ЭКВИВАЛЕНТНОСТЬ ВЕЩЕСТВЕННЫХ КВАДРАТИЧНЫХ ФОРМ
- § 39. ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ