| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 25. ОРТОГОНАЛЬНОСТЬ ВЕКТОРОВ. ОРТОНОРМИРОВАННЫЙ БАЗИС. ОРТОГОНАЛЬНО-ДОПОЛНИТЕЛЬНОЕ ПОДПРОСТРАНСТВО
Определение 28. Векторы х и у евклидова пространства  называются ортогональными, если их скалярное произведение равно нулю, т. е. если
называются ортогональными, если их скалярное произведение равно нулю, т. е. если

Согласно определению 27 угол между ненулевыми ортогональными векторами равен 
Таким образом, понятие ортогональности является естественным обобщением понятия перпендикулярности. Поэтому для обозначения ортогональности векторов используют знак 
Если  то
то  т. е. нулевой вектор оказывается ортогональным к любому вектору.
т. е. нулевой вектор оказывается ортогональным к любому вектору.
Из аксиомы 13° следует, что если  то и
то и  т. е. ортогональность двух векторов сохраняется при умножении любого из них на произвольное вещественное число.
т. е. ортогональность двух векторов сохраняется при умножении любого из них на произвольное вещественное число.
Упражнения
(см. скан)
(см. скан)
Отметим два свойства ортогональности векторов. Свойство 1. Любая система ненулевых попарно ортогональных векторов

линейно независима.
Допустим, что система (3) линейно зависима. Тогда существуют не равные одновременно нулю числа  такие, что
такие, что

Не нарушая общности, положим  Умножив обе части (4) скалярно на
Умножив обе части (4) скалярно на  и учитывая ортогональность вектора к остальным, получим, что
и учитывая ортогональность вектора к остальным, получим, что

откуда, в силу  следует, что
следует, что  Отсюда по аксиоме, 14° получаем
Отсюда по аксиоме, 14° получаем  что противоречит условию. Следовательно, допущение о линейной зависимости системы (3) неверно.
что противоречит условию. Следовательно, допущение о линейной зависимости системы (3) неверно.
Свойство 2. Если вектор  ортогонален к каждому из векторов
ортогонален к каждому из векторов

то он ортогонален к каждому из векторов линейного подпространства  натянутого на векторы
натянутого на векторы 
В самом деле, пусть  где
где  произвольные вещественные числа. Согласно условию и аксиомам
произвольные вещественные числа. Согласно условию и аксиомам  имеем:
имеем:

Свойство 2 является обобщением на любое евклидово пространство теоремы о двух перпендикулярах из элементарной геометрии (сделайте чертеж). Говорят, что вектор  ортогонален к подпространству
ортогонален к подпространству  и пишут
и пишут  если
если  где
где  -любой вектор из
-любой вектор из 
Упражнение
(см. скан)
Определение 29. Векторы  отличные от нулевого, образуют ортогональный базис
отличные от нулевого, образуют ортогональный базис  -мерного евклидова пространства, если они попарно ортогональны.
-мерного евклидова пространства, если они попарно ортогональны.
Определение 30. Векторы  евклидова пространства размерности
евклидова пространства размерности  образуют ортонормированный базис, если они попарно ортогональны и каждый имеет длину, равную 1, т. е. если
образуют ортонормированный базис, если они попарно ортогональны и каждый имеет длину, равную 1, т. е. если

Существование ортогональных базисов доказывается конструктивно с помощью так называемого процесса ортогонализации.
Теорема 24. Во всяком  -мерном евклидовом пространстве
-мерном евклидовом пространстве  существуют ортогональные (а также и ортонормированные) базисы.
существуют ортогональные (а также и ортонормированные) базисы.
Доказательство. По условию в пространстве  имеется некоторый базис, состоящий из векторов
имеется некоторый базис, состоящий из векторов

Будем строить новый, ортогональный базис  Положим:
Положим:

Вектор  будем искать в виде
будем искать в виде

Вещественный множитель  подбираем так, чтобы было
подбираем так, чтобы было  (Из чертежа 5 видно, какими соображениями следует руководствоваться при подборе
(Из чертежа 5 видно, какими соображениями следует руководствоваться при подборе 
Алгебраически выбор  производится так. Должно быть
производится так. Должно быть  т. е.
т. е.


Черт. 5
Отсюда однозначно находим:

Заметим, что  иначе было бы
иначе было бы  что означает линейную зависимость системы векторов
что означает линейную зависимость системы векторов 
Если  то процесс окончен. Если
то процесс окончен. Если  то, построив и
то, построив и  ищем
ищем  в форме
в форме

где  находим из условий
находим из условий  . А именно, из
. А именно, из  следует:
следует:

откуда

Аналогично из  находим:
находим:

В результате имеем:

откуда следует, что 
Если  то процесс окончен, в противном случае продолжаем его. Если уже построены векторы
то процесс окончен, в противном случае продолжаем его. Если уже построены векторы  то вектор
то вектор  ищем в форме
ищем в форме

где коэффициенты  находим из условия
находим из условия 
Получим:

Этот процесс носит название процесса ортогонализации. Он продолжается до исчерпания векторов базиса  Полученные векторы
Полученные векторы  по построению попарно ортогональны и отличны от нулевого, следовательно, они образуют ортогональный базис.
по построению попарно ортогональны и отличны от нулевого, следовательно, они образуют ортогональный базис.
Для получения ортонормированного базиса остается нормировать векторы 
Из теоремы 8 следует, что любой вектор  можно включить в состав базиса линейного пространства
можно включить в состав базиса линейного пространства  Заметим, что и в теореме 24 доказано также нечто большее, чем в ней
Заметим, что и в теореме 24 доказано также нечто большее, чем в ней
утверждалось, а именно: любой вектор  длины 1 можно дополнить до ортонормированного базиса пространства
длины 1 можно дополнить до ортонормированного базиса пространства 
Следующая теорема показывает значение ортонормированных базисов в определении скалярного произведения.
Теорема 25. 1) В ортонормированном базисе евклидова пространства скалярное произведение любых двух векторов равно сумме произведений соответствующих координат:

где и  координаты векторов х и у в указанном базисе.
координаты векторов х и у в указанном базисе.
2) Обратно, если в некотором базисе  евклидова пространства
евклидова пространства  скалярное произведение любых двух векторов
скалярное произведение любых двух векторов  задается формулой (5), то этот базис является ортонормированным.
задается формулой (5), то этот базис является ортонормированным.
Доказательство. 1) Пусть  ортонормированный базис пространства
ортонормированный базис пространства  так что
так что

По аксиомам  для векторов
для векторов

будем иметь выражение скалярного произведения в координатах в общем виде:

Учитывая условие ортонормированности векторов базиса, получаем наиболее простой вид для выражения скалярного произведения:

2) Пусть теперь в некотором базисе  для произвольных векторов
для произвольных векторов

имеет место (5):

Применим эту формулу для базисных векторов. Так как

то

Следовательно, векторы нашего базиса ортонормированы.
Упражнения
(см. скан)
В качестве дополнения к свойству 2 ортогональных векторов докажем теперь, что совокупность  векторов пространства
векторов пространства  ортогональных ненулевому вектору
ортогональных ненулевому вектору  есть подпространство размерности
есть подпространство размерности 
Выберем ортогональный базис пространства Ею содержащий вектор  Значит,
Значит,

а потому

Пусть  произвольный вектор пространства
произвольный вектор пространства 

Потребуем, чтобы  Тогда
Тогда  т. е.
т. е.

Отсюда  а потому
а потому 
Таким образом, любой вектор  линейно выражается через векторы
линейно выражается через векторы  А так как последние линейно независимы, то по определению 4 они составляют базис пространства
А так как последние линейно независимы, то по определению 4 они составляют базис пространства  Следовательно, по теореме
Следовательно, по теореме 
Определение 31. Ортогональным дополнением подпространства  пространства
пространства  называется совокупность
называется совокупность  всех векторов из
всех векторов из  ортогональных к
ортогональных к 
Докажем, что  является подпространством пространства
является подпространством пространства  Пусть
Пусть  Это означает, что если х — произвольный вектор из
Это означает, что если х — произвольный вектор из  то
то  и потому
и потому

Следовательно,  Кроме того, для произвольного вещественного числа а и любого
Кроме того, для произвольного вещественного числа а и любого  имеем:
имеем:

Следовательно,  По теореме 7 получаем, что
По теореме 7 получаем, что  подпространство.
подпространство.
Тот факт, что подпространство  названо дополнением подпространства
названо дополнением подпространства  объясняется следующей теоремой.
объясняется следующей теоремой.
Теорема 26. Пространство  есть прямая сумма подпространств
есть прямая сумма подпространств 
Доказательство. Согласно определению 8 достаточно доказать, что  Пусть
Пусть  Тогда по определению пространства
Тогда по определению пространства  Отсюда по аксиоме
Отсюда по аксиоме 
Таким образом,  Покажем, теперь, что
Покажем, теперь, что  Пусть
Пусть  ортогональный базис пространства
ортогональный базис пространства  Дополним этот базис до базиса всего пространства
Дополним этот базис до базиса всего пространства  векторами
векторами  После выполнения ортогонализации получим ортогональный базис
После выполнения ортогонализации получим ортогональный базис

пространства  Тогда при
Тогда при  будем иметь
будем иметь  Следовательно,
Следовательно, 
Пусть  любой вектор из
любой вектор из  и
и

Так как 

Упражнения
[7], № 1366, 1367.
Пусть  линейное подпространство пространства
линейное подпространство пространства  Докажем, что любой вектор х из
Докажем, что любой вектор х из  однозначно представляется в виде
однозначно представляется в виде  где
где  Вектор у называется ортогональной проекцией вектора на подпространство
Вектор у называется ортогональной проекцией вектора на подпространство  ортогональной составляющей вектора относительно
ортогональной составляющей вектора относительно 
Пусть  некоторый базис подпространства
некоторый базис подпространства  Будем искать вектор у, требуемый задачей в виде
Будем искать вектор у, требуемый задачей в виде

где числа  найдем из условия ортогональности вектора
найдем из условия ортогональности вектора 
Из  следует, что
следует, что  а отсюда
а отсюда

Таким образом, получаем систему для отыскания чисел 

Если базис  ортонормален, то система (7) обращается в систему
ортонормален, то система (7) обращается в систему

откуда находятся и притом однозначно коэффициенты 
Так как базис всегда можно ортонормировать, а исходное условие  не зависит от базиса, то тем самым доказано существование и единственность вектора у, такого, что
не зависит от базиса, то тем самым доказано существование и единственность вектора у, такого, что 
Отсюда следует, что при произвольном базисе  определитель системы (7)
определитель системы (7)

отличен от нуля (так называемый определитель Грама векторов 
Таким образом, числа  находим из системы (7), а затем по формуле (6) и сам вектор у. Найдя вектор у, полагаем
находим из системы (7), а затем по формуле (6) и сам вектор у. Найдя вектор у, полагаем  .
.
Пример. Найти ортогональную проекцию у и ортогональную составляющую  вектора
вектора  на линейное пространство
на линейное пространство  натянутое на векторы
натянутое на векторы

Решение. Система векторов  базис
базис  Пусть
Пусть

Так как

то система (7) принимает вид:

отсюда получаем: 

Упражнения
[7], № 1370—1372; [10], № 906.
Расстоянием от вектора х до линейного многообразия  называется минимум расстояний от данного вектора до векторов многообразия, т. е. минимум длин векторов
называется минимум расстояний от данного вектора до векторов многообразия, т. е. минимум длин векторов  и, где
и, где  вектор из
вектор из 
Докажем, что указанное расстояние равно длине ортогональной составляющей  векторов
векторов  относительно линейного подпространства
относительно линейного подпространства 
Пусть  где у — ортогональная проекция вектора
где у — ортогональная проекция вектора  на
на  его ортогональная составляющая относительно
его ортогональная составляющая относительно  так что
так что 
Имеем:

Здесь  а потому
а потому

Так как первое слагаемое не зависит от и, то  достигается при
достигается при  который равен нулю (при
который равен нулю (при  Следовательно,
Следовательно,

что и требовалось доказать.
Упражнение
[7], № 1374.
Теперь докажем, что из всех векторов линейного подпространства  наименьший угол с данным вектором
наименьший угол с данным вектором  образует ортогональная проекция у вектора
образует ортогональная проекция у вектора  на
на 
Пусть  где у и 2 имеют тот же смысл, что и выше. Тогда
где у и 2 имеют тот же смысл, что и выше. Тогда

а поэтому

Пусть теперь у — произвольный вектор из  Учитывая, что
Учитывая, что

получаем:

что и доказывает утверждение.
Угол между вектором х и его ортогональной проекцией на подпространство  называется углом между
называется углом между 
Упражнения
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Глава I. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- § 2. ПРОСТЕЙШИЕ СВОЙСТВА ЛИНЕЙНЫХ ПРОСТРАНСТВ
- § 3. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- § 4. БАЗИС ЛИНЕЙНОГО ПРОСТРАНСТВА. КООРДИНАТЫ ВЕКТОРА ОТНОСИТЕЛЬНО БАЗИСА
- § 5. РАЗМЕРНОСТЬ ЛИНЕЙНОГО ПРОСТРАНСТВА
- § 6. ИЗОМОРФИЗМ ЛИНЕЙНЫХ ПРОСТРАНСТВ
- § 7. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ВЕКТОРА ПРИ ИЗМЕНЕНИИ БАЗИСА
- § 8. ПОДПРОСТРАНСТВА ЛИНЕЙНОГО ПРОСТРАНСТВА
- § 9. ЛИНЕЙНАЯ ОБОЛОЧКА ИЛИ ПОДПРОСТРАНСТВО, НАТЯНУТОЕ НА ДАННУЮ СИСТЕМУ ВЕКТОРОВ
- § 10. ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ ОДНОРОДНОЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 11. ЛИНЕЙНОЕ МНОГООБРАЗИЕ. ЛИНЕЙНОЕ МНОГООБРАЗИЕ РЕШЕНИЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- Глава II. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
- § 12. ПОНЯТИЕ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ МАТРИЦЕЙ
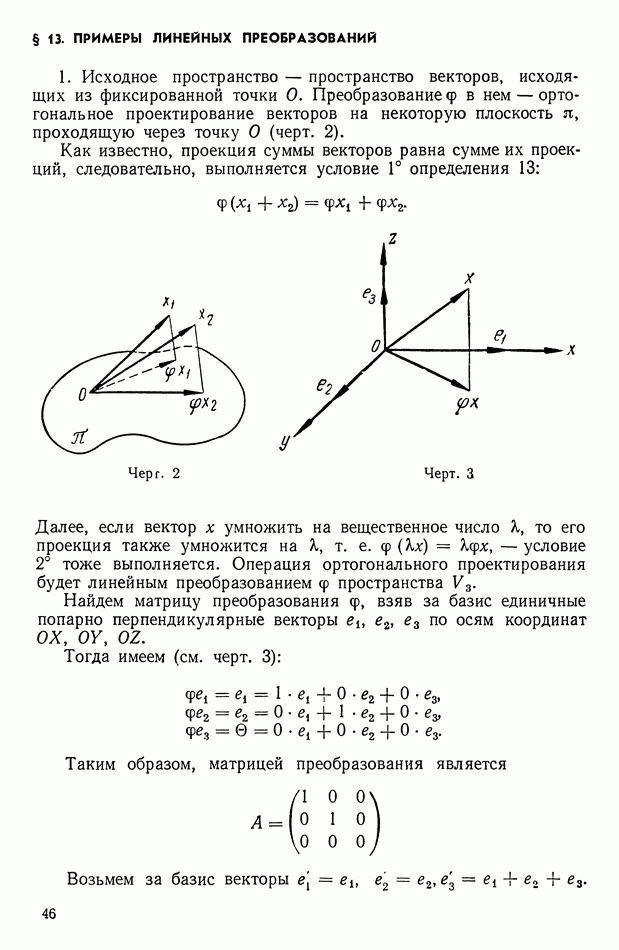
- § 13. ПРИМЕРЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ
- § 14. СВЯЗЬ МЕЖДУ МАТРИЦАМИ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ В РАЗЛИЧНЫХ БАЗИСАХ
- § 15. ДЕЙСТВИЯ НАД ЛИНЕЙНЫМИ ПРЕОБРАЗОВАНИЯМИ И МАТРИЦАМИ. КОЛЬЦО ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ И КОЛЬЦО МАТРИЦ
- § 16. ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ. ВЫРОЖДЕННЫЕ И НЕВЫРОЖДЕННЫЕ ПРЕОБРАЗОВАНИЯ. РАНГ И ЯДРО ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- § 17. ОБ ИНВАРИАНТНЫХ ПОДПРОСТРАНСТВАХ И ИНДУЦИРОВАННЫХ ПРЕОБРАЗОВАНИЯХ
- § 18. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- § 19. ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН МАТРИЦЫ И ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. СУЩЕСТВОВАНИЕ СОБСТВЕННЫХ ВЕКТОРОВ
- § 20. О ПРИВЕДЕНИИ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ К ДИАГОНАЛЬНОЙ ФОРМЕ
- § 21. О СОБСТВЕННЫХ ВЕКТОРАХ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ С СИММЕТРИЧЕСКОЙ МАТРИЦЕЙ
- Глава III. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- § 22. ПОНЯТИЕ ЕВКЛИДОВА ПРОСТРАНСТВА. ПРИМЕРЫ
- § 23. ДЛИНА ВЕКТОРА. УГОЛ МЕЖДУ ВЕКТОРАМИ. НЕРАВЕНСТВО КОШИ—БУНЯКОВСКОГО
- § 24. ПОНЯТИЕ МЕТРИЧЕСКОГО ПРОСТРАНСТВА
- § 25. ОРТОГОНАЛЬНОСТЬ ВЕКТОРОВ. ОРТОНОРМИРОВАННЫЙ БАЗИС. ОРТОГОНАЛЬНО-ДОПОЛНИТЕЛЬНОЕ ПОДПРОСТРАНСТВО
- § 26. ИЗОМОРФИЗМ ЕВКЛИДОВЫХ ПРОСТРАНСТВ
- § 27. ОРТОГОНАЛЬНЫЕ МАТРИЦЫ
- § 28. ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА
- § 29. СИММЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА
- § 30. ПРЕДСТАВЛЕНИЕ НЕВЫРОЖДЕННОГО ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА В ВИДЕ ПРОИЗВЕДЕНИЯ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ НА СИММЕТРИЧЕСКОЕ
- § 31. ТЕОРЕМА О ТРАНСФОРМИРОВАНИИ СИММЕТРИЧЕСКОЙ МАТРИЦЫ В ДИАГОНАЛЬНУЮ МАТРИЦУ С ПОМОЩЬЮ ОРТОГОНАЛЬНОЙ
- Глава IV. КВАДРАТИЧНЫЕ ФОРМЫ
- § 32. ПОНЯТИЕ КВАДРАТИЧНОЙ ФОРМЫ
- § 33. ПРЕОБРАЗОВАНИЕ МАТРИЦЫ КВАДРАТИЧНОЙ ФОРМЫ ПРИ ЛИНЕЙНОЙ ЗАМЕНЕ ПЕРЕМЕННЫХ. КАНОНИЧЕСКИЙ ВИД КВАДРАТИЧНОЙ ФОРМЫ
- § 34. ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ
- § 35. НАХОЖДЕНИЕ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ, ПРИВОДЯЩЕГО ВЕЩЕСТВЕННУЮ КВАДРАТИЧНУЮ ФОРМУ К КАНОНИЧЕСКОМУ ВИДУ
- § 36. МЕТОД ЛАГРАНЖА ПРИВЕДЕНИЯ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ
- § 37. ЗАКОН ИНЕРЦИИ КВАДРАТИЧНЫХ ФОРМ
- § 38. ЭКВИВАЛЕНТНОСТЬ ВЕЩЕСТВЕННЫХ КВАДРАТИЧНЫХ ФОРМ
- § 39. ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ