| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
Манометрические упругие элементы — трубчатые пружины, сильфоны, мембраны — выполняются в виде тонкостенных оболочек, деформирующихся под действием давления. Они несут функции упругих преобразователей давления во многих манометрических приборах.
Если манометрический упругий элемент преобразует давление в перемещение, то одним из основных его показателей является упругая характеристика — зависимость между перемещением (ходом) упругого элемента и давлением.
В некоторых приборах, например, в тех, где используется принцип силовой компенсации, давление  преобразуется манометрическим упругим элементом в усилие
преобразуется манометрическим упругим элементом в усилие  при этом ход упругого элемента практически равен нулю. В подобном случае важным параметром манометрического элемента является его эффективная площадь
при этом ход упругого элемента практически равен нулю. В подобном случае важным параметром манометрического элемента является его эффективная площадь  т. е. та часть площади упругого элемента, произведение которой на давление дает величину усилия
т. е. та часть площади упругого элемента, произведение которой на давление дает величину усилия 
Одним из основных критериев качества измерительного упругого элемента является точность, с которой производится преобразование измеряемого параметра. Погрешности упругого элемента связаны главным образом с несовершенством упругих свойств материала, которое является причиной гистерезиса, упругого последействия, ползучести манометрического элемента.
В условиях переменной температуры изменение модуля упругости материала и линейных размеров манометрического элемента приводят к его температурной погрешности.
Сведения о материалах для упругих элементов даны работе [16].
Манометрические трубчатые пружины. Манометрическая трубчатая пружина представляет собой тонкостенную кривую трубку вытянутого поперечного сечения (рис. XV.9, а). При подаче давления во внутреннюю полость трубки ее поперечное сечение деформируется, принимая форму, показанную штриховой линией на рис. XV.9, б. При этом продольное волокно а - а трубки переходит на дугу большого радиуса, а волокно b - b на дугу меньшего радиуса. Поскольку волокна стремятся сохранить свою первоначальную длину, поперечные сечения трубки будут поворачиваться
против часовой стрелки (рис. XV.9, в), пружина разгибается, а ее конец получит некоторое перемещение X.
Чаще всего трубчатые пружины выполняются в виде одновитковых — пружин Бурдона. При требованиях больших перемещений используются многовитковые пружины: винтовые, спиральные и  -образные (рис. XV. 10).
-образные (рис. XV. 10).
Пружина Бурдона является наиболее распространенным типом манометрических упругих элементов. Ее применяют в показывающих, регистрирующих и регулирующих манометрах, в термометрах, вакуумметрах, уровнемерах, расходомерах и в других манометрических приборах.
На рис. XV. 11 изображены формы поперечных сечений трубчатых пружин. Самыми распространенными формами являются плоскоовальная, эллиптическая и  -образная (рис. XV. 11, а — в).
-образная (рис. XV. 11, а — в).

Рис. XV.9. Пружина Бурдона: а — схема; б — деформация сечения трубки; в — деформация элемента трубки

Рис. XV. 10. Разновидности манометрических трубчатых пружин: а — винтовая; б — спиральная; в — S-образная
Пружина эллиптического сечения обладает большей чувствительностью. Трубки с формой сечения, показанной на рис. XV. 11, г, имеют минимальный начальный объем и используются в манометрических термометрах. Форма сечения, изображенная на рис. XV. 11, д обеспечивает пружине повышенную прочность.
Для измерения высоких давлений (порядка тысяч и десятков тысяч  применяется специальная конструкция трубчатых пружин, перемещения которых под действием давления происходят не вследствие деформации поперечного сечения, как в пружине Бурдона, а в результате появления изгибающего момента, обусловленного эксцентрисистетом внутреннего отверстия относительно наружного контура поперечного сечения (рис. XV, 11, е).
применяется специальная конструкция трубчатых пружин, перемещения которых под действием давления происходят не вследствие деформации поперечного сечения, как в пружине Бурдона, а в результате появления изгибающего момента, обусловленного эксцентрисистетом внутреннего отверстия относительно наружного контура поперечного сечения (рис. XV, 11, е).
В приборах высокого давления (порядка сотен  применяются витые трубчатые пружины, представляющие собой закрученную трубку (рис. XV. 12). Принцип работы витой пружины, как и пружины Бурдона, основан на деформации поперечного сечения под действием давления.
применяются витые трубчатые пружины, представляющие собой закрученную трубку (рис. XV. 12). Принцип работы витой пружины, как и пружины Бурдона, основан на деформации поперечного сечения под действием давления.
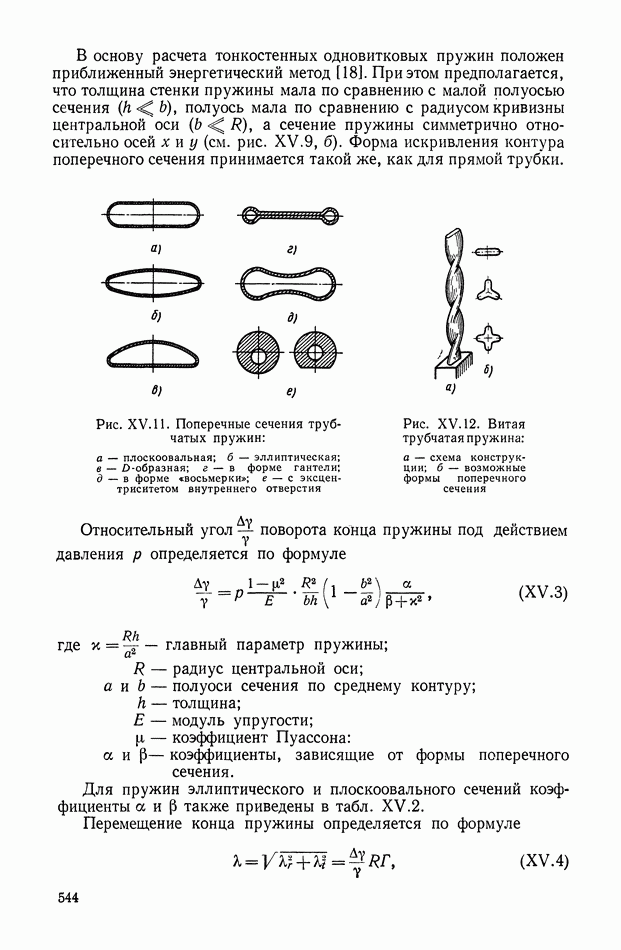
В основу расчета тонкостенных одновитковых пружин положен приближенный энергетический метод [18]. При этом предполагается, что толщина стенки пружины мала по сравнению с малой полуосью сечения  полуось мала по сравнению с радиусом кривизны центральной оси
полуось мала по сравнению с радиусом кривизны центральной оси  а сечение пружины симметрично относительно осей х и у (см. рис. XV.9, б). Форма искривления контура поперечного сечения принимается такой же, как для прямой трубки.
а сечение пружины симметрично относительно осей х и у (см. рис. XV.9, б). Форма искривления контура поперечного сечения принимается такой же, как для прямой трубки.

Рис.  Поперечные сечения трубчатых пружин: а — плоскоовальная; б — эллиптическая; в — D-образная; г — в форме гантели; д — в форме «восьмерки»; е — с эксцентриситетом внутреннего отверстия
Поперечные сечения трубчатых пружин: а — плоскоовальная; б — эллиптическая; в — D-образная; г — в форме гантели; д — в форме «восьмерки»; е — с эксцентриситетом внутреннего отверстия

Рис. XV. 12. Витая трубчатая пружина: а — схема конструкции; б — возможные формы поперечного сечения
Относительный угол  поворота конца пружины под действием давления
поворота конца пружины под действием давления  определяется по формуле
определяется по формуле

где  — главный параметр пружины;
— главный параметр пружины;
R — радиус центральной оси;
 — полуоси сечения по среднему контуру;
— полуоси сечения по среднему контуру;
 — толщина;
— толщина;
Е — модуль упругости;
 — коэффициент Пуассона:
— коэффициент Пуассона:
 коэффициенты, зависящие от формы поперечного сечения.
коэффициенты, зависящие от формы поперечного сечения.
Для пружин эллиптического и плоскоовального сечений коэффициенты  также приведены в табл. XV.2.
также приведены в табл. XV.2.
Перемещение конца пружины определяется по формуле

где  радиальная составляющая;
радиальная составляющая;
 — перемещение в направлении касательной;
— перемещение в направлении касательной;

Изменение объема внутренней полости пружины в зависимости от давления  выражается формулой
выражается формулой

 или через перемещение X конца пружины
или через перемещение X конца пружины

Значения коэффициента  приведены в табл. XV.2.
приведены в табл. XV.2.
Если конец пружины Бурдона закрепить неподвижно и подать в нее давление, то момент, с которым она будет воздействовать на заделку, равен величине тягового момента:

Коэффициенты  и I даны в табл. XV.2.
и I даны в табл. XV.2.
Если конец пружины Бурдона может поворачиваться и перемещаться в радиальном направлении, а перемещение в окружном направлении невозможно, то тяговая сила

Тяговая сила при ограничении перемещения конца пружины в радиальном направлении

Коэффициенты  определяются выражениями
определяются выражениями

В трубчатой пружине, нагруженной давлением, возникает двухосное напряженное состояние. Распределение напряжений вдоль контура поперечного сечения довольно сложно, и положение опасной точки может быть в различных местах в зависимости от соотношения размеров пружины. Для пружин плоскоовального сечения с отношением осей  и при главном параметре
и при главном параметре

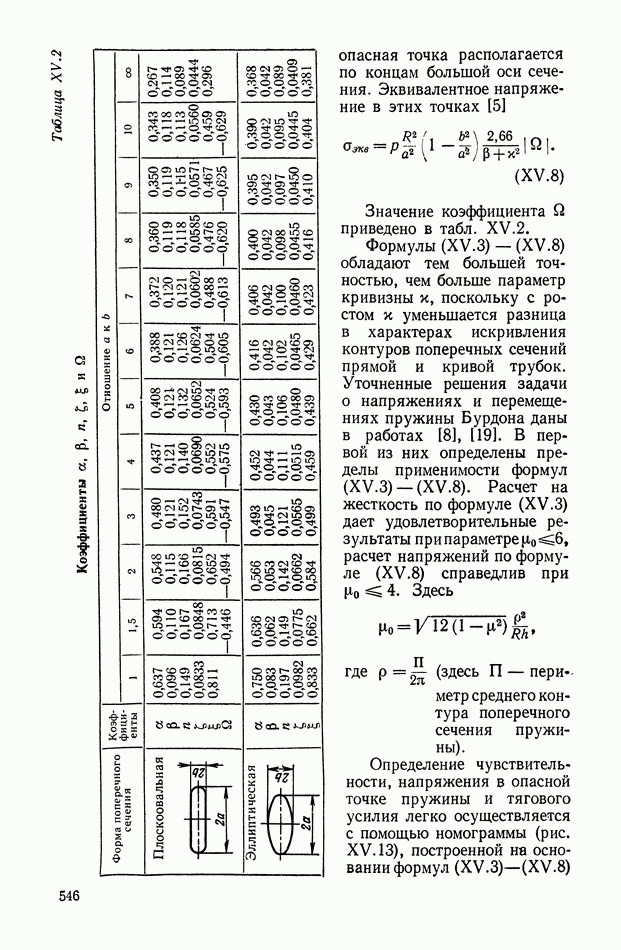
Таблица XV.2 (см. скан) Коэффициенты 
опасная точка располагается по концам большой оси сечения. Эквивалентное напряжение в этих точках [5]

Значение коэффициента  приведено в табл. XV.2.
приведено в табл. XV.2.
Формулы (XV.3) — (XV.8) обладают тем большей точностью, чем больше параметр кривизны к, поскольку с ростом х уменьшается разница в характерах искривления контуров поперечных сечений прямой и кривой трубок. Уточненные решения задачи о напряжениях и перемещениях пружины Бурдона даны в работах [8], [19]. В первой из них определены пределы применимости формул (XV.3) — (XV.8). Расчет на жесткость по формуле (XV.3) дает удовлетворительные результаты при параметре  расчет напряжений по формуле (XV.8) справедлив при
расчет напряжений по формуле (XV.8) справедлив при  Здесь
Здесь

где  (здесь П — периметр среднего контура поперечного сечения пружины).
(здесь П — периметр среднего контура поперечного сечения пружины).
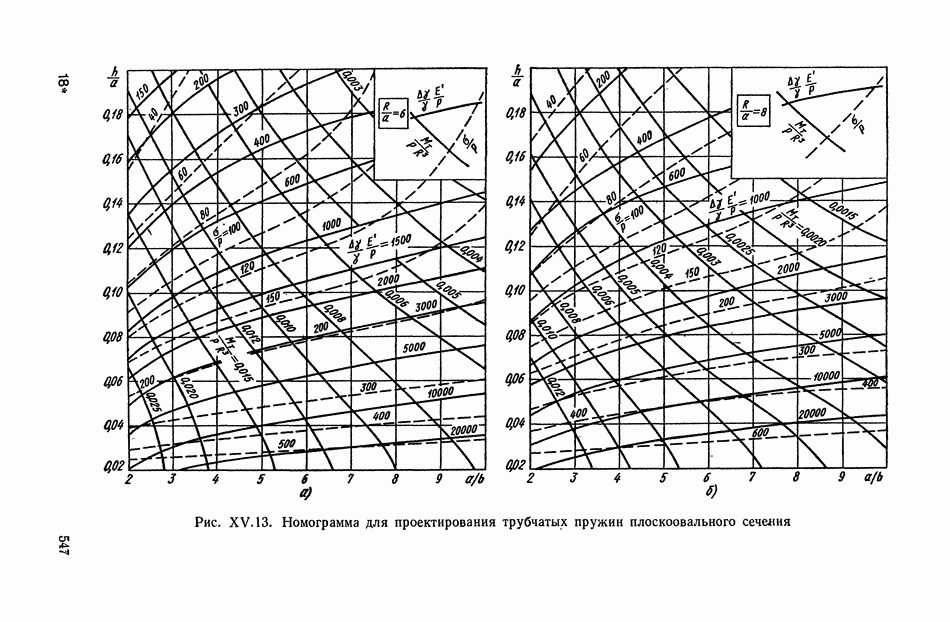
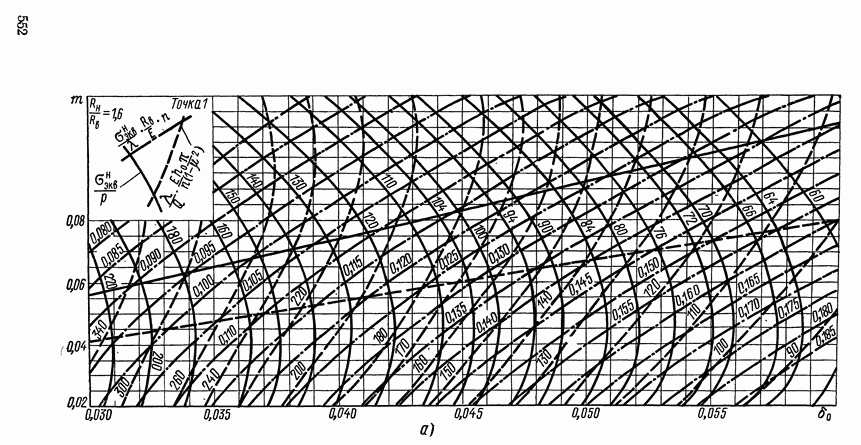
Определение чувствительности, напряжения в опасной точке пружины и тягового усилия легко осуществляется с помощью номограммы (рис. XV. 13), построенной на основании формул 

(кликните для просмотра скана)
для пружин плоскоовальной формы поперечного сечения при  .
.
В координатах  построены три семейства кривых: постоянной чувствительности
построены три семейства кривых: постоянной чувствительности  напряжений
напряжений  и тягового момента
и тягового момента  Здесь
Здесь  — относительный угол поворота концевого сечения;
— относительный угол поворота концевого сечения;  упругая постоянная материала; через а обозначено наибольшее эквивалентное напряжение
упругая постоянная материала; через а обозначено наибольшее эквивалентное напряжение  — тяговый момент.
— тяговый момент.
Если размеры пружины известны, то с помощью номограммы можно легко провести поверочный расчет. Номограмма может также служить целям проектирования трубчатой пружины.
Пример. Определить перемещение X, тяговую силу  и запас прочности трубчатой пружины манометра на
и запас прочности трубчатой пружины манометра на  если размеры пружины известны:
если размеры пружины известны:  , сечение имеет плоскоовальную форму. Материал пружины — сплав
, сечение имеет плоскоовальную форму. Материал пружины — сплав  модуль упругости
модуль упругости  предел текучести
предел текучести 
Определим сначала относительные размеры пружины

Затем, по номограмме (рис. XV. 19, а) находим

откуда в соответствии с выражениями (XV.4) и (XV.7) получим 
Запас прочности пружины будет равен

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
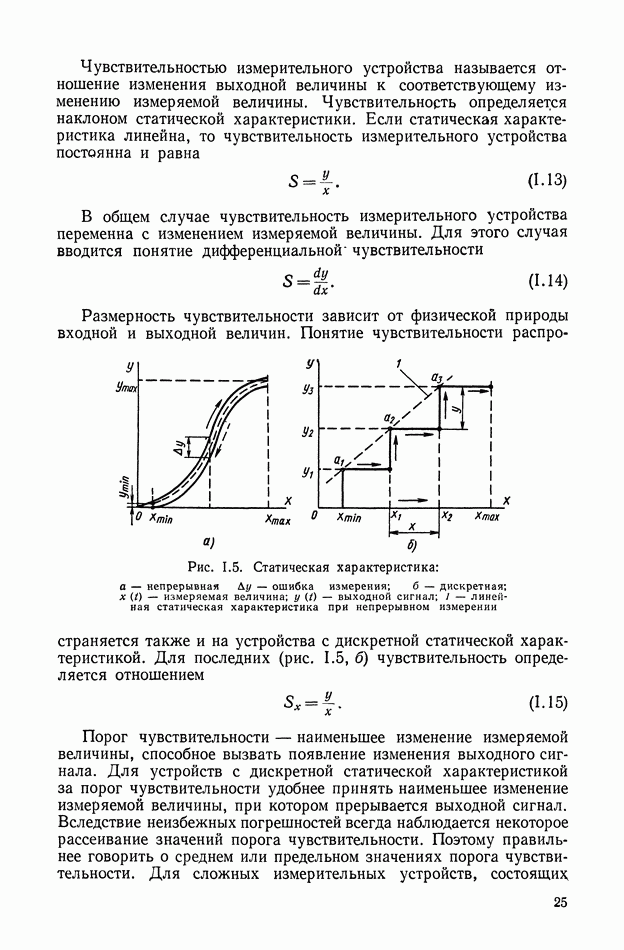
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
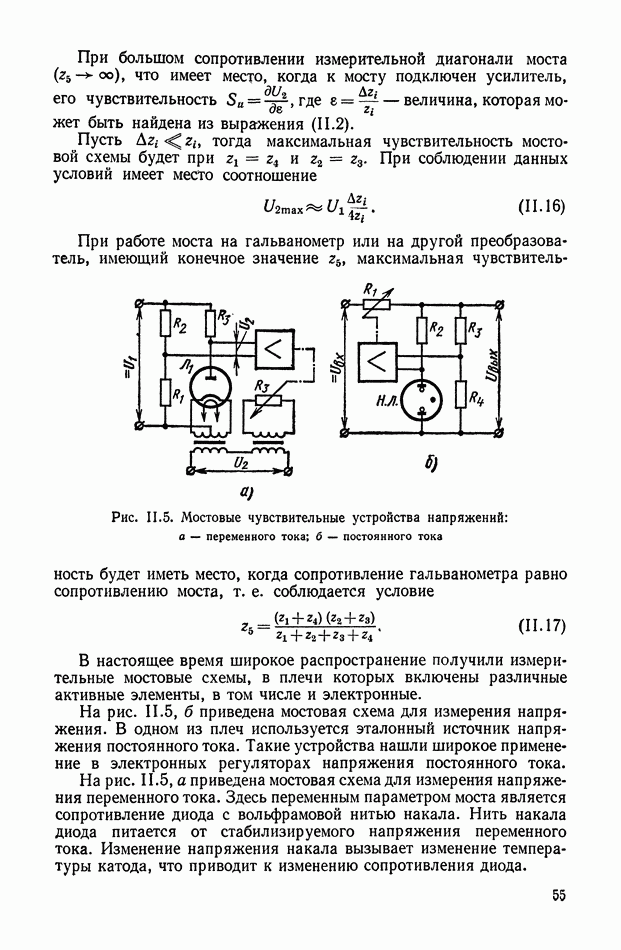
- 1. МОСТОВЫЕ СХЕМЫ
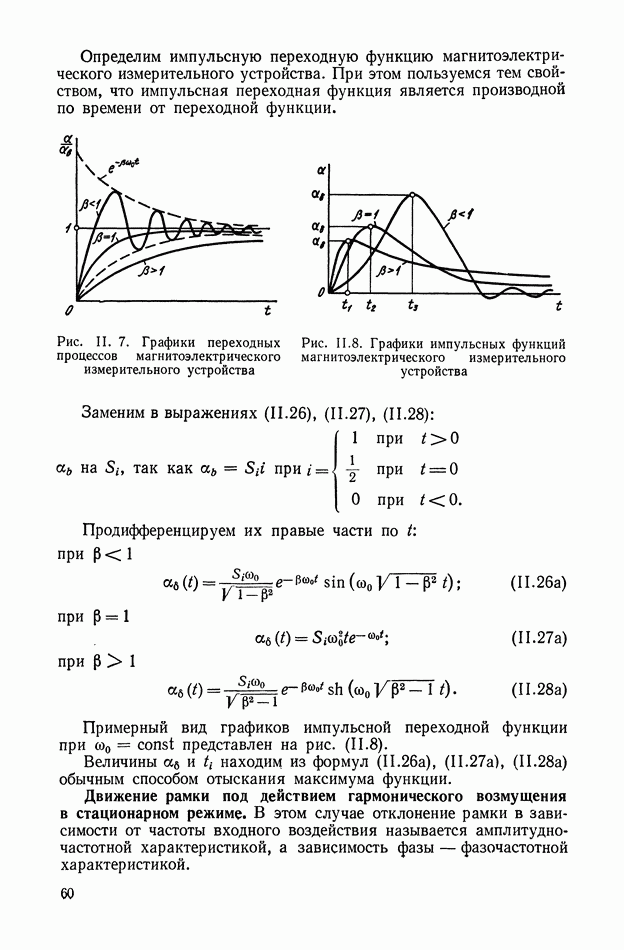
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
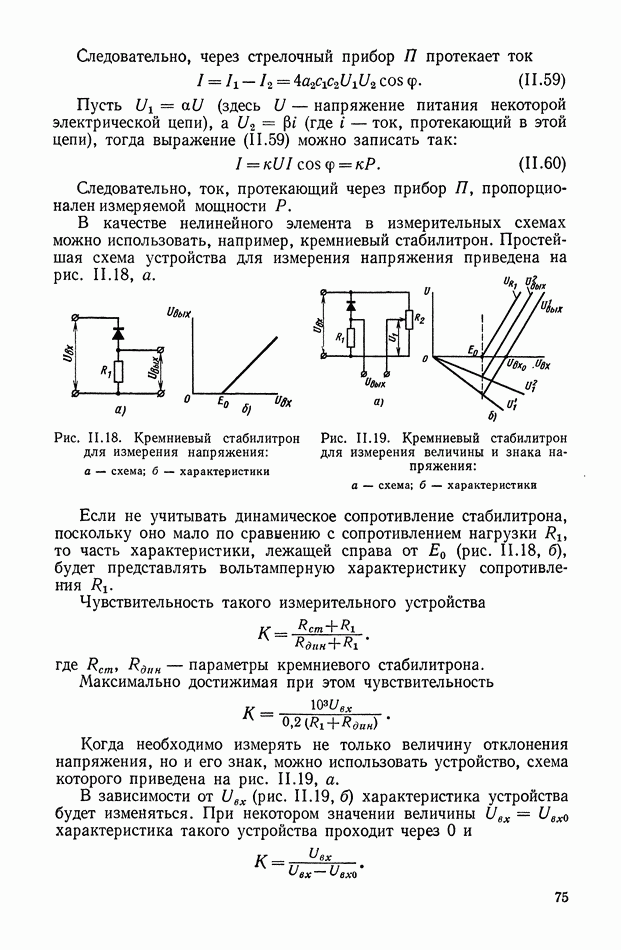
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
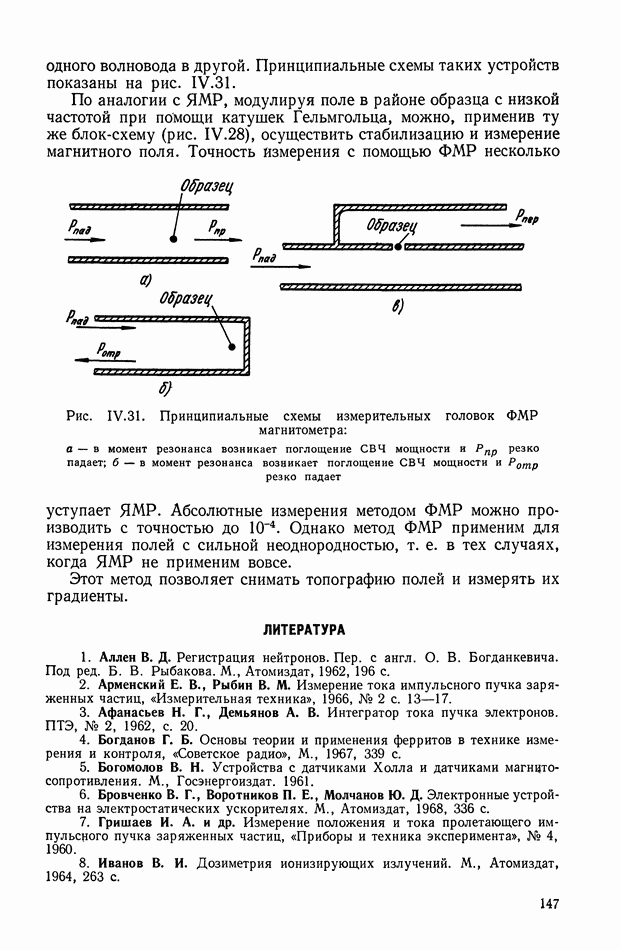
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
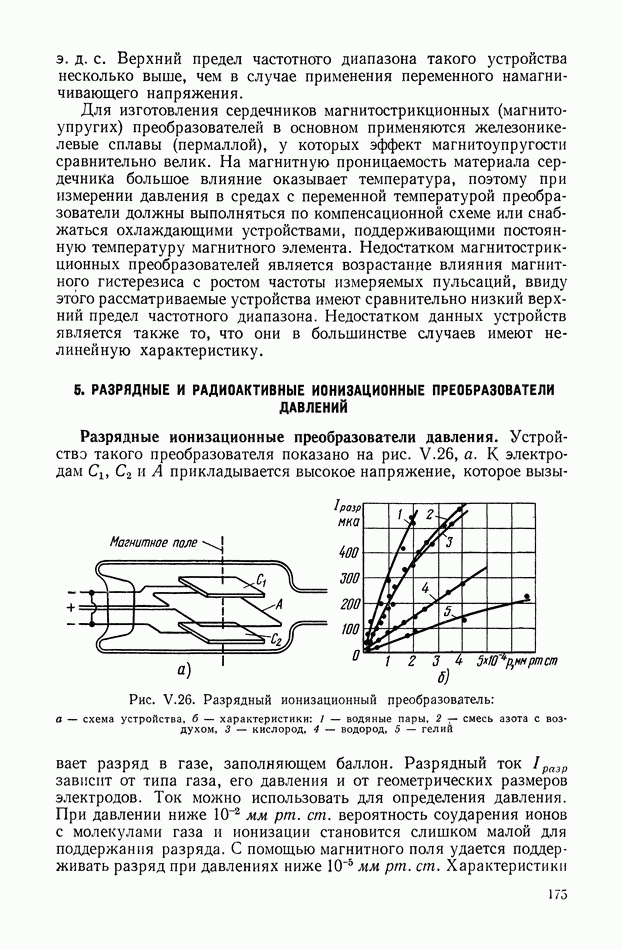
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 1. МОДУЛЯТОРЫ
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
- Двухполупериодные демодуляторы на диодах.
- Однополупериодные усилители-демодуляторы.
- Двухполупериодные усилители-демодуляторы.
- Демодуляторы на транзисторных ключах.
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
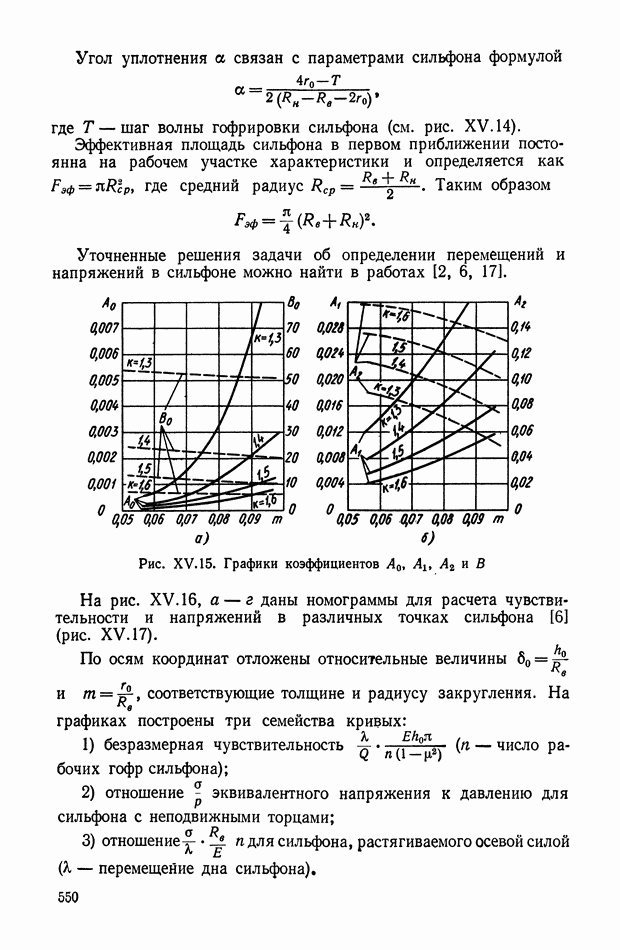
- Сильфоны.
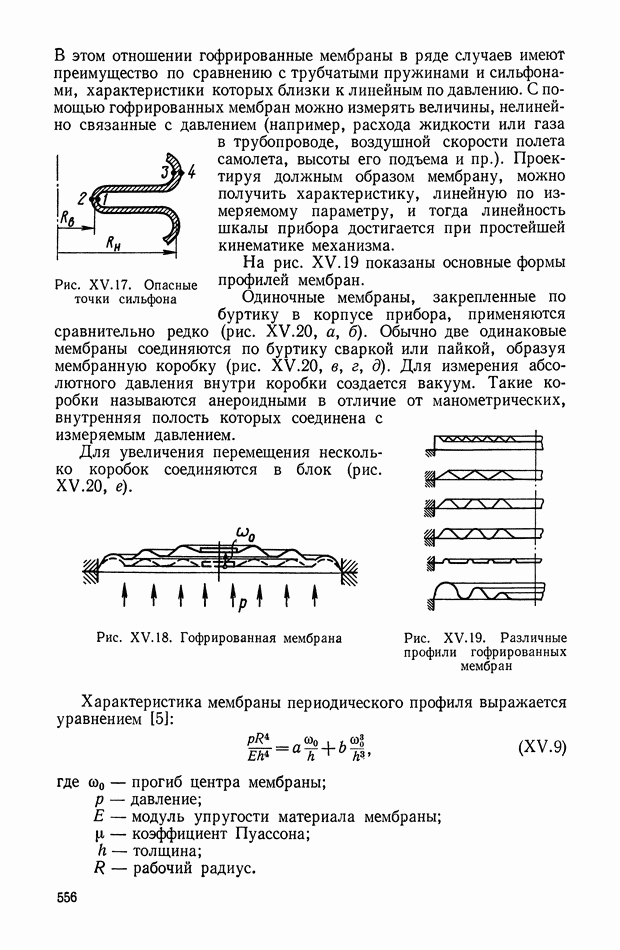
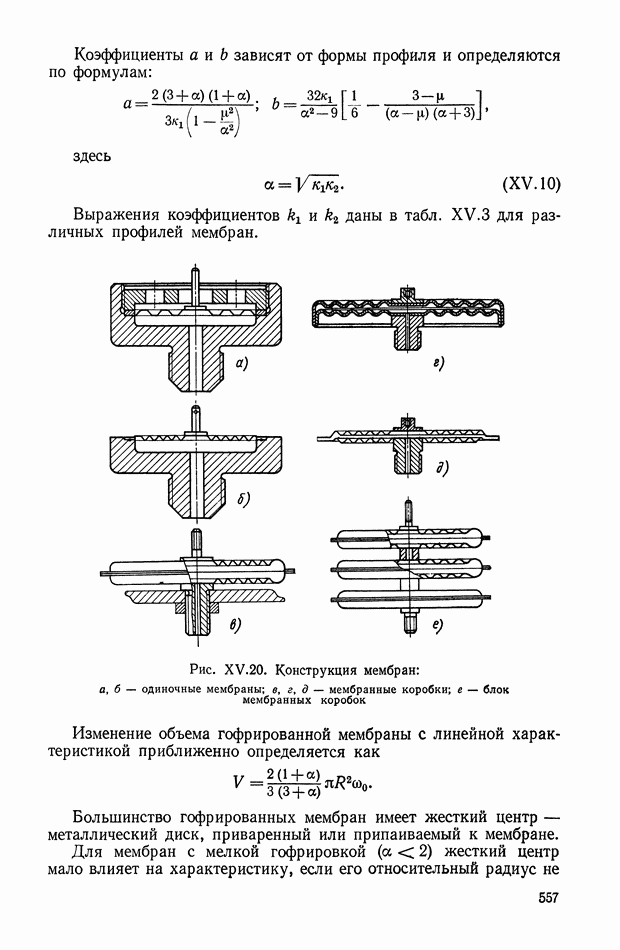
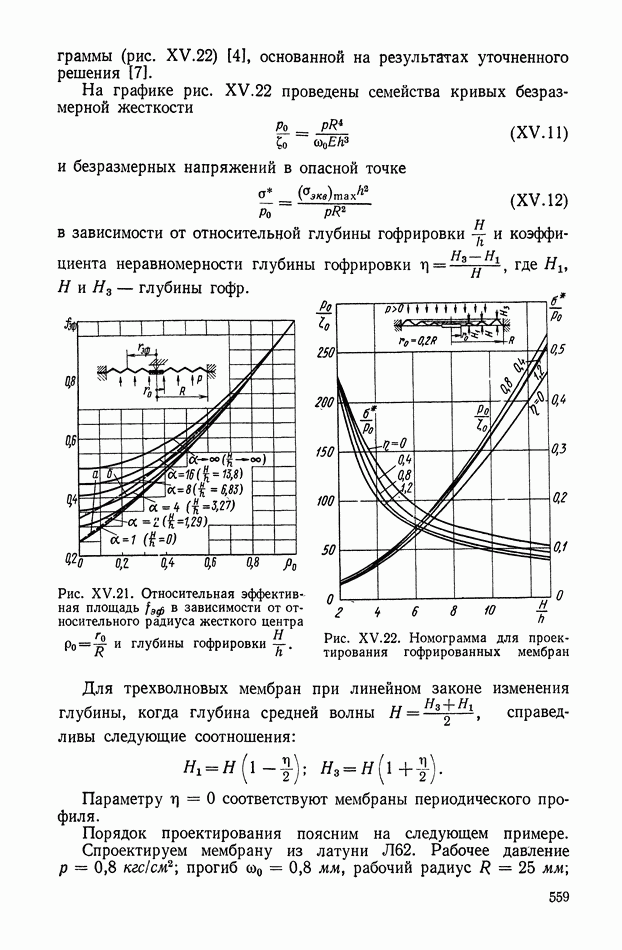
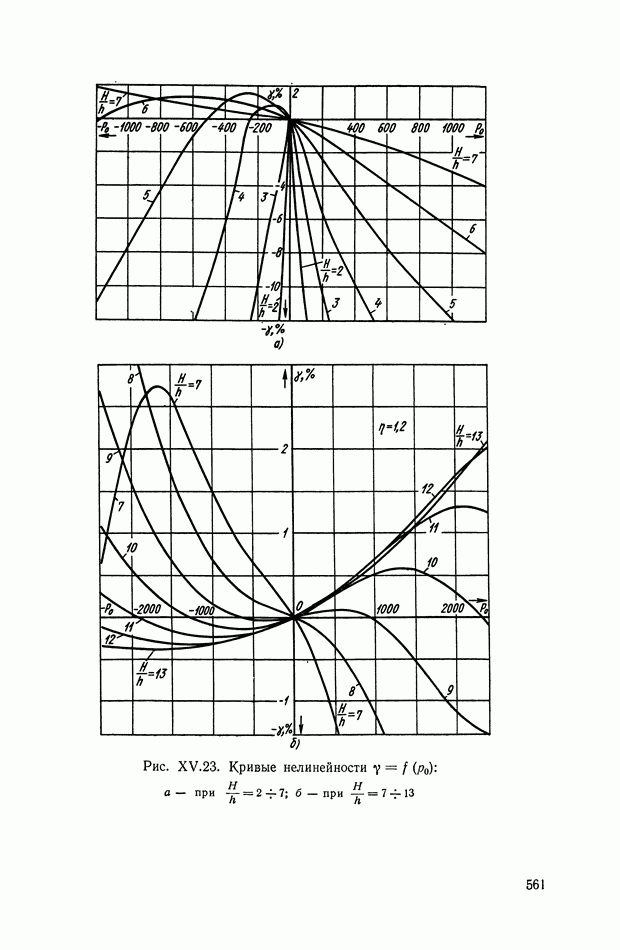
- Гофрированные мембраны.
- Гибкие диафрагмы.
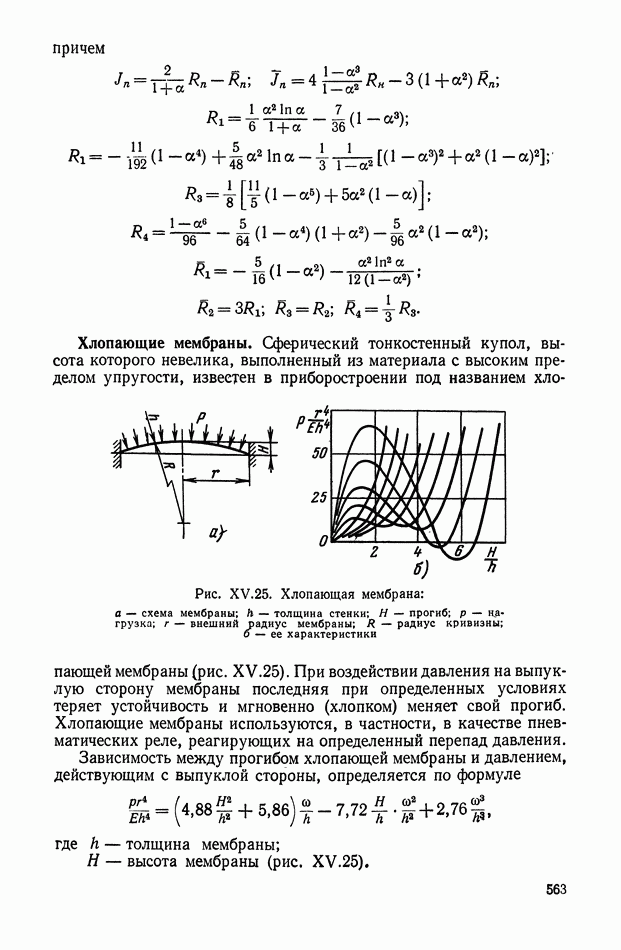
- Хлопающие мембраны.
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
- Пневмоэлектроконтактные преобразователи линейных величин.
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
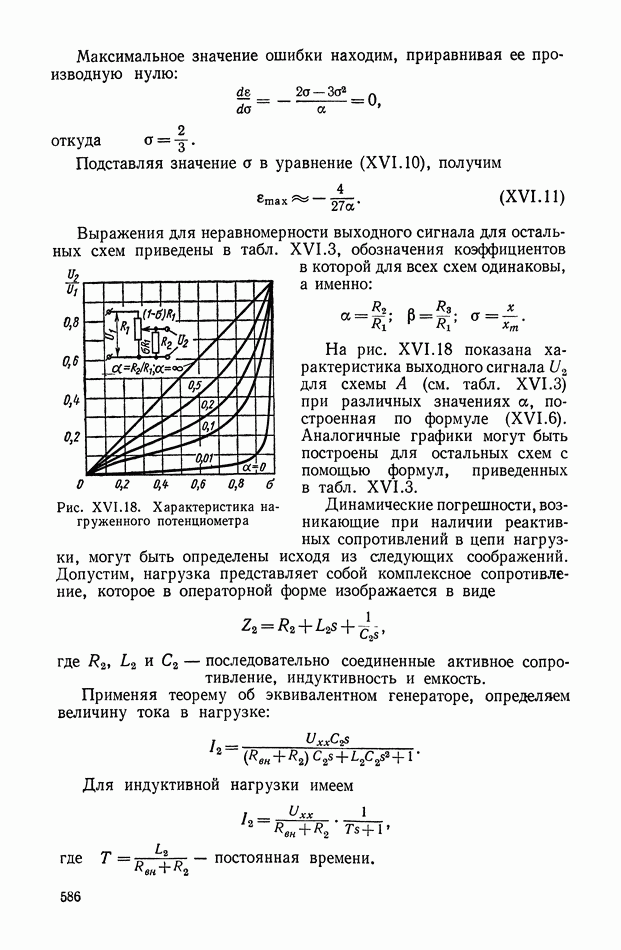
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
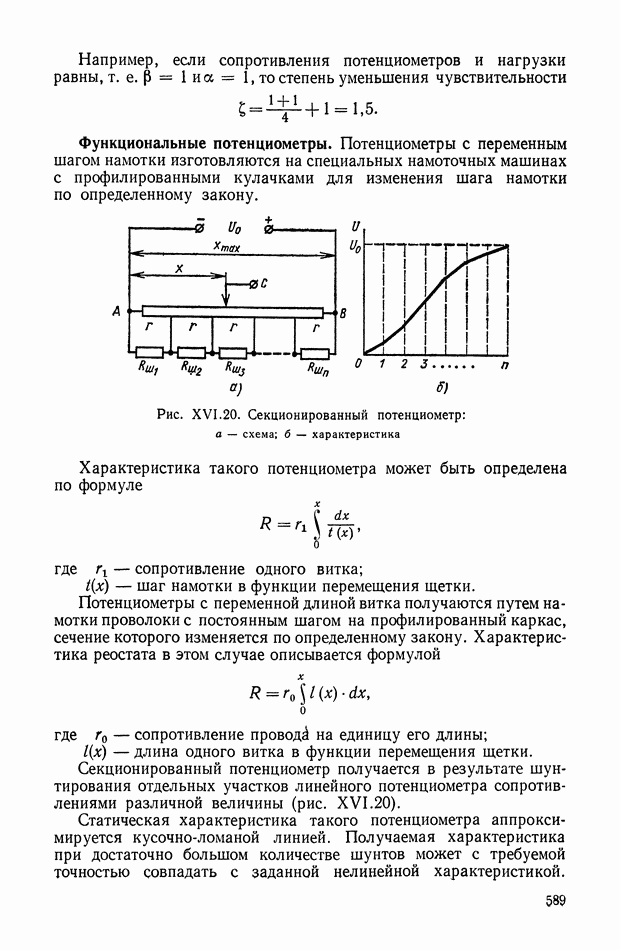
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
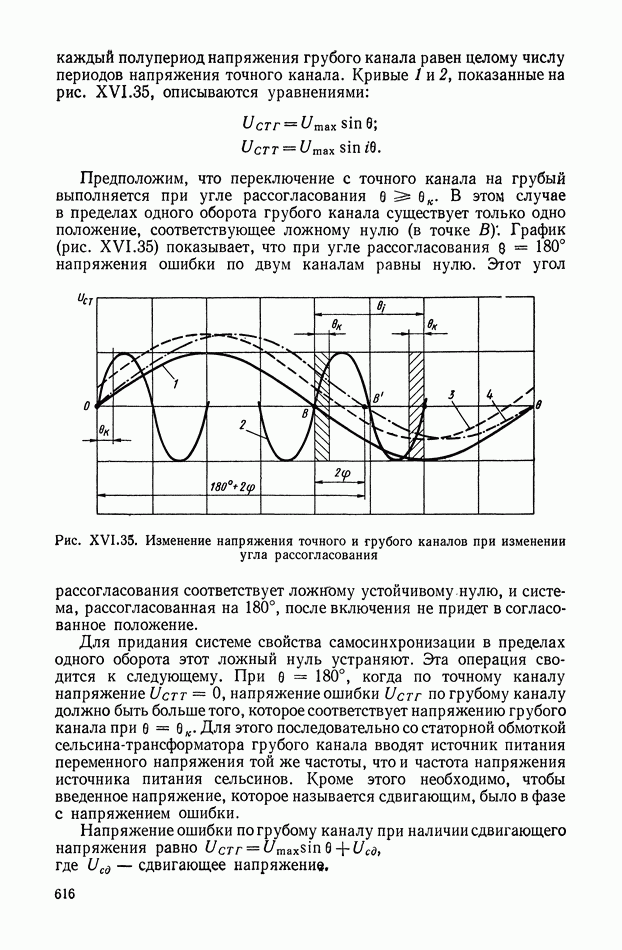
- Работа сельсинов в трансформаторном режиме.
- Устранение ложного нуля в двухскоростной системе.
- Схемы синхронизаторов.
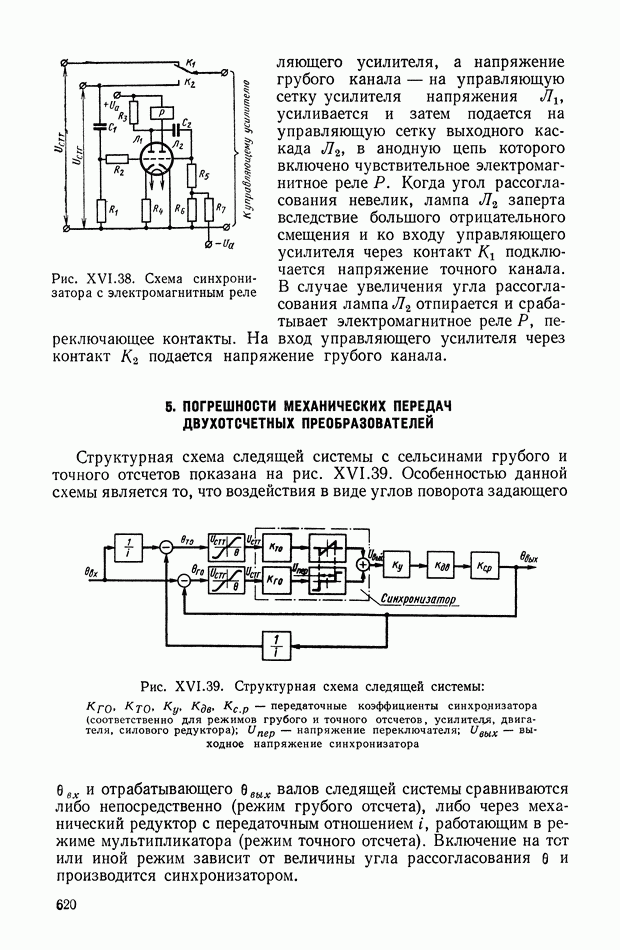
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
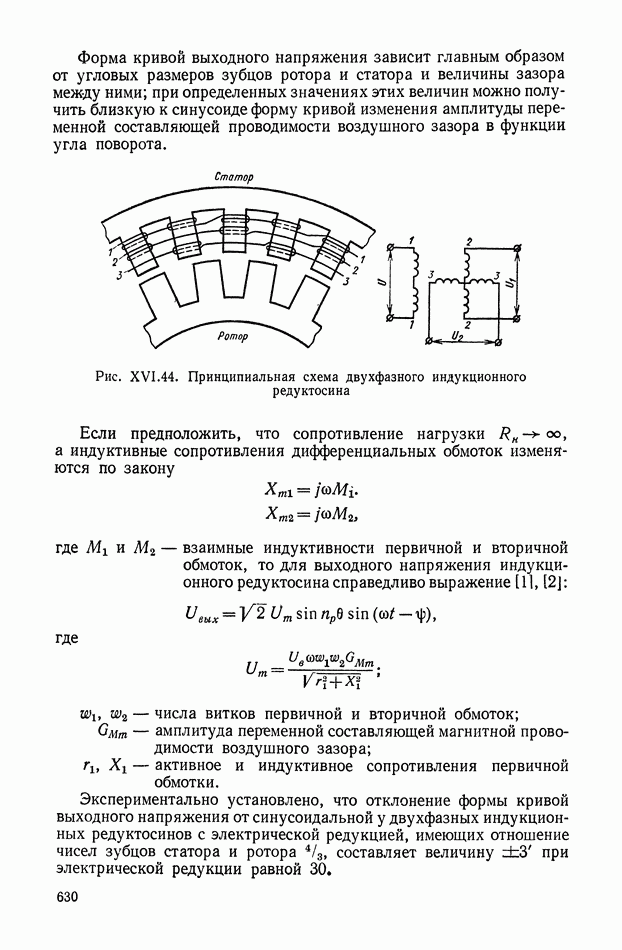
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
- Индукционные редуктосины.
- Индуктосины.
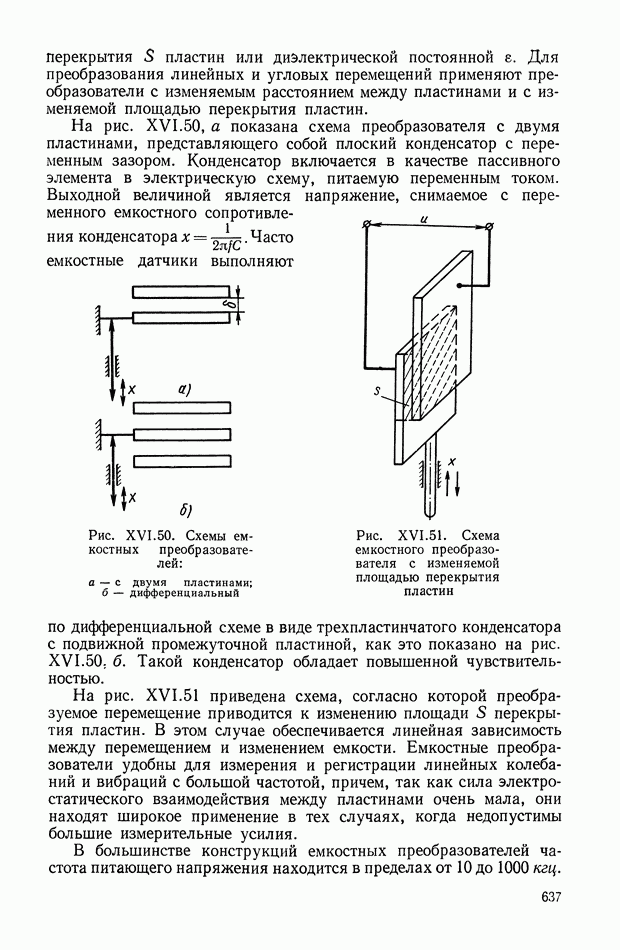
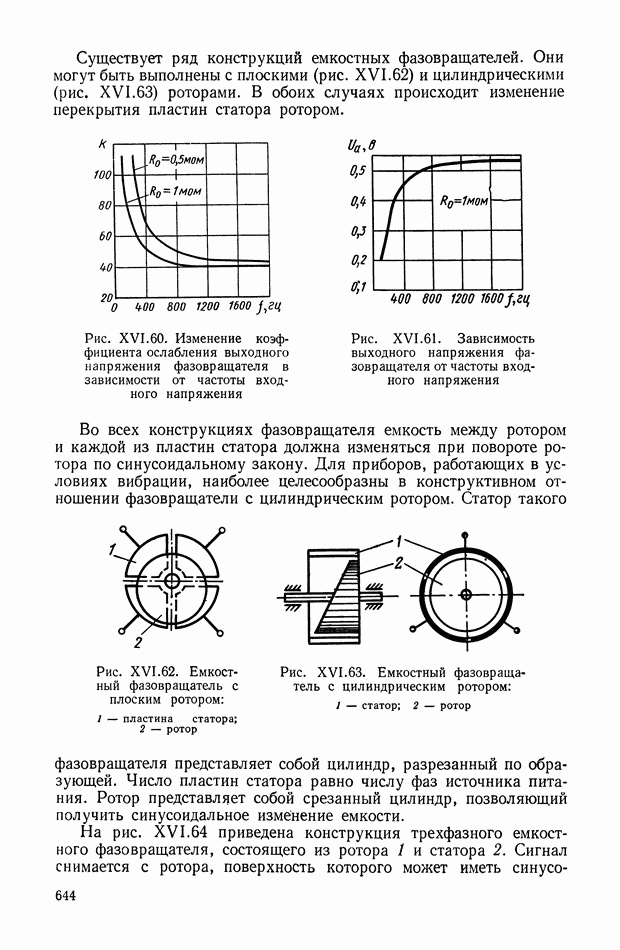
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
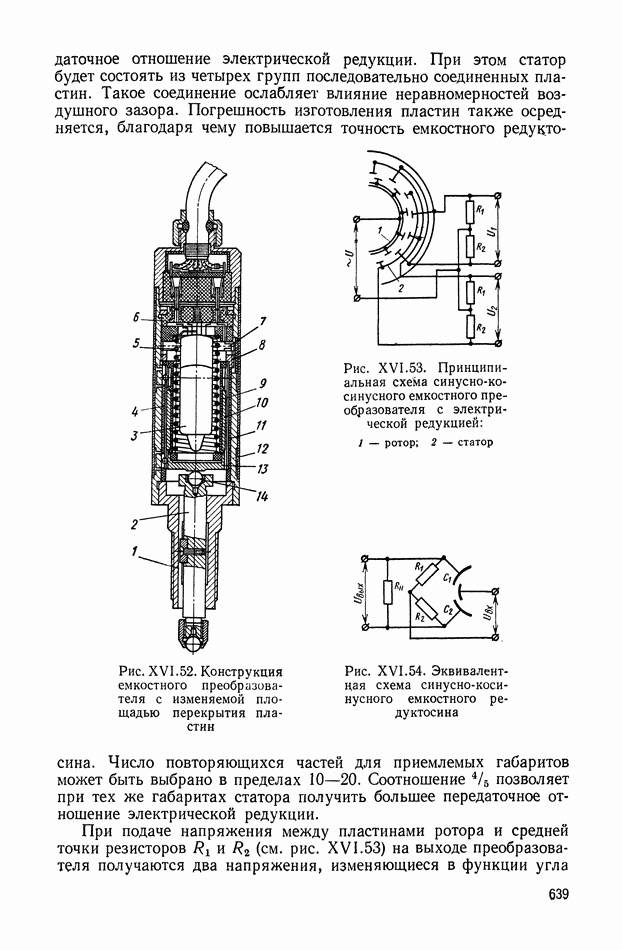
- Емкостный редуктосин.
- Емкостный фазовращатель.
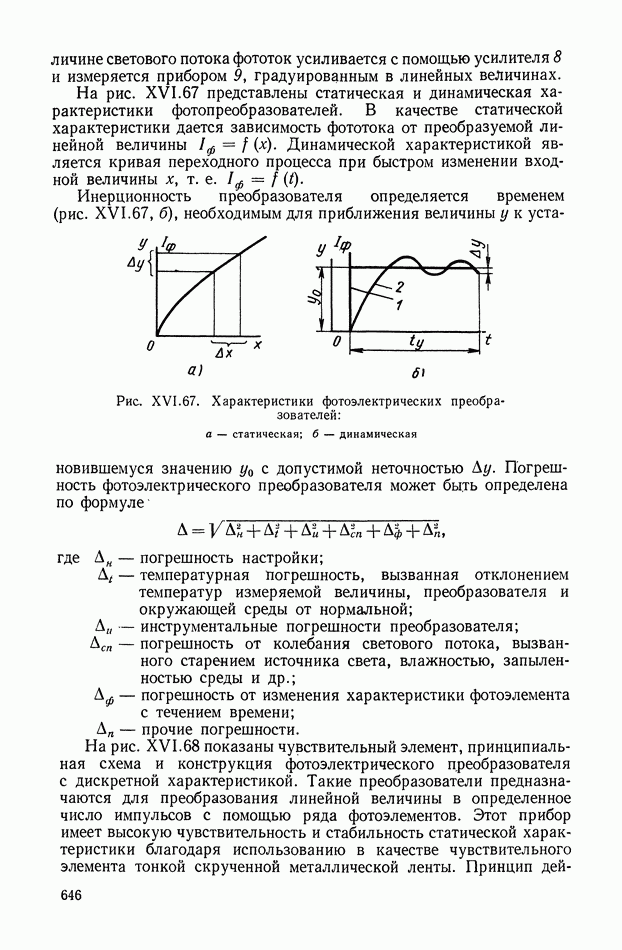
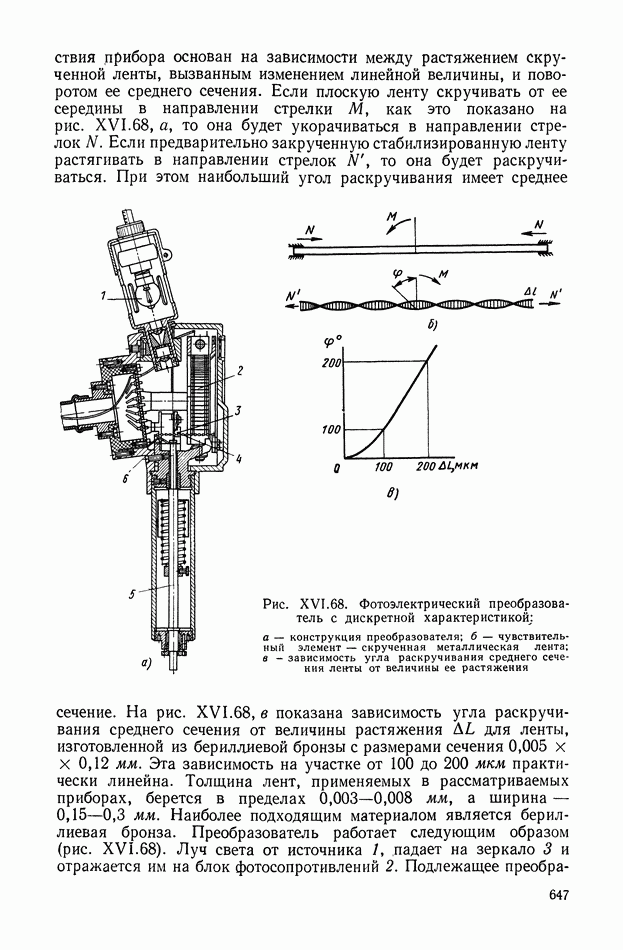
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
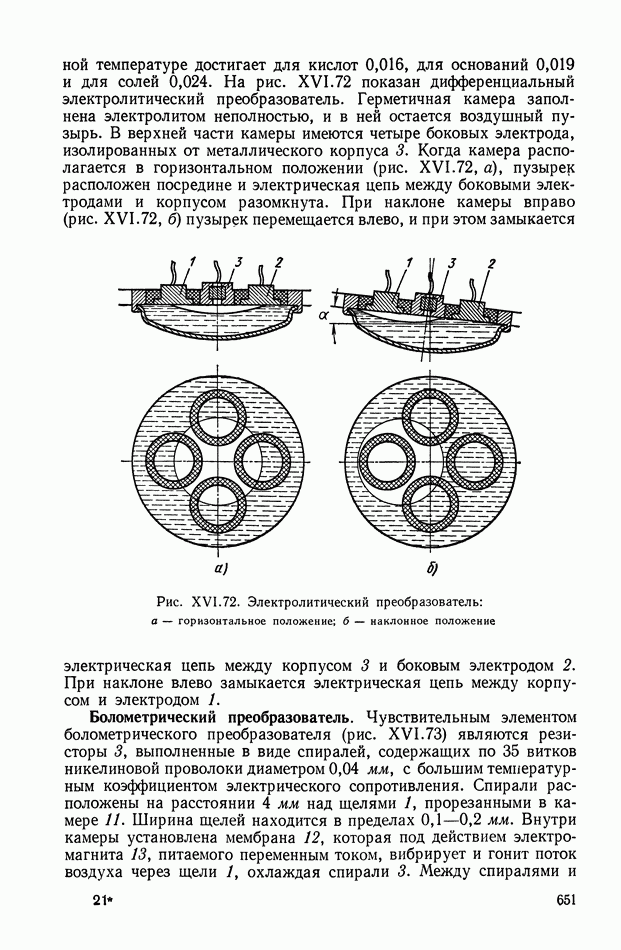
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ