| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
Статическая характеристика. Основным требованием, предъявляемым к измерительному устройству, является обеспечение определенной функцирнальной связи между изменением измеряемой величины на входе и изменением выходного сигнала.
У измерительных устройств с непрерывной характеристикой при таком же непрерывном изменении измеряемой величины от  до
до  выходной сигнал у также изменяется непрерывно от
выходной сигнал у также изменяется непрерывно от  до
до  (рис. 1.5). Зависимость
(рис. 1.5). Зависимость  называется статической характеристикой измерительного устройства. В целях обеспечения постоянной чувствительности измерительного устройства важно получить зависимость
называется статической характеристикой измерительного устройства. В целях обеспечения постоянной чувствительности измерительного устройства важно получить зависимость  линейной или близкой к линейной на заданном интервале изменения х. У измерительных устройств с дискретной характеристикой при непрерывном изменении входной измеряемой величины выходной сигнал представляет собой дискретную функцию. Например, при изменении измеряемой величины х от
линейной или близкой к линейной на заданном интервале изменения х. У измерительных устройств с дискретной характеристикой при непрерывном изменении входной измеряемой величины выходной сигнал представляет собой дискретную функцию. Например, при изменении измеряемой величины х от  до
до  выходной сигнал изменяется скачком от
выходной сигнал изменяется скачком от  до 1/2 при
до 1/2 при  от
от  до
до  при
при  (рис. 1.5, б). При изменении измеряемой величины в промежутках от
(рис. 1.5, б). При изменении измеряемой величины в промежутках от  до
до  от
от  до
до  и от
и от  до
до  величина у остается постоянной, равной соответственно
величина у остается постоянной, равной соответственно  Точки
Точки  на рис. 1.5, б соответствуют кривой 1 — статической характеристике, которая имела бы место при непрерывном характере изменения измеряемой величины.
на рис. 1.5, б соответствуют кривой 1 — статической характеристике, которая имела бы место при непрерывном характере изменения измеряемой величины.
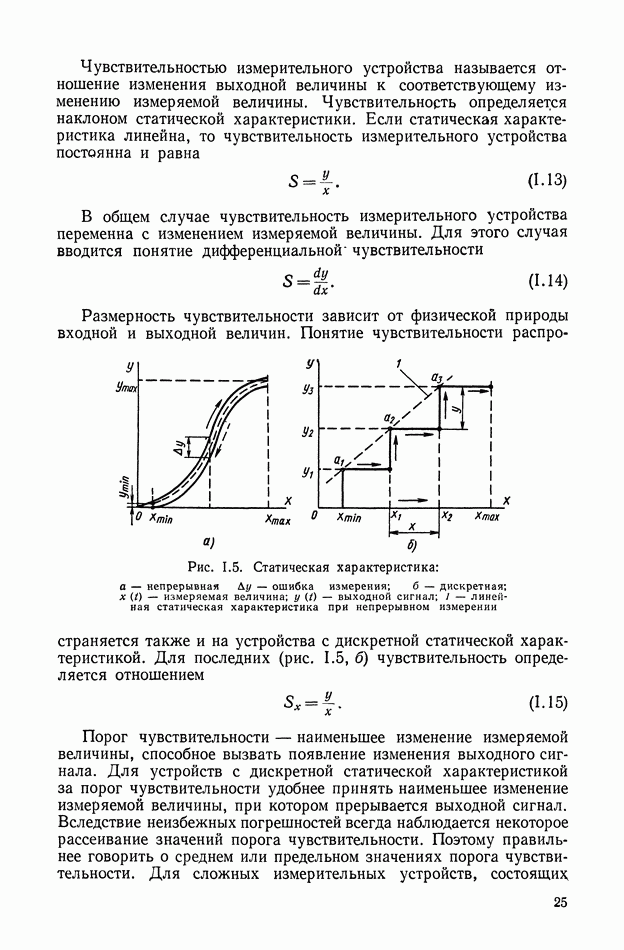
Чувствительностью измерительного устройства называется отношение изменения выходной величины к соответствующему изменению измеряемой величины. Чувствительность определяется наклоном статической характеристики. Если статическая характеристика линейна, то чувствительность измерительного устройства постоянна и равна

В общем случае чувствительность измерительного устройства переменна с изменением измеряемой величины. Для этого случая вводится понятие дифференциальной чувствительности

Размерность чувствительности зависит от физической природы входной и выходной величин.

Рис. 1.5. Статическая характеристика: а — непрерывная  — ошибка измерения; б — дискретная;
— ошибка измерения; б — дискретная;  — измеряемая величина;
— измеряемая величина;  — выходной сигнал; 1 — линейная статическая характеристика при непрерывном измерении
— выходной сигнал; 1 — линейная статическая характеристика при непрерывном измерении
Понятие чувствительности распространяется также и на устройства с дискретной статической характеристикой. Для последних (рис. 1.5, б) чувствительность определяется отношением

Порог чувствительности — наименьшее изменение измеряемой величины, способное вызвать появление изменения выходного сигнала. Для устройств с дискретной статической характеристикой за порог чувствительности удобнее принять наименьшее изменение измеряемой величины, при котором прерывается выходной сигнал. Вследствие неизбежных погрешностей всегда наблюдается некоторое рассеивание значений порога чувствительности. Поэтому правильнее говорить о среднем или предельном значениях порога чувствительности. Для сложных измерительных устройств, состоящих,
из ряда последовательно соединенных элементов, чувствительность определяется по формуле

где  — чувствительность
— чувствительность  звена.
звена.
Для расчета чувствительности при параллельном соединении элементов применима формула

Наконец, при расположении элементов, как указано на рис. 1.2, общая чувствительность измерительного устройства

где  относится к элементам основной цепи, а
относится к элементам основной цепи, а  — к элементам обратной связи.
— к элементам обратной связи.
Погрешности измерительных устройств. Погрешностью измерительного устройства называется разность между результатом измерения некоторой величины и ее действительным значением:

Погрешность измерительного устройства по своему характеру является сложной и неопределенно изменяющейся вследствие влияния многих причин, порождаемых относительным несовершенством конструкции, условиями технологического процесса изготовления, а также условиями его эксплуатации. В связи с этим погрешности измерительных устройств могут быть классифицированы следующим образом:
статические и динамические, в зависимости от условий и режимов эксплуатации;
систематические, случайные и грубые, в зависимости от характера их проявления и возможностей устранения.
Статические и динамические погрешности. Статической погрешностью называется погрешность, возникающая при установившемся значении измеряемой величины и неизменных внешних условиях.
Динамической погрешностью называется погрешность, возникающая при изменениях измеряемой величины и внешних воздействий.
Методические и инструментальные погрешности. Методические погрешности зависят от выбранного метода измерения и принципа
действия измерительного устройства. Они появляются также при неправильной установке измерительного устройства.
Инструментальные погрешности происходят от конструктивных недостатков измерительного устройства, от отклонений его характеристик и параметров вследствие неточности изготовления, под влиянием изменения внешних условий, вследствие естественного старения материалов и т. п.
Систематические, случайные и грубые погрешности. Систематическими погрешностями называются постоянные по величине и знаку или изменяющиеся по определенному закону погрешности, повторяющиеся при многократных измерениях. Систематические погрешности определяются путем многократного измерения одной и той же величины при постоянных прочих условиях и устраняются посредством регулировочных и юстировочных устройств или введением коррекций с помощью специальных элементов, предусматриваемых для этой цели в конструкции измерительного устройства. Систематические погрешности подразделяются на прогрессивные и периодические, а также погрешности, изменяющиеся по сложному закону во времени. Прогрессивными называются непрерывно возрастающие или убывающие погрешности. К ним могут быть отнесены, например, погрешности от износа деталей, контактов и др. Периодическими называются погрешности равномерно изменяющиеся. по величине и знаку, возникающие при функционировании измерительных устройств. Погрешности, изменяющиеся по сложному закону, происходят от совместного действия нескольких систематических погрешностей.
Методы расчета неслучайных погрешностей детально освещены в специальной литературе и поэтому в настоящей книге не приводятся.
Случайные погрешности представляют собой погрешности, неопределенным образом изменяющиеся по величине и знаку. Они определяют точность измерительного устройства. Случайные погрешности происходят от совместного проявления большого числа причин. К этим причинам относятся неизбежные и неучитываемые деформации и смещения деталей и узлов измерительного устройства, например, вследствие зазоров, колебаний окружающей температуры и т. д. Случайные погрешности возникают вследствие помех и большого уровня шумов в элементах измерительного устройства. Случайные погрешности в значительной степени неустранимы. По ним производится оценка точности как самих измерительных устройств, так и методов измерения. Случайные погрешности при многократных измерениях одной и той же величины вызывают рассеивание значений выходного сигнала, называемое также нестабильностью или вариацией сигнала. В идеальном случае при отсутствии случайных погрешностей значения выходного сигнала совпадали бы и соответствовали точно истинному значению измеряемой величины. Вследствие случайной погрешности истинное значение измеряемой величины неизвестно, поэтому при подсчете случайных погрешностей
за измеренное значение принимают среднее арифметическое х из полученных  измерений
измерений  т. е.
т. е.

где  — частота появления значения
— частота появления значения 
 — число измерений.
— число измерений.
Случайные погрешности являются случайными величинами и также, как последние, могут быть охарактеризованы с помощью понятий и характеристик теории вероятностей. В связи с этим ниже приводятся наиболее распространенные в практике измерительной техники расчетные формулы. Среднее арифметическое является наиболее достоверным значением измеряемой величины:


Рис. 1.6. Случайная погрешность с нормальным законом распределения:  — измеряемая величина;
— измеряемая величина;  — плотность распределения
— плотность распределения
При  определяет математическое ожидание случайной величины. При большом числе независимых причин, вызывающих появление случайных погрешностей, плотность распределения выражается законом Гаусса (нормальное распределение — рис. 1.6):
определяет математическое ожидание случайной величины. При большом числе независимых причин, вызывающих появление случайных погрешностей, плотность распределения выражается законом Гаусса (нормальное распределение — рис. 1.6):

где  — плотность распределения вероятности; а — среднее квадратическое отклонение.
— плотность распределения вероятности; а — среднее квадратическое отклонение.
Случайную погрешность принято оценивать либо средним квадратическим ее значением  либо вероятным значением
либо вероятным значением  , либо предельным
, либо предельным  Средняя квадратическая погрешность отдельных измерений определяется по формуле
Средняя квадратическая погрешность отдельных измерений определяется по формуле

Дисперсией называется величина

Средняя квадратическая погрешность является основной и исходной при подсчете других, упомянутых выше погрешностей.
Вероятная (средняя) погрешность определяется в зависимости от а по формуле

Как правило, при многократных измерениях одной и той же величины половина всех случайных погрешностей будет больше вероятности и половина — меньше ее. Точность измерительных устройств принято характеризовать предельной погрешностью, определяемой по формуле

Случайные погрешности при нормальном законе распределения не могут по абсолютной величине превышать предельное значение. Между средним квадратическим значением а погрешности единичного измерения и средним квадратическим значением  погрешности среднего арифметического имеется следующая зависимость, называемая «правилом
погрешности среднего арифметического имеется следующая зависимость, называемая «правилом 

где  — число замеров, для которых подсчитывается среднее арифметическое значение х. Предельная погрешность
— число замеров, для которых подсчитывается среднее арифметическое значение х. Предельная погрешность  среднего арифметического
среднего арифметического


Рис. 1.7. Систематическая и случайная погрешности
Таким образом, точность среднего арифметического значения измеряемой величины в  раз выше по сравнению с точностью единичных измерений. На рис. 1.7 схематически показаны систематические и случайные погрешности. Первые определяются по величине среднего арифметического для данной точки, а вторые — через среднее квадратическое отклонение описанным выше способом.
раз выше по сравнению с точностью единичных измерений. На рис. 1.7 схематически показаны систематические и случайные погрешности. Первые определяются по величине среднего арифметического для данной точки, а вторые — через среднее квадратическое отклонение описанным выше способом.
Грубые погрешности представляют собой погрешности, превосходящие предельное  значение случайной погрешности. Они происходят от резких изменений внешних условий измерения, например вследствие толчков, резкого колебания температуры, загрязнений и т. п. Общая случайная погрешность измерительного устройства определяется по формуле
значение случайной погрешности. Они происходят от резких изменений внешних условий измерения, например вследствие толчков, резкого колебания температуры, загрязнений и т. п. Общая случайная погрешность измерительного устройства определяется по формуле

где  — частная погрешность;
— частная погрешность;
 — весовой коэффициент для
— весовой коэффициент для  звена.
звена.
Такова методика, принятая в настоящее время для оценки погрешности обычных измерительных средств. Эта методика базируется на нормальном законе распределения и аддитивности отдельных составляющих.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 1. МОСТОВЫЕ СХЕМЫ
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 1. МОДУЛЯТОРЫ
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
- Двухполупериодные демодуляторы на диодах.
- Однополупериодные усилители-демодуляторы.
- Двухполупериодные усилители-демодуляторы.
- Демодуляторы на транзисторных ключах.
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
- Сильфоны.
- Гофрированные мембраны.
- Гибкие диафрагмы.
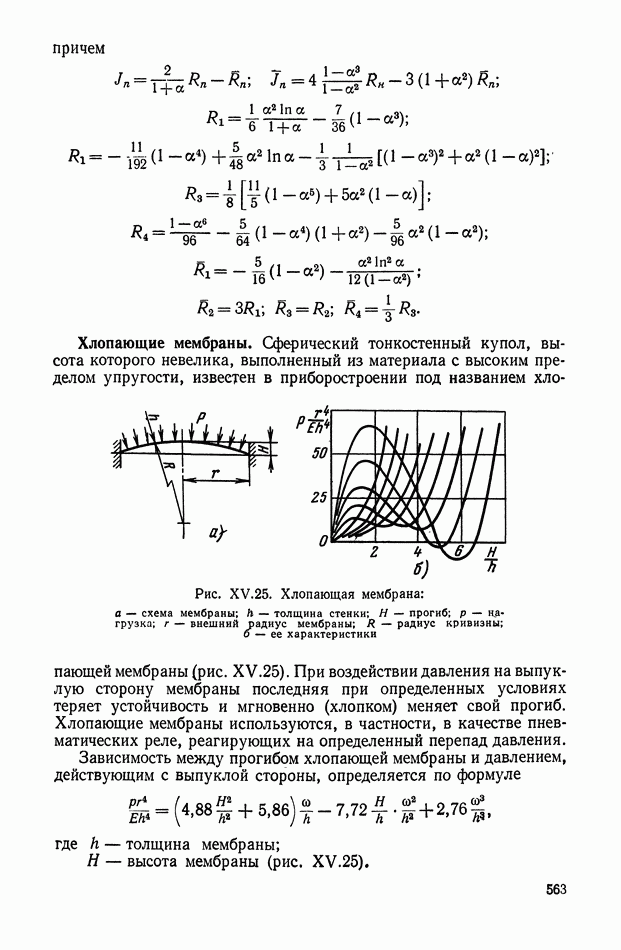
- Хлопающие мембраны.
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
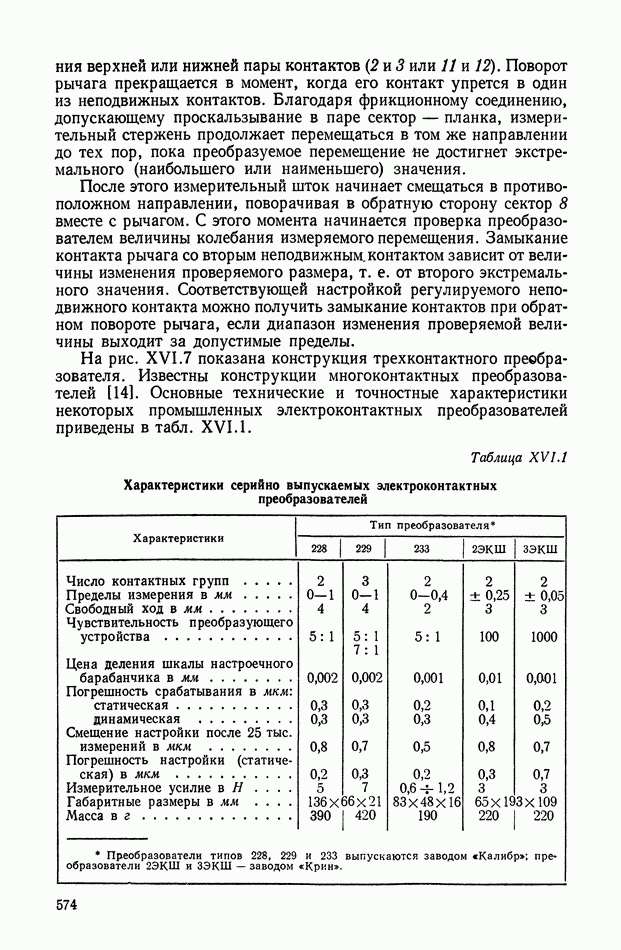
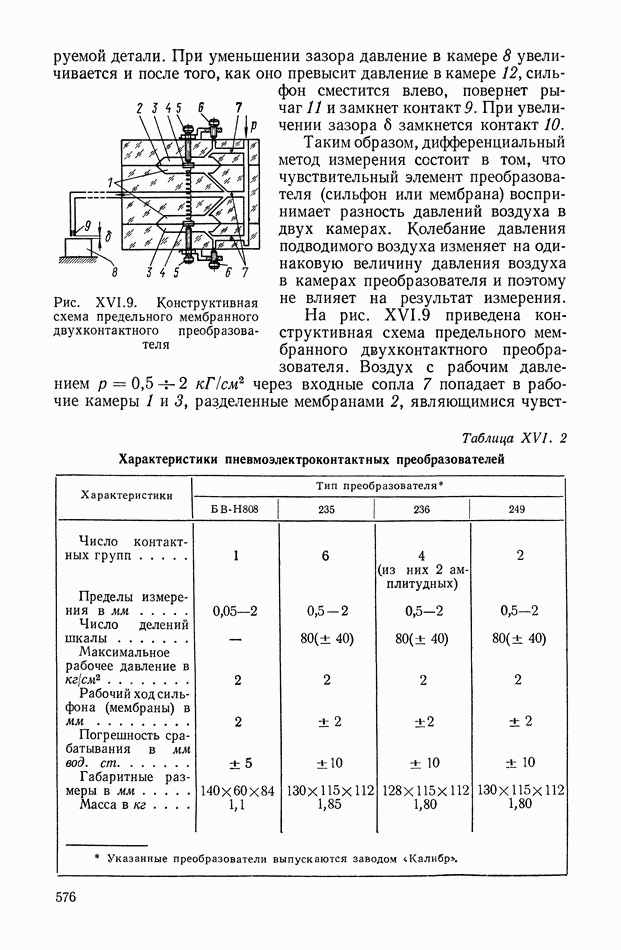
- Пневмоэлектроконтактные преобразователи линейных величин.
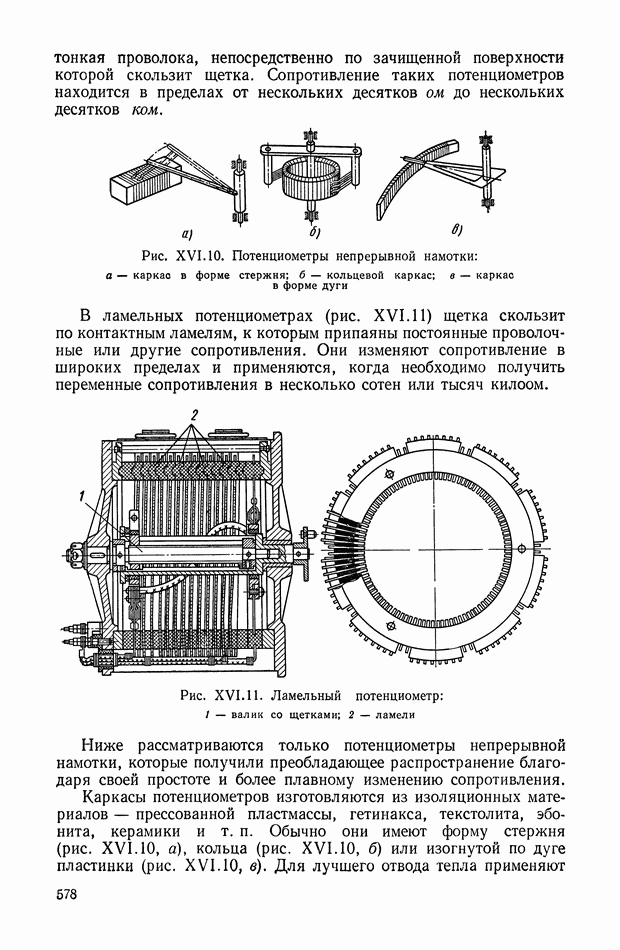
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
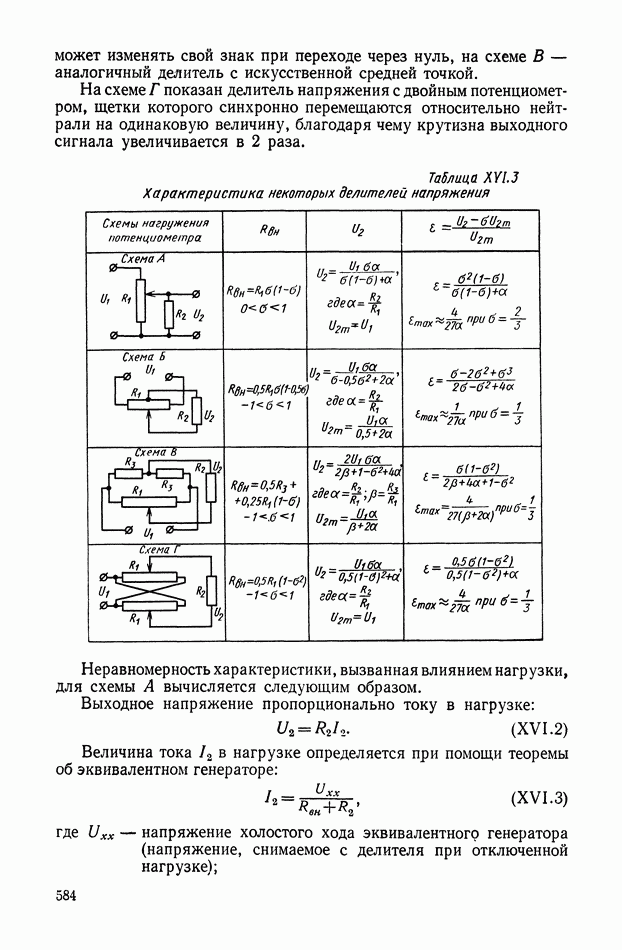
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
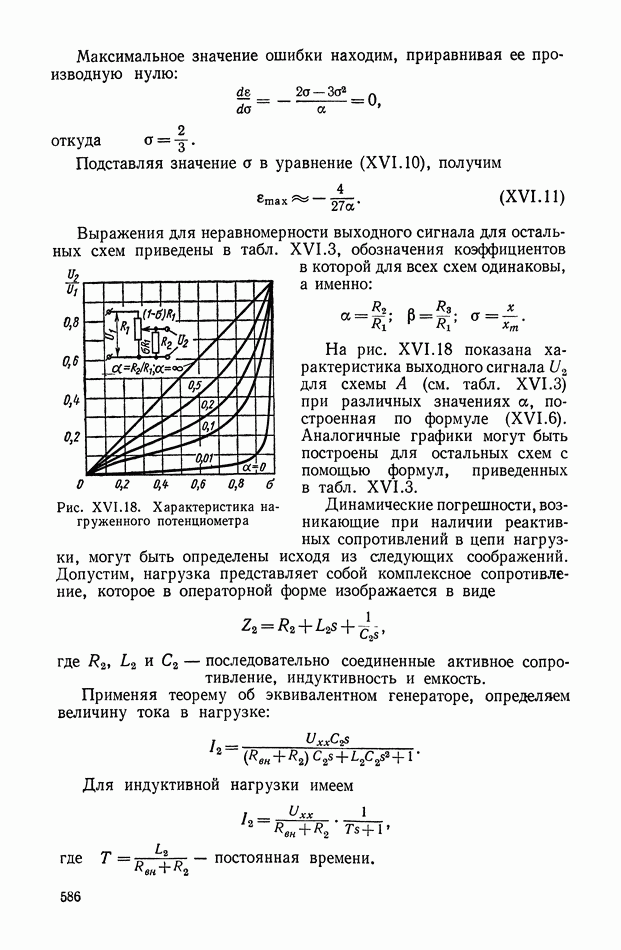
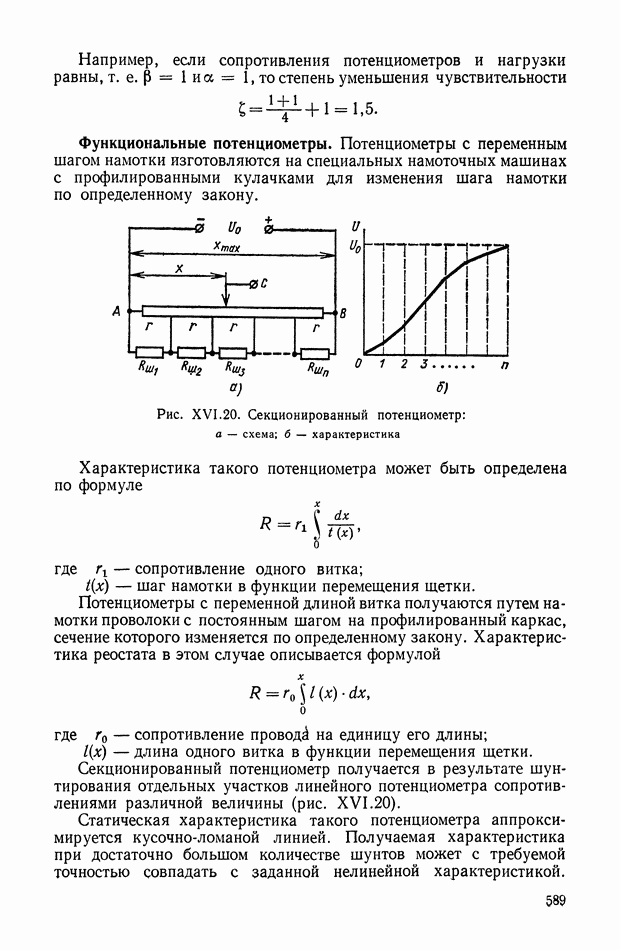
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
- Работа сельсинов в трансформаторном режиме.
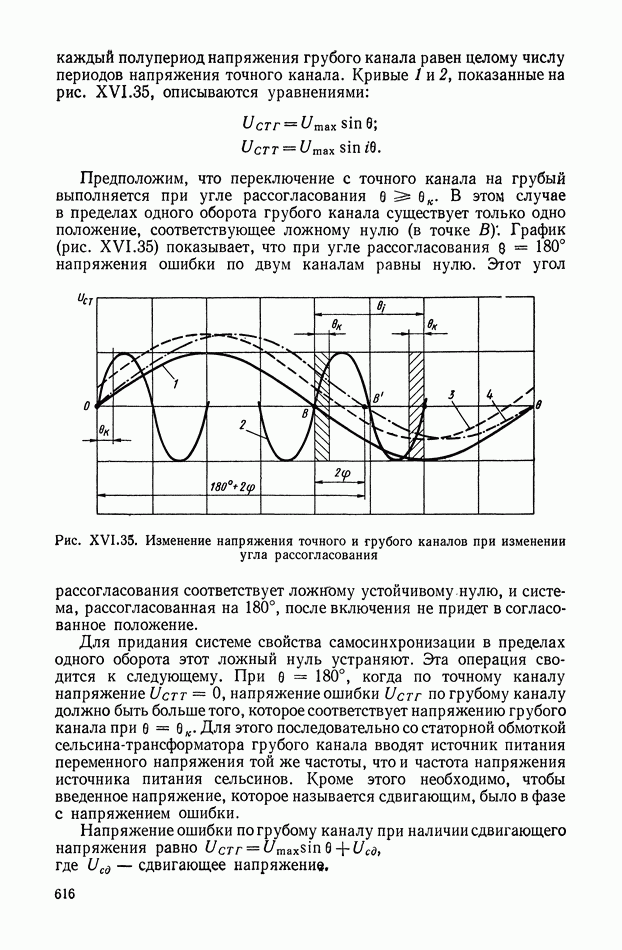
- Устранение ложного нуля в двухскоростной системе.
- Схемы синхронизаторов.
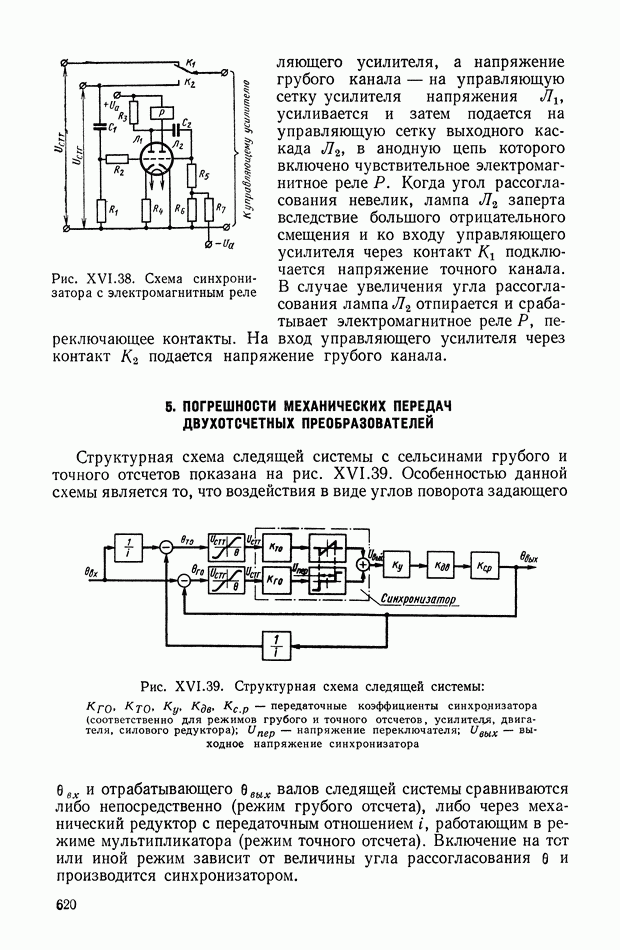
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
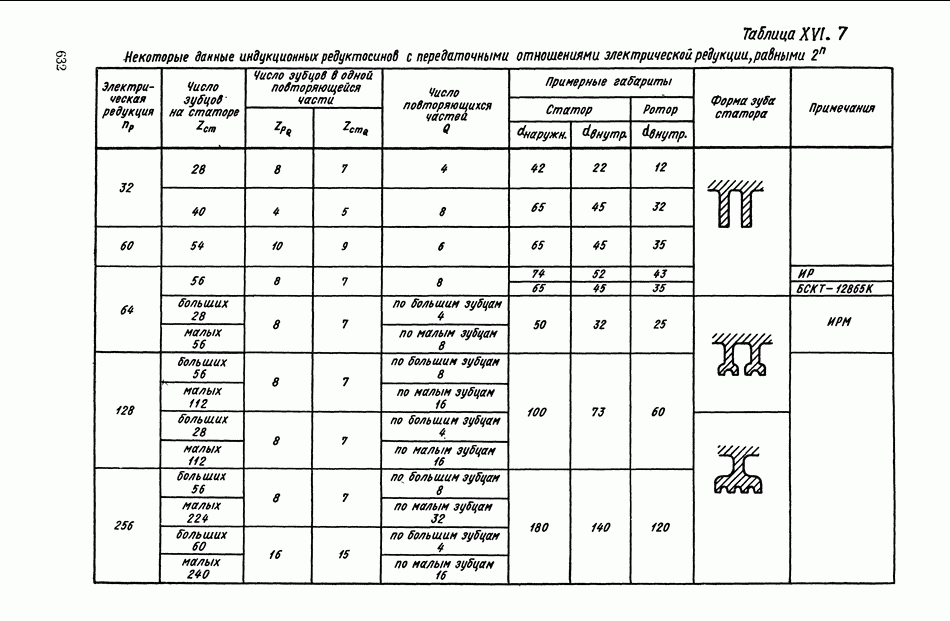
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
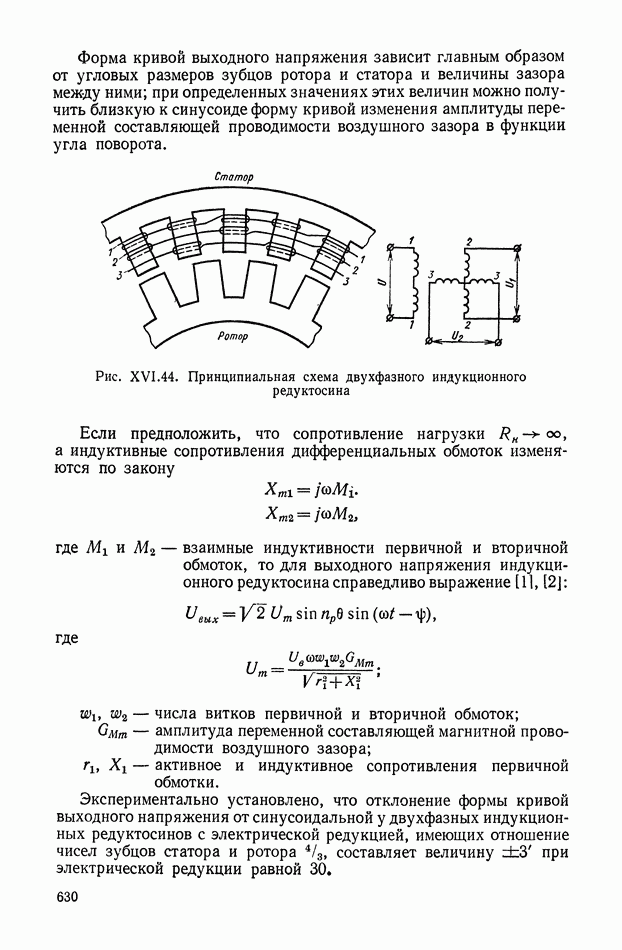
- Индукционные редуктосины.
- Индуктосины.
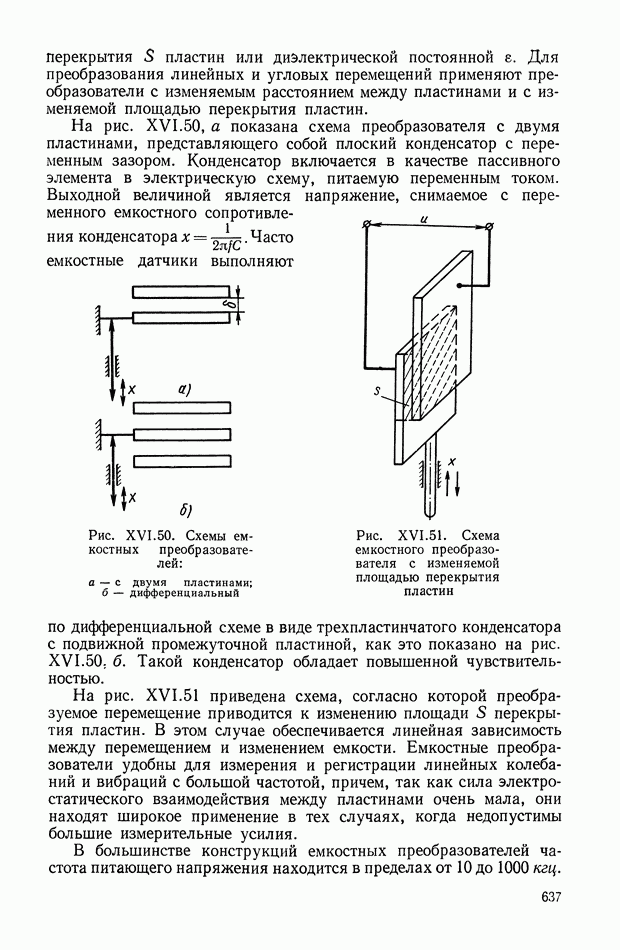
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
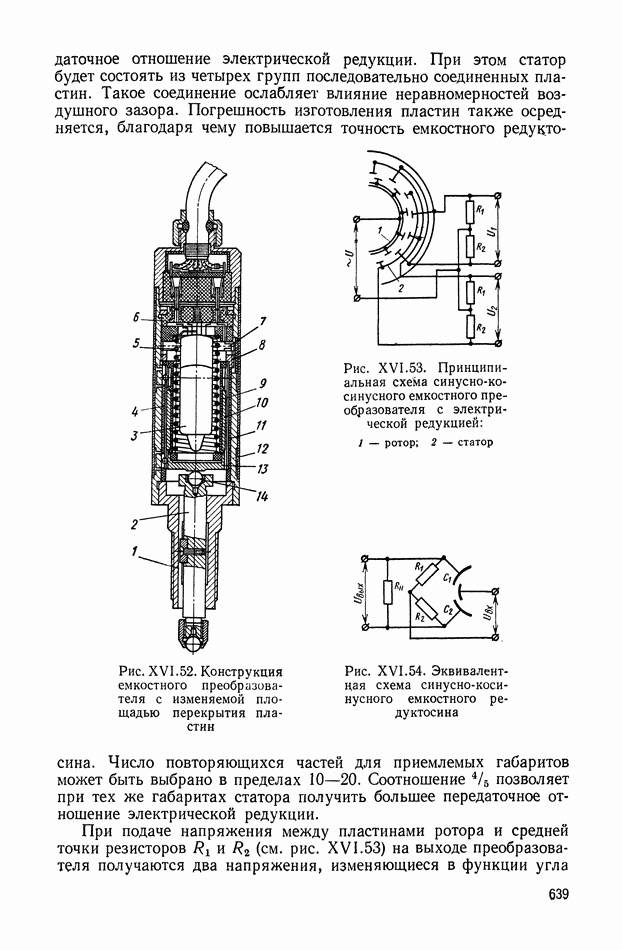
- Емкостный редуктосин.
- Емкостный фазовращатель.
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ