| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
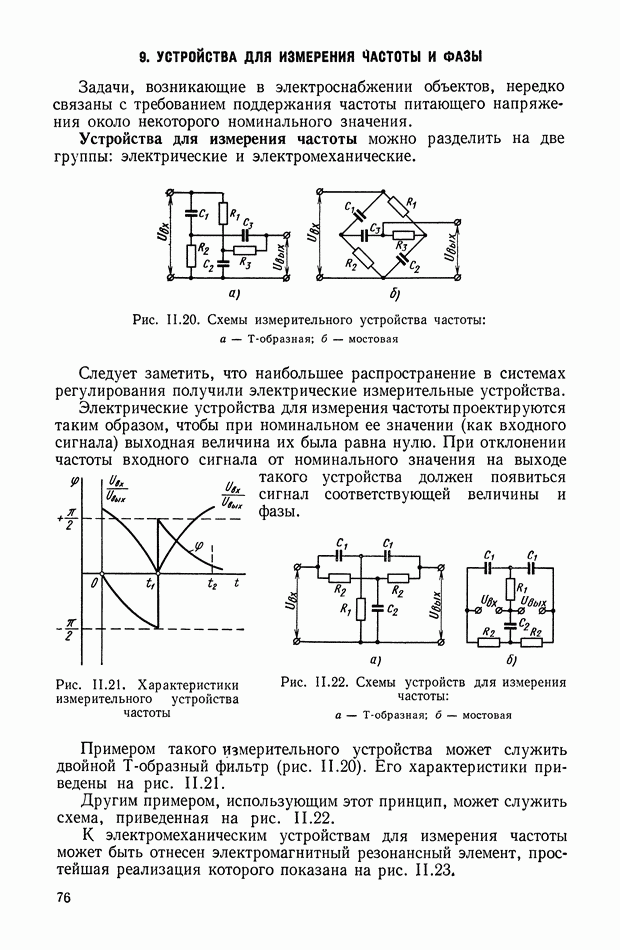
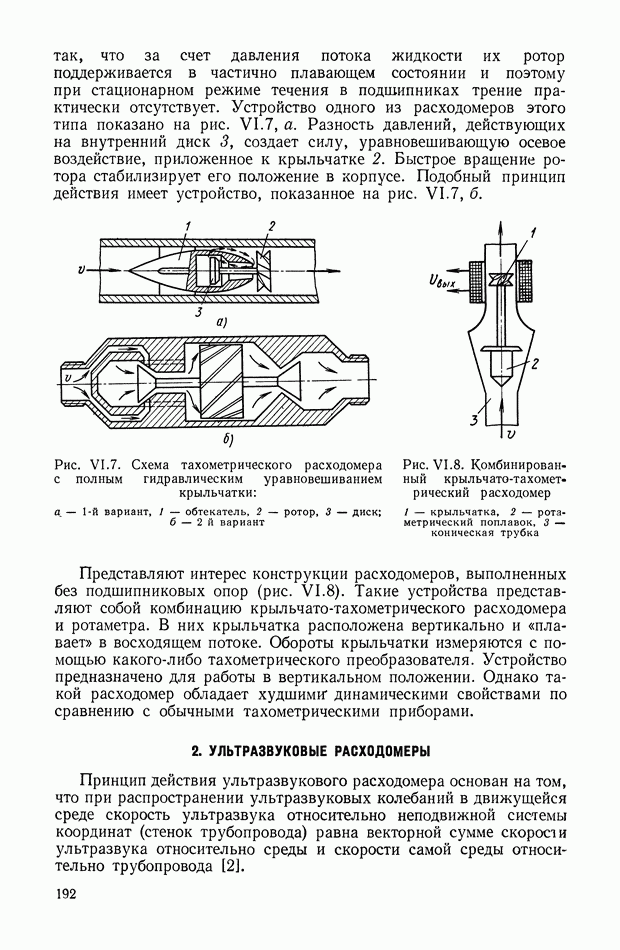
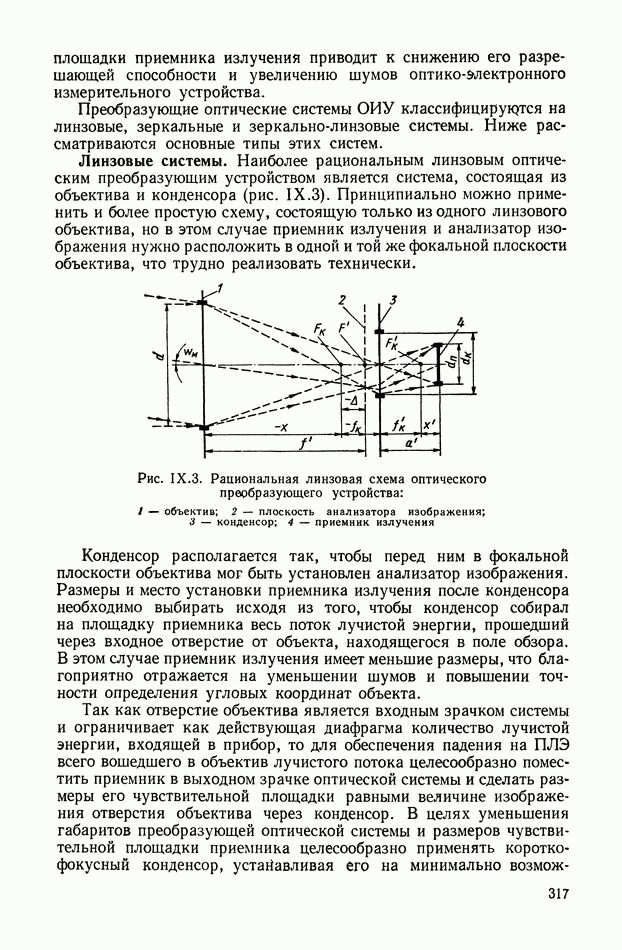
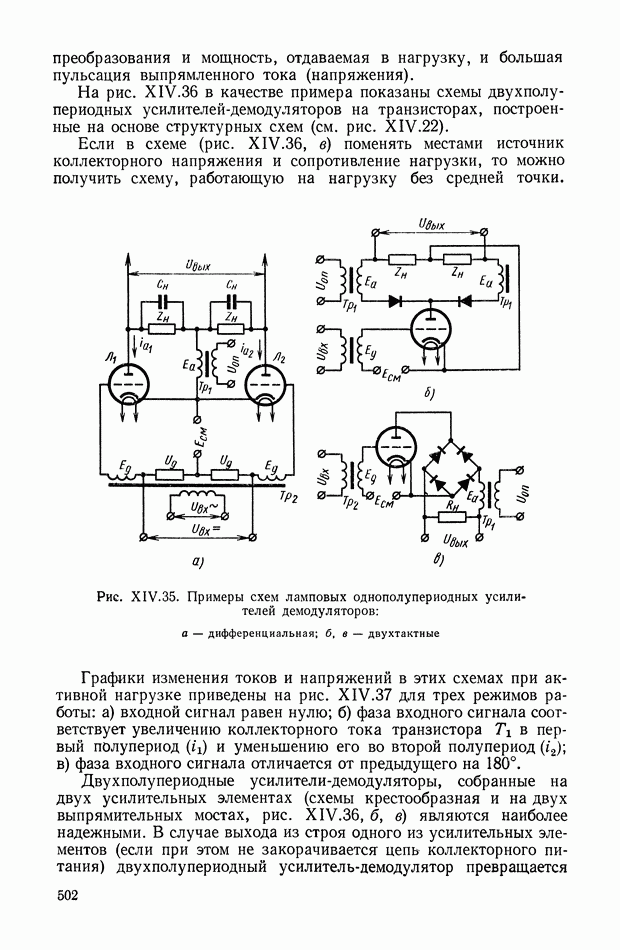
Схемы пружинных акселерометров. Принципиальная схема пружинного акселерометра, предназначенного для измерения линейных ускорений, приведена на рис. VII. 13.

Рис. VII. 13. Схема пружинного акселерометра для измерения линейных ускорений
Чувствительным элементом служит инерционная масса  подвешенная на двух пружинах 2, прикрепленных в точках
подвешенная на двух пружинах 2, прикрепленных в точках  к корпусу 3, жестко связанному с движущимся объектом. Линия
к корпусу 3, жестко связанному с движущимся объектом. Линия  называемая измерительной осью, параллельна той оси движущегося объекта, по которой нужно измерить ускорение х. При отсутствии ускорений натяжение пружин одинаково и масса располагается в среднем (нейтральном) положении. Если объект движется с постоянным линейным ускорением х, то масса перемещается на некоторую величину
называемая измерительной осью, параллельна той оси движущегося объекта, по которой нужно измерить ускорение х. При отсутствии ускорений натяжение пружин одинаково и масса располагается в среднем (нейтральном) положении. Если объект движется с постоянным линейным ускорением х, то масса перемещается на некоторую величину  при которой инерционная сила
при которой инерционная сила  возникающая вследствие ускоренного движения массы в абсолютном пространстве, уравновешивается силой Рупр упругости пружин. Выражая эти силы через параметры прибора
возникающая вследствие ускоренного движения массы в абсолютном пространстве, уравновешивается силой Рупр упругости пружин. Выражая эти силы через параметры прибора

где  — инерционная масса;
— инерционная масса;
 — суммарная жесткость двух, пружин, получим условие равновесия (при
— суммарная жесткость двух, пружин, получим условие равновесия (при  ):
):

отсюда величина установившегося смещения массы

где  — чувствительность прибора;
— чувствительность прибора; 
Для успокоения колебаний инерционной массы в переходном режиме служит демпфер 4, создающий силу, пропорциональную скорости перемещения массы относительно корпуса 3. Применяют магнитноиндукционные, жидкостные или воздушные демпферы. У воздушных демпферов из-за сжимаемости воздуха демпфирующая сила запаздывает по отношению к скорости движения подвижной системы, что является их недостатком. Для получения электрического сигнала перемещение массы преобразуется в электрическую величину с помощью потенциометрического преобразователя 5. Могут быть использованы также индуктивные, емкостные и другие преобразователи.
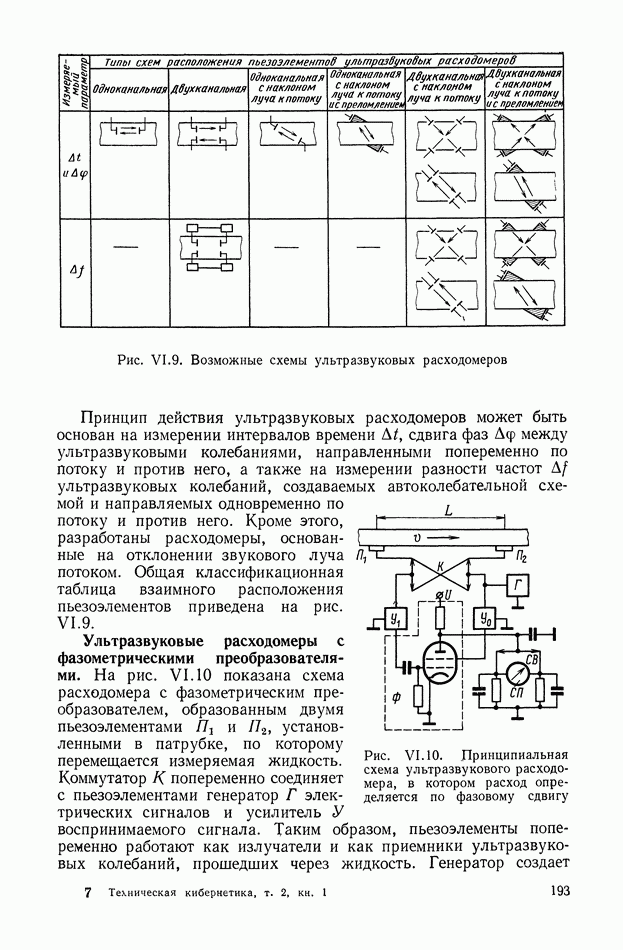
Инструментальные погрешности акселерометров возникают в результате влияния ряда внешних и внутренних факторов, к числу которых относятся силы трения и люфты в опорах и направляющих, гистерезис и упругое последействие измерительной пружины, изменение модуля упругости пружины при изменении окружающей температуры, неравномерность характеристики преобразователя перемещений, изменение характеристики преобразователя перемещений при изменении окружающей температуры и режимов электрического питания и др. Точность акселерометра определяется главным образом величиной рассеяния погрешностей относительно среднего значения. Мерой рассеяния служит среднее квадратическое отклонение погрешности, величина которого в значительной степени зависит от соотношения между силами трения в опорах и направляющих и инерционными силами, развиваемыми массой при ее движении с ускорением. В связи с этим одним из наиболее ответственных элементов конструкции является подвес подвижной системы акселерометра, обеспечивающий необходимую степень свободы инерционной массы. Конструкция также должна обеспечивать сведение к минимуму влияния боковых ускорений, направленных перпендикулярно измерительной оси. Конструкция подвеса с направляющей для поступательного движения инерционного элемента проста (рис. VII. 14,а), но обладает значительной нечувствительностью, величина которой пропорциональна составляющей ускорения у, направленной перпендикулярно оси чувствительности и прижимающей массу к направляющей. Подвеска массы на направляющей с трением качения (см. рис. VII. 14, б) более рациональна. Зона нечувствительности при этом для одинаковой массы уменьшается примерно в  раз (где R — радиус ролика,
раз (где R — радиус ролика,  — радиус опорной цапфы ролика).
— радиус опорной цапфы ролика).
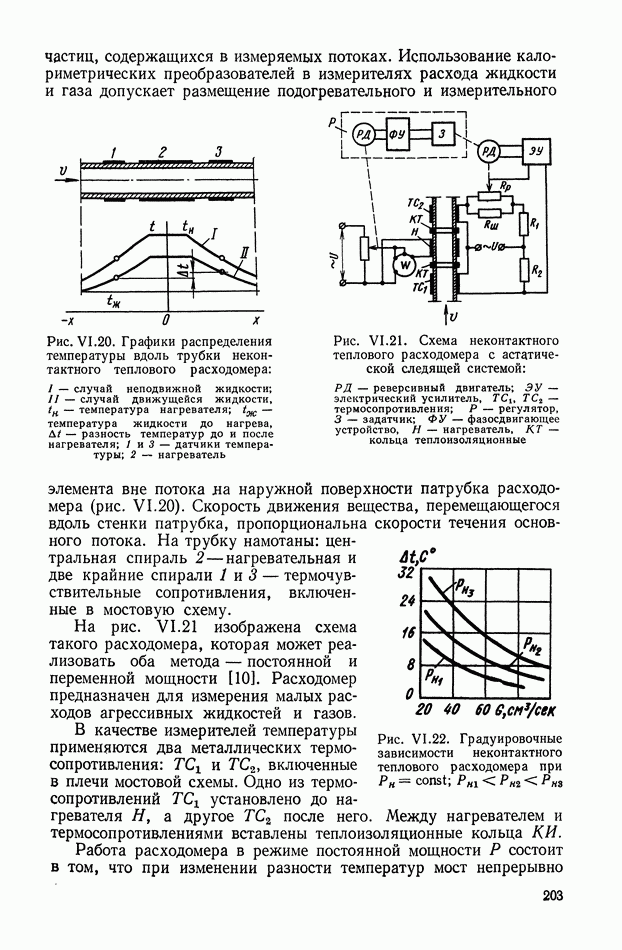
Маятниковый подвес инерционной массы (рис. VII. 15) позволяет уменьшить зону нечувствительности. Измерительная ось 
такого элемента перпендикулярна линии  соединяющей ось вращения с центром тяжести маятника, находящегося в нейтральном положении.
соединяющей ось вращения с центром тяжести маятника, находящегося в нейтральном положении.

Рис. VII. 14. Подвес инерционной массы на направляющей: а — с трением скольжения; б — с трением качения
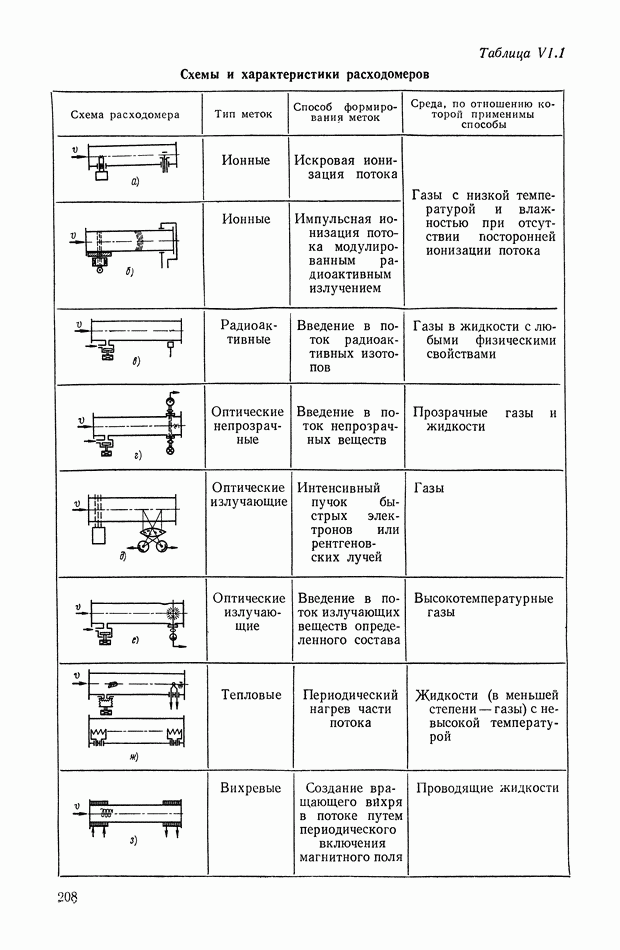
При постоянном линейном ускорении  направленном по измерительной оси
направленном по измерительной оси  равновесному положению маятника 1 при отклонении от нейтрали
равновесному положению маятника 1 при отклонении от нейтрали  будет соответствовать угол а (рис. VII. 16), при котором момент инерционной силы уравновешивается моментом пружины 2:
будет соответствовать угол а (рис. VII. 16), при котором момент инерционной силы уравновешивается моментом пружины 2:

где  — масса маятника;
— масса маятника;
 — расстояние от оси вращения до центра тяжести маятника;
— расстояние от оси вращения до центра тяжести маятника;  — угловая жесткость пружины.
— угловая жесткость пружины.

Рис. VII. 15. Маятниковый подвес

Рис. VII. 16. Схема действия инерционных сил на маятниковый чувствительный элемент
Как видно  угол а не пропорционален ускорению х. При малых а
угол а не пропорционален ускорению х. При малых а  можно приближенно считать установившийся угол отклонения маятника пропорциональным линейному ускорению:
можно приближенно считать установившийся угол отклонения маятника пропорциональным линейному ускорению:

где  — чувствительность прибора;
— чувствительность прибора; 
Маятниковый подвес по сравнению с подвесом на направляющих позволяет уменьшить зону нечувствительности при одинаковой массе примерно в  раз, где
раз, где  — радиус опорной цапфы маятника.
— радиус опорной цапфы маятника.
При одновременном действии продольного и поперечного ускорений х и у (рис. VII. 16, б) условием равновесия системы будет равенство нулю алгебраической суммы моментов инерционных сил и сил упругости пружины:

При малых углах можно принять  Тогда
Тогда  откуда
откуда

Пользуясь выражениями (VII.18) и (VII.19), можно определить относительную ошибку в измерении ускорения х, возникающую под влиянием ускорения у:

поскольку

Таким образом, относительная ошибка маятникового акселерометра, вызванная влиянием боковых ускорений, уменьшается с понижением чувствительности  Эту ошибку, как и ошибку, обусловленную влиянием угловых ускорений, действующих вокруг оси подвеса, можно скомпенсировать применением двух параллельных маятников, кинематически связанных между собой антипараллелограммом (рис. VII.17, а) или парой зубчатых масс (рис. VII. 17, б).
Эту ошибку, как и ошибку, обусловленную влиянием угловых ускорений, действующих вокруг оси подвеса, можно скомпенсировать применением двух параллельных маятников, кинематически связанных между собой антипараллелограммом (рис. VII.17, а) или парой зубчатых масс (рис. VII. 17, б).
Для устранения сил сухого трения, люфтов и исключения влияния поперечных ускорений у и угловых ускорений  в линейных акселерометрах иногда применяют упругий подвес (рис. VII.18) с закреплением инерционной массы на двух плоских пружинах или мембранах.
в линейных акселерометрах иногда применяют упругий подвес (рис. VII.18) с закреплением инерционной массы на двух плоских пружинах или мембранах.
Пружинные акселерометры, предназначенные для измерения угловых ускорений, отличаются тем, что обладают лишь одной степенью свободы вращательного движения относительно измерительной оси  (рис. VII. 19).
(рис. VII. 19).
Мерой измеряемого углового ускорения  служит угловое перемещение а инерционной массы 2, при котором момент инерционных сил Мин уравновешивается моментом упругих сил Мупр противодействующей пружины 1. Выражая моменты через параметры прибора
служит угловое перемещение а инерционной массы 2, при котором момент инерционных сил Мин уравновешивается моментом упругих сил Мупр противодействующей пружины 1. Выражая моменты через параметры прибора

где  — момент инерции массы относительно оси
— момент инерции массы относительно оси  — угловатая жесткость пружины,
— угловатая жесткость пружины,
получим условие равновесия 

Отсюда установившийся угол поворота массы

Угловой акселерометр содержит демпфер 4, потенциометр 3 или преобразователь угловых перемещений другого типа. Инструментальная точность угловых акселерометров определяется в основном теми же факторами, что и точность линейных акселерометров.

Рис. VII. 17. Кинематические схемы компенсации влияния поперечных ускорений у и угловых ускорений  а — схема с антипараллелограммом; б — схема с зубчатой передачей
а — схема с антипараллелограммом; б — схема с зубчатой передачей

Рис. VII. 18. Упругий подвес линейного акселерометра: 1 — масса; 2 и 3 — плоские пружины
Конструкция подвеса должна обеспечивать минимальный момент трения и люфт. Подвес углового акселерометра должен минимизировать влияние угловых ускорений относительно осей, перпендикулярных измерительной оси  а также влияние линейных ускорений, направленных по любой оси. Для этого инерционная масса должна быть тщательно сбалансирована относительно оси вращения.
а также влияние линейных ускорений, направленных по любой оси. Для этого инерционная масса должна быть тщательно сбалансирована относительно оси вращения.
В конструкции углового акселерометра могут быть использованы опоры с трением скольжения, с трением качения (шарикоподшипники) и упругие подвесы (рис. VII.20).
В прецизионных акселерометрах, предназначенных для измерения как линейных, так и угловых ускорений, применяют специальные виды подвесов, позволяющих снизить порог чувствительности акселерометра до весьма малого уровня. К таким относится поплавковый акселерометр, в котором маятник помещен внутрь пустотелого цилиндрического поплавка, погруженного в жидкость. Объем поплавка выбирают из расчета равенства подъемной силы весу подвижной системы. Трение поверхности поплавка о жидкость можно использовать для создания демпфирующего момента. В
случае несовпадения центра гидростатических сил с осью вращения поплавка возникает дополнительная погрешность акселерометра при изменении окружающей температуры, поскольку изменяются удельный вес жидкости и, соответственно, подъемная сила поплавка. Для уменьшения этой погрешности применяют объемную балансировку поплавка с целью совмещения центра гидростатических сил с осью вращения и термостатируют прибор. В прецизионных акселерометрах могут быть использованы и другие способы снижения трения в опорах подвеса, например, возможно использование газодинамических опор, взвешивание инерционной массы в электромагнитном или электростатическом поле и др.

Рис. VII. 19. Схема пружинного акселерометра для измерения угловых ускорений

Рис. VII.20. Упругий подвес углового акселерометра: а — с торсионом; б — с крестообразным пружинами
Динамические характеристики акселерометров. Уравнение движения подвижной системы акселерометра для измерения линейных ускорений (см. рис. VII. 13) можно записать в виде

где х — измеряемое ускорение;
 — относительные ускорение, скорость и перемещение массы
— относительные ускорение, скорость и перемещение массы 
— коэффициенты демпфирования и жесткость.
Разделив все члены уравнения (VI 1.21) на си перепишем его следующим образом:

где  — постоянная времени акселерометра;
— постоянная времени акселерометра;  степень успокоения
степень успокоения 
Принимая х за входную координату,  — за выходную, получим передаточную функцию акселерометра в виде
— за выходную, получим передаточную функцию акселерометра в виде

Уравнение движения подвижной системы акселерометра, измеряющего угловые ускорения (рис. VII. 19), имеет вид

или

где  — измеряемое угловое ускорение;
— измеряемое угловое ускорение;
 — относительное угловое ускорение, скорость и отклонение массы;
— относительное угловое ускорение, скорость и отклонение массы;
 — момент инерции массы;
— момент инерции массы;  — коэффициент углового демпфирования и жесткость;
— коэффициент углового демпфирования и жесткость;

Принимая  за входную,
за входную,  за выходную величину, получим передаточную функцию, аналогичную (VI 1.23). Установим связь между собственной частотой <и диапазоном измерения акселерометра. Для акселерометра, измеряющего линейные ускорения с поступательным перемещением массы, собственная частота недемпфированных колебаний
за выходную величину, получим передаточную функцию, аналогичную (VI 1.23). Установим связь между собственной частотой <и диапазоном измерения акселерометра. Для акселерометра, измеряющего линейные ускорения с поступательным перемещением массы, собственная частота недемпфированных колебаний

где  — диапазон измерения;
— диапазон измерения;
 — максимальный ход массы, отвечающий в статике ускорению
— максимальный ход массы, отвечающий в статике ускорению  .
.
Обозначив  — ускорение силы тяжести), можно собственную частоту выразить через
— ускорение силы тяжести), можно собственную частоту выразить через  — статический прогиб массы под влиянием силы тяжести:
— статический прогиб массы под влиянием силы тяжести:

Для акселерометра с маятниковым подвесом (рис. VII. 15) выражение для собственной частоты имеет вид

где  — максимальное линейное перемещение центра тяжести;
— максимальное линейное перемещение центра тяжести;
 — линейное перемещение центра тяжести под действием силы веса;
— линейное перемещение центра тяжести под действием силы веса;
 — максимальный угол поворота маятника, соответствующий в статике ускорению
— максимальный угол поворота маятника, соответствующий в статике ускорению 
 - момент инерции подвижной системы;
- момент инерции подвижной системы;
 — момент инерции маятника с массой
— момент инерции маятника с массой  подвижной системы, условно сосредоточенной в центре ее тяжести;
подвижной системы, условно сосредоточенной в центре ее тяжести;
 — коэффициент увеличения момента инерции из-за пространственной протяженности массы.
— коэффициент увеличения момента инерции из-за пространственной протяженности массы.
Наконец, для акселерометра, измеряющего угловые ускорения с диапазоном измерения  имеем:
имеем:

откуда собственная частота

где  — максимальный угол поворота инерционного элемента, отвечающий в статике угловому ускорению г|Зт.
— максимальный угол поворота инерционного элемента, отвечающий в статике угловому ускорению г|Зт.
Рассмотрим теперь зависимость динамической ошибки акселерометра от его параметров и условий измерения.
При собственных колебаниях подвижной системы акселерометра в уравнениях (VI 1.22) и (VI 1.24) получается одинаковый результат для относительной динамической ошибки:

где

 — установившиеся значения
— установившиеся значения  ; х — безразмерное время;
; х — безразмерное время; 
Принимая безразмерное время, в течение которого динамическая ошибка 6 уменьшается до допустимой величины  и впредь не будет ее превышать, за длительность переходного процесса хппу находим оптимальное значение
и впредь не будет ее превышать, за длительность переходного процесса хппу находим оптимальное значение  при котором величина
при котором величина  будет минимальной.
будет минимальной.

Рис. VII.21. Графики безразмерной динамической ошибки
Графики безразмерной динамической ошибки  в соответствии с выражением (VI 1.25) показывают, что оптимальным будет такое значение
в соответствии с выражением (VI 1.25) показывают, что оптимальным будет такое значение  при котором минимум функции (VI 1.25) после первого перехода ее через нуль соответствует нижней границе допустимой ошибки, т. е. кривой 1 на (рис. VII.21). Этой кривой соответствует минимальное время переходного процесса
при котором минимум функции (VI 1.25) после первого перехода ее через нуль соответствует нижней границе допустимой ошибки, т. е. кривой 1 на (рис. VII.21). Этой кривой соответствует минимальное время переходного процесса  соответствующее допустимой ошибке в точке А.
соответствующее допустимой ошибке в точке А.
Допустим, что  Тогда период колебаний увеличивается, функция (VI 1.25) будет изображаться кривой 2, которая располагается правее кривой 1 и входит в зону допустимых ошибок в точке В, для которой
Тогда период колебаний увеличивается, функция (VI 1.25) будет изображаться кривой 2, которая располагается правее кривой 1 и входит в зону допустимых ошибок в точке В, для которой 
При  период колебаний уменьшается, но минимум функции выходит за пределы зоны
период колебаний уменьшается, но минимум функции выходит за пределы зоны  , следовательно, время
, следовательно, время  переходного
переходного
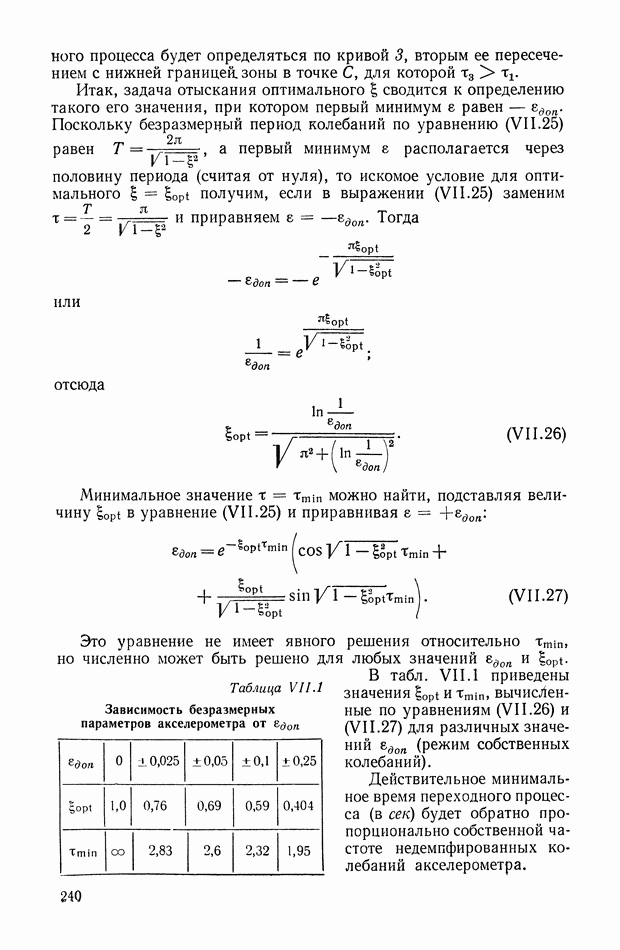
него процесса будет определяться по кривой 3, вторым ее пересечением с нижней границей, зоны в точке С, для которой 
Итак, задача отыскания оптимального  сводится к определению такого его значения, при котором первый минимум
сводится к определению такого его значения, при котором первый минимум  равен — едоп. Поскольку безразмерный период колебаний по уравнению (VI 1.25) равен
равен — едоп. Поскольку безразмерный период колебаний по уравнению (VI 1.25) равен  а первый минимум 8 располагается через половину периода (считая от нуля), то искомое условие для оптимального
а первый минимум 8 располагается через половину периода (считая от нуля), то искомое условие для оптимального  получим, если в выражении (VI 1.25) заменим
получим, если в выражении (VI 1.25) заменим  и приравняем
и приравняем  . Тогда
. Тогда

или

отсюда

Минимальное значение  можно найти, подставляя величину
можно найти, подставляя величину  в уравнение (VI 1.25) и приравнивая
в уравнение (VI 1.25) и приравнивая 

Это уравнение не имеет явного решения относительно  но численно может быть решено для любых значений гдоп и
но численно может быть решено для любых значений гдоп и 
В табл. VII. 1 приведены значения  и
и  вычисленные по уравнениям (VI 1.26) и (VI 1.27) для различных значений гдоп (режим собственных колебаний).
вычисленные по уравнениям (VI 1.26) и (VI 1.27) для различных значений гдоп (режим собственных колебаний).
Действительное минимальное время переходного процесса (в сек) будет обратно пропорционально собственной частоте недемпфированных колебаний акселерометра.
Таблица VI 1.1
Зависимость безразмерных параметров акселерометра от 

Например, при  Мсек получим
Мсек получим

Для вынужденных колебаний акселерометра ограничимся рассмотрением лишь синусоидального закона изменения входной величины

где А — амплитуда входного ускорения;
х — входная величина;
 — круговая частота.
— круговая частота.
Установившиеся колебания выходной величины  определяемые подстановкой
определяемые подстановкой  в выражение передаточной функции (VI 1.23), вычисляются по формуле
в выражение передаточной функции (VI 1.23), вычисляются по формуле

где В — амплитуда колебаний выходного сигнала,

Обозначив  получим коэффициент увеличения амплитуды:
получим коэффициент увеличения амплитуды:

Сдвиг фаз выходного сигнала равен

Если сдвиг фаз не регламентирован, то выбор оптимального значения  при синусоидальном характере изменения измеряемого ускорения зависит от допустимой ошибки по амплитуде
при синусоидальном характере изменения измеряемого ускорения зависит от допустимой ошибки по амплитуде  . В этом случае имеется оптимальное значение
. В этом случае имеется оптимальное значение  при котором полоса пропускания частот
при котором полоса пропускания частот  будет максимальной. Под полосой пропускания частот понимается предельное значение
будет максимальной. Под полосой пропускания частот понимается предельное значение  , при котором коэффициент х не выходит за пределы
, при котором коэффициент х не выходит за пределы  .
.

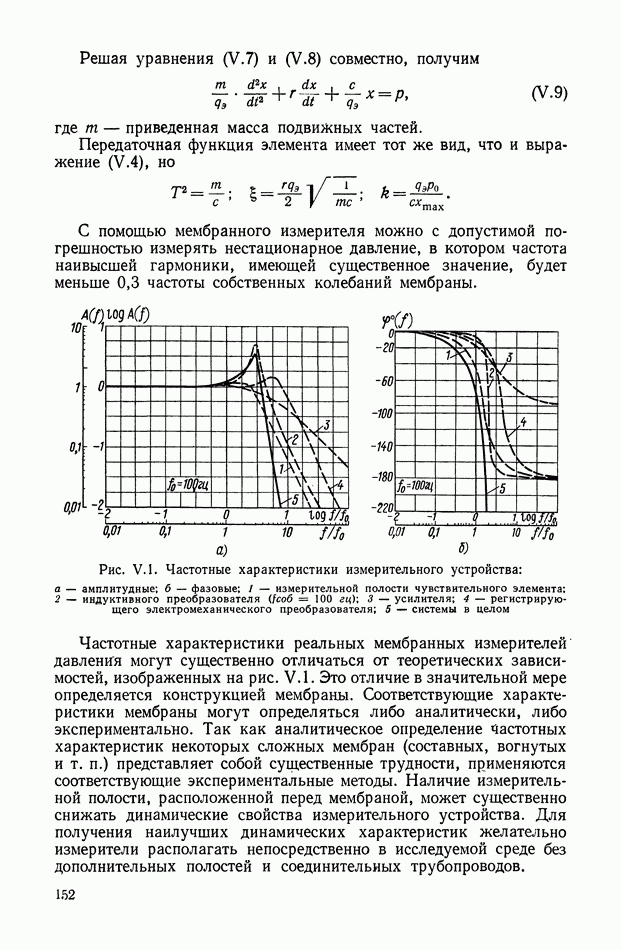
Рис. VI 1.22. Амплитудно-частотные характеристики
Наибольшей полосе пропускания  соответствует значение
соответствует значение  при котором максимум амплитудно-частотной характеристики совпадает с верхней границей
при котором максимум амплитудно-частотной характеристики совпадает с верхней границей  зоны допустимой динамической ошибки (кривая 1 на рис. VI 1.22). При этом полоса пропускания
зоны допустимой динамической ошибки (кривая 1 на рис. VI 1.22). При этом полоса пропускания  определяется точкой А пересечения кривой 1, построенной по уравнению (VII.28) с нижней границей
определяется точкой А пересечения кривой 1, построенной по уравнению (VII.28) с нижней границей  зоны допустимой ошибки. Эта полоса пропускания
зоны допустимой ошибки. Эта полоса пропускания  и Является максимальной,
и Является максимальной,
Предположим, что  . В этом случае функция
. В этом случае функция  изображается кривой 2, ниспадающая ветвь которой проходит левее кривой 1 и пересекает нижнюю границу зоны в точке В, для которой
изображается кривой 2, ниспадающая ветвь которой проходит левее кривой 1 и пересекает нижнюю границу зоны в точке В, для которой 
Если же  то максимум функции
то максимум функции  выходит за пределы верхней границы
выходит за пределы верхней границы  и, следовательно, полоса пропускания будет определяться по кривой 3. Эта кривая первый раз пересекает верхнюю границу зоны в точке С, для которой
и, следовательно, полоса пропускания будет определяться по кривой 3. Эта кривая первый раз пересекает верхнюю границу зоны в точке С, для которой 
Таким образом, задача отыскания оптимального  сводится к нахождению такого значения Е, для которого максимум функции (VI 1.28) равен
сводится к нахождению такого значения Е, для которого максимум функции (VI 1.28) равен  .
.
Для нахождения максимума х произведем в уравнении (VI 1.28) замену  и приравняем нулю первую производную
и приравняем нулю первую производную  по у:
по у:

Первое решение, получаемое при  соответствует минимуму х, а второе — максимуму х, которое получается, если приравнять числитель нулю:
соответствует минимуму х, а второе — максимуму х, которое получается, если приравнять числитель нулю:

откуда

Подставляя полученное значение  в уравнение (VI 1.28) и приравнивая
в уравнение (VI 1.28) и приравнивая  , находим условие для оптимального коэффициента
, находим условие для оптимального коэффициента 

отсюда

Максимальную безразмерную полосу пропускания частот  можно определить, подставляя в уравнение (VI 1.28) значения
можно определить, подставляя в уравнение (VI 1.28) значения  ,
,

отсюда, заменив предварительно  по формуле (VI 1.29) получим
по формуле (VI 1.29) получим

В общем случае колебания линейной измерительной системы акселерометра складываются из собственных и вынужденных колебаний. График переходной функции при этом определяется полным решением дифференциального уравнения (VI 1.22) или (VI 1.24) и зависит от характера изменения ускорения, измеряемого акселерометром [6].
Таблица VI 1.2
Зависимость безразмерных параметров акселерометра от 

В табл: VI 1.2 приведены значения  вычисленные по уравнениям (VI 1.29) и (VI 1.30) для различных значений гдоп (режим вынужденных колебаний).
вычисленные по уравнениям (VI 1.29) и (VI 1.30) для различных значений гдоп (режим вынужденных колебаний).
Действительная максимальная полоса пропускания  будет пропорциональна собственной частоте недемпфированных колебаний акселерометра.
будет пропорциональна собственной частоте недемпфированных колебаний акселерометра.
Например, при 

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 1. МОСТОВЫЕ СХЕМЫ
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
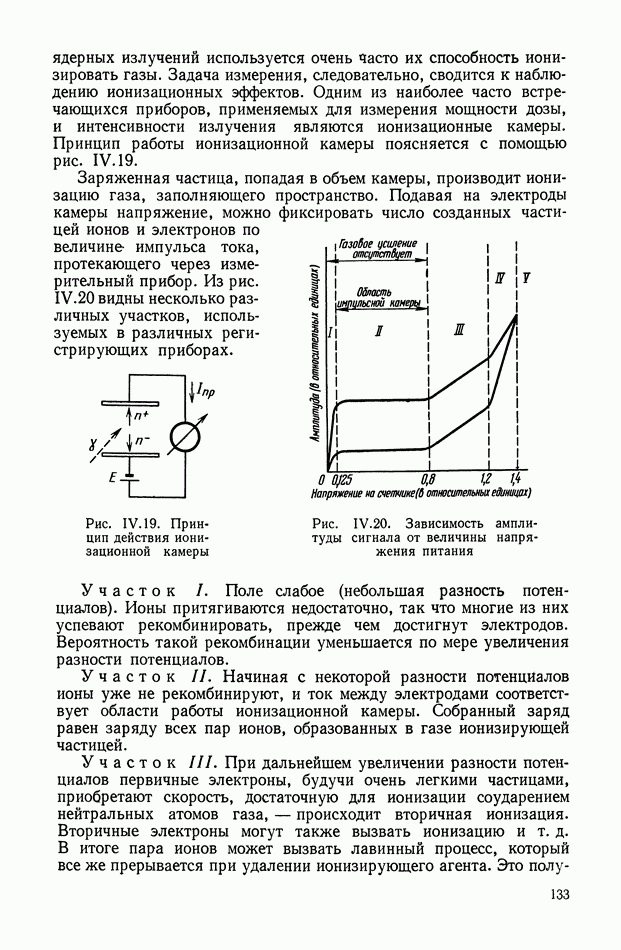
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
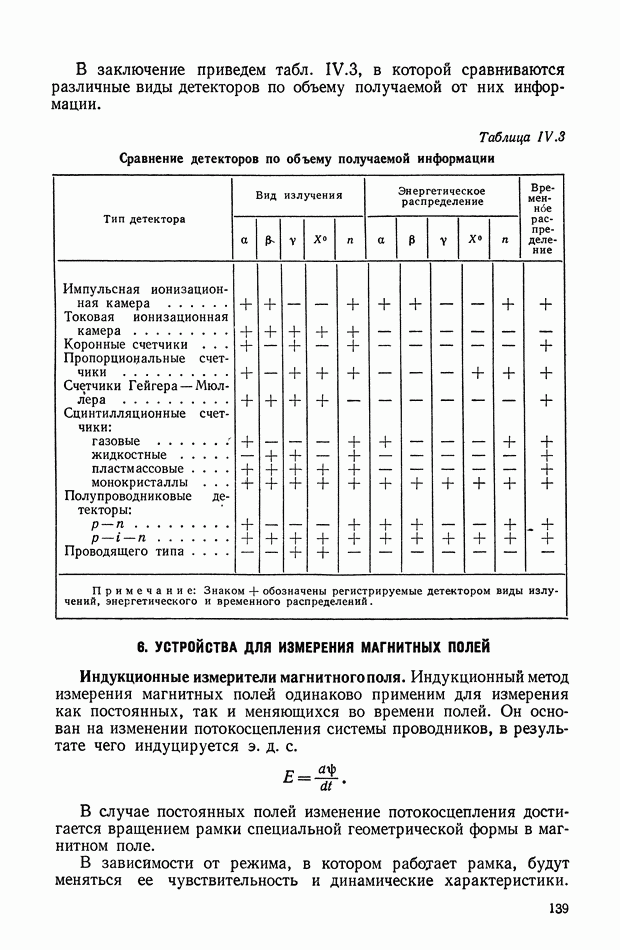
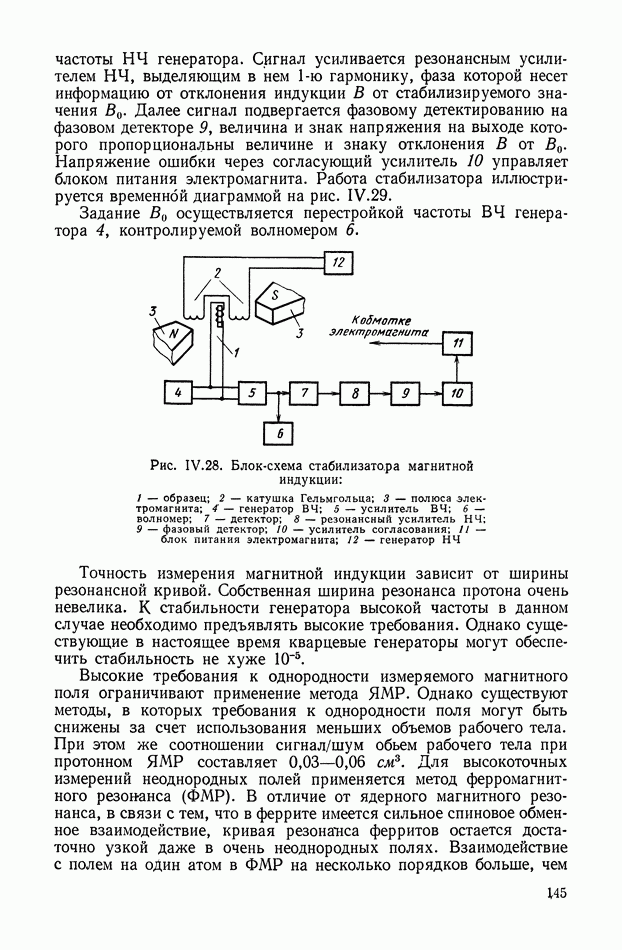
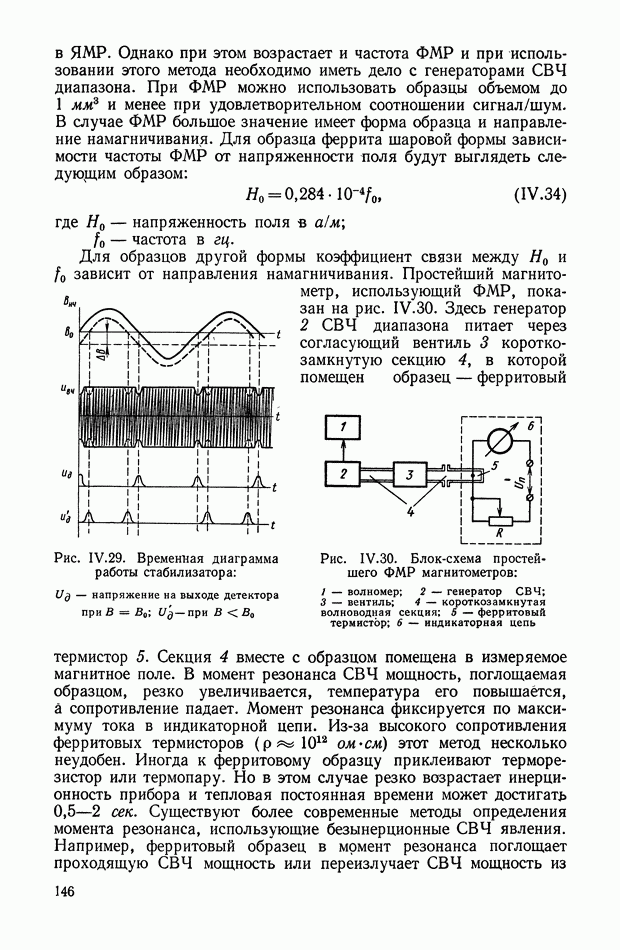
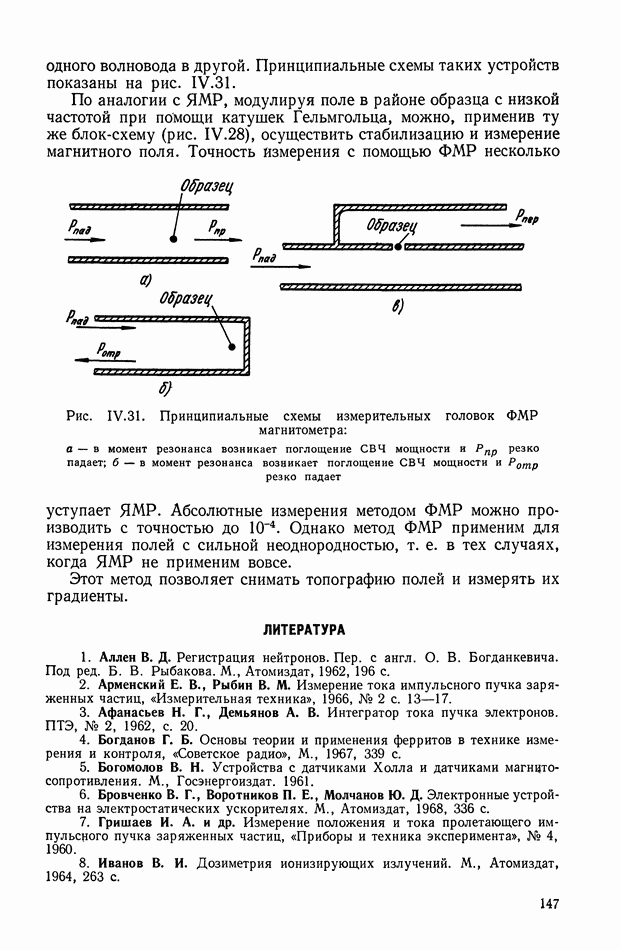
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
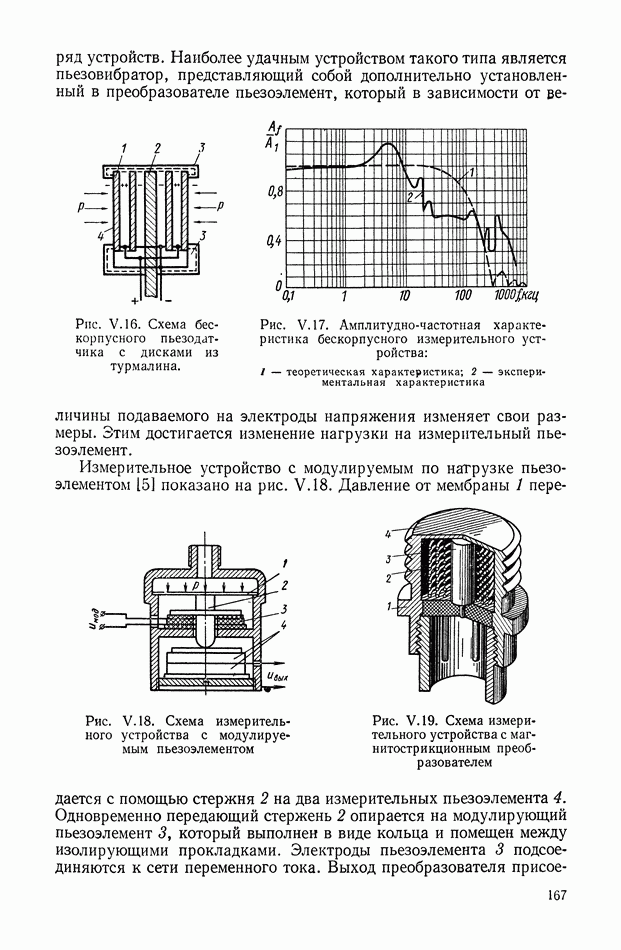
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
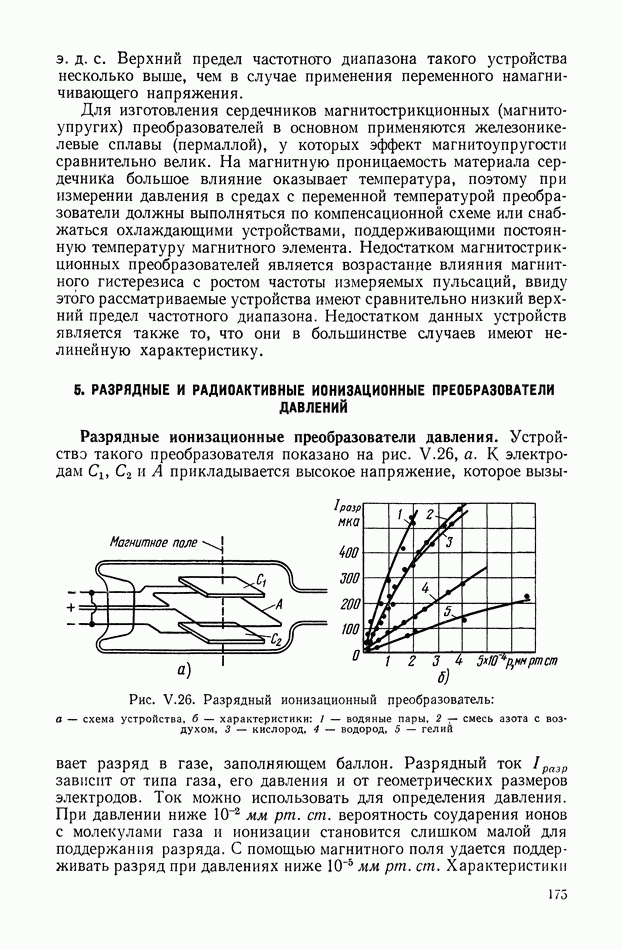
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
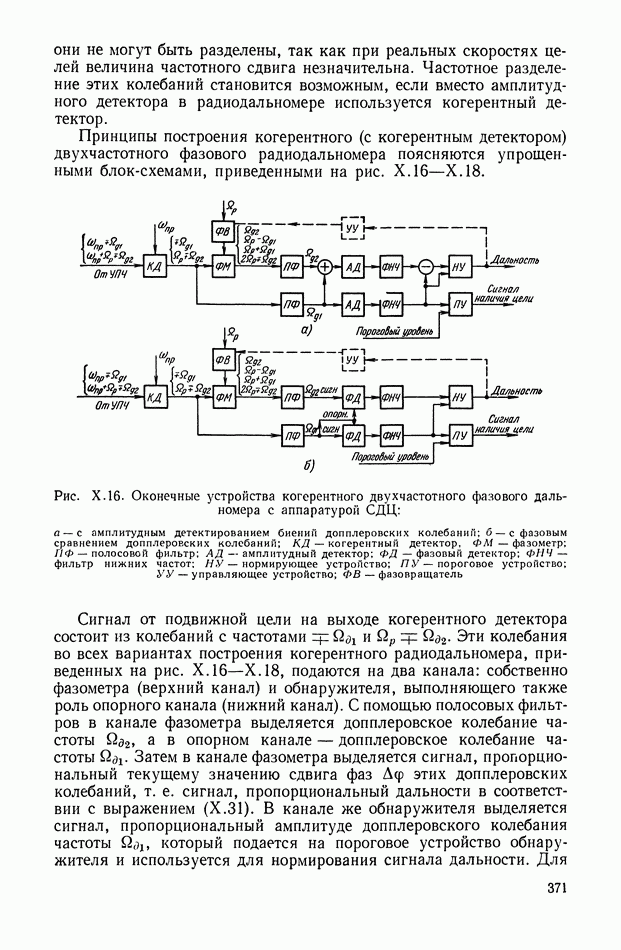
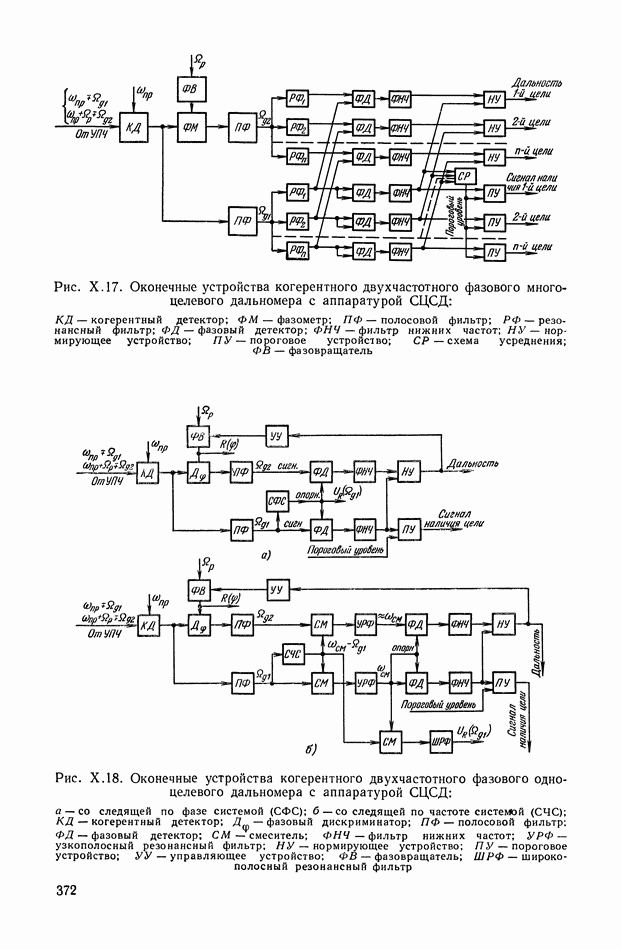
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
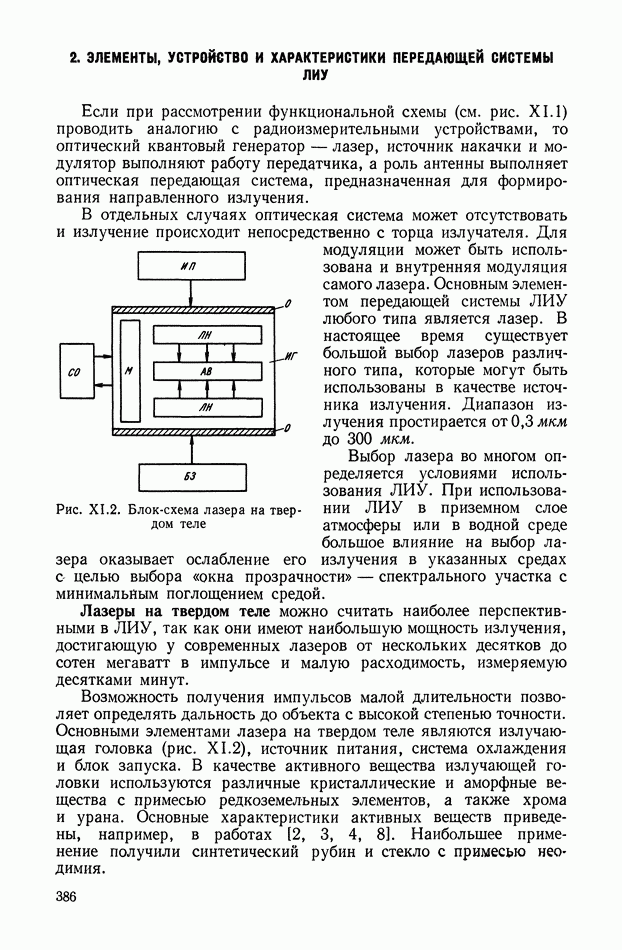
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 1. МОДУЛЯТОРЫ
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
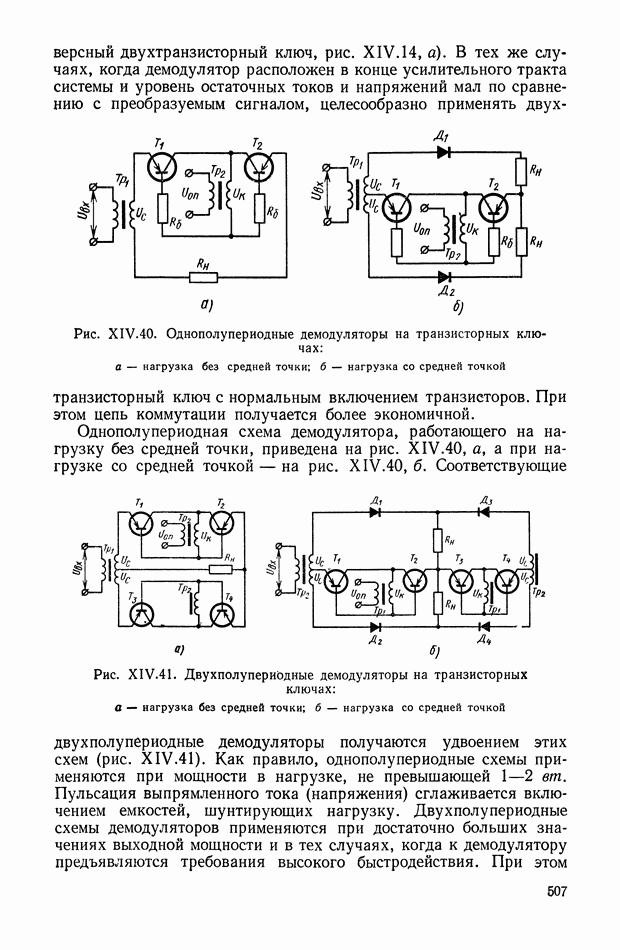
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
- Двухполупериодные демодуляторы на диодах.
- Однополупериодные усилители-демодуляторы.
- Двухполупериодные усилители-демодуляторы.
- Демодуляторы на транзисторных ключах.
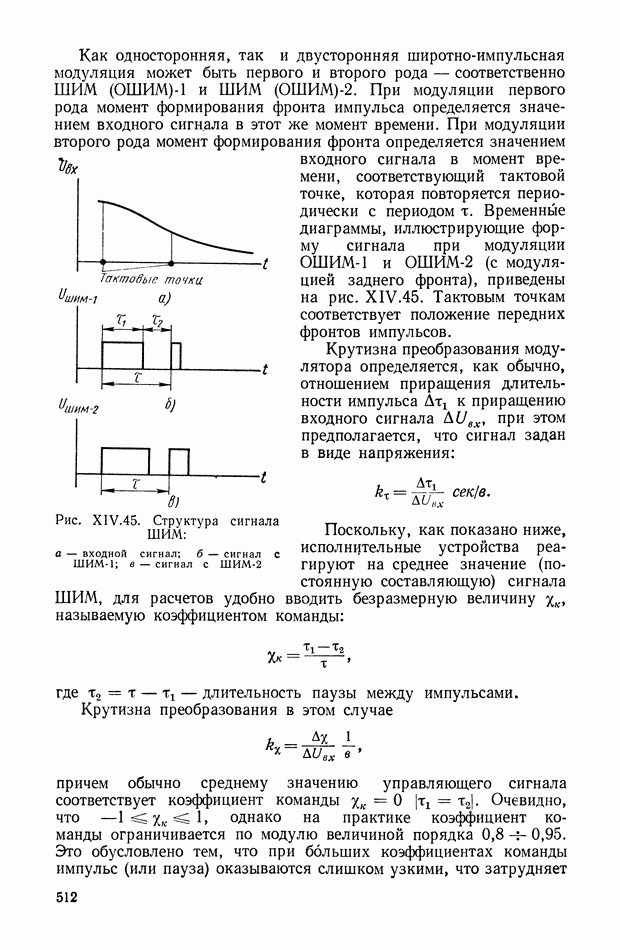
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
- Сильфоны.
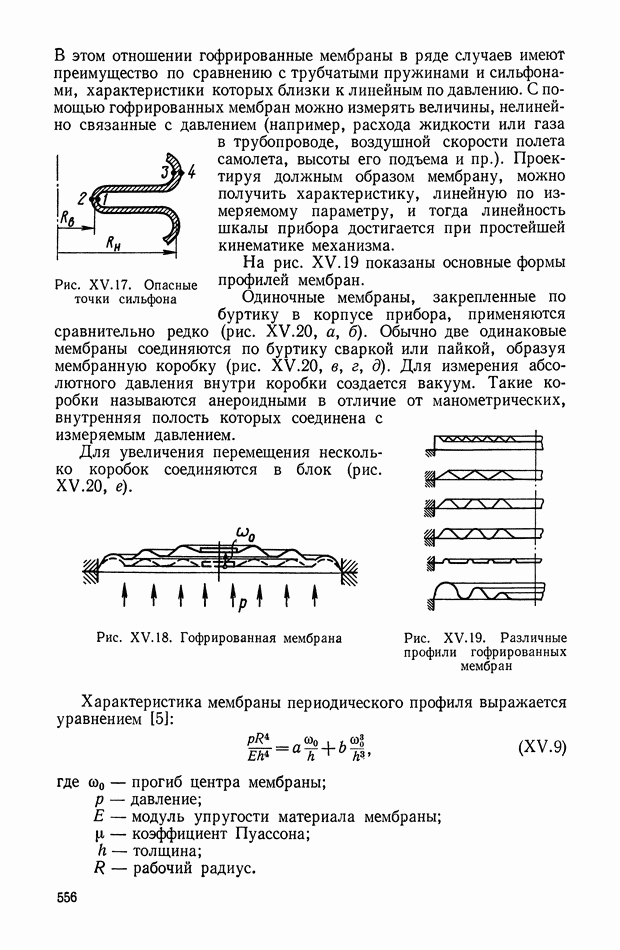
- Гофрированные мембраны.
- Гибкие диафрагмы.
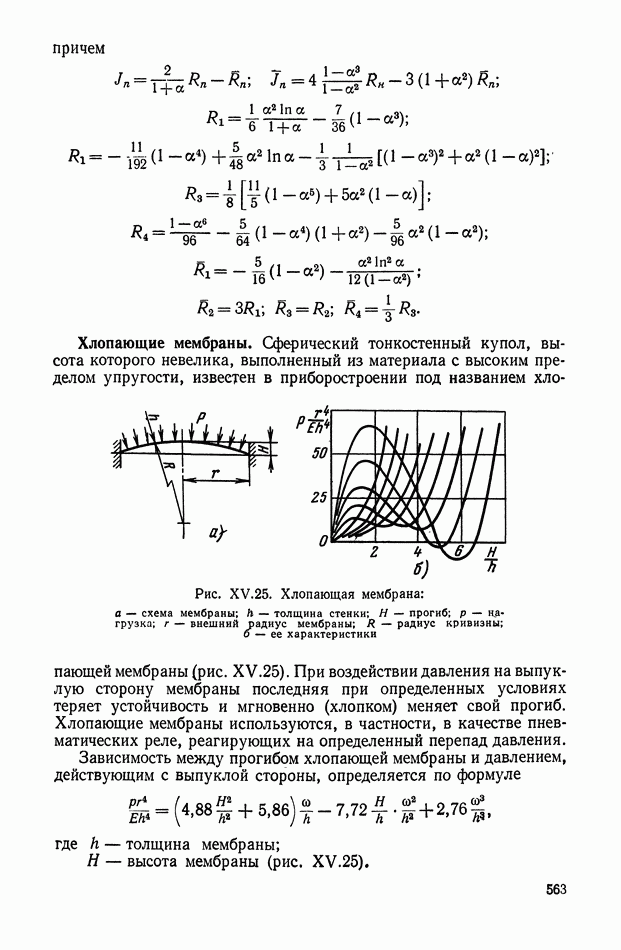
- Хлопающие мембраны.
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
- Пневмоэлектроконтактные преобразователи линейных величин.
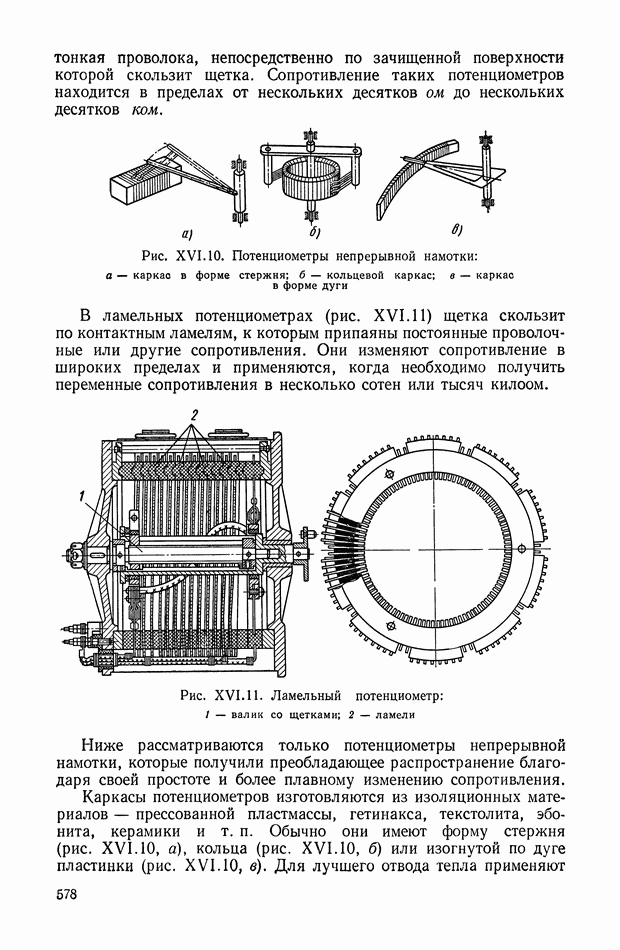
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
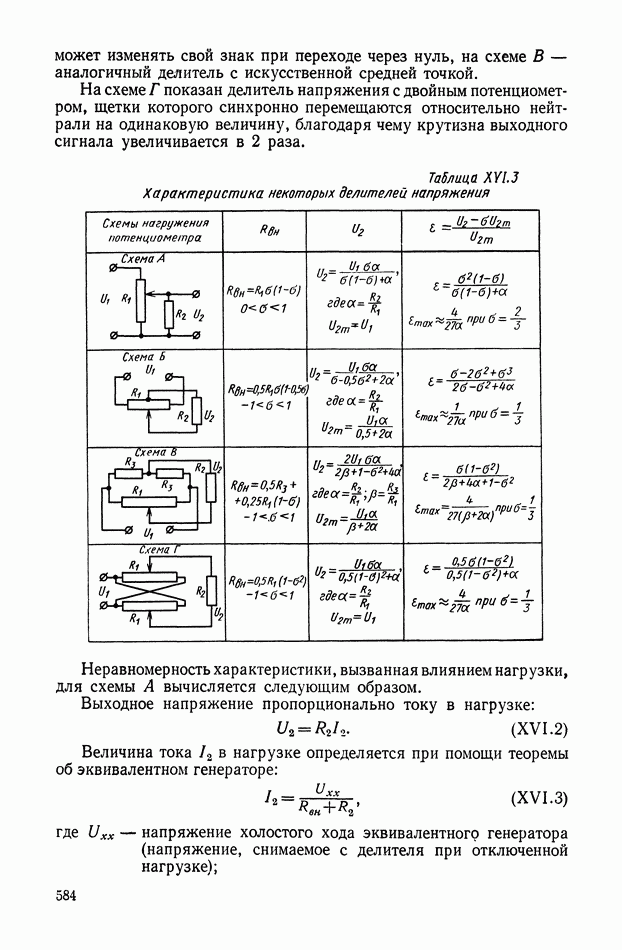
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
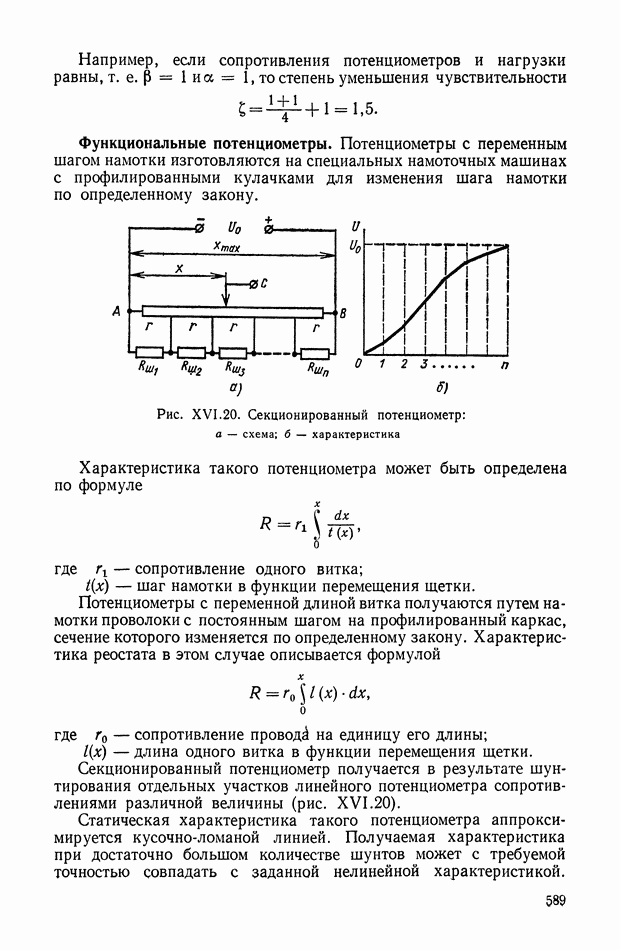
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
- Работа сельсинов в трансформаторном режиме.
- Устранение ложного нуля в двухскоростной системе.
- Схемы синхронизаторов.
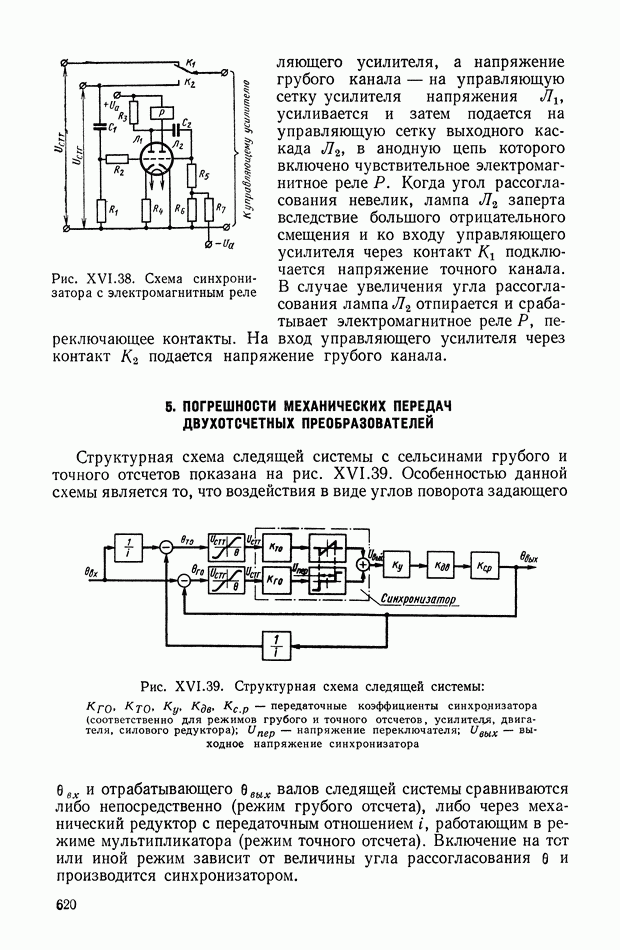
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
- Индукционные редуктосины.
- Индуктосины.
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- Емкостный редуктосин.
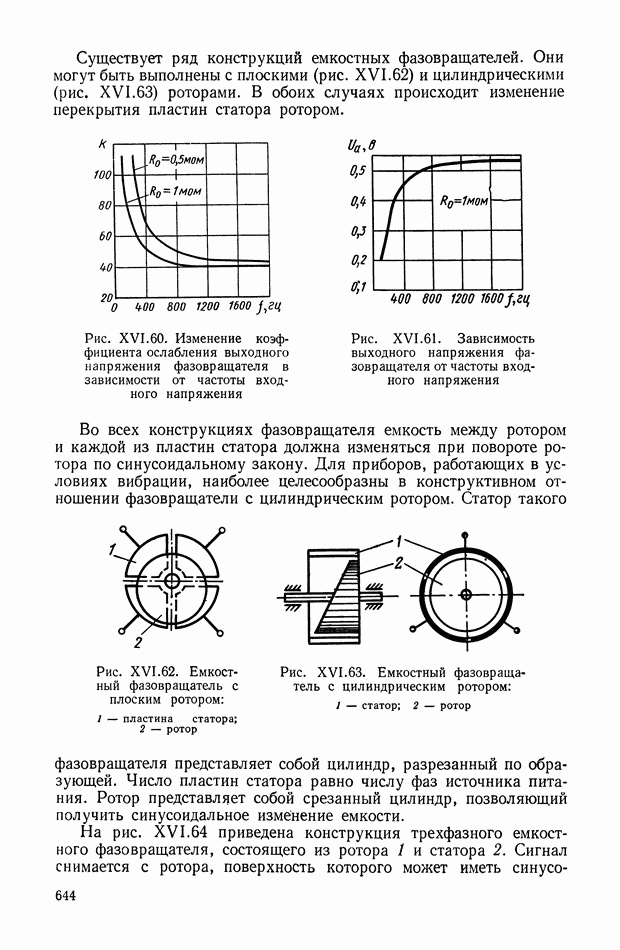
- Емкостный фазовращатель.
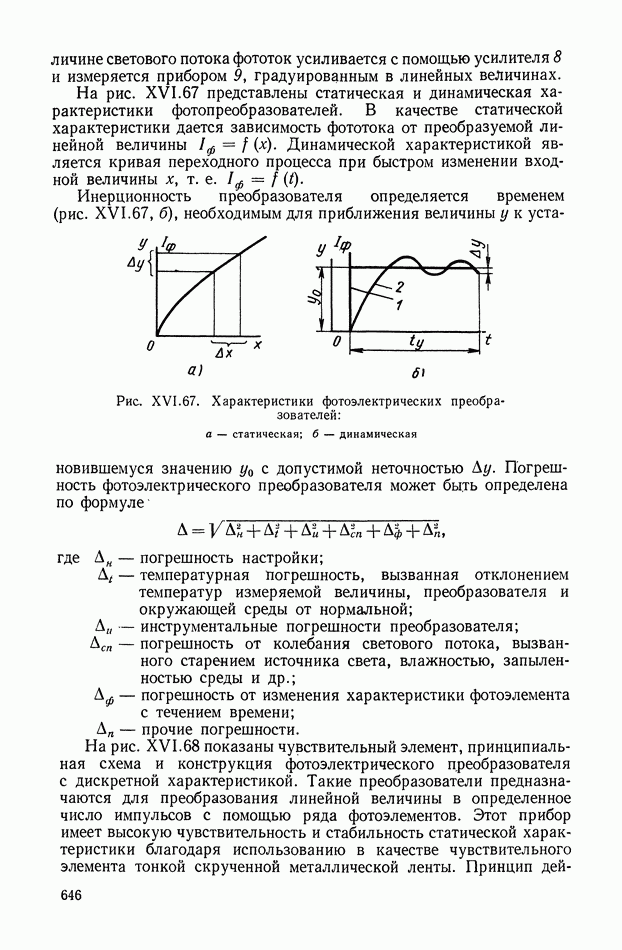
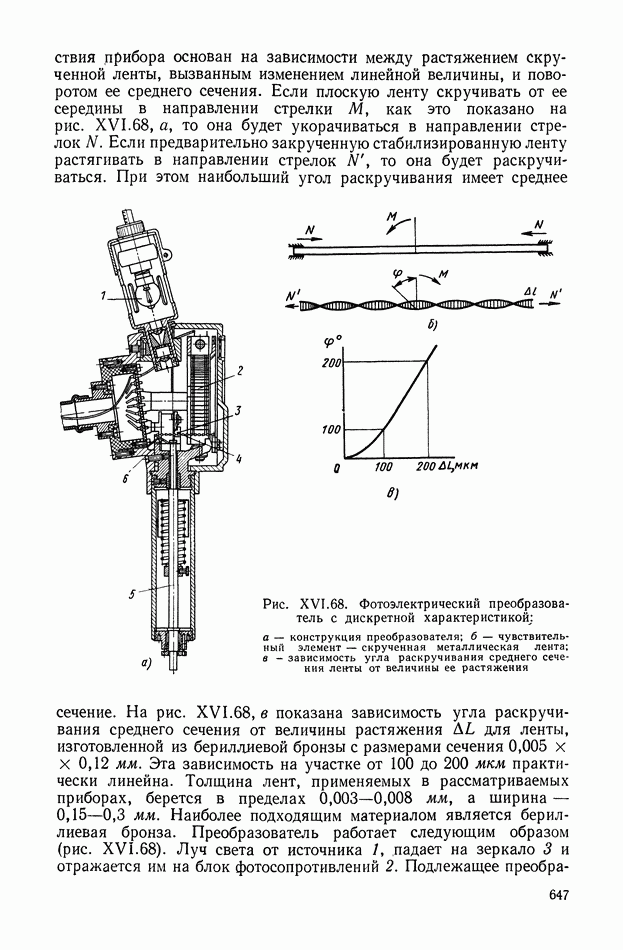
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
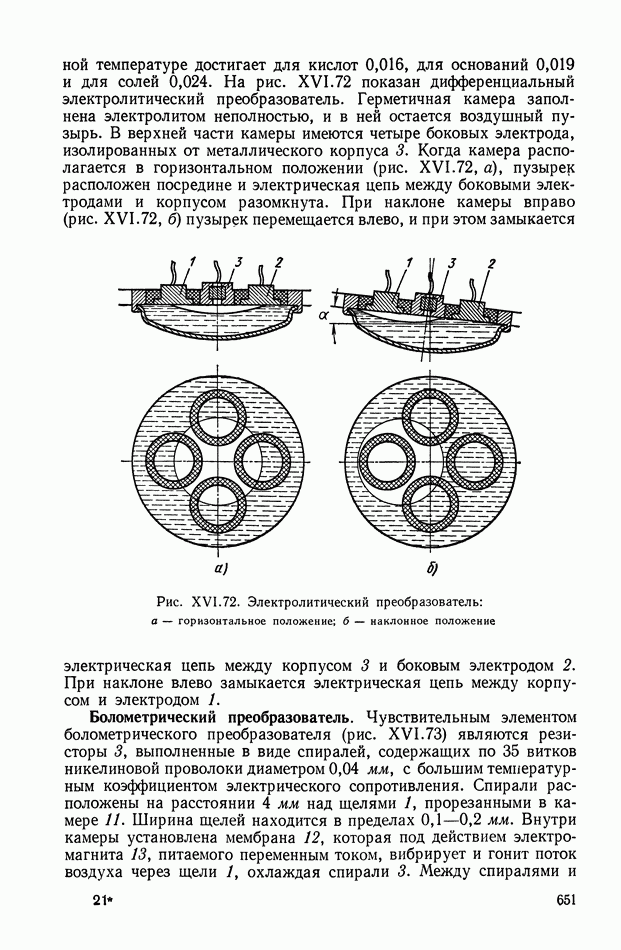
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ