| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. КОЛИЧЕСТВО ИНФОРМАЦИИ
Количество информации при равновероятности всех элементов сообщения. Определим количество информации, содержащееся в сообщении сначала в простейшем случае, когда число символов или элементов (например, букв в алфавите), из которых может быть составлено сообщение, равно  а число символов в сообщении равно
а число символов в сообщении равно  При этом мы предположим, что выбор каждого из символов равновероятен. При
При этом мы предположим, что выбор каждого из символов равновероятен. При  число возможных сообщений, т. е. число возможных комбинаций выбора двух элементов из
число возможных сообщений, т. е. число возможных комбинаций выбора двух элементов из  равно
равно  Точно также при
Точно также при  число возможных сообщений равно
число возможных сообщений равно  Если же число элементов в сообщении равно
Если же число элементов в сообщении равно  , то число возможных сообщений
, то число возможных сообщений

Это число можно было бы выбрать в качестве меры количества информации. Однако это не вполне удобно, потому что такая мера не удовлетворяет условию аддитивности, заключающемуся в том, что вдвое более длинное сообщение, естественно, должно содержать и вдвое большее количество информации. Это условие аддитивности или пропорциональности количества информации числу  будет удовлетворено, если в качестве меры количества информации выбрать не само число
будет удовлетворено, если в качестве меры количества информации выбрать не само число  а его логарифм, т. е. условиться, что количество информации
а его логарифм, т. е. условиться, что количество информации  определяется выражением
определяется выражением

Остается выбрать основание логарифмов а. Для этого рассмотрим простейший возможный случай, когда сообщение состоит из одного единственного элемента, а общее число элементов равно двум, т. е. когда  . В этом случае
. В этом случае

Если количество информации, получаемое при таких условиях, принять равным единице, то это определит выбор в качестве основания логарифмов а числа, равного двум. Итак, количество информации в сообщении определяется выражением

или, так как в рассматриваемом случае  то
то

Выше количество информации в сообщении было определено как логарифм от общего числа возможных сообщений. Количество
информации можно определить так же, как отрицательный логарифм вероятности выбора одного сообщения из всей возможной совокупности сообщений. Действительно, если выбор каждого из сообщений равновероятен, то вероятность Р выбора одного из  сообщений
сообщений

Следовательно, согласно выражению (1.31)

Количество информации, связанное с измерением физической величины. Рассмотрим какую-либо физическую величину х, например температуру, напряжение, давление и т.  изменяющуюся в пределах от Хщах до
изменяющуюся в пределах от Хщах до  Пусть
Пусть  Если даже величина X изменяется непрерывно, то при ее измерении прибор остается нечувствительным к ее изменениям в пределах некоторого приращения
Если даже величина X изменяется непрерывно, то при ее измерении прибор остается нечувствительным к ее изменениям в пределах некоторого приращения  зависящего от разрешающей способности прибора. Поэтому при измерении можно получить лишь конечное число дискретных значений величины х, равное
зависящего от разрешающей способности прибора. Поэтому при измерении можно получить лишь конечное число дискретных значений величины х, равное

Так, например, если отсчет производится между 0 и 1 в и минимальное приращение, которое чувствует прибор, равно 0,01 в, то максимальное Число отсчетов будет равно 
Минимальная ошибка Да: называется разрешающей способностью системы. Предположим, что минимальная относительная ошибка  — не должна превышать
— не должна превышать  . Тогда требуемая разрешающая способность
. Тогда требуемая разрешающая способность

Рассмотрим переменную, изменяющуюся со скоростью, равной 0,01 от ее полного диапазона изменения в секунду. Предположим, что мы можем измерить переменную в статическом режиме с точностью до 1%. Если отсчет может быть произведен быстро, скажем, в течение 0,001 сек, то во время отсчета переменная может измениться лишь очень незначительно, а именно на 
Наоборот, если для отсчета требуется значительный промежуток времени, например, 10 сек, то переменная может измениться на  Другими словами, чем быстрее изменяется переменная, тем больше потеря точности в течение интервала измерения. Промежуток времени
Другими словами, чем быстрее изменяется переменная, тем больше потеря точности в течение интервала измерения. Промежуток времени  необходимый для того, чтобы переменная изменилась на величину
необходимый для того, чтобы переменная изменилась на величину  равную разрешающей способности прибора,
равную разрешающей способности прибора,

Наименьший промежуток времени, который требуется для того, чтобы переменная изменилась на величину 

Минимальное время, за которое переменная может измениться на величину 

Подставляя выражение (1.36) в формулу (1.38) и учитывая соотношение (1.39), получим

Определим теперь количество информации, получаемое при измерении переменной х в рассматриваемых условиях. При этом количество информации определяется просто как логарифм полного числа возможных состояний системы или измеряемых значений переменной, характеризующей ее поведение. Если мы не располагаем никакими предварительными сведениями о процессе, то каждый из  возможных отсчетов одинаково вероятен. Итак, вероятность Р любого из
возможных отсчетов одинаково вероятен. Итак, вероятность Р любого из  описывается формулой
описывается формулой

Подставляя выражение (1.35) в формулу (1.33) и учитывая соотношение (1.34), получим для количества информации, связанного с одним отсчетом в статике, выражение

или

В динамическом режиме, когда переменная изменяется на заметную величину за время  определяемое выражением (1.40), максимальная скорость изменения информации, которая еще может регистрироваться системой
определяемое выражением (1.40), максимальная скорость изменения информации, которая еще может регистрироваться системой

Применим полученные формулы для  чтобы сравнить дискретный и непрерывный регистрирующие приборы по их способности передавать данное количество информации в единицу времени.
чтобы сравнить дискретный и непрерывный регистрирующие приборы по их способности передавать данное количество информации в единицу времени.
Пусть дискретный прибор производит 1000 измерений в секунду, каждое из которых дает 7 единиц количества информации, так что
допустимая для него скорость изменения информации равна  . В то же время пусть прибор непрерывного действия имеет время прохождения всей шкалы, равное 0,01 сек, и ошибку измерения
. В то же время пусть прибор непрерывного действия имеет время прохождения всей шкалы, равное 0,01 сек, и ошибку измерения  тогда
тогда 

Таким образом, для рассмотренного примера количество информации в единицу времени на выходе дискретного прибора больше, чем на выходе непрерывного.
Количество информации при неравновероятности выбора элементов сообщения. Рассмотрим сообщения, каждое из которых состоит из большого числа элементов, равного  выбираемых из
выбираемых из  элементов:
элементов:  причем вероятности выбора этих элементов не равны и определяются числами
причем вероятности выбора этих элементов не равны и определяются числами  .
.
Каждое такое сообщение содержит  элементов
элементов  элементов
элементов  Отличие между сообщениями заключается лишь в порядке следования элементов. Так как вероятность выбора
Отличие между сообщениями заключается лишь в порядке следования элементов. Так как вероятность выбора  элементов
элементов  равна и так как выбор каждого из элементов есть событие, не зависимое от выбора других элементов, то вероятность Р выбора каждого такого сообщения при достаточно большом
равна и так как выбор каждого из элементов есть событие, не зависимое от выбора других элементов, то вероятность Р выбора каждого такого сообщения при достаточно большом  одинакова и равна
одинакова и равна

Но при этом

следовательно,

Количество информации, содержащееся в сообщении, согласно выражениям (1.34) и (1.35)

В частном случае, когда все элементы сообщения равновероятны, формула (1.47) сводится к формуле (1.32). Действительно, при этом

и

поэтому

Заметим, что этот частный случай соответствует максимальному возможному количеству информации, содержащемуся в сообщении из  элементов.
элементов.
Действительно, предположим сначала, что мы производим выбор между двумя возможными сообщениями, вероятности которых равны  для первого и
для первого и  для второго. Величина 3 имеет максимум, равный единице, тогда, когда оба сообщения одинаково вероятны
для второго. Величина 3 имеет максимум, равный единице, тогда, когда оба сообщения одинаково вероятны  т. е. когда имеется полная свобода выбора между сообщениями. Как только одно сообщение делается более вероятным, чем другое
т. е. когда имеется полная свобода выбора между сообщениями. Как только одно сообщение делается более вероятным, чем другое  то значение 3 убывает. А когда одно сообщение очень вероятно
то значение 3 убывает. А когда одно сообщение очень вероятно  то 3 очень мало.
то 3 очень мало.
В предельном случае, когда одна вероятность равна 1 (достоверность), а все остальные — нулю (невозможность), то 3 равно нулю (никакой неопределенности, никакой свободы выбора — никакой информации). То же и в случае произвольного числа выборов: 3 имеет максимум, когда все выборы равновероятны, и 3 близка к нулю, корда вероятность одного из сообщений велика. Чем больше число возможных решений, тем больше 3.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 1. МОСТОВЫЕ СХЕМЫ
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 1. МОДУЛЯТОРЫ
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
- Двухполупериодные демодуляторы на диодах.
- Однополупериодные усилители-демодуляторы.
- Двухполупериодные усилители-демодуляторы.
- Демодуляторы на транзисторных ключах.
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
- Сильфоны.
- Гофрированные мембраны.
- Гибкие диафрагмы.
- Хлопающие мембраны.
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
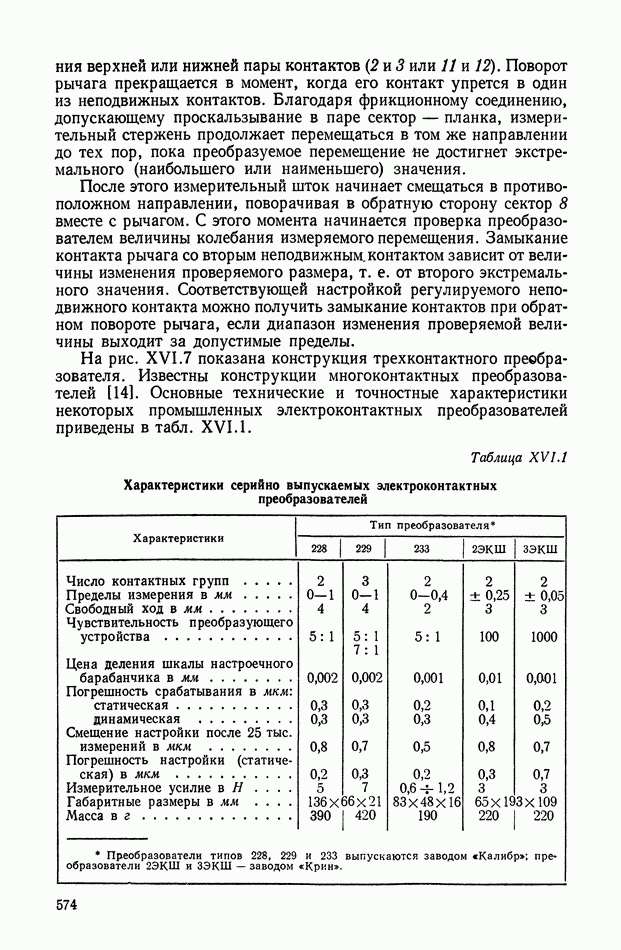
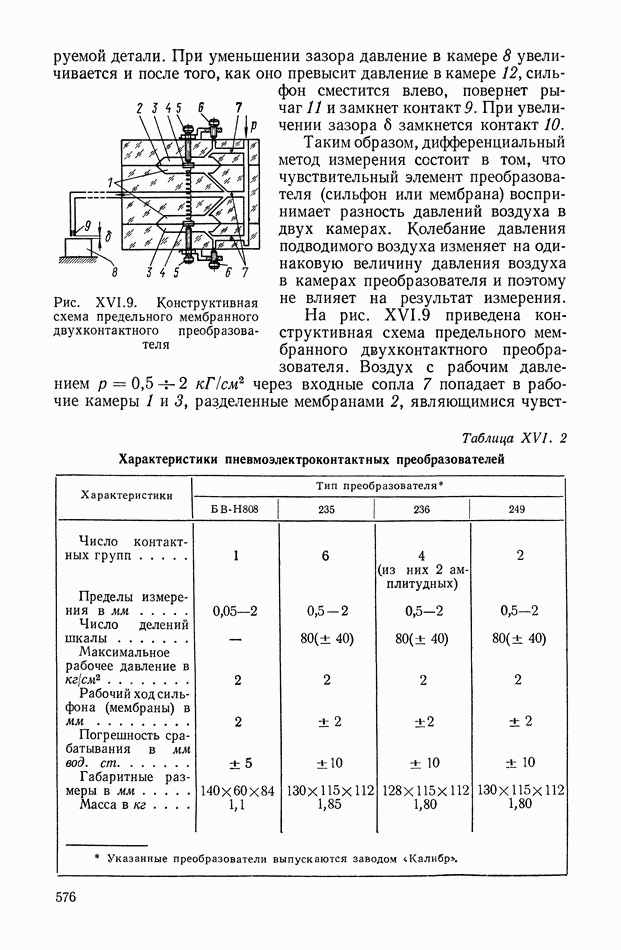
- Пневмоэлектроконтактные преобразователи линейных величин.
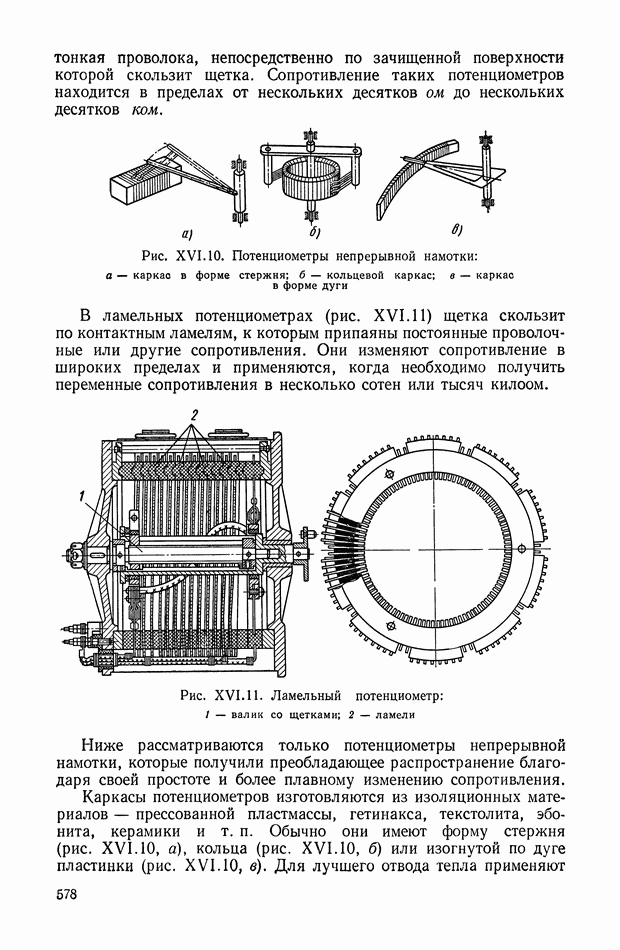
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
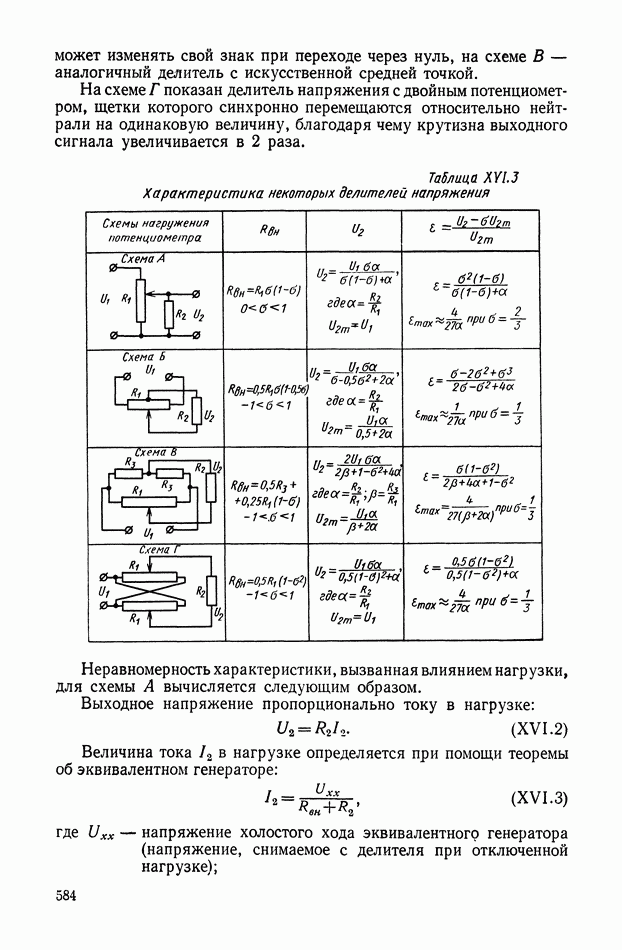
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
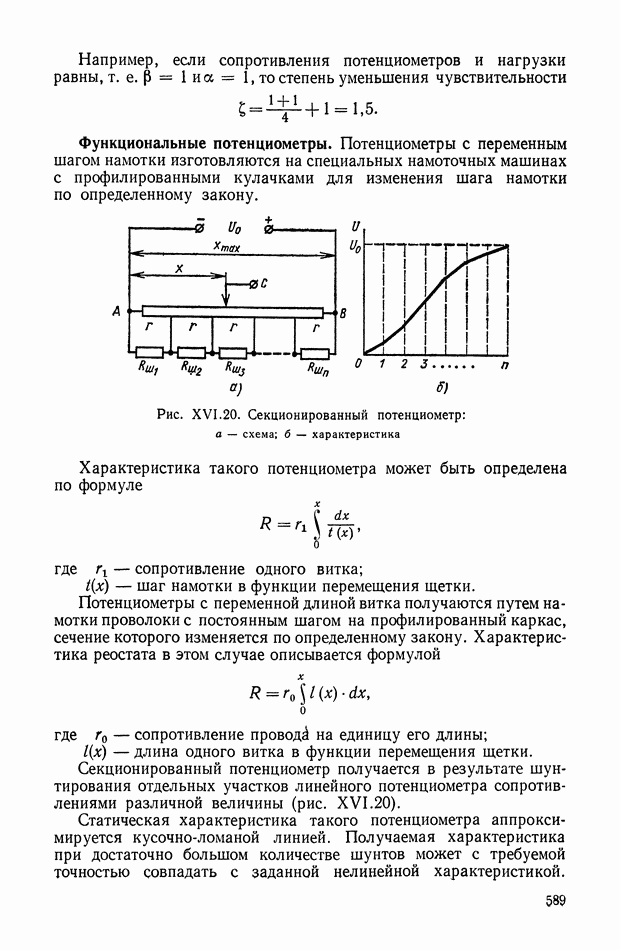
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
- Работа сельсинов в трансформаторном режиме.
- Устранение ложного нуля в двухскоростной системе.
- Схемы синхронизаторов.
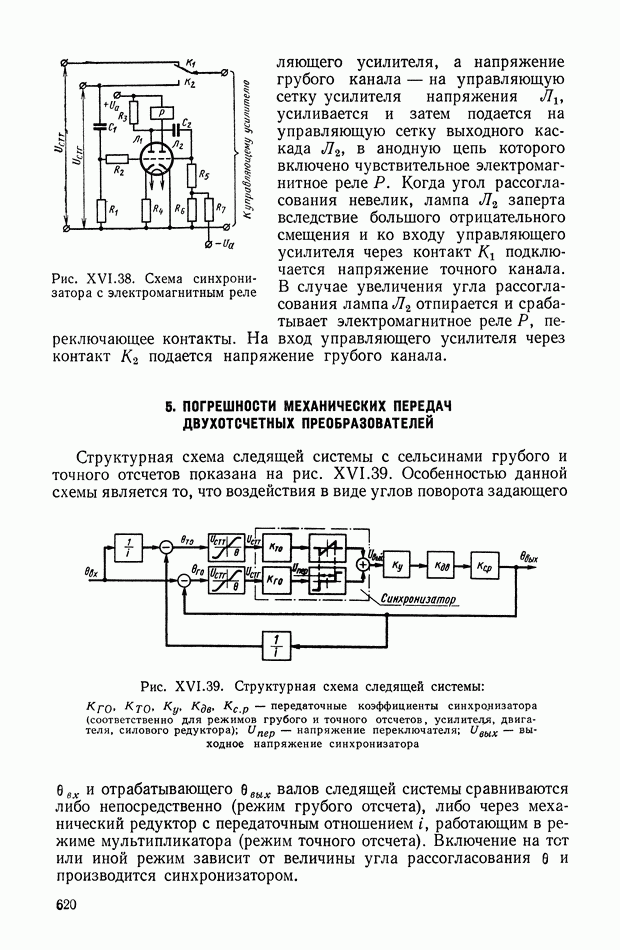
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
- Индукционные редуктосины.
- Индуктосины.
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- Емкостный редуктосин.
- Емкостный фазовращатель.
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ