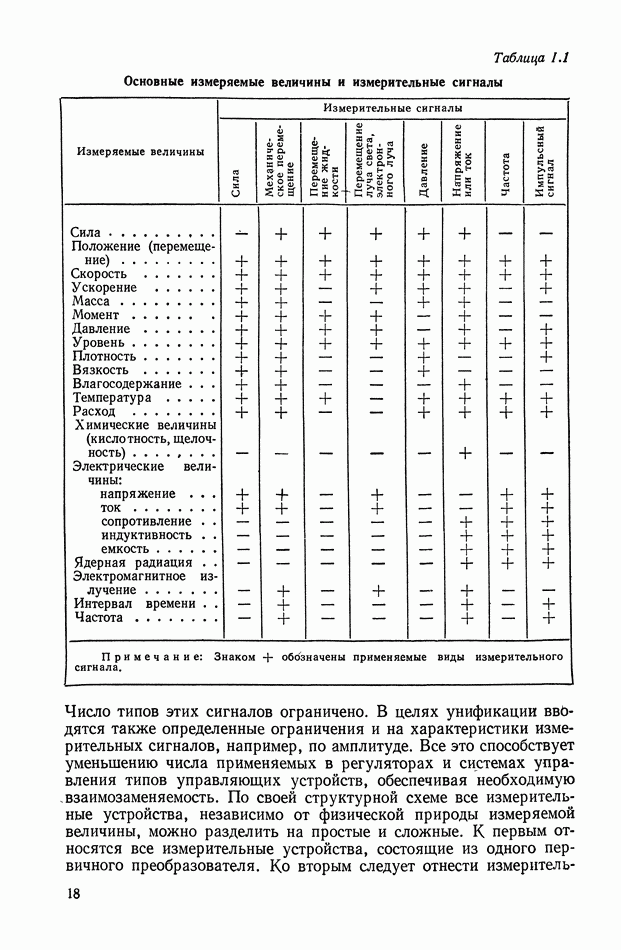
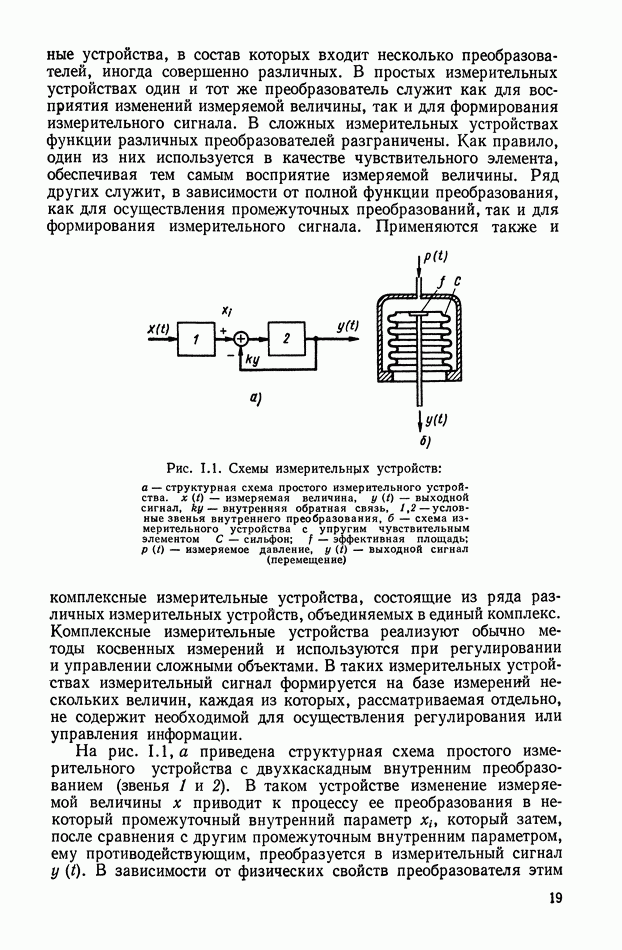
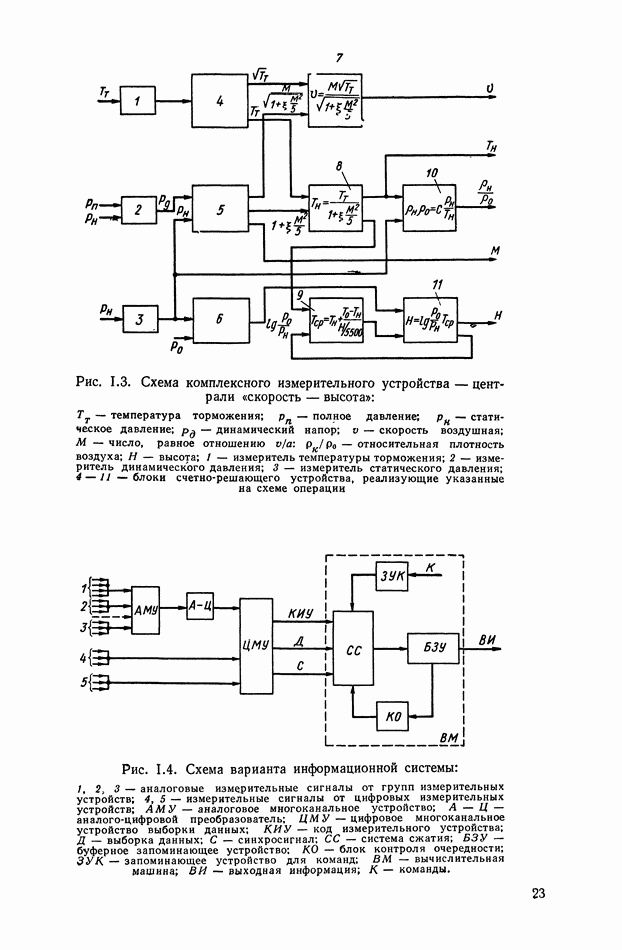
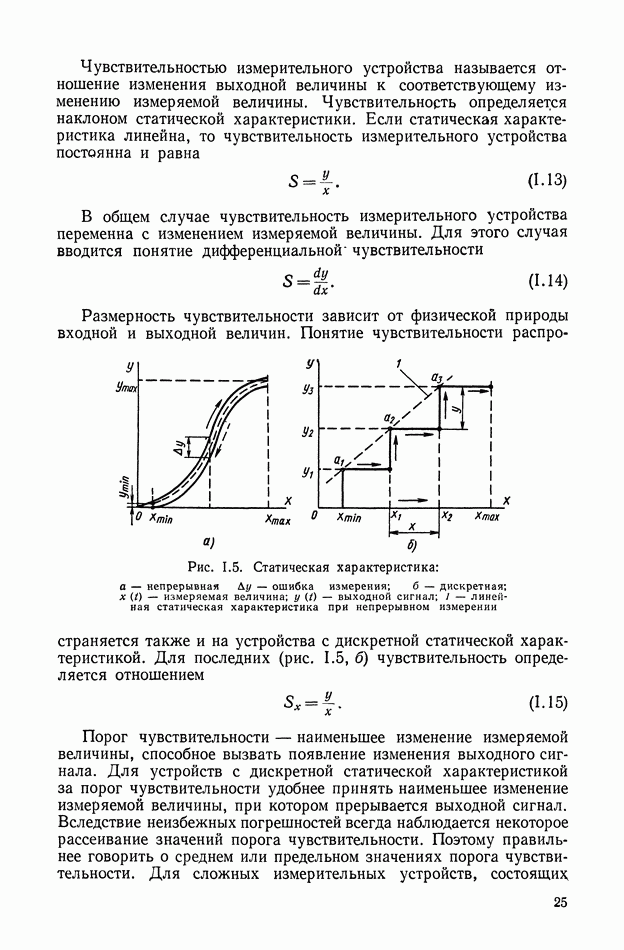
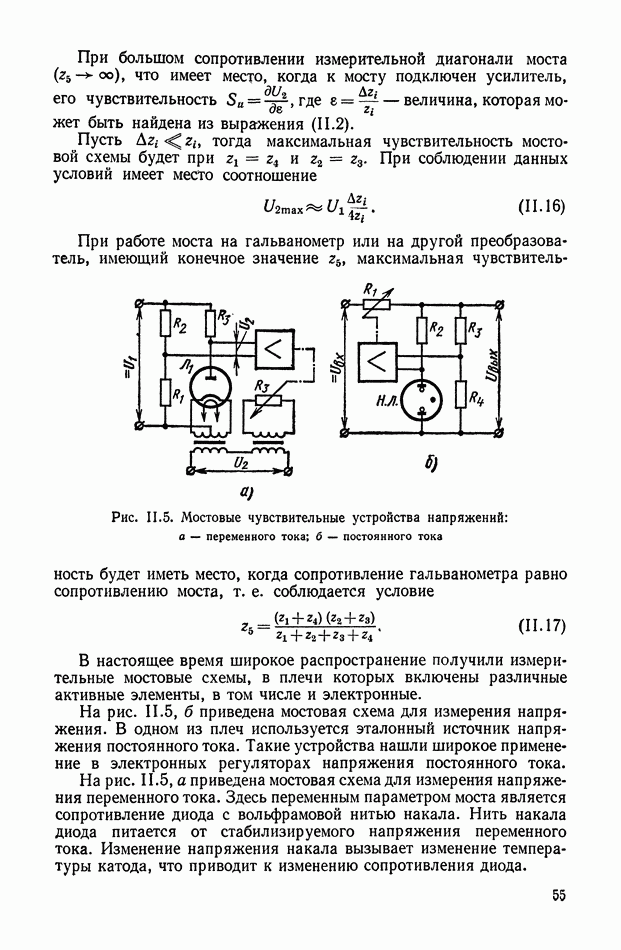
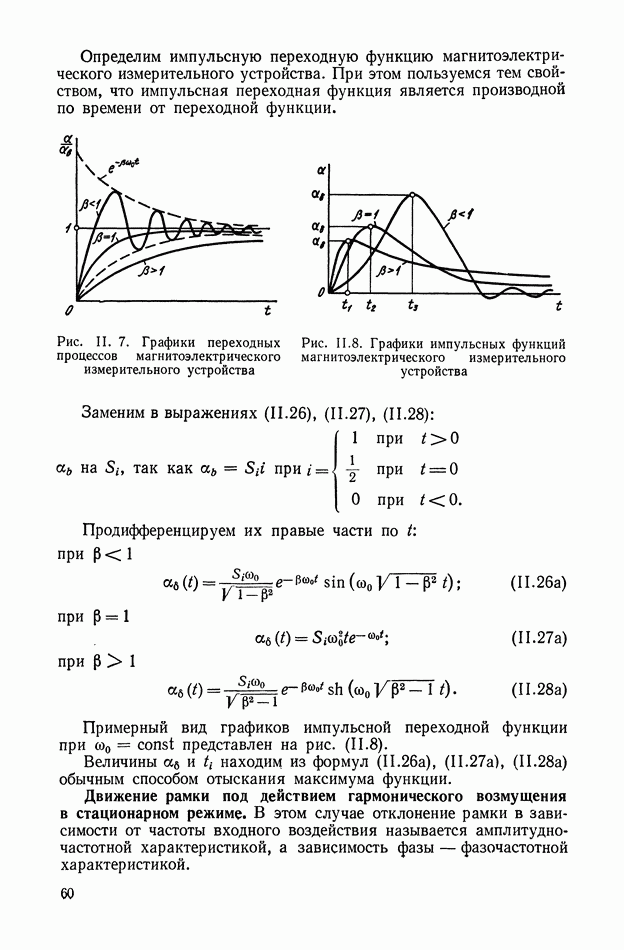
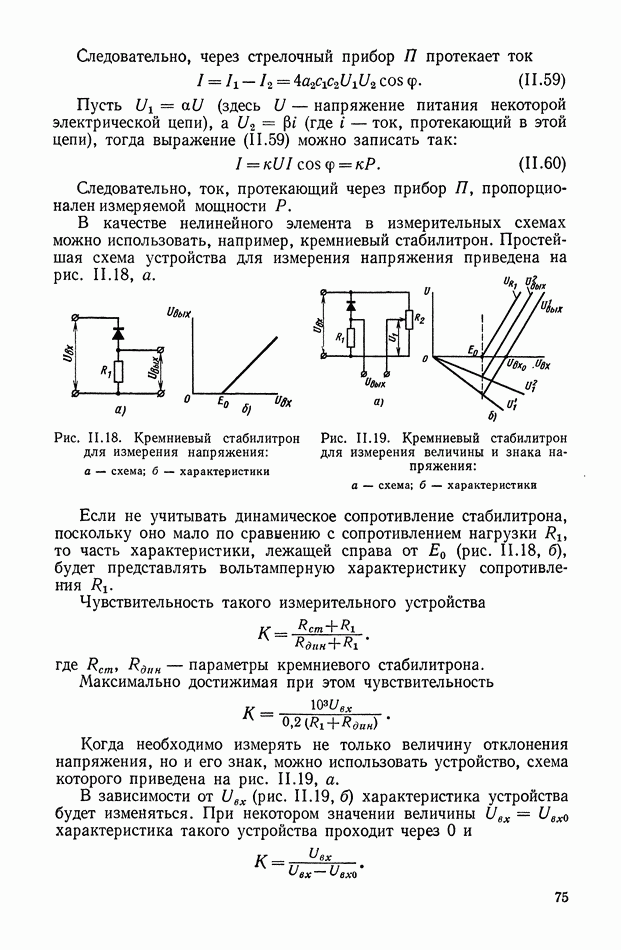
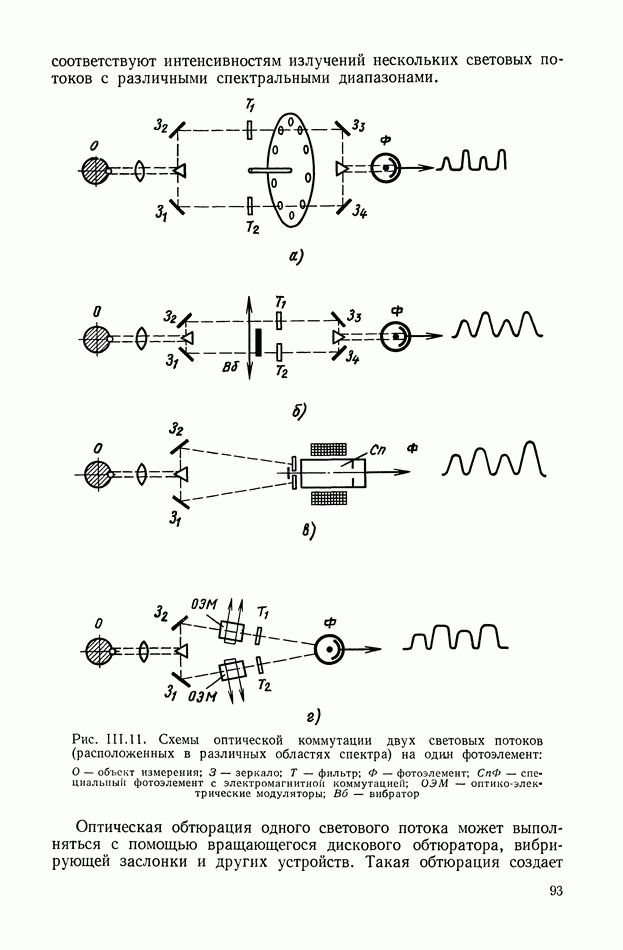
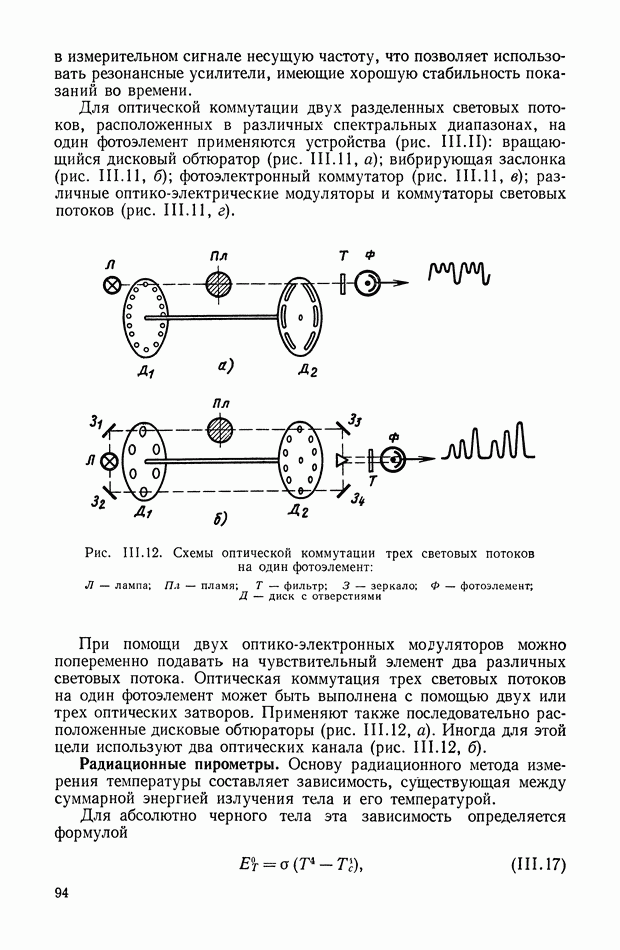
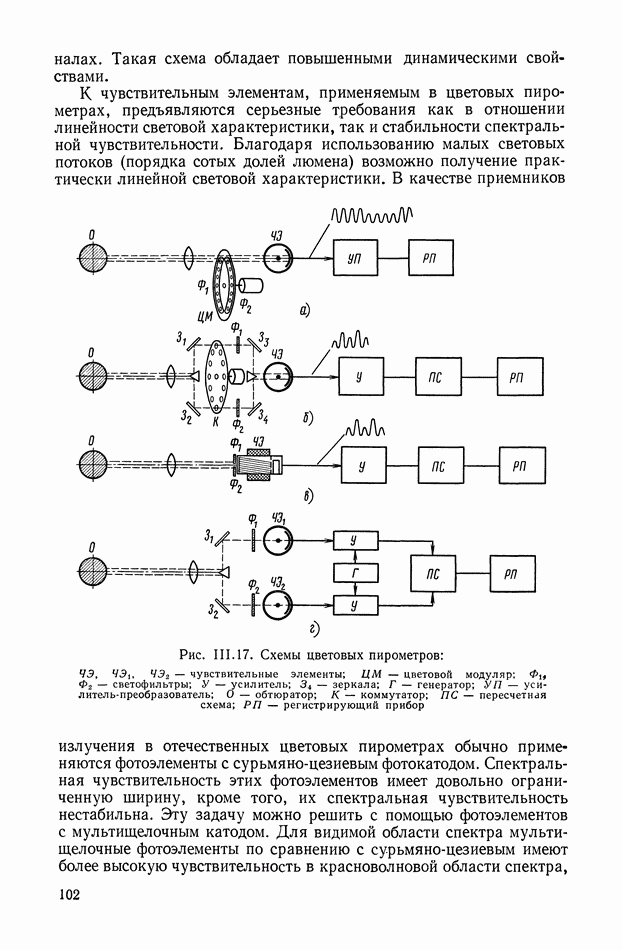
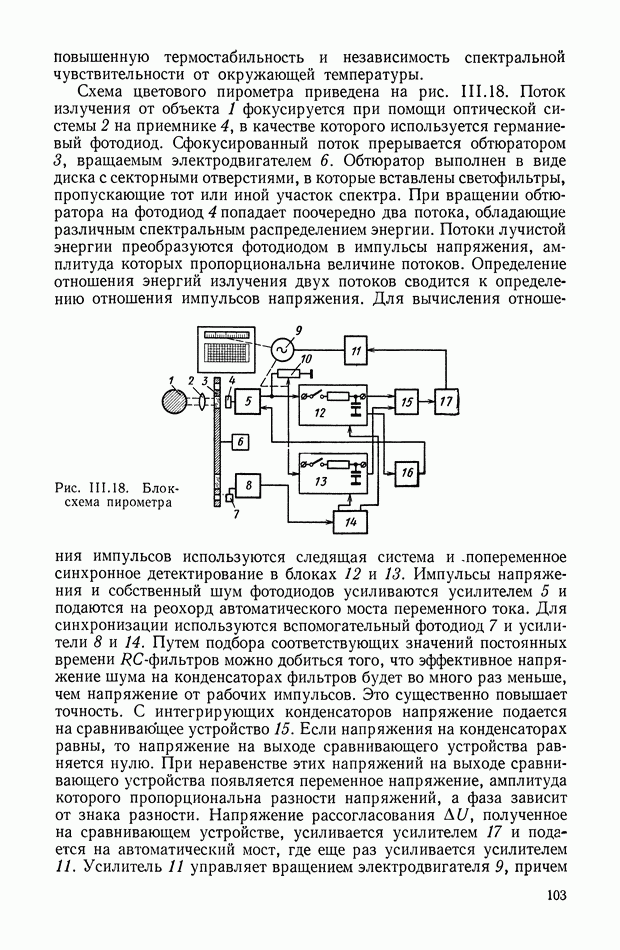
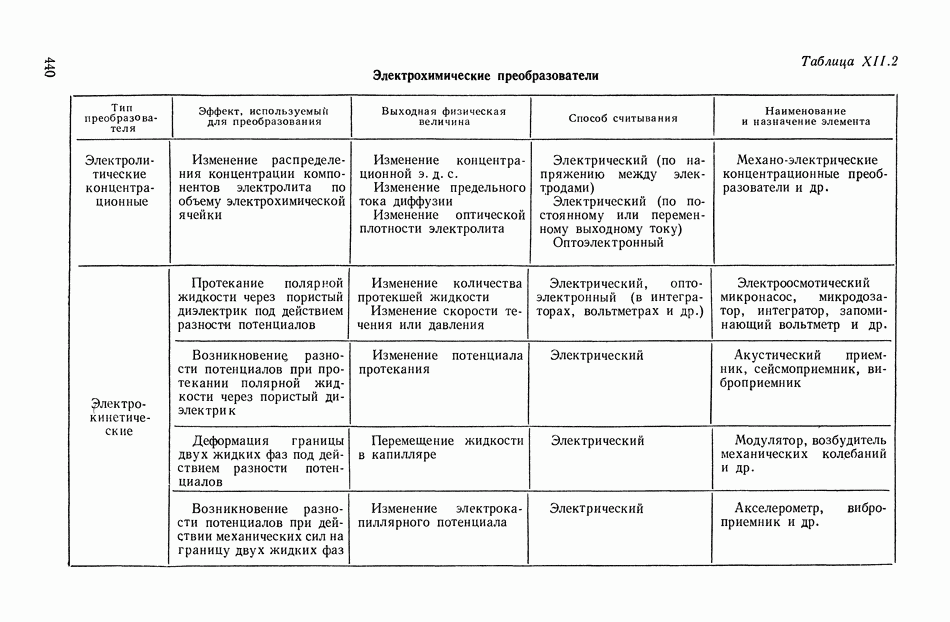
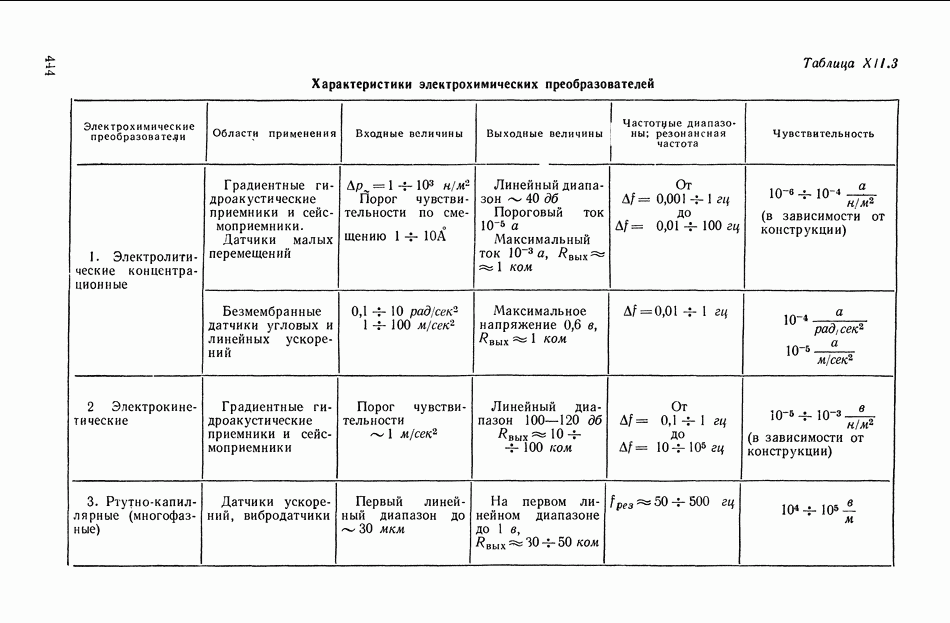
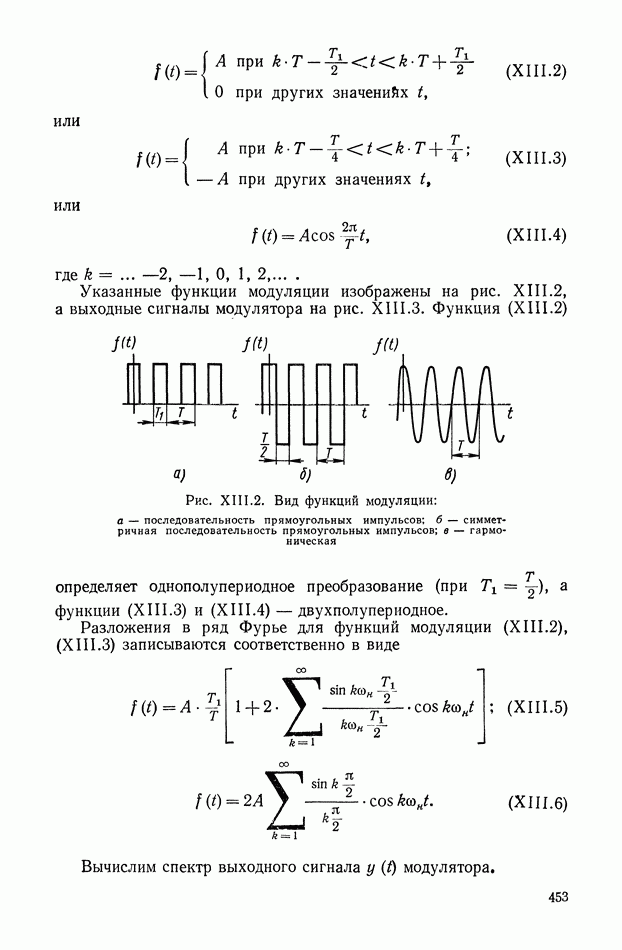
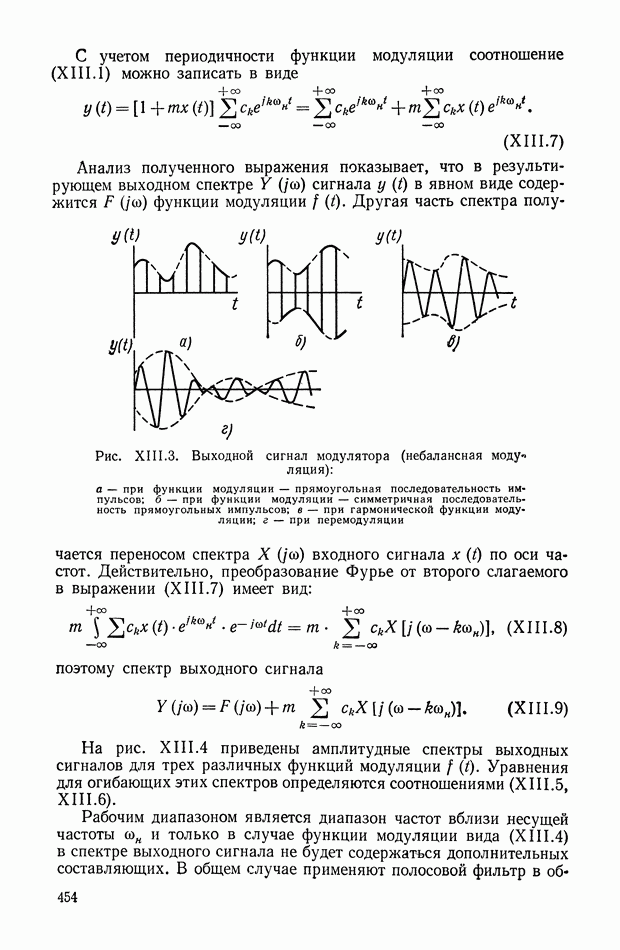
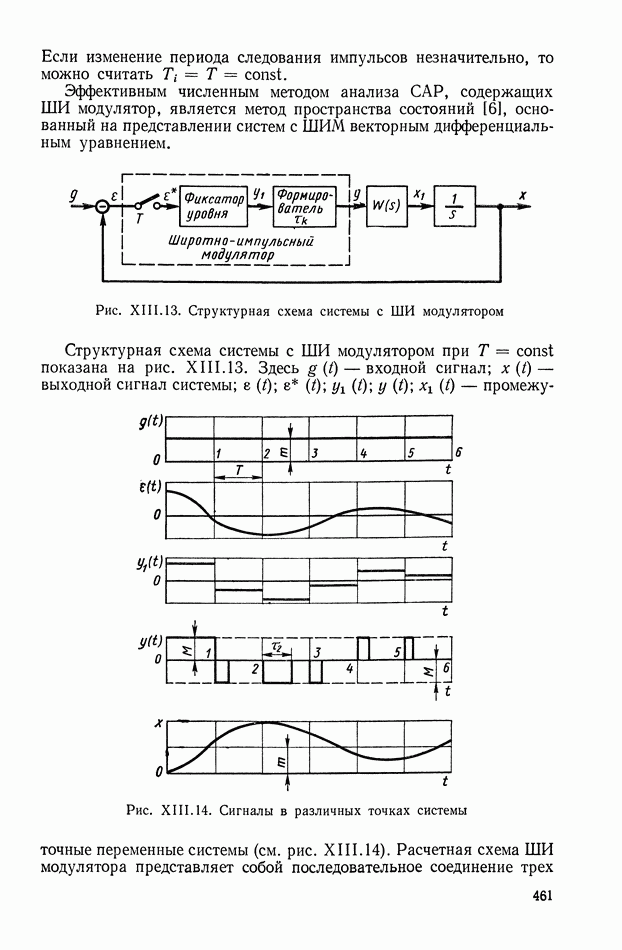
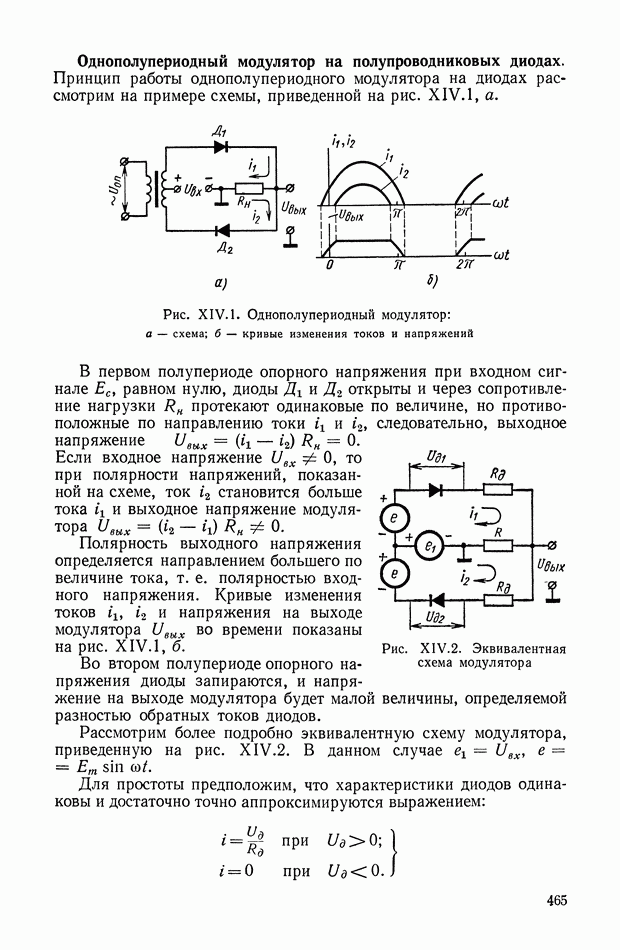
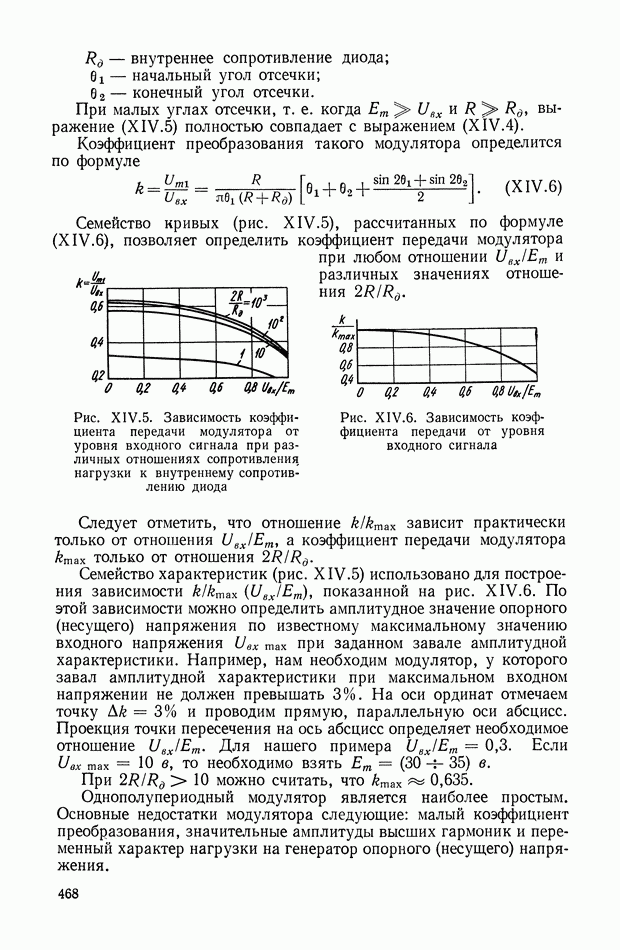
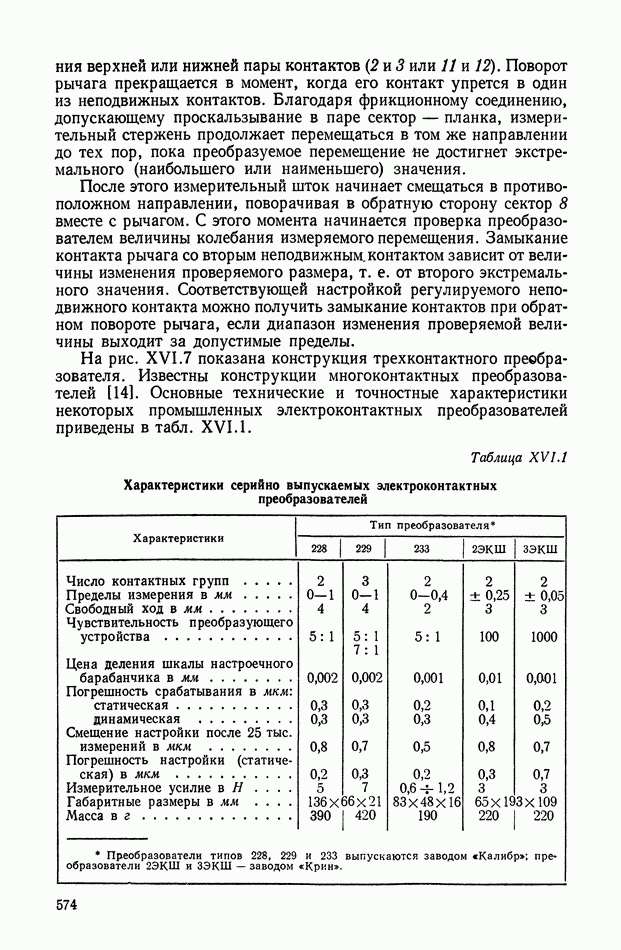
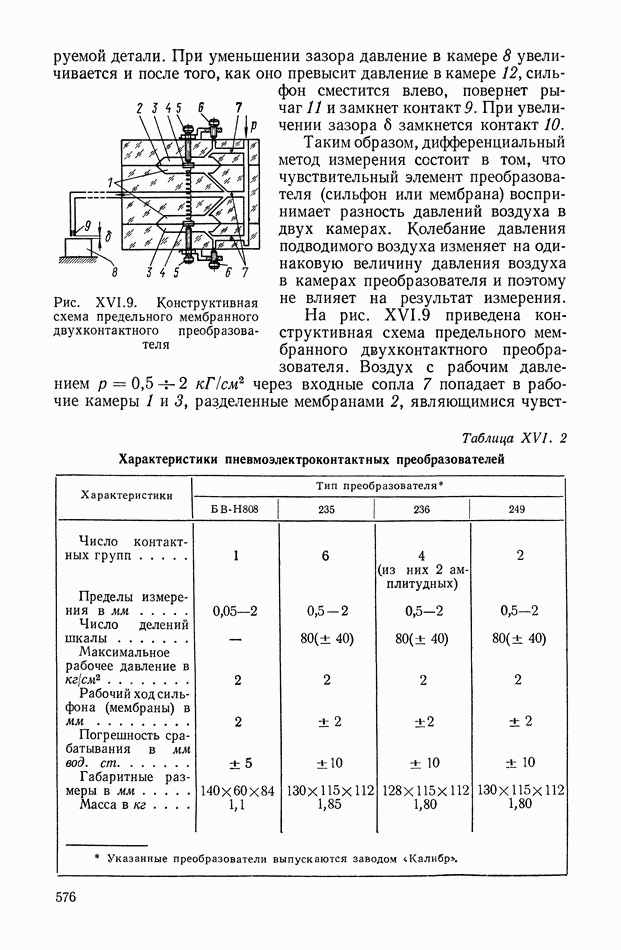
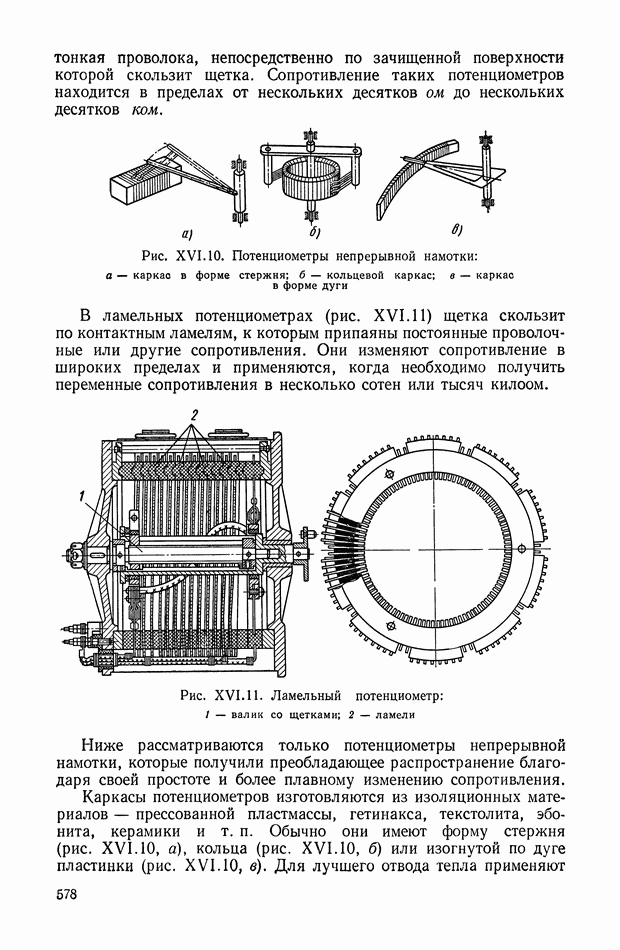
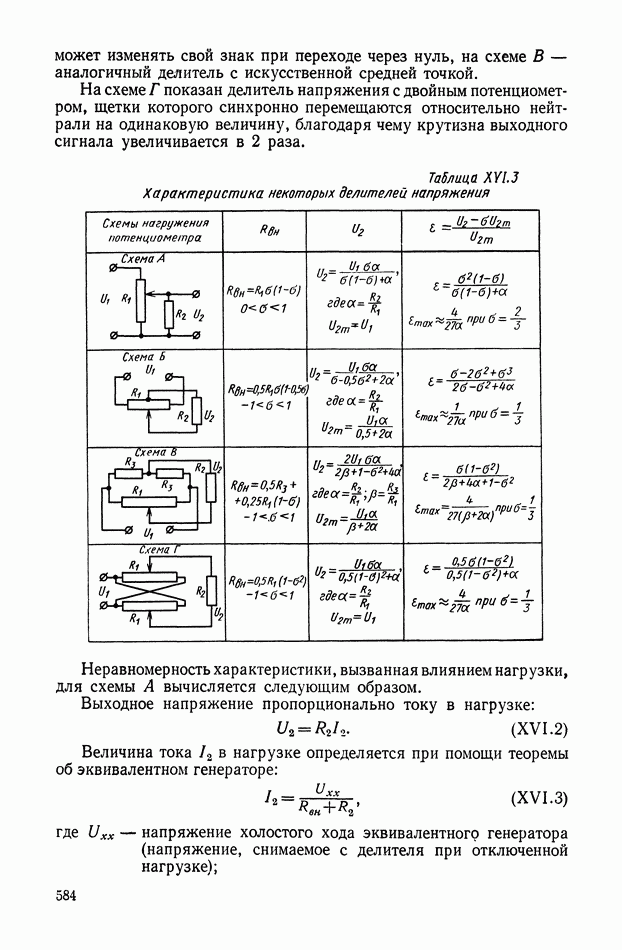
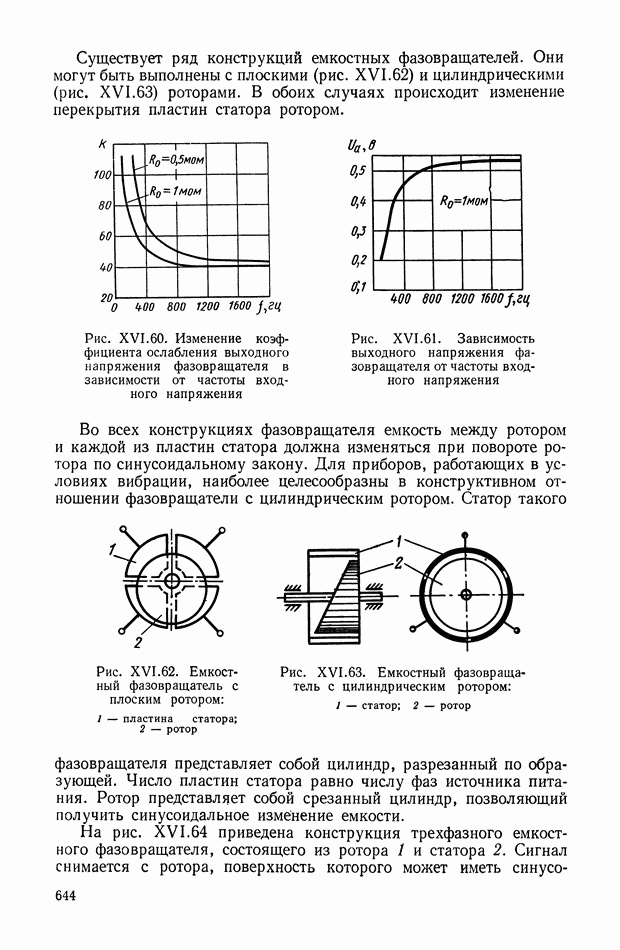
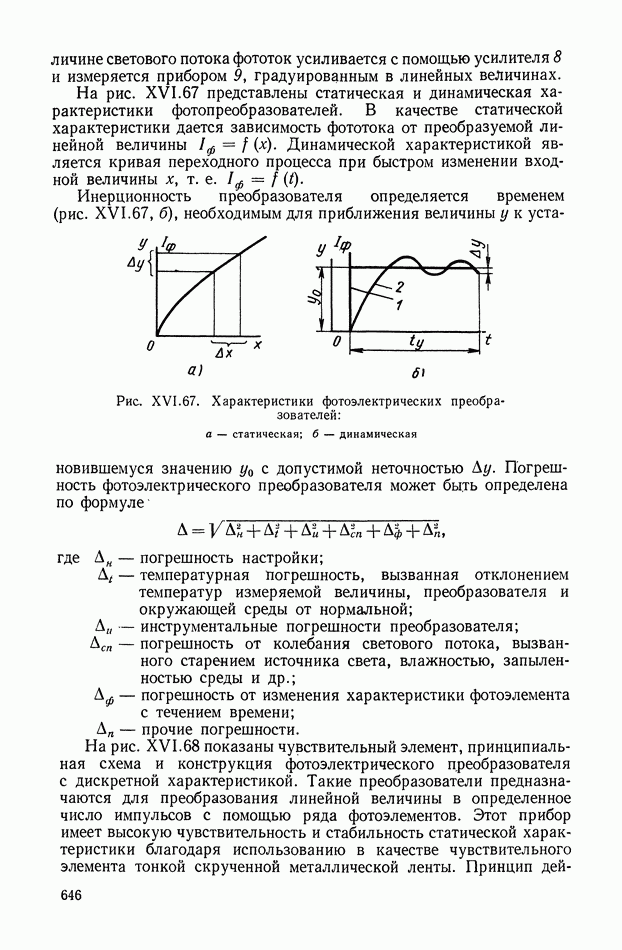
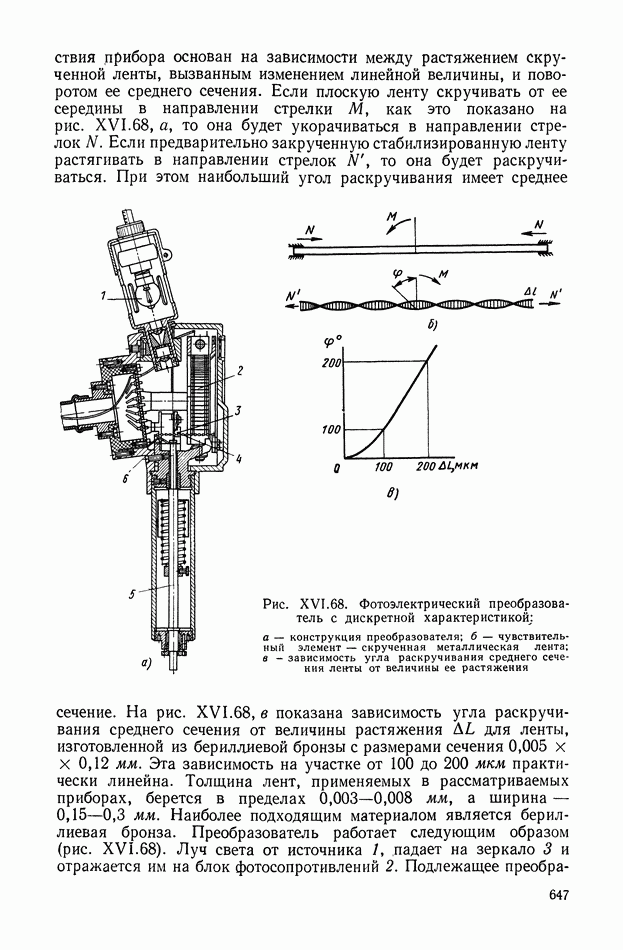
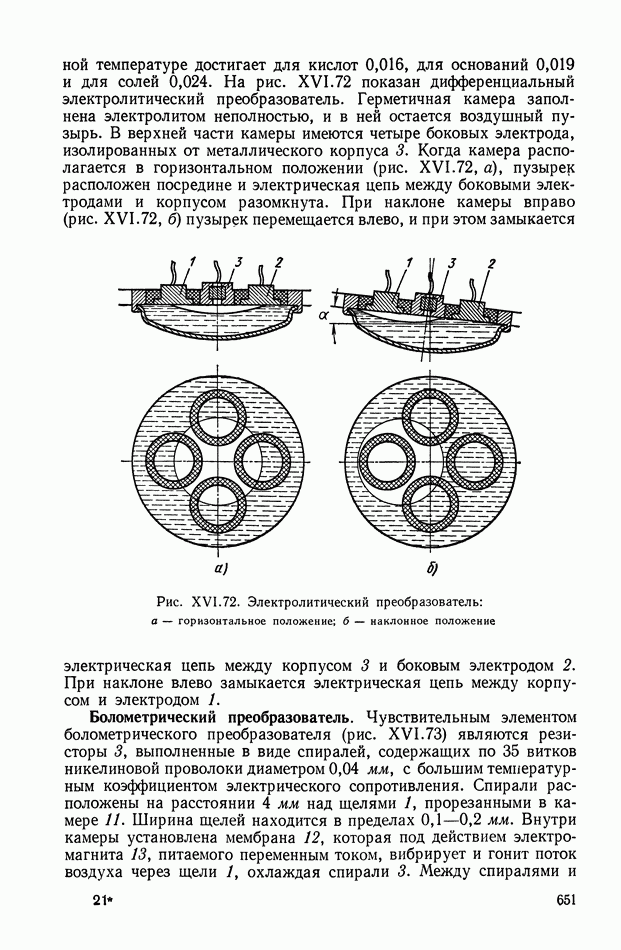
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
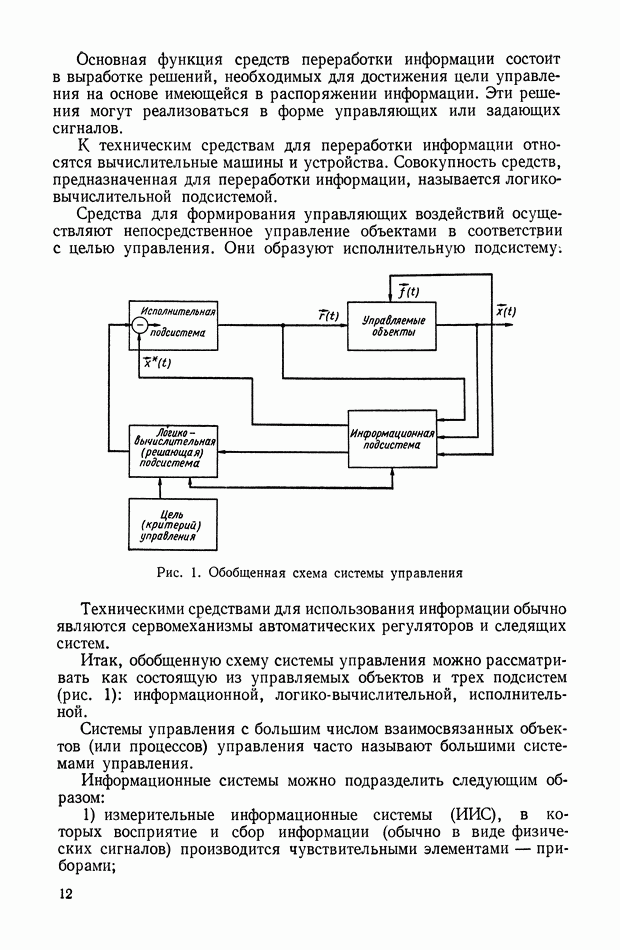
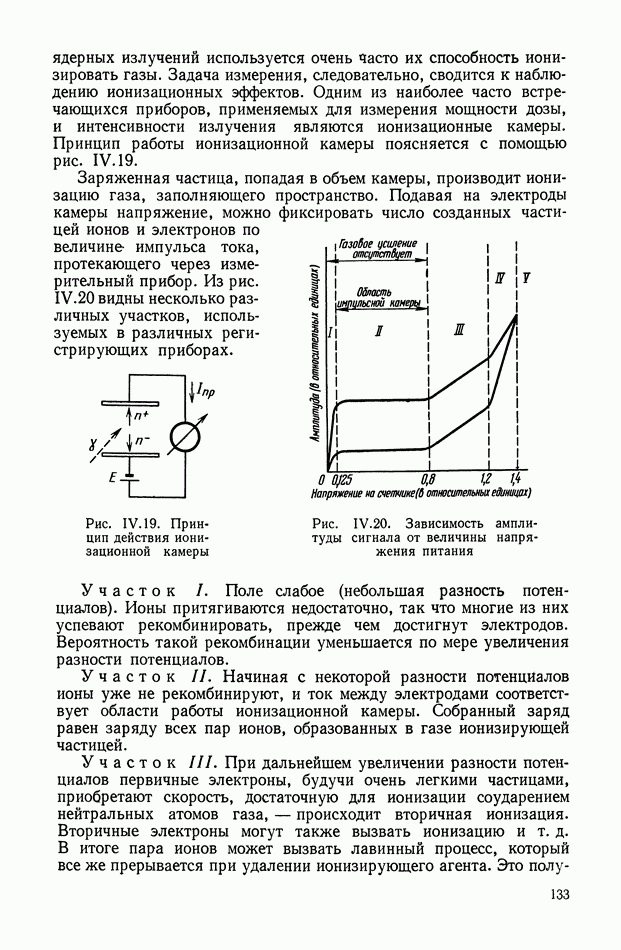
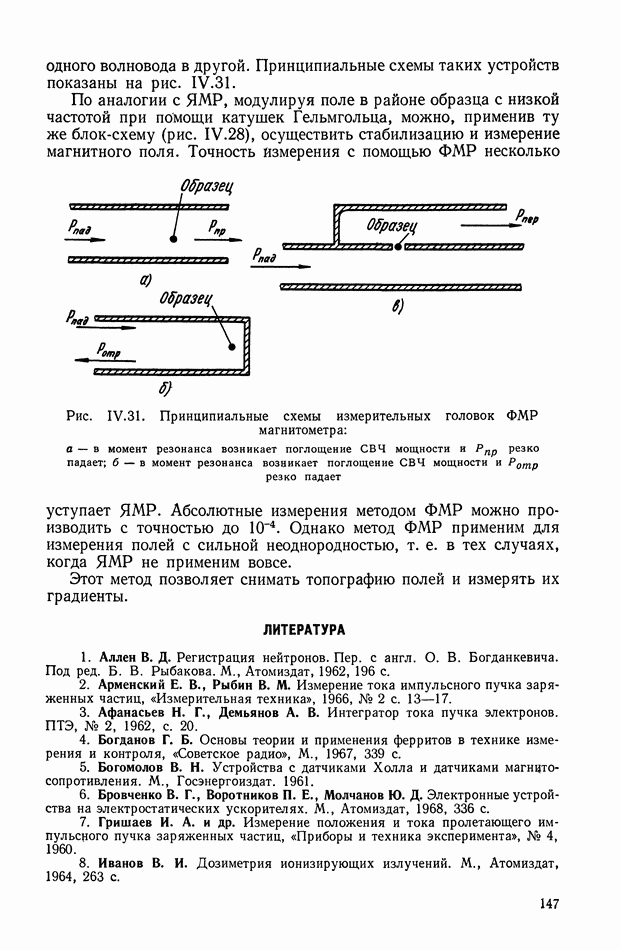
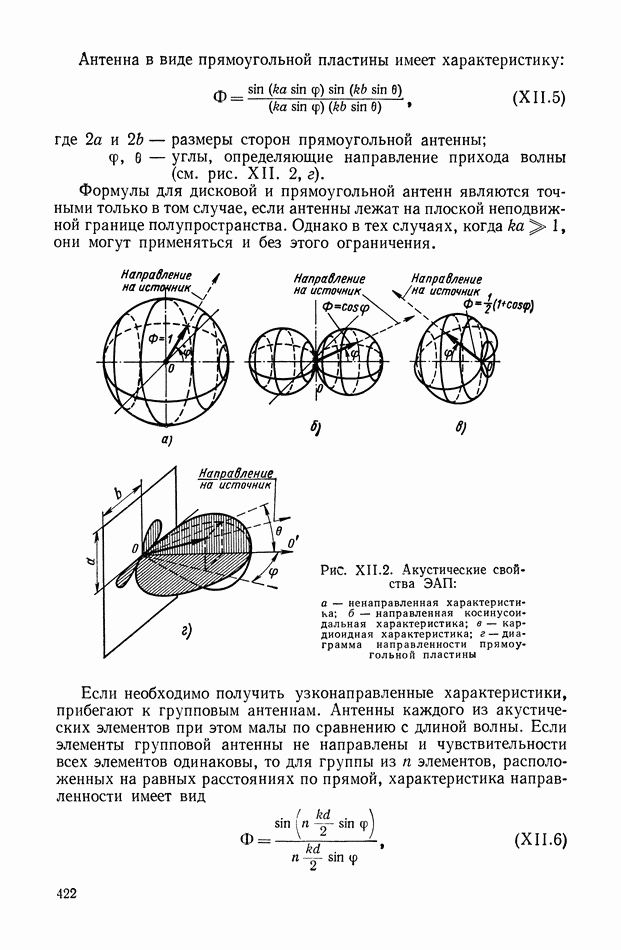
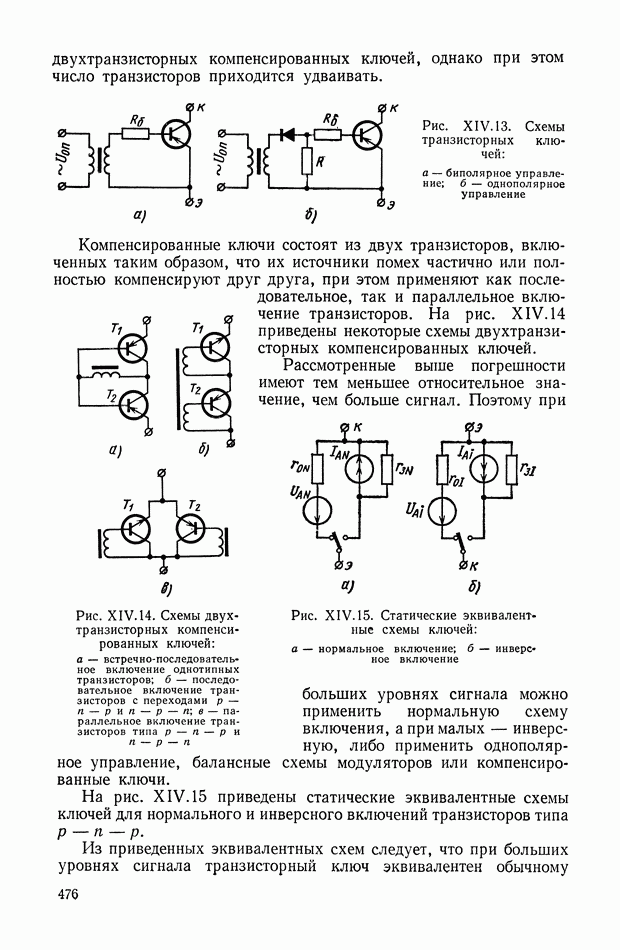
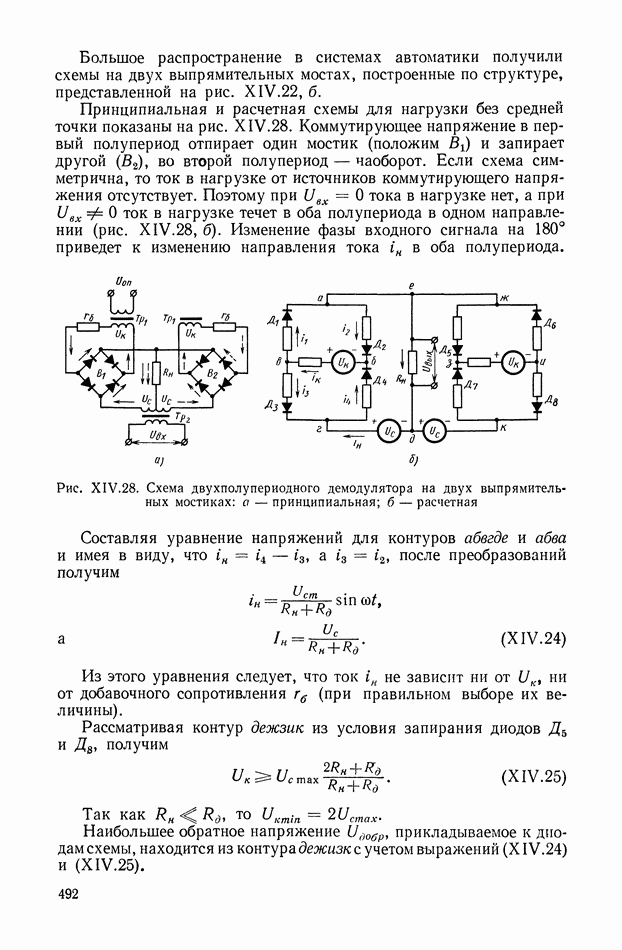
Для обеспечения ротору гироскопа (рис. VIII.2) свободы вращения вокруг «неподвижной» точки применяют карданов подвес. Если центр тяжести гироскопа совпадает с его «неподвижной» точкой (точкой пересечения осей карданова подвеса), то такой гироскоп называется астатическим.

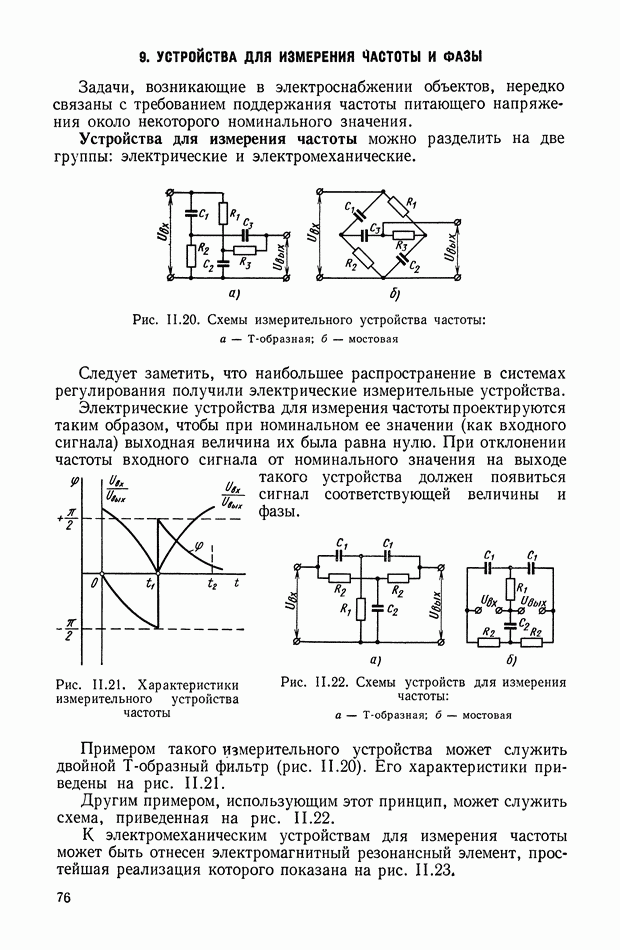
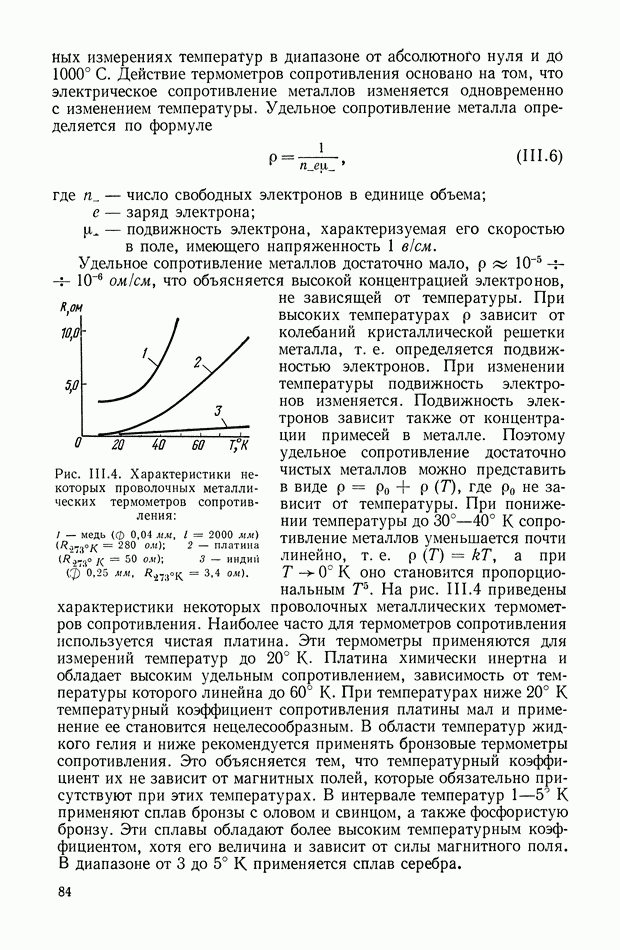
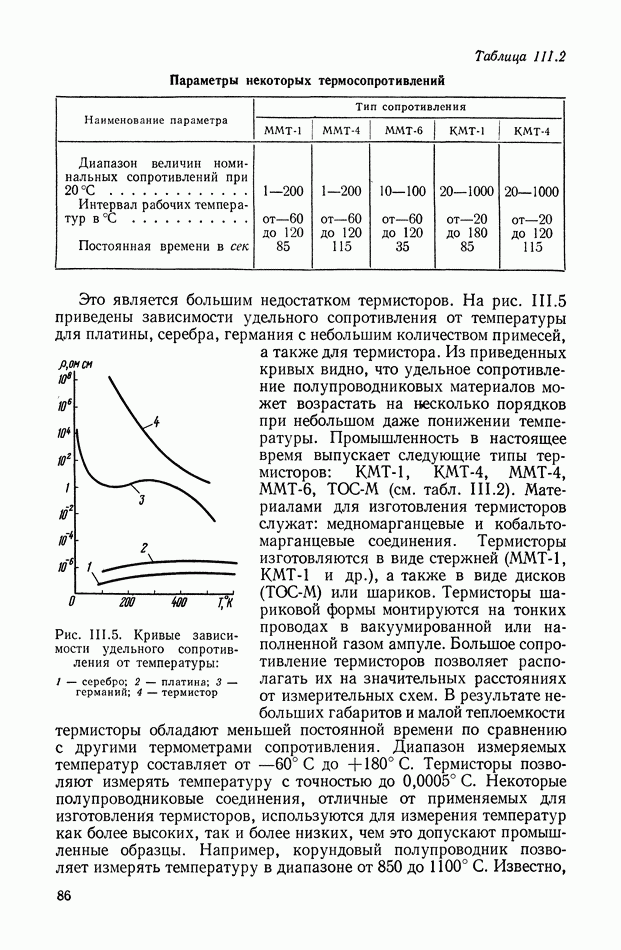
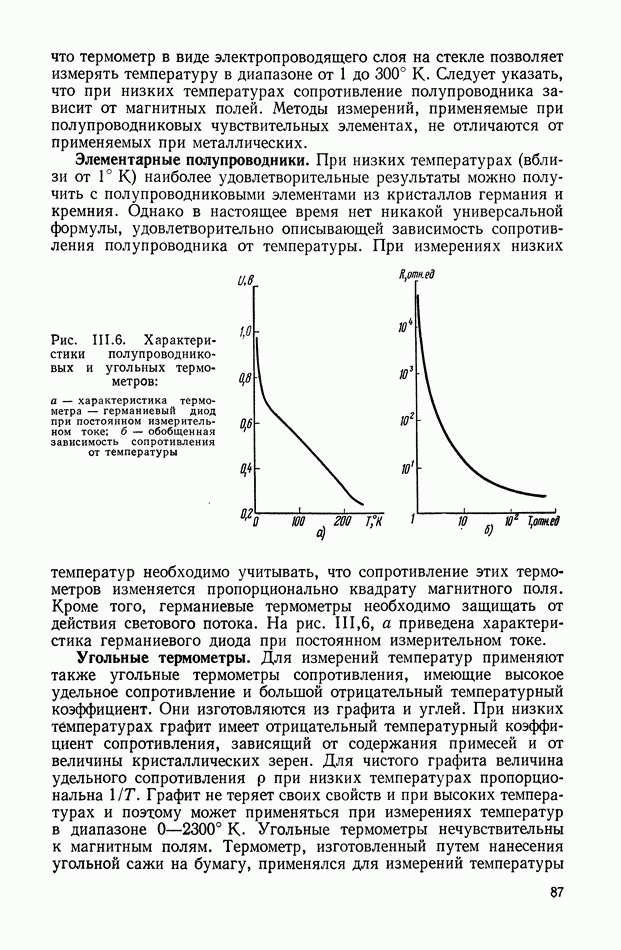
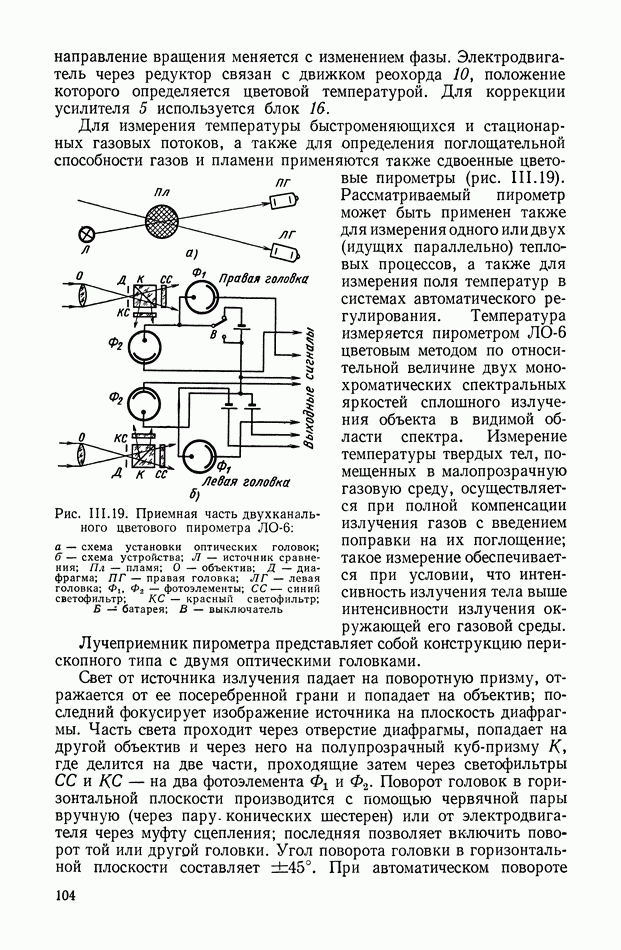
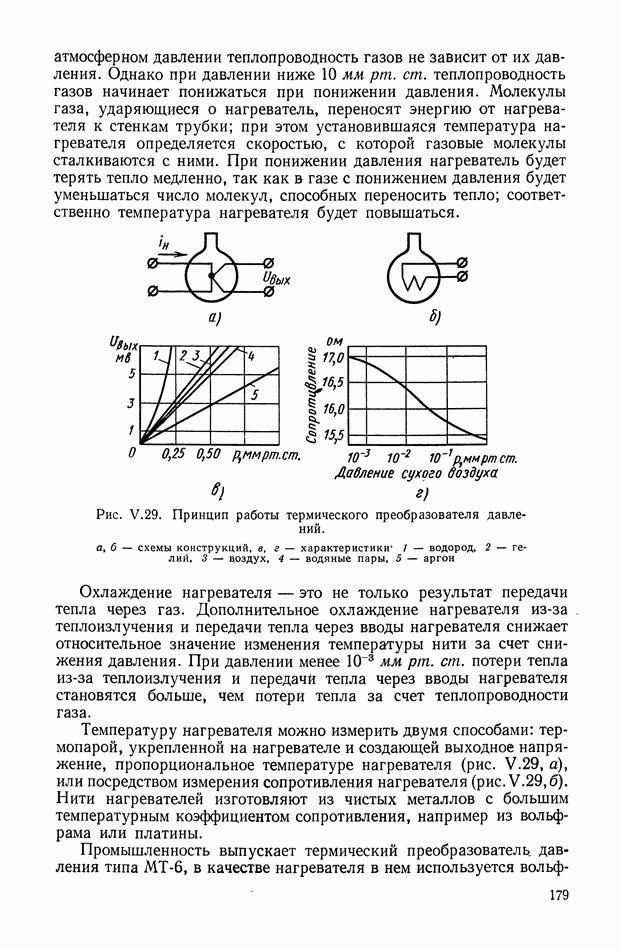
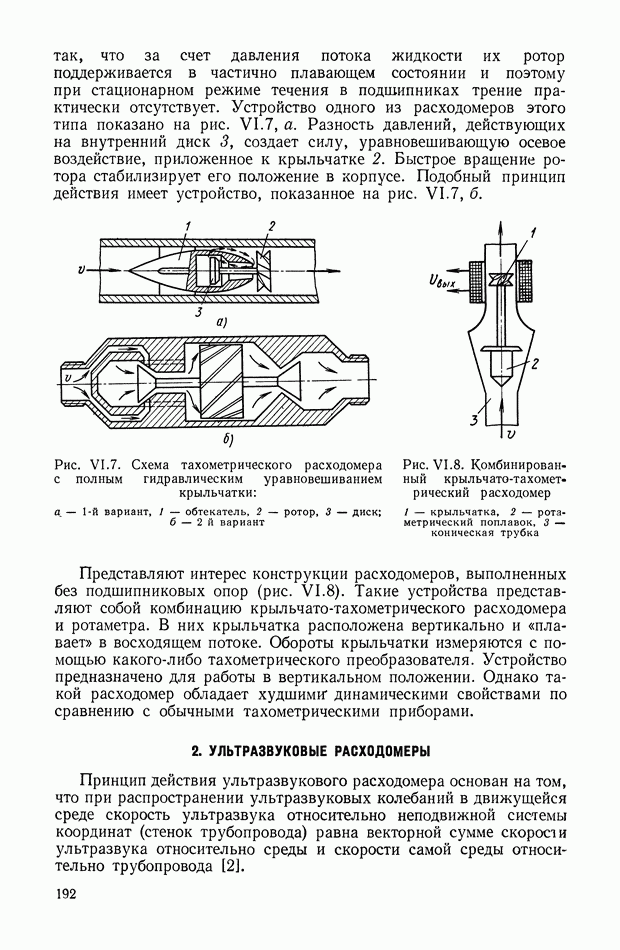
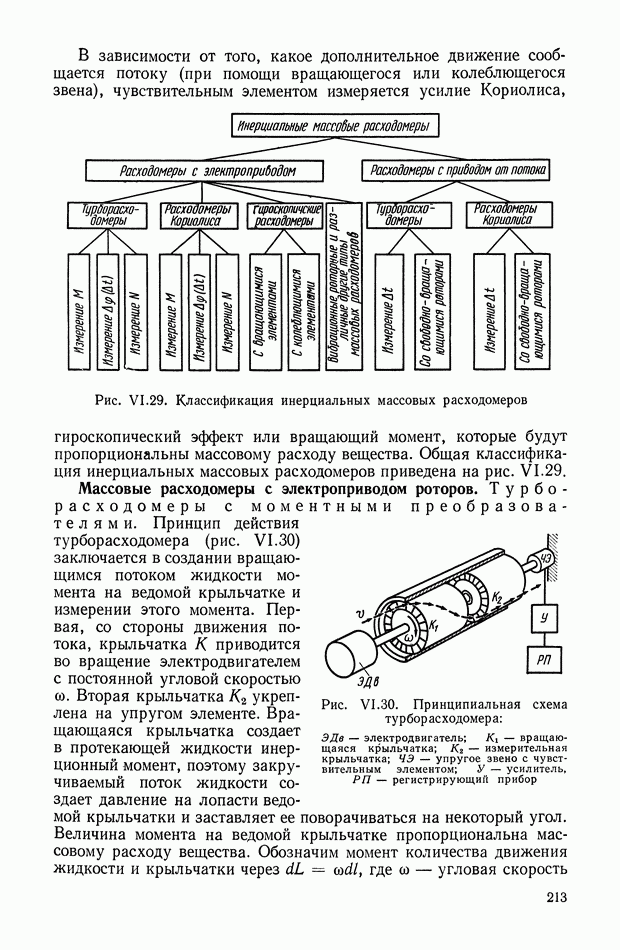
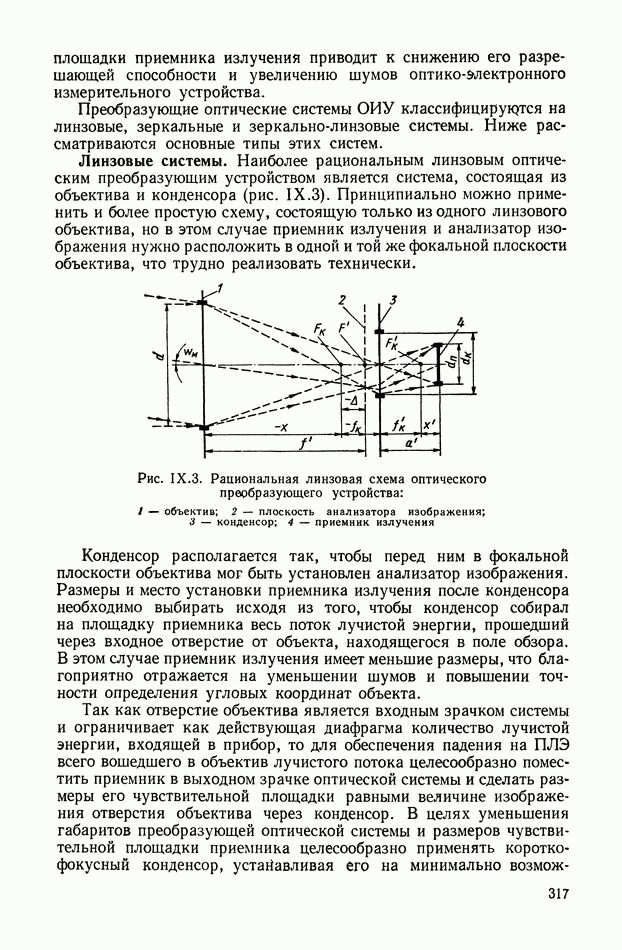
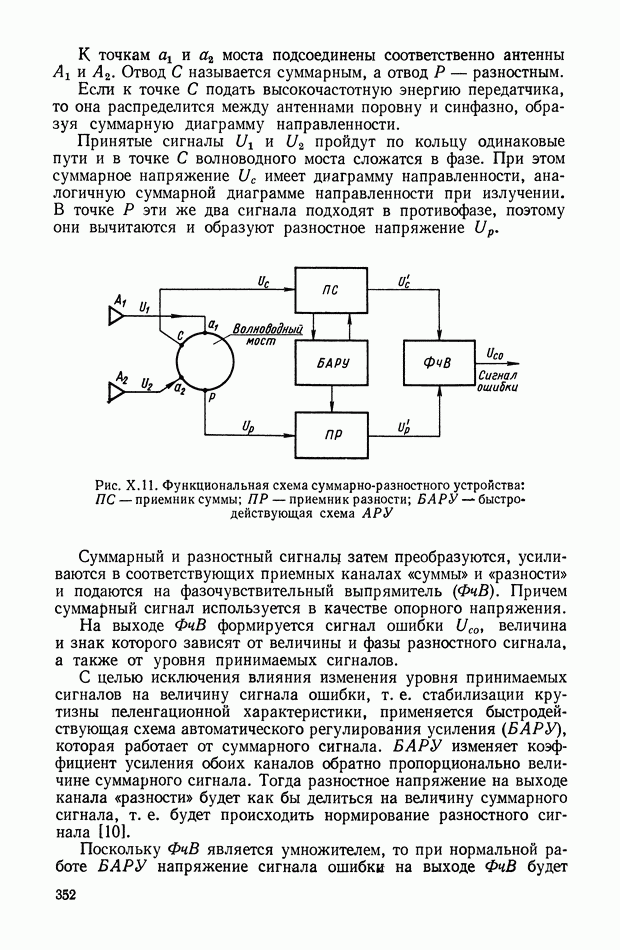
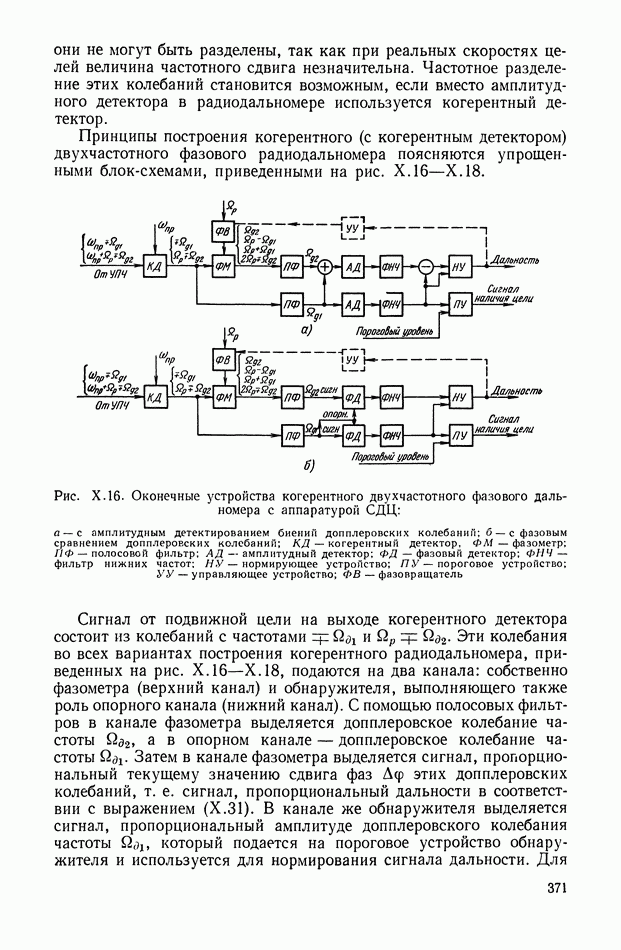
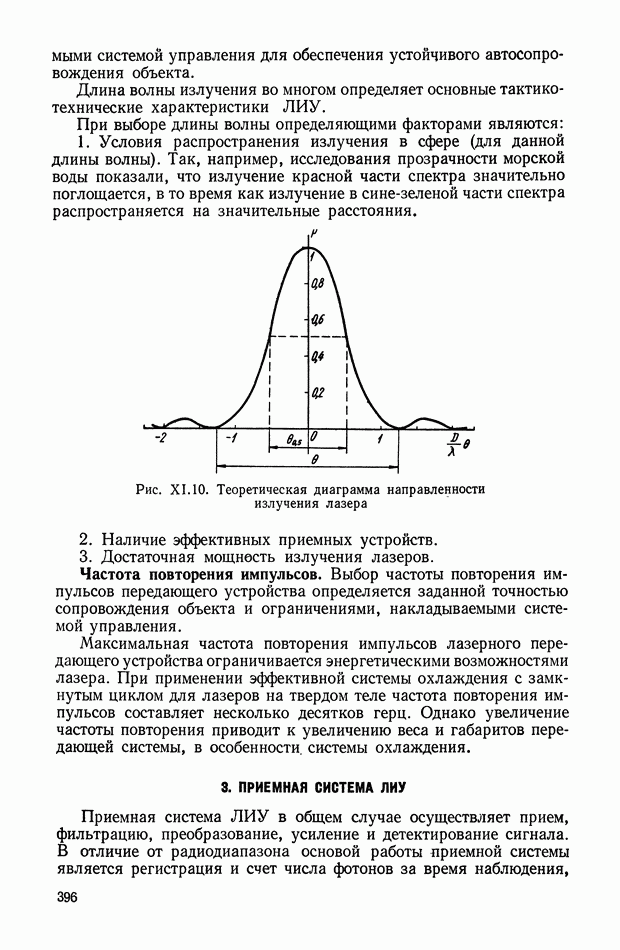
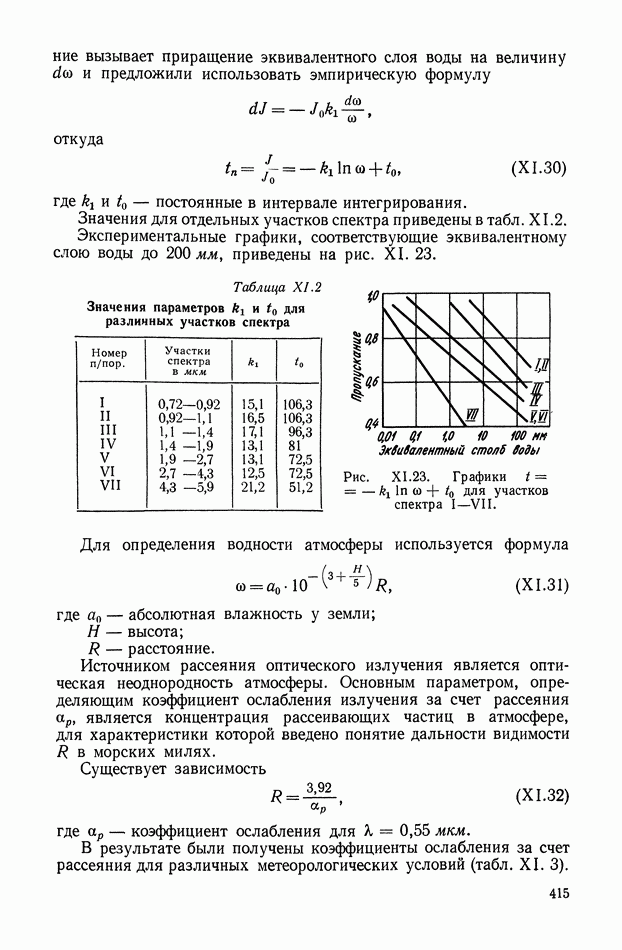
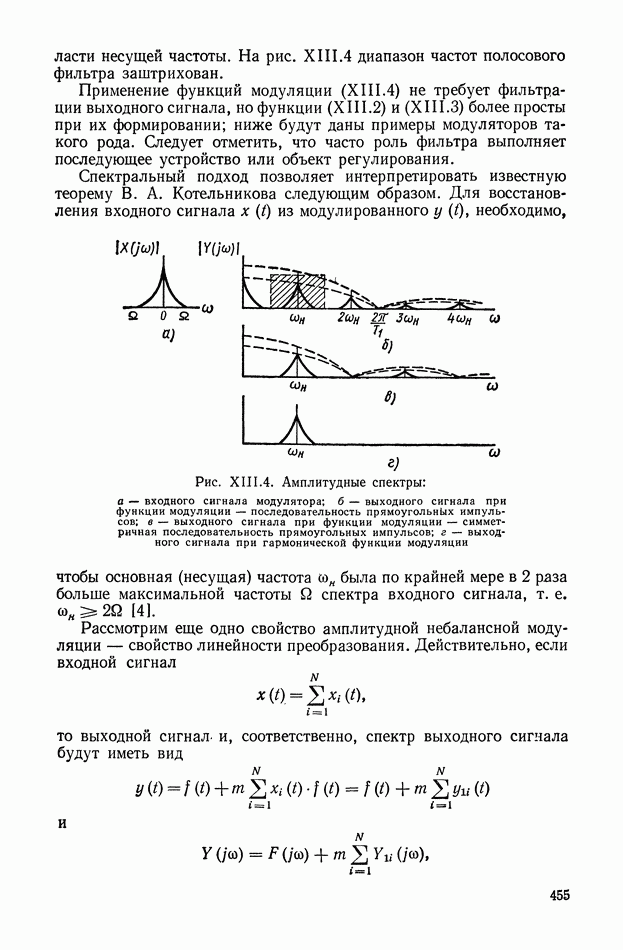
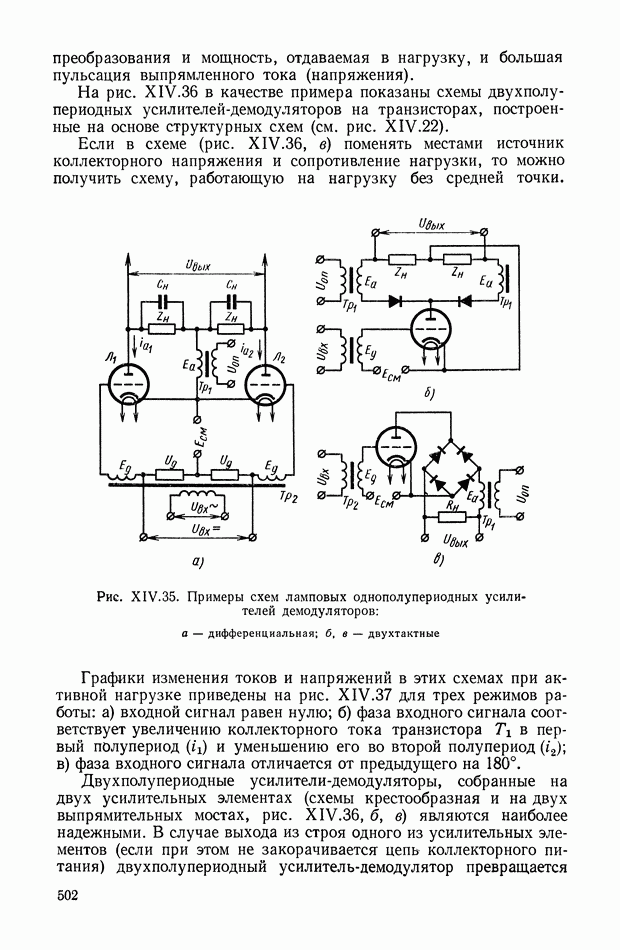
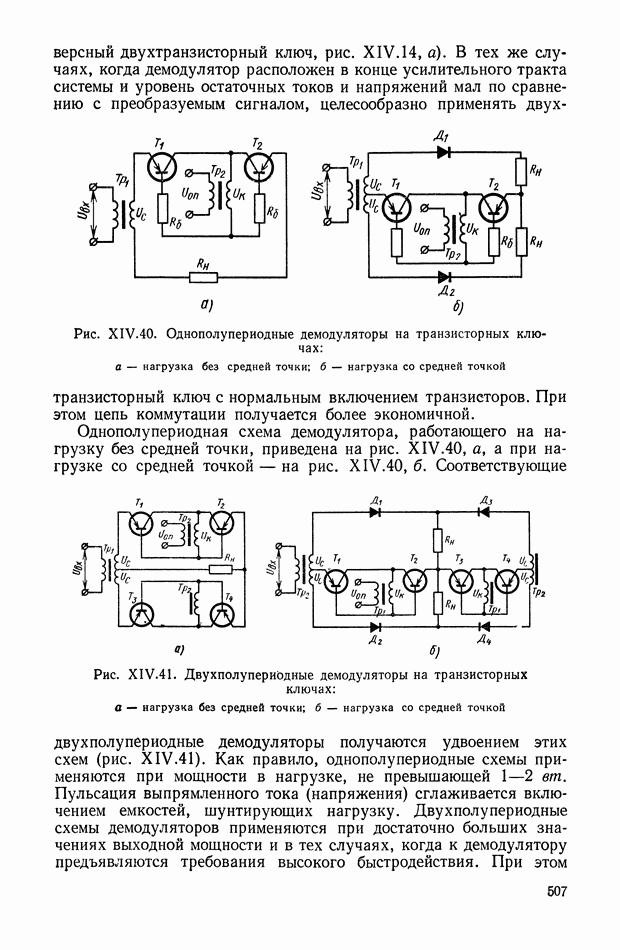
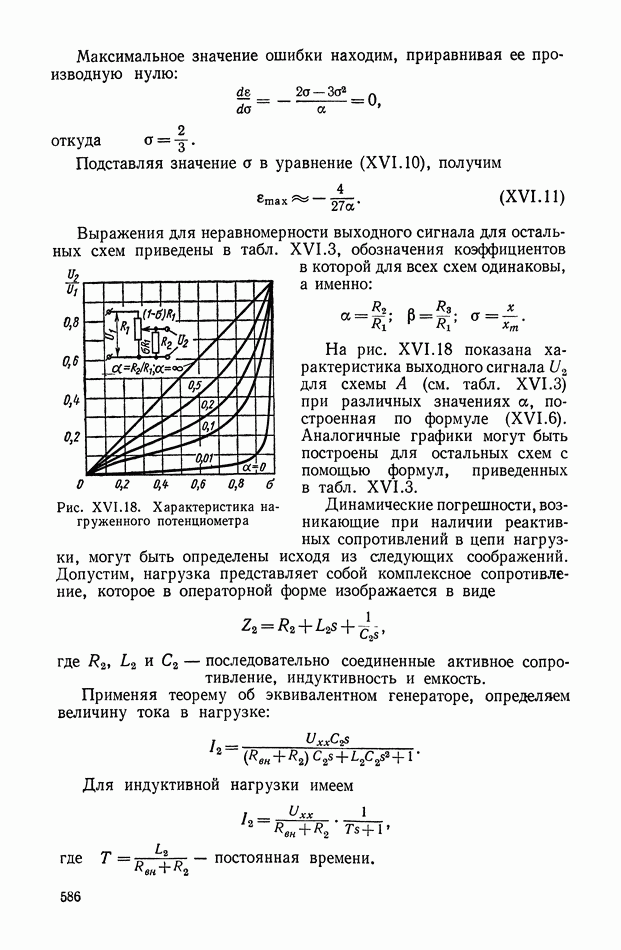
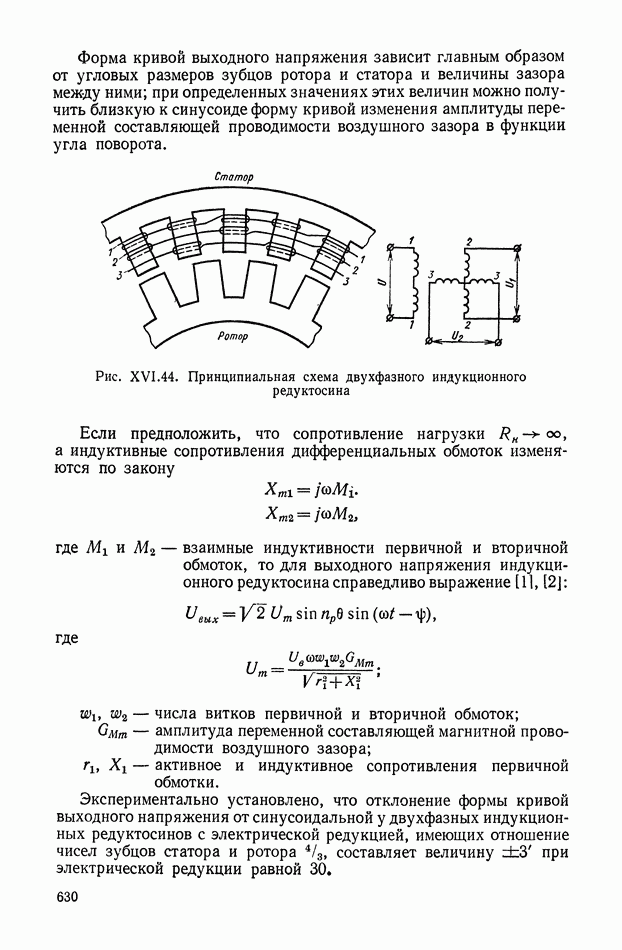
Рис. VIII.2. Астатический гироскоп в кардановом подвесе
Астатические гироскопы применяются в качестве измерительных элементов, определяющих заданное направление в пространстве, и, в частности, как временные «хранители» направления истинной вертикали, направления меридиана или ортодромии и являются датчиками автопилота, прицела, антенны, определяющими положение объекта относительно заданного направления в пространстве.
Принцип действия астатического гироскопа основан на использовании способности вектора кинетического момента Н сохранять заданное направление в пространстве при отсутствии внешних моментов. Тогда направление оси ротора гироскопа в пространстве служит исходной базой для определения положения движущегося объекта, антенны и Др.
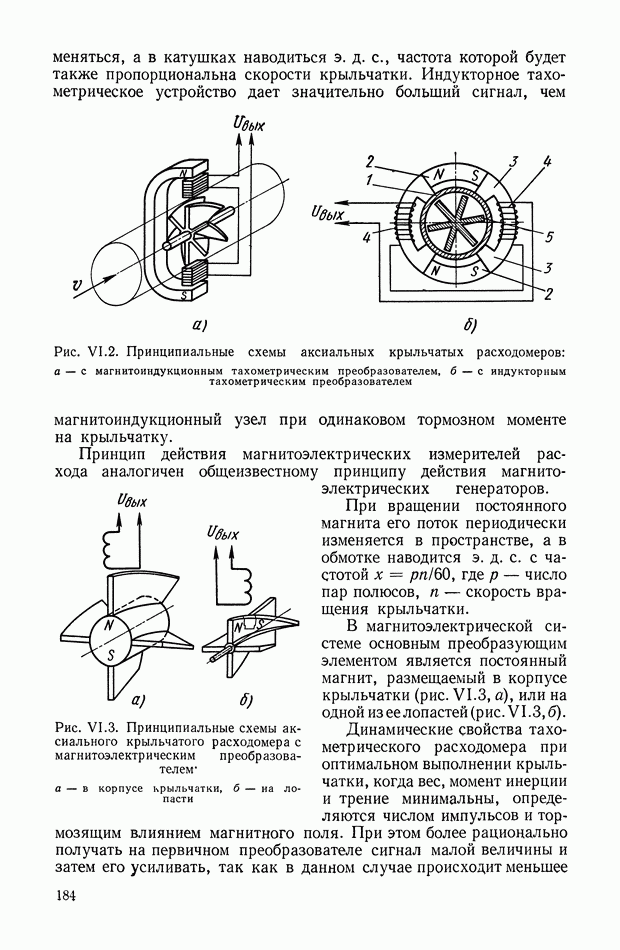
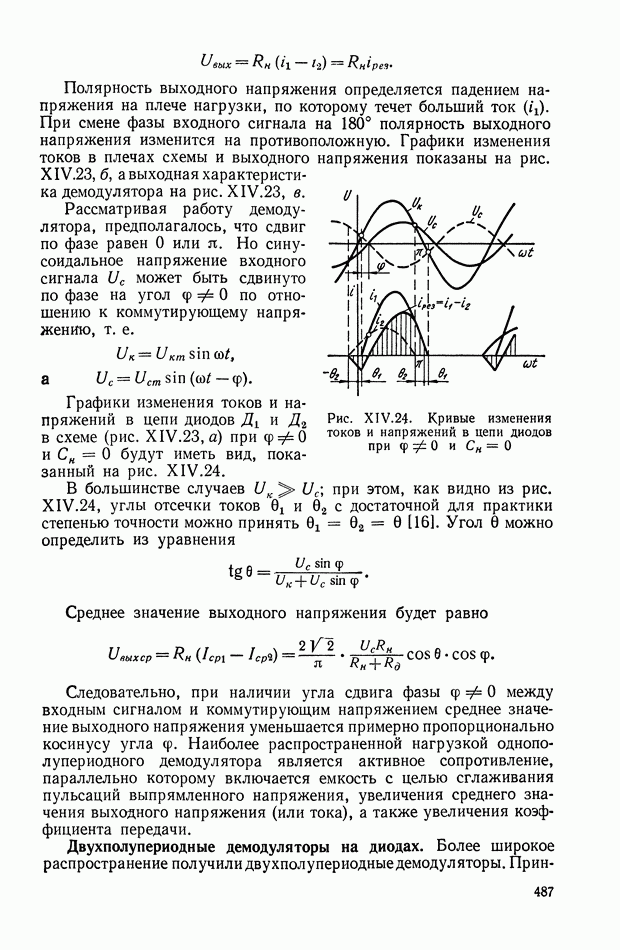
В процессе эксплуатации ось ротора астатического гироскопа, подверженная действию моментов внешних сил, совершает вынужденные колебания и постепенно отклоняется от заданного направления в пространстве.
Скорость отклонения оси ротора гироскопа в пространстве называется собственной скоростью прецессии гироскопа, или просто «уходом», и является наиболее важной характеристикой точности прибора.
Обычно для астатического гироскопа, как и для остальных гироскопических элементов, различают следующие составляющие собственной скорости прецессии:
а) случайную составляющую  вызванную действием вредных моментов, не зависящих от силы тяжести (моменты трения, моменты от токоподводов, моменты «тяжения» от электростатических и магнитных полей и т. д.);
вызванную действием вредных моментов, не зависящих от силы тяжести (моменты трения, моменты от токоподводов, моменты «тяжения» от электростатических и магнитных полей и т. д.);
б) составляющую со пропорциональную перегрузке, вызванную действием инерционных моментов, возникающих вследствие несовпадения центра тяжести гироскопа с центром карданова подвеса;
в) составляющую  пропорциональную квадрату перегрузки, вызванную действием вредных моментов, возникающих вследствие неравножесткости элементов карданова подвеса в различных направлениях;
пропорциональную квадрату перегрузки, вызванную действием вредных моментов, возникающих вследствие неравножесткости элементов карданова подвеса в различных направлениях;
г) динамическую составляющую  вызванную угловыми колебаниями оси ротора в пространстве, возникающими вследствие воздействия угловых колебаний основания, нутационных колебаний гироскопа и т. д.
вызванную угловыми колебаниями оси ротора в пространстве, возникающими вследствие воздействия угловых колебаний основания, нутационных колебаний гироскопа и т. д.
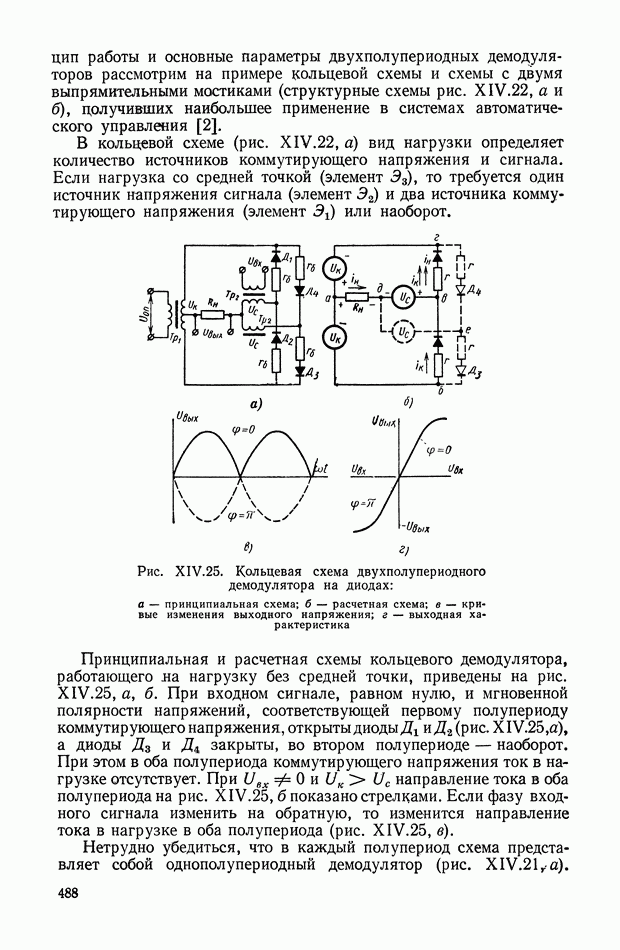
Первые три составляющие являются инструментальными погрешностями, четвертая — методической. Для современных астатических гироскопов, используемых на практике, 
Кроме погрешностей, вызванных отклонением вектора Н от заданного направления, в астатических гироскопах различают также геометрические (карданные) погрешности. Эти погрешности имеют место и при равенстве нулю собственной скорости прецессии и вызваны тем, что определение положения объекта, антенны, прицела относительно вектора Н производится посредством измерения углов поворота гироскопа вокруг внутренней и наружной осей кардана, направления которых вообще не совпадают с осями отсчета в выбранной системе координат.
Величина карданных погрешностей определяется с помощью формул сферической тригонометрии или матричной алгебры.
Уравнения движения астатического гироскопа [8]. Представим себе гироскоп (см. рис. VIII.2), с внутренней рамкой карданова подвеса которого связан правый трехгранник  Оси координат
Оси координат  связаны с летательным аппаратом
связаны с летательным аппаратом 
Положение гироскопа относительно системы координат, связанной с ЛА, определяется углами  (см. рис. VIII.2) поворота оси ротора гироскопа вокруг осей наружной и внутренней рамок его карданова подвеса.
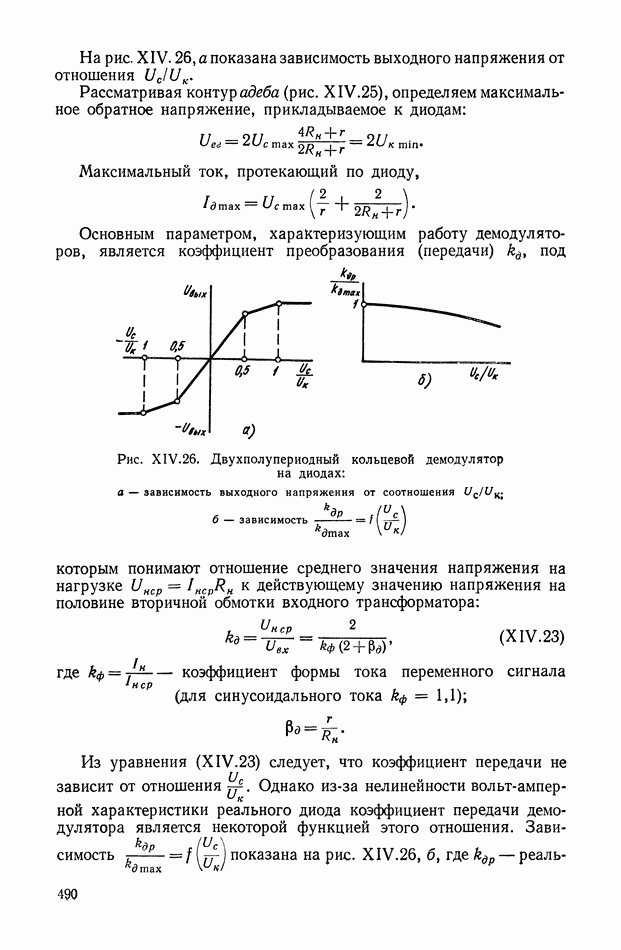
(см. рис. VIII.2) поворота оси ротора гироскопа вокруг осей наружной и внутренней рамок его карданова подвеса.
Вводим обозначения:
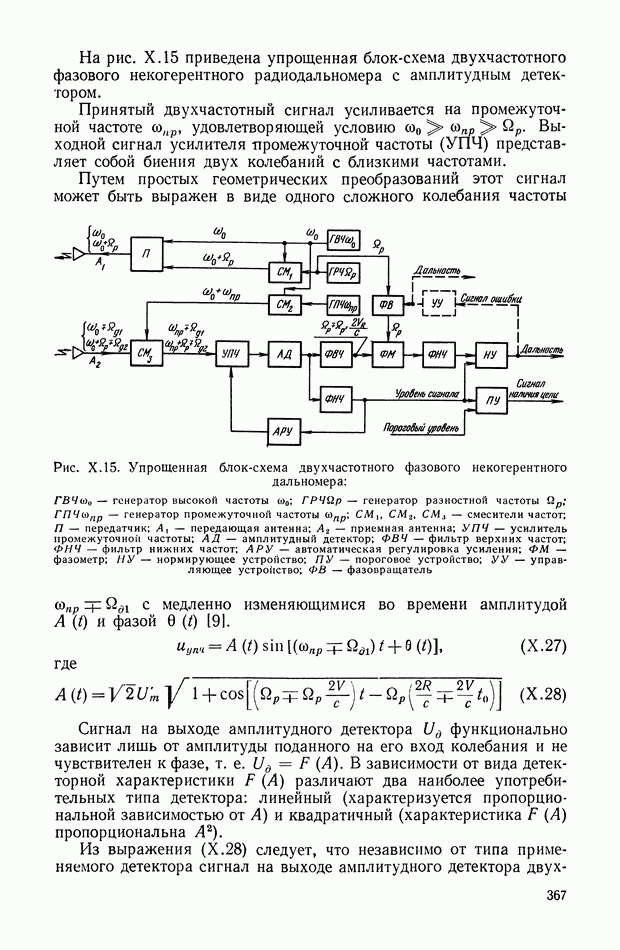
А и С — экваториальный и осевой моменты инерции ротора гироскопа;
 — моменты инерции внутренней рамки карданова подвеса относительно осей
— моменты инерции внутренней рамки карданова подвеса относительно осей 
 — моменты инерции наружной рамки карданова подвеса относительно осей
— моменты инерции наружной рамки карданова подвеса относительно осей 
 — проекции переносной угловой скорости вращения трехгранника
— проекции переносной угловой скорости вращения трехгранника  на его ребра;
на его ребра;
 проекции переносной угловой скорости наружной рамки карданова подвеса на ось
проекции переносной угловой скорости наружной рамки карданова подвеса на ось  и на ось
и на ось 
 — абсолютная угловая скорость вращения ротора гироскопа вокруг оси
— абсолютная угловая скорость вращения ротора гироскопа вокруг оси 
Проектируя моменты, действующие вокруг осей внутренней и наружной рамок карданова подвеса, на оси  получаем уравнения движения астатического гироскопа в подвижных осях координат:
получаем уравнения движения астатического гироскопа в подвижных осях координат:

Уравнениями (VIII.4) удобно пользоваться при исследовании движения гироскопа, заключенного в кардановом подвесе на движущемся объекте, когда возмущение их  задано и необходимо найти движение гироскопа, определяемое координатами
задано и необходимо найти движение гироскопа, определяемое координатами  Эти уравнения могут быть использованы также для определения динамической составляющей собственной скорости прецессии
Эти уравнения могут быть использованы также для определения динамической составляющей собственной скорости прецессии 
Свободное движение гироскопа, заключенного в кардановом подвесе. Для астатического гироскопа, установленного на неподвижном основании при отсутствии внешних возмущений  и уравнения (VIII.4) принимают вид
и уравнения (VIII.4) принимают вид

Движение свободного гироскопа описывается системой нелинейных дифференциальных уравнений 
Переходя к вариациям координат  полагая
полагая

и ограничиваясь первым приближением линеаризованных уравне  получим
получим

Исключая координату Др, имеем

При этом, как это следует из решения системы нелинейных дифференциальных уравнений (VIII.5),

где 
 — амплитуда нутационных колебаний гироскопа, представ ляющих собой решение уравнений (VIII.6),
— амплитуда нутационных колебаний гироскопа, представ ляющих собой решение уравнений (VIII.6),

Частота нутационных колебаний гироскопа

Согласно уравнениям (VIII.7) и (VIII.8) астатический гироскоп, заключенный в кардановом подвесе, совершает нутационные колебания малой амплитуды и одновременно поворачивается вокруг оси наружной рамки карданова подвеса с угловой скоростью 
Малая величина  определяемая выражением (VIII.7), представляет собой динамическую составляющую собственной скорости прецессии, обусловленную нутационными колебаниями гироскопа.
определяемая выражением (VIII.7), представляет собой динамическую составляющую собственной скорости прецессии, обусловленную нутационными колебаниями гироскопа.
Основное свойство свободного гироскопа (см. рис. VIII. 1) — сохранять направление оси его ротора неизменным в абсолютном пространстве; для гироскопа в карданном подвесе это свойство сохраняется с точностью до  При
При  гироскоп не является указателем направления, неизменного в абсолютном пространстве.
гироскоп не является указателем направления, неизменного в абсолютном пространстве.
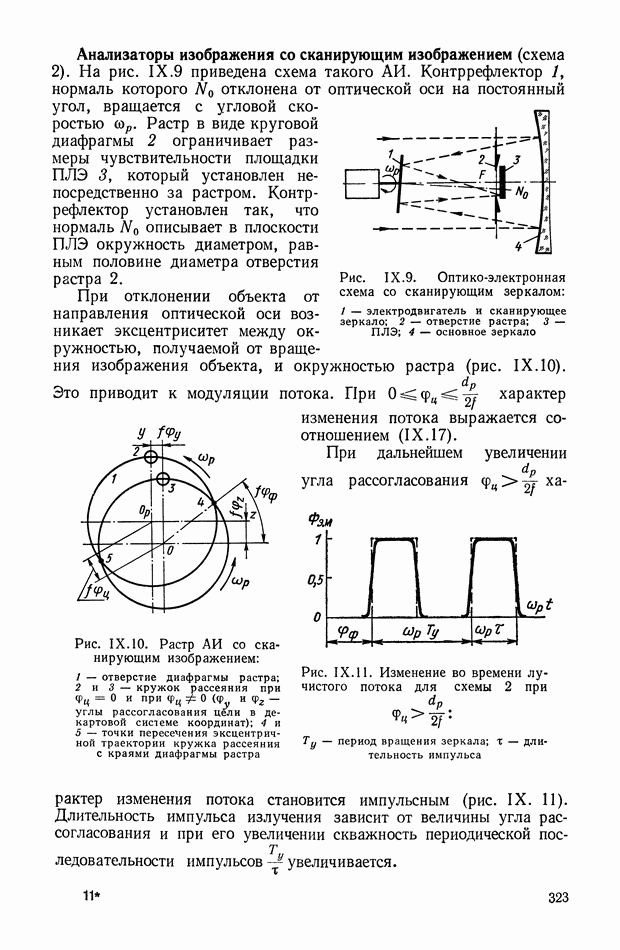
Вынужденное движение. Определим реакцию астатического гироскопа на возмущающий момент  действующий вокруг оси
действующий вокруг оси  Полагая, что вокруг оси
Полагая, что вокруг оси  так же действует диссипативный момент
так же действует диссипативный момент  , и опуская значок
, и опуская значок  вариации из уравнения (VIII.5), получим уравнения движения астатического гироскопа первого приближения
вариации из уравнения (VIII.5), получим уравнения движения астатического гироскопа первого приближения

Обозначая  при условии, что при
при условии, что при  а также
а также  определим реакцию гироскопа на возмущение
определим реакцию гироскопа на возмущение  типа единичного скачка
типа единичного скачка

В установившемся режиме движения гироскопа вторые и третьи члены уравнений (VIII.11) стремятся к нулю и, следовательно, имеем

Гироскоп поворачивается в направлении действия момента внешних сил на угол а, называемый «нутационным броском», и поворачивается вокруг оси  внутренней рамки кардана с угловой скоростью
внутренней рамки кардана с угловой скоростью  (прецессия гироскопа).
(прецессия гироскопа).
Реакция астатического гироскопа на гармоническое возмущение может быть определена с помощью передаточных функций

Перепишем дифференциальные уравнения (VIII.10) воператорной форме 

Из уравнений (VIII. 13) имеем

Применяя к уравнениям (VII 1.14) преобразование Лапласа, получим искомые передаточные функции

где 

Для реальных параметров астатических гироскопов собственная частота 
Это означает, что нутационные колебания совершаются с высокой частотой и малой амплитудой и их в большинстве случаев можно не учитывать. Физически нутационные колебания вызываются наличием инерционных членов  в уравнениях (VIII. 10). В связи с этим на практике вместо полных уравнений (VIII. 10) часто используются укороченные (усеченные, прецессионные) уравнения, которые при отсутствии диссипативного момента имеют вид
в уравнениях (VIII. 10). В связи с этим на практике вместо полных уравнений (VIII. 10) часто используются укороченные (усеченные, прецессионные) уравнения, которые при отсутствии диссипативного момента имеют вид

Тогда соответствующие передаточные функции

т. e. гироскоп является интрегатором внешнего момента.
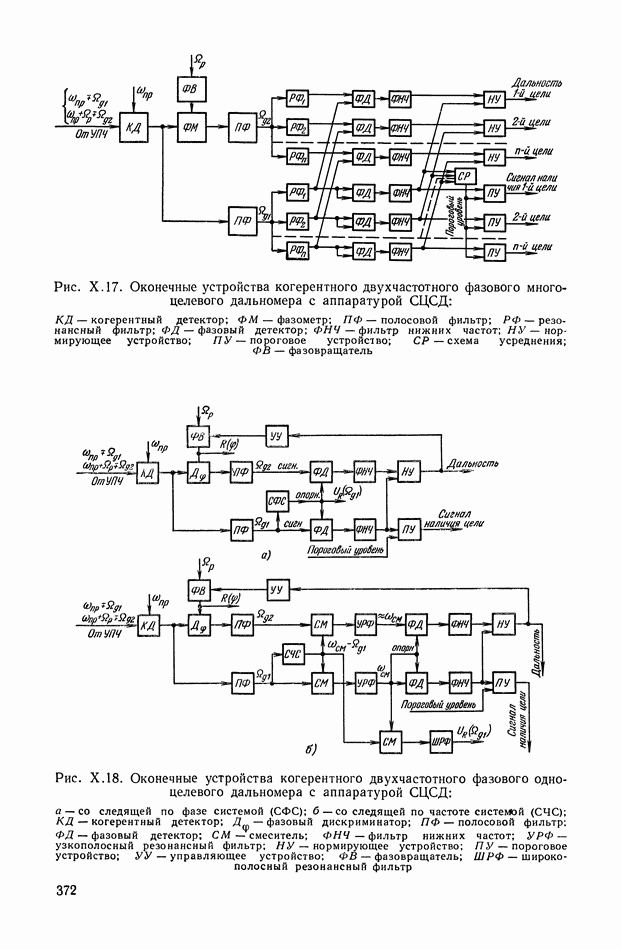
Определение собственной скорости прецессии. Для определения  используются уравнения
используются уравнения  . В качестве примера найдем при малых гармонических колебаниях летательного аппарата вокруг продольной оси
. В качестве примера найдем при малых гармонических колебаниях летательного аппарата вокруг продольной оси  (рис. VIII.2) с угловой скоростью у [8]. При этом
(рис. VIII.2) с угловой скоростью у [8]. При этом

Используя значения  (VIII.18) из уравнений (VIII.4), найдем приближенное значение возмущающего момента, действующего вокруг оси
(VIII.18) из уравнений (VIII.4), найдем приближенное значение возмущающего момента, действующего вокруг оси  и возникающего вследствие карданного поворота рамок гироскопа, а именно
и возникающего вследствие карданного поворота рамок гироскопа, а именно

Если  где
где  — частота возмущающих колебаний летательного аппарата, то
— частота возмущающих колебаний летательного аппарата, то

и, следовательно,

Считая, что  воспользуемся уравнениями
воспользуемся уравнениями  для нахождения амплитуды угловых колебаний оси ротора гироскопа вокруг осей внутренней и наружной рамок его карданова подвеса. При этом вследствие периодического наклона оси х внутренней рамки карданова подвеса гироскопа с частотой
для нахождения амплитуды угловых колебаний оси ротора гироскопа вокруг осей внутренней и наружной рамок его карданова подвеса. При этом вследствие периодического наклона оси х внутренней рамки карданова подвеса гироскопа с частотой  и прецессии гироскопа вокруг оси
и прецессии гироскопа вокруг оси  с угловой скоростью
с угловой скоростью  ось ротора гироскопа поворачивается в абсолютном пространстве вокруг оси наружной рамки карданова подвеса с угловой скоростью, среднее значение которой
ось ротора гироскопа поворачивается в абсолютном пространстве вокруг оси наружной рамки карданова подвеса с угловой скоростью, среднее значение которой

Аналогичным образом легко определите, что в случае малых периодических колебаний ЛА с угловой скоростью у

где Т — период колебаний.
Если у — стационарная случайная функция, то математическое ожидание  определится:
определится:

где  дисперсия 7.
дисперсия 7.
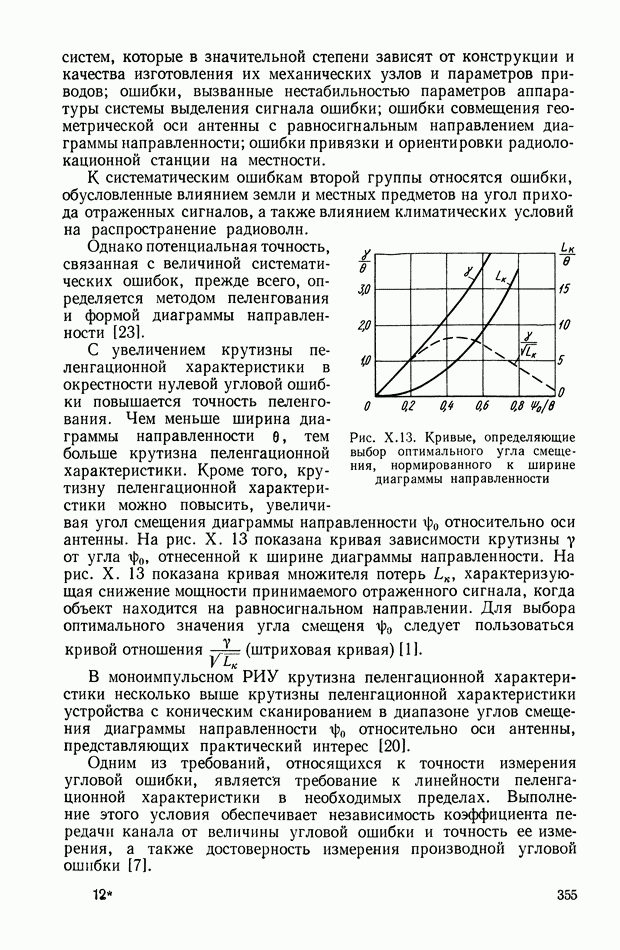
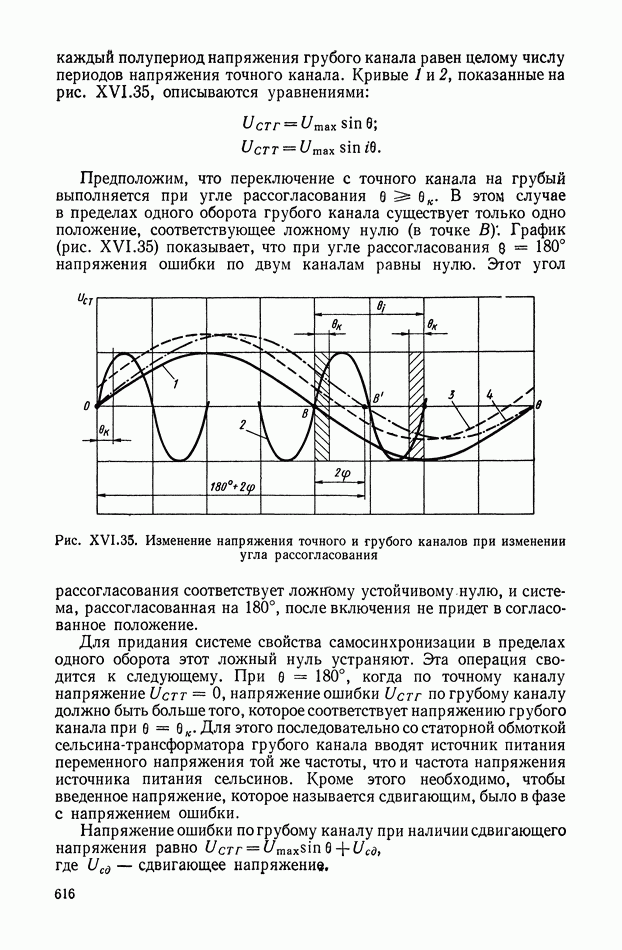
Скорость прецессии  достигает наибольшей величины при гармонических угловых вибрациях основания в случае резонанса, когда частота вибрации
достигает наибольшей величины при гармонических угловых вибрациях основания в случае резонанса, когда частота вибрации  равна частоте нутационных колебаний гироскопа
равна частоте нутационных колебаний гироскопа  Тогда с учетом выражения (VIII. 15)
Тогда с учетом выражения (VIII. 15)

где X — коэффициент динамичности гироскопа.
Составляющие  зависят от возмущающих моментов (трение, дисбаланс и т. д.), действующих вокруг осей карданова подвеса.
зависят от возмущающих моментов (трение, дисбаланс и т. д.), действующих вокруг осей карданова подвеса.
Для примера определим составляющие собственной скорости прецессии  вокруг оси наружной рамки карданова подвеса.
вокруг оси наружной рамки карданова подвеса.
Пользуясь уравнениями (V 111.16), в предположении, что момент вокруг внутренней оси кардана  находим
находим

В свою очередь,

где  — момент, не зависящий от силы тяжести;
— момент, не зависящий от силы тяжести;
 — момент, пропорциональный перегрузке;
— момент, пропорциональный перегрузке;
 — момент, пропорциональный квадрату перегрузки.
— момент, пропорциональный квадрату перегрузки.
При проектировании прибора  определяется либо как сумма моментов трения, моментов от токоподводов и т.
определяется либо как сумма моментов трения, моментов от токоподводов и т.  либо по аналогии с существующими конструкциями. Для изготовленного прибора
либо по аналогии с существующими конструкциями. Для изготовленного прибора  определяется на основании экспериментальных исследований.
определяется на основании экспериментальных исследований.
Обычно  является случайной величиной, распределенной по нормальному закону со среднеквадратическим отклонением
является случайной величиной, распределенной по нормальному закону со среднеквадратическим отклонением  Тогда
Тогда  и за время
и за время  вектор Н повернется в пространстве вокруг оси наружной рамки кардана на угол
вектор Н повернется в пространстве вокруг оси наружной рамки кардана на угол  причем
причем  (VIII.23), где
(VIII.23), где  среднеквадратическое значение случайной составляющей собственной скорости прецессии
среднеквадратическое значение случайной составляющей собственной скорости прецессии  .
.

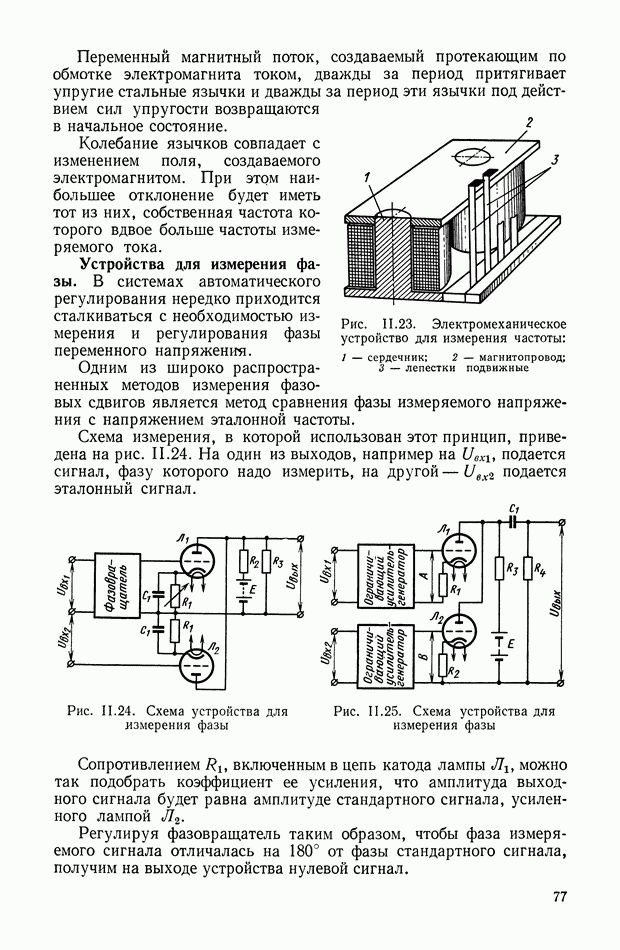
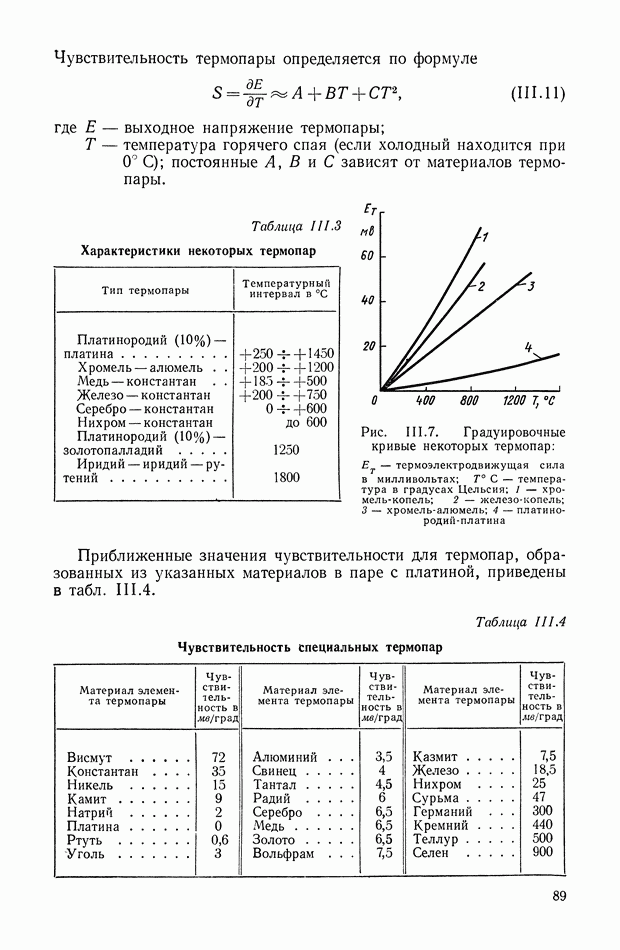
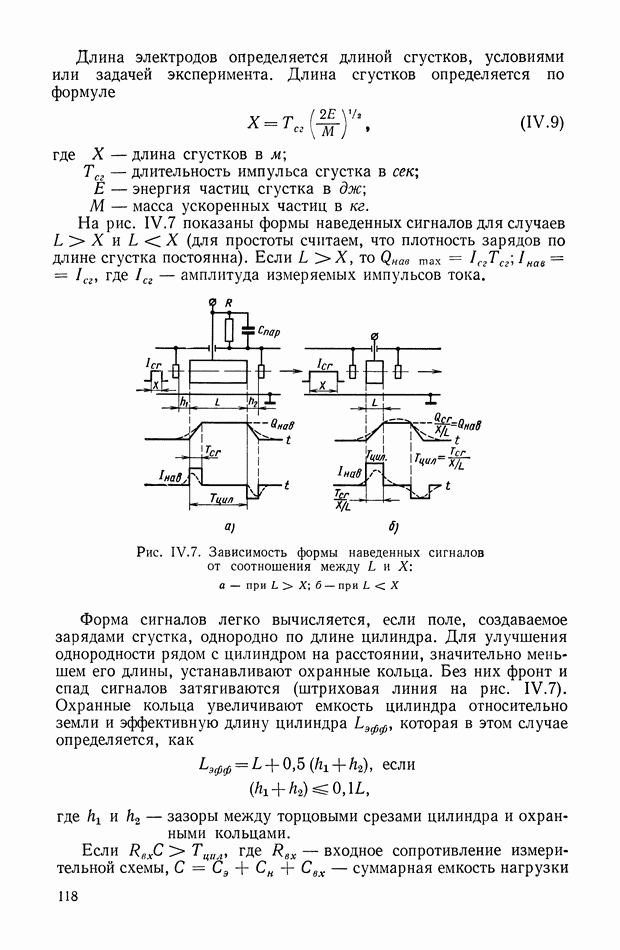
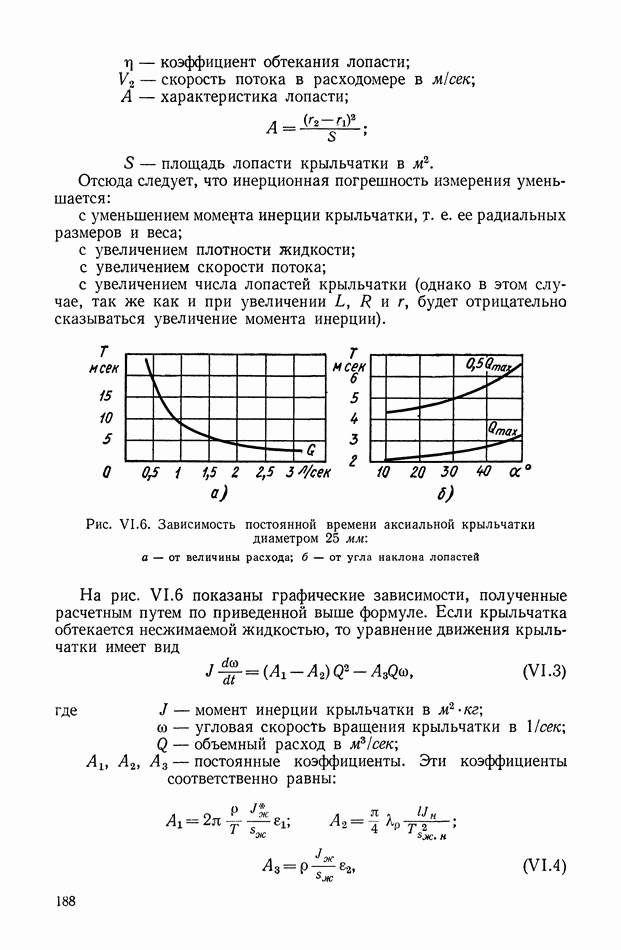
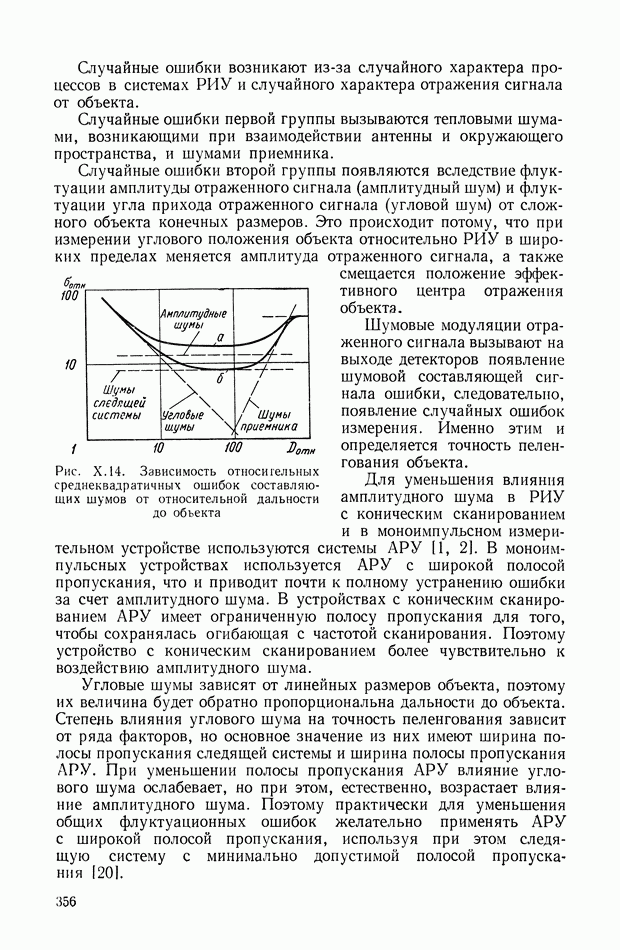
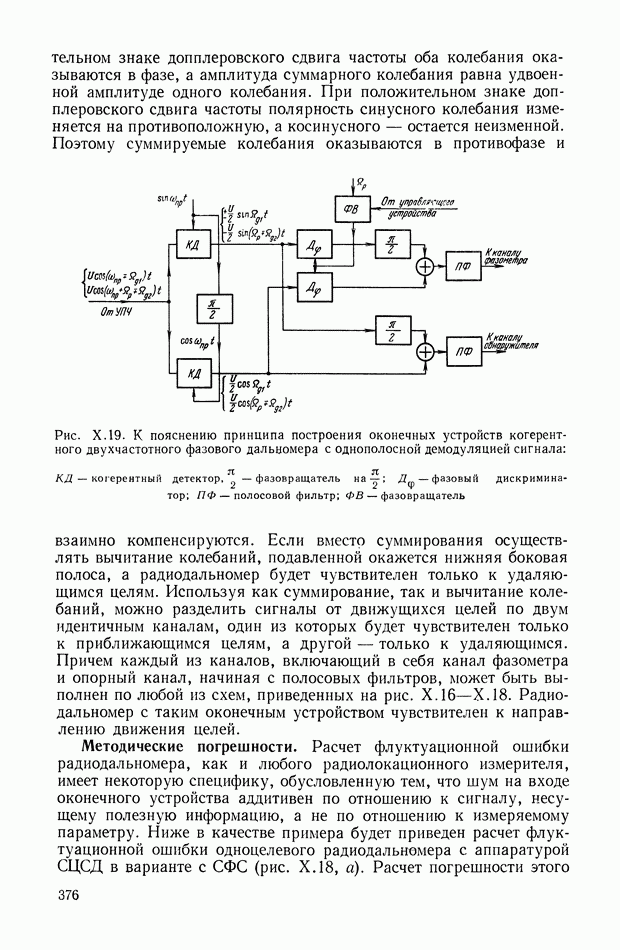
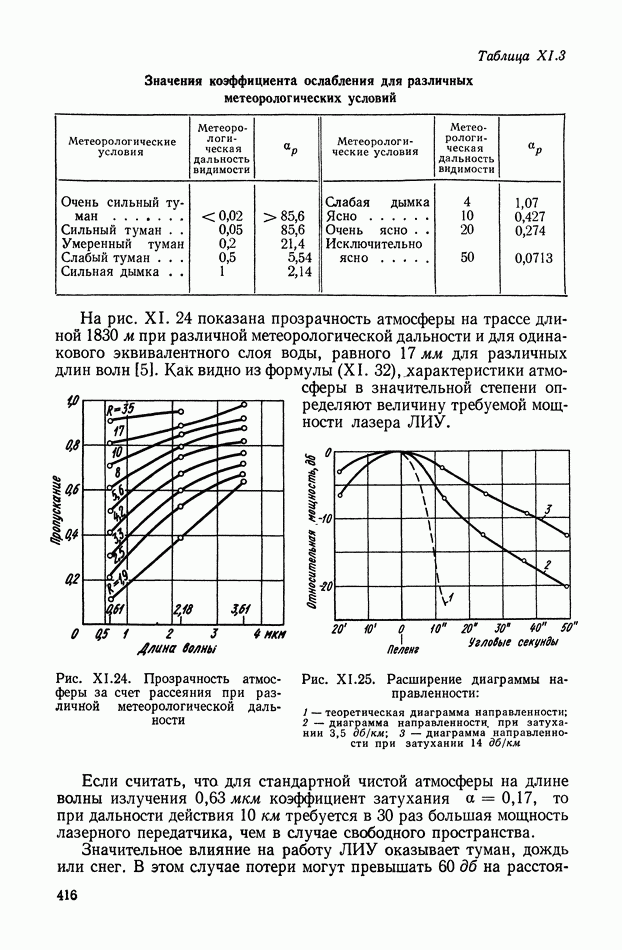
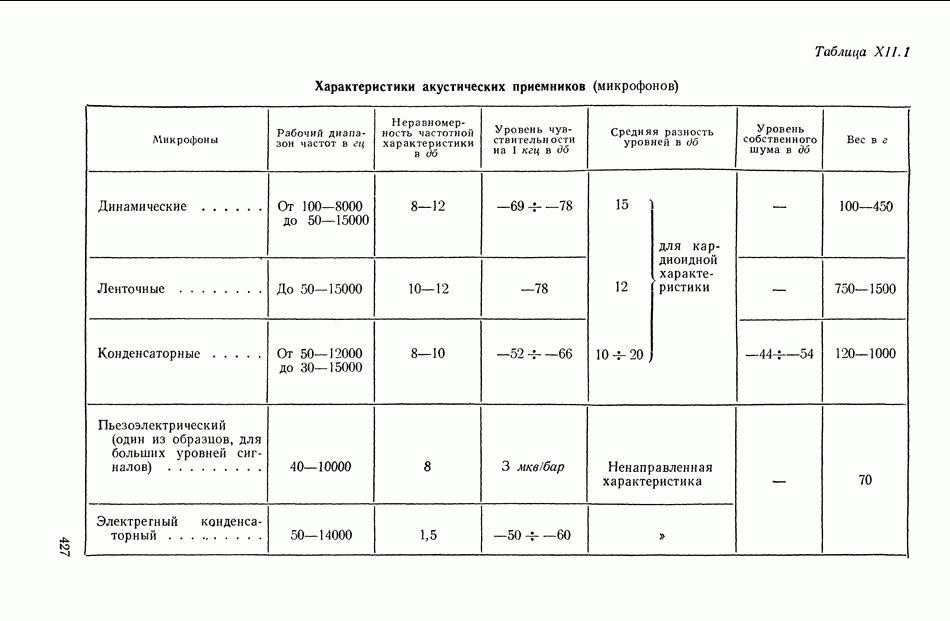
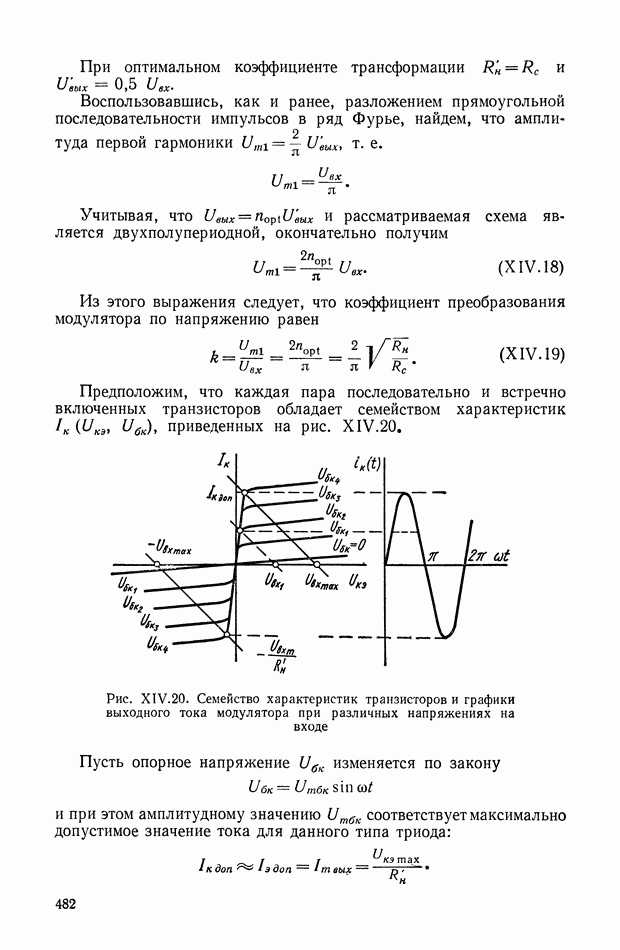
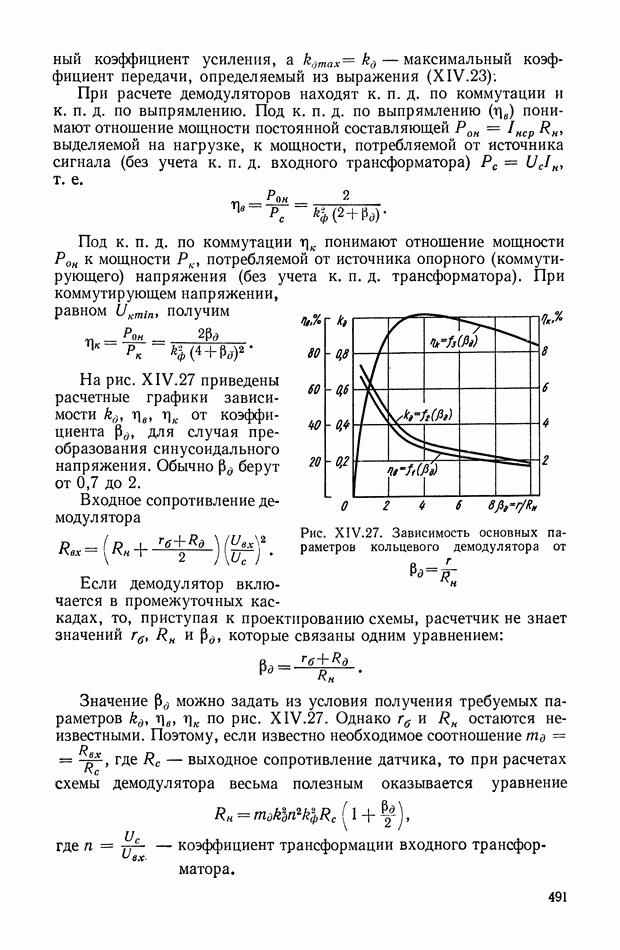
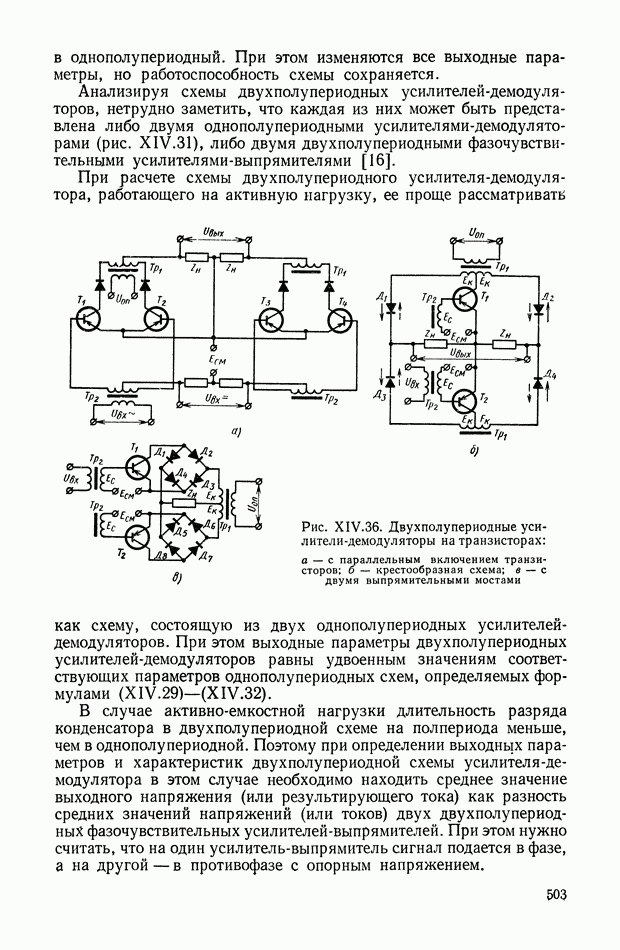
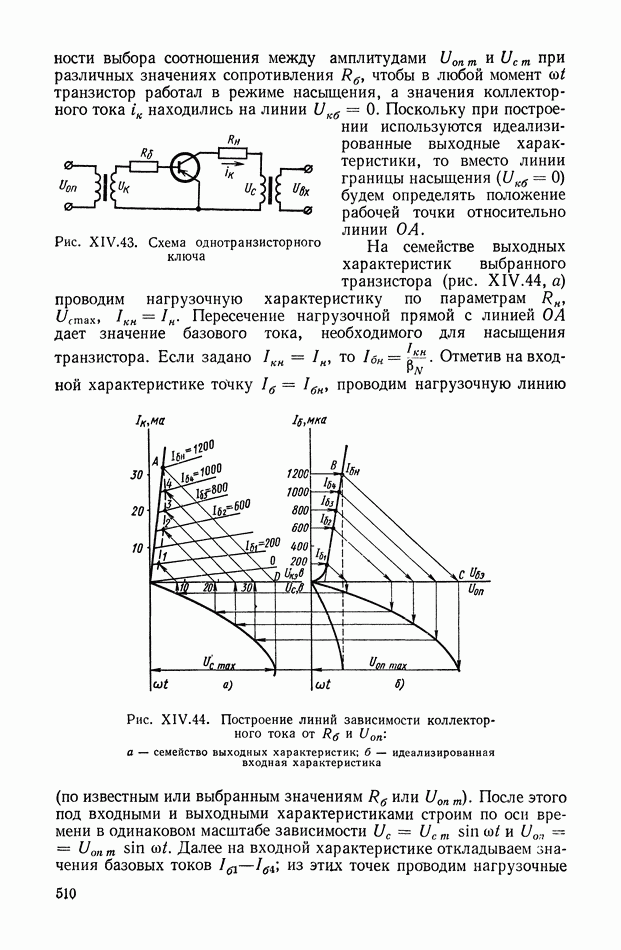
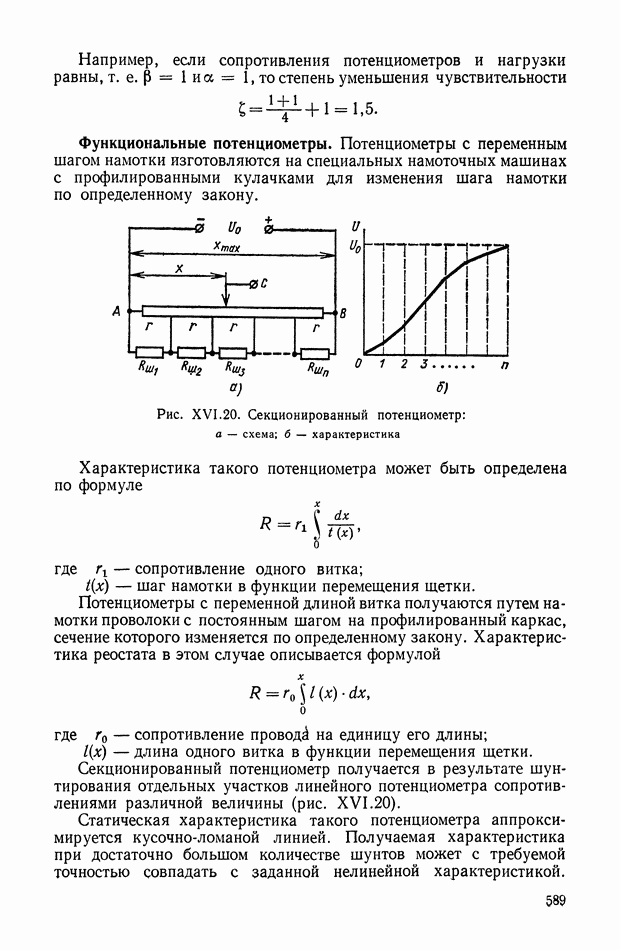
Рис. VIII.3. К определению момента от смещения центра тяжести
Момент  определяется (рис. VII 1.3) в виде
определяется (рис. VII 1.3) в виде

где Р — вес гироузла;
 — смещение центра тяжести вдоль оси
— смещение центра тяжести вдоль оси 
— перегрузки вдоль оси 
Величина смещения центра тяжести вдоль оси  определяется либо по аналогии с существующими конструкциями, либо на основании экспериментальных данных. В установившемся тепловом режиме или в течение сравнительно короткого отрезка времени
определяется либо по аналогии с существующими конструкциями, либо на основании экспериментальных данных. В установившемся тепловом режиме или в течение сравнительно короткого отрезка времени  можно рассматривать как независимые случайные величины, распределенные по нормальному закону. Тогда
можно рассматривать как независимые случайные величины, распределенные по нормальному закону. Тогда

и за время  за счет смещения центра тяжести вдоль оси
за счет смещения центра тяжести вдоль оси  вектор Н повернется на угол
вектор Н повернется на угол  причем
причем

средне-квадратическое значение удельной скорости прецессии, пропорциональной 
В статике, момент от неравножесткости определится по формуле

где  — жесткость упругой связи между кожухом и ротором вдоль оси
— жесткость упругой связи между кожухом и ротором вдоль оси  — вес ротора.
— вес ротора.
Для уменьшения  стремятся, чтобы
стремятся, чтобы  были по возможности максимальны и при номинальных значениях всех параметров равны друг другу. Величина коэффициента
были по возможности максимальны и при номинальных значениях всех параметров равны друг другу. Величина коэффициента  является центрированной случайной величиной. Тогда
является центрированной случайной величиной. Тогда

и за время  за счет неравножесткости вектор Н повернется на угол
за счет неравножесткости вектор Н повернется на угол  причем
причем

где
— среднеквадратическое значение удельной составляющей собственной скорости прецессии, пропорциональной квадрату перегрузки.
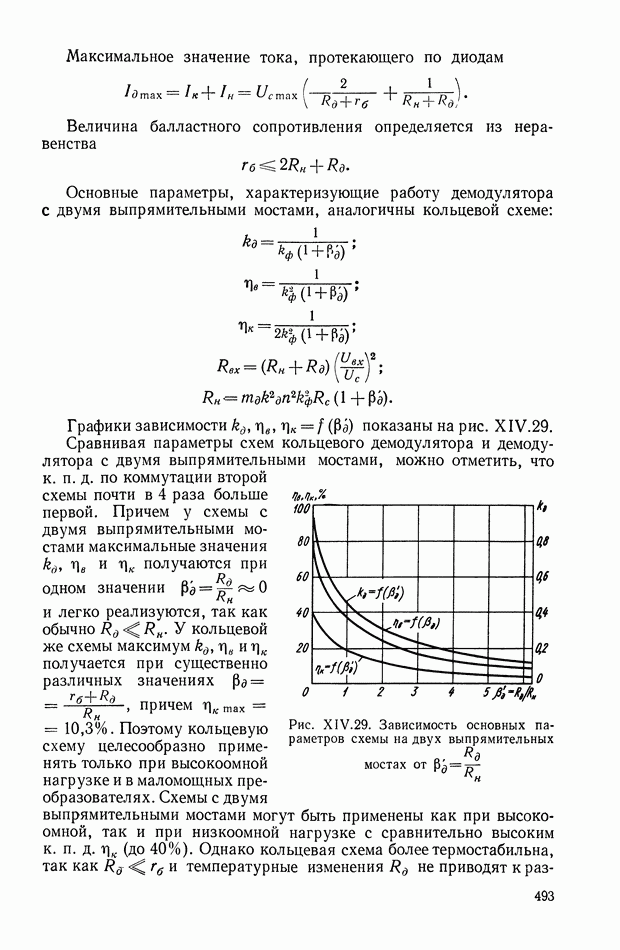
Параметры  являются наиболее важными характеристиками точности прибора.
являются наиболее важными характеристиками точности прибора.
Результирующий угол поворота вектора в пространстве равен сумме случайных величин  которые по своей физической природе являются независимыми, т. е.
которые по своей физической природе являются независимыми, т. е.

Аналогичным образом при вычислении  можно учесть влияние линейных вибраций, непостоянство угла
можно учесть влияние линейных вибраций, непостоянство угла  возрастание момента трения в подшипниках внутренней оси кардана под действием радиальной и осевой перегрузок и т. д.
возрастание момента трения в подшипниках внутренней оси кардана под действием радиальной и осевой перегрузок и т. д.
Окончательное значение погрешности сохранения заданного направления вектора Я определяется суммой  и динамической составляющей.
и динамической составляющей.
Рабочие углы. Рабочий диапазон углов по осям кардана является важной технической характеристикой астатического гироскопа. Так как с увеличением угла увеличиваются методические и инструментальные погрешности гироскопа и снижается нутационная частота, то при проектировании прибора и всей системы в целом, стремятся, чтобы  По этим же причинам рабочий угол
По этим же причинам рабочий угол  как правило, не превышает 45—60°.
как правило, не превышает 45—60°.
Рабочий угол поворота по наружной оси кардана не оказывает существенного влияния на точность астатического гироскопа, В случае необходимости неограниченное значение угла  обеспечивается применением коллекторных токоподводов по наружной оси кардана. При применении гибких токоподводов
обеспечивается применением коллекторных токоподводов по наружной оси кардана. При применении гибких токоподводов  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 1. МОСТОВЫЕ СХЕМЫ
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
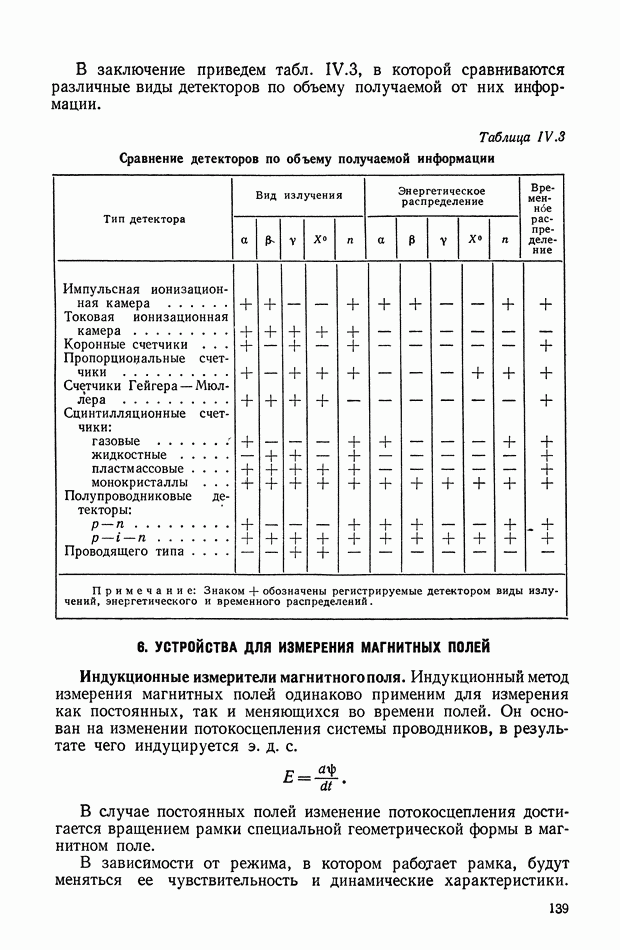
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
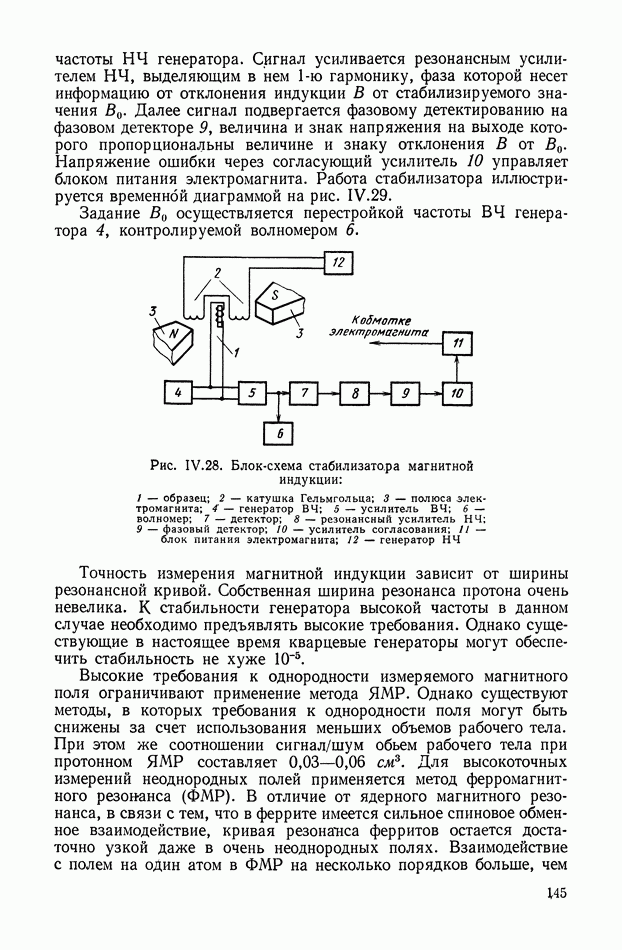
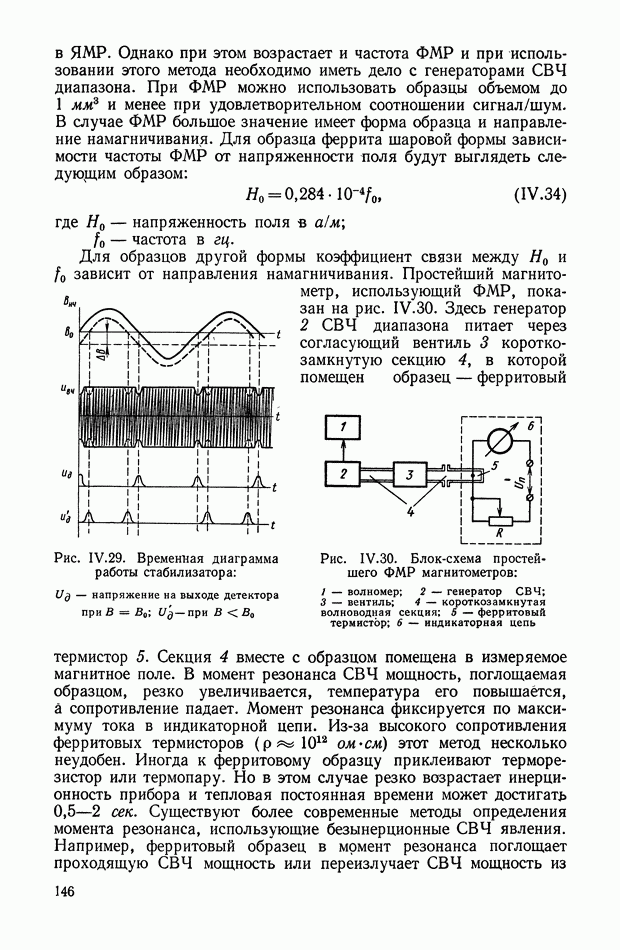
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
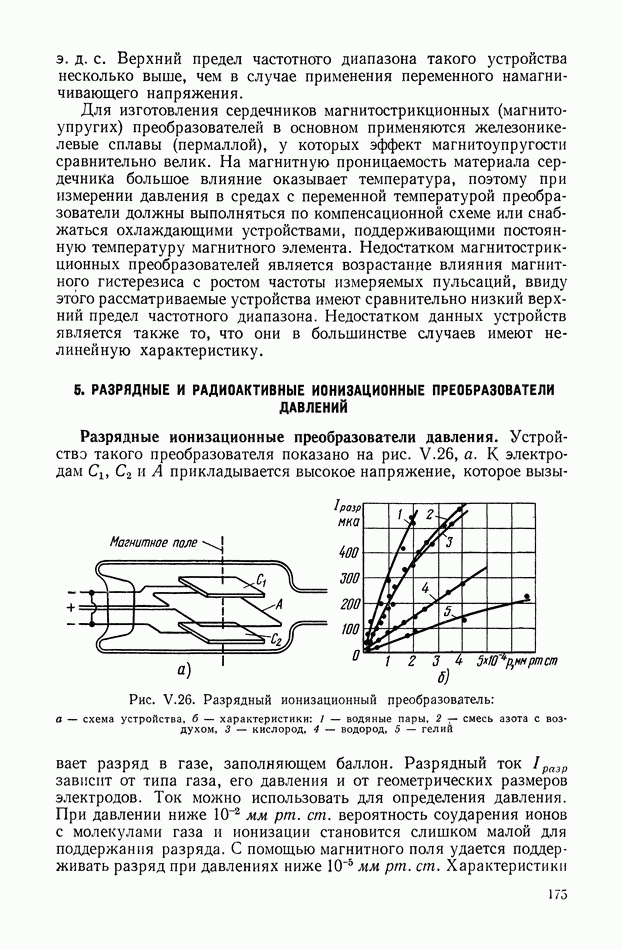
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
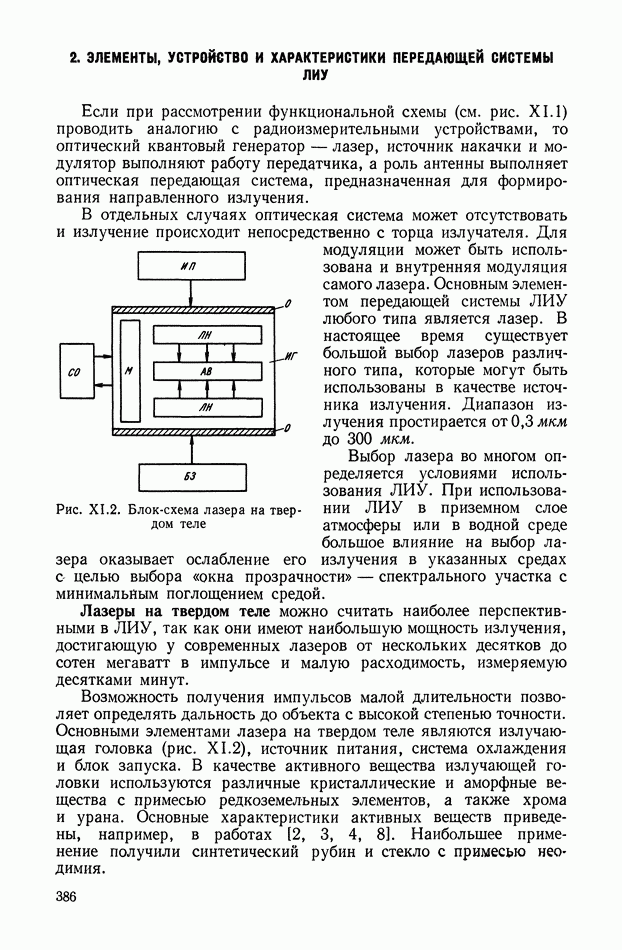
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
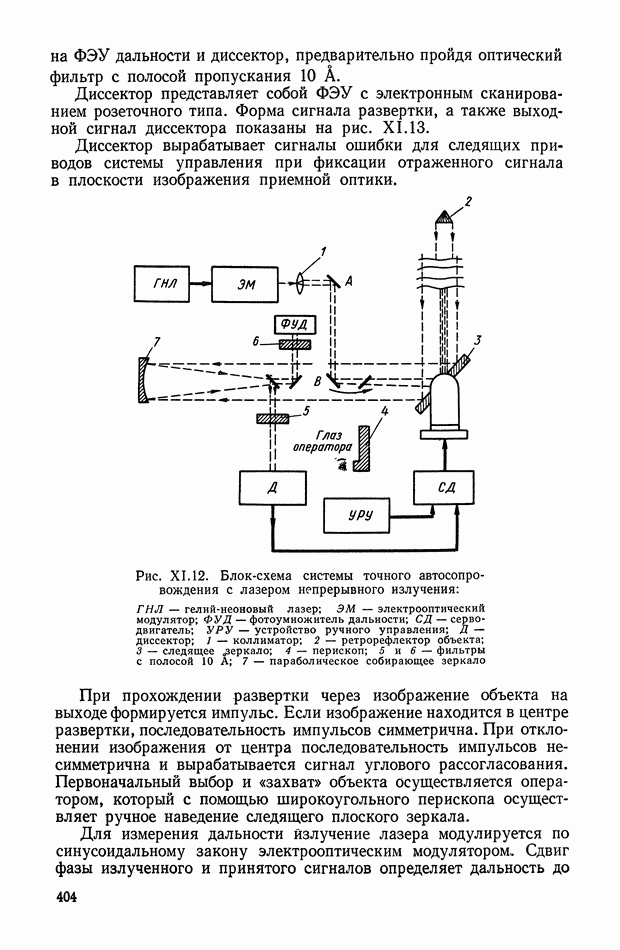
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
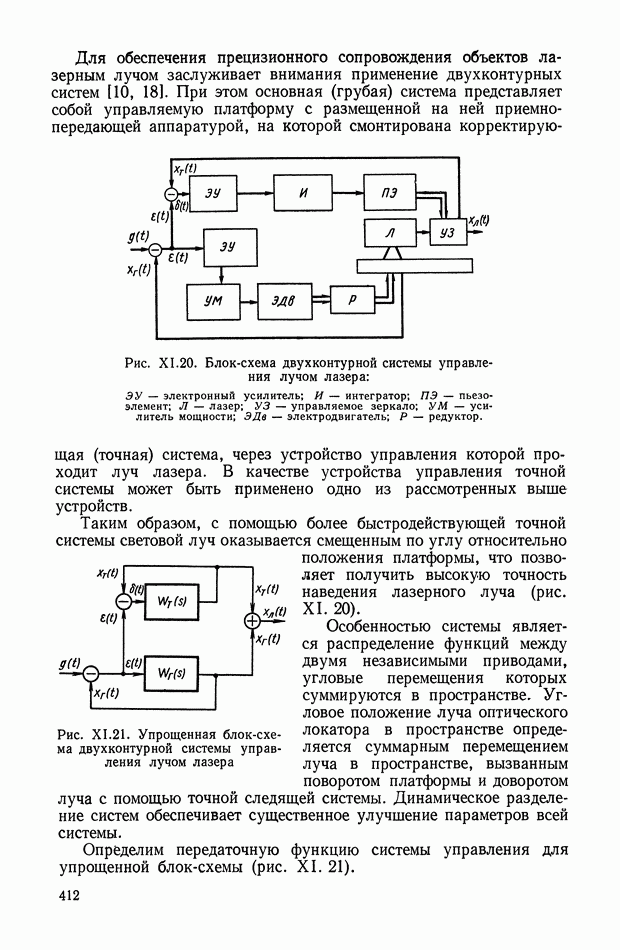
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
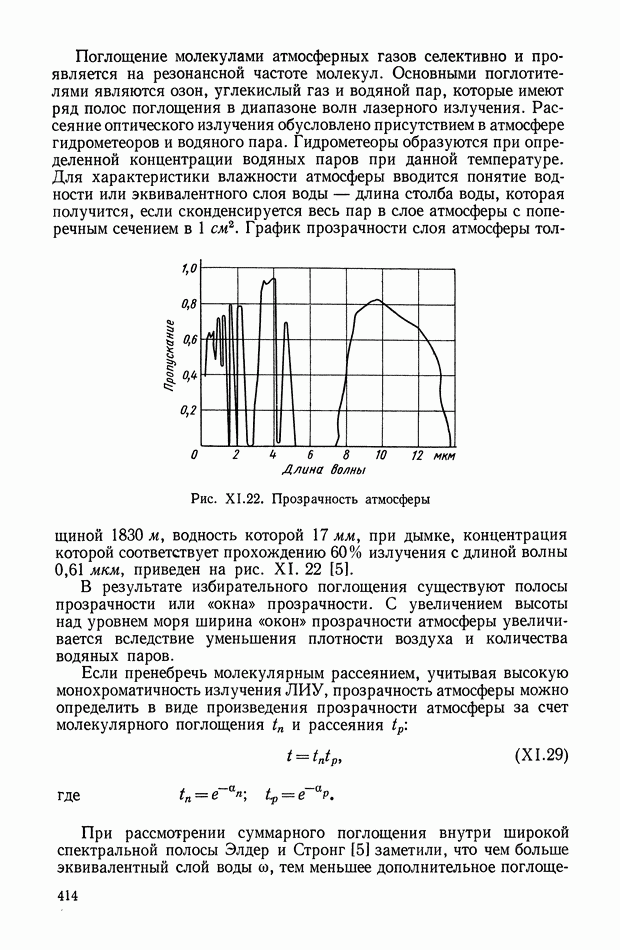
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 1. МОДУЛЯТОРЫ
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
- Двухполупериодные демодуляторы на диодах.
- Однополупериодные усилители-демодуляторы.
- Двухполупериодные усилители-демодуляторы.
- Демодуляторы на транзисторных ключах.
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
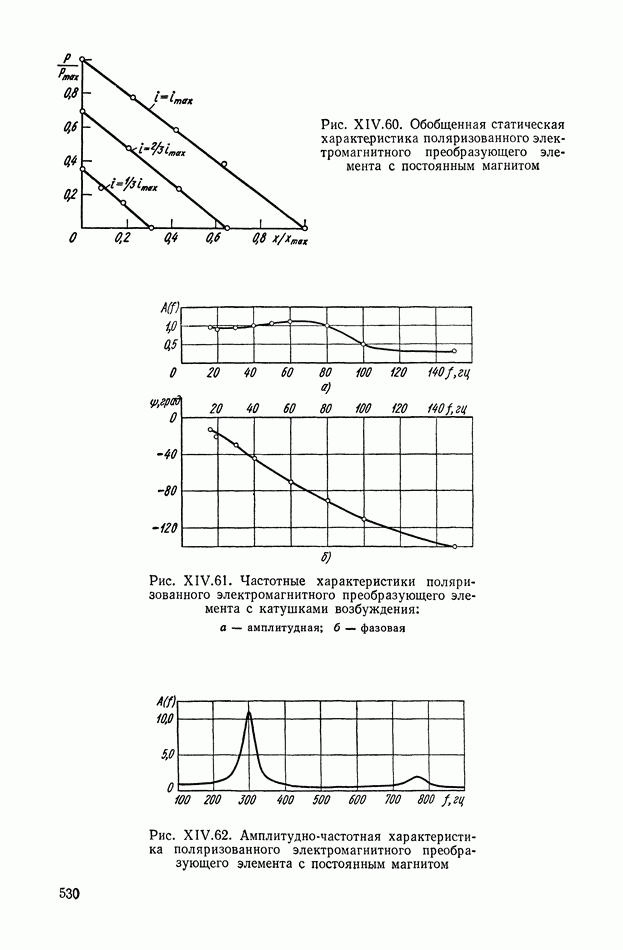
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
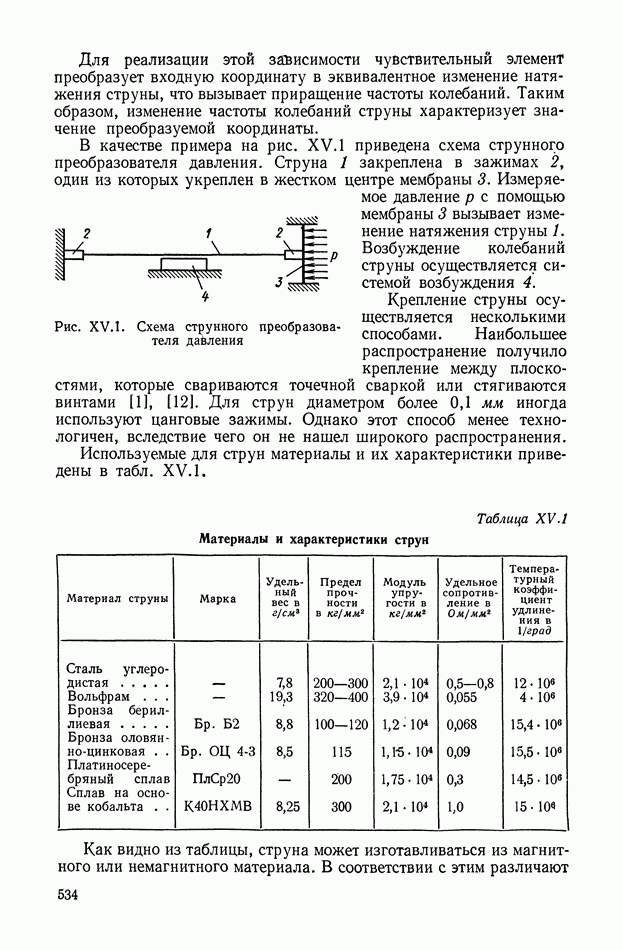
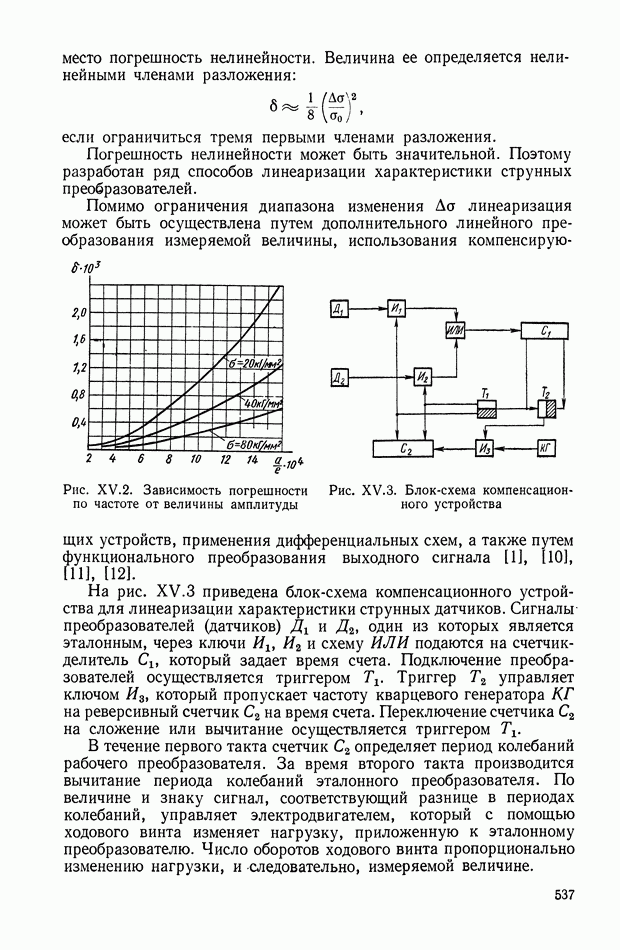
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
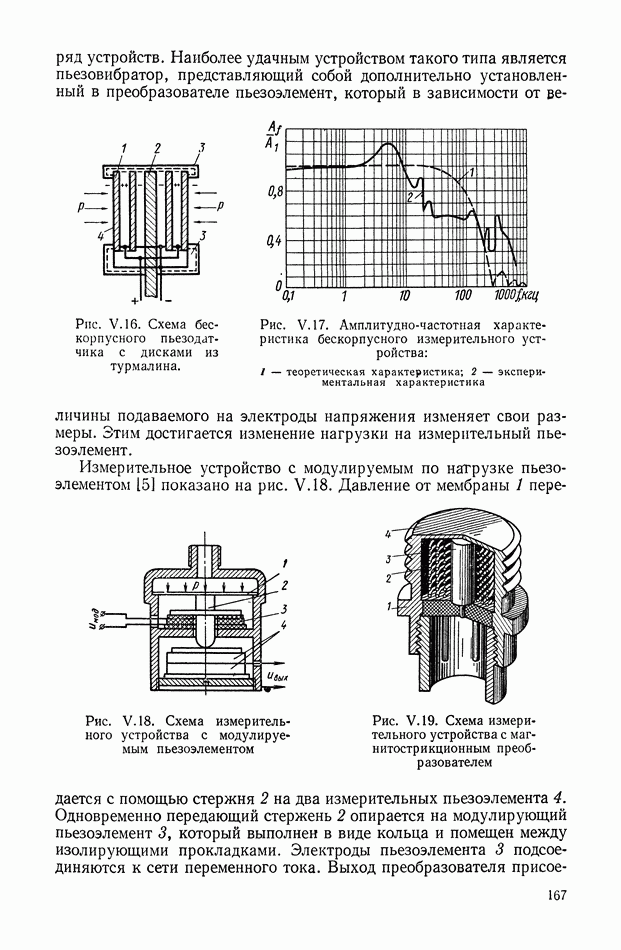
- Сильфоны.
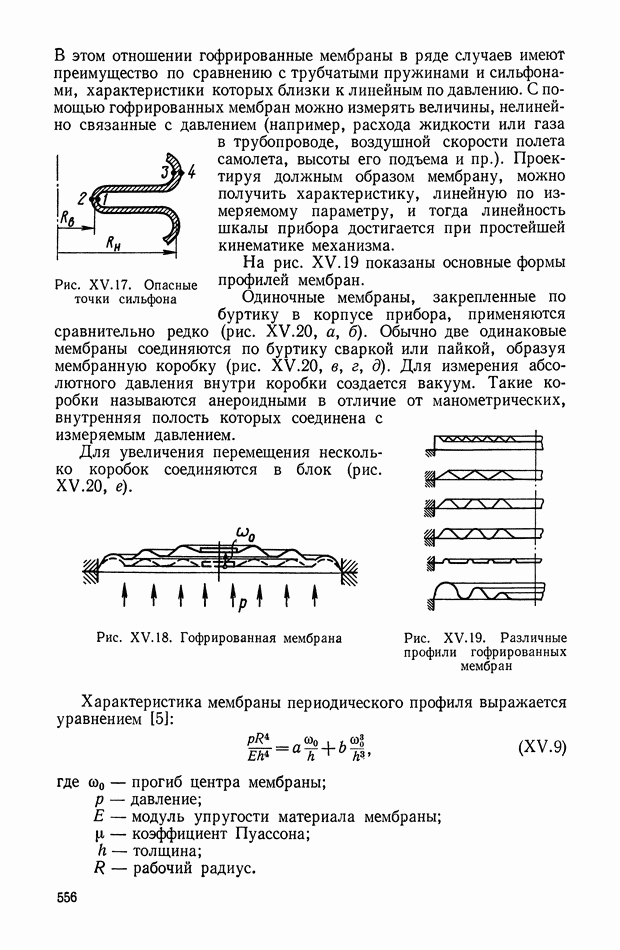
- Гофрированные мембраны.
- Гибкие диафрагмы.
- Хлопающие мембраны.
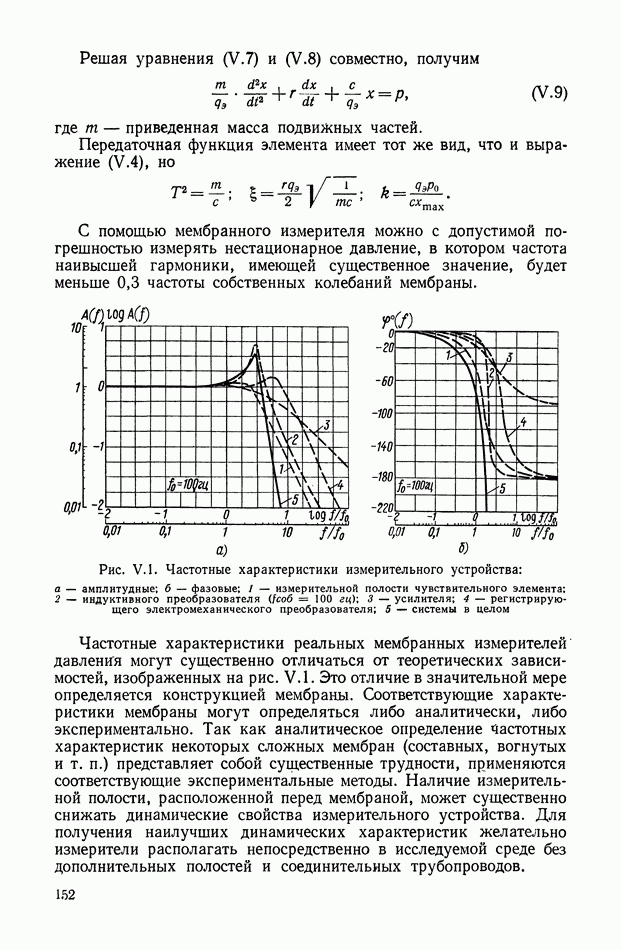
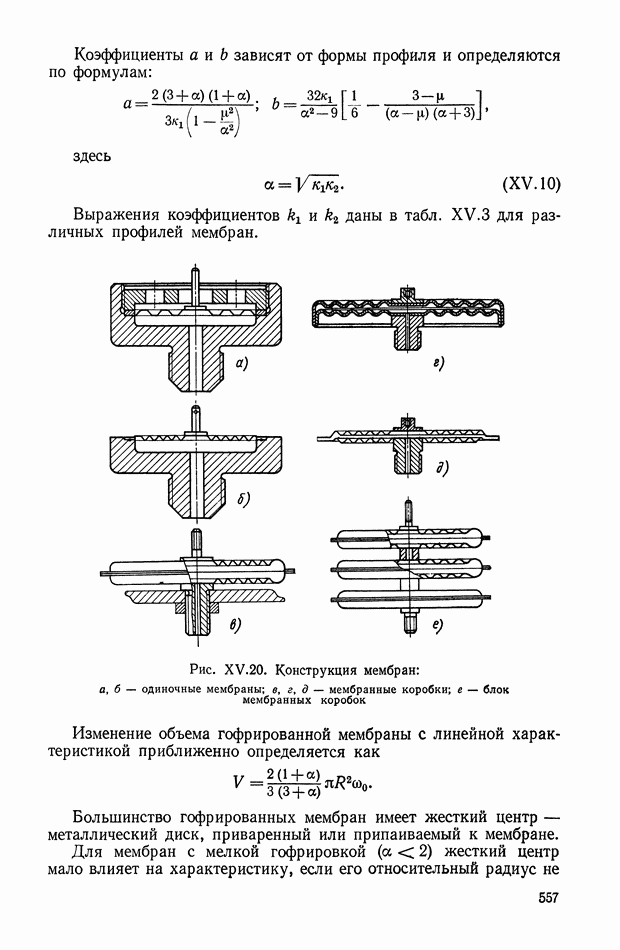
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
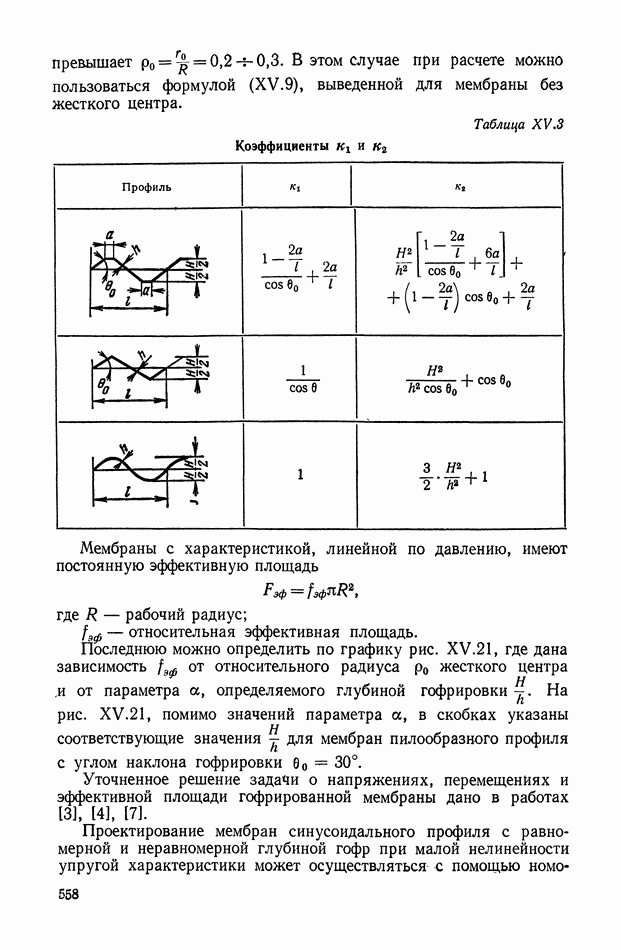
- Пневмоэлектроконтактные преобразователи линейных величин.
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
- Работа сельсинов в трансформаторном режиме.
- Устранение ложного нуля в двухскоростной системе.
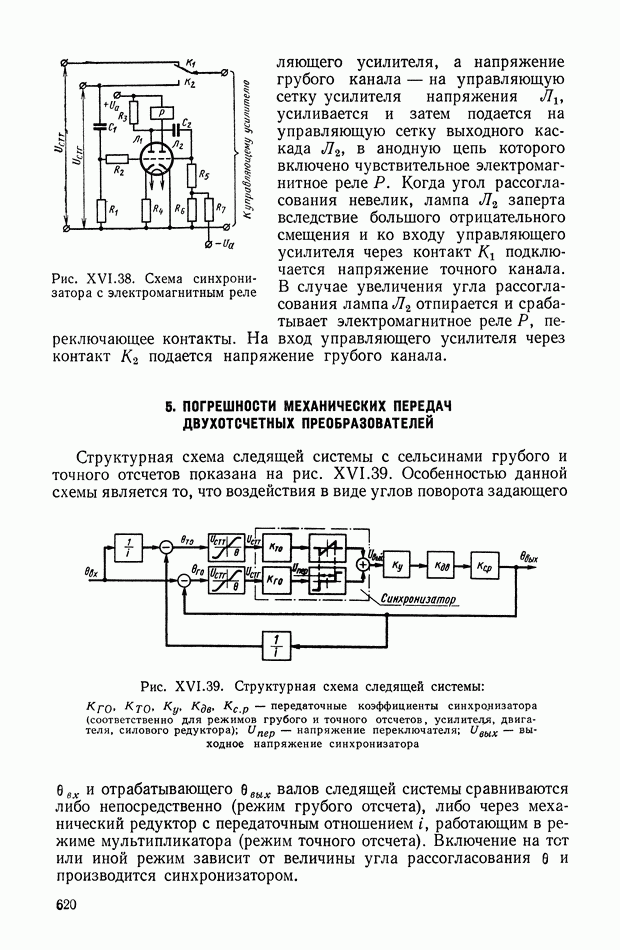
- Схемы синхронизаторов.
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
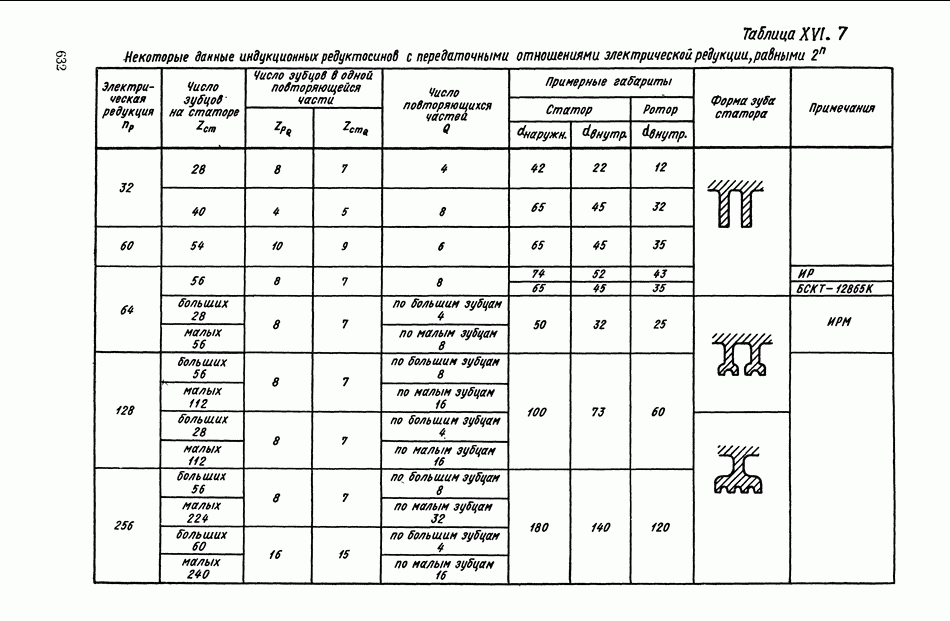
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
- Индукционные редуктосины.
- Индуктосины.
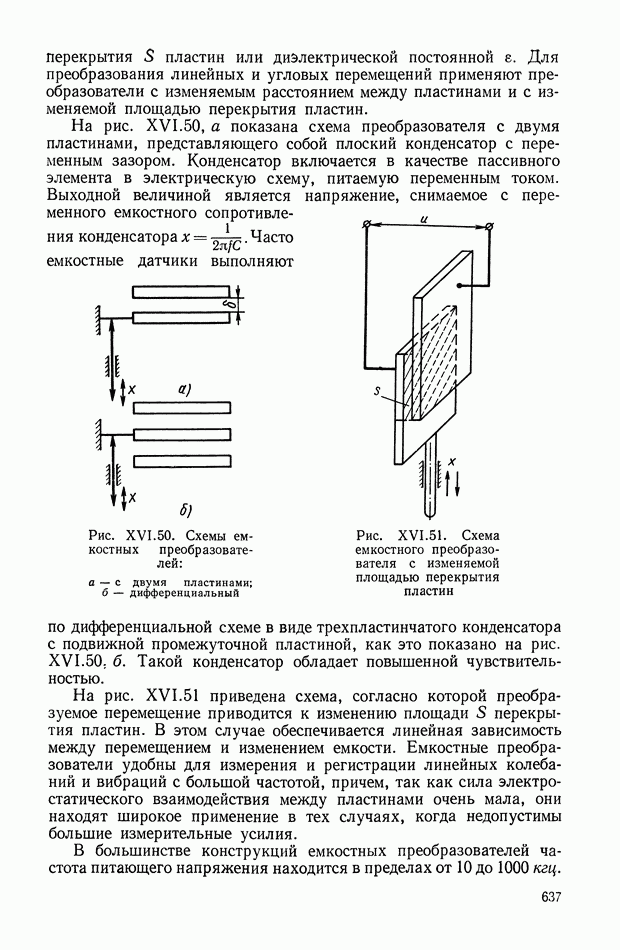
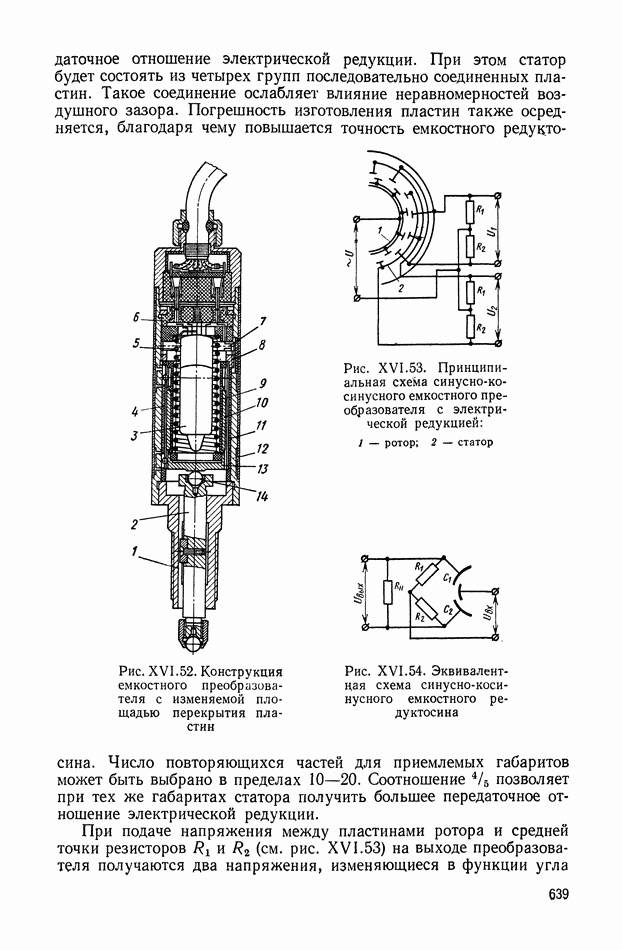
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- Емкостный редуктосин.
- Емкостный фазовращатель.
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ