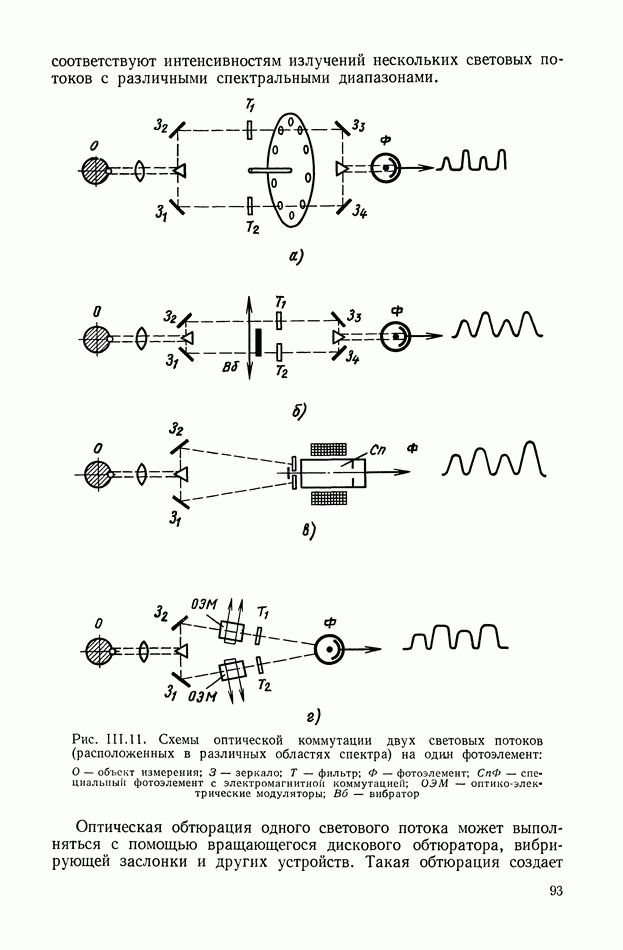
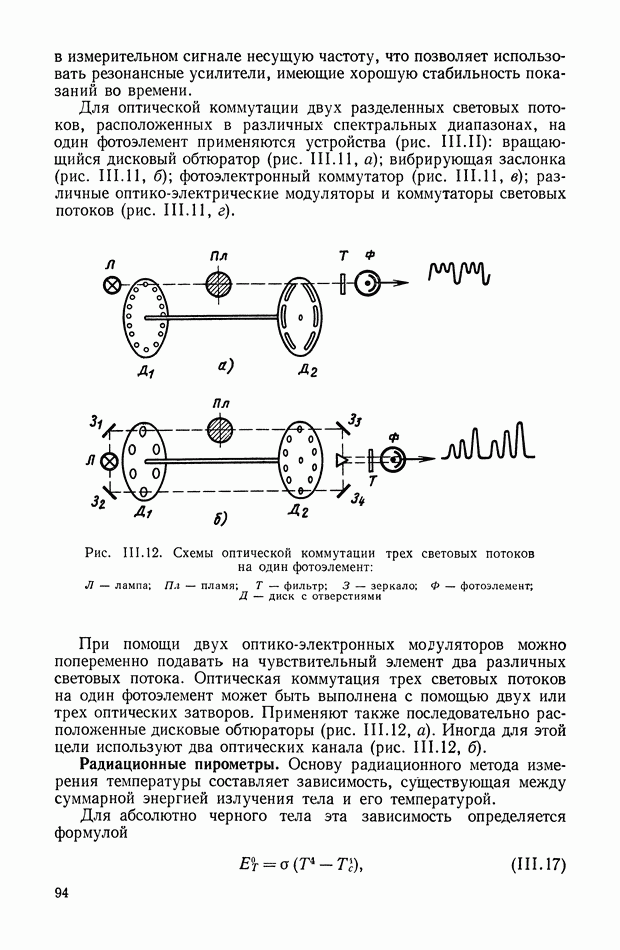
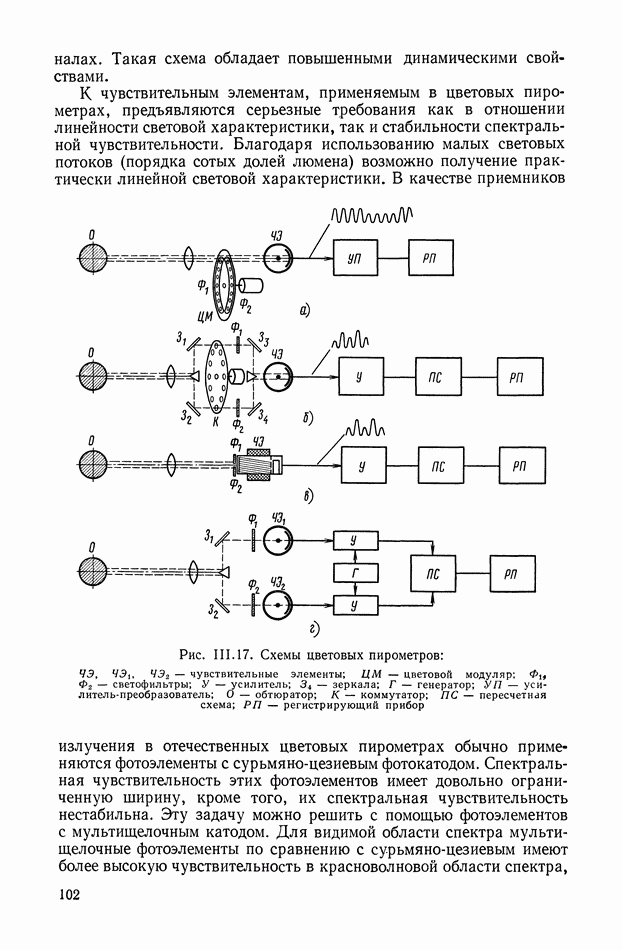
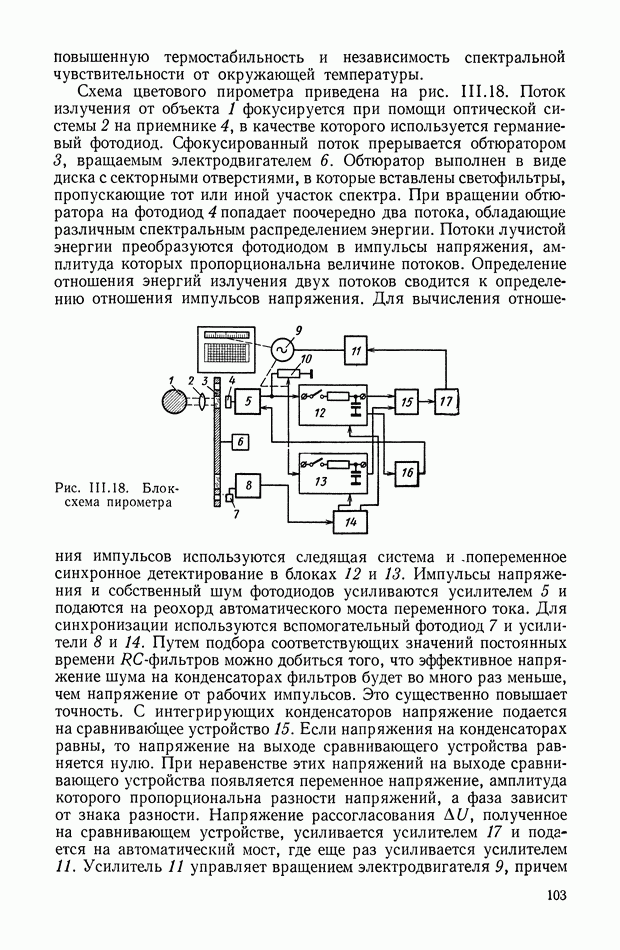
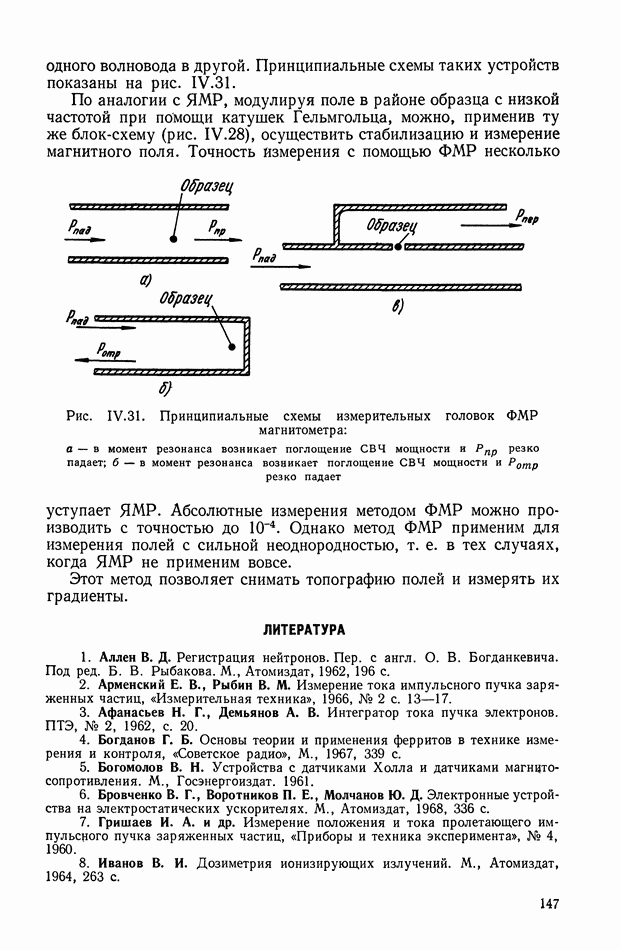
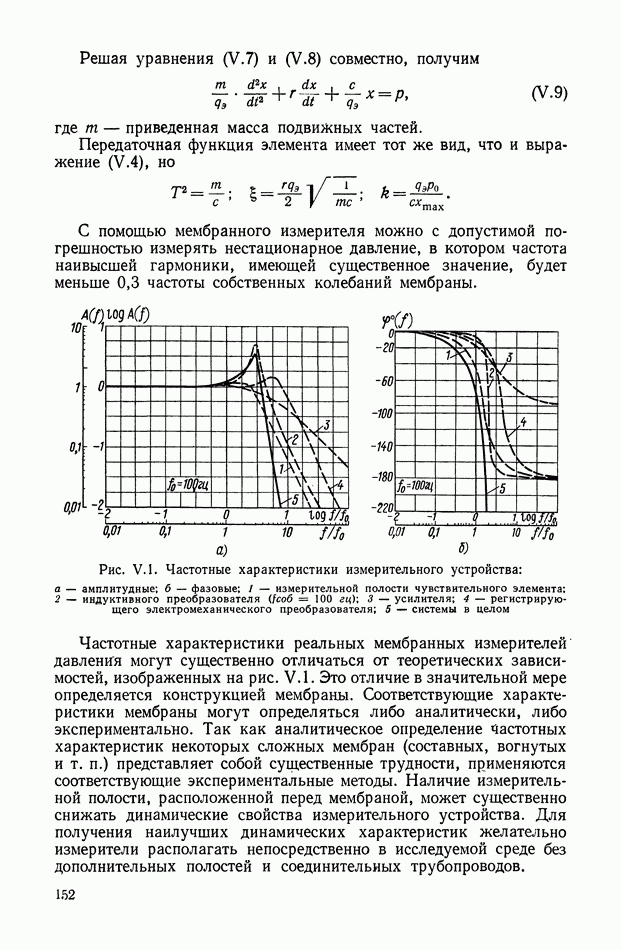
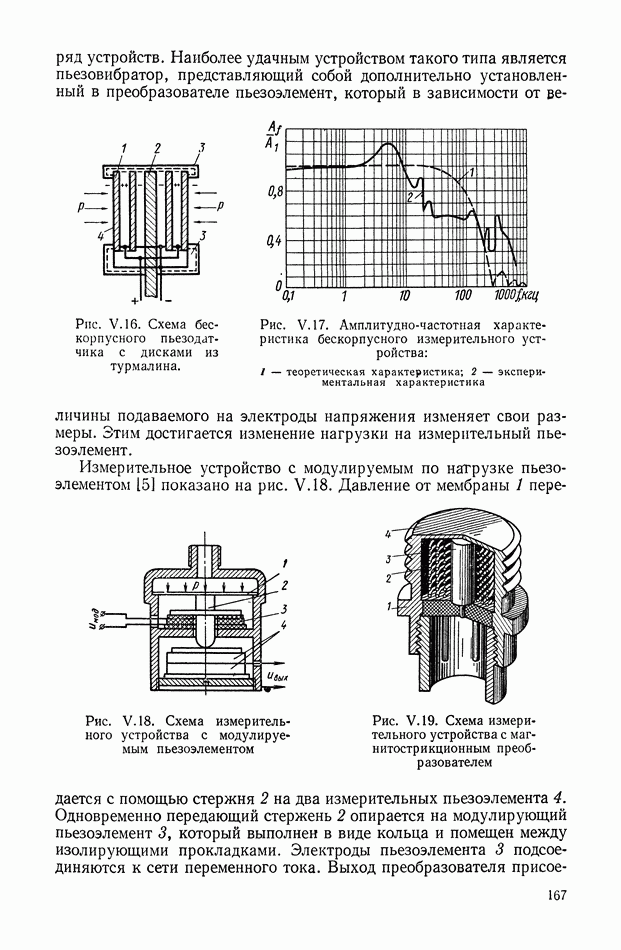
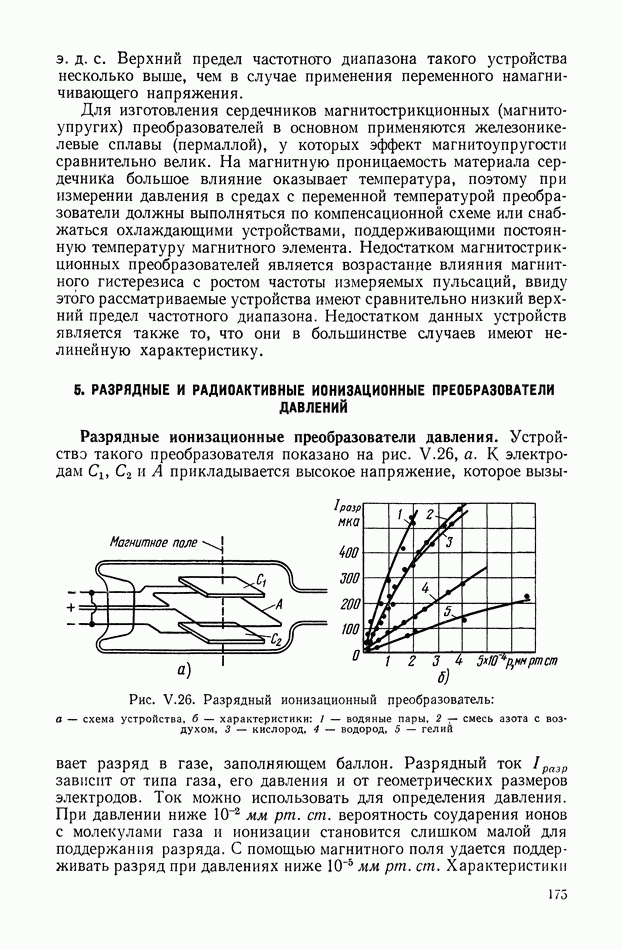
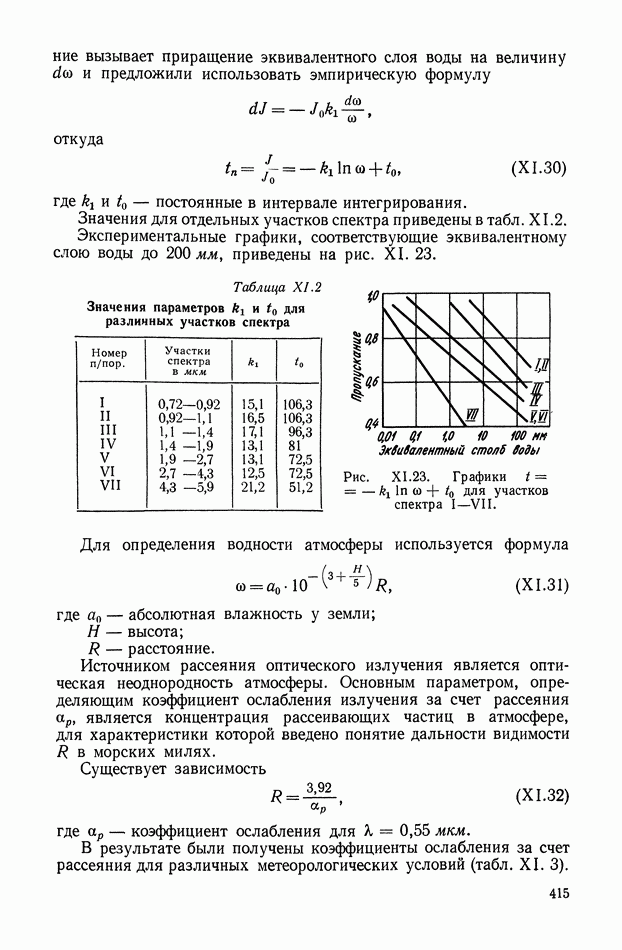
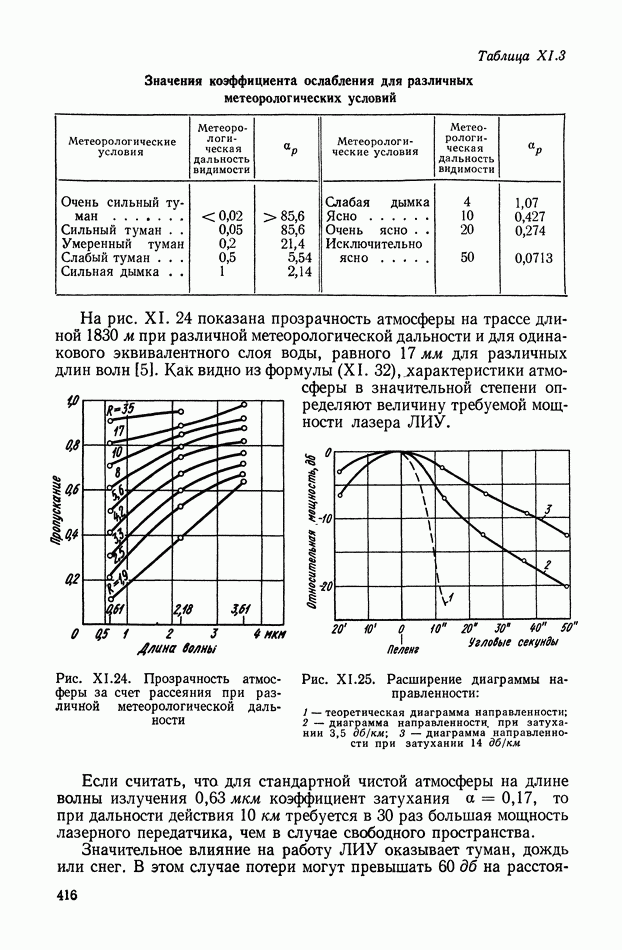
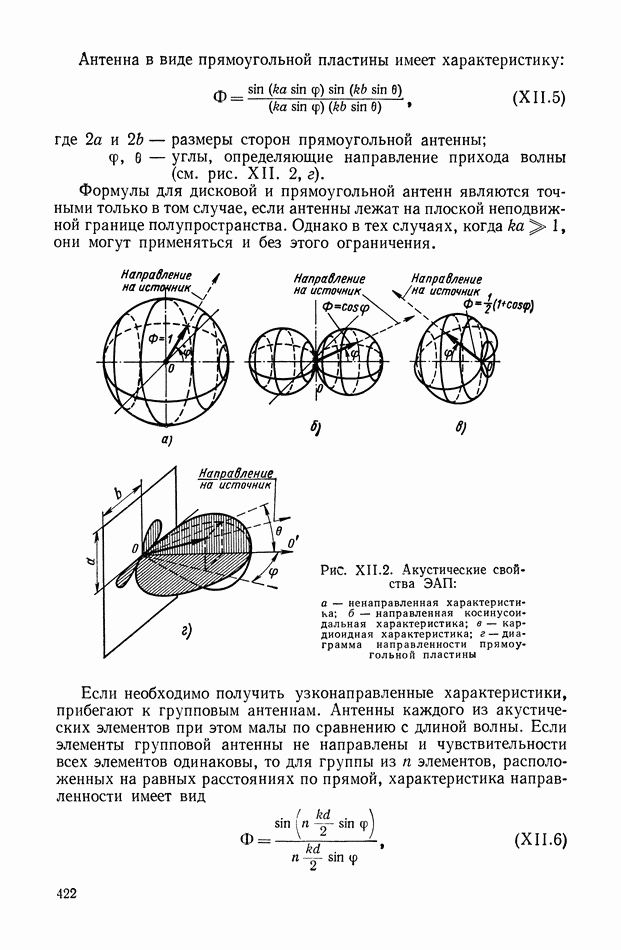
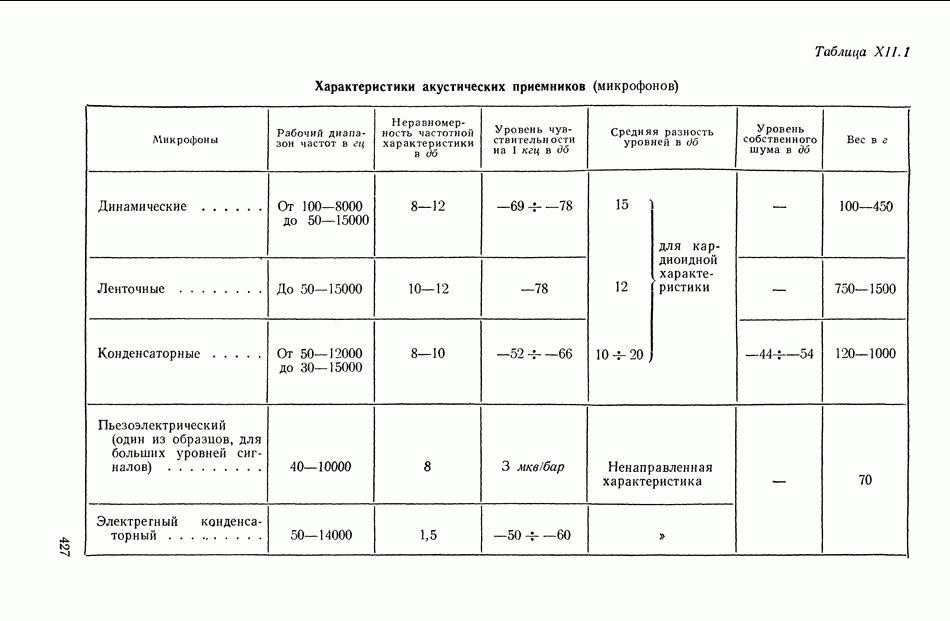
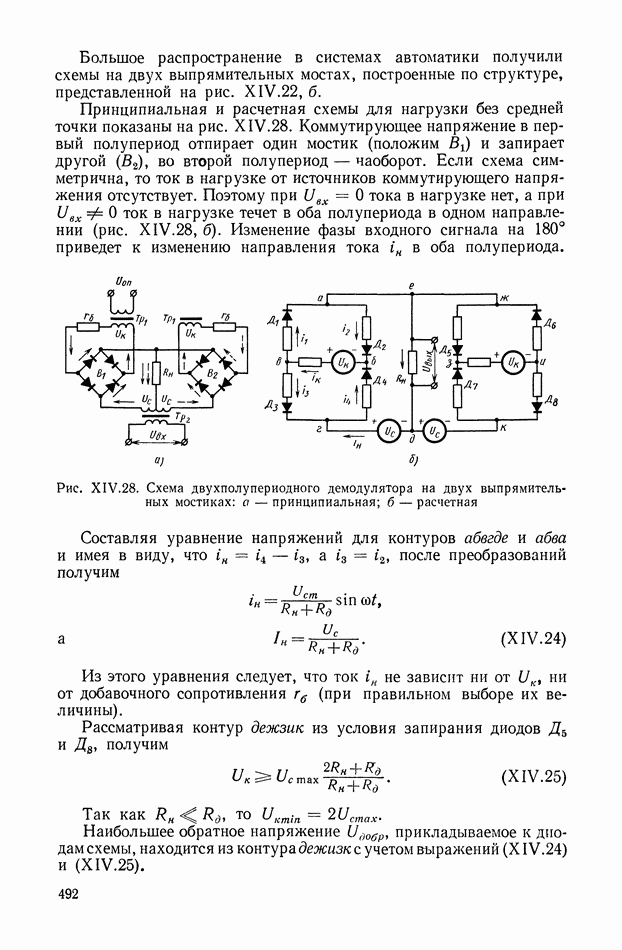
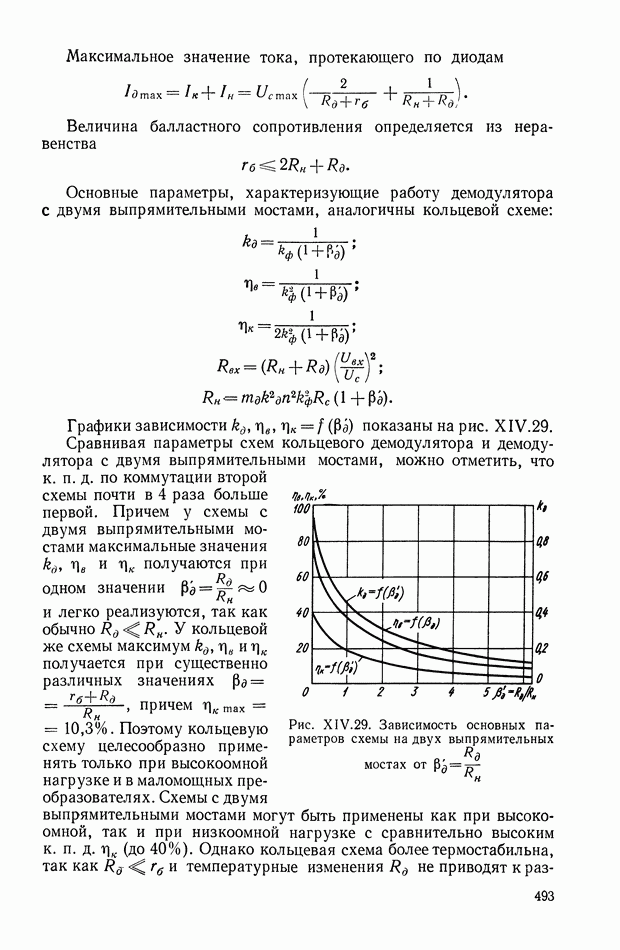
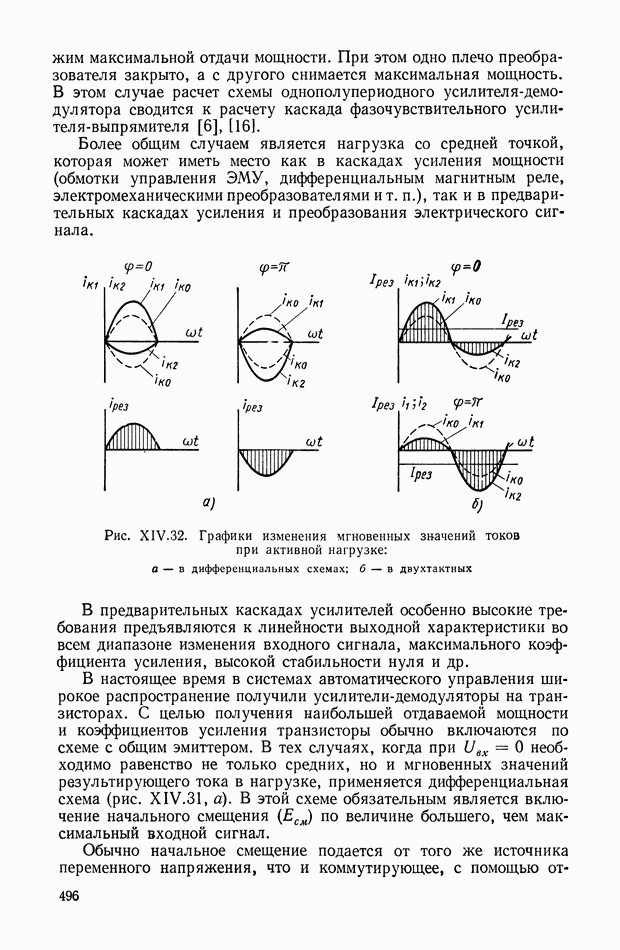
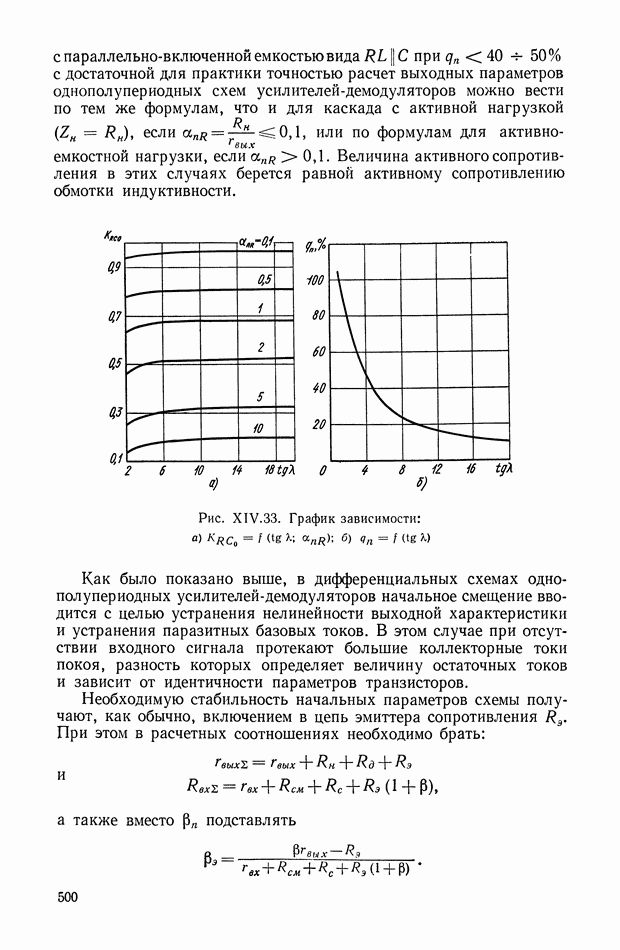
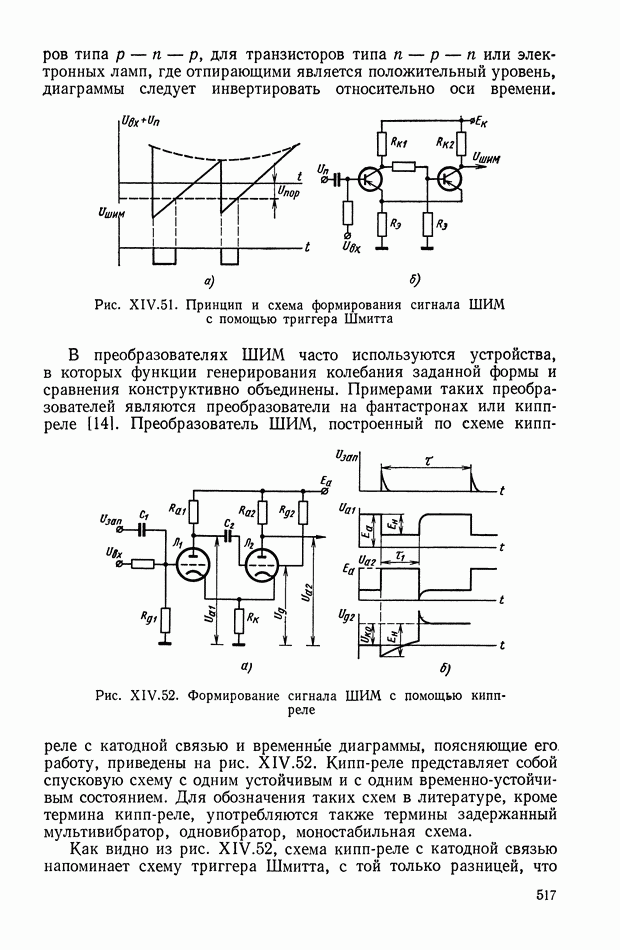
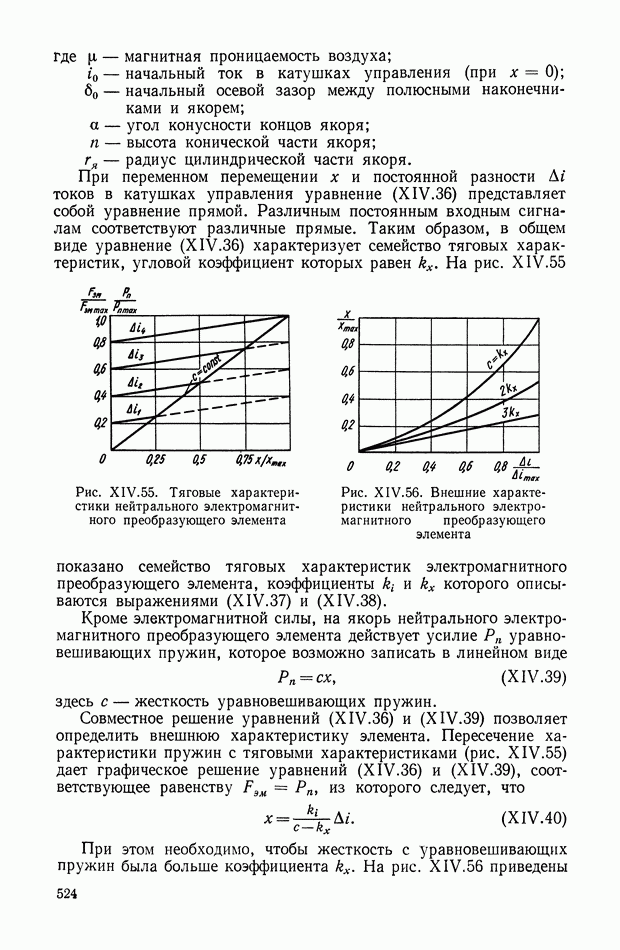
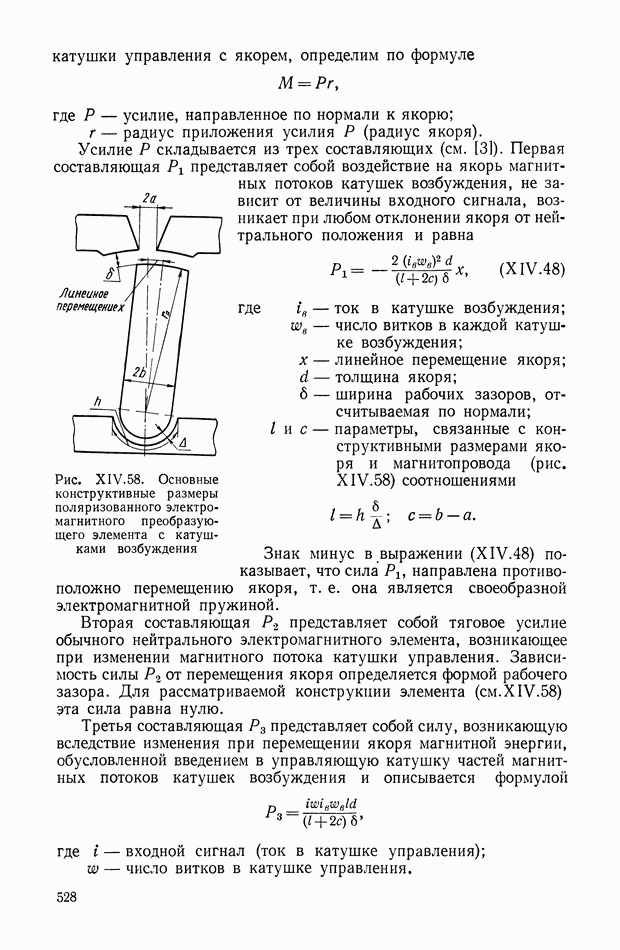
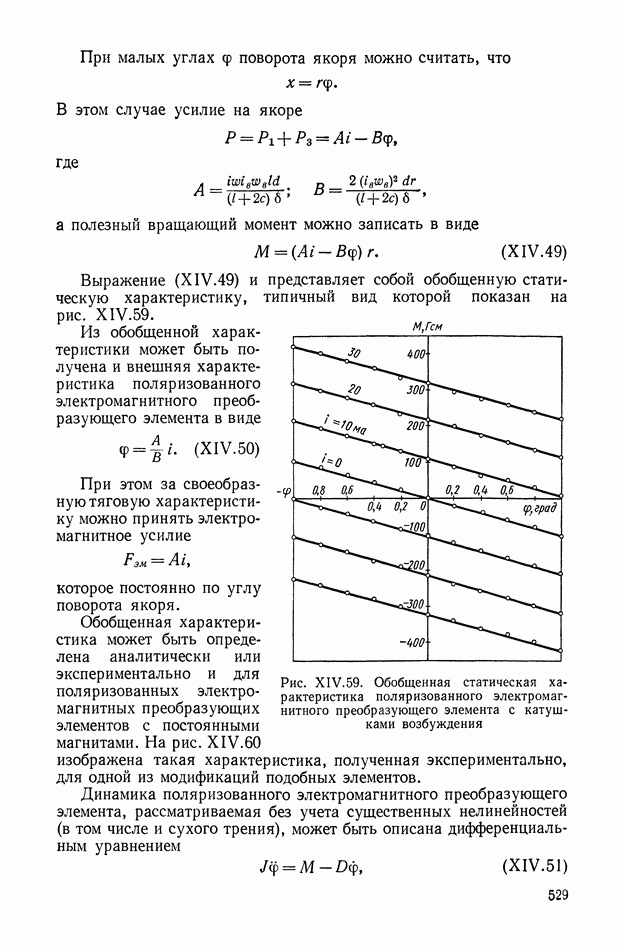
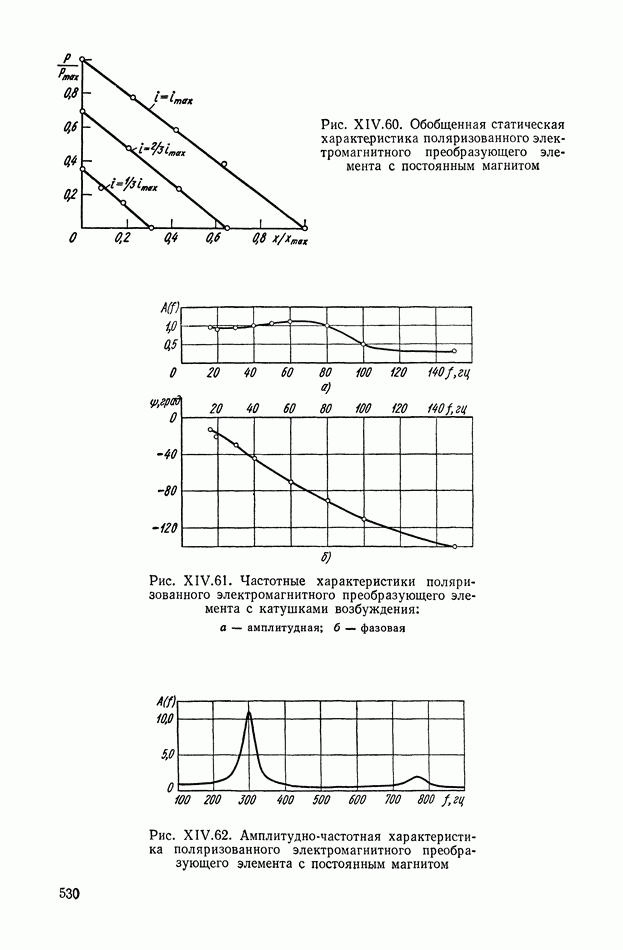
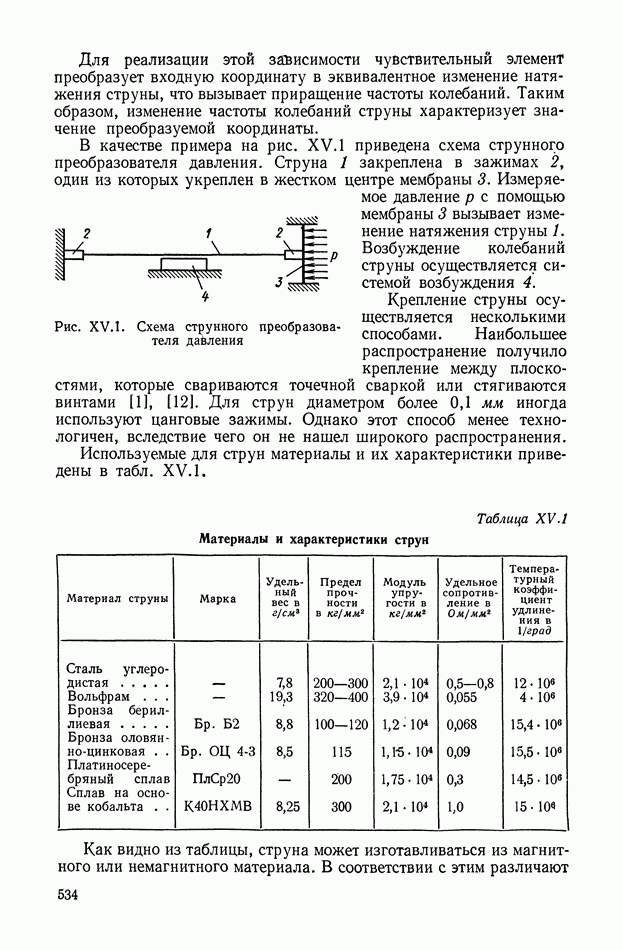
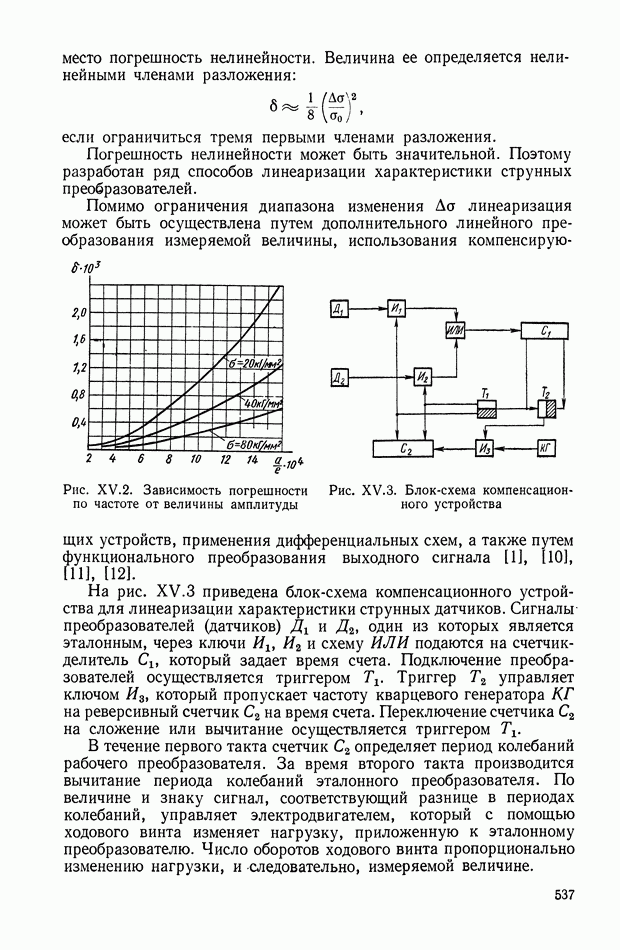
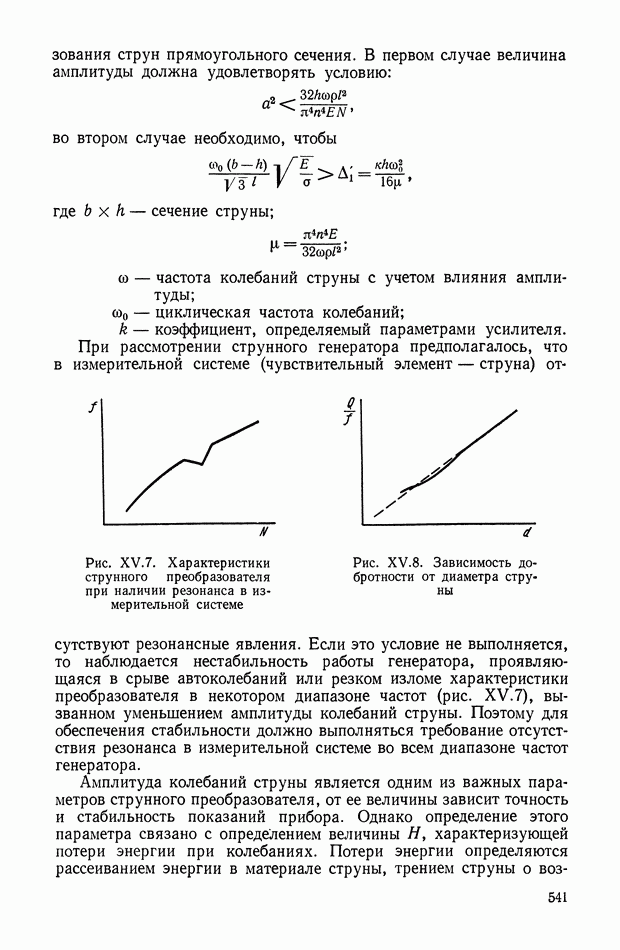
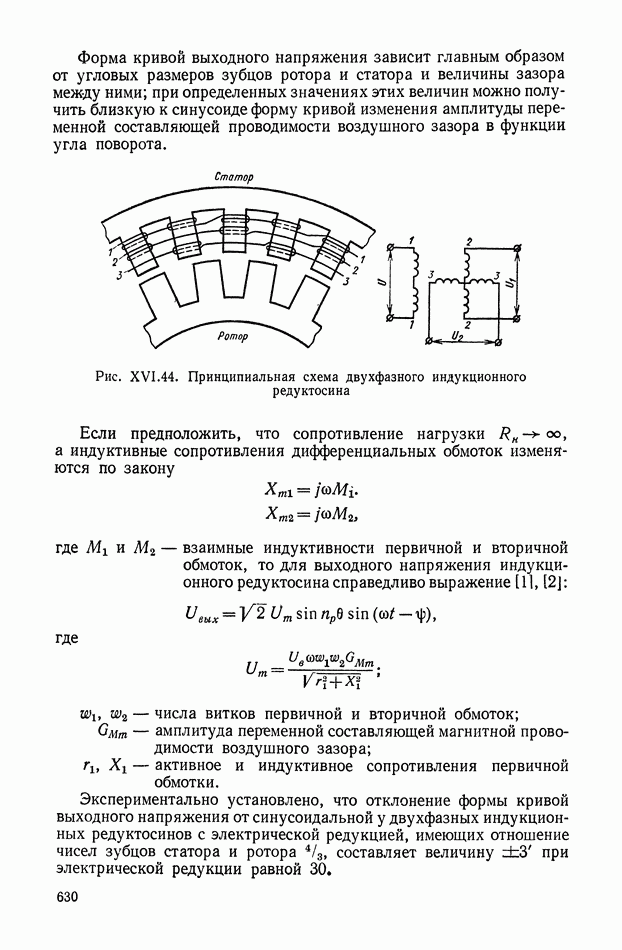
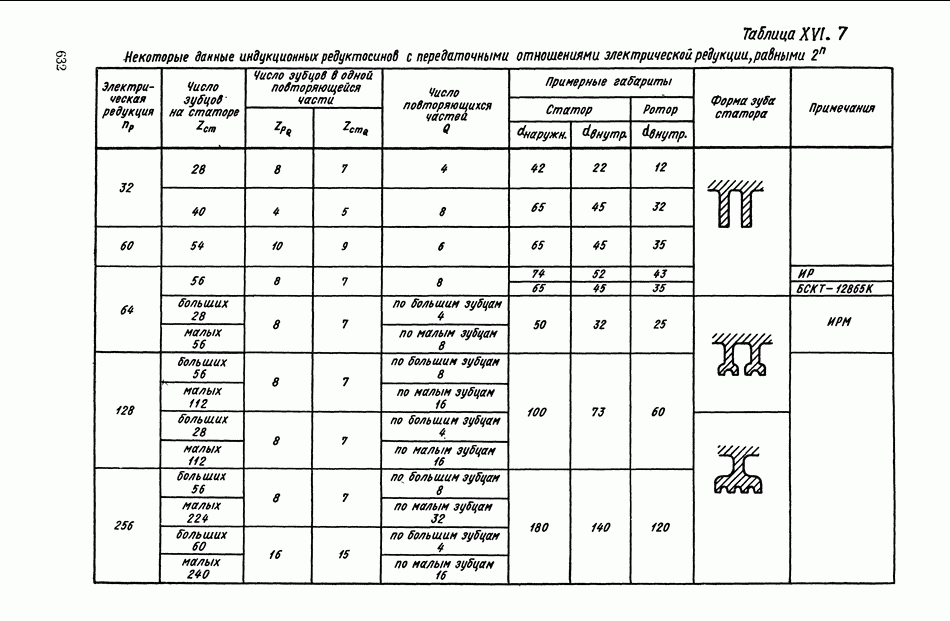
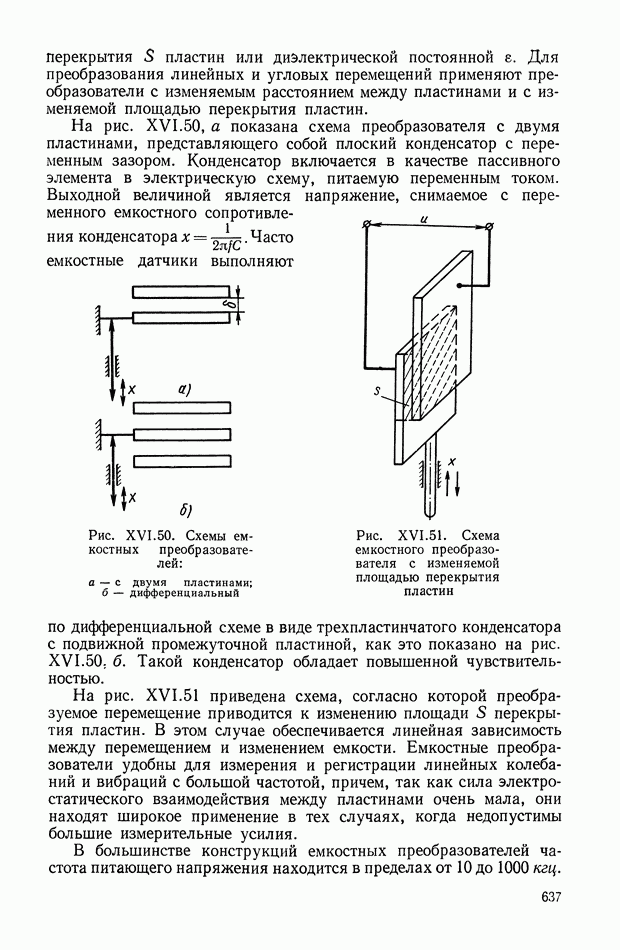
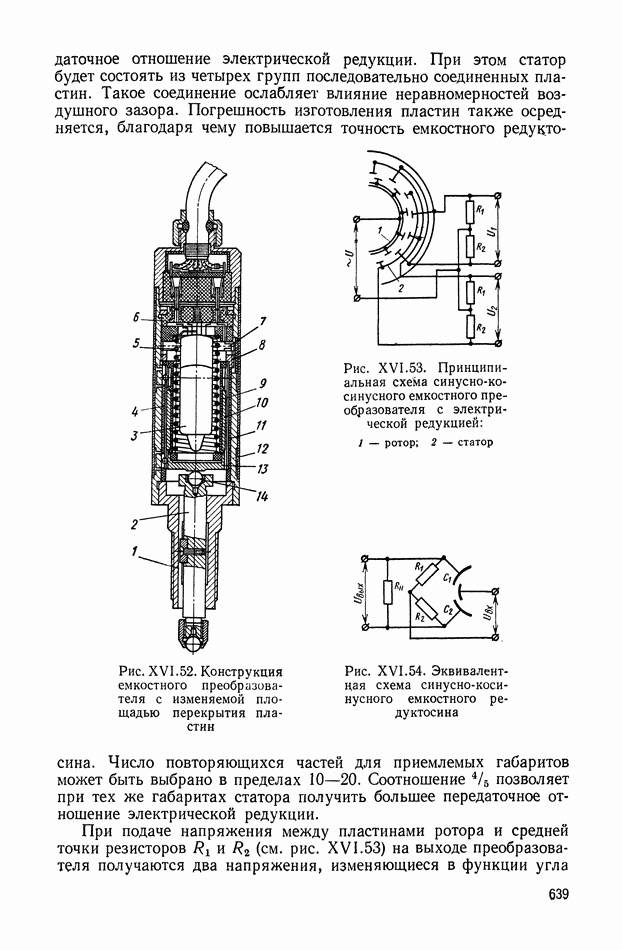
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
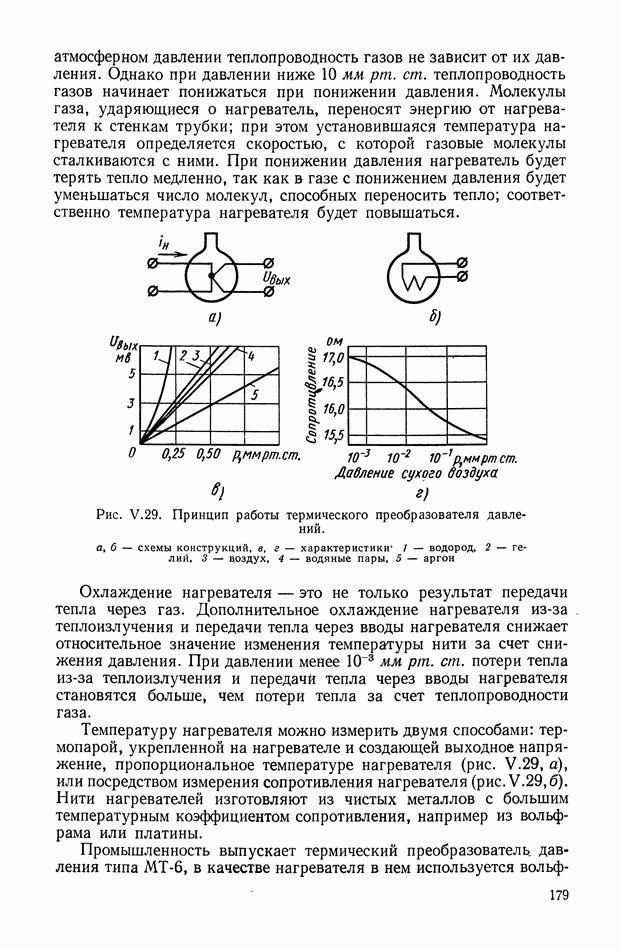
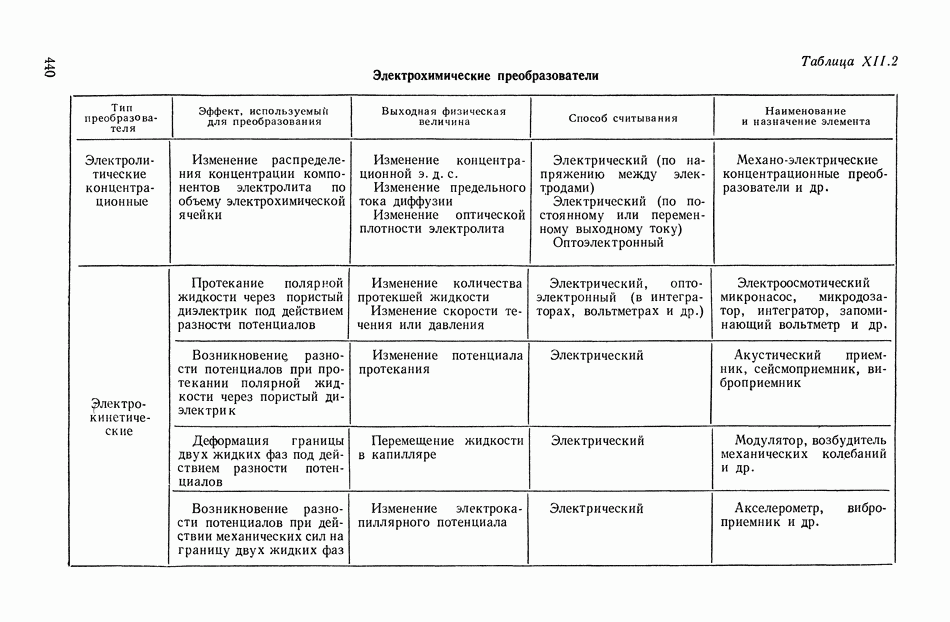
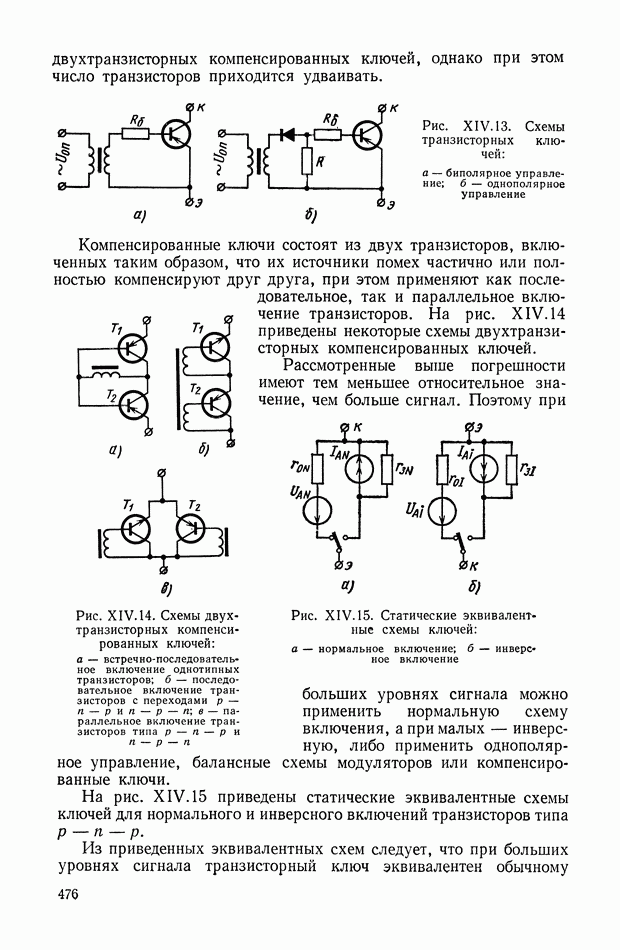
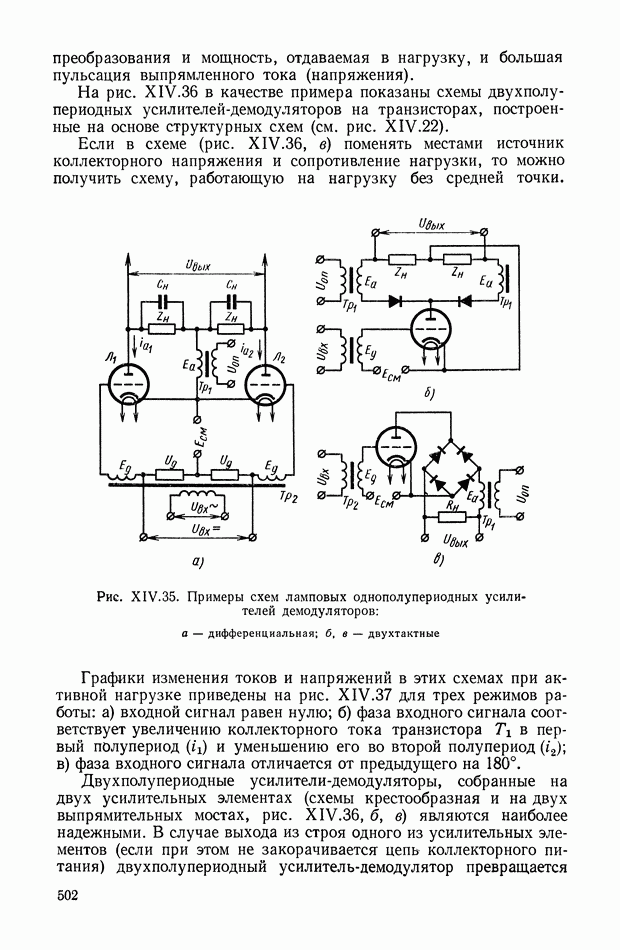
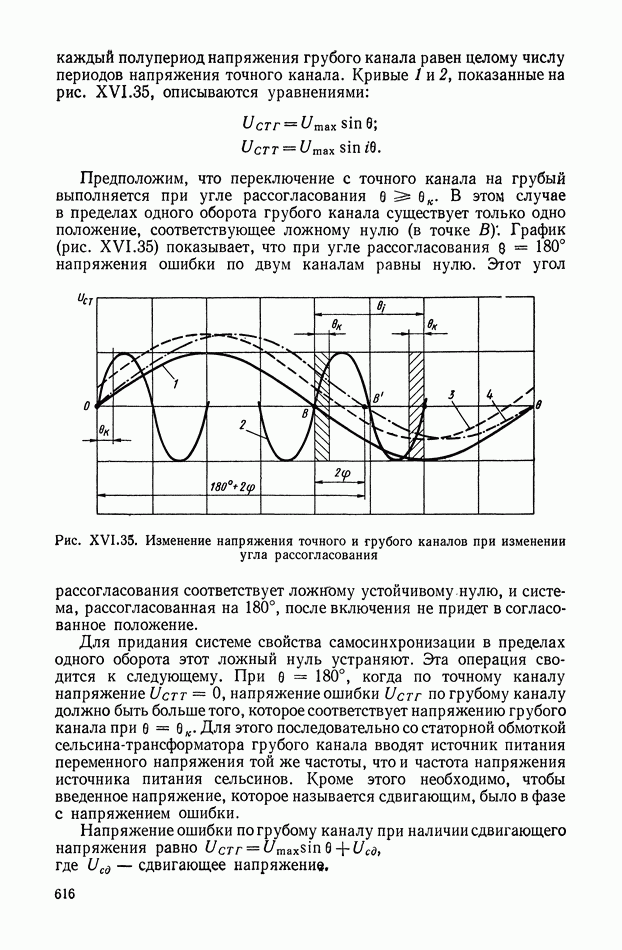
Индикаторный режим работы сельсинов.
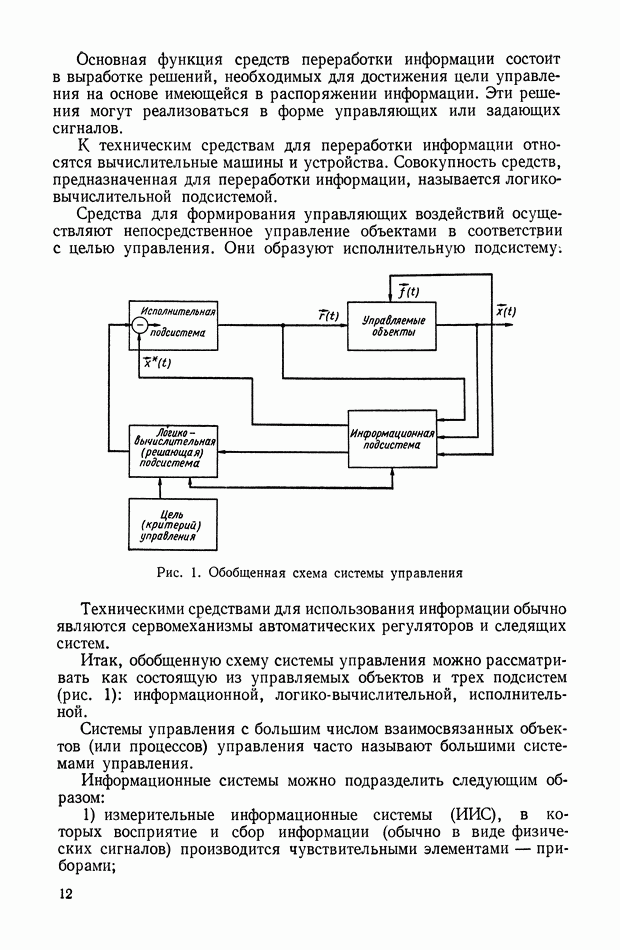
Система уравнений сельсинов» работающих в индикаторном режиме, может быть составлена на основании схемы рис. XVI. 27.
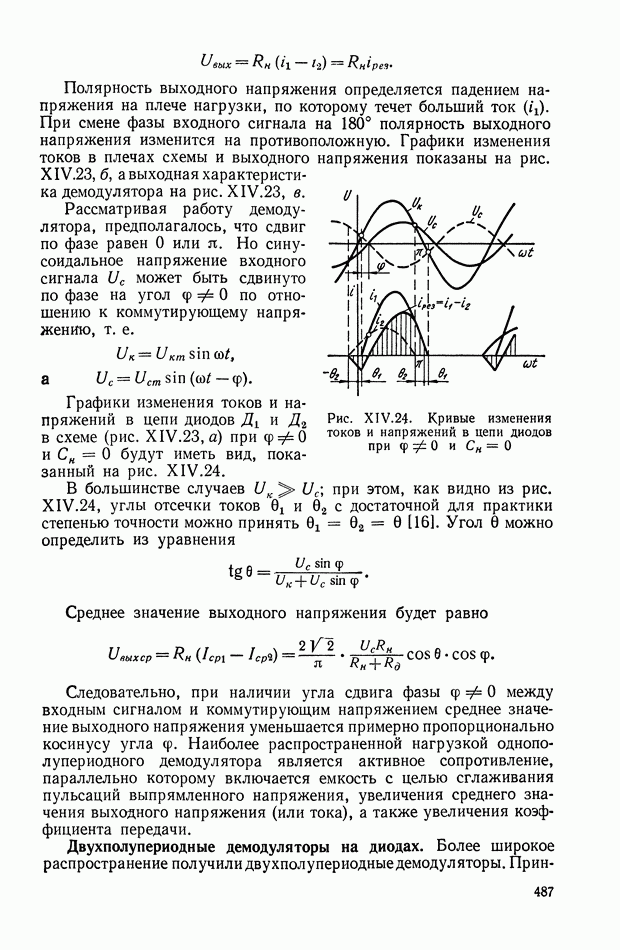
Полагая, что сельсин-датчик и сельсин-приемник имеют одинаковые параметры и что при напряжении возбуждения  одинаковом для датчика и приемника, в обмотках вторичной цепи датчика возникают напряжения
одинаковом для датчика и приемника, в обмотках вторичной цепи датчика возникают напряжения  а в обмотках вторичной цепи приемника — напряжения
а в обмотках вторичной цепи приемника — напряжения  получим систему уравнений в следующем виде:
получим систему уравнений в следующем виде:


где  — токи в первой, второй и третьей фазах и обмотке возбуждения датчика соответственно;
— токи в первой, второй и третьей фазах и обмотке возбуждения датчика соответственно;
 — токи в первой, второй и третьей фазах и обмотке возбуждения приемника соответственно;
— токи в первой, второй и третьей фазах и обмотке возбуждения приемника соответственно;
 активное сопротивление обмоток вторичнои цепи и обмоток возбуждения соответственно;
активное сопротивление обмоток вторичнои цепи и обмоток возбуждения соответственно;
 — потокосцепления фазовых обмоток и обмоток возбуждения датчика и приемника соответственно.
— потокосцепления фазовых обмоток и обмоток возбуждения датчика и приемника соответственно.
Из теории электрических машин переменного тока известно, что потокосцепления, входящие в систему уравнений (XVI. 17), могут быть записаны в виде формул:

где

 индуктивности первой, второй и третьей фазовых обмоток соответственно;
индуктивности первой, второй и третьей фазовых обмоток соответственно;
 — коэффициенты взаимоиндукции между первой и второй, первой и третьей, второй и третьей фазовыми обмотками соответственно;
— коэффициенты взаимоиндукции между первой и второй, первой и третьей, второй и третьей фазовыми обмотками соответственно;
 — коэффициенты взаимоиндукции между первой, второй и третьей фазовыми обмотками и обмоткой возбуждения соответственно.
— коэффициенты взаимоиндукции между первой, второй и третьей фазовыми обмотками и обмоткой возбуждения соответственно.
В формулах (XVI. 19)  является амплитудным значением взаимоиндуктивности фазы, определяемым как полуразность между максимальным и минимальным значениями взаимоиндуктивности;
является амплитудным значением взаимоиндуктивности фазы, определяемым как полуразность между максимальным и минимальным значениями взаимоиндуктивности;  представляет среднее значение взаимоиндуктивности фазы и определяется как полусумма максимального и минимального значений взаимоиндуктивности. Аналогичным образом определяются
представляет среднее значение взаимоиндуктивности фазы и определяется как полусумма максимального и минимального значений взаимоиндуктивности. Аналогичным образом определяются 
Для получения потокосцеплений датчика в системах уравнений (XVI. 18) и (XVI. 19) вместо индекса  нужно поставить индекс
нужно поставить индекс  а вместо угла
а вместо угла  — угол
— угол  Для получения потокосцеплений приемника индекс
Для получения потокосцеплений приемника индекс  и угол
и угол  заменяют соответственно на
заменяют соответственно на  и
и 
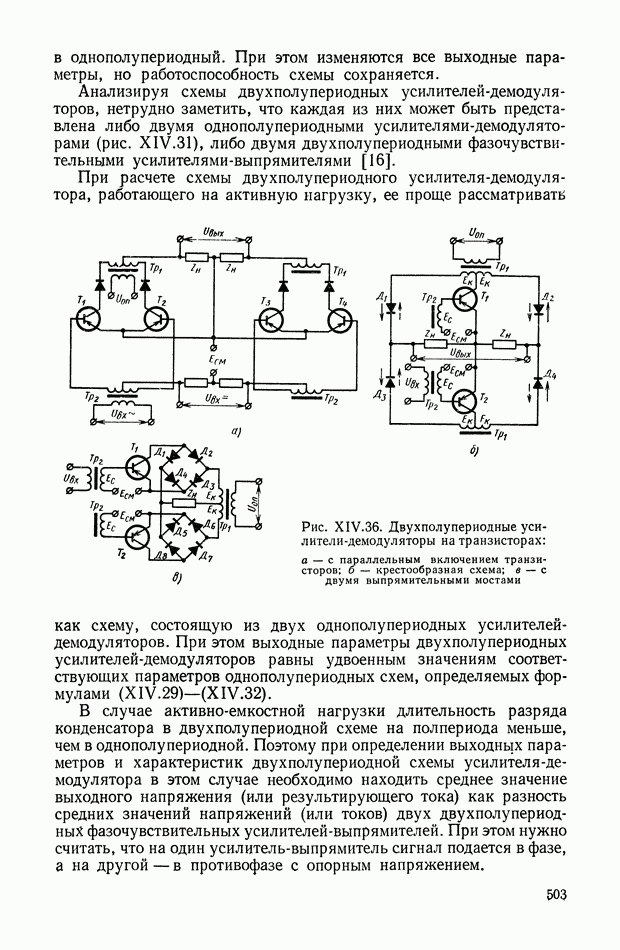
Решение системы уравнений (XVI. 17) представляет известные трудности. Система может быть решена, если физические процессы в сельсинах рассматривать не вдоль магнитных осей вторичных фазовых обмоток, а вдоль продольной оси, совпадающей с направлением магнитной оси обмотки возбуждения, и поперечной оси, имеющей направление, перпендикулярное первому [10].
Система уравнений (XVI. 17) может быть преобразована к виду

или

где

 — продольная составляющая тока во вторичной цепи датчика;
— продольная составляющая тока во вторичной цепи датчика;
 — поперечная составляющая тока во вторичной цепи датчика;
— поперечная составляющая тока во вторичной цепи датчика;  — продольная составляющая тока во вторичной цепи приемника;
— продольная составляющая тока во вторичной цепи приемника;
 — поперечная составляющая тока во вторичной цепи приемника;
— поперечная составляющая тока во вторичной цепи приемника;
 угол рассогласования;
угол рассогласования;

 — угловая скорость вращения датчика и приемника.
— угловая скорость вращения датчика и приемника.
Входящий в коэффициенты  оператор
оператор  при решении системы уравнений относительно токов
при решении системы уравнений относительно токов  или
или  и 2 обычно заменяется величиной
и 2 обычно заменяется величиной  т. е. считается, что
т. е. считается, что  . В этом случае полученные формулы для токов будут характеризовать установившийся режим в индикаторной синхронной передаче.
. В этом случае полученные формулы для токов будут характеризовать установившийся режим в индикаторной синхронной передаче.
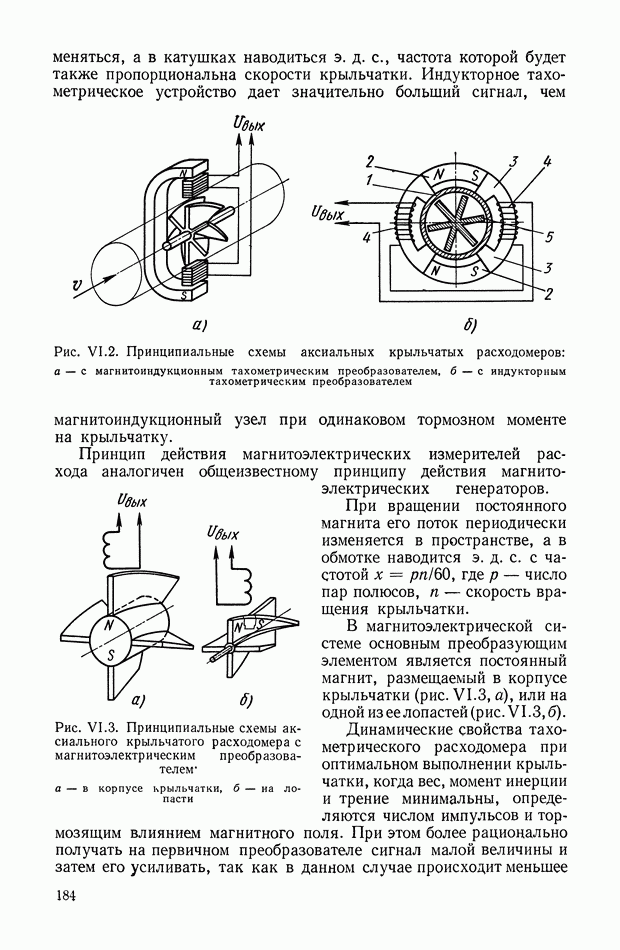
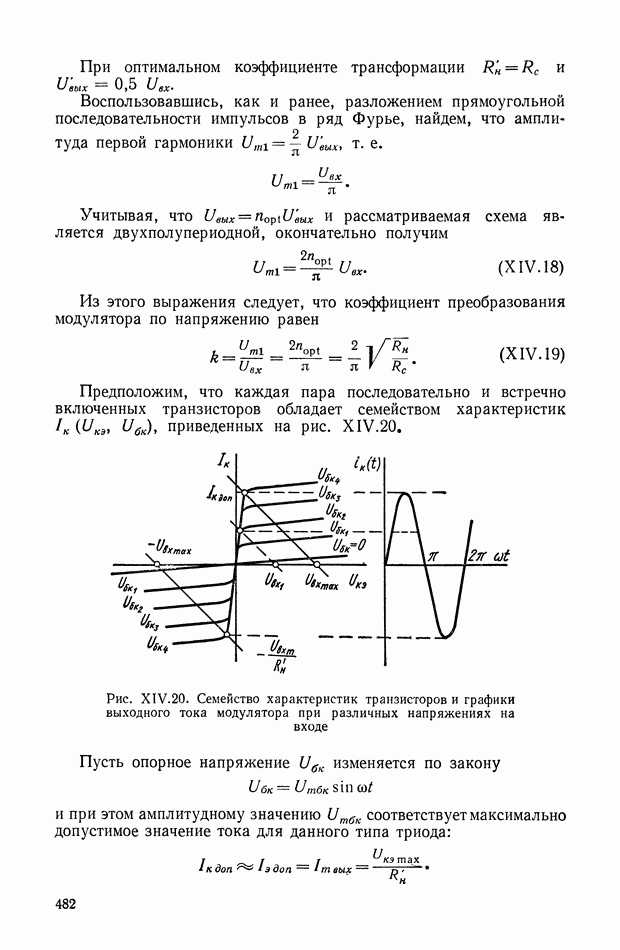
Синхронизирующий момент. Из теории электрических машин переменного тока известно, что электромагнитный момент определяется выражением

где

Синхронизирующий момент сельсина-датчика или сельсина-приемника может быть определен выражением (XVI.21), если в него подставить значения потокосцеплений  и
и  Например, синхронизирующий момент на валу сельсина-приемника
Например, синхронизирующий момент на валу сельсина-приемника

где

Выражение (XVI.22) показывает, что синхронизирующий момент сельсина имеет две составляющие, одна из которых носит реактивный характер и обусловлена наличием явно выраженных полюсов, а вторая — взаимодействием потока возбуждения с поперечной
составляющей вторичного тока. Нужно сказать, что первая составляющая момента  не является основной и ею в большинстве случаев можно пренебречь, так как режим работы индикаторной синхронной передачи обычно соответствует малым углам рассогласования, при которых размагничивающее действие продольной составляющей вторичного тока
не является основной и ею в большинстве случаев можно пренебречь, так как режим работы индикаторной синхронной передачи обычно соответствует малым углам рассогласования, при которых размагничивающее действие продольной составляющей вторичного тока  мало, и она практически равна нулю. В тех случаях, когда сельсины не имеют явно выраженных полюсов, реактивная составляющая вообще отсутствует, так как
мало, и она практически равна нулю. В тех случаях, когда сельсины не имеют явно выраженных полюсов, реактивная составляющая вообще отсутствует, так как 
Таким образом, синхронизирующий момент сельсина без большого ущерба для практических расчетов в области малых углов рассогласования может определяться по выражению

Подставляя в уравнения (XVI.22) и (XVI.23) токи  получим теоретическую зависимость синхронизирующего момента не только от угла рассогласования, но и от скорости вращения роторов сельсинов индикаторной синхронной передачи.
получим теоретическую зависимость синхронизирующего момента не только от угла рассогласования, но и от скорости вращения роторов сельсинов индикаторной синхронной передачи.
Воспользовавшись формулой (XVI.22), нетрудно показать, что синхронизирующий момент сельсина в синхронной передаче при постоянном угле рассогласования с возрастанием скорости убывает.
Найдем зависимость синхронизирующего момента от угла рассогласования  при постоянной скорости. Полагая, что скорость равна нулю и сельсины не имеют явно выраженных полюсов, а также активное сопротивление обмотки возбуждения мало по сравнению с ее индуктивным сопротивлением, используя уравнение (XVI.23) и находя значения токов
при постоянной скорости. Полагая, что скорость равна нулю и сельсины не имеют явно выраженных полюсов, а также активное сопротивление обмотки возбуждения мало по сравнению с ее индуктивным сопротивлением, используя уравнение (XVI.23) и находя значения токов  получим
получим

где

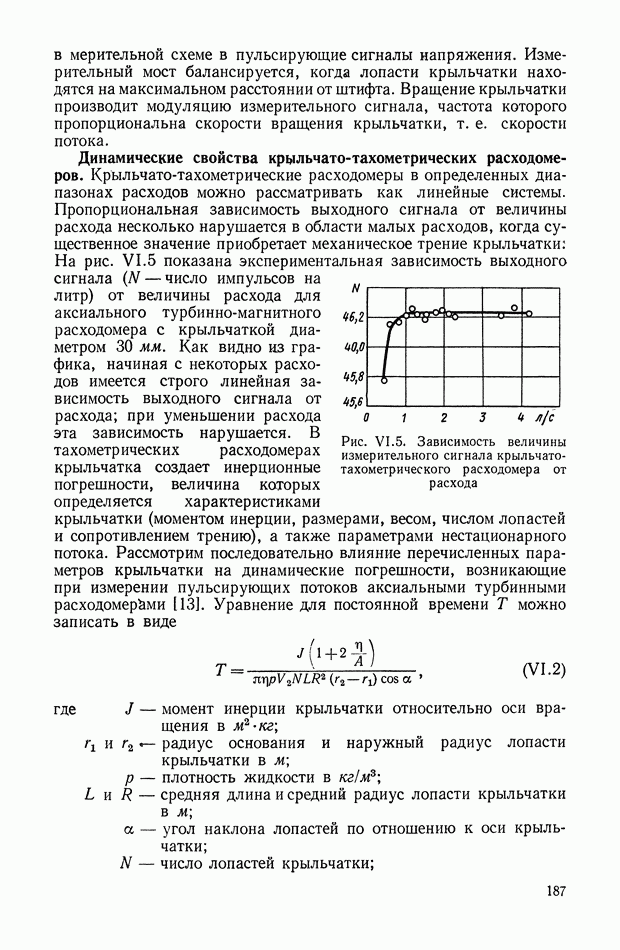
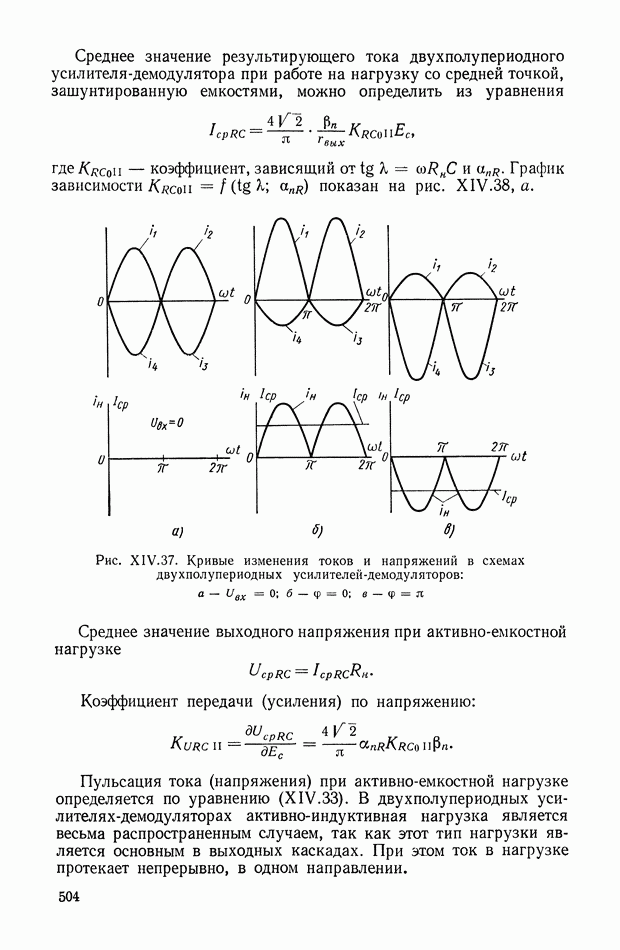
Характер изменения синхронизирующего момента при изменении угла рассогласования, как показывает уравнение (XVI.24), может быть различным и зависит от соотношения параметров  , которые определяются выражениями (XVI.26) и (XVI. 27). Так, например, при
, которые определяются выражениями (XVI.26) и (XVI. 27). Так, например, при  график функции
график функции  приведенный на рис. XVI.30, соответствует кривой У, а при
приведенный на рис. XVI.30, соответствует кривой У, а при  — кривой 2. Обычно
— кривой 2. Обычно  поэтому зависимость
поэтому зависимость  сельсинов с неявно выраженными полюсами имеет вид кривой 1. Наличие явно выраженных полюсов, как это следует из уравнения (XVI.22),
сельсинов с неявно выраженными полюсами имеет вид кривой 1. Наличие явно выраженных полюсов, как это следует из уравнения (XVI.22),
обусловливает реактивную составляющую момента, которая увеличивает результирующий синхронизирующий момент. Благодаря этому возрастает и крутизна кривой  в области малых углов рассогласования.
в области малых углов рассогласования.

Рис. XVI.30 Кривые изменения синхронизирующего момента для различных соотношений параметров  : кривые 1—3 имеют соответственно
: кривые 1—3 имеют соответственно  (при
(при  )
)
Удельный статический синхронизирующий момент. Крутизна кривой, представляющей зависимость синхронизирующего момента от угла рассогласования, в точке  характеризуемая производной
характеризуемая производной

обычно называется удельным статическим синхронизирующим моментом.
Величину удельного момента можно выразить через параметры сельсина. Поскольку удельный момент характеризуется крутизной характеристики  в начале координат, то при определении
в начале координат, то при определении  принимаем
принимаем  Следовательно, удельный момент может быть вычислен по формуле (XVI.23), в которой поперечная составляющая тока и ток в обмотке возбуждения определяются уравнениями
Следовательно, удельный момент может быть вычислен по формуле (XVI.23), в которой поперечная составляющая тока и ток в обмотке возбуждения определяются уравнениями

В уравнении (XVI .29) в правой части составляющая  ввиду малости
ввиду малости  может быть принята равной нулю.
может быть принята равной нулю.
При малых значениях 0 получим следующее выражение для синхронизирующего момента:

Подставляя в уравнение (XVI.30) значения коэффициентов  и с и представляя угол рассогласования в градусах, а синхронизирующий момент в
и с и представляя угол рассогласования в градусах, а синхронизирующий момент в  получим
получим

где

откуда удельный момент

Работа сельсина-датчика с несколькими параллельно включенными приемниками. Можно показать, что при работе датчика с  приемниками в случае, когда сопротивления фазы датчика и фазы приемника равны и соответствуют величине
приемниками в случае, когда сопротивления фазы датчика и фазы приемника равны и соответствуют величине  синхронизирующий момент датчика
синхронизирующий момент датчика  и синхронизирующий момент приемника
и синхронизирующий момент приемника  определяются выражениями
определяются выражениями

где  синхронизирующий момент сельсина при
синхронизирующий момент сельсина при 
Таким образом при работе датчика с  приемниками синхронизирующий момент каждого сельсина-приемника уменьшается в
приемниками синхронизирующий момент каждого сельсина-приемника уменьшается в  раз по сравнению с тем случаем, когда датчик работает на одйн приемник. В результате этого снижается удельный момент и, как правило, увеличивается ошибка при передаче показаний. Для предотвращения снижения точности необходимо, чтобы сопротивление фазы сельсина-датчика было в
раз по сравнению с тем случаем, когда датчик работает на одйн приемник. В результате этого снижается удельный момент и, как правило, увеличивается ошибка при передаче показаний. Для предотвращения снижения точности необходимо, чтобы сопротивление фазы сельсина-датчика было в  раз меньше сопротивления фазы сельсина-приемника, тогда
раз меньше сопротивления фазы сельсина-приемника, тогда

Синхронизирующий момент приемника оказывается равным синхронизирующему моменту, возникающему в сельсине при работе одного датчика на один приемник, у которого 
При определении влияния числа приемников  на величину синхронизирующего момента предполагалось, что сопротивление линий равно нулю. В действительности этого нет, в особенности если передача ведется на большие расстояния. Если учесть сопротивление линии
на величину синхронизирующего момента предполагалось, что сопротивление линий равно нулю. В действительности этого нет, в особенности если передача ведется на большие расстояния. Если учесть сопротивление линии  то синхронизирующий момент с увеличением
то синхронизирующий момент с увеличением  будет уменьшаться, что приведет к увеличению ошибки.
будет уменьшаться, что приведет к увеличению ошибки.
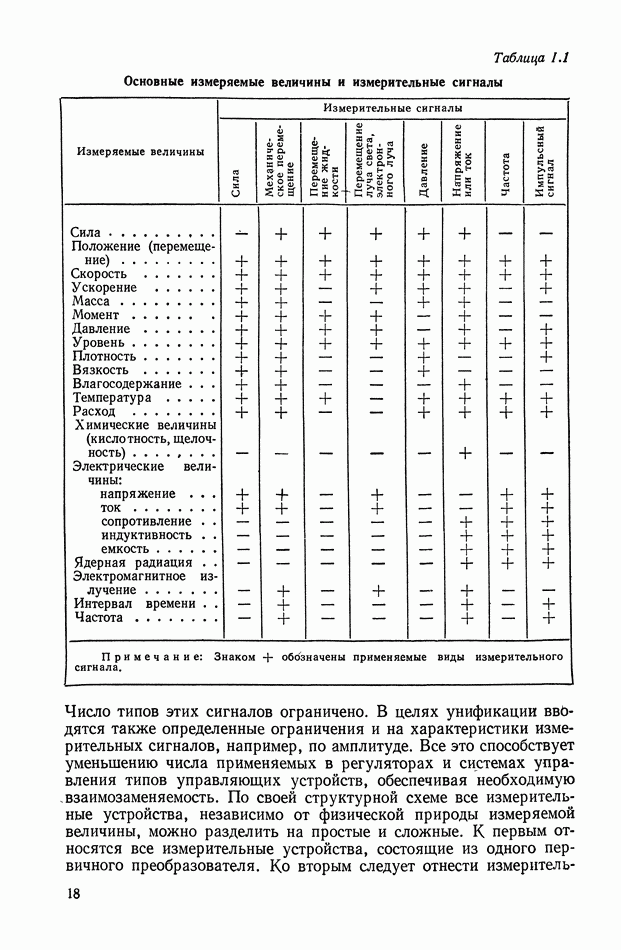
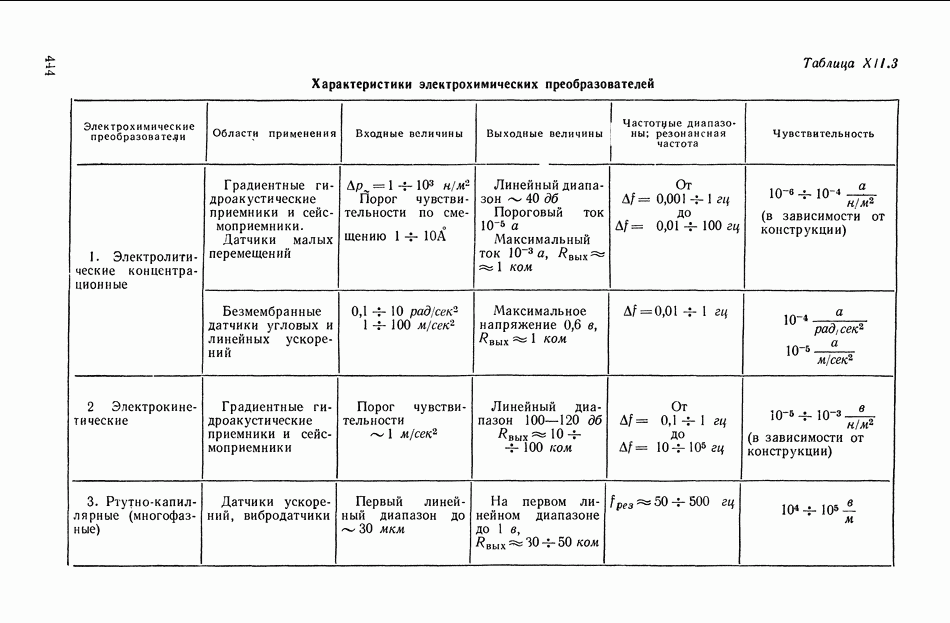
Классы точности индикаторных сельсинов. Статическая точность работы синхронной передачи прежде всего определяется нагрузкой или внешним моментом на валу приемника, а также собственной ошибкой сельсинов, величина которой нормализуется классом точности и, наконец, ошибкой, возникающей в процессе эксплуатации с течением времени.
Собственная ошибка сельсинов зависит от особенностей конструктивного выполнения сельсинов.
К основным факторам, влияющим на собственную ошибку, следует отнести момент сил трения, который складывается из момента трения в подшипниках и в случае применения контактных сельсинов момента трения токосъемных щеток на кольцах коллектора. Собственная ошибка, обусловленная моментом трения, может быть определена по формуле

Это выражение соответствует утверждению, что сельсин-приемник будет неподвижен до тех пор, пока синхронизирующий момент  не станет равным или большим момента трения
не станет равным или большим момента трения 
Вторым фактором, обусловливающим собственную ошибку сельсина, следует считать неточную балансировку ротора приемника.
Подробнее о собственной ошибке сельсина можно найти, например, в работе [16].
В зависимости от величины собственной ошибки сельсины группируются по классам. Классы определяются по средней максимальной ошибке, равной полусумме абсолютных максимальных отклонений от согласованного положения со знаком плюс и со знаком минус, т. е.

где  — абсолютная величина максимального отклонения со знаком плюс;
— абсолютная величина максимального отклонения со знаком плюс;
 абсолютная величина максимального отклонения со знаком минус.
абсолютная величина максимального отклонения со знаком минус.
К первому классу относятся сельсины, допустимая ошибка которых составляет  , ко второму классу — сельсины с ошибкой
, ко второму классу — сельсины с ошибкой  и к третьему классу — сельсины ошибка которых составляет
и к третьему классу — сельсины ошибка которых составляет  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
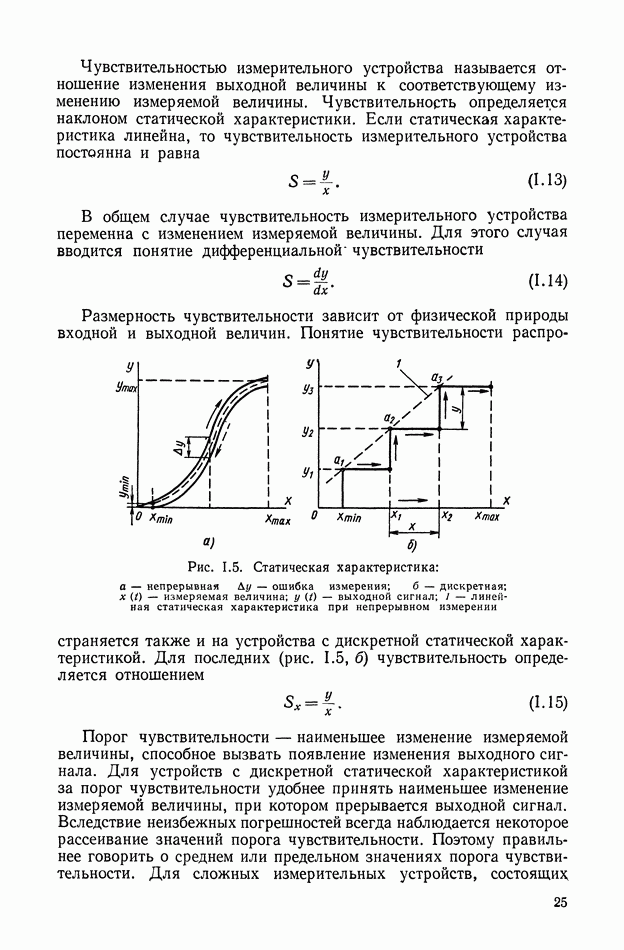
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
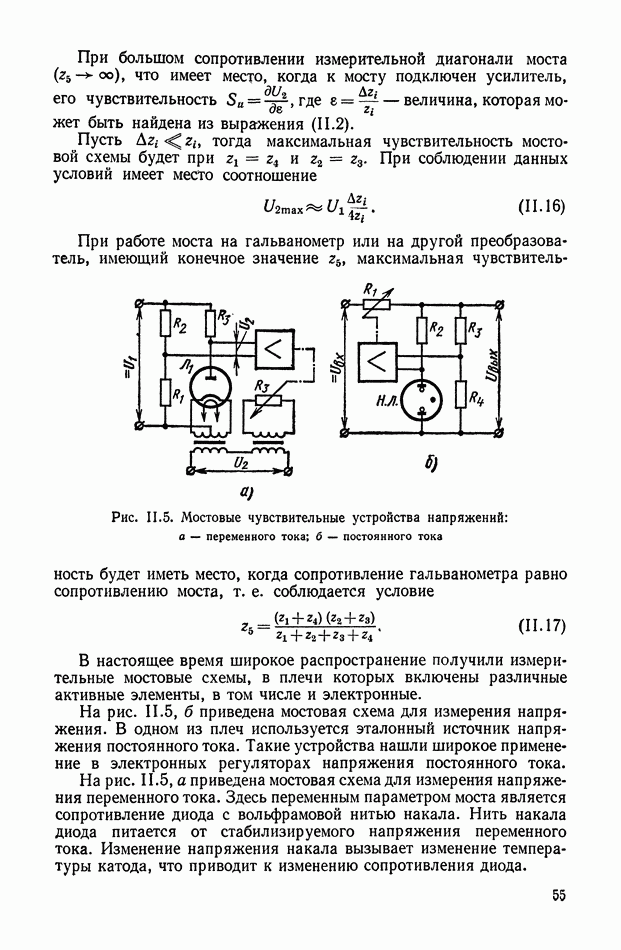
- 1. МОСТОВЫЕ СХЕМЫ
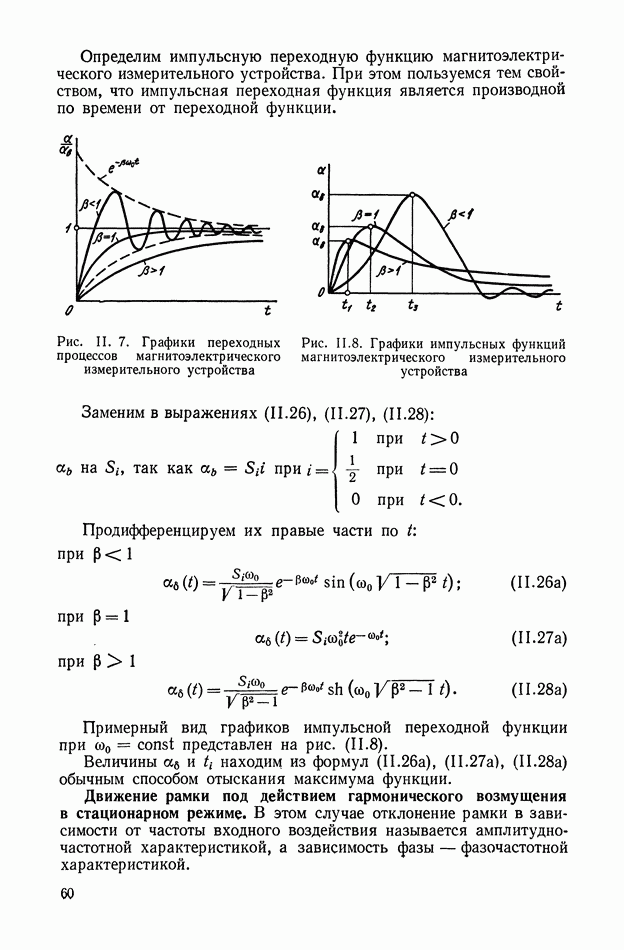
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
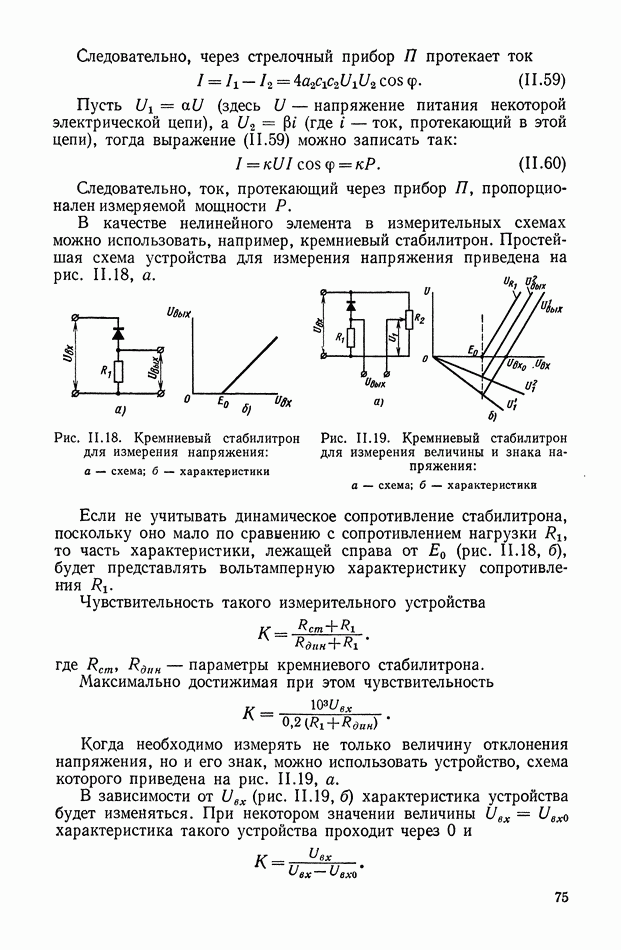
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
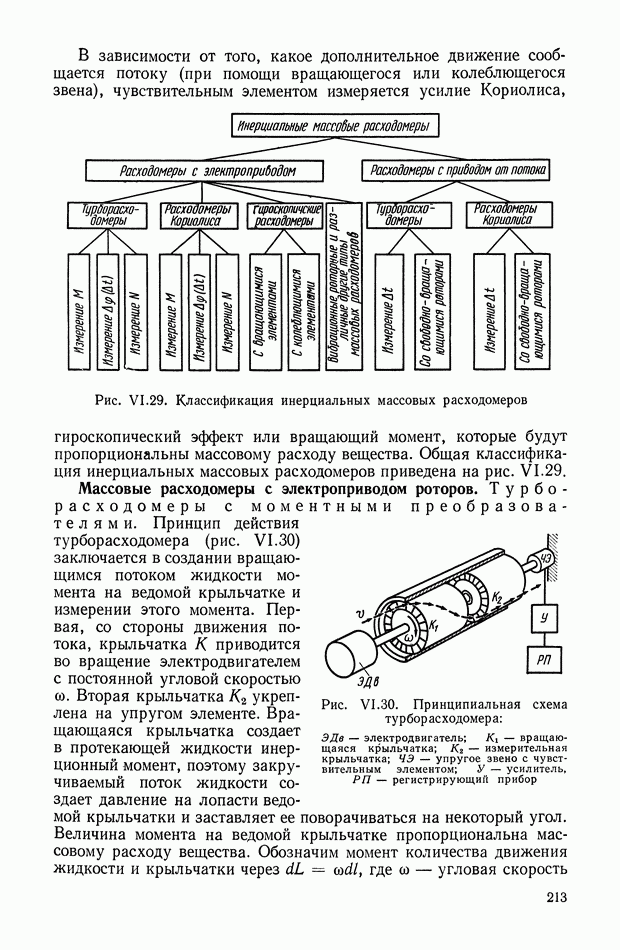
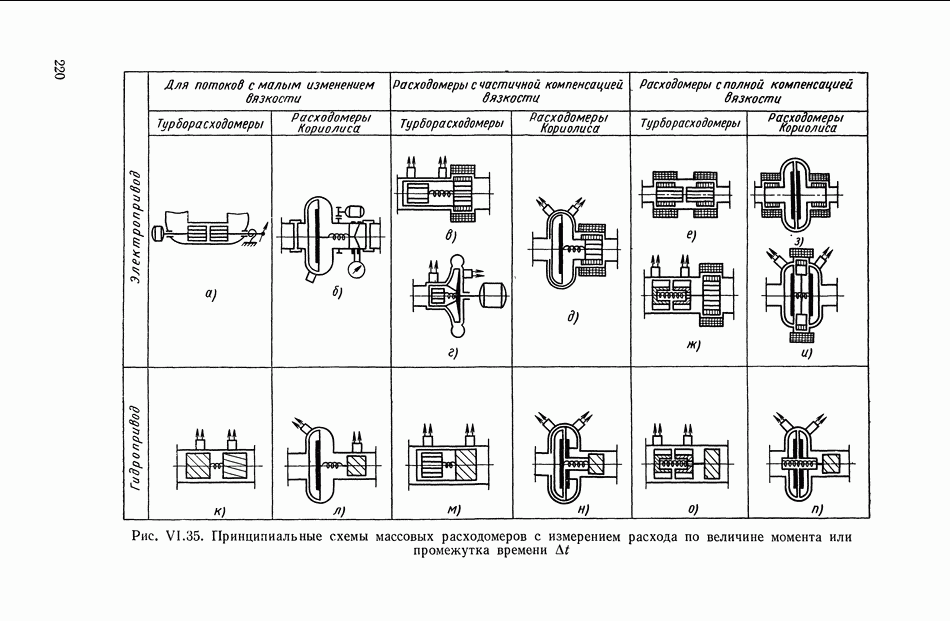
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
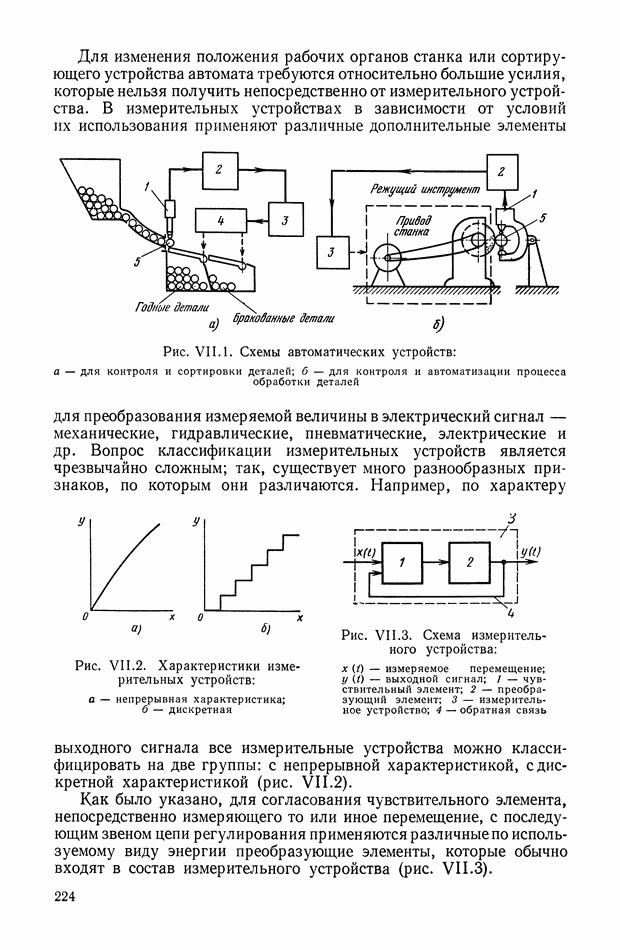
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
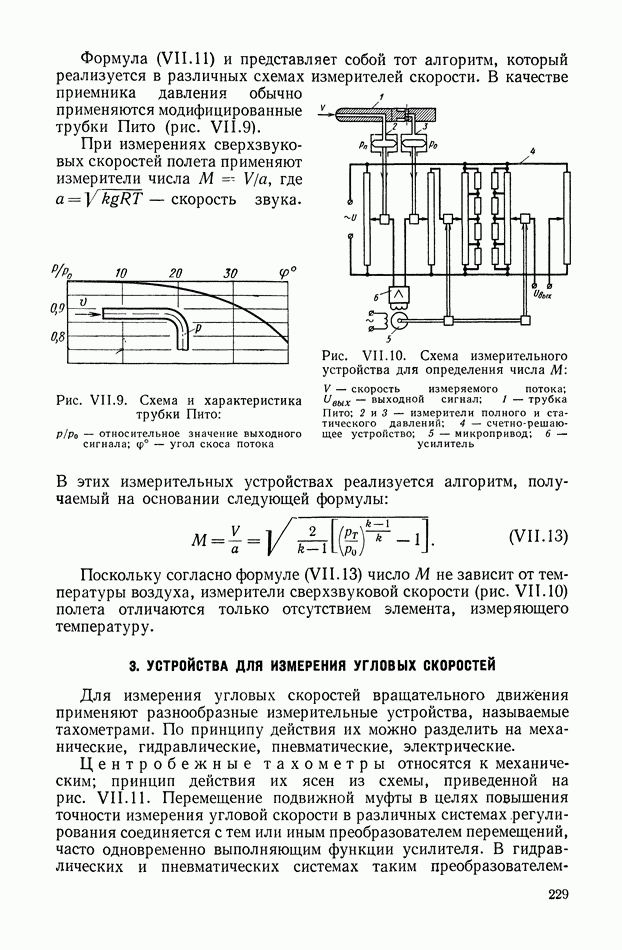
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
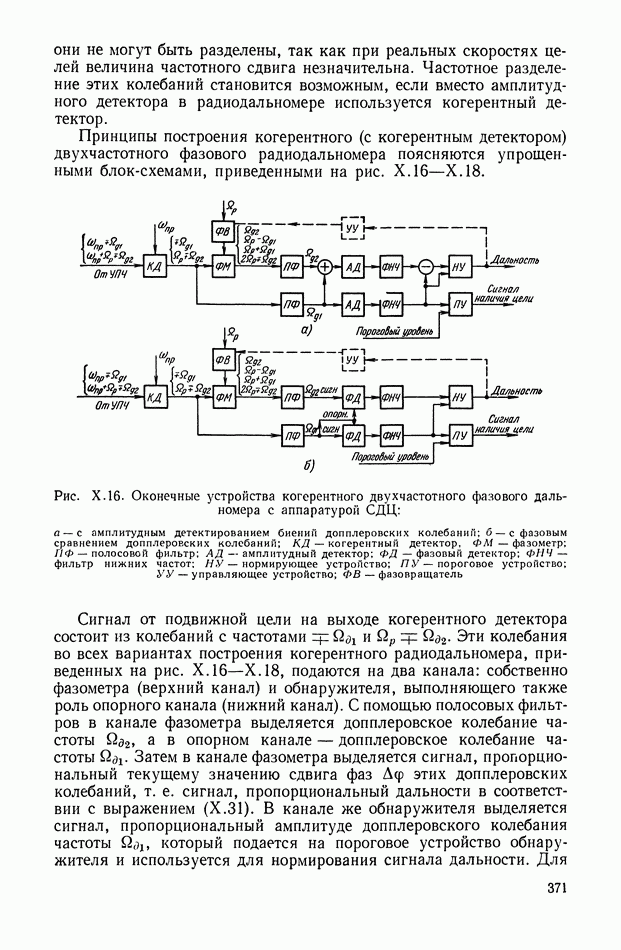
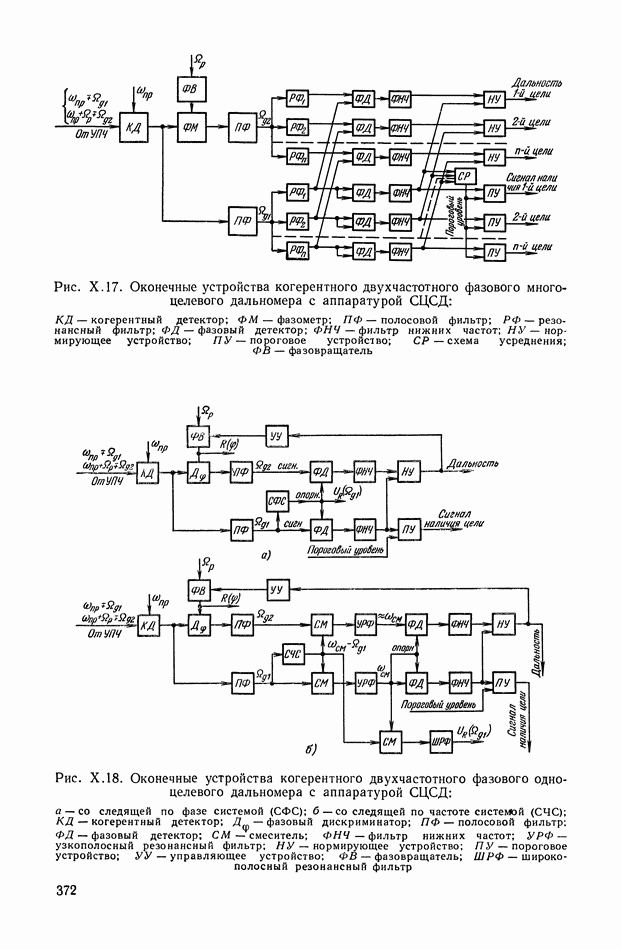
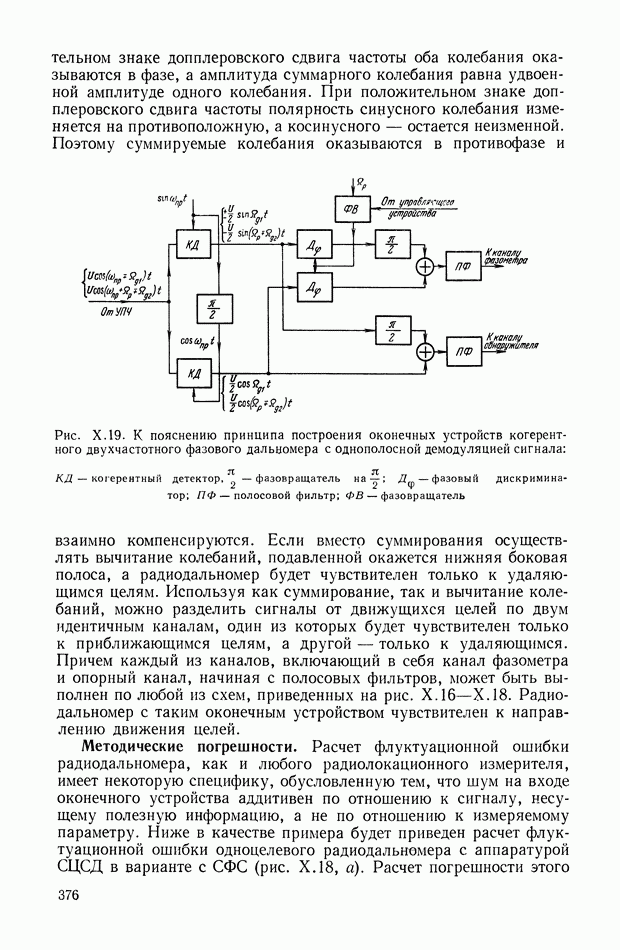
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
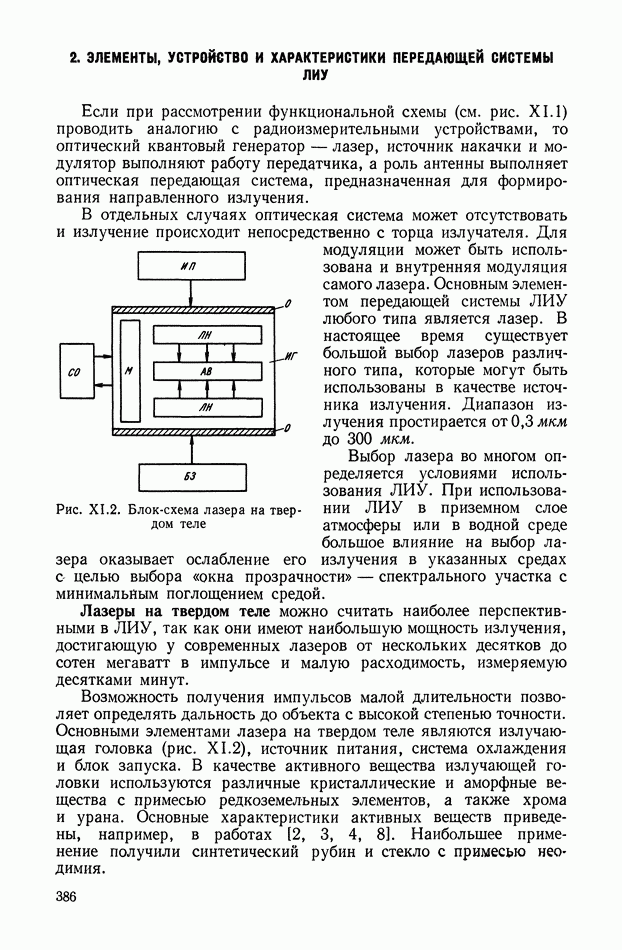
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
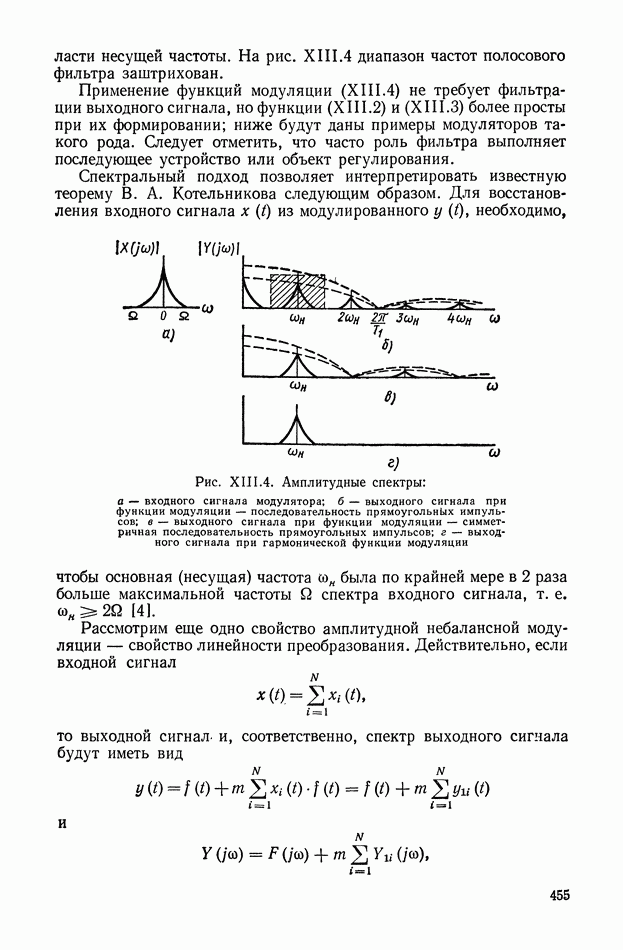
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
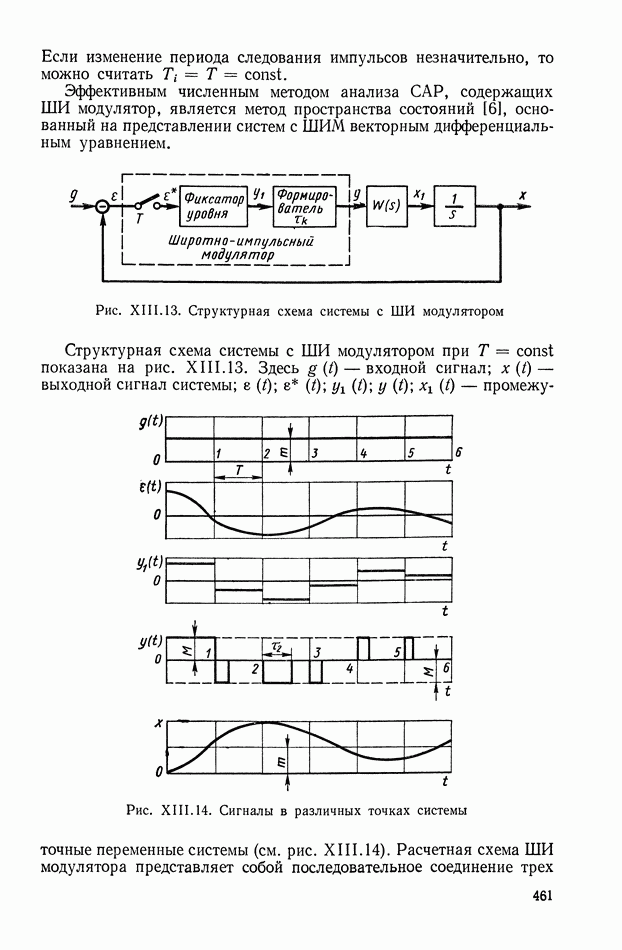
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
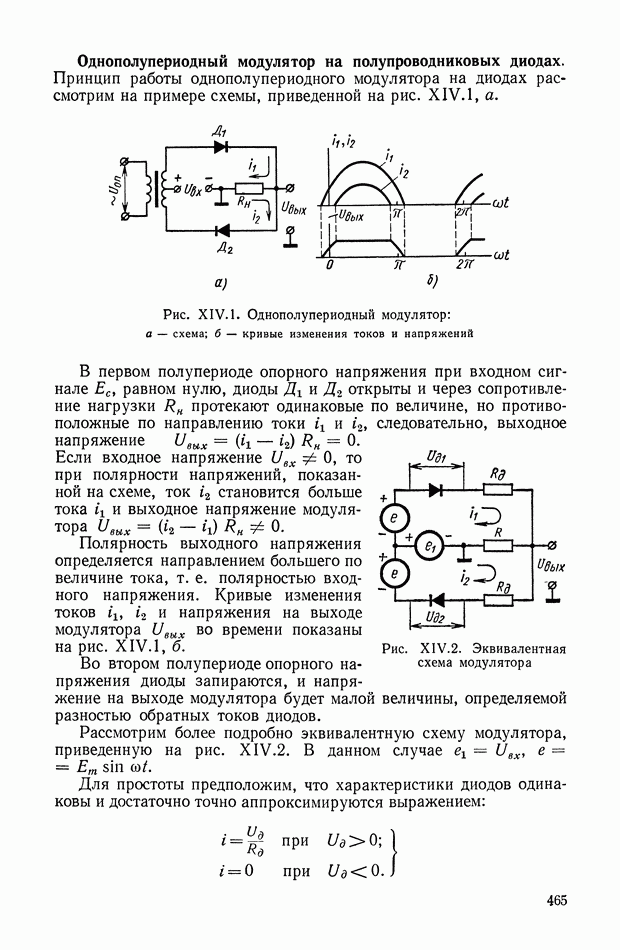
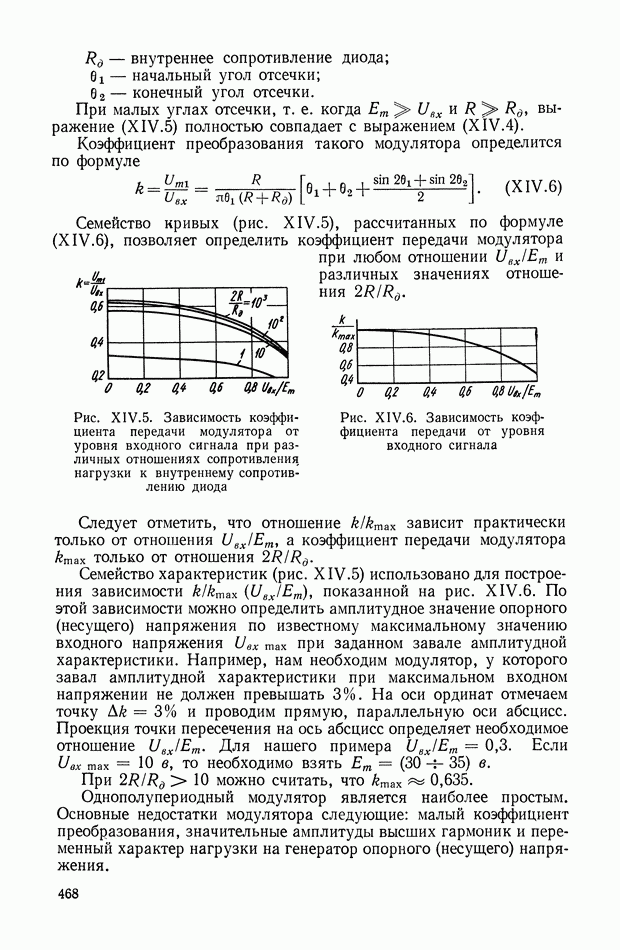
- 1. МОДУЛЯТОРЫ
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
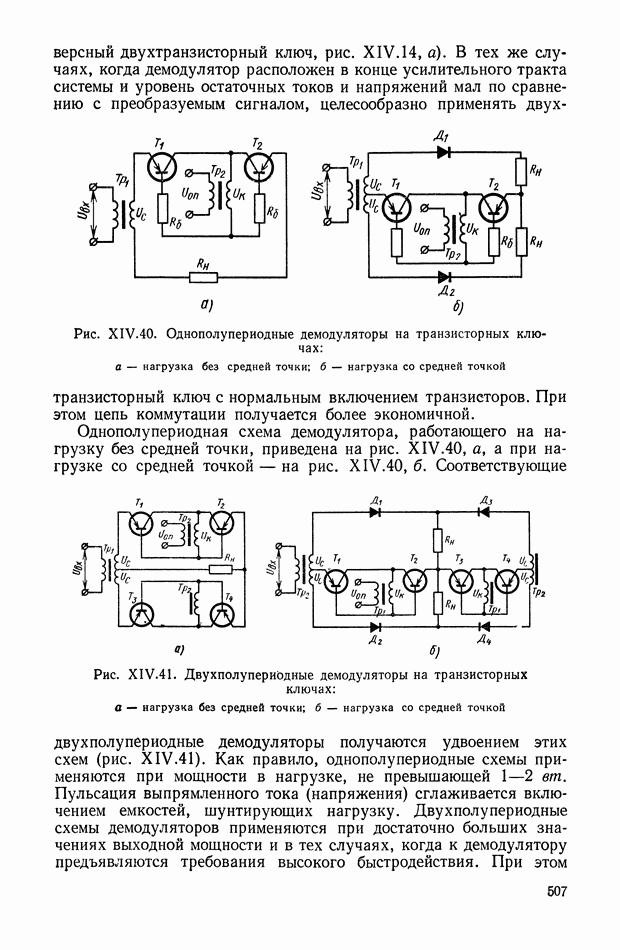
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
- Двухполупериодные демодуляторы на диодах.
- Однополупериодные усилители-демодуляторы.
- Двухполупериодные усилители-демодуляторы.
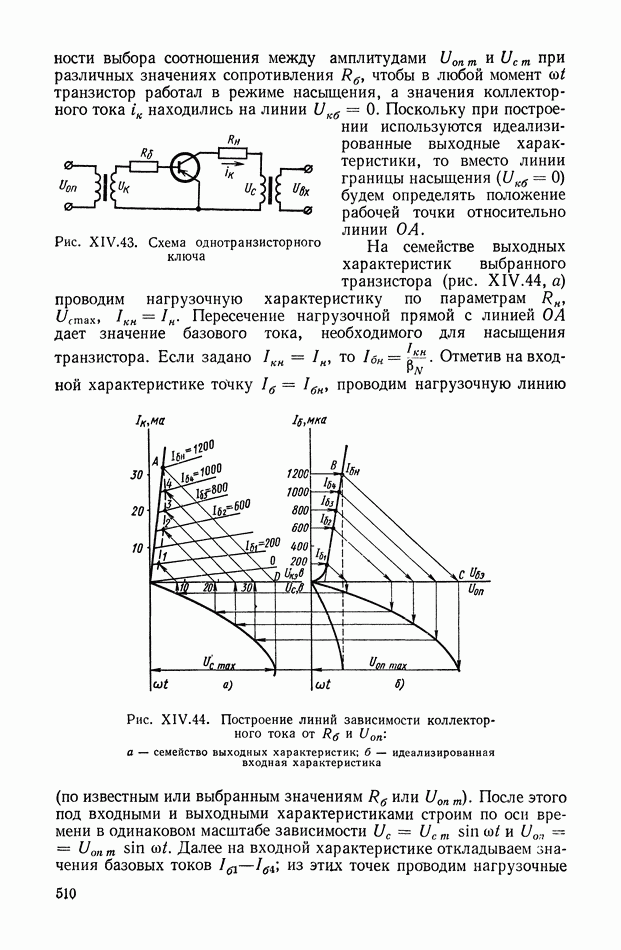
- Демодуляторы на транзисторных ключах.
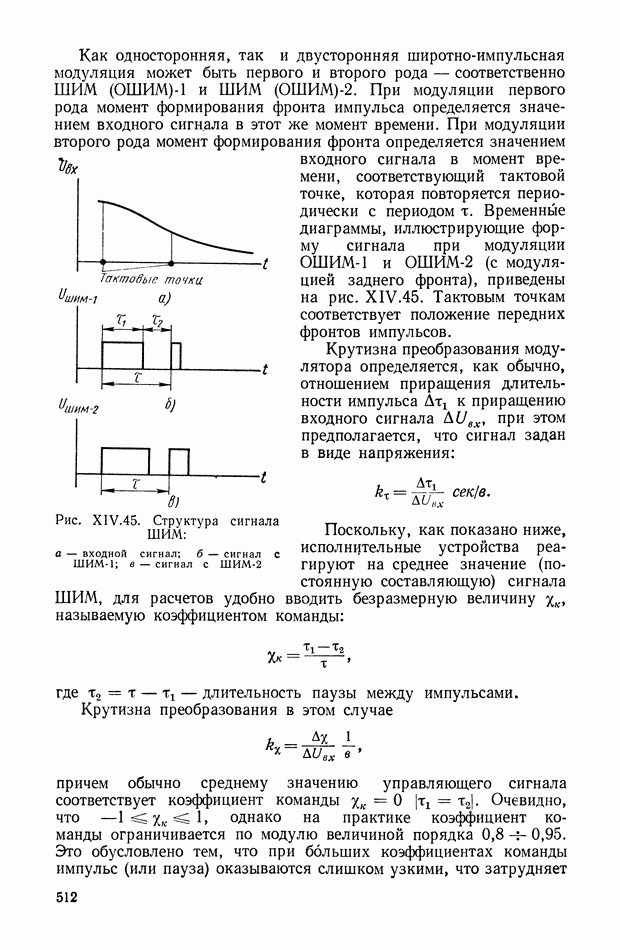
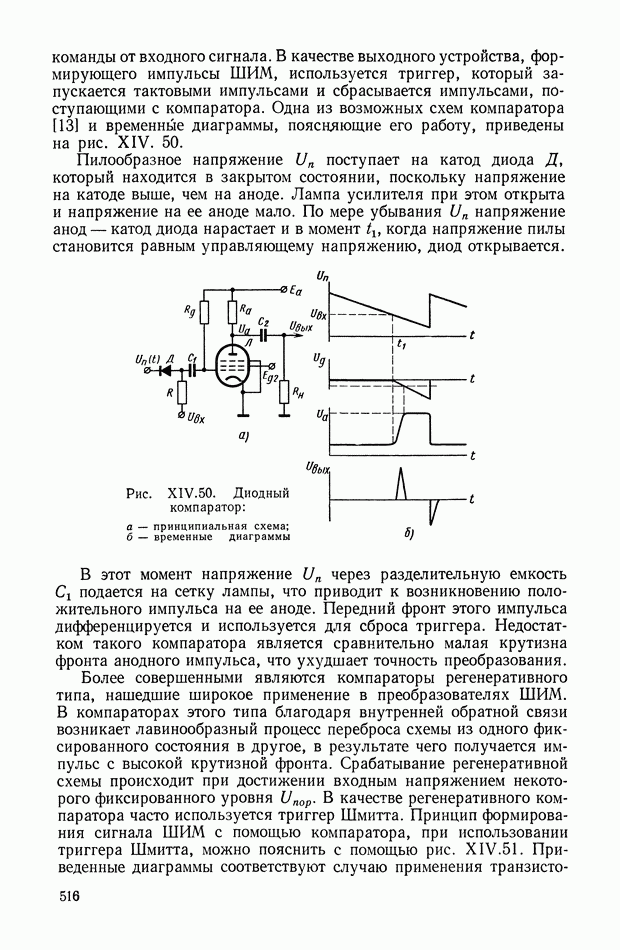
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
- Сильфоны.
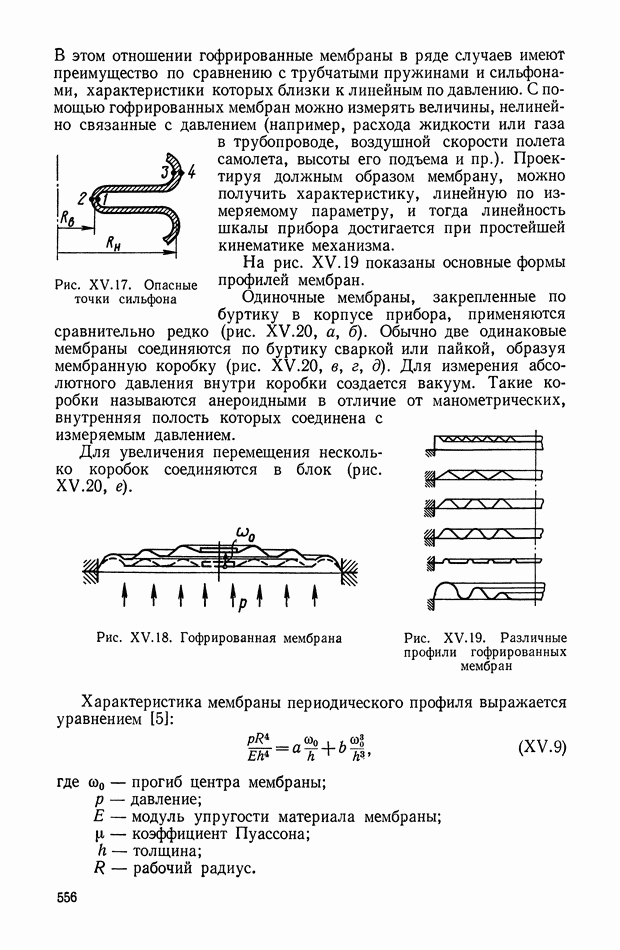
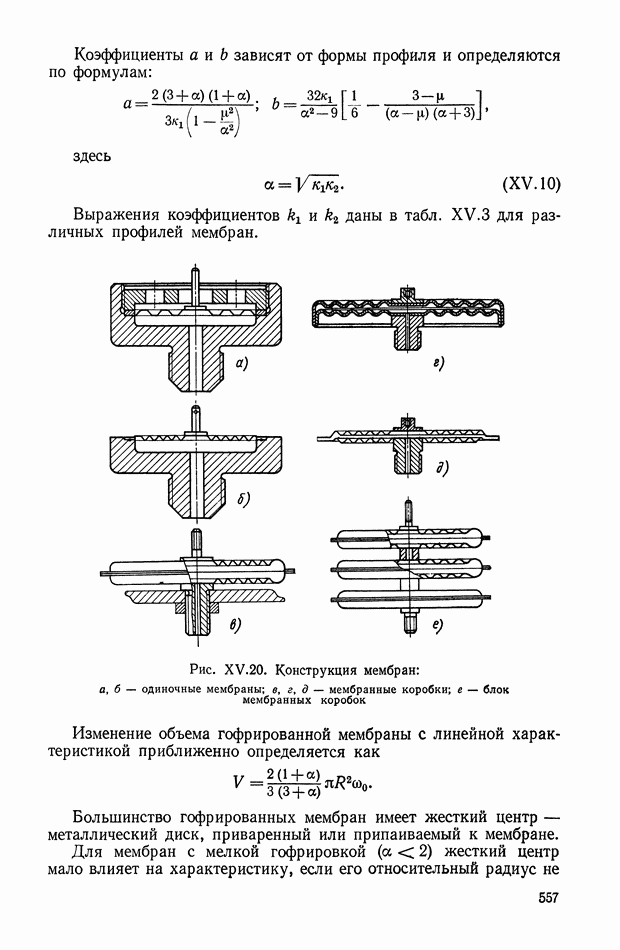
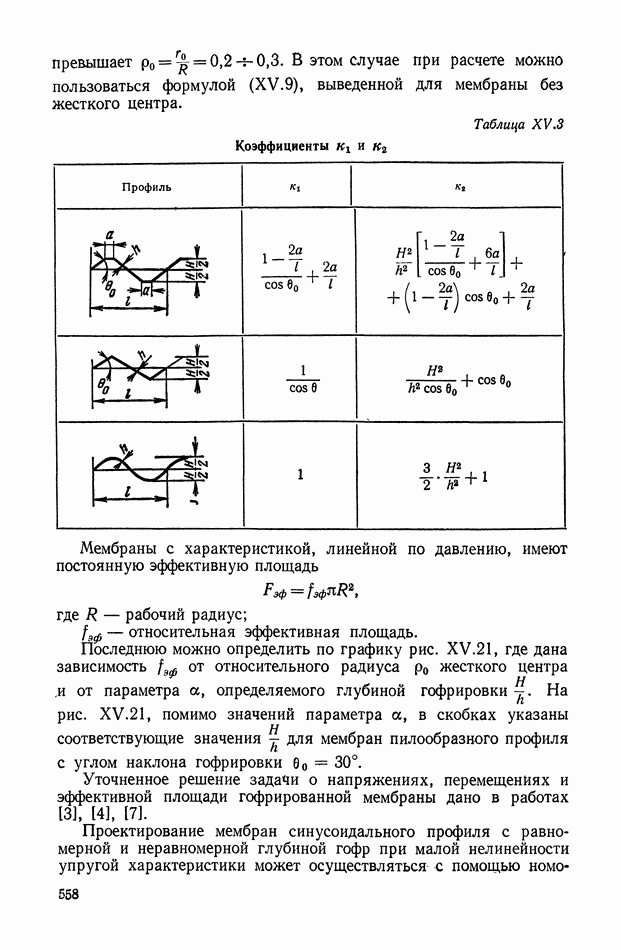
- Гофрированные мембраны.
- Гибкие диафрагмы.
- Хлопающие мембраны.
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
- Пневмоэлектроконтактные преобразователи линейных величин.
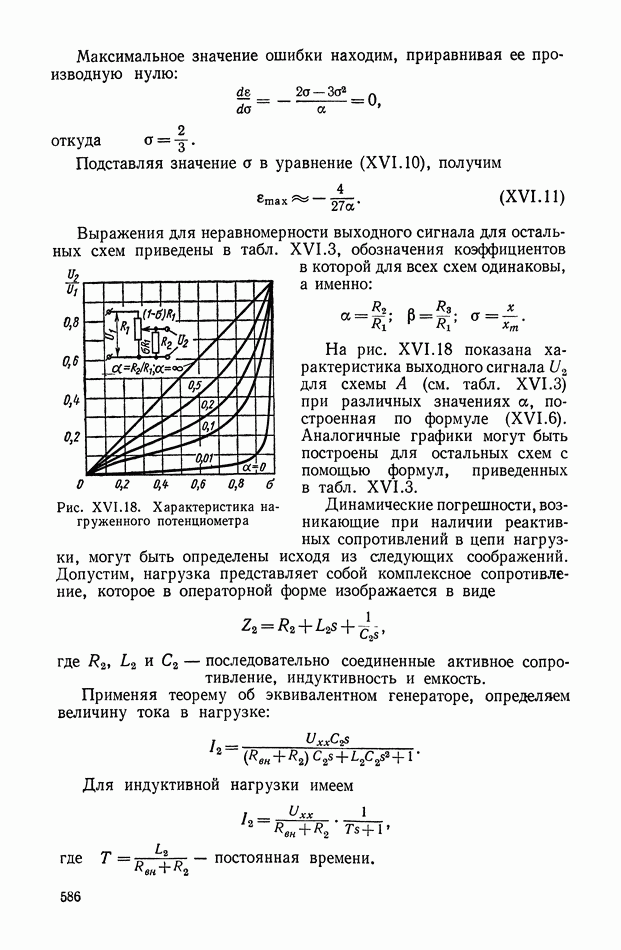
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
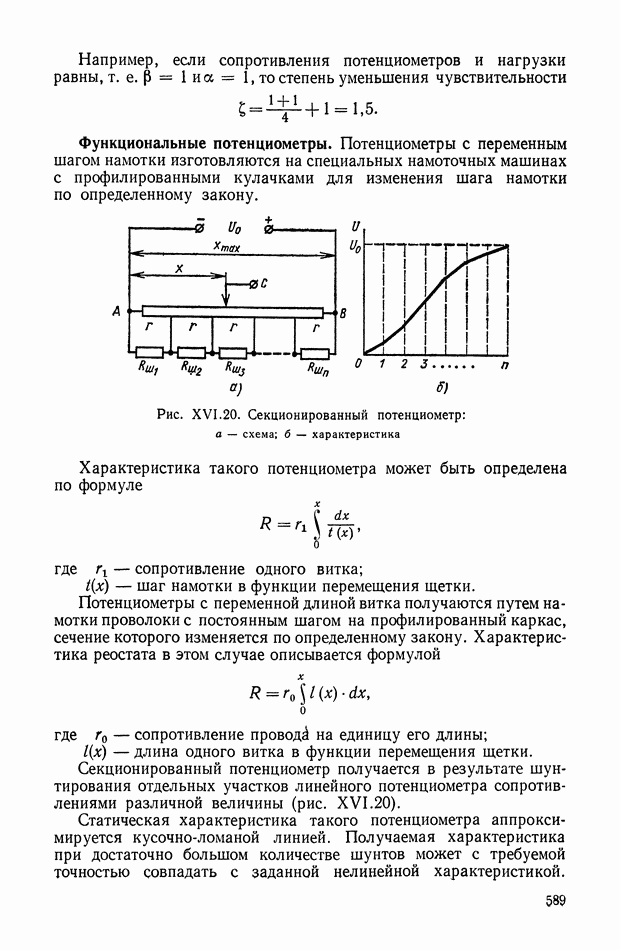
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
- Работа сельсинов в трансформаторном режиме.
- Устранение ложного нуля в двухскоростной системе.
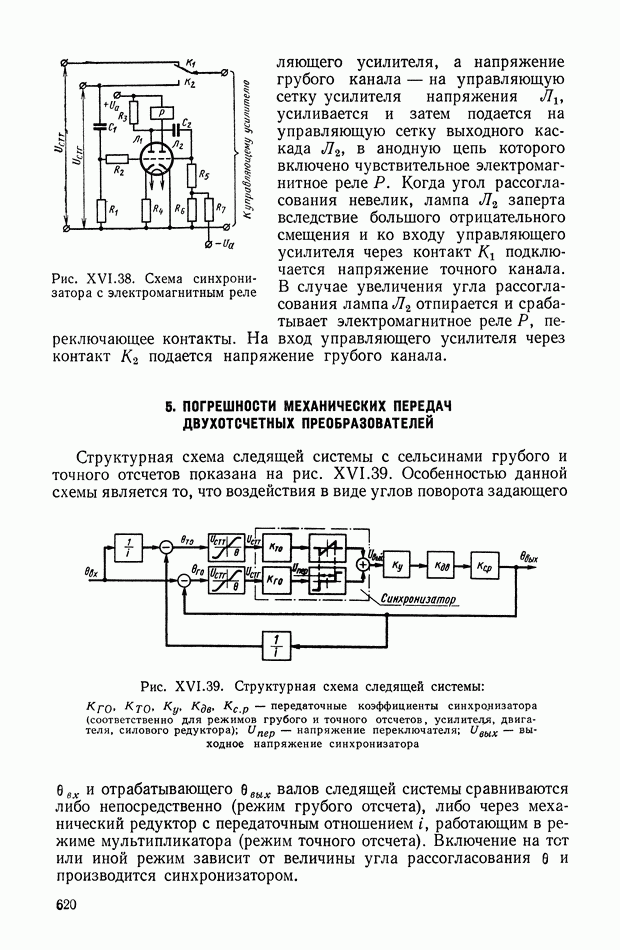
- Схемы синхронизаторов.
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
- Индукционные редуктосины.
- Индуктосины.
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- Емкостный редуктосин.
- Емкостный фазовращатель.
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ