| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
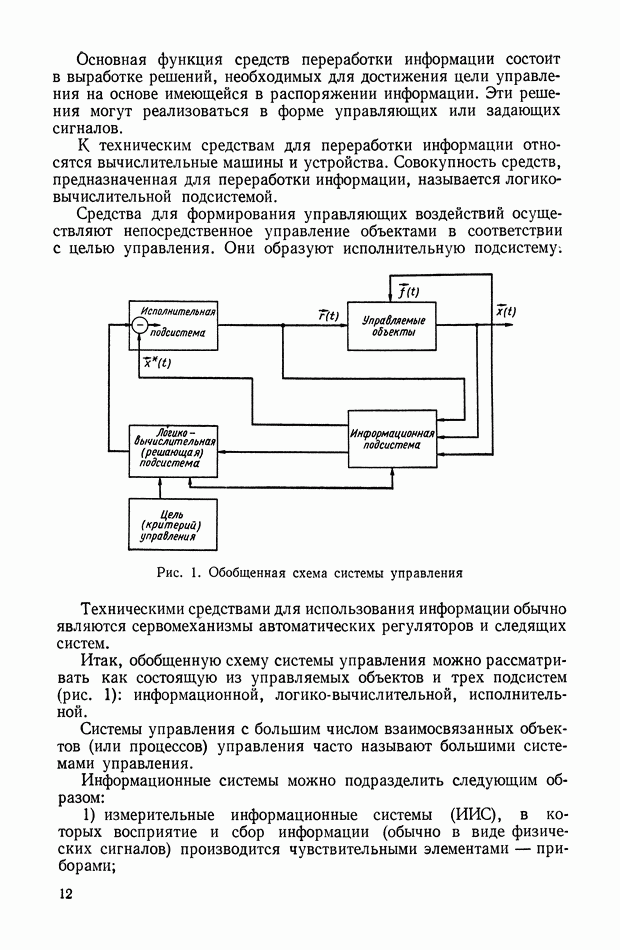
В настоящей главе рассматриваются гироскопические приборы и системы, представляющие собой измерительные элементы автопилотов, головок самонаведения летательных и морских аппаратов, гирорулевых систем инерциальной навигации и др., предназначенные для определения положения объекта (корабля, самолета или ракеты) в пространстве и для измерения угловых и линейных скоростей и ускорений движения различных объектов.
Гироскопические приборы и системы применяются в авиации, ракетной технике и морском флоте, а также на космических кораблях для определения курса и направления истинной вертикали, для автоматического управления самолетами, ракетами и судами; в артиллерии, авиации и на танках они используются для сохранения заданного направления прицела. Кроме этого, в горнорудной и нефтяной промышленности эти устройства применяются при прокладке шахт и тоннелей, при бурении скважин для определения соответствующих направлений и т. д.
На кораблях и самолетах, плавание и полет которых происходит в основном при установившемся режиме движения, а время выполнения маневров невелико, применяют курсовые системы и гироскопические вертикали, корректируемые с помощью физического маятника и магнитного компаса.
На летательных аппаратах, непрерывно выполняющих сложные маневры с большими ускорениями, в качестве курсовых приборов и гировертикалей используются гироскопические приборы, не корректируемые физическим маятником или магнитным компасом.
Такие приборы и системы представляют собой гироскопические стабилизаторы.
Широкое применение гироскопических стабилизаторов объясняется тем, что гироскопы, устанавливаемые на платформе гиростабилизатора, обладают повышенной сопротивляемостью по отношению к моментам внешних сил и в большей мере, чем обычные «негироскопические» твердые тела, наделены способностью сохранять направление оси своего ротора неизменным в инерциальном пространстве.
Простейшим гироскопическим стабилизатором является астатический гироскоп.
Для придания гироскопу необходимой свободы вращения его заключают в специальный подвес. Наиболее широкое применение нашел карданов подвес с прецизионными шарикоподшипниковыми опорами, хотя в отдельных случаях в зависимости от требуемой точности и условий эксплуатации используются гидростатический, газодинамический, электростатический, магнитный и другие типы подвесов.
В настоящее время за рубежом ведутся широкие работы по созданию гироскопических приборов, в которых отсутствует быстровращающееся твердое тело (лазерные и ядерные гироскопы). Однако указанные приборы не вышли пока из стадии лабораторных исследований.
1. ОБЩИЕ СВЕДЕНИЯ
Приборы и системы, представляющие собой гироскопические чувствительные элементы, строятся с использованием симметричных быстровращающихся гироскопов; при этом в основу методов исследования таких приборов положена теория быстровращающегося симметричного гороскопа [2], [5], [8].

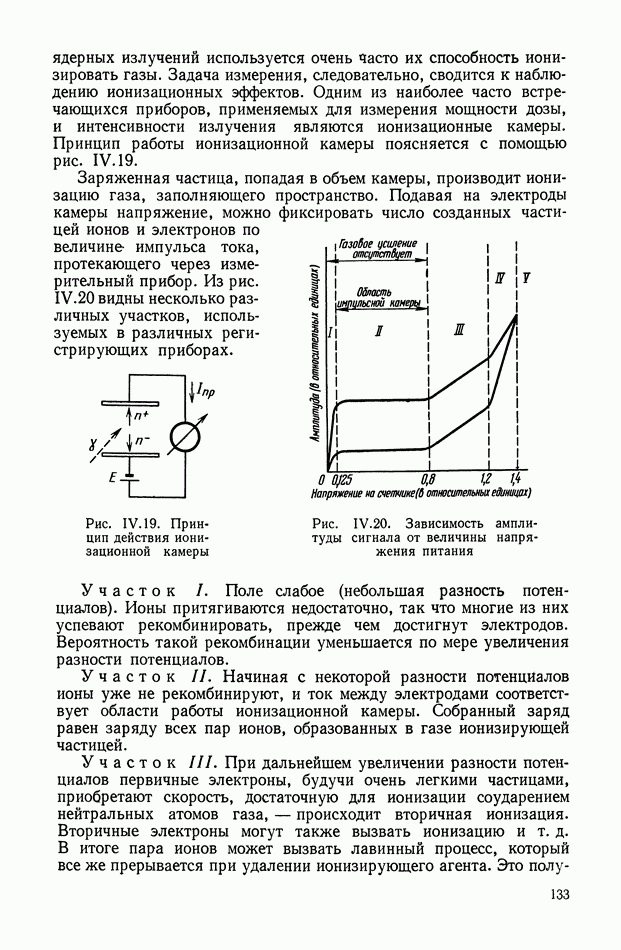
Рис. VIII. 1. Симметричный быстровращающийся гироскоп
Симметричным быстровращающимся гироскопом (рис. VIII. 1) называют быстровращающееся твердое тело, одна из точек О которого закреплена, а эллипсоид инерции относительно этой точки является эллипсоидом вращения; ось вращения эллипсоида инерции совпадает .с осью собственного вращения гироскопа.
Если на гироскоп не действует момент внешних сил, то такой гироскоп называют свободным.
В случае, если осевой момент инерции С больше экваториального момента инерции Л, как это показано на рис. VIII. 1, то кинематику свободного движения симметричного гироскопа можно представить как равномерное качение без скольжения круглого конуса П (полодии), жестко скрепленного с гироскопом, по поверхности другого конуса Г (герполодий), неподвижного в абсолютном пространстве.
При этом ось конуса герполодии совпадает с направлением вектора  — момента количества движения гироскопа, а ось
— момента количества движения гироскопа, а ось  фигуры гироскопа является осью конуса полодии. Вектор мгновенной угловой скорости со вращения гироскопа лежит на соприкасающейся
фигуры гироскопа является осью конуса полодии. Вектор мгновенной угловой скорости со вращения гироскопа лежит на соприкасающейся
образующих конусов Г и П. Такое движение гироскопа называют свободной регулярной прецессией, или нутадией.
У быстровращающегося гироскопа угол между вектором 0 и осью  практически бывает малым. В этом случае свободное движение оси
практически бывает малым. В этом случае свободное движение оси  фигуры гироскопа представляет собой быстрое дрожание оси фигуры с малой амплитудой около вектора 0, направление которого сохраняется неподвижным в абсолютном пространстве.
фигуры гироскопа представляет собой быстрое дрожание оси фигуры с малой амплитудой около вектора 0, направление которого сохраняется неподвижным в абсолютном пространстве.
Если на гироскоп действует момент М внешних сил, то его движение в соответствии с законом моментов количества движения определяется уравнением

Векторная производная по времени от вектора  момента количества движения гироскопа равна вектору М равнодействующей момента внешних сил, действующих на гироскоп.
момента количества движения гироскопа равна вектору М равнодействующей момента внешних сил, действующих на гироскоп.
Амплитуда нутационных колебаний гироскопа мала и практически затухает под влиянием диссипативных моментов, поэтому в технических приложениях часто движение вектора  отождествляют с движением оси
отождествляют с движением оси  фигуры гироскопа.
фигуры гироскопа.
В этом случае уравнение (VIII. 1) преобразуется к виду

где Н — постоянный по модулю кинетический момент гироскопа. Тогда имеем

где  — абсолютная угловая скорость поворота оси фигуры гироскопа.
— абсолютная угловая скорость поворота оси фигуры гироскопа.
Рассматривая движение гироскопа в подвижной системе координат, переносная угловая скорость которой равна  получим
получим

где  — угловая скорость поворота оси
— угловая скорость поворота оси  фигуры гироскопа относительно подвижной системы координат.
фигуры гироскопа относительно подвижной системы координат.
Если центр тяжести (ц. т.) гироскопа не совпадает с точкой О его опоры и положение центра тяжести гироскопа относительно точки О определяется радиусом-вектором  то уравнение движения гироскопа преобразуется к виду
то уравнение движения гироскопа преобразуется к виду

где  — масса гироскопа;
— масса гироскопа;
 — абсолютное ускорение точки О опоры гироскопа. Векторное произведение
— абсолютное ускорение точки О опоры гироскопа. Векторное произведение  называется гироскопическим моментом, представляющим собой специфическое инерционное сопротивление, которое гироскоп оказывает внешнему моменту.
называется гироскопическим моментом, представляющим собой специфическое инерционное сопротивление, которое гироскоп оказывает внешнему моменту.
В процессе поворота оси  гироскопа в пространстве с абсолютной угловой скоростью
гироскопа в пространстве с абсолютной угловой скоростью  в каждый момент времени момент внешних сил, действующий на гироскоп через соответствующие связи, уравновешивается гироскопическим моментом, приложенным к связям.
в каждый момент времени момент внешних сил, действующий на гироскоп через соответствующие связи, уравновешивается гироскопическим моментом, приложенным к связям.
Гироскопический момент  равен по величине
равен по величине  момент перпендикулярен плоскости, заключающей вектор Н кинетического момента и вектор угловой скорости
момент перпендикулярен плоскости, заключающей вектор Н кинетического момента и вектор угловой скорости  , и направлен таким образом, что стремится совместить первый вектор со вторым по кратчайшему пути.
, и направлен таким образом, что стремится совместить первый вектор со вторым по кратчайшему пути.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
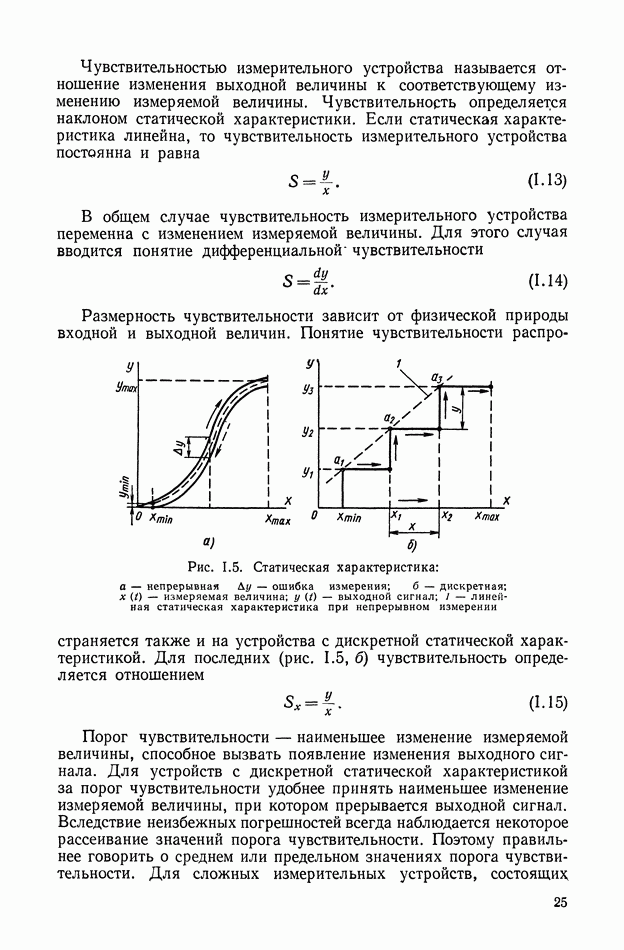
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
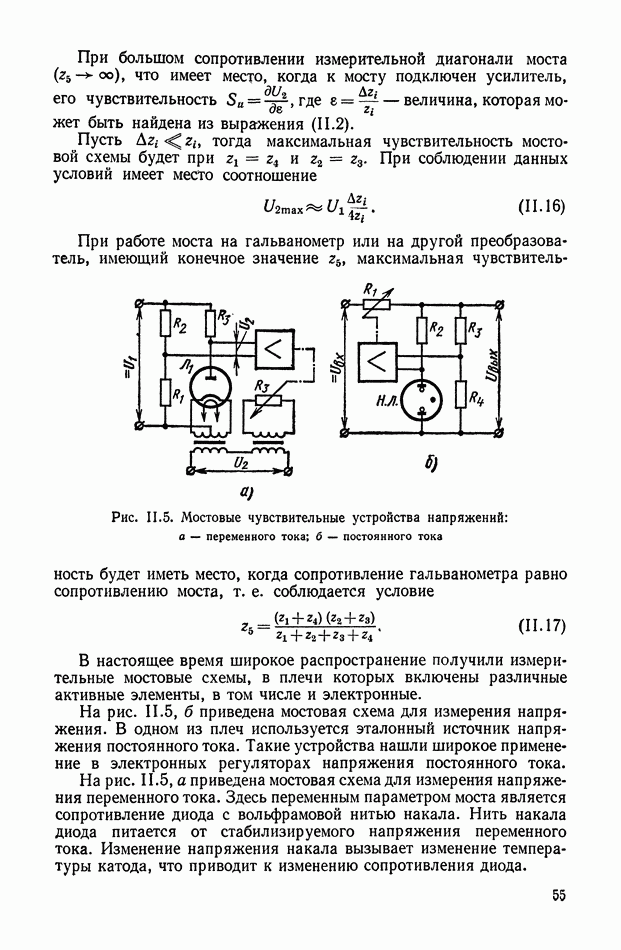
- 1. МОСТОВЫЕ СХЕМЫ
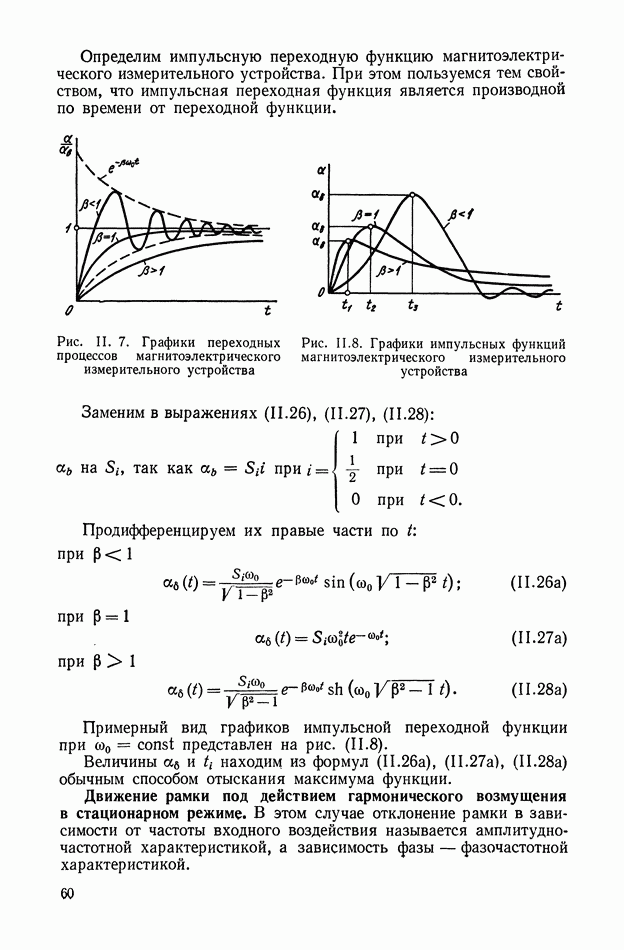
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
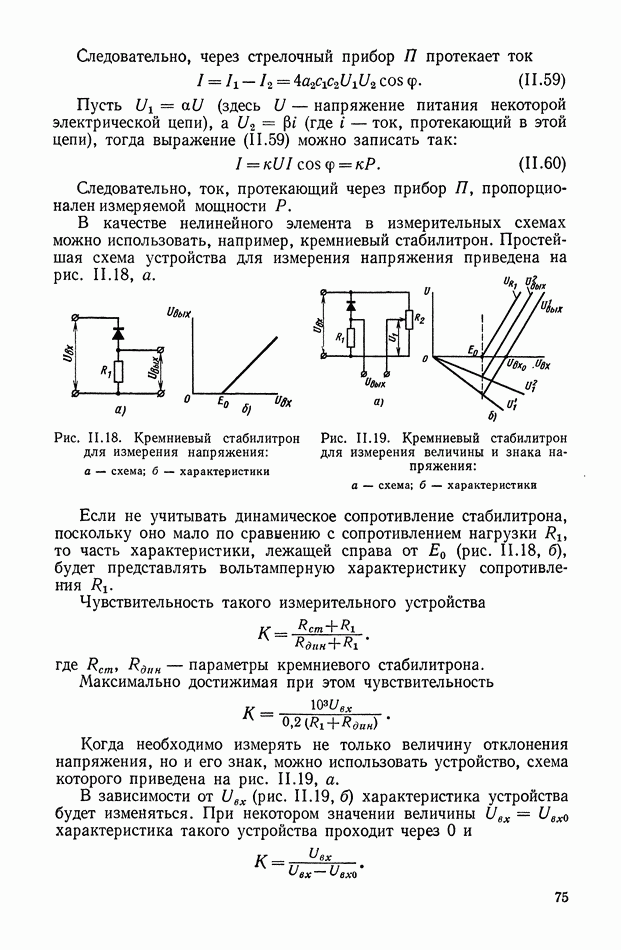
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
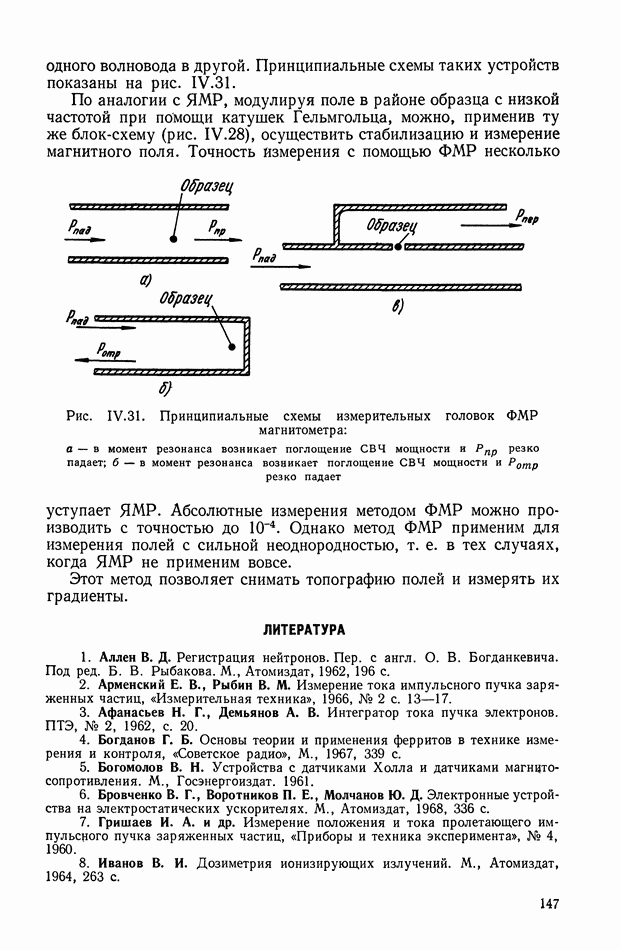
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
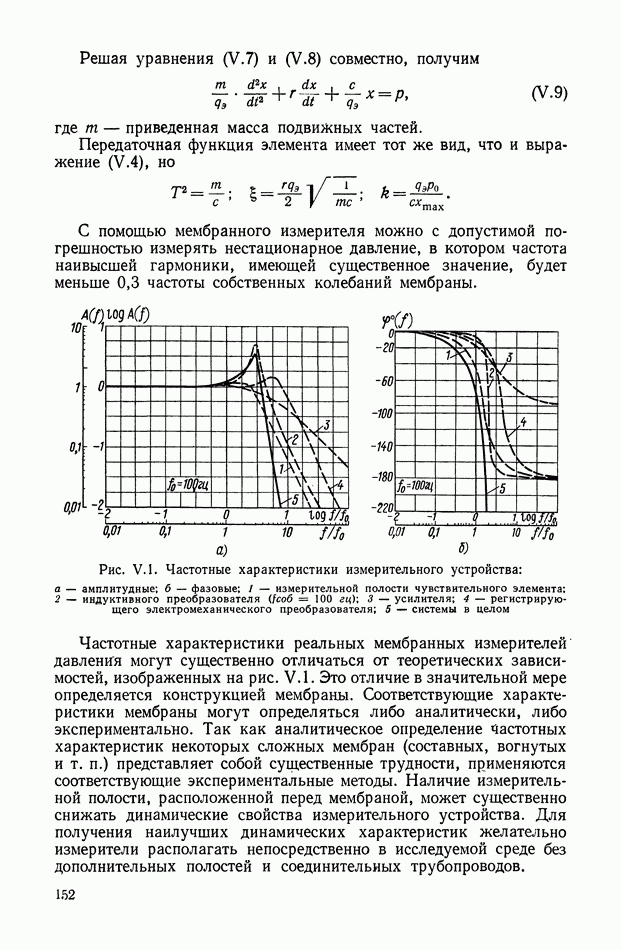
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
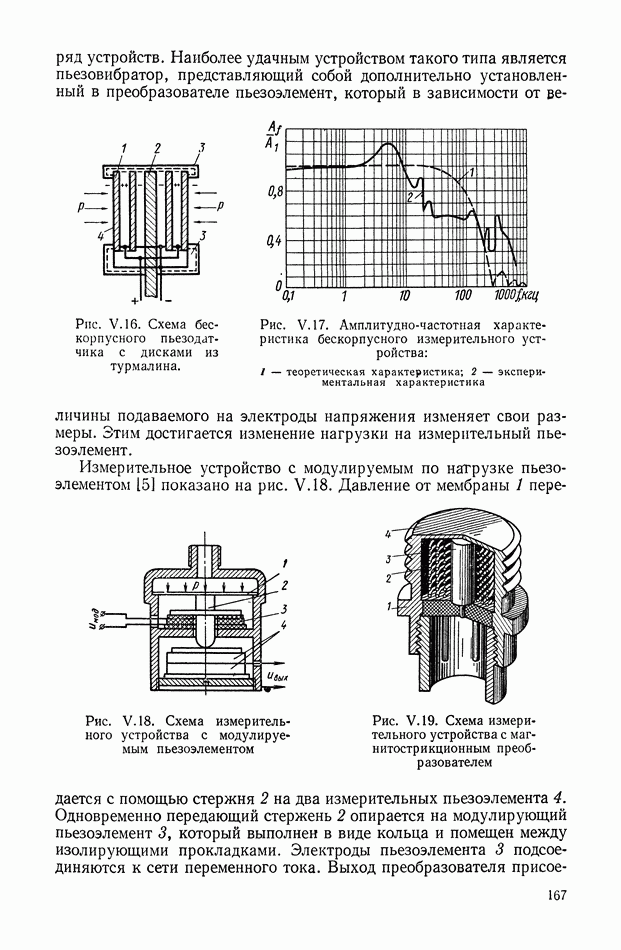
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
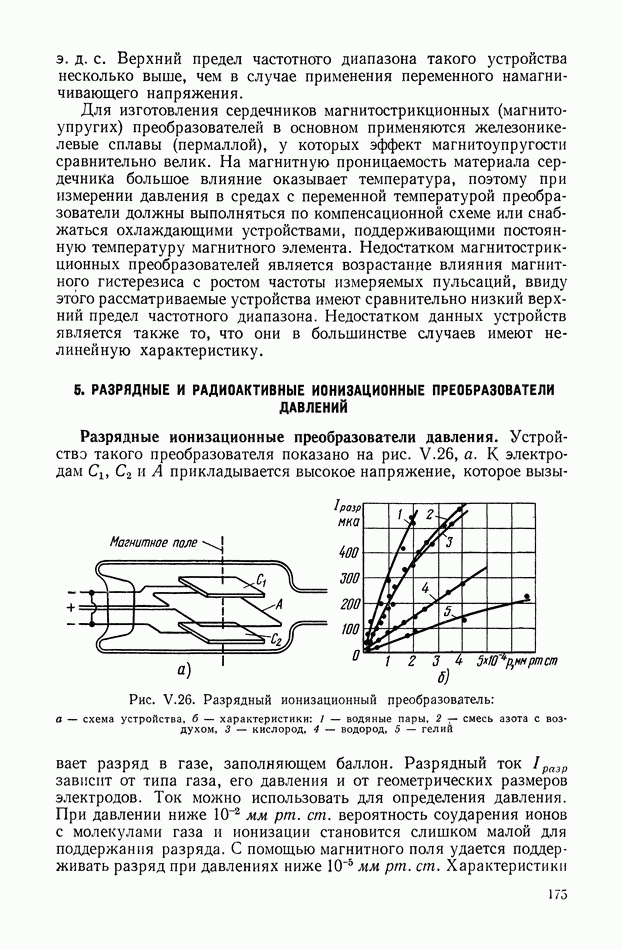
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
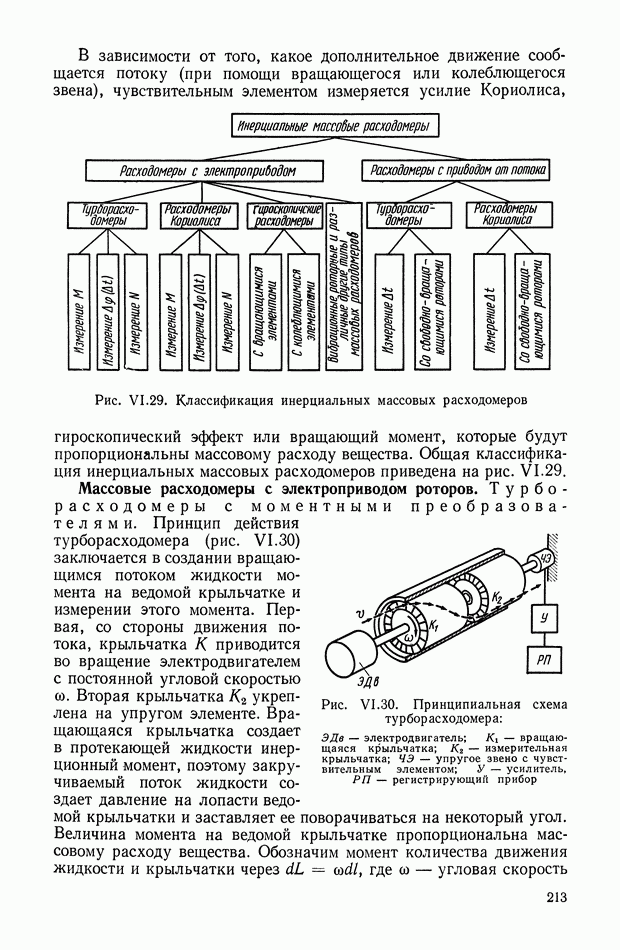
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
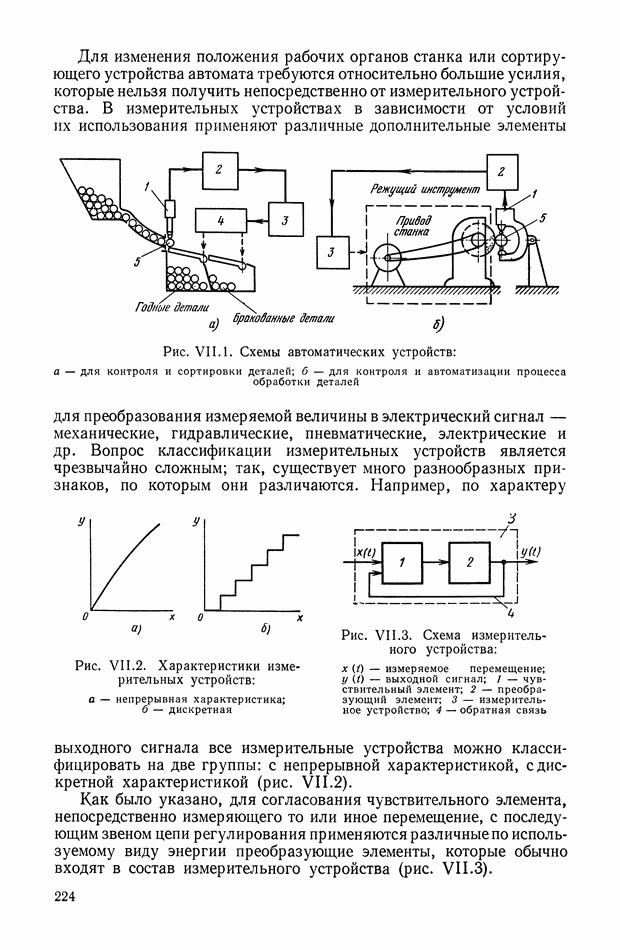
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
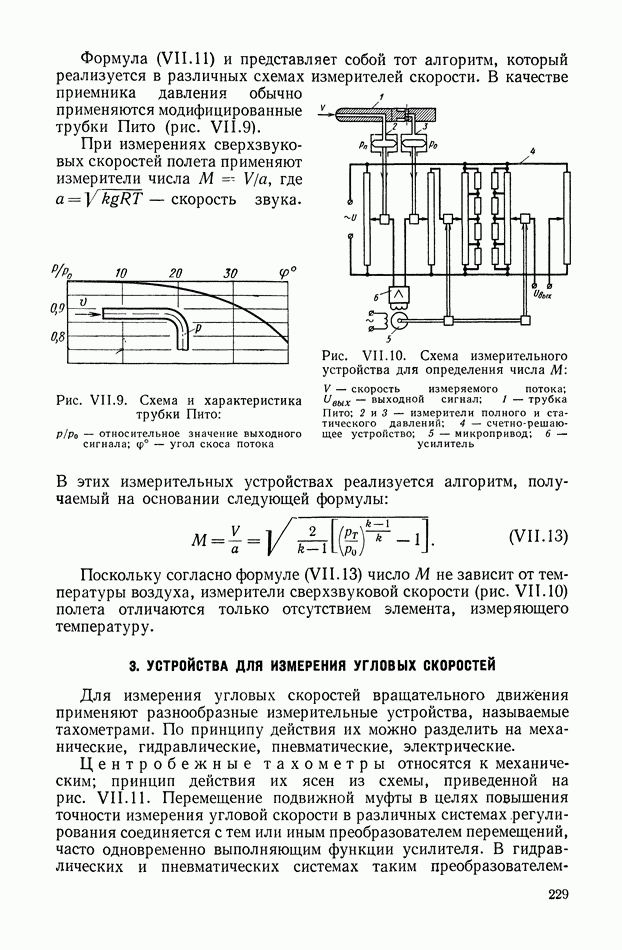
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
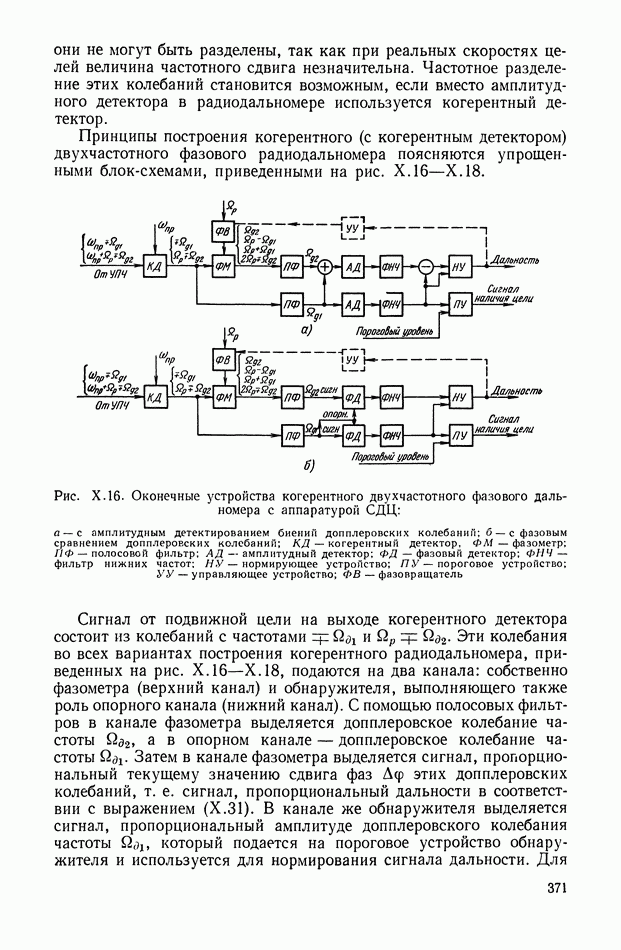
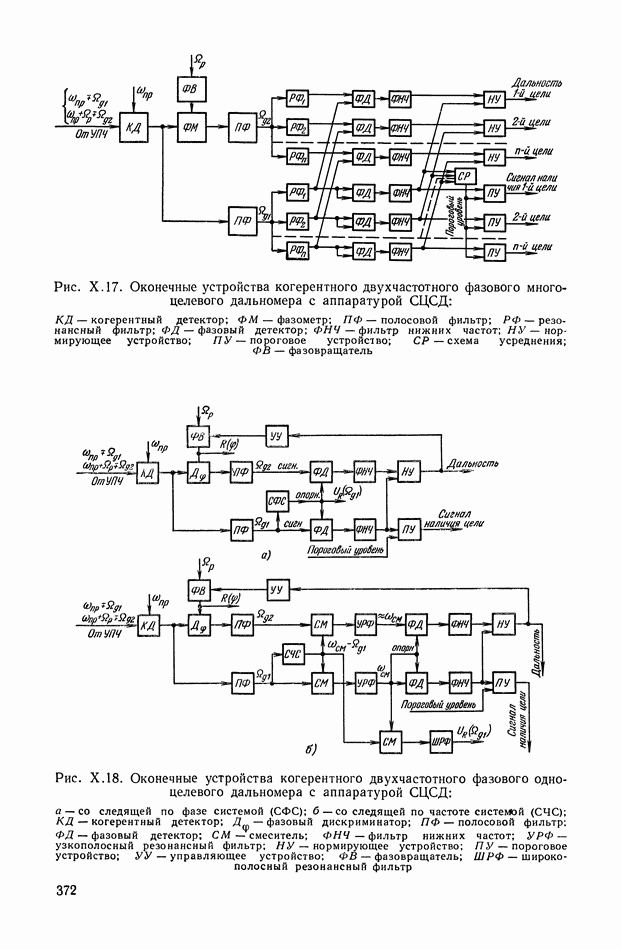
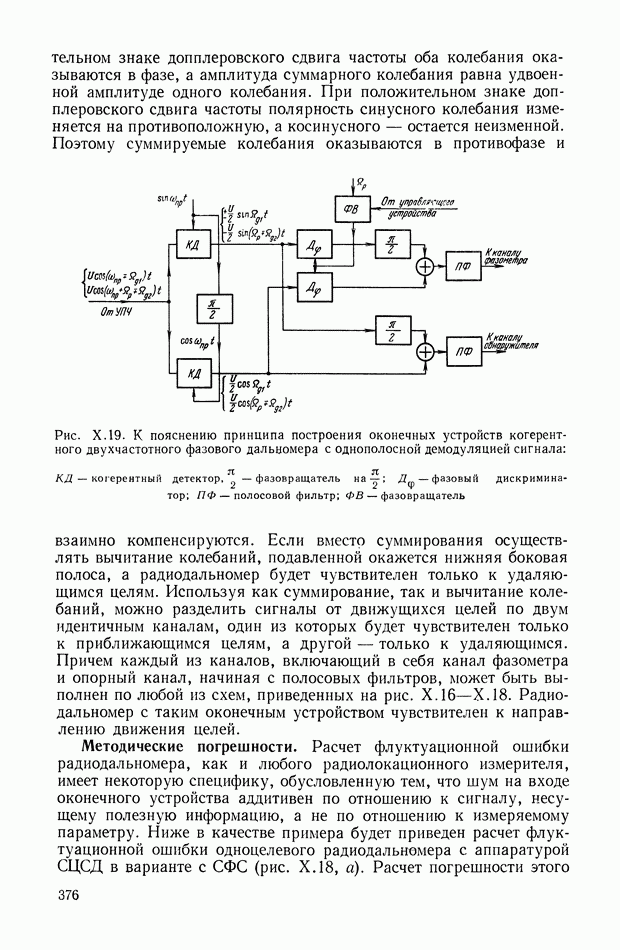
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
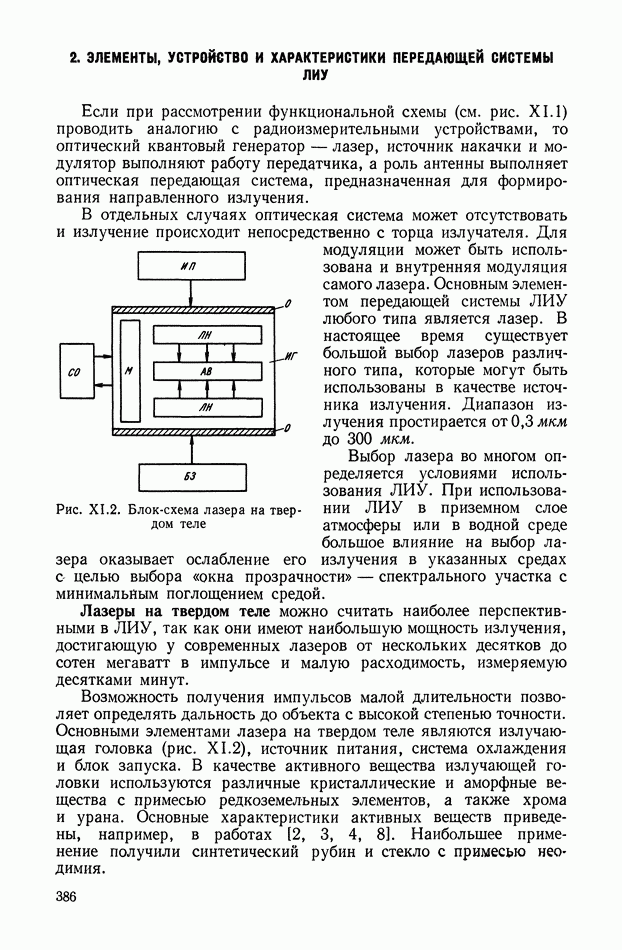
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 1. МОДУЛЯТОРЫ
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
- Двухполупериодные демодуляторы на диодах.
- Однополупериодные усилители-демодуляторы.
- Двухполупериодные усилители-демодуляторы.
- Демодуляторы на транзисторных ключах.
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
- Сильфоны.
- Гофрированные мембраны.
- Гибкие диафрагмы.
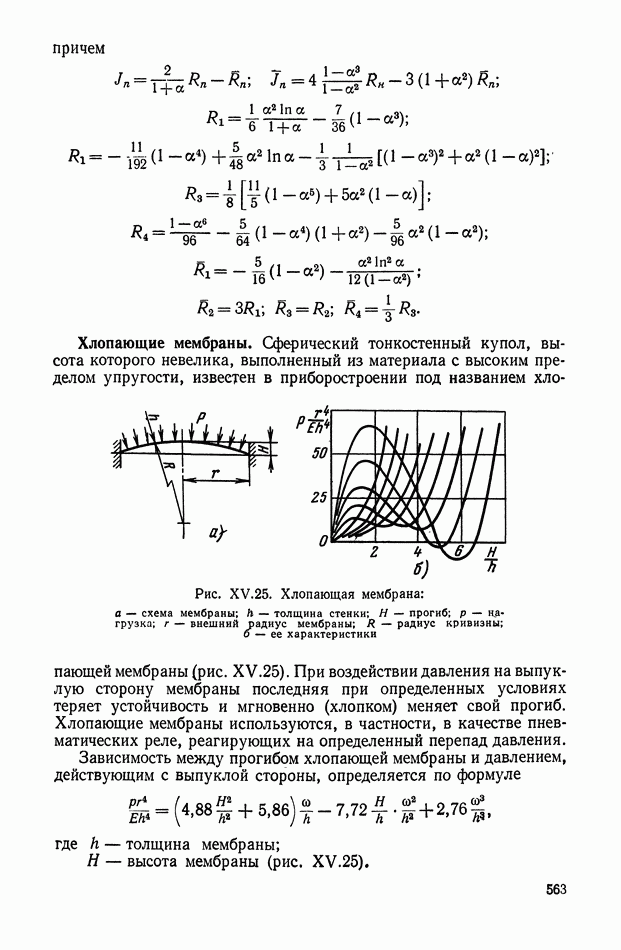
- Хлопающие мембраны.
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
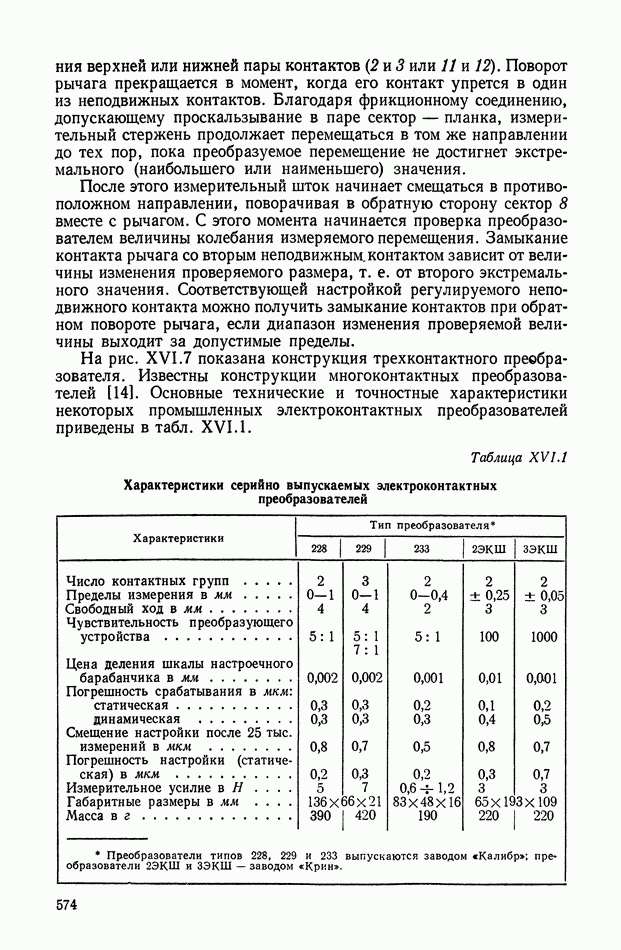
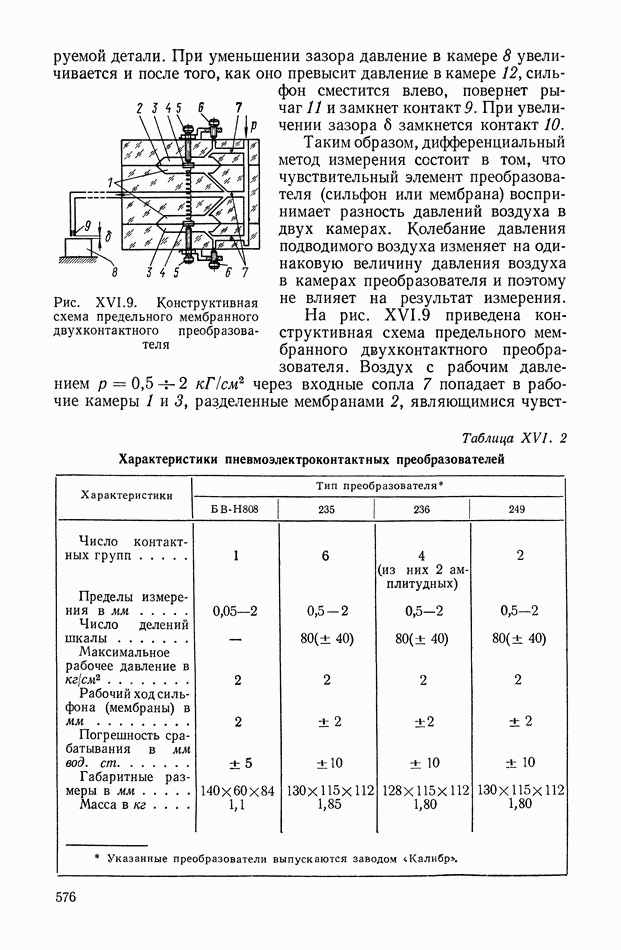
- Пневмоэлектроконтактные преобразователи линейных величин.
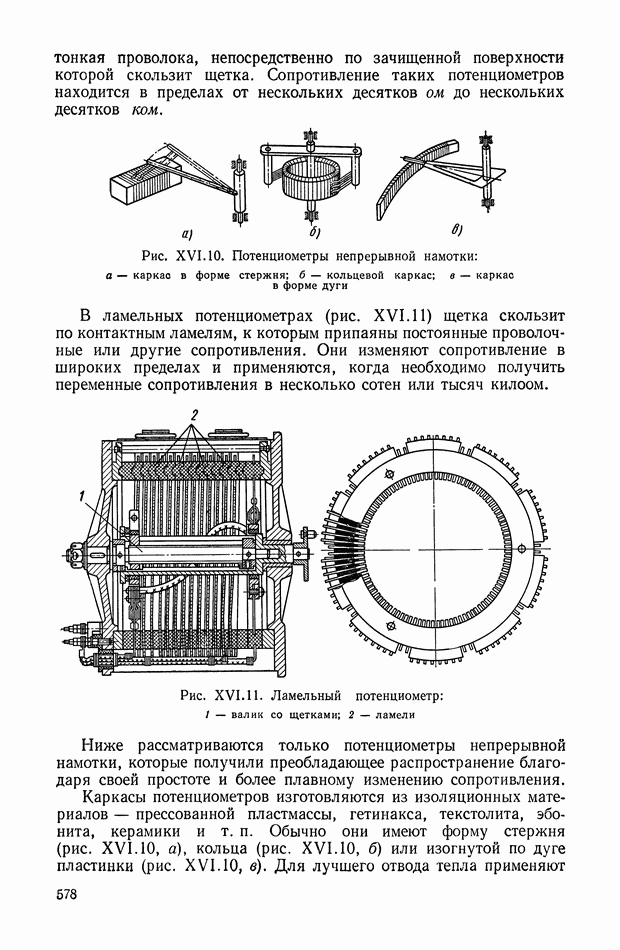
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
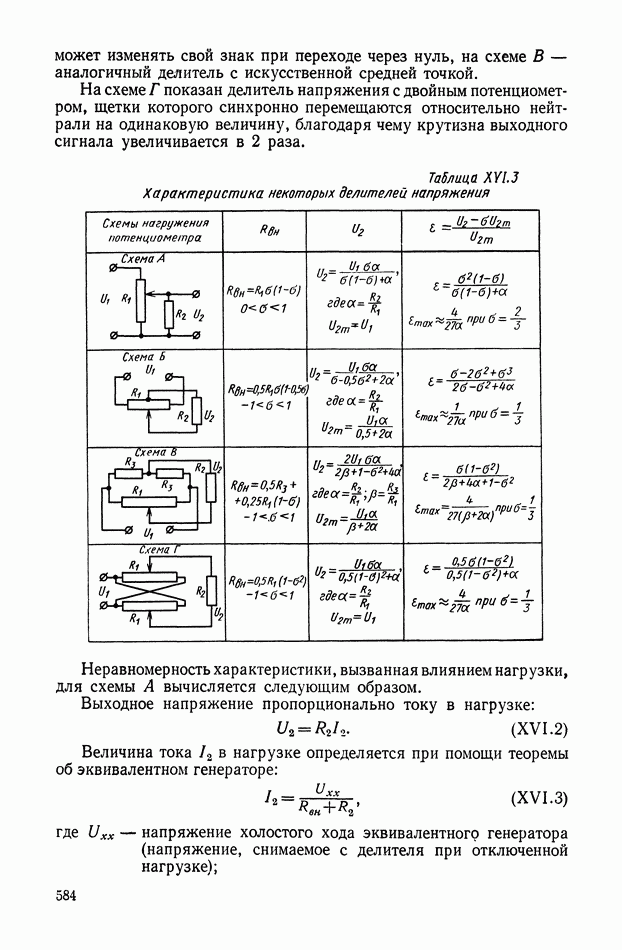
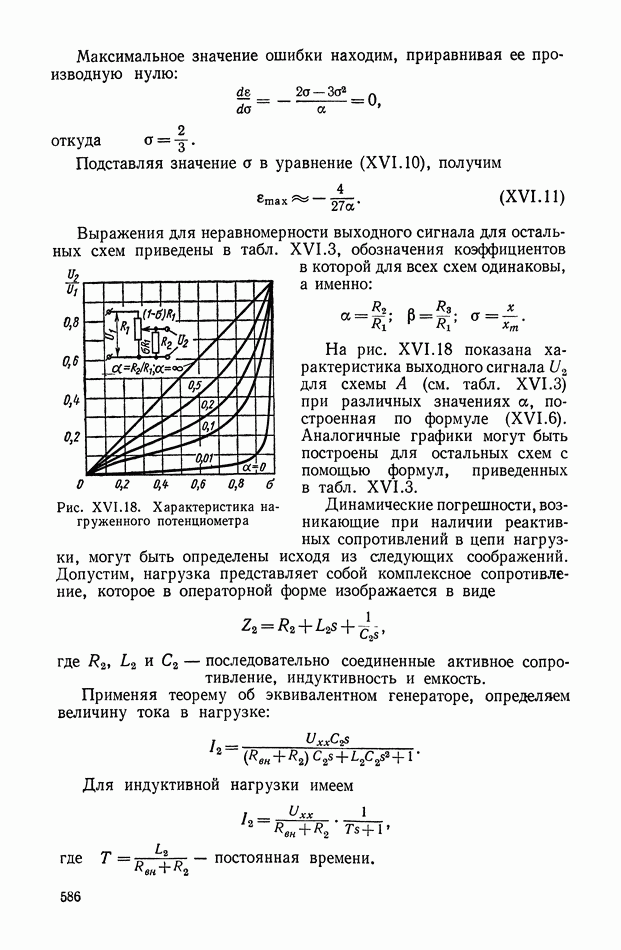
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
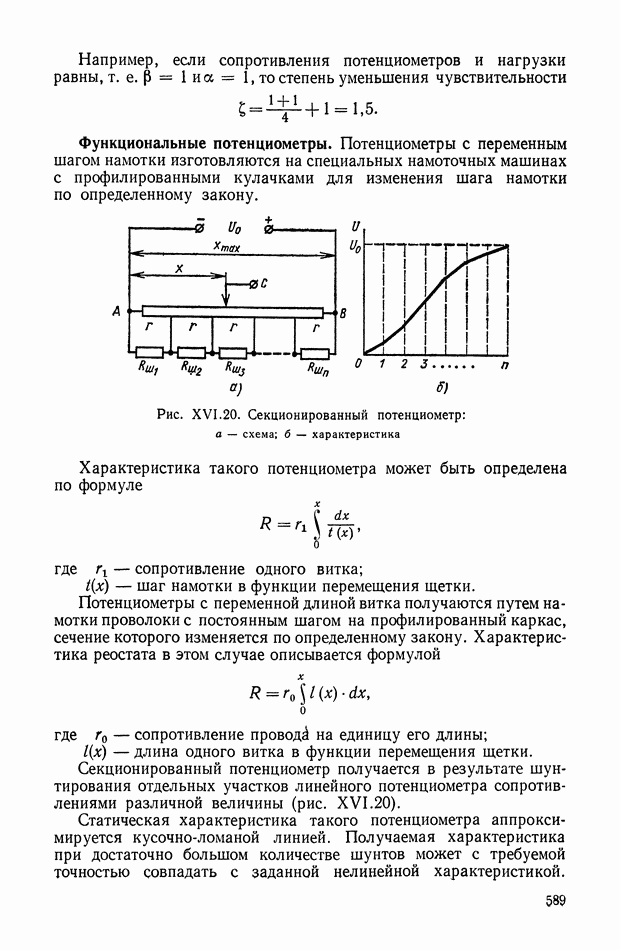
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
- Работа сельсинов в трансформаторном режиме.
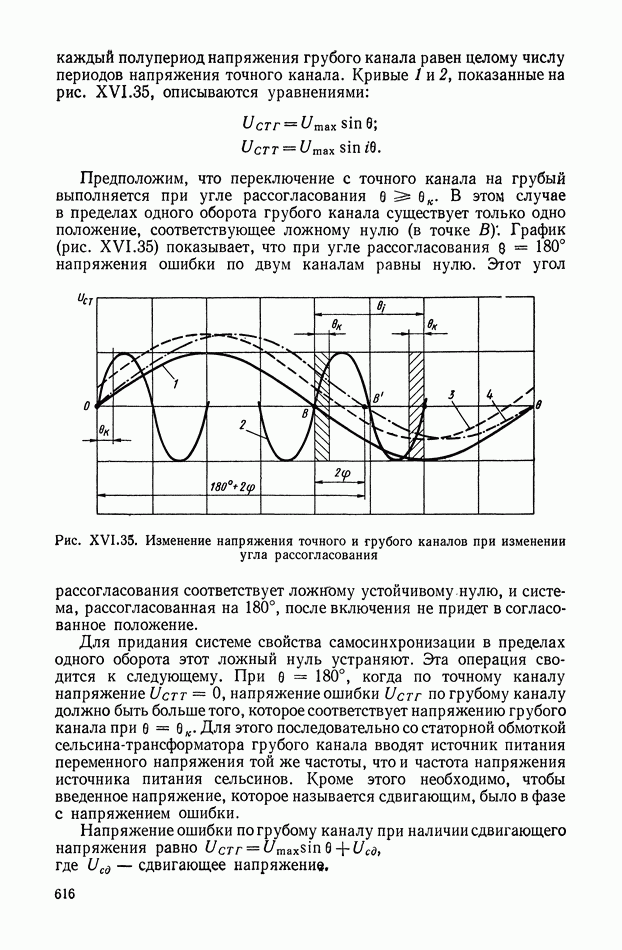
- Устранение ложного нуля в двухскоростной системе.
- Схемы синхронизаторов.
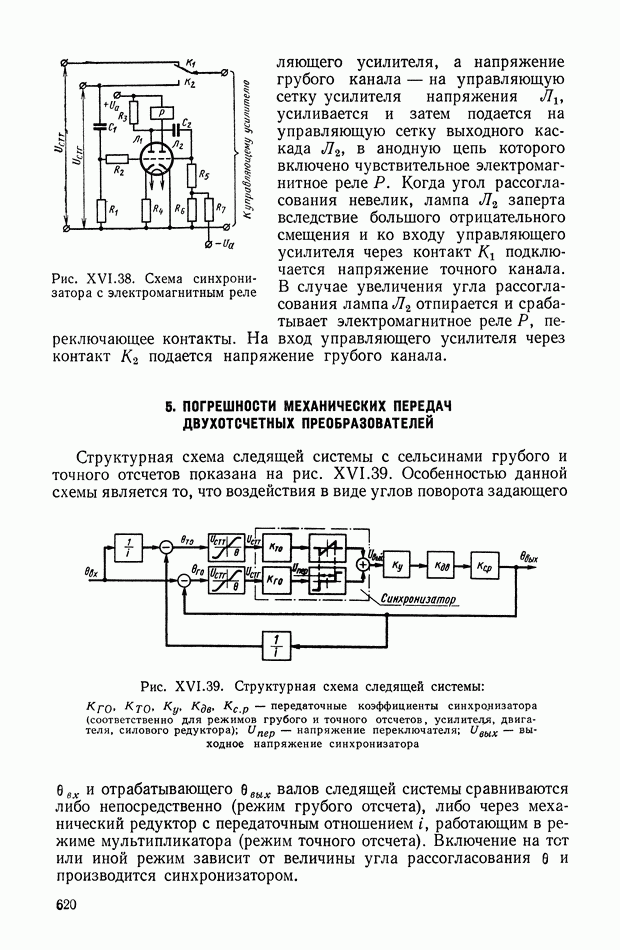
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
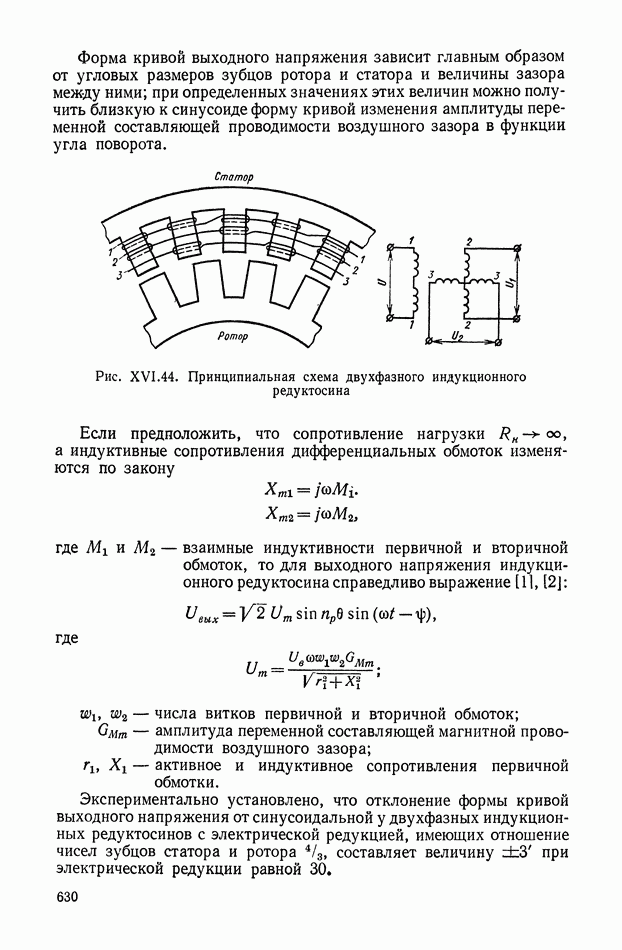
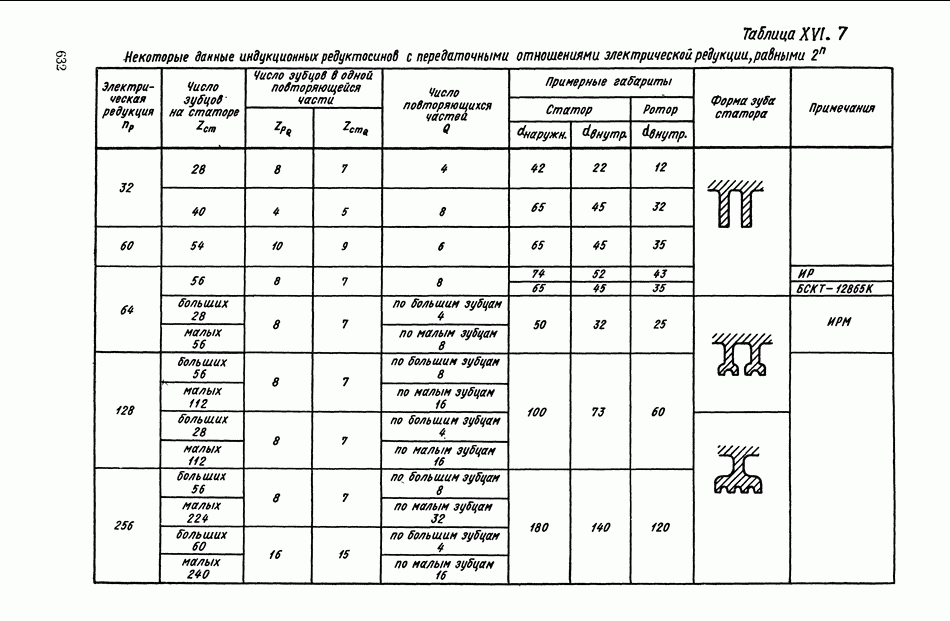
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
- Индукционные редуктосины.
- Индуктосины.
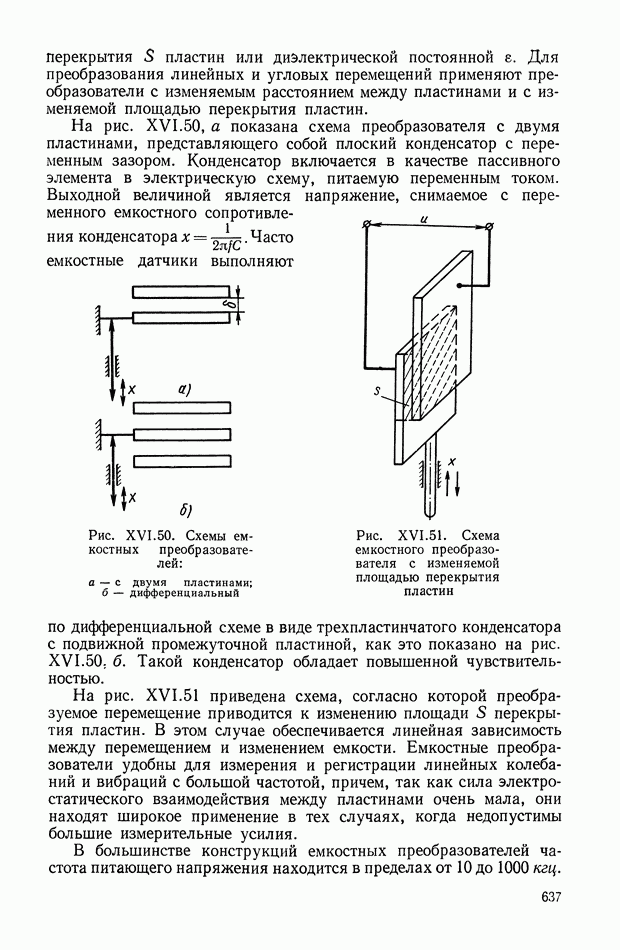
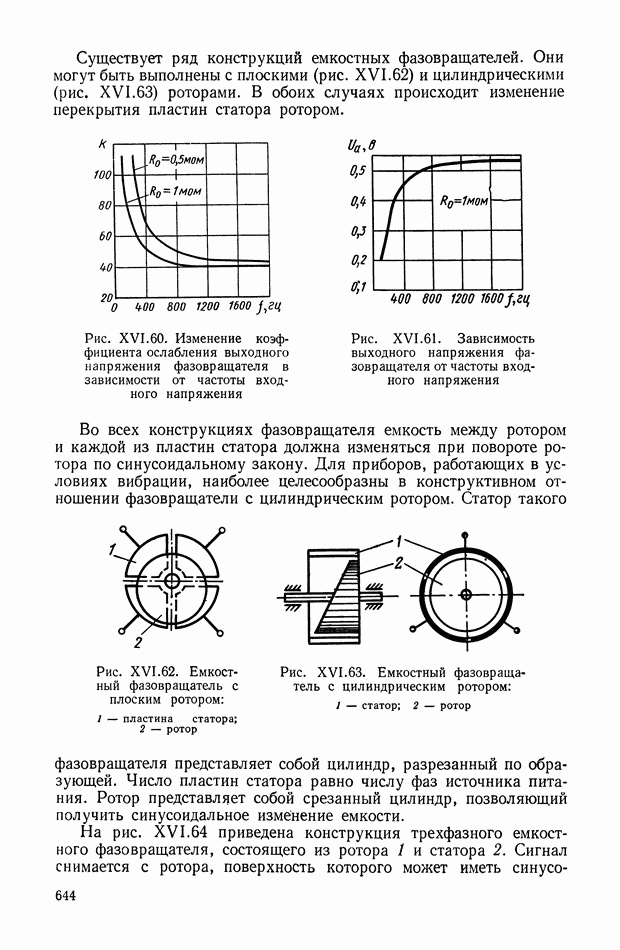
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
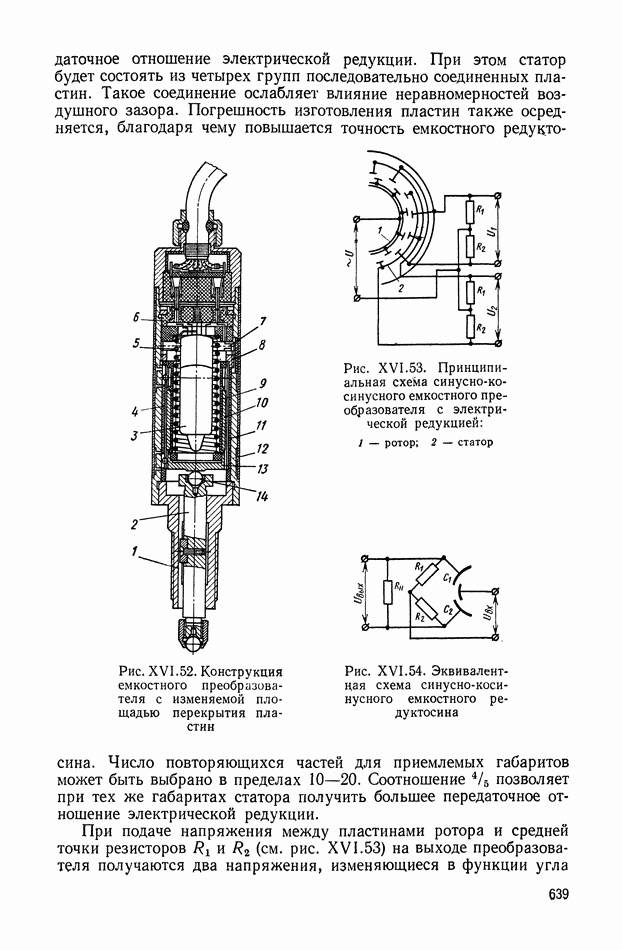
- Емкостный редуктосин.
- Емкостный фазовращатель.
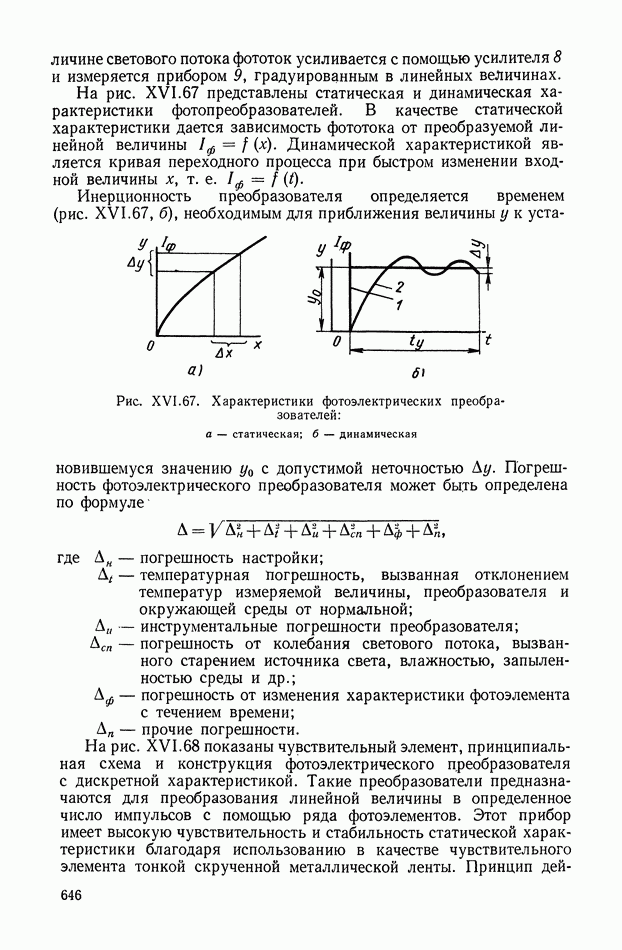
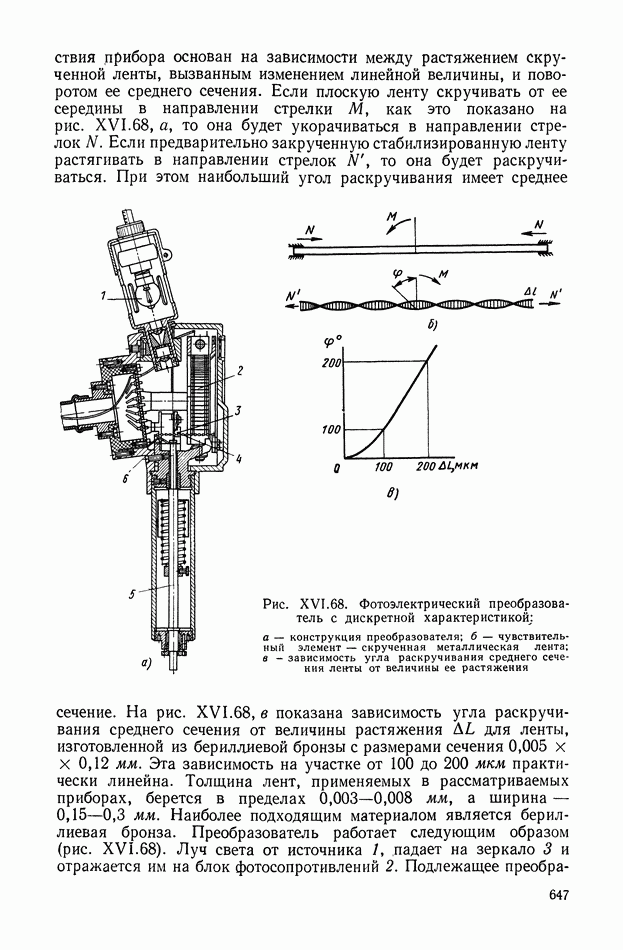
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
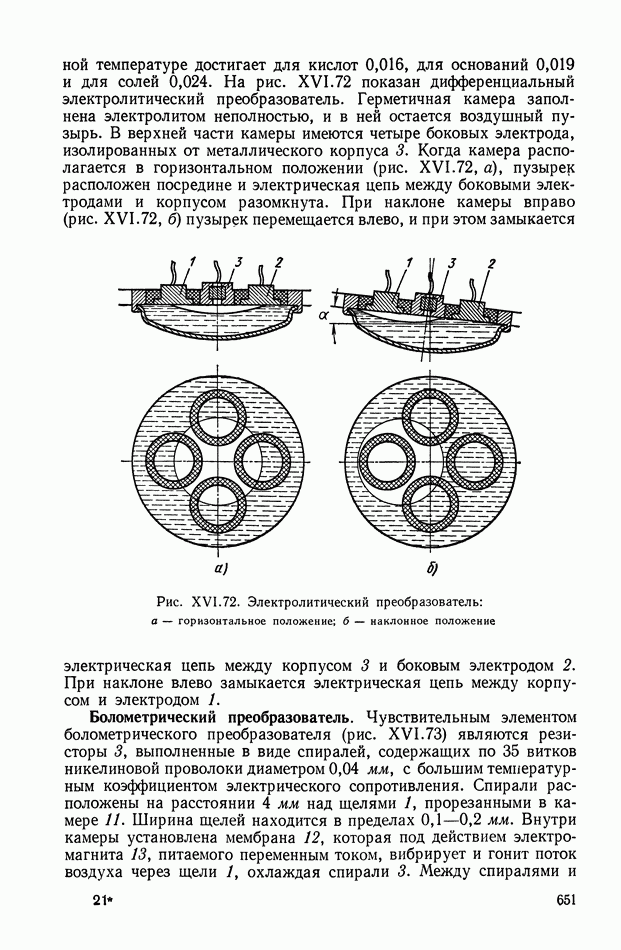
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ