| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
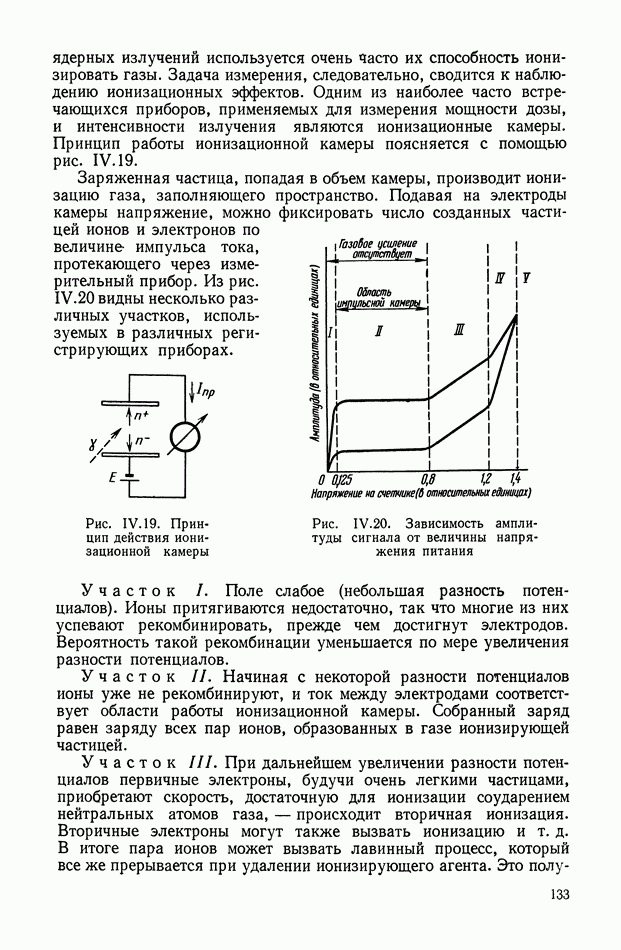
Гофрированные мембраны.
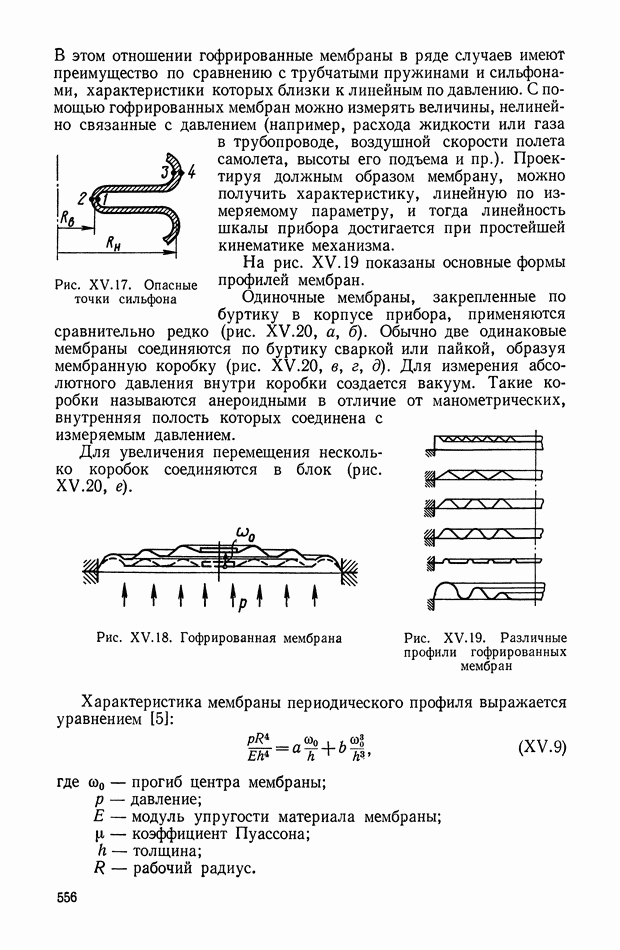
Мембрана представляет собой Гибкую круглую пластинку, способную получать значительные упругие прогибы  под действием давления
под действием давления  (рис. X.V.18).
(рис. X.V.18).
Гофрированные мембраны применяются чаще плоских, так как они могут надежно работать при значительно больших прогибах. В зависимости от формы профиля характеристика мембраны может быть линейной, затухающей или возрастающей по давлению.

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
В этом отношении гофрированные мембраны в ряде случаев имеют преимущество по сравнению с трубчатыми пружинами и сильфонами, характеристики которых близки к линейным по давлению. С помощью гофрированных мембран можно измерять величины, нелинейно связанные с давлением (например, расхода жидкости или газа в трубопроводе, воздушной скорости полета самолета, высоты его подъема и пр.). Проектируя должным образом мембрану, можно получить характеристику, линейную по измеряемому параметру, и тогда линейность шкалы прибора достигается при простейшей кинематике механизма.
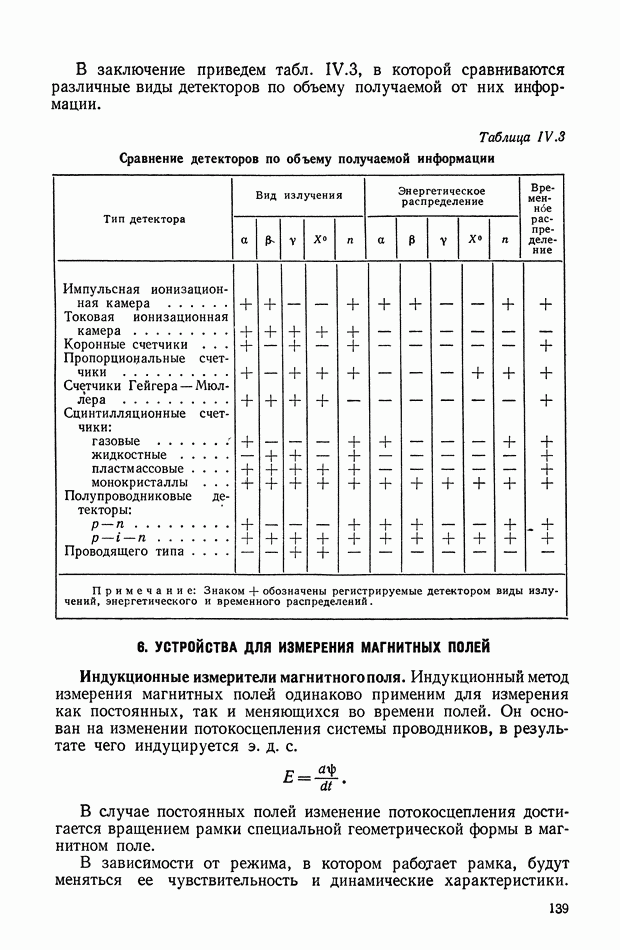
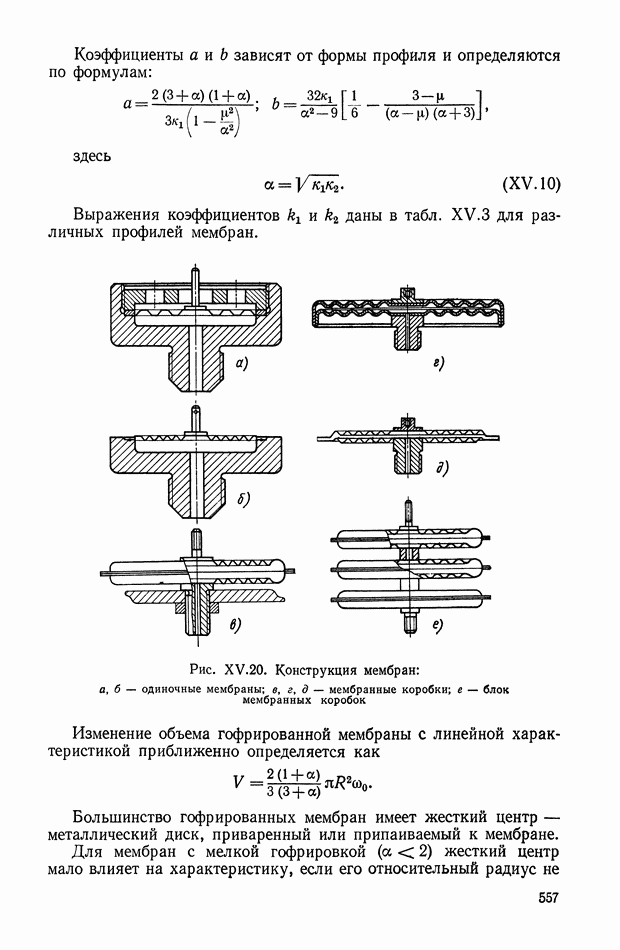
На рис. XV. 19 показаны основные формы профилей мембран.
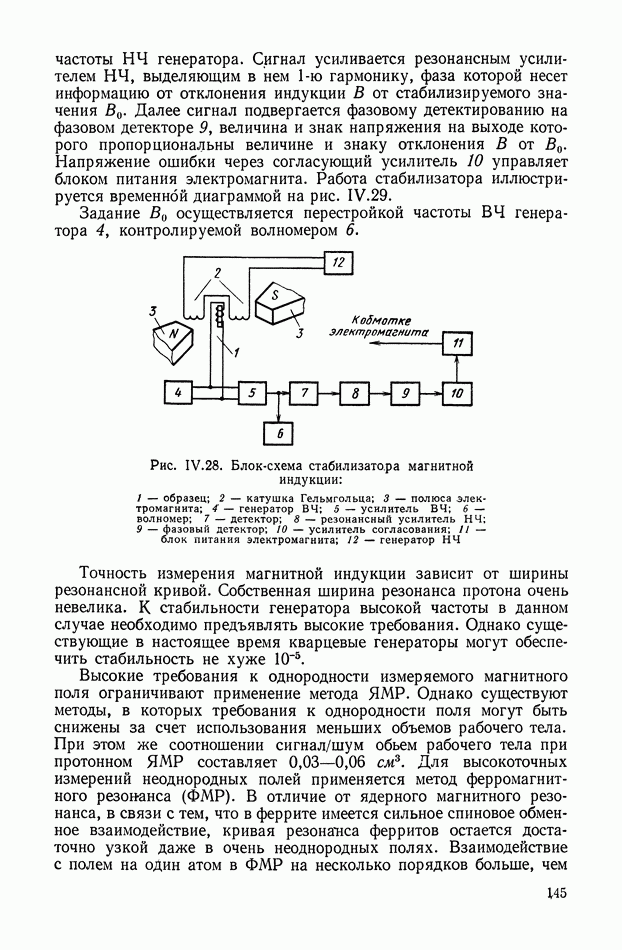
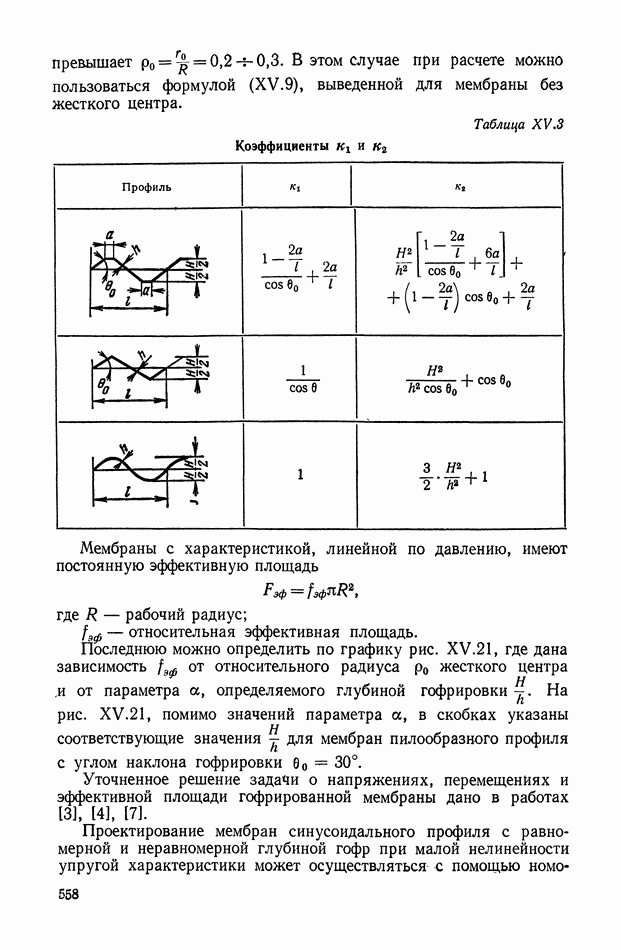
Одиночные мембраны, закрепленные по буртику в корпусе прибора, применяются сравнительно редко (рис. XV.20, а, б). Обычно две одинаковые мембраны соединяются по буртику сваркой или пайкой, образуя мембранную коробку (рис. XV.20, в, г, д). Для измерения абсолютного давления внутри коробки создается вакуум. Такие коробки называются анероидными в отличие от манометрических, внутренняя полость которых соединена с измеряемым давлением.
Для увеличения перемещения несколько коробок соединяются в блок (рис. XV.20, в).

Рис. XV. 17. Опасные точки сильфона

Рис. XV. 18. Гофрированная мембрана

Рис. XV. 19. Различные профили гофрированных мембран
Характеристика мембраны периодического профиля выражается уравнением [5]:

где  — прогиб центра мембраны;
— прогиб центра мембраны;
 — давление;
— давление;
Е — модуль упругости материала мембраны;
 — коэффициент Пуассона;
— коэффициент Пуассона;
 — толщина;
— толщина;
R — рабочий радиус.
Коэффициенты  зависят от формы профиля и определяются по формулам:
зависят от формы профиля и определяются по формулам:

здесь

Выражения коэффициентов и  даны в табл. XV.3 для различных профилей мембран.
даны в табл. XV.3 для различных профилей мембран.

Рис. XV.20. Конструкция мембран: а, б — одиночные мембраны; в, г, д — мембранные коробки; е — блок мембранных коробок
Изменение объема гофрированной мембраны с линейной характеристикой приближенно определяется как

Большинство гофрированных мембран имеет жесткий центр — металлический диск, приваренный или припаиваемый к мембране.
Для мембран с мелкой гофрировкой  жесткий центр мало влияет на характеристику, если его относительный радиус не
жесткий центр мало влияет на характеристику, если его относительный радиус не
превышает  . В этом случае при расчете можно пользоваться формулой (XV.9), выведенной для мембраны без жесткого центра.
. В этом случае при расчете можно пользоваться формулой (XV.9), выведенной для мембраны без жесткого центра.
Таблица XV.3 (см. скан) Коэффициенты 
Мембраны с характеристикой, линейной по давлению, имеют постоянную эффективную площадь

где R — рабочий радиус;
 — относительная эффективная площадь.
— относительная эффективная площадь.
Последнюю можно определить по графику рис. XV.21, где дана зависимость  от относительного радиуса
от относительного радиуса  жесткого центра и от параметра а, определяемого глубиной гофрировки На рис. XV.21, помимо значений параметра а, в скобках указаны соответствующие значения
жесткого центра и от параметра а, определяемого глубиной гофрировки На рис. XV.21, помимо значений параметра а, в скобках указаны соответствующие значения  для мембран пилообразного профиля с углом наклона гофрировки
для мембран пилообразного профиля с углом наклона гофрировки  .
.
Уточненное решение задачи о напряжениях, перемещениях и эффективной площади гофрированной мембраны дано в работах 13], [4], [7].
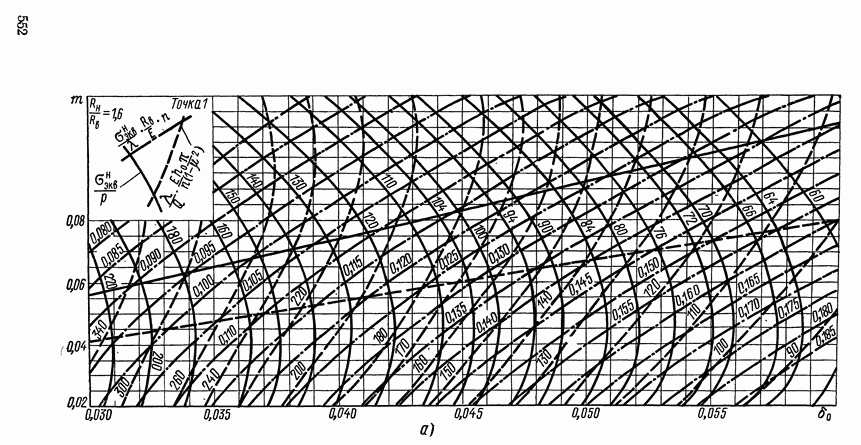
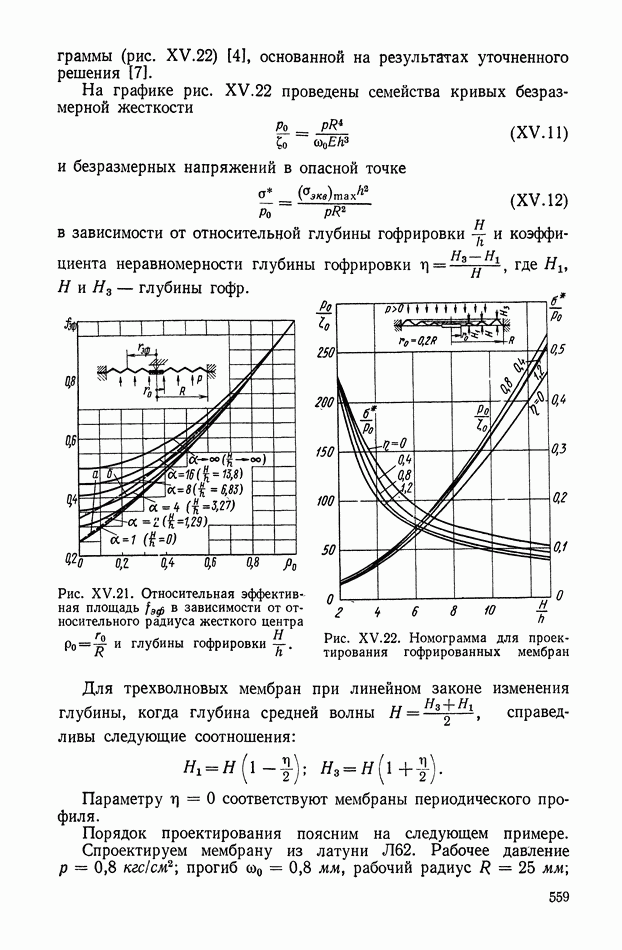
Проектирование мембран синусоидального профиля с равномерной и неравномерной глубиной гофр при малой нелинейности упругой характеристики может осуществляться с помощью
номограммы (рис. XV.22) [4], основанной на результатах уточненного решения 17].
На графике рис. XV.22 проведены семейства кривых безразмерной жесткости

и безразмерных напряжений в опасной точке

в зависимости от относительной глубины гофрировки и коэффициента неравномерности глубины гофрировки  , где
, где  — глубины гофр.
— глубины гофр.

Рис. XV.21. Относительная эффективная площадь  в зависимости от относительного радиуса жесткого центра
в зависимости от относительного радиуса жесткого центра  и глубины гофрировки
и глубины гофрировки

Рис. XV.22. Номограмма для проектирования гофрированных мембран
Для трехволновых мембран при линейном законе изменения глубины, когда глубина средней волны  справедливы следующие соотношения:
справедливы следующие соотношения:

Параметру  соответствуют мембраны периодического профиля.
соответствуют мембраны периодического профиля.
Порядок проектирования поясним на следующем примере. Спроектируем мембрану из латуни  Рабочее давление
Рабочее давление  прогиб
прогиб  , рабочий радиус
, рабочий радиус  мм;
мм;
модуль упругости  предел текучести
предел текучести  величина нелинейности у должна быть меньше
величина нелинейности у должна быть меньше  коэффициент запаса по текучести
коэффициент запаса по текучести 
Выберем мембрану неравномерной глубины гофрировки с коэффициентом  Зададимся рядом значений параметра глубины
Зададимся рядом значений параметра глубины  в по кривым рис. XV.22 находим соответствующие величины
в по кривым рис. XV.22 находим соответствующие величины 
Из формулы (XV. 11) находим толщину

для каждого значения 
Зная безразмерные напряжения  по формуле (XV. 12) вычисляем эквивалентные напряжения в опасной точке:
по формуле (XV. 12) вычисляем эквивалентные напряжения в опасной точке:

Результаты вычислений приведены в табл. XV.4.
Таблица XV.4 (см. скан)
Числовые данные к примеру расчета мембран
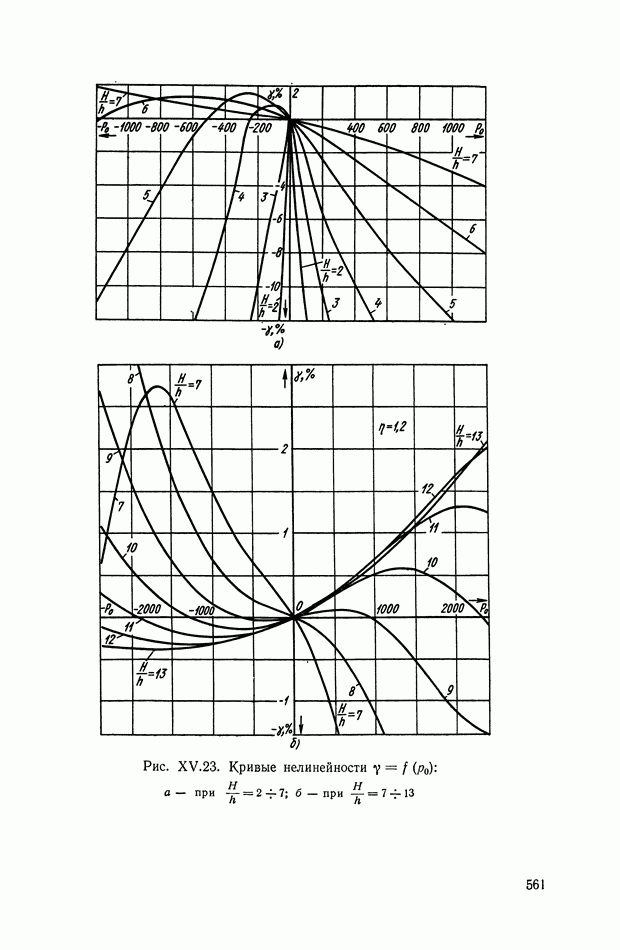
Нелинейность упругой характеристики можно оценить по рис. XV.23, где приведены кривые нелинейности для мембран неравномерного профиля при  в зависимости от безразмерного давления
в зависимости от безразмерного давления  График нелинейности для мембран периодического профиля приведен в работе [4]. Подсчитывая для спроектированного ряда мембран параметр
График нелинейности для мембран периодического профиля приведен в работе [4]. Подсчитывая для спроектированного ряда мембран параметр  находим по рис. XV.23 величину нелинейности у.
находим по рис. XV.23 величину нелинейности у.
Полученный ряд мембран удовлетворяет заданным требованиям по жесткости и габаритам. Наименьшие рабочие напряжения  возникают в мембране с относительной глубиной
возникают в мембране с относительной глубиной  ее нелинейность
ее нелинейность  также удовлетворяет заданным требованиям.
также удовлетворяет заданным требованиям.

(кликните для просмотра скана)
Коэффициент запаса

Реальный чувствительный элемент никогда не совпадает полностью с расчетной схемой, поэтому необходима экспериментальная проверка полученных результатов и соответствующая корректировка геометрии чувствительного элемента.

Рис. XV.24. Гибкая мембрана:  — внешний радиус;
— внешний радиус;  — радиус жесткого центра;
— радиус жесткого центра;  — прогиб
— прогиб
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
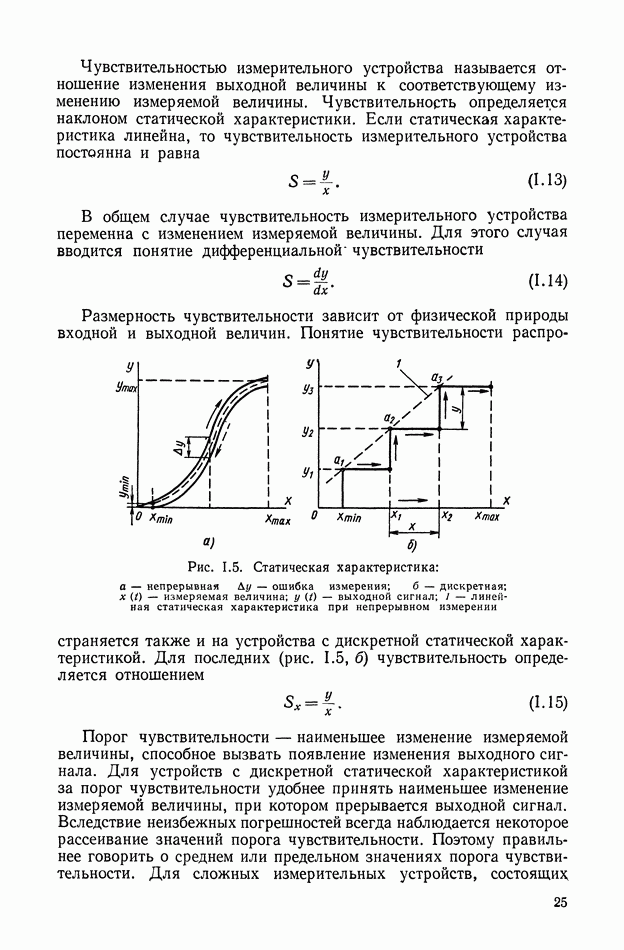
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
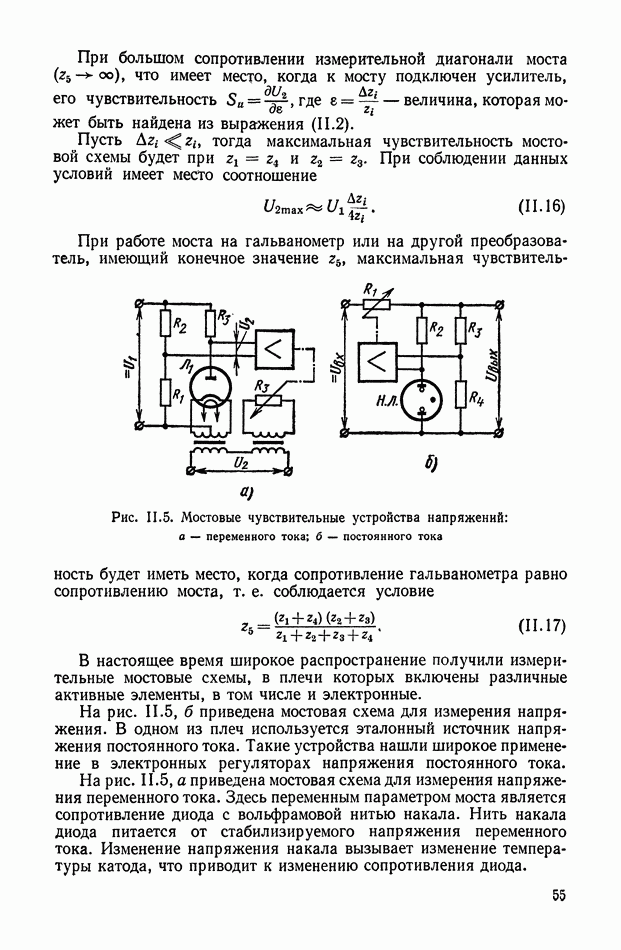
- 1. МОСТОВЫЕ СХЕМЫ
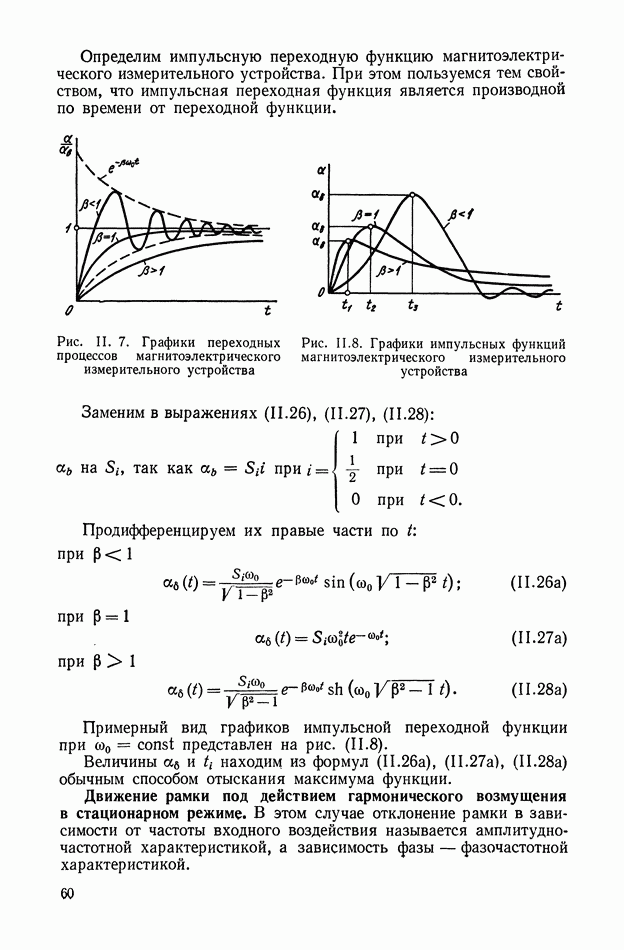
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
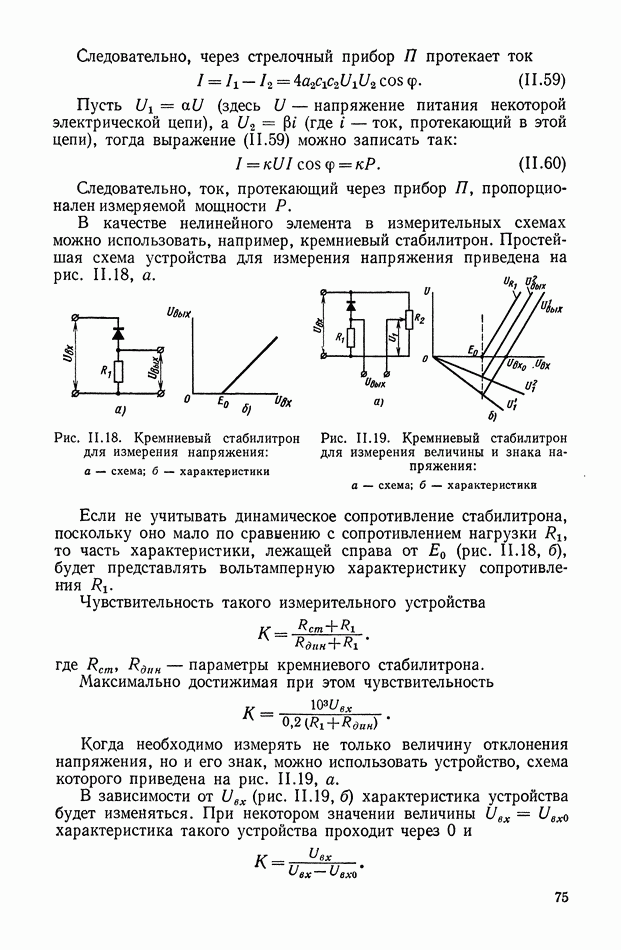
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
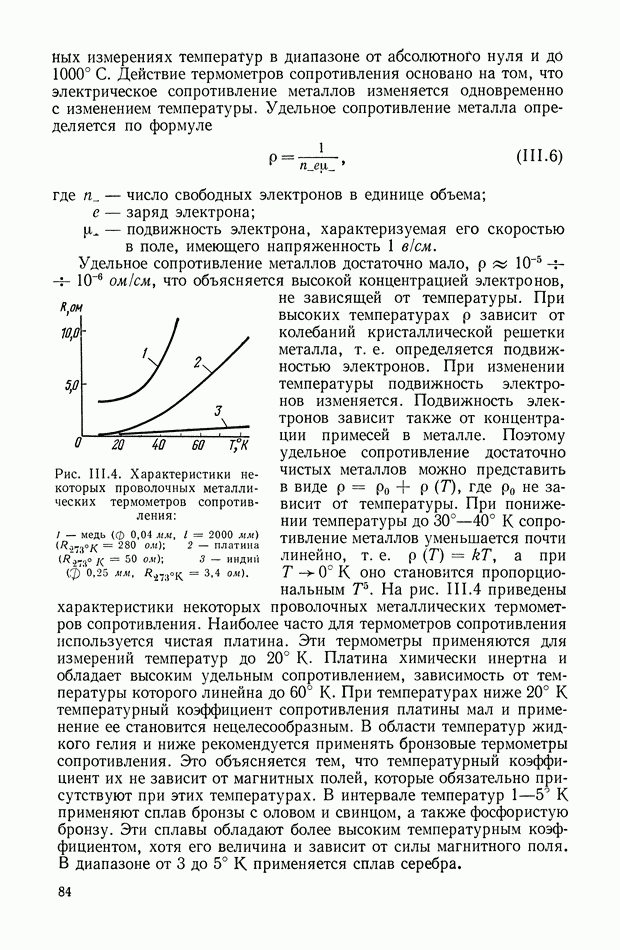
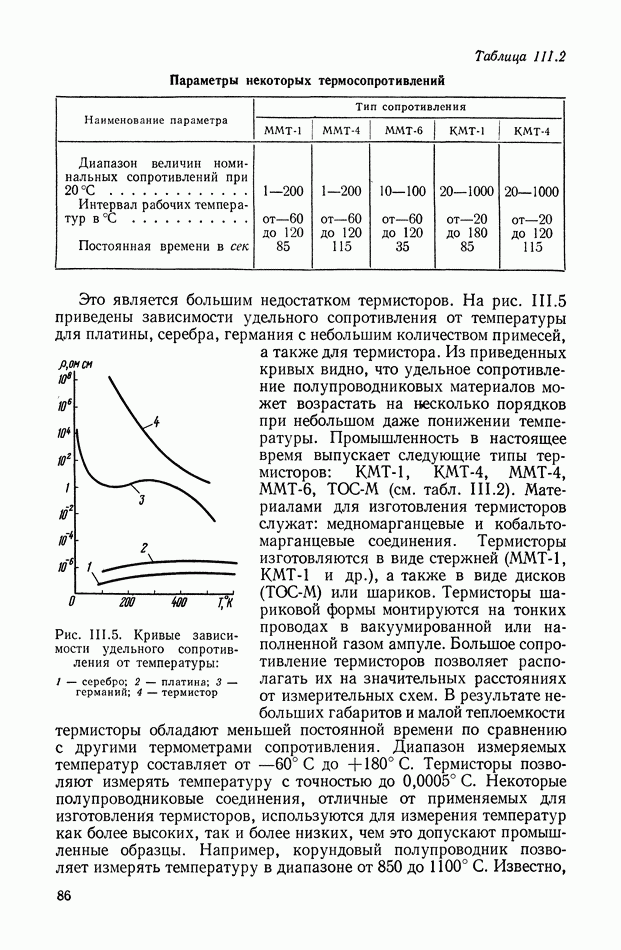
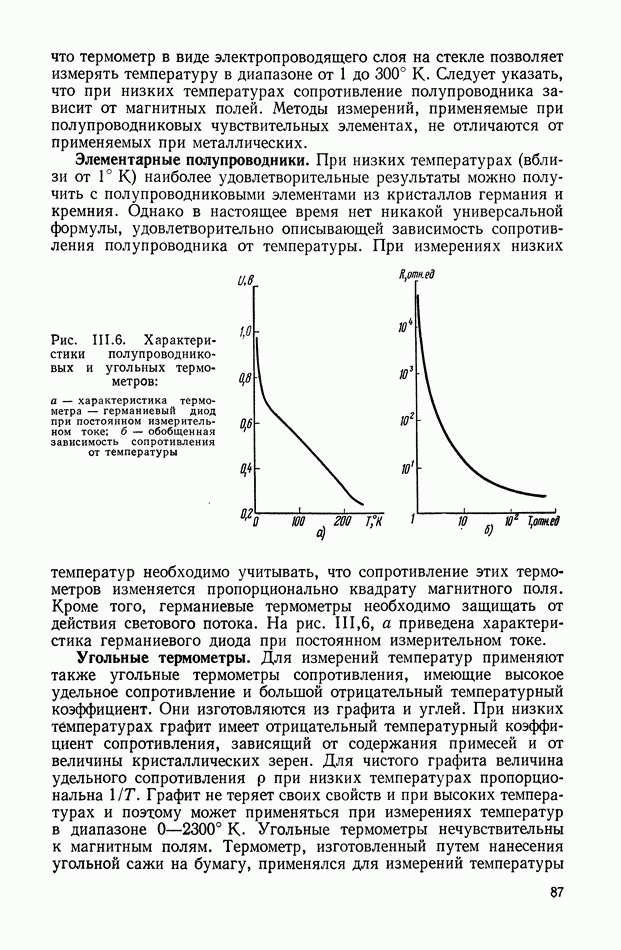
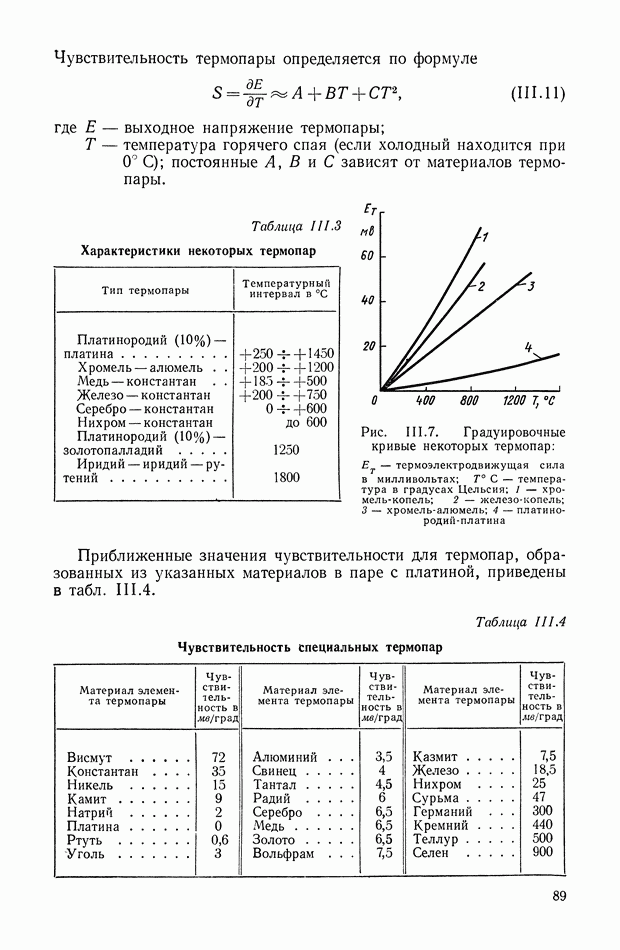
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
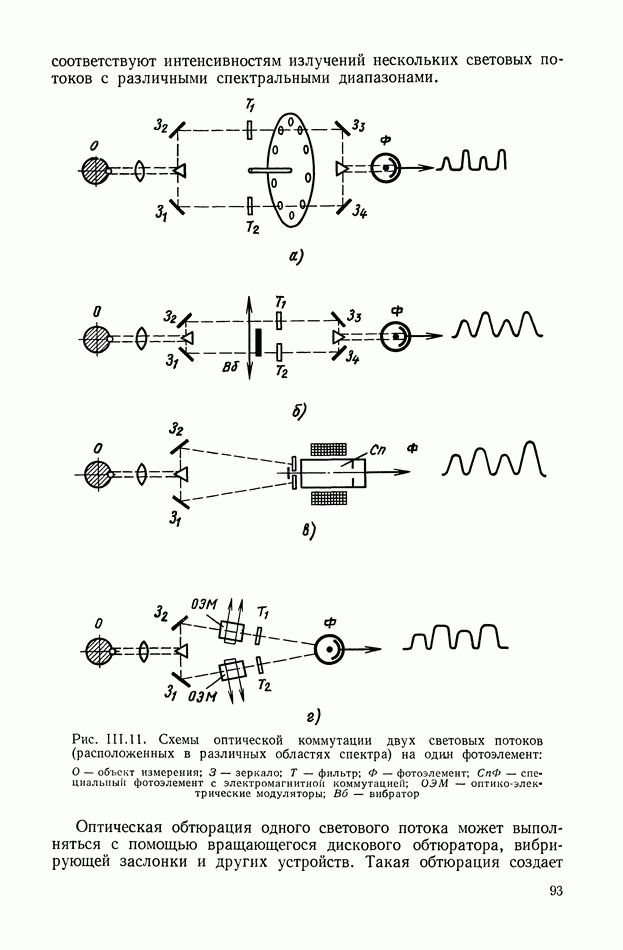
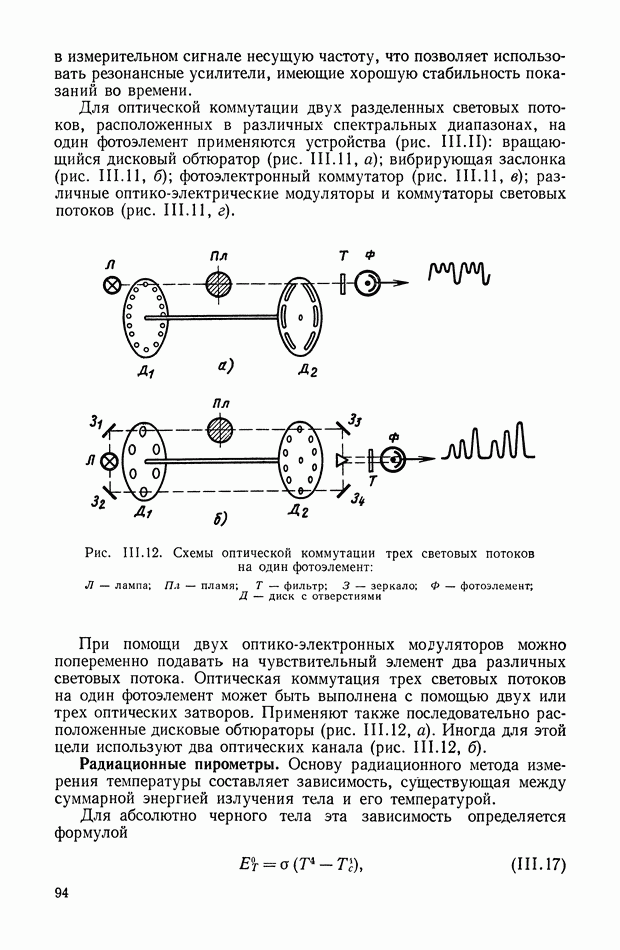
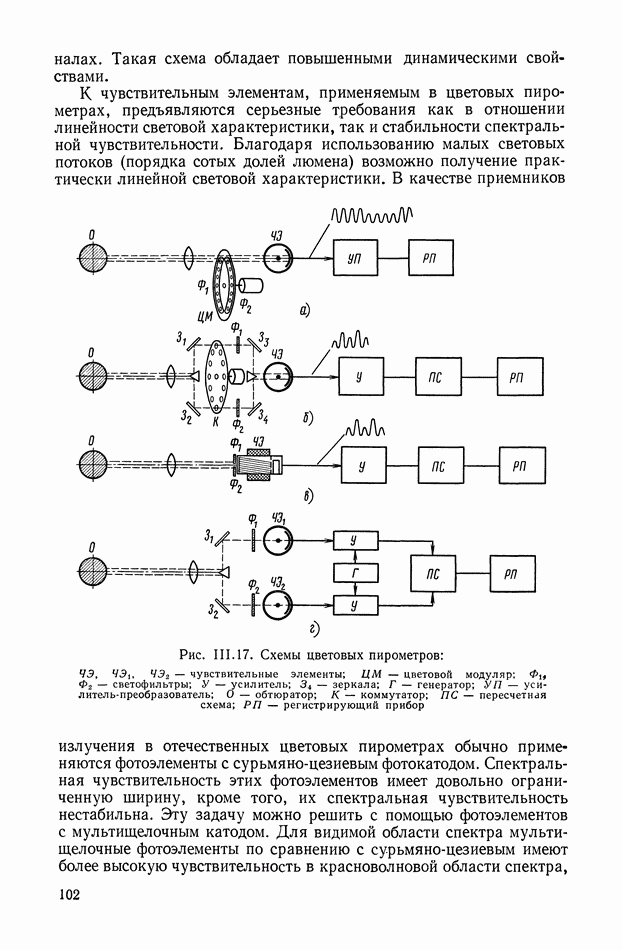
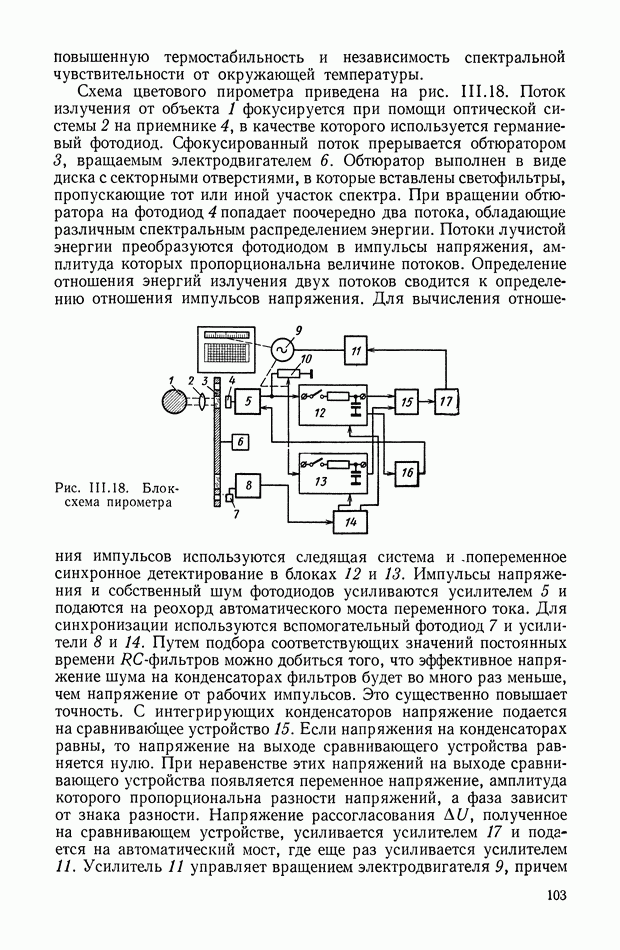
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
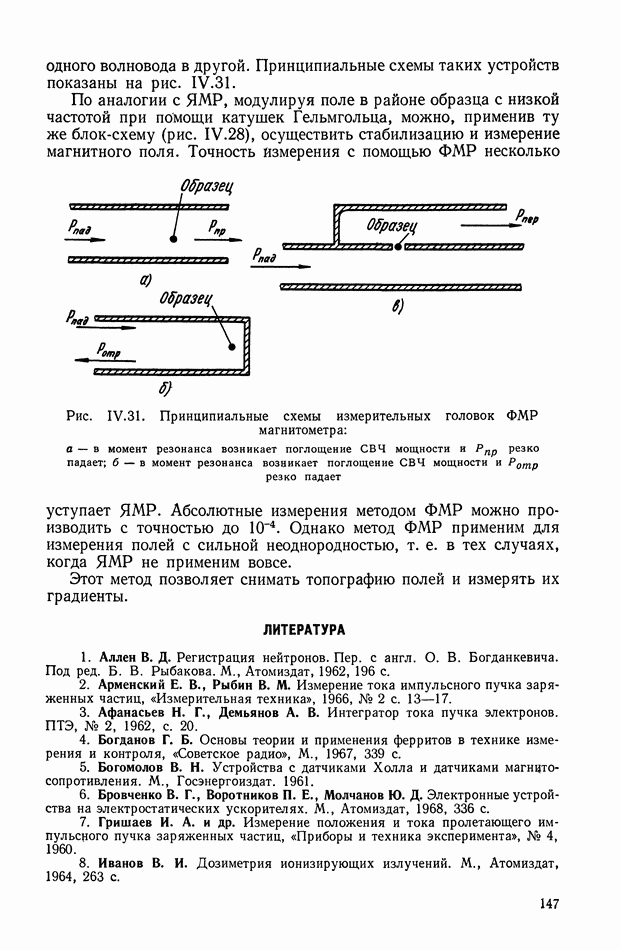
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
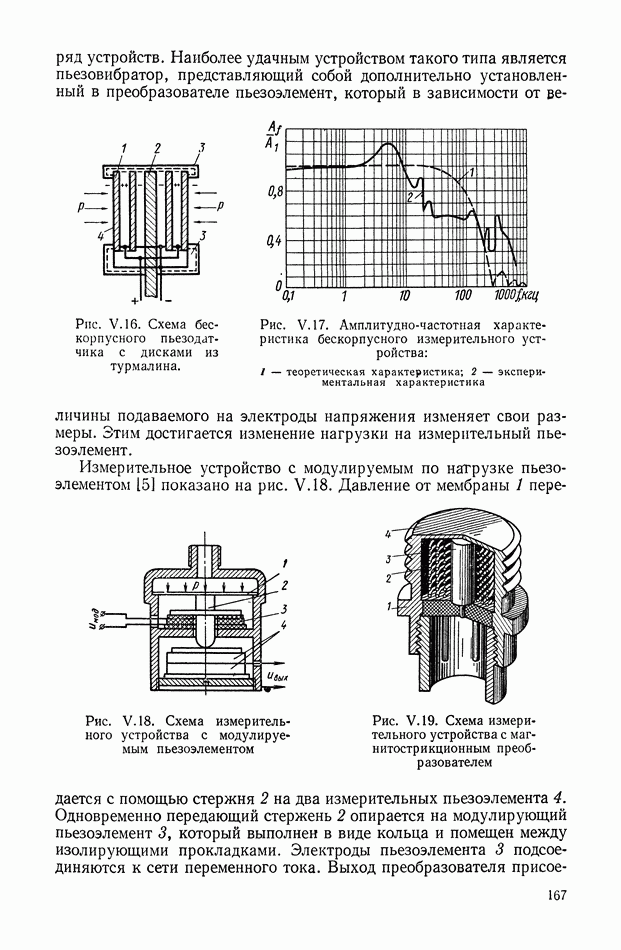
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
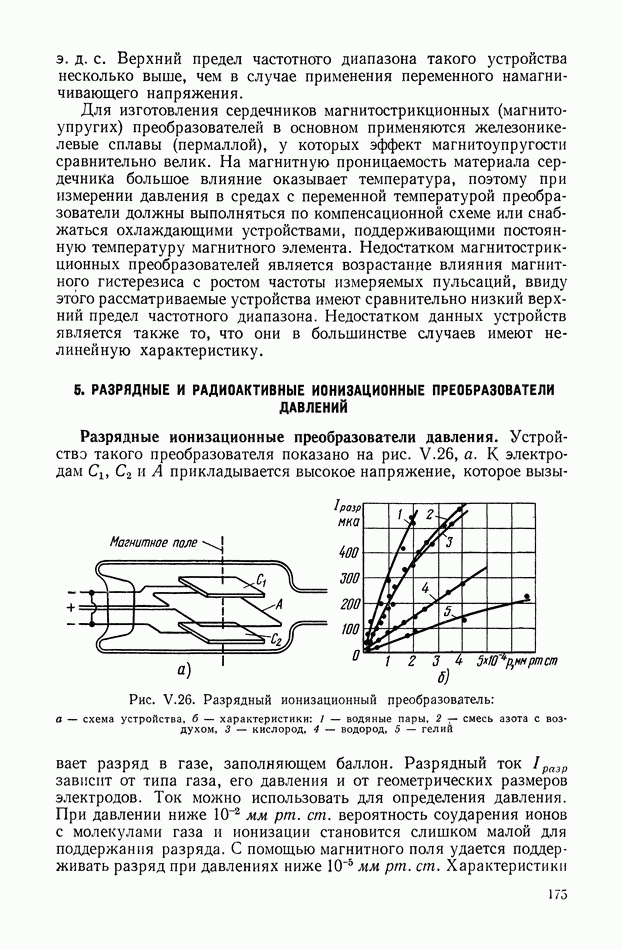
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
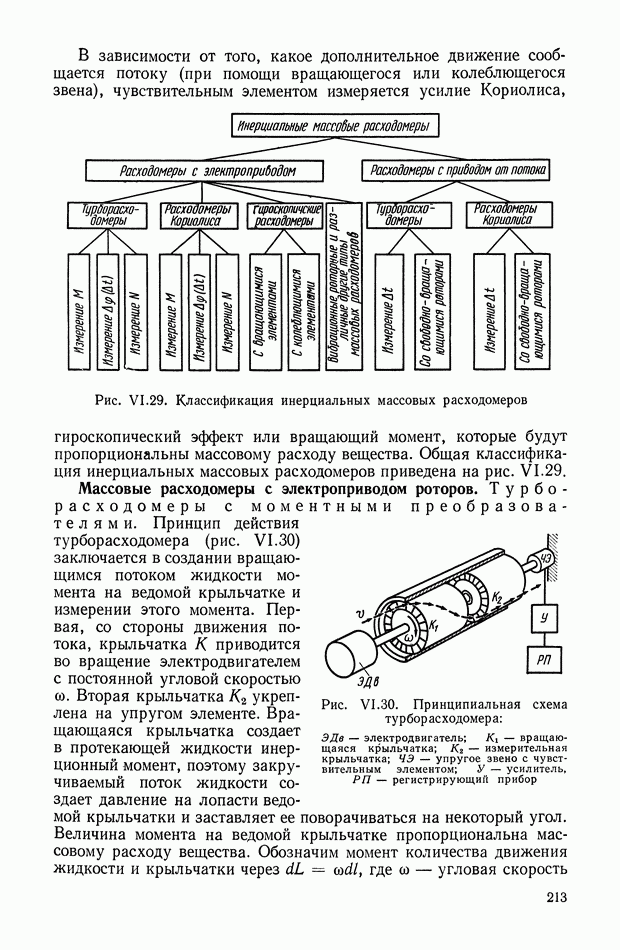
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
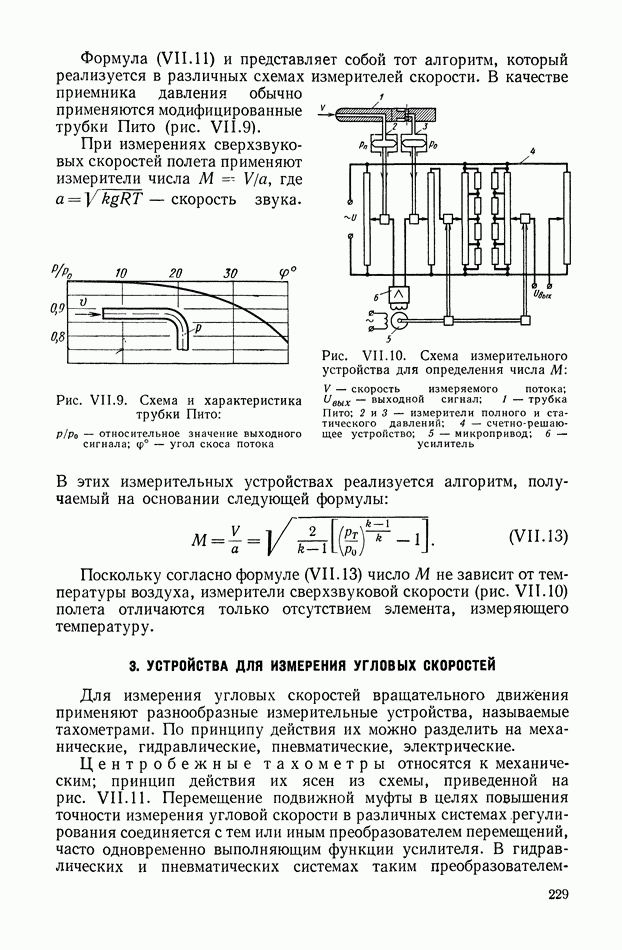
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
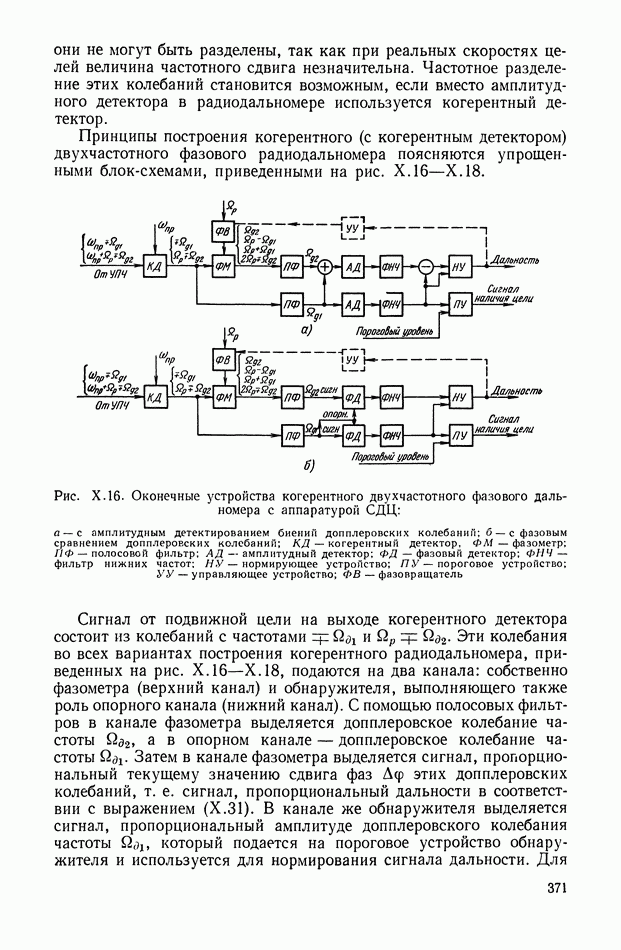
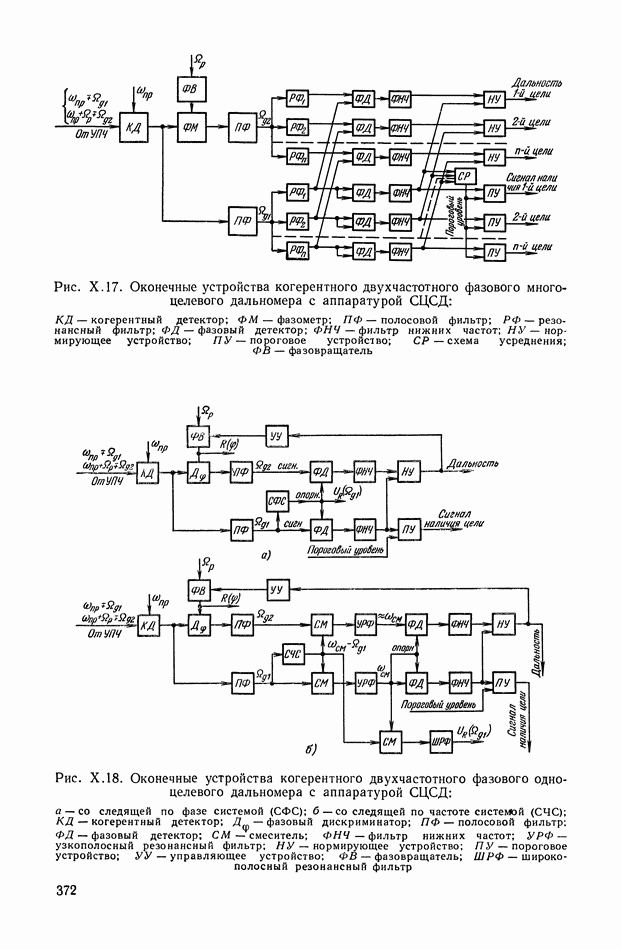
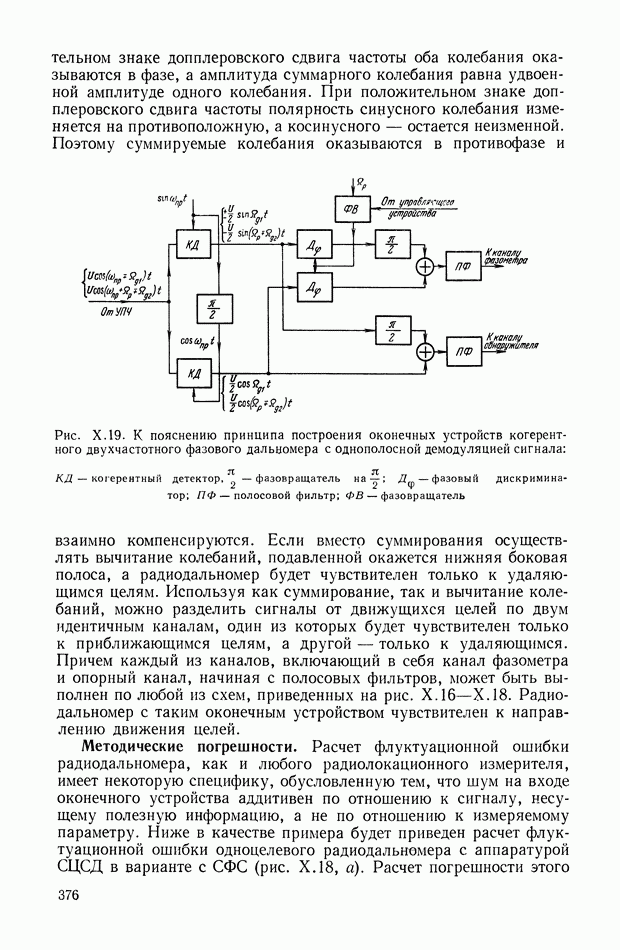
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
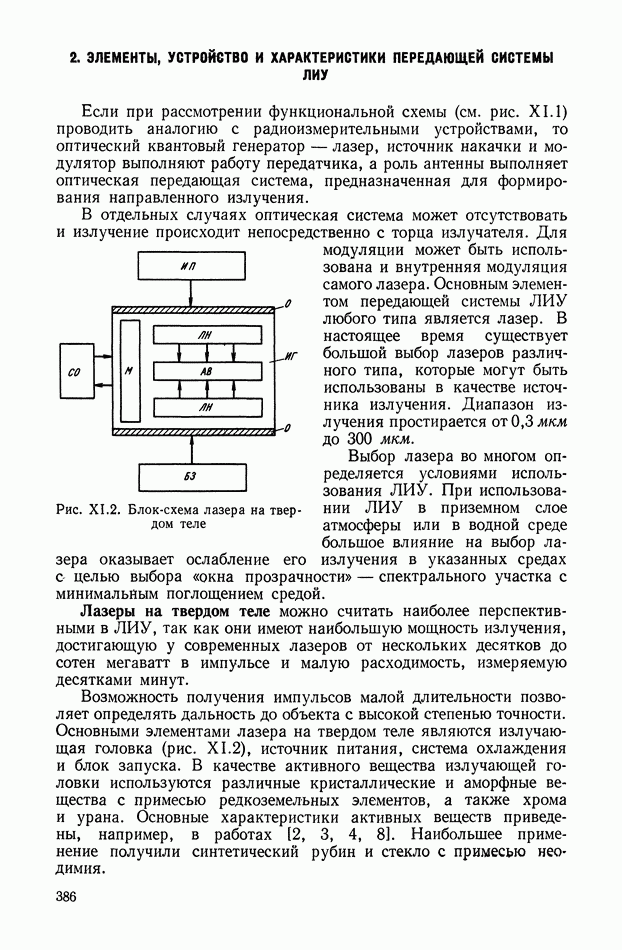
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
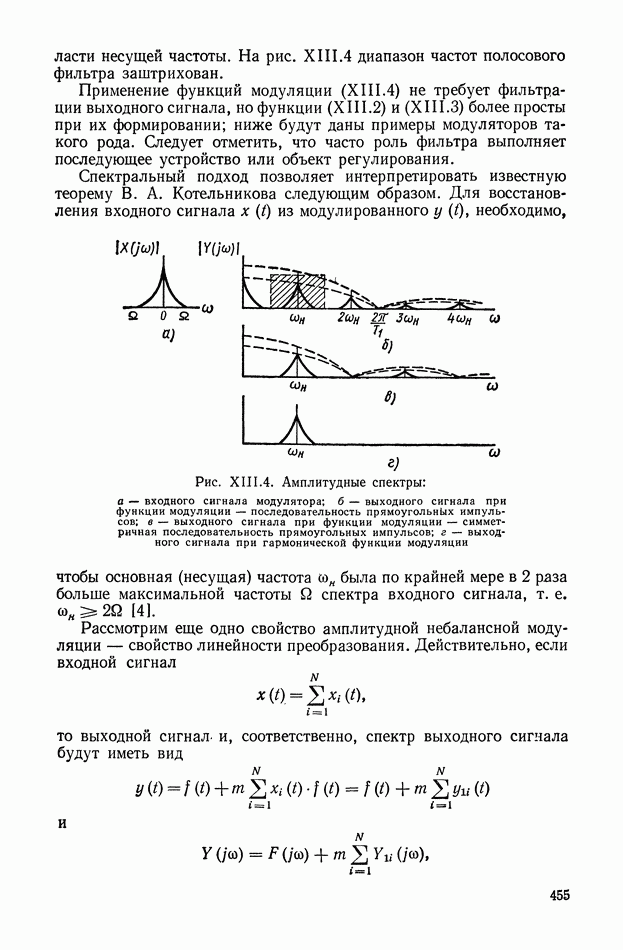
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
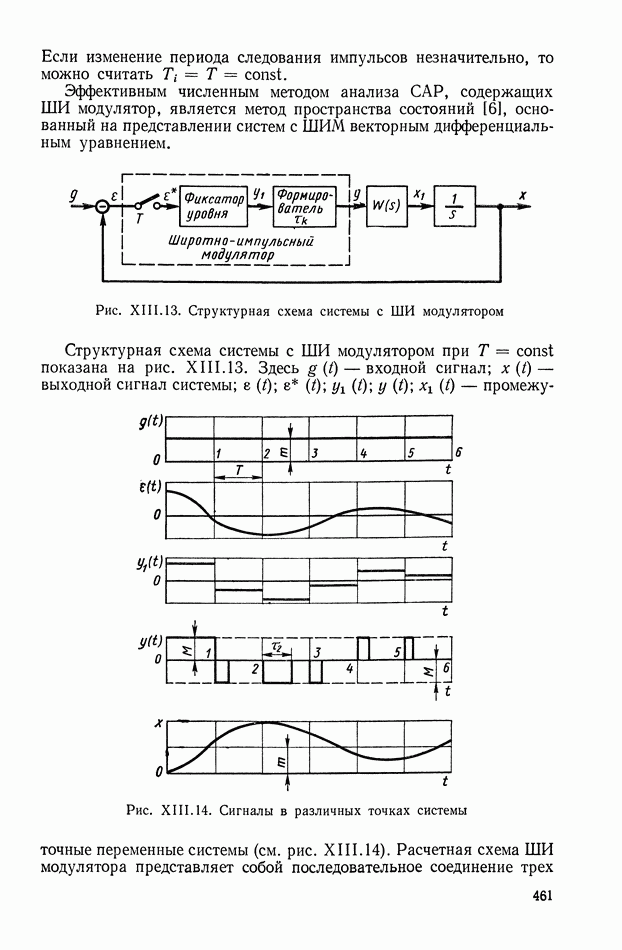
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 1. МОДУЛЯТОРЫ
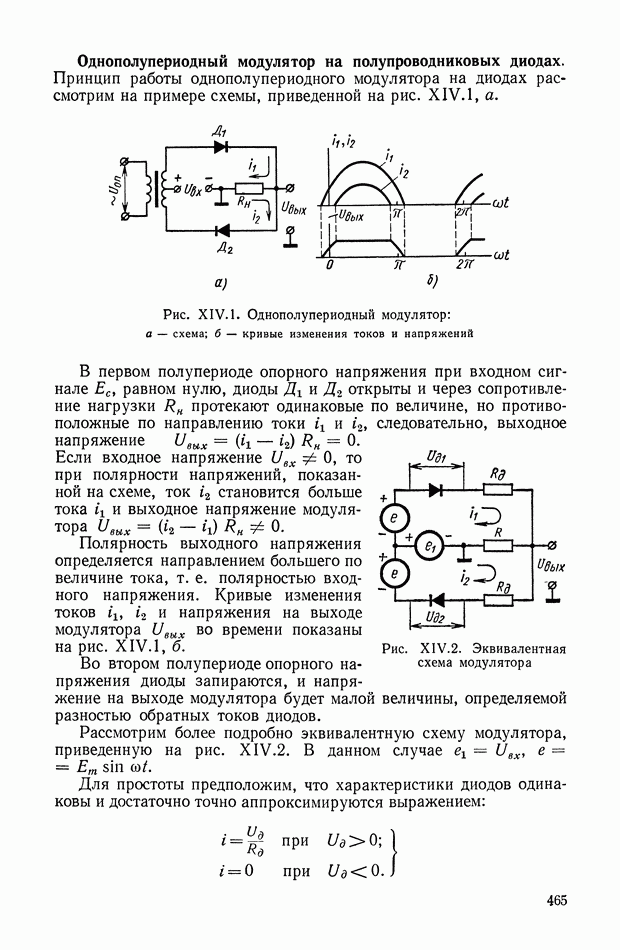
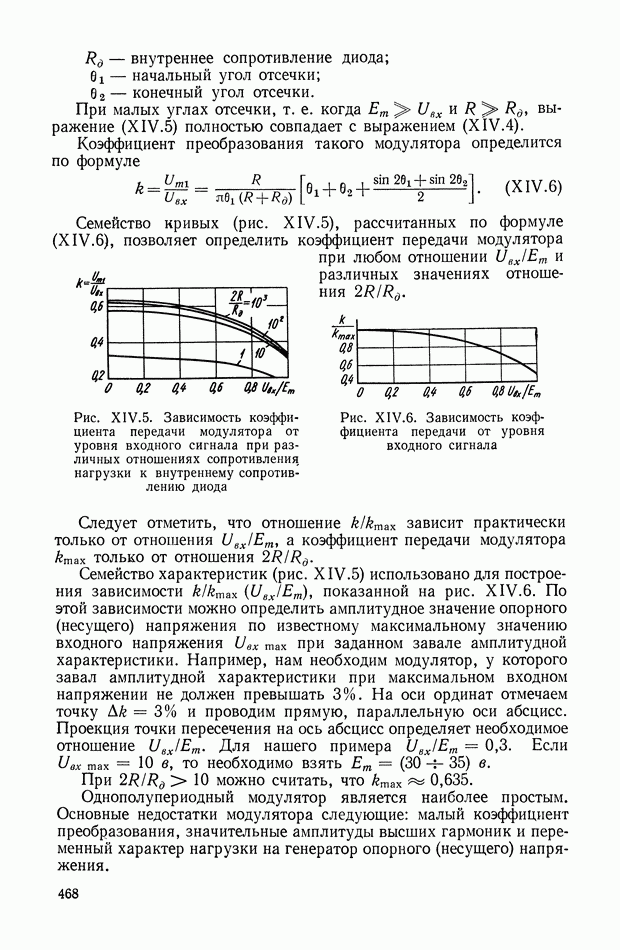
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
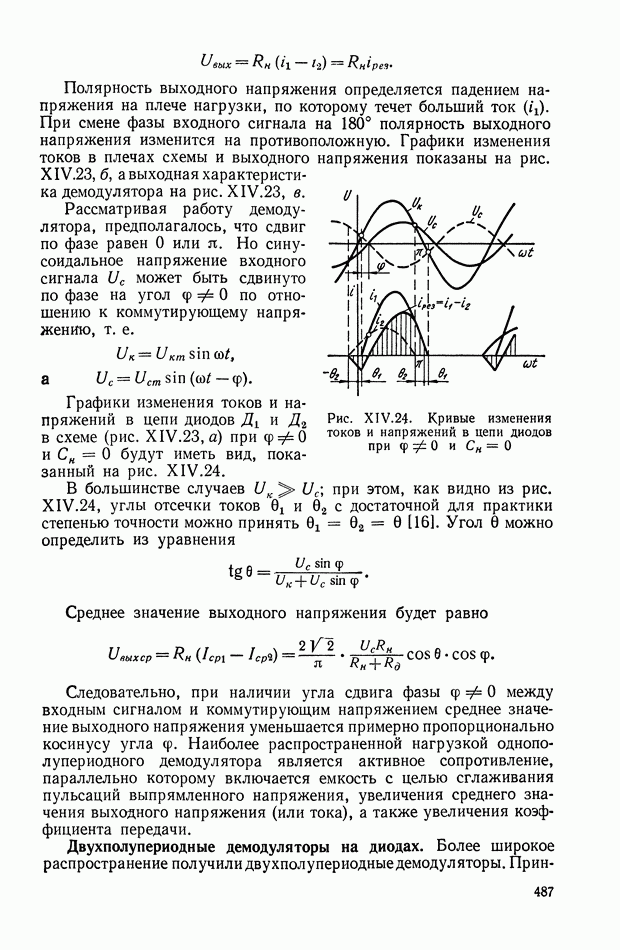
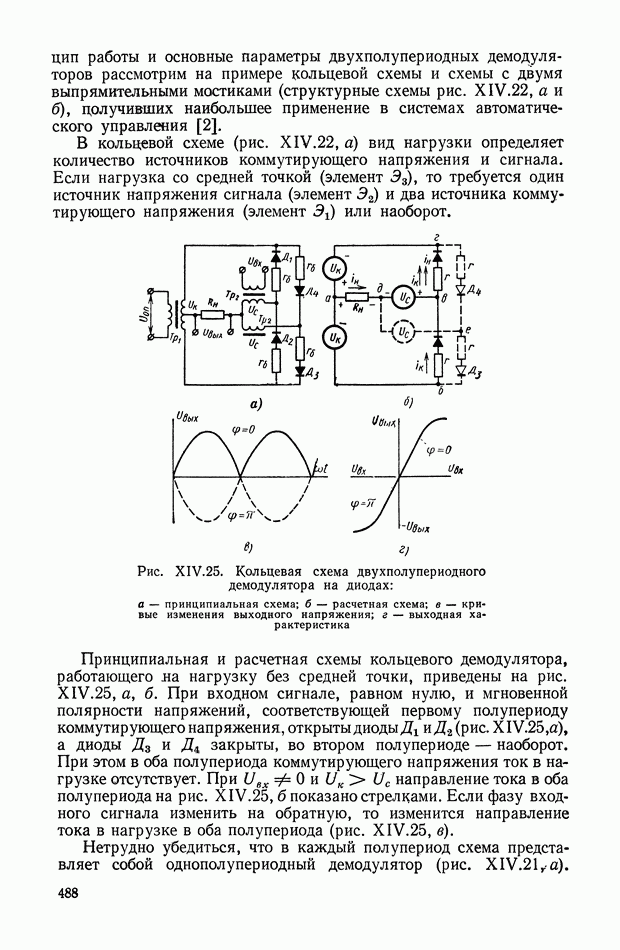
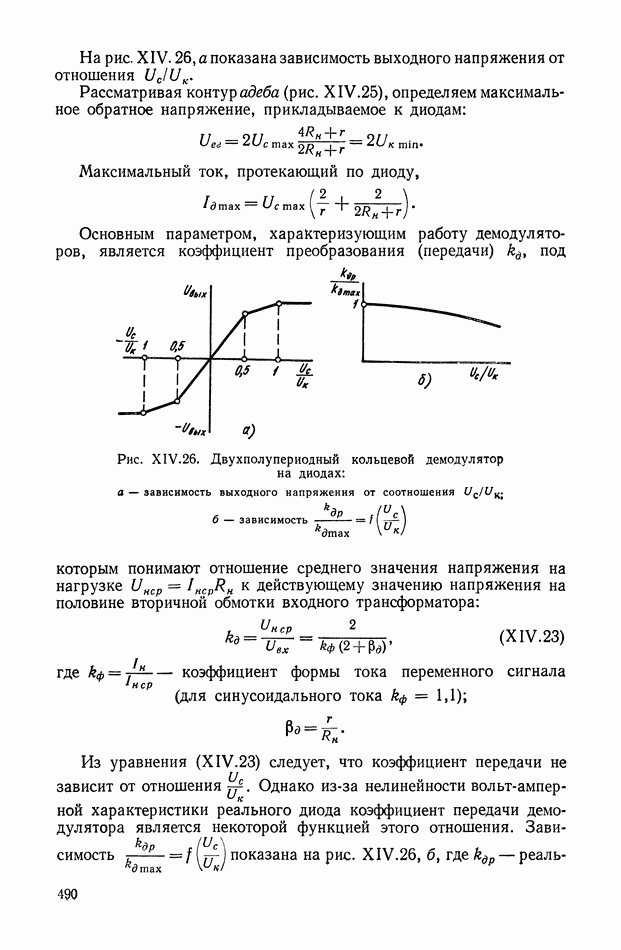
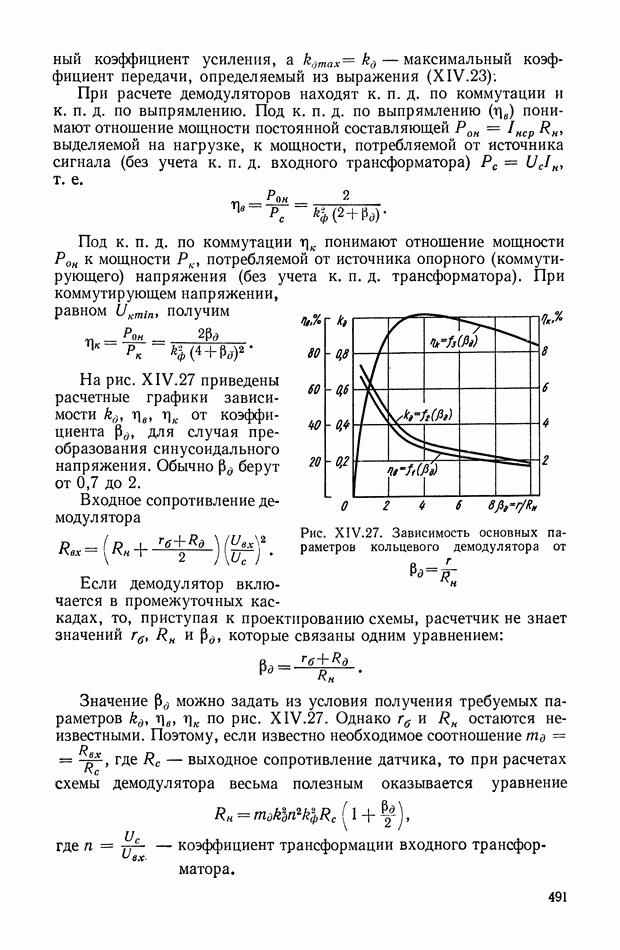
- Двухполупериодные демодуляторы на диодах.
- Однополупериодные усилители-демодуляторы.
- Двухполупериодные усилители-демодуляторы.
- Демодуляторы на транзисторных ключах.
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
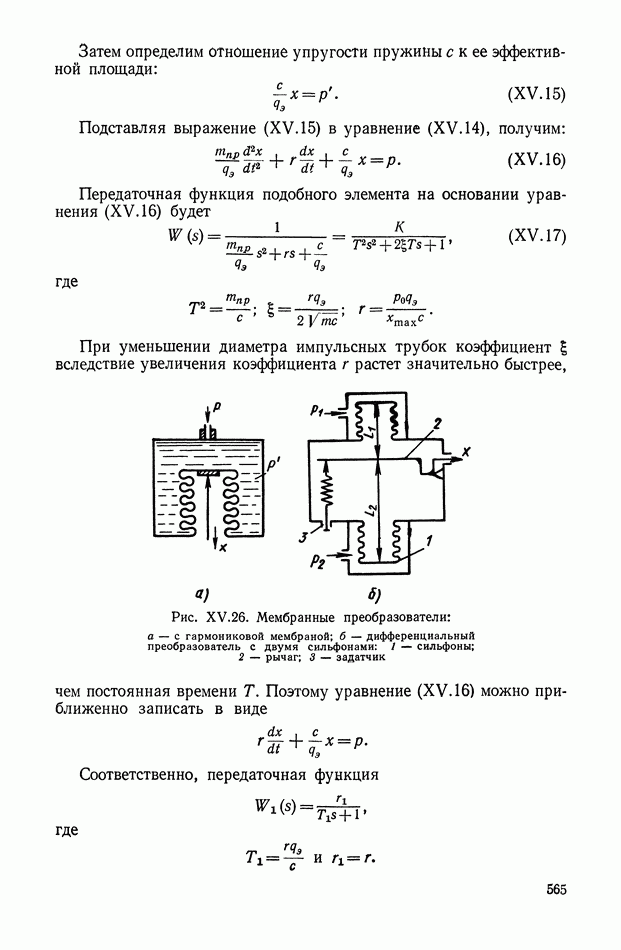
- Сильфоны.
- Гофрированные мембраны.
- Гибкие диафрагмы.
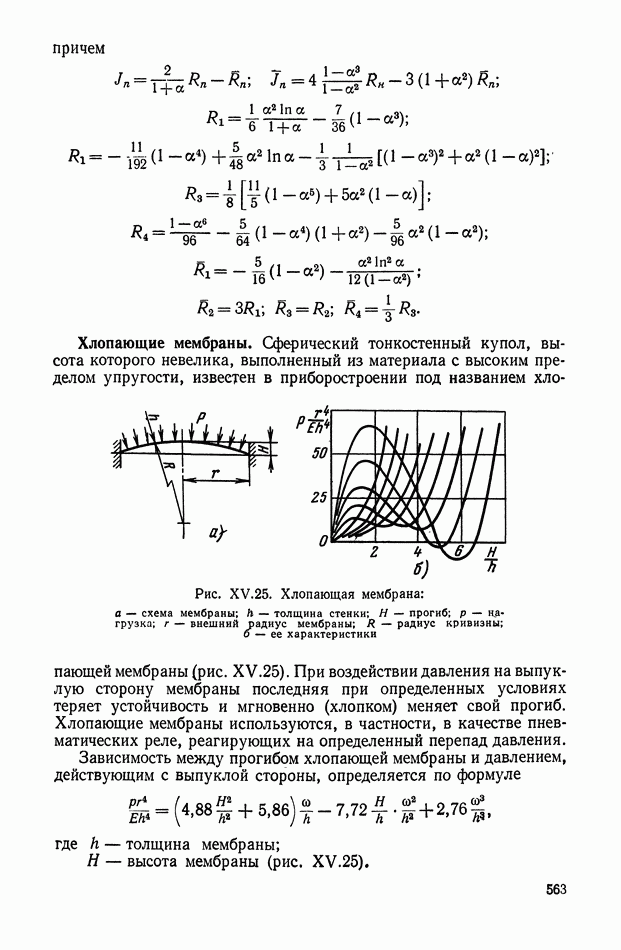
- Хлопающие мембраны.
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
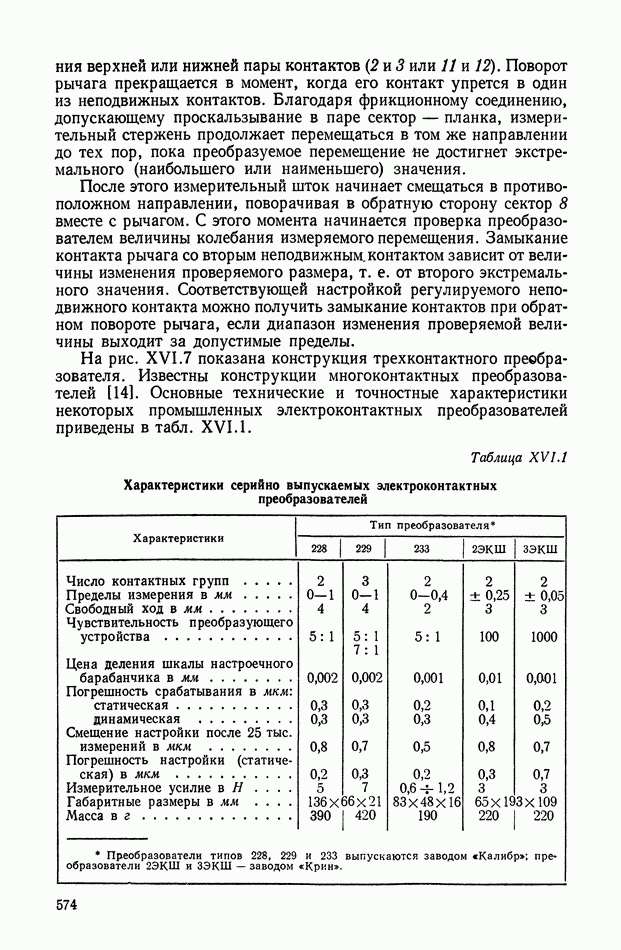
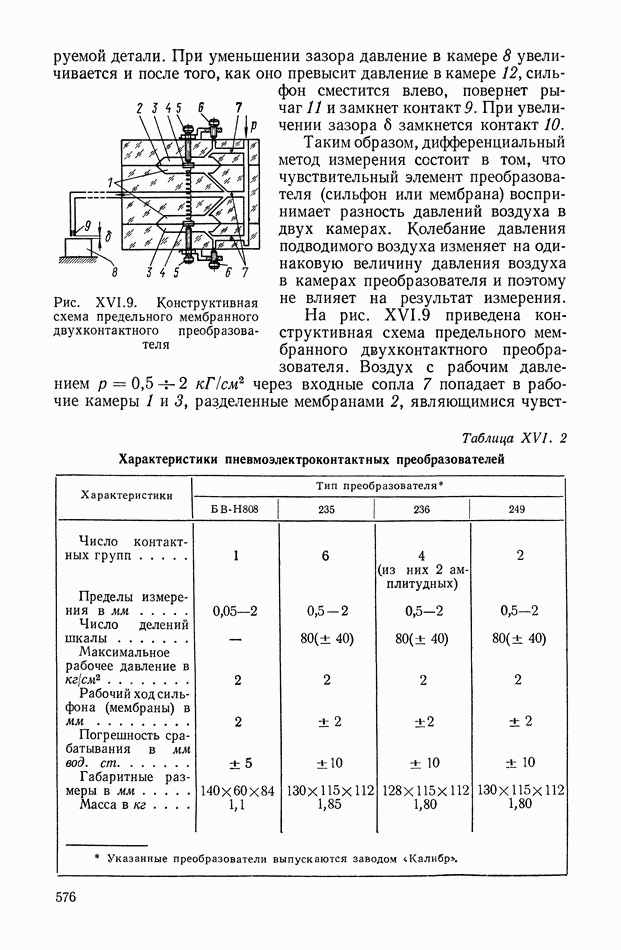
- Пневмоэлектроконтактные преобразователи линейных величин.
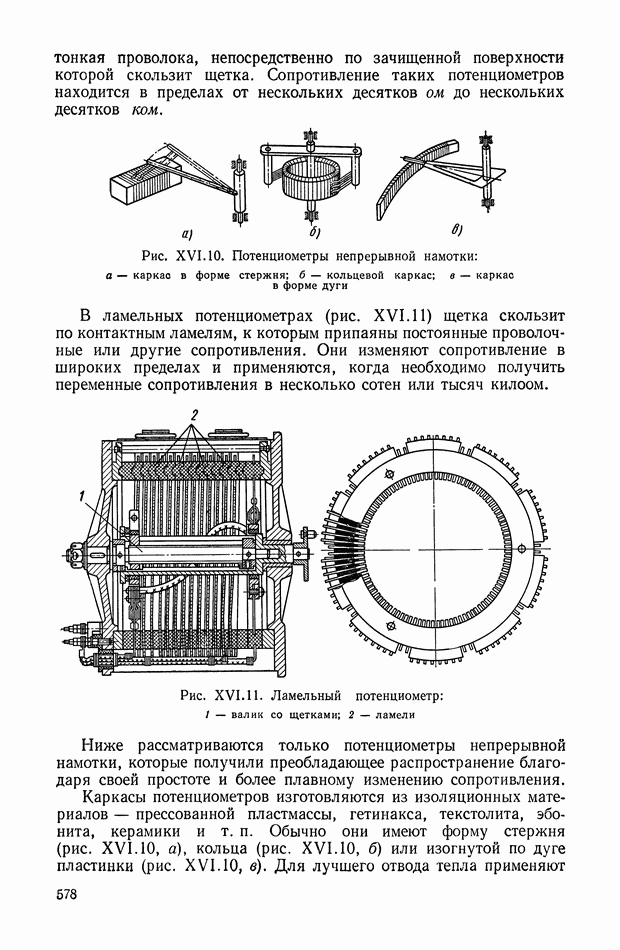
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
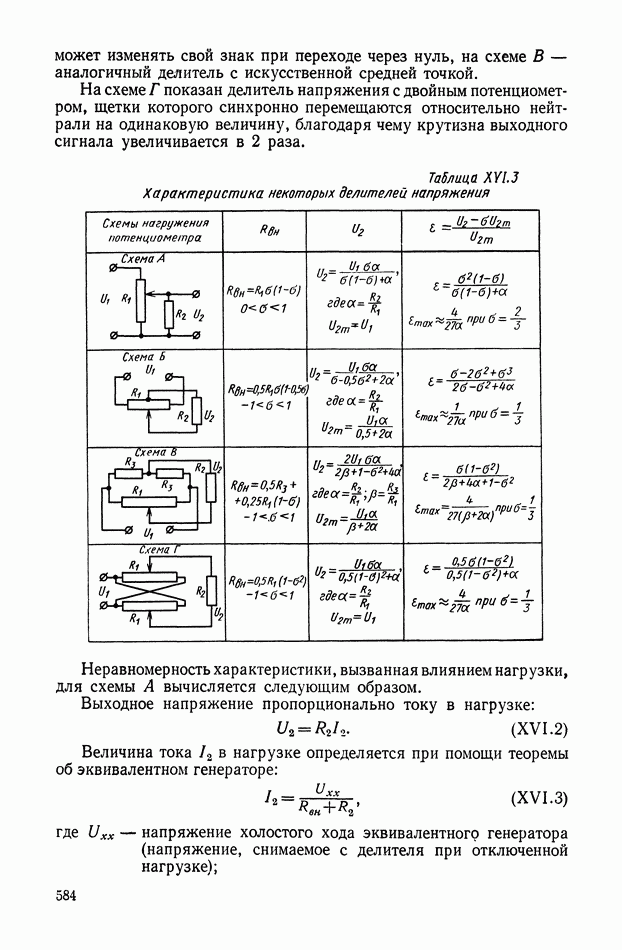
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
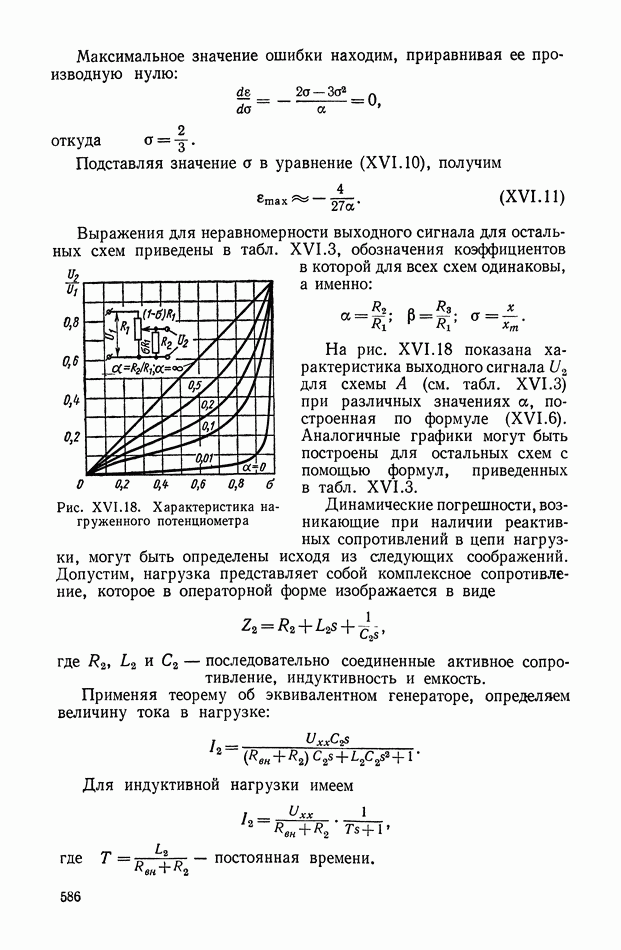
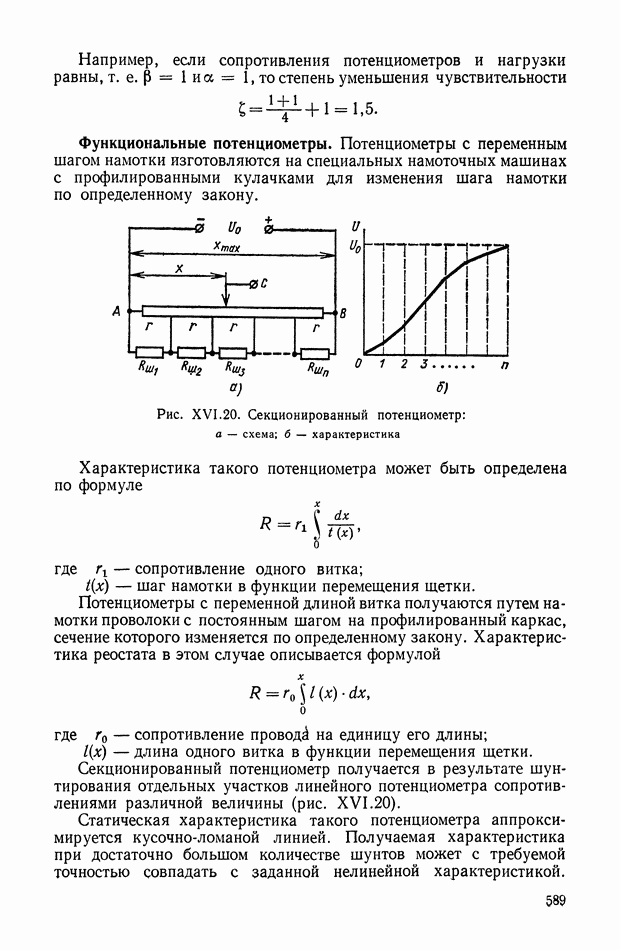
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
- Работа сельсинов в трансформаторном режиме.
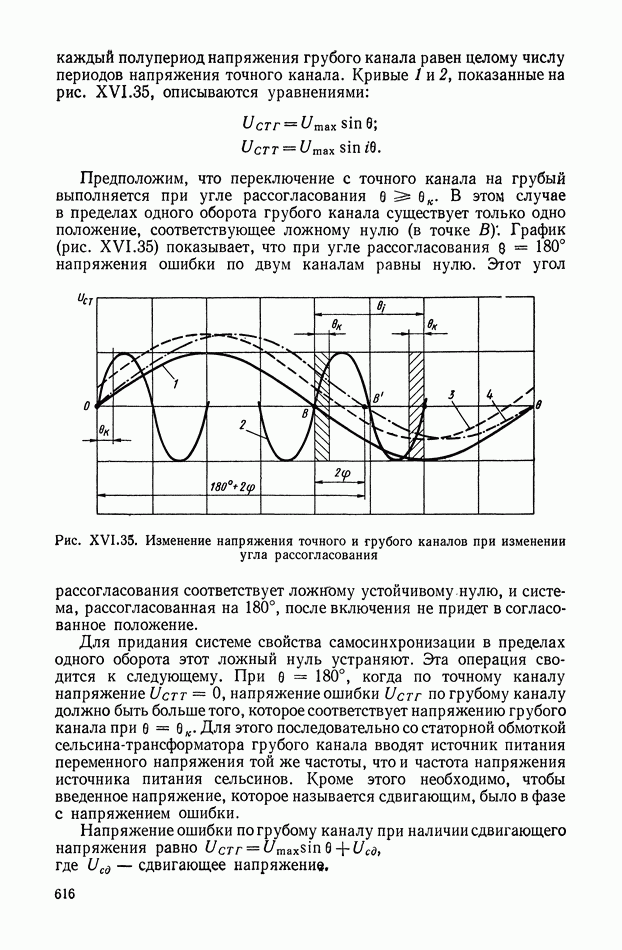
- Устранение ложного нуля в двухскоростной системе.
- Схемы синхронизаторов.
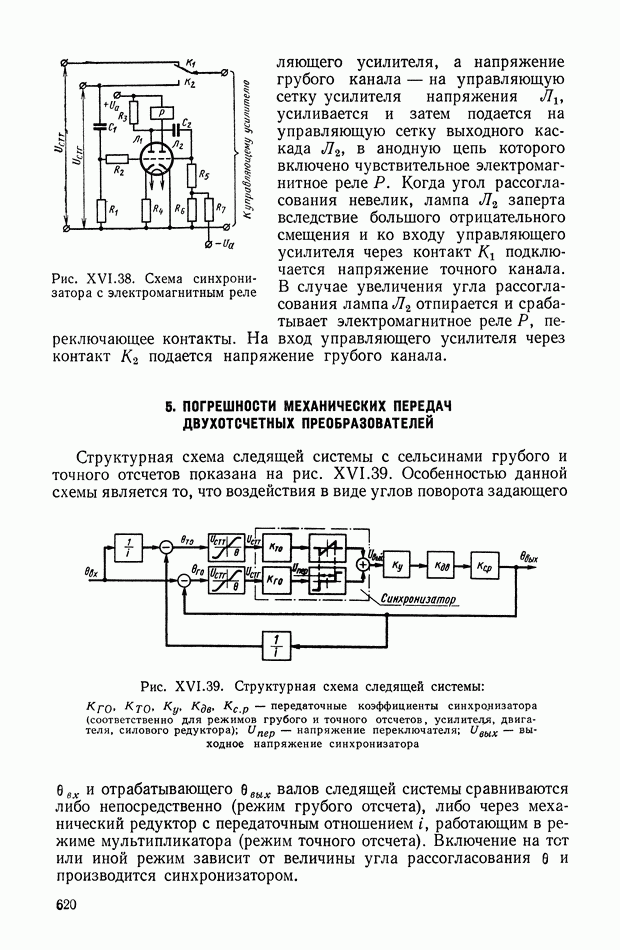
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
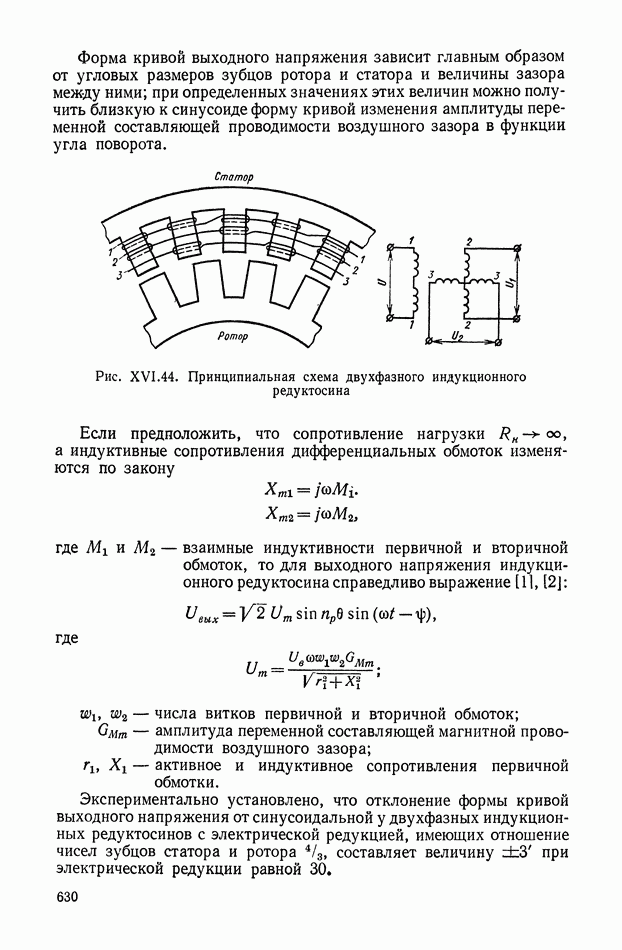
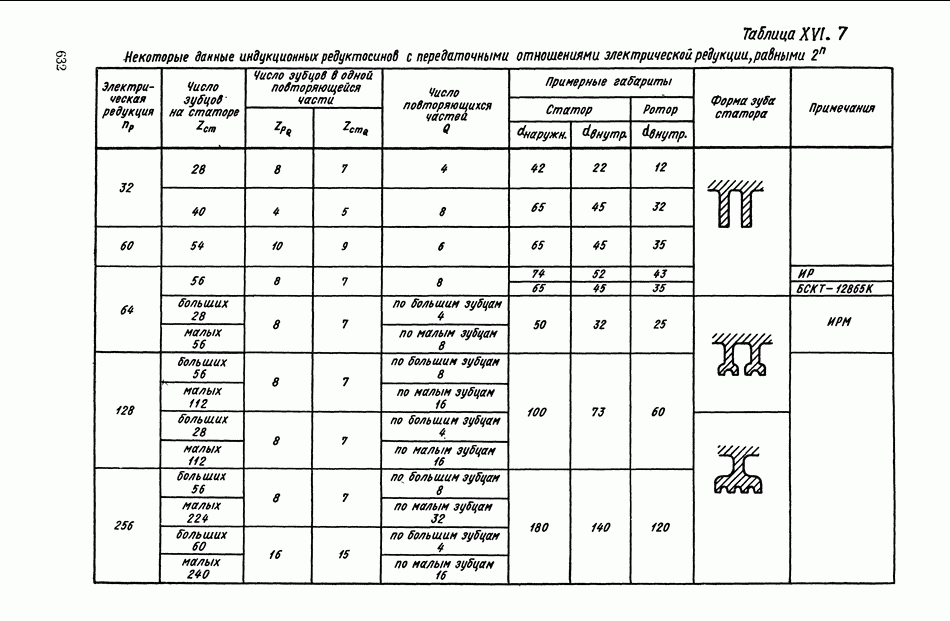
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
- Индукционные редуктосины.
- Индуктосины.
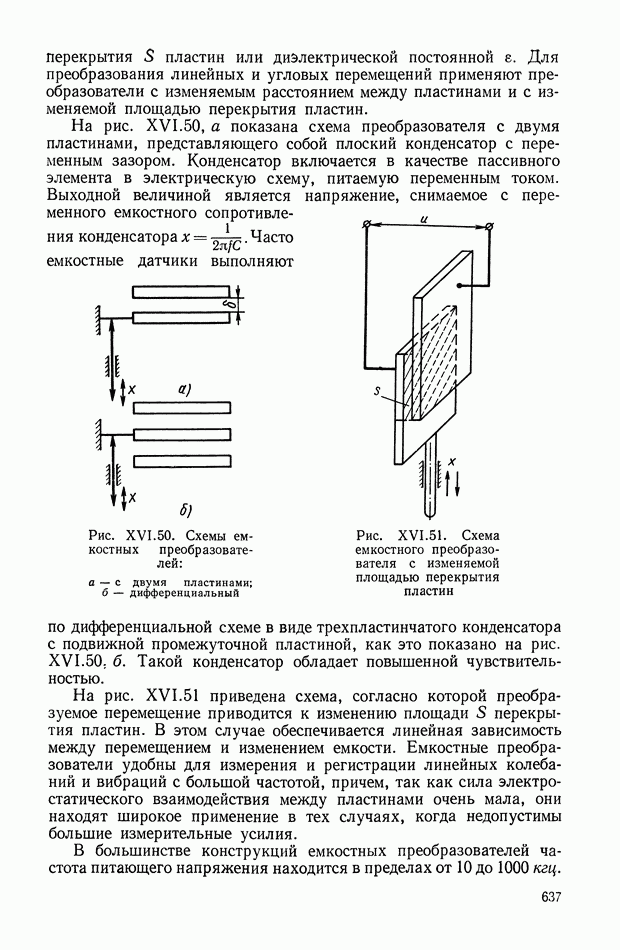
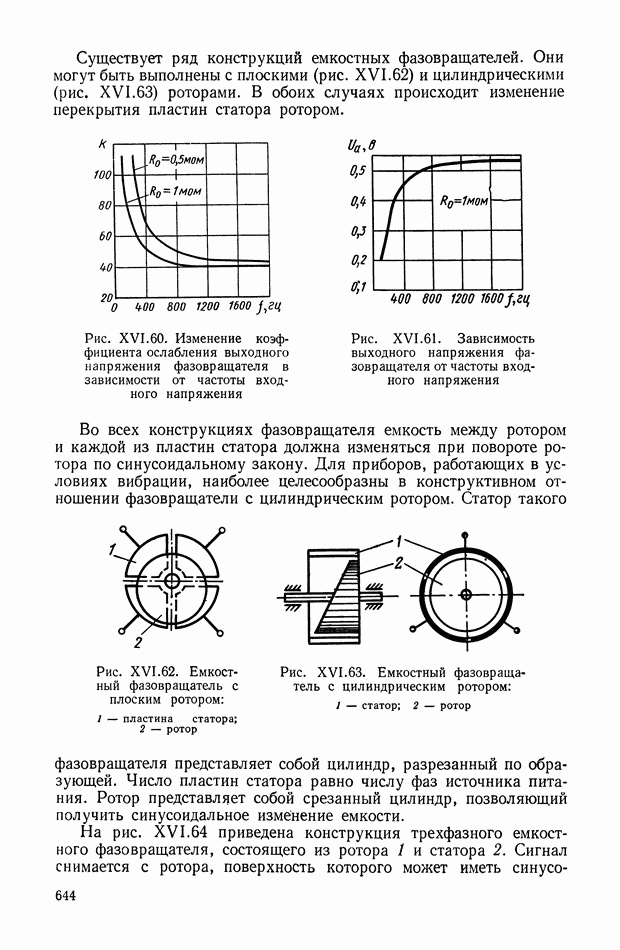
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
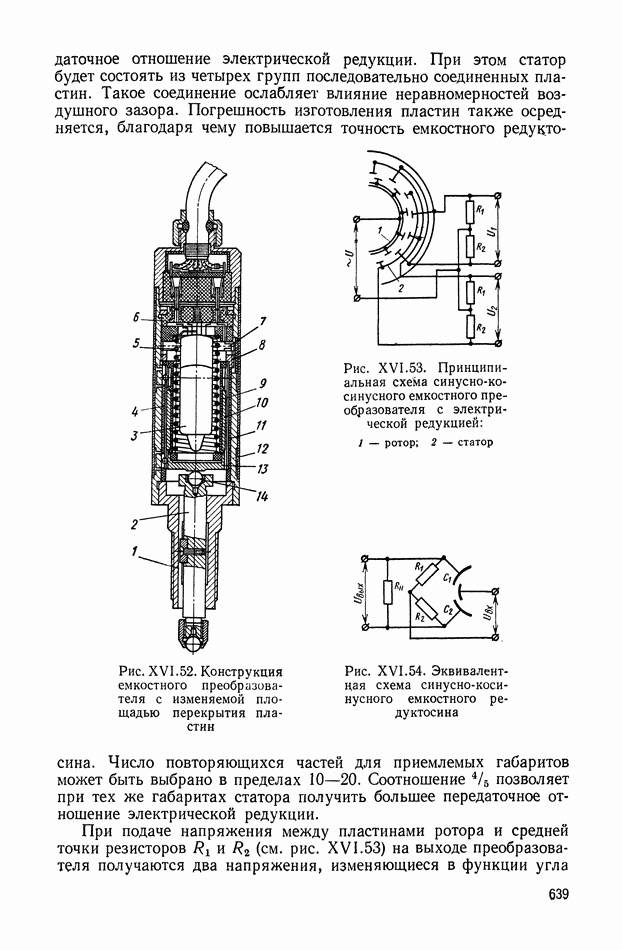
- Емкостный редуктосин.
- Емкостный фазовращатель.
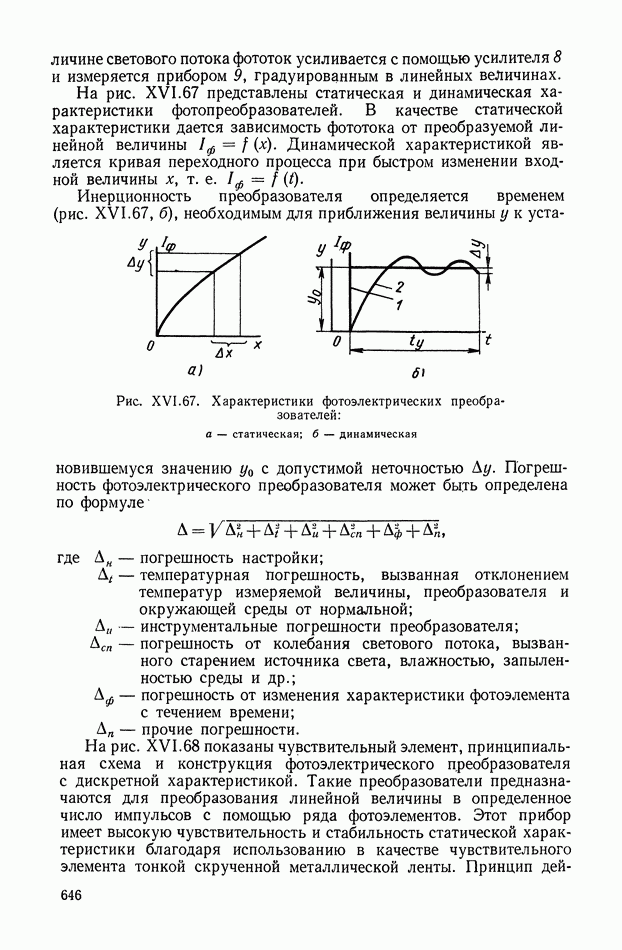
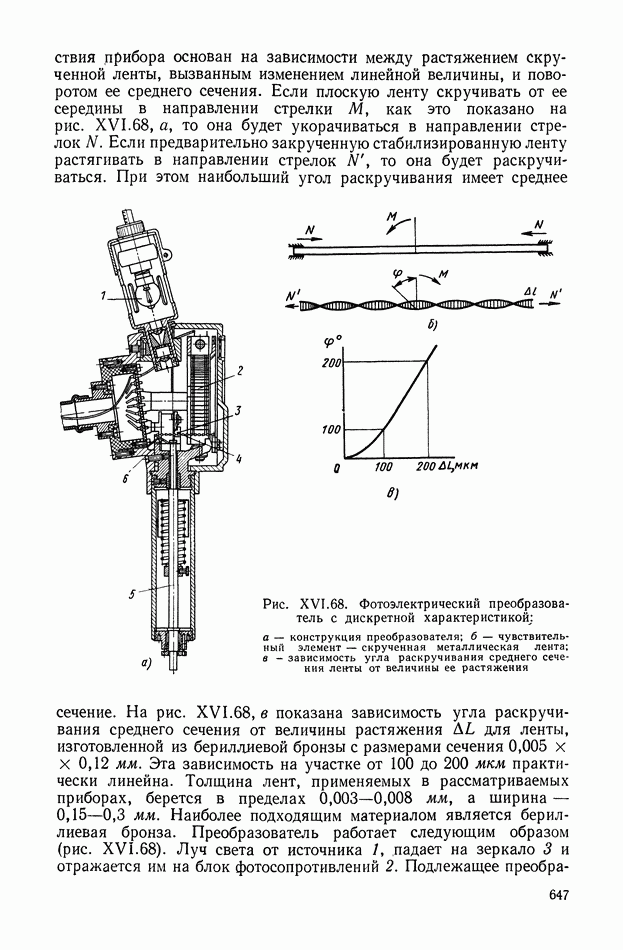
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
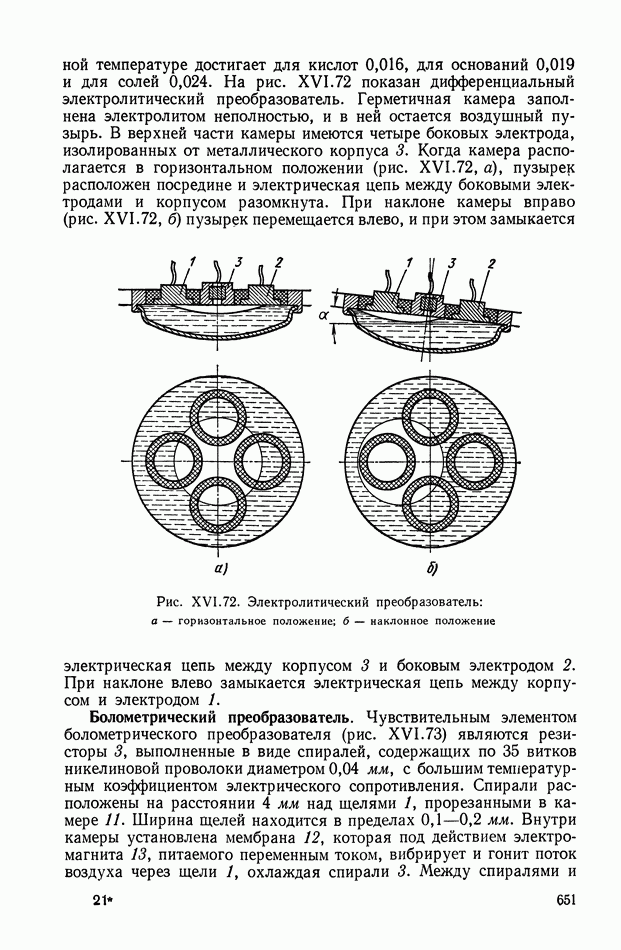
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ