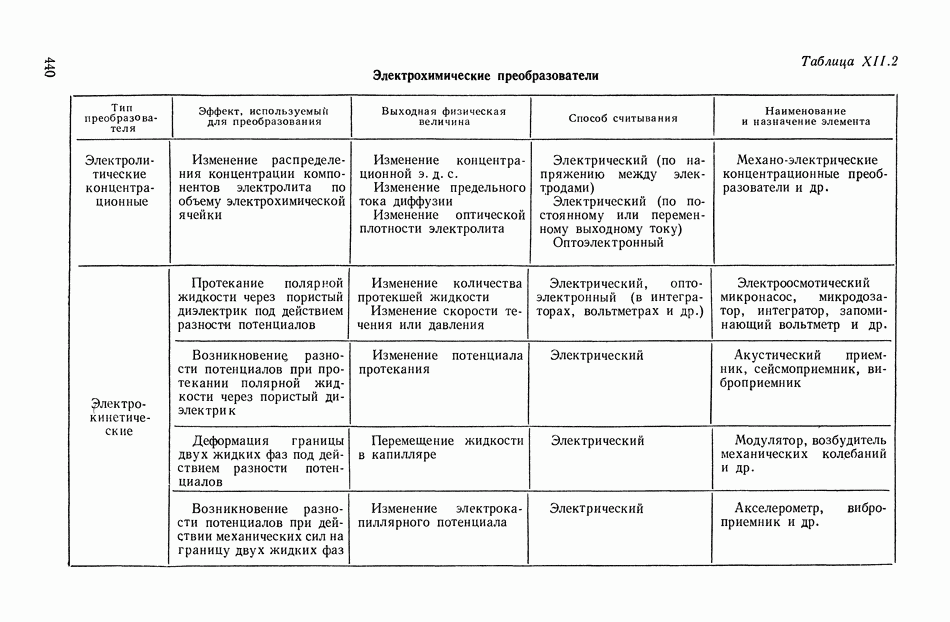
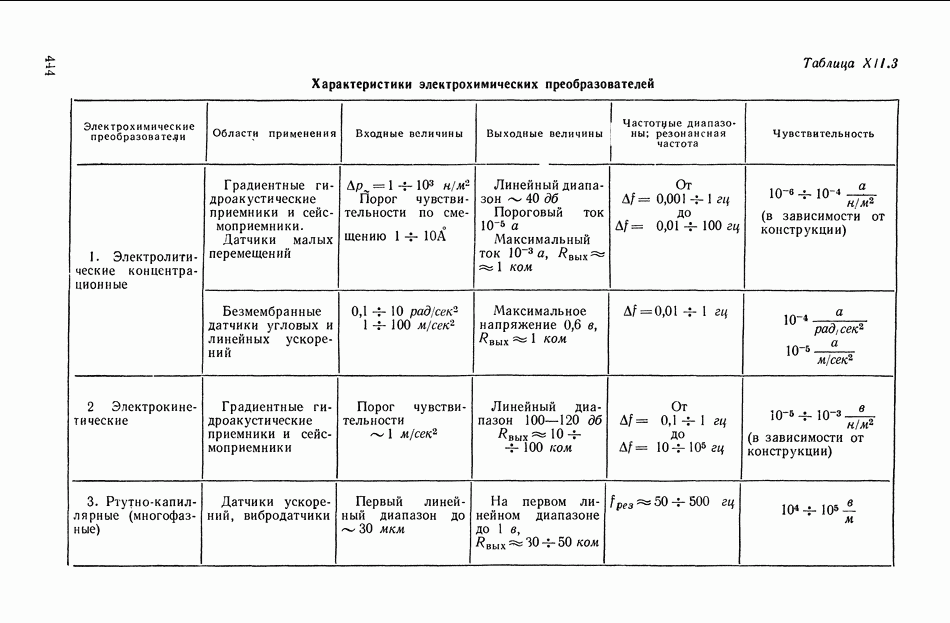
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
Амплитудная небалансная модуляция. Выражение для выходного сигнала преобразователя  можно записать следующим образом:
можно записать следующим образом:

где

где  — коэффициент амплитудной модуляции, выбираемый из условия
— коэффициент амплитудной модуляции, выбираемый из условия  для любых
для любых 
 — входной сигнал модулятора;
— входной сигнал модулятора;
 — функция модуляции, т. е. периодическая функция с периодом Т.
— функция модуляции, т. е. периодическая функция с периодом Т.
В этом случае преобразователь называется небалансным модулятором, или модулятором с несущей частотой [3].
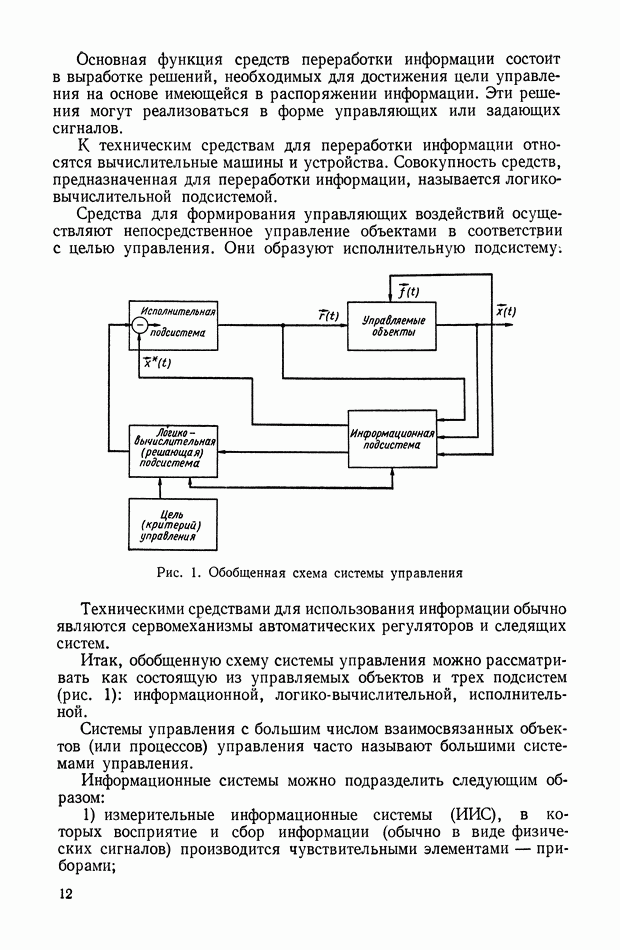
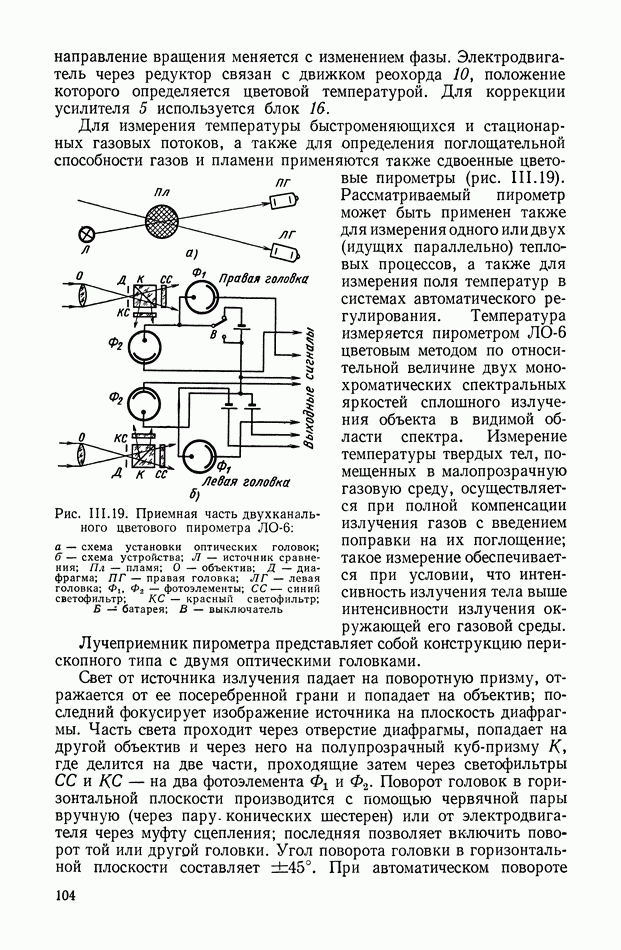
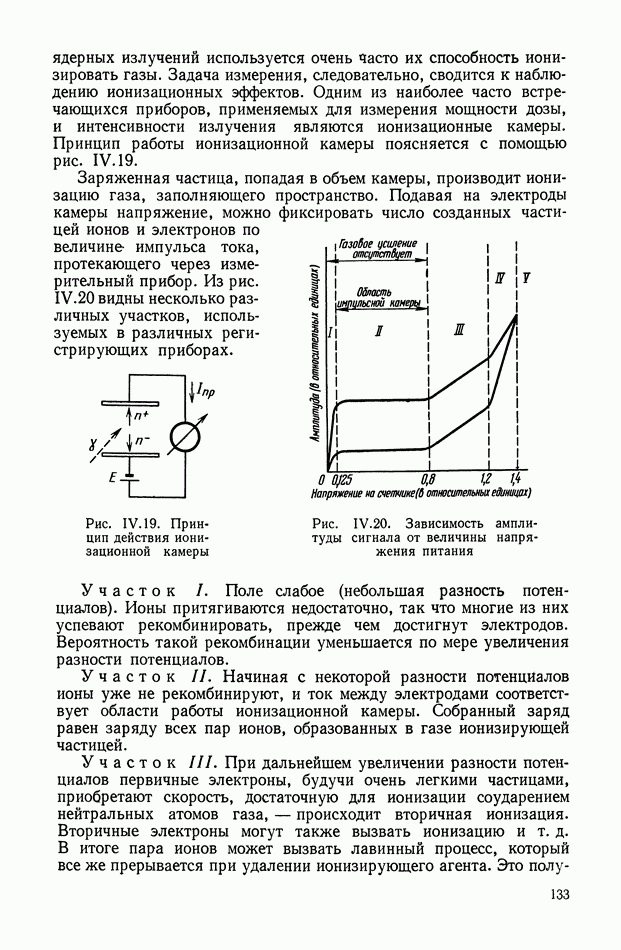
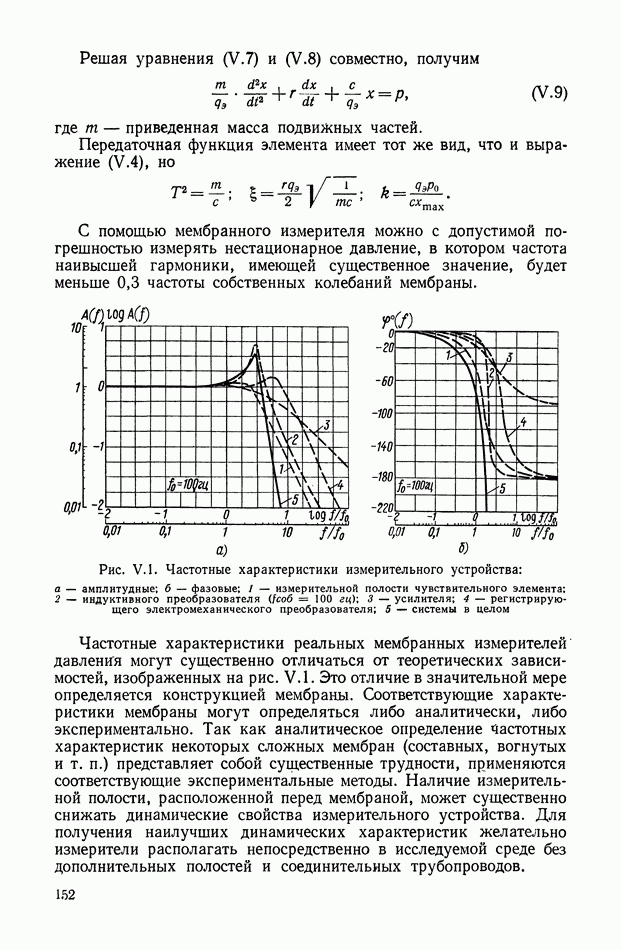
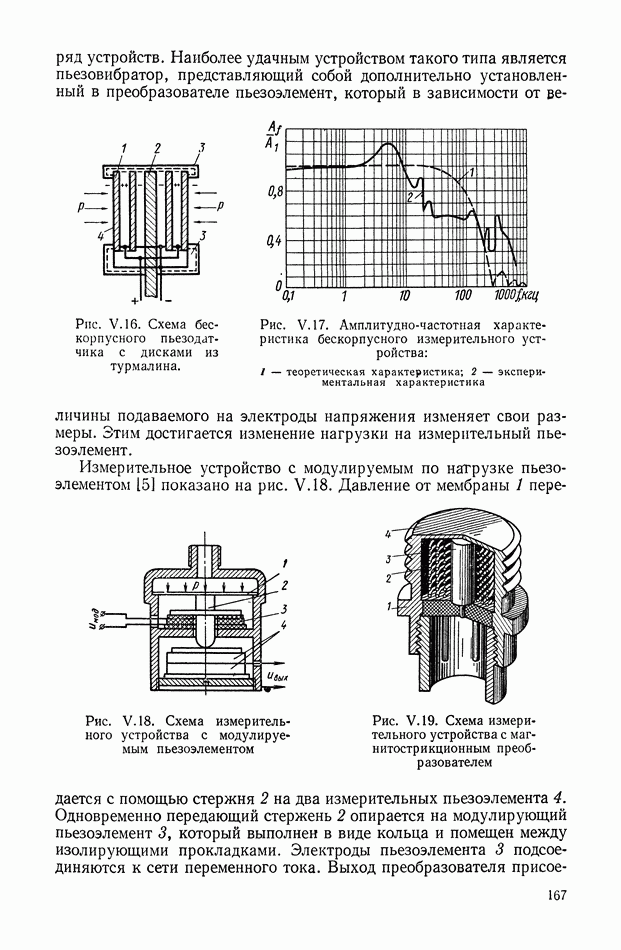
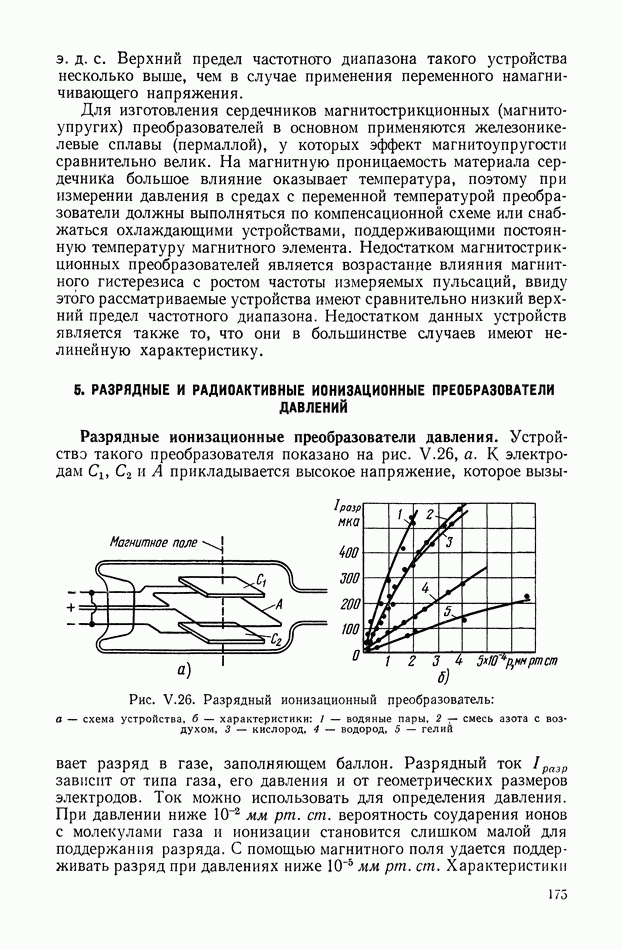
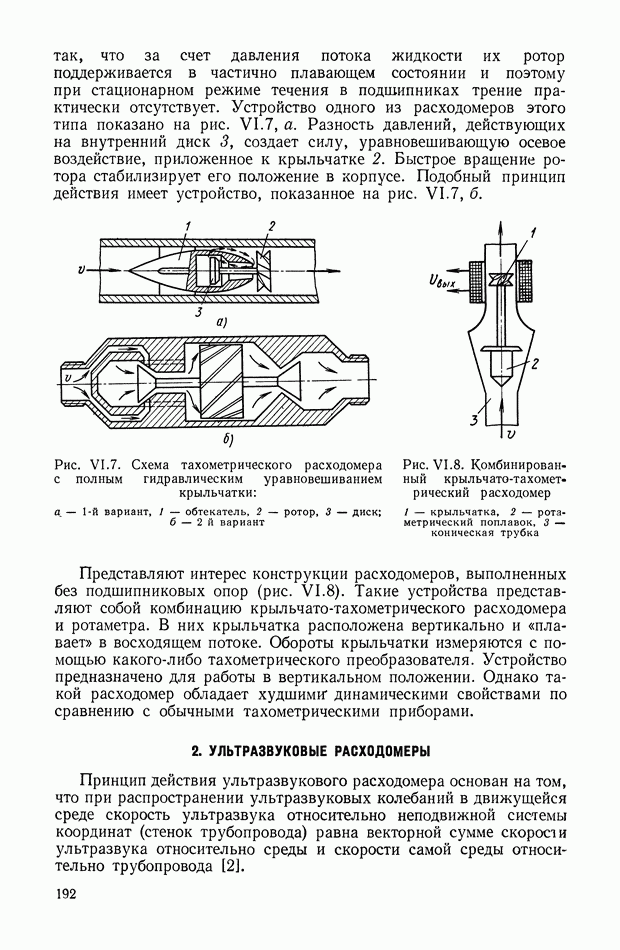
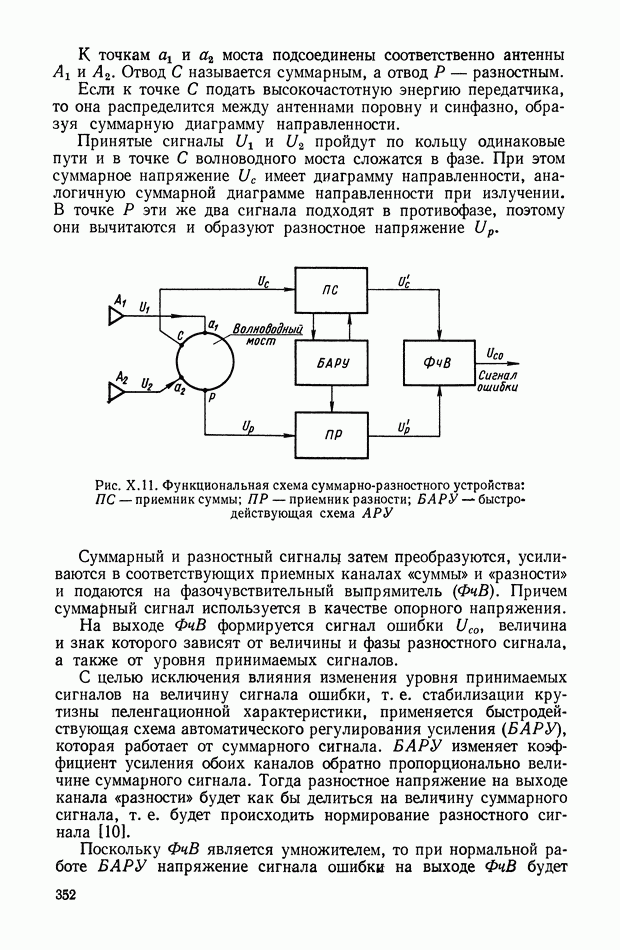
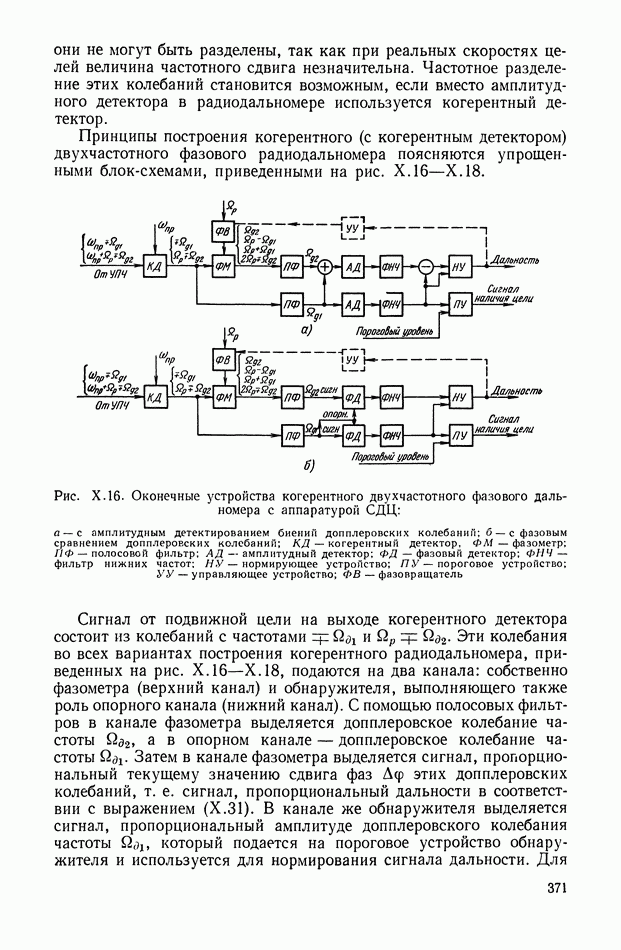
Структурная схема, соответствующая выражению (XIII.1), приведена на рис. XIII.I.
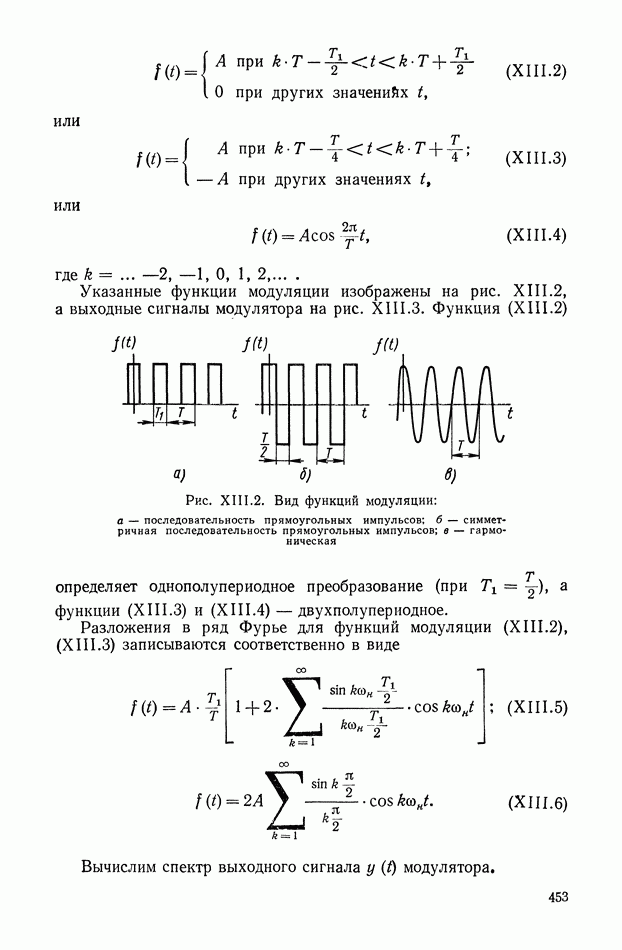
В качестве функций модуляции наиболее часто используются следующие:

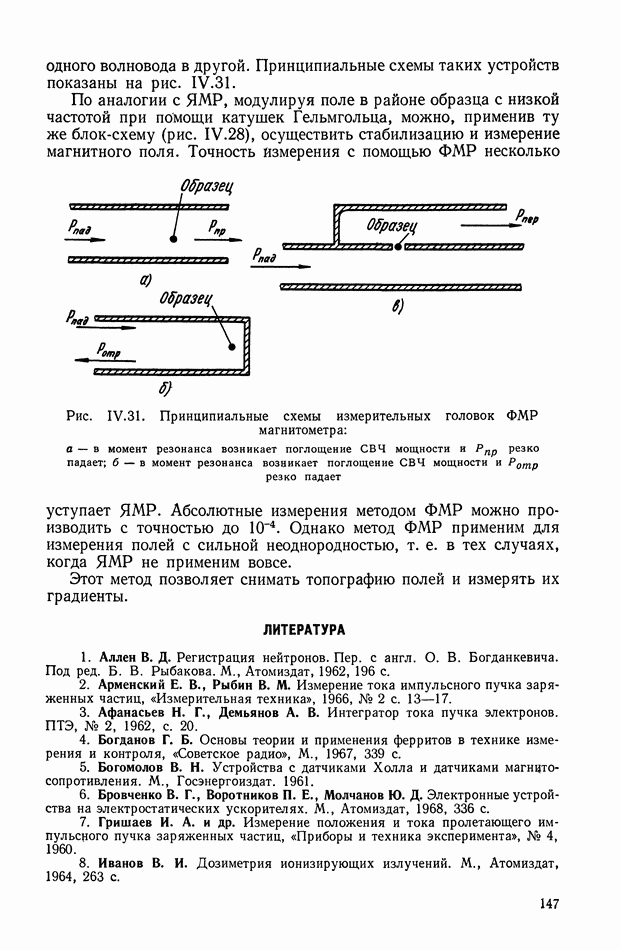
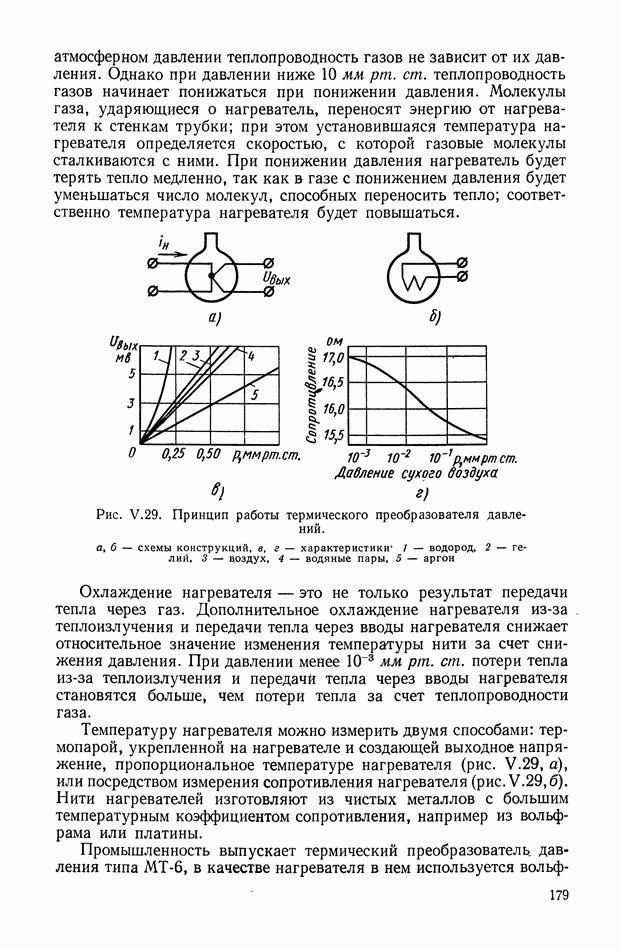
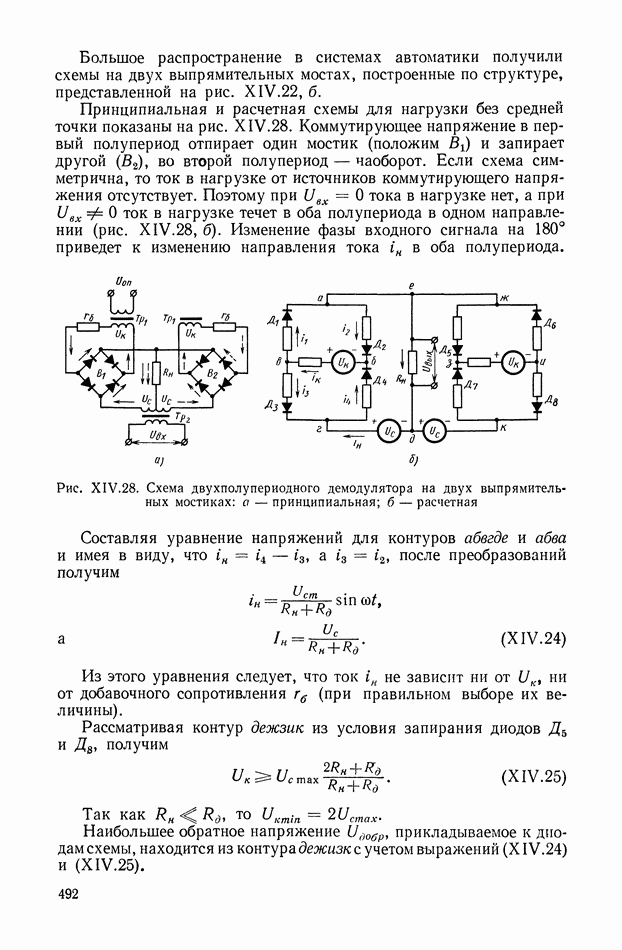
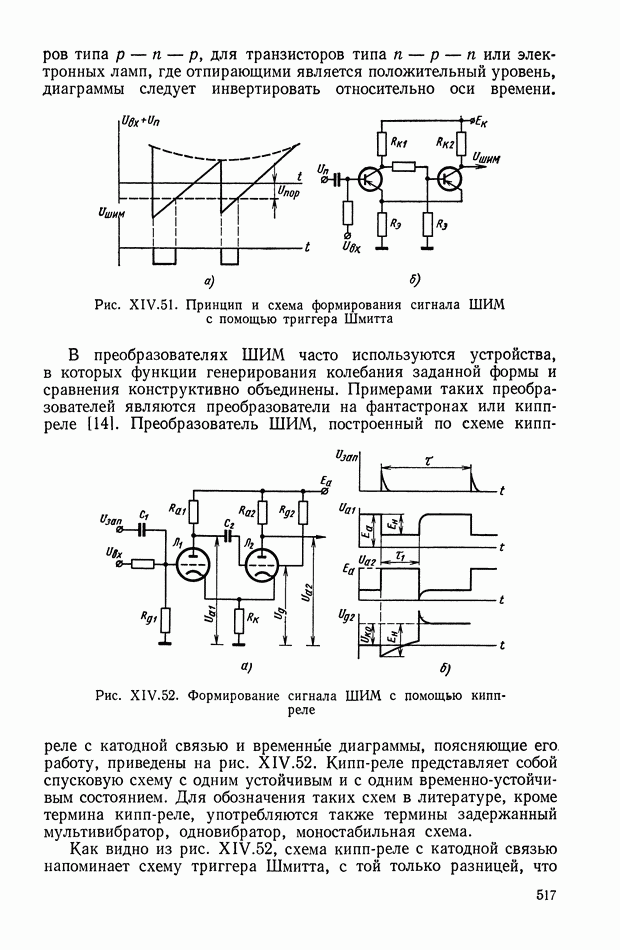
Рис. XIII.1. Структурное изображение амплитудной небалансной модуляции: Ф — фильтр;  — коэффициент амплитудной модуляции.
— коэффициент амплитудной модуляции.

или

или

где
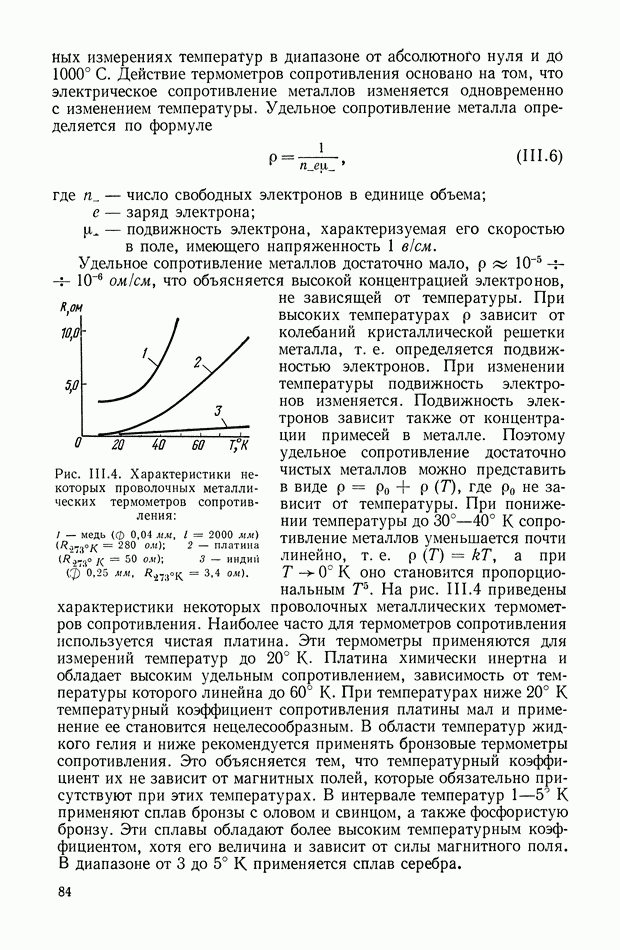
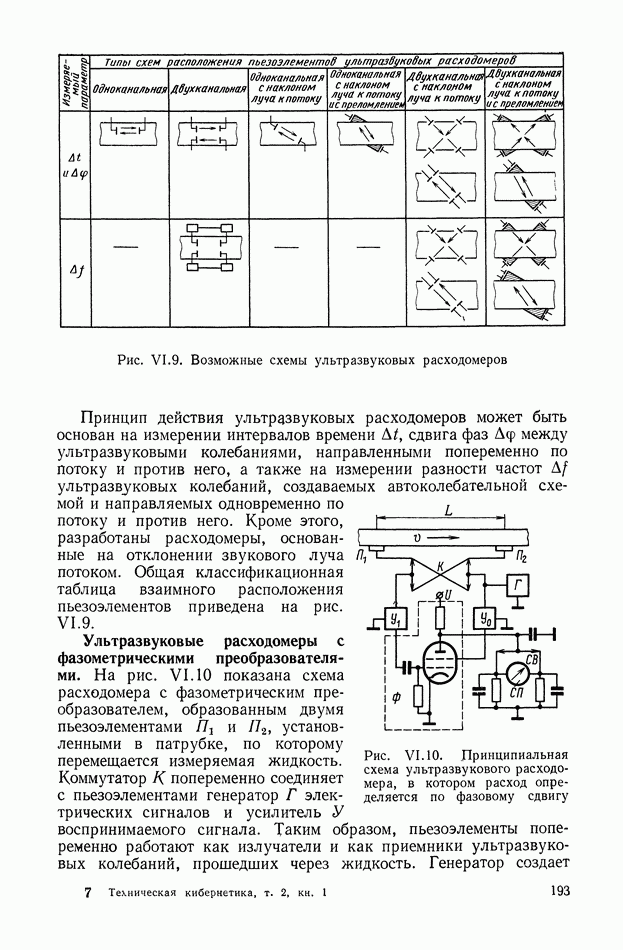
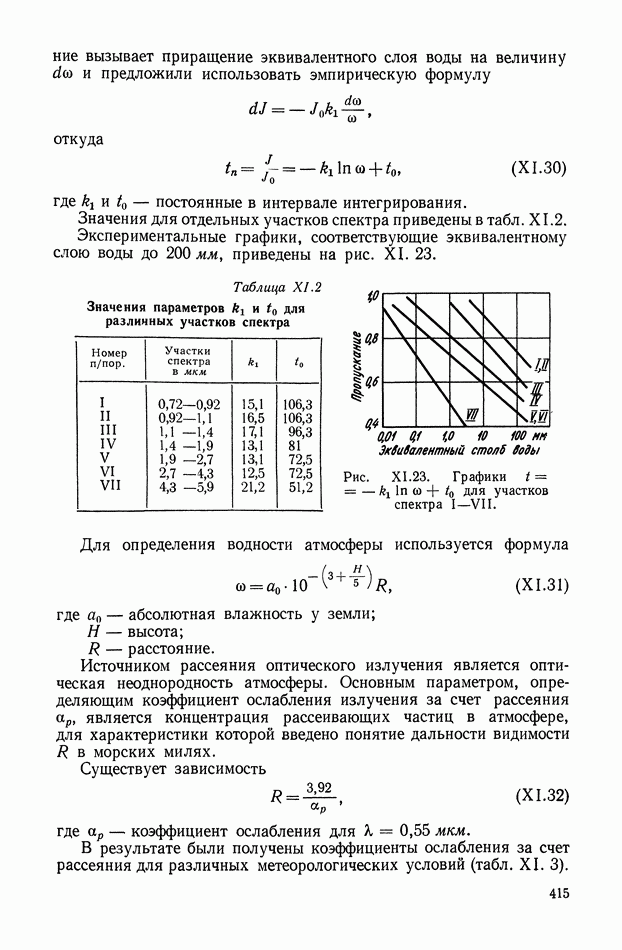
Указанные функции модуляции изображены на рис. XIII.2, а выходные сигналы модулятора на рис. XIII.3.

Рис. XIII.2. Вид функций модуляции: а — последовательность прямоугольных импульсов; б — симметричная последовательность прямоугольных импульсов; в — гармоническая
Функция (XIII.2) определяет однопол у пер йодное преобразование (при  ), а функции (XIII.3) и (XIII.4) — двухполупериодное.
), а функции (XIII.3) и (XIII.4) — двухполупериодное.
Разложения в ряд Фурье для функций модуляции (XIII.2), (XII 1.3) записываются соответственно в виде

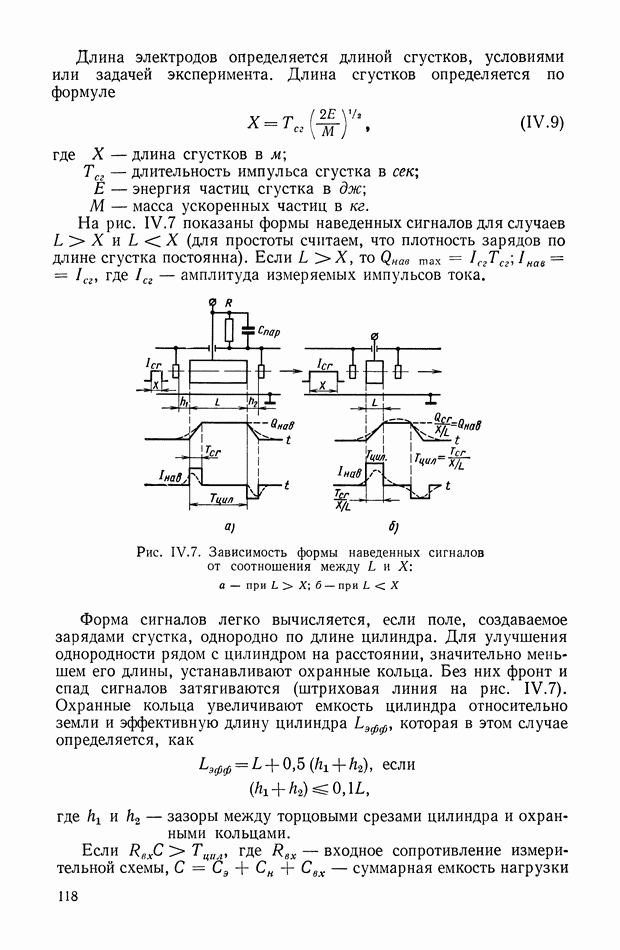
Вычислим спектр выходного сигнала  модулятора.
модулятора.
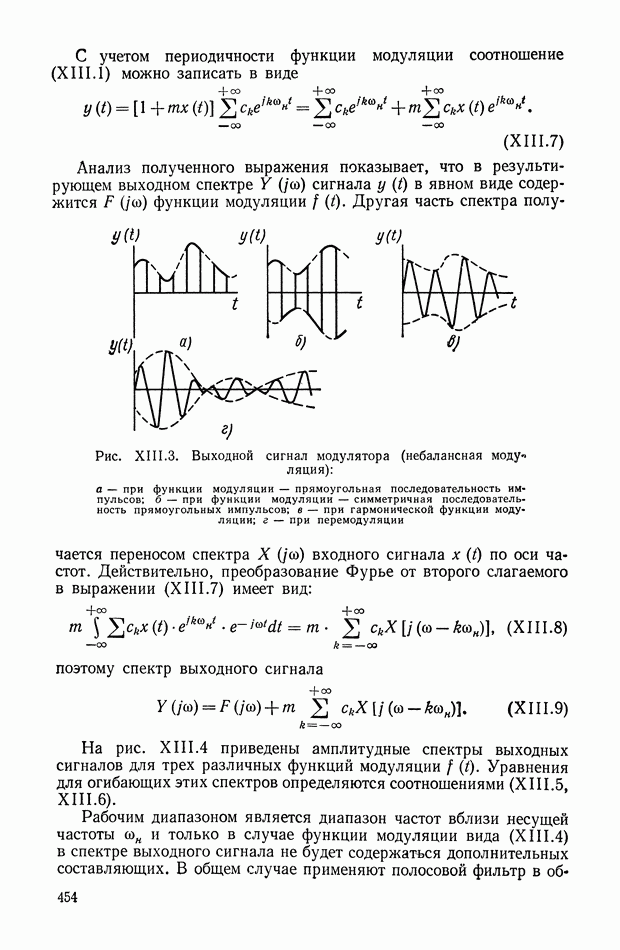
С учетом периодичности функции модуляции соотношение (XIII.1) можно записать в виде

Анализ полученного выражения показывает, что в результирующем выходном спектре  сигнала
сигнала  в явном виде содержится
в явном виде содержится  функции модуляции
функции модуляции 

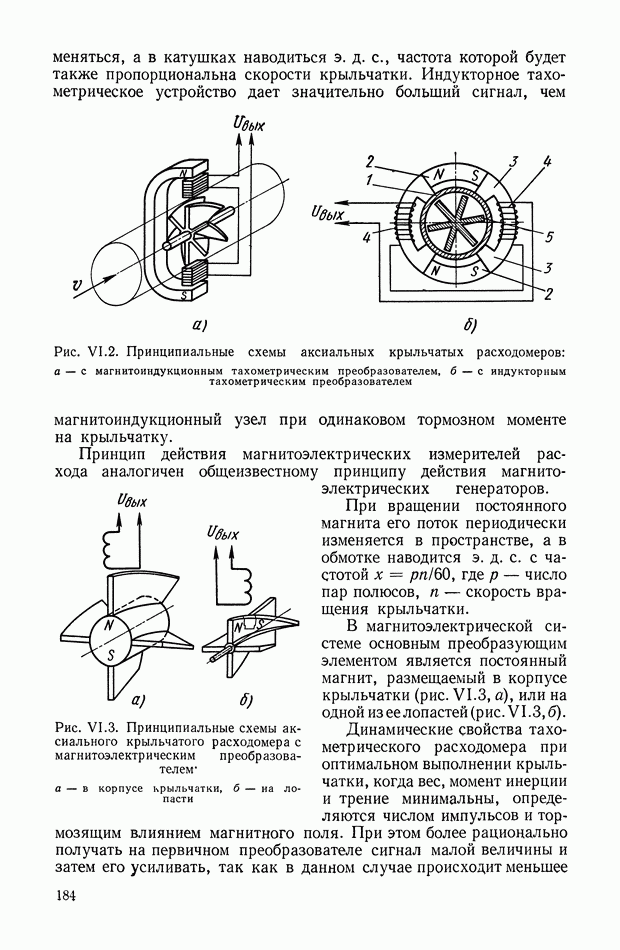
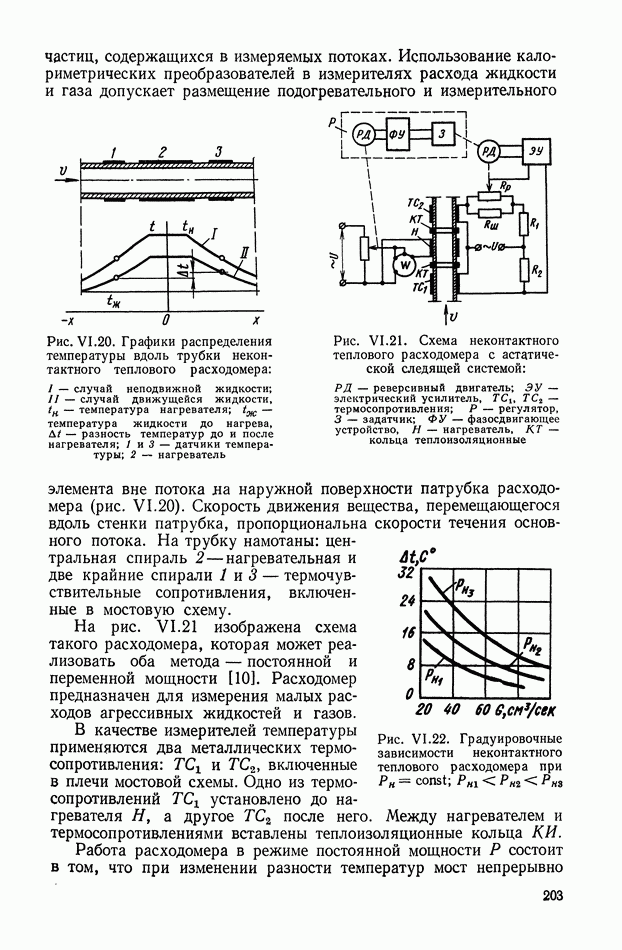
Рис. XIII.3. Выходной сигнал модулятора (небалансная модуляция): а — при функции модуляции — прямоугольная последовательность импульсов; б — при функции модуляции — симметричная последовательность прямоугольных импульсов; в — при гармонической функции модуляции;  — при перемодуляции
— при перемодуляции
Другая часть спектра получается переносом спектра  входного сигнала
входного сигнала  по оси частот. Действительно, преобразование Фурье от второго слагаемого в выражении (XIII.7) имеет вид:
по оси частот. Действительно, преобразование Фурье от второго слагаемого в выражении (XIII.7) имеет вид:

поэтому спектр выходного сигнала

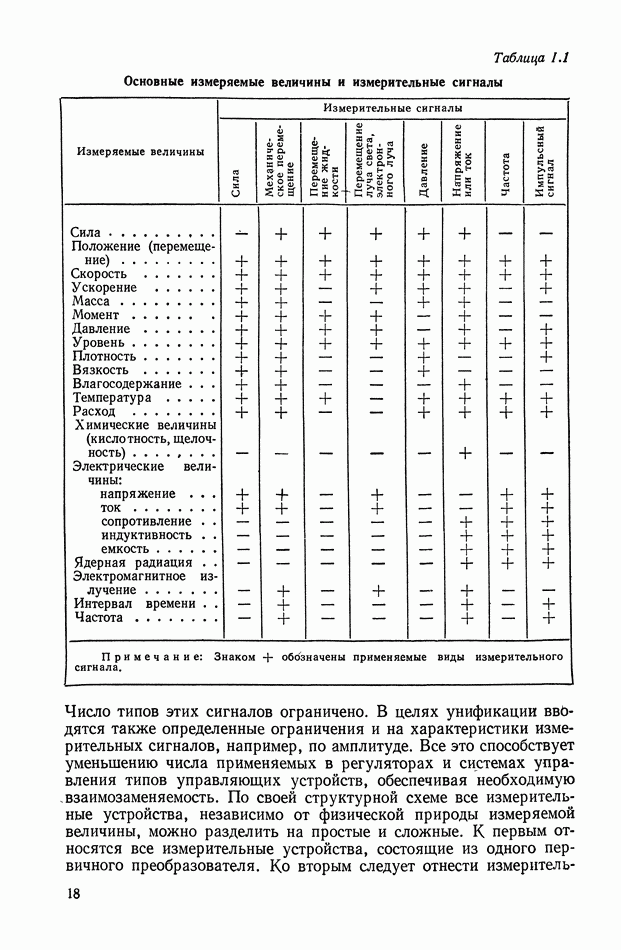
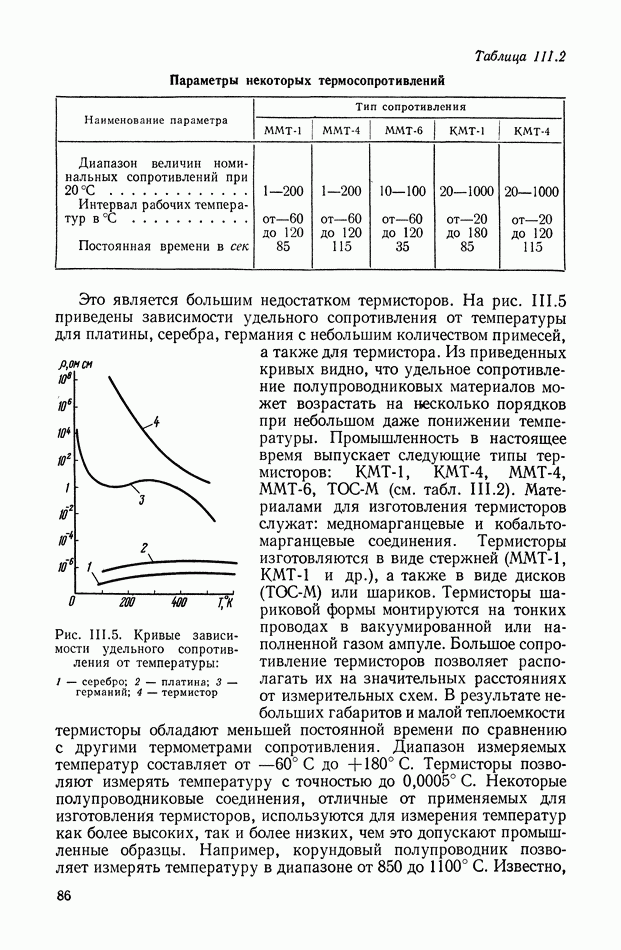
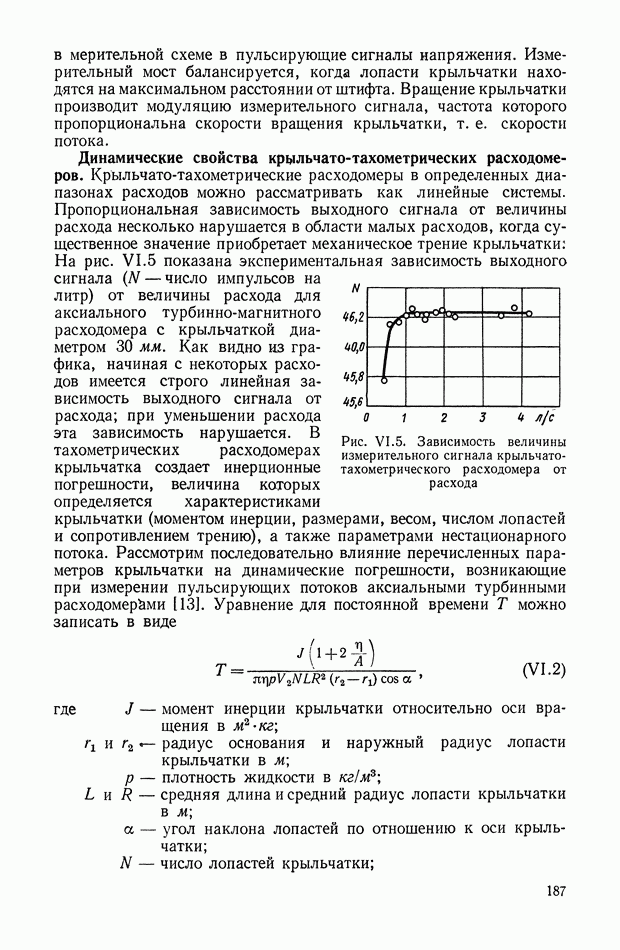
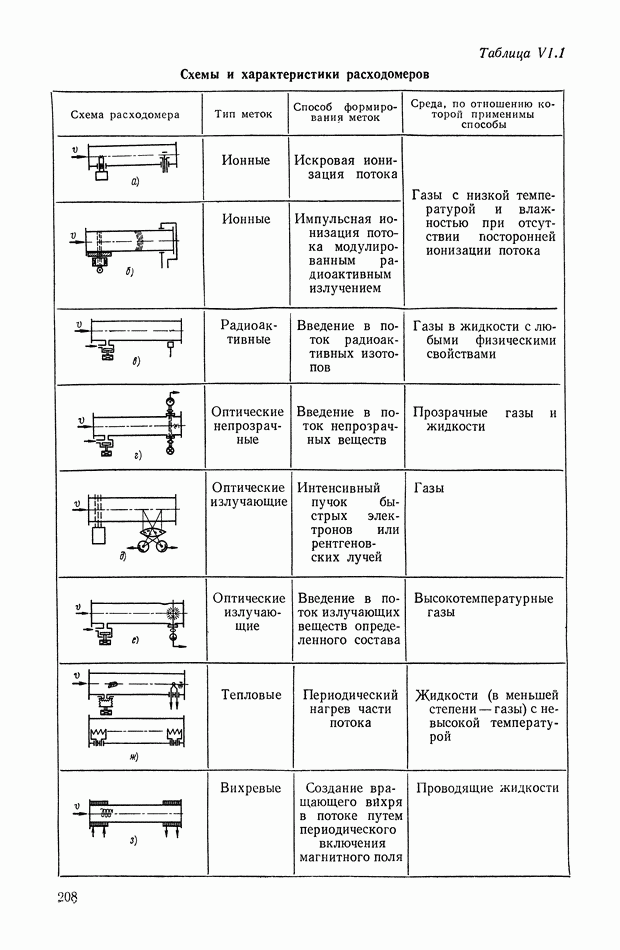
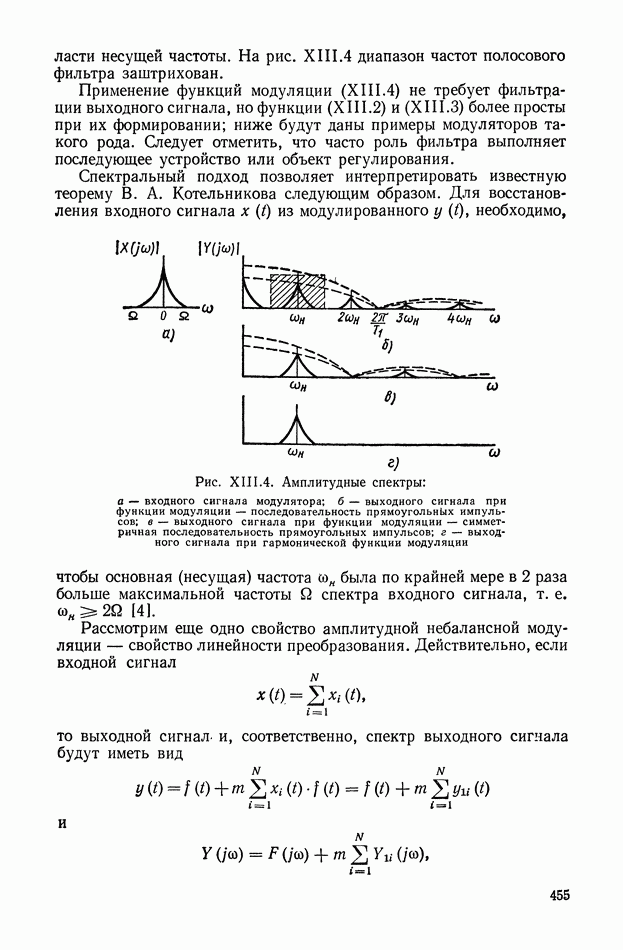
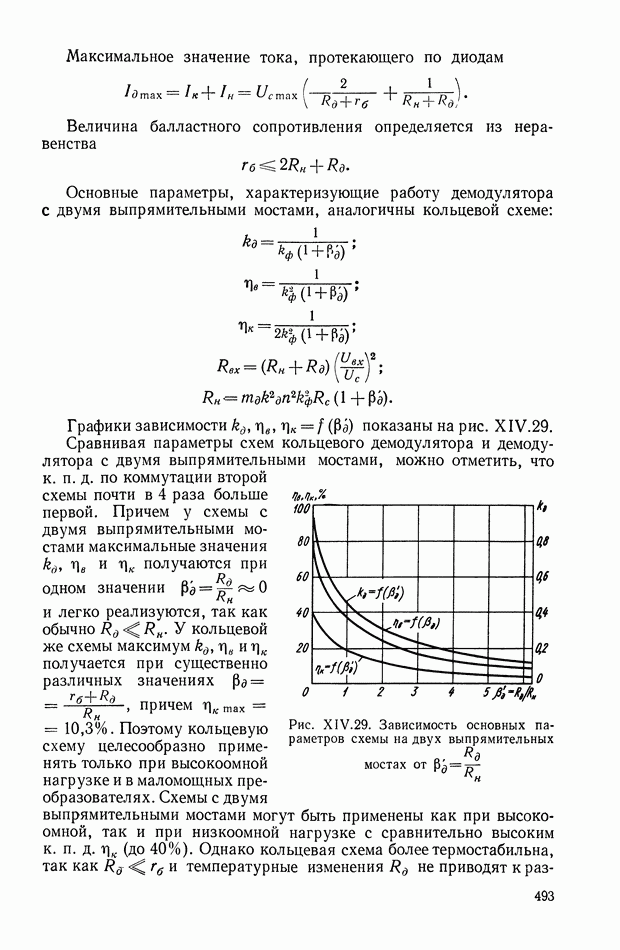
На рис. XIII.4 приведены амплитудные спектры выходных сигналов для трех различных функций модуляции  Уравнения для огибающих этих спектров определяются соотношениями (XIII.5, XIII.6).
Уравнения для огибающих этих спектров определяются соотношениями (XIII.5, XIII.6).
Рабочим диапазоном является диапазон частот вблизи несущей частоты  и только в случае функции модуляции вида (XIII.4) в спектре выходного сигнала не будет содержаться дополнительных составляющих. В общем случае применяют полосовой фильтр в
и только в случае функции модуляции вида (XIII.4) в спектре выходного сигнала не будет содержаться дополнительных составляющих. В общем случае применяют полосовой фильтр в
области несущей частоты. На рис. XIII.4 диапазон частот полосового фильтра заштрихован.
Применение функций модуляции (XIII.4) не требует фильтрации выходного сигнала, но функции (XIII.2) и (XIII.3) более просты при их фюрмировании; ниже будут даны примеры модуляторов такого рода. Следует отметить, что часто роль фильтра выполняет последующее устройство или объект регулирования.
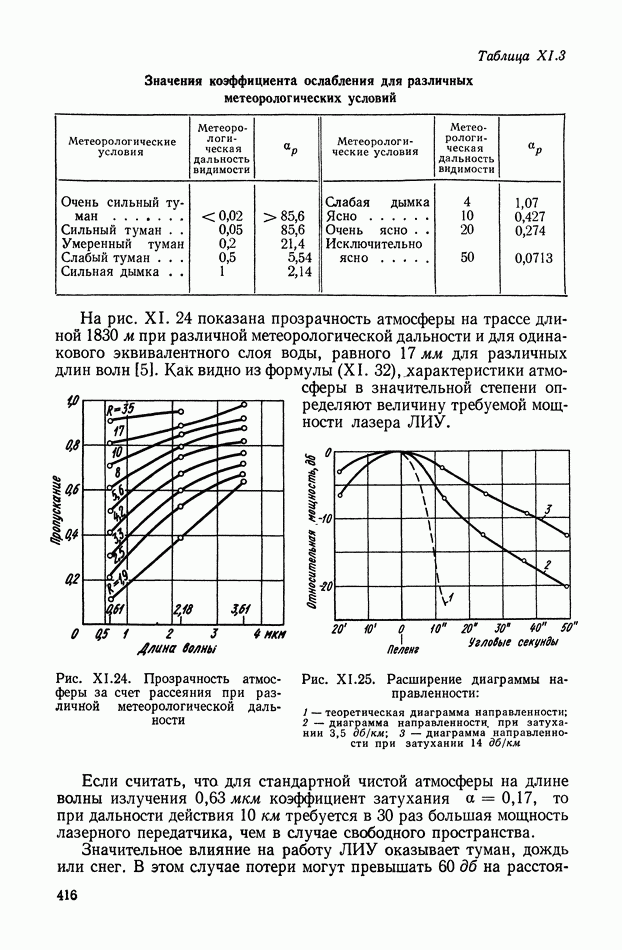
Спектральный подход позволяет интерпретировать известную теорему В. А. Котельникова следующим образом.

Рис. XII 1.4. Амплитудные спектры: а — входного сигнала модулятора; б — выходного сигнала при функции модуляции — последовательность прямоугольных импульсов; в — выходного сигнала при функции модуляции — симметричная последовательность прямоугольных импульсов; г — выходного сигнала при гармонической функции модуляции
Для восстановления входного сигнала  из модулированного
из модулированного  необходимо, чтобы основная (несущая) частота (он была по крайней мере в 2 раза больше максимальной частоты
необходимо, чтобы основная (несущая) частота (он была по крайней мере в 2 раза больше максимальной частоты  спектра входного сигнала, т. е.
спектра входного сигнала, т. е. 
Рассмотрим еще одно свойство амплитудной небалансной модуляции — свойство линейности преобразования. Действительно, если входной сигнал

то выходной сигнал и, соответственно, спектр выходного сигнала будут иметь вид

и

где

Свойство линейности позволяет получать спектр выходного сигнала для аддитивного входного сигнала.
При амплитудной небалансной модуляции важно, чтобы выполнялось условие  для любых что исключает перемодуляцию. На рис. XIII.3, 2 показан пример перемодулированного сигнала.
для любых что исключает перемодуляцию. На рис. XIII.3, 2 показан пример перемодулированного сигнала.
С учетом фильтрации выходной спектр модулятора

где  — комплексно-сопряженные числа.
— комплексно-сопряженные числа.
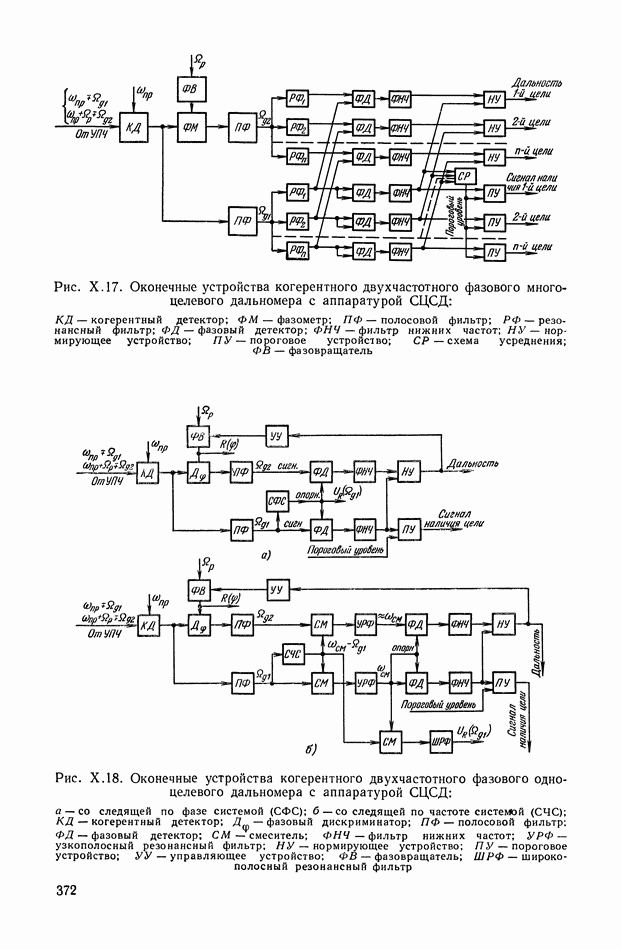
Амплитудная балансная модуляция. Выражение для выходного сигнала  преобразователя (модулятора) можно записать в виде
преобразователя (модулятора) можно записать в виде

где  — периодическая функция модуляции.
— периодическая функция модуляции.
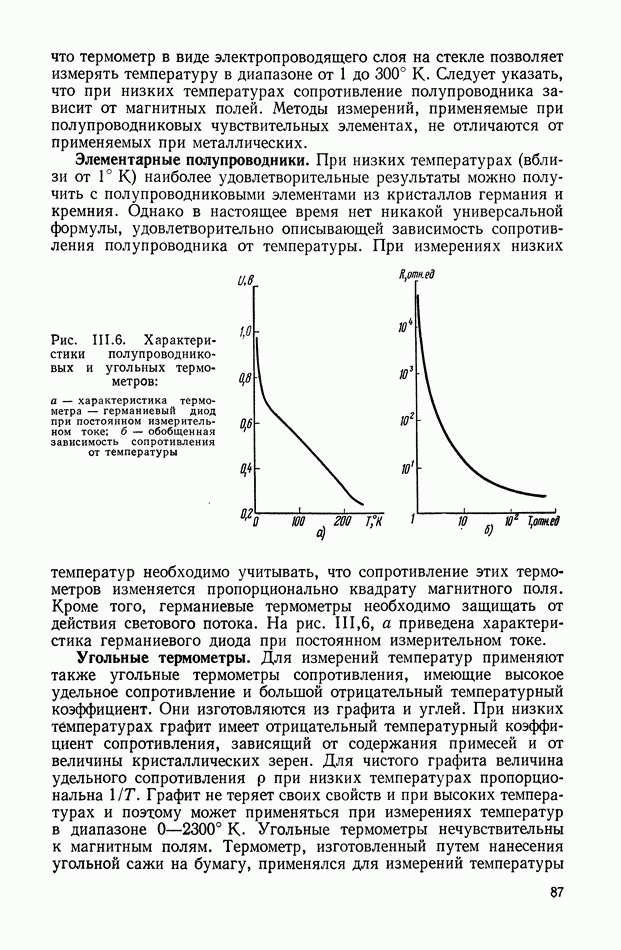
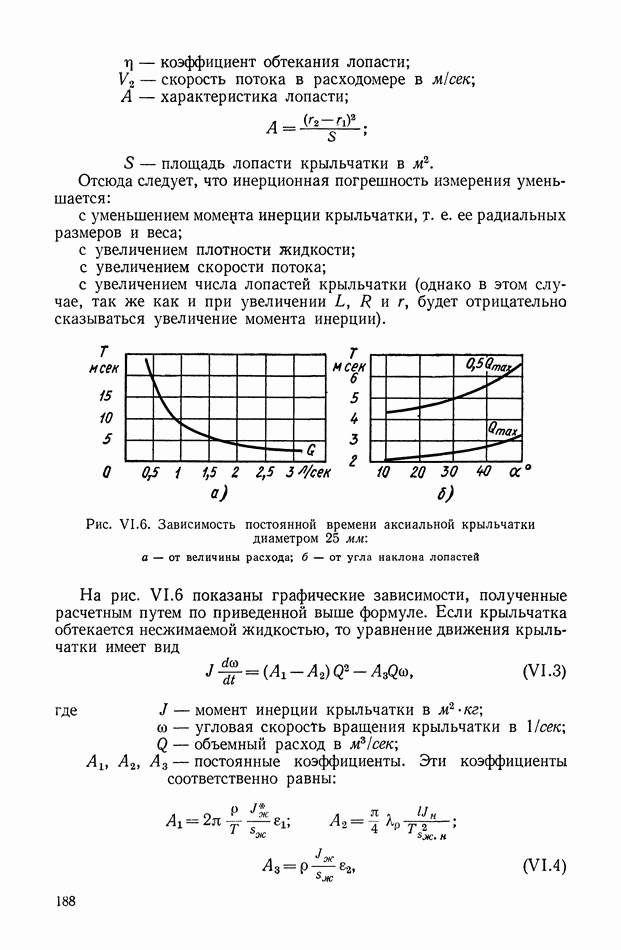
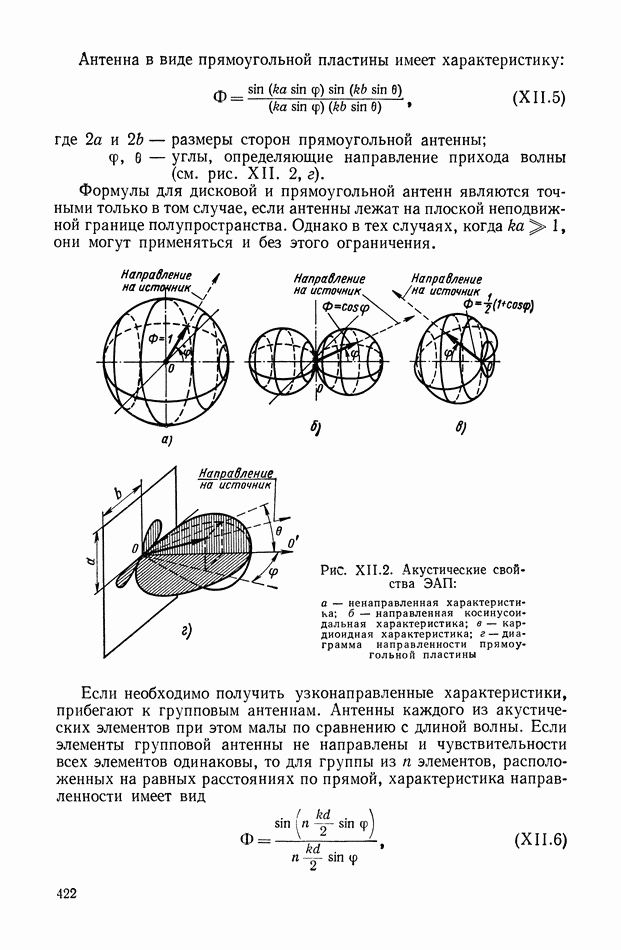
Структурная схема, соответствующая выражению (XIII. 11) приведена на рис. XIII.5. Вид модулированных сигналов для функций модуляции (XII 1.3) и (XIII.4) показан на рис. XIII.6.

Рис. XIII. 5. Структурное изображение амплитудной балансной модуляции: Ф — фильтр.
Результирующий спектр выходного сигнала модулятора отличается от спектра выходного сигнала при небалансной амплитудной модуляции только отсутствием линейчатого спектра  функции модуляции. Амплитудная балансная модуляция также обладает свойством линейности, что позволяет использовать принцип суперпозиции при нахождении спектра выходного сигнала. Фильтр, представленный на рис. XIII.5, выполняет ту же роль, что и фильтр, приведенный на рис. XIII.1.
функции модуляции. Амплитудная балансная модуляция также обладает свойством линейности, что позволяет использовать принцип суперпозиции при нахождении спектра выходного сигнала. Фильтр, представленный на рис. XIII.5, выполняет ту же роль, что и фильтр, приведенный на рис. XIII.1.
Модулированный сигнал типа (XIII. 11) соответствует выходным сигналам сельсинов-трансформаторов, индукционных и др. преобразователей, работающих в системе регулирования.
Отметим, что спектры сигналов с более сложными видами модуляции часто вычисляют на основе эквивалентного перехода к амплитудной модуляции [21.
Рассмотренные схемы амплитудной модуляции (рис. XIII.1 и XII 1.5) объединяют в себе как непрерывные, так и импульсные виды модуляции, что зависит от выбранной функцией модуляции. Если  определяется выражением (XIII.4), то это соответствует
определяется выражением (XIII.4), то это соответствует
непрерывной амплитудной модуляции (AM), а если  имеет вид выражения (XIII.2), — то амплитудно-импульсной модуляции
имеет вид выражения (XIII.2), — то амплитудно-импульсной модуляции  рода
рода 

Рис. XIII.6. Выходной сигнал модулятора (балансная модуляция): а — при функции модуляции последовательность прямоугольных импульсов; б — при функции модуляции — симметричная последовательность прямоугольных импульсов; в — при гармонической функции модуляции.
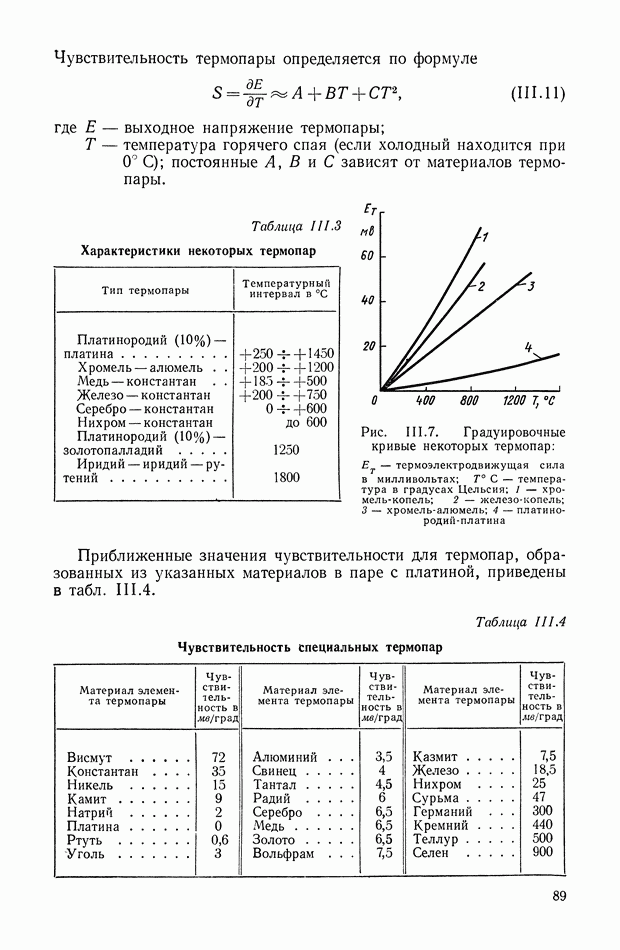
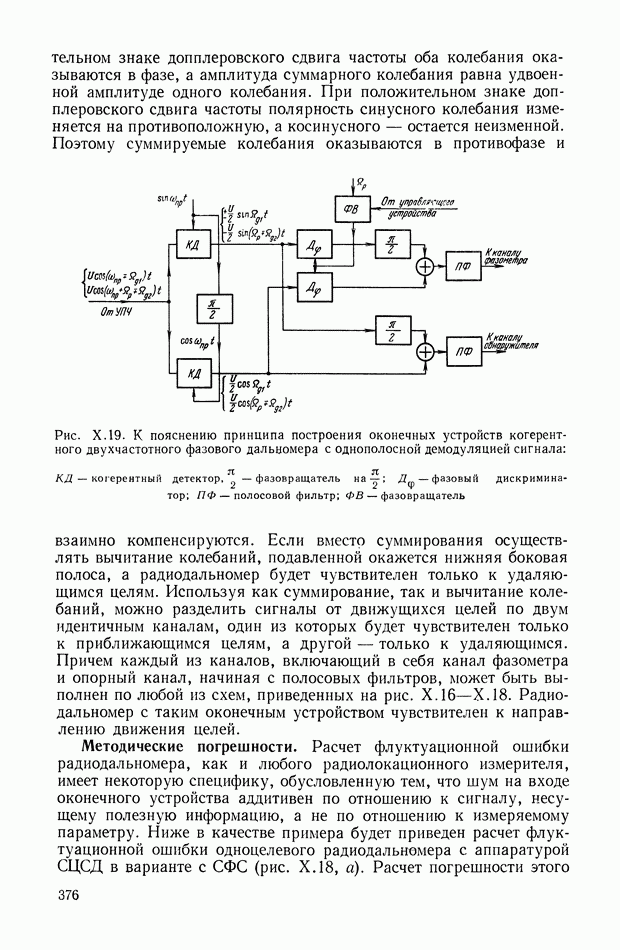
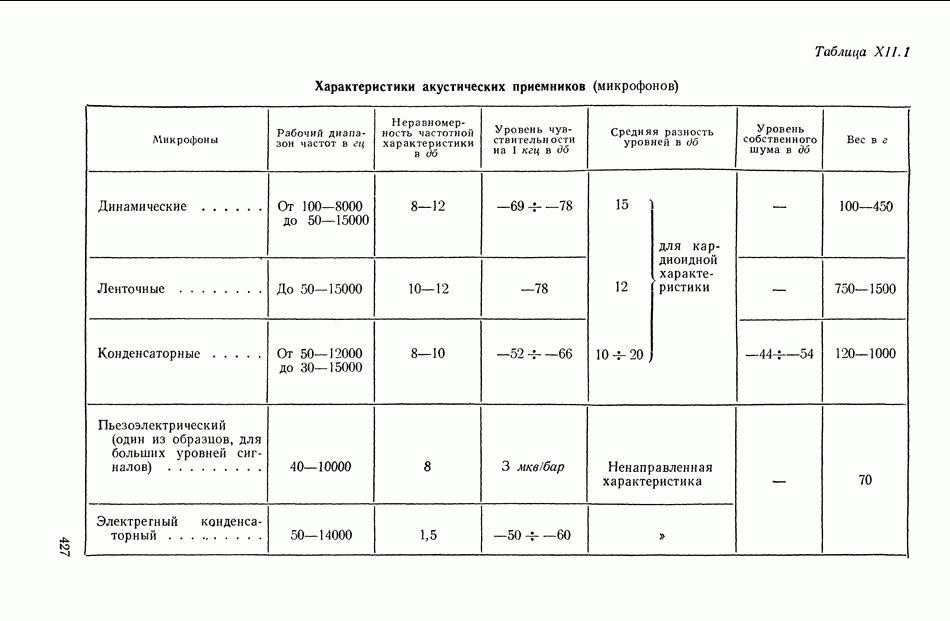
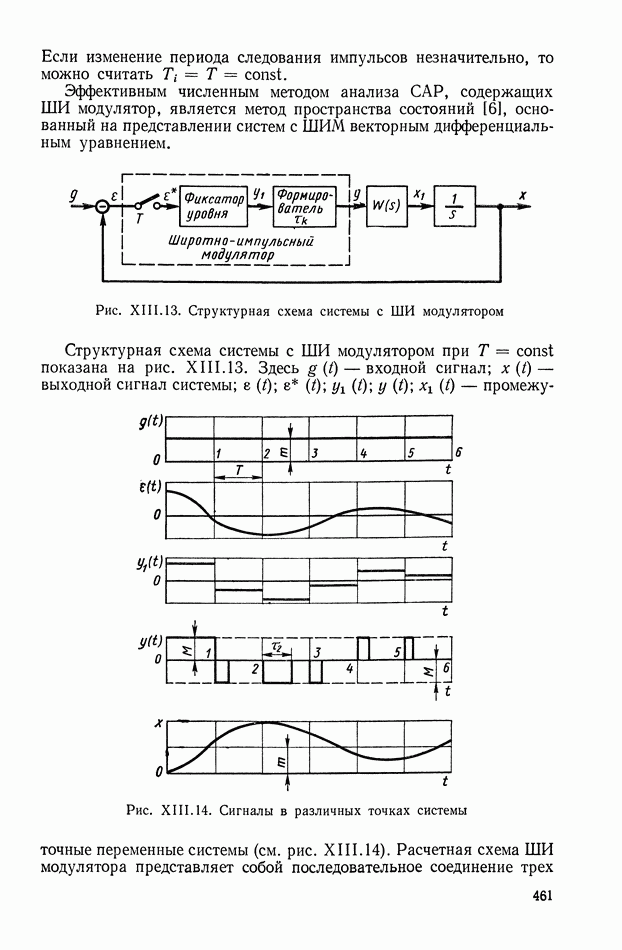
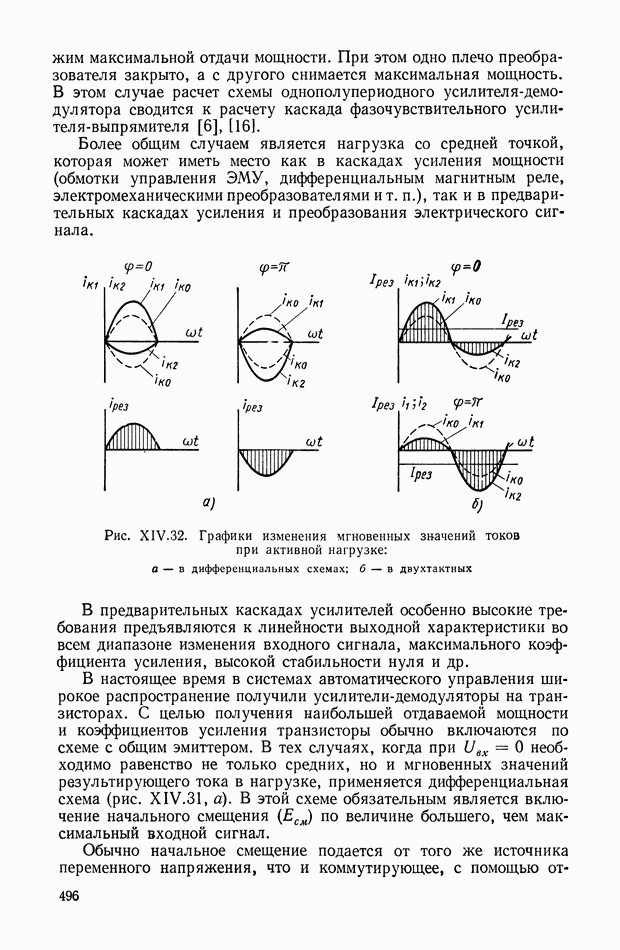
При использовании ЦВМ в системе управления или в импульсной системе можно считать, что ввод информации осуществляется в дискретные моменты времени, длительность которых составляет малую величину.

Рис. XII 1.7. Прохождение сигнала: а — через дискретный преобразователь (ключ); б — через последовательное соединение дискретного преобразователя и фильтра
Это соответствует функции модуляции (XIII.2) при  Устройство, выполняющее такое преобразование, называется дискретным преобразователем или просто ключом (рис. XIII.7).
Устройство, выполняющее такое преобразование, называется дискретным преобразователем или просто ключом (рис. XIII.7).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
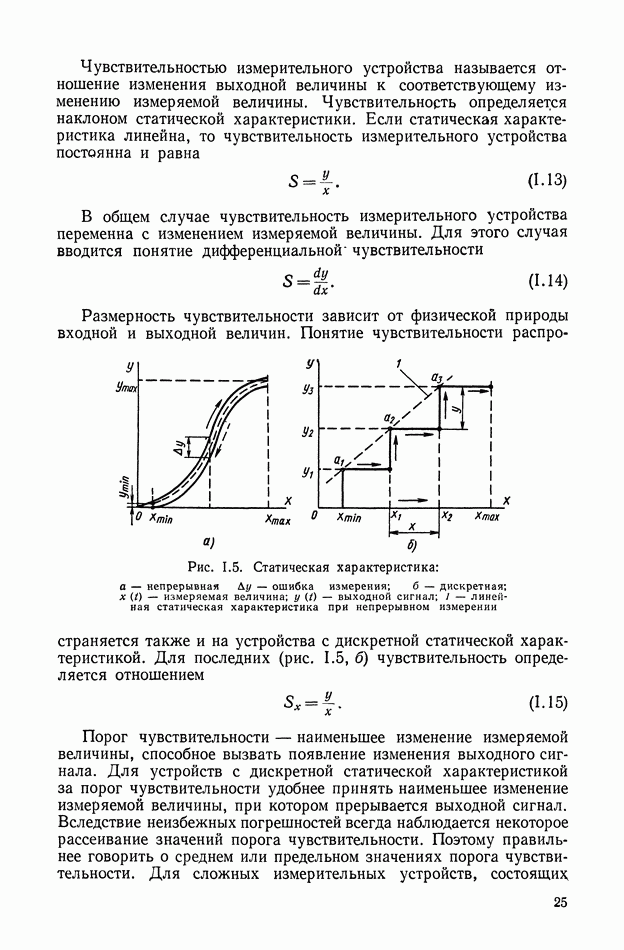
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
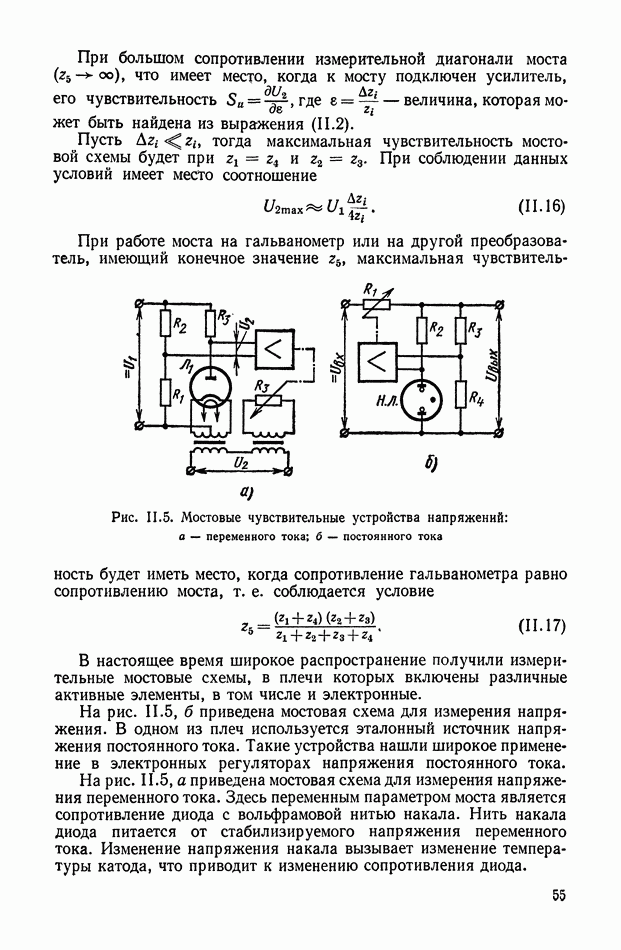
- 1. МОСТОВЫЕ СХЕМЫ
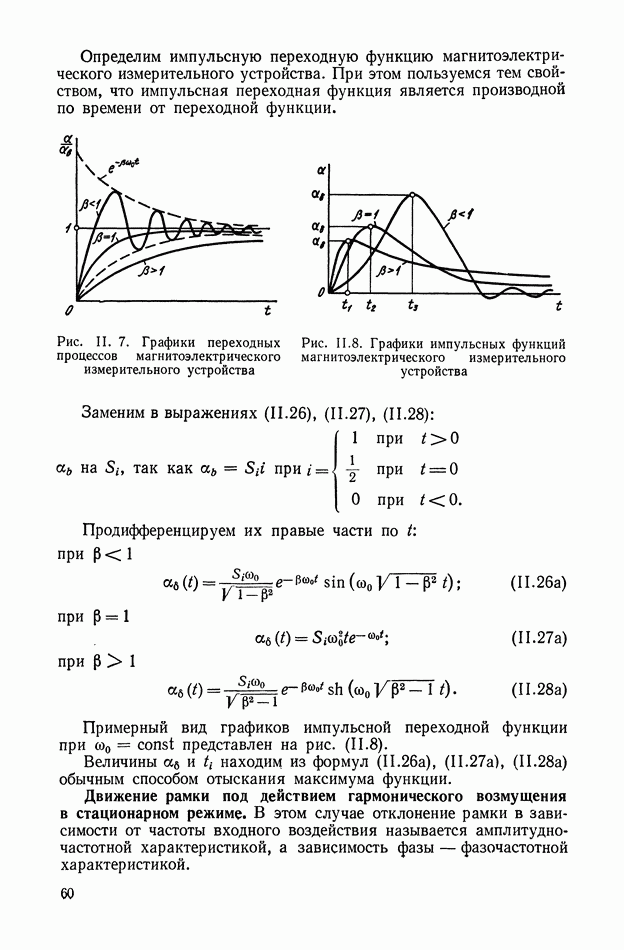
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
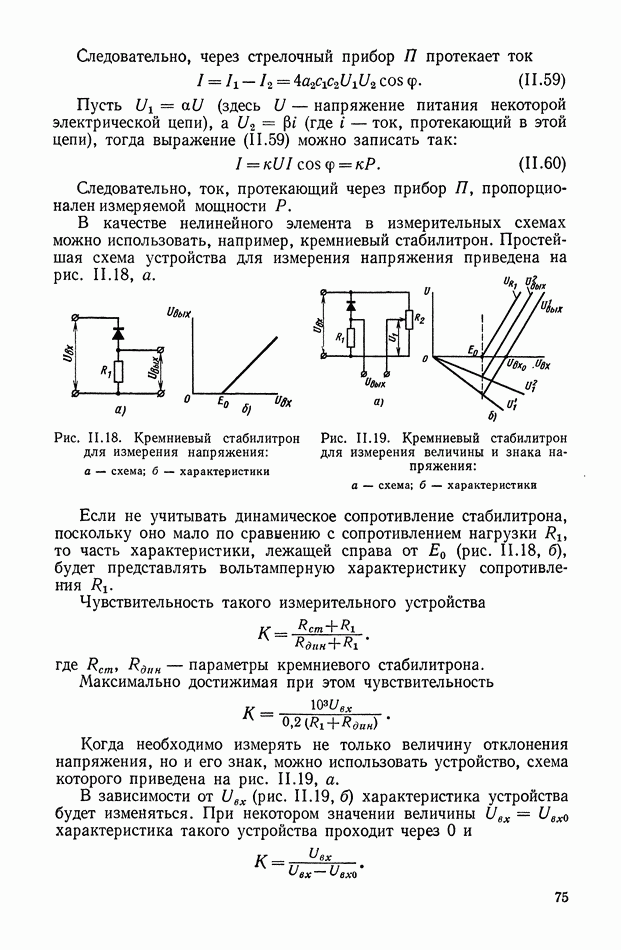
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
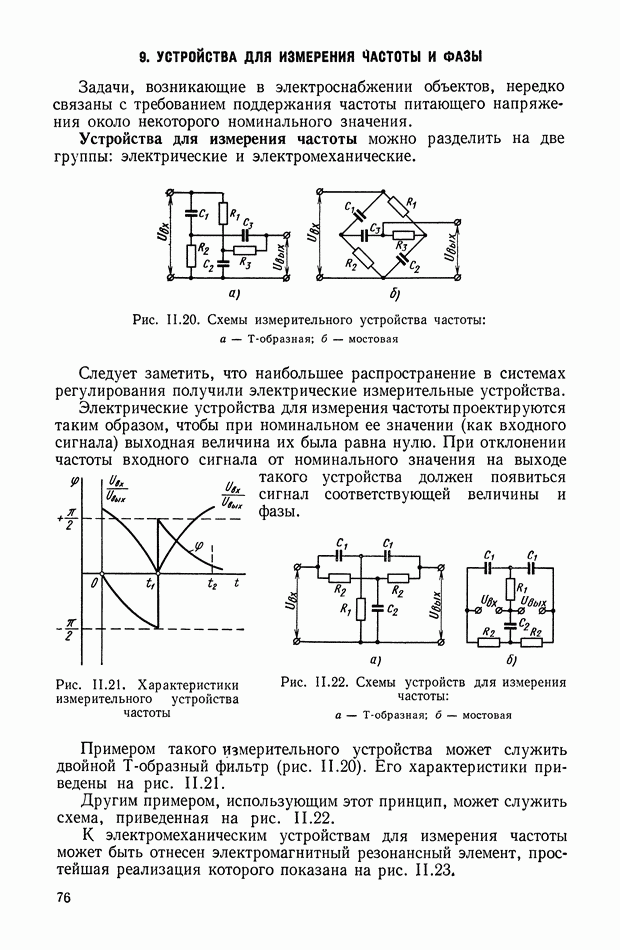
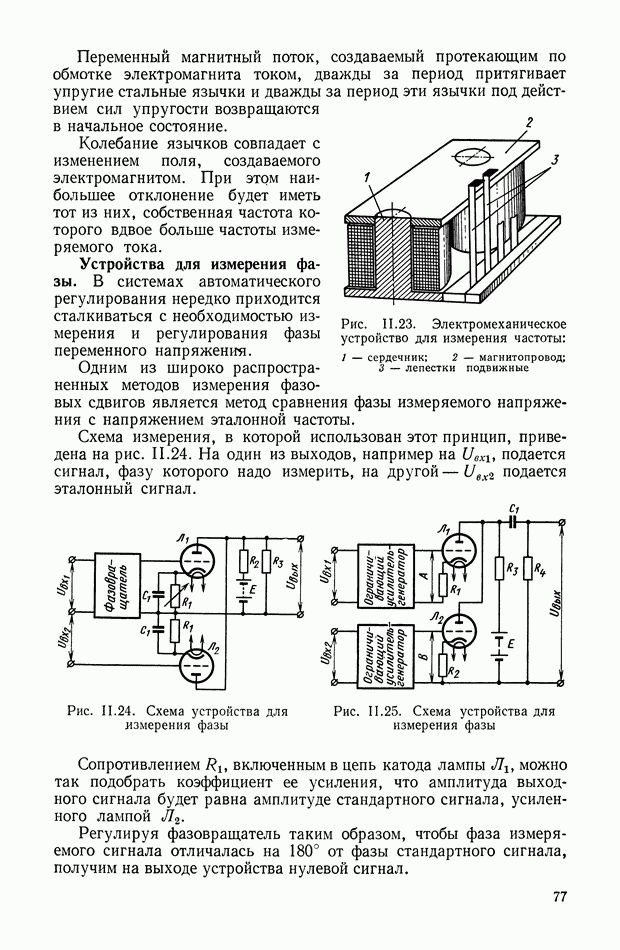
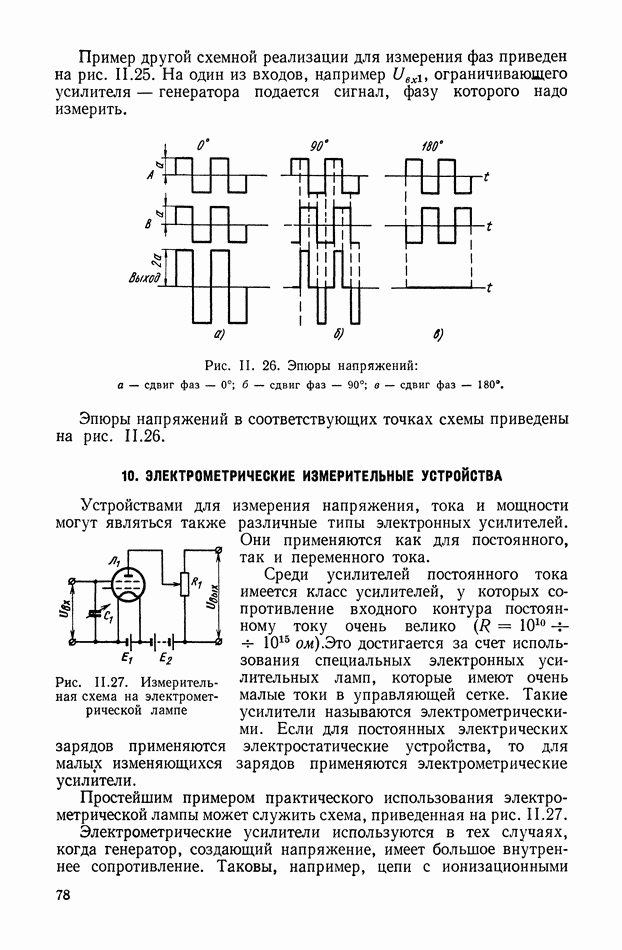
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
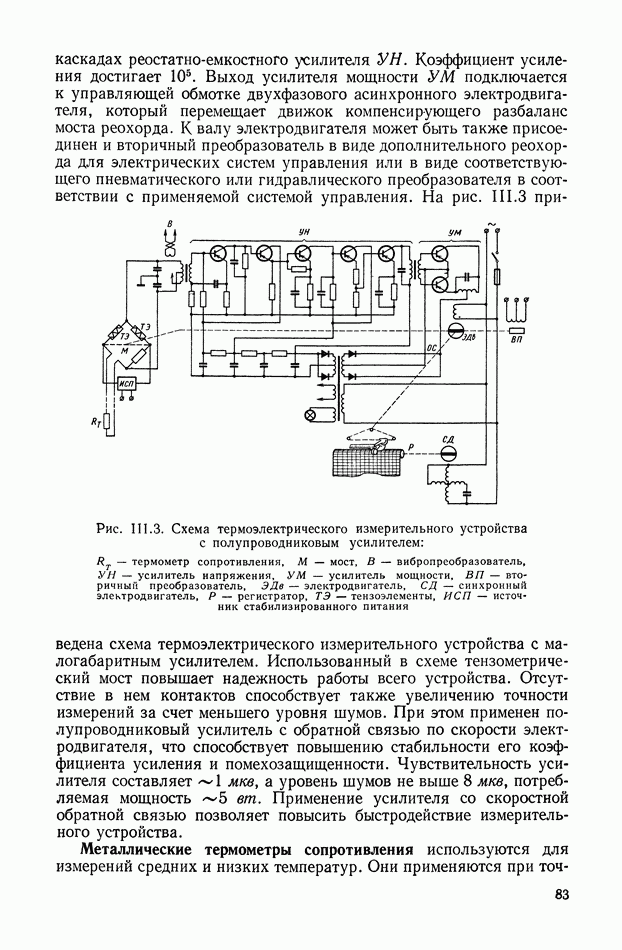
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
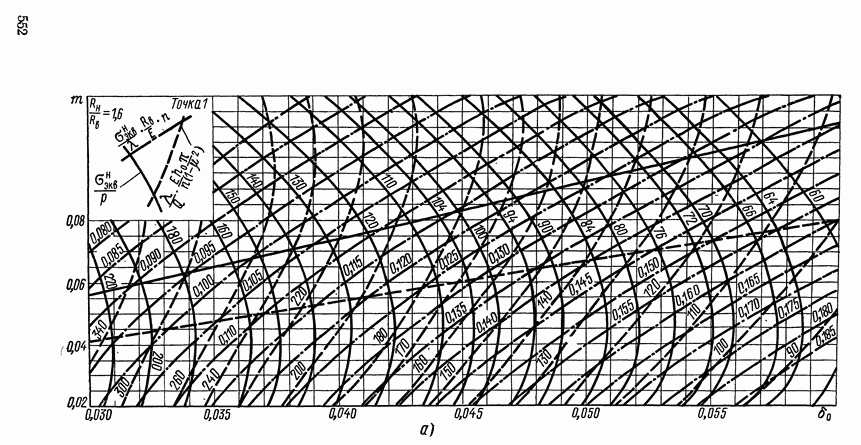
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
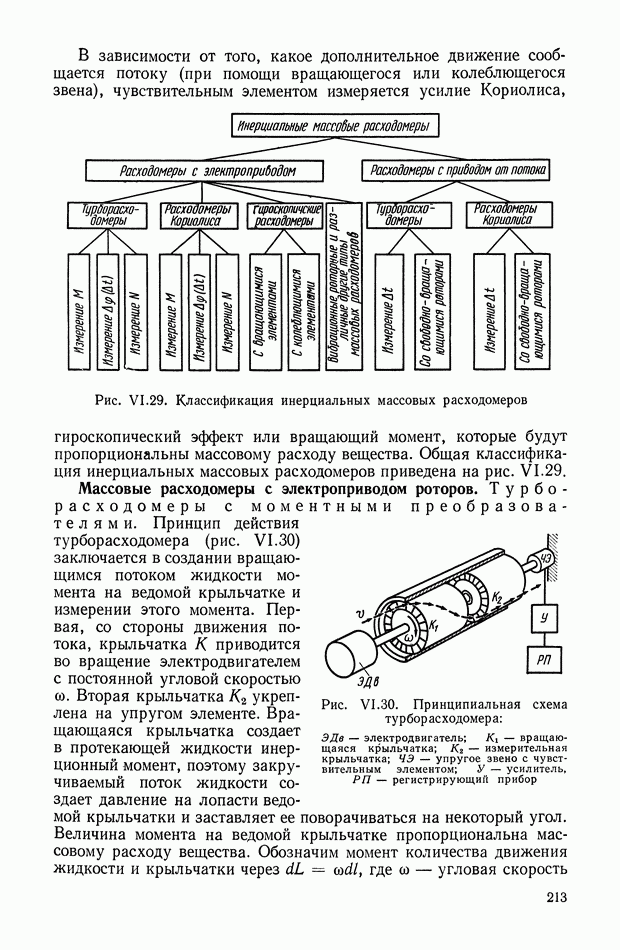
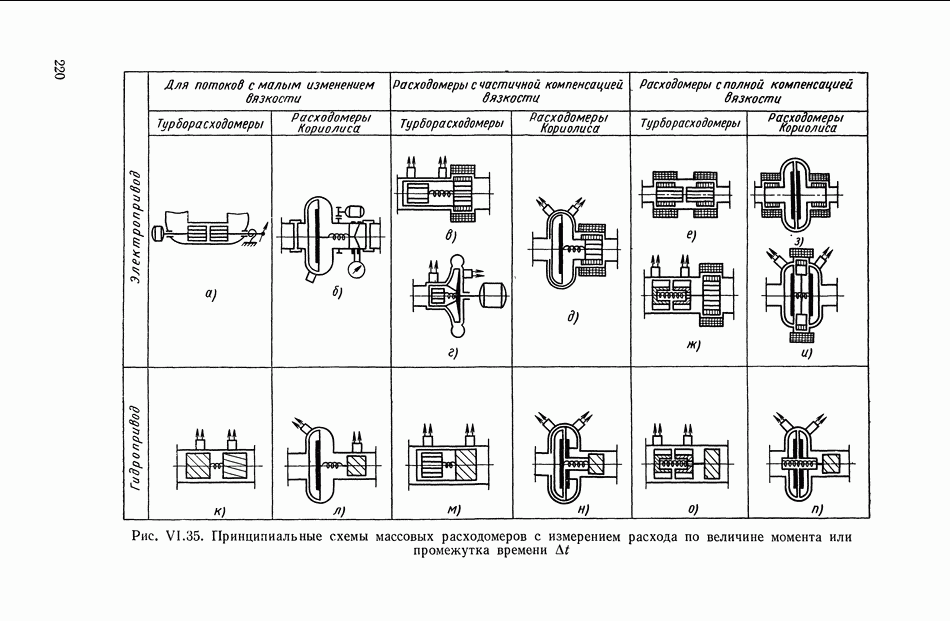
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
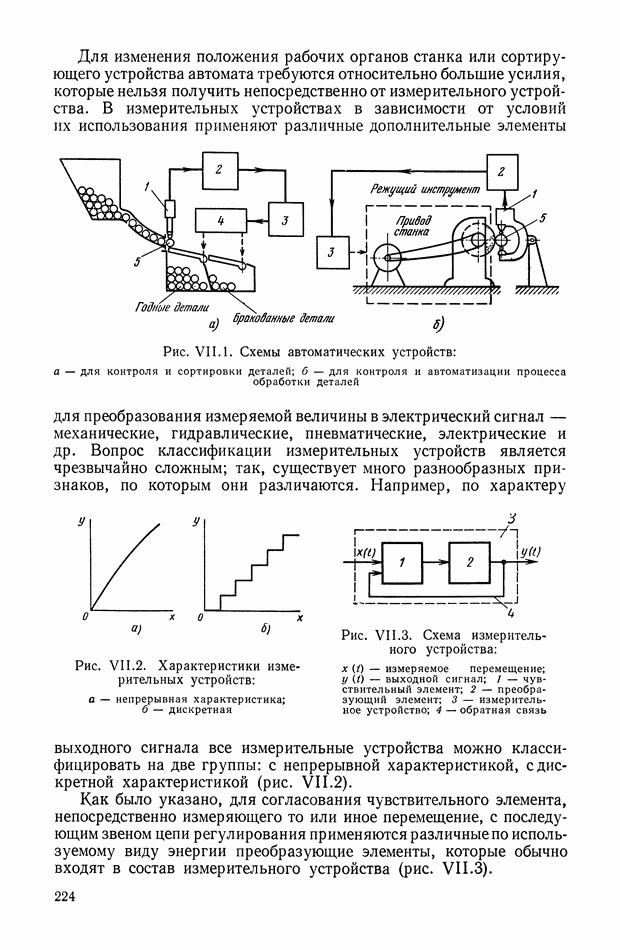
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
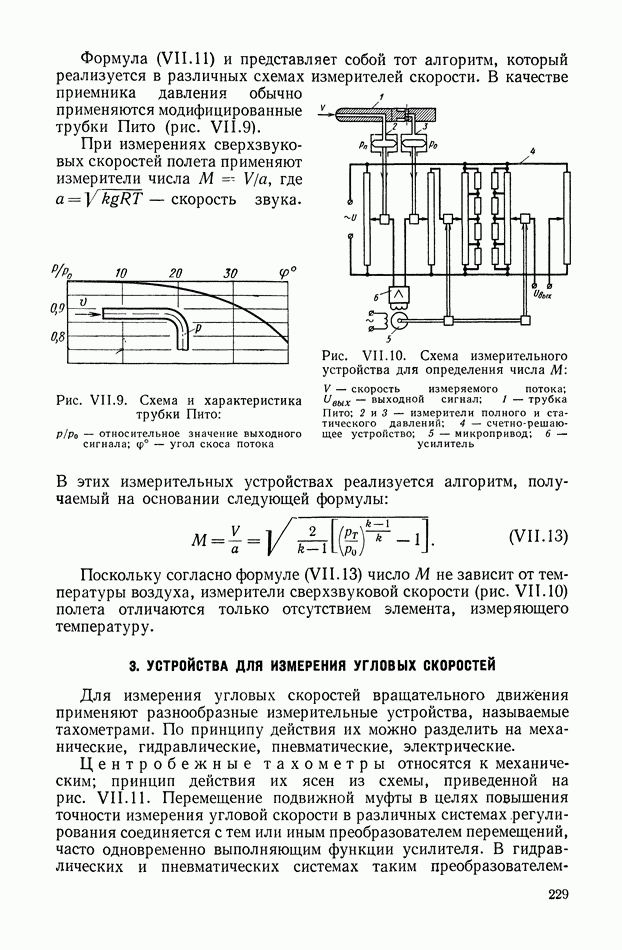
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
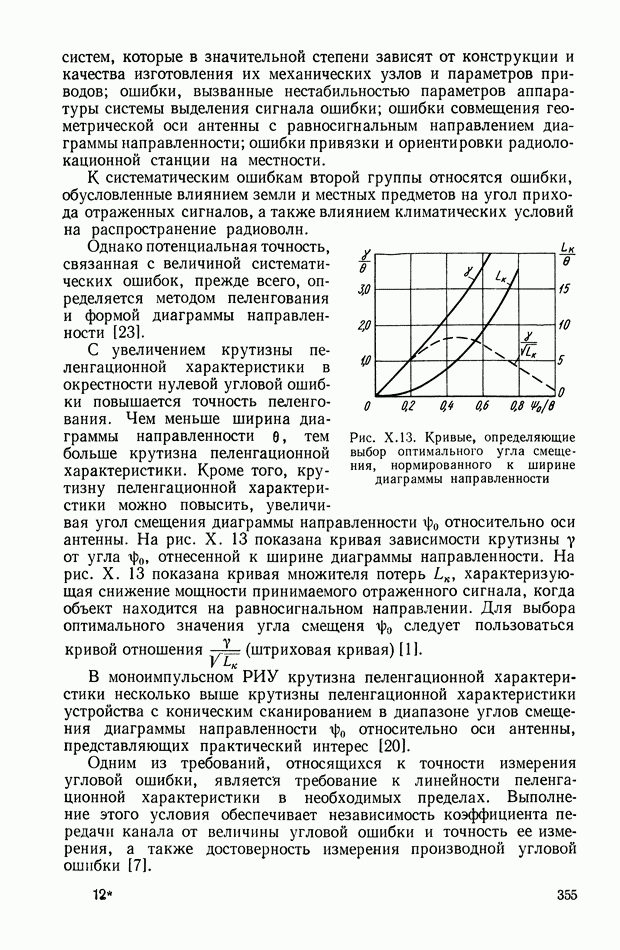
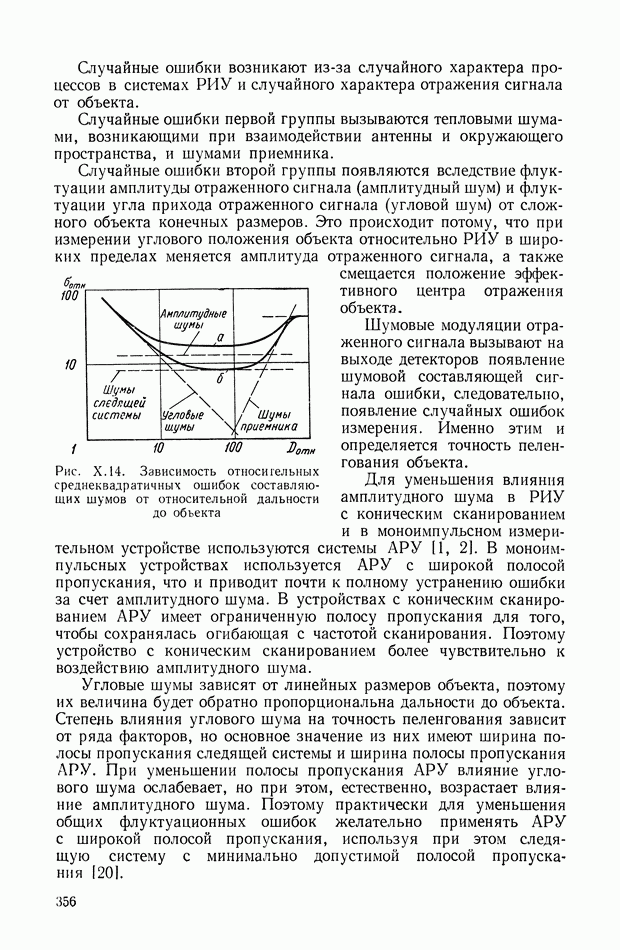
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
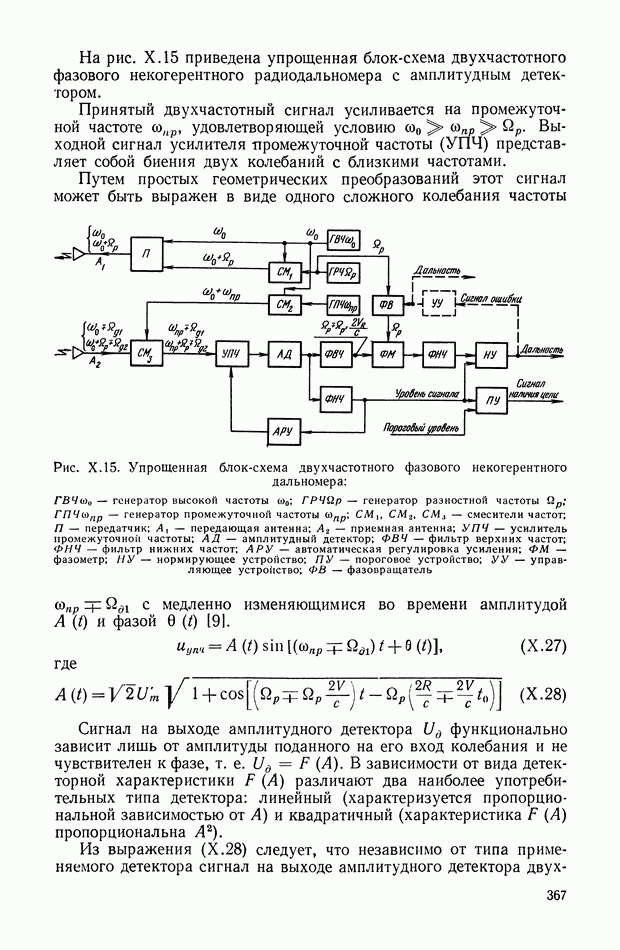
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
- 1. МОДУЛЯТОРЫ
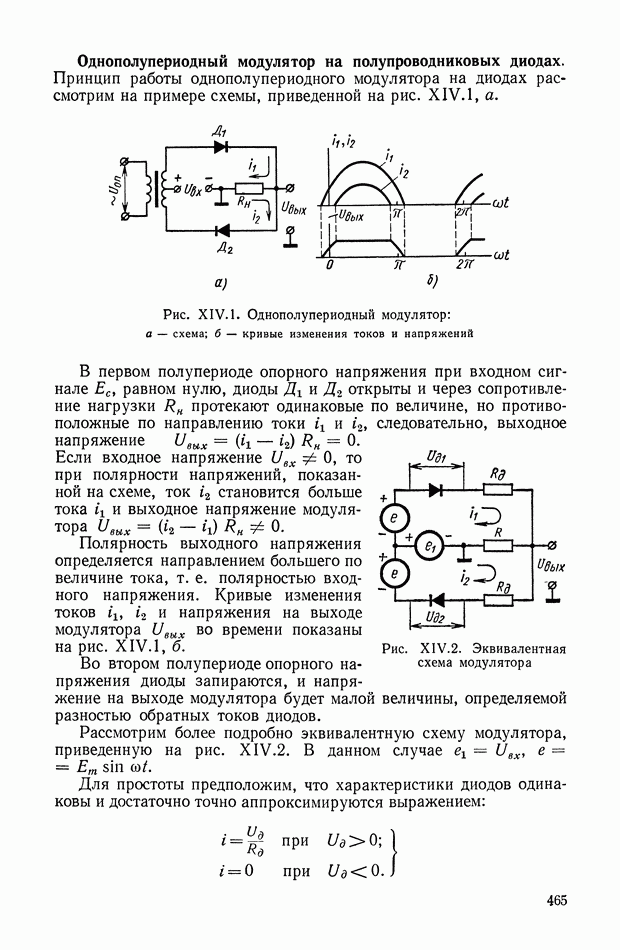
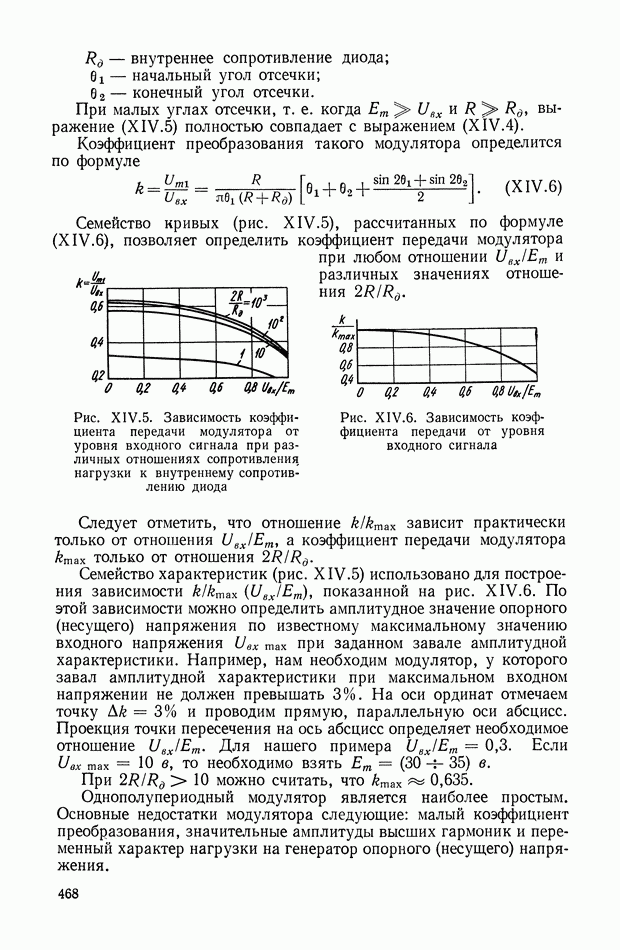
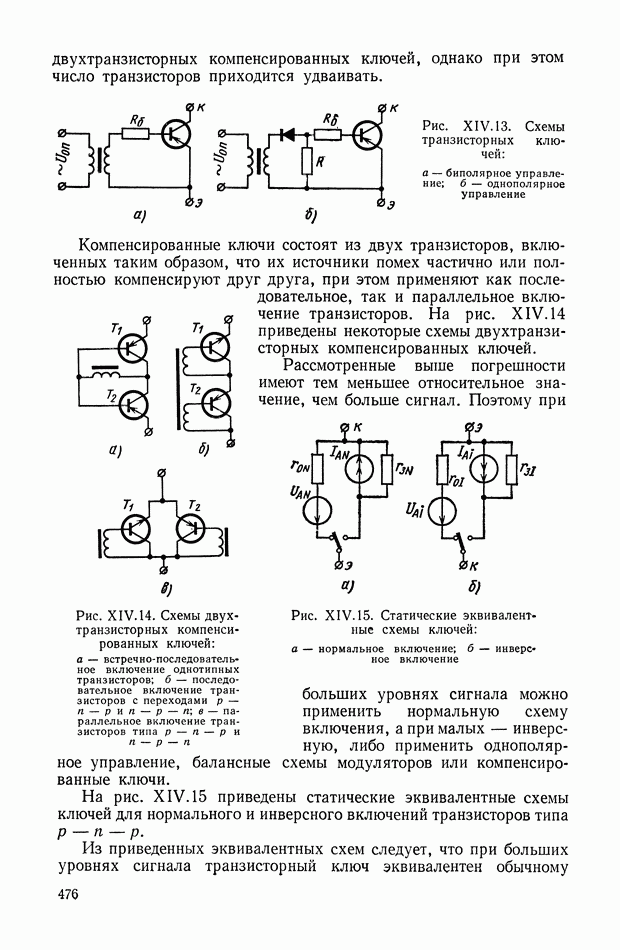
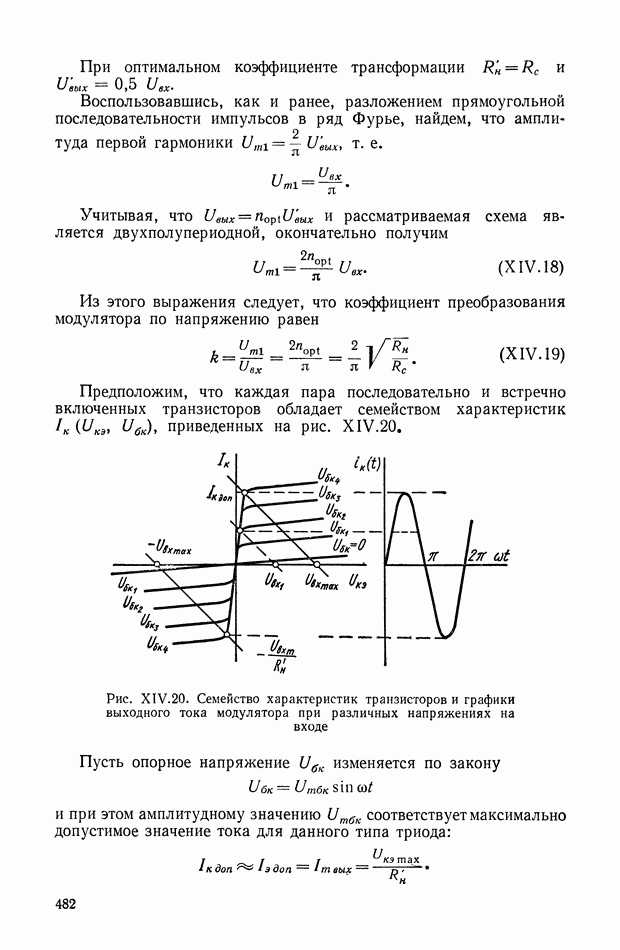
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
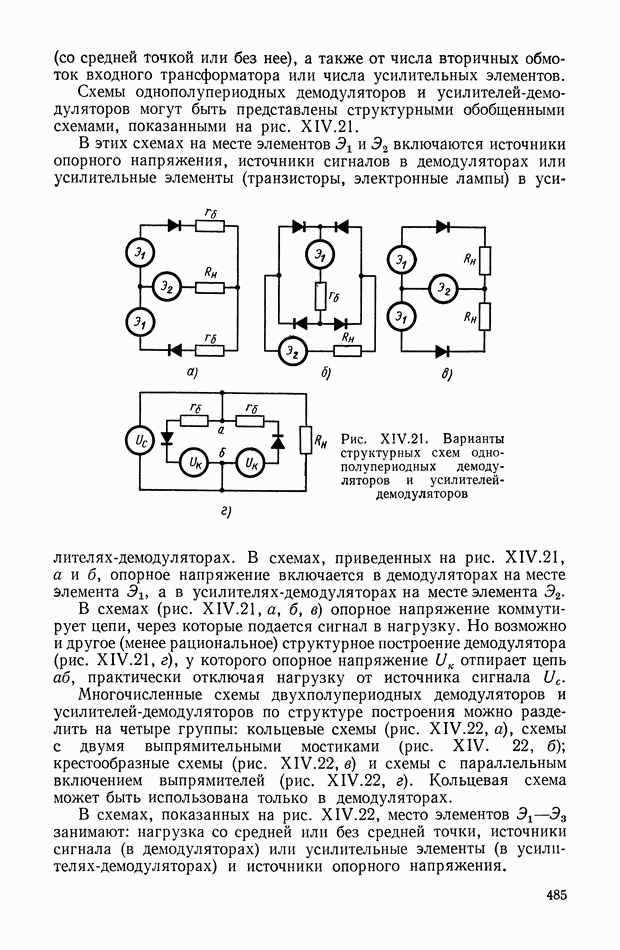
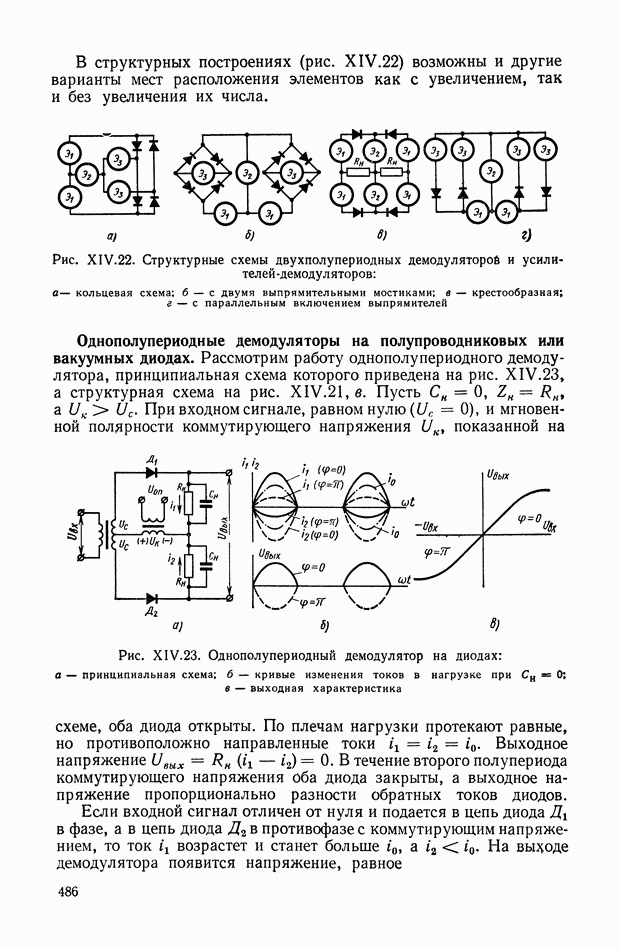
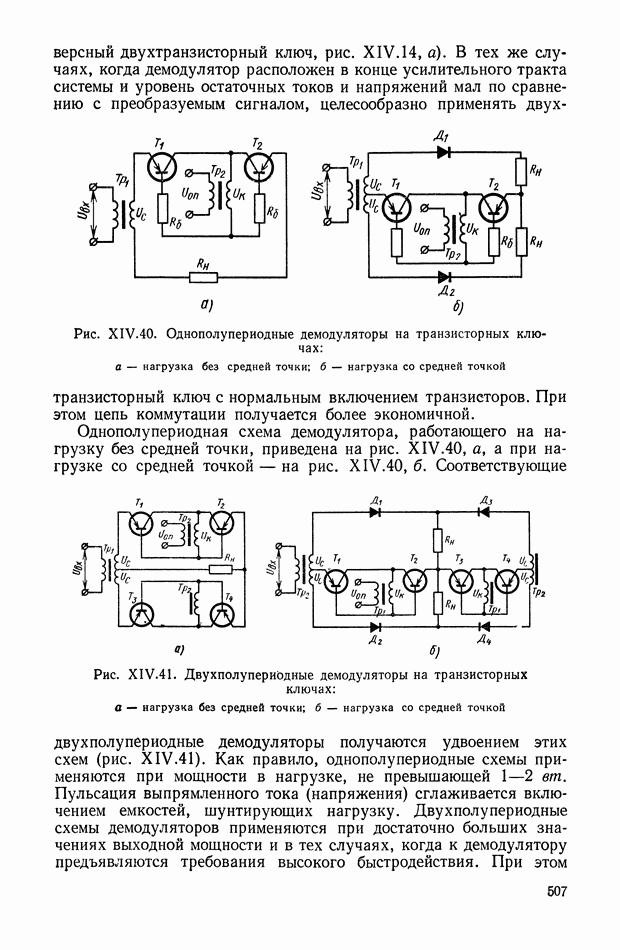
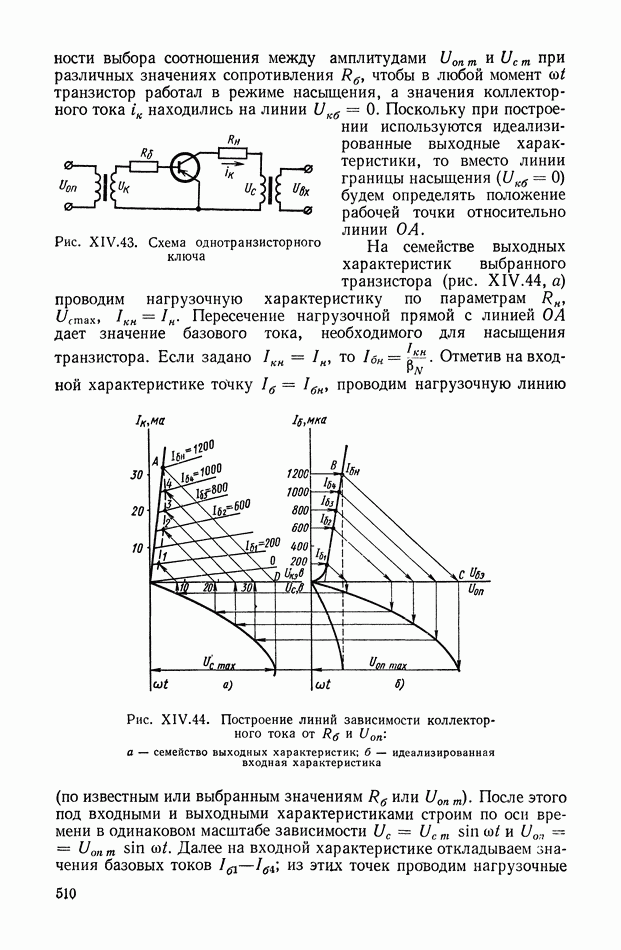
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
- Двухполупериодные демодуляторы на диодах.
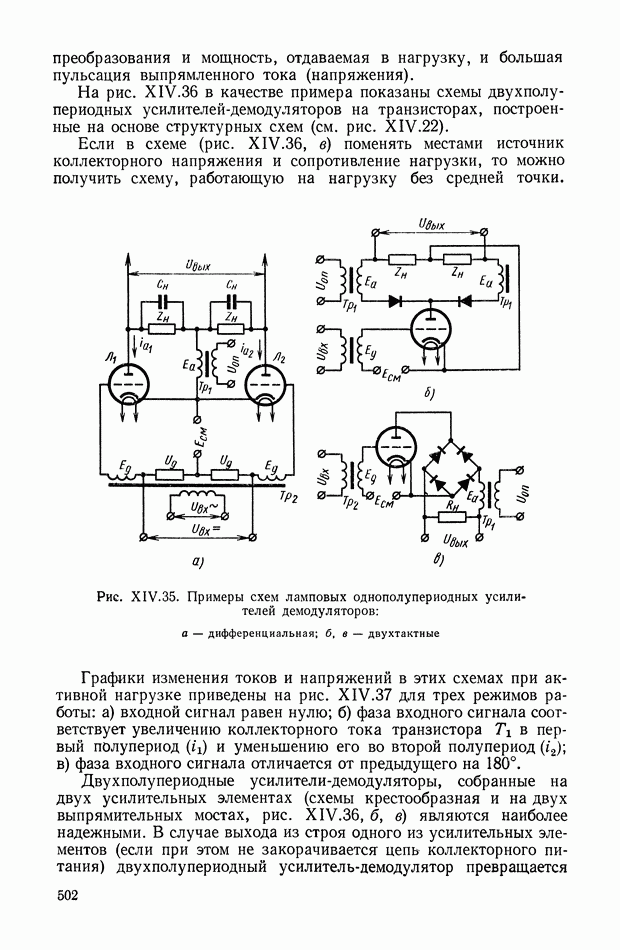
- Однополупериодные усилители-демодуляторы.
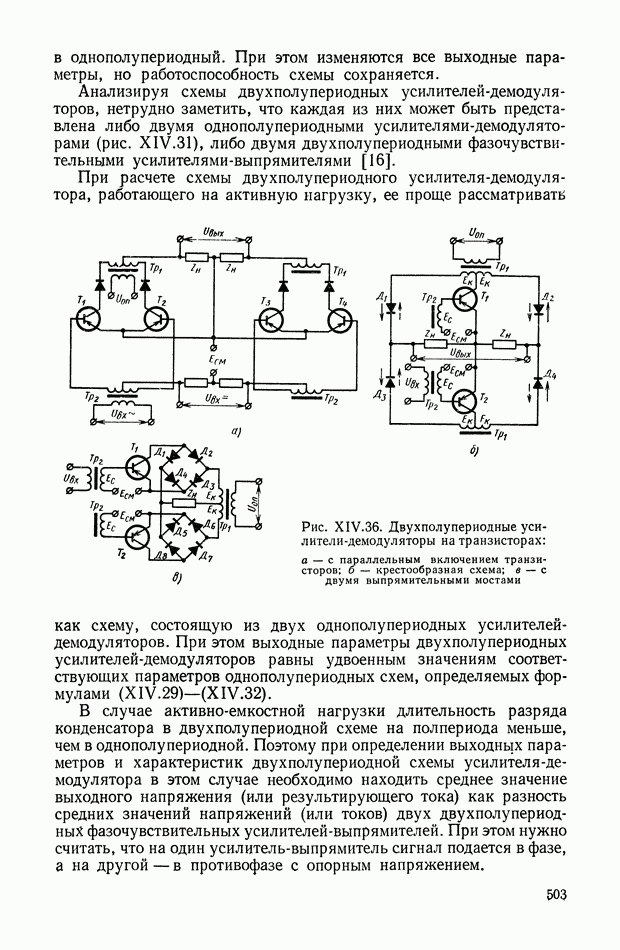
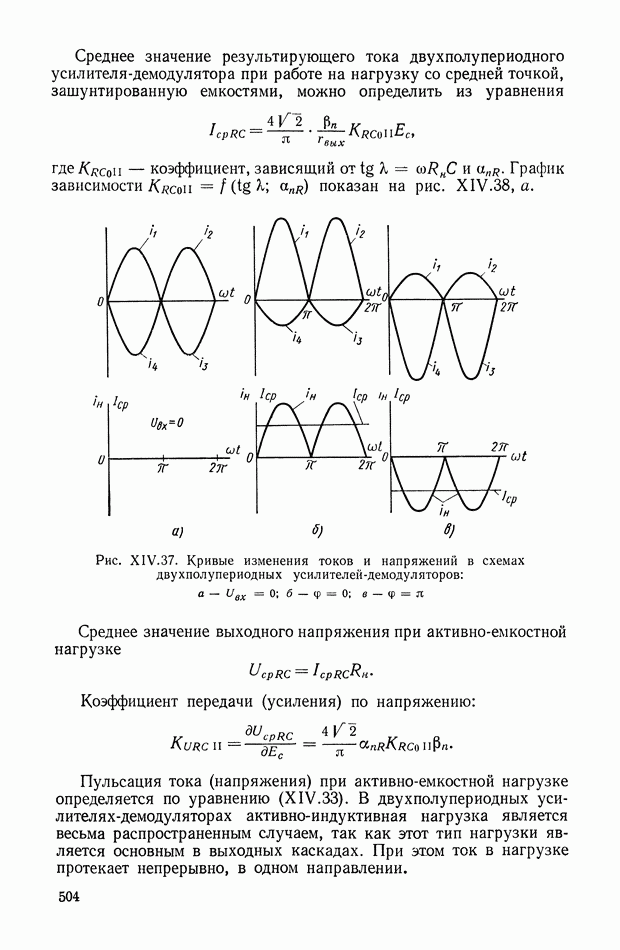
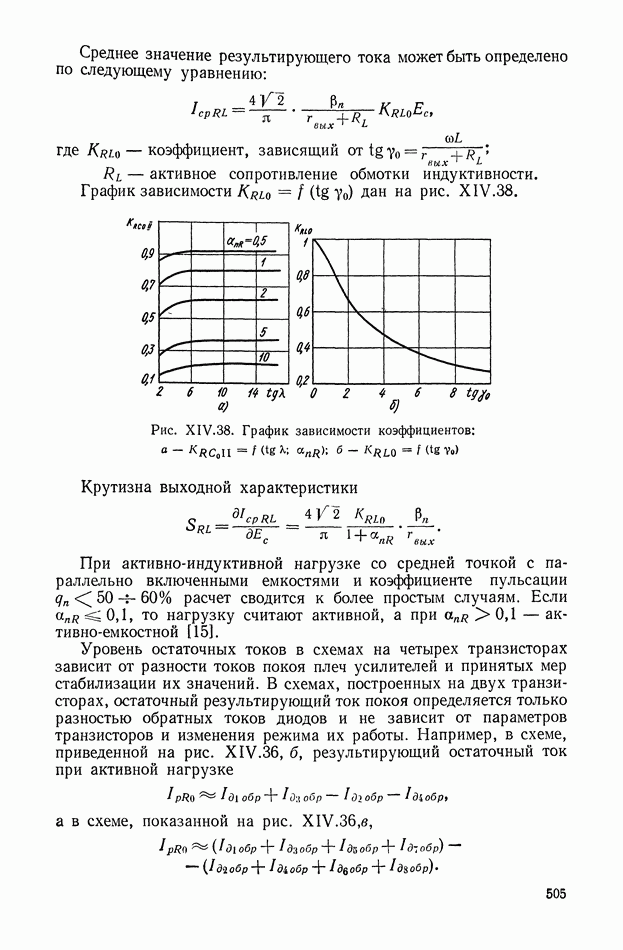
- Двухполупериодные усилители-демодуляторы.
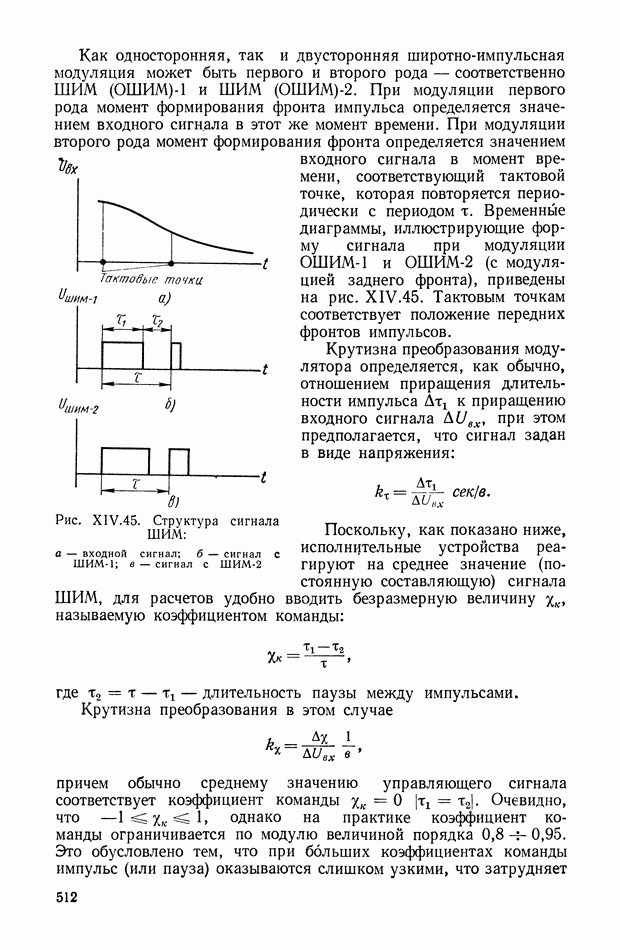
- Демодуляторы на транзисторных ключах.
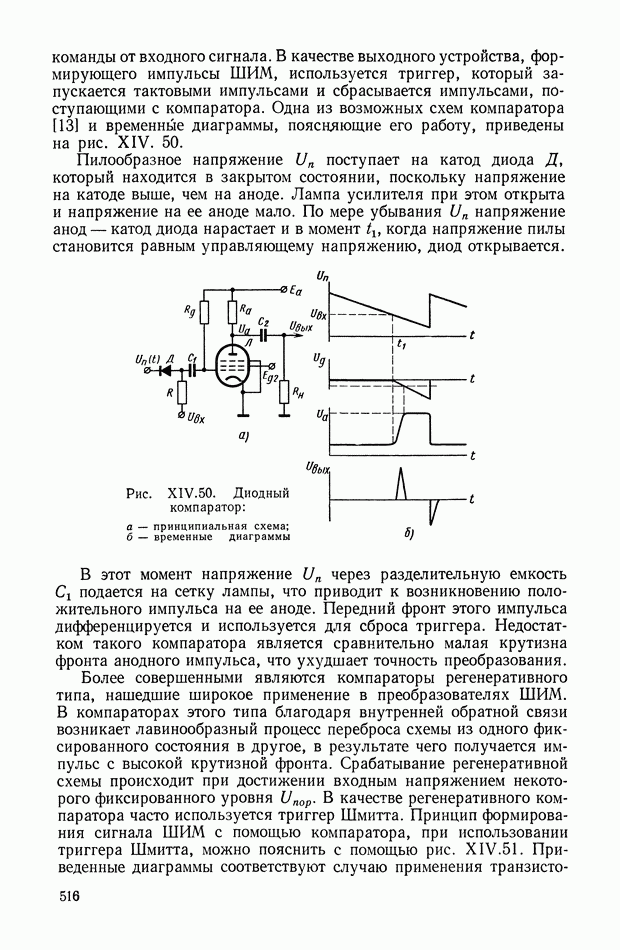
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
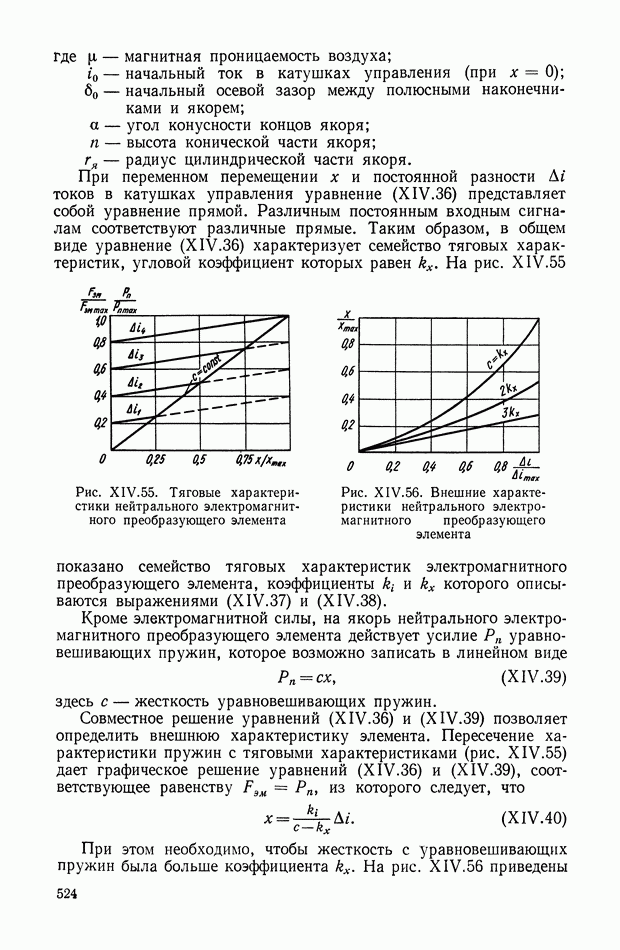
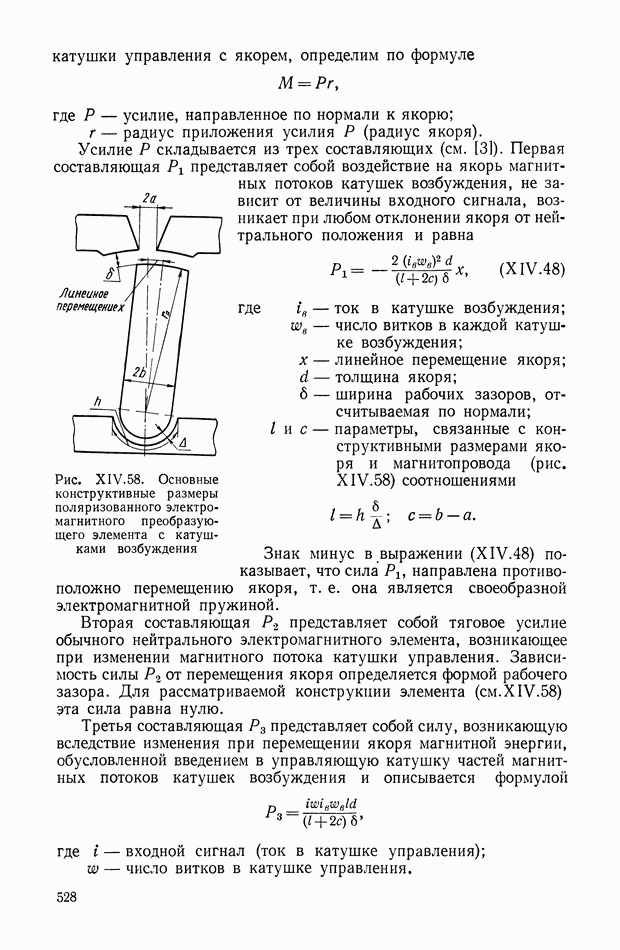
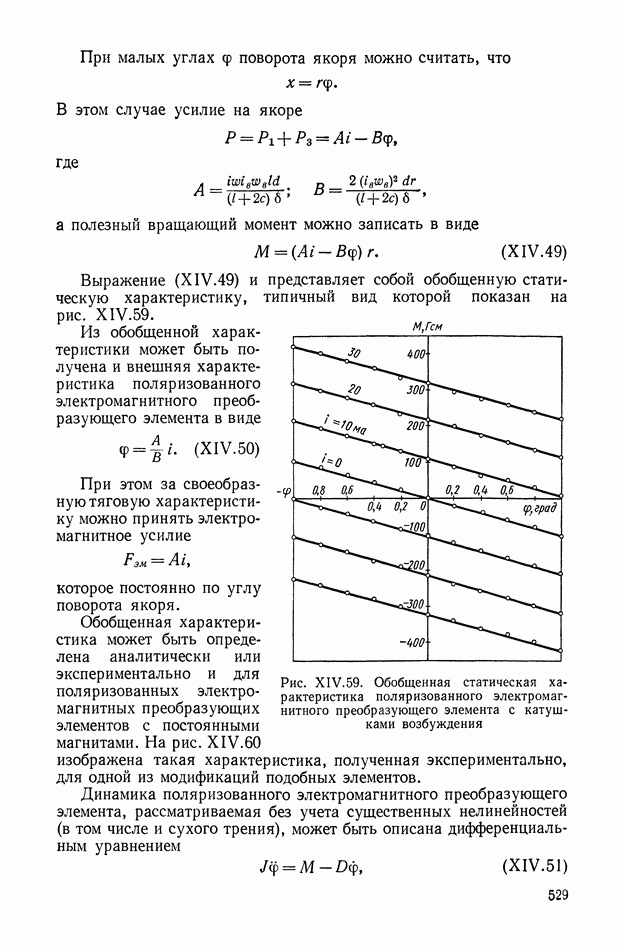
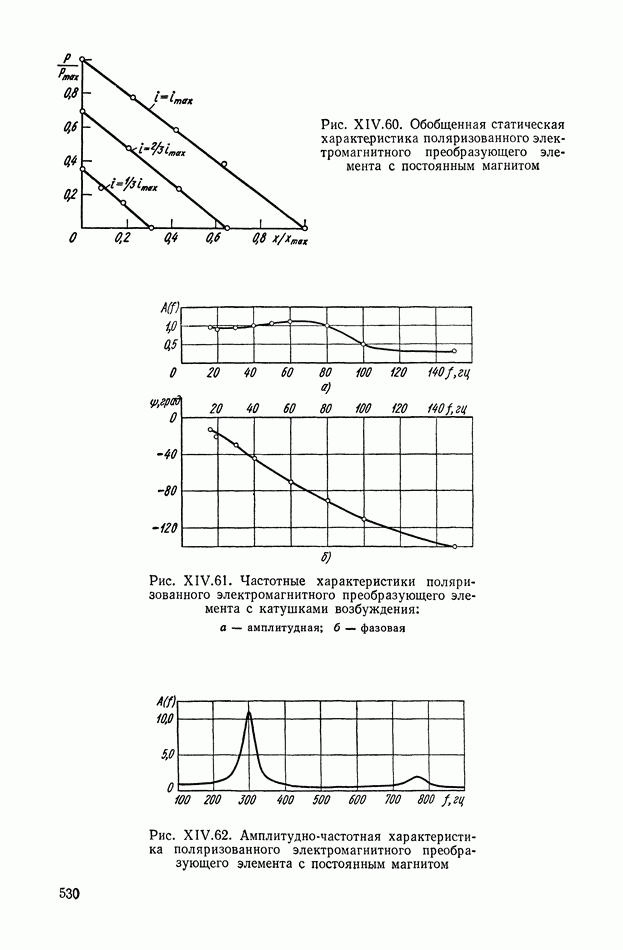
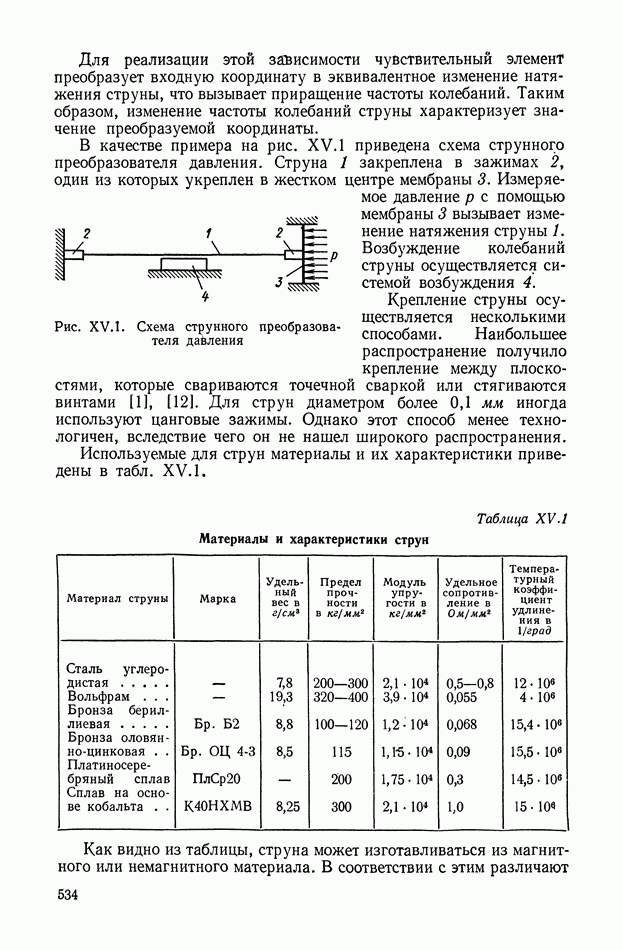
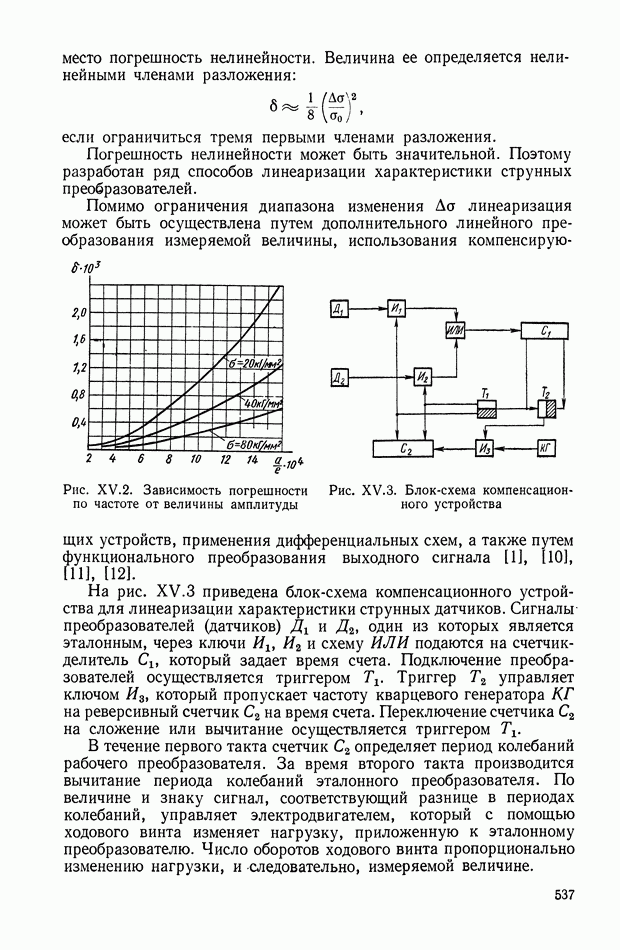
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
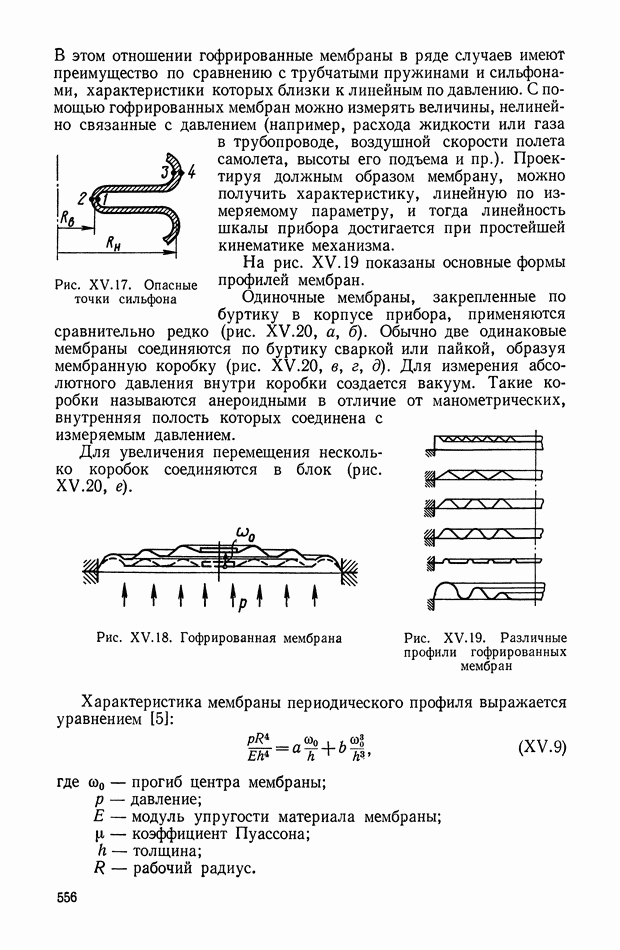
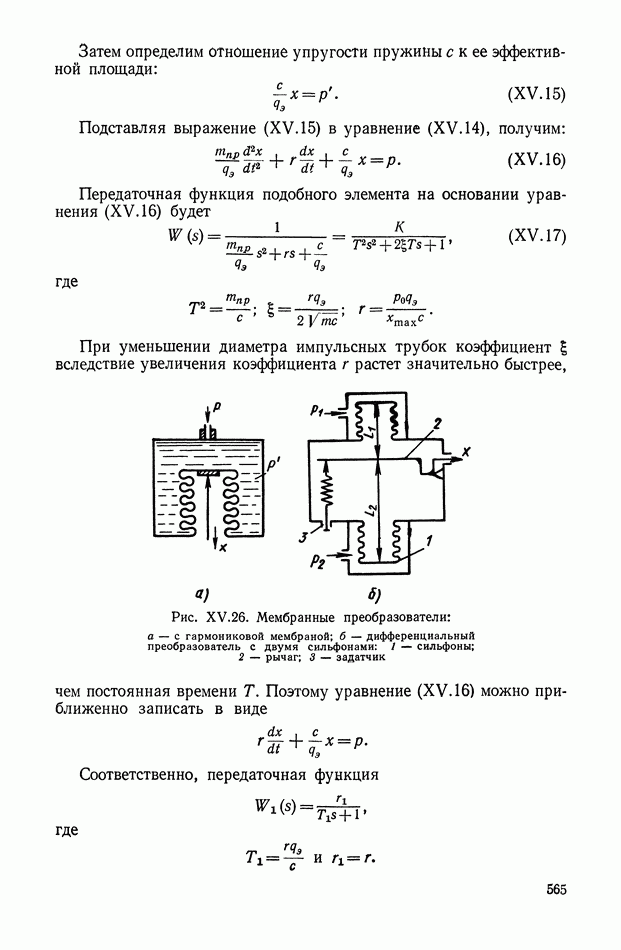
- Сильфоны.
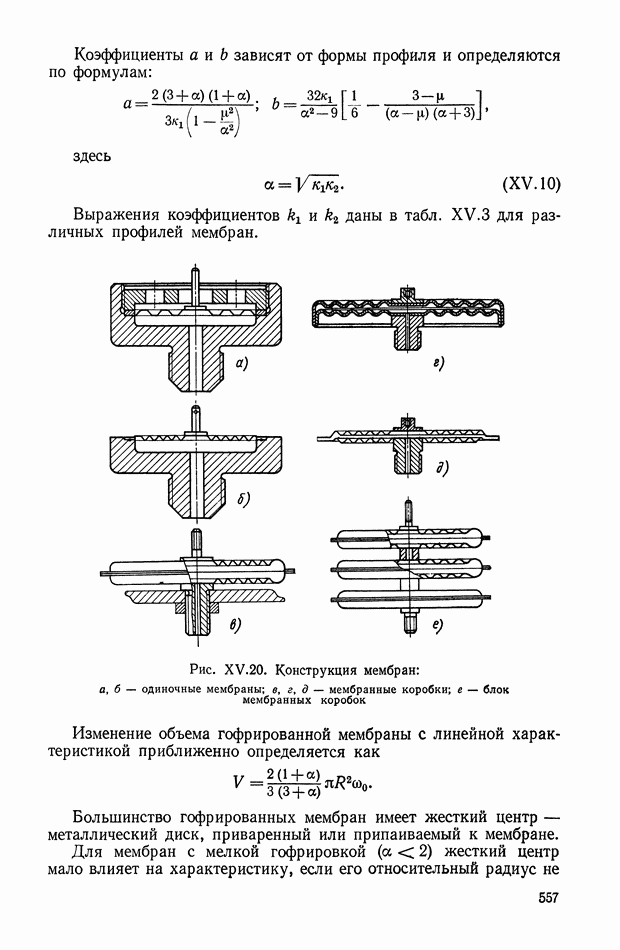
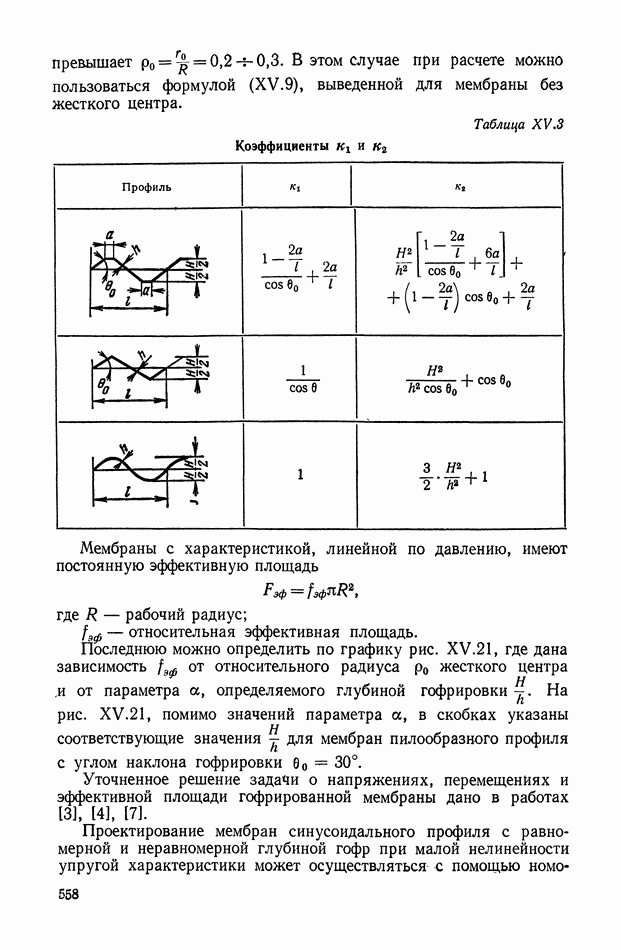
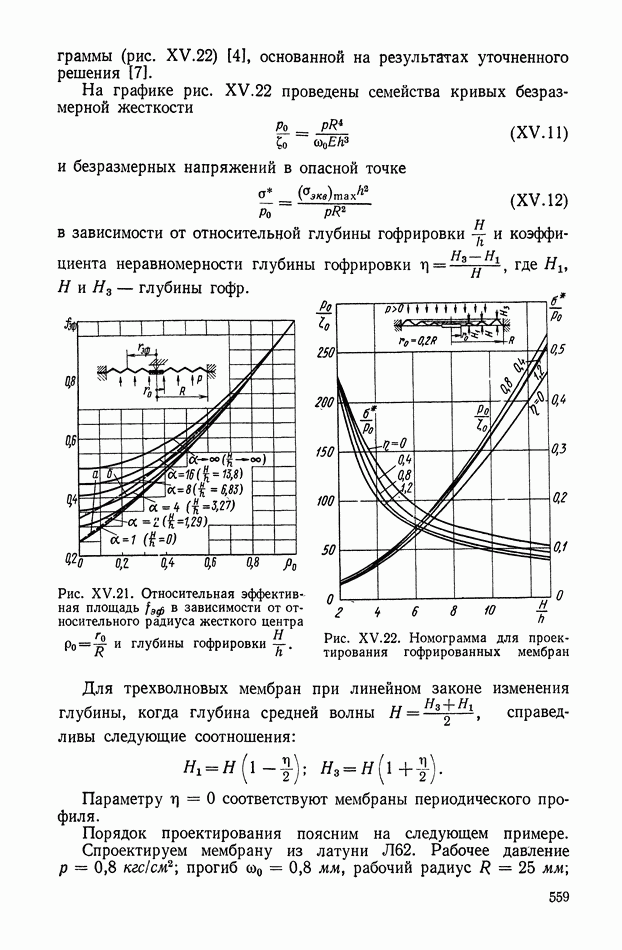
- Гофрированные мембраны.
- Гибкие диафрагмы.
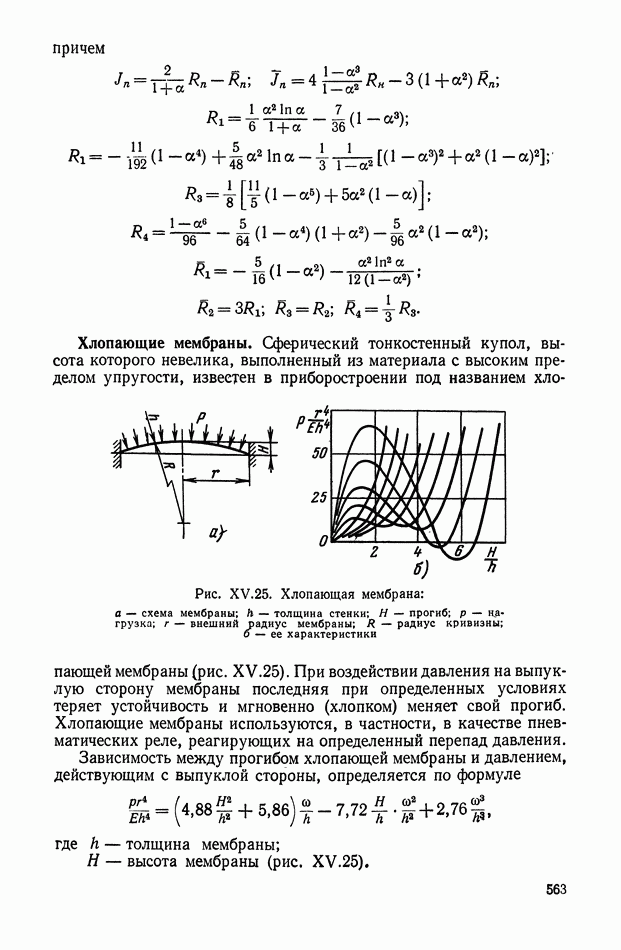
- Хлопающие мембраны.
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
- Пневмоэлектроконтактные преобразователи линейных величин.
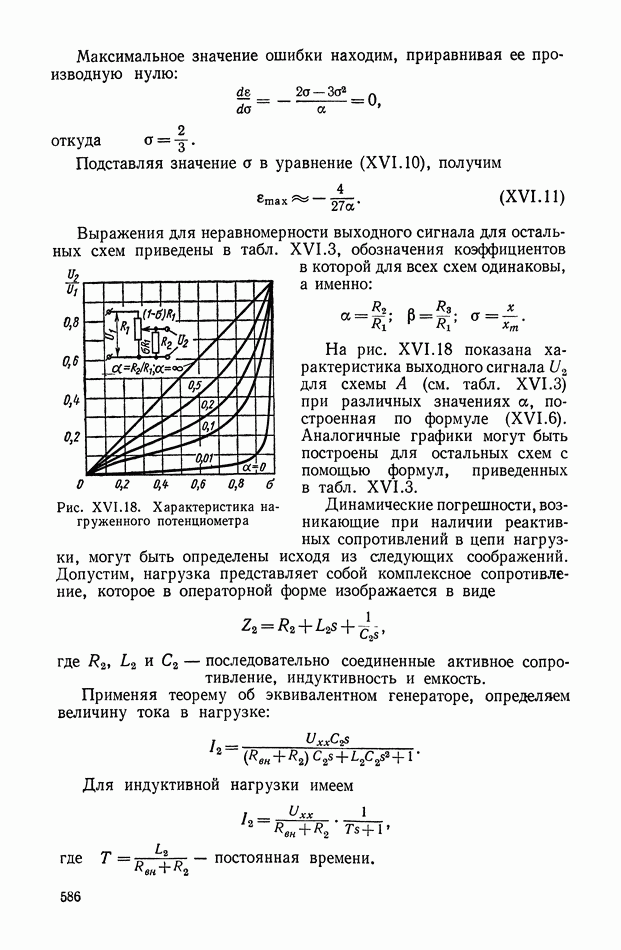
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
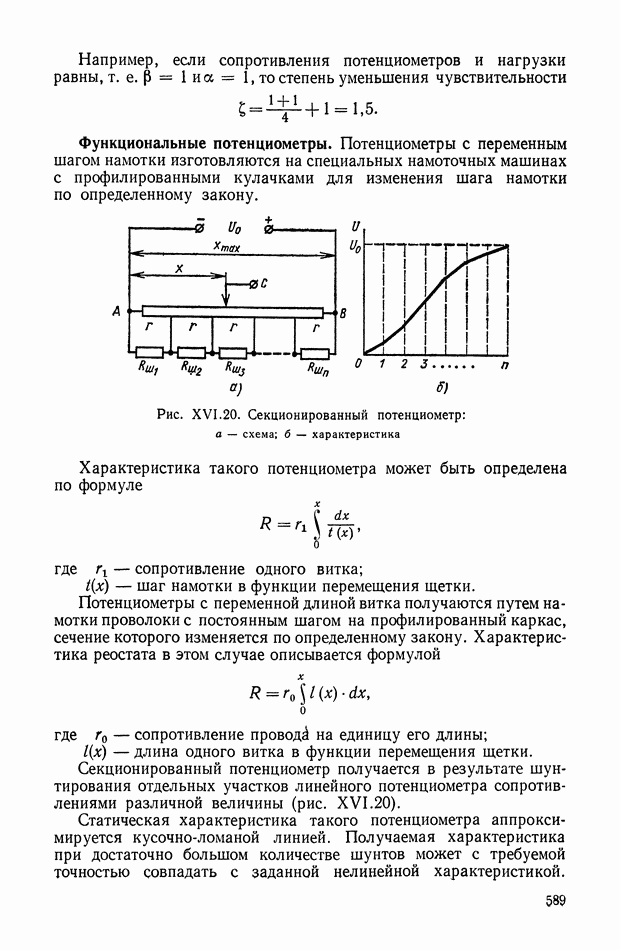
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
- Работа сельсинов в трансформаторном режиме.
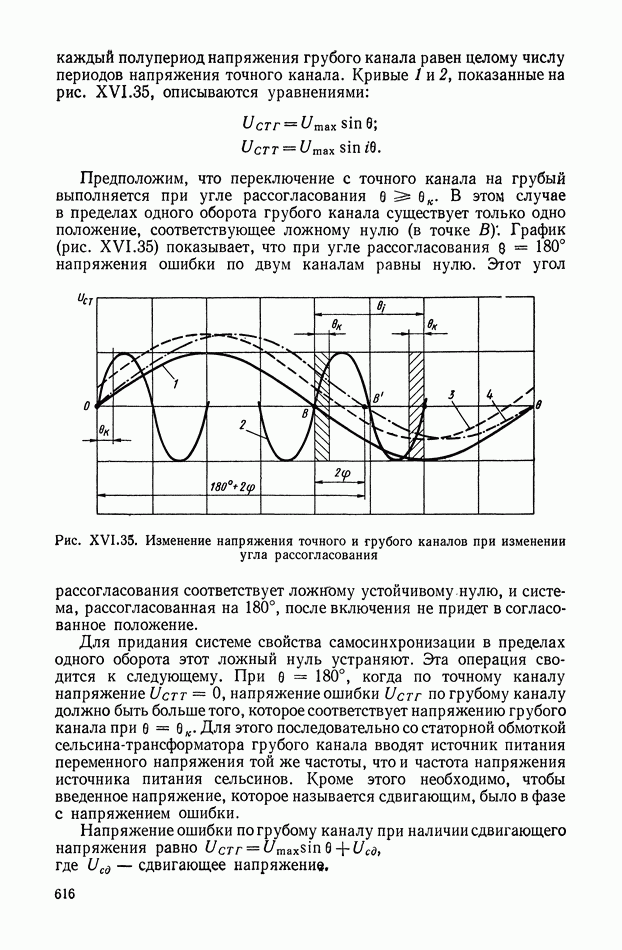
- Устранение ложного нуля в двухскоростной системе.
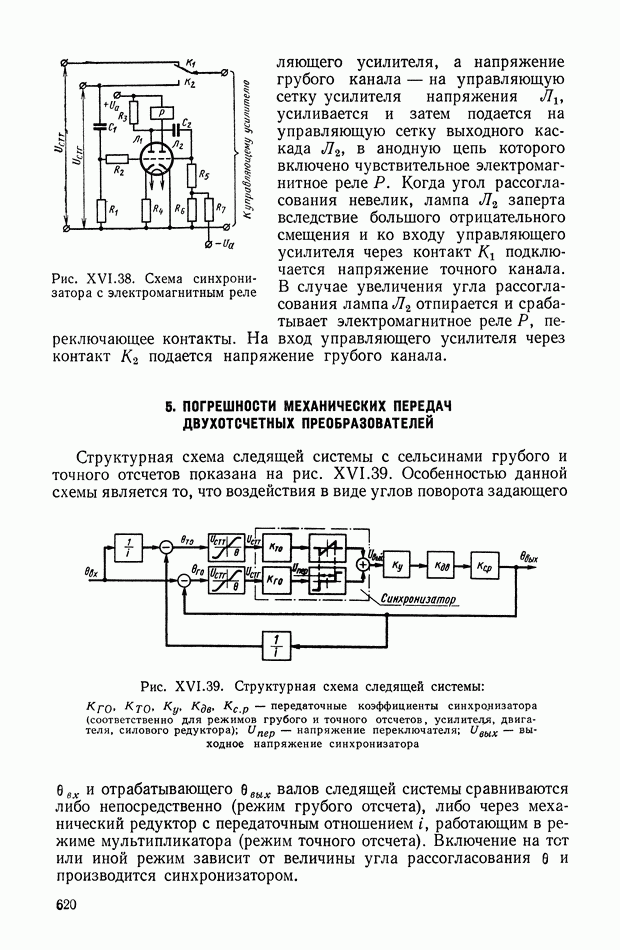
- Схемы синхронизаторов.
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
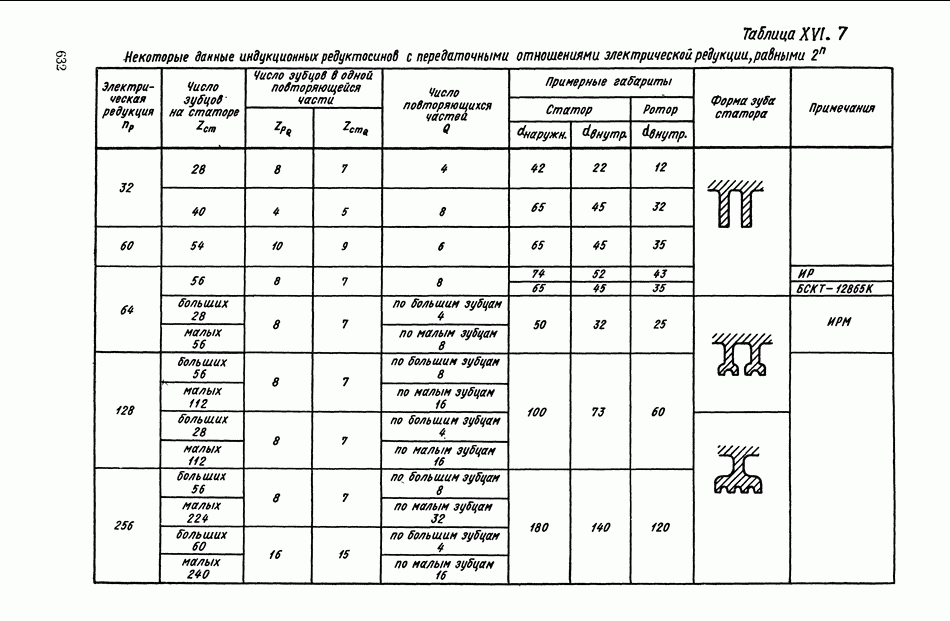
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
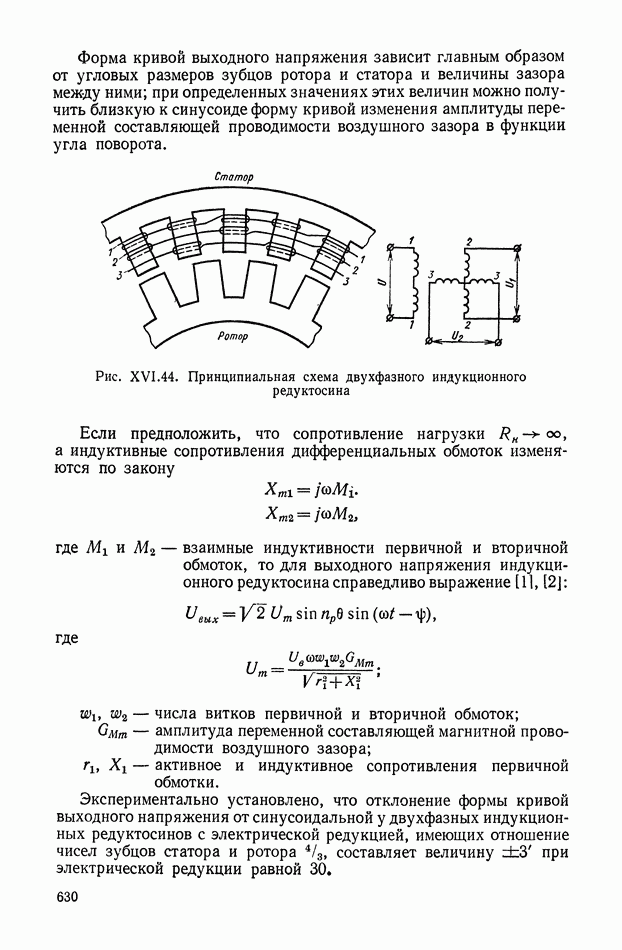
- Индукционные редуктосины.
- Индуктосины.
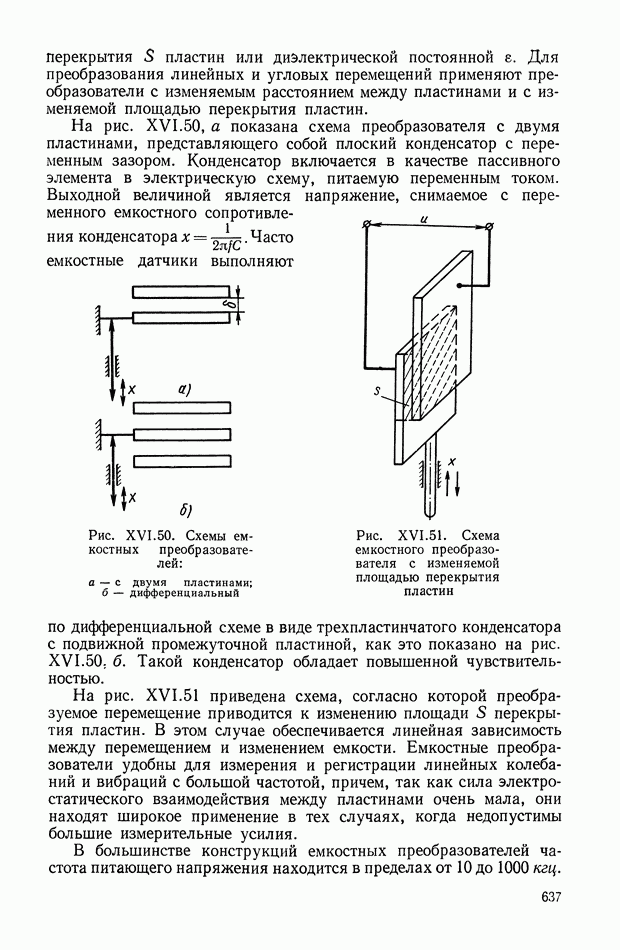
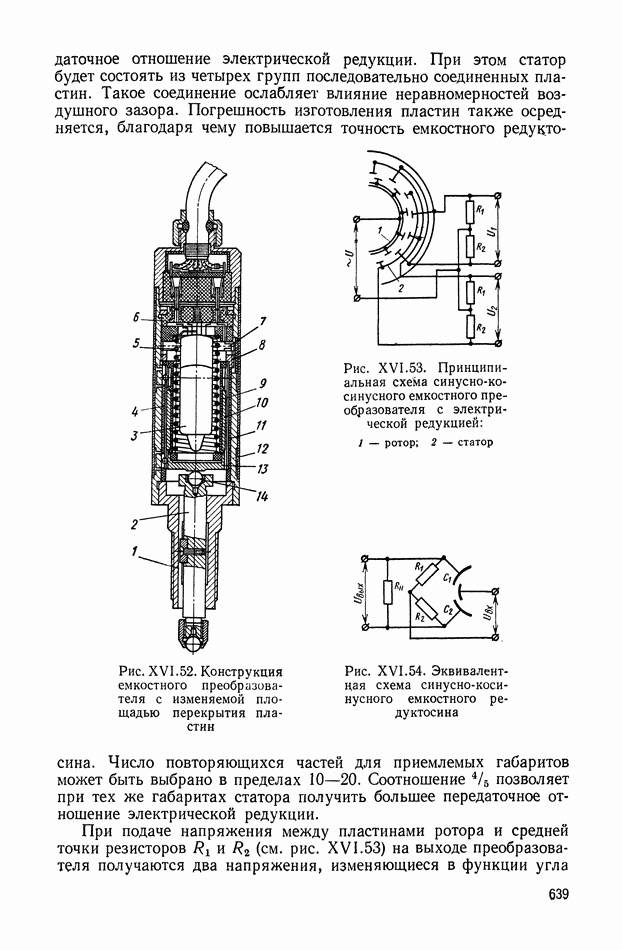
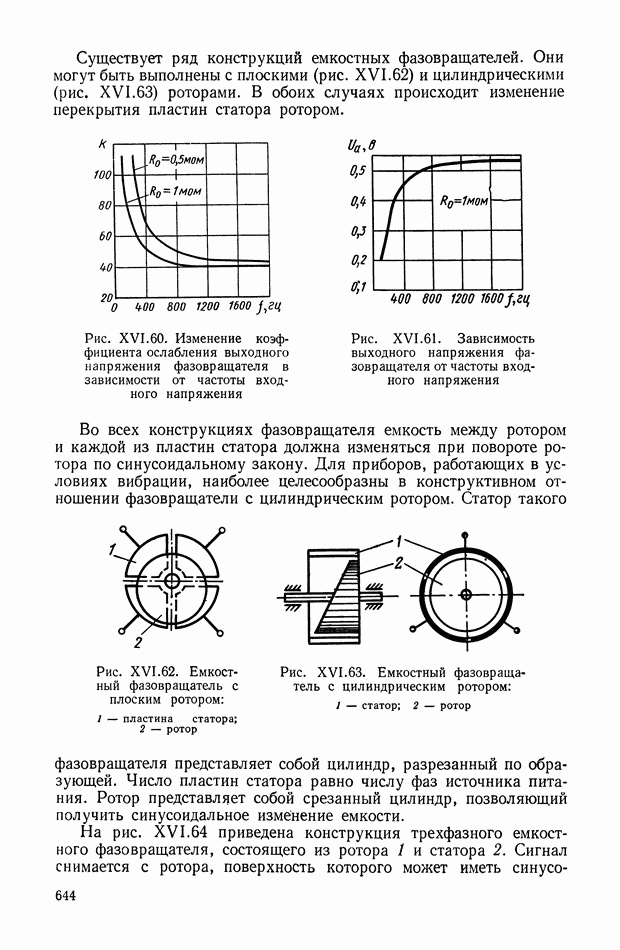
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
- Емкостный редуктосин.
- Емкостный фазовращатель.
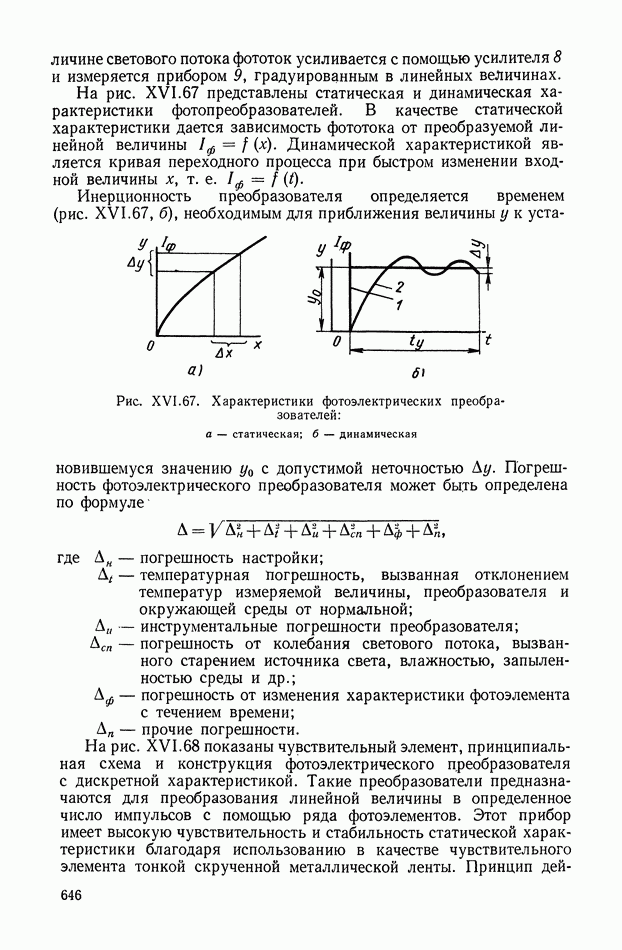
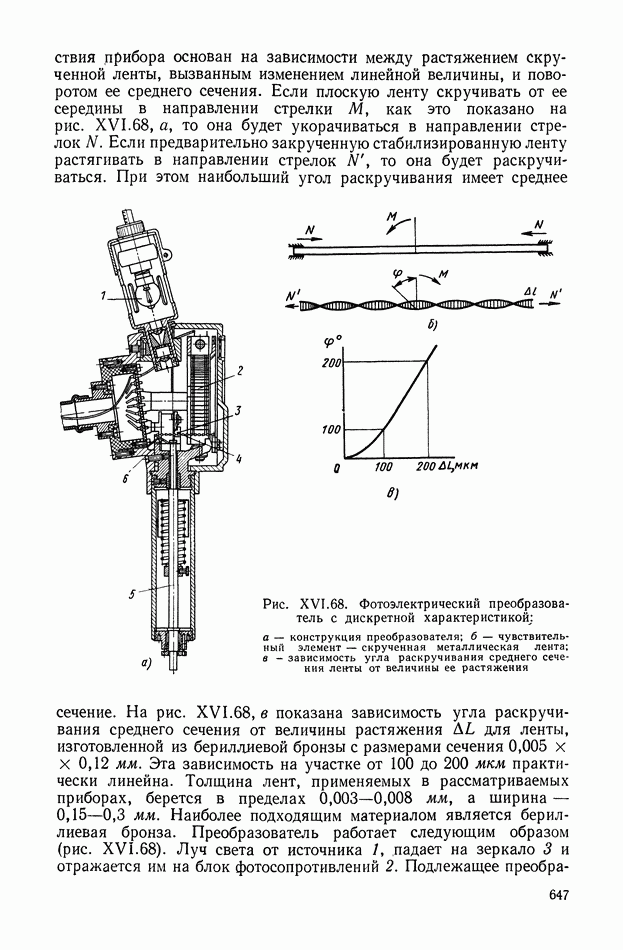
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
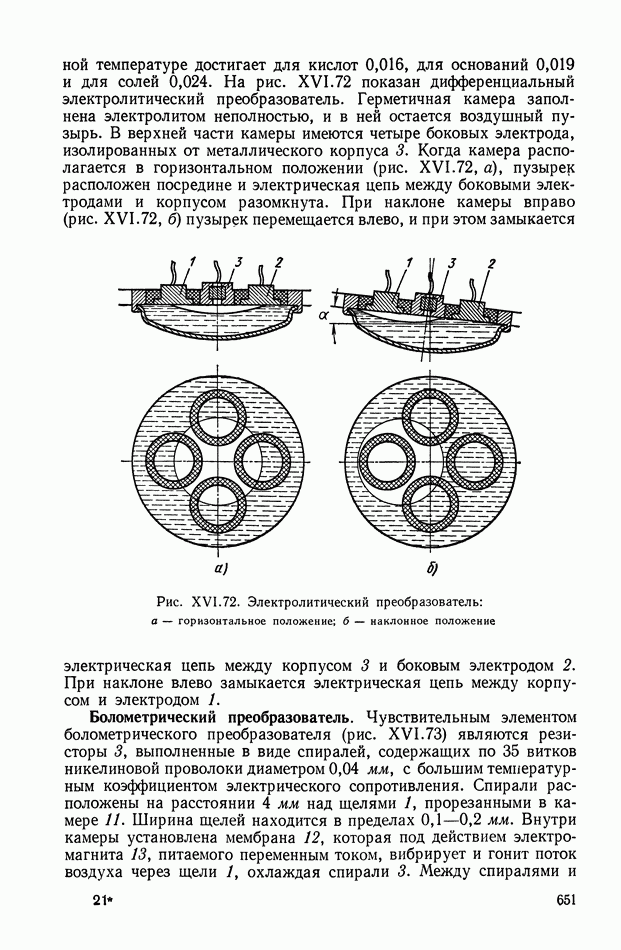
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
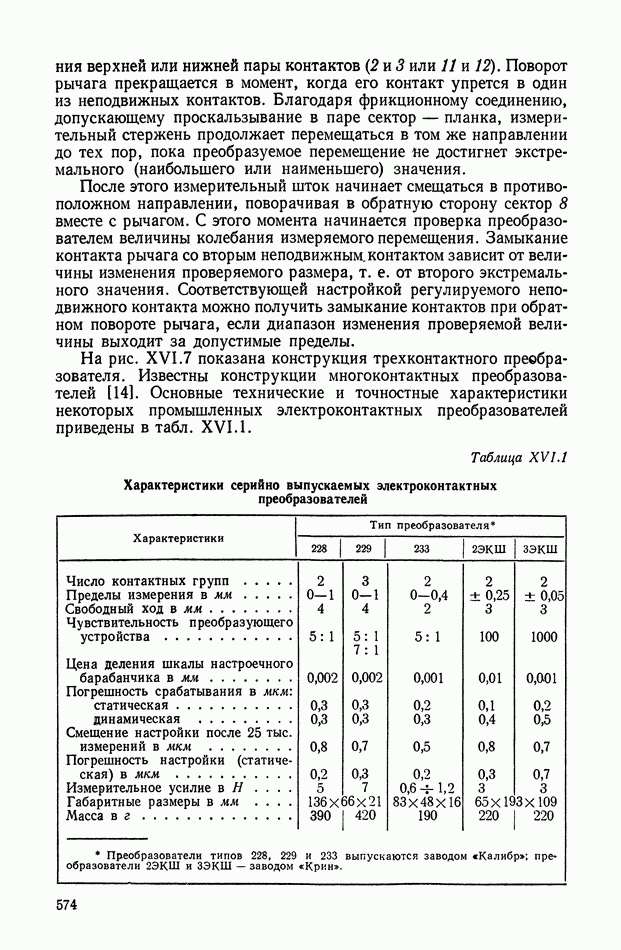
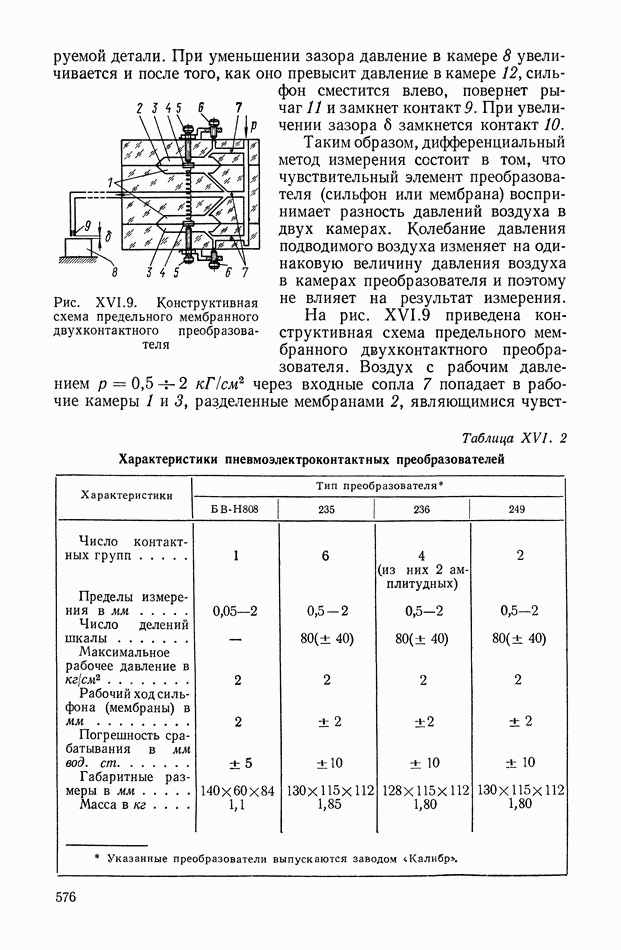
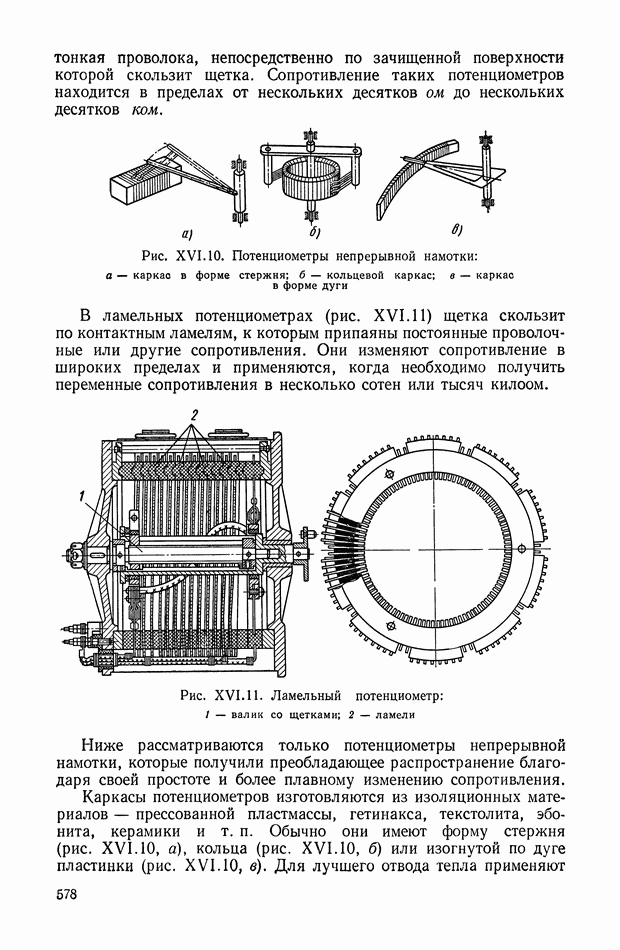
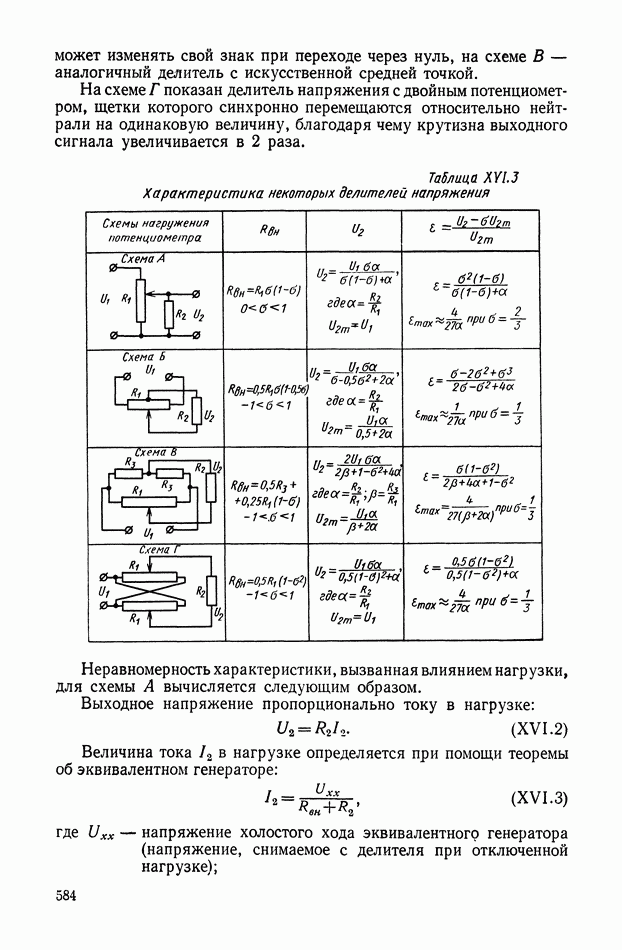
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ