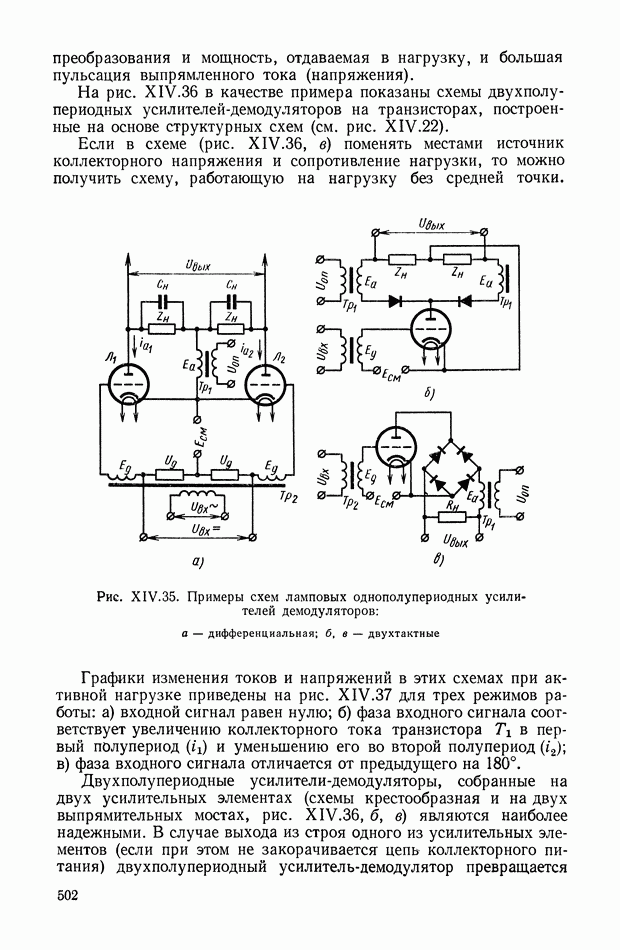
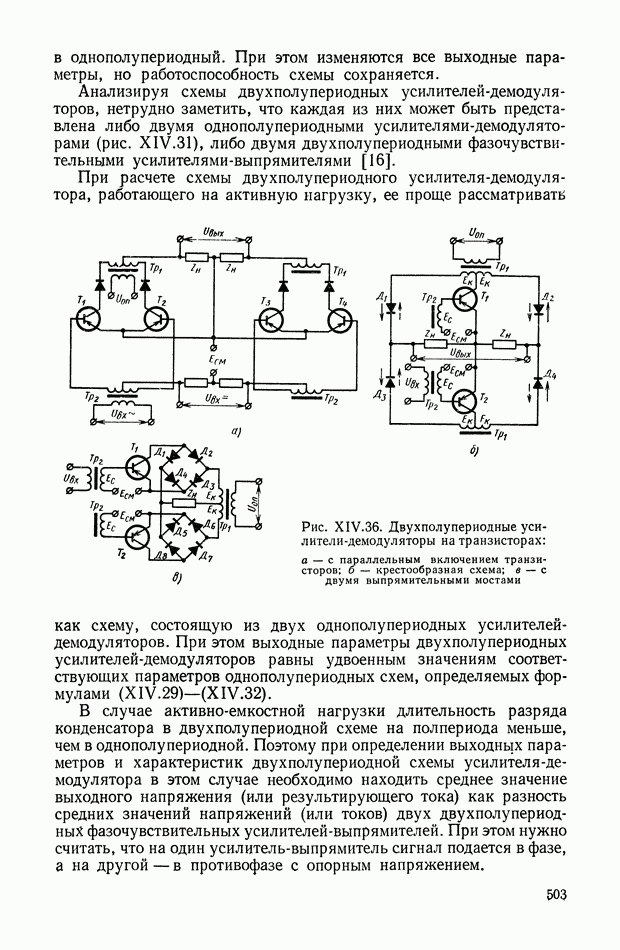
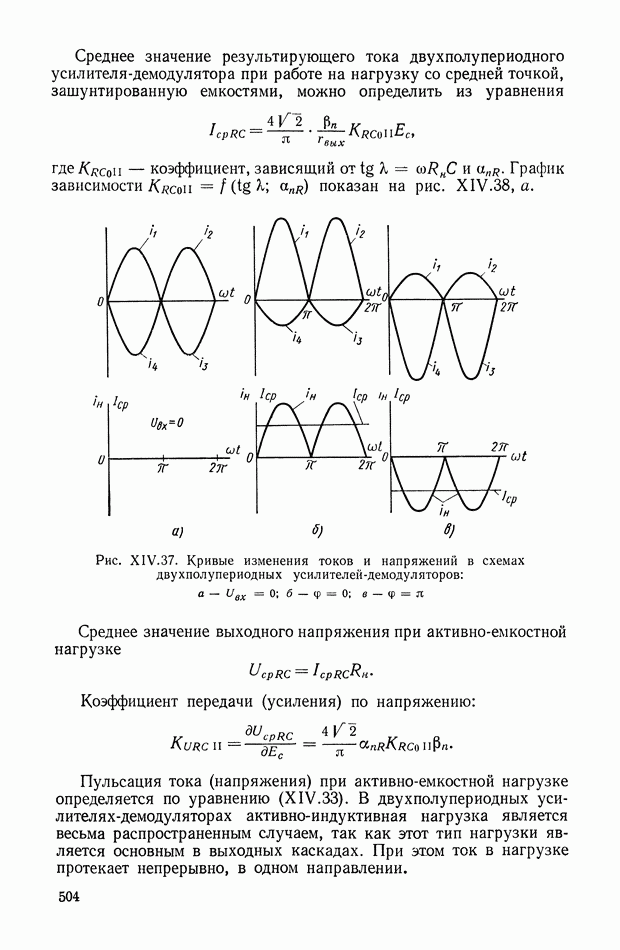
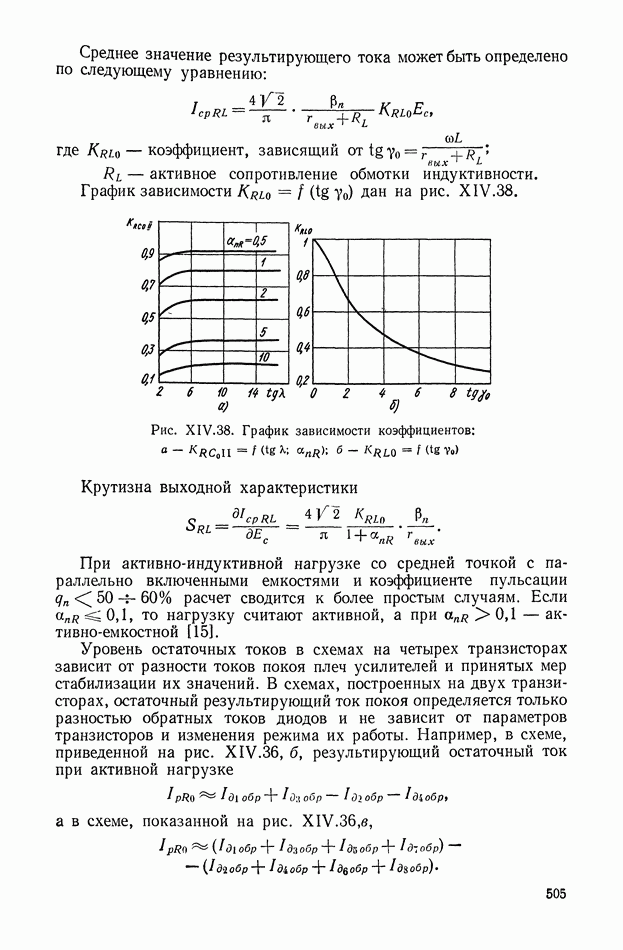
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
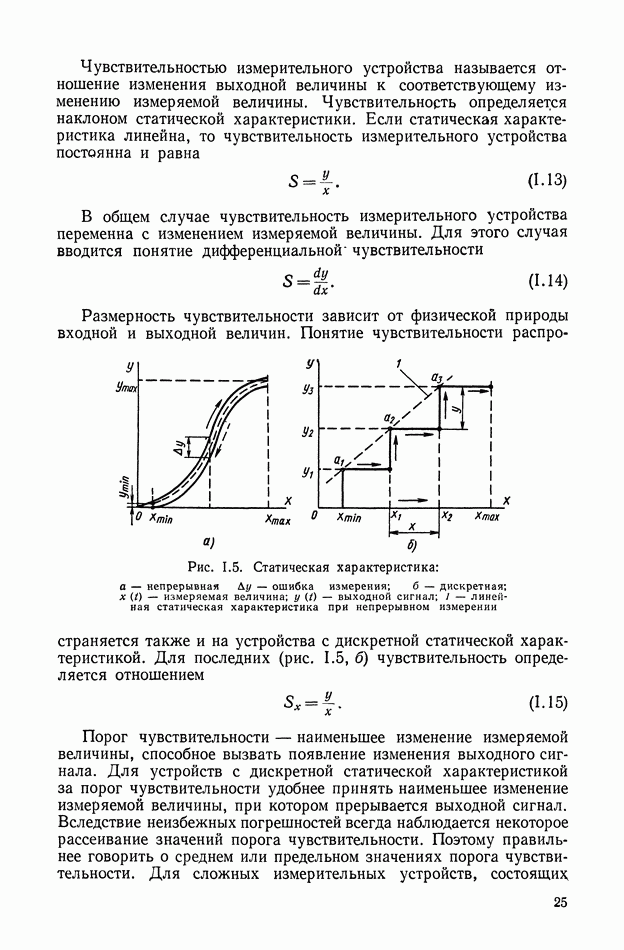
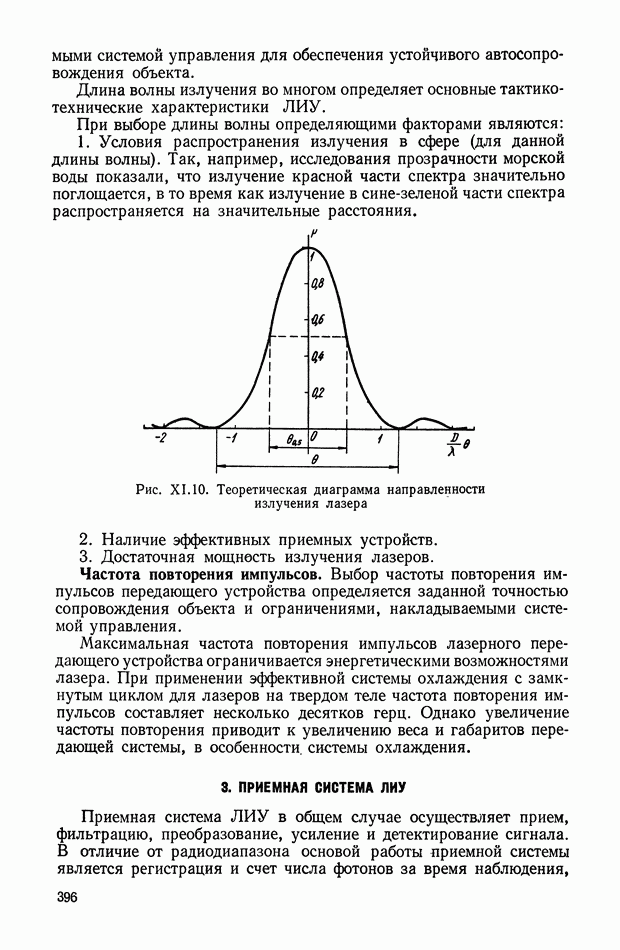
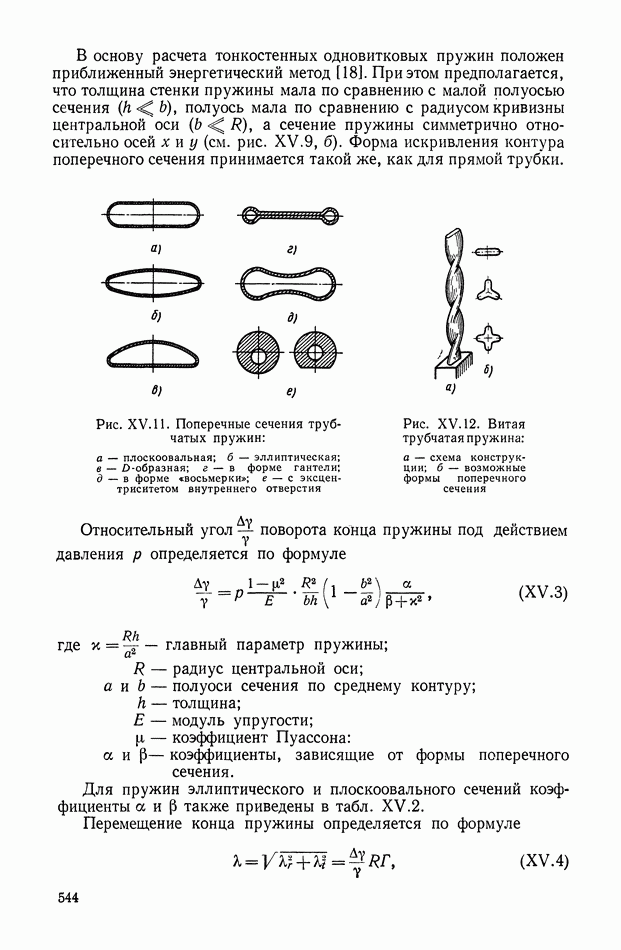
Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
Если потенциометр работает в схеме делителя напряжения, то его выходное напряжение зависит от нагрузки. Из-за этого могут возникнуть дополнительные статические и динамические погрешности.
Статическая погрешность выражается в том, что под влиянием нагрузки появляется добавочная неравномерность характеристики, а динамическая погрешность возникает в случае, если нагрузка содержит реактивное сопротивление. При этом ток в нагрузке зависит не только от перемещения щетки потенциометра, но также от скорости этого перемещения.
Рассмотрим вначале влияние чисто активной нагрузки на характеристику потенциометра.
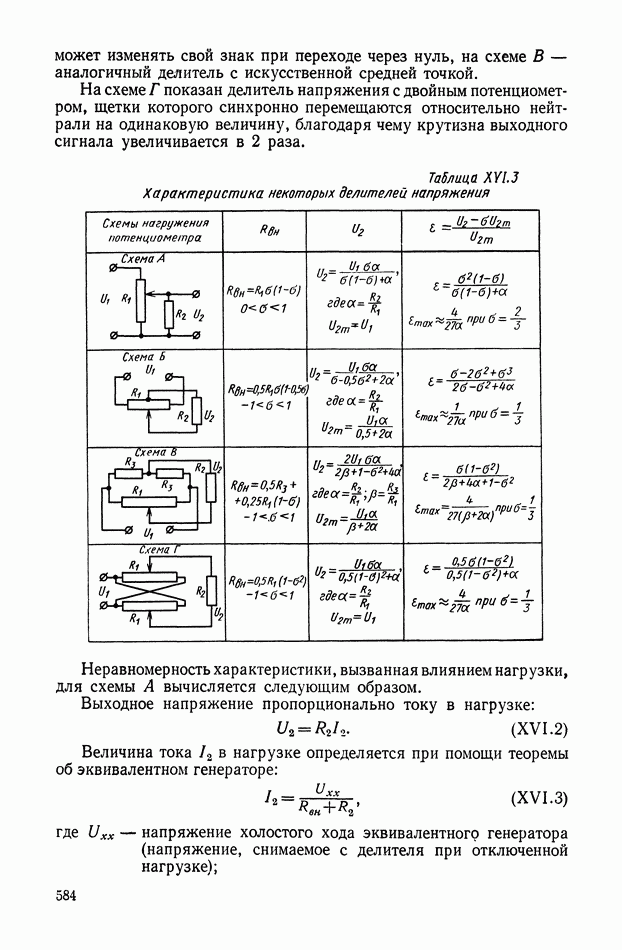
Наиболее часто применяемые схемы делителей напряжения приведены в табл. XVI.3. Во всех схемах через  обозначено сопротивление потенциометра,
обозначено сопротивление потенциометра,  — сопротивление нагрузки,
— сопротивление нагрузки,  — сопротивления дополнительных шунтов,
— сопротивления дополнительных шунтов,  — напряжение источника питания,
— напряжение источника питания,  — напряжение на нагрузке.
— напряжение на нагрузке.
На схеме А (см. табл. XVI.3) показан простейший делитель напряжения, у которого напряжение  на нагрузке
на нагрузке  может изменяться от нуля до максимального значения, не изменяя знака.
может изменяться от нуля до максимального значения, не изменяя знака.
На схемах Б, В и Г представлены делители, у которых выходное напряжение  может изменять знак. На схеме Б показан делитель напряжения со средней точкой, в котором напряжение
может изменять знак. На схеме Б показан делитель напряжения со средней точкой, в котором напряжение  на нагрузке
на нагрузке
может изменять свой знак при переходе через нуль, на схеме В — аналогичный делитель с искусственной средней точкой.
На схеме Г показан делитель напряжения с двойным потенциометром, щетки которого синхронно перемещаются относительно нейтрали на одинаковую величину, благодаря чему крутизна выходного сигнала увеличивается в 2 раза.
Таблица XYI.3 (см. скан) Характеристика некоторых делителей напряжения
Неравномерность характеристики, вызванная влиянием нагрузки, для схемы А вычисляется следующим образом.
Выходное напряжение пропорционально току в нагрузке:

Величина тока  в нагрузке определяется при помощи теоремы об эквивалентном генераторе:
в нагрузке определяется при помощи теоремы об эквивалентном генераторе:

где  — напряжение холостого хода эквивалентного генератора (напряжение, снимаемое с делителя при отключенной нагрузке);
— напряжение холостого хода эквивалентного генератора (напряжение, снимаемое с делителя при отключенной нагрузке);
 — внутреннее сопротивление эквивалентного генератора (сопротивление между выходными клеммами делителя при отключенной нагрузке и закороченном источнике питания; при этом внутренним сопротивлением источника питания пренебрегаем).
— внутреннее сопротивление эквивалентного генератора (сопротивление между выходными клеммами делителя при отключенной нагрузке и закороченном источнике питания; при этом внутренним сопротивлением источника питания пренебрегаем).
Напряжение холостого хода находим по формуле

где  — относительное перемещение щетки.
— относительное перемещение щетки.
Внутреннее сопротивление делителя

Подставляя уравнения  (XVI.4) и (XVI.5) в уравнение (XVI.2) и обозначая
(XVI.4) и (XVI.5) в уравнение (XVI.2) и обозначая  получим
получим

Относительная неравномерность характеристики имеет вид

где  — максимальное значение
— максимальное значение  (при
(при 
— расчетное значение выходного напряжения для случая, когда  изменяется пропорционально а в пределах от 0 до
изменяется пропорционально а в пределах от 0 до 
Принимая во внимание, что  и
и  перепишем выражение (XVI.7) следующим образом:
перепишем выражение (XVI.7) следующим образом:

Подставив уравнение (XVI.6) в формулу (XVI.8), получим окончательное выражение, которое характеризует неравномерность выходного сигнала, вызванную влиянием нагрузки:

Знак минус свидетельствует о том, что действительный сигнал будет меньше расчетного.
Упростим выражение (XVI.9), учитывая, что сопротивление нагрузки обычно значительно больше сопротивления потенциометра (а 1). Поэтому в знаменателе выражения (XIV. 9) можно пренебречь произведением  , которое ни при каких значениях а не превышает 0,25.
, которое ни при каких значениях а не превышает 0,25.
Приближенно неравномерность выходного сигнала определяется по формуле

Максимальное значение ошибки находим, приравнивая ее производную нулю:

откуда 
Подставляя значение а в уравнение (XVI. 10), получим

Выражения для неравномерности выходного сигнала для остальных схем приведены в табл. XVI.3, обозначения коэффициентов в которой для всех схем одинаковы, а именно:


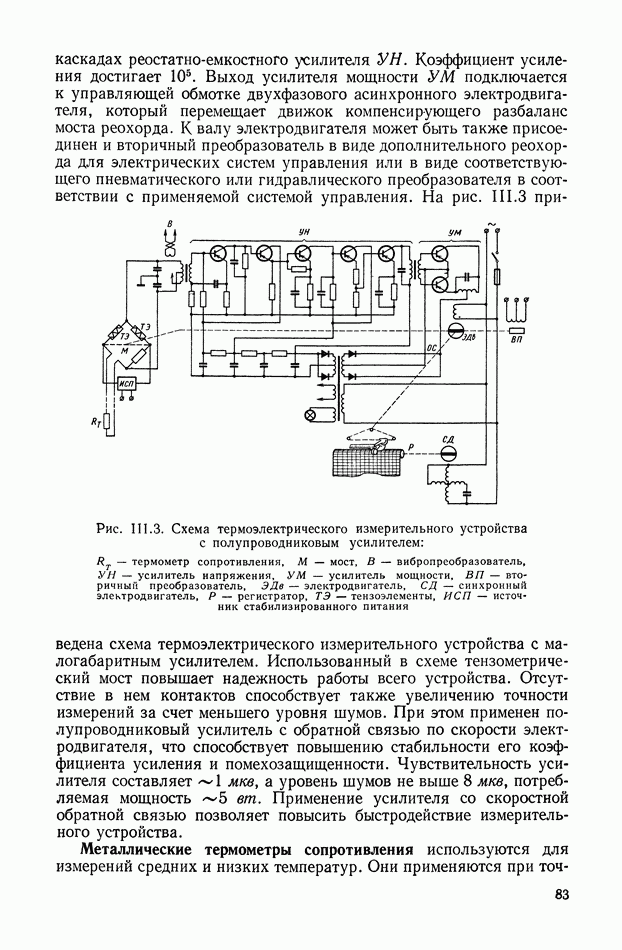
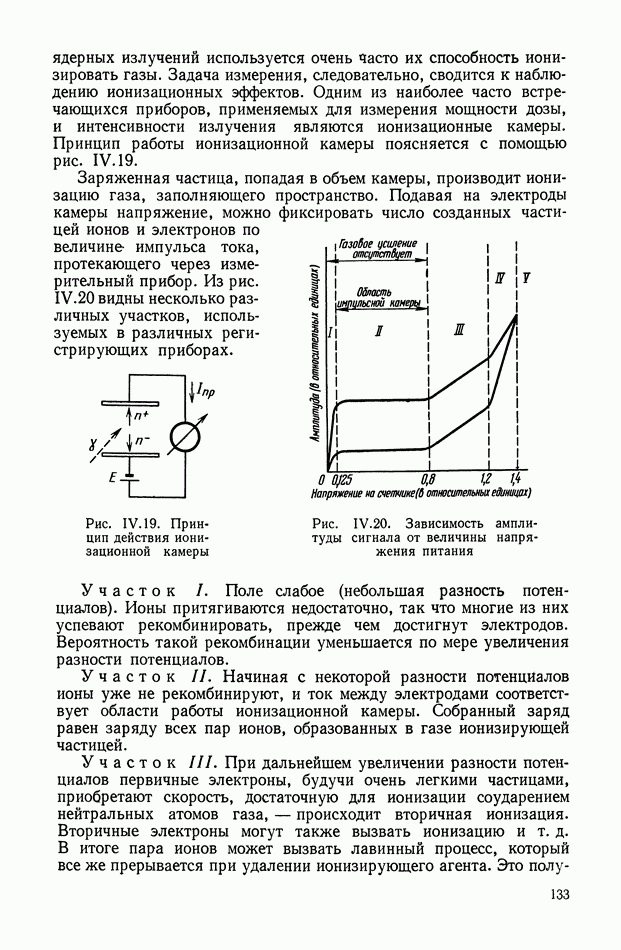
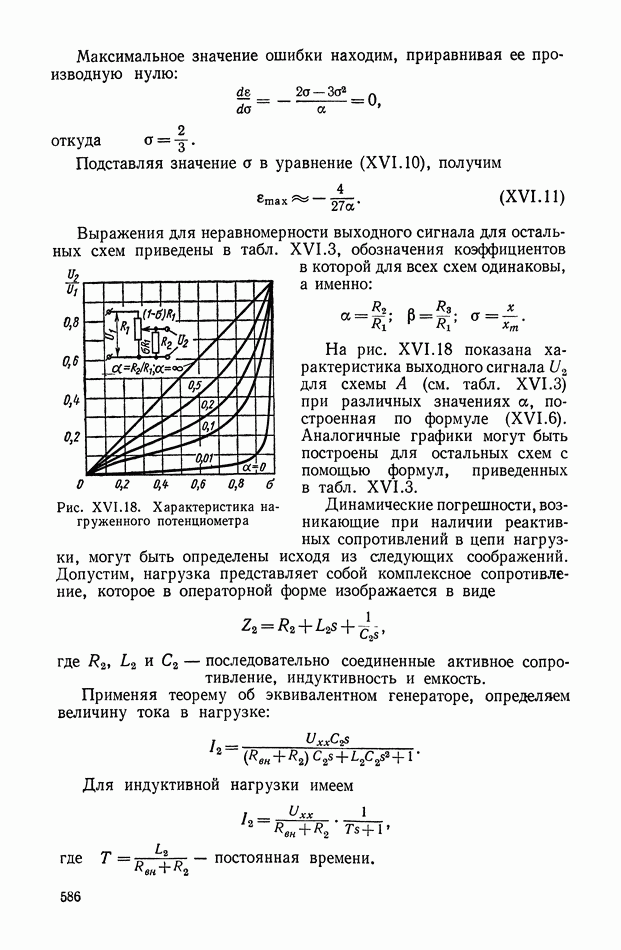
Рис. XVI. 18. Характеристика нагруженного потенциометра
На рис. XVI. 18 показана характеристика выходного сигнала  для схемы А (см. табл. XVI.3) при различных значениях а, построенная по формуле (XVI.6). Аналогичные графики могут быть построены для остальных схем с помощью формул, приведенных в табл. XVI.3.
для схемы А (см. табл. XVI.3) при различных значениях а, построенная по формуле (XVI.6). Аналогичные графики могут быть построены для остальных схем с помощью формул, приведенных в табл. XVI.3.
Динамические погрешности, возникающие при наличии реактивных сопротивлений в цепи нагрузки, могут быть определены исходя из следующих соображений. Допустим, нагрузка представляет собой комплексное сопротивление, которое в операторной форме изображается в виде

где  — последовательно соединенные активное сопротивление, индуктивность и емкость.
— последовательно соединенные активное сопротивление, индуктивность и емкость.
Применяя теорему об эквивалентном генераторе, определяем величину тока в нагрузке:

Для индуктивной нагрузки имеем 

где  постоянная времени.
постоянная времени.
Учитывая, что  где а — коэффициент пропорциональности, равный
где а — коэффициент пропорциональности, равный  для схем А, Г и
для схем А, Г и  для схем Б, В, получим
для схем Б, В, получим

Принимая  за входную, а ток
за входную, а ток  в нагрузке — за выходную величину, определим передаточную функцию делителя напряжений
в нагрузке — за выходную величину, определим передаточную функцию делителя напряжений

где  величина
величина  необходимая для подсчета значений
необходимая для подсчета значений  и
и  определяется по формулам, приведенным в табл. XVI.3.
определяется по формулам, приведенным в табл. XVI.3.
Передаточный коэффициент  и постоянная времени Т являются непостоянными величинами, так как
и постоянная времени Т являются непостоянными величинами, так как  зависит от а; но практически принимают
зависит от а; но практически принимают  , кроме того, при малых вариациях а, что характерно для регуляторов, можно приближенно считать
, кроме того, при малых вариациях а, что характерно для регуляторов, можно приближенно считать  и соответственно
и соответственно 

Рис. XVI .19. Следящая система
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ I. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
- 2. СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. ПОНЯТИЕ ИНФОРМАЦИИ
- 4. КОЛИЧЕСТВО ИНФОРМАЦИИ
- 5. ИНФОРМАЦИЯ ПРИ ИЗМЕРЕНИЯХ
- 6. ИНФОРМАТИВНОСТЬ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 7. ОЦЕНКА ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- ГЛАВА II. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
- 1. МОСТОВЫЕ СХЕМЫ
- 2. МАГНИТОЭЛЕКТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 4. ЭЛЕКТРОМАГНИТНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 5. ЭЛЕКТРОСТАТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 6. ИНДУКЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЛОГОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 8. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
- 9. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ И ФАЗЫ
- 10. ЭЛЕКТРОМЕТРИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА III. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕПЛОВЫХ ВЕЛИЧИН
- 2. ИОНИЗАЦИОННЫЕ ИЗМЕРИТЕЛИ ТЕМПЕРАТУР, ПАРАМАГНИТНЫЕ И ШУМОВЫЕ ТЕРМОМЕТРЫ
- 3. ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- ГЛАВА IV. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ИЗЛУЧЕНИЙ
- 1. ЦИЛИНДР ФАРАДЕЯ
- 2. КОЛЛИМАТОРЫ, ДИАФРАГМЫ И МИШЕНИ
- 3. ЭЛЕКТРОИКДУКЦИОННЫЕ И МАГНИТОИНДУКЦИОННЫЕ ИЗМЕРИТЕЛИ ТОКА ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ
- 4. ИЗМЕРИТЕЛИ ВТОРИЧНОЙ ЭМИССИИ (ЭМИССИОННЫЕ ИЗМЕРИТЕЛИ)
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ n- И y-ИЗЛУЧЕНИЯ
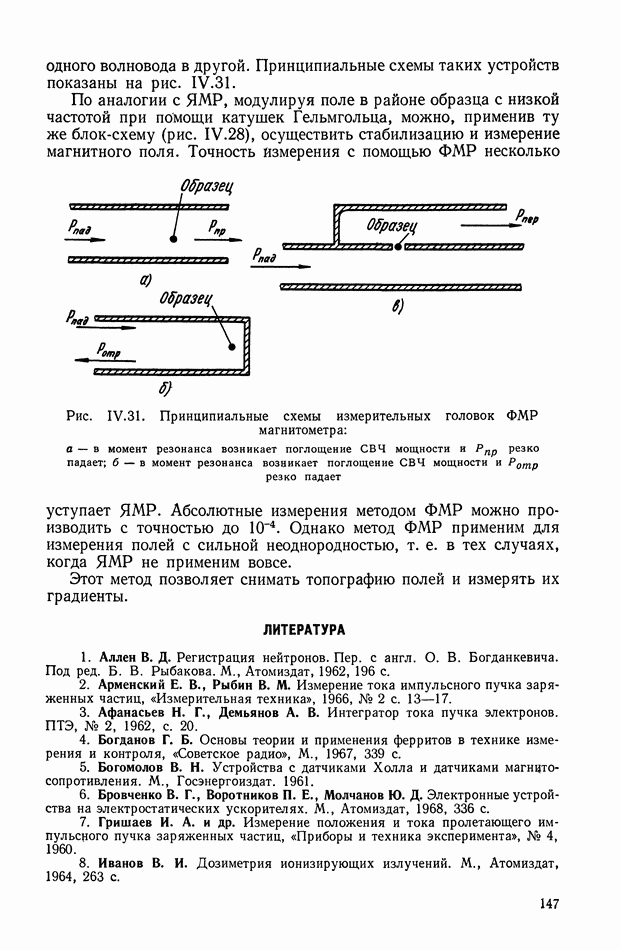
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ МАГНИТНЫХ ПОЛЕЙ
- ГЛАВА V. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
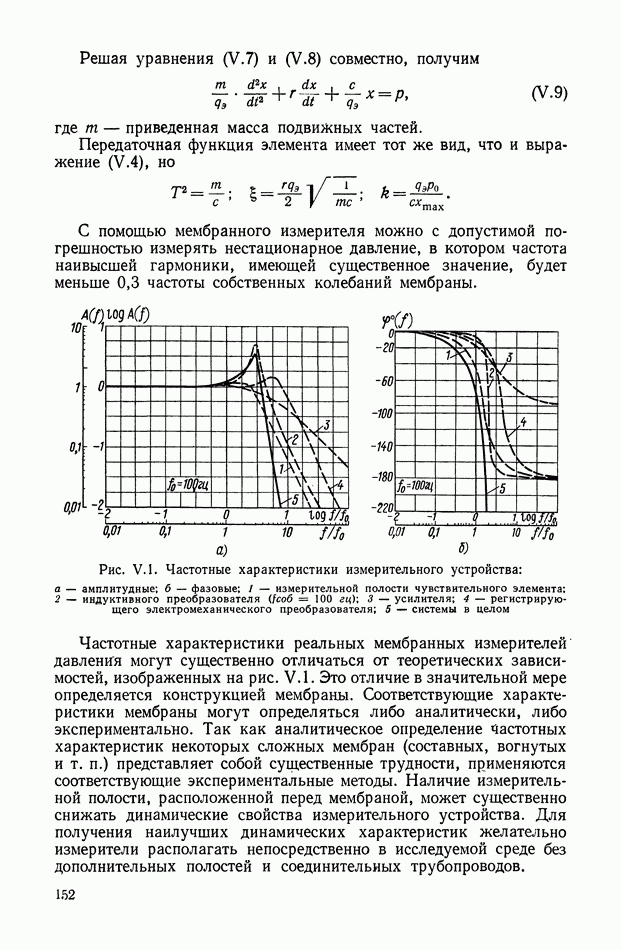
- 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ УСТРОЙСТВ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ
- 2. УСТРОЙСТВА ИЗМЕРЕНИЯ ДАВЛЕНИЯ С УПРУГИМИ ЧУВСТВИТЕЛЬНЫМИ ЭЛЕМЕНТАМИ
- 3. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАТЕЛЯМИ, ИЗМЕНЯЮЩИМИ ФИЗИЧЕСКИЕ СВОЙСТВА ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ
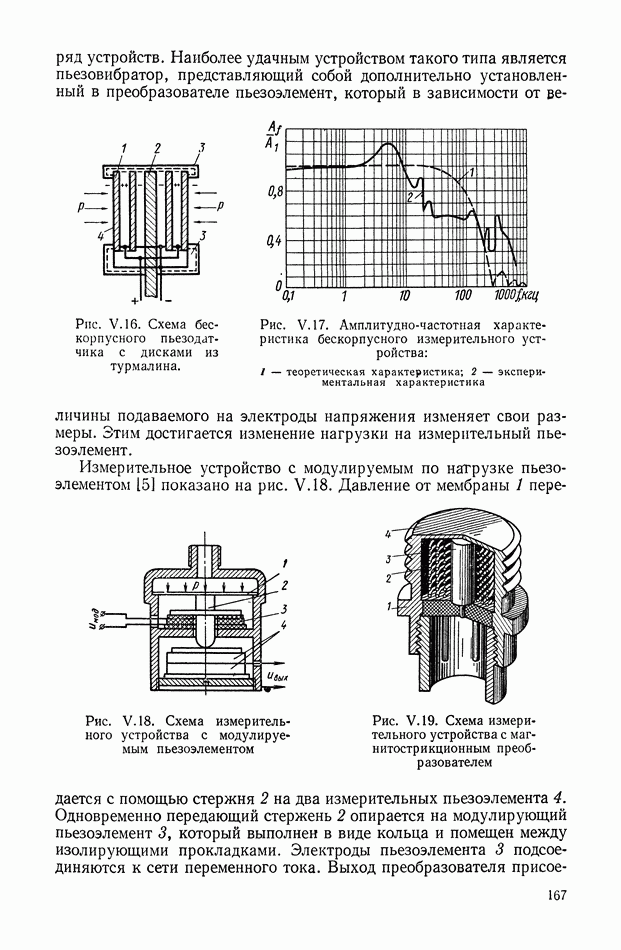
- 4. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ И МАГНИТОСТРИКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
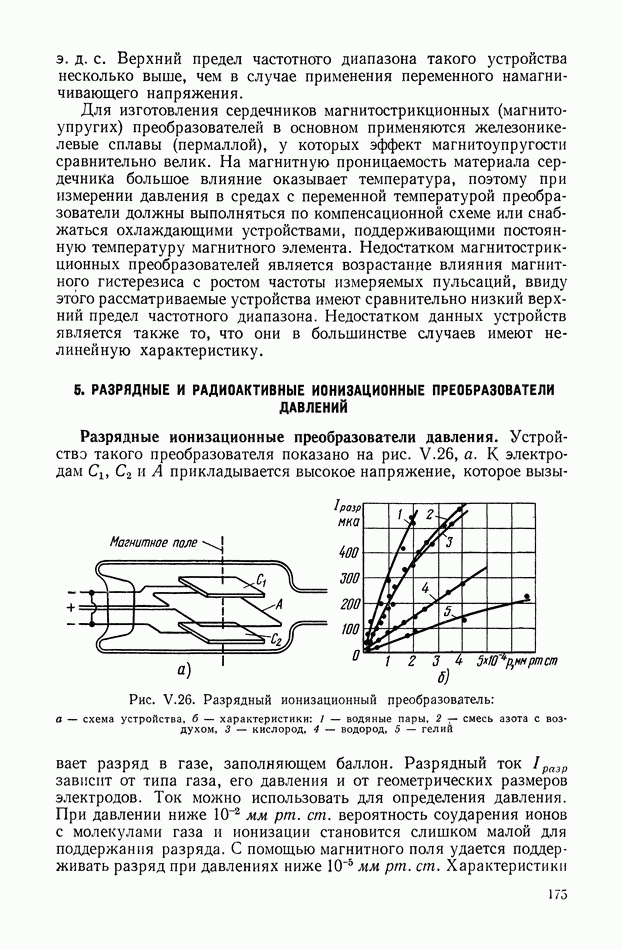
- 5. РАЗРЯДНЫЕ И РАДИОАКТИВНЫЕ ИОНИЗАЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- 6. ЭЛЕКТРОННЫЕ И ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ДАВЛЕНИЙ
- ГЛАВА VI. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ РАСХОДА
- 2. УЛЬТРАЗВУКОВЫЕ РАСХОДОМЕРЫ
- 3. ИНДУКЦИОННЫЕ РАСХОДОМЕРЫ
- 4. ТЕПЛОВЫЕ РАСХОДОМЕРЫ
- 5. ОПТИЧЕСКИЕ РАСХОДОМЕРЫ
- 6. РАСХОДОМЕРЫ С МАРКЕРНЫМИ ПРЕОБРАЗОВАТЕЛЯМИ
- 7. РАСХОДОМЕРЫ ПЕРЕМЕННОГО ПЕРЕПАДА ДАВЛЕНИЙ
- 8. РАСХОДОМЕРЫ С ПРЕОБРАЗОВАТЕЛЯМИ СКОРОСТНОГО НАПОРА
- 9. ИНЕРЦИАЛЬНЫЕ МАССОВЫЕ РАСХОДОМЕРЫ
- ГЛАВА VII. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- 1. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ
- 2. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ СКОРОСТЕЙ
- 4. АКСЕЛЕРОМЕТРЫ. ИХ НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ
- 5. ПРУЖИННЫЕ АКСЕЛЕРОМЕТРЫ
- 6. КОМПЕНСАЦИОННЫЕ АКСЕЛЕРОМЕТРЫ
- 7. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЕЙ УРОВНЯ
- ГЛАВА VIII. ГИРОСКОПИЧЕСКИЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ ОРИЕНТАЦИИ ОБЪЕКТА
- 2. АСТАТИЧЕСКИЕ ГИРОСКОПЫ
- 3. ОДНООСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 4. ДВУХОСНЫЕ ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 5. ТРЕХОСНЫЕ, ИЛИ ПРОСТРАНСТВЕННЫЕ, ГИРОСКОПИЧЕСКИЕ СТАБИЛИЗАТОРЫ
- 8. ДИФФЕРЕНЦИРУЮЩИЕ И ИНТЕГРИРУЮЩИЕ ГИРОСКОПЫ
- 7. ГИРОСКОПИЧЕСКИЕ ВЕРТИКАЛИ
- 8. КУРСОВЫЕ ГИРОСКОПИЧЕСКИЕ СИСТЕМЫ
- ГЛАВА IX. ОПТИКО-ЭЛЕКТРОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ (ОИУ)
- 1. ОПТИЧЕСКИЕ СИСТЕМЫ ОПТИКО-ЭЛЕКТРОННЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ОИУ)
- 2. АНАЛИЗАТОРЫ ИЗОБРАЖЕНИЯ ОИУ
- 3. ПРИЕМНИКИ ЛУЧИСТОЙ ЭНЕРГИИ ОИУ
- ГЛАВА X. РАДИОЛОКАЦИОННЫЕ УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ И ДАЛЬНОСТИ
- 2. ПЕЛЕНГАЦИОННЫЕ РИУ
- 3. ТОЧНОСТЬ ИЗМЕРЕНИЯ УГЛОВЫХ КООРДИНАТ РИУ
- 4. ФИЗИЧЕСКИЕ ПРИНЦИПЫ И МЕТОДЫ ИЗМЕРЕНИЯ ДАЛЬНОСТИ
- 5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДАЛЬНОМЕРНЫХ РИУ
- 6. ПРИНЦИПЫ ПОСТРОЕНИЯ И МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ РАДИОДАЛЬНОМЕРОВ
- ГЛАВА XI. ЛАЗЕРНЫЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ПРИНЦИПЫ РАБОТЫ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ (ЛИУ)
- 2. ЭЛЕМЕНТЫ, УСТРОЙСТВО И ХАРАКТЕРИСТИКИ ПЕРЕДАЮЩЕЙ СИСТЕМЫ ЛИУ
- 3. ПРИЕМНАЯ СИСТЕМА ЛИУ
- 4. СИСТЕМА УПРАВЛЕНИЯ ЛИУ
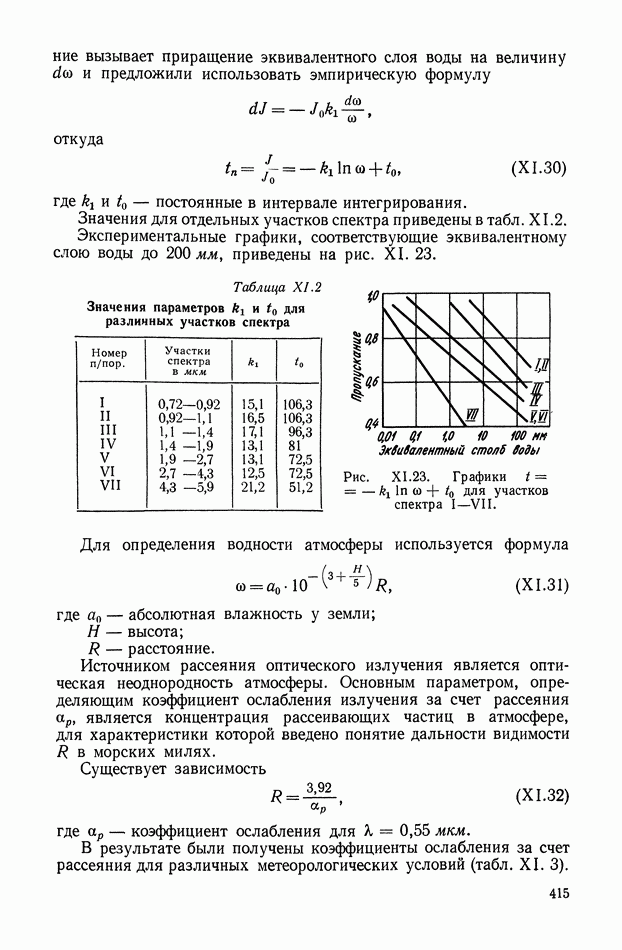
- 5. ВЛИЯНИЕ АТМОСФЕРЫ НА РАБОТУ ЛИУ
- ГЛАВА XII. ЭЛЕКТРОАКУСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА И ПРЕОБРАЗОВАТЕЛИ
- 1. ОБЩИЕ ХАРАКТЕРИСТИКИ ОБРАТИМЫХ ЭЛЕКТРОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
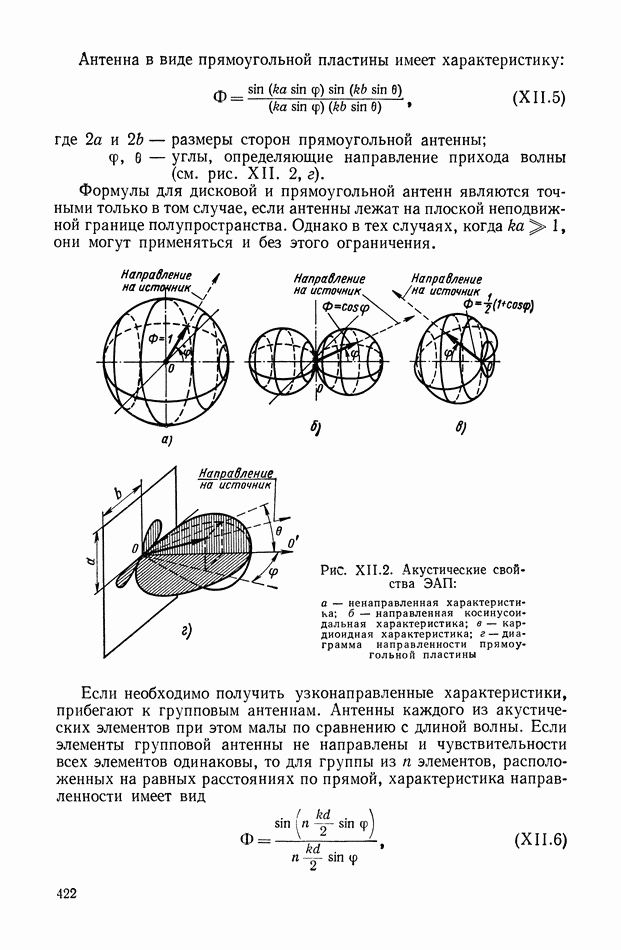
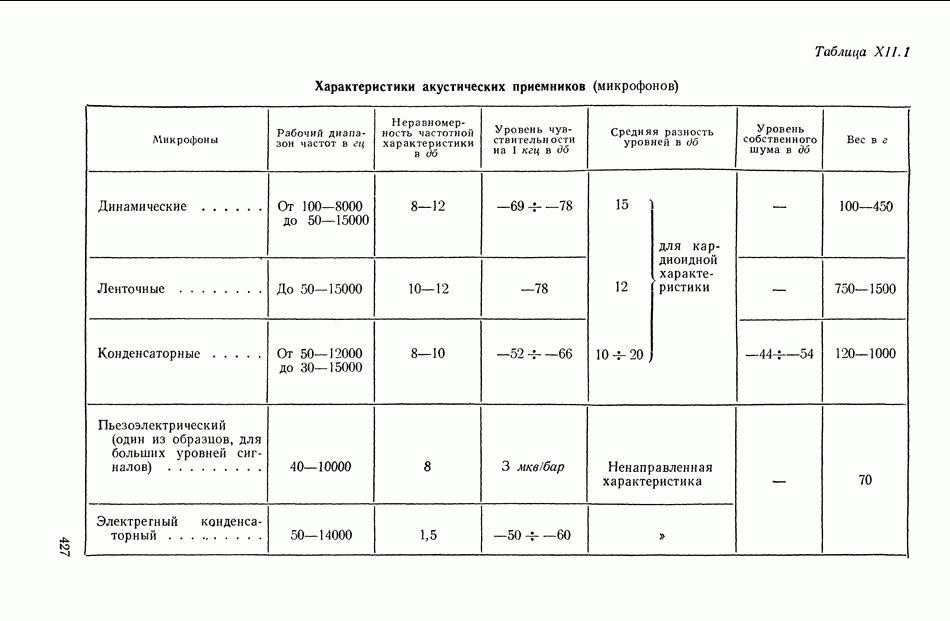
- 2. СВОЙСТВА АКУСТИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ
- 3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 4. МАГНИТОСТРИКЦИОННЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 5. ПЬЕЗОЭЛЕКТРИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 6. ЭЛЕКТРОСТАТИЧЕСКИЕ (КОНДЕНСАТОРНЫЕ) ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 7. ПЬЕЗОРЕЗИСТИВНЫЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
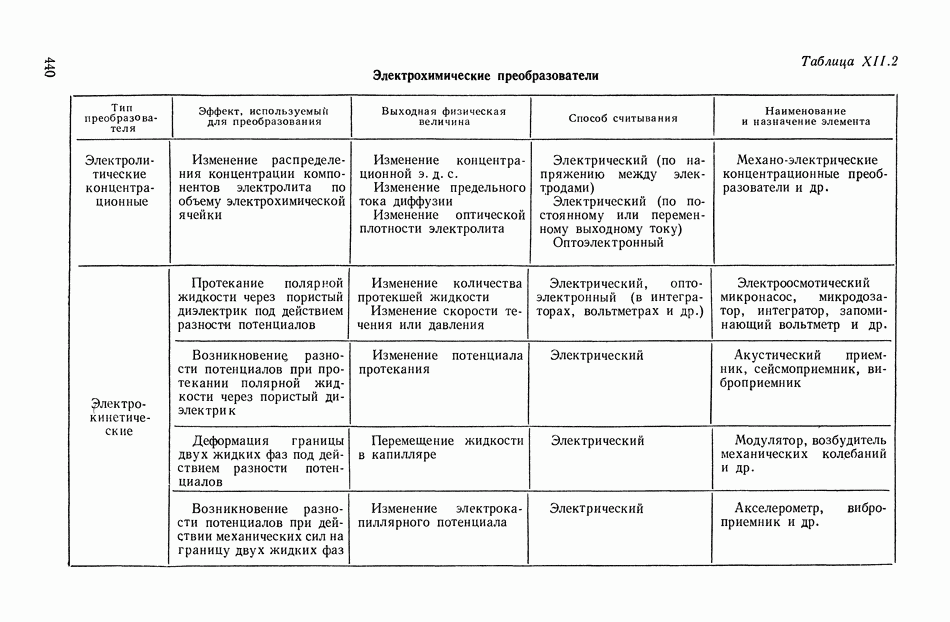
- 8. ЭЛЕКТРОХИМИЧЕСКИЕ ЭЛЕКТРОАКУСТИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- РАЗДЕЛ II. ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА
- ГЛАВА XIII. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
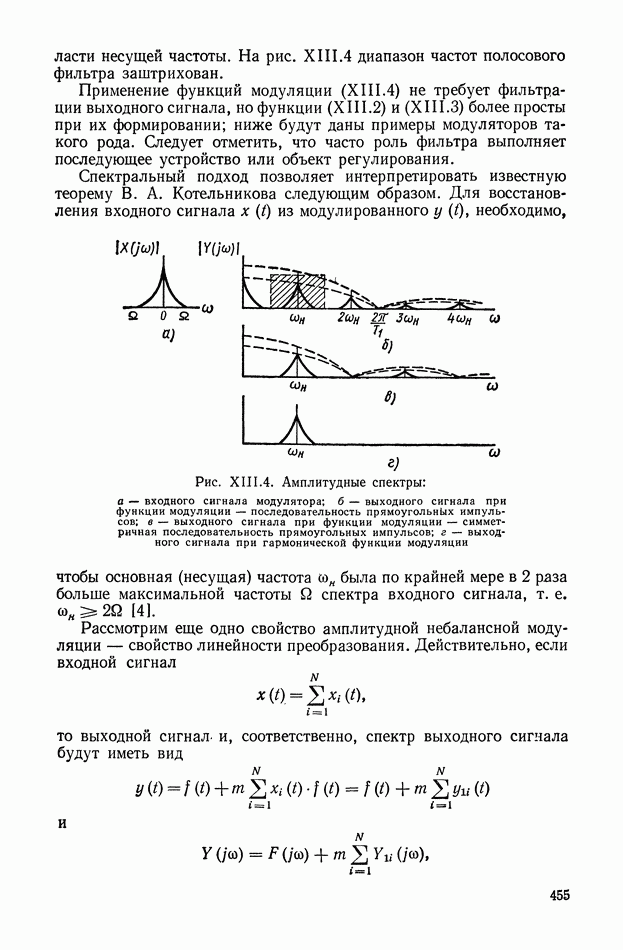
- 2. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ МОДУЛЯТОР
- 3. ПРЕОБРАЗОВАНИЕ СПЕКТРОВ ПРИ ПРОХОЖДЕНИИ СИГНАЛОВ ЧЕРЕЗ ДЕМОДУЛЯТОР
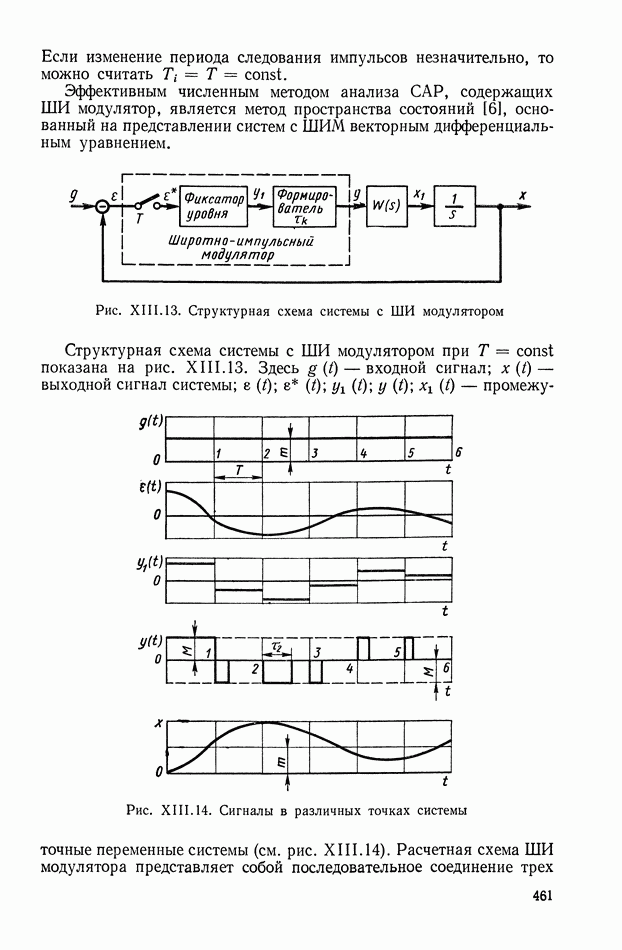
- 4. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ
- ГЛАВА XIV. ПРЕОБРАЗОВАТЕЛИ ЭЛЕКТРИЧЕСКИХ СИГНАЛОВ
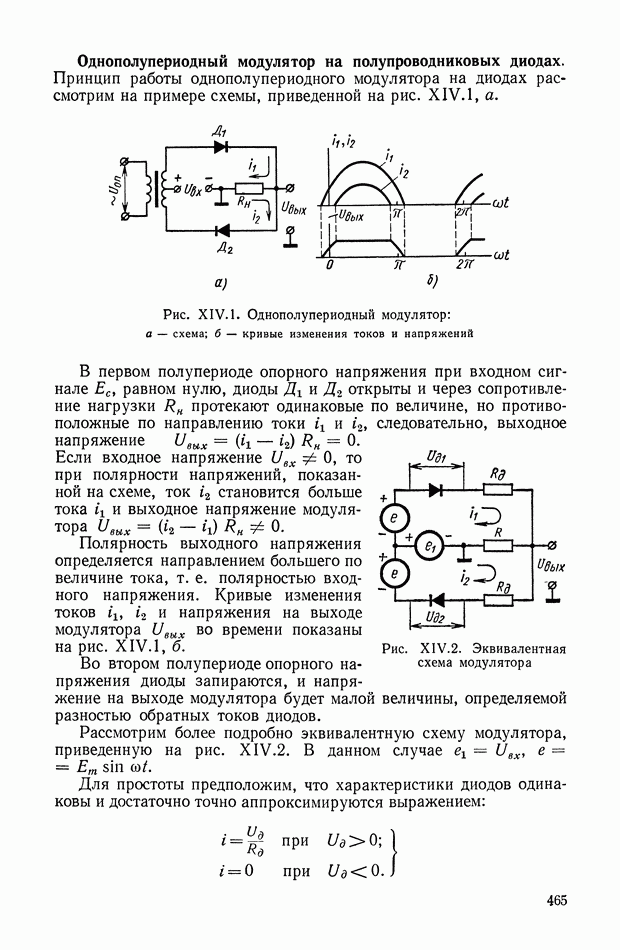
- 1. МОДУЛЯТОРЫ
- Двухполупериодный кольцевой модулятор на диодах.
- Усилители-модуляторы на электронных лампах.
- Модуляторы на транзисторах.
- Модуляторы на транзисторных ключах с реостатно-емкостным выходом.
- Модуляторы на транзисторных ключах с трансформаторным выходом.
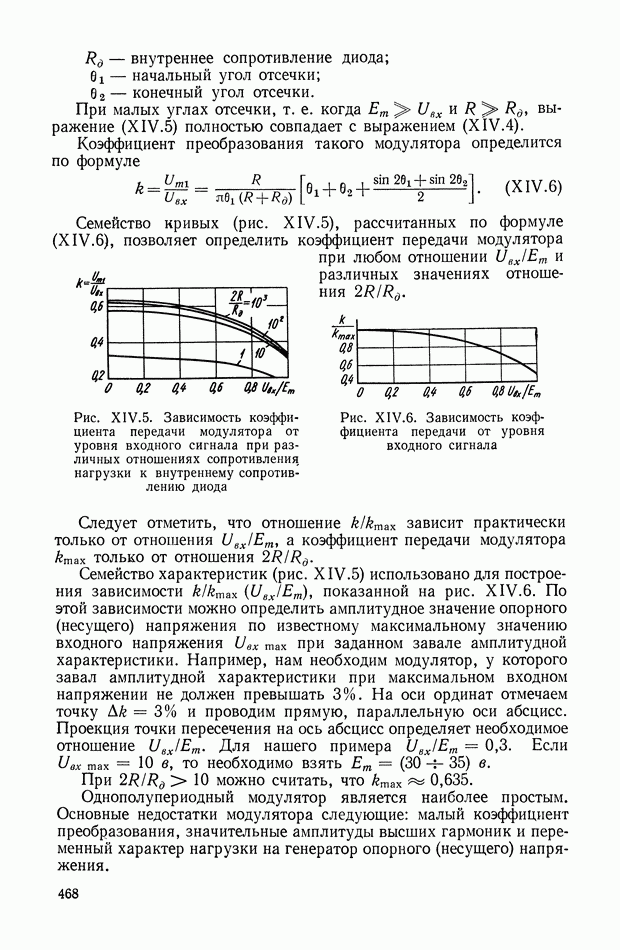
- 2. ФАЗОЧУВСТВИТЕЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ ПЕРЕМЕННОГО ТОКА В ПОСТОЯННЫЙ
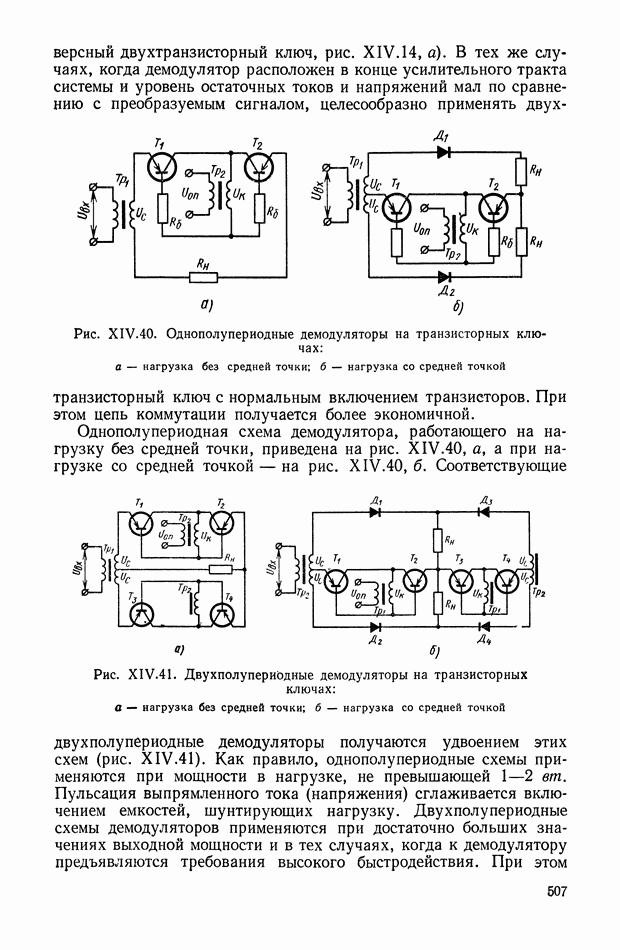
- Однополупериодные демодуляторы на полупроводниковых или вакуумных диодах.
- Двухполупериодные демодуляторы на диодах.
- Однополупериодные усилители-демодуляторы.
- Двухполупериодные усилители-демодуляторы.
- Демодуляторы на транзисторных ключах.
- 3. ШИРОТНО-ИМПУЛЬСНЫЕ ПРЕОБРАЗОВАТЕЛИ УПРАВЛЯЮЩИХ СИГНАЛОВ
- 4. ЭЛЕКТРОМАГНИТНЫЕ ПРЕОБРАЗУЮЩИЕ ЭЛЕМЕНТЫ
- Статика и динамика электромагнитных преобразующих элементов нейтрального типа.
- Статика и динамика электромагнитных преобразующих элементов поляризованного типа.
- ГЛАВА XV. ПРЕОБРАЗОВАТЕЛИ УСИЛИЙ И ДАВЛЕНИЙ
- 2. УПРУГИЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ПРЕОБРАЗОВАТЕЛЕЙ ДАВЛЕНИЯ
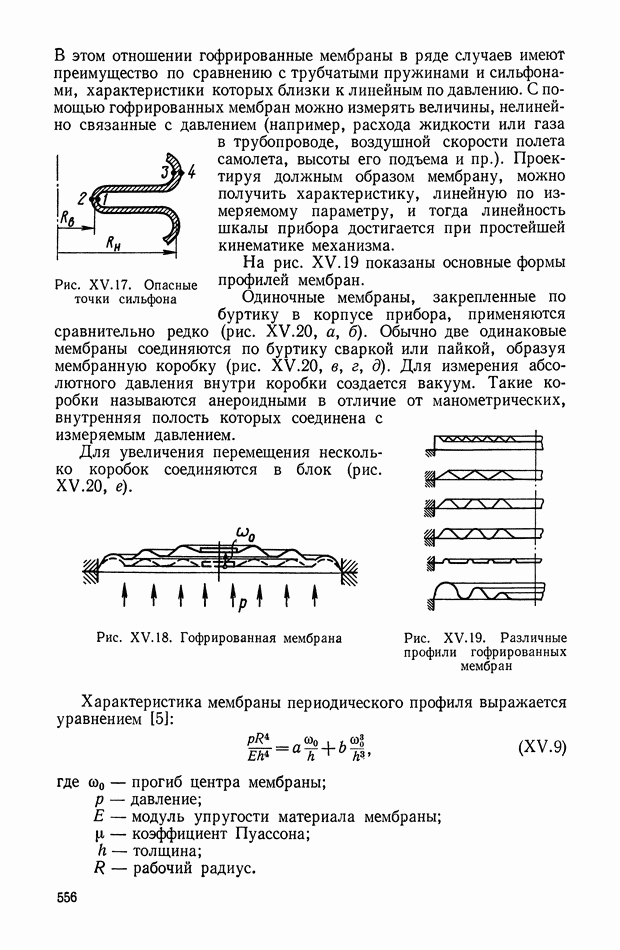
- Сильфоны.
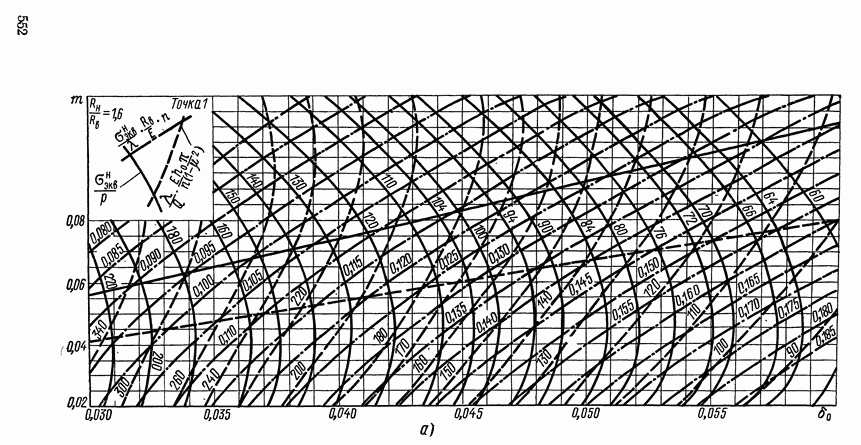
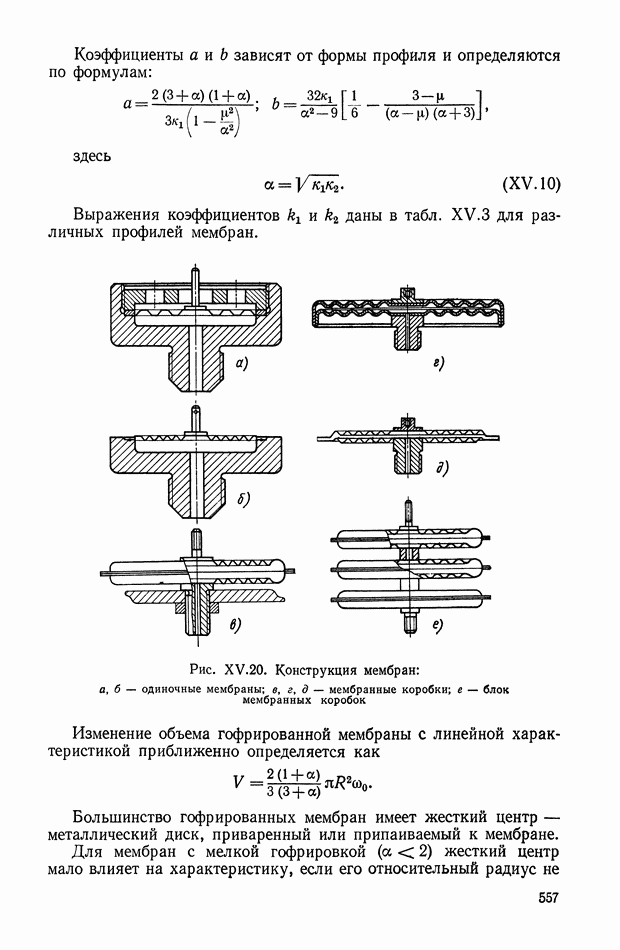
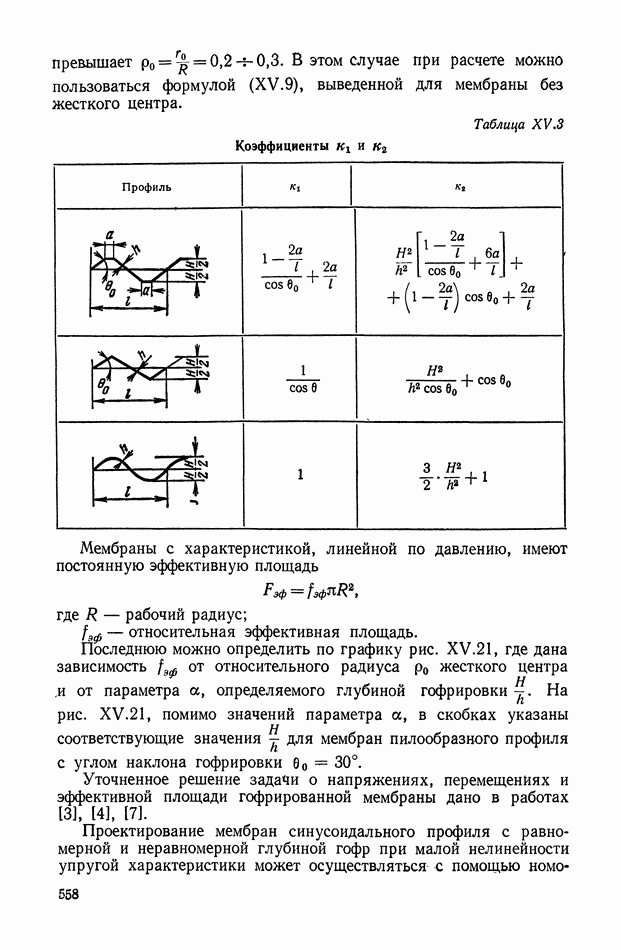
- Гофрированные мембраны.
- Гибкие диафрагмы.
- Хлопающие мембраны.
- 3. ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- ГЛАВА XVI. ПРЕОБРАЗОВАТЕЛИ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ
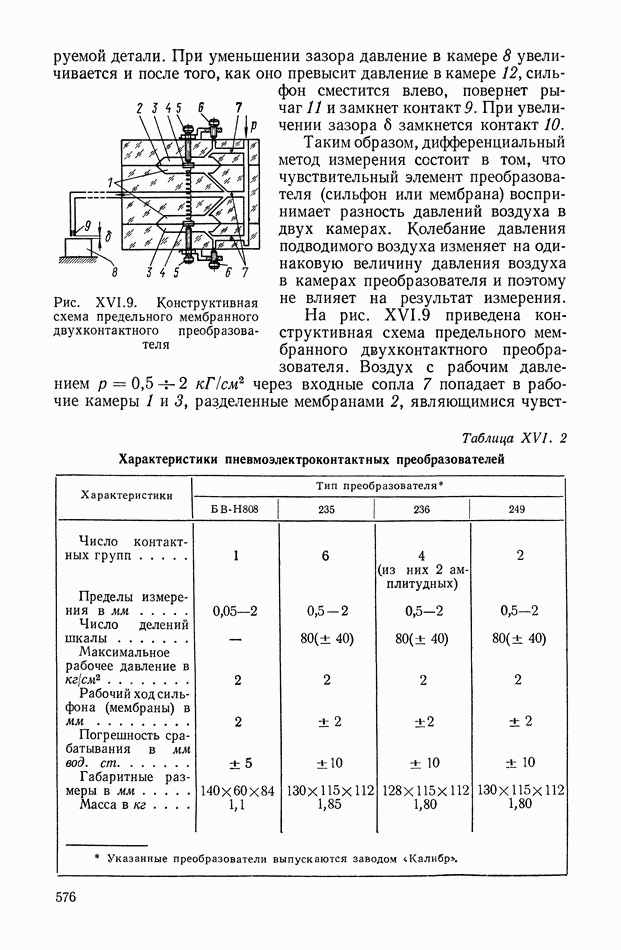
- Пневмоэлектроконтактные преобразователи линейных величин.
- 2. ПОТЕНЦИОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- Влияние нагрузки при использовании потенциометров в качестве делителей напряжения.
- Влияние нагрузки при использовании потенциометров в измерительных устройствах следящих систем.
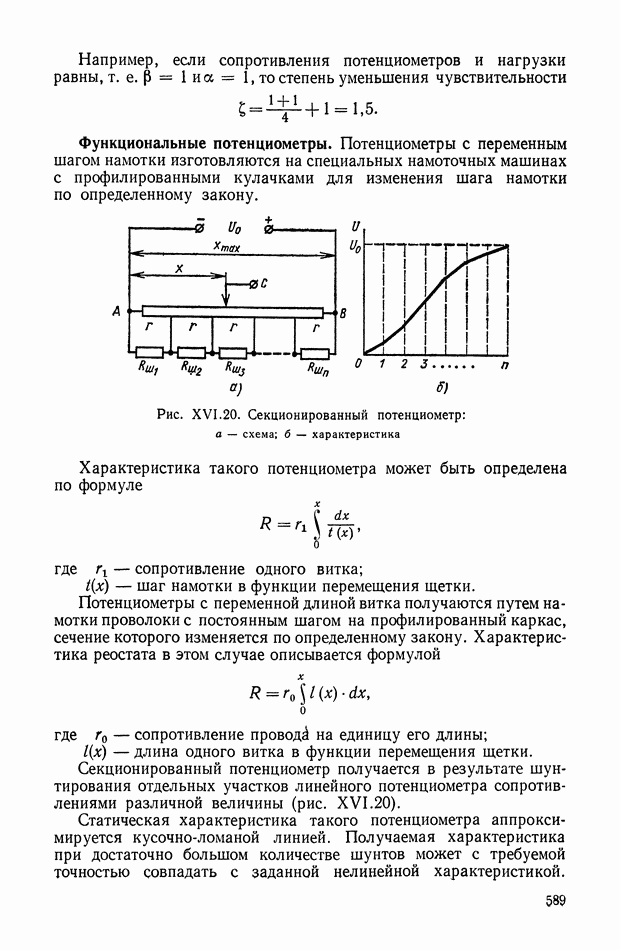
- Функциональные потенциометры.
- 3. ИНДУКТИВНЫЕ И ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. СЕЛЬСИНЫ
- Индикаторный режим работы сельсинов.
- Работа сельсинов в трансформаторном режиме.
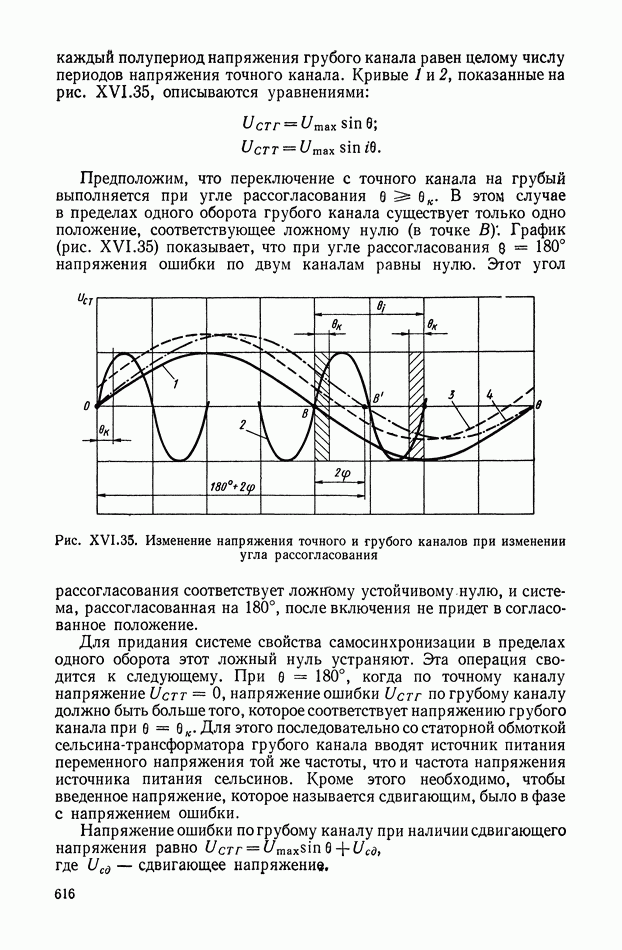
- Устранение ложного нуля в двухскоростной системе.
- Схемы синхронизаторов.
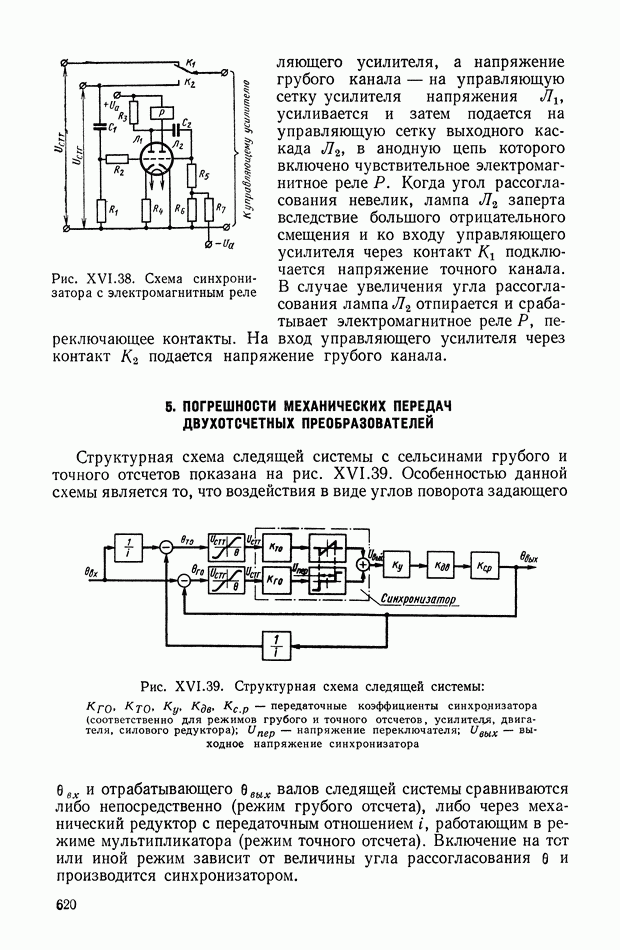
- 5. ПОГРЕШНОСТИ МЕХАНИЧЕСКИХ ПЕРЕДАЧ ДВУХОТСЧЕТНЫХ ПРЕОБРАЗОВАТЕЛЕЙ
- 6. ИНДУКЦИОННЫЕ ПРЕОБРАЗОВАТЕЛИ С ЭЛЕКТРИЧЕСКОЙ РЕДУКЦИЕЙ
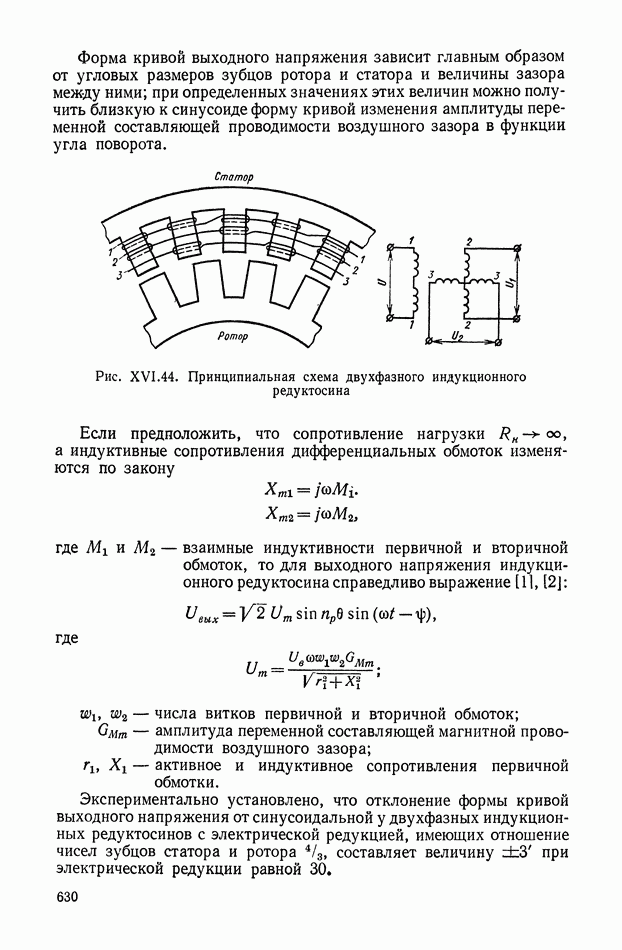
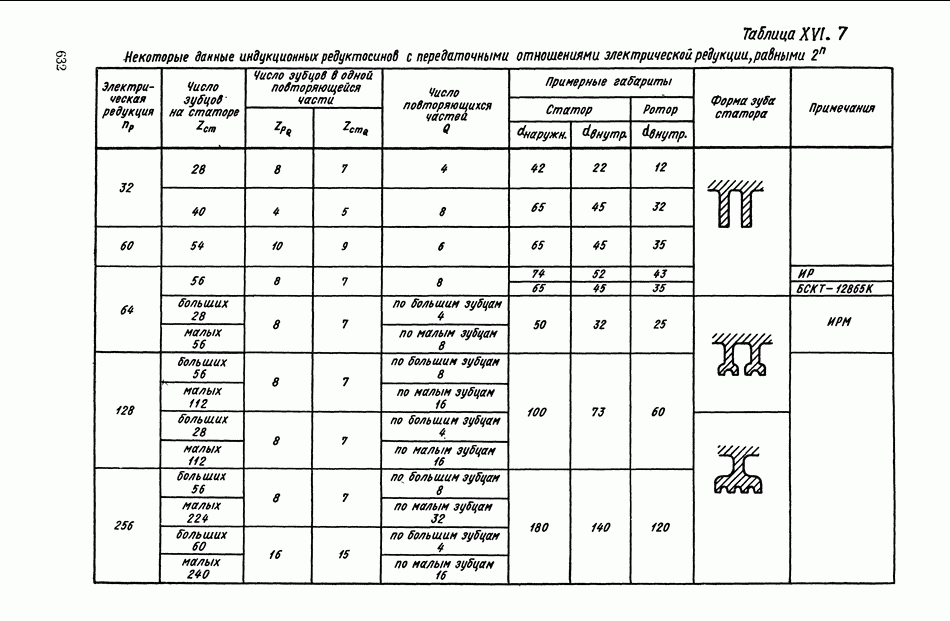
- Индукционные редуктосины.
- Индуктосины.
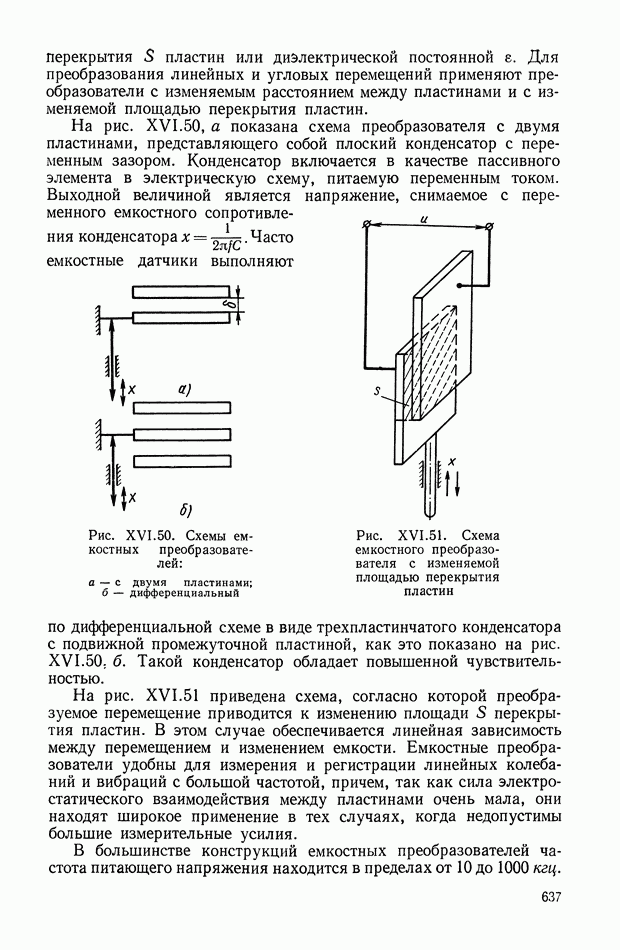
- 7. ЕМКОСТНЫЕ ПРЕОБРАЗОВАТЕЛИ
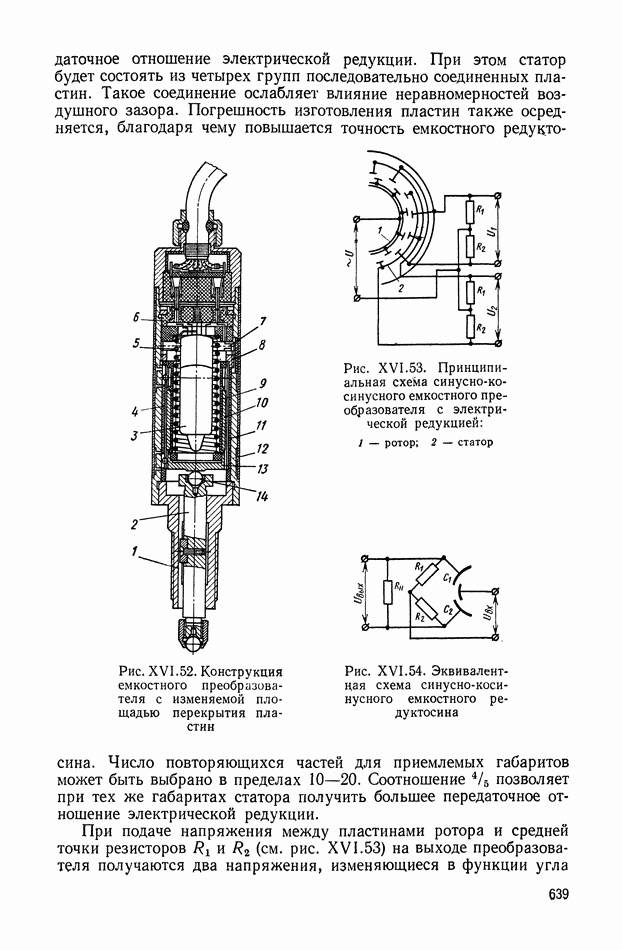
- Емкостный редуктосин.
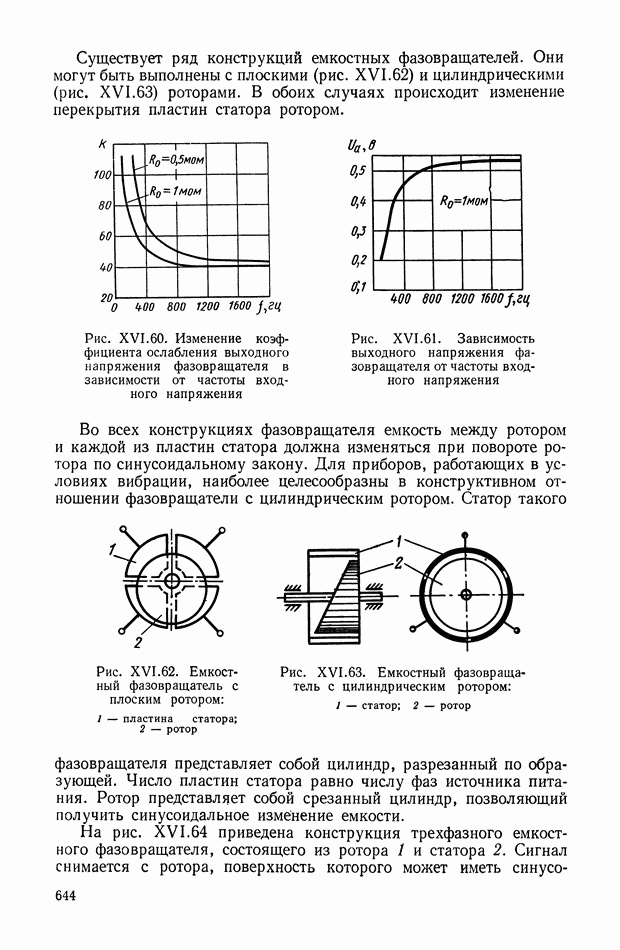
- Емкостный фазовращатель.
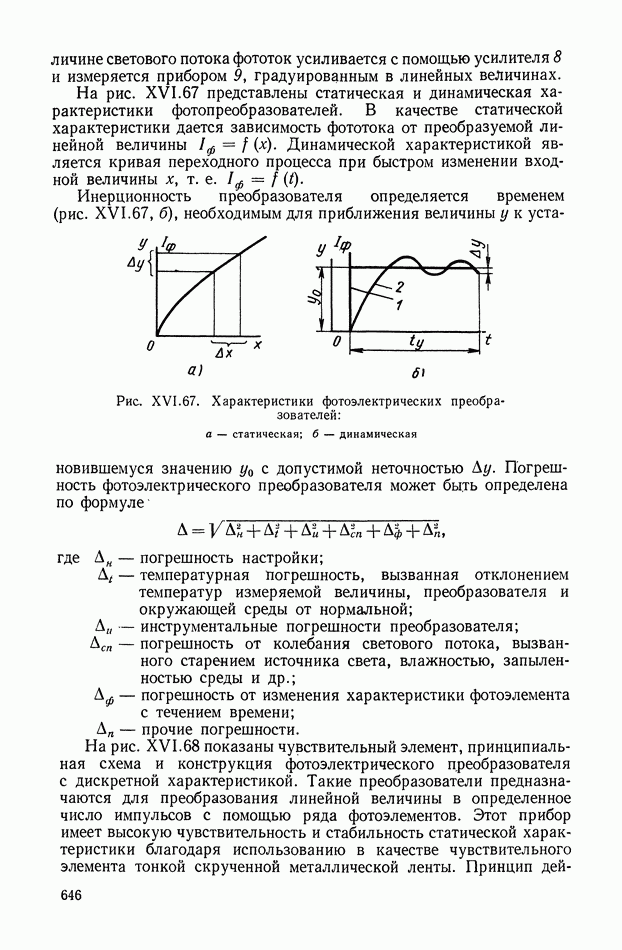
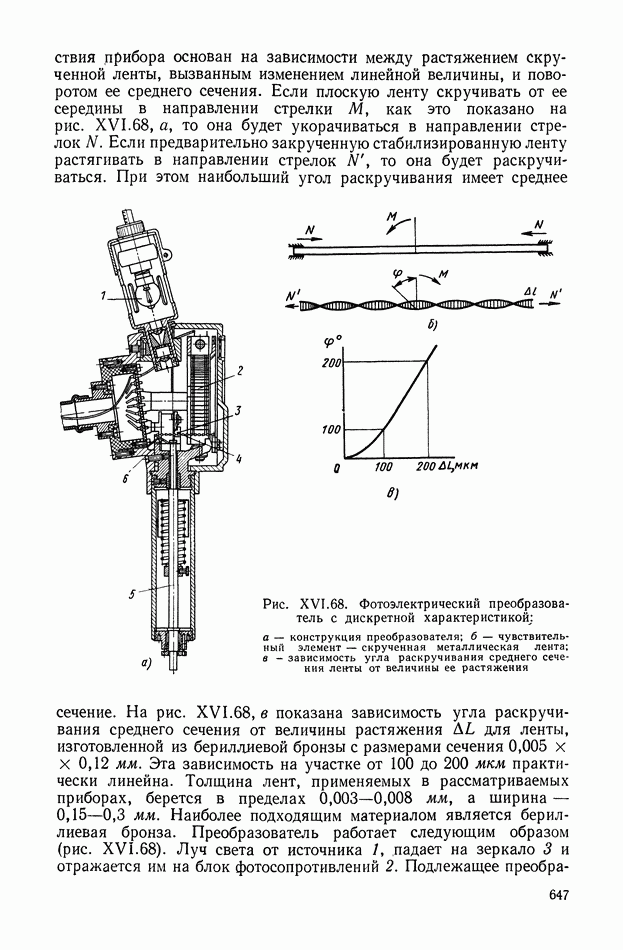
- 8. ФОТОЭЛЕКТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
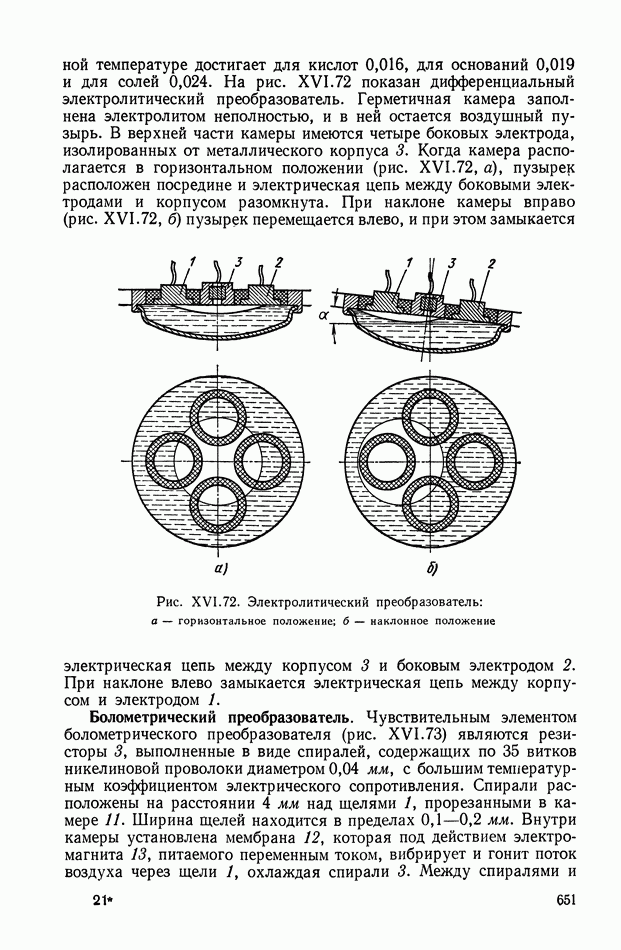
- 9. ЭЛЕКТРОННЫЕ, ЭЛЕКТРОННОЛИТИЧЕСКИЕ И БОЛОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ
- 10. ТЕНЗОПРЕОБРАЗОВАТЕЛИ
- БИБЛИОГРАФИЯ ПО РАЗДЕЛАМ КНИГИ