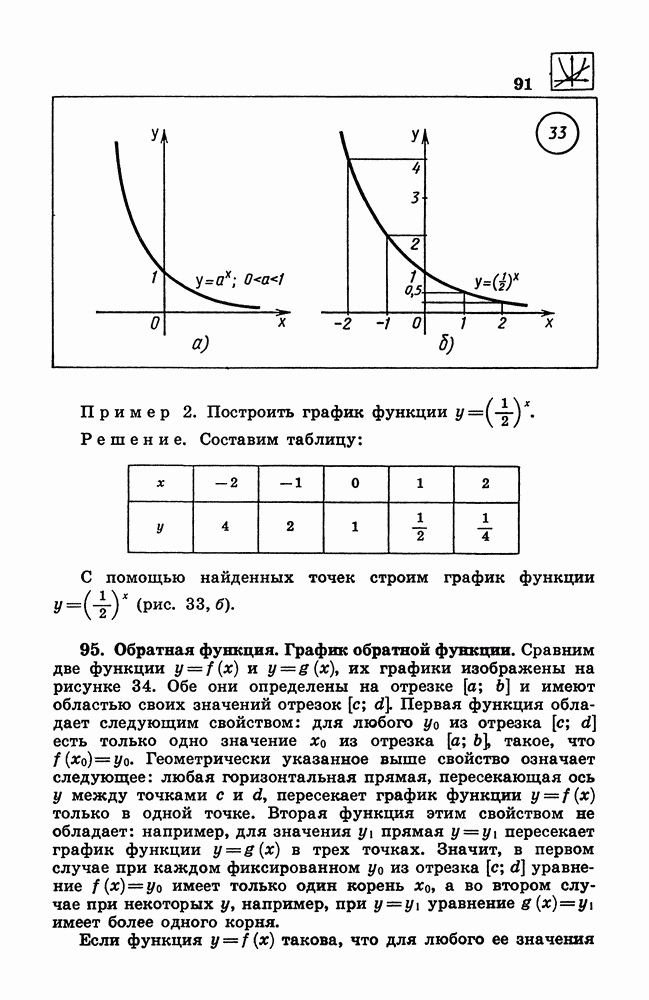
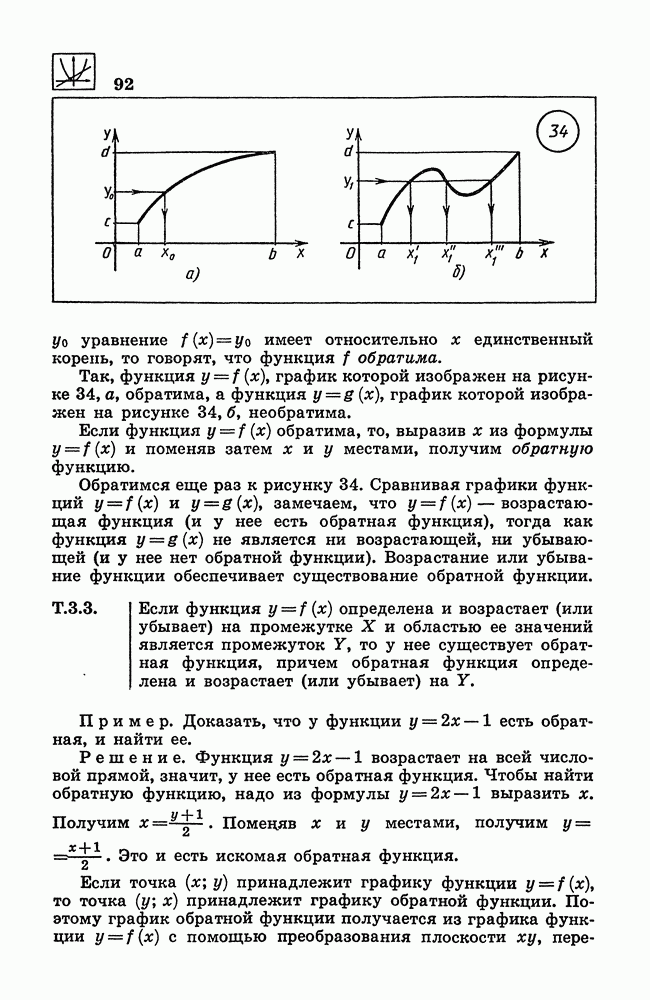
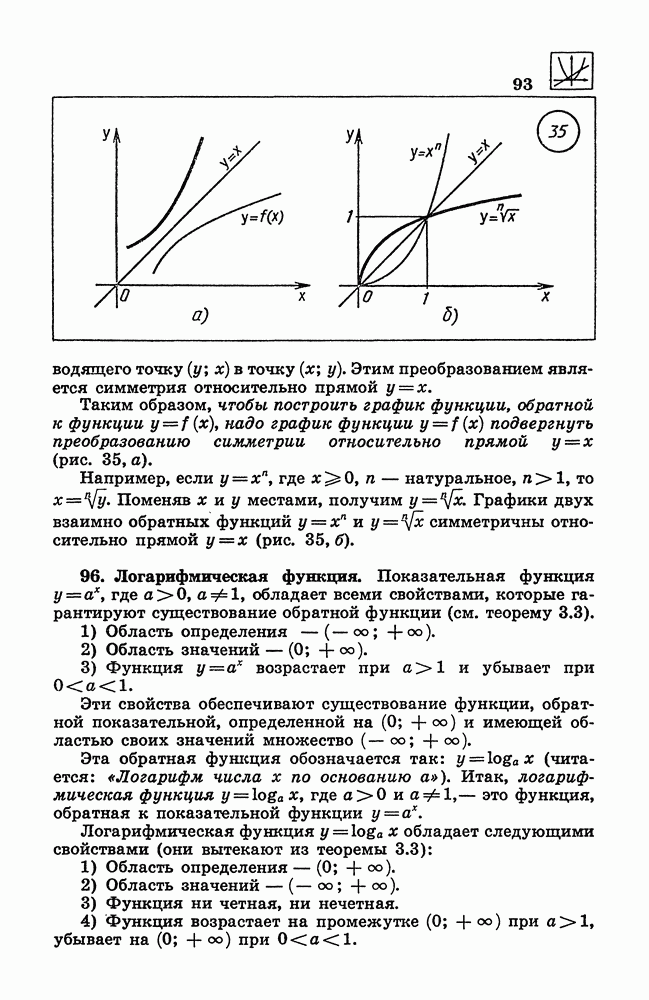
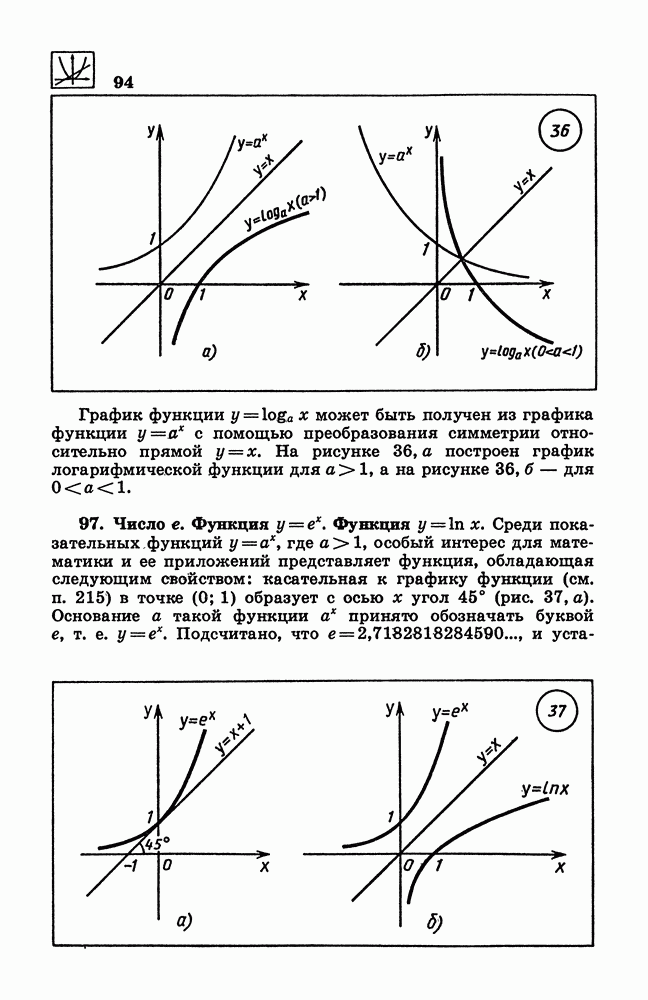
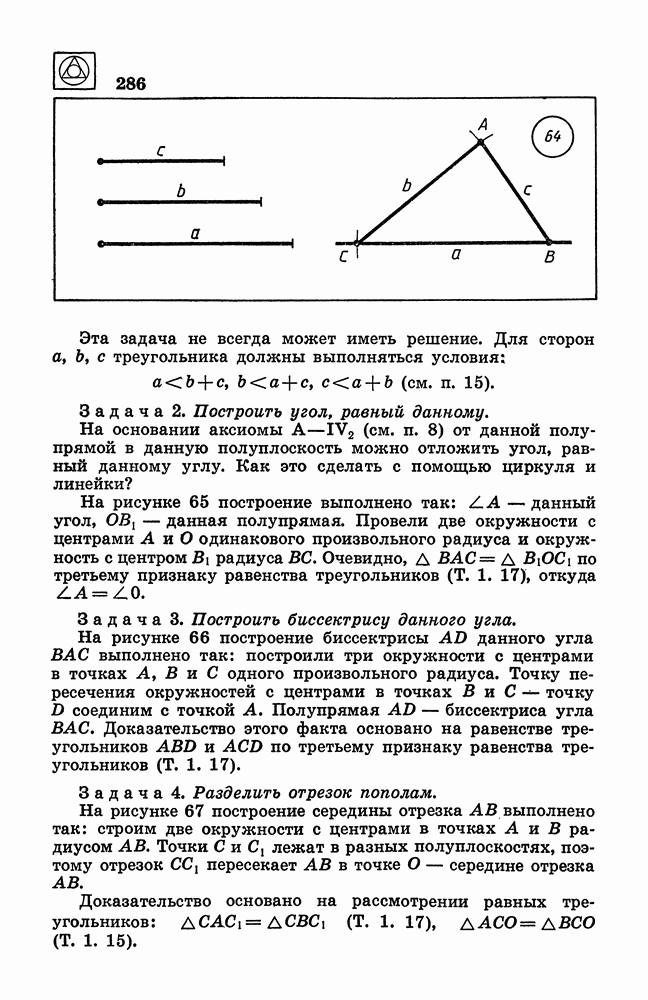
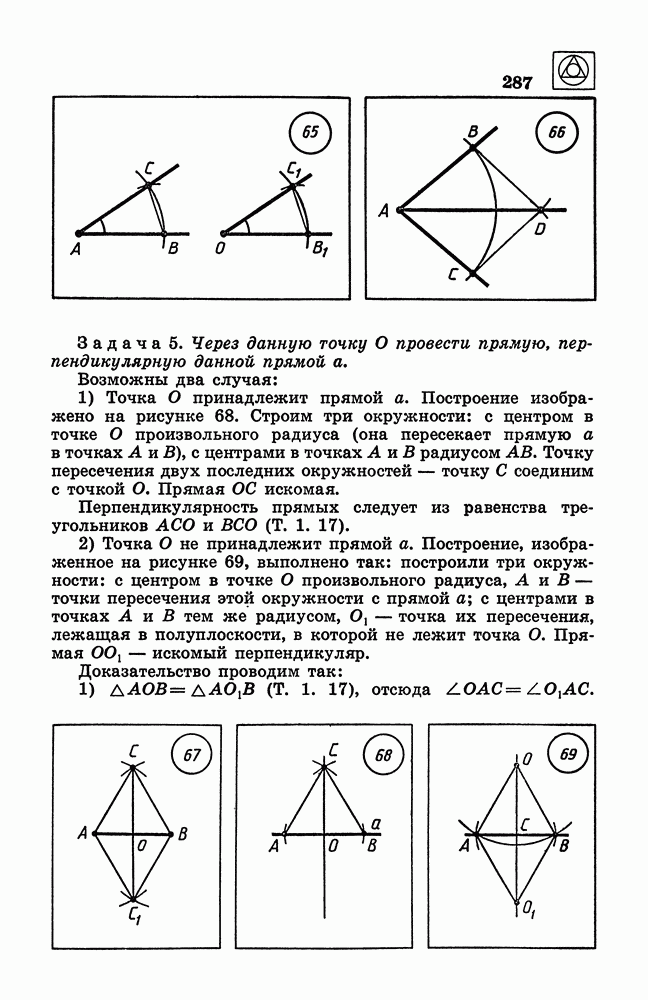
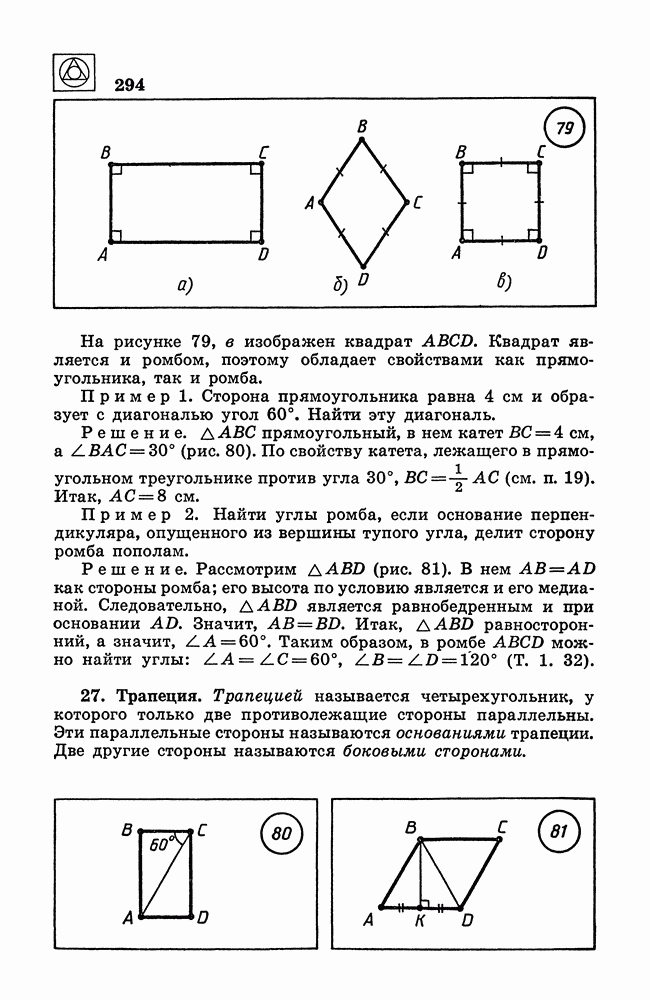
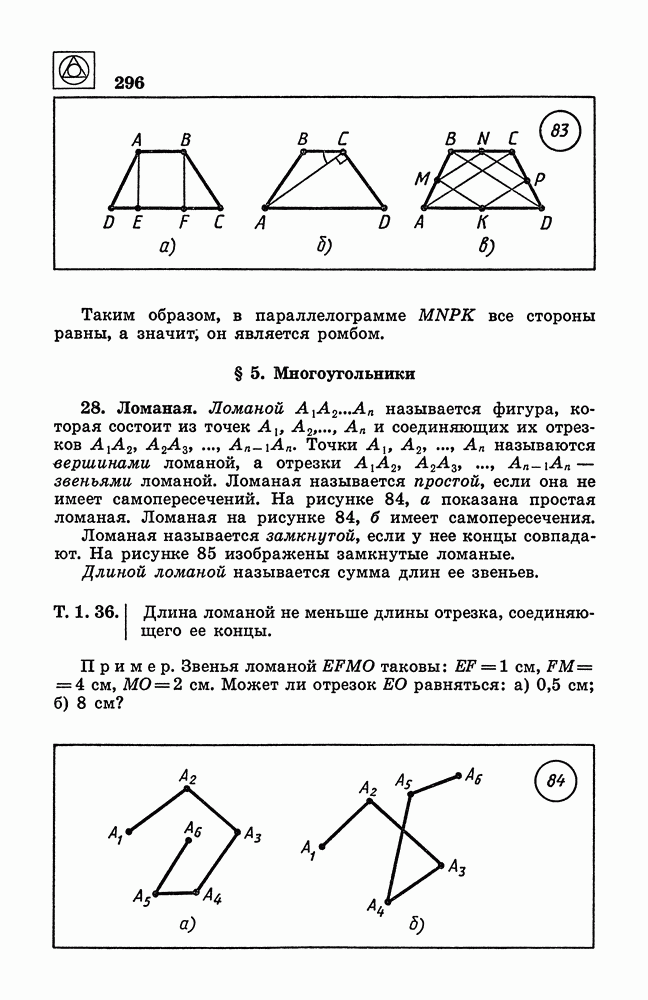
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
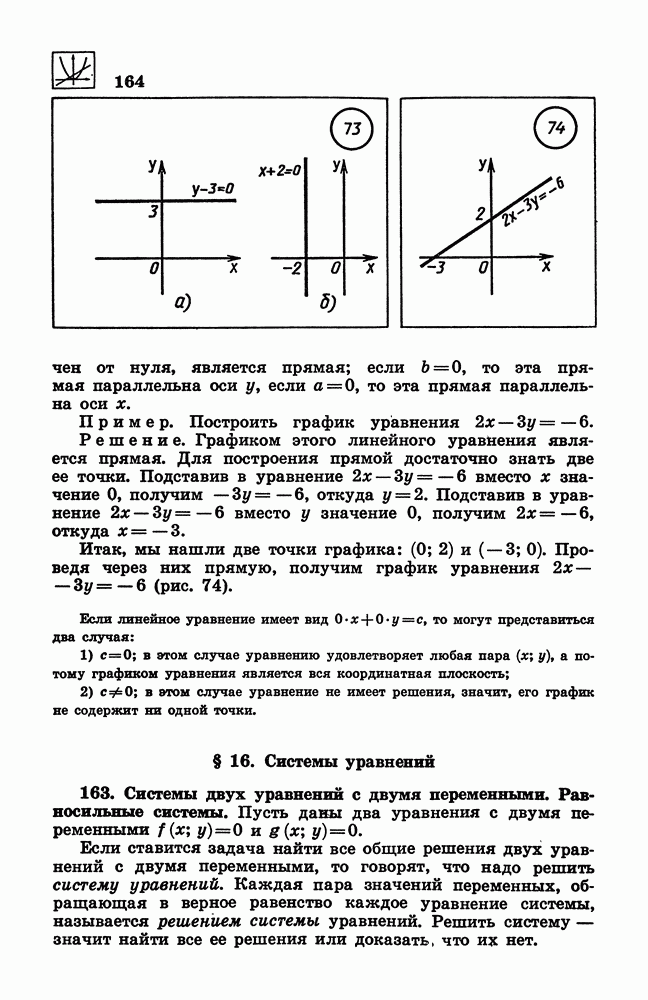
64. Площади поверхностей тел вращения.
Воспользовавшись данным в предыдущем пункте определением площади поверхности, можно получить формулы, по которым вычисляются площади поверхностей различных тел вращения. Площадь сферы находится по формуле

где  — радиус сферы.
— радиус сферы.
Площадь поверхности сферического сегмента находится по формуле

где  — радиус сферы,
— радиус сферы,  высота сегмента.
высота сегмента.
Площадь боковой поверхности цилиндра находится по формуле

где  — радиус основания цилиндра,
— радиус основания цилиндра,  его высота. Для нахождения площади полной поверхности цилиндра надо к площади боковой поверхности прибавить удвоенную площадь основания.
его высота. Для нахождения площади полной поверхности цилиндра надо к площади боковой поверхности прибавить удвоенную площадь основания.
Площадь боковой поверхности конуса находится по формуле

где  — радиус основания конуса,
— радиус основания конуса,  его образующая. Для нахождения площади полной поверхности конуса нужно к площади его боковой поверхности прибавить площадь основания.
его образующая. Для нахождения площади полной поверхности конуса нужно к площади его боковой поверхности прибавить площадь основания.
Площадь боковой поверхности усеченного конуса находится по формуле

где  соответственно радиусы оснований,
соответственно радиусы оснований,  его образующая.
его образующая.
Пример 1. В конус, радиус основания которого  и высота Н, вписан цилиндр. Найдите размеры цилиндра, при которых площадь его боковой поверхности имеет наибольшее значение.
и высота Н, вписан цилиндр. Найдите размеры цилиндра, при которых площадь его боковой поверхности имеет наибольшее значение.
Решение. Обозначим радиус основания цилиндра через  его высоту через
его высоту через  (рис. 187). Из подобия
(рис. 187). Из подобия  и
и

 следует, что
следует, что  откуда
откуда  Подставив в формулу
Подставив в формулу  значение
значение  , получим
, получим 
Рассмотрим  как функцию
как функцию  и иссдедуем ее на экстремум. Для этого найдем ее производную
и иссдедуем ее на экстремум. Для этого найдем ее производную 
Очевидно,  при
при  . В этой точке функция
. В этой точке функция  имеет максимум. Итак, наибольшее значение площадь боковой поверхности цилиндра принимает при
имеет максимум. Итак, наибольшее значение площадь боковой поверхности цилиндра принимает при 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- СЛОВО К УЧАЩИМСЯ
- ГЛАВА I. ЧИСЛА
- § 1. Натуральные числа
- 2. Арифметические действия над натуральными числами.
- 3. Деление с остатком.
- 4. Признаки делимости.
- 5. Разложение натурального числа на простые множители.
- 6. Наибольший общий делитель нескольких натуральных чисел.
- 7. Наименьшее общее кратное нескольких натуральных чисел.
- 8. Употребление букв в алгебре. Переменные.
- § 2. Рациональные числа
- 10. Равенство дробей. Основное свойство дроби. Сокращение дробей.
- 11. Приведение дробей к общему знаменателю.
- 12. Арифметические действия над обыкновенными дробями.
- 13. Десятичные дроби.
- 14. Арифметические действия над десятичными дробями.
- 15. Проценты.
- 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь.
- 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь.
- 18. Координатная прямая.
- 19. Множество рациональных чисел.
- § 3. Действительные числа
- 21. Действительные числа. Числовая прямая.
- 22 Обозначения некоторых числовых множеств.
- 23. Сравнение действительных чисел.
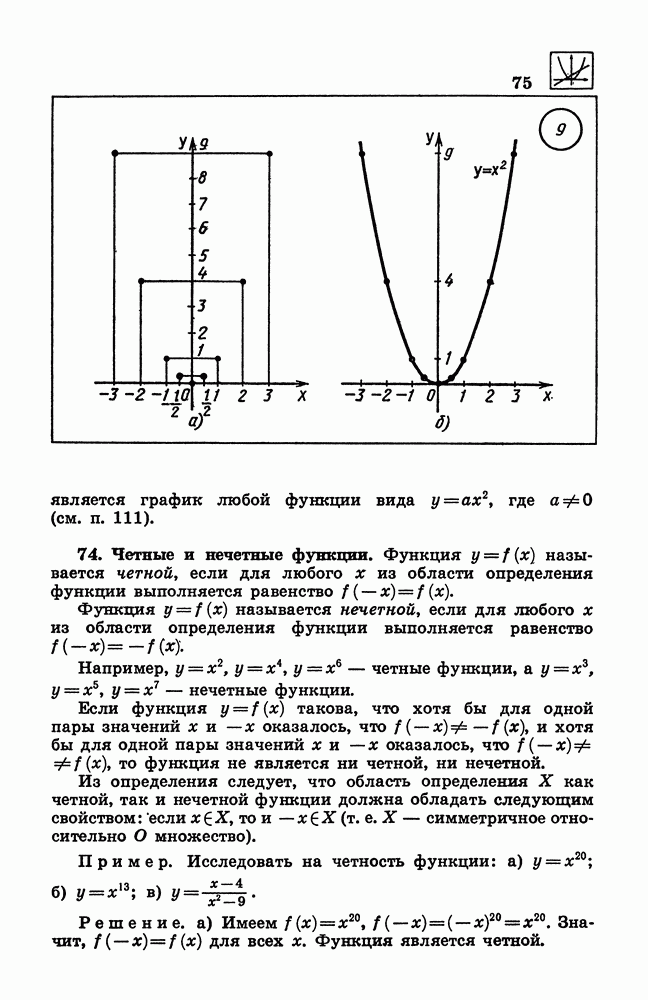
- 25. Числовые промежутки.
- 26. Модуль действительного числа.
- 27. Формула расстояния между двумя точками координатной прямой.
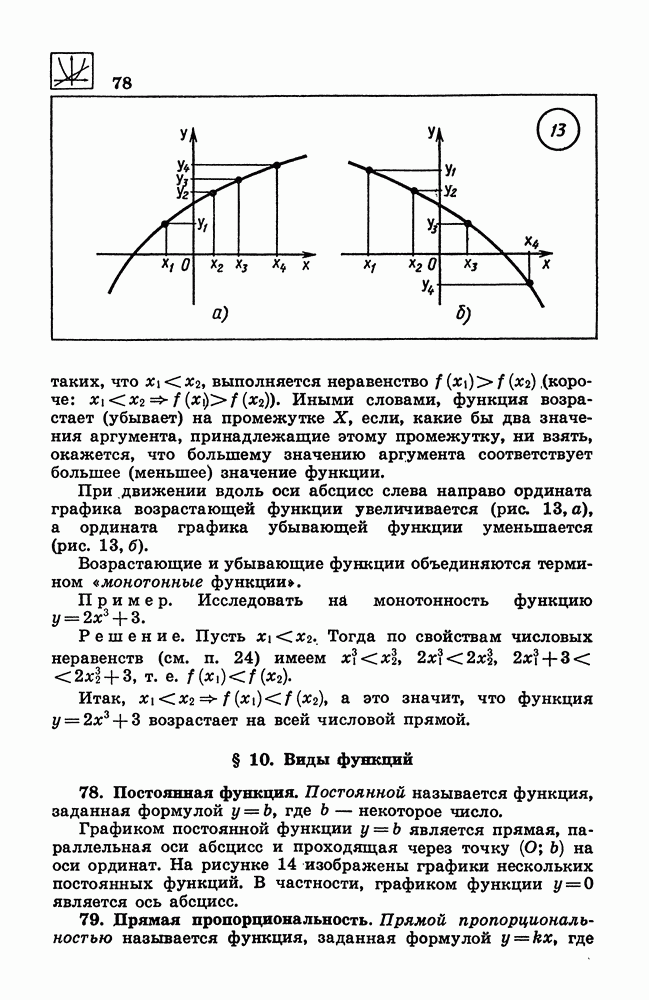
- 28. Правила действий над действительными числами.
- 29. Свойства арифметических действий над действительными числами.
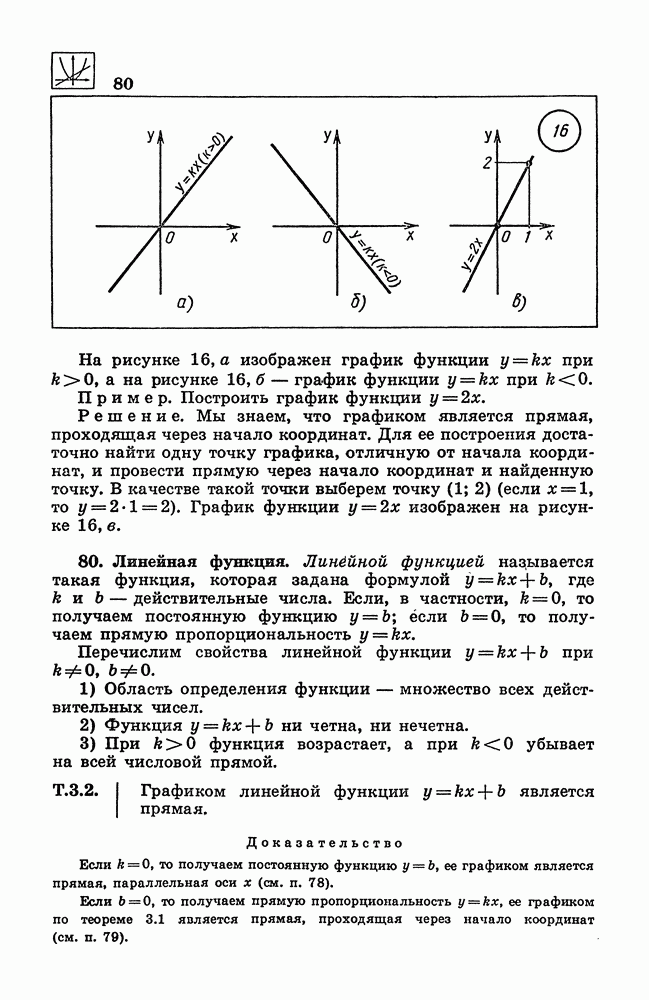
- 30. Пропорции.
- 31. Целая часть числа. Дробная часть числа.
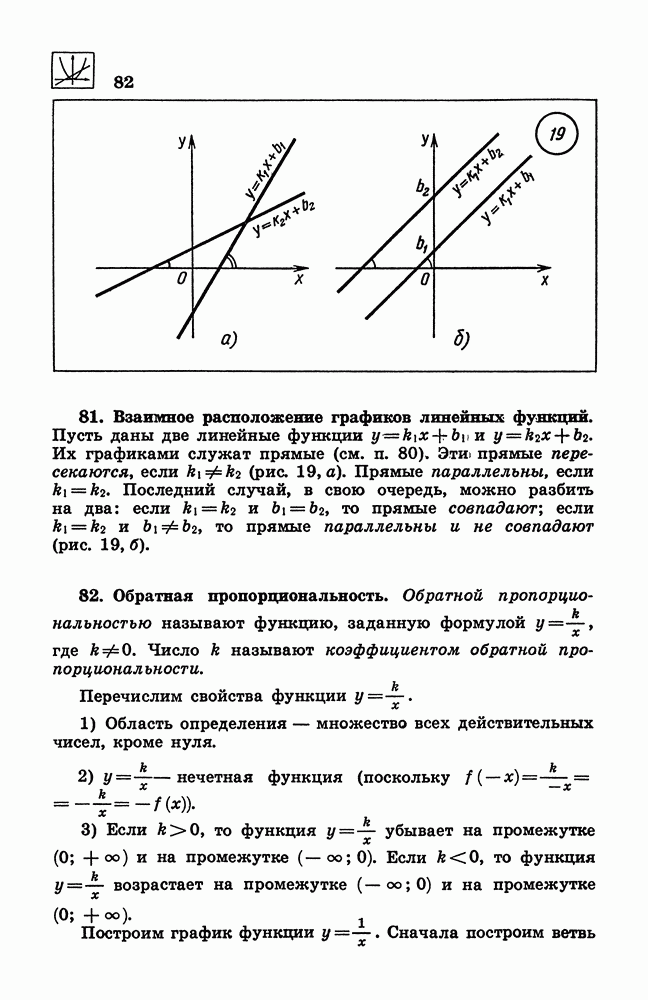
- 32. Степень с натуральным показателем.
- 33. Степень с нулевым показателем. Степень с отрицательным целым показателем.
- 34. Стандартный вид положительного действительного числа.
- 35. Определение арифметического корня.
- 36. Корень нечетной степени из отрицательного числа.
- 37. Степень с дробным показателем.
- 38. Свойства степеней с рациональными показателями.
- 39. Приближенные значения чисел. Абсолютная и относительная погрешности.
- 40. Десятичные приближения действительного числа по недостатку и по избытку.
- 41. Правило извлечения квадратного корня из натурального числа.
- 42. Понятие о степени с иррациональным показателем.
- 43. Свойства степеней с действительными показателями.
- § 4. Комплексные числа
- 45. Арифметические операции над комплексными числами.
- 46. Алгебраическая форма комплексного числа.
- 47. Отыскание комплексных корней уравнений.
- ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
- 49. Допустимые значения переменных.
- 50. Понятие тождественного преобразования выражения. Тождество.
- § 6. Целые рациональные выражения
- 52. Многочлены. Приведение многочленов к стандартному виду.
- 53. Формулы сокращенного умножения.
- 54. Разложение многочленов на множители.
- 55. Многочлены от одной переменной.
- 56. Разложение квадратного трехчлена на линейные множители.
- 57. Разложение на множители двучлена x^n-a^n.
- 58. Возведение двучлена в натуральную степень (бином Ньютона).
- § 7. Дробные рациональные выражения
- 60. Сокращение рациональных дробей.
- 61. Приведение рациональных дробей к общему знамена телю.
- 62. Сложение и вычитание рациональных дробей.
- 63. Умножение и деление рациональных дробей.
- 64. Возведение рациональной дроби в целую степень.
- 65. Преобразование рациональных выражений.
- § 8. Иррациональные выражения
- 67. Тождество sqrt(a^2)=|a|
- 68. Преобразование иррациональных выражений.
- Глава III. ФУНКЦИИ И ГРАФИКИ
- 70. Аналитическое задание функции.
- 71. Табличное задание функции.
- 72. Числовая плоскость. Координатная плоскость, оси координат.
- 73. График функции, заданной аналитически.
- 74. Четные и нечетные функции.
- 75. График четной функции. График нечетной функции.
- 76. Периодические функции.
- 77. Монотонные функции.
- § 10. Виды функций
- 79. Прямая пропорциональность.
- 80. Линейная функция.
- 81. Взаимное расположение графиков линейных функций.
- 82. Обратная пропорциональность.
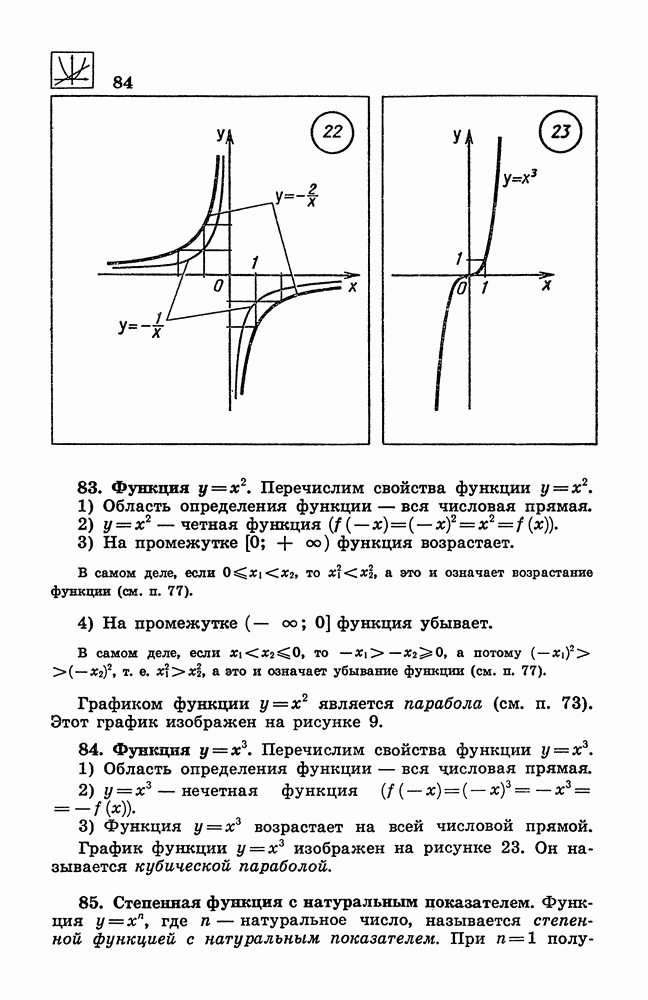
- 83. Функция у = x^2.
- 84. Функция y = x^3.
- 85. Степенная функция с натуральным показателем.
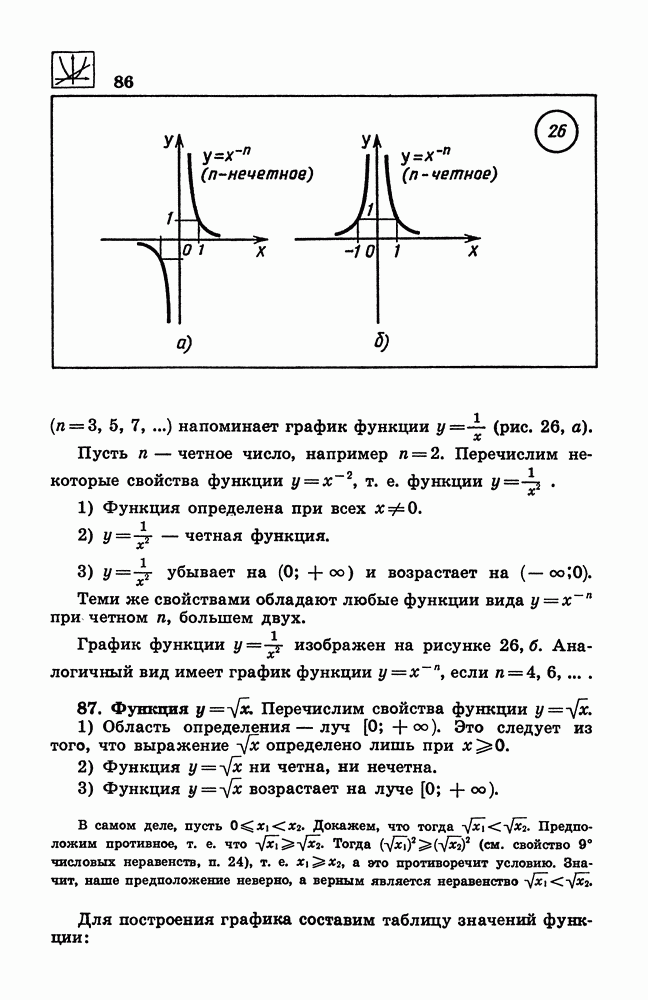
- 86. Степенная функция с целым отрицательным показателем.
- 87. Функция y = sqrt(x)
- 88. Функция y = x^(1/3)
- 89. Функция y = x^(1/n)
- 90. Степенная функция с положительным дробным показателем.
- 91. Степенная функция с отрицательным дробным показателем.
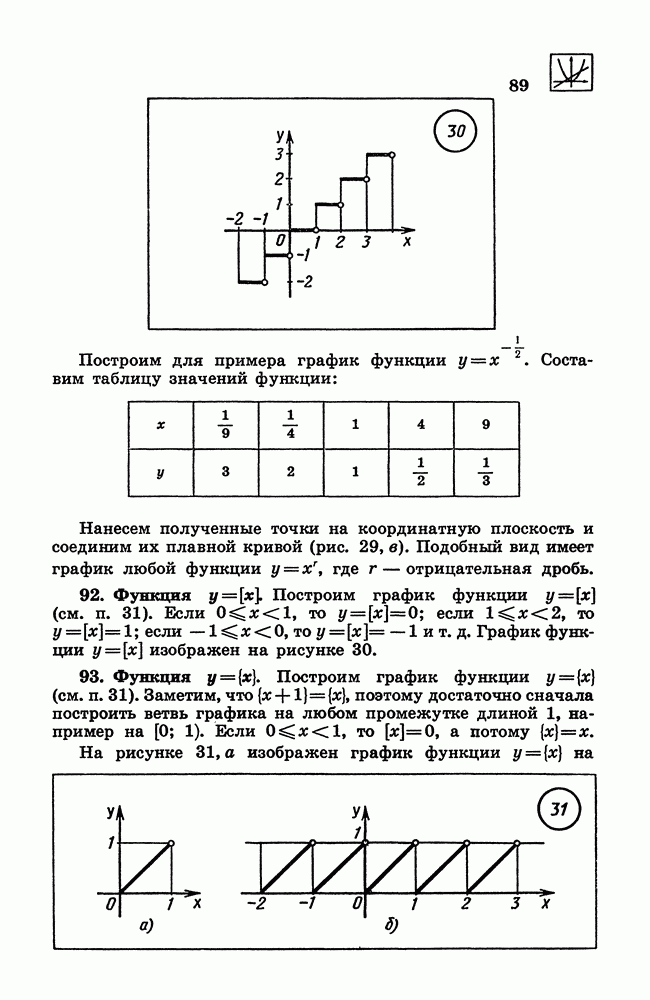
- 92. Функция у = [x].
- 93. Функция у = {х}.
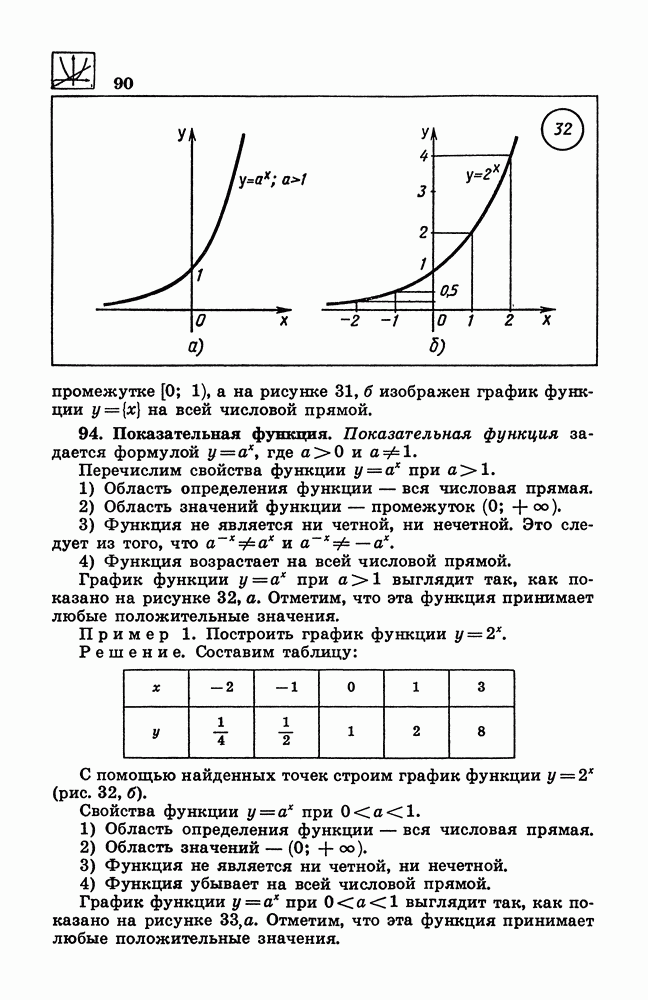
- 94. Показательная функция.
- 95. Обратная функция. График обратной функции.
- 96. Логарифмическая функция.
- 97. Число е. Функция у = е^x. Функция у = ln х.
- 98. Определение тригонометрических функций.
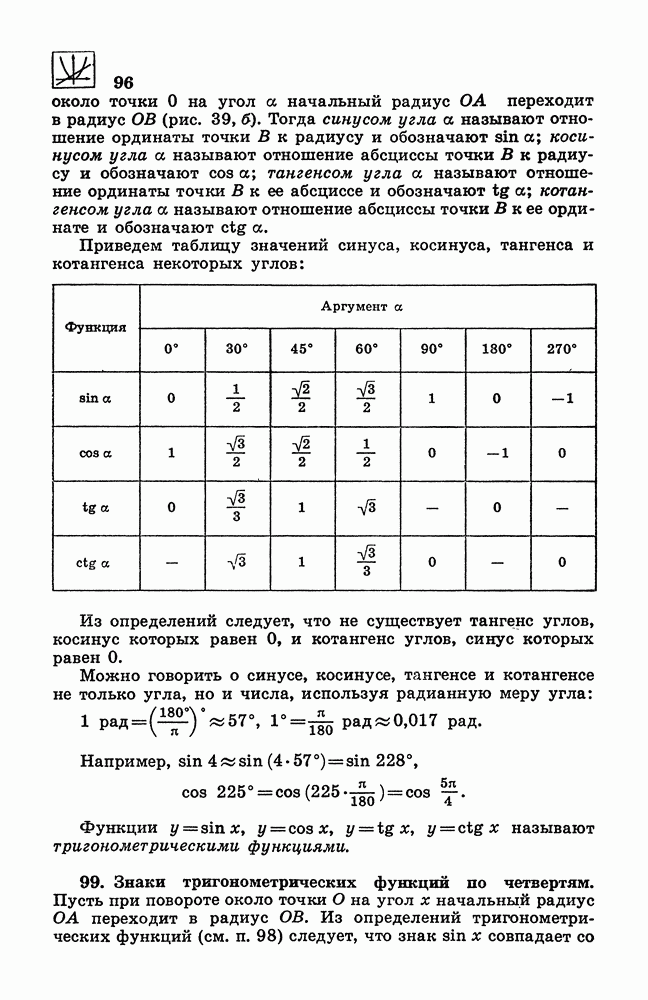
- 99. Знаки тригонометрических функций по четвертям.
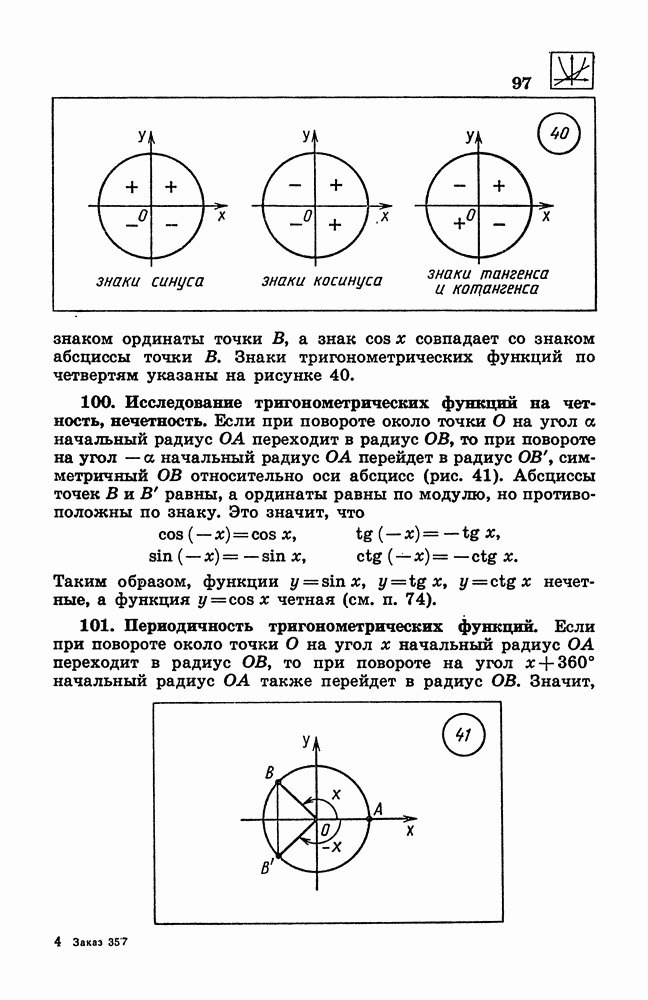
- 100. Исследование тригонометрических функций на четность, нечетность.
- 101. Периодичность тригонометрических функций.
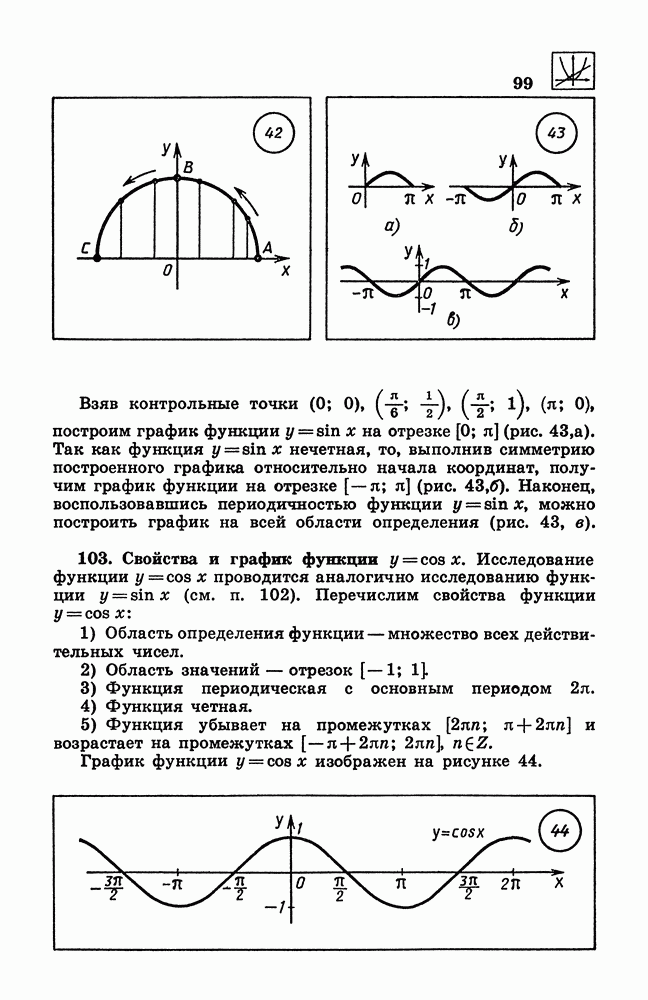
- 102. Свойства и график функции y = sin x.
- 103. Свойства и график функции у = cos x.
- 104. Свойства и график функции у = tg х.
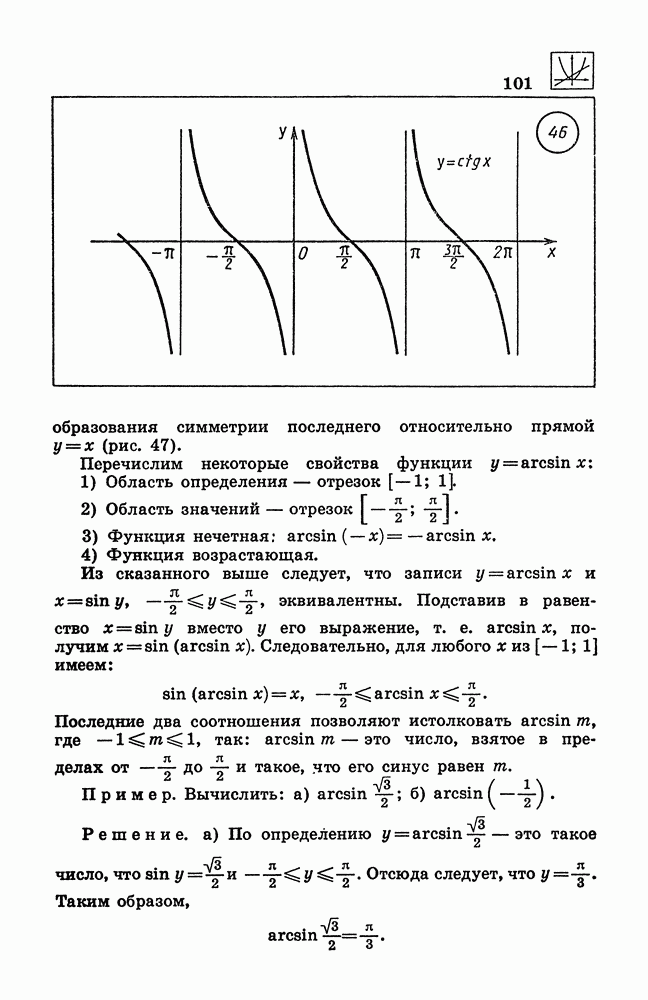
- 105. Свойства и график функции y = ctg x.
- 106. Функция у = arcsin х.
- 107. Функция y = arccos x.
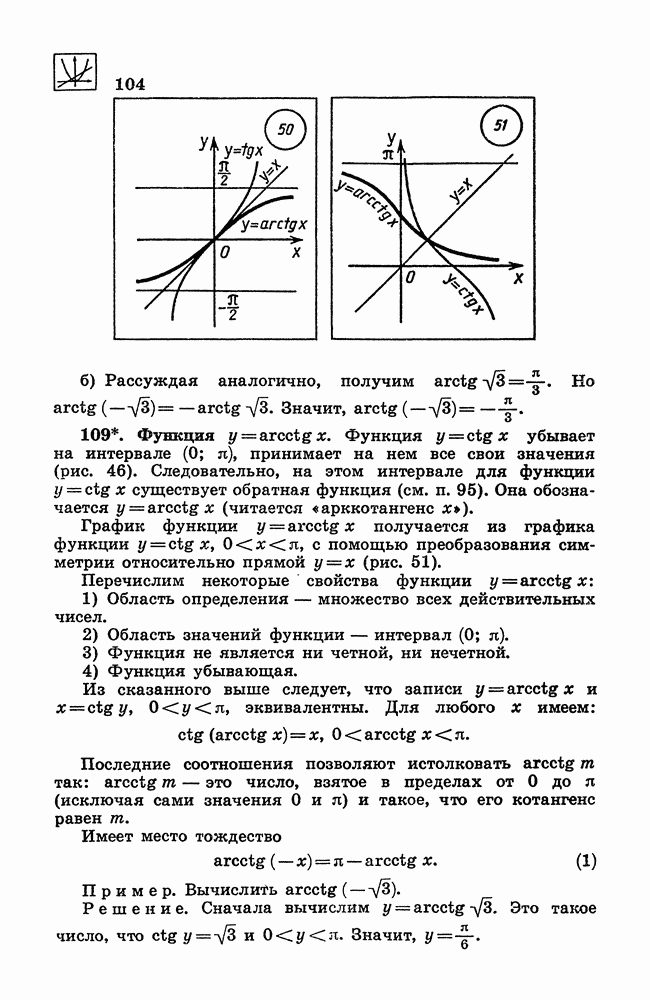
- 108. Функция у = arctg x.
- 109. Функция y = arcctg х.
- § 11. Преобразования графиков
- 111. Графики функций y = ax^2, y = ax^3.
- 112. Построение графика функции y = f(x-m)+n
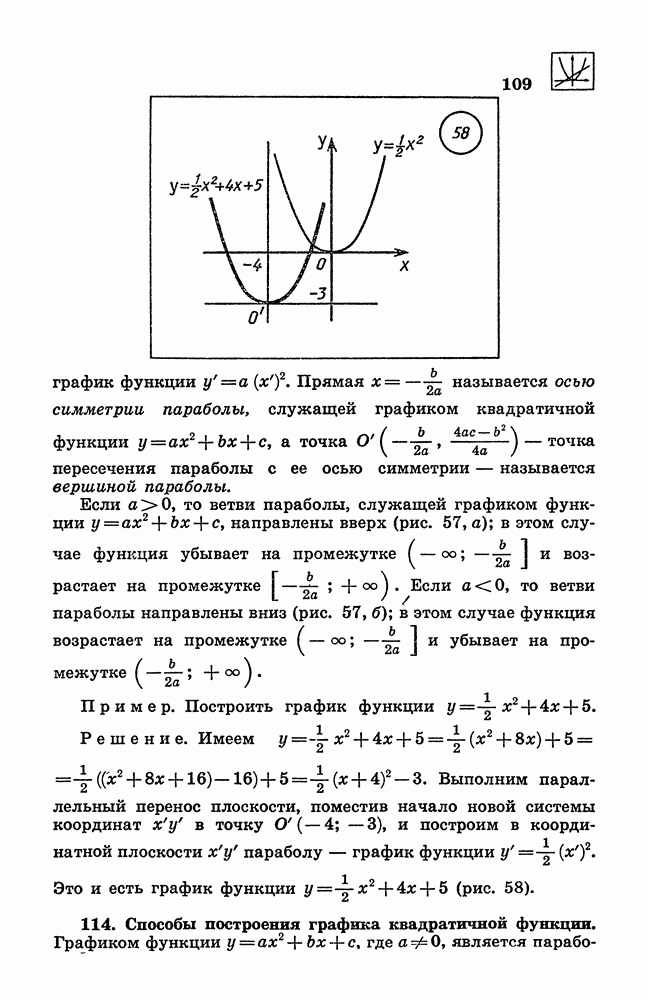
- 113. График квадратичной функции.
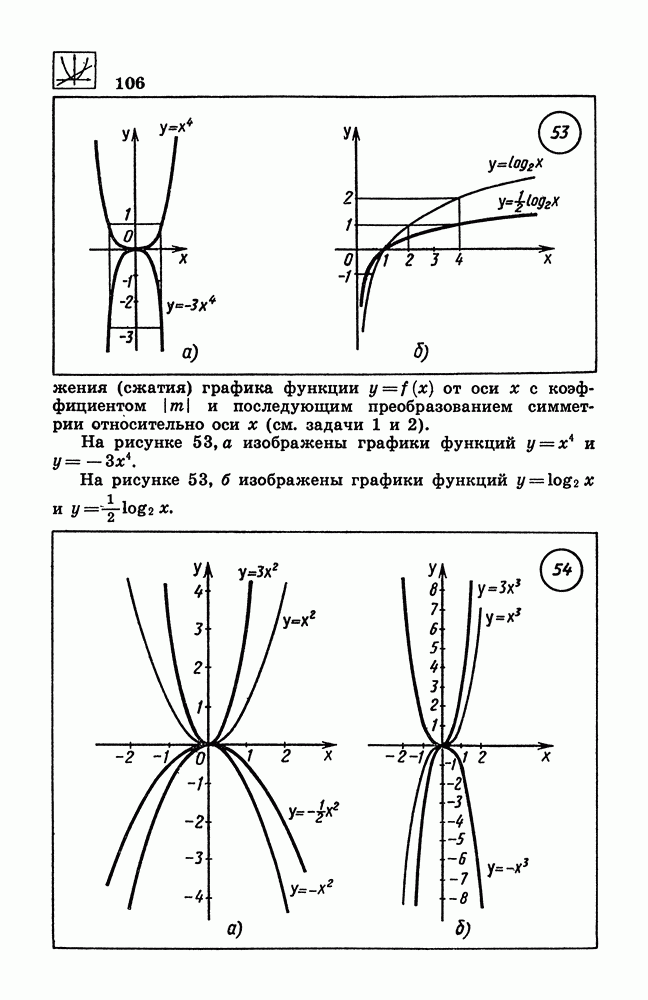
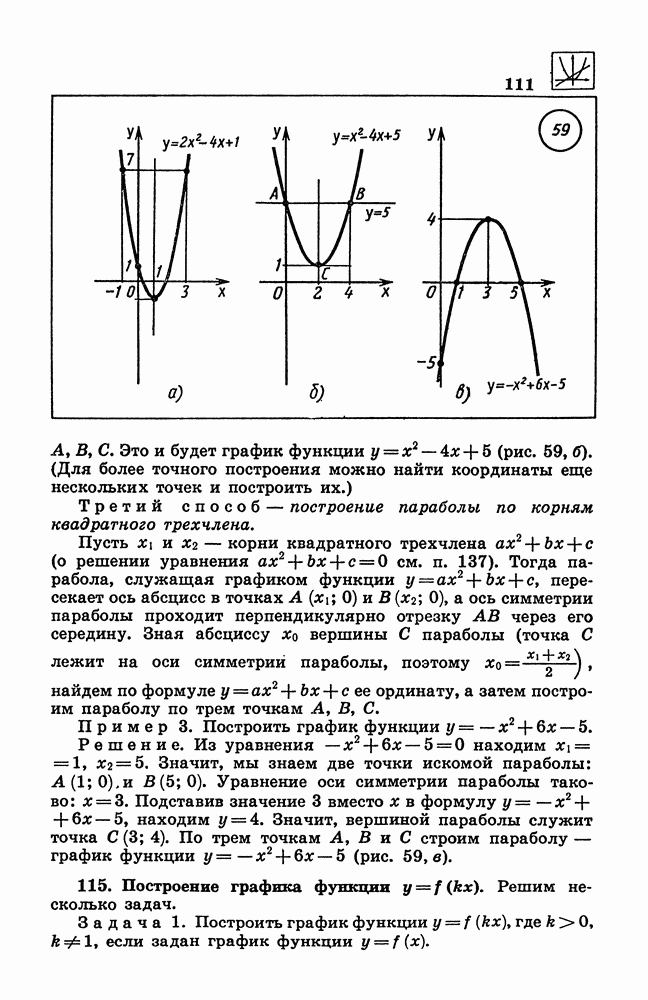
- 114. Способы построения графика квадратичной функции
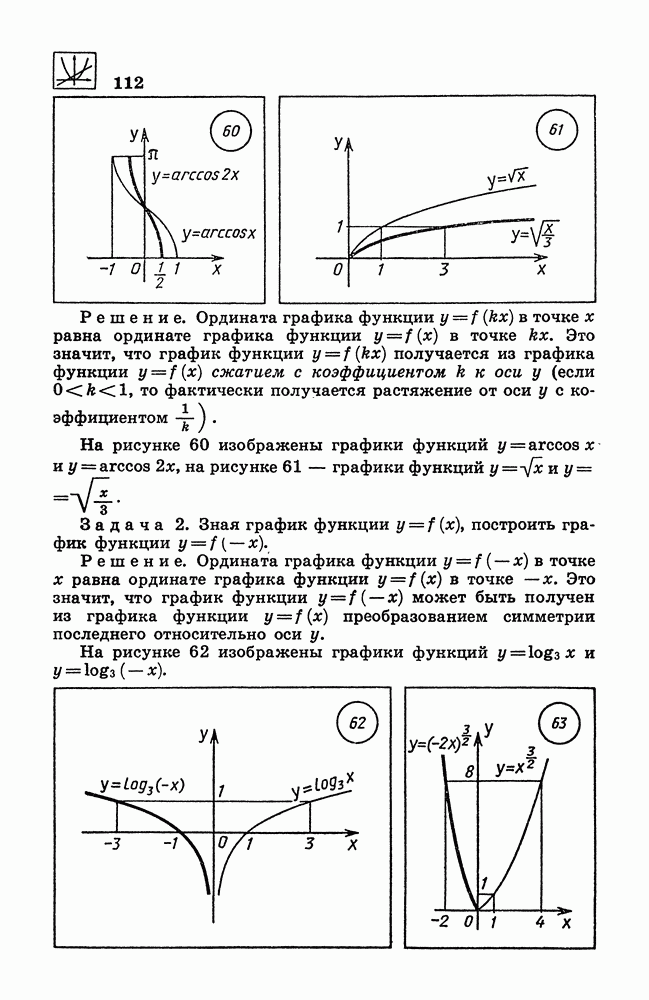
- 115. Построение графика функции y = f(kx).
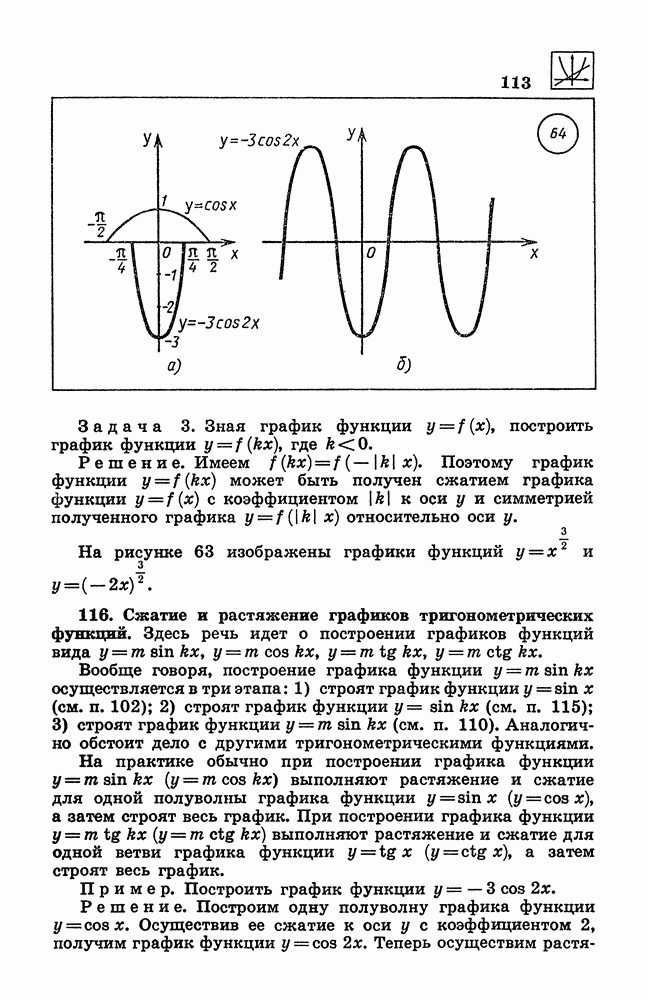
- 116. Сжатие и растяжение графиков тригонометрических функций.
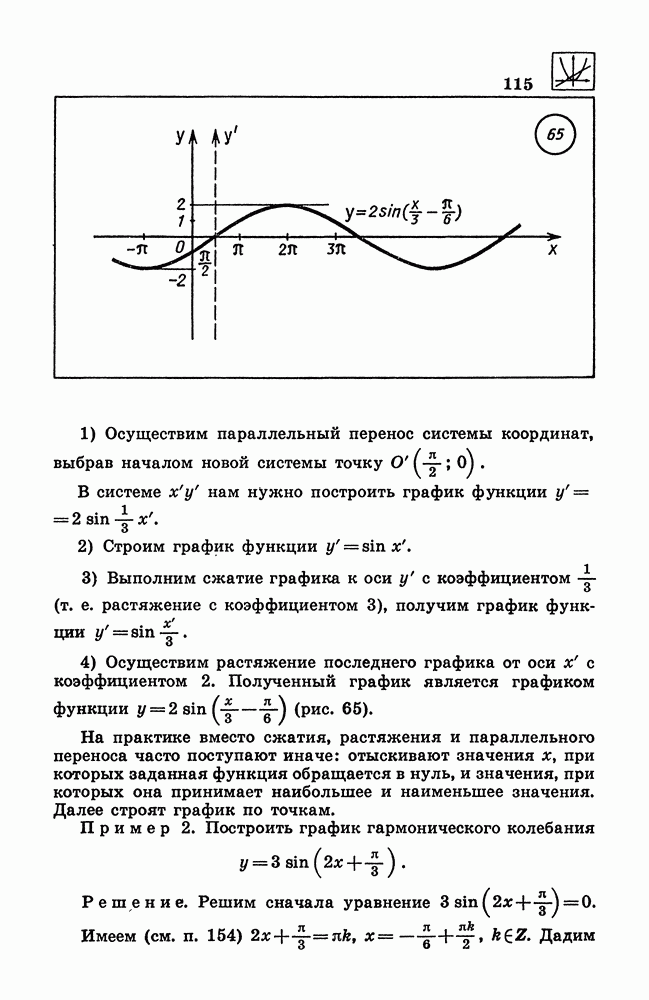
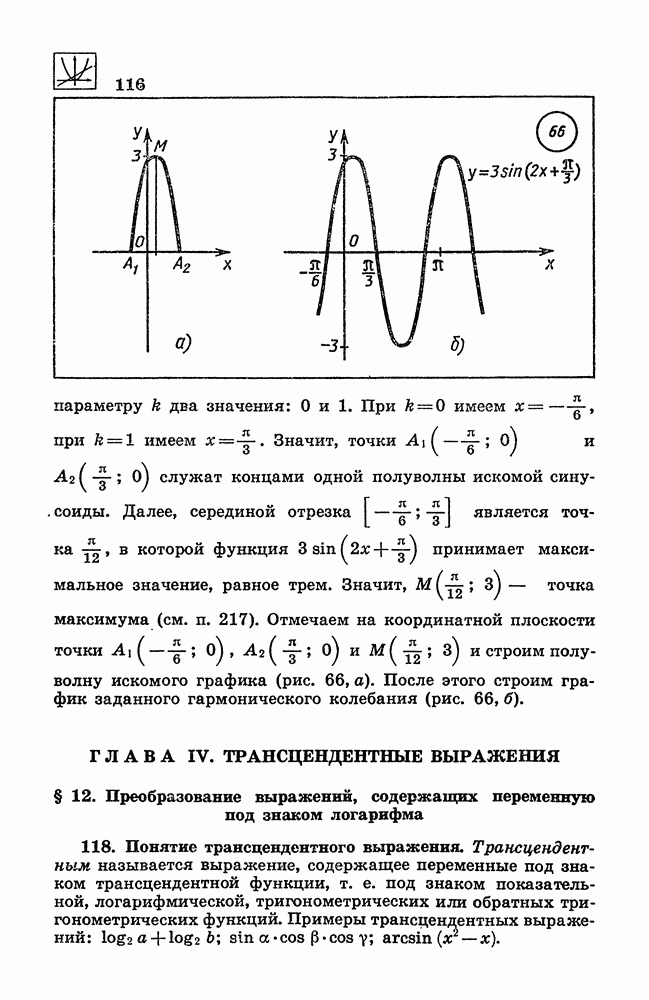
- 117. График гармонического колебания
- ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ
- § 12. Преобразование выражений, содержащих переменную под знаком логарифма
- 119. Определение логарифма положительного числа по данному основанию.
- 120. Свойства логарифмов.
- 121. Переход к новому основанию логарифма.
- 122. Логарифмирование и потенцирование.
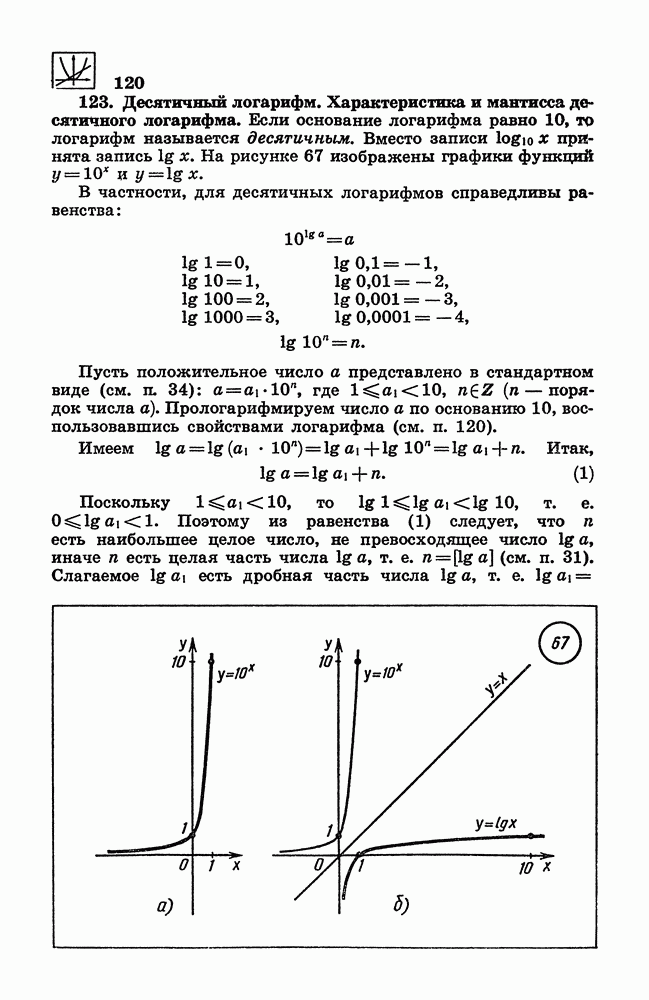
- 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма.
- § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений
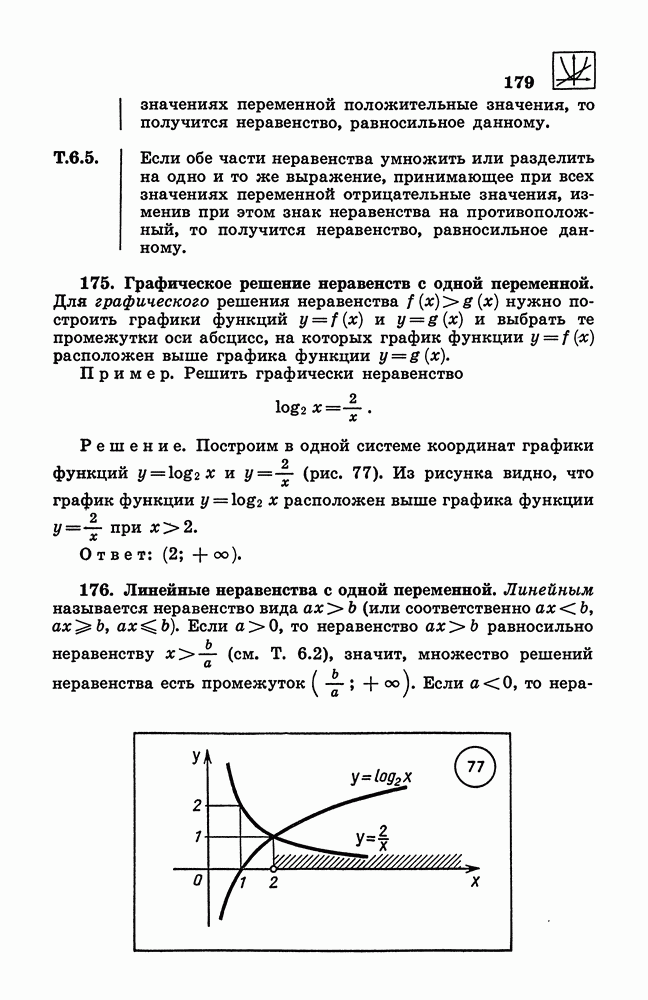
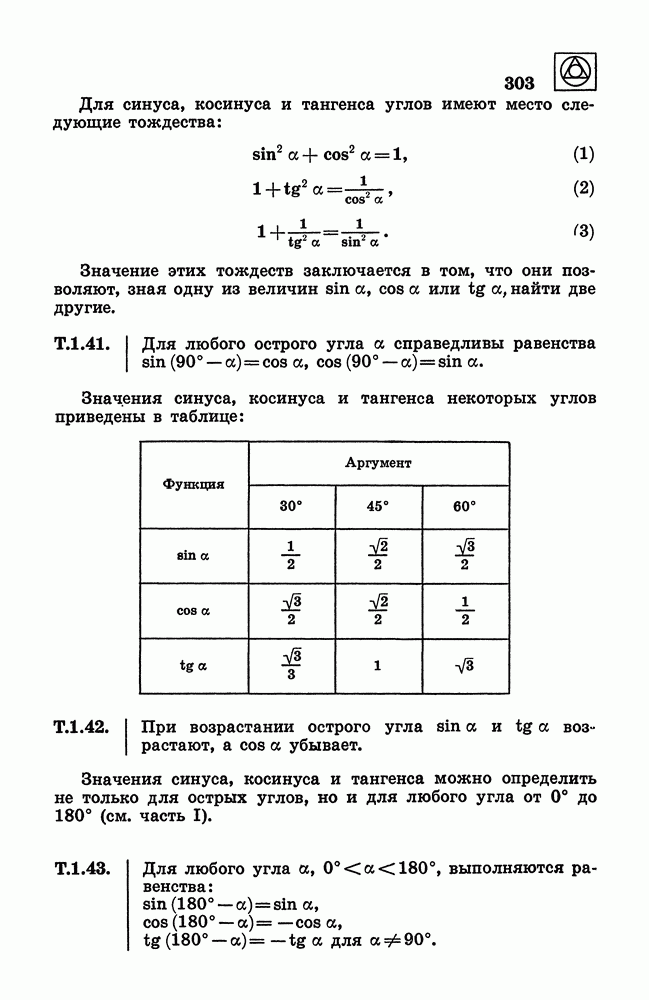
- 125. Формулы сложения и вычитания аргументов.
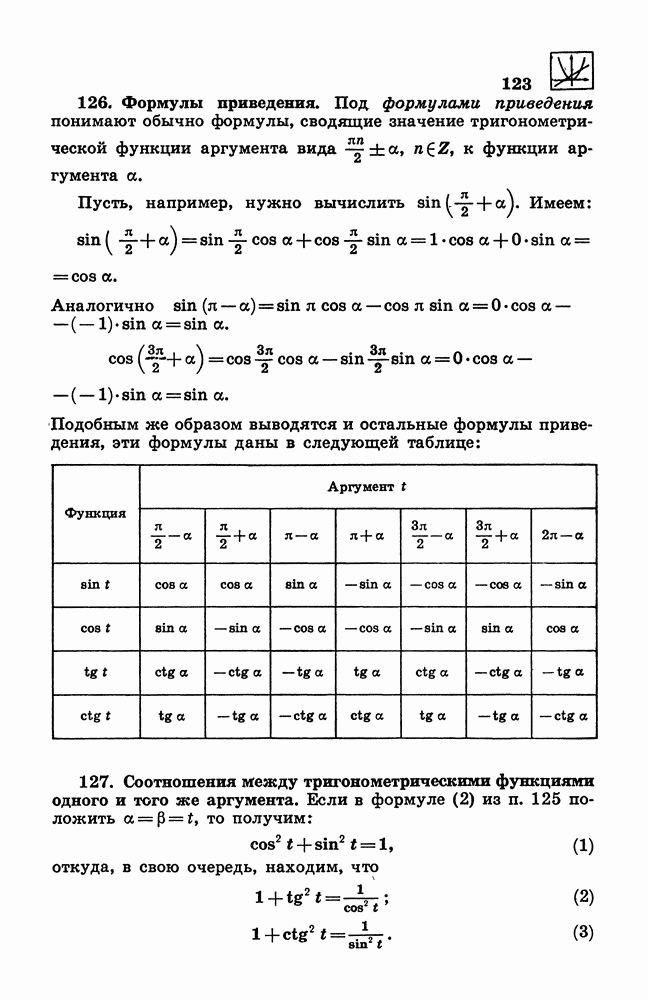
- 126. Формулы приведения.
- 127. Соотношения между тригонометрическими функциями одного и того же аргумента.
- 128. Формулы двойного угла.
- 129. Формулы понижения степени.
- 130. Преобразование суммы тригонометрических функций в произведение.
- 131. Преобразование произведения тригонометрических функций в сумму.
- 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a).
- 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции.
- ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
- § 14. Уравнения с одной переменной
- 135. Равносильность уравнений.
- 136. Линейные уравнения.
- 137. Квадратные уравнения.
- 138. Неполные квадратные уравнения.
- 139. Теорема Виета.
- 140. Системы и совокупности уравнений.
- 141. Уравнения, содержащие переменную под знаком модуля.
- 142. Понятие следствия уравнения. Посторонние корни.
- 143. Уравнения с переменной в знаменателе.
- 144. Область определения уравнения.
- 145. Рациональные уравнения.
- 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители.
- 147. Решение уравнений методом введения новой переменной.
- 148. Биквадратные уравнения.
- 149. Решение задач с помощью составления уравнений.
- 150. Иррациональные уравнения.
- 151. Показательные уравнения.
- 152. Логарифмические уравнения.
- 153. Примеры решения показательно-логарифмических уравнений.
- 154. Простейшие тригонометрические уравнения.
- 155. Методы решения тригонометрических уравнений.
- 156. Универсальная подстановка (для тригонометрических уравнений).
- 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений).
- 158. Графическое решение уравнений.
- 159. Уравнения с параметром.
- § 15. Уравнения с двумя переменными
- 161. График уравнения с двумя переменными.
- 162. Линейное уравнение с двумя переменными и его график.
- § 16. Системы уравнений
- 164. Решение систем двух уравнений с двумя переменными методом подстановки.
- 165. Решение систем двух уравнений с двумя переменными методом сложения.
- 167. Графическое решение систем двух уравнений с двумя переменными.
- 168. Исследование системы двух линейных уравнений с двумя переменными.
- 169. Решение систем двух уравнений с двумя переменными методами умножения и деления.
- 170. Системы показательных и логарифмических уравнений.
- 171. Системы тригонометрических уравнений с двумя переменными.
- 172. Системы трех уравнений с тремя переменными.
- 173. Решение задач с помощью составления систем уравнений.
- Глава VI. НЕРАВЕНСТВА
- § 17. Решение неравенств с переменной
- 175. Графическое решение неравенств с одной переменной.
- 176. Линейные неравенства с одной переменной.
- 177. Системы неравенств с одной переменной.
- 178. Совокупность неравенств с одной переменной.
- 179. Дробно-линейные неравенства.
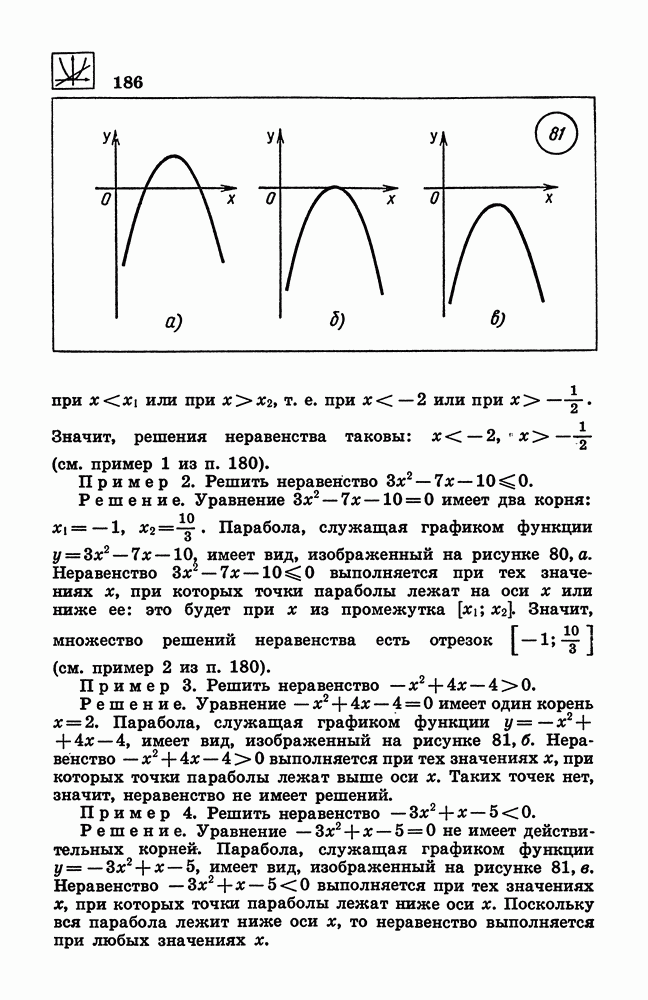
- 180. Неравенства второй степени.
- 181. Графическое решение неравенств второй степени.
- 182. Неравенства с модулями.
- 183. Решение рациональных неравенств методом промежутков.
- 184. Показательные неравенства.
- 185. Логарифмические неравенства.
- 186. Иррациональные неравенства.
- 187. Решение тригонометрических неравенств.
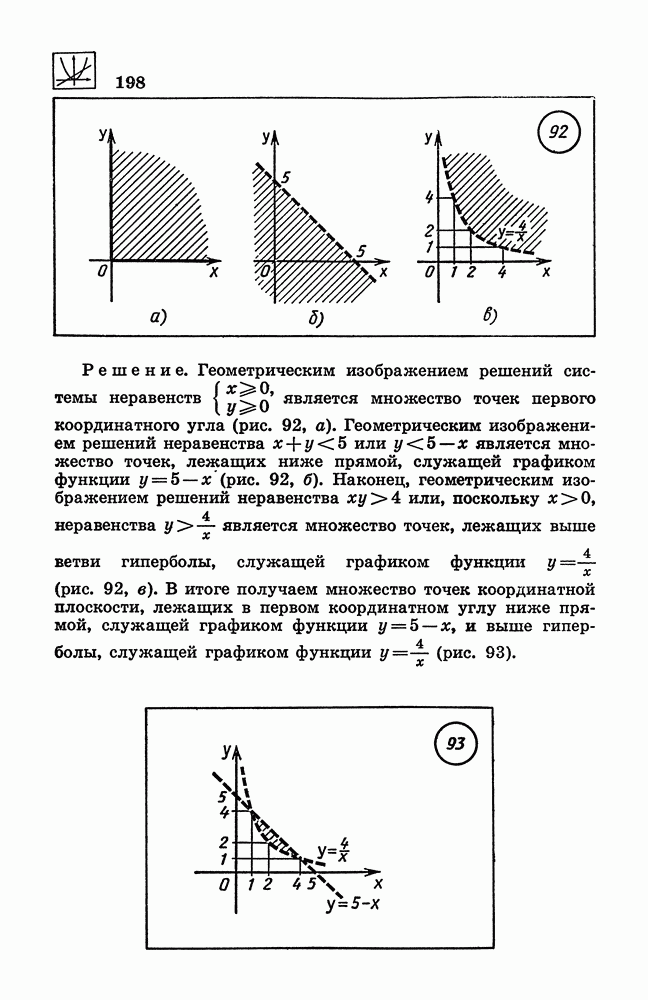
- 188. Неравенства и системы неравенств с двумя переменными.
- § 18. Доказательство неравенств
- 190. Синтетический метод доказательства неравенств.
- 191. Доказательство неравенств методом от противного.
- 192. Использование неравенств при решении уравнений.
- ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- § 19. Числовые последовательности
- 194. Способы задания последовательности.
- 195. Возрастание и убывание последовательности.
- 196. Определение арифметической прогрессии.
- 197. Свойства арифметической прогрессии
- 198. Определение геометрической прогрессии.
- 199. Свойства геометрической прогрессии.
- 200. Понятие о пределе последовательности.
- 201. Вычисление пределов последовательностей.
- 202. Сумма бесконечной геометрической прогрессии при |q| < 1.
- § 20. Предел функции
- 204. Вычисление пределов функции при х->оо.
- 205. Предел функции в точке. Непрерывные функции.
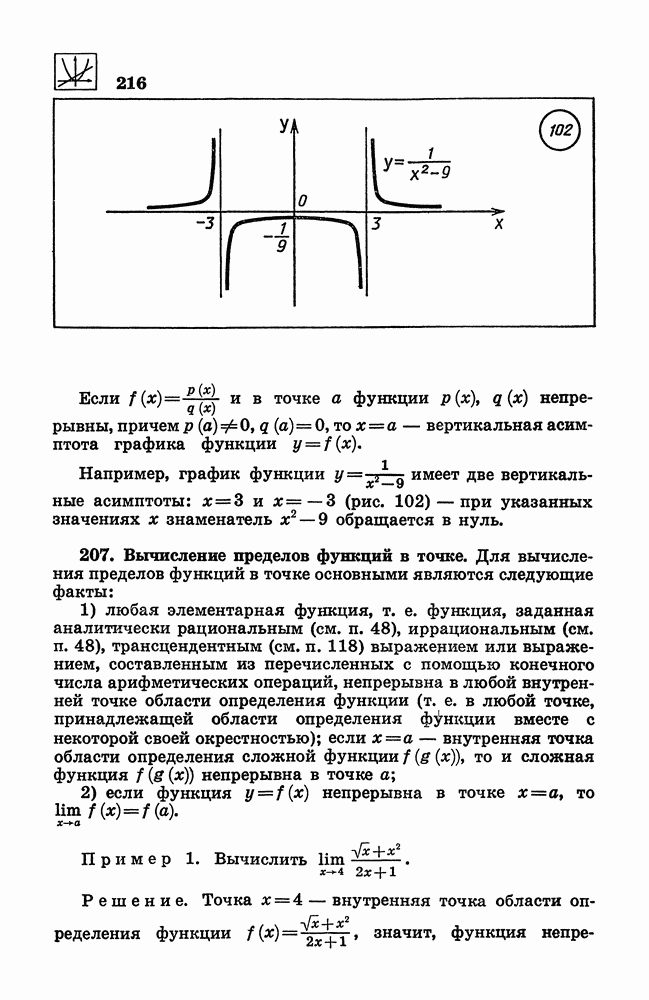
- 206. Вертикальная асимптота.
- 207. Вычисление пределов функций в точке.
- § 21. Производная и ее применения
- 209. Определение производной.
- 210. Формулы дифференцирования. Таблица производных.
- 211. Дифференцирование суммы, произведения, частного.
- 212. Сложная функция и ее дифференцирование.
- 213. Физический смысл производной.
- 214. Вторая производная и ее физический смысл.
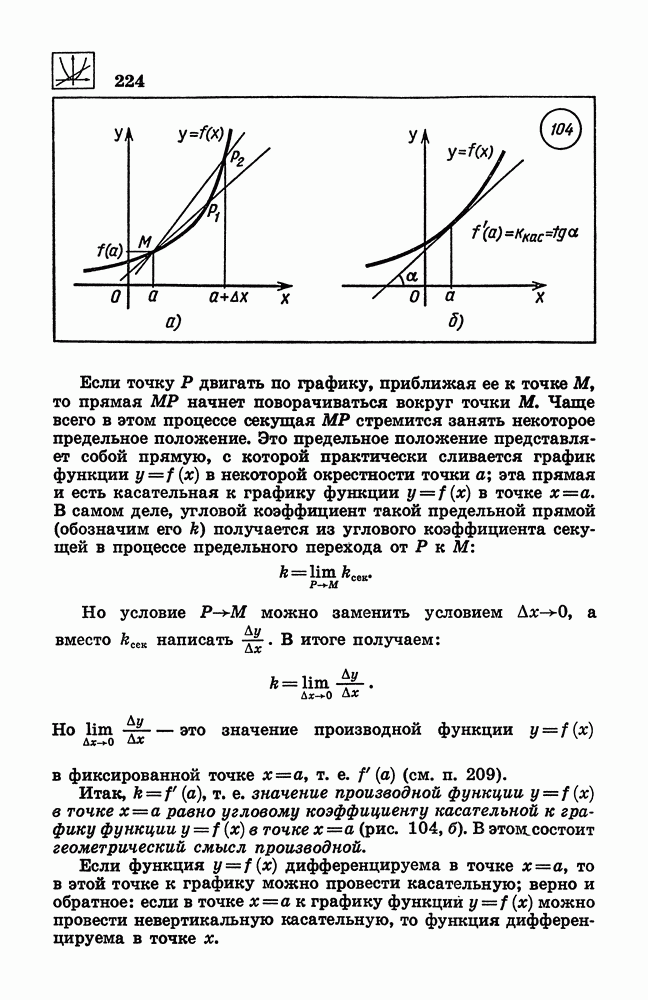
- 215. Касательная к графику функции.
- 216. Применение производной к исследованию функций на монотонность.
- 217. Применение производной к исследованию функций на экстремум.
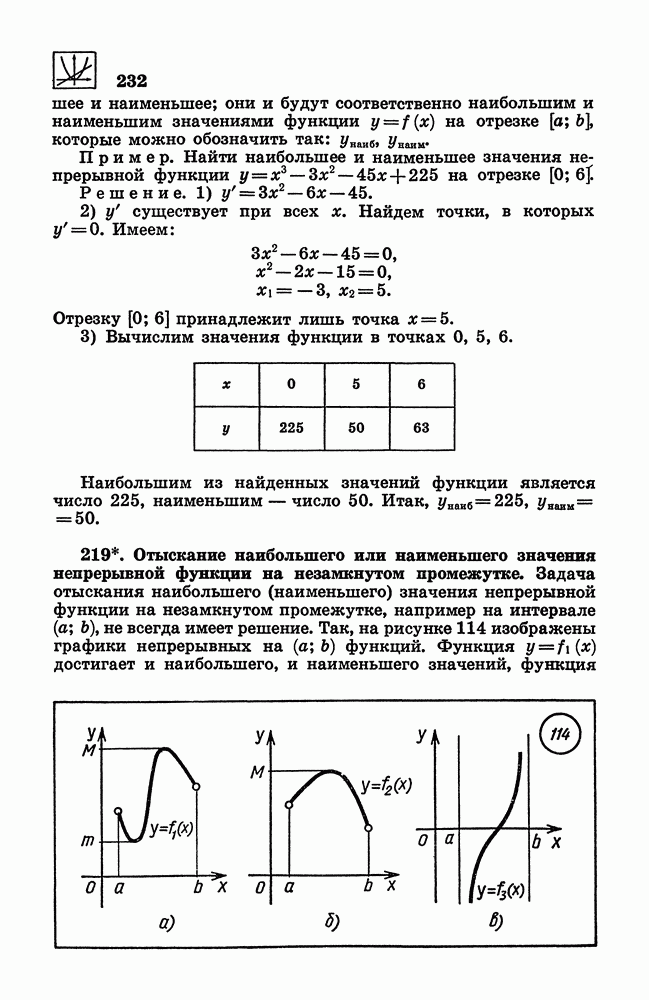
- 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке.
- 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке.
- 220. Задачи на отыскание наибольших или наименьших значений величин.
- 221. Применение производной для доказательства тождеств.
- 222. Применение производной для доказательства неравенств.
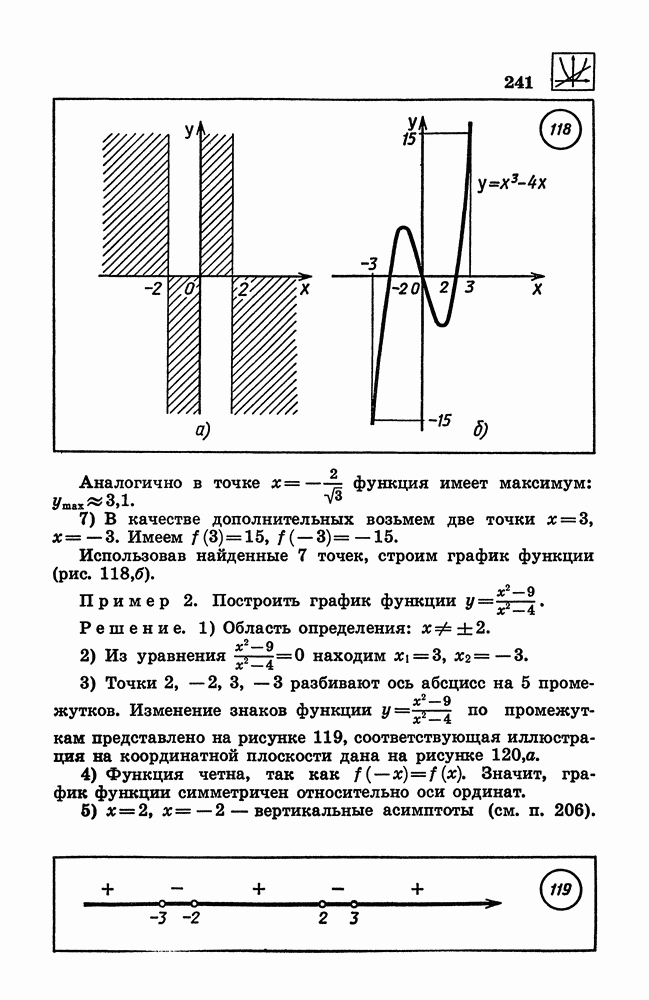
- 223. Общая схема построения графика функции.
- § 22. Первообразная и интеграл
- 225. Таблица первообразных.
- 226. Правила вычисления первообразных.
- 227. Интеграл.
- 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница).
- 229. Правила вычисления интегралов.
- 230. Использование интеграла для вычисления площадей плоских фигур.
- ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ
- 2. Точка. Прямая.
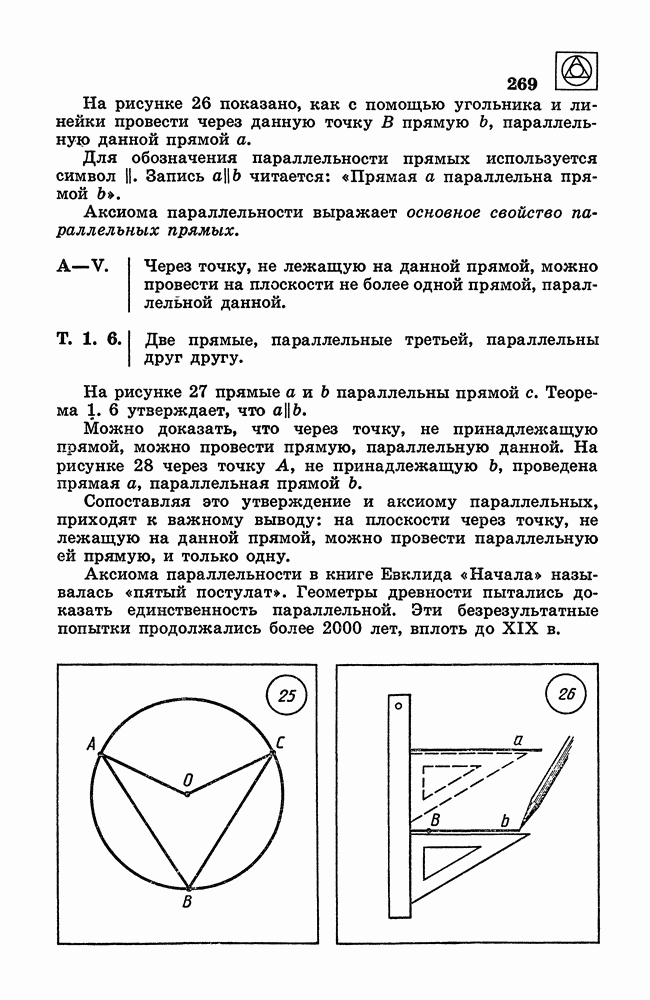
- 3. Определения. Аксиомы. Теоремы.
- § 2. Основные свойства простейших геометрических фигур
- 5. Луч.
- 6. Окружность. Круг.
- 7. Полуплоскость.
- 8. Угол. Градусная мера угла.
- 9. Смежные и вертикальные углы.
- 10. Центральные и вписанные углы.
- 11. Параллельные прямые.
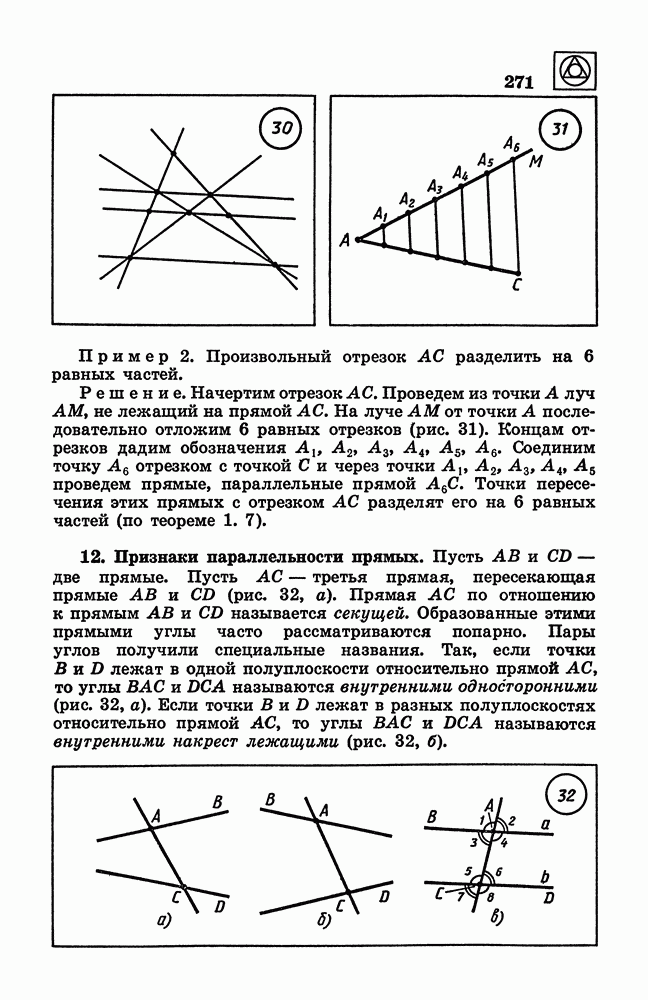
- 12. Признаки параллельности прямых.
- 13. Перпендикулярные прямые.
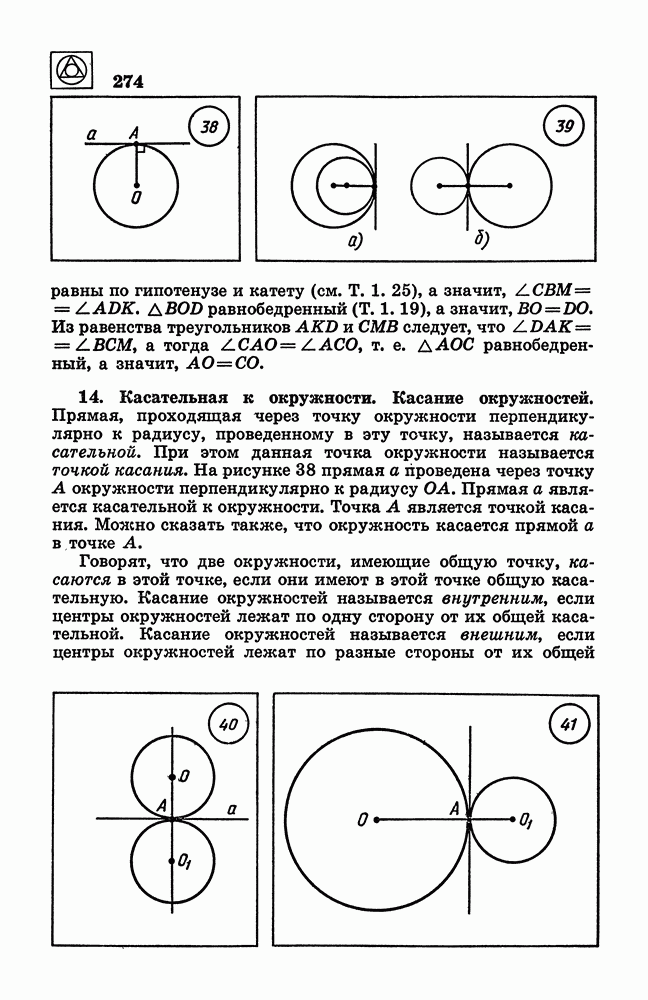
- 14. Касательная к окружности.
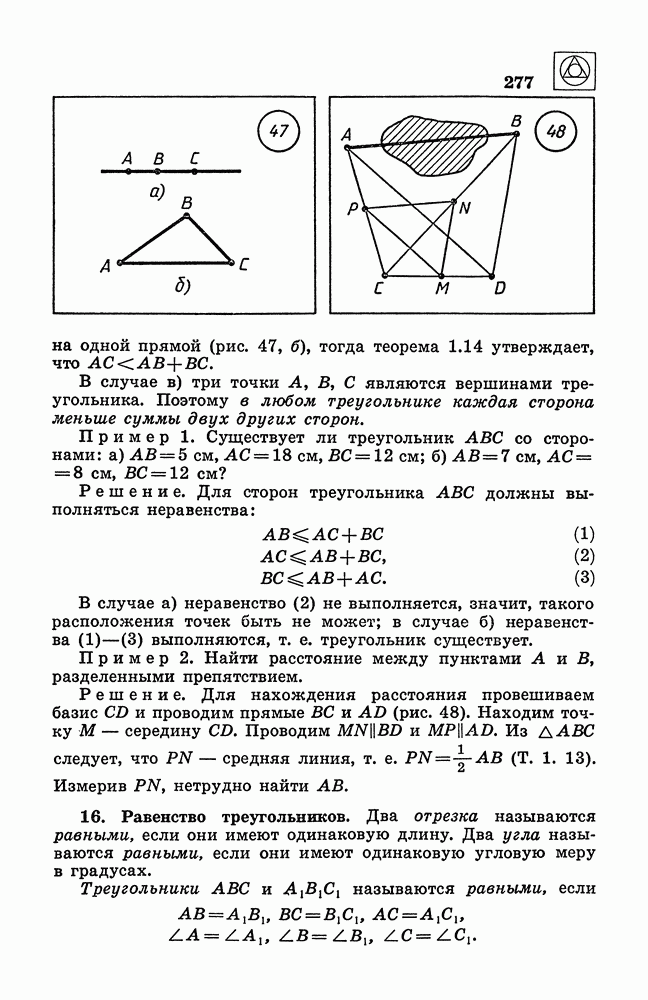
- 15. Треугольники.
- 16. Равенство треугольников.
- 17. Равнобедренный треугольник.
- 18. Сумма углов треугольника.
- 19. Прямоугольный треугольник. Теорема Пифагора.
- 20. Окружности, вписанные в треугольник и описанные около треугольника.
- § 3. Геометрические построения на плоскости
- 22. Простейшие задачи на построение.
- 23. Геометрическое место точек на плоскости.
- § 4. Четырехугольники
- 25. Параллелограмм.
- 26. Прямоугольник. Ромб. Квадрат.
- 27. Трапеция.
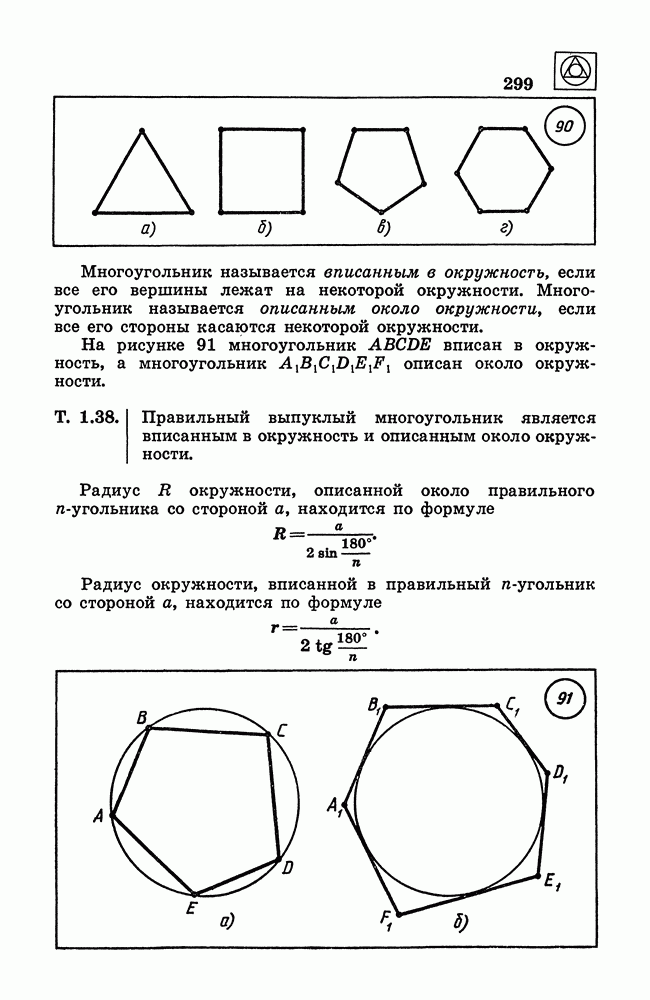
- § 5. Многоугольники
- 29. Выпуклые многоугольники.
- 30. Правильные многоугольники.
- 31. Длина окружности.
- § 6. Решение треугольников
- 33. Соотношения между сторонами и углами в прямоугольном треугольнике.
- 34. Теорема косинусов. Теорема синусов.
- 35. Решение треугольников.
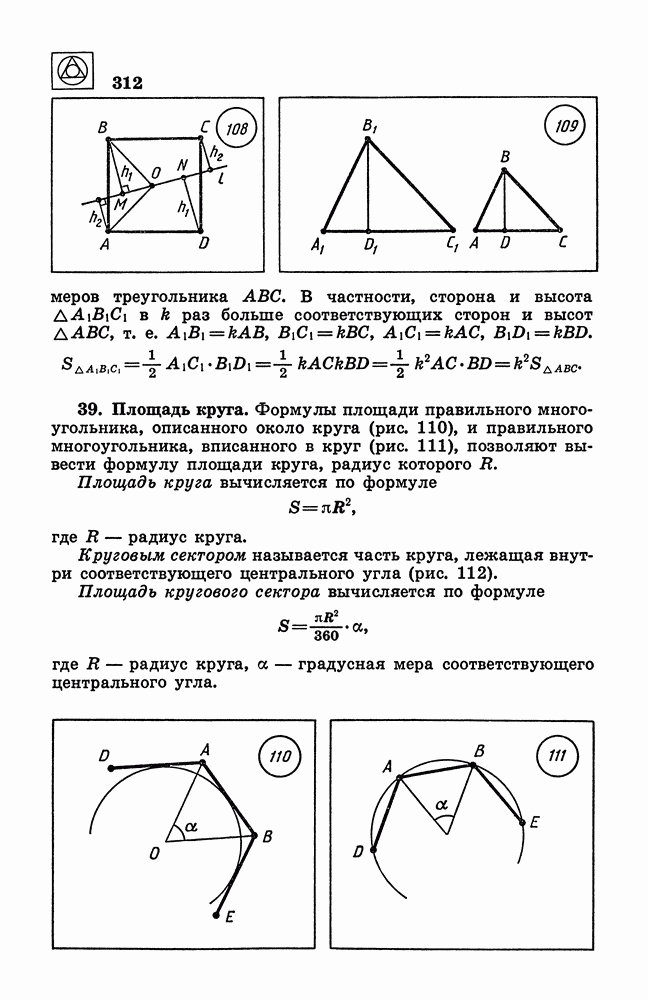
- § 7. Площади плоских фигур
- 37. Площади многоугольников.
- 38. Площади подобных фигур.
- 39. Площадь круга.
- ГЛАВА II. Прямые и плоскости в пространстве
- § 9. Параллельность прямых и плоскостей
- 42. Параллельность прямой и плоскости.
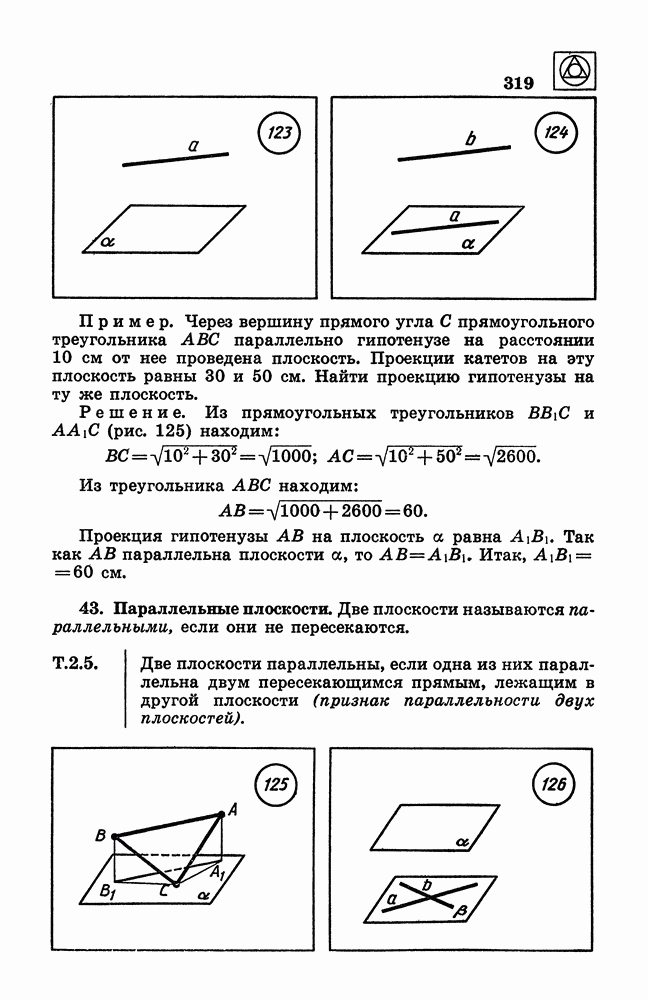
- 43. Параллельные плоскости.
- § 10. Перпендикулярность прямых и плоскостей
- 45. Перпендикуляр и наклонная к плоскости.
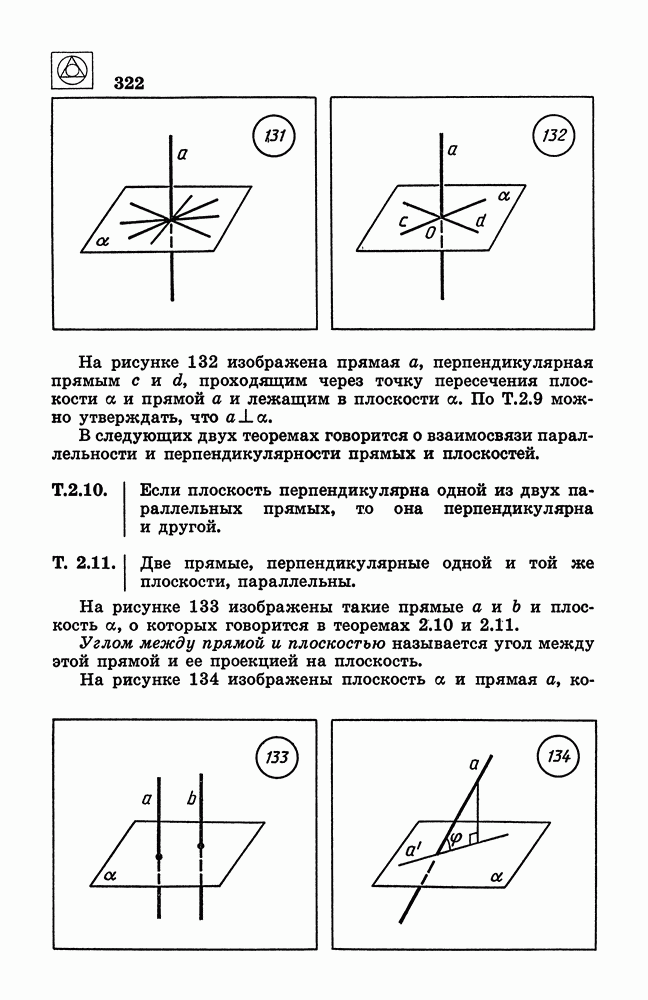
- 46. Перпендикулярность плоскостей.
- ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ
- § 11. Многогранники
- 48. Многогранные углы. Многогранники.
- 49. Призма. Параллелепипед. Куб.
- 50. Пираприда.
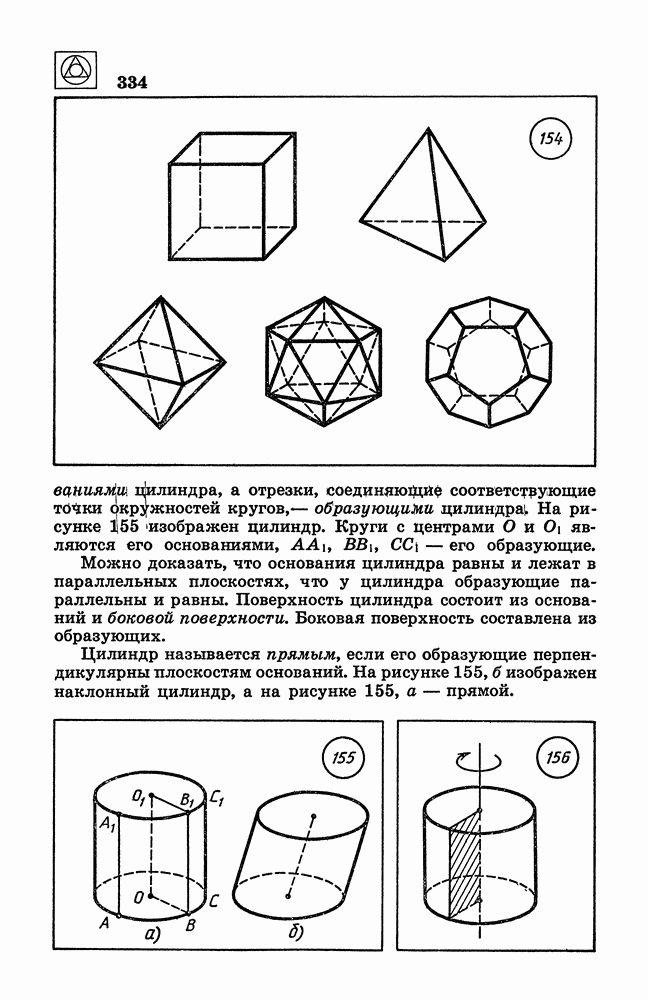
- 51. Правильные многогранники.
- § 12. Тела вращения
- 53. Конус.
- 54. Шар.
- § 13. Изображение пространственных фигур на плоскости
- 56. Ортогональное проектирование.
- 57. Геометрическое место точек в пространстве.
- § 14. Объемы тел
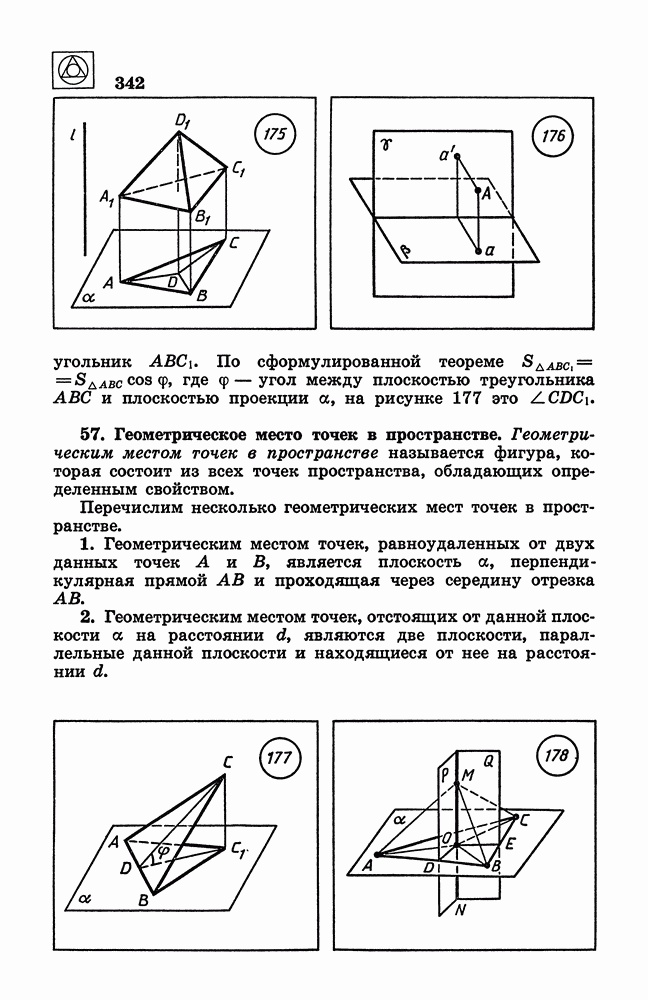
- 59. Объем параллелепипеда, призмы и пирамиды.
- 60. Объем цилиндра и конуса.
- 61. Общая формула объемов тел вращения.
- § 15. Площади поверхностей тел
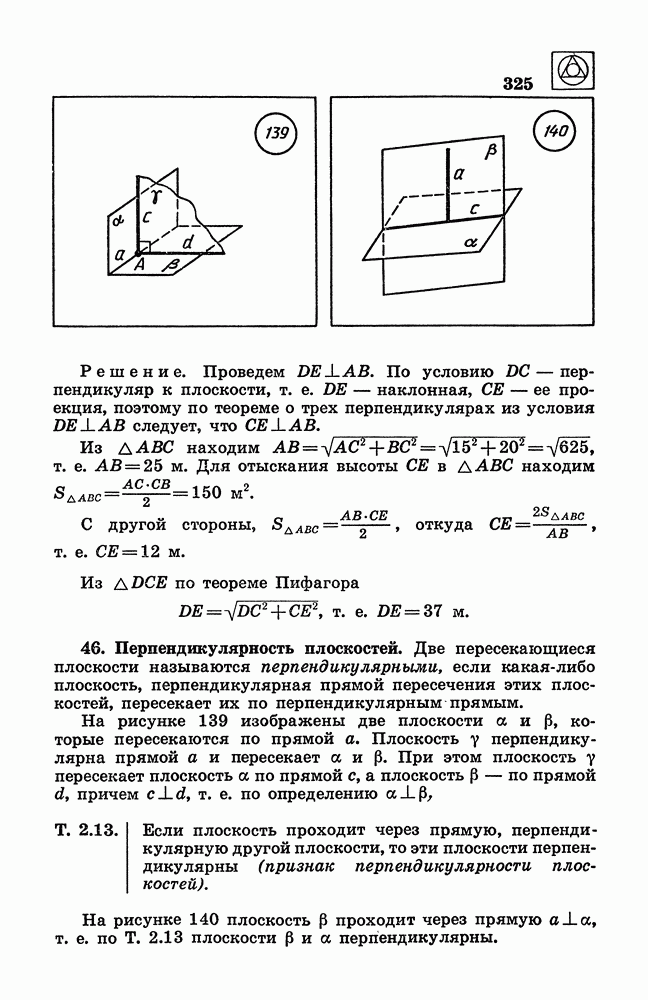
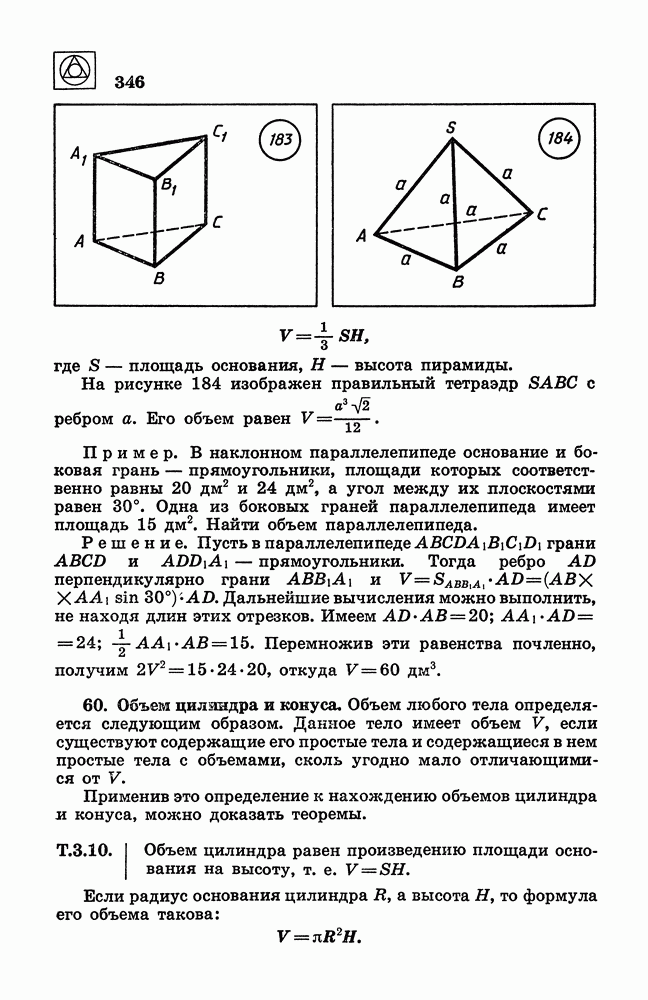
- 63. Понятие площади поверхности.
- 64. Площади поверхностей тел вращения.
- ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ
- § 16. Координаты на плоскости и в пространстве
- 66. Координаты середины отрезка.
- § 17. Уравнения фигур на плоскости
- 68. Пересечение двух окружностей.
- 69. Уравнение прямой.
- 70. Пересечение прямой и окружности.
- § 18. Уравнения фигур в пространстве
- 72. Уравнение сферы.
- 73. Взаимное расположение сферы и плоскости.
- 74. Пересечение двух сфер.
- ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР
- 76. Понятие движения.
- § 20. Подобие фигур
- 78. Подобные фигуры.
- ГЛАВА VI. ВЕКТОРЫ
- 80. Понятие вектора.
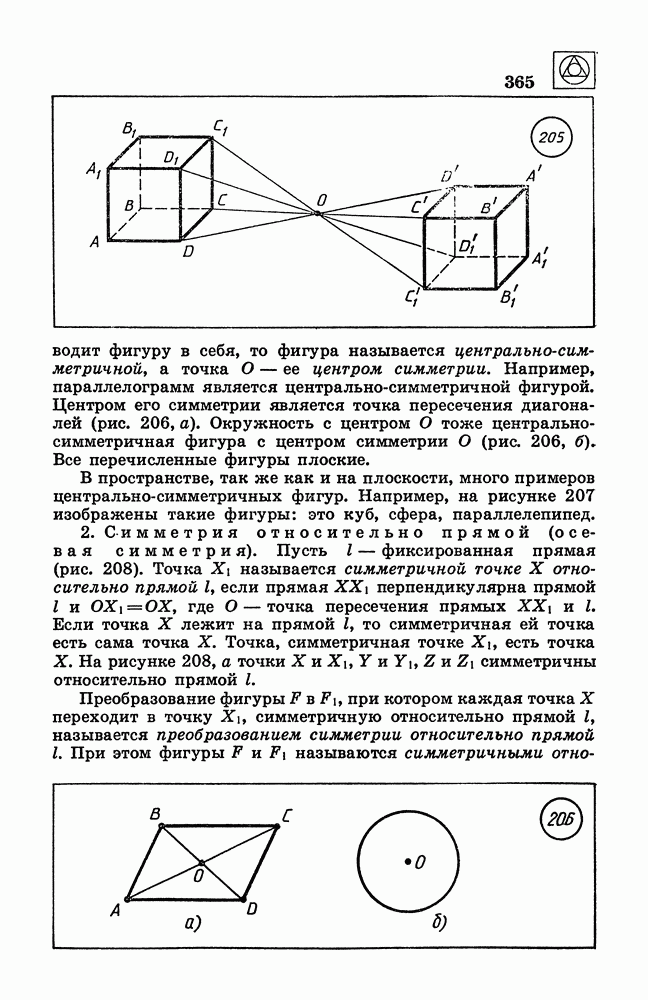
- 81. Координаты вектора.
- § 22. Операции над векторами
- 83. Умножение вектора на число. Коллинеарные векторы.
- 84. Скалярное произведение векторов.
- ПРИЛОЖЕНИЯ
- ГЕОМЕТРИЯ