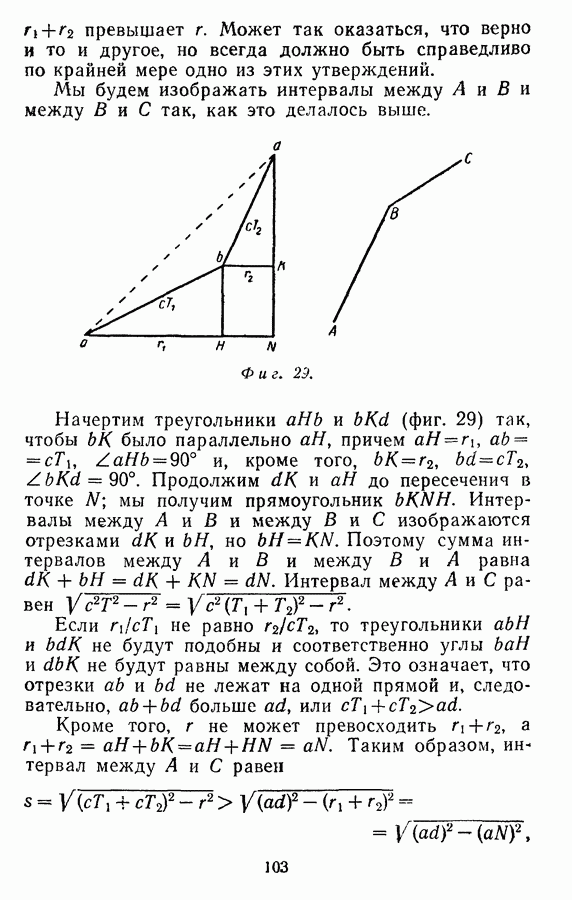| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Применение гипотезы Эйнштейна
Никто не в состоянии обнаружить движение относительно эфира. Неподвижный наблюдатель О без труда измерит скорость, с которой гребец  удаляется от него. Она будет равна по величине и противоположна по направлению скорости, с которой, по мнению гребца
удаляется от него. Она будет равна по величине и противоположна по направлению скорости, с которой, по мнению гребца  от него удаляется наблюдатель О. Если каждый из них выразит измеренную им скорость в долях скорости света, то результаты будут иметь одинаковую величину и противоположные знаки. Таким образом, понятие относительной скорости не приводит к каким-либо трудностям. Однако и
от него удаляется наблюдатель О. Если каждый из них выразит измеренную им скорость в долях скорости света, то результаты будут иметь одинаковую величину и противоположные знаки. Таким образом, понятие относительной скорости не приводит к каким-либо трудностям. Однако и  с равным основанием считают, что именно он находится в состоянии покоя относительно эфира, и производят свои измерения, основываясь на этом предположении. Таким образом, они глядят на мир с разных точек зрения.
с равным основанием считают, что именно он находится в состоянии покоя относительно эфира, и производят свои измерения, основываясь на этом предположении. Таким образом, они глядят на мир с разных точек зрения.
Поэтому, чтобы объяснить загадку двух лодок, мы должны рассмотреть по отдельности точку зрения каждого из участников, гребцов  и постороннего наблюдателя О, который, как мы будем считать, находится вместе с
и постороннего наблюдателя О, который, как мы будем считать, находится вместе с  в момент их старта. Чтобы провести более близкую аналогию с опытом Майкельсона — Морли, представим себе, что берега реки исчезли и единственное, что попадает в поле нашего зрения, — это безбрежная водная гладь, лишенная каких-либо ориентиров, а именно этого и требует представление об эфире.
в момент их старта. Чтобы провести более близкую аналогию с опытом Майкельсона — Морли, представим себе, что берега реки исчезли и единственное, что попадает в поле нашего зрения, — это безбрежная водная гладь, лишенная каких-либо ориентиров, а именно этого и требует представление об эфире.
По утверждению О, однообразный океан перемещается в направлении от  к С со скоростью 4 м/сек
к С со скоростью 4 м/сек
Чтобы доказать это, он опускает на воду кусок пробки и следит за тем, как она движется в направлении к С со скоростью 4 м/сек. Гребцы  утверждают, что вода неподвижна; каждый, сидя в своей лодке, опускает на воду кусок пробки, который остается в том самом месте, где его опустили. Наблюдатель О утверждает, естественно, что куски плывут с той же скоростью, что и лодки. Затем
утверждают, что вода неподвижна; каждый, сидя в своей лодке, опускает на воду кусок пробки, который остается в том самом месте, где его опустили. Наблюдатель О утверждает, естественно, что куски плывут с той же скоростью, что и лодки. Затем  приходят к единому мнению, что О движется от них в направлении от С к
приходят к единому мнению, что О движется от них в направлении от С к  со скоростью 4 м/сек; они считают, что пробка, опущенная на воду наблюдателем О, стоит на месте, а движется в направлении от них сам О.
со скоростью 4 м/сек; они считают, что пробка, опущенная на воду наблюдателем О, стоит на месте, а движется в направлении от них сам О.

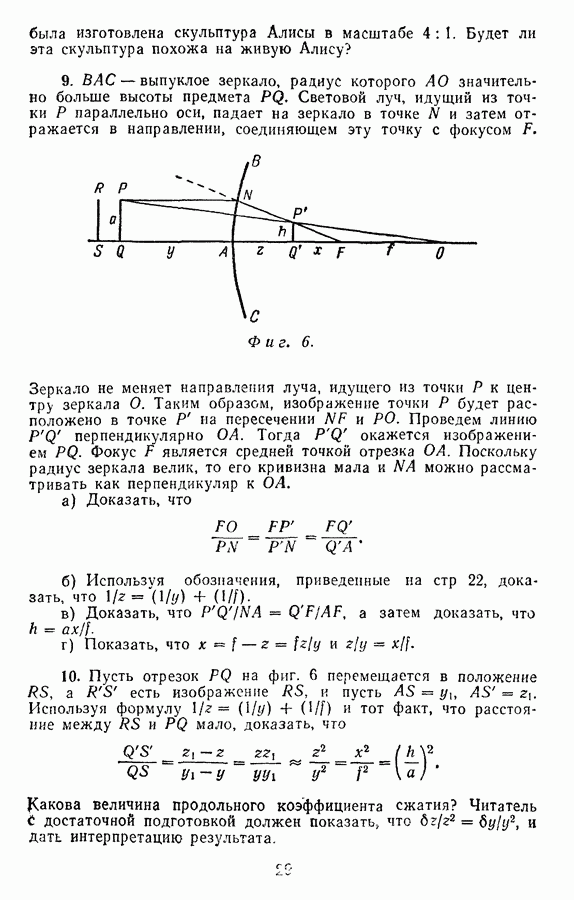
Фиг. 12.
Утверждение о том, что скорость света абсолютно постоянна или что каждый, к  измеряет скорость света, получает один и тот же результат, применительно к движению лодок означает следующее:
измеряет скорость света, получает один и тот же результат, применительно к движению лодок означает следующее:  измеряя скорость, с которой лодка плывет по воде, получат один и тот же результат, ибо лодка является аналогом светового сигнала в опыте Майкельсона — Морли. Мы будем считать, что это стандартное значение скорости составляет 5 м/сек.
измеряя скорость, с которой лодка плывет по воде, получат один и тот же результат, ибо лодка является аналогом светового сигнала в опыте Майкельсона — Морли. Мы будем считать, что это стандартное значение скорости составляет 5 м/сек.
В этих условиях нам надлежит объяснить определенные экспериментальные результаты, а именно тот факт, что лодки (т. е. световые сигналы) возвратятся в  в один и тот же момент времени.
в один и тот же момент времени.
Будем считать, что отрезки  и
и  представляют собой деревянные планки, плавающие на воде. По мнению
представляют собой деревянные планки, плавающие на воде. По мнению  эти планки неподвижны, как и вода, которая им кажется также неподвижной.
эти планки неподвижны, как и вода, которая им кажется также неподвижной.
Наблюдатель О считает, что планки плывут вместе с водой, как гребцы  . У гребцов
. У гребцов  и наблюдателя О имеется метровая линейка;
и наблюдателя О имеется метровая линейка;  она расположена вдоль отрезка
она расположена вдоль отрезка  а
а  вдоль отрезка
вдоль отрезка  наблюдатель О сравнивает свою линейку с линейкой
наблюдатель О сравнивает свою линейку с линейкой  наложив одну на другую; линейки совпадают. Пока линейка, принадлежащая гребцу
наложив одну на другую; линейки совпадают. Пока линейка, принадлежащая гребцу  расположена перпендикулярно течению, она будет
расположена перпендикулярно течению, она будет
идентична линейке наблюдателя О. Однако после того как  сравнив свою линейку с линейкой
сравнив свою линейку с линейкой  ориентирует ее по течению вдоль отрезка
ориентирует ее по течению вдоль отрезка  то, с точки зрения наблюдателя О, эта линейка сократится, хотя как
то, с точки зрения наблюдателя О, эта линейка сократится, хотя как  так и
так и  останутся в неведении о происшедшем и не должны осознать этот факт, поскольку они не имеют никакого представления о течении, уносящем их с собой (об этом см. дальше).
останутся в неведении о происшедшем и не должны осознать этот факт, поскольку они не имеют никакого представления о течении, уносящем их с собой (об этом см. дальше).
В данном случае  удовлетворятся непосредственными измерениями длин отрезков
удовлетворятся непосредственными измерениями длин отрезков  и
и  и получат величину 90 м. Не зная о наличии течения,
и получат величину 90 м. Не зная о наличии течения,  придут к выводу, что время, затраченное на плавание к
придут к выводу, что время, затраченное на плавание к  и С и обратно к
и С и обратно к  в обоих случаях составляет
в обоих случаях составляет  сек. По окончании плавания их часы должны подтвердить этот вывод, ибо в противном случае гребцы обнаружили бы наличие течения и смогли вычислить его скорость.
сек. По окончании плавания их часы должны подтвердить этот вывод, ибо в противном случае гребцы обнаружили бы наличие течения и смогли вычислить его скорость.
Пусть О хронометрирует плавание  . В соответствии с тем, что говорилось на стр. 34, ему кажется, что
. В соответствии с тем, что говорилось на стр. 34, ему кажется, что  движется вдоль
движется вдоль  туда и обратно со скоростью 3 м/сек и поэтому затрачивает на всю поездку
туда и обратно со скоростью 3 м/сек и поэтому затрачивает на всю поездку  сек. Следовательно, О утверждает, что часы
сек. Следовательно, О утверждает, что часы  отсчитывают всего лишь 36 сек вместо 60 сек. Таким образом, по мнению О, часы
отсчитывают всего лишь 36 сек вместо 60 сек. Таким образом, по мнению О, часы  отстают.
отстают.
Поскольку  затрачивают в точности одно и то же время на свои поездки, то по часам О гребцу
затрачивают в точности одно и то же время на свои поездки, то по часам О гребцу  также потребуется 60 сек. Однако опять-таки на основании сказанного на стр. 34 наблюдатель О считает, что
также потребуется 60 сек. Однако опять-таки на основании сказанного на стр. 34 наблюдатель О считает, что  движется вперед от
движется вперед от  к С со скоростью 9 м/сек, а возвращается из
к С со скоростью 9 м/сек, а возвращается из  со скоростью 1 м/сек. Следовательно, если
со скоростью 1 м/сек. Следовательно, если  то полное время составило бы
то полное время составило бы  сек. Однако по часам О полное время составляет всего 60 сек. Поэтому О считает, что длина пути
сек. Однако по часам О полное время составляет всего 60 сек. Поэтому О считает, что длина пути  равна лишь
равна лишь  (Заметим для проверки, что
(Заметим для проверки, что  сек.)
сек.)
Но измеряя длину  с помощью своей метровой линейки, гребец
с помощью своей метровой линейки, гребец  получил 90 м. Поэтому О вынужден заключить, что длина линейки гребца
получил 90 м. Поэтому О вынужден заключить, что длина линейки гребца  равна
равна  Итак, О утверждает, что течение
Итак, О утверждает, что течение
вызывает сокращение длины метровой линейки  когда ее располагают по течению, до
когда ее располагают по течению, до 
Кроме того, поскольку время поездки по часам  составляет 36 сек, то О считает, что часы
составляет 36 сек, то О считает, что часы  отстают в точности так же, как часы гребца
отстают в точности так же, как часы гребца  Эти результаты можно подытожить следующим образом.
Эти результаты можно подытожить следующим образом.
Наблюдатель О утверждает, что: 1) в системе, где находятся гребцы  часы идут медленнее; по прошествии 5 мин их стрелки показывают лишь 3 мин (60/36 = 5/3); 2) в этой системе метровая линейка отмеряет
часы идут медленнее; по прошествии 5 мин их стрелки показывают лишь 3 мин (60/36 = 5/3); 2) в этой системе метровая линейка отмеряет  если ее располагают вдоль
если ее располагают вдоль  т. е. под прямым углом к направлению течения, а вдоль
т. е. под прямым углом к направлению течения, а вдоль  (направления течения) она отмеряет всего
(направления течения) она отмеряет всего 
Гребцы  утверждают, что: 1) их часы идут точно; 2) их метровые линейки сохраняют истинную длину независимо от их расположения.
утверждают, что: 1) их часы идут точно; 2) их метровые линейки сохраняют истинную длину независимо от их расположения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Введение
- ГЛАВА ПЕРВАЯ. Научный прогресс
- Система Птолемея
- Система Коперника
- Всемирное тяготение
- Механика Галилея и Ньютона
- Измерительные приборы
- Искусственное расширение предела человеческих чувств
- Здравый смысл
- ГЛАВА ВТОРАЯ. Алиса в Зазеркалье
- Может ли Природа ввести в заблуждение?
- Выпуклое зеркало
- Жизнь за зеркалом
- Сжатие в направлении, перпендикулярном оси
- Сжатие в направлении вдоль оси
- Геометрия в мире Алисы
- ГЛАВА ТРЕТЬЯ. Скорость света
- Абсолютное движение
- По течению
- Опыт Майкельсона — Морли
- Какова же разгадка?
- Гипотеза Эйнштейна
- Применение гипотезы Эйнштейна
- Кто же прав?
- ГЛАВА ЧЕТВЕРТАЯ. ЧАСЫ
- Наблюдения в различных местах
- Синхронизация часов
- Мнение постороннего наблюдателя
- Что думают другие наблюдатели
- Одновременные события
- Единство пространства и времени
- ГЛАВА ПЯТАЯ. Алгебраические соотношения между событиями в двух системах
- Измерительные линейки
- Сравнение часов наблюдателей A и C с часами наблюдателя O
- Ход часов
- Расстояние и промежуток времени между двумя событиями
- Мнение наблюдателя А о данных наблюдателя О
- Скорость света
- ГЛАВА ШЕСТАЯ. Интервал между событиями
- Измерение различными наблюдателями интервала между двумя событиями
- Формальное рассмотрение интервала
- Вещественная и мнимая части интервала
- Последовательность двух событий во времени
- Собственное время
- ГЛАВА СЕДЬМАЯ. Четвертое измерение
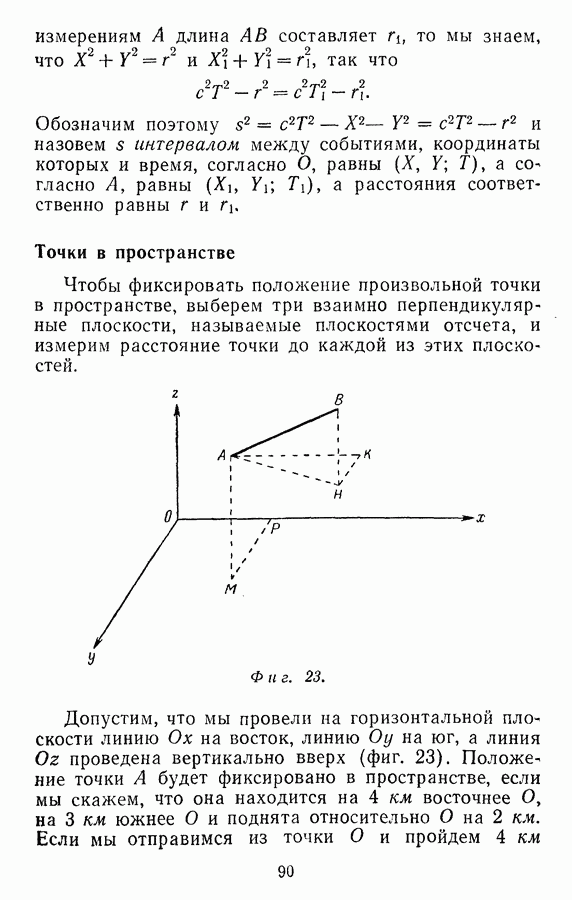
- Точки в пространстве
- Четырехмерное пространство-время
- Плоский мир
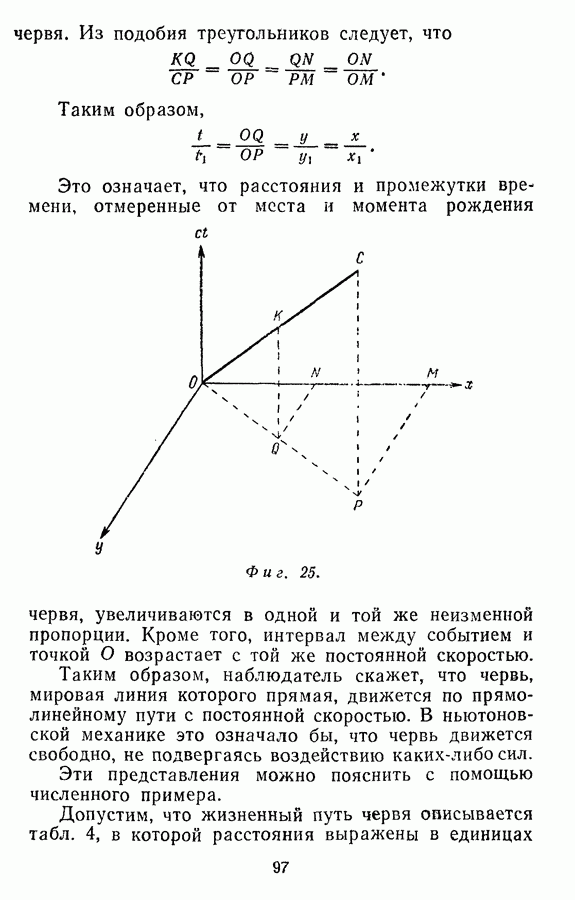
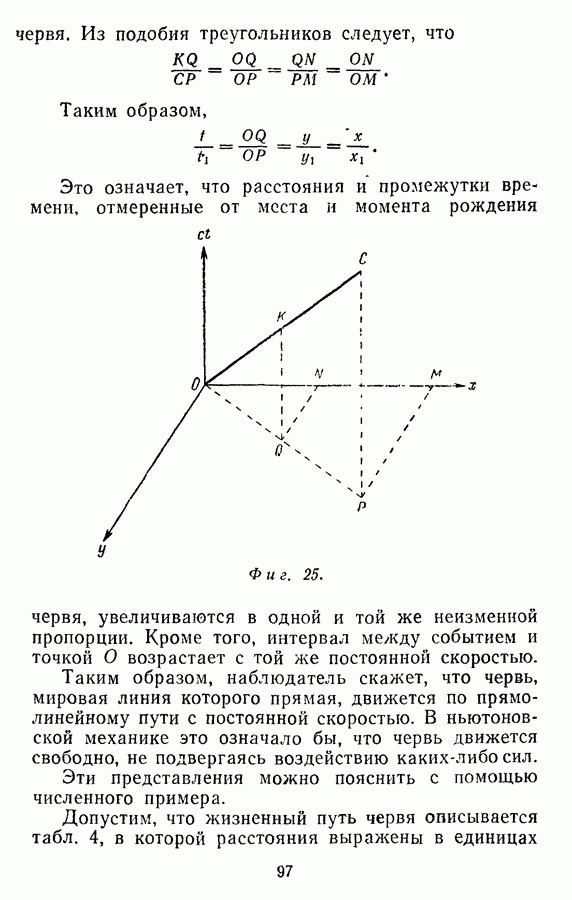
- Прямолинейные мировые линии
- Прямолинейные мировые линии
- Криволинейные мировые линии
- Прямолинейные и криволинейные мировые линии
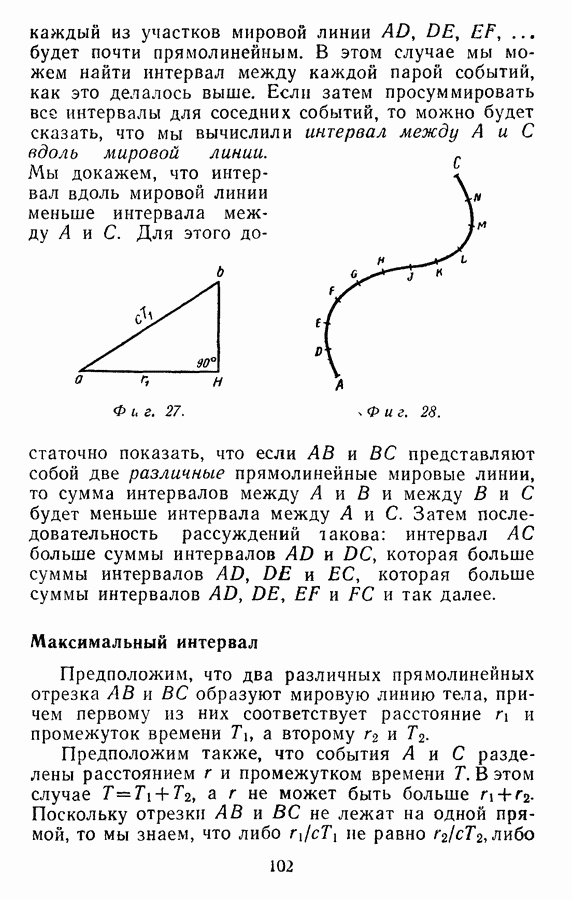
- Интервал вдоль мировой линии
- Максимальный интервал
- Геодезический закон движения
- ГЛАВА ВОСЬМАЯ. Масса и импульс
- Поперечная скорость
- Коэффициент увлечения Френеля
- Масса
- Эйнштейновское определение массы
- Законы сохранения массы и импульса
- Импульс и интервал
- Принципы специальной теории относительности
- ГЛАВА ДЕВЯТАЯ. Общая теория относительности
- Силовое поле
- Принцип эквивалентности
- Искривление пространства-времени
- Жизнь на вращающемся диске
- Поле силы тяжести
- ГЛАВА ДЕСЯТАЯ. Проверка общей теории относительности Энштейна
- Смещение спектральных линий
- Искривление светового луча
- Общие выводы