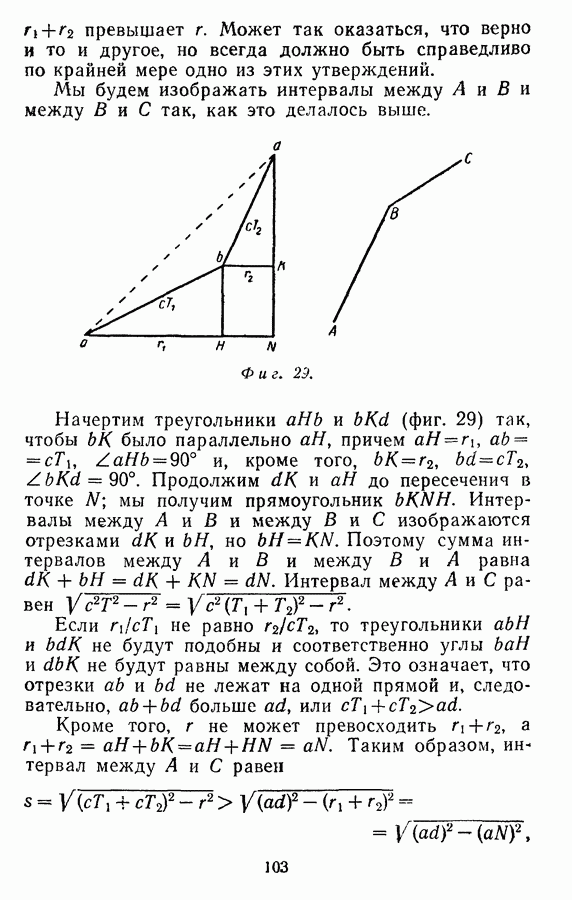| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА СЕДЬМАЯ. Четвертое измерение
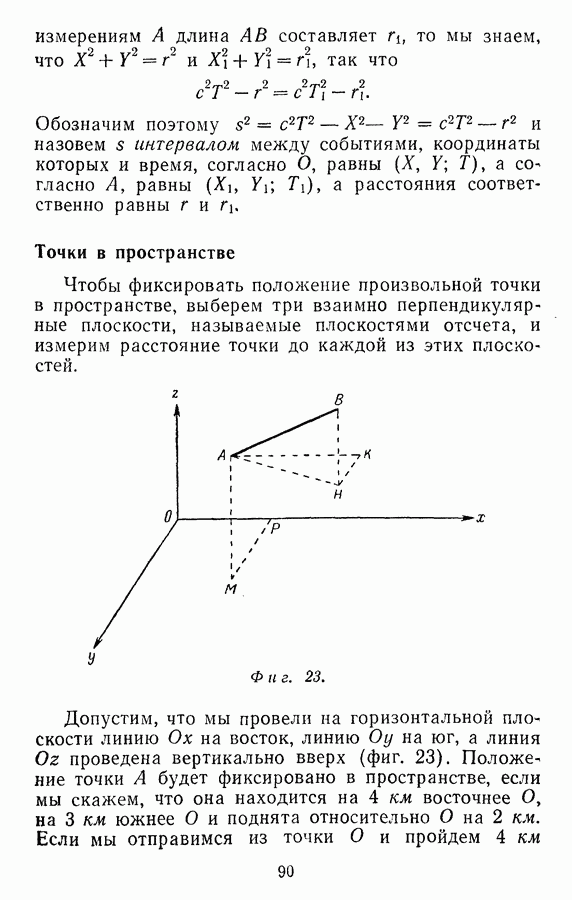
До сих пор мы рассматривали только такие события, которые происходили на прямой линии, соединяющей различные системы. Все сказанное легко распространить также на события, происходящие в любых точках пространства.
Точки на плоскости
Если на плоскости провести две взаимно перпендикулярные линии, то положение любой точки можно будет задать с помощью расстояния до этих линий. Например, выберем точку О и проведем от нее линию  на восток и линию
на восток и линию  на север (фиг. 22). Допустим, что точка А расположена в 5 км к востоку и в 3 км к северу от точки
на север (фиг. 22). Допустим, что точка А расположена в 5 км к востоку и в 3 км к северу от точки  тем самым мы фиксируем ее положение. Если мы направимся из О и пройдем 5 км в направлении оси
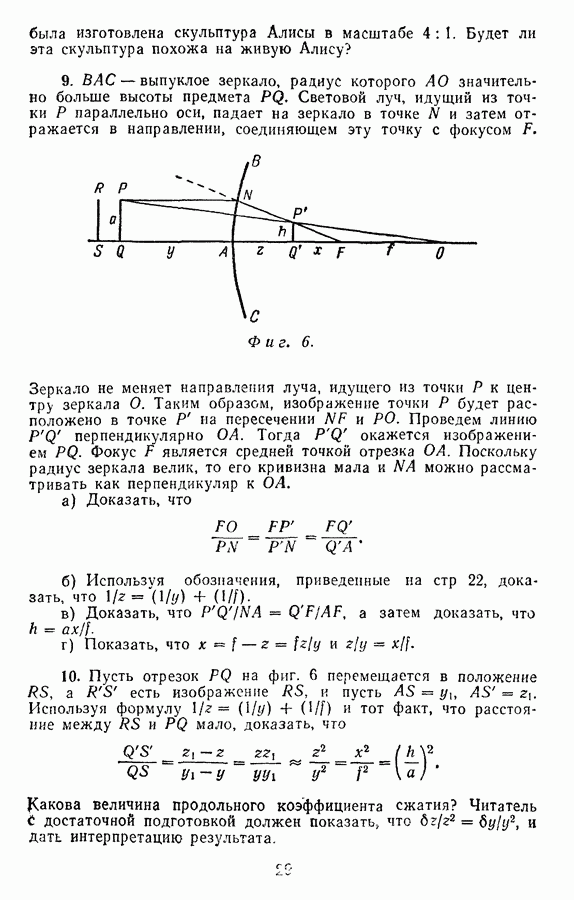
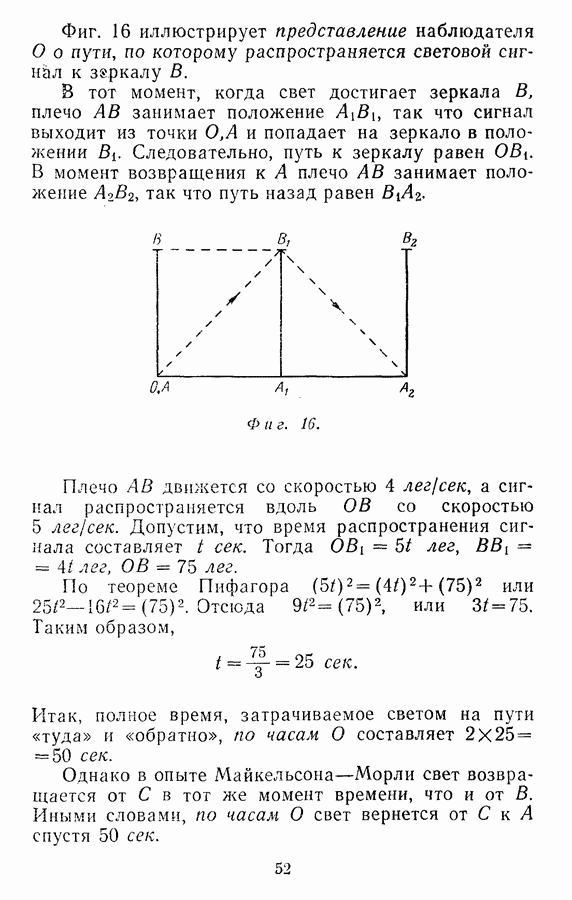
тем самым мы фиксируем ее положение. Если мы направимся из О и пройдем 5 км в направлении оси  т. е. на восток к точке
т. е. на восток к точке  а затем 3 км в направлении оси у, т. е. на север вдоль
а затем 3 км в направлении оси у, т. е. на север вдоль  то попадем в точку А. Числа 5 и 3 называются координатами точки А. Мы говорим, что точка А задана
то попадем в точку А. Числа 5 и 3 называются координатами точки А. Мы говорим, что точка А задана  или что ее координаты (5,3); координата
или что ее координаты (5,3); координата  всегда указывается первой. Допустим, что В — другая точка на плоскости с координатами (9,6). Тогда мы можем попасть из
всегда указывается первой. Допустим, что В — другая точка на плоскости с координатами (9,6). Тогда мы можем попасть из 
переместившись вдоль оси  еще на
еще на  и вдоль оси у на
и вдоль оси у на  На фиг. 22
На фиг. 22  и
и  Таким образом,
Таким образом,

Аналогично, если расстояние между  по оси
по оси  составляет X, а по оси у составляет У, так что
составляет X, а по оси у составляет У, так что  и
и  то
то

Координаты точки представляют собой просто расстояния от точки О, измеренные в направлении осей х и у.

Фиг. 22.
Если нам известны координаты двух любых точек  то расстояние от
то расстояние от  до В в координатах х и у можно найти, производя, как и выше, вычитание соответствующих координат этих точек.
до В в координатах х и у можно найти, производя, как и выше, вычитание соответствующих координат этих точек.
Допустим теперь, что, по утверждению наблюдателя О, система  удаляется от него в направлении
удаляется от него в направлении  со скоростью
со скоростью  и что событие
и что событие  происходит в точке
происходит в точке  а событие II — в точке В спустя время
а событие II — в точке В спустя время  . В этом случае наблюдатель О говорит, что расстояние и промежуток времени между событиями равны X (вдоль оси х), Y (вдоль оси у) и Т. В системе
. В этом случае наблюдатель О говорит, что расстояние и промежуток времени между событиями равны X (вдоль оси х), Y (вдоль оси у) и Т. В системе  промежуток времени оказывается иным, скажем
промежуток времени оказывается иным, скажем  Расстояние вдоль оси
Расстояние вдоль оси  тоже другое, скажем
тоже другое, скажем  а расстояние вдоль оси у сохраняется прежним, так как линейки наблюдателей
а расстояние вдоль оси у сохраняется прежним, так как линейки наблюдателей  одинаковы в направлении, перпендикулярном скорости, т. е.
одинаковы в направлении, перпендикулярном скорости, т. е. 
Мы уже доказали, что  Поскольку
Поскольку  , то
, то  Но если по измерениям О длина
Но если по измерениям О длина  равна
равна  а по
а по
измерениям А длина  составляет
составляет  то мы знаем, что
то мы знаем, что  и так что
и так что

Обозначим поэтому  и назовем
и назовем  интервалом между событиями, координаты которых и время, согласно О, равны
интервалом между событиями, координаты которых и время, согласно О, равны  а согласно А, равны
а согласно А, равны  а расстояния соответственно равны
а расстояния соответственно равны 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Введение
- ГЛАВА ПЕРВАЯ. Научный прогресс
- Система Птолемея
- Система Коперника
- Всемирное тяготение
- Механика Галилея и Ньютона
- Измерительные приборы
- Искусственное расширение предела человеческих чувств
- Здравый смысл
- ГЛАВА ВТОРАЯ. Алиса в Зазеркалье
- Может ли Природа ввести в заблуждение?
- Выпуклое зеркало
- Жизнь за зеркалом
- Сжатие в направлении, перпендикулярном оси
- Сжатие в направлении вдоль оси
- Геометрия в мире Алисы
- ГЛАВА ТРЕТЬЯ. Скорость света
- Абсолютное движение
- По течению
- Опыт Майкельсона — Морли
- Какова же разгадка?
- Гипотеза Эйнштейна
- Применение гипотезы Эйнштейна
- Кто же прав?
- ГЛАВА ЧЕТВЕРТАЯ. ЧАСЫ
- Наблюдения в различных местах
- Синхронизация часов
- Мнение постороннего наблюдателя
- Что думают другие наблюдатели
- Одновременные события
- Единство пространства и времени
- ГЛАВА ПЯТАЯ. Алгебраические соотношения между событиями в двух системах
- Измерительные линейки
- Сравнение часов наблюдателей A и C с часами наблюдателя O
- Ход часов
- Расстояние и промежуток времени между двумя событиями
- Мнение наблюдателя А о данных наблюдателя О
- Скорость света
- ГЛАВА ШЕСТАЯ. Интервал между событиями
- Измерение различными наблюдателями интервала между двумя событиями
- Формальное рассмотрение интервала
- Вещественная и мнимая части интервала
- Последовательность двух событий во времени
- Собственное время
- ГЛАВА СЕДЬМАЯ. Четвертое измерение
- Точки в пространстве
- Четырехмерное пространство-время
- Плоский мир
- Прямолинейные мировые линии
- Прямолинейные мировые линии
- Криволинейные мировые линии
- Прямолинейные и криволинейные мировые линии
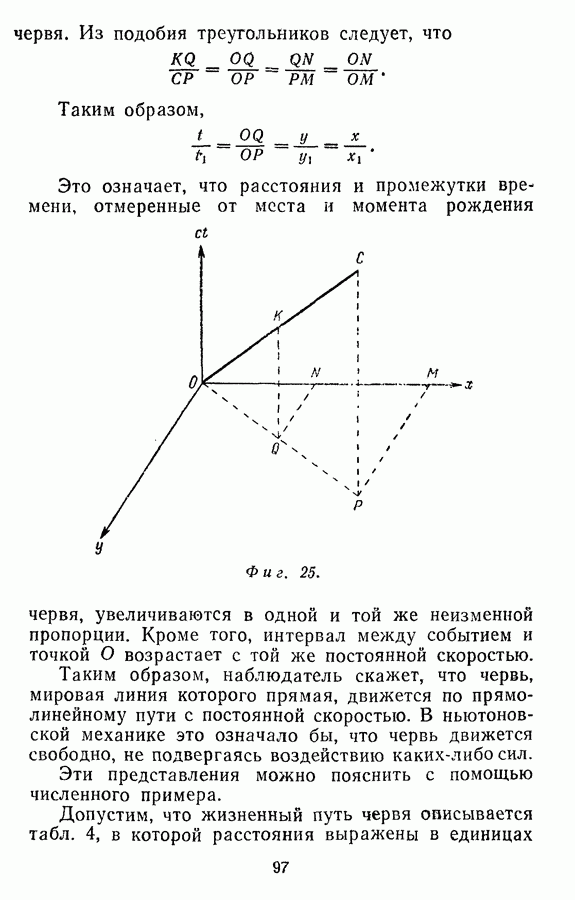
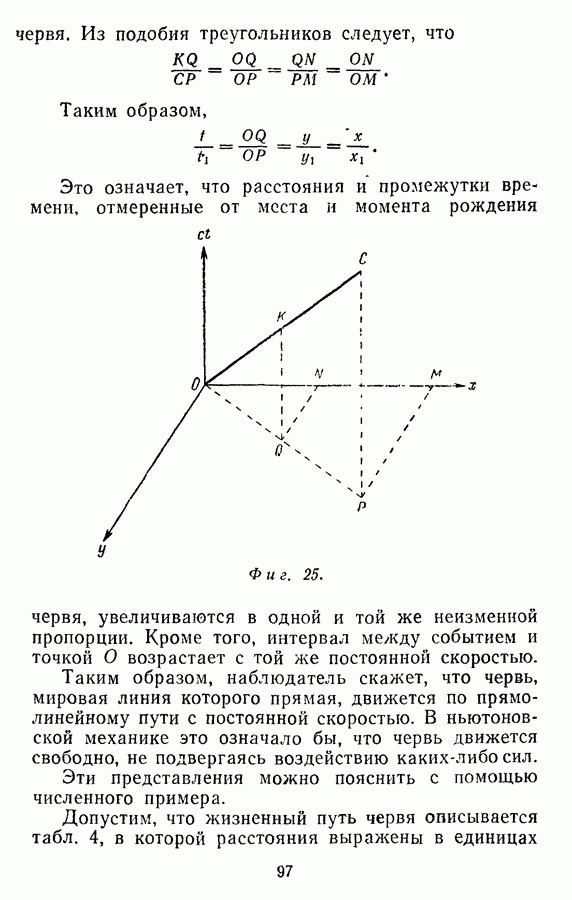
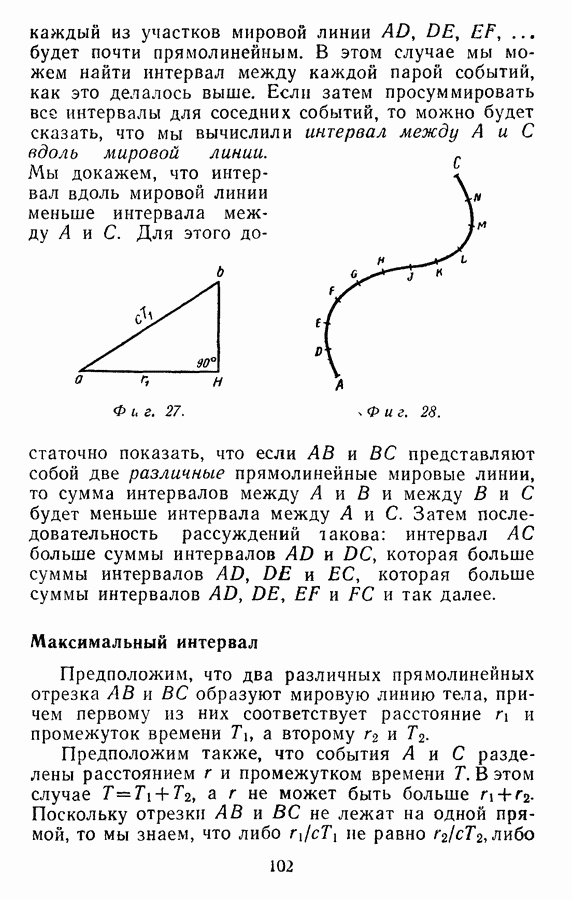
- Интервал вдоль мировой линии
- Максимальный интервал
- Геодезический закон движения
- ГЛАВА ВОСЬМАЯ. Масса и импульс
- Поперечная скорость
- Коэффициент увлечения Френеля
- Масса
- Эйнштейновское определение массы
- Законы сохранения массы и импульса
- Импульс и интервал
- Принципы специальной теории относительности
- ГЛАВА ДЕВЯТАЯ. Общая теория относительности
- Силовое поле
- Принцип эквивалентности
- Искривление пространства-времени
- Жизнь на вращающемся диске
- Поле силы тяжести
- ГЛАВА ДЕСЯТАЯ. Проверка общей теории относительности Энштейна
- Смещение спектральных линий
- Искривление светового луча
- Общие выводы