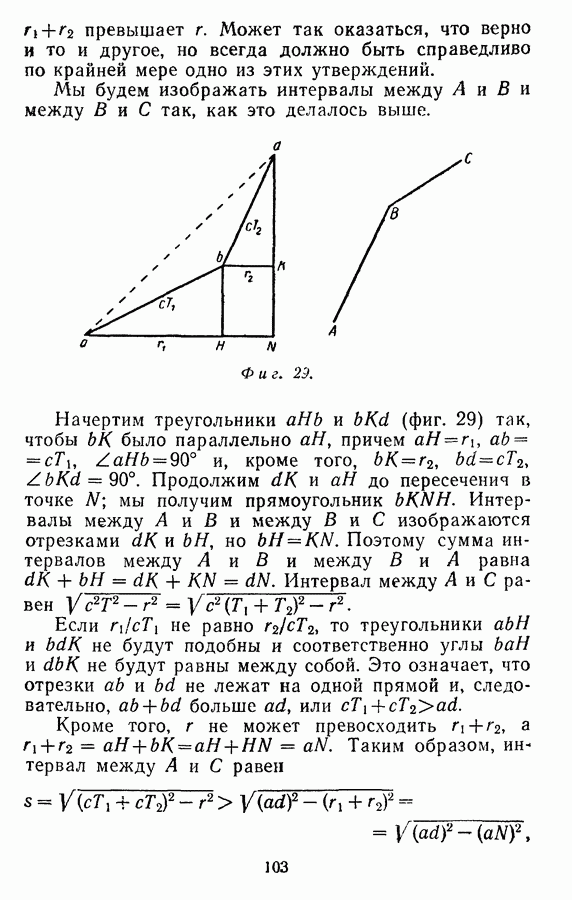| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Поле силы тяжести
Наличие вещества порождает в его окрестности поле силы тяжести. Но вместо того, чтобы говорить о существовании силового поля, мы теперь говорим о наличии искривления пространства-времени.
Инвариантное выражение для интервала между двумя событиями  было получено в предположении, что пространство-время однородно. Так как в окрестности вещества это предположение несправедливо, выражение для
было получено в предположении, что пространство-время однородно. Так как в окрестности вещества это предположение несправедливо, выражение для  при наличии поля силы тяжести потребует модификации, чтобы сохранять свойства при переходе от одной системы к другой. Автоматически возникает необходимость в новой геометрии с иными формулами, связывающими измеряемые величины.
при наличии поля силы тяжести потребует модификации, чтобы сохранять свойства при переходе от одной системы к другой. Автоматически возникает необходимость в новой геометрии с иными формулами, связывающими измеряемые величины.
В последнее столетие были исследованы различные варианты геометрии. До этого считалось, что единственной логически последовательной является геометрия Евклида. Характерной особенностью геометрии Евклида является то, что сумма углов треугольника там равна двум прямым углам. Но сейчас общепризнано существование в такой же степени по
следовательных геометрий, противоречащих геометрии Евклида. В так называемой гиперболической геометрии сумма углов каждого треугольника меньше двух прямых, а в эллиптической геометрии сумма углов треугольника всегда больше двух прямых. Если мы спросим, какая же из этих геометрий истинная, то единственный ответ, который можно дать в этом случае, таков: та, которая применима к нашему миру.
Гаусс пытался ответить на этот вопрос, измеряя углы большого треугольника, вершинами которого служили вершины трех гор. Однако отличие суммы этих углов от двух прямых углов оказалось меньше вероятной ошибки эксперимента. Нет сомнений в том, что только треугольники со сторонами астрономических масштабов могут дать убедительный ответ на поставленный таким образом вопрос. Эксперимент Гаусса вряд ли мог привести к решению этой проблемы. Существующие в настоящее время аргументы указывают на то, что геометрия нашей Вселенной — эллиптическая. Подобное утверждение содержит допущение, что Вселенная имеет конечную протяженность, конечна, но безгранична, подобно тому как поверхность сферы конечна, но не имеет границы.
В наши дни каждому образованному человеку понятны основные положения ньютоновской механики. Но содержание «Начал», в которых приведено формальное рассмотрение, способен воспринять лишь специалист. Точно так же лишь специалист-математик способен оценить и понять тот путь, которым шел Эйнштейн при выводе законов геометрии пространства-времени нашей Вселенной и формулировке этих законов в наиболее общем виде. Однако характер идей, отличающих теорию Эйнштейна от механики Ньютона, можно проиллюстрировать, не прибегая к математическим выкладкам. Кроме того, можно дать простую формулировку эйнштейновского закона тяготения в наиболее интересном, с нашей точки зрения, специальном случае, а именно для области пространства-времени в окрестности Солнца.
Допустим, что  — центр массивного тела, подобного Солнцу, а
— центр массивного тела, подобного Солнцу, а  два события, происходящие в
два события, происходящие в
соседних точках пространства-времени. Проведем из  перпендикуляр
перпендикуляр  к линии, проходящей через 5 и
к линии, проходящей через 5 и  Так как событие
Так как событие  происходит вблизи
происходит вблизи  то можно считать
то можно считать  и
и  малыми по сравнению с
малыми по сравнению с  Предположим, кроме того, что промежуток времени между
Предположим, кроме того, что промежуток времени между  равен
равен  причем
причем  также мало. Если теперь
также мало. Если теперь  гравитационный радиус массивного тела, находящегося в точке
гравитационный радиус массивного тела, находящегося в точке  то интервал между
то интервал между  будет равен
будет равен

Метод расчета  приведен в упражнениях 5 и 6 на стр. 140. Для Солнца
приведен в упражнениях 5 и 6 на стр. 140. Для Солнца  лаке, а для Земли
лаке, а для Земли  лаке. Отметим, что если
лаке. Отметим, что если  то
то  т. е. мы получим обычное выражение для интервала в специальной теории относительности. Подстановка
т. е. мы получим обычное выражение для интервала в специальной теории относительности. Подстановка  эквивалентна, конечно, отсутствию вещества и его влияния на свойства пространства-времени, в котором происходят рассматриваемые события. Таким образом, введение дополнительных членов, содержащих
эквивалентна, конечно, отсутствию вещества и его влияния на свойства пространства-времени, в котором происходят рассматриваемые события. Таким образом, введение дополнительных членов, содержащих  характеризует те изменения в формулах, которые возникают вследствие искривления пространства-времени в окрестности отдельного массивного тела.
характеризует те изменения в формулах, которые возникают вследствие искривления пространства-времени в окрестности отдельного массивного тела.
Если тело свободно движется в окрестности другого массивного тела, то его траектория будет такой, что интервал вдоль этой траектории, вычисленный по приведенной выше формуле, будет максимальным. Ньютоновский закон всемирного тяготения заменяется геометрической формулой Эйнштейна для области пространства-времени, геометрическим пространственно-временным законом. Формулу Эйнштейна можно

Фиг. 33.
проверить, рассматривая траектории планет около Солнца. Если интервал вычисляется по приведенной выше формуле, то будут ли эти траектории геодезическими линиями в пространстве-времени? Хорошо известно, что траектории планет очень точно совпадают с результатами расчетов, выполненных на основе механики Ньютона. Именно благодаря этому согласию наблюдаемых орбит с вычисленными на основе ньютоновского закона всемирного тяготения этот закон был общепризнанным вплоть до времен Эйнштейна. Но мы увидим в следующей главе, что, сколь бы хорошим ни было согласие расчетов с результатами наблюдений, замена законов механики Ньютона геометрическим законом Эйнштейна обеспечивает еще более высокую точность: эти законы можно рассматривать как первое приближение к закону Эйнштейна.
УПРАЖНЕНИЯ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Введение
- ГЛАВА ПЕРВАЯ. Научный прогресс
- Система Птолемея
- Система Коперника
- Всемирное тяготение
- Механика Галилея и Ньютона
- Измерительные приборы
- Искусственное расширение предела человеческих чувств
- Здравый смысл
- ГЛАВА ВТОРАЯ. Алиса в Зазеркалье
- Может ли Природа ввести в заблуждение?
- Выпуклое зеркало
- Жизнь за зеркалом
- Сжатие в направлении, перпендикулярном оси
- Сжатие в направлении вдоль оси
- Геометрия в мире Алисы
- ГЛАВА ТРЕТЬЯ. Скорость света
- Абсолютное движение
- По течению
- Опыт Майкельсона — Морли
- Какова же разгадка?
- Гипотеза Эйнштейна
- Применение гипотезы Эйнштейна
- Кто же прав?
- ГЛАВА ЧЕТВЕРТАЯ. ЧАСЫ
- Наблюдения в различных местах
- Синхронизация часов
- Мнение постороннего наблюдателя
- Что думают другие наблюдатели
- Одновременные события
- Единство пространства и времени
- ГЛАВА ПЯТАЯ. Алгебраические соотношения между событиями в двух системах
- Измерительные линейки
- Сравнение часов наблюдателей A и C с часами наблюдателя O
- Ход часов
- Расстояние и промежуток времени между двумя событиями
- Мнение наблюдателя А о данных наблюдателя О
- Скорость света
- ГЛАВА ШЕСТАЯ. Интервал между событиями
- Измерение различными наблюдателями интервала между двумя событиями
- Формальное рассмотрение интервала
- Вещественная и мнимая части интервала
- Последовательность двух событий во времени
- Собственное время
- ГЛАВА СЕДЬМАЯ. Четвертое измерение
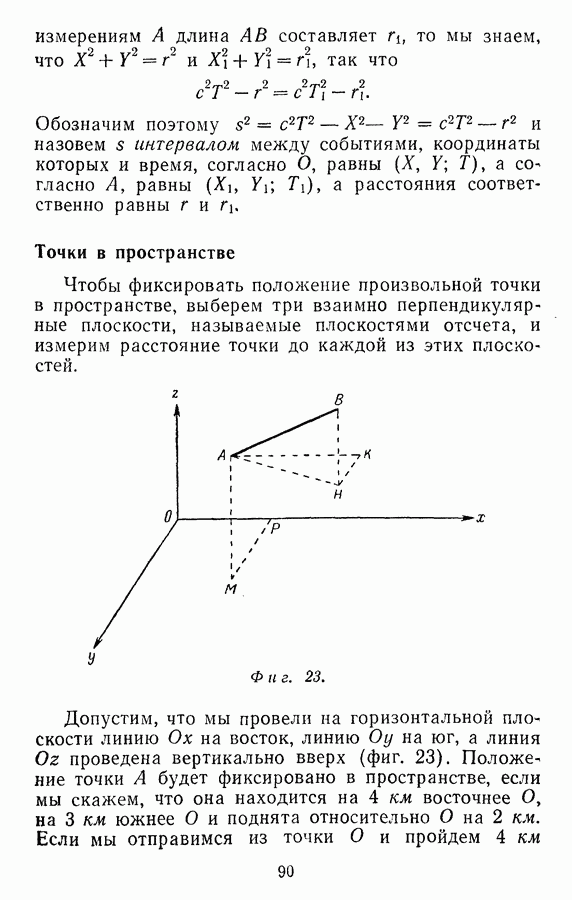
- Точки в пространстве
- Четырехмерное пространство-время
- Плоский мир
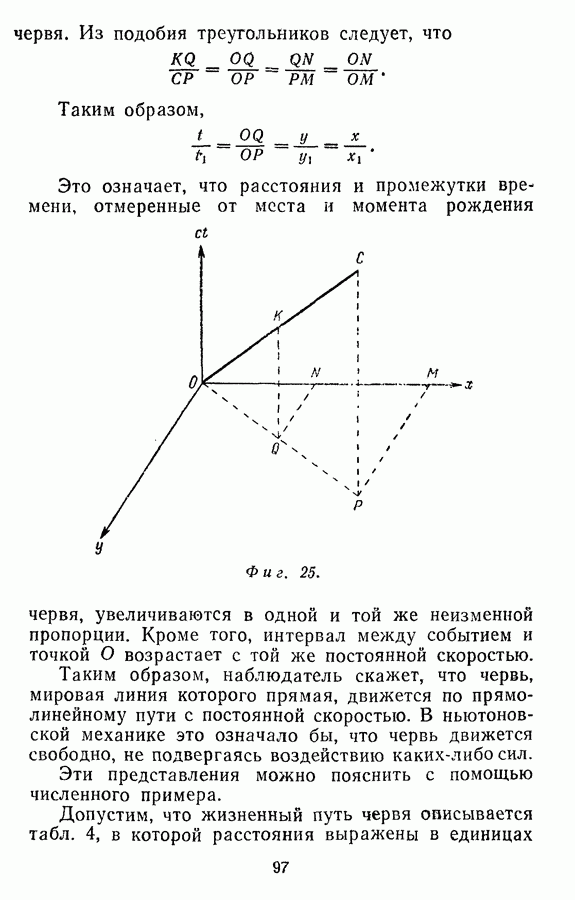
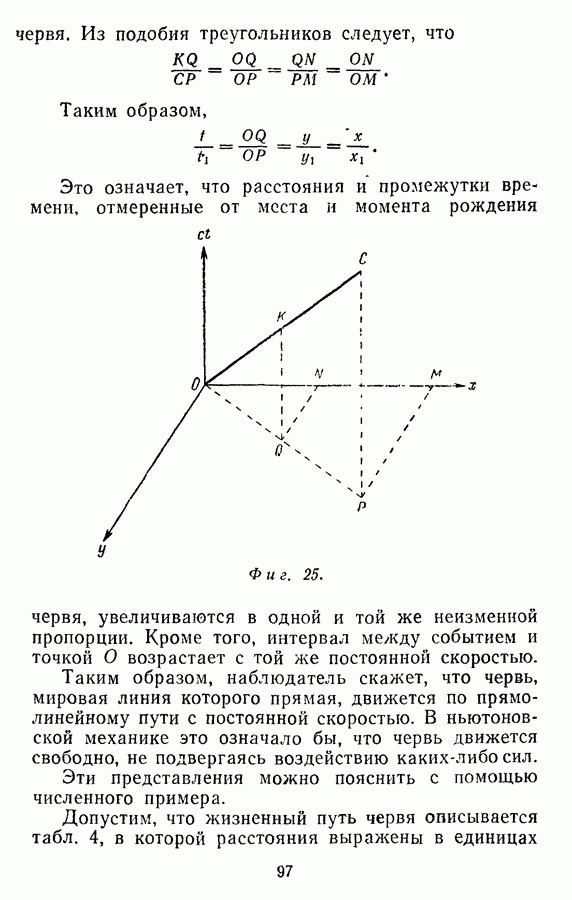
- Прямолинейные мировые линии
- Прямолинейные мировые линии
- Криволинейные мировые линии
- Прямолинейные и криволинейные мировые линии
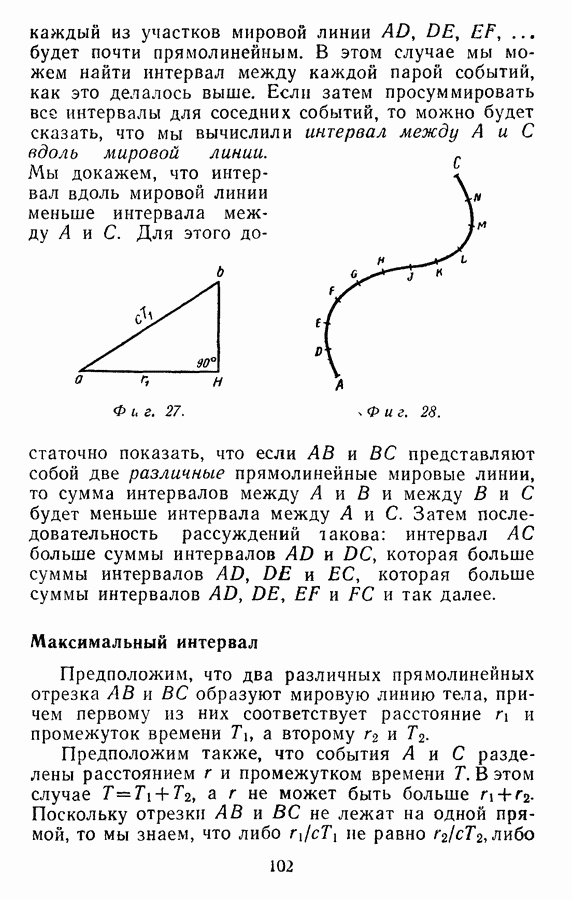
- Интервал вдоль мировой линии
- Максимальный интервал
- Геодезический закон движения
- ГЛАВА ВОСЬМАЯ. Масса и импульс
- Поперечная скорость
- Коэффициент увлечения Френеля
- Масса
- Эйнштейновское определение массы
- Законы сохранения массы и импульса
- Импульс и интервал
- Принципы специальной теории относительности
- ГЛАВА ДЕВЯТАЯ. Общая теория относительности
- Силовое поле
- Принцип эквивалентности
- Искривление пространства-времени
- Жизнь на вращающемся диске
- Поле силы тяжести
- ГЛАВА ДЕСЯТАЯ. Проверка общей теории относительности Энштейна
- Смещение спектральных линий
- Искривление светового луча
- Общие выводы