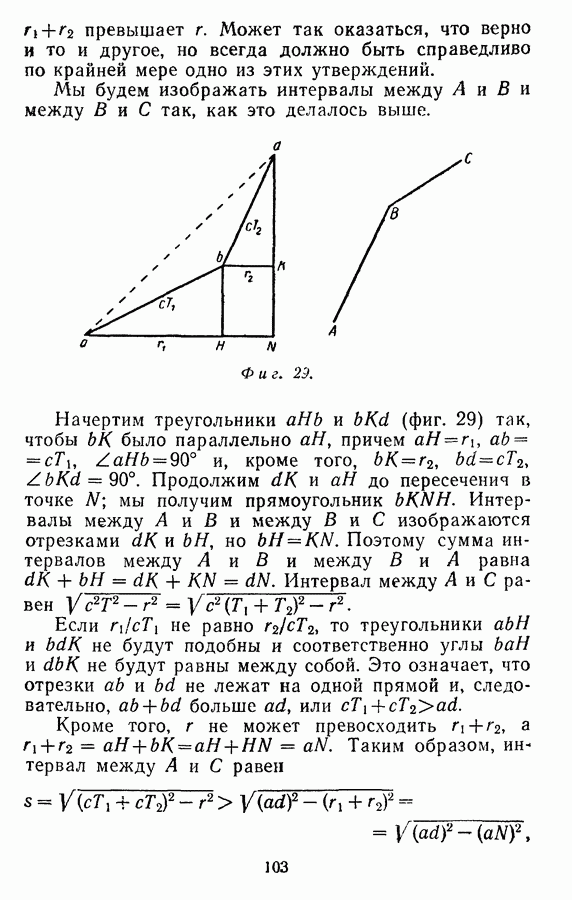| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Интервал вдоль мировой линии
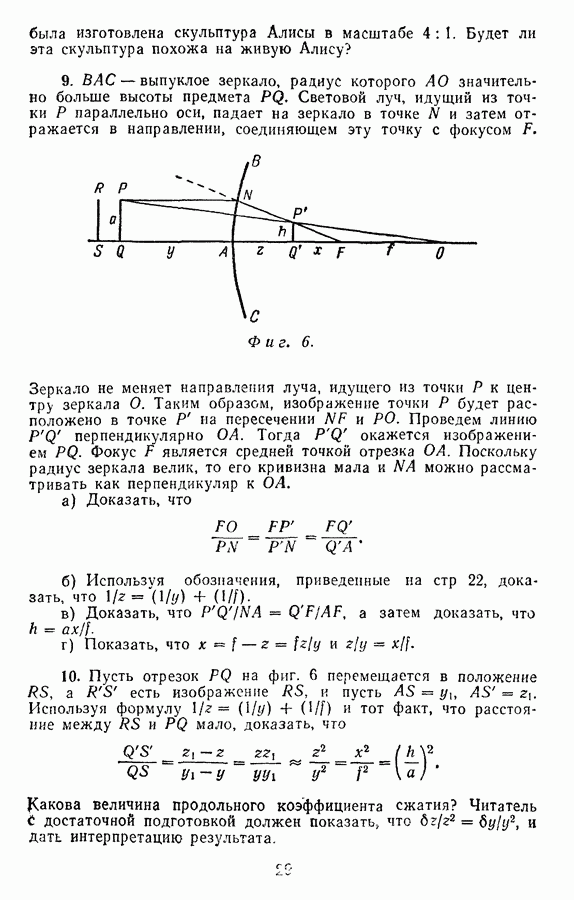
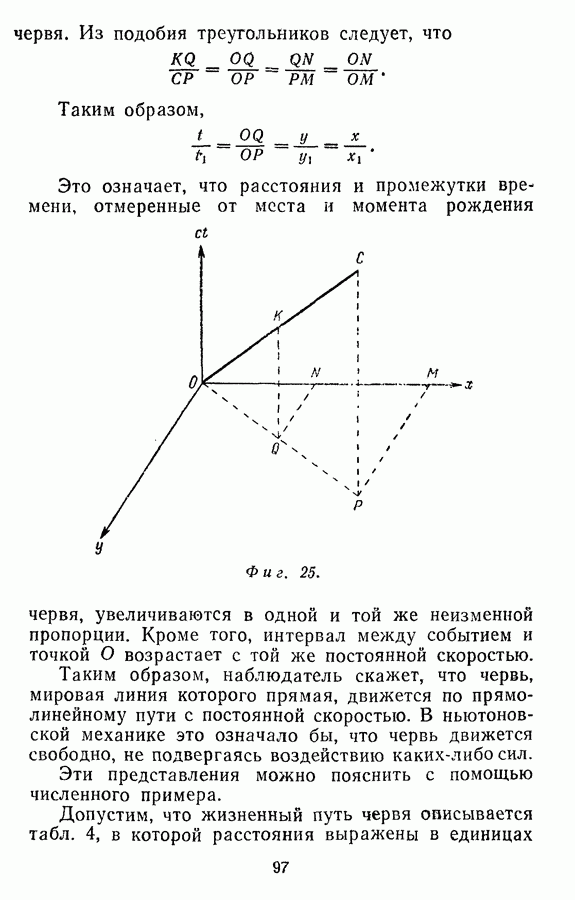
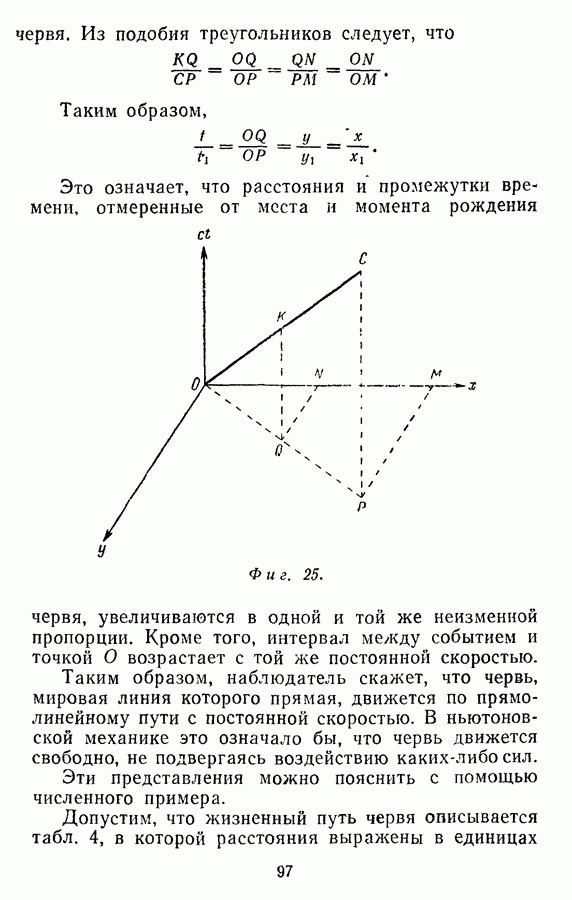
Если мировая линия  прямолинейная, то в наших прежних обозначениях интервал между
прямолинейная, то в наших прежних обозначениях интервал между  будет равен
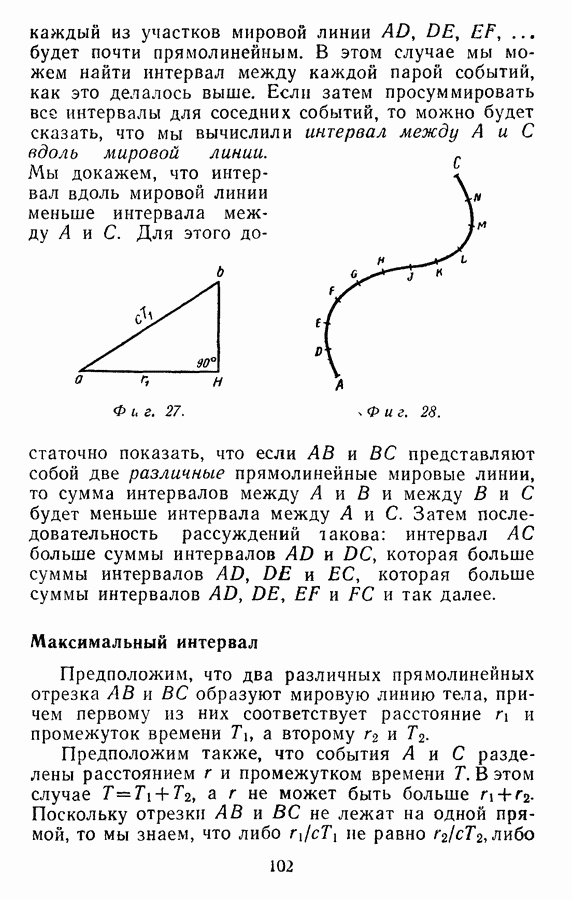
будет равен  Интервал можно изобразить прямоугольным треугольником
Интервал можно изобразить прямоугольным треугольником  (фиг. 27), в котором сторона
(фиг. 27), в котором сторона  сторона
сторона  а угол
а угол  . В этом случае, по теореме Пифагора,
. В этом случае, по теореме Пифагора,  , так что
, так что

Сторона  характеризует величину интервала
характеризует величину интервала 
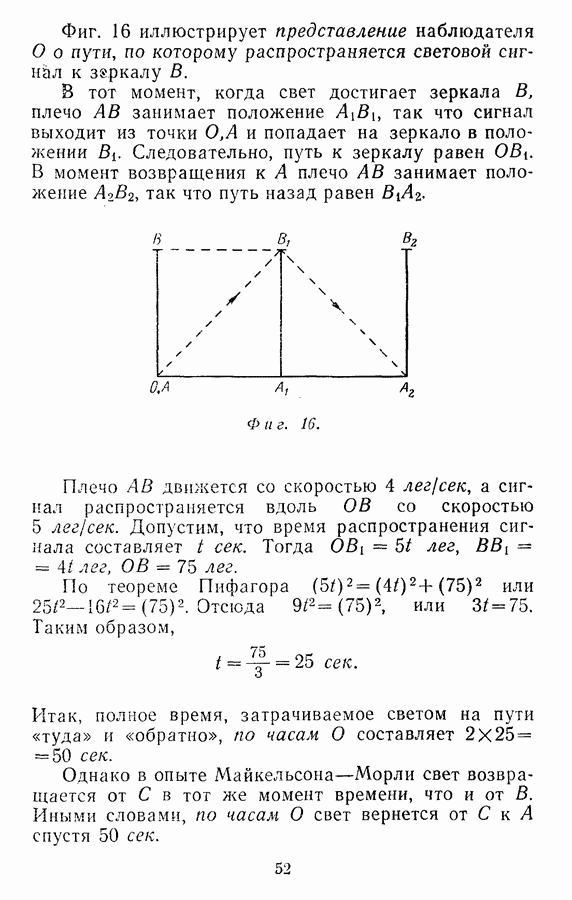
Теперь предположим, что мировая линия  криволинейная. Рассмотрим последовательность многочисленных событий:
криволинейная. Рассмотрим последовательность многочисленных событий:  (фиг. 28). Если число событий выбрано достаточно большим, то
(фиг. 28). Если число событий выбрано достаточно большим, то
каждый из участков мировой линии  будет почти прямолинейным. В этом случае мы можем найти интервал между каждой парой событий, как это делалось выше. Если затем просуммировать все интервалы для соседних событий, то можно будет сказать, что мы вычислили интервал между
будет почти прямолинейным. В этом случае мы можем найти интервал между каждой парой событий, как это делалось выше. Если затем просуммировать все интервалы для соседних событий, то можно будет сказать, что мы вычислили интервал между  вдоль мировой линии. Мы докажем, что интервал вдоль мировой линии меньше интервала между
вдоль мировой линии. Мы докажем, что интервал вдоль мировой линии меньше интервала между 

Фиг. 27.

Фиг. 28.
Для этого достаточно показать, что если  и
и  представляют собой две различные прямолинейные мировые линии, то сумма интервалов между
представляют собой две различные прямолинейные мировые линии, то сумма интервалов между  и между
и между  будет меньше интервала между
будет меньше интервала между  Затем последовательность рассуждений такова: интервал
Затем последовательность рассуждений такова: интервал  больше суммы интервалов
больше суммы интервалов  и
и  которая больше суммы интервалов
которая больше суммы интервалов  и
и  которая больше суммы интервалов
которая больше суммы интервалов  и
и  и так далее.
и так далее.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Введение
- ГЛАВА ПЕРВАЯ. Научный прогресс
- Система Птолемея
- Система Коперника
- Всемирное тяготение
- Механика Галилея и Ньютона
- Измерительные приборы
- Искусственное расширение предела человеческих чувств
- Здравый смысл
- ГЛАВА ВТОРАЯ. Алиса в Зазеркалье
- Может ли Природа ввести в заблуждение?
- Выпуклое зеркало
- Жизнь за зеркалом
- Сжатие в направлении, перпендикулярном оси
- Сжатие в направлении вдоль оси
- Геометрия в мире Алисы
- ГЛАВА ТРЕТЬЯ. Скорость света
- Абсолютное движение
- По течению
- Опыт Майкельсона — Морли
- Какова же разгадка?
- Гипотеза Эйнштейна
- Применение гипотезы Эйнштейна
- Кто же прав?
- ГЛАВА ЧЕТВЕРТАЯ. ЧАСЫ
- Наблюдения в различных местах
- Синхронизация часов
- Мнение постороннего наблюдателя
- Что думают другие наблюдатели
- Одновременные события
- Единство пространства и времени
- ГЛАВА ПЯТАЯ. Алгебраические соотношения между событиями в двух системах
- Измерительные линейки
- Сравнение часов наблюдателей A и C с часами наблюдателя O
- Ход часов
- Расстояние и промежуток времени между двумя событиями
- Мнение наблюдателя А о данных наблюдателя О
- Скорость света
- ГЛАВА ШЕСТАЯ. Интервал между событиями
- Измерение различными наблюдателями интервала между двумя событиями
- Формальное рассмотрение интервала
- Вещественная и мнимая части интервала
- Последовательность двух событий во времени
- Собственное время
- ГЛАВА СЕДЬМАЯ. Четвертое измерение
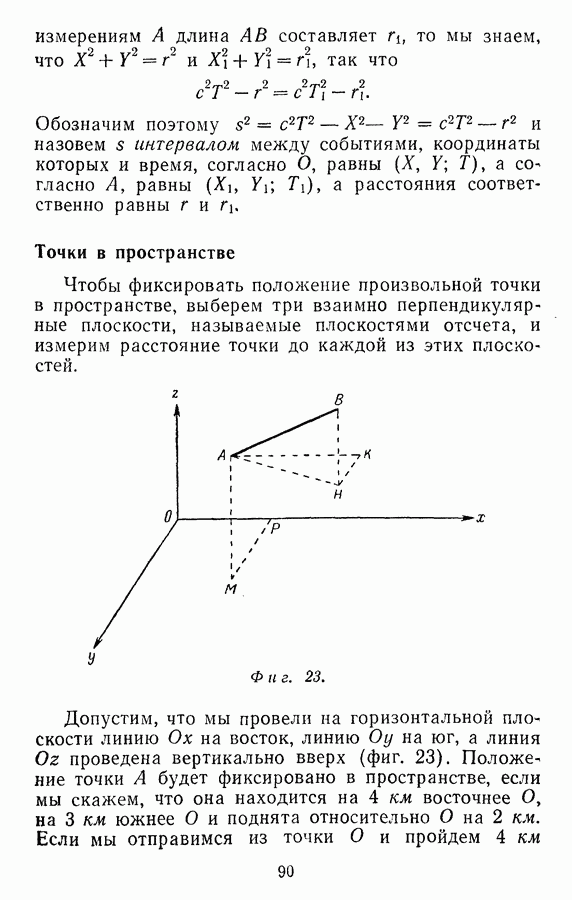
- Точки в пространстве
- Четырехмерное пространство-время
- Плоский мир
- Прямолинейные мировые линии
- Прямолинейные мировые линии
- Криволинейные мировые линии
- Прямолинейные и криволинейные мировые линии
- Интервал вдоль мировой линии
- Максимальный интервал
- Геодезический закон движения
- ГЛАВА ВОСЬМАЯ. Масса и импульс
- Поперечная скорость
- Коэффициент увлечения Френеля
- Масса
- Эйнштейновское определение массы
- Законы сохранения массы и импульса
- Импульс и интервал
- Принципы специальной теории относительности
- ГЛАВА ДЕВЯТАЯ. Общая теория относительности
- Силовое поле
- Принцип эквивалентности
- Искривление пространства-времени
- Жизнь на вращающемся диске
- Поле силы тяжести
- ГЛАВА ДЕСЯТАЯ. Проверка общей теории относительности Энштейна
- Смещение спектральных линий
- Искривление светового луча
- Общие выводы