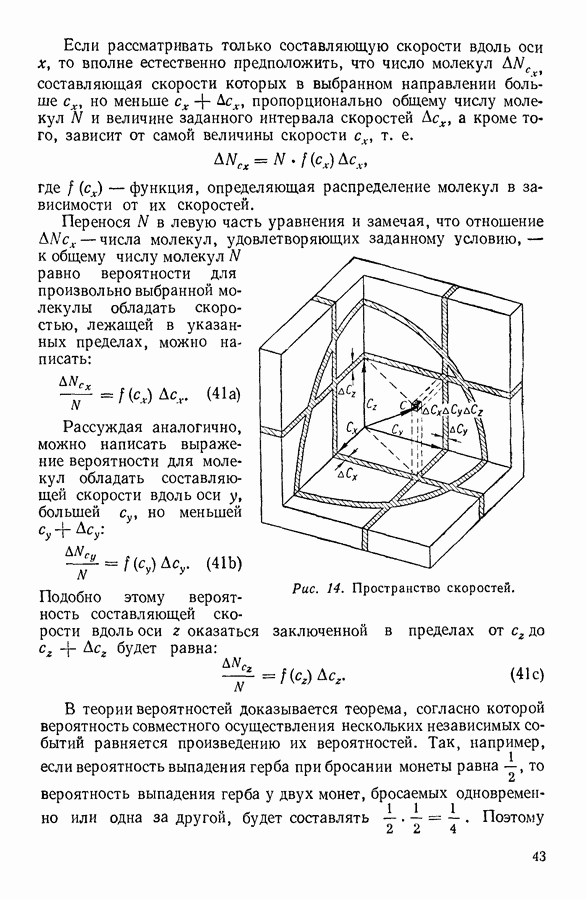
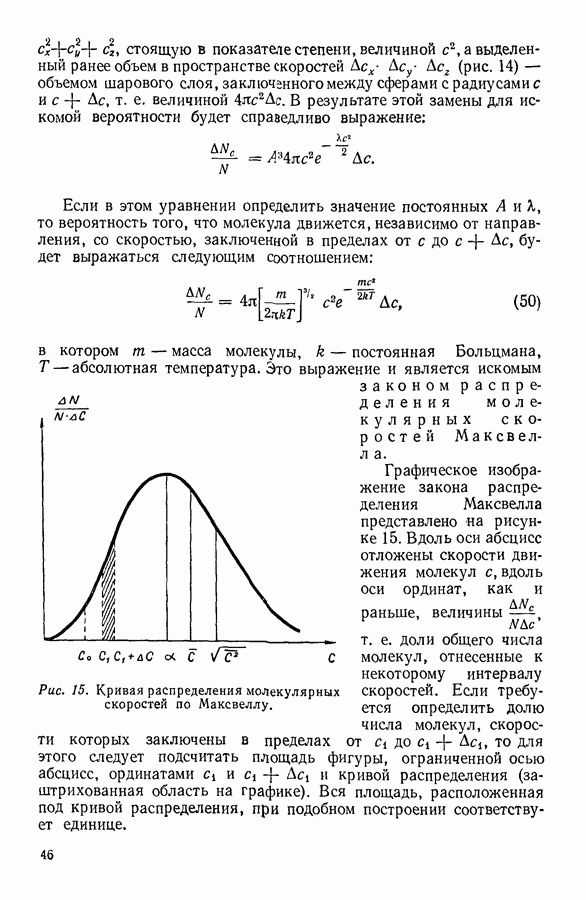
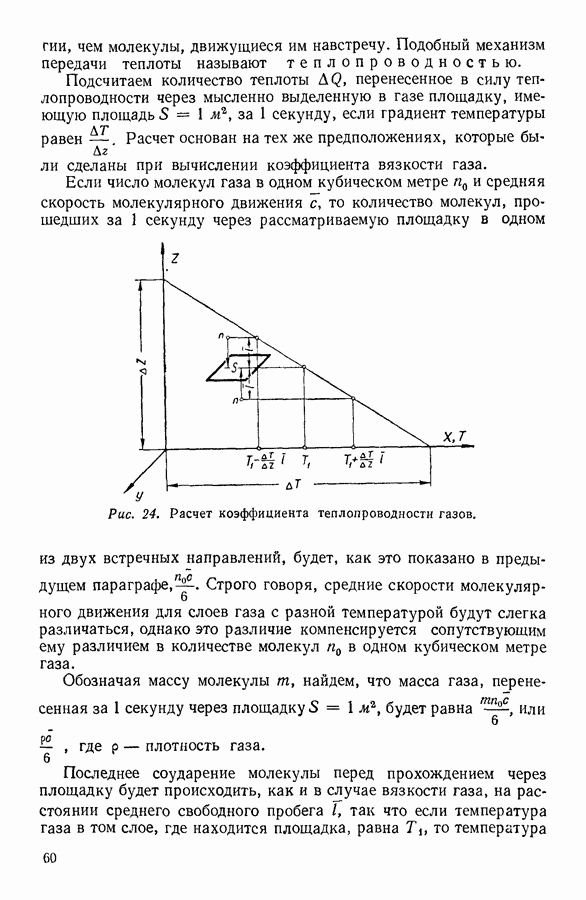
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
Замечательные работы  Перрена, сыгравшие исключительную роль в деле утверждения молекулярных представлений, связаны с использованием полученной выше барометрической формулы. Основная идея опытов Перрена сводилась к предположению, что законы молекулярно-кинетической теории определяют поведение не только атомов и молекул, но и гораздо более крупных частиц, состоящих из многих тысяч молекул. Исходя из весьма общих соображений, которые здесь не будут рассматриваться, можно предполагать, что средние кинетические энергии очень мелких частиц, совершающих броуновское движение в жидкости, совпадают со средними кинетическими энергиями молекул газа, если только температура жидкости и температура газа одинаковы. Точно так же распределение по высоте частиц, взвешенных в жидкости, подчиняется тому же закону, что и распределение по высоте молекул газа. Подобный вывод очень важен, поскольку на основании его возможна количественная проверка закона распределения. Проверку можно осуществить путем непосредственного подсчета с помощью микроскопа количества взвешенных частиц, находящихся в жидкости на разной высоте.
Перрена, сыгравшие исключительную роль в деле утверждения молекулярных представлений, связаны с использованием полученной выше барометрической формулы. Основная идея опытов Перрена сводилась к предположению, что законы молекулярно-кинетической теории определяют поведение не только атомов и молекул, но и гораздо более крупных частиц, состоящих из многих тысяч молекул. Исходя из весьма общих соображений, которые здесь не будут рассматриваться, можно предполагать, что средние кинетические энергии очень мелких частиц, совершающих броуновское движение в жидкости, совпадают со средними кинетическими энергиями молекул газа, если только температура жидкости и температура газа одинаковы. Точно так же распределение по высоте частиц, взвешенных в жидкости, подчиняется тому же закону, что и распределение по высоте молекул газа. Подобный вывод очень важен, поскольку на основании его возможна количественная проверка закона распределения. Проверку можно осуществить путем непосредственного подсчета с помощью микроскопа количества взвешенных частиц, находящихся в жидкости на разной высоте.
Уравнение (36) распределения частиц по высоте

удобно в этом случае переписать, разделив числитель и знаменатель дроби, стоящей в правой части уравнения, на число Авогадро 
При этом следует заметить, что отношение - соответствует массе частицы  а отношение равно
а отношение равно  средней кинетическои энергии частицы
средней кинетическои энергии частицы  [сравните уравнение (28)]. Вводя эти обозначения, получим:
[сравните уравнение (28)]. Вводя эти обозначения, получим:

Если теперь опытным путем определить количества частиц и  соответствующие двум различным значениям
соответствующие двум различным значениям  то можно будет написать:
то можно будет написать:

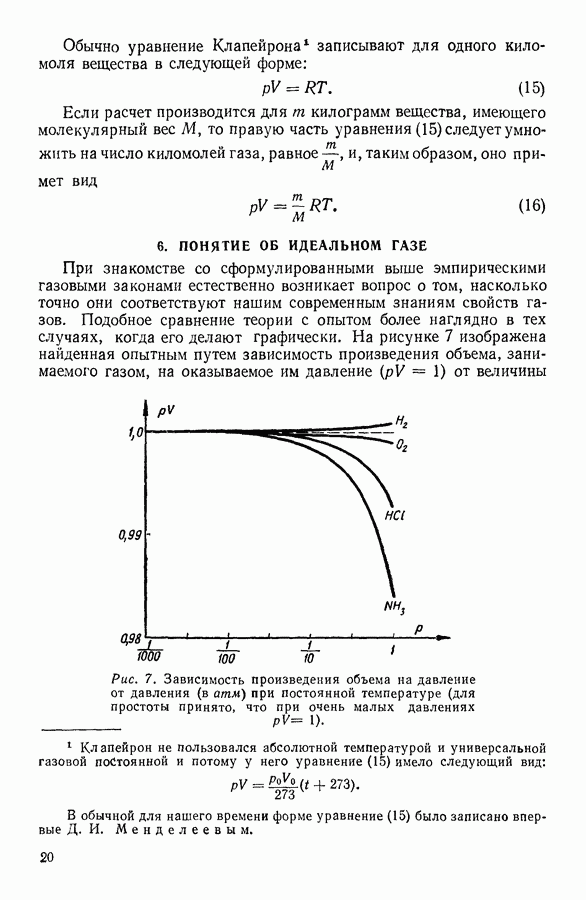
Вычитая из первого уравнения второе, найдем:

Из этого соотношения можно определить  если только знать массу частицы
если только знать массу частицы 
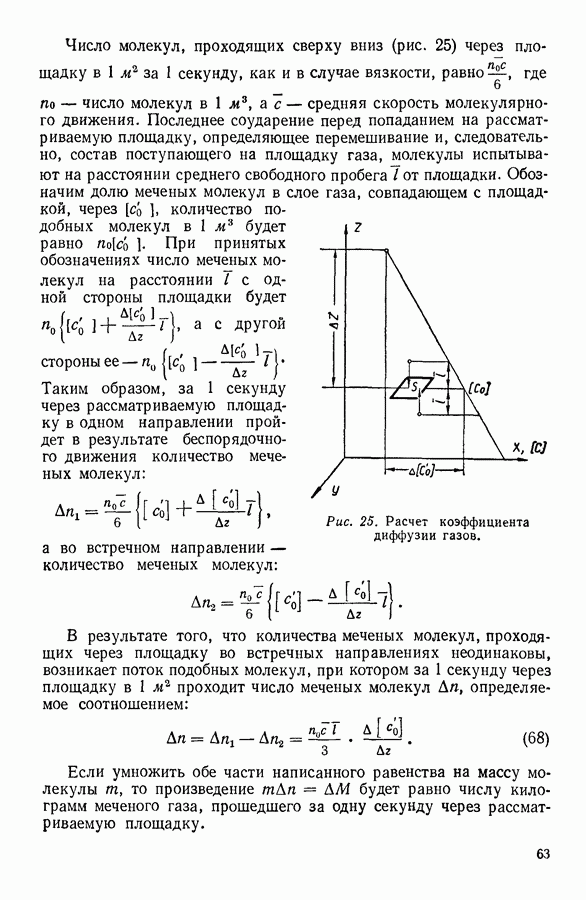
При всей простоте и ясности основной идеи опыты Перрена были связаны с преодолением больших трудностей. В качестве объекта исследования им были выбраны водные эмульсии мастики и гуммигута, которые подвергались центрифугированию для получения эмульсий, состоящих из зернышек одинакового размера. Размер зернышек, которые считались шариками, определялся по скорости их оседания. За движением отдельного зернышка следить было невозможно и потому наблюдалась скорость оседания верхней границы эмульсии, т. е. средняя скорость оседания многих тысяч зернышек. Зная плотность эмульгированного вещества и определяя размеры зернышек эмульсии, можно было вычислить их массы. Далее необходимо было определить числа  С этой целью к предметному стеклышку для микроскопических наблюдений Перрен приклеил второе стекло с просверленным в нем круглым отверстием, так что образовалась цилиндрическая прозрачная кювета. Поместив в кювету каплю эмульсии и закрыв для предотвращения испарения кювету покровным стеклышком, можно было с помощью микроскопа наблюдать зернышки эмульсии. Если воспользоваться объективом с небольшой глубиной поля зрения, то в микроскопе будут видны только зернышки, расположенные в очень тонком слое жидкости. Практически в этих опытах можно сосчитать лишь небольшое количество зернышек, поскольку их число непрерывно меняется. Для преодоления этого затруднения в фокальной
С этой целью к предметному стеклышку для микроскопических наблюдений Перрен приклеил второе стекло с просверленным в нем круглым отверстием, так что образовалась цилиндрическая прозрачная кювета. Поместив в кювету каплю эмульсии и закрыв для предотвращения испарения кювету покровным стеклышком, можно было с помощью микроскопа наблюдать зернышки эмульсии. Если воспользоваться объективом с небольшой глубиной поля зрения, то в микроскопе будут видны только зернышки, расположенные в очень тонком слое жидкости. Практически в этих опытах можно сосчитать лишь небольшое количество зернышек, поскольку их число непрерывно меняется. Для преодоления этого затруднения в фокальной
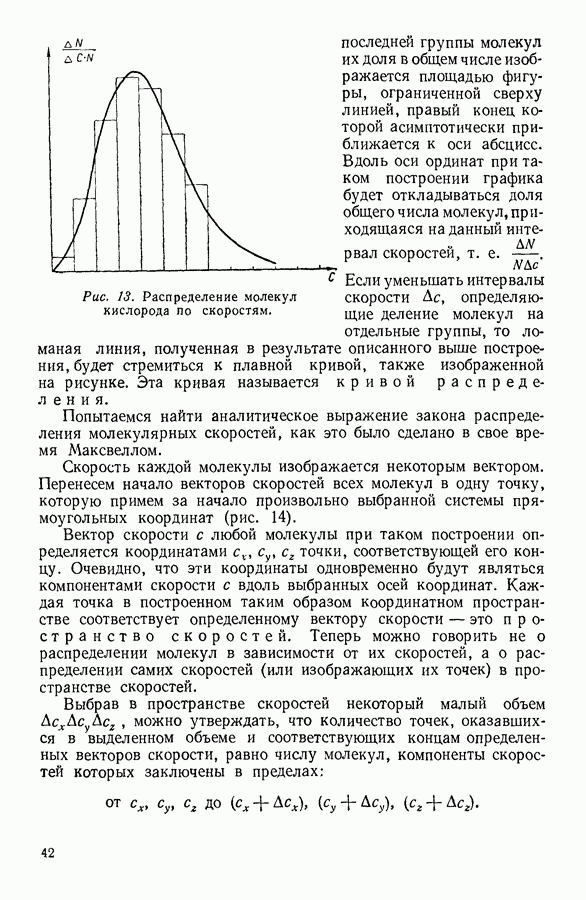
плоскости окуляра помещался непрозрачный экран с маленьким круглым отверстием. Благодаря этому поле зрения микроскопа сильно уменьшалось, и наблюдатель мог сразу определить, сколько зернышек в данный момент находится в поле зрения (рис. 12).
Повторяя подобные наблюдения через правильные промежутки времени, записывая наблюдаемые числа зерен и усредняя полученные данные, Перрен показал, что среднее число зерен на данном уровне стремится к некоторому определенному пределу, соответствующему плотности эмульсии на этом уровне. Для того чтобы проиллюстрировать трудоемкость этих опытов, можно указать, что для получения точного результата необходимо было производить несколько тысяч измерений.

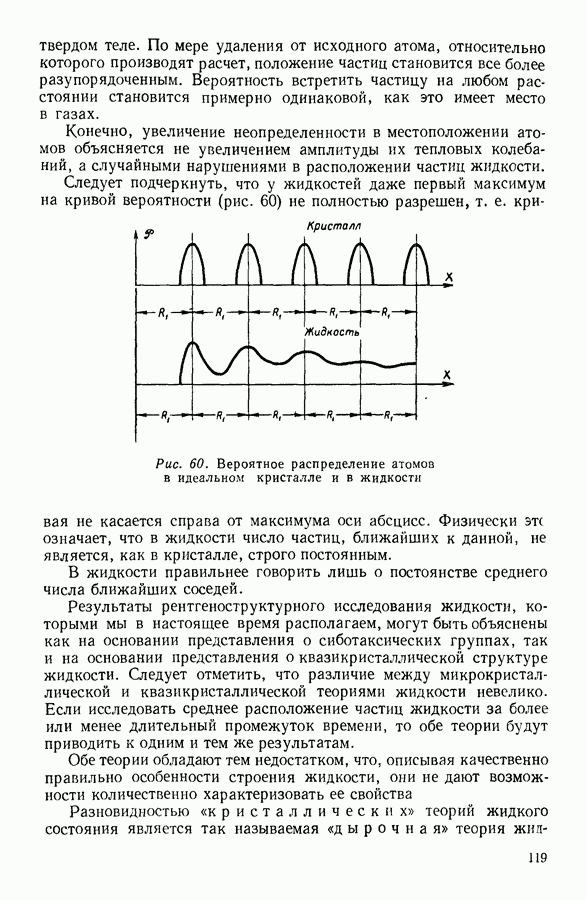
Рис. 12. Распределение зерен эмульсии.
Определив с желаемой степенью точности плотность эмульсии на некотором уровне  Перрен перемещал микроскоп в вертикальном направлении и измерял плотность эмульсии на втором уровне
Перрен перемещал микроскоп в вертикальном направлении и измерял плотность эмульсии на втором уровне  Тщательно выполненные измерения показали, что распределение зернышек эмульсии по высоте подчиняется барометрической формуле (уравнение 37).
Тщательно выполненные измерения показали, что распределение зернышек эмульсии по высоте подчиняется барометрической формуле (уравнение 37).
Воспользовавшись найденными значениями плотности зерен эмульсии на разных уровнях, Перрен вычислил среднюю кинетическую энергию частицы  воспользовавшись соотношением
воспользовавшись соотношением

определил экспериментально число Авогадро 
Найденные таким образом значения числа Авогадро колебались от  до
до 
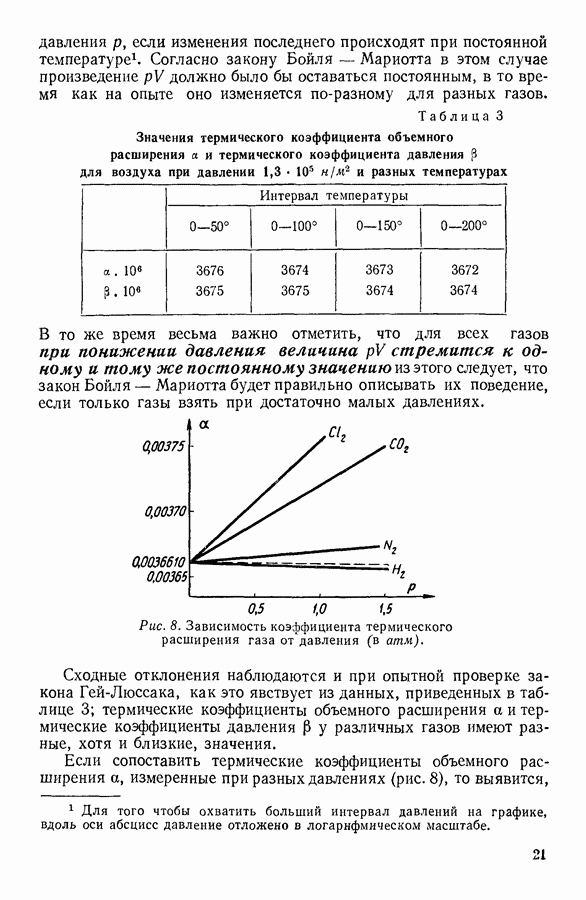
Число Авогадро можно определить различными способами. В своей работе Перрен сопоставляет найденные им величины со значениями числа Авогадро, определенными двенадцатью другими методами, и подчеркивает, что самые разнообразные методы определения  приводят к весьма близким величинам, чего не могло бы быть, если бы основные положения молекулярно-кинетической теории не отражали бы правильно явления, объективно существующие в природе.
приводят к весьма близким величинам, чего не могло бы быть, если бы основные положения молекулярно-кинетической теории не отражали бы правильно явления, объективно существующие в природе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
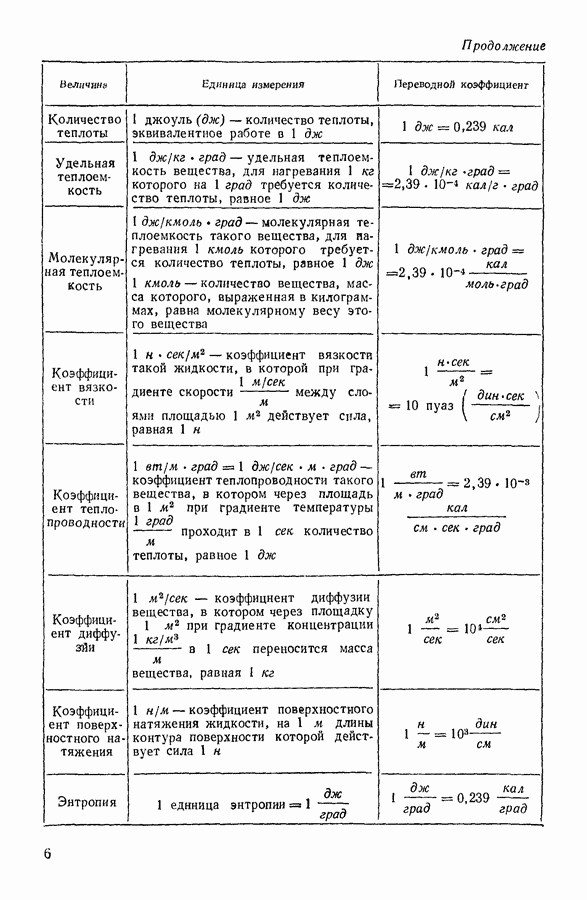
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
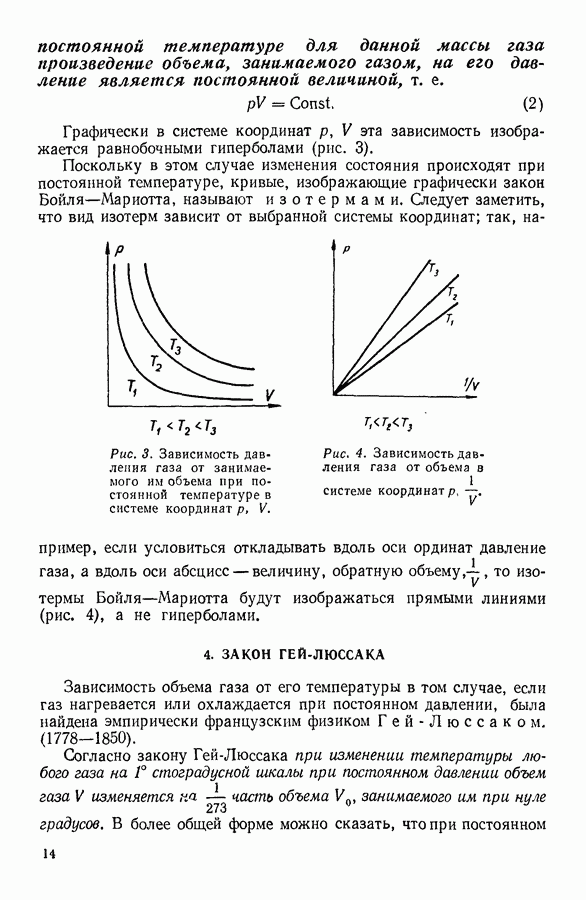
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
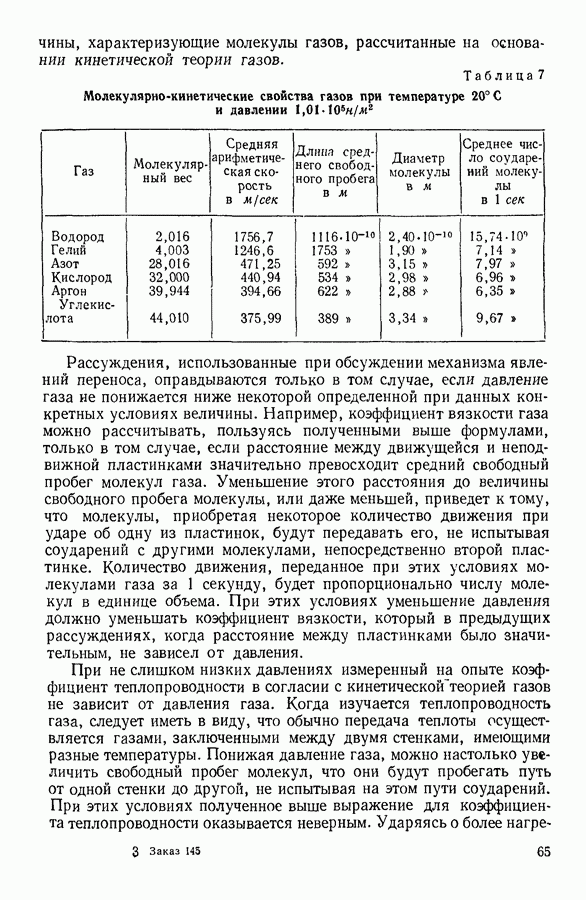
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
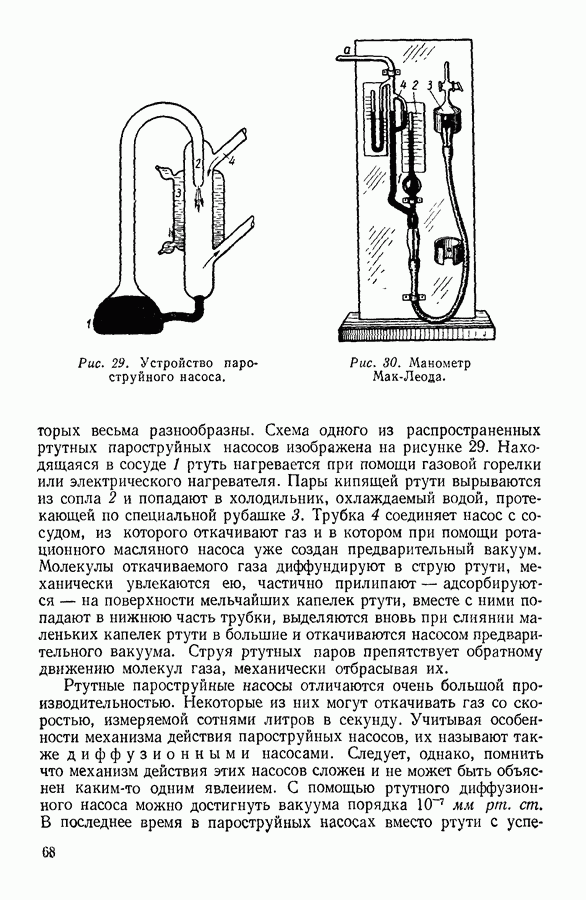
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
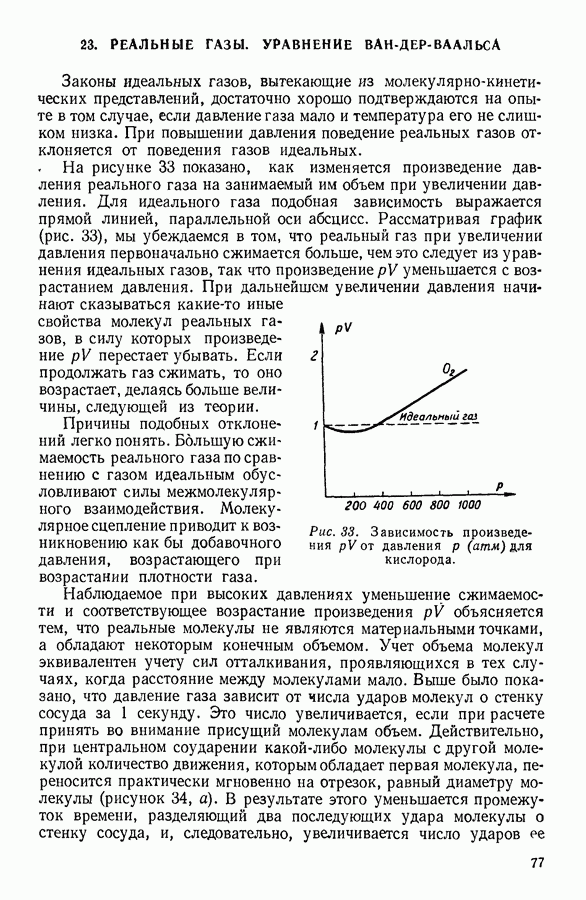
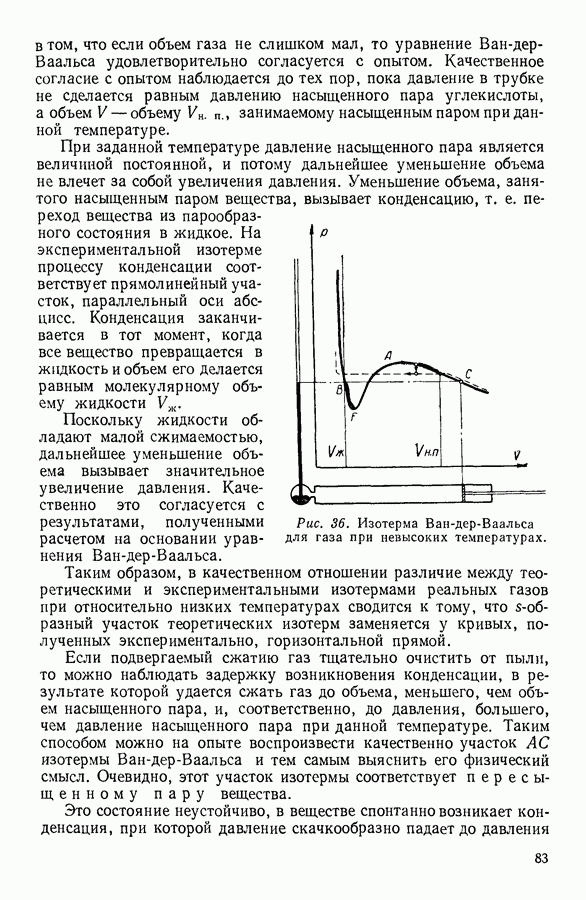
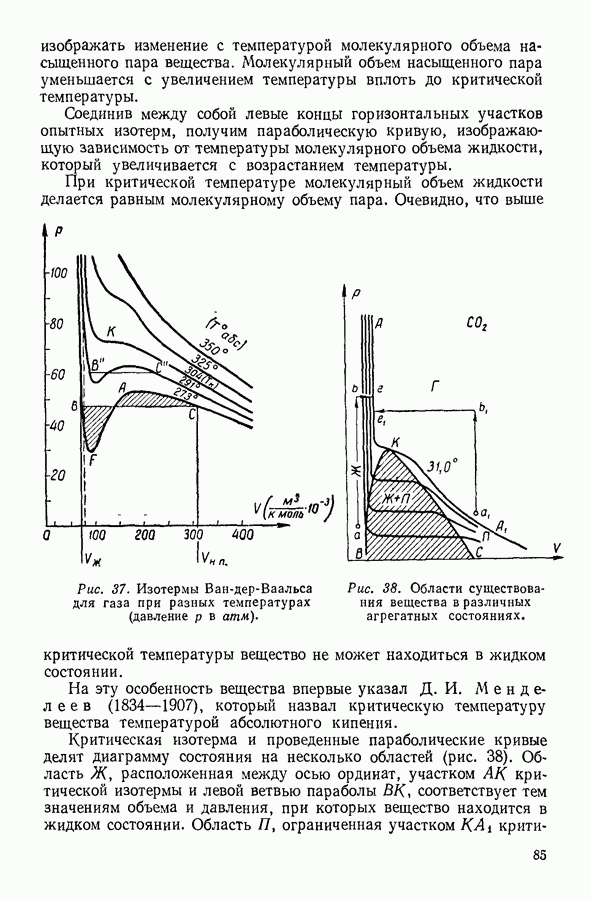
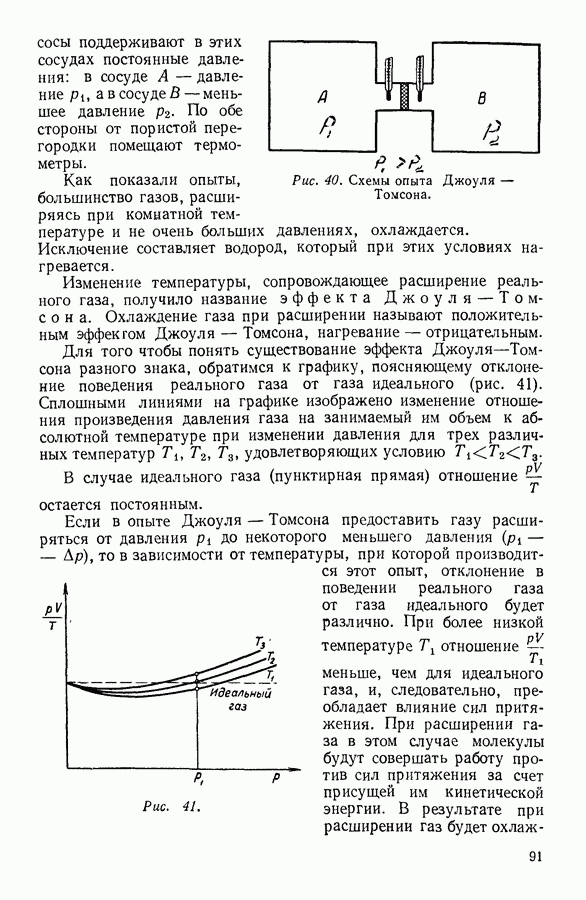
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
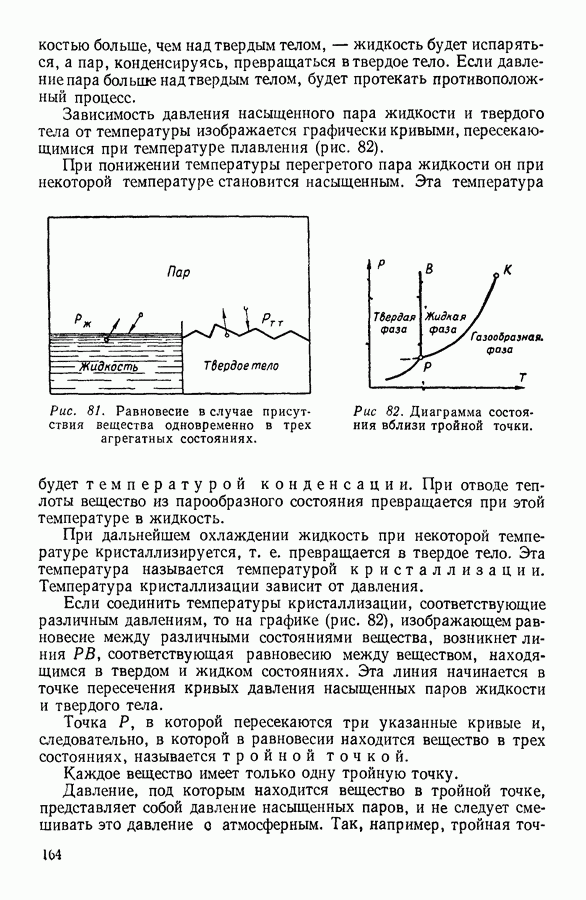
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
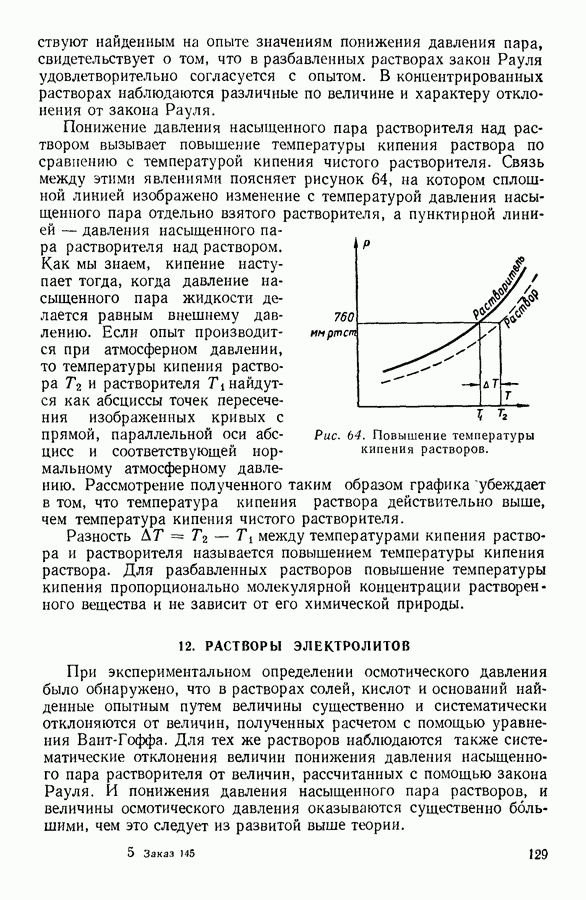
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
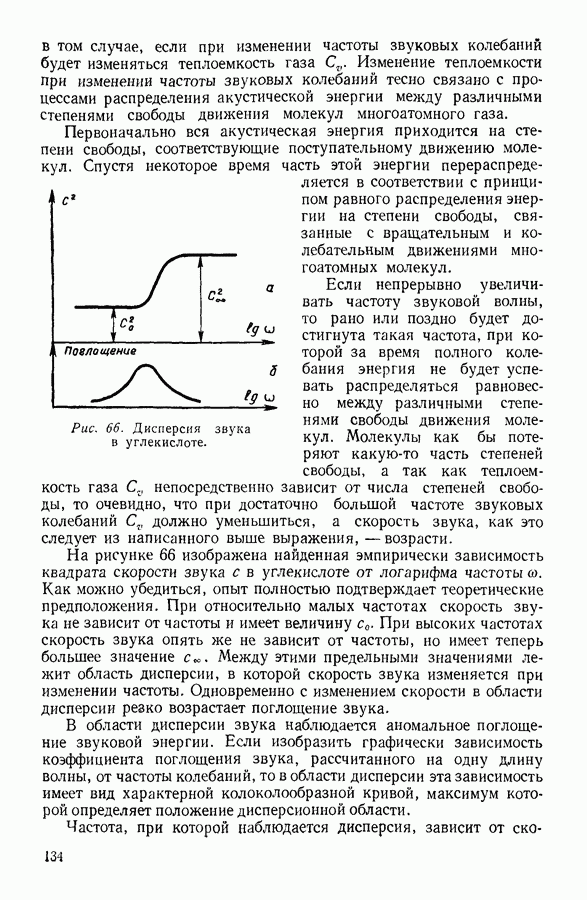
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
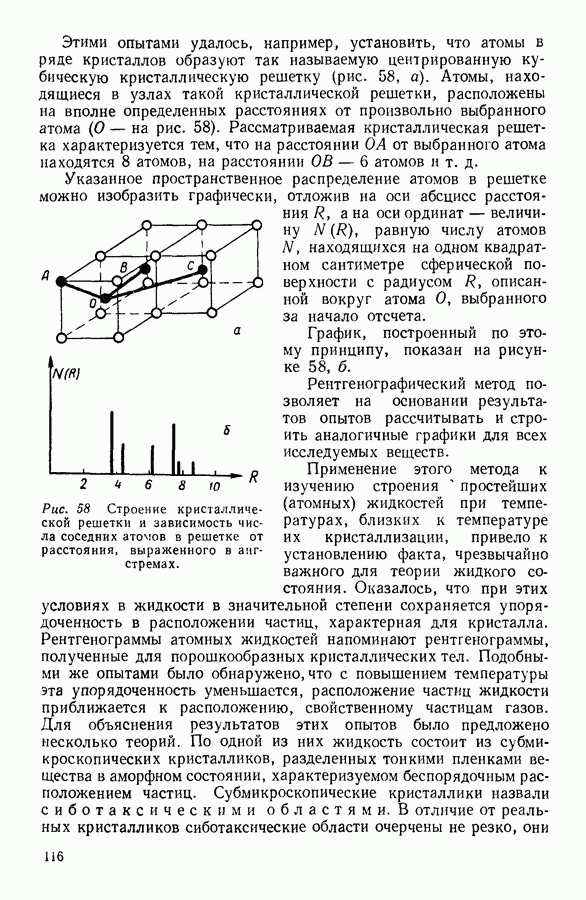
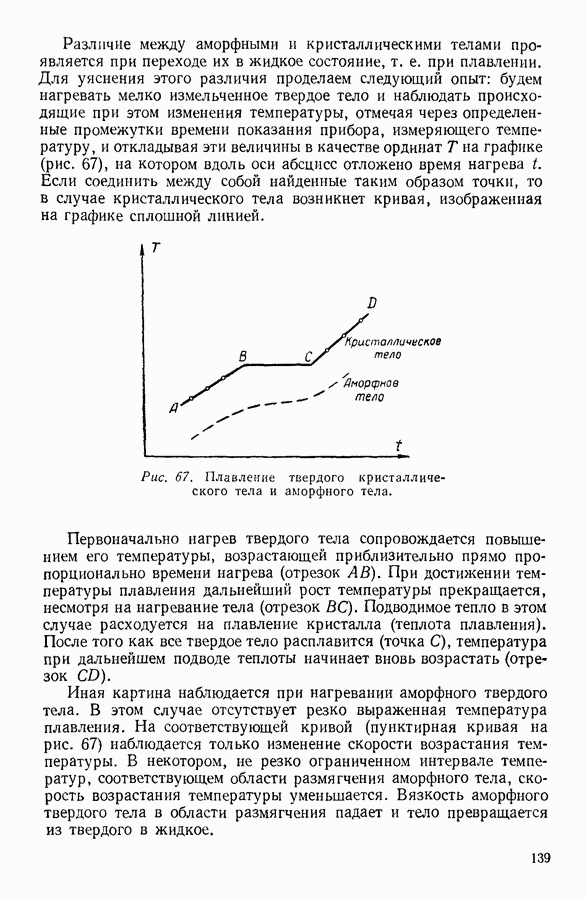
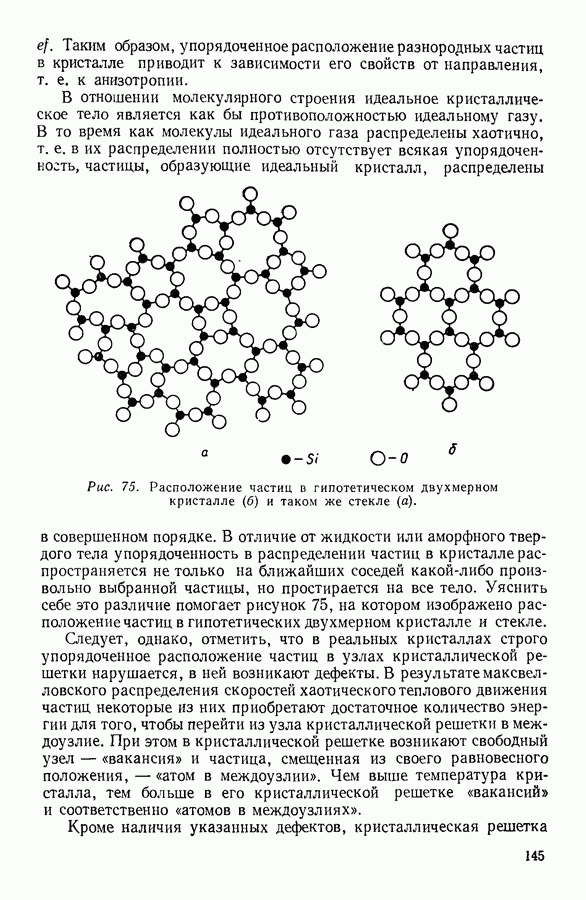
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
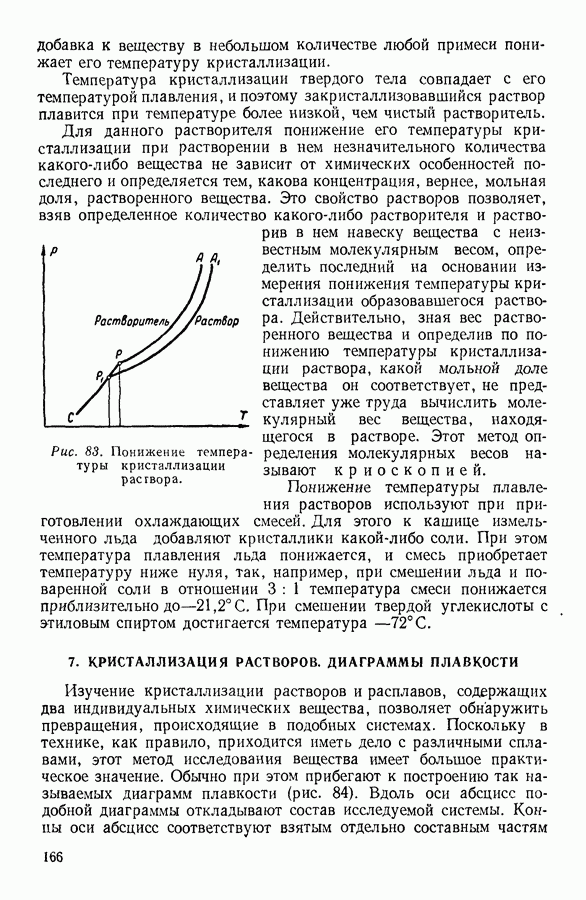
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
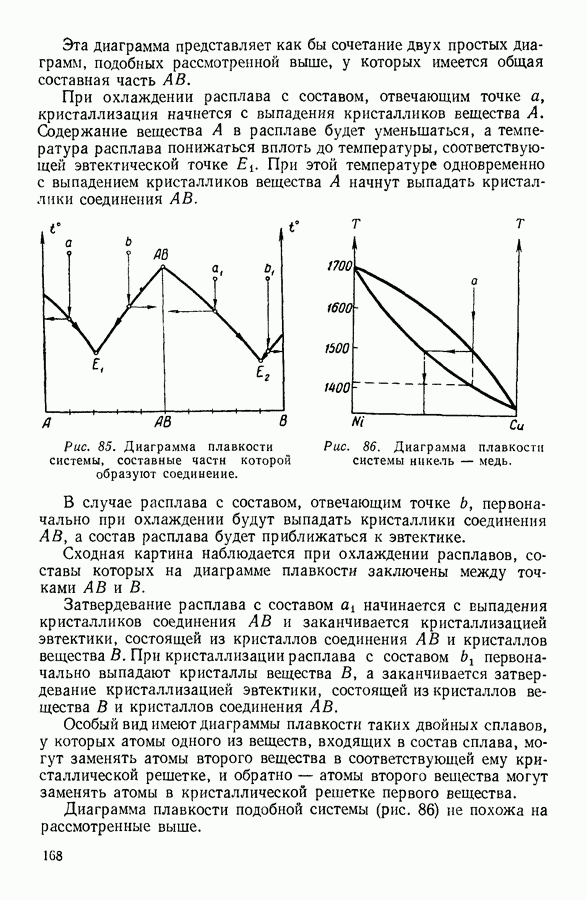
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
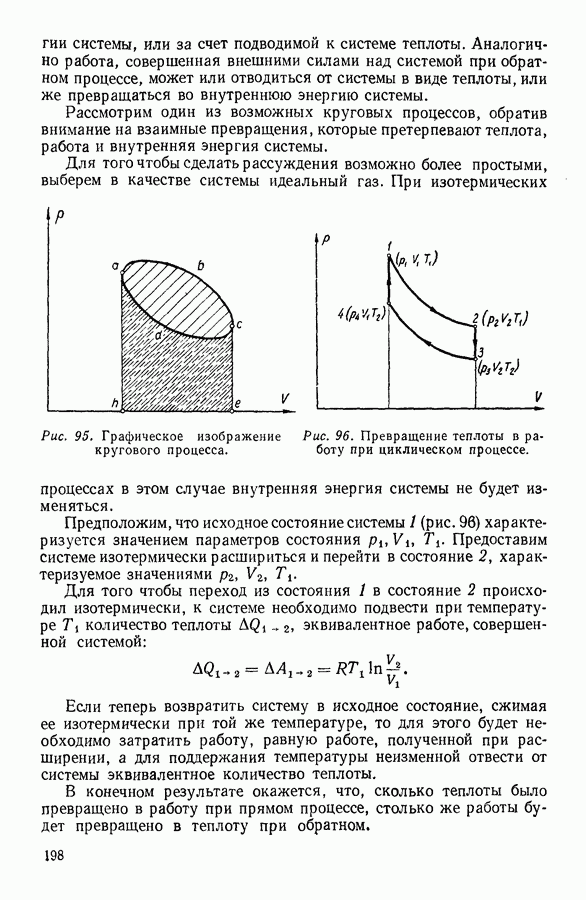
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
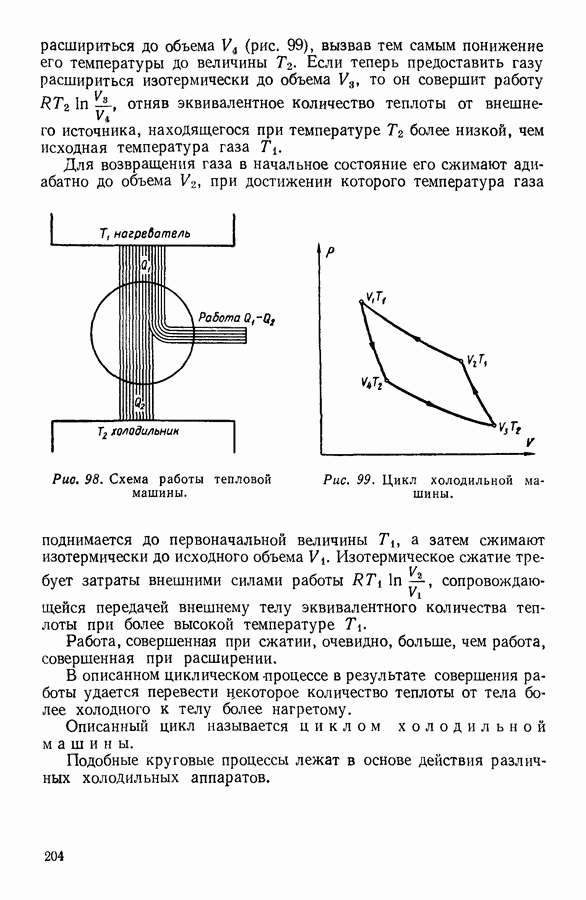
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
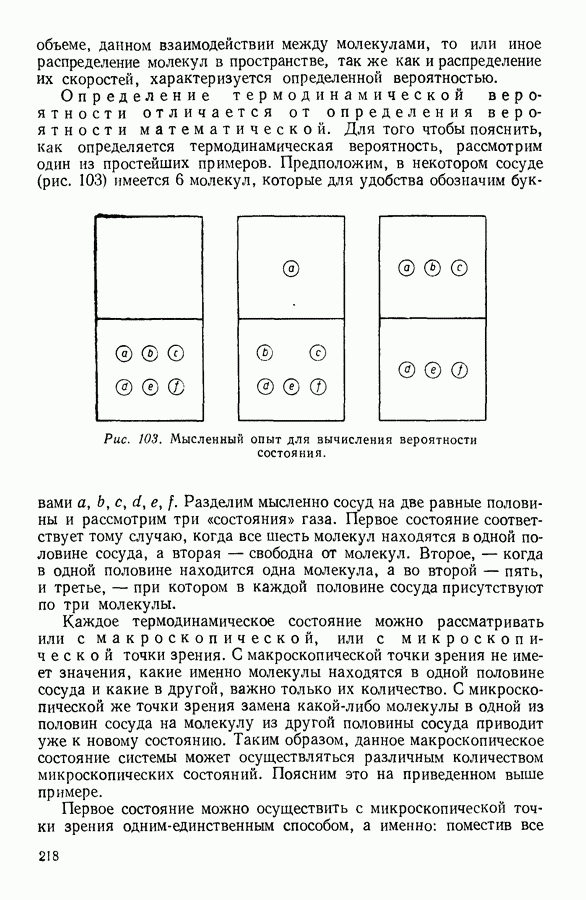
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»