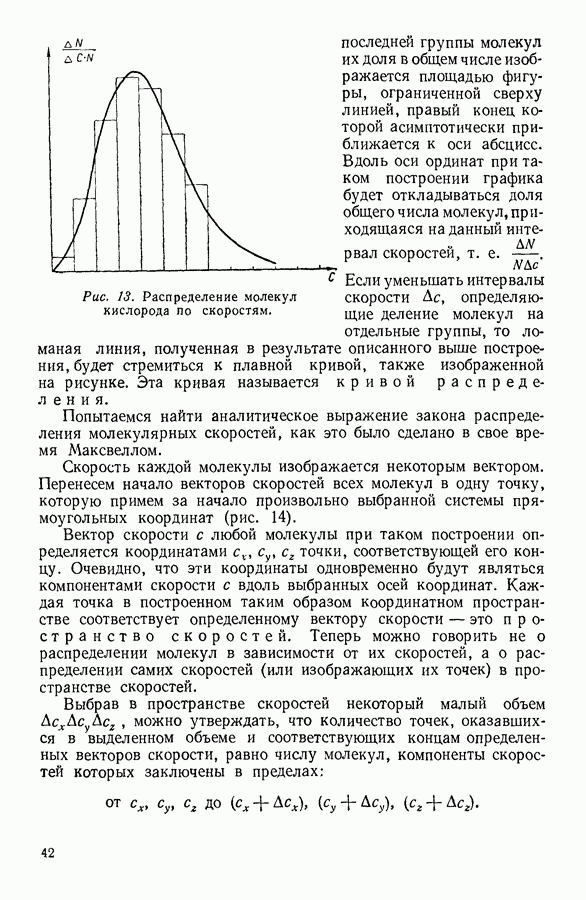
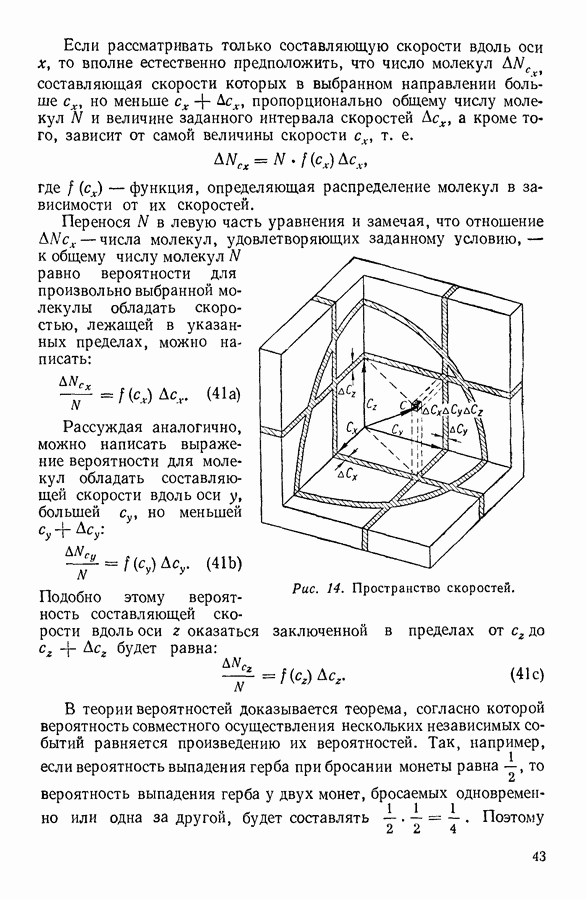
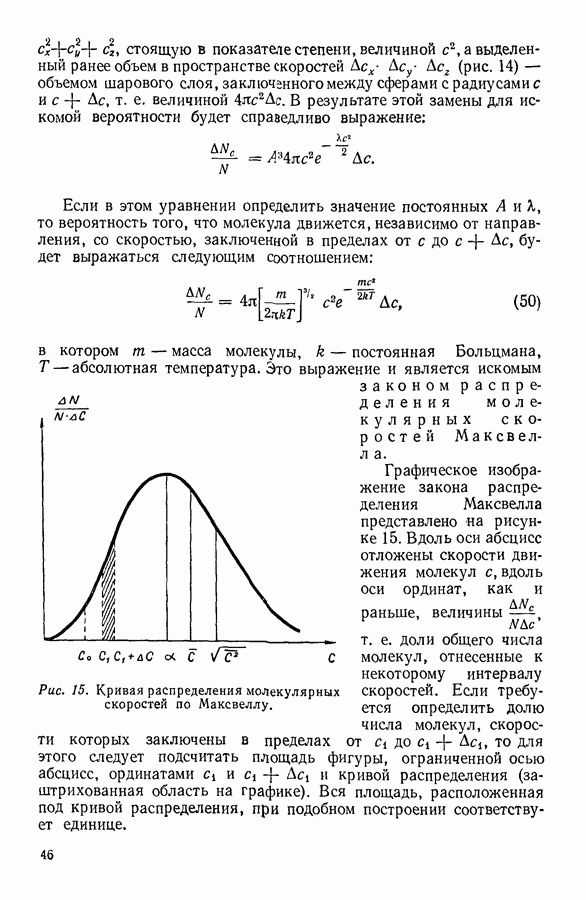
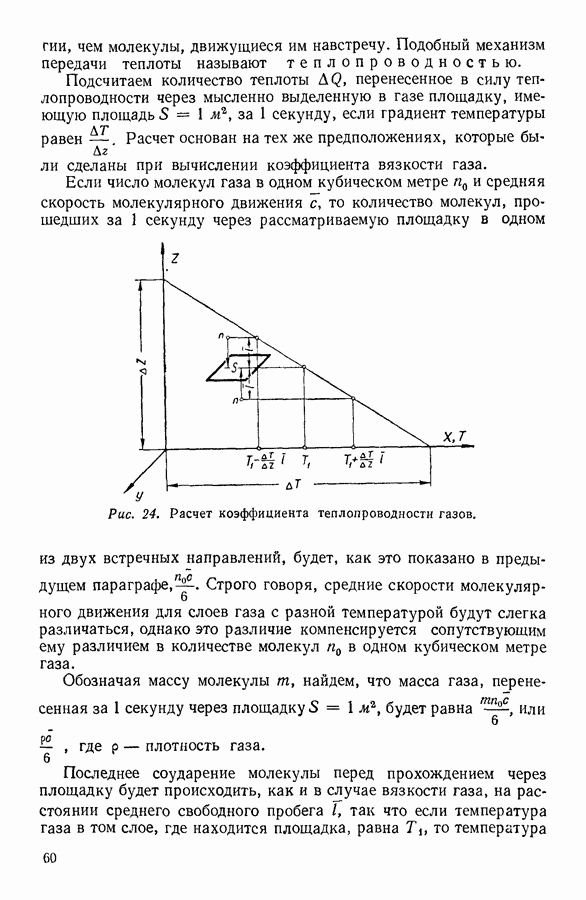
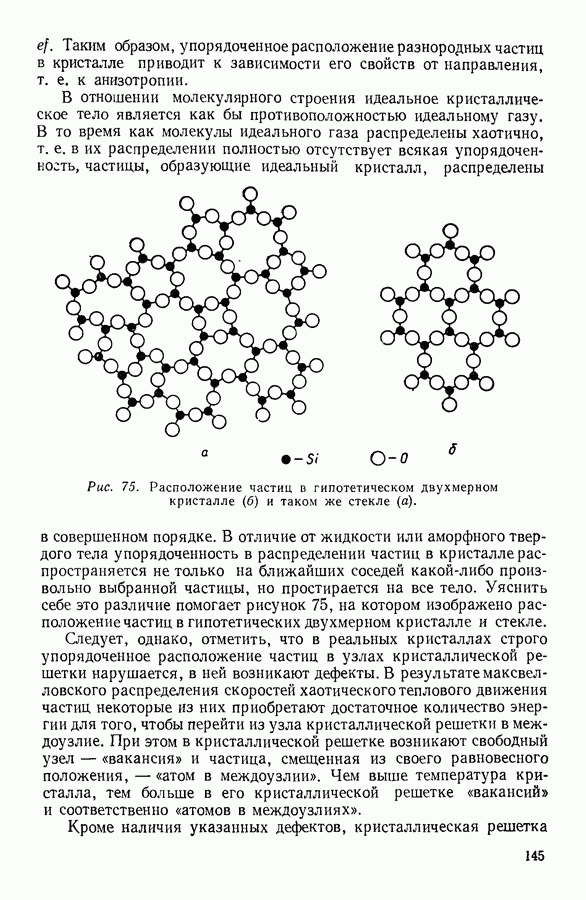
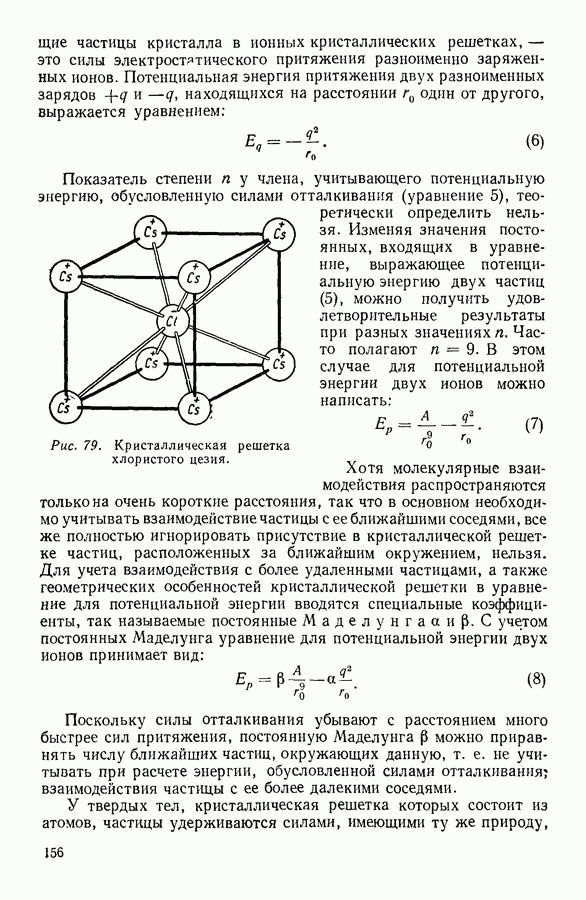
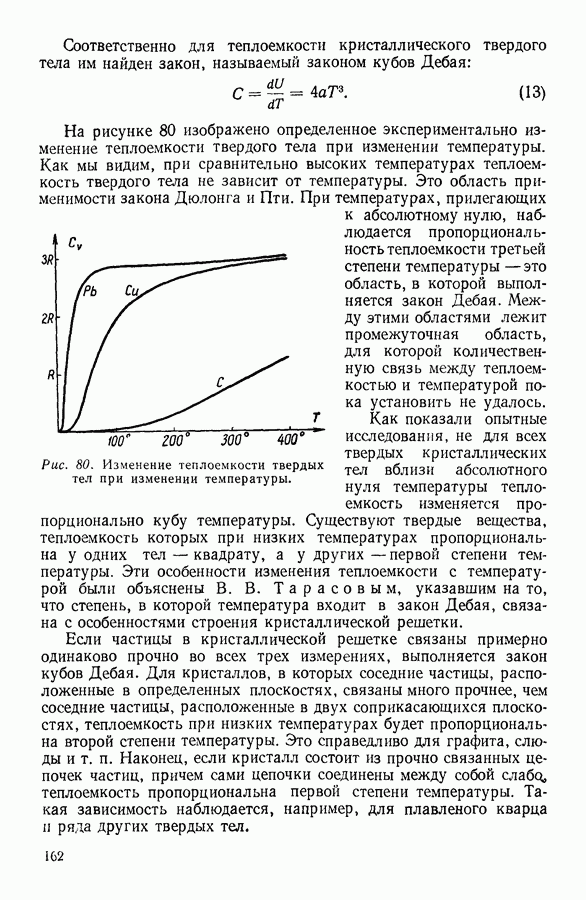
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
Натяжение, существующее в поверхностном слое, вызывает в том случае, если поверхность жидкости изогнута, возникновение давления, называемого лапласовским, поскольку Лаплас впервые обратил на него внимание.
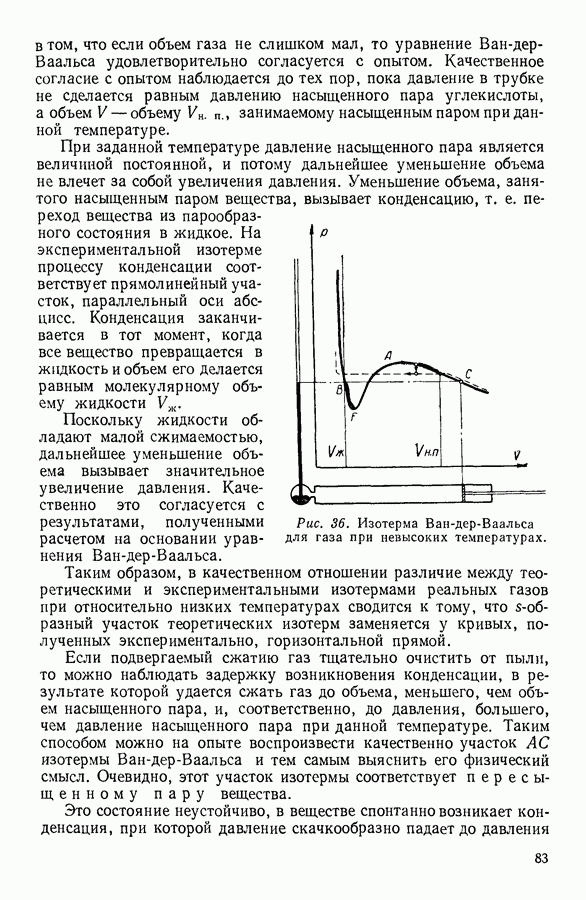
Лапласовское давление  как это ясно из рассмотрения рисунка 52, направлено внутрь жидкости, если поверхность жидкости выпуклая, и в сторону паровой фазы, если поверхность — вогнутая.
как это ясно из рассмотрения рисунка 52, направлено внутрь жидкости, если поверхность жидкости выпуклая, и в сторону паровой фазы, если поверхность — вогнутая.
С целью определения лапласовского давления подсчитаем работу, необходимую для дифференциально малого увеличения объема мыльного пузыря.
Свободная энергия  поверхности мыльного пузыря радиуса
поверхности мыльного пузыря радиуса  равна, согласно сказанному выше, произведению площади поверхности пузыря на коэффициент поверхностного натяжения а. Учитывая, что оболочка пузыря имеет две поверхности (внешнюю и внутреннюю) площадью по
равна, согласно сказанному выше, произведению площади поверхности пузыря на коэффициент поверхностного натяжения а. Учитывая, что оболочка пузыря имеет две поверхности (внешнюю и внутреннюю) площадью по  каждая, можно написать:
каждая, можно написать:


Рис. 52. Возникновение лапласовского давления.
Пленка мыльного пузыря оказывает давление  на заключенный в пузыре воздух, и поэтому при увеличении радиуса пузыря на элементарно малую величину
на заключенный в пузыре воздух, и поэтому при увеличении радиуса пузыря на элементарно малую величину  внешние силы должны совершить работу против этого давления, равную
внешние силы должны совершить работу против этого давления, равную  Эта работа затрачивается на увеличение свободной энергии
Эта работа затрачивается на увеличение свободной энергии  поверхности пузыря, которая возрастает при увеличении его радиуса.
поверхности пузыря, которая возрастает при увеличении его радиуса.
Приравнивая увеличение свободной энергии работе, совершенной внешними силами,  и подставляя вместо объема V его значение, равное для шара
и подставляя вместо объема V его значение, равное для шара  а вместо свободной энергии
а вместо свободной энергии  ее значение из уравнения (9), найдем:
ее значение из уравнения (9), найдем:

или

Если рассматривать не мыльный пузырь, а пузырек, возникший в толще жидкости, то, поскольку последний обладает только одной поверхностью, избыточное давление в нем будет в половину меньше подсчитанного, т. е.

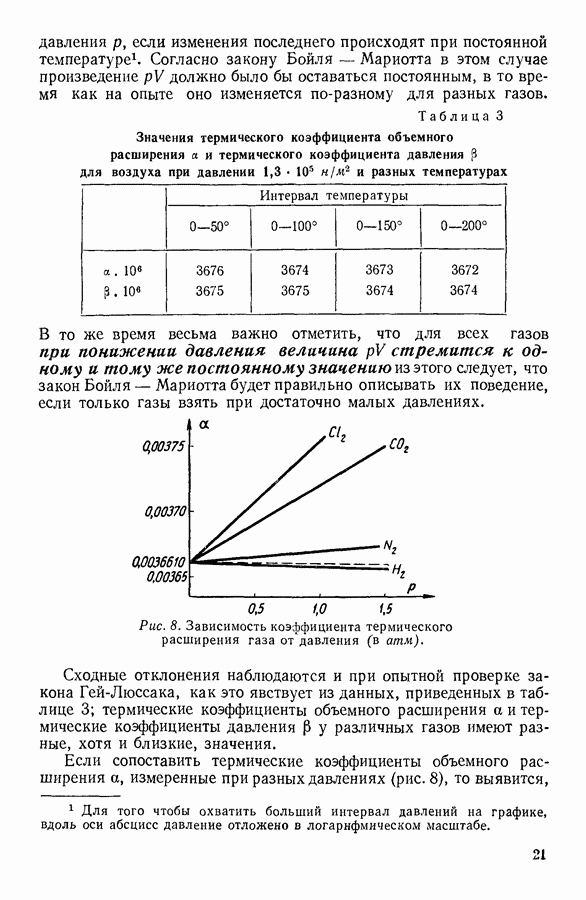
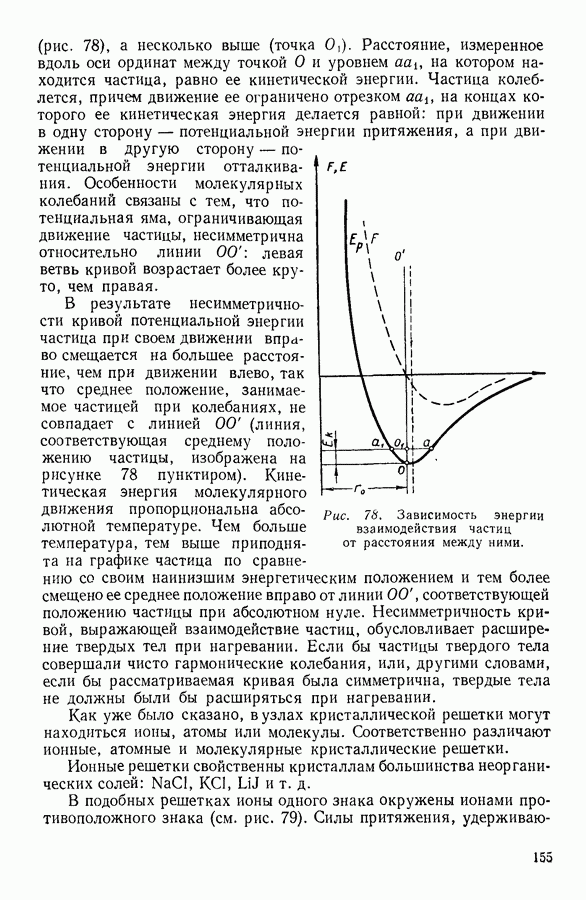
Полученные соотношения подтверждают, что лапласовское давление обусловлено кривизной поверхности. В случае плоской поверхности, для которой радиус кривизны бесконечно велик, лапласовское давление обращается в нуль. Следует обратить внимание также на то, что по мере увеличения радиуса пузырька лапласовское давление уменьшается, а не увеличивается, как это наблюдается в том случае, когда избыточное давление обусловлено упругостью пленки (резиновый мяч).
В пузырьках, размеры которых не очень малы, лапласовское давление незначительно по сравнению с атмосферным и его можно обычно не учитывать. При уменьшении же радиуса пузырька оно возрастает и может достигать очень больших величин. Так, например, в возникшем в воде пузырьке радиусом  лапласовское давление составит около
лапласовское давление составит около 
В технике приходится считаться с тем, что при различных процессах в жидкости могут возникать наполненные паром пузырьки. Это наблюдается при быстром движении жидкости в трубе, при распространении в ней интенсивных звуковых и ультразвуковых волн, при пропускании в жидкость через узкое сопло перегретого пара жидкости и т. п. Явления возникновения пузырьков в жидкости называют кавитацией, а пузырьки — кавитационными пузырьками. Кавитация возникает, в частности, при вращении гребных винтов кораблей.
Сжатие и полное исчезновение кавитационных пузырьков сопровождается возникновением огромных давлений, измеряемых тысячами атмосфер. Эти давления являются одной из причин своеобразных явлений, наблюдаемых при кавитации. Так, например, кавитация может вызывать разрушение гребных винтов кораблей, дробить большие молекулы органических соединений, вызывать химические превращения, свечение воды и т. д.
Если поверхность жидкости имеет кривизну, отличную от сферической, лапласовское давление может быть подсчитано при помощи уравнения:

в котором  радиусы кривизны двух произвольно проведенных взаимно перпендикулярных нормальных сечений.
радиусы кривизны двух произвольно проведенных взаимно перпендикулярных нормальных сечений.
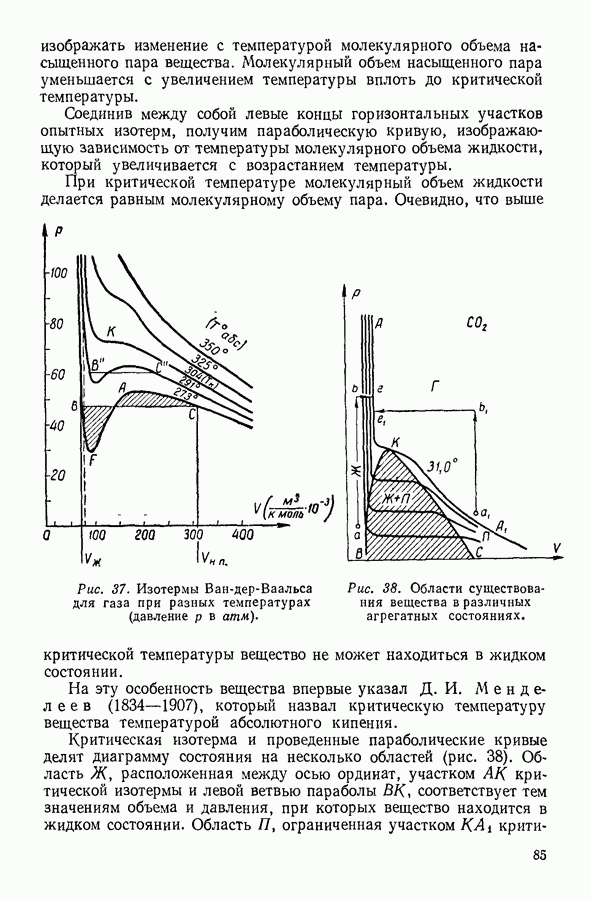
Для того чтобы уяснить значение последнего уравнения, подсчитаем лапласовское давление в жидкости, удерживающейся в силу капиллярности между двумя параллельными пластинками (рис. 53). Проведем два взаимно перпендикулярных нормальных сечения одно из которых проходит вдоль образующей цилиндрической поверхности жидкости. Поскольку радиус кривизны, соответствующий последнему сечению, бесконечно велик, то 

Рис. 53. Поведение жидкости, заключенной между двумя параллельными плоскими пластинками.
Очевидно, в рассматриваемом случае лапласовское давление будет равно:

В описанном опыте стремление поверхности жидкости к сокращению будет стягивать пластинки, если жидкость их смачивает, и расталкивать, если не смачивает.
Пример. Требуется определить давление, которое может расплющить каплю ртути весом  между тонкими стеклянными пластинками в лепешку радиусом 0,9 см. Плотность ртути
между тонкими стеклянными пластинками в лепешку радиусом 0,9 см. Плотность ртути  Поверхностное натяжение
Поверхностное натяжение 
Решение. Объем капли ртути

где  масса ртути.
масса ртути.
Площадь одного из оснований лепешки:

Расстояние между пластинами:

Радиус кривизны края ртутной лепешки:

Давление, необходимое для того чтобы расплющить ртутную капельку в лепешку:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
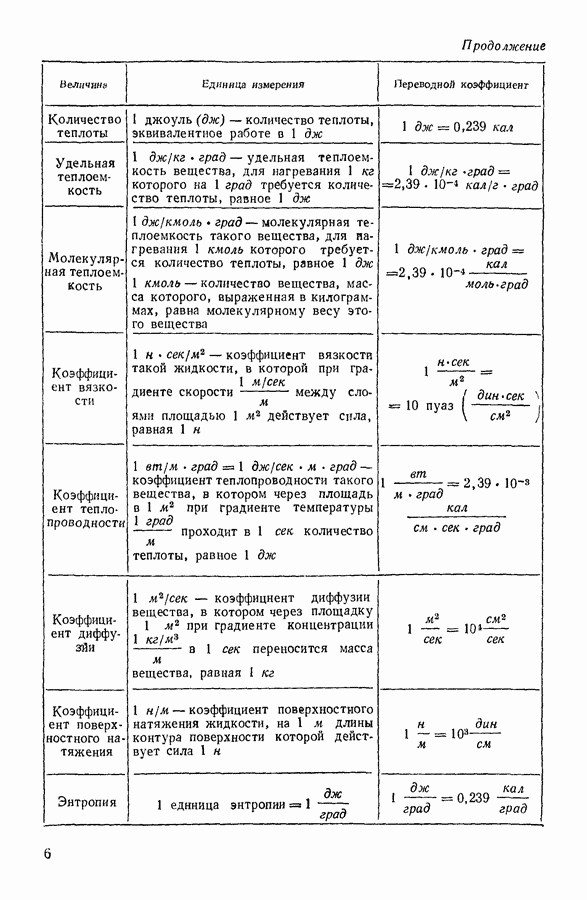
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
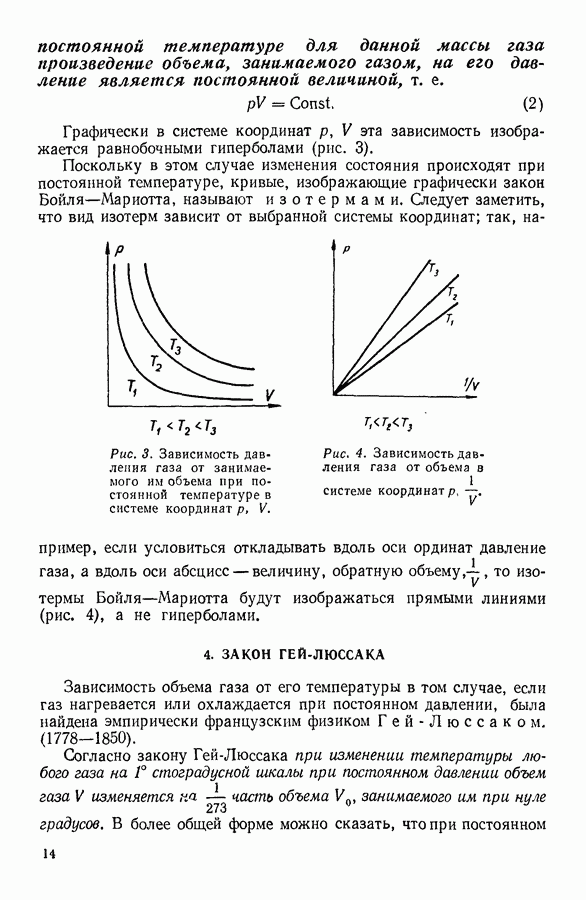
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
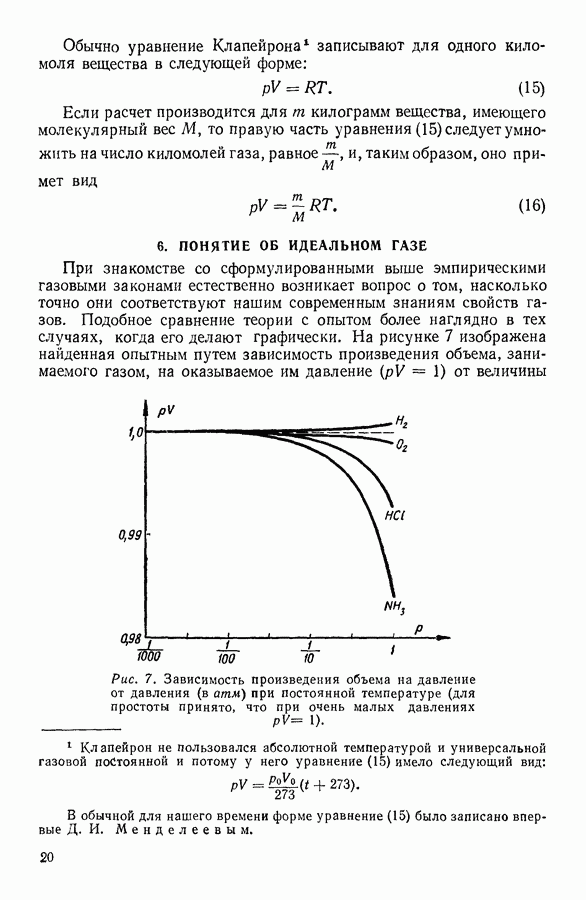
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
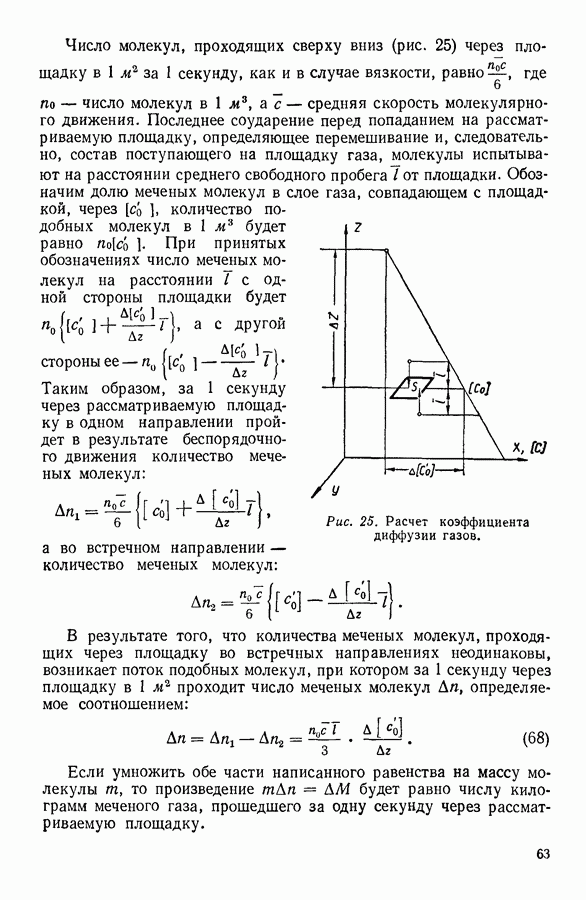
- 18. ДИФФУЗИЯ ГАЗОВ
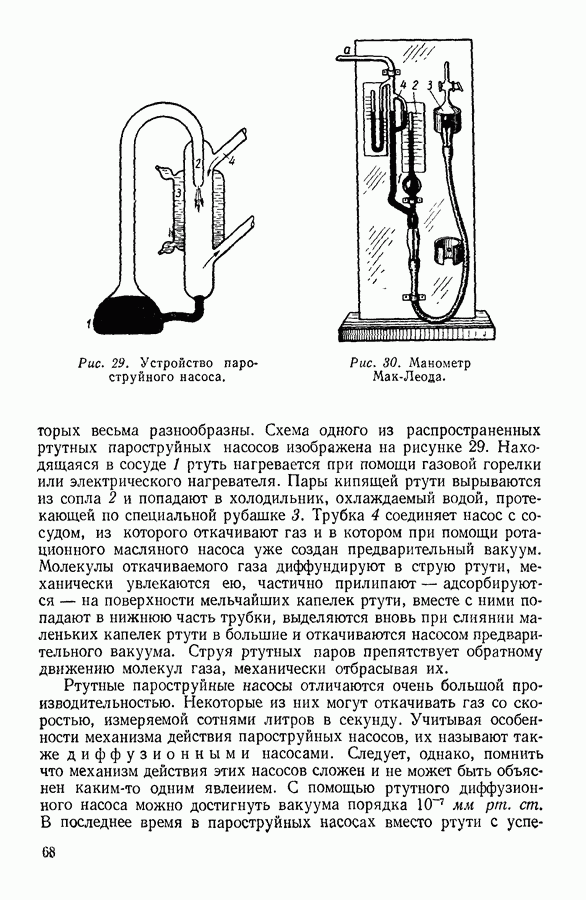
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
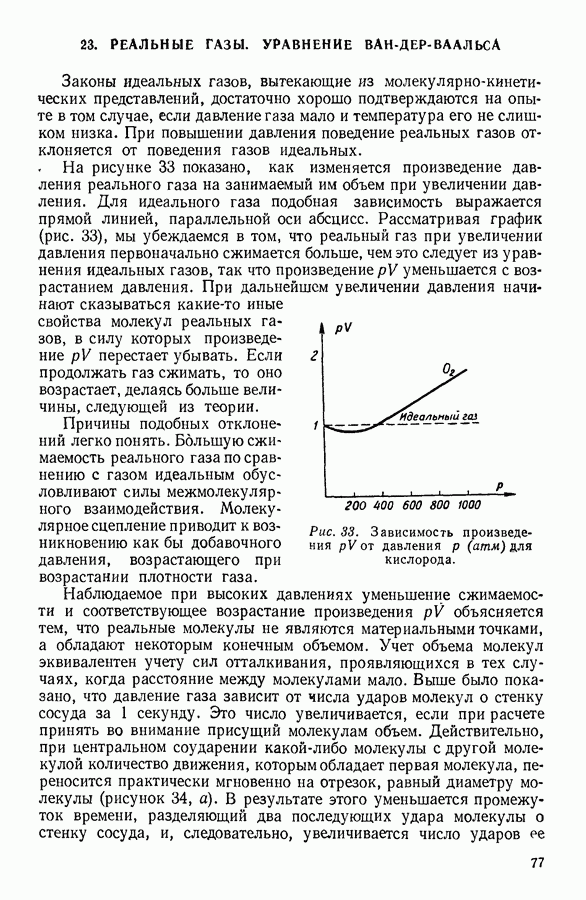
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
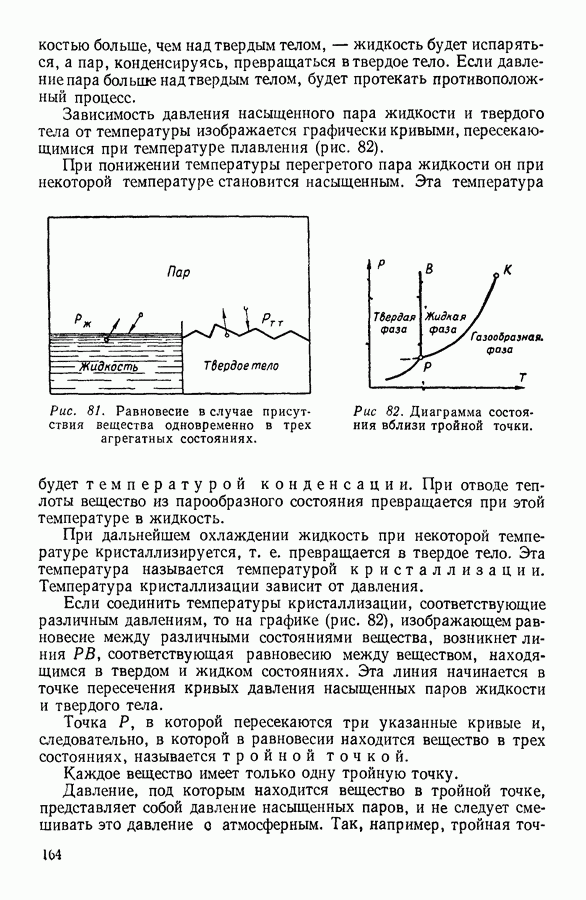
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
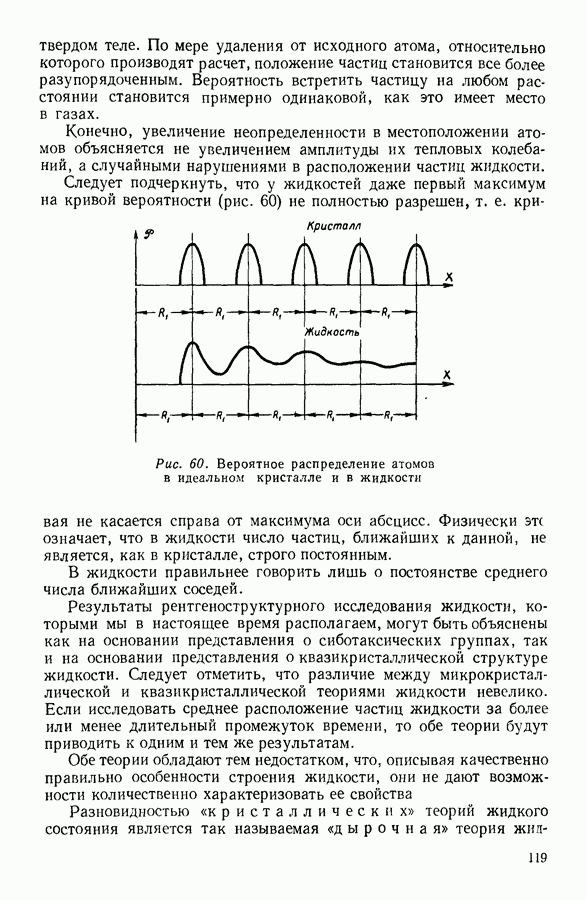
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
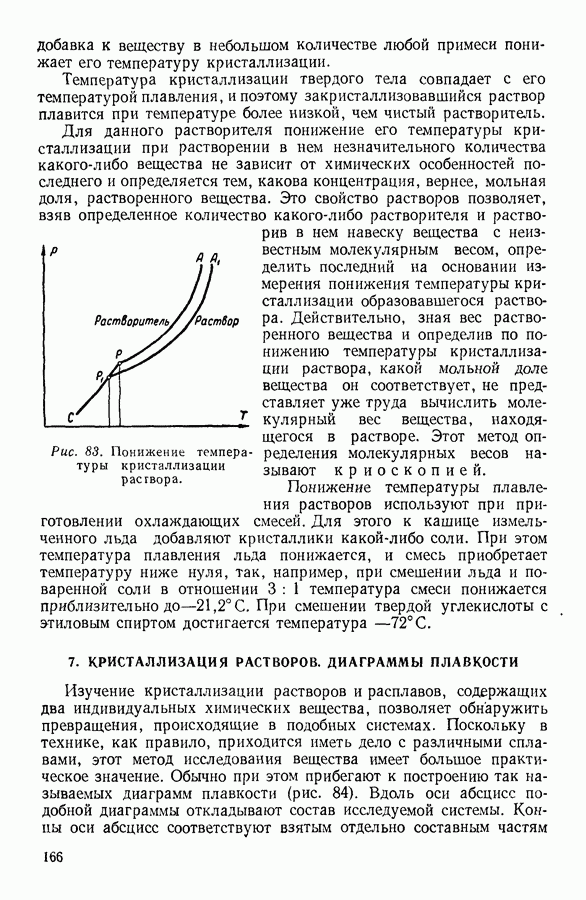
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
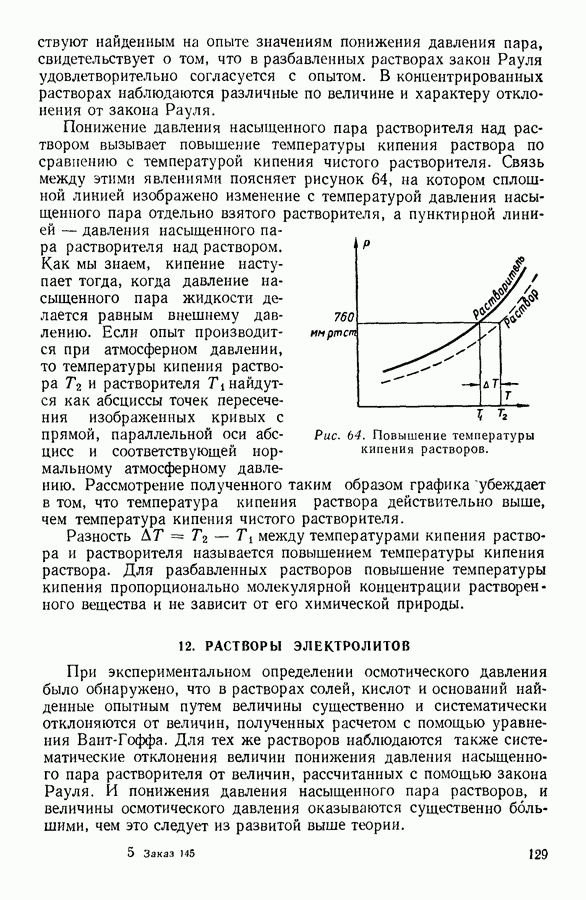
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
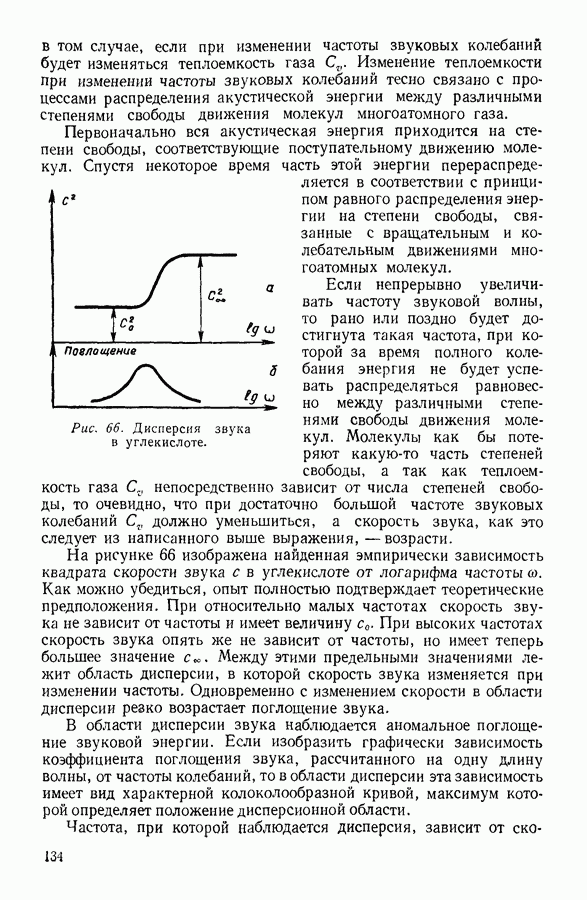
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
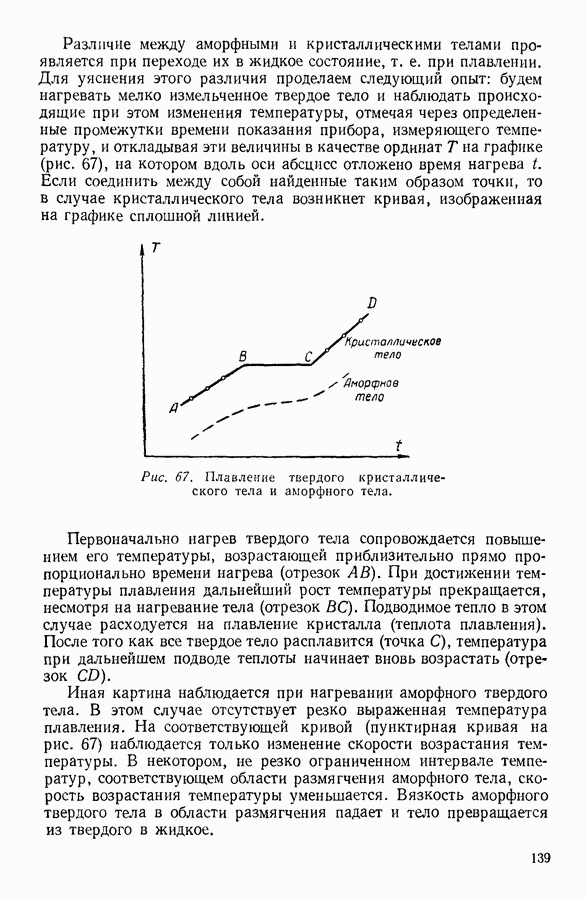
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
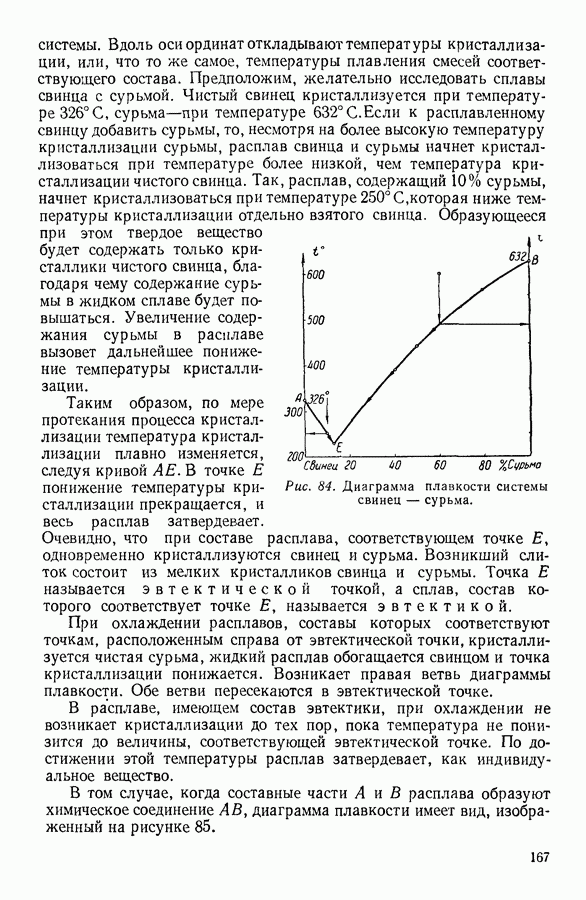
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
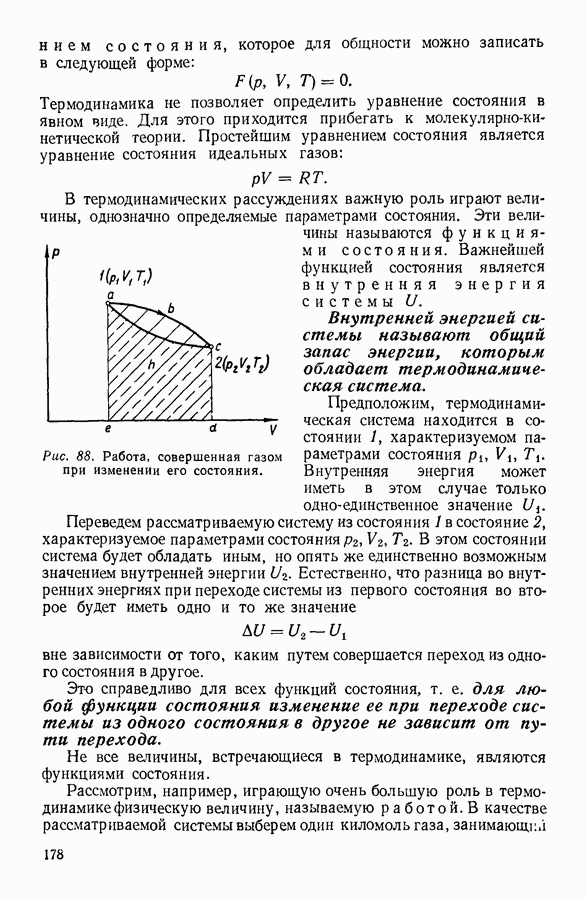
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
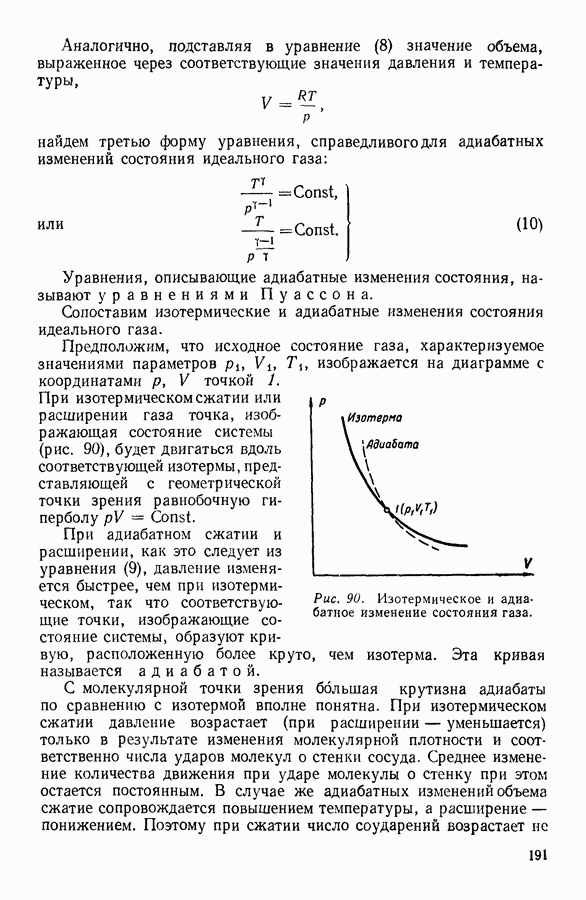
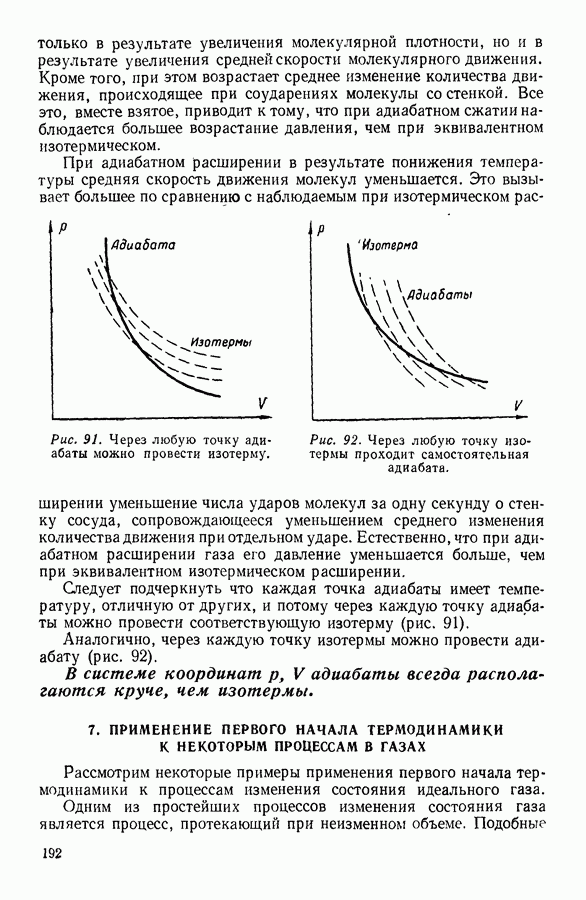
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
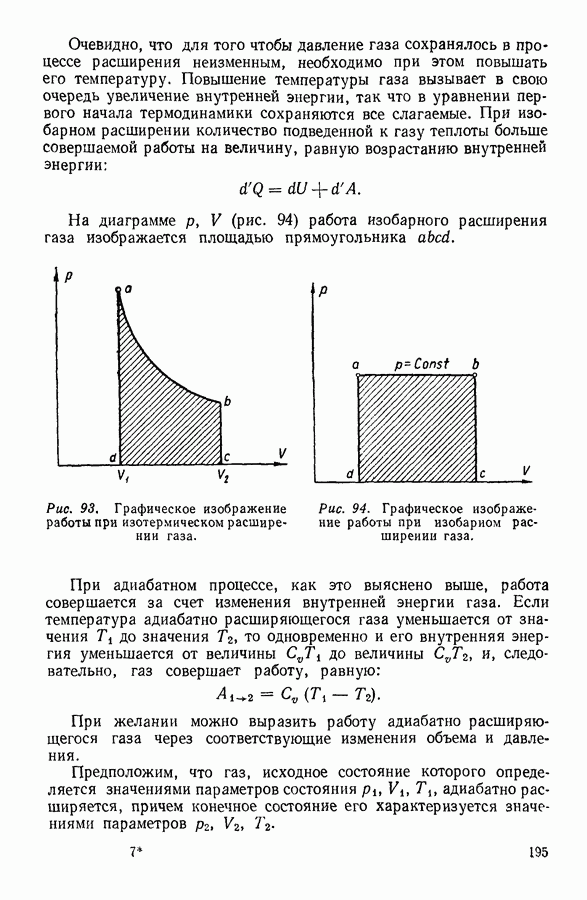
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
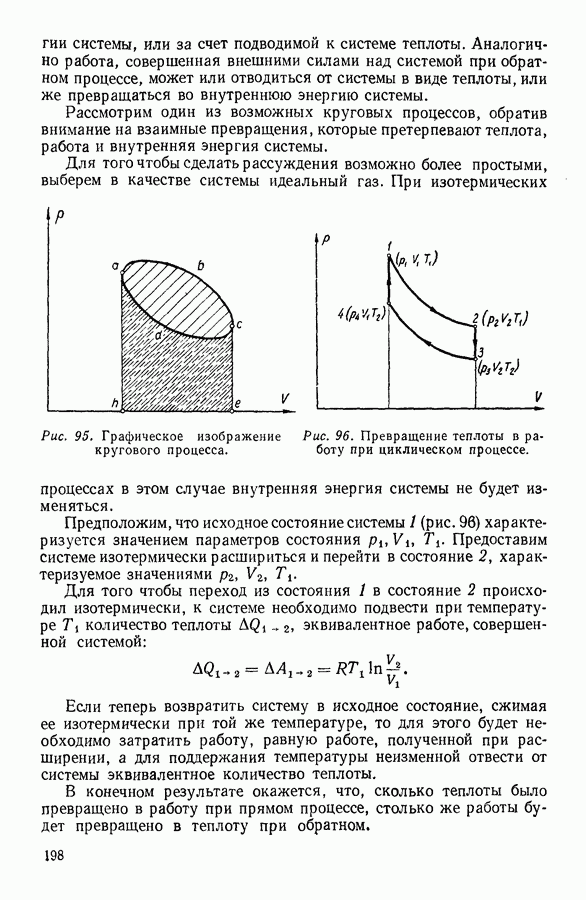
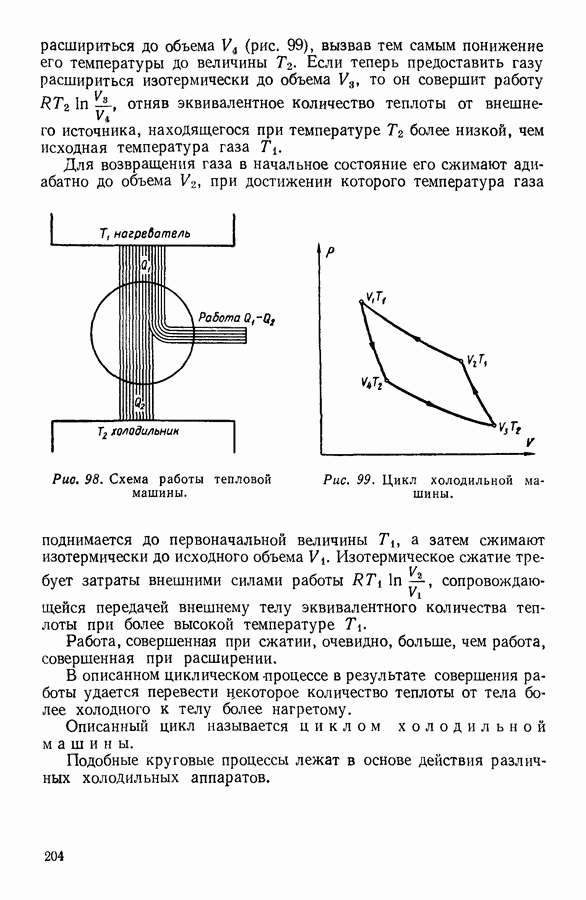
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
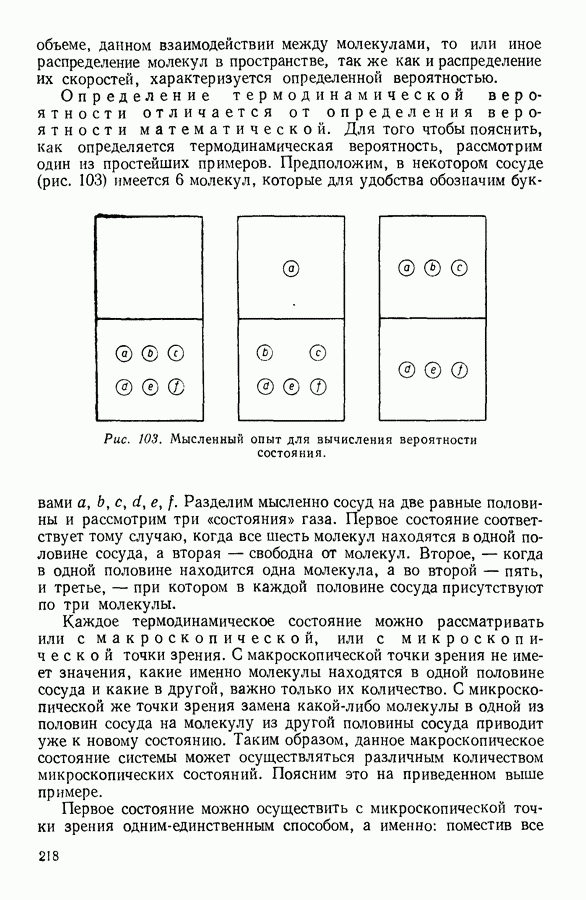
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»