| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
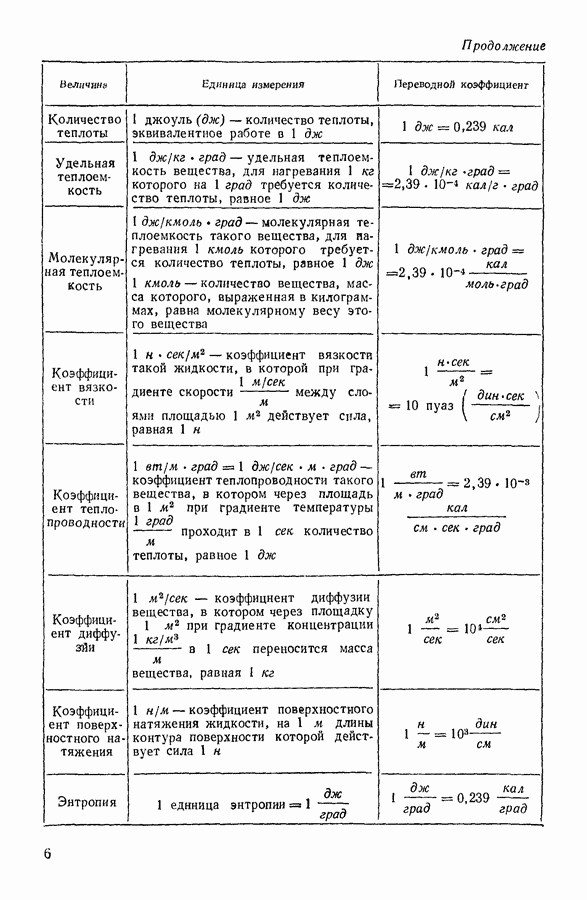
17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
При соприкосновении двух газов, имеющих разную температуру, газ с более высокой температурой охлаждается, а газ с более низкой температурой нагревается. Обычно основную роль в выравнивании температуры играет перемешивание газов, или конвекция, обусловленная возникновением в газе потоков, имеющих разную плотность.
Можно, однако, осуществить опыт таким образом, что в газе будет отсутствовать конвекция, но в то же время будет существовать постоянный градиент температуры, обусловливающий постоянный поток теплоты.
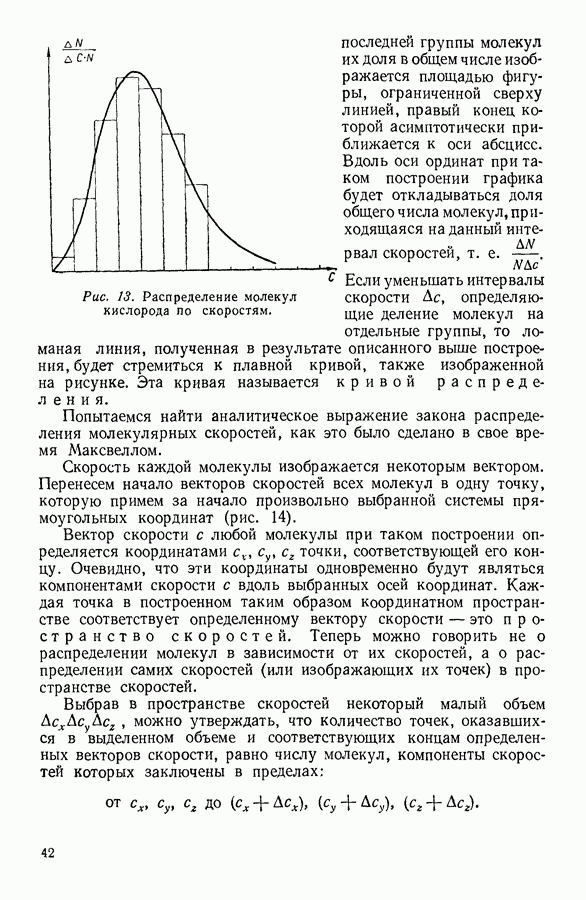
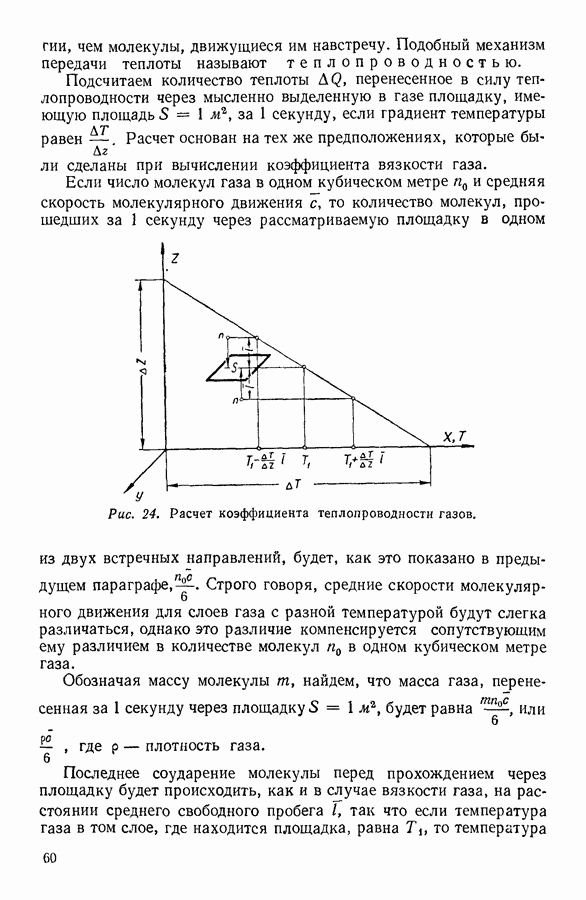
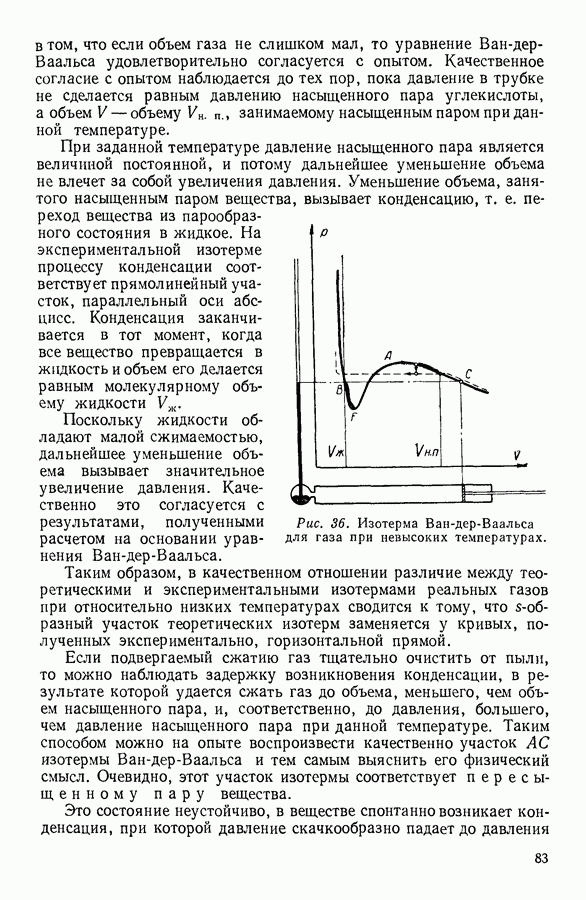
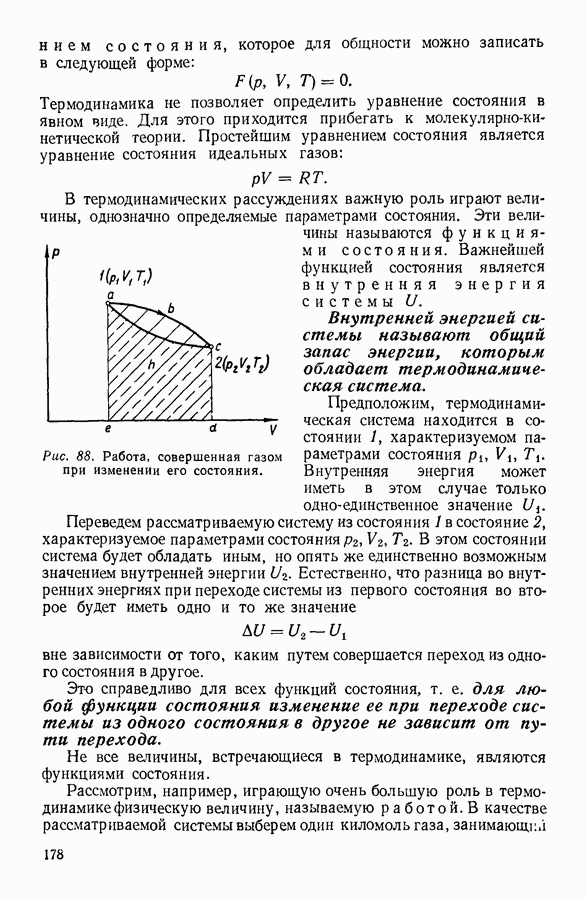
В этом случае перенос теплоты осуществляется в результате беспорядочного теплового движения молекул, которые, проходя через мысленно выделенную площадку 5 (рис. 24), переносят в одном направлении в среднем большее количество кинетической
энергии, чем молекулы, движущиеся им навстречу. Подобный механизм передачи теплоты называют теплопроводностью.
Подсчитаем количество теплоты  перенесенное в силу теплопроводности через мысленно выделенную в газе площадку, имеющую площадь
перенесенное в силу теплопроводности через мысленно выделенную в газе площадку, имеющую площадь  за 1 секунду, если градиент температуры равен
за 1 секунду, если градиент температуры равен  Расчет основан на тех же предположениях, которые были сделаны при вычислении коэффициента вязкости газа.
Расчет основан на тех же предположениях, которые были сделаны при вычислении коэффициента вязкости газа.
Если число молекул газа в одном кубическом метре  и средняя скорость молекулярного движения с, то количество молекул, прошедших за 1 секунду через рассматриваемую площадку в одном из двух встречных направлений, будет, как это показано в предыдущем параграфе,
и средняя скорость молекулярного движения с, то количество молекул, прошедших за 1 секунду через рассматриваемую площадку в одном из двух встречных направлений, будет, как это показано в предыдущем параграфе, 

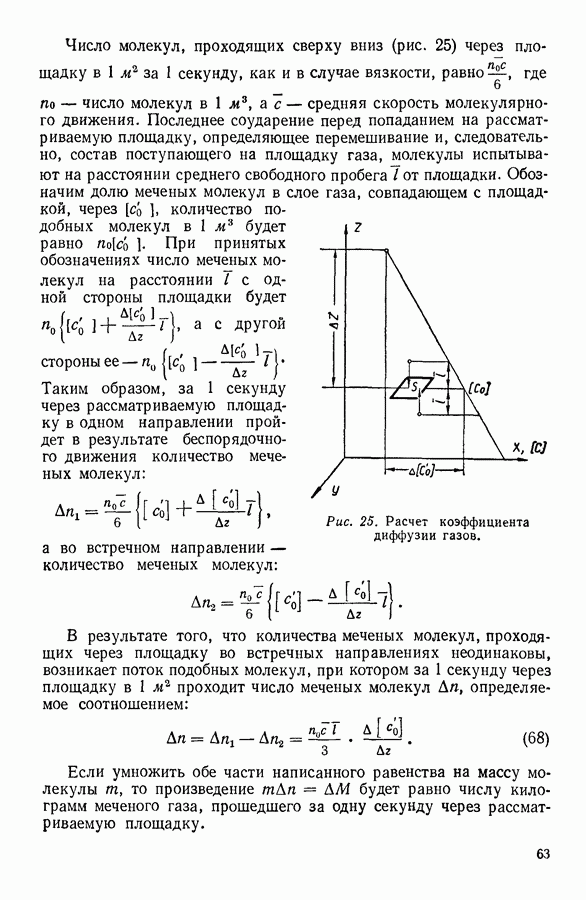
Рис. 24. Расчет коэффициента теплопроводности газов.
Строго говоря, средние скорости молекулярного движения для слоев газа с разной температурой будут слегка различаться, однако это различие компенсируется сопутствующим ему различием в количестве молекул  в одном кубическом метре газа.
в одном кубическом метре газа.
Обозначая массу молекулы  найдем, что масса газа, перенесенная за 1 секунду через площадку
найдем, что масса газа, перенесенная за 1 секунду через площадку  будет равна или
будет равна или  где
где  плотность газа.
плотность газа.
Последнее соударение молекулы перед прохождением через площадку будет происходить, как и в случае вязкости газа, на расстоянии среднего свободного пробега I, так что если температура газа в том слое, где находится площадка, равна  то температура
то температура
более нагретого газа, поступающего на площадку, будет  а более холодного газа
а более холодного газа 
Обозначив удельную теплоемкость газа  можно для количества теплоты
можно для количества теплоты  перенесенного в результате беспорядочного теплового движения молекул за 1 секунду через площадку
перенесенного в результате беспорядочного теплового движения молекул за 1 секунду через площадку  в одном направлении, написать выражение:
в одном направлении, написать выражение:

а для количества теплоты  перенесенного во встречном направлении, выражение:
перенесенного во встречном направлении, выражение:

Таким образом, в результате беспорядочного теплового движения молекул возникает непрерывный поток теплоты через рассматриваемую площадку. За 1 секунду через площадку  проходит количество теплоты
проходит количество теплоты  равное:
равное:

Еще до возникновения молекулярно-кинетической трактовки явления теплопроводности французский математик и физик Фурье (1768—1830) нашел, что количество теплоты, проходящее через площадку в  за 1 секунду, пропорционально градиенту температуры, т. е.
за 1 секунду, пропорционально градиенту температуры, т. е.

Коэффициент пропорциональности К называют коэффициентом теплопроводности. Сравнивая уравнения (65) и (66), можно расшифровать значение коэффициента теплопроводности газа

Коэффициент теплопроводности связан простой зависимостью с коэффициентом вязкости. Из уравнений (64) и (67) следует, что

В такой простой форме это соотношение плохо согласуется с опытом. Однако более строгие рассуждения показывают, что выводы молекулярно-кинетической теории правильно описывают наблюдаемое соотношение коэффициентов вязкости и теплопроводности.
Анализ уравнения (67) приводит к заключению, что коэффициент теплопроводности газа не должен зависеть от давления. Экспериментальная проверка подтверждает этот вывод. Коэффициент теплопроводности сохраняет постоянное значение вплоть до весьма малых давлений, при которых уже основные положения теории оказываются неприменимыми, и величина К начинает изменяться при изменении давления.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
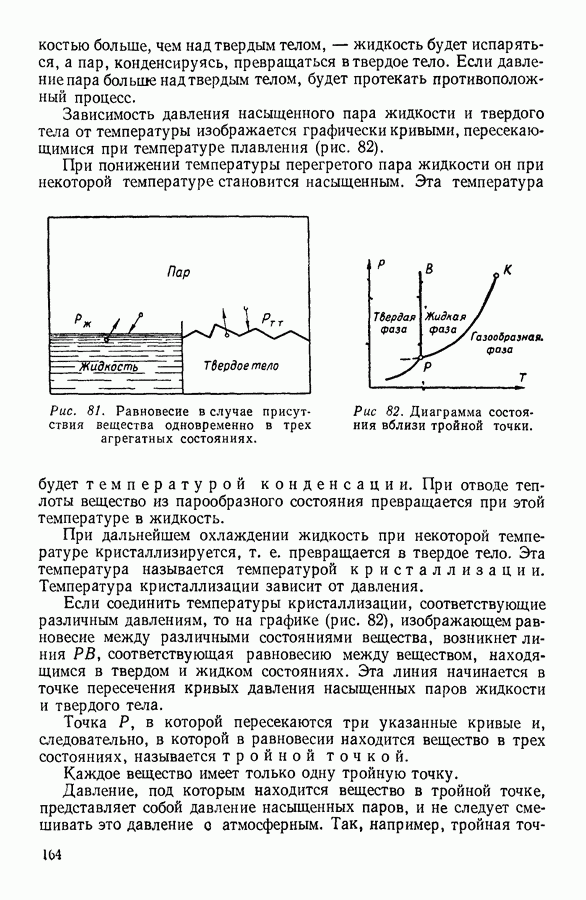
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
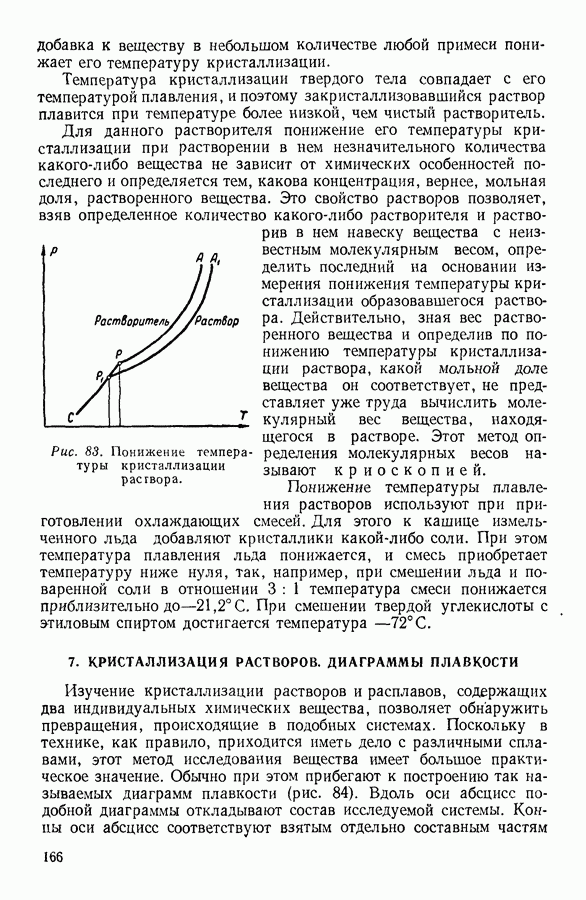
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
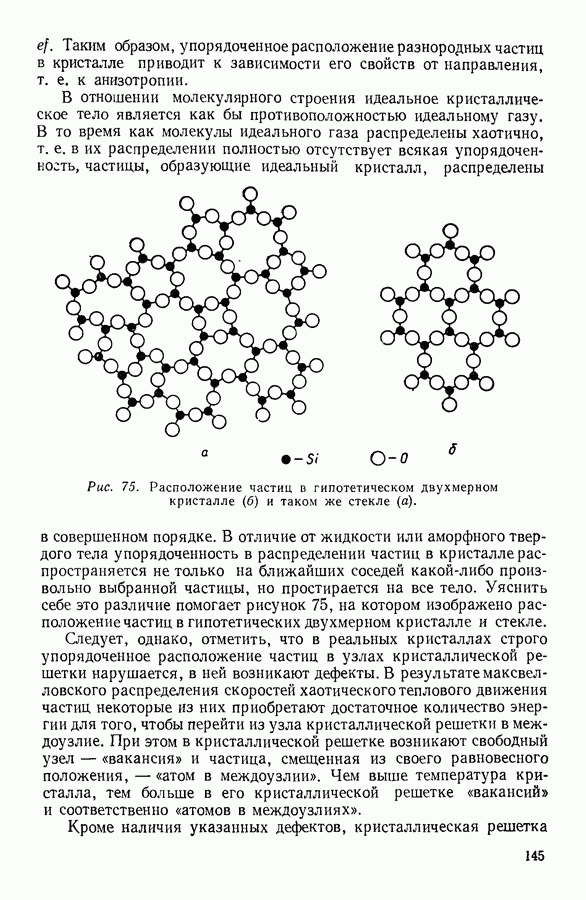
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
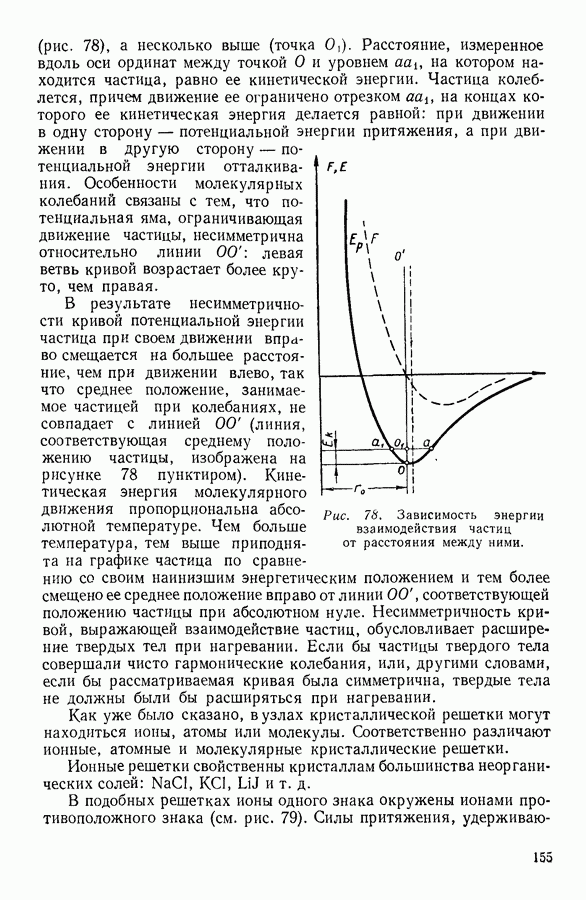
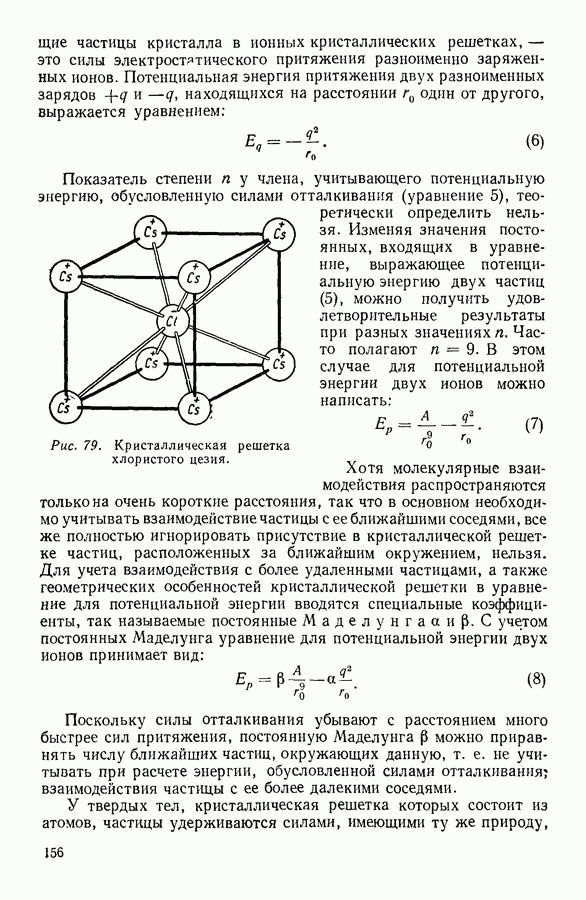
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
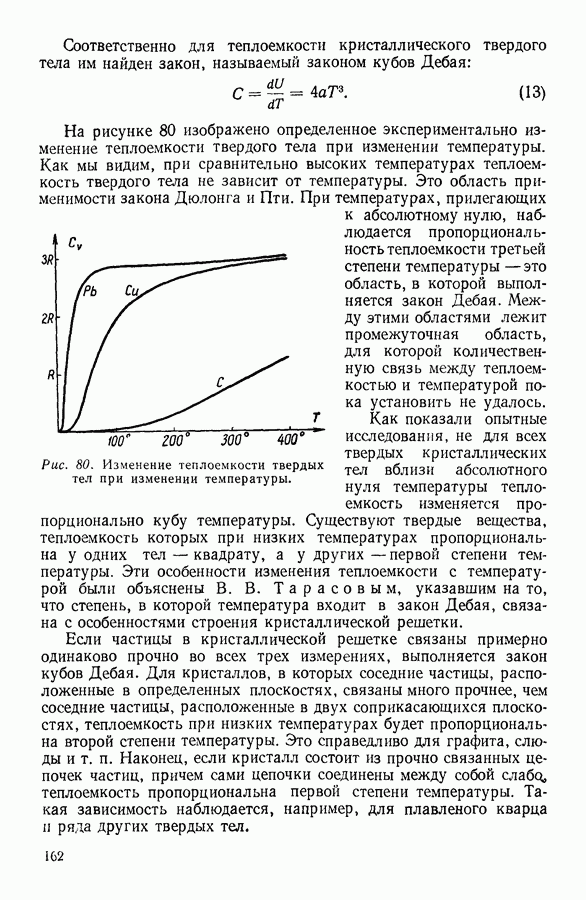
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
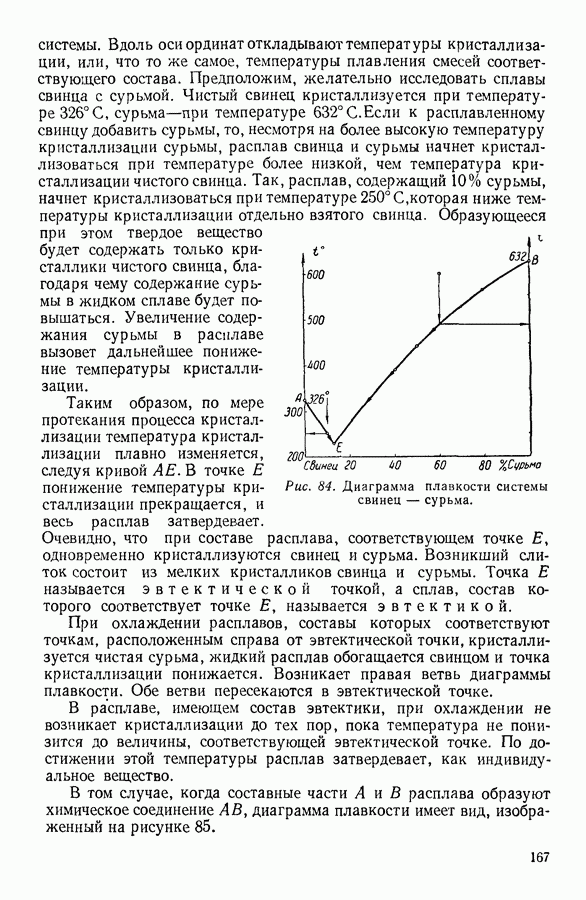
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»