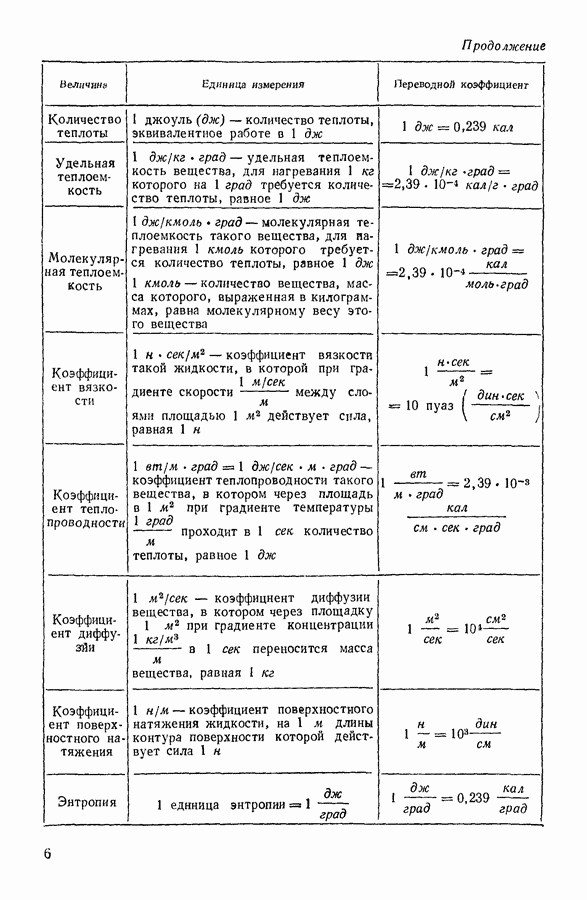
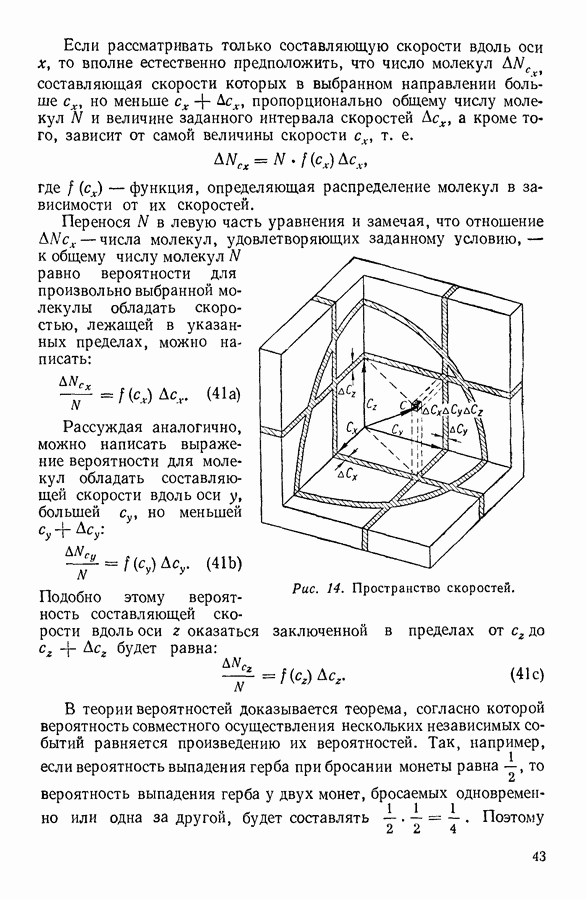
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
Как уже указывалось выше, коэффициент полезного действия цикла Карно имеет одно и то же значение для любого вещества и зависит только от температур, при которых осуществляются изотермические расширение и сжатие. Больше того, при изменениях параметров состояния, т. е. давления, объема и температуры, в цикле Карно может происходить изменение агрегатного состояния вещества, например испарение жидкости или конденсация пара, и все же коэффициент полезного действия будет определяться уравнением (14), полученным в предыдущем параграфе.
Эта особенность цикла Карно позволяет использовать его Для нахождения важных термодинамических соотношений.
В качестве примера получим этим способом уравнение Клапейрона — Клаузиуса, устанавливающее связь между давлением насыщенного пара жидкости и температурой.

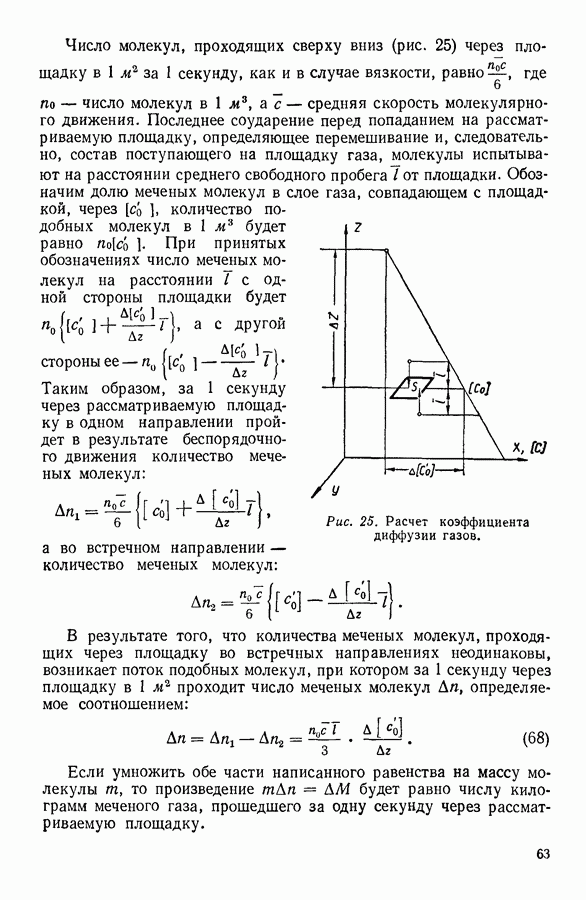
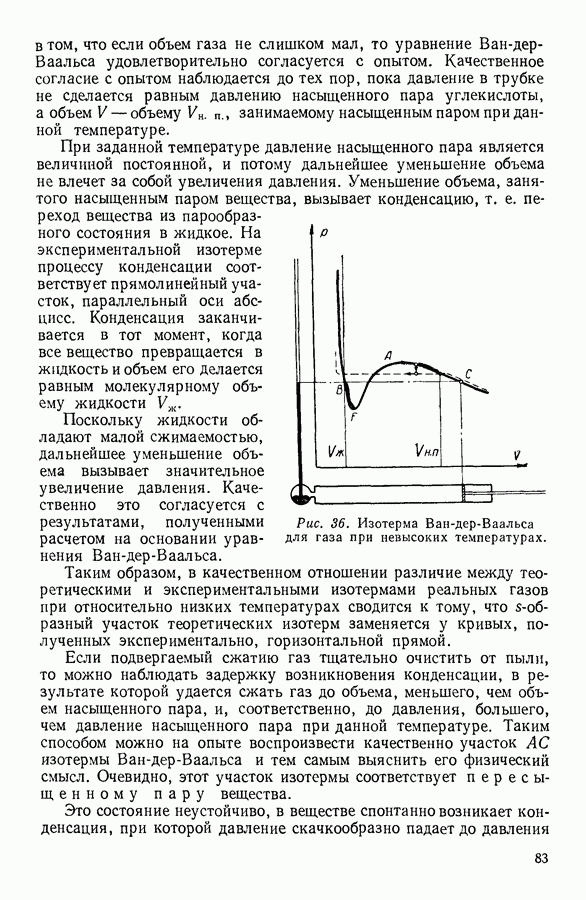
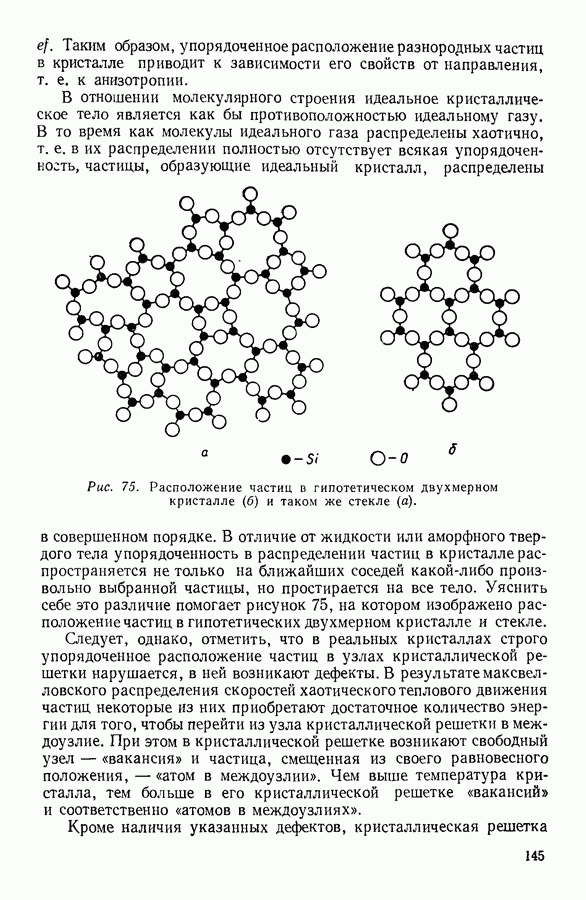
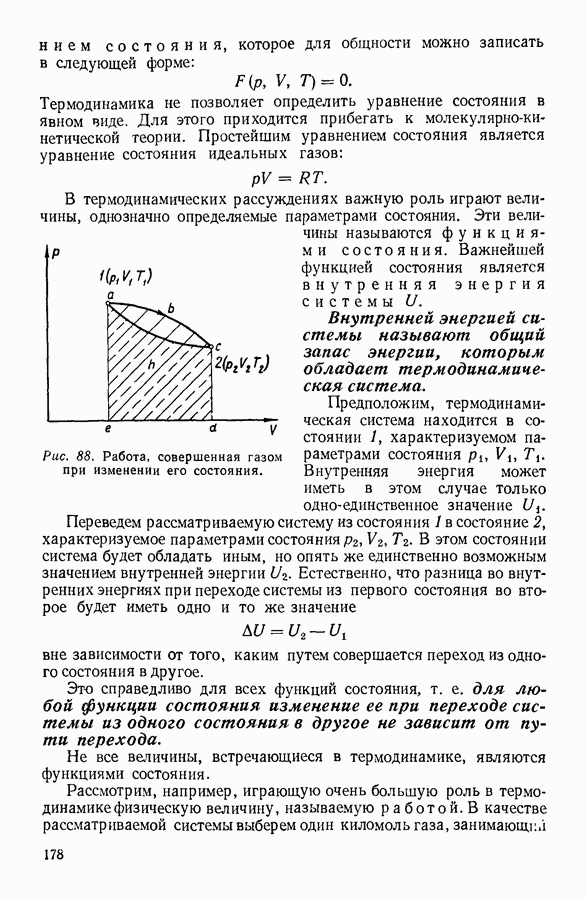
Рис. 100. К выводу уравнения Клапейрона — Клаузиуса методом циклов.
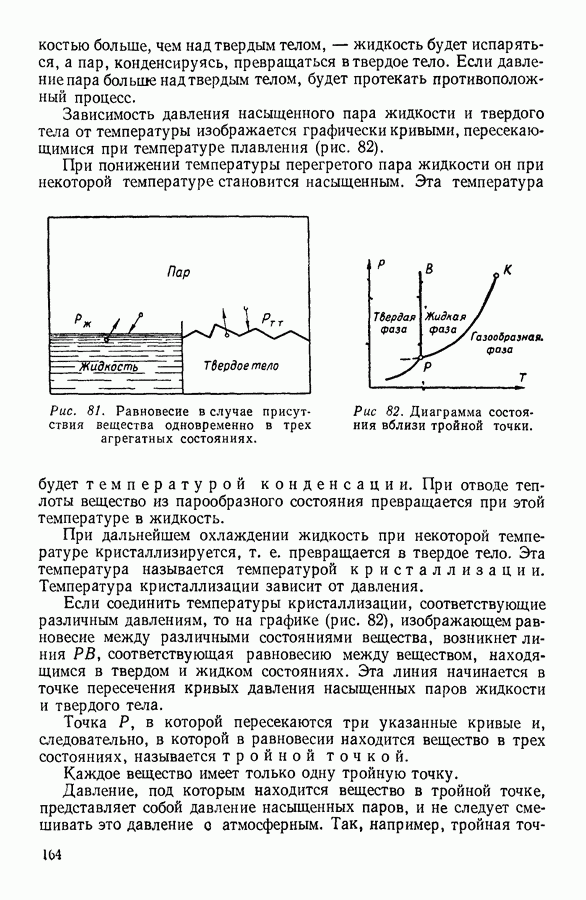
Пусть рассматриваемая система состоит из жидкости, находящейся при температуре  в равновесии с собственным паром, давление которого при этой температуре
в равновесии с собственным паром, давление которого при этой температуре 
Обозначим молекулярный объем жидкости при температуре  через Уж, а молекулярный объем пара —
через Уж, а молекулярный объем пара — 
На диаграмме  (рис. 100) начальное состояние системы изображается точкой а. Предоставим системе возможность изотермически расшириться и перейти в состояние, изображенное на диаграмме точкой
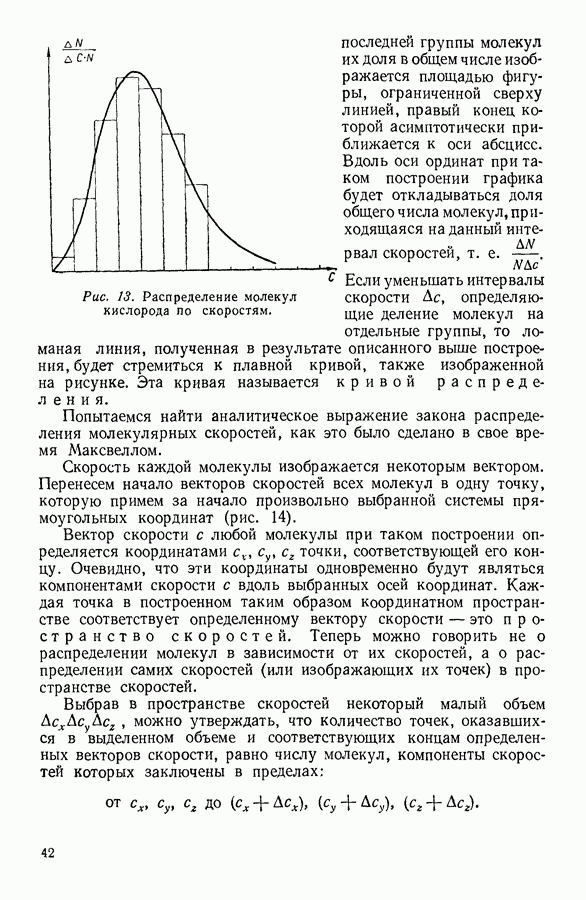
(рис. 100) начальное состояние системы изображается точкой а. Предоставим системе возможность изотермически расшириться и перейти в состояние, изображенное на диаграмме точкой  Поскольку система состоит из жидкости, находящейся в равновесии с собственным паром, изотермическое расширение происходит при постоянном давлении
Поскольку система состоит из жидкости, находящейся в равновесии с собственным паром, изотермическое расширение происходит при постоянном давлении  и сопровождается испарением
и сопровождается испарением  киломолей жидкости.
киломолей жидкости.
В жидком состоянии  киломолей вещества занимают объем
киломолей вещества занимают объем  а в виде насыщенного пара они занимают объем
а в виде насыщенного пара они занимают объем  В результате возрастание объема при переходе системы из точки а в точку
В результате возрастание объема при переходе системы из точки а в точку  составит
составит  Уж).
Уж).
Для того чтобы испарение жидкости происходило изотермически, к системе необходимо подвести количество теплоты, равное произведению числа киломолей испаряющейся жидкости  на молекулярную теплоту испарения X, т. е.
на молекулярную теплоту испарения X, т. е. 
Из состояния, соответствующего точке  система переводится адцабатно, в результате дифференциально малого увеличения объема, в состояние, соответствующее точке с, где температура на величину
система переводится адцабатно, в результате дифференциально малого увеличения объема, в состояние, соответствующее точке с, где температура на величину  меньше исходной. Давление насыщенного пара уменьшается соответственно на величину
меньше исходной. Давление насыщенного пара уменьшается соответственно на величину 
Уменьшая объем, систему изотермически переводят из состояния с в состояние, соответствующее точке  которое определяется тем условием, чтобы адиабатное сжатие системы до исходного объема сопровождалось подъемом температуры до первоначального значения
которое определяется тем условием, чтобы адиабатное сжатие системы до исходного объема сопровождалось подъемом температуры до первоначального значения 
Изотермическое сжатие  происходит при постоянном давлении, т. е. изобарно, и сопровождается конденсацией некоторого количества пара.
происходит при постоянном давлении, т. е. изобарно, и сопровождается конденсацией некоторого количества пара.
Выражение для коэффициента полезного действия рассматриваемого дифференциального цикла Карно можно записать в виде соотношения:

в котором  соответствует количеству теплоты, превращенному в результате циклического изменения состояния системы в работу, а произведение
соответствует количеству теплоты, превращенному в результате циклического изменения состояния системы в работу, а произведение  количеству теплоты, подведенному к системе при изотермическом расширении. Графически (рис. 100) работа
количеству теплоты, подведенному к системе при изотермическом расширении. Графически (рис. 100) работа  изображается площадью фигуры
изображается площадью фигуры  равной произведению одного из оснований
равной произведению одного из оснований  или
или  на высоту, которая, как это ясно из графика, определяется изменением давления насыщенного пара
на высоту, которая, как это ясно из графика, определяется изменением давления насыщенного пара 
Поскольку основание рассматриваемой фигуры  равно разности объемов, занимаемых
равно разности объемов, занимаемых  киломолями вещества в жидком и парообразном состояниях, т. е.
киломолями вещества в жидком и парообразном состояниях, т. е.  , то для работы, совершенной веществом в течение описанного цикла, будет справедливо выражение:
, то для работы, совершенной веществом в течение описанного цикла, будет справедливо выражение:

Воспользовавшись полученным выражением, можно записать коэффициент полезного действия рассматриваемого циклического процесса в форме следующего соотношения:

или, преобразуя его в более обычную форму, получим:

Последнее соотношение и называют уравнением Клапейрона— Клаузиуса.
Воспользовавшись уравнением Клапейрона-Клаузиуса, удобно сравнить термодинамический и молекулярно-кинетический методы решения одной из физико-химических проблем.
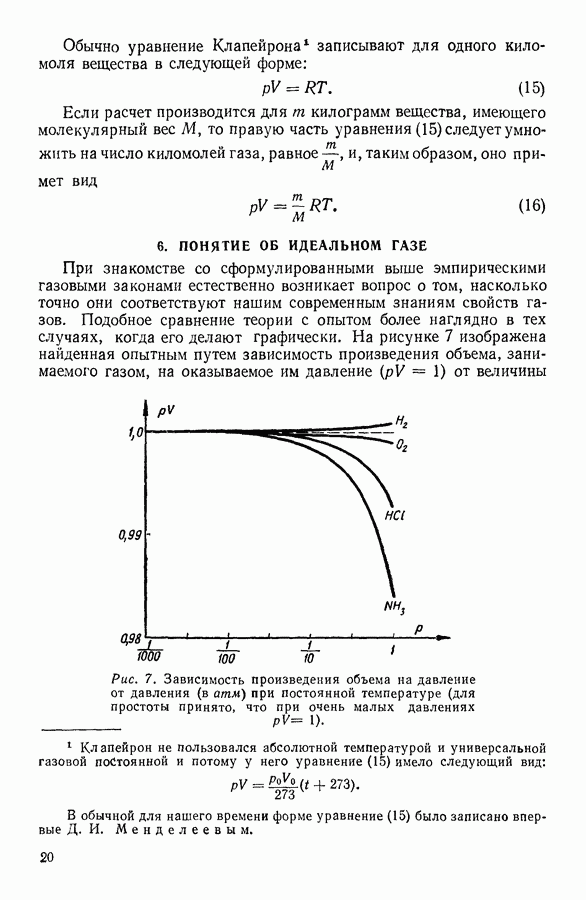
Предположим, требуется найти зависимость между упругостью насыщенного пара жидкости и температурой. В дифференциальной форме эта зависимость дается совершенно строго уравнением Клапейрона-Клаузиуса, однако в такой форме это уравнение не удобно для практического применения. Интегрирование полученного уравнения связано, как это сделается ясным ниже, с целым рядом приближенно верных предположений.
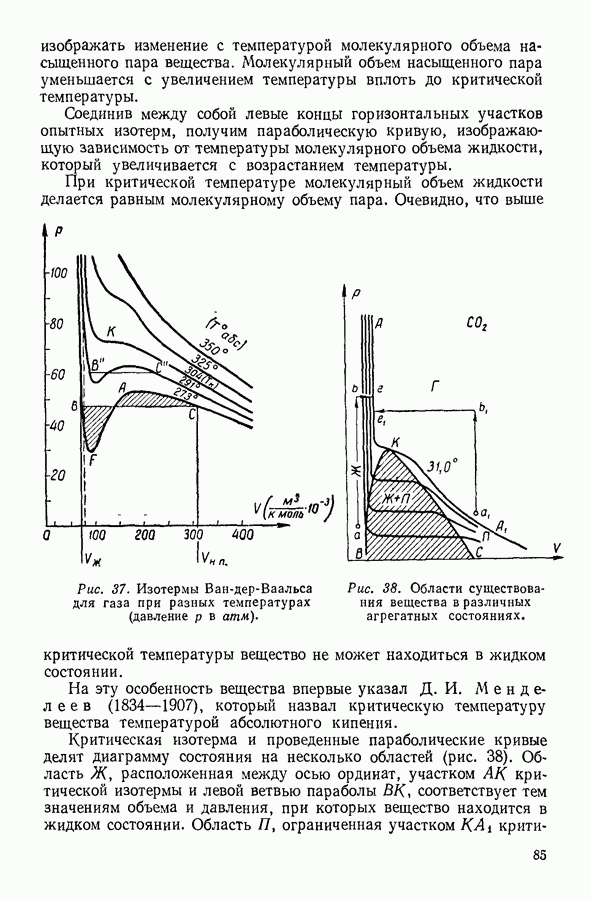
При температурах, далеких от критической, молекулярный объем жидкости  много меньше молекулярного объема насыщенного пара
много меньше молекулярного объема насыщенного пара  поэтому в разности, стоящей в правой части уравнения (15), молекулярным объемом жидкости можно пренебречь и записать уравнение Клапейрона — Клаузиуса в форме:
поэтому в разности, стоящей в правой части уравнения (15), молекулярным объемом жидкости можно пренебречь и записать уравнение Клапейрона — Клаузиуса в форме:

Если теперь предположить, что при небольших давлениях свойства насыщенного пара подобны свойствам идеального газа и для величины молекулярного объема пара  справедливо выражение:
справедливо выражение:

то уравнение Клапейрона-Клаузиуса примет вид:

или

Предположив далее, что теплота испарения X не зависит от температуры, можно проинтегрировать написанное уравнение и найти для давления насыщенного пара следующее соотношение:

или

где А — постоянная.
Но, как показывает опыт, теплота испарения зависит от температуры. Это является одной из причин плохого согласия с опытом уравнения (17). Приняв в качестве первого приближения, что теплота испарения линейно убывает с температурой:

где а — постоянная величина, и подставив это значение X в уравнение (16), найдем:

Интегрирование последнего уравнения приводит к зависимости давления насыщенного пара от температуры, лучше согласующейся с опытом, а именно:

Здесь  постоянные, значения которых находятся из опыта.
постоянные, значения которых находятся из опыта.
Отказываясь от сделанных выше приближенно верных предположений, можно получить более строгие и одновременно более сложные решения данной физико-химической задачи.
Ту же проблему можно решить молекулярно-кинетическим методом. Для этой цели будем считать, что средние скорости движения молекул жидкости и пара одинаковы, а следовательно, одинаковы и средние кинетические энергии молекул жидкости и находящегося с ней в равновесии пара.
Поскольку переход жидкости в пар требует затраты энергии в форме теплоты, называемой теплотой испарения, то очевидно, что потенциальные энергии молекул вещества в жидком и парообразном состоянии различаются между собой. Разница в потенциальной энергии  молекул одного киломоля вещества в жидком и парообразном состояниях в первом приближении равна молекулярной теплоте испарения
молекул одного киломоля вещества в жидком и парообразном состояниях в первом приближении равна молекулярной теплоте испарения  В кинетической теории было показано, что если молекулы вещества могут находиться в одной из двух областей, переход между которыми связан с изменением потенциальной энергии на величину
В кинетической теории было показано, что если молекулы вещества могут находиться в одной из двух областей, переход между которыми связан с изменением потенциальной энергии на величину  то при равновесии молекулярные плотности вещества в этих двух областях будут различны. Если обозначить числа молекул в одном кубическом метре в первой и во второй области соответственно
то при равновесии молекулярные плотности вещества в этих двух областях будут различны. Если обозначить числа молекул в одном кубическом метре в первой и во второй области соответственно  то можно написать (сравните стр. 37):
то можно написать (сравните стр. 37):

где  изменение потенциальной энергии одного киломоля вещества при переходе его из второй области в первую,
изменение потенциальной энергии одного киломоля вещества при переходе его из второй области в первую,  универсальная газовая постоянная и
универсальная газовая постоянная и  абсолютная температура.
абсолютная температура.
Применяя это уравнение к случаю равновесия между жидкостью и паром, найдем:

Здесь пп и  числа молекул в
числа молекул в  соответственно пара и жидкости.
соответственно пара и жидкости.
Число молекул в одном кубическом метре жидкости  сравнительно мало зависит от температуры и в первом приближении, при небольших изменениях температуры, может считаться постоянным.
сравнительно мало зависит от температуры и в первом приближении, при небольших изменениях температуры, может считаться постоянным.
Предположив, что пар подчиняется закону идеальных газов, найдем далее, что число молекул пара в одном кубическом метре  связано с давлением
связано с давлением  и температурой
и температурой  соотношением:
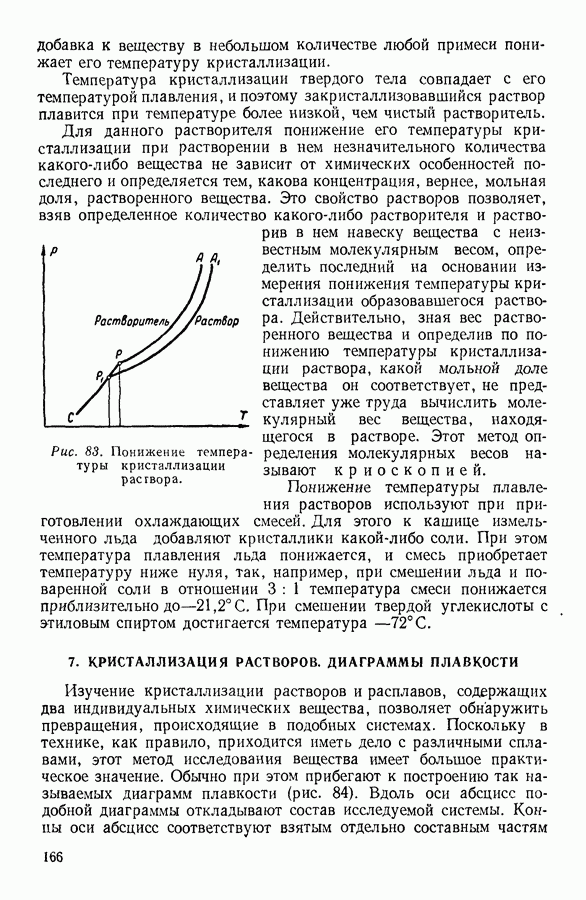
соотношением:

в котором  постоянная Больцмана.
постоянная Больцмана.
Подставляя из последнего уравнения значение  в уравнение (19), получим:
в уравнение (19), получим:

или

Логарифмирование этого уравнения приводит к выражению:

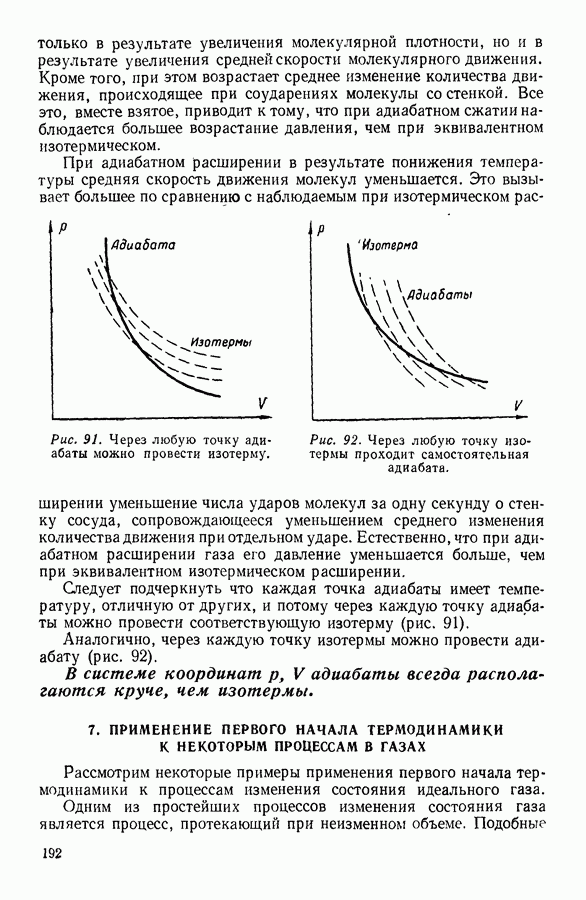
Последнее уравнение качественно совпадает с уравнением (18), полученным выше термодинамическим методом.
Некоторое отличие уравнения, полученного молекулярно-кинетическим методом от аналогичного уравнения, полученного термодинамически, обусловлено тем, что в обоих случаях для получения окончательного выражения пришлось использовать лишь приближенно верные предположения.
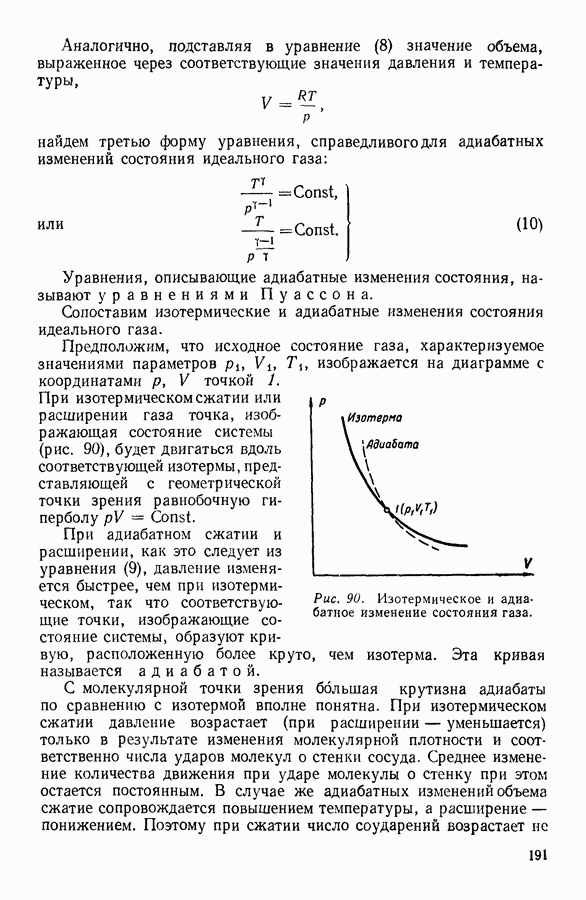
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
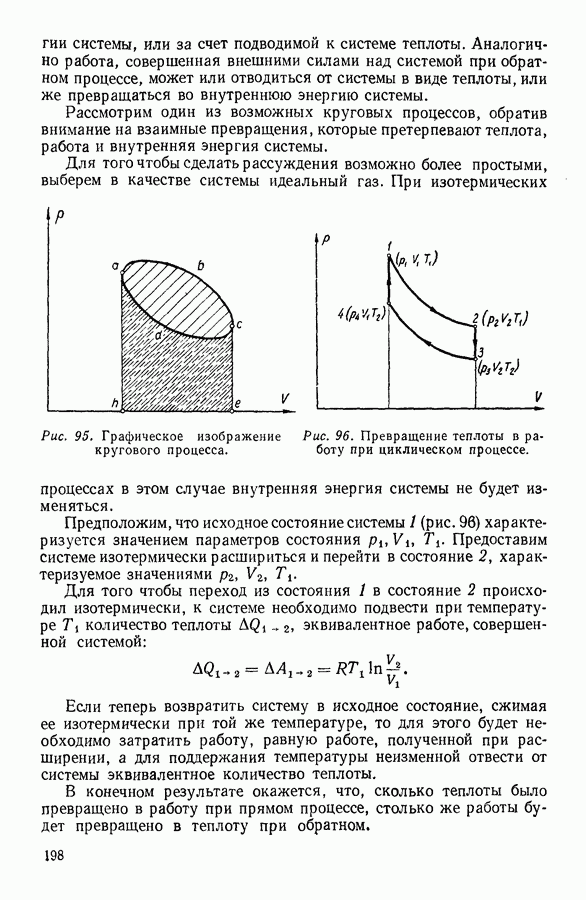
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
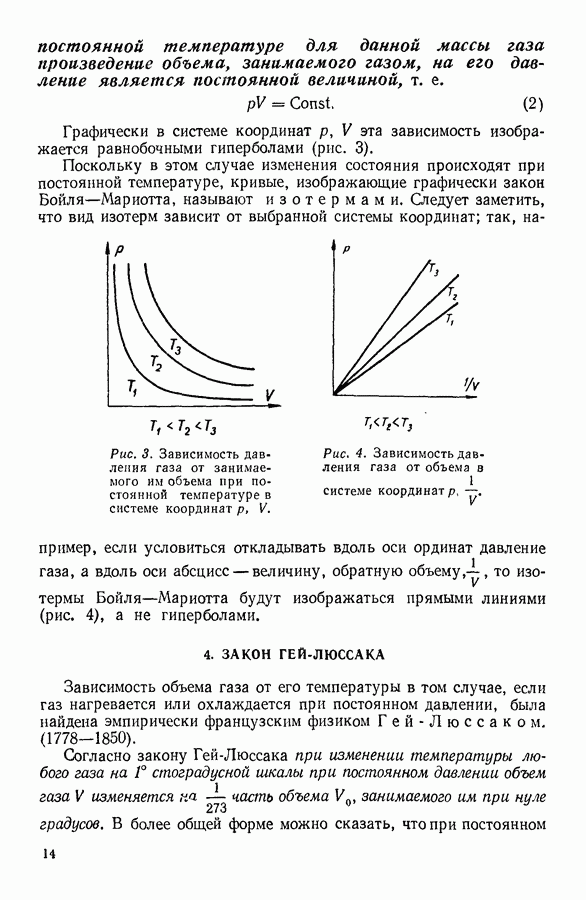
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
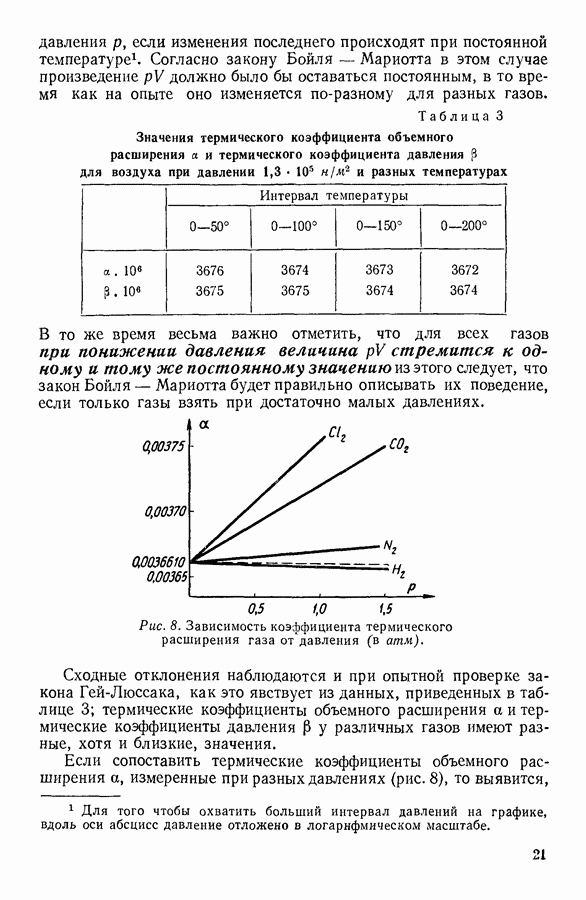
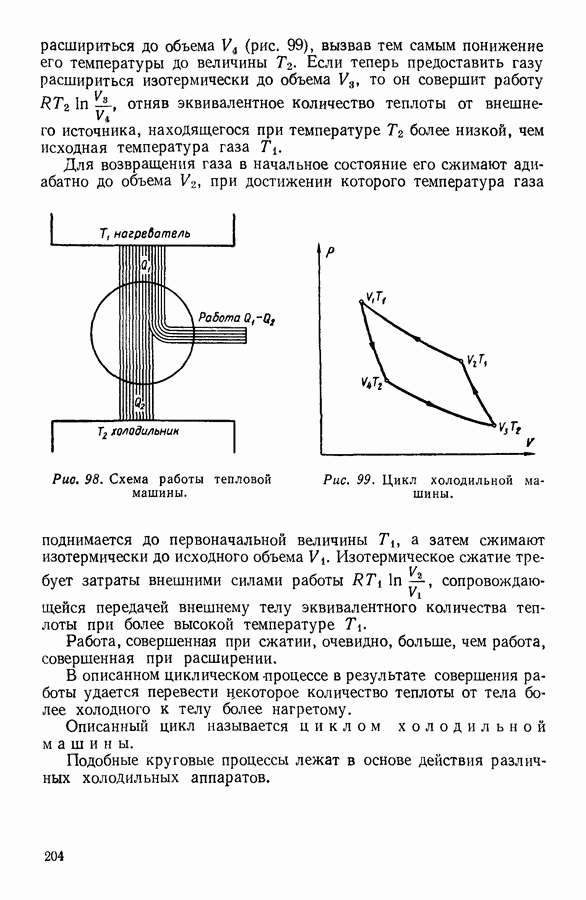
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
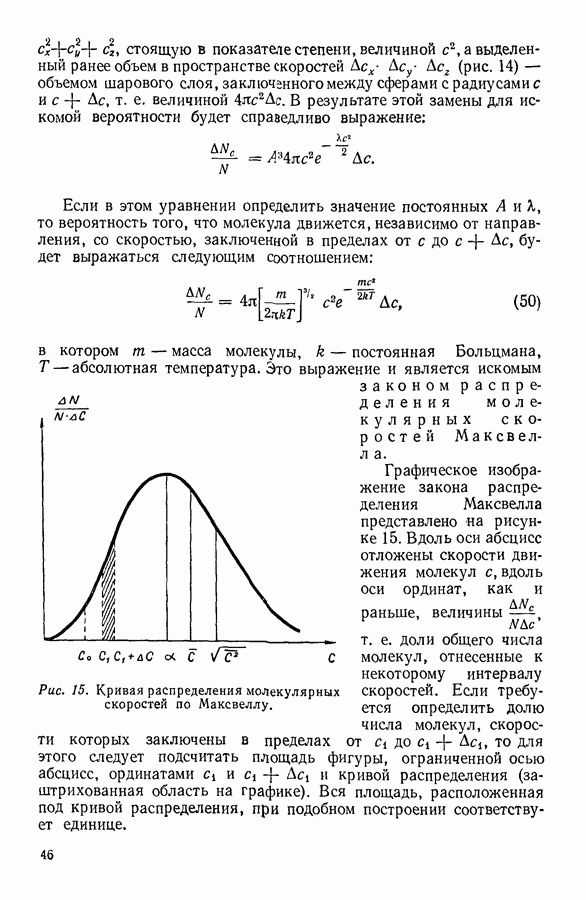
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
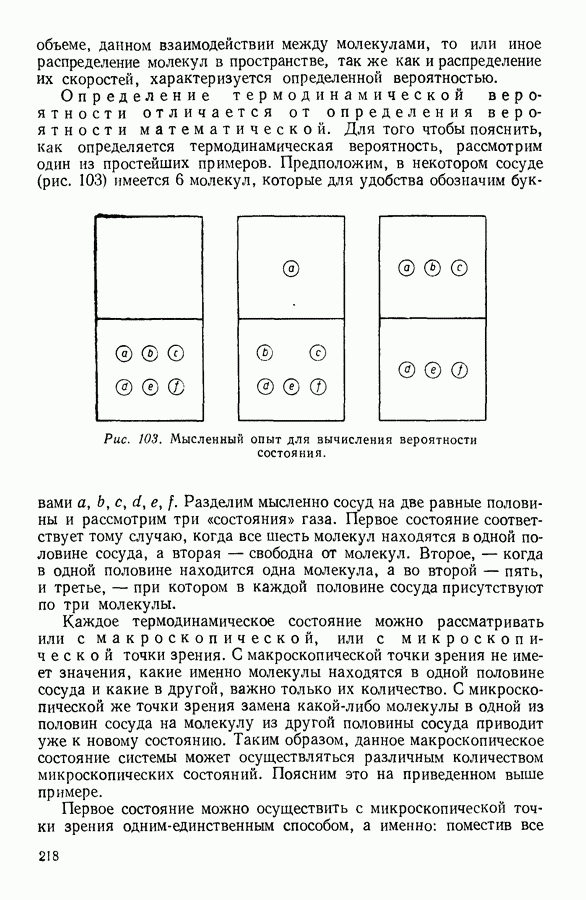
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
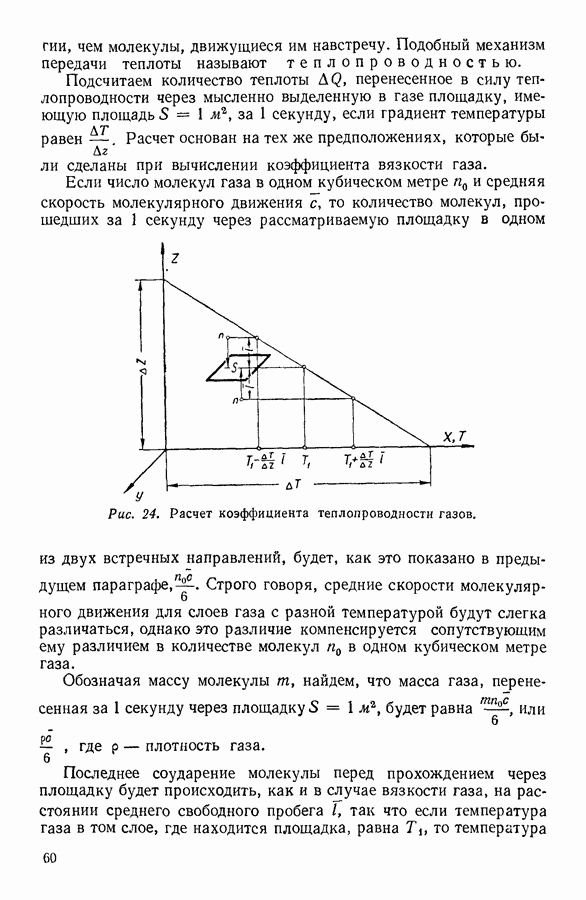
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
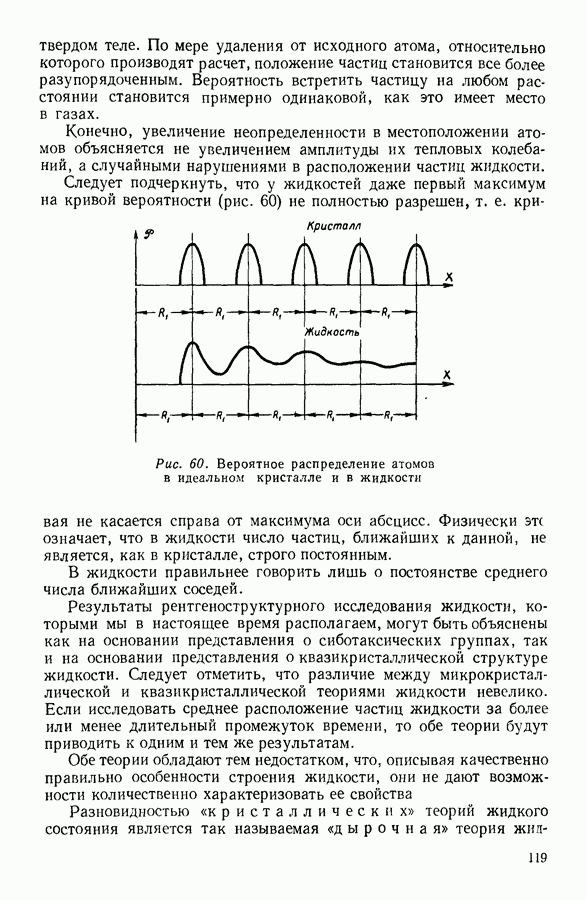
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
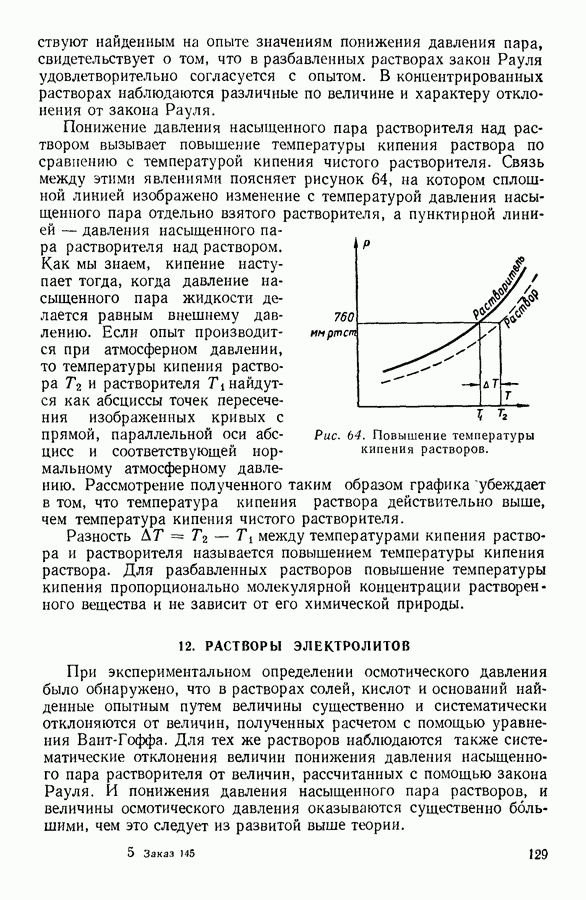
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
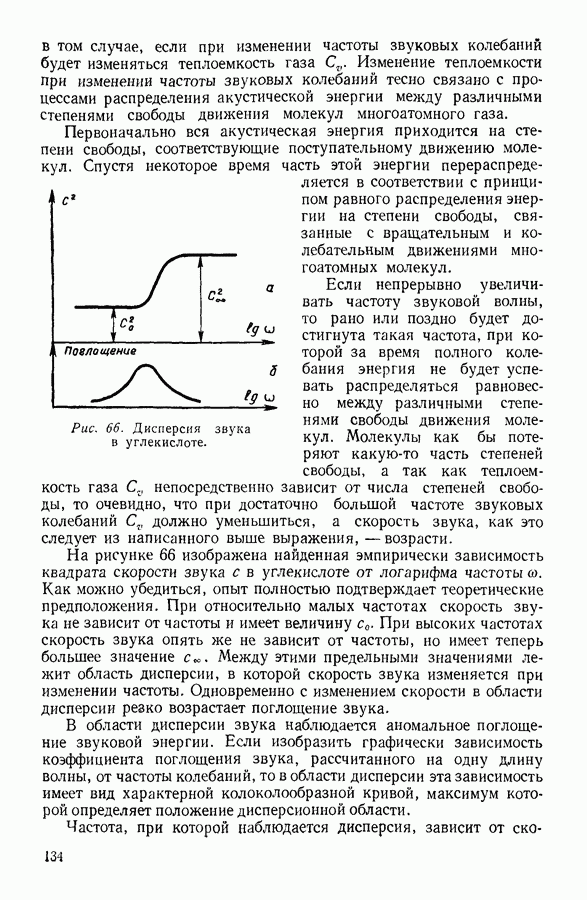
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
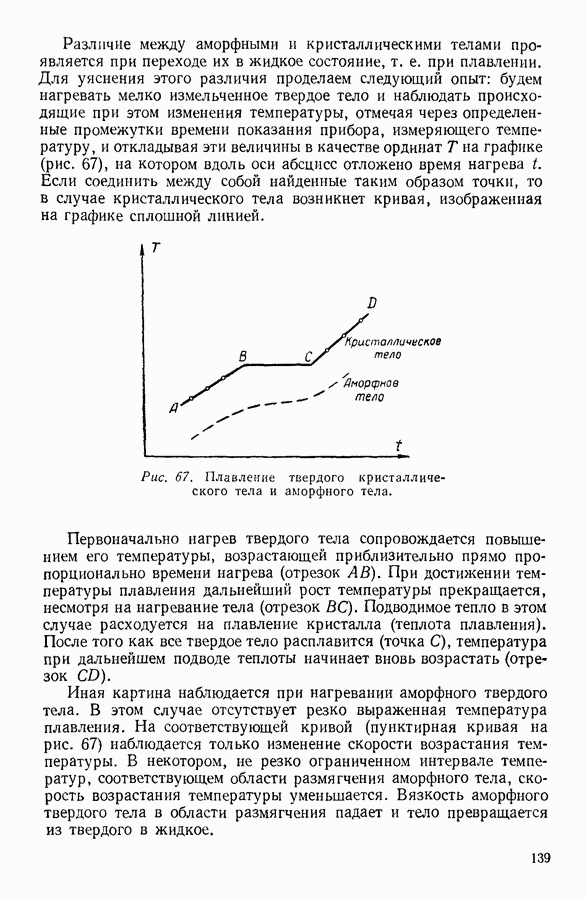
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
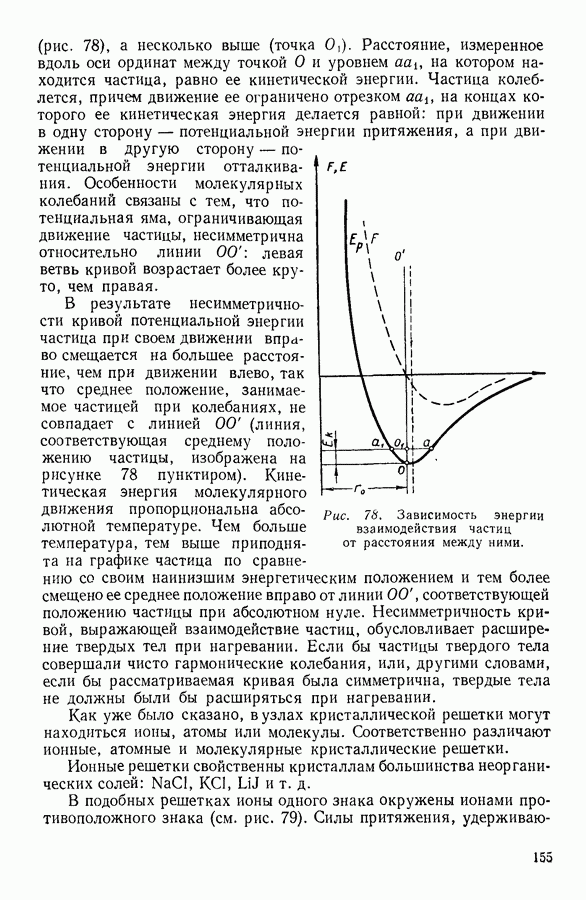
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
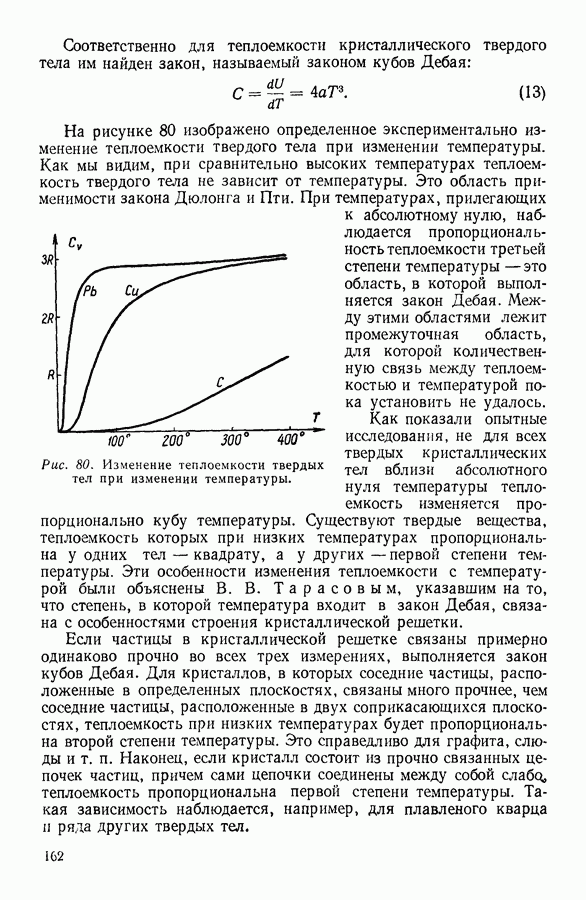
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
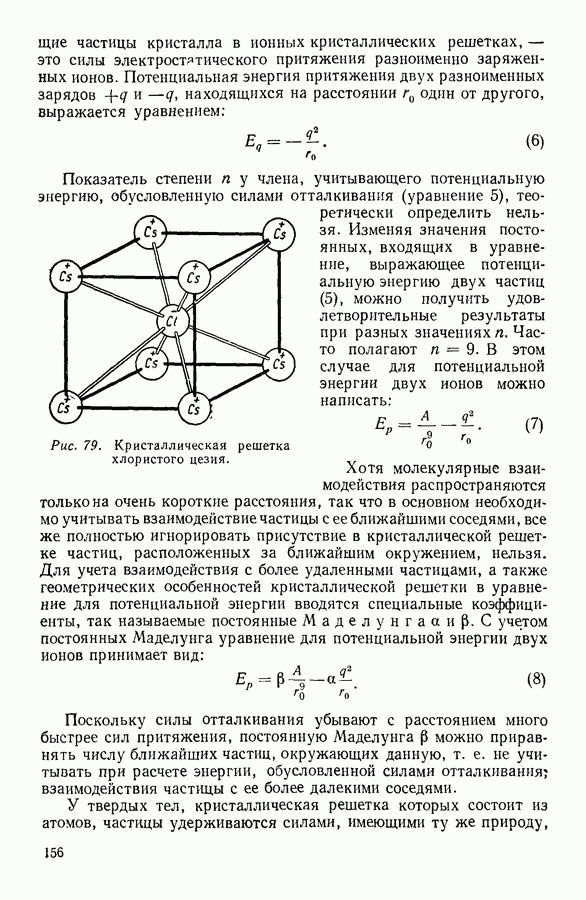
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»