24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА

Уравнение Ван-дер-Ваальса - алгебраическое уравнение третьей степени относительно объема. Раскрыв скобки и расположив члены уравнения Ван-дер-Ваальса по убывающим степеням объема, можно записать последнее в следующем виде:

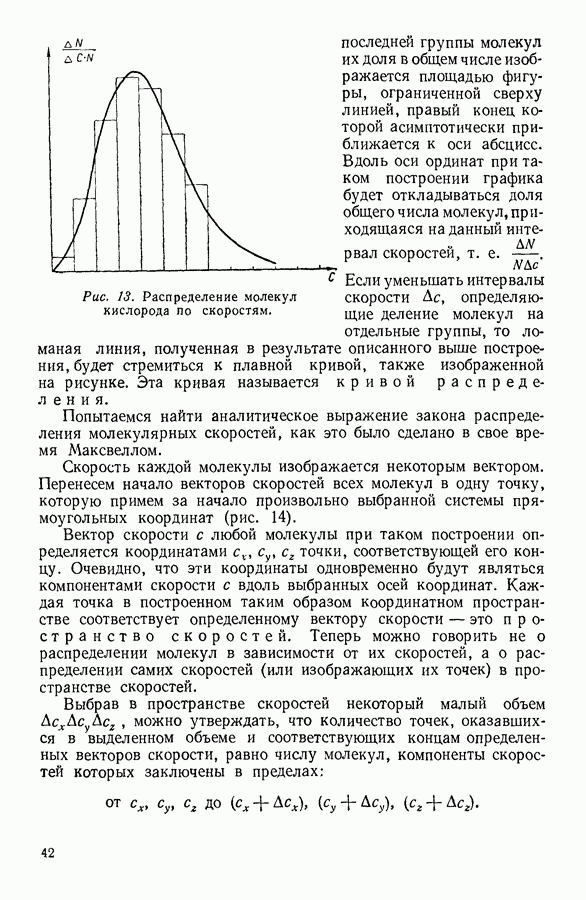
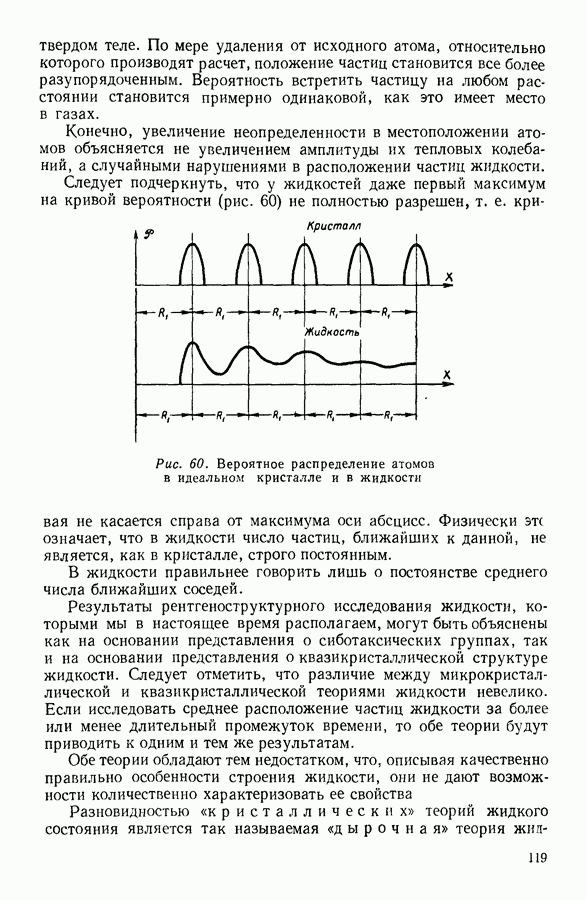
Особенности этого уравнения наиболее наглядно выявляются при графическом изображении полученной с его помощью зависимости давления газа от занимаемого им объема.

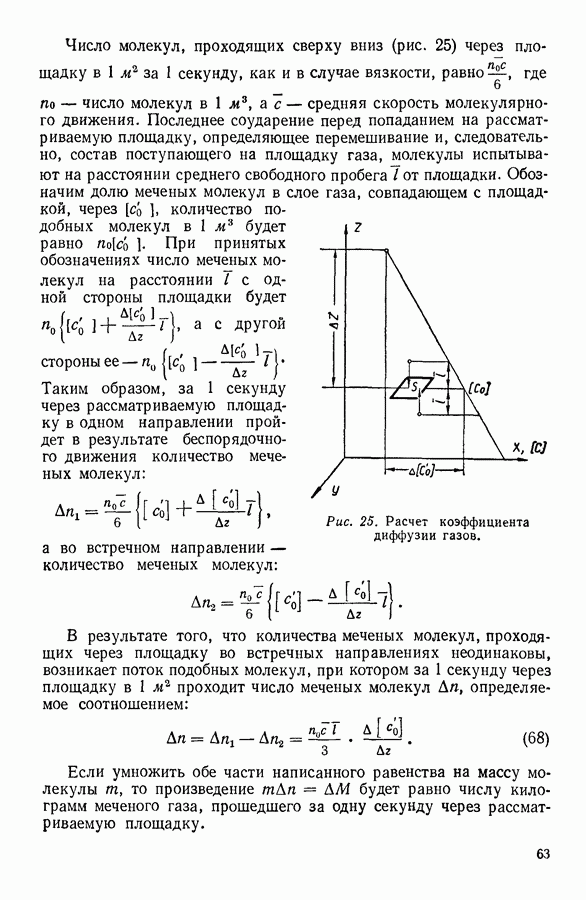
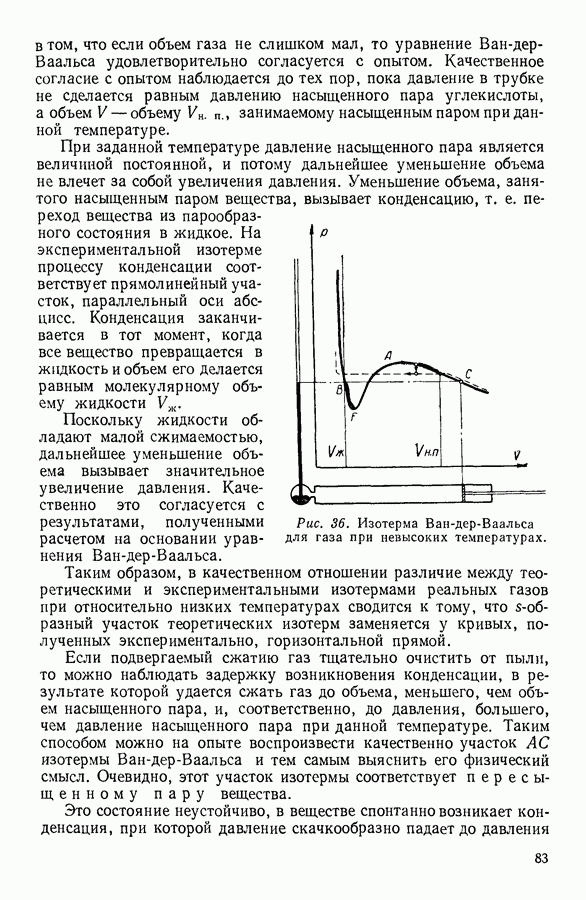
На рисунке 36 изображена подобная зависимость для того случая, когда температура газа не слишком высока. Вдоль оси абсцисс отложен объем, вдоль оси ординат — давление газа. Кривая, которая изображена на графике, рассчитана при постоянной температуре и, следовательно, является изотермой. Для того чтобы проанализировать физический смысл отдельных участков полученной изотермы, рассмотрим мысленный опыт, схема которого изображена на том же рисунке. Параллельно оси абсцисс расположена толстостенная стеклянная трубка, наполненная углекислотой и закрытая с правого конца поршнем. К левому концу трубки прикреплен ртутный манометр. Положение поршня непосредственно указывает объем, занимаемый газом. Давление газа регистрируется по положению уровня ртути в манометре.

Пересечение прямых, одна из которых параллельна оси абсцисс на уровне ртути в манометре, а вторая — параллельна оси ординат и указывает положение поршня в трубке, наполненной газом, происходит в точке С, изображающей на расположенной выше диаграмме определенное состояние газа. Перемещая поршень и отмечая указанным способом состояния газа, можно с помощью подобного прибора выяснить, насколько правильно передает уравнение Ван-дер-Ваальса поведение реального газа.

Результаты подобного опыта изображены на рисунке 36 пунктирной линией. Сопоставляя рассчитанную теоретически кривую с кривой, построенной на основании опыта, мы убеждаемся

втом, что если объем газа не слишком мал, то уравнение Ван-дер-Ваальса удовлетворительно согласуется с опытом. Качественное согласие с опытом наблюдается до тех пор, пока давление в трубке не сделается равным давлению насыщенного пара углекислоты, а объем V — объему занимаемому насыщенным паром при данной температуре.

При заданной температуре давление насыщенного пара является величиной постоянной, и потому дальнейшее уменьшение объема не влечет за собой увеличения давления. Уменьшение объема, занятого насыщенным паром вещества, вызывает конденсацию, т. е. переход вещества из парообразного состояния в жидкое. На экспериментальной изотерме процессу конденсации соответствует прямолинейный участок, параллельный оси абсцисс. Конденсация заканчивается в тот момент, когда все вещество превращается в жидкость и объем его делается равным молекулярному объему жидкости .

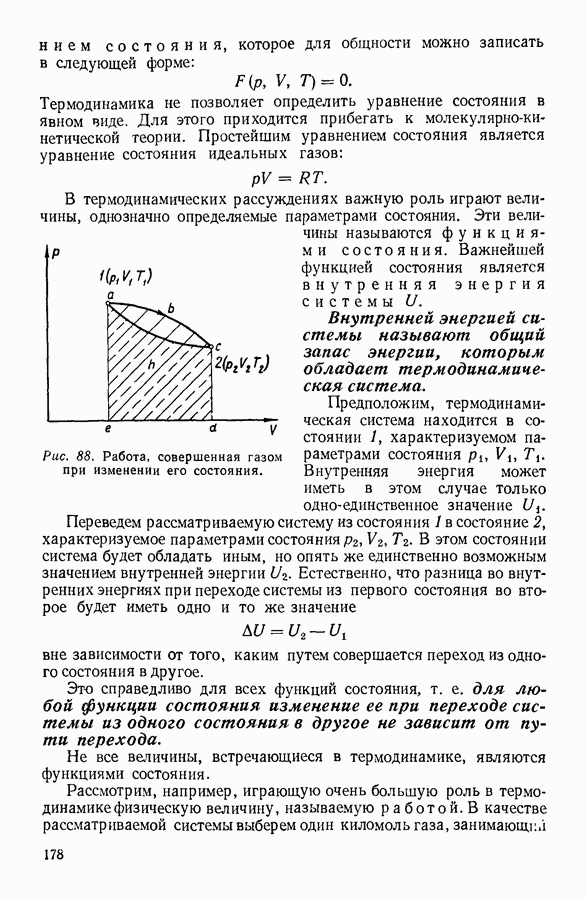
Рис. 36. Изотерма Ван-дер-Ваальса для газа при невысоких температурах.

Поскольку жидкости обладают малой сжимаемостью, дальнейшее уменьшение объема вызывает значительное увеличение давления. Качественно это согласуется с результатами, полученными расчетом на основании уравнения Ван-дер-Ваальса.

Таким образом, в качественном отношении различие между теоретическими и экспериментальными изотермами реальных газов при относительно низких температурах сводится к тому, что -образный участок теоретических изотерм заменяется у кривых, полученных экспериментально, горизонтальной прямой.

Если подвергаемый сжатию газ тщательно очистить от пыли, то можно наблюдать задержку возникновения конденсации, в результате которой удается сжать газ до объема, меньшего, чем объем насыщенного пара, и, соответственно, до давления, большего, чем давление насыщенного пара при данной температуре. Таким способом можно на опыте воспроизвести качественно участок изотермы Ван-дер-Ваальса и тем самым выяснить его физический смысл. Очевидно, этот участок изотермы соответствует пересыщенному пару вещества.

Это состояние неустойчиво, в веществе спонтанно возникает конденсация, при которой давление скачкообразно падает до давления

насыщенного пара (подобный процесс на рисунке 36 изображен стрелкой).

Точно так же при изотермическом увеличении объема сжатой жидкости экспериментально можно наблюдать задержку образования паровой фазы, несмотря на то что объем, занимаемый жидкостью, превышает ее молекулярный объем.

Давление в системе при этом будет ниже соответствующего данной температуре давления насыщенного пара жидкости. Задержка возникновения паровой фазы позволяет экспериментально воспроизвести в качественном согласии с теорией участок изотермы Ван-дер-Ваальса. Эта часть теоретической изотермы соответствует неустойчивому состоянию растянутой жидкости. Иногда это состояние называют состоянием перегретой жидкости в том смысле, что при данном значении молекулярного объема и температуры часть жидкости должна была бы находиться в парообразном состоянии, в то время как на опыте паровая фаза отсутствует.

Участок изотермы Ван-дер-Ваальса соответствует совершенно неустойчивому состоянию вещества, при котором давление в системе должно было бы уменьшаться при уменьшении объема системы и расти при его увеличении. На опыте это состояние не реализуется.

Таким образом, уравнение Ван-дер-Ваальса качественно правильно передает изменение давления вещества при изменении объема как в случае пара, так и в случае жидкости.

Уравнение предсказывает наличие неустойчивых состояний, а именно — состояния перегретого пара и состояния растянутой жидкости. Однако теория Ван-дер-Ваальса не учитывает возможности одновременного присутствия вещества в парообразном и жидком состояниях.

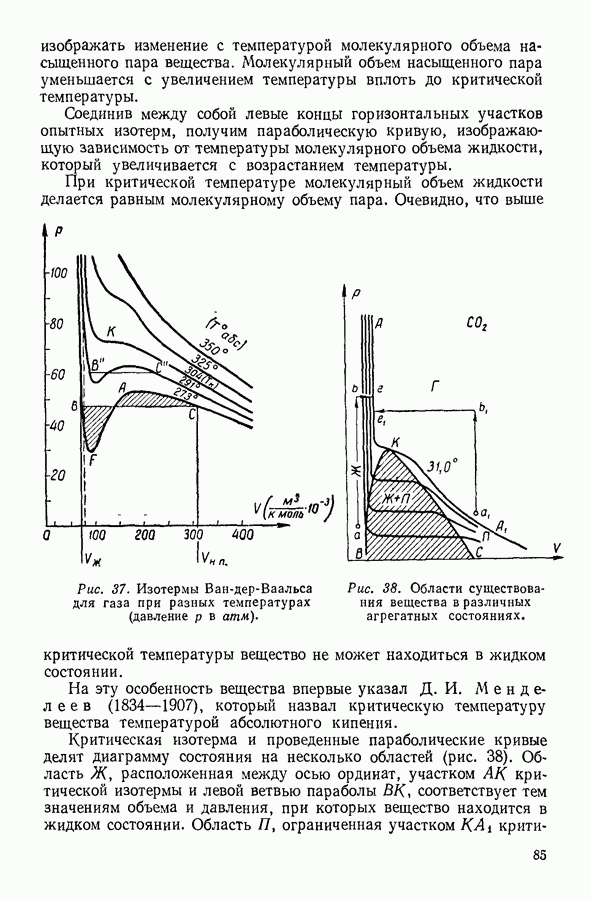
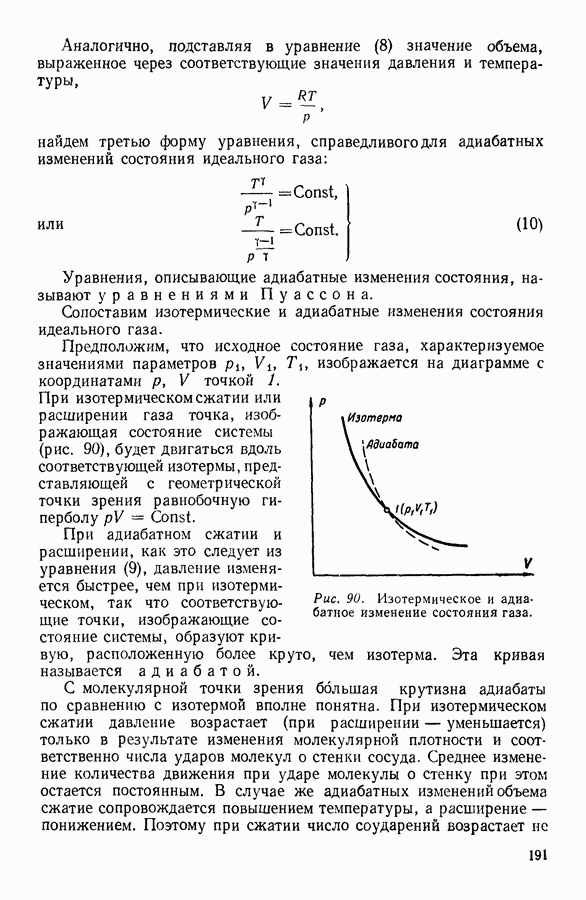
Если изобразить на графике изотермы Ван-дер-Ваальса, рассчитанные теоретически при разных значениях температуры, то получится семейство кривых, подобное изображенному на рисунке 37. Как можно убедиться, при повышении температуры -образный участок изотермы Ван-дер-Ваальса уменьшается, другими словами, уменьшается разница между молекулярными объемами насыщенного пара и жидкости. При некоторой температуре называемой критической температурой, -образный участок изотермы исчезает. На соответствующей изотерме, которую называют критической, вместо -образного участка наблюдается точка перегиба К, которая называется критической точкой. При более высоких температурах изотермы Ван-дер-Ваальса напоминают изотермы идеальных газов.

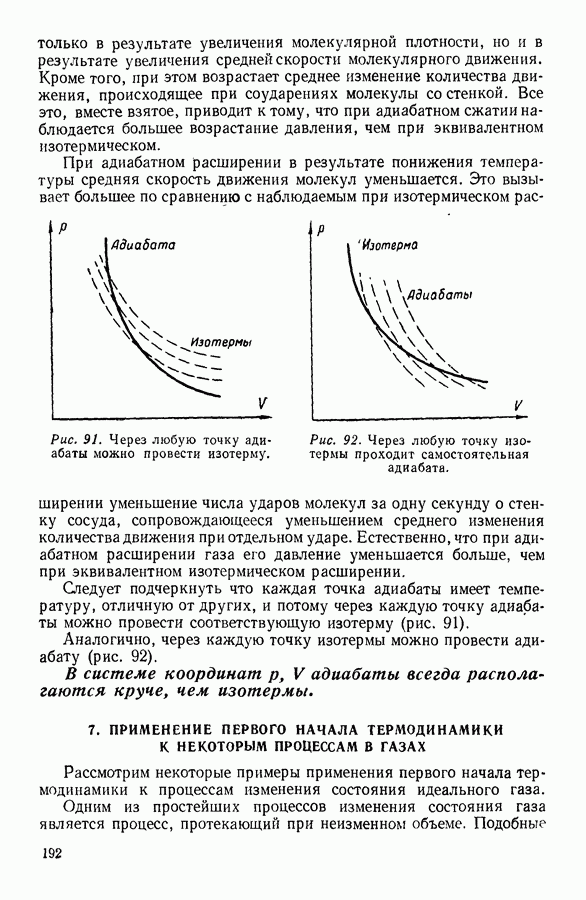
Экспериментально поведение реальных газов было изучено Эндрьюсом (1813—1885), найденные им изотермы изображены на рисунке 38.

Если соединить между собой правые концы горизонтальных участков экспериментальных изотерм, то полученная кривая будет

изображать изменение с температурой молекулярного объема насыщенного пара вещества. Молекулярный объем насыщенного пара уменьшается с увеличением температуры вплоть до критической температуры.

Соединив между собой левые концы горизонтальных участков опытных изотерм, получим параболическую кривую, изображающую зависимость от температуры молекулярного объема жидкости, который увеличивается с возрастанием температуры.

При критической температуре молекулярный объем жидкости делается равным молекулярному объему пара.

Рис. 37. Изотермы Ван-дер-Ваальса для газа при разных температурах (давление в атм).

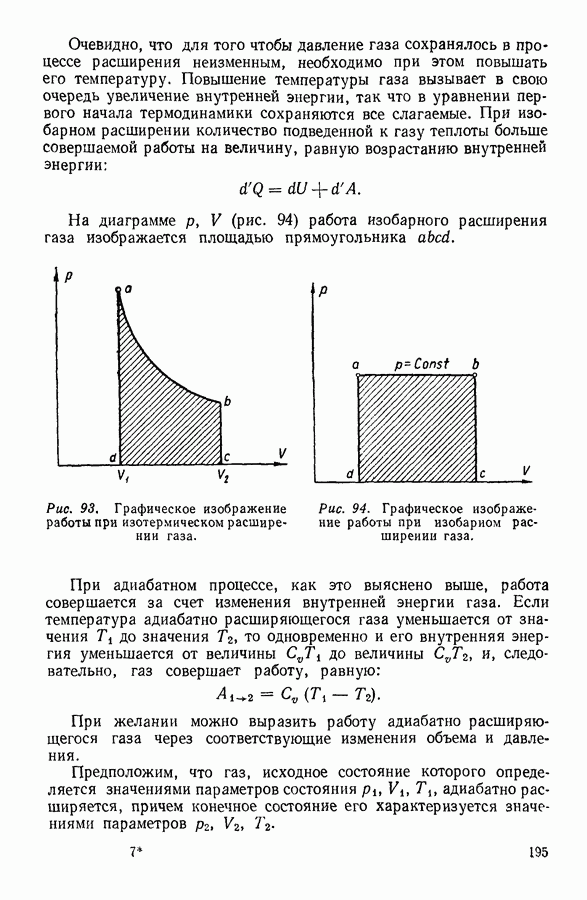
Рис. 38. Области существования вещества в различных агрегатных состояниях.

Очевидно, что выше критической температуры вещество не может находиться в жидком состоянии.

На эту особенность вещества впервые указал Д. И. Менделеев (1834—1907), который назвал критическую температуру вещества температурой абсолютного кипения.

Критическая изотерма и проведенные параболические кривые делят диаграмму состояния на несколько областей (рис. 38). Область расположенная между осью ординат, участком критической изотермы и левой ветвью параболы соответствует тем значениям объема и давления, при которых вещество находится в жидком состоянии. Область ограниченная участком

критической изотермы и правой ветвью параболы выделяет значения давления и объема, соответствующие веществу в парообразном состоянии. Выше критической изотермы расположена область вещества в газообразном состоянии. Наконец, область, ограниченная осью абсцисс и параболой соответствует одновременному присутствию вещества в жидком и парообразном состояниях. Это область, в которой вещество находится одновременно в двух различных агрегатных состояниях, или гетерогенная область.

Таким образом, сжатие вещества при температуре ниже критической вызывает при определенном давлении его конденсацию, в то время как любое сжатие вещества при температурах выше критической не вызывает конденсации. При температурах выше критической, увеличивая давление, нельзя превратить газообразное вещество в жидкое.

Теория Ван-дер-Ваальса указывает на возможность непрерывного перехода вещества из жидкого состояния в газообразное без распадения вещества на две фазы. Непрерывный переход из жидкого состояния в газообразное изображен на рисунке 38 стрелками. Отрезки изображают нагрев вещества до критической температуры. Давление в системе при этом возрастает выше критического давления. Дальнейшее изменение состояния вещества может заключаться или в изотермическом расширении, при котором давление уменьшается до критического и жидкость в критической точке превращается в пар, или же в изобарном нагревании, при котором вещество превращается в газ при давлении выше критического.

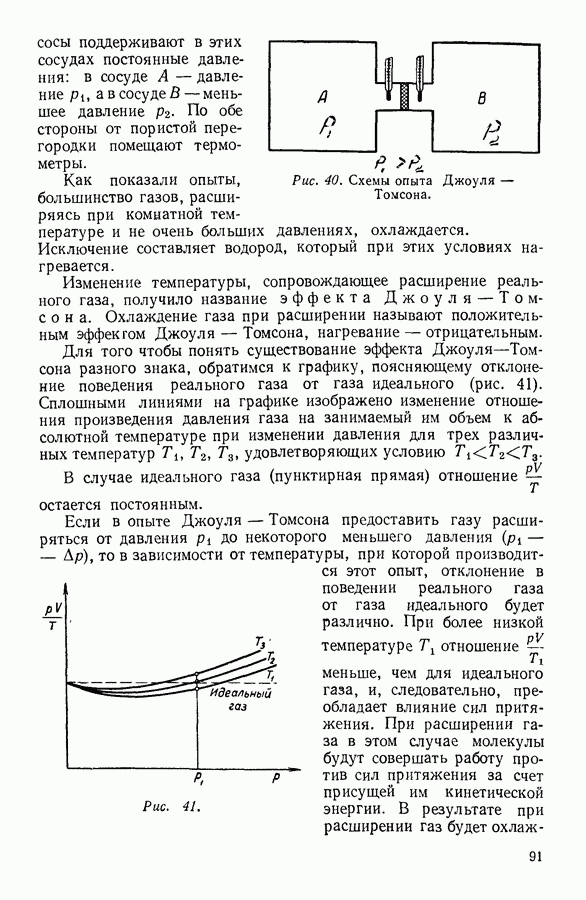
Естественно, что возможен и обратный непрерывный, т. е. не сопровождающийся распадением вещества на две фазы, переход из газообразного состояния в жидкое. Этот переход показан на диаграмме стрелками