| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
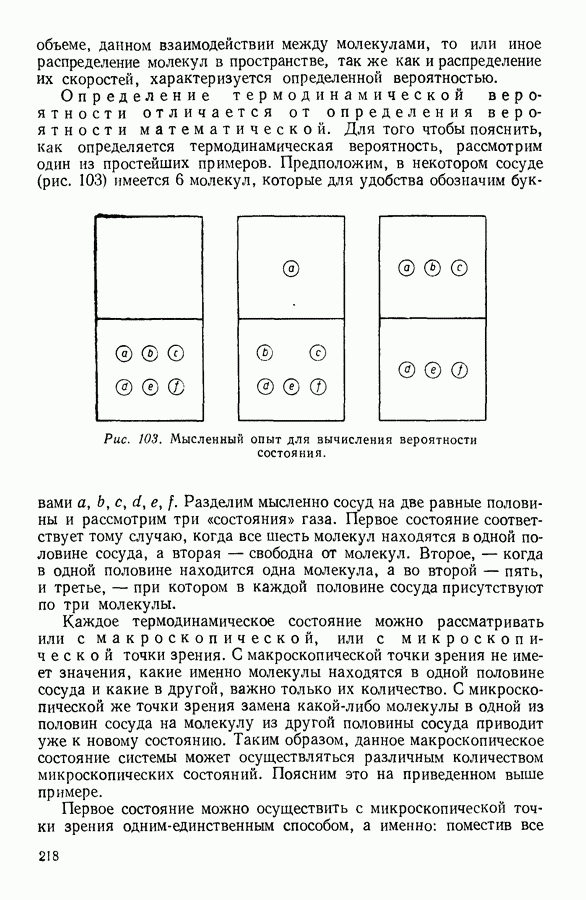
8. КРУГОВЫЕ ПРОЦЕССЫ
В термодинамических рассуждениях большое значение имеет рассмотрение различных круговых процессов.
Круговым процессом, или циклом называется такая последовательность превращений, в результате которой система, выйдя из какого-либо исходного состояния, вновь в него возвращается.
На диаграмме состояния круговой процесс изображается замкнутой кривой.
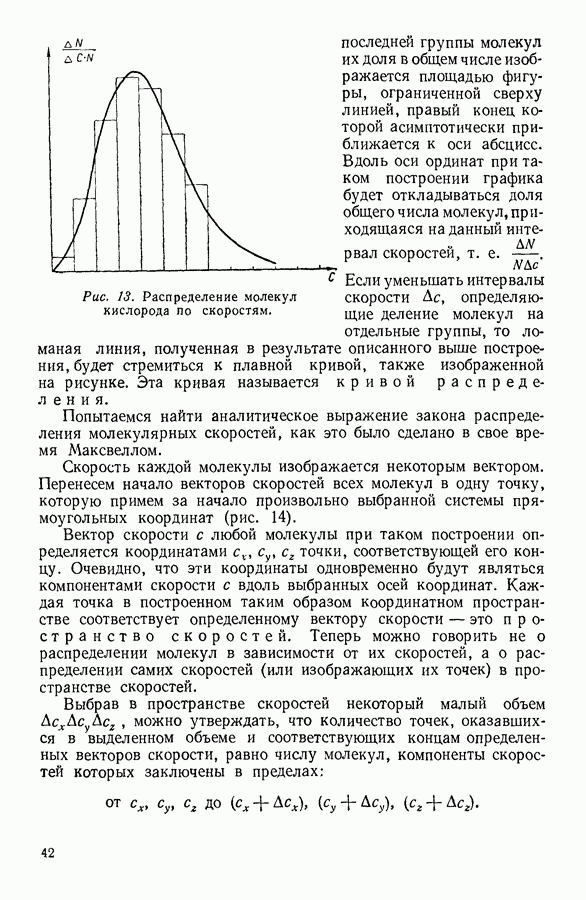
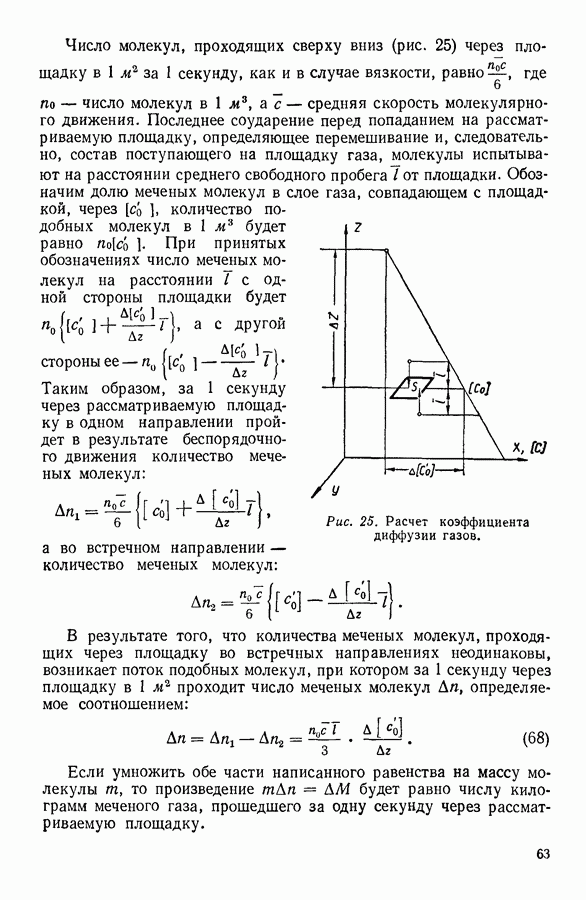
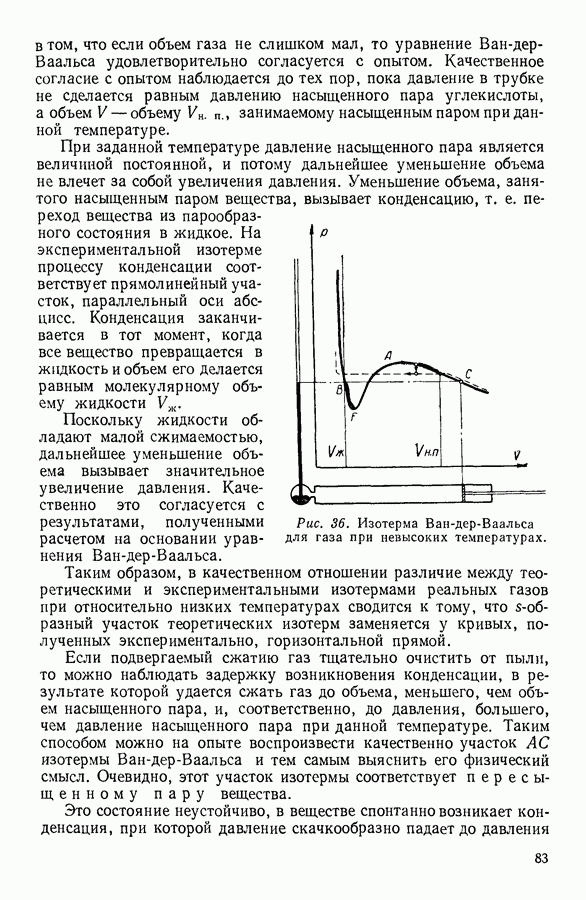
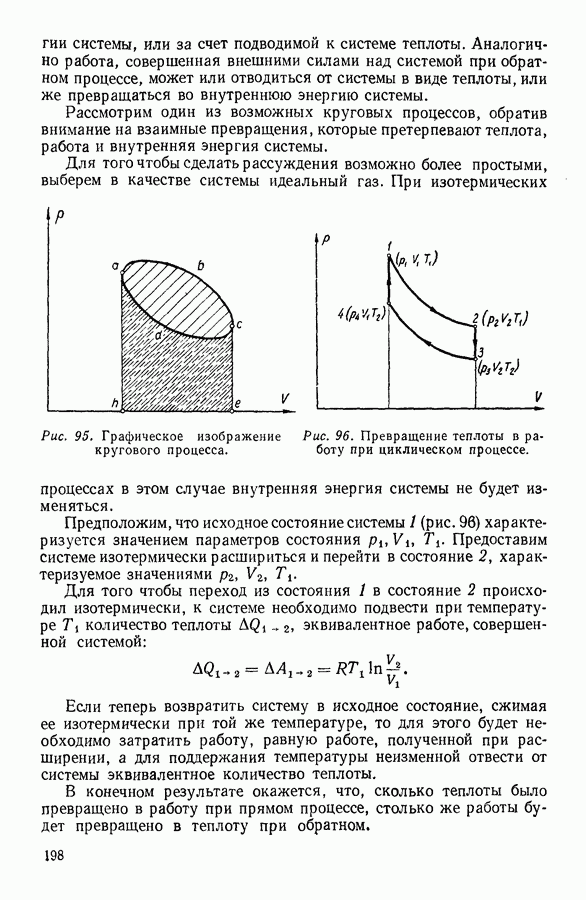
При изображении кругового процесса на графике с координатами  (рис. 95) он, естественно, распадается на процесс расширения системы
(рис. 95) он, естественно, распадается на процесс расширения системы  и на процесс сжатия
и на процесс сжатия 
Процесс расширения системы связан с совершением ею работы, в то время как сжатие системы вызывается работой внешних сил над системой.
На графике (рис. 95) работа, совершаемая системой при расширении, численно равна площади фигуры  а работа, совершаемая внешними силами, возвращающими систему в исходное состояние, — площади фигуры
а работа, совершаемая внешними силами, возвращающими систему в исходное состояние, — площади фигуры  Разность этих площадей, равная площади фигуры
Разность этих площадей, равная площади фигуры  соответствует разнице между работой, полученной при расширении системы
соответствует разнице между работой, полученной при расширении системы  и работой, совершенной для возвращения системы в исходное состояние
и работой, совершенной для возвращения системы в исходное состояние
Согласно первому началу термодинамики работа при расширении системы может совершаться или за счет внутренней
энергии системы, или за счет подводимой к системе теплоты. Аналогично работа, совершенная внешними силами над системой при обратном процессе, может или отводиться от системы в виде теплоты, или же превращаться во внутреннюю энергию системы.
Рассмотрим один из возможных круговых процессов, обратив внимание на взаимные превращения, которые претерпевают теплота, работа и внутренняя энергия системы.
Для того чтобы сделать рассуждения возможно более простыми, выберем в качестве системы идеальный газ.

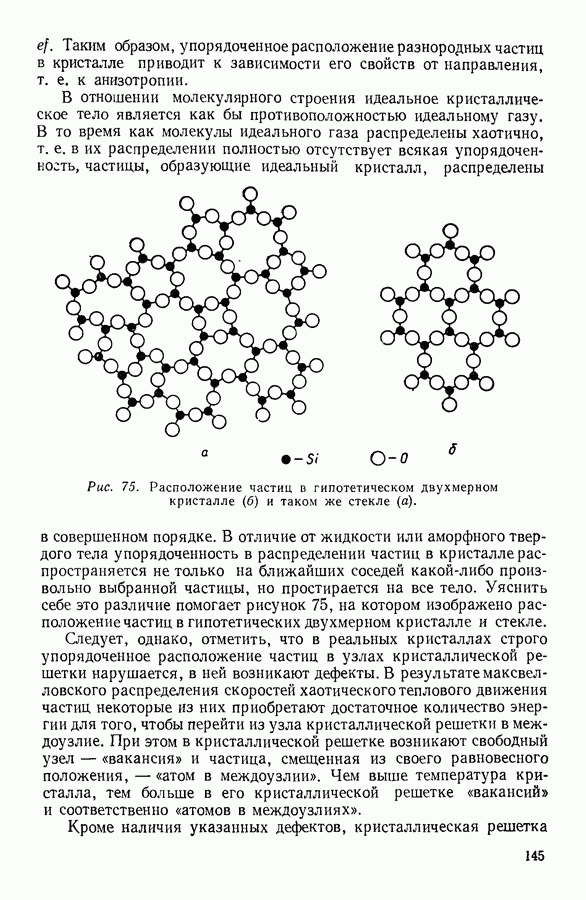
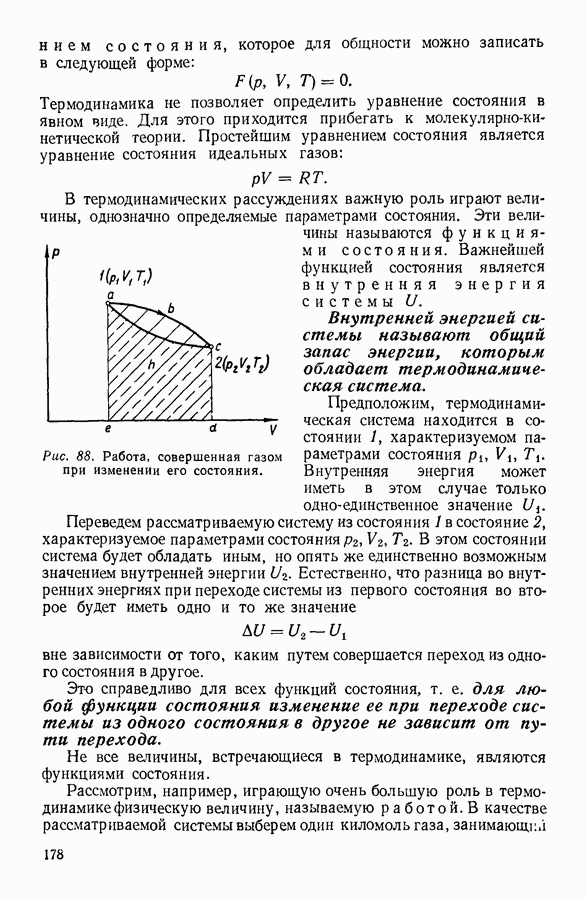
Рис. 95. Графическое изображение кругового процесса.

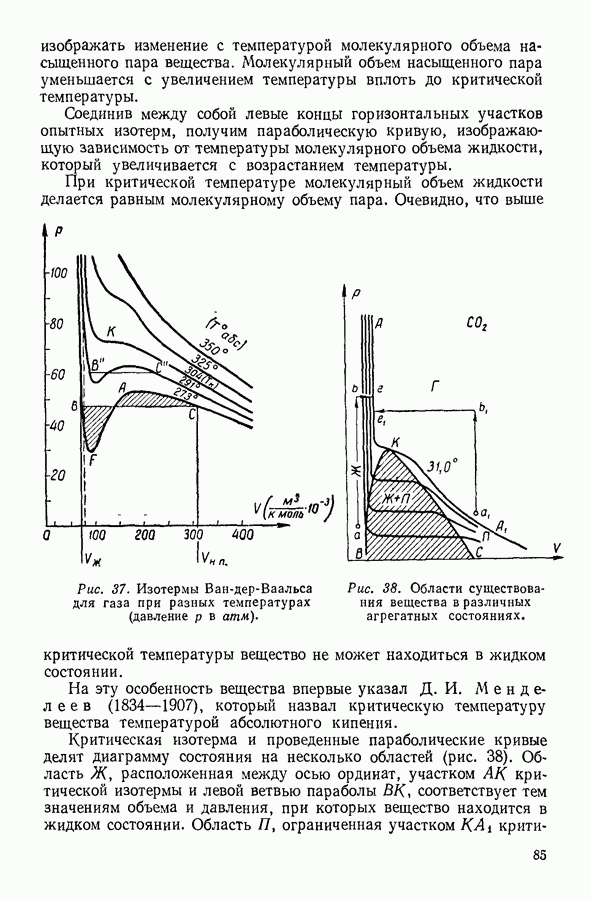
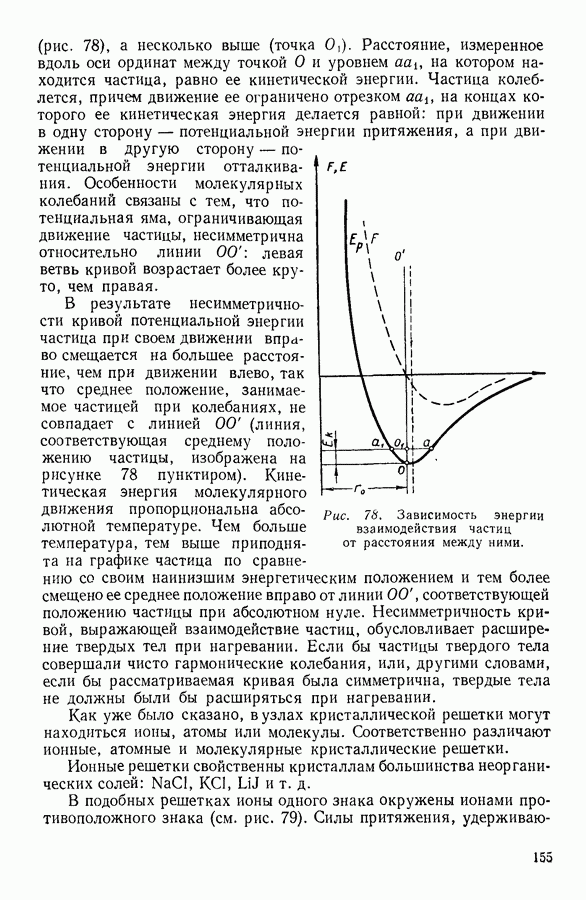
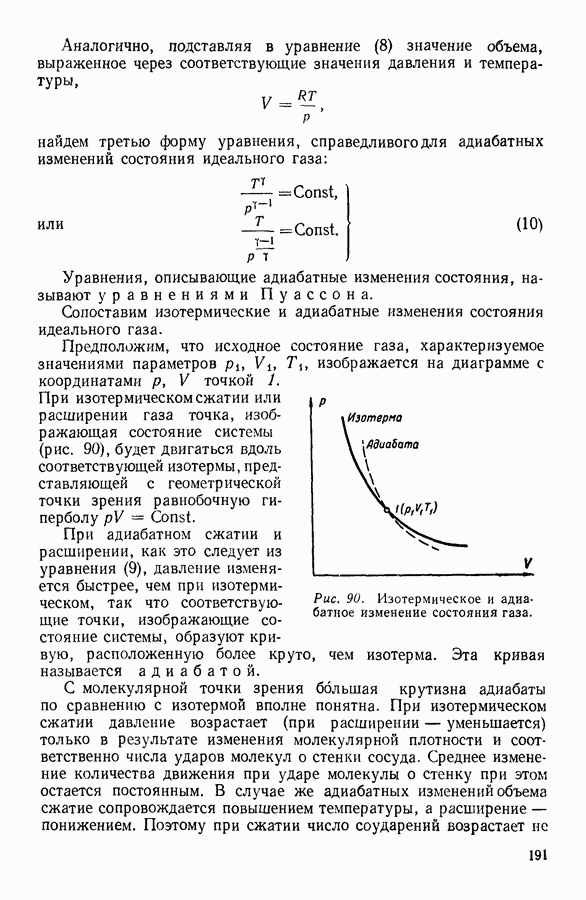
Рис. 96. Превращение теплоты в работу при циклическом процессе.
При изотермических процессах в этом случае внутренняя энергия системы не будет изменяться.
Предположим, что исходное состояние системы 1 (рис. 96) характеризуется значением параметров состояния  Предоставим системе изотермически расшириться и перейти в состояние 2, характеризуемое значениями
Предоставим системе изотермически расшириться и перейти в состояние 2, характеризуемое значениями 
Для того чтобы переход из состояния 1 в состояние 2 происходил изотермически, к системе необходимо подвести при температуре  количество теплоты
количество теплоты  эквивалентное работе, совершенной системой:
эквивалентное работе, совершенной системой:

Если теперь возвратить систему в исходное состояние, сжимая ее изотермически при той же температуре, то для этого будет необходимо затратить работу, равную работе, полученной при расширении, а для поддержания температуры неизменной отвести от системы эквивалентное количество теплоты.
В конечном результате окажется, что, сколько теплоты было превращено в работу при прямом процессе, столько же работы будет превращено в теплоту при обратном.
Можно, однако, поступить иначе.
Предположим, например, что по достижении системой состояния 2 мы понизим ее температуру до величины  сохранив объем неизменным. Давление в системе при этом должно уменьшиться до величины
сохранив объем неизменным. Давление в системе при этом должно уменьшиться до величины  Система перейдет в некоторое состояние 3, характеризуемое параметрами
Система перейдет в некоторое состояние 3, характеризуемое параметрами 
Переход из состояния 2 в 3 потребует отвода от системы количества теплоты  равного
равного

Если теперь сжать газ изотермически до первоначального объема, то система перейдет в состояние 4, характеризуемое параметрами 
Для этого перехода потребуется затратить работу  и для поддержания неизменной температуры отвести от системы эквивалентное количество теплоты:
и для поддержания неизменной температуры отвести от системы эквивалентное количество теплоты:

Как мы видим, на сжатие газа затрачена меньшая работа, чем была получена при его расширении.
Рассмотренный процесс, однако, не является еще циклическим. Для замыкания цикла необходимо газ нагреть при постоянном объеме, повысив его температуру до исходной. При этом к системе необходимо подвести количество теплоты  равное
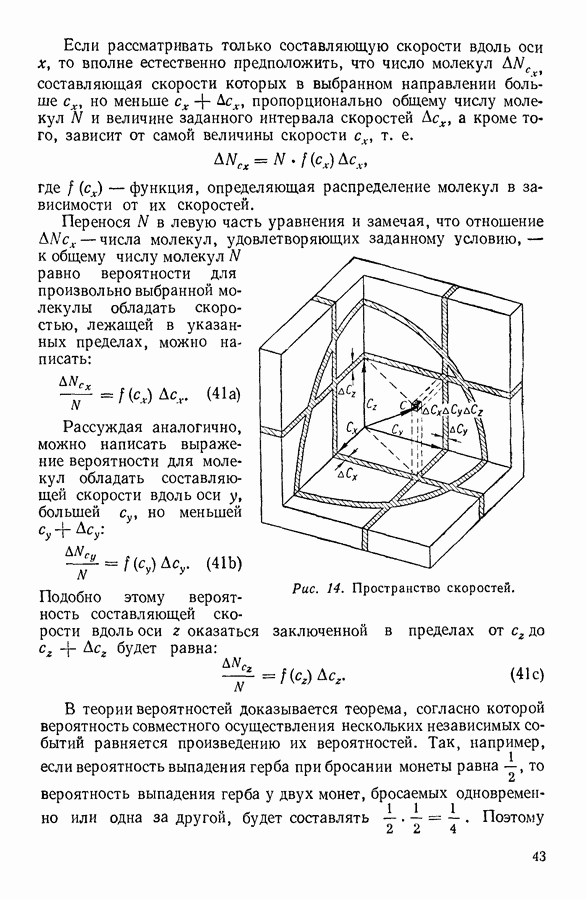
равное

В результате нагревания цикл замкнется, система возвратится в исходное состояние с параметрами 
Проанализируем рассмотренный круговой процесс.
Прежде всего обратим внимание на то, что количество теплоты  отнятое от системы при переходе ее из состояния 2 в состояние 3, равно количеству теплоты
отнятое от системы при переходе ее из состояния 2 в состояние 3, равно количеству теплоты  сообщенному системе при переходе ее из состояния 4 в 1, и поэтому эти количества теплоты взаимно сокращаются.
сообщенному системе при переходе ее из состояния 4 в 1, и поэтому эти количества теплоты взаимно сокращаются.
Таким образом, следует рассмотреть только изотермическое расширение системы при переходе ее из состояния 1 в состояние 2 и изотермическое сжатие при переходе от состояния 3 к 4.
При изотермическом расширении системы к ней при температуре  подводится количество теплоты
подводится количество теплоты  и система совершает работу
и система совершает работу  эквивалентную этому количеству теплоты.
эквивалентную этому количеству теплоты.
При изотермическом сжатии системы внешние силы совершают работу  и от системы при более низкой температуре отводится эквивалентное количество теплоты
и от системы при более низкой температуре отводится эквивалентное количество теплоты 
Разность работ  представляет работу данного циклического процесса. Эта работа выражается на графике площадью фигуры, ограниченной контуром цикла. Она эквивалентна
представляет работу данного циклического процесса. Эта работа выражается на графике площадью фигуры, ограниченной контуром цикла. Она эквивалентна
разности количеств теплоты, подведенной при расширении и отведенной при сжатии системы.
С практической точки зрения интересны циклические процессы, сопровождающиеся превращениями теплоты в работу.
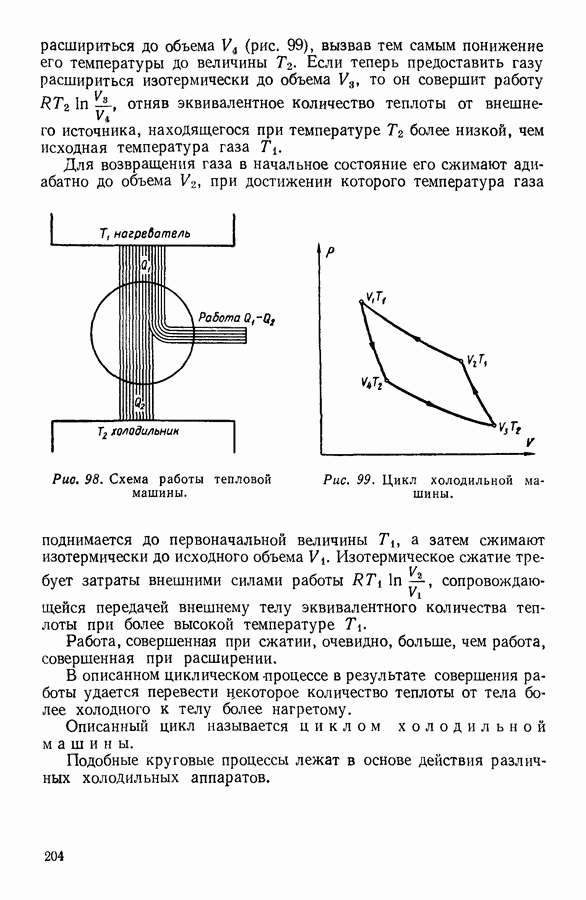
В рассмотренном циклическом процессе от некоторого источника забиралось количество теплоты  при температуре и подводилось к рассматриваемой системе. Часть подведенной к системе теплоты превращалась в работу, а остаток отводился от системы опять же в форме теплоты
при температуре и подводилось к рассматриваемой системе. Часть подведенной к системе теплоты превращалась в работу, а остаток отводился от системы опять же в форме теплоты  но при более низкой температуре
но при более низкой температуре  Такое положение является общим.
Такое положение является общим.
При любом циклическом процессе, предназначенном для превращения теплоты в работу, к системе подводится некоторое количество энергии в форме теплоты при более высокой температуре, часть подведенной энергии превращается в работу, а часть отводится опять же в форме теплоты, но при более низкой температуре. Циклический процесс, при котором к системе подводилось бы некоторое количество теплоты и все без остатка превращалось бы в работу, вообще невозможен.
Для характеристики эффективности циклического процесса в отношении превращения теплоты в работу вводится физическая величина, называемая коэффициентом поленного действия цикла,  равная отношению работы
равная отношению работы  практически используемой в данном циклическом процессе, к работе, которую можно было бы получить при превращении в нее всего количества теплоты, подведенного к системе:
практически используемой в данном циклическом процессе, к работе, которую можно было бы получить при превращении в нее всего количества теплоты, подведенного к системе:

или, учитывая эквивалентность между теплотой и работой,

Превращения теплоты в работу, подобные описанным выше, используются в различных тепловых машинах. Чем ближе коэффициент полезного действия цикла к единице, тем более совершенна с термодинамической точки зрения данная машина. Наиболее совершенным в отношении коэффициента полезного действия является циклический процесс, рассмотренный впервые французским физиком Сади Карно (1796—1832) и носящий его имя.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
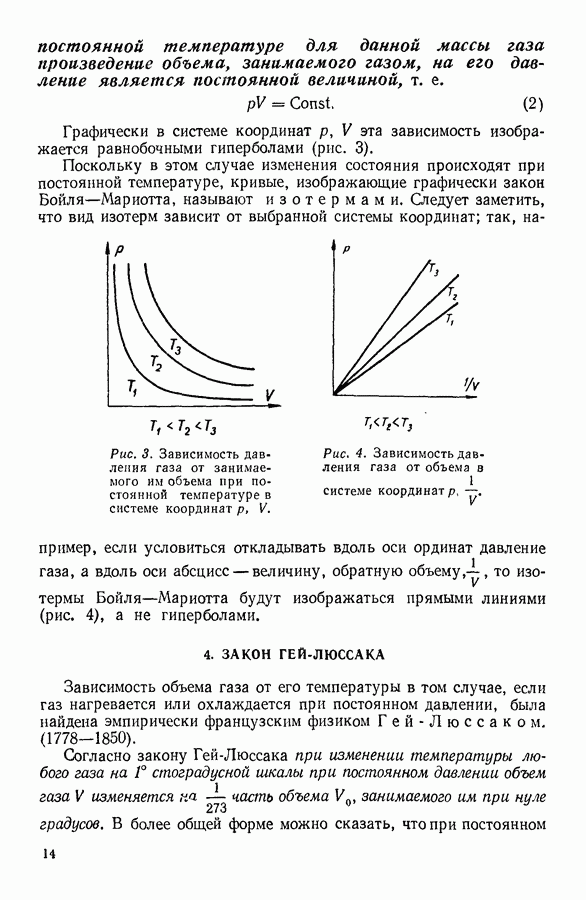
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
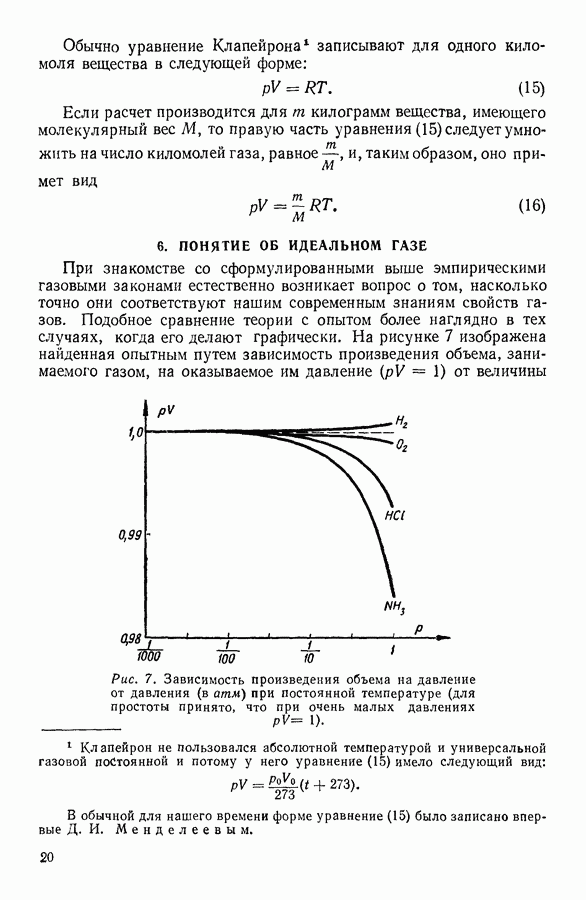
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
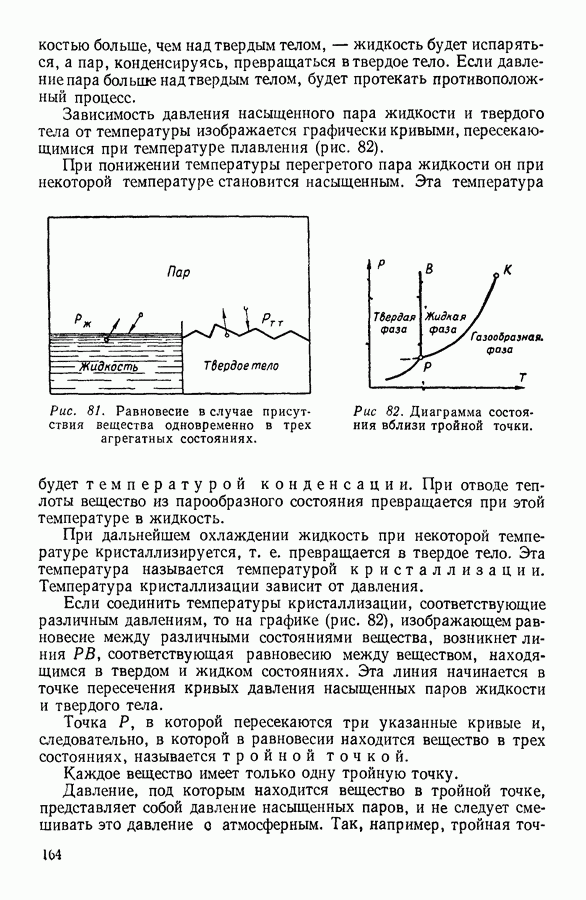
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
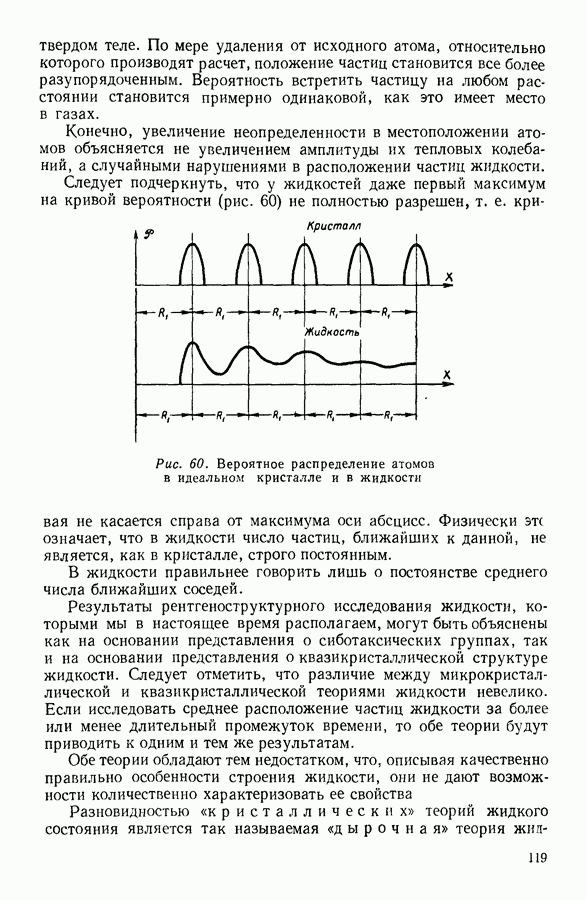
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
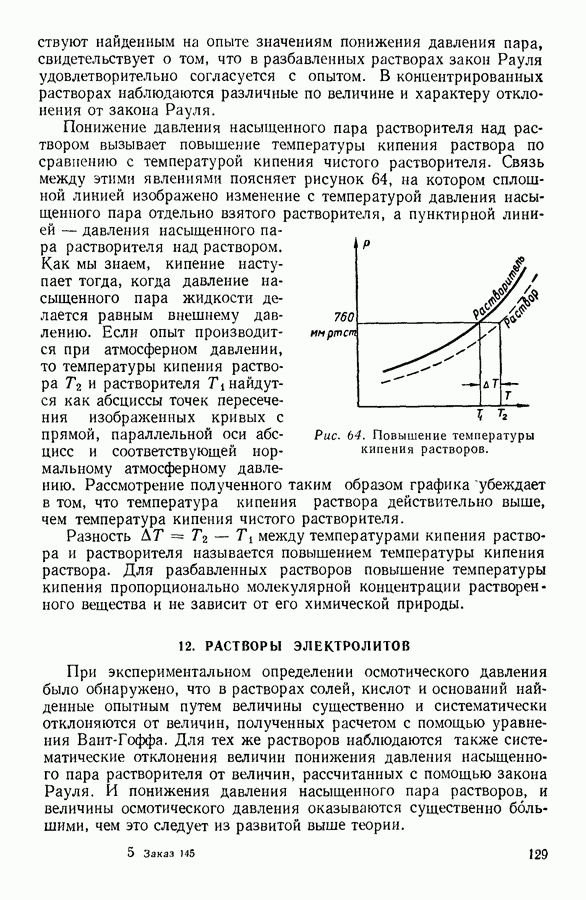
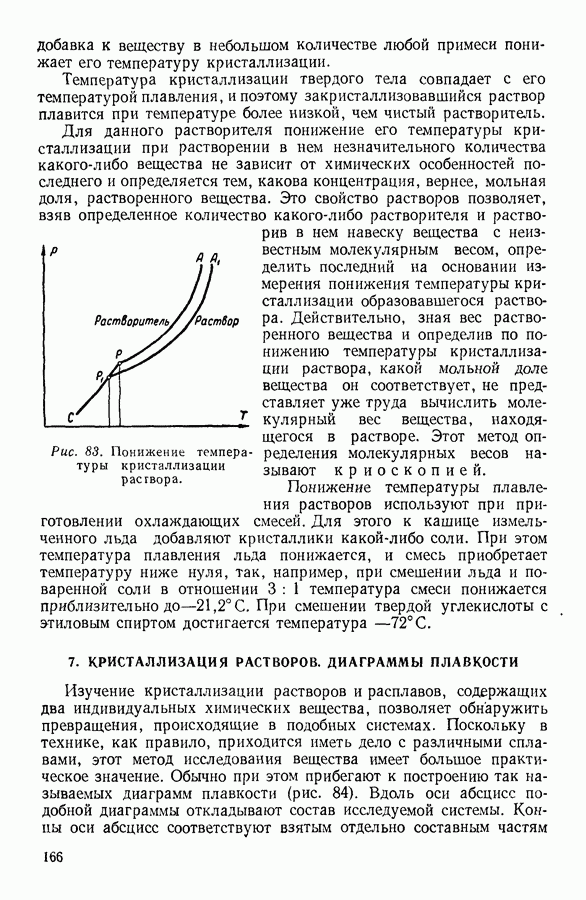
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
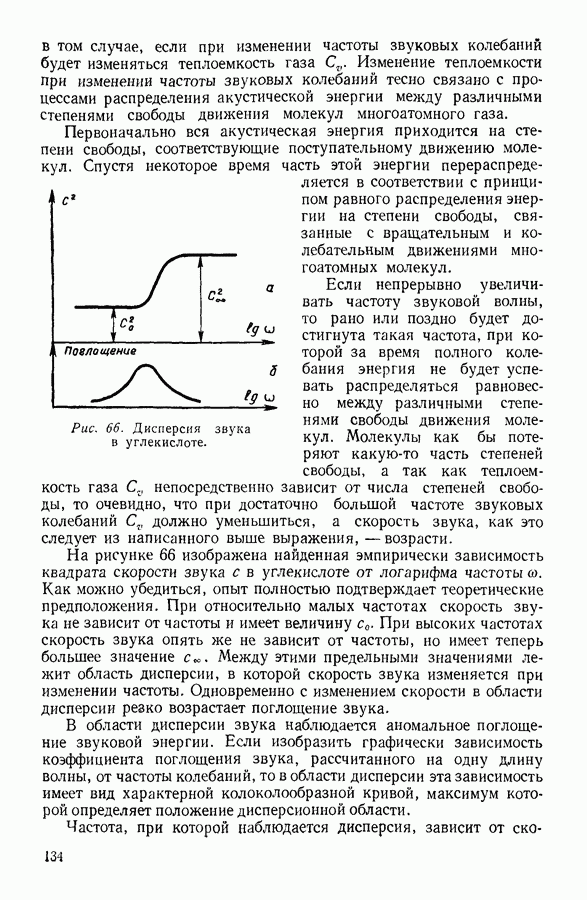
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
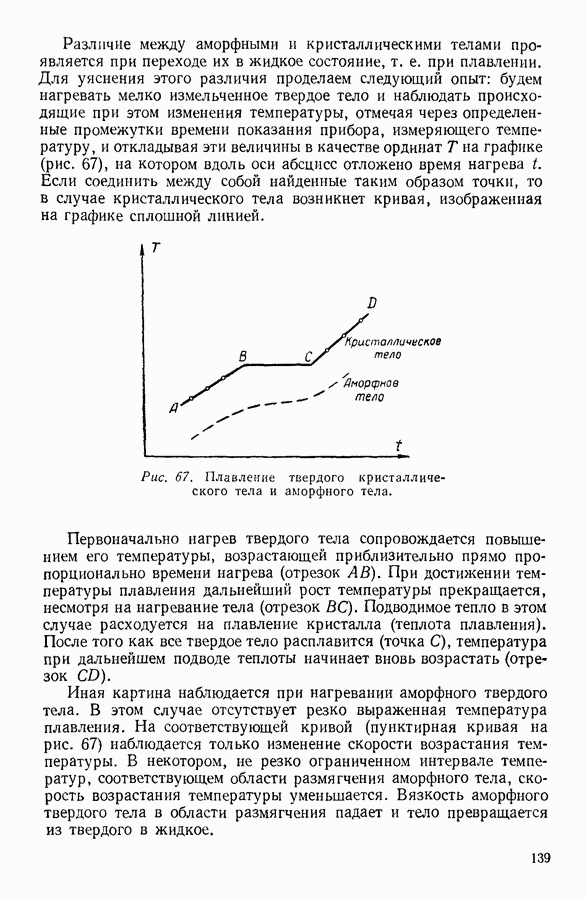
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
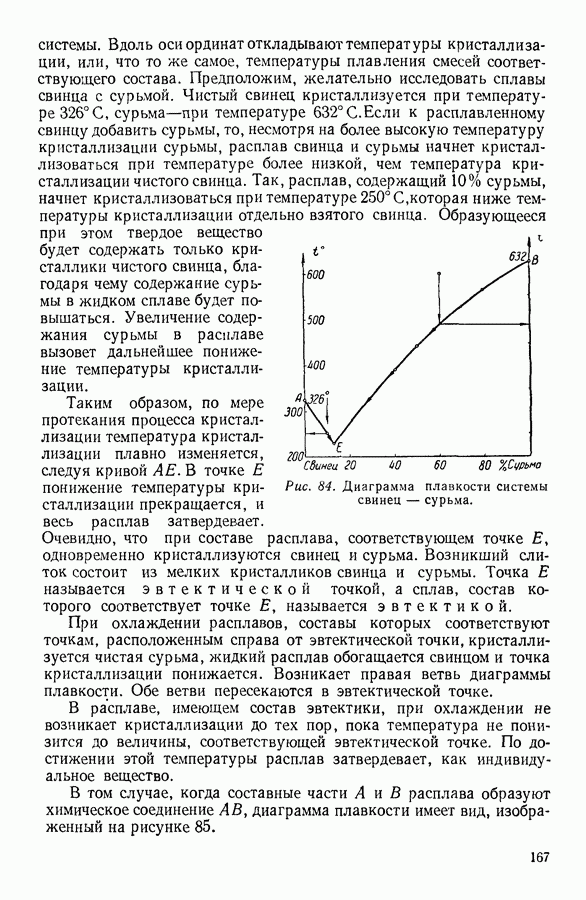
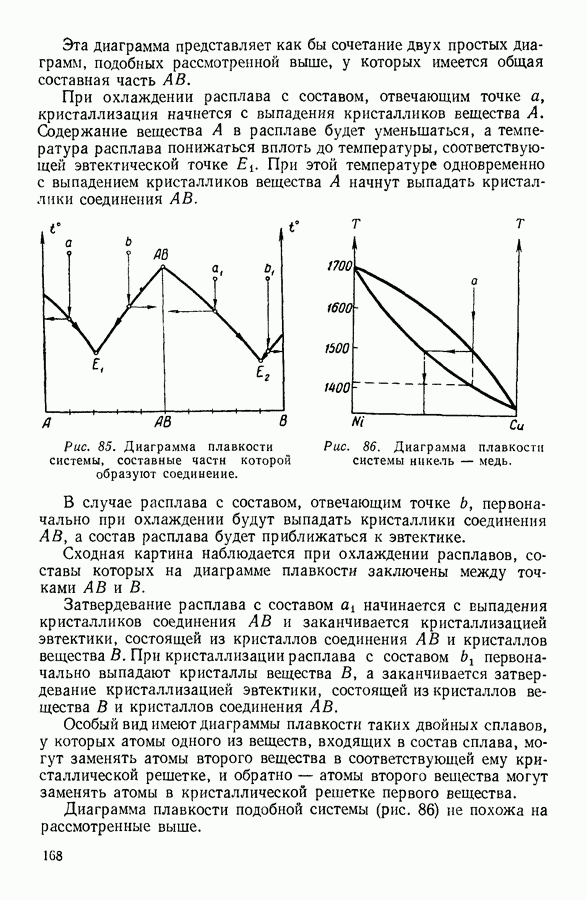
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»