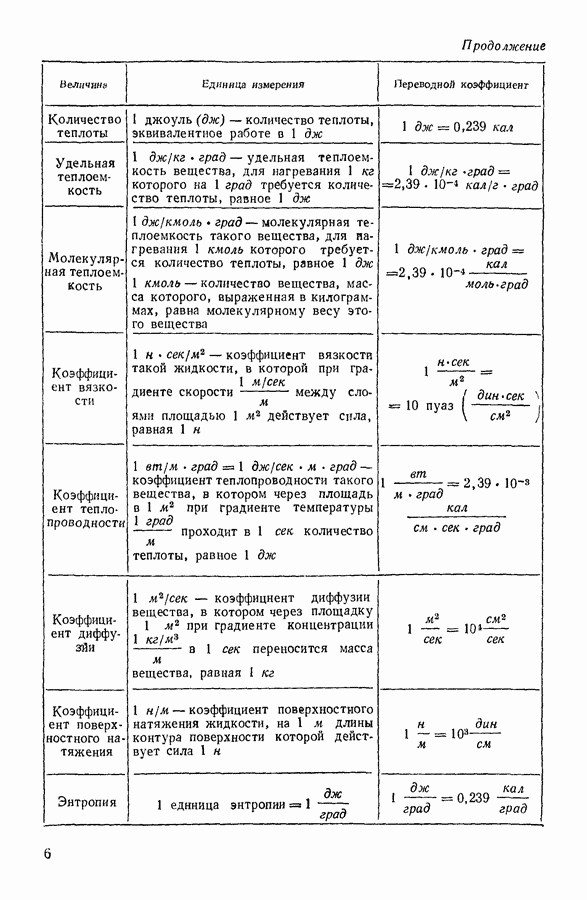
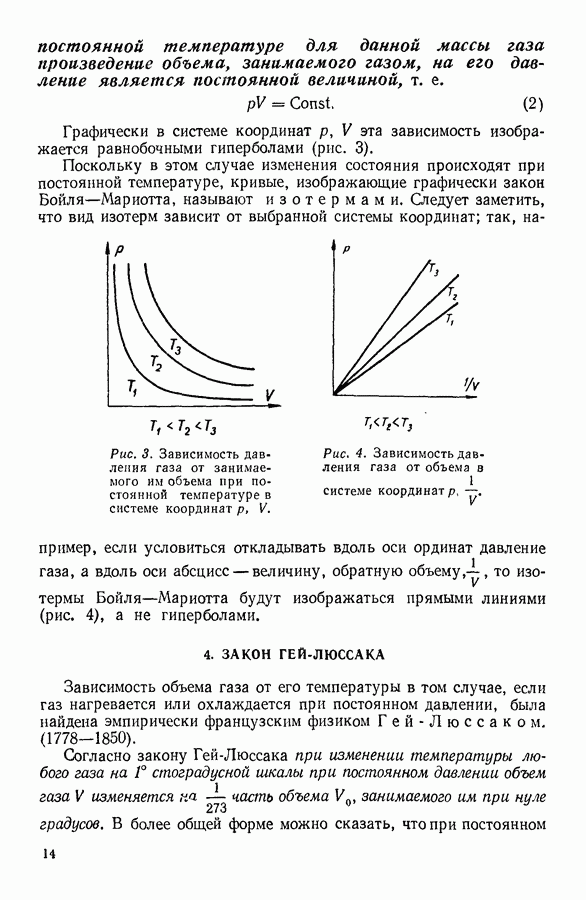
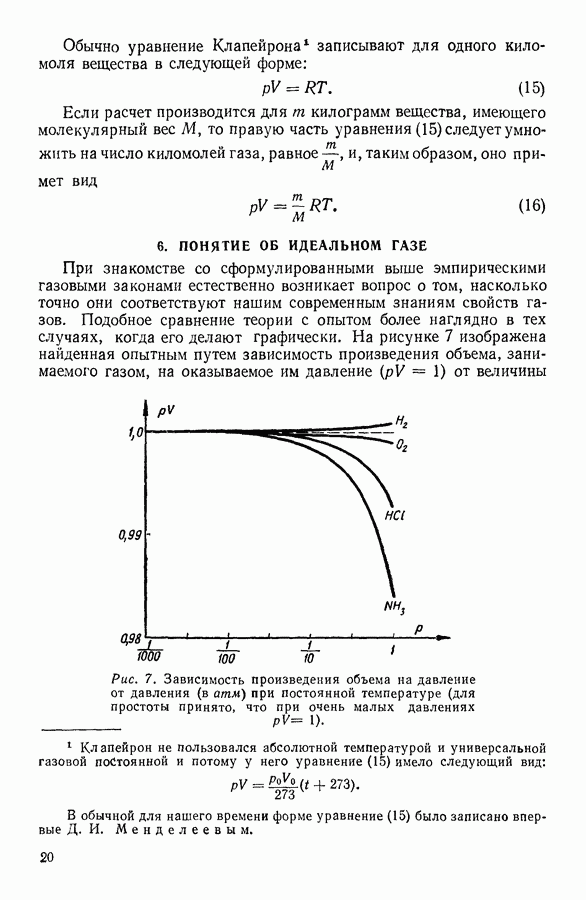
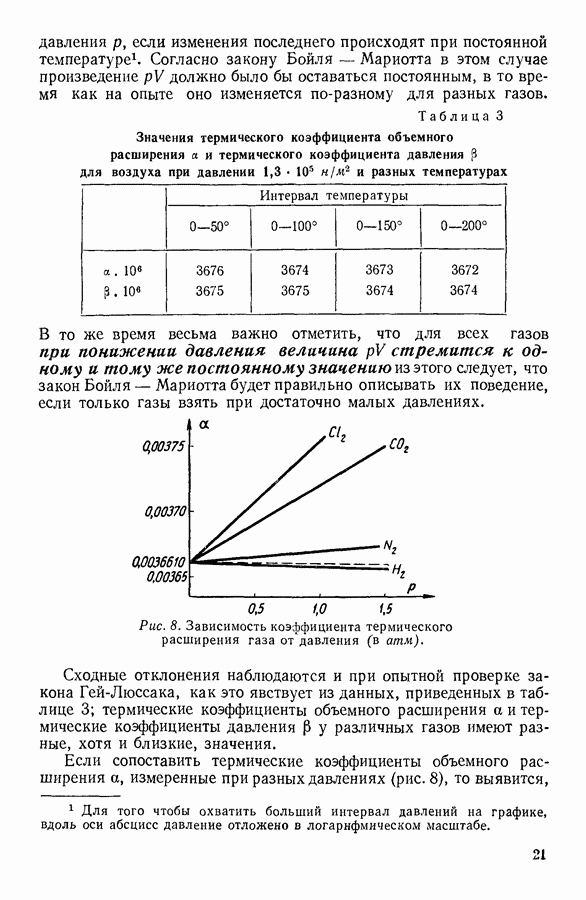
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
В современной молекулярно-кинетической теории материи различные агрегатные состояния вещества связывают с различной степенью упорядоченности в расположении его частиц. Для газообразного состояния характерно полностью беспорядочное, хаотичное расположение молекул. В противоположность этому в идеальном кристалле частицы расположены в строгом порядке, распространяющемся на весь кристалл. Правильное расположение частиц в кристаллических твердых телах подтверждается экспериментально опытами по рассеянию рентгеновских лучей кристаллами.
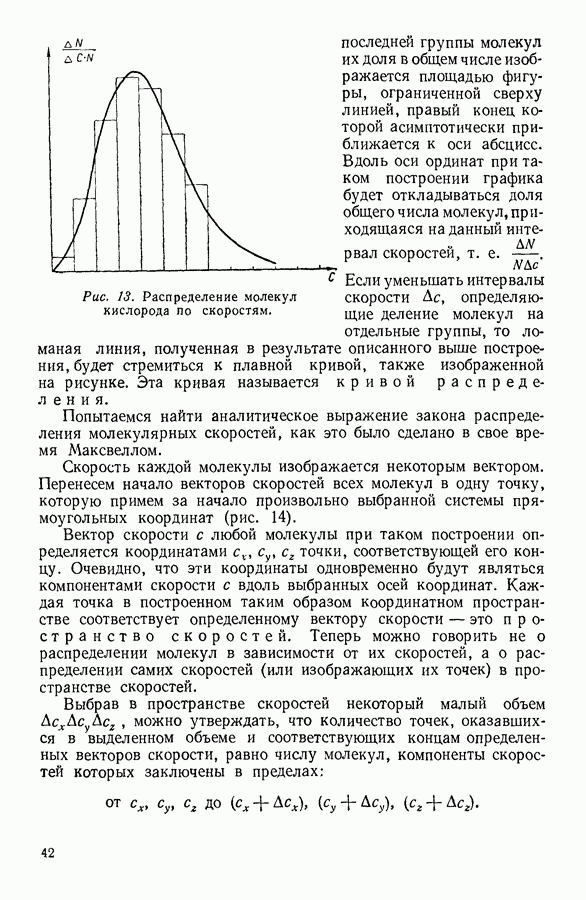
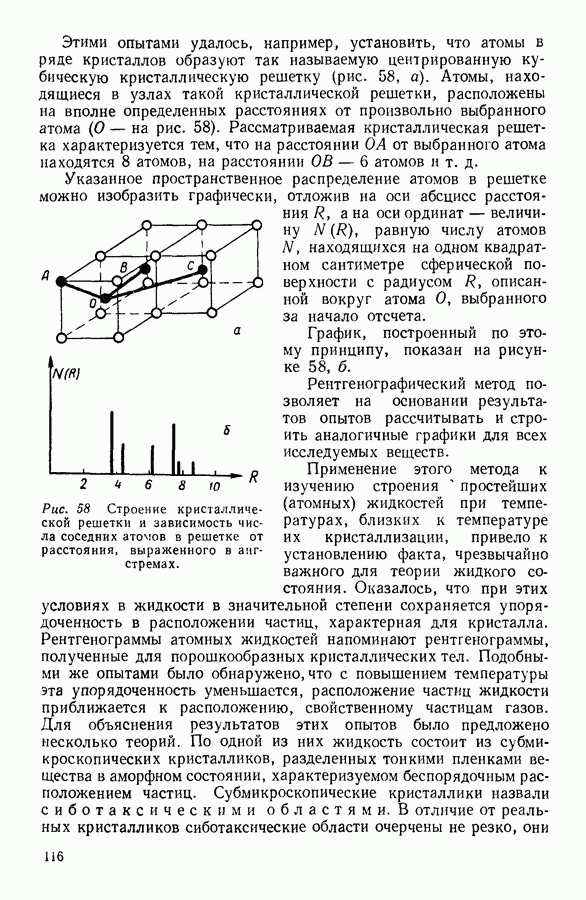
Этими опытами удалось, например, установить, что атомы в ряде кристаллов образуют так называемую центрированную кубическую кристаллическую решетку (рис. 58, а). Атомы, находящиеся в узлах такой кристаллической решетки, расположены на вполне определенных расстояниях от произвольно выбранного атома (О — на рис. 58). Рассматриваемая кристаллическая решетка характеризуется тем, что на расстоянии  от выбранного атома находятся 8 атомов, на расстоянии
от выбранного атома находятся 8 атомов, на расстоянии  атомов и т. д.
атомов и т. д.
Указанное пространственное распределение атомов в решетке можно изобразить графически, отложив на оси абсцисс расстояния  а на оси ординат — величину
а на оси ординат — величину  равную числу атомов
равную числу атомов  находящихся на одном квадратном сантиметре сферической поверхности с радиусом
находящихся на одном квадратном сантиметре сферической поверхности с радиусом  описанной вокруг атома О, выбранного за начало отсчета.
описанной вокруг атома О, выбранного за начало отсчета.
График, построенный по этому принципу, показан на рисунке 58, б.

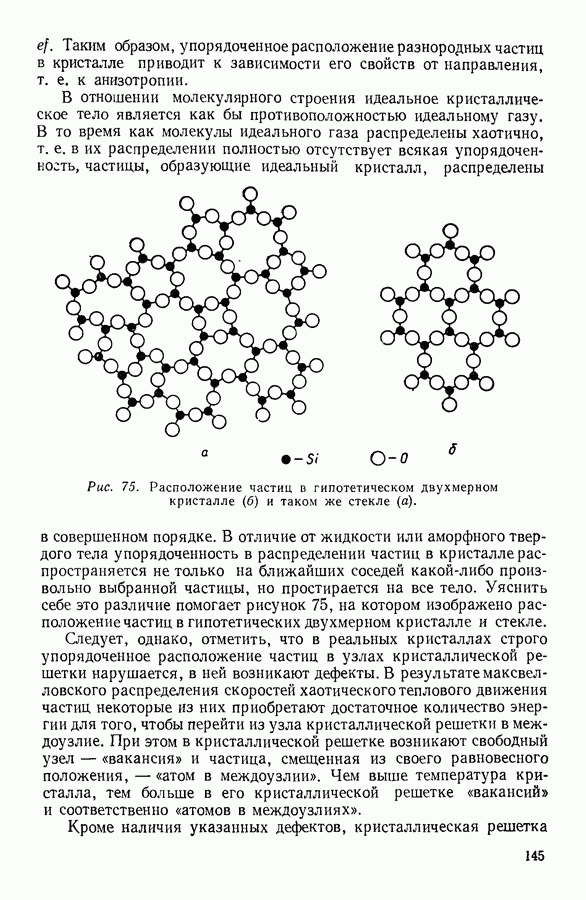
Рис. 58 Строение кристаллической решетки и зависимость числа соседних атомов в решетке от расстояния, выраженного в ангстремах.
Рентгенографический метод позволяет на основании результатов опытов рассчитывать и строить аналогичные графики для всех исследуемых веществ.
Применение этого метода к изучению строения простейших (атомных) жидкостей при температурах, близких к температуре их кристаллизации, привело к установлению факта, чрезвычайно важного для теории жидкого состояния. Оказалось, что при этих условиях в жидкости в значительной степени сохраняется упорядоченность в расположении частиц, характерная для кристалла. Рентгенограммы атомных жидкостей напоминают рентгенограммы, полученные для порошкообразных кристаллических тел. Подобными же опытами было обнаружено, что с повышением температуры эта упорядоченность уменьшается, расположение частиц жидкости приближается к расположению, свойственному частицам газов. Для объяснения результатов этих опытов было предложено несколько теорий. По одной из них жидкость состоит из субмикроскопических кристалликов, разделенных тонкими пленками вещества в аморфном состоянии, характеризуемом беспорядочным расположением частиц. Субмикроскопические кристаллики назвали сиботаксическими областями. В отличие от реальных кристалликов сиботаксические области очерчены не резко, они
плавно переходят в области неупорядоченного расположения, частиц. Кроме того, сиботаксические области непостоянны, они непрерывно разрушаются и возникают вновь. Наличие областей упорядоченного расположения частиц приводит к тому, что у большинства молекул жидкости соседние с ними частицы располагаются в определенном, характерном для данной жидкости порядке. Однако благодаря хаотической ориентации отдельных сиботаксических групп в отношении друг друга упорядоченное расположение молекул распространяется только на ближайших к данной молекуле соседей.

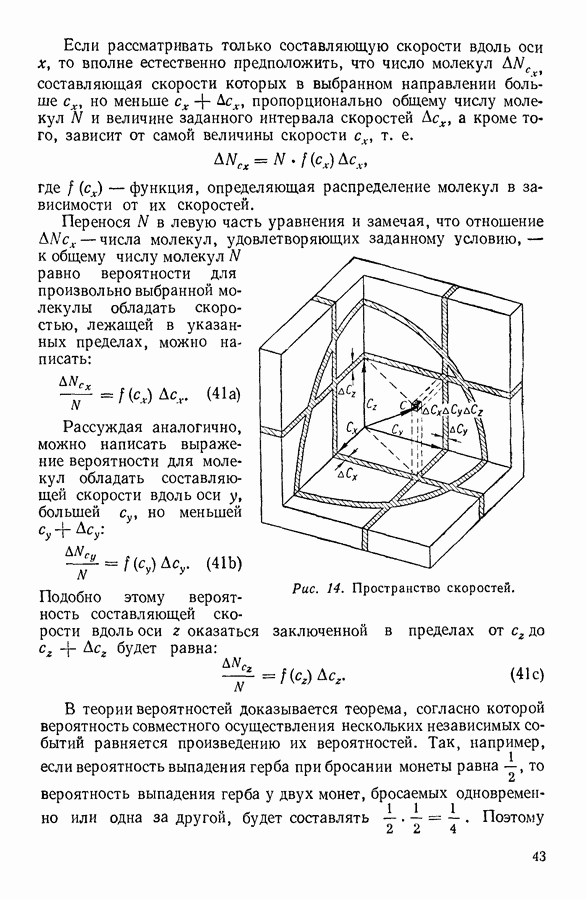
Рис. 59. Сравнение строения идеального кристалла и жидкости.
На расстоянии трех-четырех молекулярных диаметров упорядоченность уменьшается столь сильно, что теряет смысл говорить о правильном порядке в расположении частиц вещества.
В настоящее время считается общепризнанным, что жидкости свойственна упорядоченность ближнего порядка в расположении ее частиц в отличие от кристаллов, которые характеризуются упорядоченностью дальнего порядка.
Различие в строении кристаллического тела и жидкости схематично показано на рисунке 59. Слева на рисунке изображено строение идеального гипотетического кристалла. Его структурные частицы в любом месте кристалла занимают строго определенное положение относительно друг друга. Однако в жидкостях (на рисунке — справа), в окрестности произвольно выбранной молекулы О, соседние молекулы могут иметь расположение, как весьма близкое к кристаллическому (направление  так и отличное от него (направление
так и отличное от него (направление  Во всяком случае, в жидкости наблюдается почти «кристаллическое» расположение соседних молекул («ближний порядок») и нарушение строгого порядка в расположении дальних молекул (отсутствие «дальнего порядка»).
Во всяком случае, в жидкости наблюдается почти «кристаллическое» расположение соседних молекул («ближний порядок») и нарушение строгого порядка в расположении дальних молекул (отсутствие «дальнего порядка»).
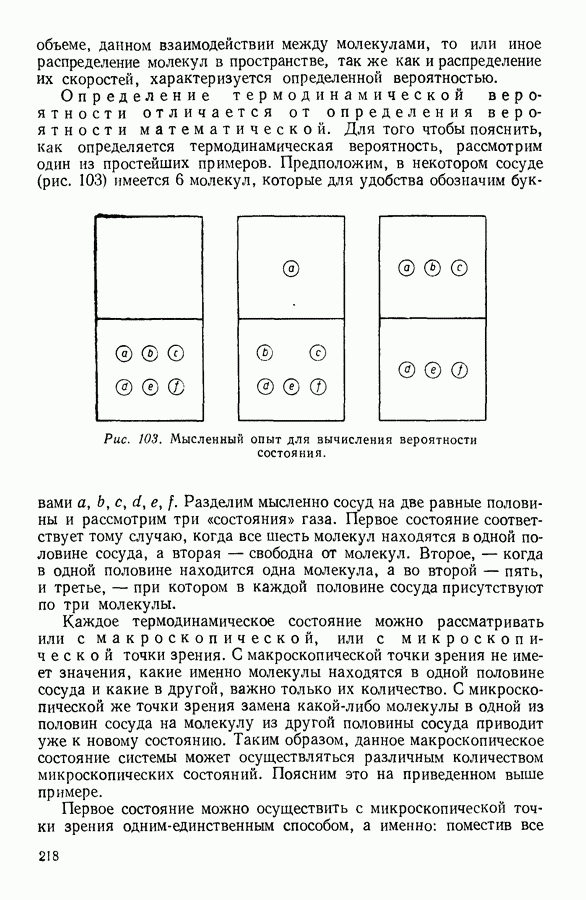
Следует также обратить внимание на то, что на рассматриваемом рисунке число частиц, расположенных упорядоченно (рис. 59, а)
одинаково с числом частиц, которые расположены неупорядоченно (рис. 59, б). Сравнение соответствующих площадей убеждает в том, что при характерном для жидкости неупорядоченном расположении частиц она занимает больший объем, чем при упорядоченном, кристаллическом.
Результаты рентгеноструктурного исследования жидкостей можно объяснить также, исходя из представления о квазикристаллической структуре жидкости. Для того чтобы пояснить это, обратимся к расположению атомов в идеальном кристалле. Если мысленно выбрать какой-либо атом в таком кристалле и постараться определить, какова вероятность встретить соседний атом на расстоянии  от первого, то при отсутствии теплового движения искомая вероятность равнялась бы нулю на расстояниях, меньших расстояния
от первого, то при отсутствии теплового движения искомая вероятность равнялась бы нулю на расстояниях, меньших расстояния  при котором она делалась бы равной единице. Это означает, что в данном направлении соседний атом всегда встречался бы на одном и том же расстоянии от исходного.
при котором она делалась бы равной единице. Это означает, что в данном направлении соседний атом всегда встречался бы на одном и том же расстоянии от исходного.
На расстояниях, больших  но меньших
но меньших  искомая вероятность вновь равнялась бы нулю, а на расстоянии
искомая вероятность вновь равнялась бы нулю, а на расстоянии  единице. Такое положение повторялось бы на всем протяжении кристалла: вероятность встретить атом равнялась бы единице для всех расстояний, кратных
единице. Такое положение повторялось бы на всем протяжении кристалла: вероятность встретить атом равнялась бы единице для всех расстояний, кратных 
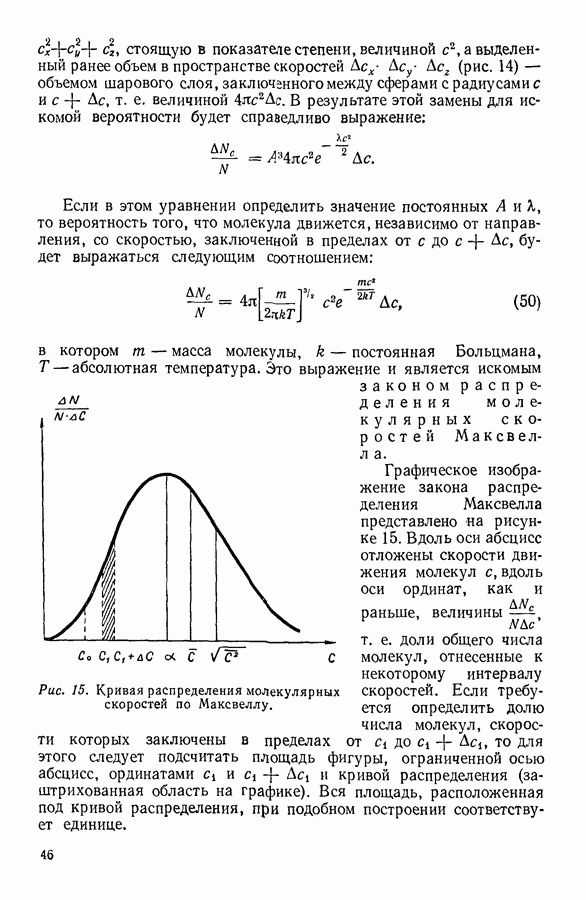
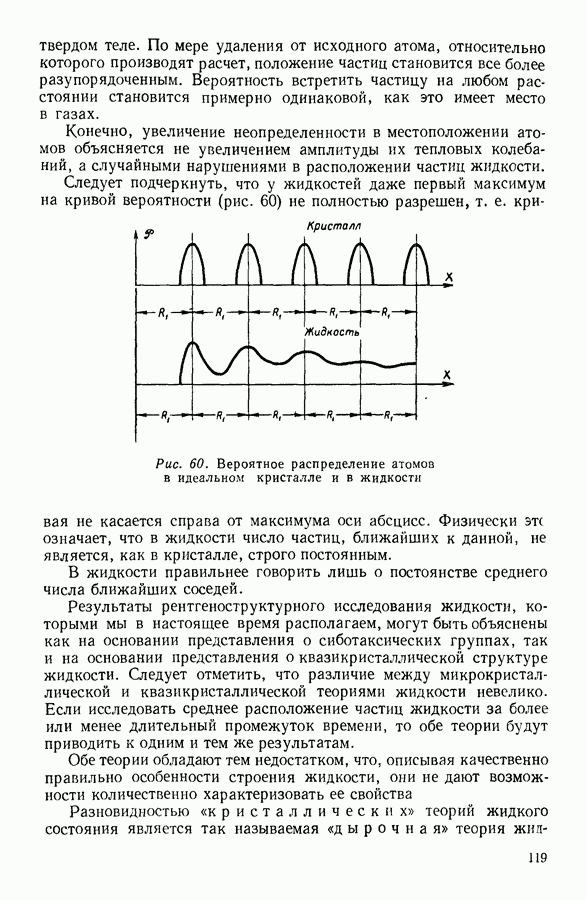
Тепловое колебательное движение атомов в кристалле приводит к тому, что вероятность встретить соседний атом будет не равна нулю также и на расстояниях, незначительно отличающихся от  В одном случае соседний атом, совершая колебания, слегка приблизится к тому, от которого ведется отсчет, а в другом случае — удалится. Графически изменение вероятности встретить атом в зависимости от расстояния между ним и атомом, выбранным за начало отсчета, изображается характерной кривой (верхняя часть рисунка 60).
В одном случае соседний атом, совершая колебания, слегка приблизится к тому, от которого ведется отсчет, а в другом случае — удалится. Графически изменение вероятности встретить атом в зависимости от расстояния между ним и атомом, выбранным за начало отсчета, изображается характерной кривой (верхняя часть рисунка 60).
Отличительной чертой графика является постоянство ширины отдельных колоколообразных участков кривой. Именно это постоянство указывает на сохранение упорядоченности на всем протяжении кристалла.
В жидкости наблюдается иная картина (рис. 60, внизу). Качественно вероятность  встретить атом на каком-либо расстоянии от исходного атома изменяется подобно тому, как это имеет место в кристалле. Однако в этом случае только первый колоколообразный участок кривой выражен в виде четкого максимума. Последующие колоколообразные участки, расширяясь, взаимно перекрываются, так что максимумы на кривой сравнительно быстро исчезают.
встретить атом на каком-либо расстоянии от исходного атома изменяется подобно тому, как это имеет место в кристалле. Однако в этом случае только первый колоколообразный участок кривой выражен в виде четкого максимума. Последующие колоколообразные участки, расширяясь, взаимно перекрываются, так что максимумы на кривой сравнительно быстро исчезают.
Таким образом, расположение близких друг к другу частиц в жидкости напоминает расположение частиц в кристаллическом
твердом теле. По мере удаления от исходного атома, относительно которого производят расчет, положение частиц становится все более разупорядоченным. Вероятность встретить частицу на любом расстоянии становится примерно одинаковой, как это имеет место в газах.
Конечно, увеличение неопределенности в местоположении атомов объясняется не увеличением амплитуды их тепловых колебаний, а случайными нарушениями в расположении частиц жидкости.
Следует подчеркнуть, что у жидкостей даже первый максимум на кривой вероятности (рис. 60) не полностью разрешен, т. е. кривая не касается справа от максимума оси абсцисс.

Рис. 60. Вероятное распределение атомов в идеальном кристалле и в жидкости
Физически это означает, что в жидкости число частиц, ближайших к данной, не является, как в кристалле, строго постоянным.
В жидкости правильнее говорить лишь о постоянстве среднего числа ближайших соседей.
Результаты рентгеноструктурного исследования жидкости, которыми мы в настоящее время располагаем, могут быть объяснены как на основании представления о сиботаксических группах, так и на основании представления о квазикристаллической структуре жидкости. Следует отметить, что различие между микрокристаллической и квазикристаллической теориями жидкости невелико. Если исследовать среднее расположение частиц жидкости за более или менее длительный промежуток времени, то обе теории будут приводить к одним и тем же результатам.
Обе теории обладают тем недостатком, что, описывая качественно правильно особенности строения жидкости, они не дают возможности количественно характеризовать ее свойства
Разновидностью «кристаллических» теорий жидкого состояния является так называемая «дырочная» теория
жидкости. Согласно этой теории жидкость уподобляется кристаллу, в котором большое количество атомов оказывается смещенным из присущих им равновесных положений. При смещении атома из равновесного положения остается как бы свободное место, которое и называется «дыркой».
Согласно теории «дырки» в жидкости — это более или менее расширенные промежутки между молекулами, возникающие спонтанно, расширяющиеся, а затем сжимающиеся и вновь исчезающие.
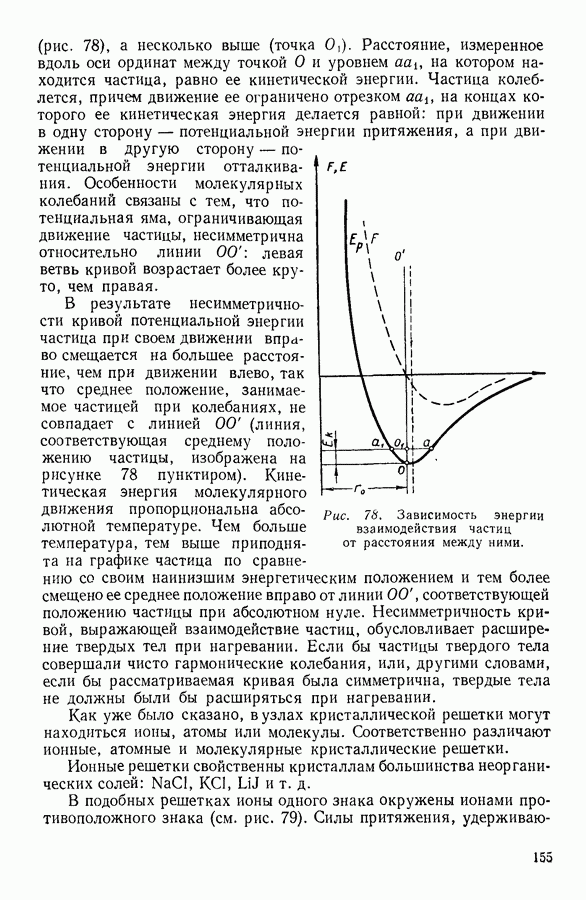
Уравнение состояния в «дырочной» теории жидкости имеет, согласно Я. И. Френкелю, следующий вид:

Здесь V — молярный объем жидкости при температуре  минимальный объем, который может занимать жидкость;
минимальный объем, который может занимать жидкость;  энергия образования дырки;
энергия образования дырки;  постоянная Больцмана;
постоянная Больцмана;  число Авогадро;
число Авогадро;  минимальный объем дырки.
минимальный объем дырки.
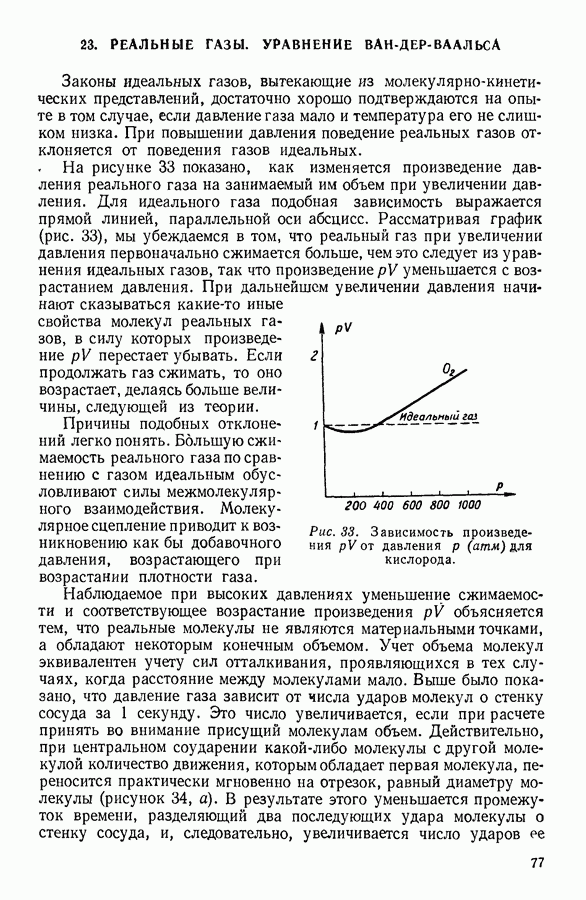
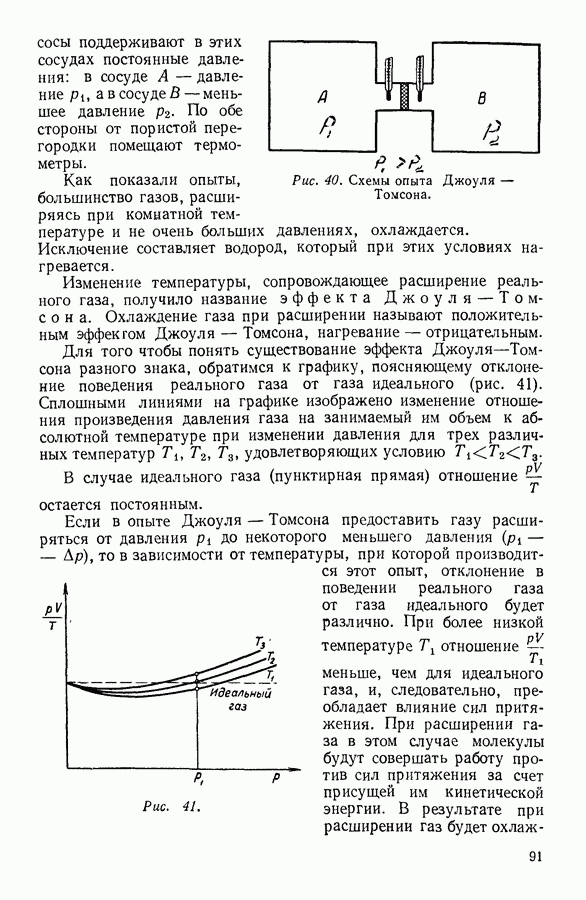
Как уже неоднократно подчеркивалось, по мере увеличения температуры сходство жидкостей с твердыми телами уменьшается и возрастает сходство их с соответствующими газами. Поэтому не удивительно, что при объяснении свойств жидкостей наряду с рассмотренными выше «кристаллическими» моделями жидкости широкое распространение приобрели теории, в которых жидкость уподобляется сильно сжатому газу. В этих теориях большую роль играет представление о свободном объеме жидкости, определить который точно затруднительно. Существующие в настоящее время методы вычисления свободного объема жидкости являются грубо приближенными и приводят, как правило, к величинам, расходящимся между собой.
Из теорий свободного объема наиболее разработана так называемая «ячеечная» теория жидкости.
Благодаря тому что молекулы жидкости расположены близко друг к другу, каждую из них можно рассматривать как заключенную в ячейку, стенки которой образуют ее ближайшие соседи. Молекулы могут меняться местами, так что молекула, находящаяся в центре мысленно выделенной ячейки, может спустя некоторое время перейти в соседнюю ячейку. Однако подобные миграции частиц происходят сравнительно редко, и большую часть времени молекула проводит внутри данной ячейки.
Движение молекулы в ячейке происходит в силовом поле, образованном ее ближайшими соседями, число которых для простых жидкостей полагают равным 12.
Поскольку данная теория применима к жидкостям, находящимся при высоких температурах, когда влияние структуры вещества практически не сказывается, можно считать силовое поле, в котором происходит движение частицы, сферически симметричным.
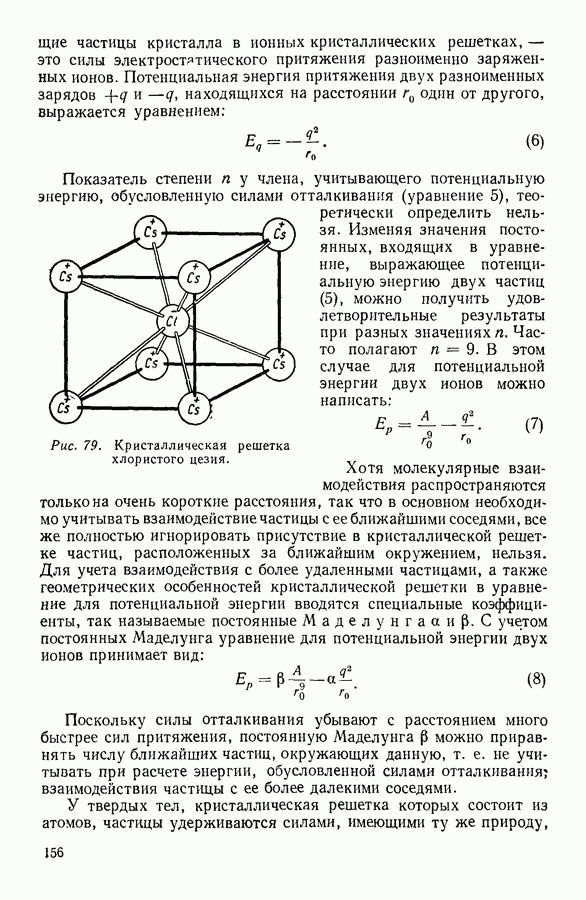
Принимая далее определенную форму зависимости потенциальной энергии молекулярного взаимодействия от расстояния между частицами и делая ряд упрощающих предположений, можно найти выражение для потенциальной энергии  частицы, находящейся в элементарной ячейке. Обычно этому выражению придают следующий вид:
частицы, находящейся в элементарной ячейке. Обычно этому выражению придают следующий вид:

где V — объем сферической ячейки, приходящейся на одну частицу, а  постоянные.
постоянные.
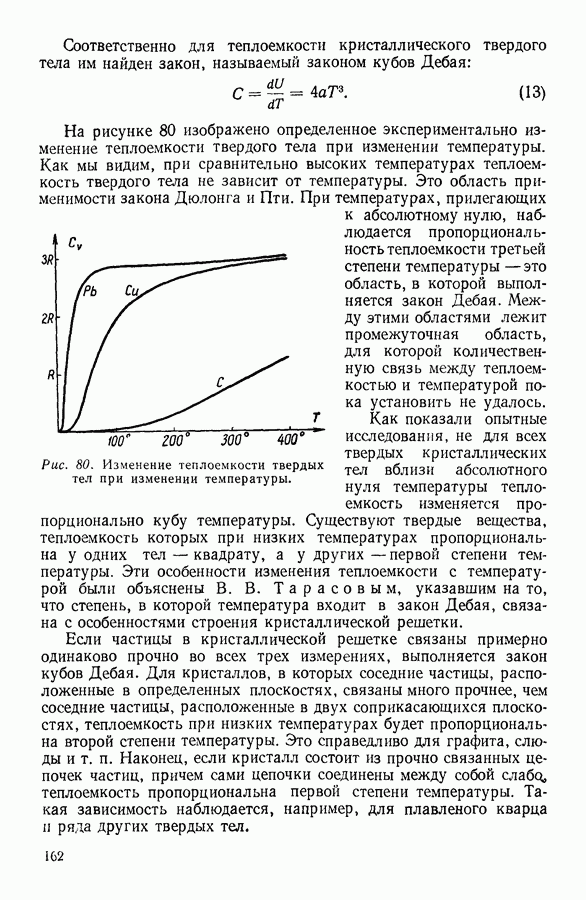
Уравнение состояния жидкости в этом случае можно будет записать в следующей форме:

Здесь  давление,
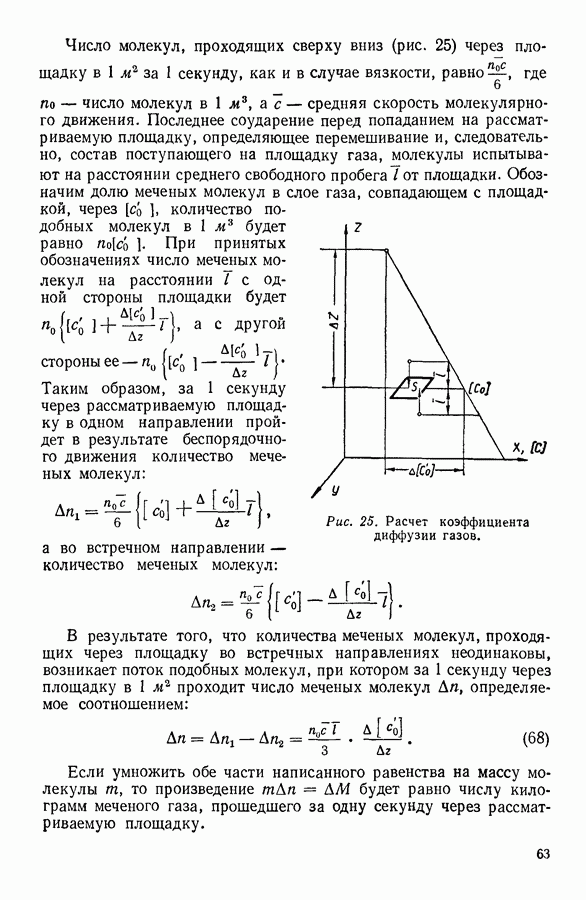
давление,  постоянная Больцмана и
постоянная Больцмана и  температура. Подставляя в последнее выражение значение
температура. Подставляя в последнее выражение значение  удается выразить количественно многие физико-химические характеристики индивидуальных жидкостей. Так, например, пользуясь ячеечной теорией жидкости, можно вычислить критические параметры различных простых веществ. Рассчитанные значения критической температуры в случае простейших газов оказались равными по абсолютной шкале для водорода 41°, неона 47°, азота 128° и аргона 160°, экспериментальные же значения соответственно равны 33°, 44°, 126° и 150° К. В приведенном примере согласие величин, рассчитанных теоретически, с величинами, найденными на опыте, вполне удовлетворительное.
удается выразить количественно многие физико-химические характеристики индивидуальных жидкостей. Так, например, пользуясь ячеечной теорией жидкости, можно вычислить критические параметры различных простых веществ. Рассчитанные значения критической температуры в случае простейших газов оказались равными по абсолютной шкале для водорода 41°, неона 47°, азота 128° и аргона 160°, экспериментальные же значения соответственно равны 33°, 44°, 126° и 150° К. В приведенном примере согласие величин, рассчитанных теоретически, с величинами, найденными на опыте, вполне удовлетворительное.
Необходимо, однако, отметить, что написанное выше выражение для давления, строго говоря, справедливо для реального газа, а не для жидкости, и потому ожидать очень хорошего согласия теории с опытом нет оснований. Несмотря на это замечание, теория свободного объема имеет свои достоинства, среди которых следует отметить простоту использованных физических моделей и возможность количественного сравнения теории с опытом.
Ячеечная теория дает возможность относительно просто объяснить свойства жидкостей и рассчитать в первом приближении некоторые их характеристики.
Теоретически более строгой является статистическая теория жидкости. В этой теории основную роль играют две физические величины. Первая из этих величин называется раднальной функцией распределения, вторая — меж молекулярным потенциалом. Радиальная
функция распределения определяет вероятность встретить произвольно выбранную пару частиц в жидкости на некотором заданном расстоянии, заключенном в пределах от  до
до  Межмолекулярный потенциал определяет взаимодействие молекул жидкости. Знание этих двух величин позволяет написать теоретически строго уравнения состояния и энергии жидкости и выразить количественно ее различные физико-химические характеристики.
Межмолекулярный потенциал определяет взаимодействие молекул жидкости. Знание этих двух величин позволяет написать теоретически строго уравнения состояния и энергии жидкости и выразить количественно ее различные физико-химические характеристики.
Радиальную функцию распределения для ряда жидкостей можно определить экспериментально на основании данных рентгено-структурного анализа. Однако значительные трудности в определении и расчете межмолекулярного потенциала для конкретных жидкостей заставляют решать полученные уравнения приближенно.
Указанное обстоятельство затрудняет количественное сопоставление статистической теории жидкости с опытом. Нельзя, однако, забывать, что эта теория качественно правильно предсказывает многие свойства жидкостей и присущие им закономерности.
Именно в возможности правильно предвидеть различные свойства вещества заключается одно из преимуществ статистической теории жидкого состояния.
В будущем, когда будет найдено теоретически строгое выражение для межмолекулярного потенциала и преодолены вычислительные затруднения, статистическая теория позволит лучше понять особенности жидкого состояния вещества.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
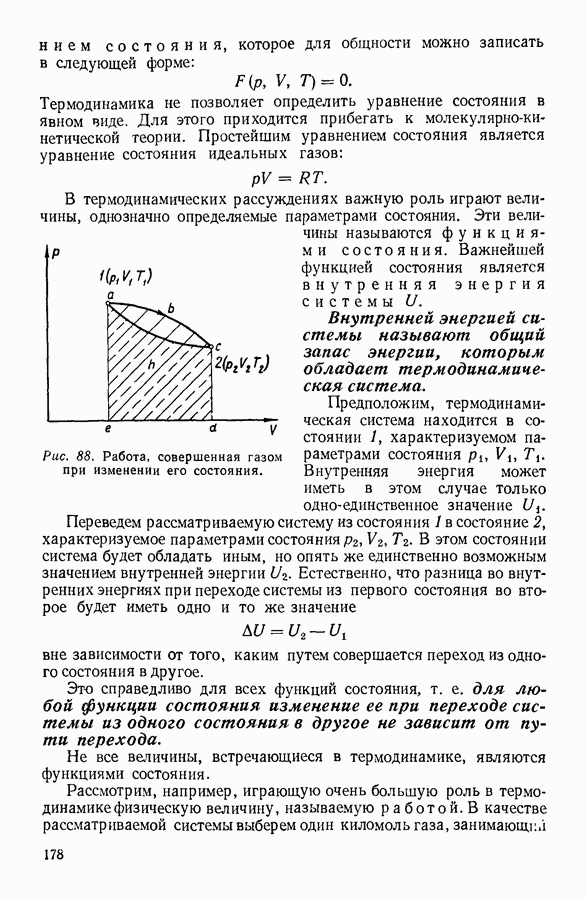
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
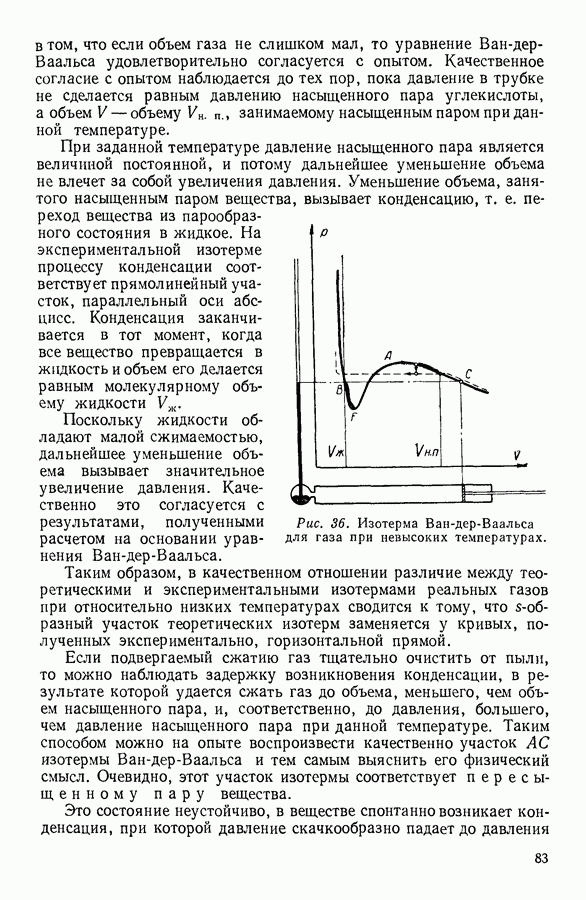
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
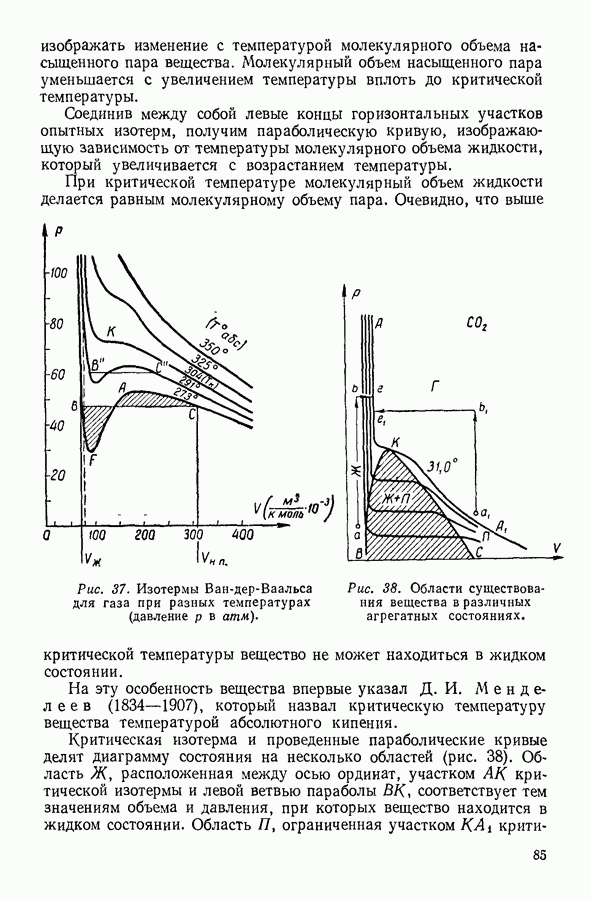
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
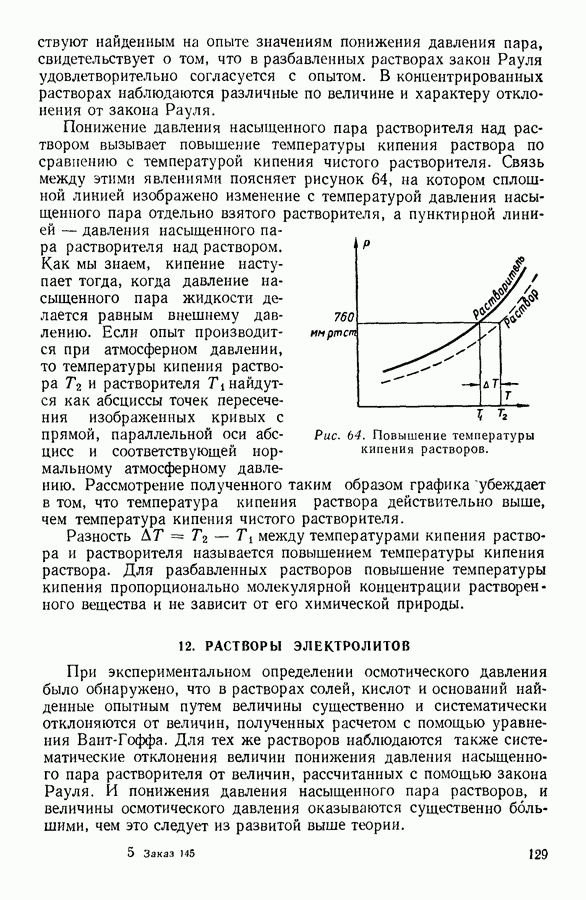
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
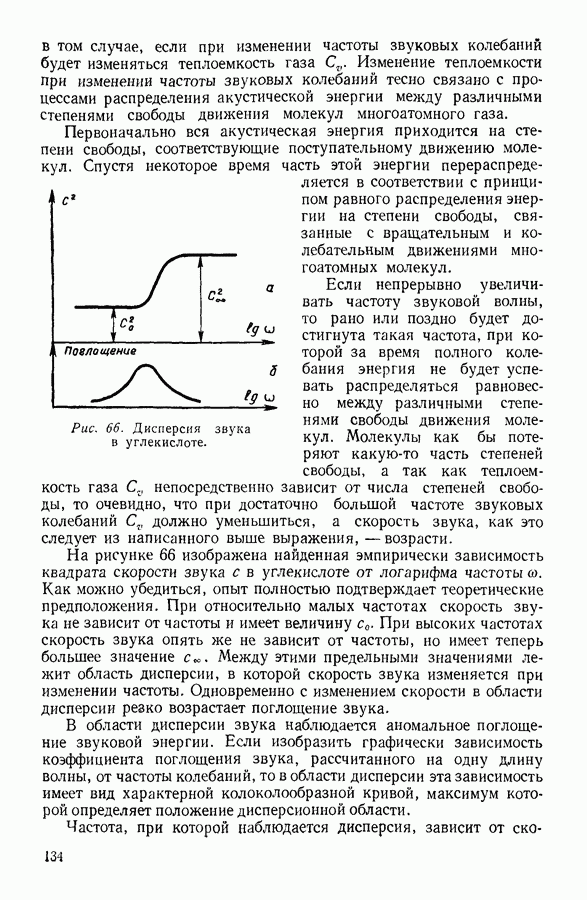
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
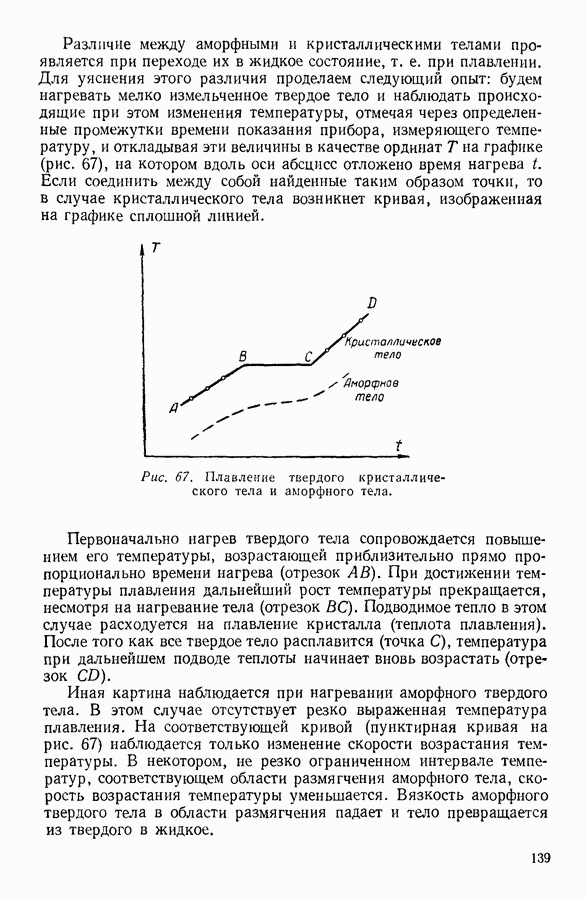
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
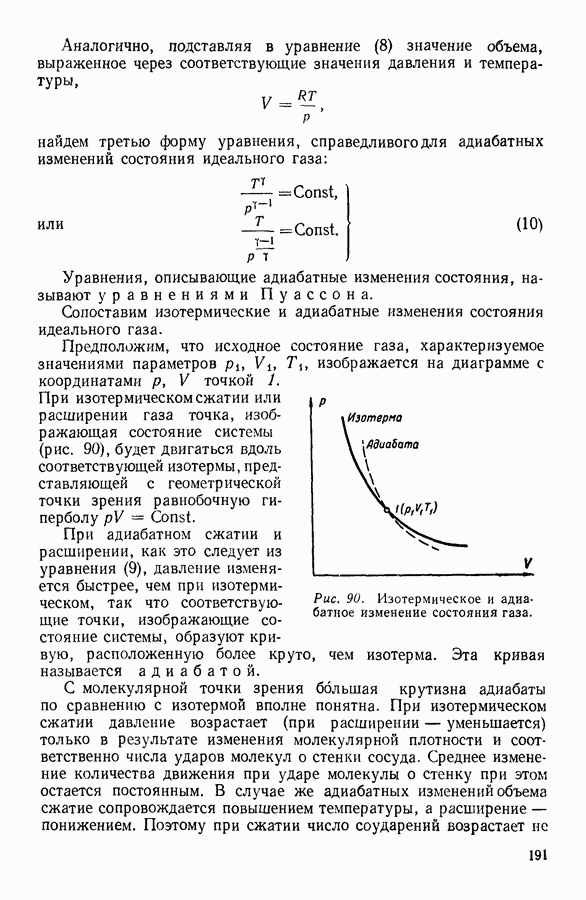
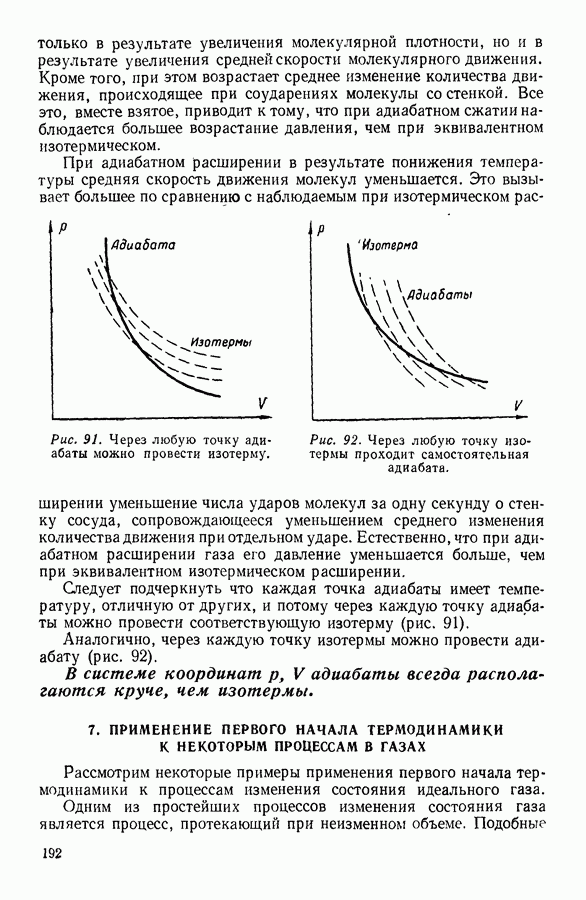
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
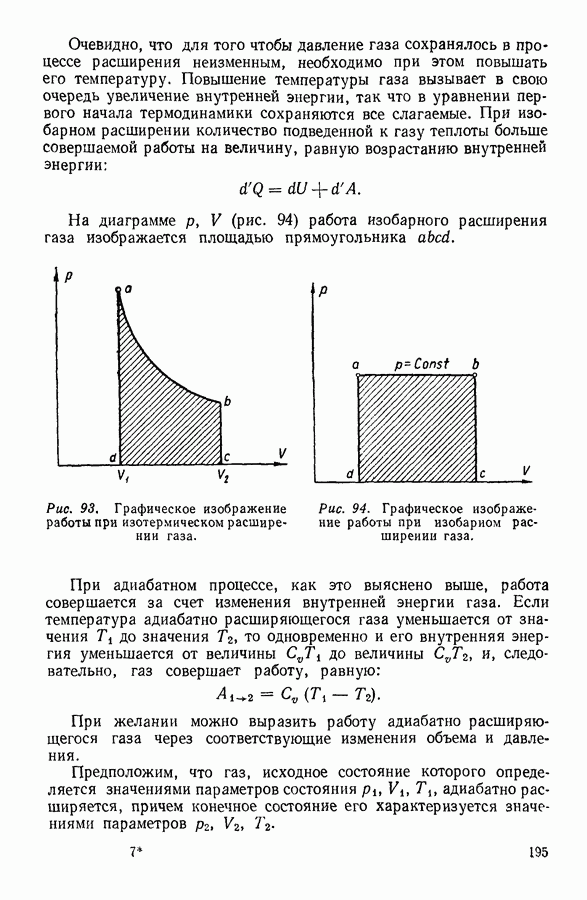
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
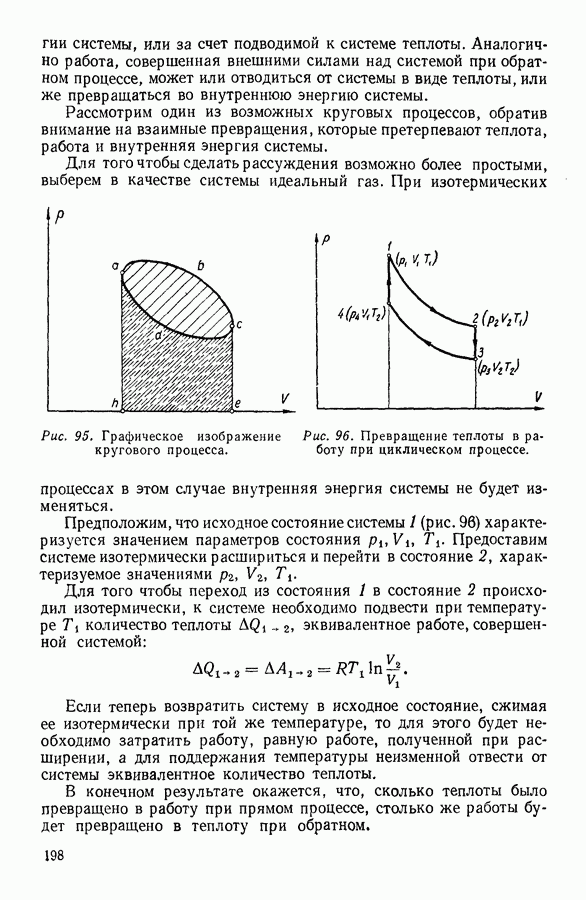
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
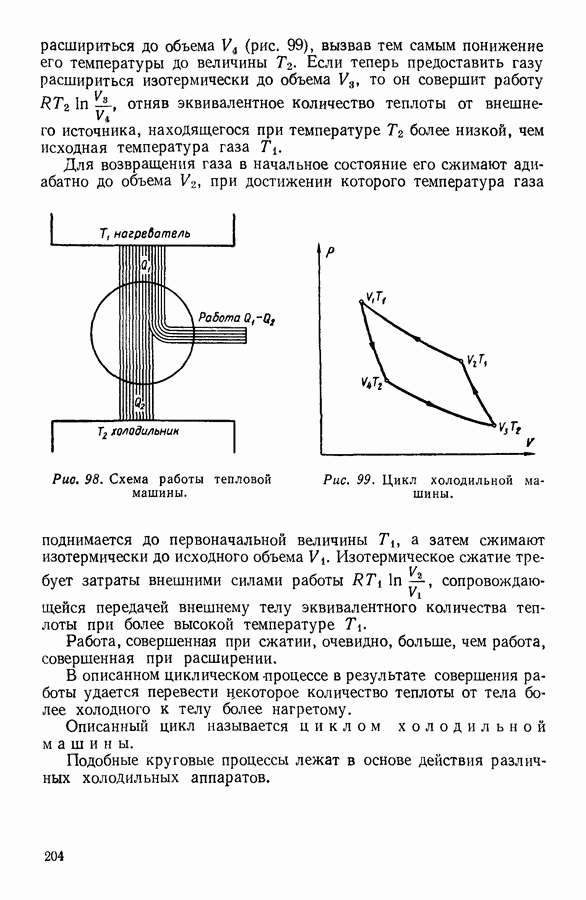
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»