| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
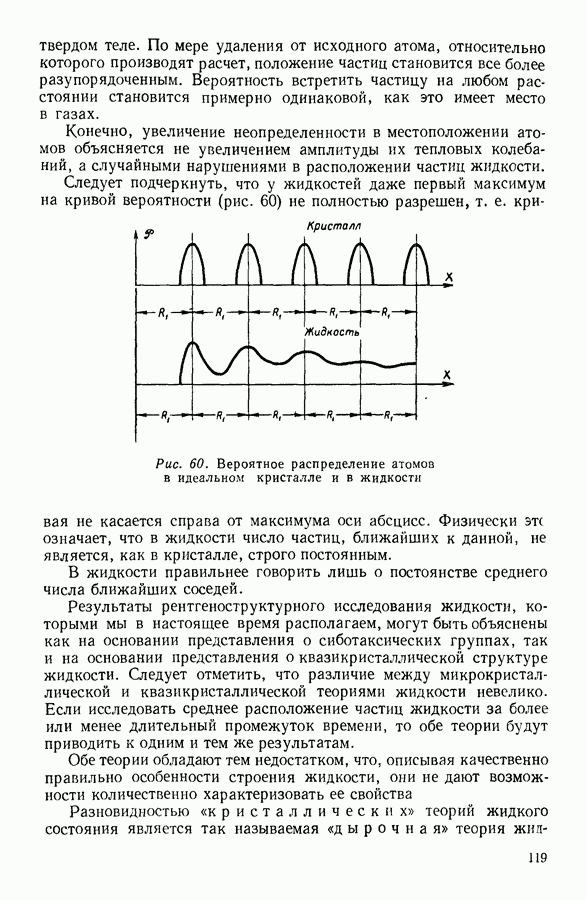
12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
В предыдущих рассуждениях принималось, что молекулы газа могут двигаться с самыми различными скоростями, начиная с очень малых и кончая бесконечно большими. Как распределяются при
этом молекулы в зависимости от их скоростей: сколько молекул движется быстро и сколько медленно — не обсуждалось. Это оправдывалось тем, что при подсчете давления распределение молекулярных скоростей не играет никакой роли. Величина давления определяется кинетической энергией молекул в единице объема вне зависимости от того, как эта кинетическая энергия делится между отдельными молекулами.
Хаотичность молекулярного движения может вообще породить сомнение в возможности решить задачу о распределении скоростей молекул. Но, как мы убедимся ниже, подобную задачу решить можно, и впервые это было сделано К. Максвеллом, нашедшим закон распределения молекул по скоростям. Строгое обоснование закона распределения принадлежит  Больцману, который показал, что, каким бы ни было в начальный момент распределение скоростей молекул, оно с неизбежностью переходит в распределение, следующее из закона Максвелла, если только температуру газа поддерживать неизменной достаточно долго.
Больцману, который показал, что, каким бы ни было в начальный момент распределение скоростей молекул, оно с неизбежностью переходит в распределение, следующее из закона Максвелла, если только температуру газа поддерживать неизменной достаточно долго.
Конечно, хаотичный характер молекулярного движения накладывает свой отпечаток на закон распределения молекул по скоростям и его формулировку. Нельзя, например, ставить вопрос о том, сколько молекул в данном объеме газа в какой-либо момент времени движется со скоростью, в точности равной  В силу случайного, беспорядочного характера движения молекул даже при очень большом числе их в рассматриваемом объеме газа может не оказаться ни одной молекулы, удовлетворяющей этому условию. По указанной причине в дальнейшем всегда будет говориться о числе молекул, скорости которых заключены в некотором интервале скоростей, скажем о числе молекул, скорости которых больше некоторой величины
В силу случайного, беспорядочного характера движения молекул даже при очень большом числе их в рассматриваемом объеме газа может не оказаться ни одной молекулы, удовлетворяющей этому условию. По указанной причине в дальнейшем всегда будет говориться о числе молекул, скорости которых заключены в некотором интервале скоростей, скажем о числе молекул, скорости которых больше некоторой величины  но меньше величины
но меньше величины 
Кроме того, нельзя гарантировать, что указанное число молекул будет во всех случаях точно соответствовать действительности. В данном случае следует говорить о вероятности встретить в газе данное число интересующих нас молекул. При этом необходимо иметь в виду, что в отличие от того, как это имеет место в обыденной жизни, когда «вероятность события» определяется на основании субъективной оценки каких-то известных данному человеку факторов, так что вероятность одного и того же события может оцениваться различными людьми по-разному, научное определение вероятности объективно и выражается числом, не зависящим от того, кто его определяет. Позднее определение вероятности будет рассмотрено более подробно. Здесь мы отметим лишь, что если газ содержит большое количество молекул, то вычисленная с помощью закона Максвелла вероятность встретить молекулу, скорость которой удовлетворяет определенным условиям, с большой точностью совпадает с долей подобных молекул среди молекул газа. Выше отмечалось, что на практике приходится иметь дело с
количествами вещества, содержащими огромное число молекул, и поэтому при решении большинства практических задач молекулярной физики законы теории вероятности выполняются с той строгостью, которая обычна для физических законов.
Для пояснения физической сущности закона распределения молекулярных скоростей рассмотрим следующий мысленный опыт. Предположим, что удалось сконструировать прибор, позволяющий не только непосредственно наблюдать хаотическое движение молекул, но и определять их скорости. Допустим, что с помощью этого прибора наблюдают поведение молекул кислорода, температура которого нуль градусов. Как указано выше, не имеет смысла пытаться определять точные значения скоростей отдельных молекул. Наблюдаемые молекулы распределяются в зависимости от их скоростей по отдельным группам. Предположим, что все молекулы делят так, что в первую группу относят те, скорости которых меньше  во вторую — те, у которых скорости заключены в пределах от 100 до
во вторую — те, у которых скорости заключены в пределах от 100 до  в третью — от 200 до
в третью — от 200 до  вплоть до молекул, движущихся со скоростями от 600 до
вплоть до молекул, движущихся со скоростями от 600 до  после чего все остальные молекулы собирают в одну общую группу. Если подобный опыт проделать несколько раз с различным, но достаточно большим количеством молекул, определяя всякий раз не просто количества молекул в указанных выше отдельных группах, а долю, которую составляют эти молекулы в общем числе молекул, скорости которых были измерены, то мы заметим, что для каждой из групп найденная таким образом доля остается неизменной.
после чего все остальные молекулы собирают в одну общую группу. Если подобный опыт проделать несколько раз с различным, но достаточно большим количеством молекул, определяя всякий раз не просто количества молекул в указанных выше отдельных группах, а долю, которую составляют эти молекулы в общем числе молекул, скорости которых были измерены, то мы заметим, что для каждой из групп найденная таким образом доля остается неизменной.
В таблице 4 приведены результаты проверки подобного мысленного опыта.
Как можно убедиться, рассматривая таблицу, молекул с очень большими и очень малыми скоростями немного. Подавляющее большинство молекул движется со скоростями, заключенными в сравнительно узких пределах.
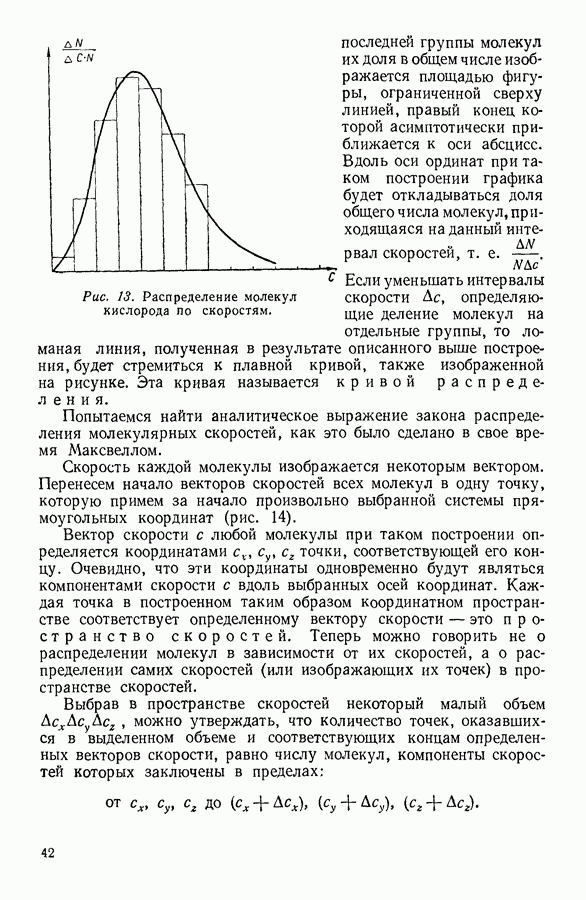
Еще более наглядно графическое изображение описанного опыта. На рисунке 13 вдоль оси абсцисс отложены скорости движения молекул. В соответствии с опытом ось абсцисс разделена на отдельные интервалы по  вплоть до
вплоть до  Доли числа молекул скорости которых лежат в указанных интервалах скоростей, изображаются на графике площадями соответствующих прямоугольников, имеющих основанием заданный интервал скоростей
Доли числа молекул скорости которых лежат в указанных интервалах скоростей, изображаются на графике площадями соответствующих прямоугольников, имеющих основанием заданный интервал скоростей  Для
Для
Таблица 4 (см. скан) Распределение молекул кислорода по скоростям при 0° С

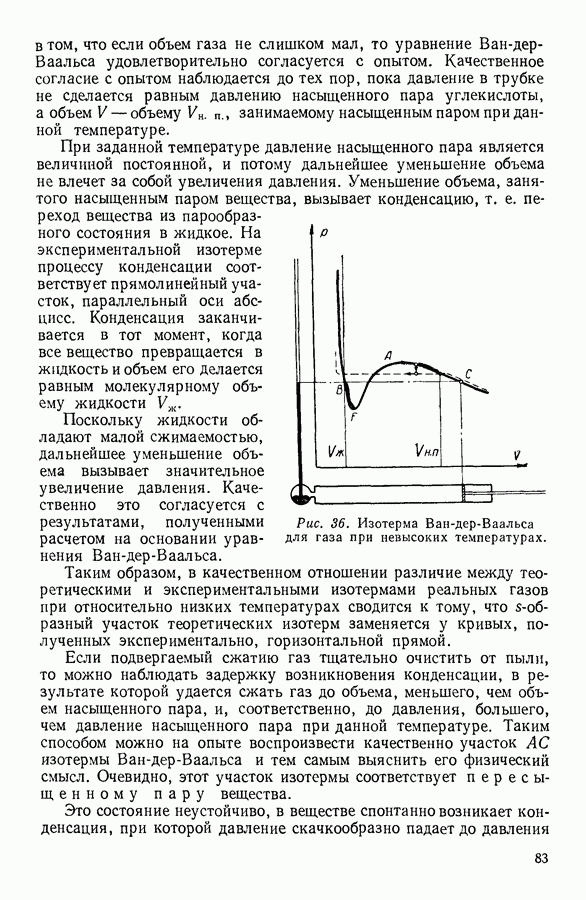
Рис. 13. Распределение молекул кислорода по скоростям.
последней группы молекул их доля в общем числе изображается площадью фигуры, ограниченной сверху линией, правый конец которой асимптотически приближается к оси абсцисс. Вдоль оси ординат при таком построении графика будет откладываться доля общего числа молекул, приходящаяся на данный интервал скоростей, т. е.  Если уменьшать интервалы скорости
Если уменьшать интервалы скорости  определяющие деление молекул на отдельные группы, то ломаная линия, полученная в результате описанного выше построения, будет стремиться к плавной кривой, также изображенной на рисунке. Эта кривая называется кривой распределения.
определяющие деление молекул на отдельные группы, то ломаная линия, полученная в результате описанного выше построения, будет стремиться к плавной кривой, также изображенной на рисунке. Эта кривая называется кривой распределения.
Попытаемся найти аналитическое выражение закона распределения молекулярных скоростей, как это было сделано в свое время Максвеллом.
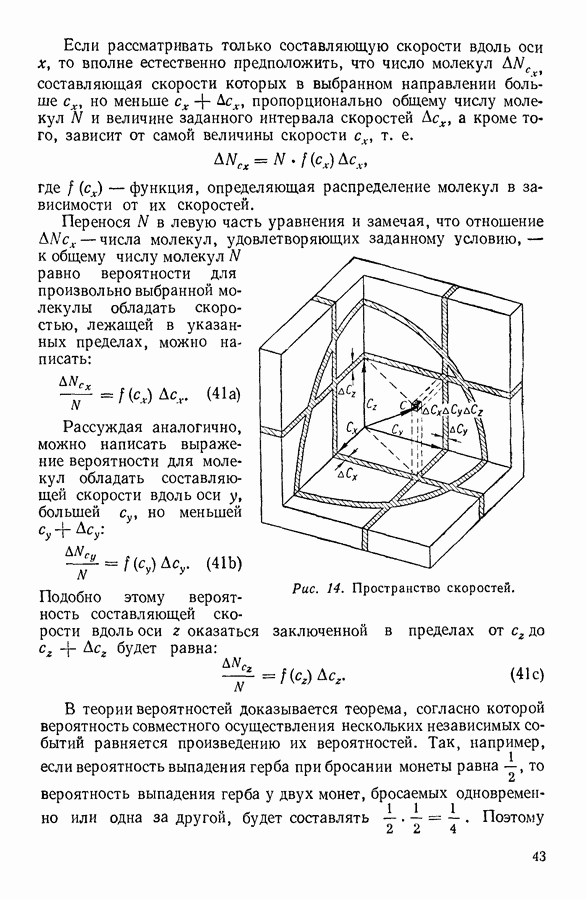
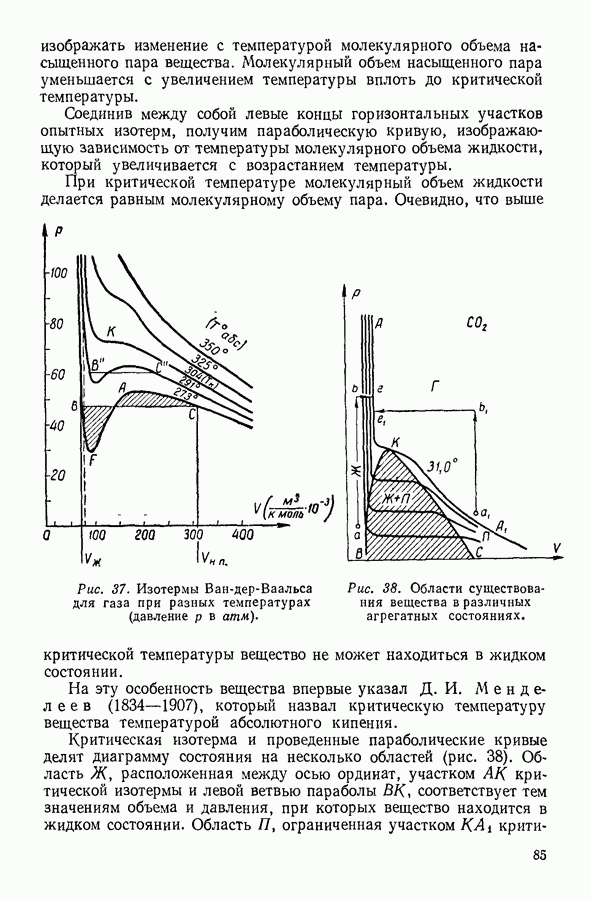
Скорость каждой молекулы изображается некоторым вектором. Перенесем начало векторов скоростей всех молекул в одну точку, которую примем за начало произвольно выбранной системы прямоугольных координат (рис. 14).
Вектор скорости с любой молекулы при таком построении определяется координатами  точки, соответствующей его концу. Очевидно, что эти координаты одновременно будут являться компонентами скорости с вдоль выбранных осей координат. Каждая точка в построенном таким образом координатном пространстве соответствует определенному вектору скорости — это пространство скоростей. Теперь можно говорить не о распределении молекул в зависимости от их скоростей, а о распределении самих скоростей (или изображающих их точек) в пространстве скоростей.
точки, соответствующей его концу. Очевидно, что эти координаты одновременно будут являться компонентами скорости с вдоль выбранных осей координат. Каждая точка в построенном таким образом координатном пространстве соответствует определенному вектору скорости — это пространство скоростей. Теперь можно говорить не о распределении молекул в зависимости от их скоростей, а о распределении самих скоростей (или изображающих их точек) в пространстве скоростей.
Выбрав в пространстве скоростей некоторый малый объем  можно утверждать, что количество точек, оказавшихся в выделенном объеме и соответствующих концам определенных векторов скорости, равно числу молекул, компоненты скоростей которых заключены в пределах:
можно утверждать, что количество точек, оказавшихся в выделенном объеме и соответствующих концам определенных векторов скорости, равно числу молекул, компоненты скоростей которых заключены в пределах:

Если рассматривать только составляющую скорости вдоль оси х, то вполне естественно предположить, что число молекул  составляющая скорости которых в выбранном направлении больше
составляющая скорости которых в выбранном направлении больше  но меньше
но меньше  пропорционально общему числу молекул
пропорционально общему числу молекул  и величине заданного интервала скоростей
и величине заданного интервала скоростей  а кроме того, зависит от самой величины скорости
а кроме того, зависит от самой величины скорости  т. е.
т. е.

где  функция, определяющая распределение молекул в зависимости от их скоростей.
функция, определяющая распределение молекул в зависимости от их скоростей.
Перенося  в левую часть уравнения и замечая, что отношение
в левую часть уравнения и замечая, что отношение  числа молекул, удовлетворяющих заданному условию, — к общему числу молекул
числа молекул, удовлетворяющих заданному условию, — к общему числу молекул  равно вероятности для произвольно выбранной молекулы обладать скоростью, лежащей в указанных пределах, можно написать:
равно вероятности для произвольно выбранной молекулы обладать скоростью, лежащей в указанных пределах, можно написать:


Рис. 14. Пространство скоростей.
Рассуждая аналогично, можно написать выражение вероятности для молекул обладать составляющей скорости вдоль оси у, большей  но меньшей
но меньшей

Подобно этому вероятность составляющей скорости вдоль оси  оказаться заключенной в пределах от
оказаться заключенной в пределах от  до
до  будет равна:
будет равна:

В теории вероятностей доказывается теорема, согласно которой вероятность совместного осуществления нескольких независимых событий равняется произведению их вероятностей. Так, например, если вероятность выпадения герба при бросании монеты равна  то вероятность выпадения герба у двух монет, бросаемых одновременно или одна за другой, будет составлять
то вероятность выпадения герба у двух монет, бросаемых одновременно или одна за другой, будет составлять  Поэтому
Поэтому
можно предположить, что вероятность для молекулы обладать скоростью, компоненты которой заключены в пределах от  до
до  найдется перемножением написанных выше вероятностей
найдется перемножением написанных выше вероятностей  т. е.
т. е.

Предположим, что нижний предел скорости с постоянен, в этом случае должно выполняться условие:

Допустим дальше, что неизменным остается и интервал скорости, т. е. элементарный объем в пространстве скоростей:

При выполнении этих двух предположений должна оставаться неизменной и вероятность  того, что молекула обладает скоростью, удовлетворяющей сформулированным выше требованиям. Если это так, то можно написать:
того, что молекула обладает скоростью, удовлетворяющей сформулированным выше требованиям. Если это так, то можно написать:

Подставляя в первое равенство значение  из уравнения (42) и принимая во внимание второе равенство, получим:
из уравнения (42) и принимая во внимание второе равенство, получим:

Разделив полученное уравнение на произведение функций

найдем

Умножив выражение (43) на произвольную величину  и сложив с уравнением (45), можно, сгруппировав члены в соответствии с индексами у
и сложив с уравнением (45), можно, сгруппировав члены в соответствии с индексами у  , написать:
, написать:

В силу произвольности величин  написанное уравнение может выполняться только в том случае, если каждый из стоящих в скобках двучленов порознь равен нулю, т. е.
написанное уравнение может выполняться только в том случае, если каждый из стоящих в скобках двучленов порознь равен нулю, т. е.

Последние уравнения легко решаются. Обозначив  и заметив, что
и заметив, что  получим:
получим:

или

откуда

где  постоянная интегрирования.
постоянная интегрирования.
Таким образом, искомое выражение вероятности  того, что скорость молекулы в направлении оси
того, что скорость молекулы в направлении оси  заключена в пределах от
заключена в пределах от  до
до  будет равна:
будет равна:

Очевидно, что аналогичные выражения можно получить для вероятности того, что скорость молекулы вдоль оси у заключена в пределах от  до
до  и для вероятности того, что скорость молекулы в направлении оси
и для вероятности того, что скорость молекулы в направлении оси  заключена в пределах от
заключена в пределах от  до
до 
Вероятность  того, что компоненты скорости молекулы вдоль трех осей координат одновременно заключены в пределах от
того, что компоненты скорости молекулы вдоль трех осей координат одновременно заключены в пределах от  до
до  найдется, как принято было выше, перемножением соответствующих вероятностей, т. е.
найдется, как принято было выше, перемножением соответствующих вероятностей, т. е.

Часто для расчета представляет интерес только абсолютная величина скорости, но не направление ее в пространстве, или, другими словами, не значения компонентов скорости  и соответствующих интервалов
и соответствующих интервалов  а лишь величина с и некоторый интервал ее
а лишь величина с и некоторый интервал ее  В этом случае следует заменить сумму
В этом случае следует заменить сумму
 стоящую в показателе степени, величиной
стоящую в показателе степени, величиной  а выделенный ранее объем в пространстве скоростей
а выделенный ранее объем в пространстве скоростей  объемом шарового слоя, заключенного между сферами с радиусами с и с
объемом шарового слоя, заключенного между сферами с радиусами с и с  величиной
величиной  В результате этой замены для искомой вероятности будет справедливо выражение:
В результате этой замены для искомой вероятности будет справедливо выражение:

Если в этом уравнении определить значение постоянных  то вероятность того, что молекула движется, независимо от направления, со скоростью, заключенной в пределах от с до с
то вероятность того, что молекула движется, независимо от направления, со скоростью, заключенной в пределах от с до с  будет выражаться следующим соотношением:
будет выражаться следующим соотношением:

в котором  масса молекулы,
масса молекулы,  постоянная Больдмана,
постоянная Больдмана,  абсолютная температура. Это выражение и является искомым законом распределения молекулярных скоростей Максвелла.
абсолютная температура. Это выражение и является искомым законом распределения молекулярных скоростей Максвелла.

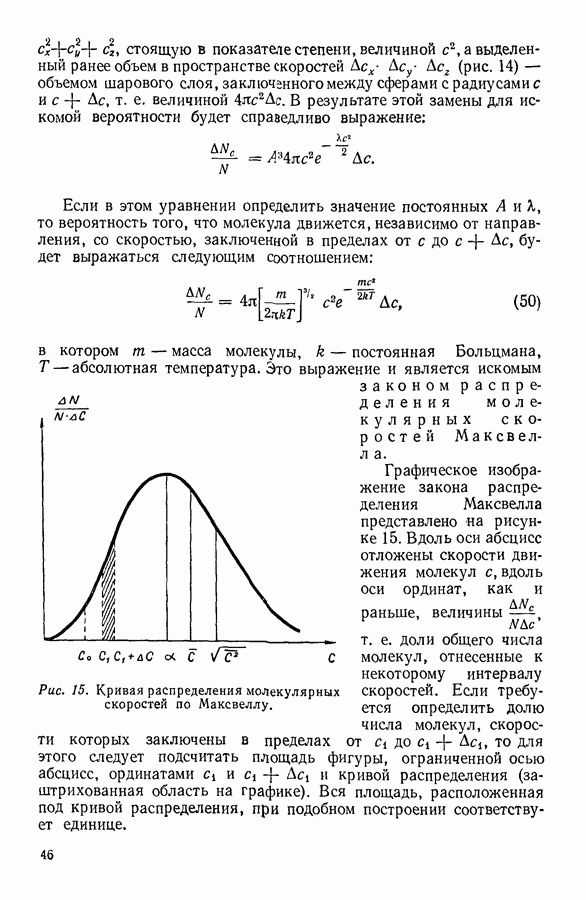
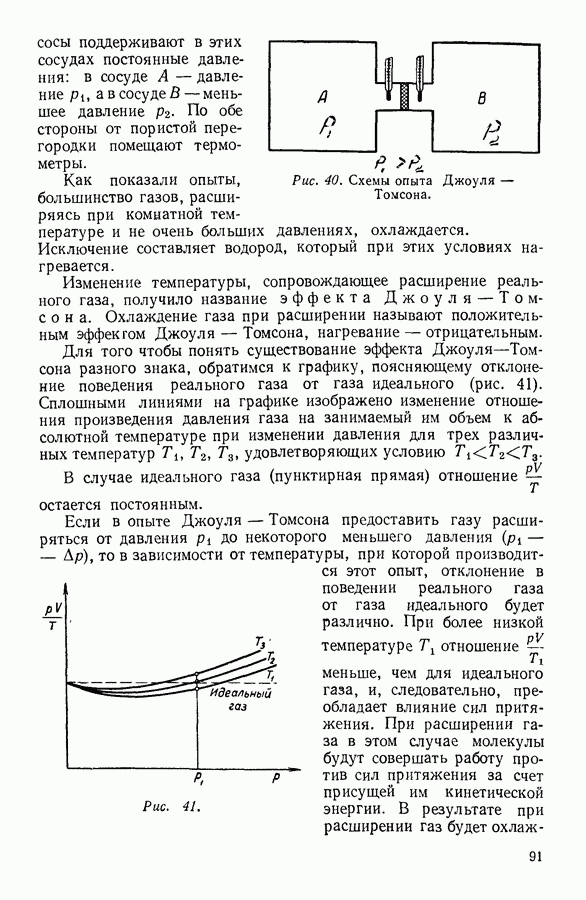
Рис. 15. Кривая распределения молекулярных скоростей по Максвеллу.
Графическое изображение закона распределения Максвелла представлено на рисунке 15. Вдоль оси абсцисс отложены скорости движения молекул  вдоль оси ординат, как и раньше, величины —
вдоль оси ординат, как и раньше, величины —  т. е. доли общего числа молекул, отнесенные к некоторому интервалу скоростей. Если требуется определить долю числа молекул, скорости которых заключены в пределах от
т. е. доли общего числа молекул, отнесенные к некоторому интервалу скоростей. Если требуется определить долю числа молекул, скорости которых заключены в пределах от  до
до  то для этого следует подсчитать площадь фигуры, ограниченной осью абсцисс, ординатами
то для этого следует подсчитать площадь фигуры, ограниченной осью абсцисс, ординатами  и кривой распределения (заштрихованная область на графике). Вся площадь, расположенная под кривой распределения, при подобном построении соответствует единице.
и кривой распределения (заштрихованная область на графике). Вся площадь, расположенная под кривой распределения, при подобном построении соответствует единице.
При практическом применении закона Максвелла иногда бывает необходимо определить долю числа молекул, скорости которых превосходят некоторое определенное значение  Искомая величина изображается на графике площадью фигуры, расположенной справа от ординаты, соответствующей скорости
Искомая величина изображается на графике площадью фигуры, расположенной справа от ординаты, соответствующей скорости  и ограниченной кривой распределения и осью абсцисс.
и ограниченной кривой распределения и осью абсцисс.
Характер кривой распределения молекулярных скоростей указывает на то, что существует некоторая скорость молекулярного движения, отличающаяся тем, что в ее окрестности на данный небольшой интервал скоростей приходится большее число молекул, чем в окрестности любой другой скорости. Эта скорость называется наивероятнейшей скоростью движения молекул. Наивероятнейшей скорости соответствует максимум на кривой распределения.
Вычисление наивероятнейшей скорости а производится по формуле:

или

Если условиться измерять скорости движения молекул не в метрах в секунду, а в относительных единицах, равных отношению скорости движения молекулы к наивероятнейшей скорости:  то закон распределения Максвелла запишется гораздо проще, а именно: доля числа молекул
то закон распределения Максвелла запишется гораздо проще, а именно: доля числа молекул  относительные скорости которых заключены в интервале от и до и
относительные скорости которых заключены в интервале от и до и  , выражается уравнением:
, выражается уравнением:

Для сравнения на графике, изображающем закон распределения (рис. 15), указаны значения средней арифметической с и средней квадратичной  скоростей.
скоростей.
На распределение молекулярных скоростей большое влияние оказывает температура. Наивероятнейшая скорость движения молекул, как это ясно из уравнения 51, пропорциональна корню квадратному из абсолютной температуры. Следовательно, при повышении температуры максимум на кривой распределения смешается вдоль оси абсцисс вправо. Поскольку же площадь, ограниченная кривой распределения и осью абсцисс, должна при этом оставаться неизменной, то очевидно, что величина ординаты, соответствующей максимуму, уменьшается — кривая делается более пологой.
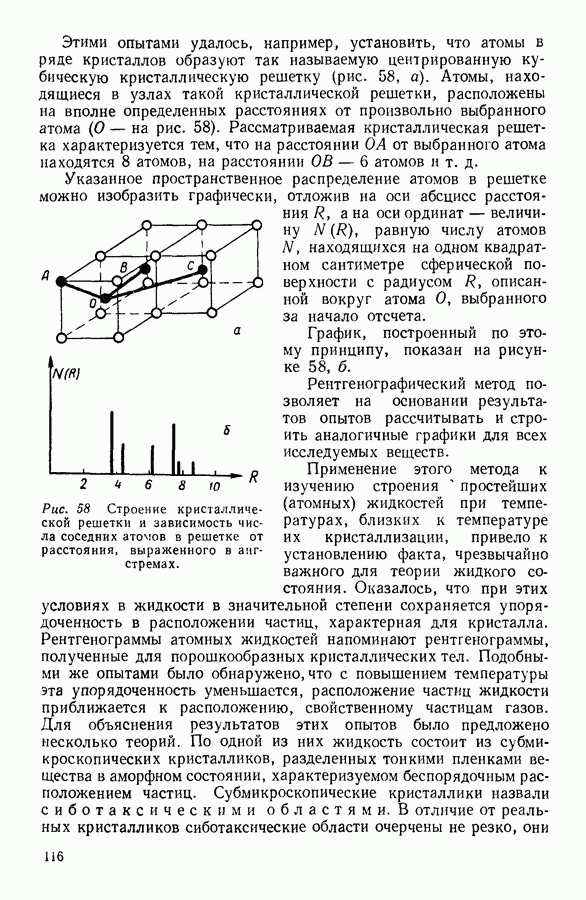
На рисунке 16 сплошная кривая соответствует абсолютной температуре 273°, а пунктирная — абсолютной температуре 373°.
Изменение кривой распределения молекулярных скоростей при изменении температуры объясняет влияние температуры на многие физико-химические процессы. Особенно велико влияние температуры на те процессы, при которых определяющим является количество молекул со скоростями, превосходящими некоторую определенную величину.

Рис. 16. Изменение распределения молекулярных скоростей при изменении температуры в кислороде (по оси ординат отложена величина 
Как явствует из графика, число подобных молекул быстро возрастает с ростом температуры. Именно это возрастание объясняет во многих случаях ускорение химических реакций при нагревании реагирующей смеси.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
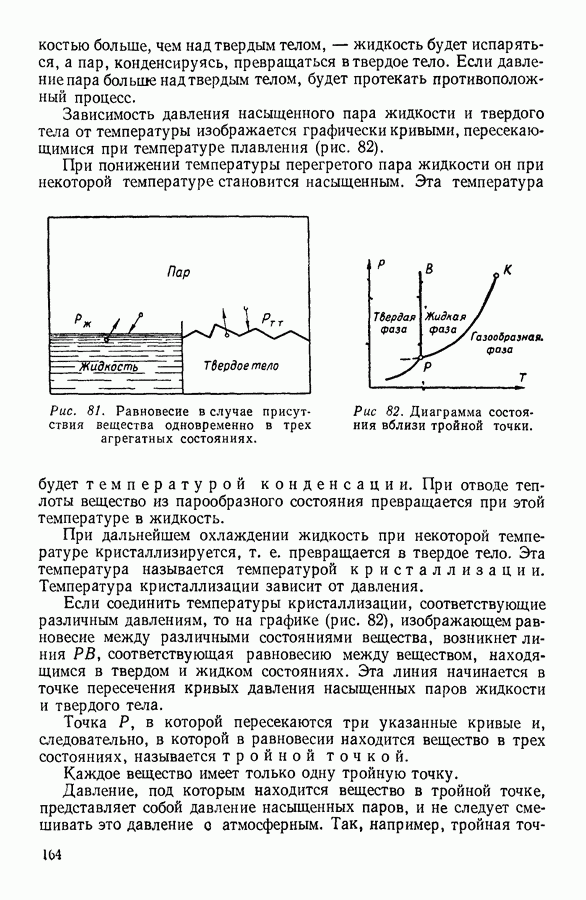
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
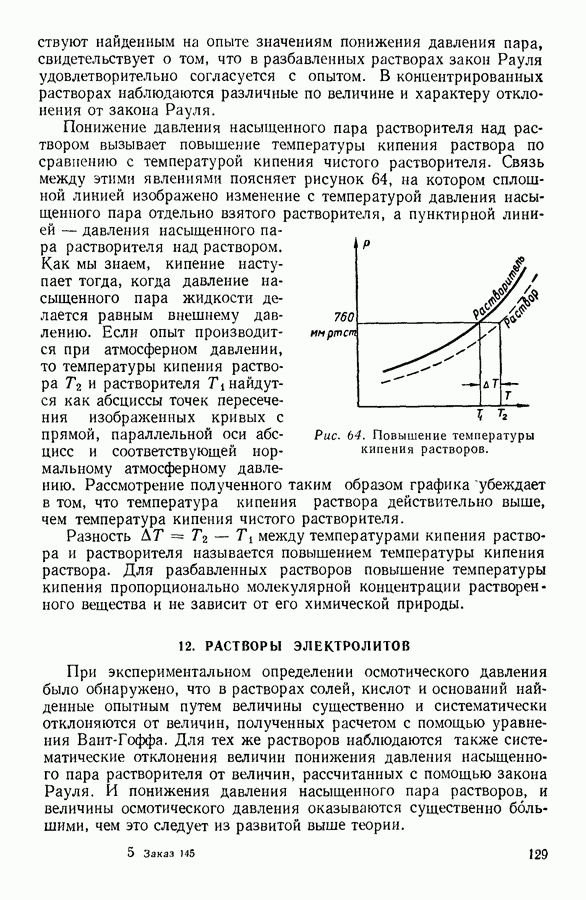
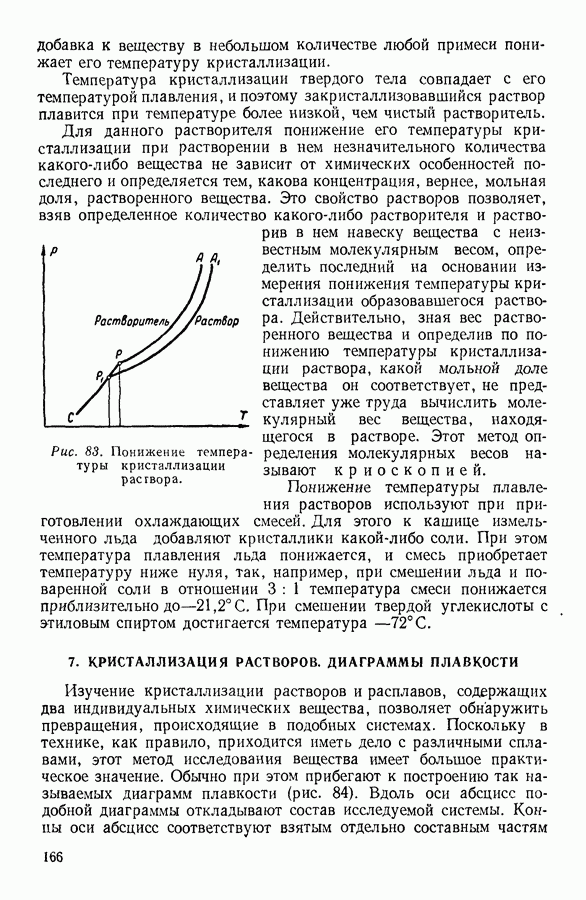
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
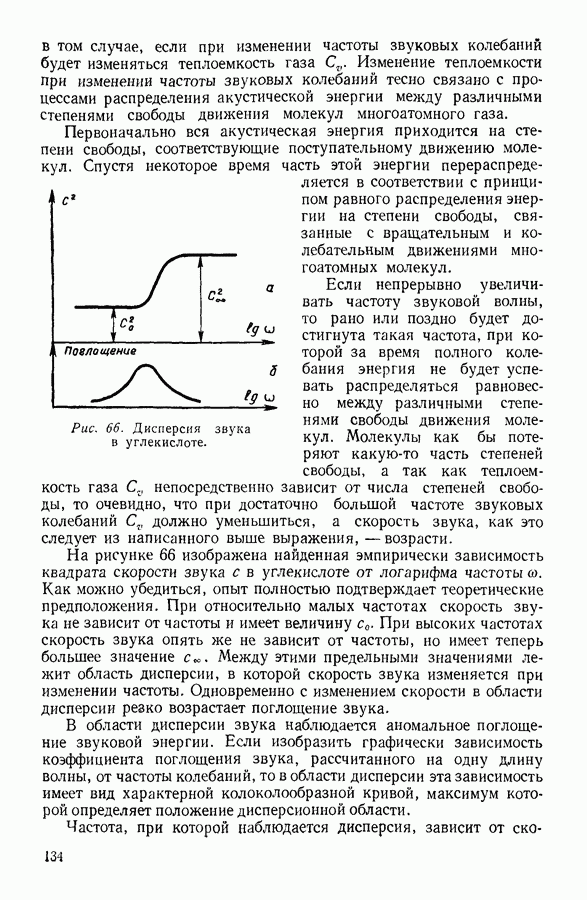
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
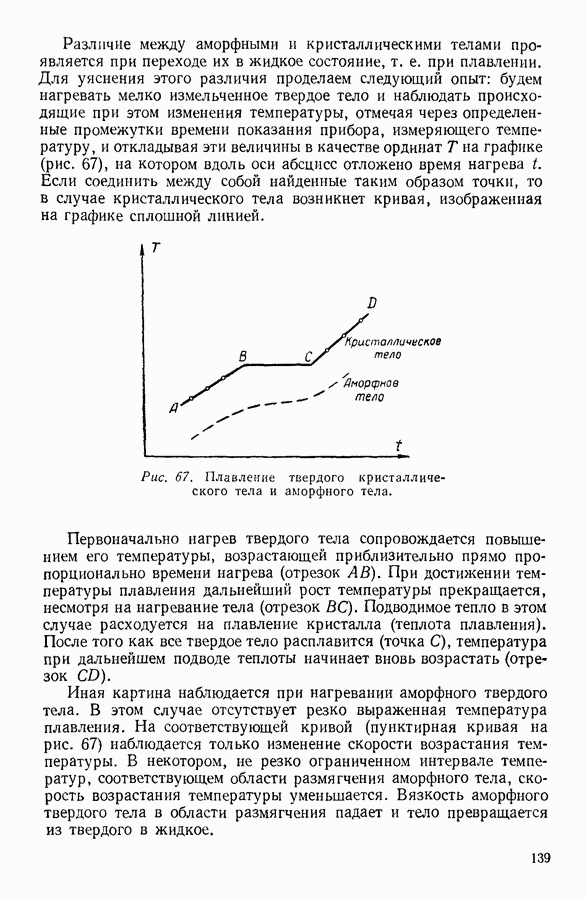
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
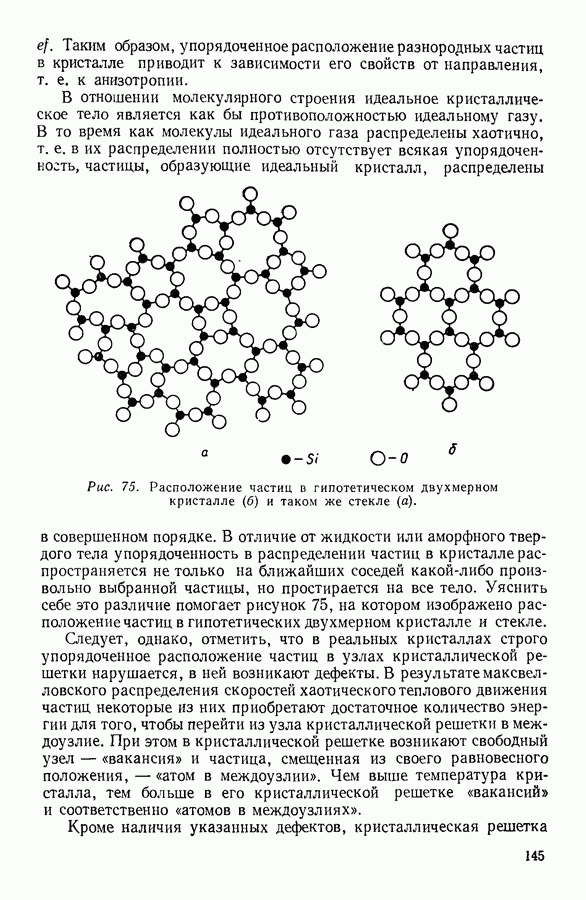
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
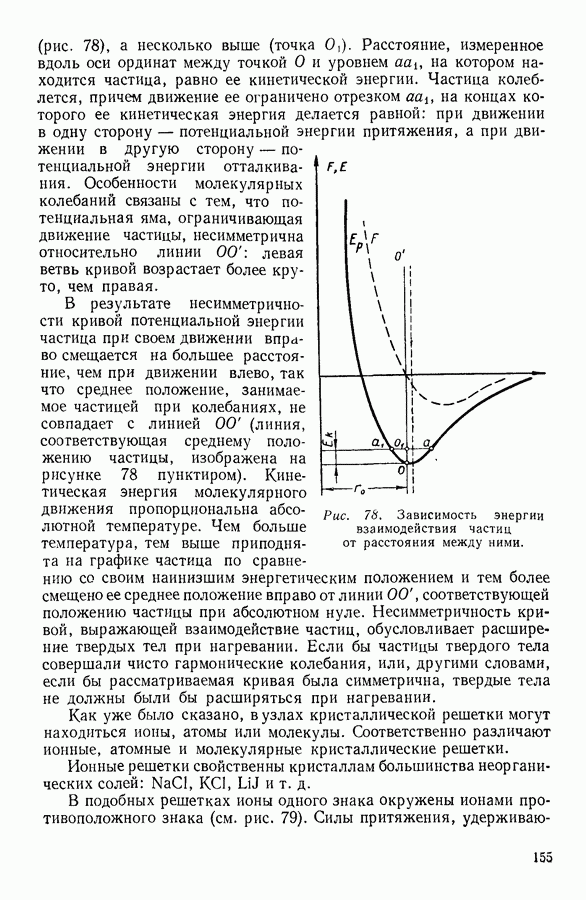
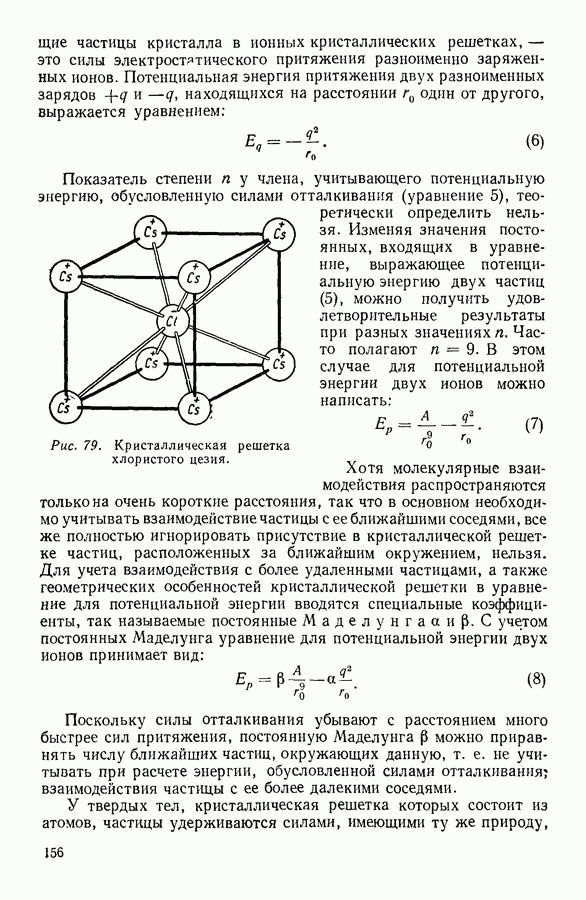
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
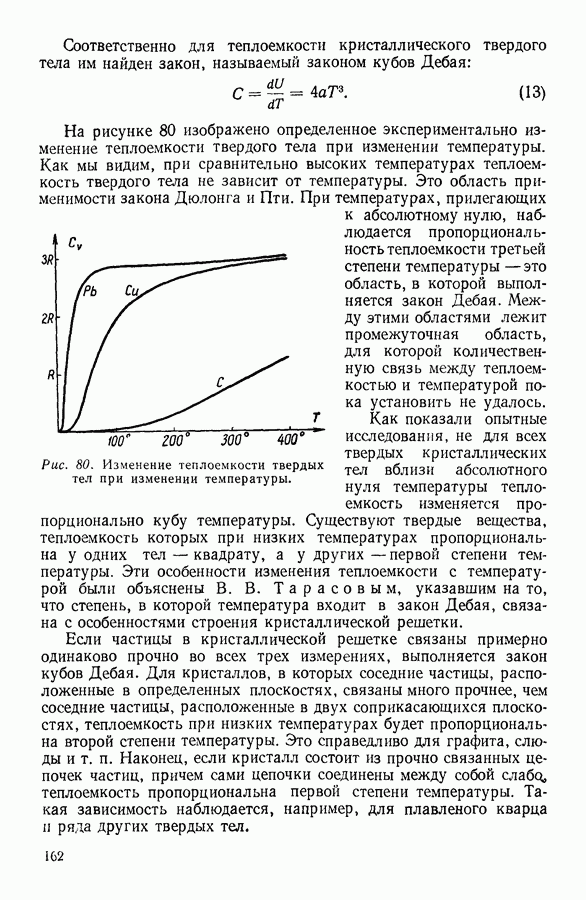
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
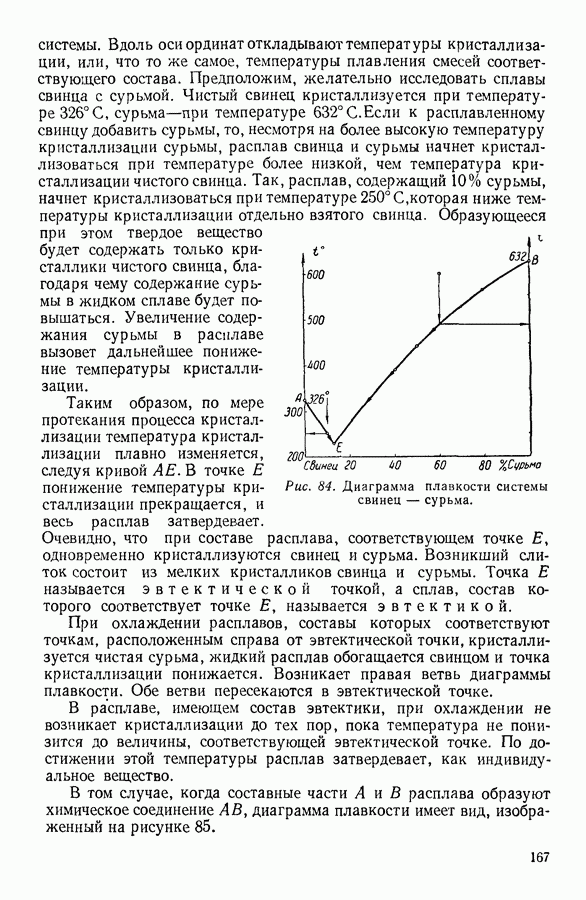
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
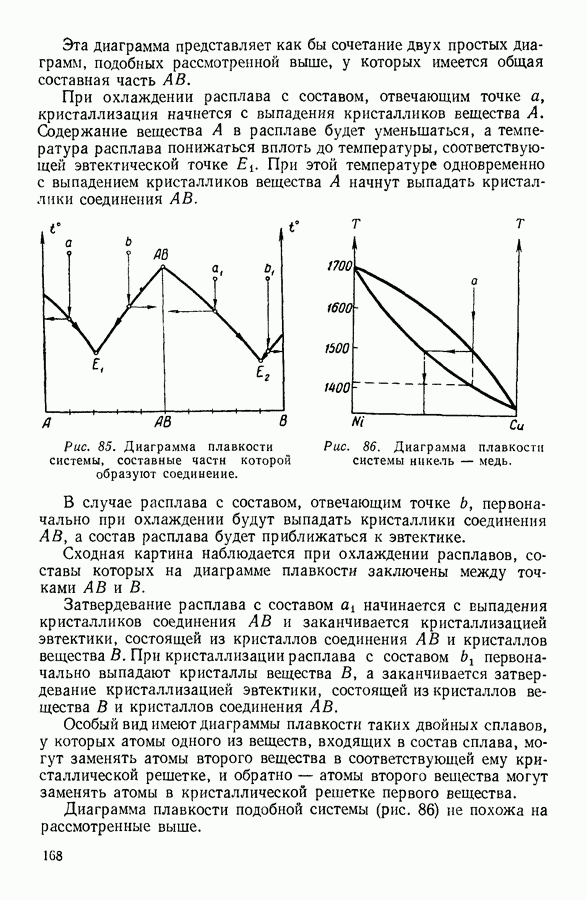
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»