| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
Законы идеальных газов, вытекающие из молекулярно-кинетических представлений, достаточно хорошо подтверждаются на опыте в том случае, если давление газа мало и температура его не слишком низка. При повышении давления поведение реальных газов отклоняется от поведения газов идеальных.
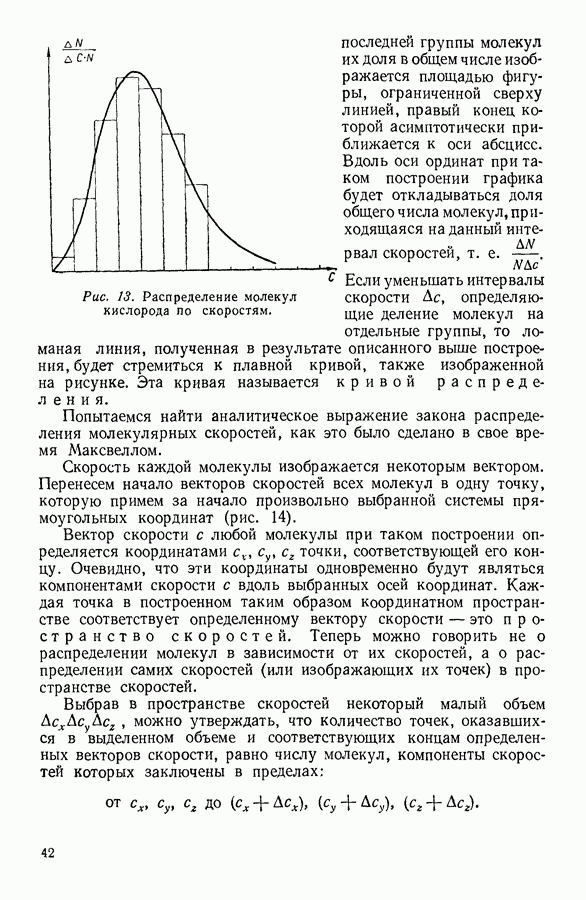
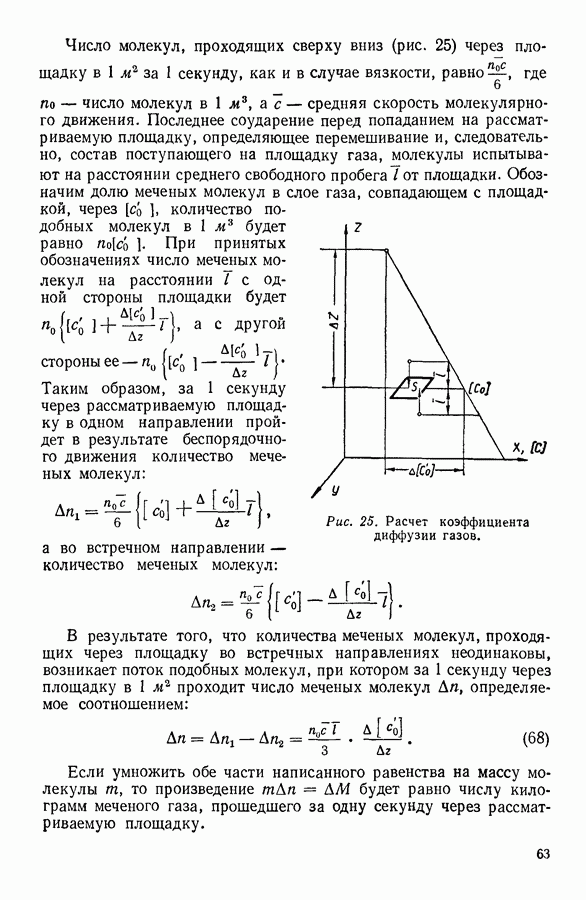
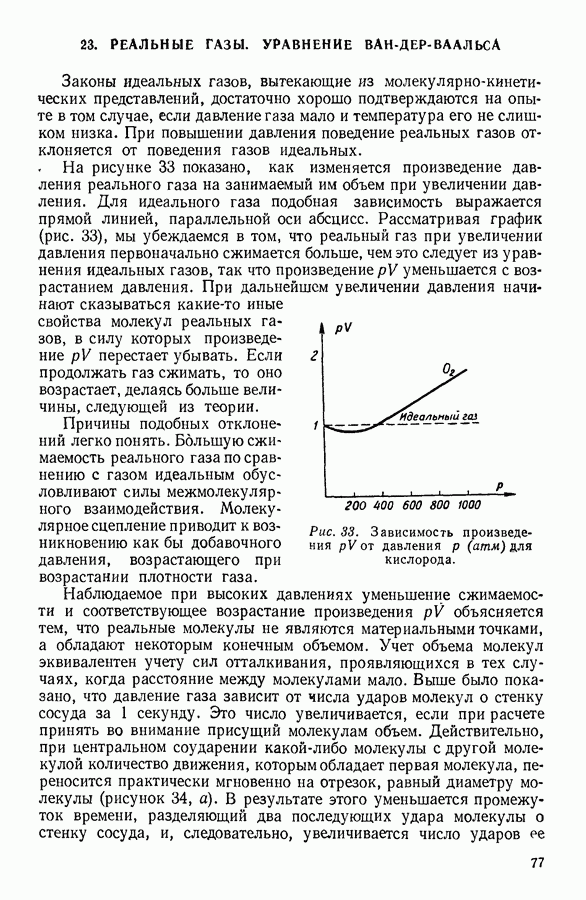
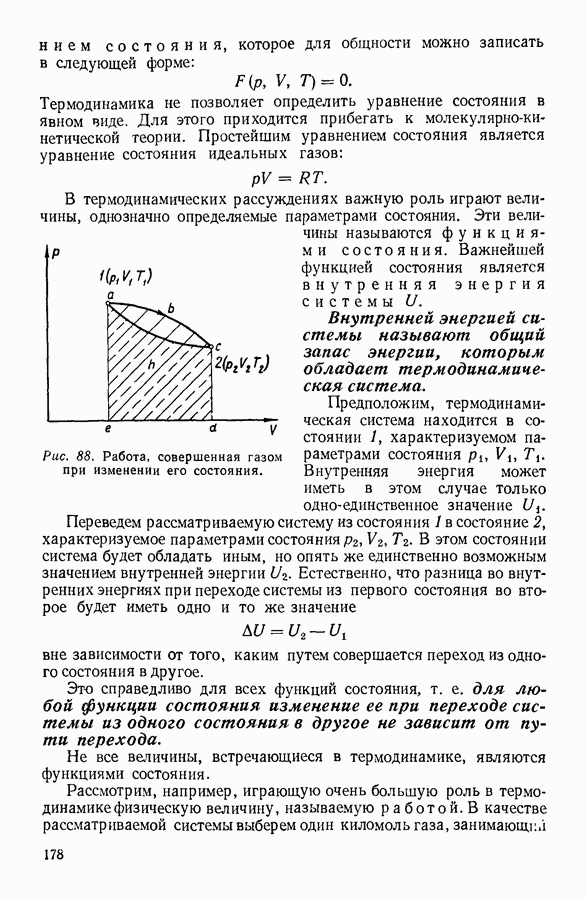
На рисунке 33 показано, как изменяется произведение давления реального газа на занимаемый им объем при увеличении давления. Для идеального газа подобная зависимость выражается прямой линией, параллельной оси абсцисс. Рассматривая график (рис. 33), мы убеждаемся в том, что реальный газ при увеличении давления первоначально сжимается больше, чем это следует из уравнения идеальных газов, так что произведение  уменьшается с возрастанием давления. При дальнейшем увеличении давления начинают сказываться какие-то иные свойства молекул реальных газов, в силу которых произведение
уменьшается с возрастанием давления. При дальнейшем увеличении давления начинают сказываться какие-то иные свойства молекул реальных газов, в силу которых произведение  перестает убывать. Если продолжать газ сжимать, то оно возрастает, делаясь больше величины, следующей из теории.
перестает убывать. Если продолжать газ сжимать, то оно возрастает, делаясь больше величины, следующей из теории.

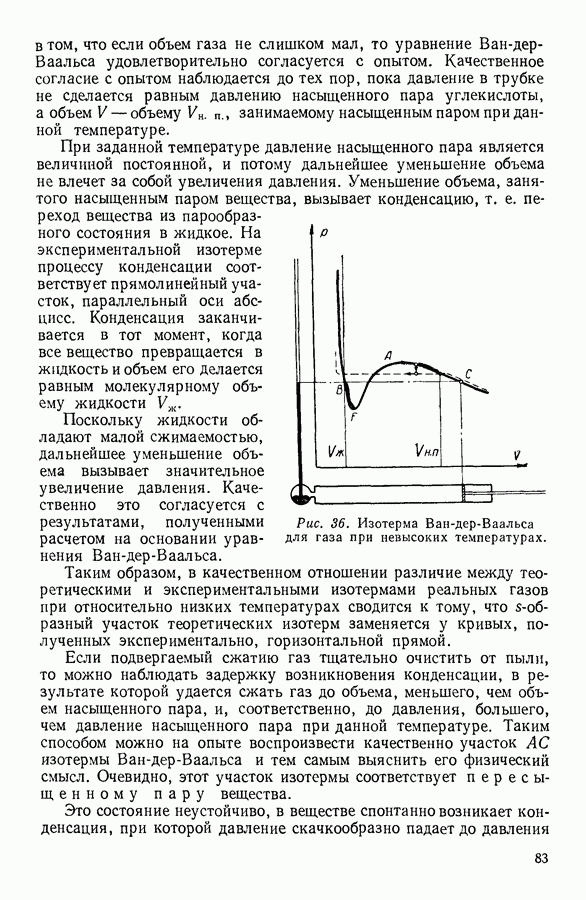
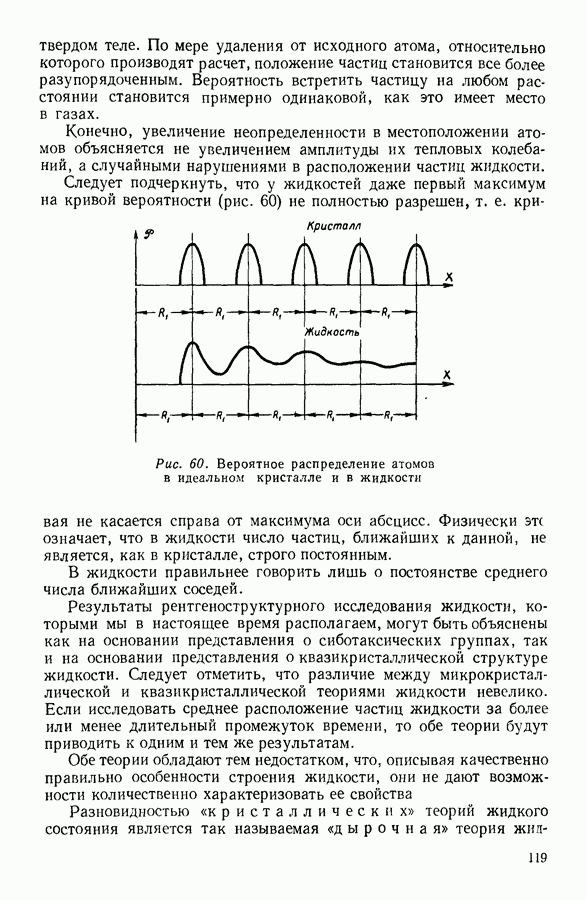
Рис. 33. Зависимость произведения  от давления
от давления  для кислорода.
для кислорода.
Причины подобных отклонений легко понять. Большую сжимаемость реального газа по сравнению с газом идеальным обусловливают силы межмолекулярного взаимодействия. Молекулярное сцепление приводит к возникновению как бы добавочного давления, возрастающего при возрастании плотности газа.
Наблюдаемое при высоких давлениях уменьшение сжимаемости и соответствующее возрастание произведения  объясняется тем, что реальные молекулы не являются материальными точками, а обладают некоторым конечным объемом. Учет объема молекул эквивалентен учету сил отталкивания, проявляющихся в тех случаях, когда расстояние между молекулами мало. Выше было показано, что давление газа зависит от числа ударов молекул о стенку сосуда за 1 секунду. Это число увеличивается, если при расчете принять во внимание присущий молекулам объем. Действительно, при центральном соударении какой-либо молекулы с другой молекулой количество движения, которым обладает первая молекула, переносится практически мгновенно на отрезок, равный диаметру молекулы (рисунок 34, а). В результате этого уменьшается промежуток времени, разделяющий два последующих удара молекулы о стенку сосуда, и, следовательно, увеличивается число ударов ее
объясняется тем, что реальные молекулы не являются материальными точками, а обладают некоторым конечным объемом. Учет объема молекул эквивалентен учету сил отталкивания, проявляющихся в тех случаях, когда расстояние между молекулами мало. Выше было показано, что давление газа зависит от числа ударов молекул о стенку сосуда за 1 секунду. Это число увеличивается, если при расчете принять во внимание присущий молекулам объем. Действительно, при центральном соударении какой-либо молекулы с другой молекулой количество движения, которым обладает первая молекула, переносится практически мгновенно на отрезок, равный диаметру молекулы (рисунок 34, а). В результате этого уменьшается промежуток времени, разделяющий два последующих удара молекулы о стенку сосуда, и, следовательно, увеличивается число ударов ее
об эту стенку за одну секунду. По мере увеличения давления возрастает плотность газа, а вместе с ней возрастает влияние собственного объема молекул — газ оказывает большее сопротивление сжатию, чем это следует из уравнения идеальных газов (уравнения Клапейрона).
Следует заметить, что на необходимость учитывать при расчете давления сильно сжатого газа собственный объем молекул указывал еще Ломоносов.

Рис. 34. Влияние собственного объема молекул на давление газа.
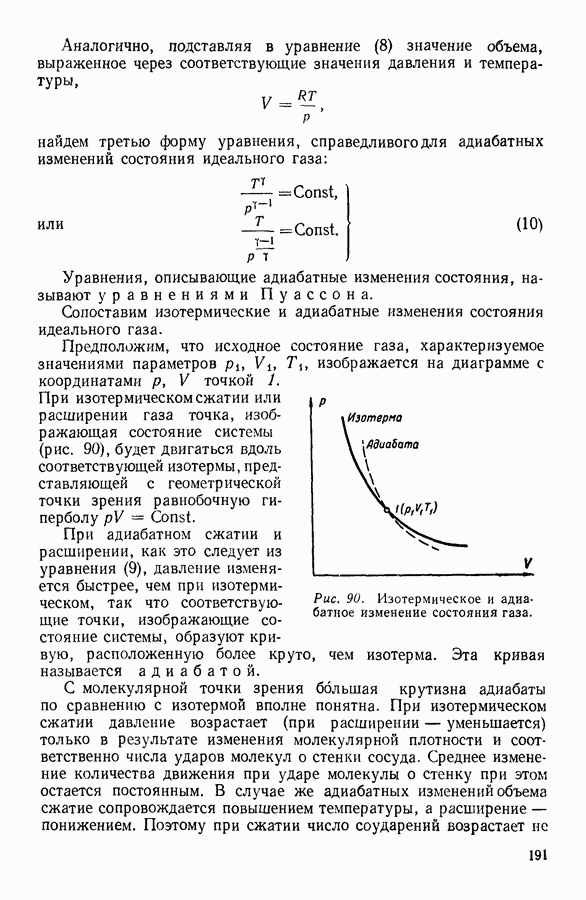
Уравнение состояния реального газа, в котором приняты во внимание обе причины, вызывающие отклонения его свойств от свойств идеальных газов, было предложено впервые голландским физиком Ван-дер-Ваальсом (1837—1923) и носит его имя. Уравнение Ван-дер-Ваальса отличается от уравнения Клапейрона наличием двух поправочных членов, один из которых учитывает влияние собственного объема молекул, а другой — влияние сил молекулярного притяжения.
Для того чтобы учесть влияние собственного объема молекул, обратим внимание на то, что при неограниченном увеличении давления объем идеального газа  стремится к нулю, а объем реального газа при тех же условиях — к некоторой предельной величине
стремится к нулю, а объем реального газа при тех же условиях — к некоторой предельной величине  Следовательно, для того чтобы в уравнении состояния идеальных газов учесть влияние собственного объема молекул, необходимо заменить в нем величину V разностью
Следовательно, для того чтобы в уравнении состояния идеальных газов учесть влияние собственного объема молекул, необходимо заменить в нем величину V разностью  Таким образом, уравнение состояния, учитывающее собственный объем молекул, будет иметь вид:
Таким образом, уравнение состояния, учитывающее собственный объем молекул, будет иметь вид:

Теоретический расчет величины  сложен. В простейшем случае, если считать молекулы газа твердыми шариками с радиусом
сложен. В простейшем случае, если считать молекулы газа твердыми шариками с радиусом  и предположить при этом, что в газе происходят только двойные соударения молекул, то можно показать, что
и предположить при этом, что в газе происходят только двойные соударения молекул, то можно показать, что  равно учетверенному
равно учетверенному
собственному объему молекул, т. е.

где  число Авогадро.
число Авогадро.
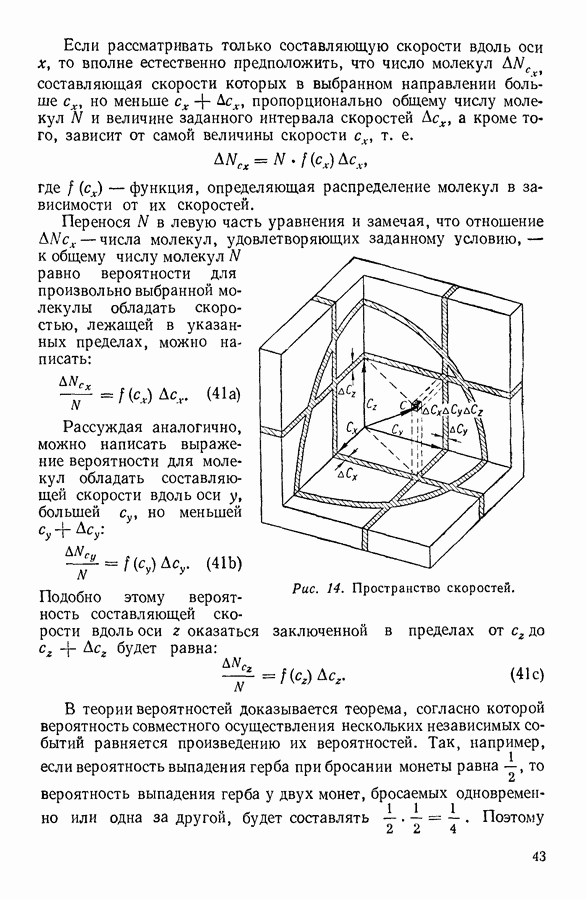
Для того чтобы пояснить, почему берется учетверенный собственный объем молекул, рассмотрим более внимательно передачу количества движения при молекулярных соударениях. При центральном ударе (рис. 34, а) импульс молекулы практически мгновенно передается на расстояние, равное диаметру молекулы  что эквивалентно вычитанию из объема, занятого газом, объема
что эквивалентно вычитанию из объема, занятого газом, объема  равного
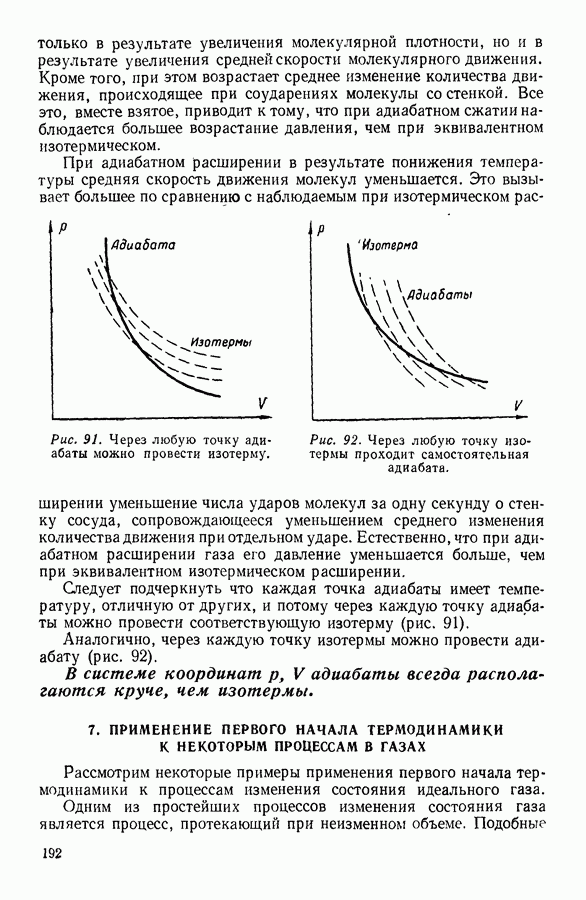
равного  т.е. восьмикратного объема молекул. Однако наряду с центральным ударом молекула будет испытывать всевозможные соударения (рис. 34, б, в, г) вплоть до скользящего удара (рис. 34, г), при котором никакой мгновенной передачи импульса в направлении движения происходить не будет и, следовательно, при котором поправка к объему равна нулю, т. е.
т.е. восьмикратного объема молекул. Однако наряду с центральным ударом молекула будет испытывать всевозможные соударения (рис. 34, б, в, г) вплоть до скользящего удара (рис. 34, г), при котором никакой мгновенной передачи импульса в направлении движения происходить не будет и, следовательно, при котором поправка к объему равна нулю, т. е. 
Приравнивая  среднему значению поправки
среднему значению поправки  получим соотношение (82).
получим соотношение (82).
Если газ сжат настолько сильно, что в нем наряду с двойными соударениями наблюдаются тройные и более сложные соударения молекул, величина поправочного члена, учитывающего влияние собственного объема молекул, будет иной.
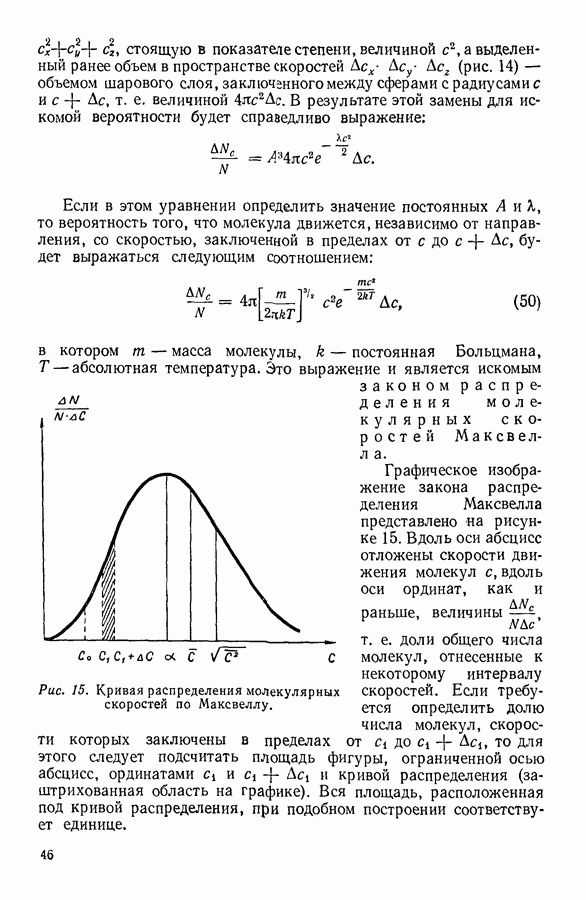
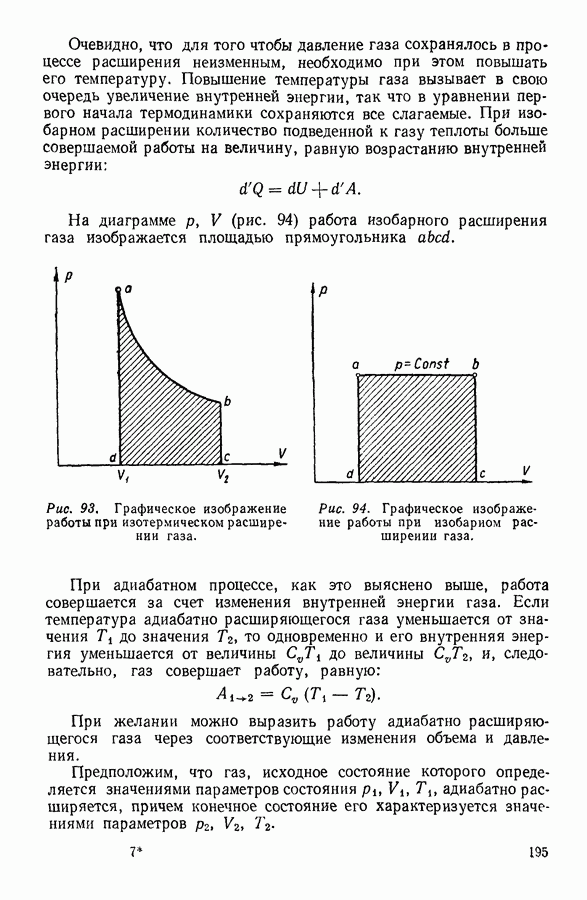
Величина поправки к давлению, обусловленная молекулярным притяжением, строго говоря, должна зависеть от плотности газа и от закона, согласно которому изменяется сила, действующая между молекулами при изменении расстояния между ними. Однако при выводе уравнения Ван-дер-Ваальса последняя зависимость не принимается во внимание. Это оказывается возможным сделать, если, учитывая подвижность молекул, предположить, что все положения какой-либо молекулы в мысленно выделенном небольшом объеме газа равновероятны. В этом случае взаимодействие любой молекулы в одном из выделенных объемов с молекулами такого же соседнего объема будет равно средней величине взаимодействия ее при всех возможных положениях, занимаемых ею относительно соседнего объема. Сказанное будет справедливо для всех молекул как в первом, так и во втором объеме. Если теперь мысленно провести плоскость внутри газа (рис. 35), то молекулы, находящиеся в малом объеме справа от этой плоскости, будут притягиваться молекулами, находящимися в таком же объеме слева от нее, с одинаковой для всех молекул средней силой. Необходимо отметить, что, строго говоря, это предположение может быть оправдано только в случае, если оно относится к разреженному газу.
На рисунке 35, а в каждом из рассматриваемых объемов находится по одной молекуле. При увеличении плотности газа в два раза число молекул в каждом из объемов удваивается (рисунок 35, б).
а сила, с которой один объем притягивает другой учетверяется. При увеличении плотности газа в три раза (рисунок 35, в) сила притяжения увеличится в 9 раз.
Из рассмотренного примера следует, что обусловленное молекулярным притяжением добавочное, или как его называют, внутреннее давление  в реальных газах возрастает прямо пропорционально квадрату плотности газа или, другими словами, обратно пропорционально квадрату молекулярного объема V, т. е.
в реальных газах возрастает прямо пропорционально квадрату плотности газа или, другими словами, обратно пропорционально квадрату молекулярного объема V, т. е.

где а — постоянная величина, различная для различных газов, зависящая от интенсивности молекулярных взаимодействий.

Рис. 35. Учет молекулярных взаимодействий.
Внутреннее давление не фиксируется манометром и потому должно добавляться к манометрическому давлению.
Учтя, таким образом, влияние на поведение газов собственного объема молекул и сил, действующих между ними, Ван-дер-Ваальс предложил записать уравнение состояния реальных газов в следующем виде:

Таблица 9 (см. скан) Сравнение наблюдаемых на опыте величин давления  и
и  при 100 °С с рассчитанными при помощи уравнения идеальных газов и уравнения Ван-дер-Ваальса
при 100 °С с рассчитанными при помощи уравнения идеальных газов и уравнения Ван-дер-Ваальса
В таблице 9 сопоставлены результаты расчета свойств газа с помощью уравнений Клапейрона и Ван-дер-Ваальса с данными опыта.
Как можно убедиться, при повышении давления уравнение Ван-дер-Ваальса лучше передает свойства реального газа, нежели уравнение Клапейрона.
Внутреннее давление  играющее роль поправочного члена, когда внешнее давление невелико, увеличивается при возрастании последнего и может при определенных условиях существенно влиять на свойства газов.
играющее роль поправочного члена, когда внешнее давление невелико, увеличивается при возрастании последнего и может при определенных условиях существенно влиять на свойства газов.
В приведенной выше форме уравнение Ван-дер-Ваальса (83) относится к одному киломолю газа, так что входящая в него величина объема газа — это молекулярный объем. При желании использовать написанное уравнение применительно к  килограммам вещества необходимо помнить, что значения постоянных
килограммам вещества необходимо помнить, что значения постоянных  в этом случае будут иными.
в этом случае будут иными.
Если молекулярный вес газа  и если желательно сохранить значения постоянных
и если желательно сохранить значения постоянных  определенных для одного киломоля вещества, то уравнение Ван-дер-Ваальса следует записывать так:
определенных для одного киломоля вещества, то уравнение Ван-дер-Ваальса следует записывать так:

В этом уравнении V — объем, занимаемый  килограммами газа.
килограммами газа.
Величины  для некоторых газов приведены в таблице 10.
для некоторых газов приведены в таблице 10.
Таблица 10 (см. скан) Постоянные в уравнении Ван-дер-Ваальса а и b для некоторых газов
В заключение следует подчеркнуть приближенный характер уравнения Ван-дер-Ваальса, которое, хотя и лучше передает поведение реальных газов, чем уравнение Клапейрона, все же мало пригодно для точных расчетов.
Вычисленные с помощью уравнения Ван-дер-Ваальса значения давления газа достаточно точно совпадают с опытом лишь при относительно высоких температурах и только в некотором интервале
давлений. Этим объясняются непрерывные поиски более совершенных уравнений, которых в настоящее время известно более 150.
При малых давлениях и соответственно больших значениях молекулярного объема V можно пренебречь в уравнении Ван-дер-Ваальса поправкой  в силу ее малости по сравнению с
в силу ее малости по сравнению с  и поправкой
и поправкой  по сравнению с молекулярным объемом
по сравнению с молекулярным объемом  Уравнение Ван-дер-Ваальса при этих условиях переходит в уравнение идеальных газов.
Уравнение Ван-дер-Ваальса при этих условиях переходит в уравнение идеальных газов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
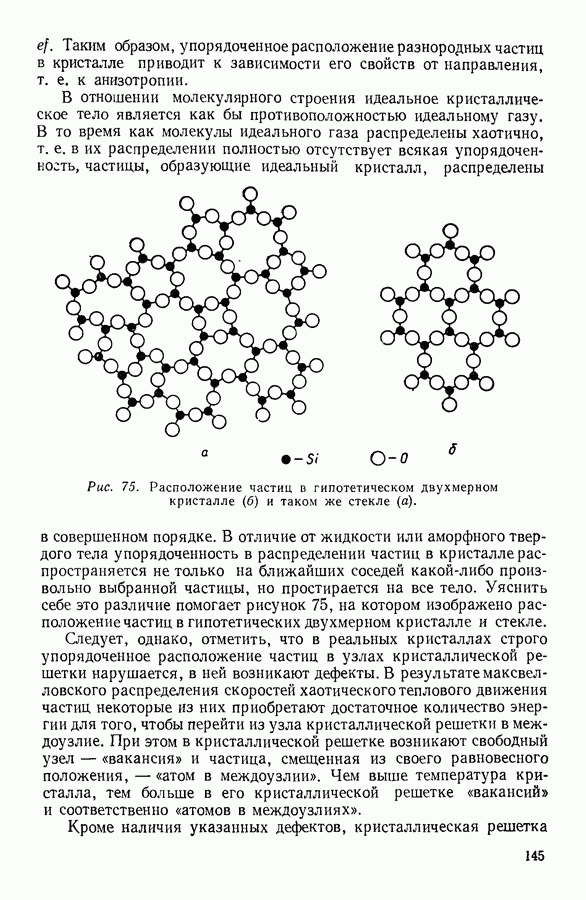
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
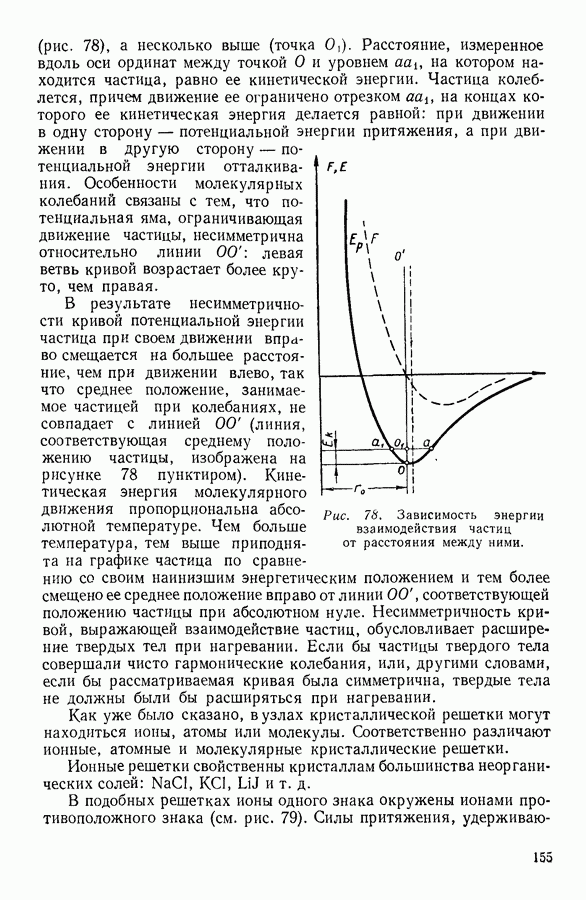
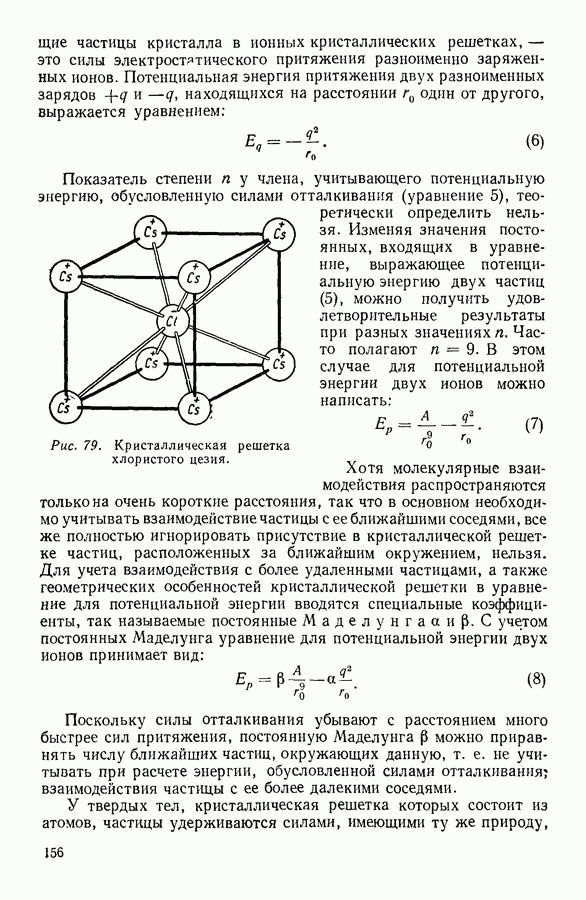
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
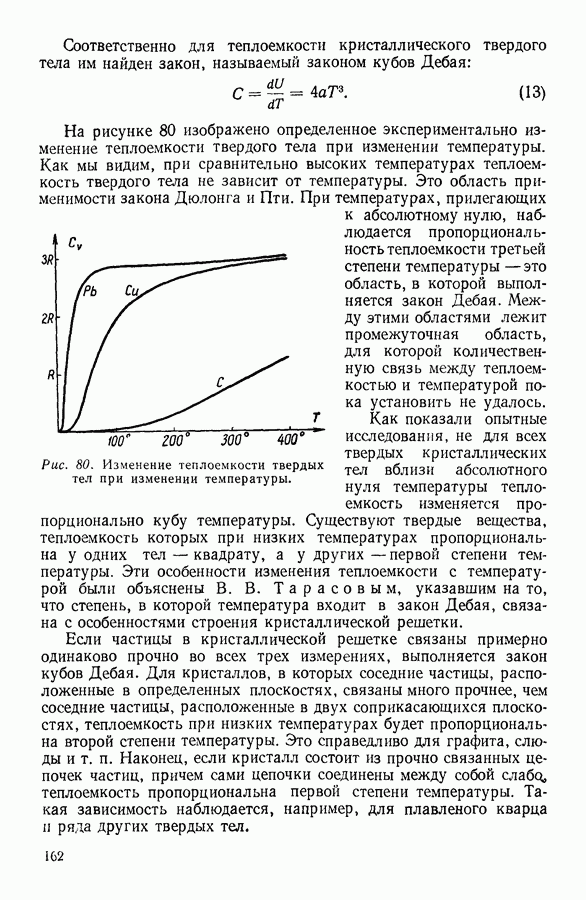
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
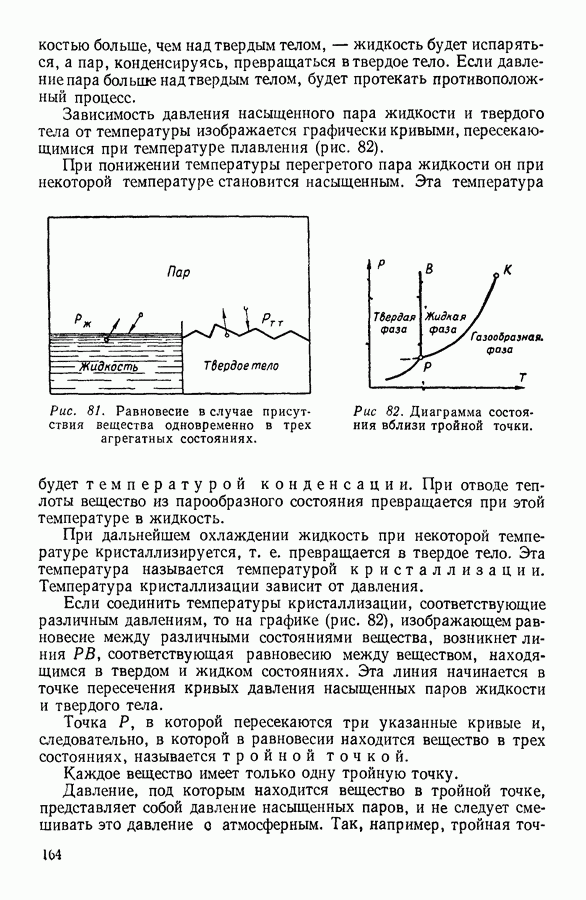
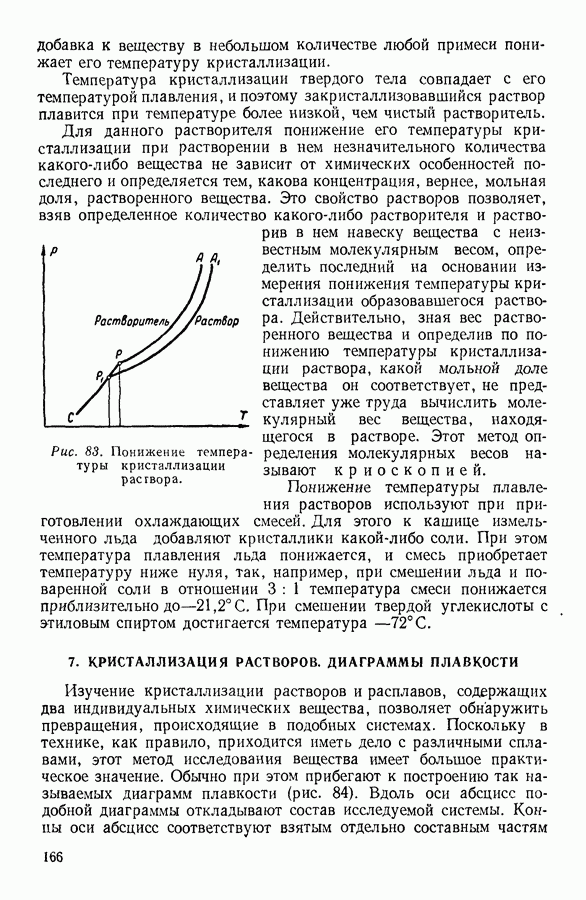
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
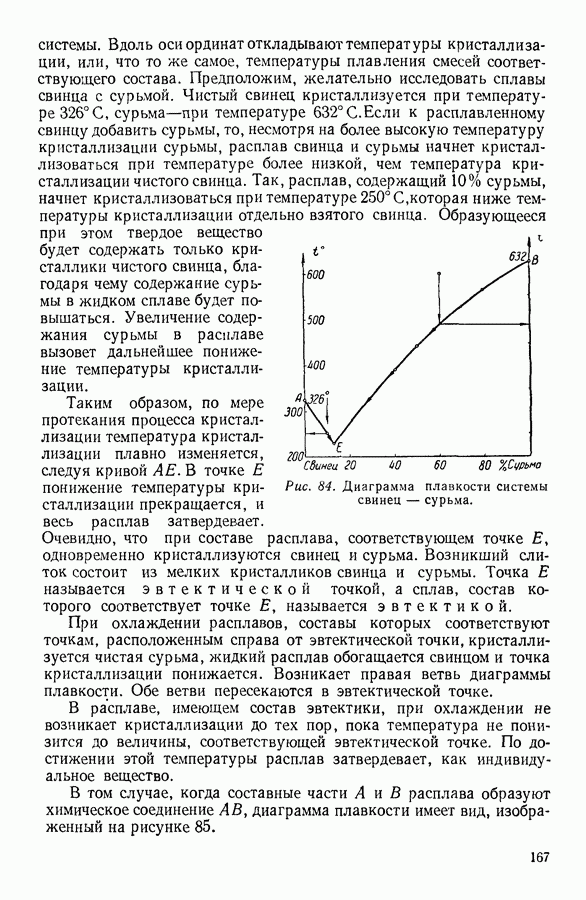
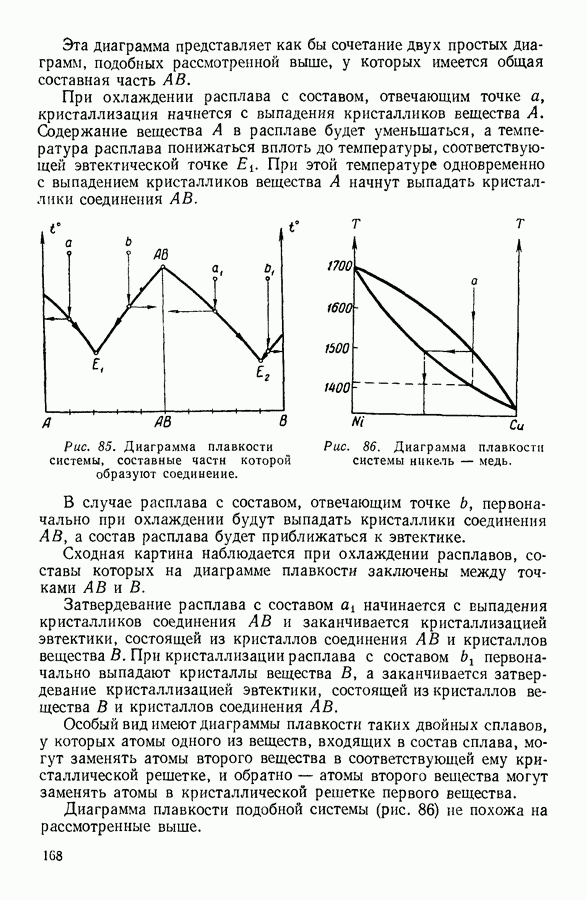
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»