10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ

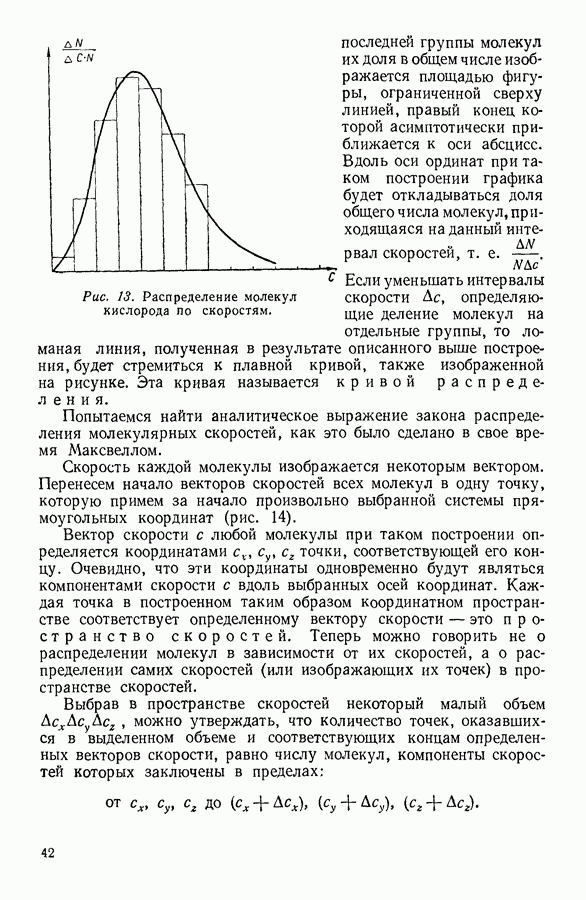
Действие силы тяжести приводит не только к возникновению избыточного давления на дно сосуда содержащего газ, но и к определенному распределению молекулярной плотности по высоте газового столба. Одновременно с измерением плотности изменяется и давление газа, измеряемое барометром.

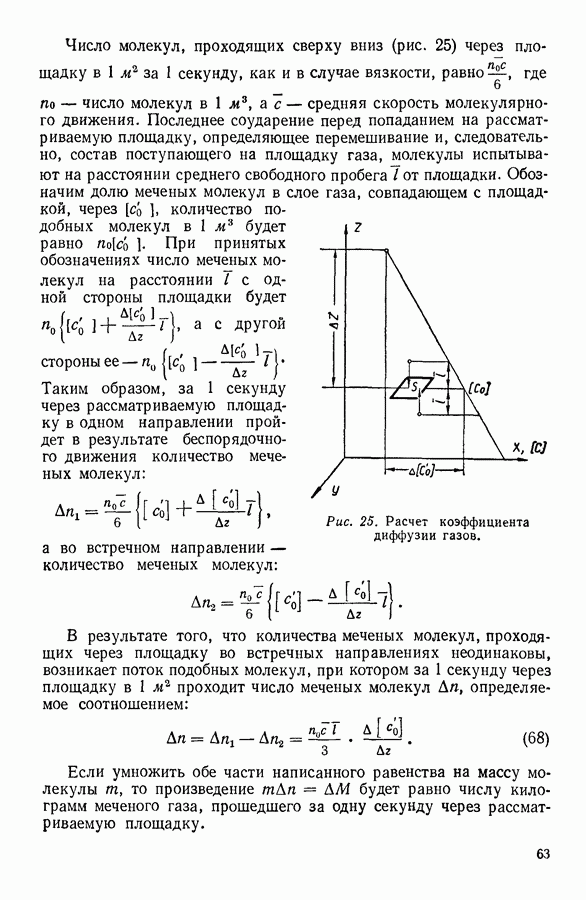
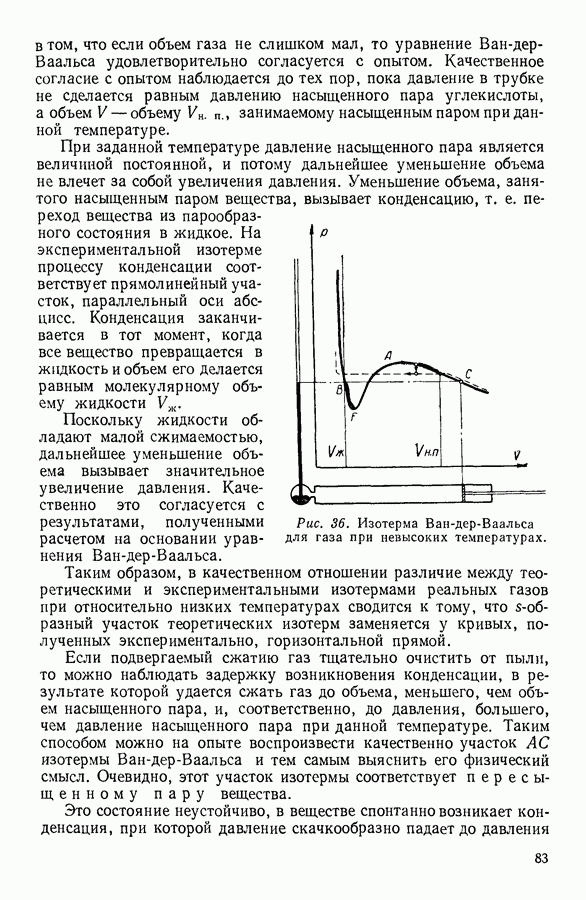
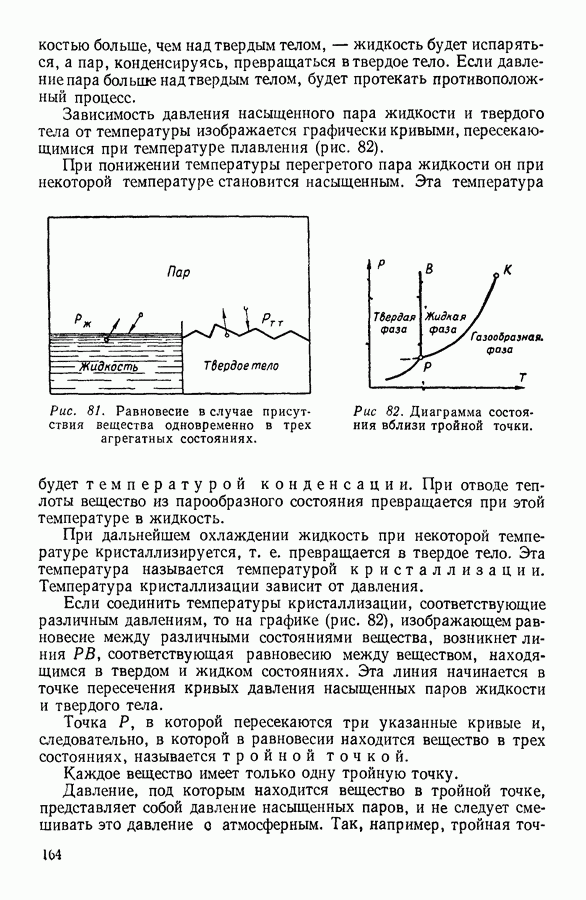
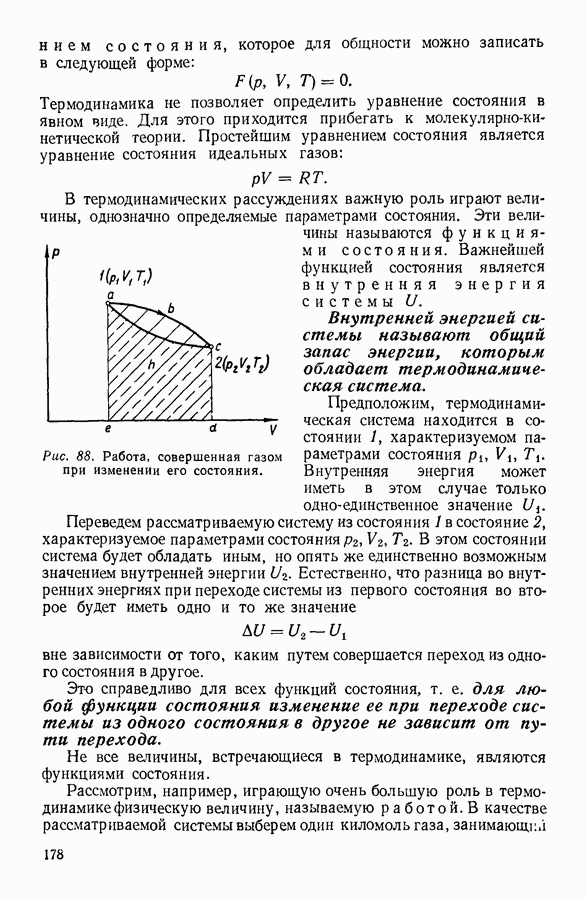
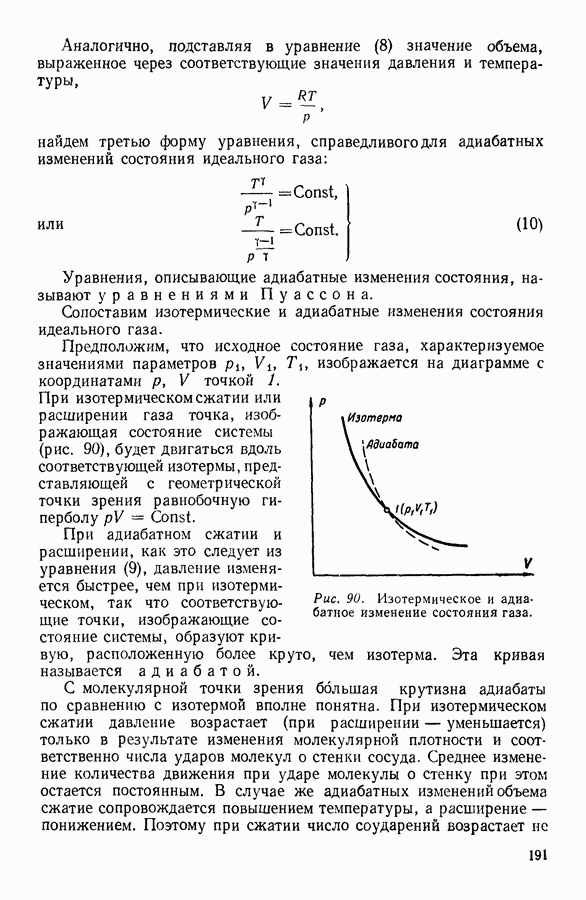
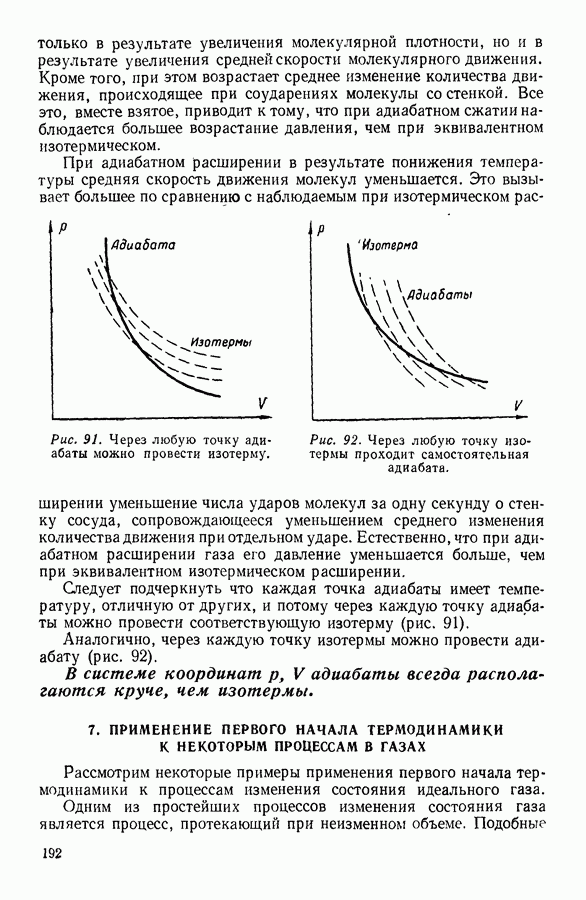
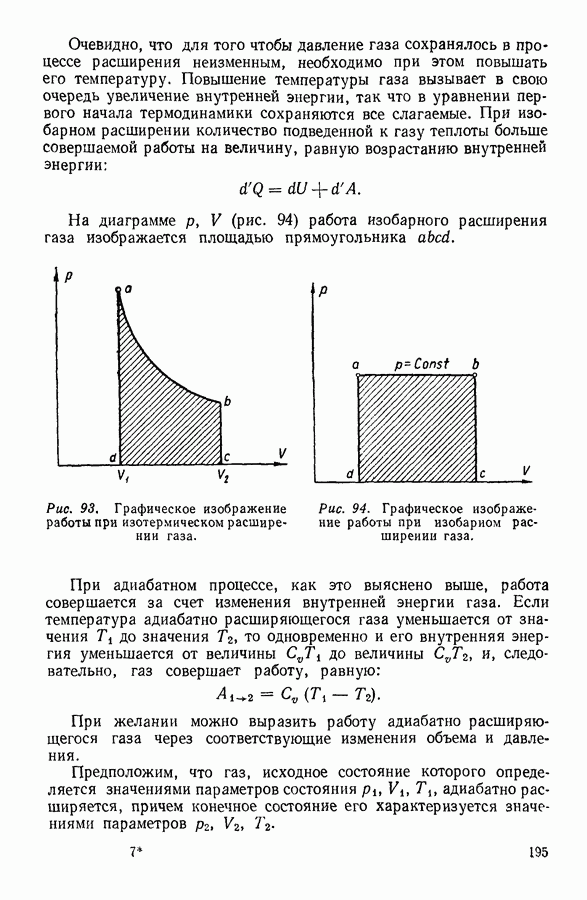
Для нахождения закона, которому подчиняется изменение плотности в свободном столбе газа, поддерживаемом при постоянной температуре, выделим мысленно столб газа с основанием в один квадратный метр (рис. 11).

Рис. 11.

Давление газа у основания столба обозначим и предположим, что в сечении столба, расположенном на высоте давление газа будет Слои газа, расположенные ниже выделенного сечения, не оказывают на него давления. Однако эти слои давят на воздух, расположенный под ними, и поэтому давление газа у основания столба будет больше, чем на высоте Для вычисления зависимости плотности газа от высоты проведем второе сечение, расположенное на дифференциально малую величину выше первого. Давление газа во втором сечении будет на величину меньше, чем в первом сечении, т. е. будет равно Уменьшение давления, очевидно равно весу столбика газа, заключенного между первым и вторым сечениями. Если обозначить число молекул в единице объема газа на высоте символом а массу молекулы то вес столбика газа, заключенного между указанными сечениями, будет равен где ускорение силы тяжести.

Как сказано выше, именно на эту величину уменьшается давление в столбе газа при переходе от первого сечения ко второму, т. е.

Воспользовавшись уравнением Клапейрона, можно написать для единицы объема газа на высоте соотношение:

где число молей газа в единице объема, равное отношению числа молекул к числу Авогадро Учитывая сказанное, получим:

Дифференцируя, найдем:

Приравнивая правые части уравнений (34) и (35), запишем:

или, преобразуя,

Замечая, что произведение представляет массу килограмм-молекулы, равную молекулярному весу газа, и интегрируя, найдем:

Для определения постоянной интегрирования заметим, что при следовательно, Таким образом, искомое уравнение принимает вид:

или

Уравнение (37) показывает, как изменяется с высотой, в результате действия силы тяжести, количество молекул в единице объема покоящегося столба газа, имеющего по всему протяжению одинаковую температуру.

Умножив обе части уравнения (37) на массу отдельной молекулы и замечая, что произведения соответствуют массам газа в одном кубическом метре, т. е. плотностям газа у основания столба и на высоте получим уравнение, передающее изменение плотности газа с высотой:

Аналогичная зависимость будет справедлива и для изменения с высотой давления газа. Именно так должно было бы изменяться давление воздуха в земной атмосфере, если бы температура в столбе воздуха была неизменной.

Уравнение, позволяющее рассчитывать изменение давления воздуха с высотой, было получено впервые французским математиком и физиком Лапласом (1749—1827) и называется барометрической формулой Лапласа.

Уравнению (37) можно придать более общую форму, если обратить внимание на то, что стоящее в показателе степени произведение равно изменению потенциальной энергии одного киломоля газа при перемещении его от уровня, на котором в кубическом метре содержится частиц, до уровня, на котором в кубическом метре частиц. Учитывая сказанное, уравнение (37) можно записать в следующем виде:

Таким образом, разница молекулярных плотностей в столбе покоящегося газа зависит от различия потенциальных энергий молекул, находящихся на разной высоте. Можно формулировать как общее правило: если имеются две области, отличающиеся одна от другой тем, что потенциальные энергии молекул в них различны, и если возможен взаимный переход молекул из одной области в другую, то при равновесии в этих областях будут различны и плотности вещества. Соотношение в плотностях в этом случае можно подсчитать, воспользовавшись уравнением (39).