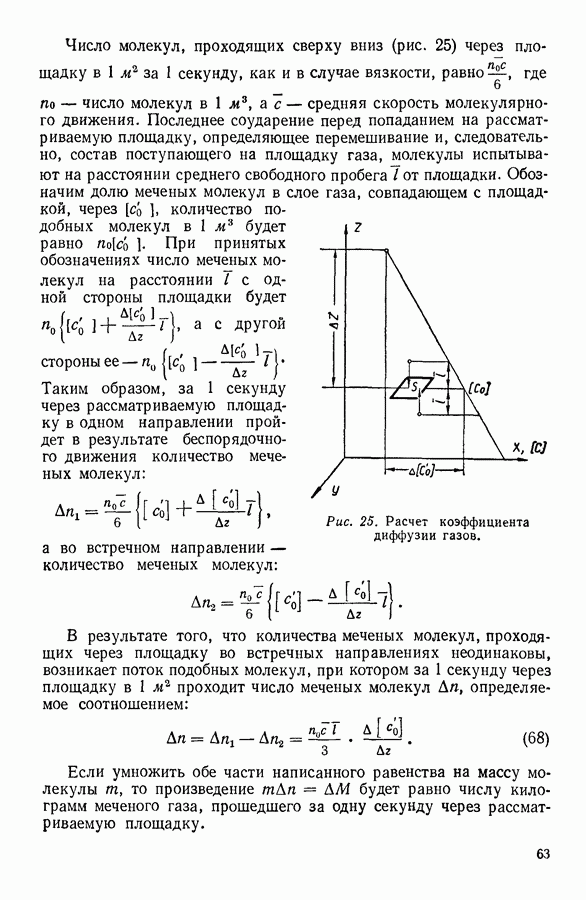
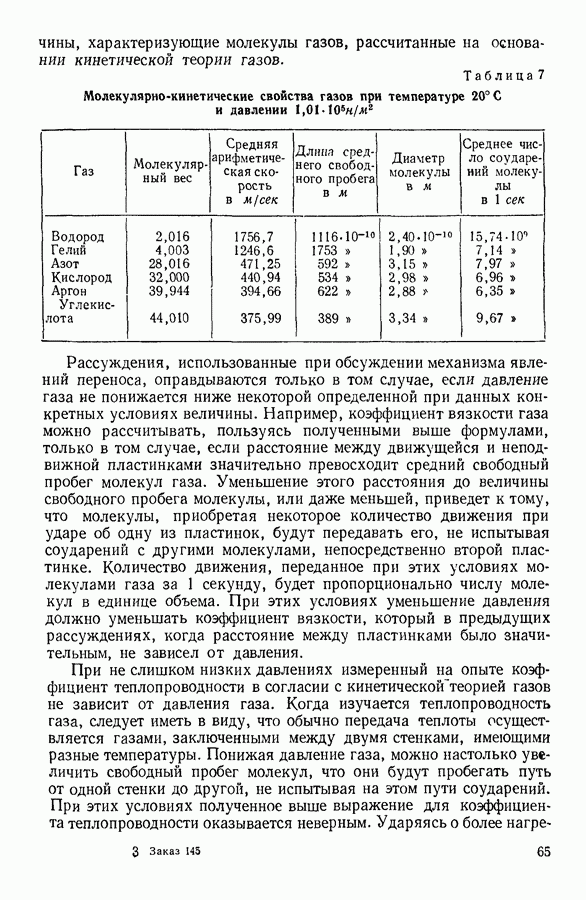
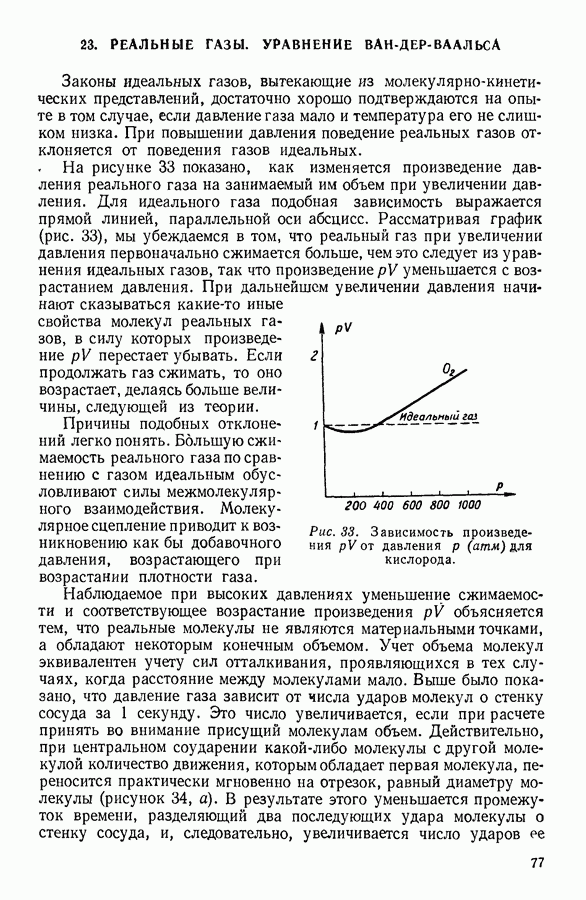
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
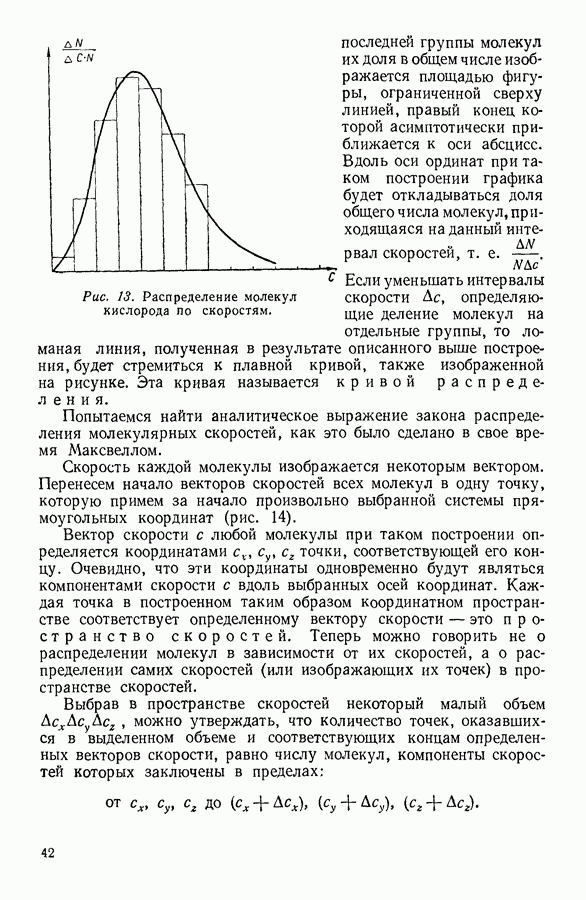
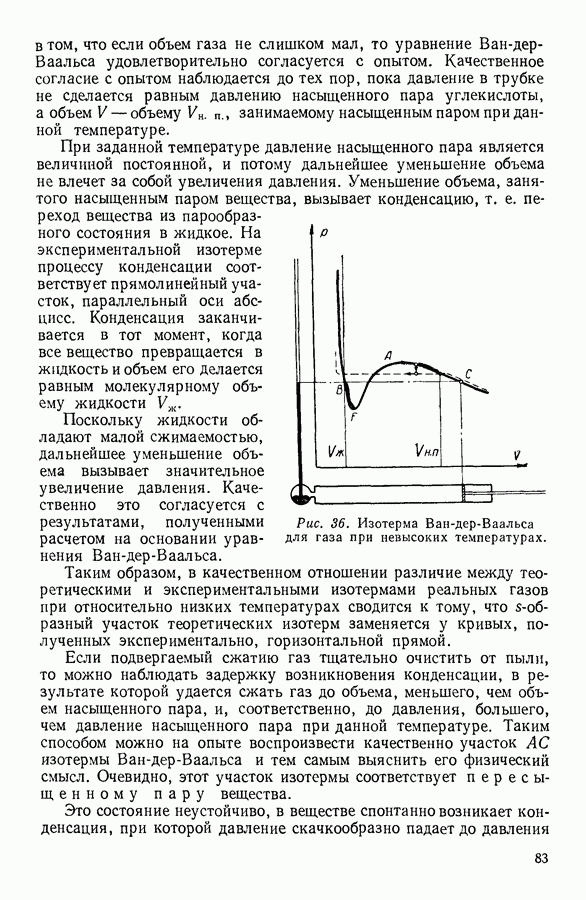
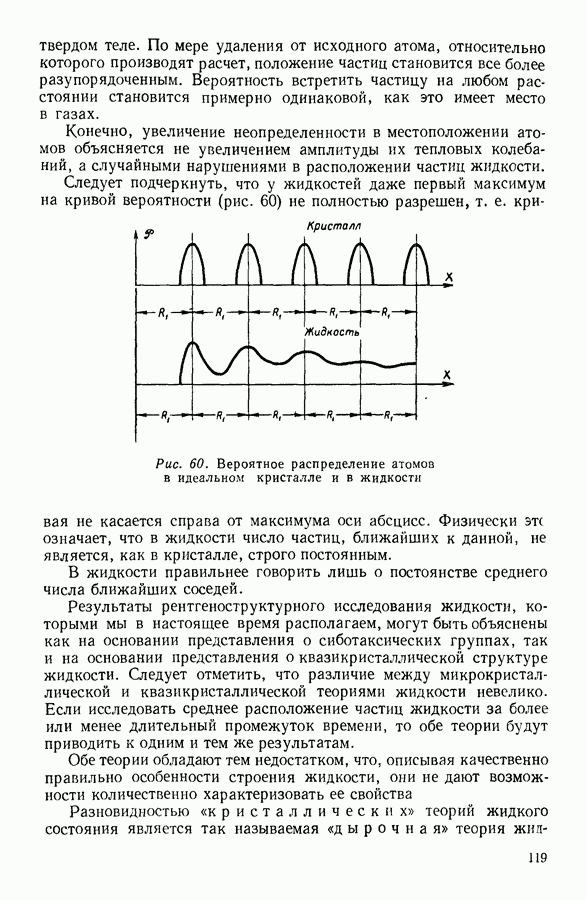
Большие скорости движения молекул, которые не только следуют из теоретических соображений, но и подтверждаются специально поставленными опытами, заставляют задуматься о причинах малых скоростей таких процессов, в которых, как казалось бы, и наблюдается непосредственно движение молекул, например процесс распространения пахучего вещества в воздухе. Это кажущееся противоречие объясняется тем, что каждая молекула при своем движении претерпевает очень большое количество соударений с другими молекулами, в результате чего ее траектория приобретает характерный вид изломанной линии (рис. 20).
Прямолинейные участки траектории  проходимые молекулой между двумя последовательными соударениями, называются свободными пробегами молекулы. Средняя арифметическая величина свободных пробегов называется средним свободным пробегом
проходимые молекулой между двумя последовательными соударениями, называются свободными пробегами молекулы. Средняя арифметическая величина свободных пробегов называется средним свободным пробегом 

где  число соударений.
число соударений.
Число свободных пробегов за какой-либо промежуток времени совпадает с числом соударений молекулы за то же время. Если за одну секунду молекула испытала  соударений, то длина ее траектории, численно равная средней скорости ее движения, будет состоять из
соударений, то длина ее траектории, численно равная средней скорости ее движения, будет состоять из  свободных пробегов. Числа соударений, испытываемых молекулой за 1 секунду, могут быть различными для различных молекул, однако можно ввести представление о среднем числе соударений
свободных пробегов. Числа соударений, испытываемых молекулой за 1 секунду, могут быть различными для различных молекул, однако можно ввести представление о среднем числе соударений  численно равном отношению средней скорости движения молекулы с к среднему свободному пробегу
численно равном отношению средней скорости движения молекулы с к среднему свободному пробегу 

От величины среднего свободного пробега зависят многие свойства газов.

Рис. 20. Траектория движения молекулы.
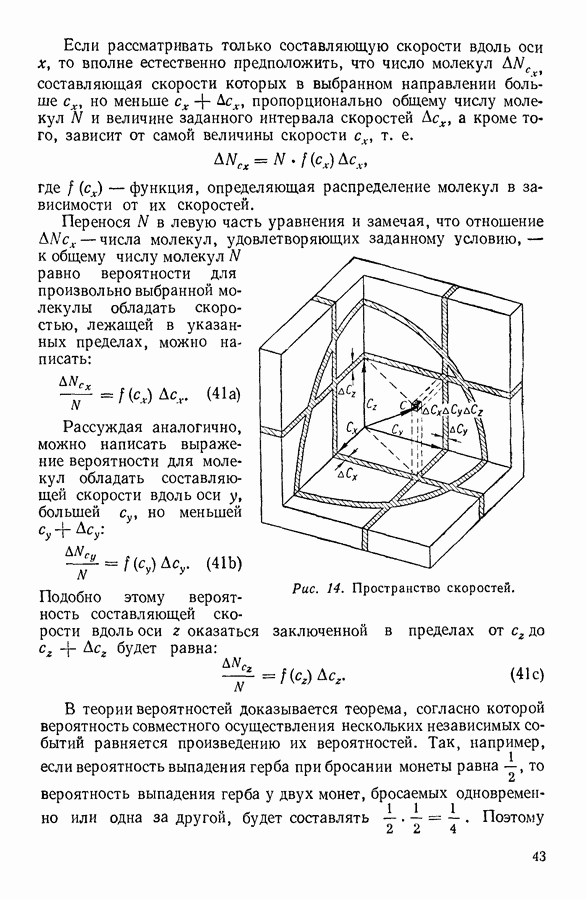
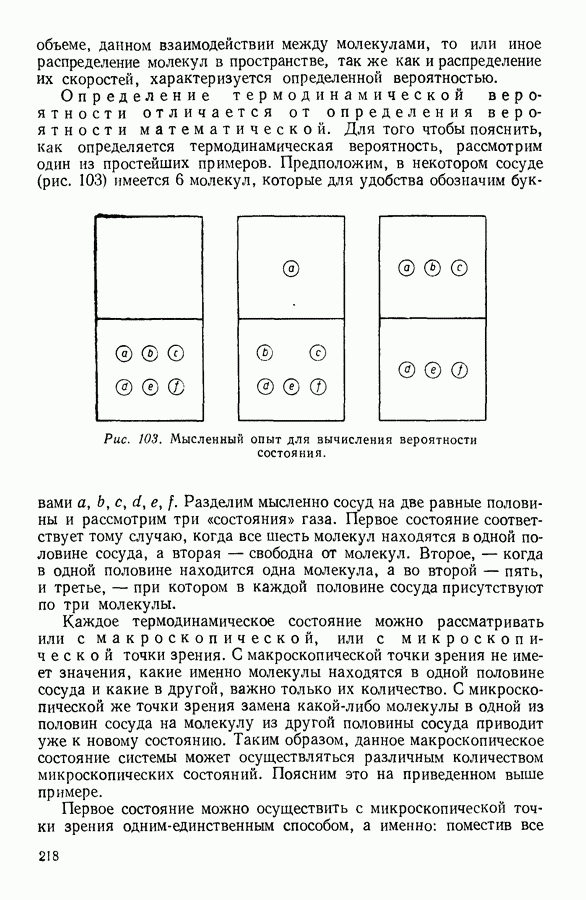
Для вычисления среднего свободного пробега молекулы предположим, что все молекулы газа, за исключением одной, неподвижны и распределены равномерно по всему объему. Будем считать далее, что скорость движущейся молекулы совпадает со средней скоростью с молекулярного движения для данного газа. Двигаясь, молекула соударяется с другими молекулами всякий раз, когда она приближается к ним настолько, что расстояние между их центрами делается равным молекулярному диаметру 
Опишем вокруг движущейся молекулы сферу радиусом, равным молекулярному диаметру, и назовем ее сферой ограждения молекулы. Всякий раз, когда движущаяся молекула сближается с какой-либо другой молекулой настолько, что центр последней оказывается на поверхности сферы ограждения, происходит соударение молекул. При движении молекулы сфера ограждения вырезает в пространстве цилиндр с основанием  Если молекула движется в течение 1 секунды, то высота этого цилиндра равна средней скорости движения молекулы с, а объем, вырезанный сферой ограждения, составляет
Если молекула движется в течение 1 секунды, то высота этого цилиндра равна средней скорости движения молекулы с, а объем, вырезанный сферой ограждения, составляет 
Очевидно, что соударения будут происходить всякий раз, когда центр встречной молекулы будет находиться внутри цилиндра, вырезанного сферой ограждения. Следовательно, для определения среднего числа соударений  достаточно подсчитать число молекул газа, центры которых находятся внутри указанного цилиндра. Это число равно произведению объема цилиндра V на количество молекул газа в единице объема
достаточно подсчитать число молекул газа, центры которых находятся внутри указанного цилиндра. Это число равно произведению объема цилиндра V на количество молекул газа в единице объема  Таким образом, среднее число соударений молекулы за одну секунду будет равно:
Таким образом, среднее число соударений молекулы за одну секунду будет равно:

При получении этого соотношения все молекулы газа, кроме одной, считались неподвижными. Более строгая теория показывает, что при учете движения всех молекул и при условии, что скорости молекулярного движения распределены согласно закону Максвелла, среднее число соударений молекулы за 1 секунду будет несколько больше и может быть подсчитано по уравнению:

Пример. Подсчитать среднее число соударений за 1 сек, молекулы кислорода при нормальном атмосферном давлении и температуре 0° С.
Решение.
Диаметр молекулы кислорода  При нормальных условиях одна килограмм-молекула кислорода занимает объем
При нормальных условиях одна килограмм-молекула кислорода занимает объем  находится
находится  молекул. Средняя арифметическая скорость движения молекулы кислорода при 0° С:
молекул. Средняя арифметическая скорость движения молекулы кислорода при 0° С:

Среднее число соударений молекулы кислорода за 1 сек при этих условиях равно:

Зная среднее число соударений молекулы, можно определить средний свободный пробег молекулы:

Пример. Подсчитать средний свободный пробег молекулы азота, если газ находится при нормальных условиях. Диаметр молекулы азога 
Решение. Число молекул в 

Средний свободный пробег молекулы азота:

Заменяя в уравнении Клапейрона универсальную газовую постоянную  произведением числа Авогадро
произведением числа Авогадро  на постоянную Больцмана
на постоянную Больцмана  можно написать:
можно написать:

или

Но отношение равно числу молекул в одном кубическом метре  следовательно,
следовательно,

Определяя из этого уравнения  и подставляя это значение в уравнение (57), получим:
и подставляя это значение в уравнение (57), получим:

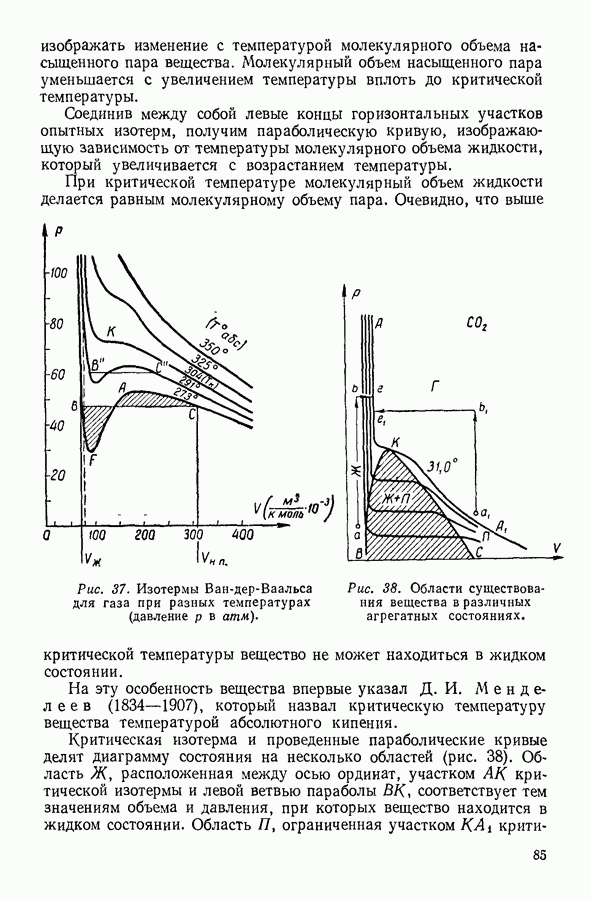
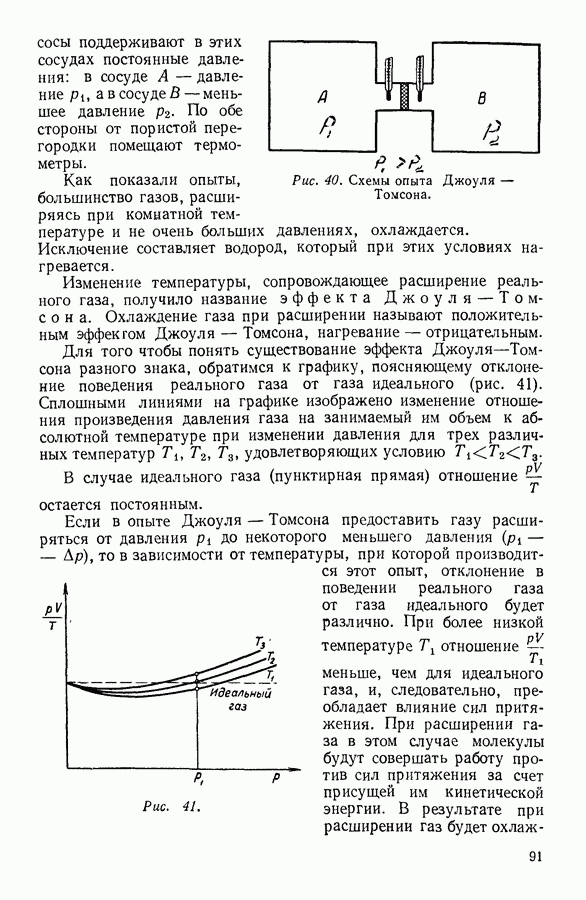
Таким образом, при постоянной температуре средний свободный пробег молекулы обратно пропорционален давлению.
При постоянной молекулярной плотности, или, что то же самое, при постоянном объеме газа, средний свободный пробег молекулы не должен зависеть от температуры.
Независимость при постоянной молекулярной плотности среднего свободного пробега молекул от температуры является
результатом того, что во всех предыдущих рассуждениях не принималось во внимание взаимодействие между молекулами. Учет молекулярных взаимодействий приводит к заключению, что при возрастании температуры средний свободный пробег молекул должен несколько увеличиваться. Если обозначить величину среднего свободного пробега молекул, рассчитанного без учета молекулярного взаимодействия, и, следовательно, независящую от температуры  , то реальная величина среднего свободного пробега
, то реальная величина среднего свободного пробега  при температуре
при температуре  может быть подсчитана с помощью уравнения:
может быть подсчитана с помощью уравнения:

где С — постоянная Сезерленда, зависящая от интенсивности молекулярных взаимодействий. Следует, однако, заметить, что учет взаимодействия молекул, проявляющегося на расстояниях, больших по сравнению с молекулярными диаметрами, в значительной степени лишает понятие свободного пробега молекул той определенности и ясности, которые без этого ему присущи. Действительно, при наличии взаимодействия на значительных расстояниях траектории сближающихся молекул будут плавно изменяться, благодаря чему границы свободного пробега делаются неопределенными.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
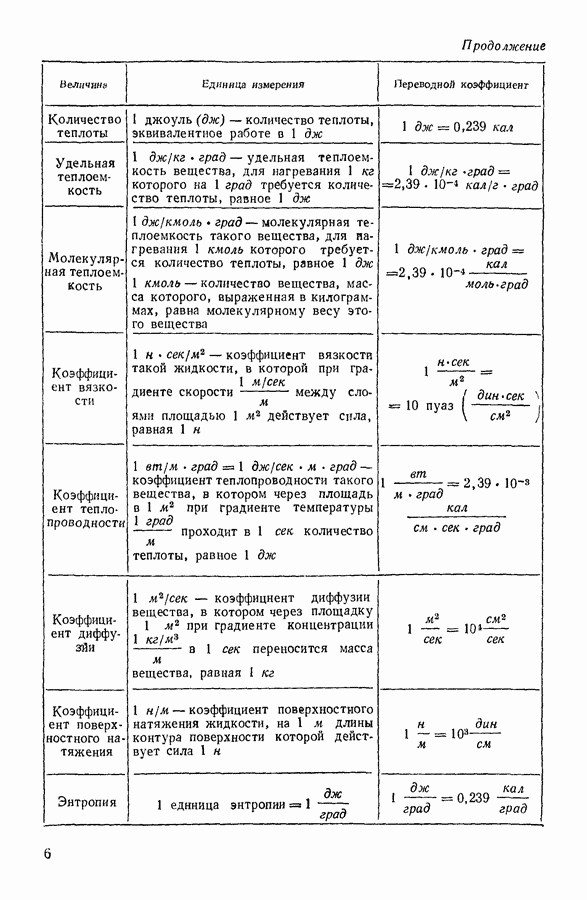
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
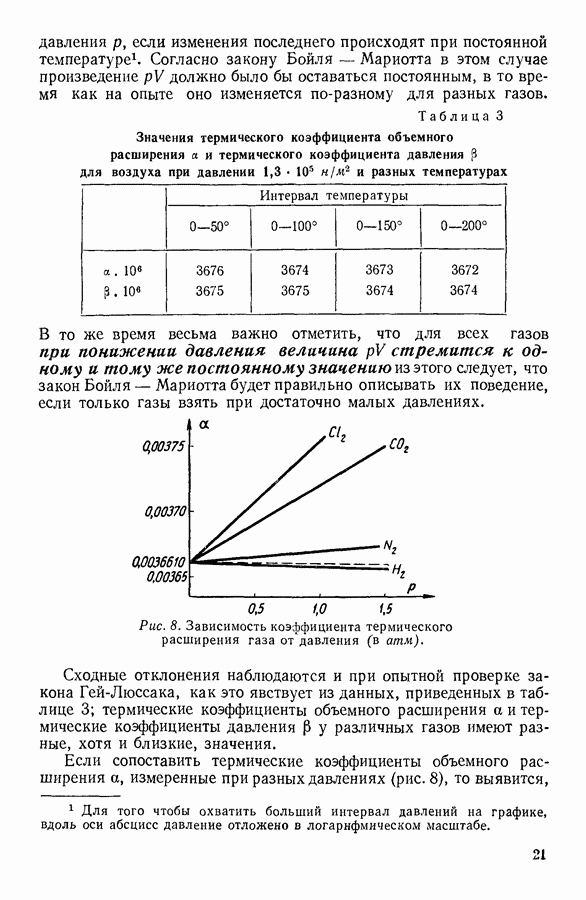
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
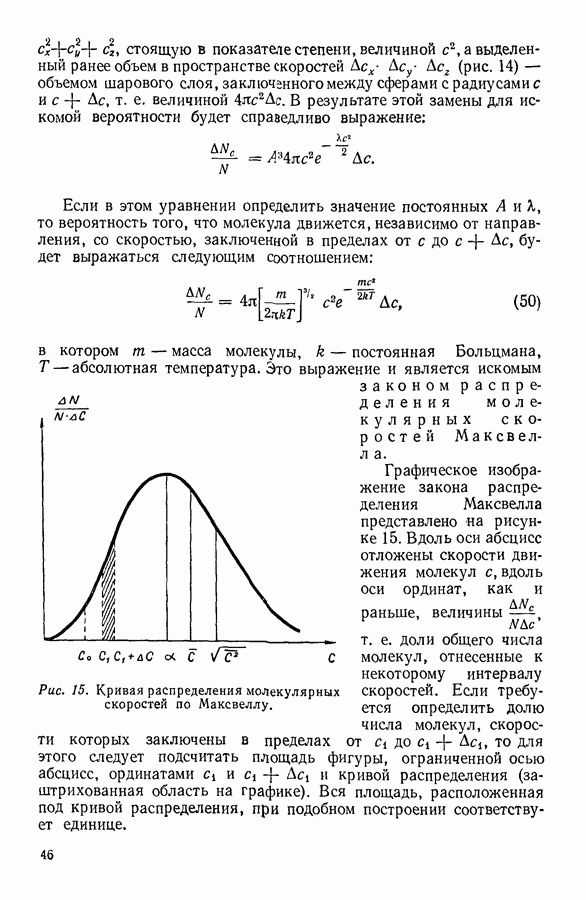
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
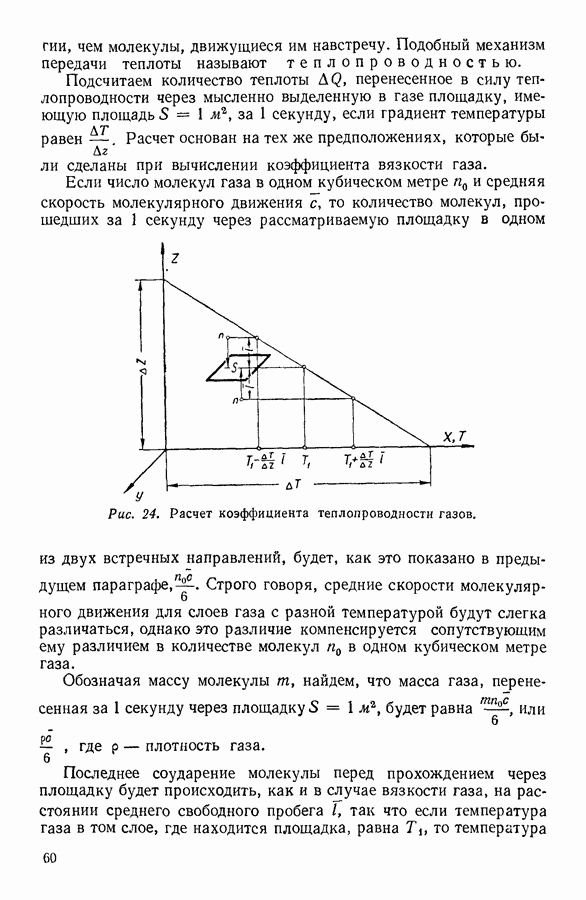
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
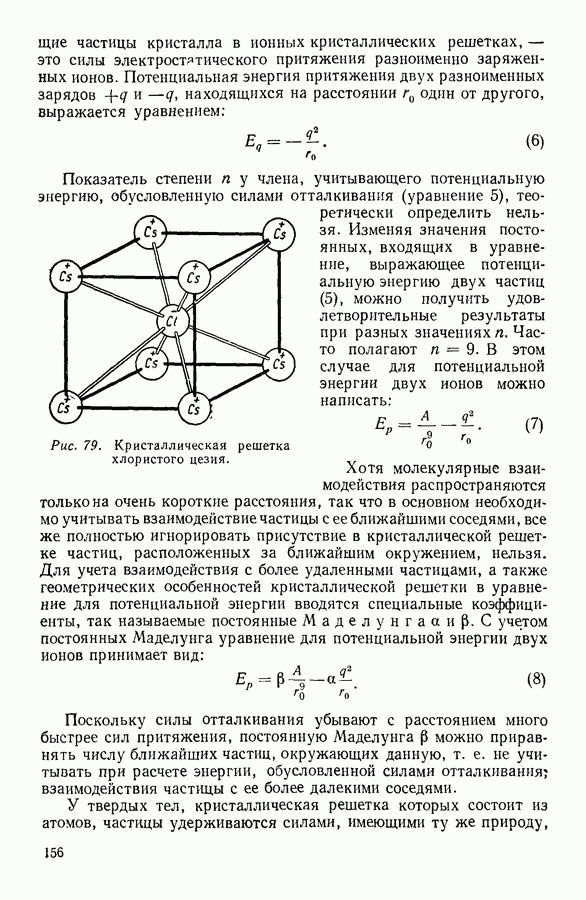
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
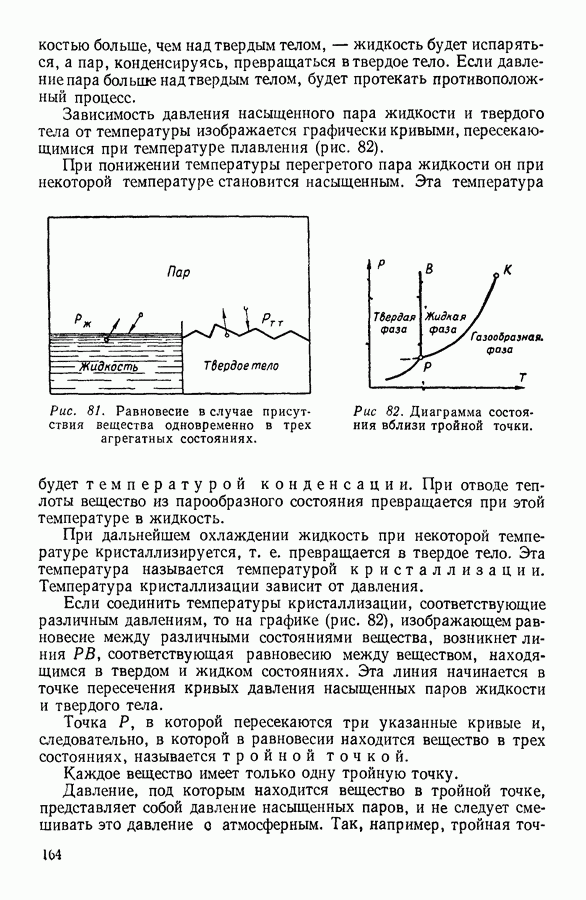
- 28. СЖИЖЕНИЕ ГАЗОВ
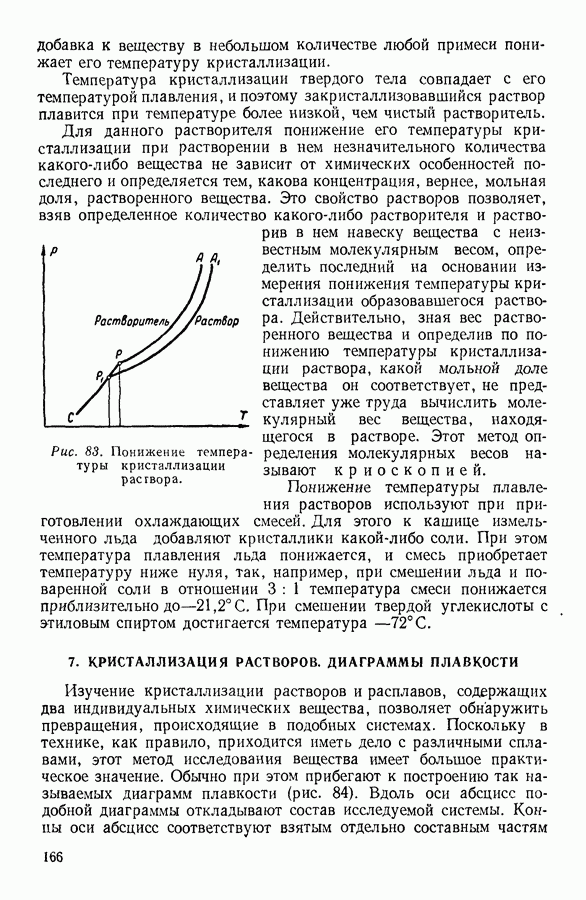
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
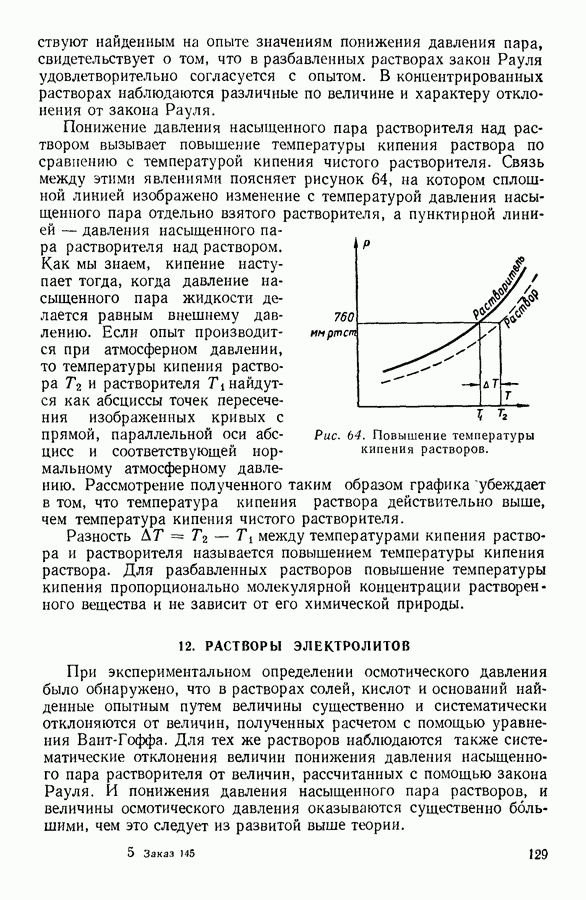
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
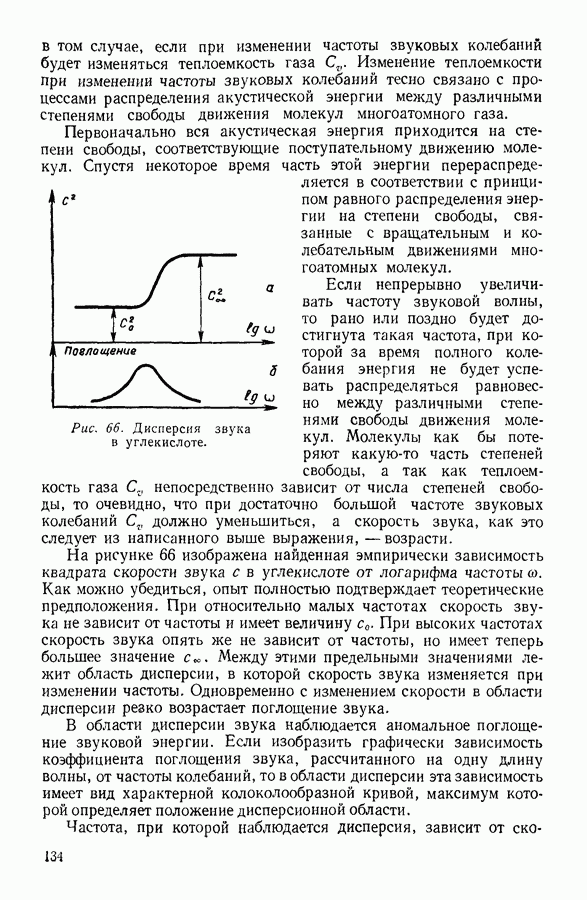
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
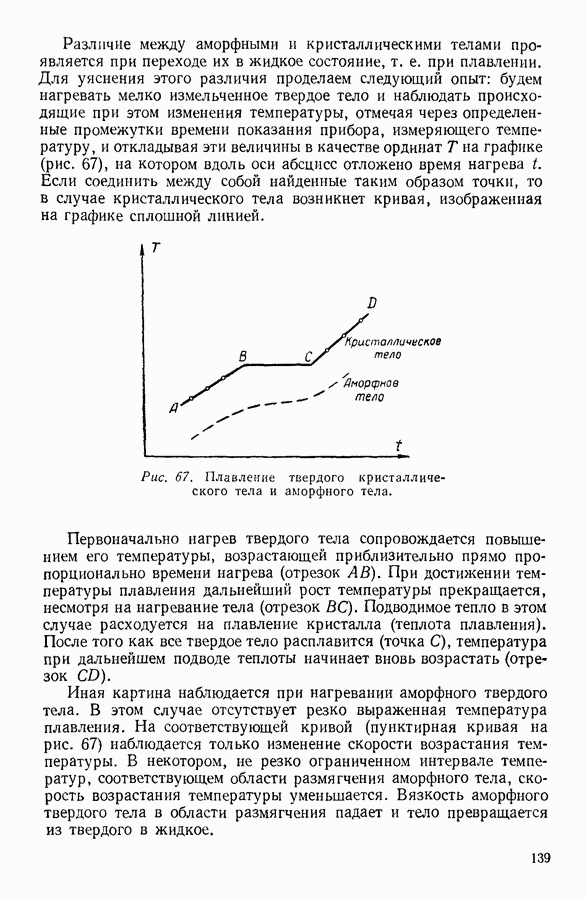
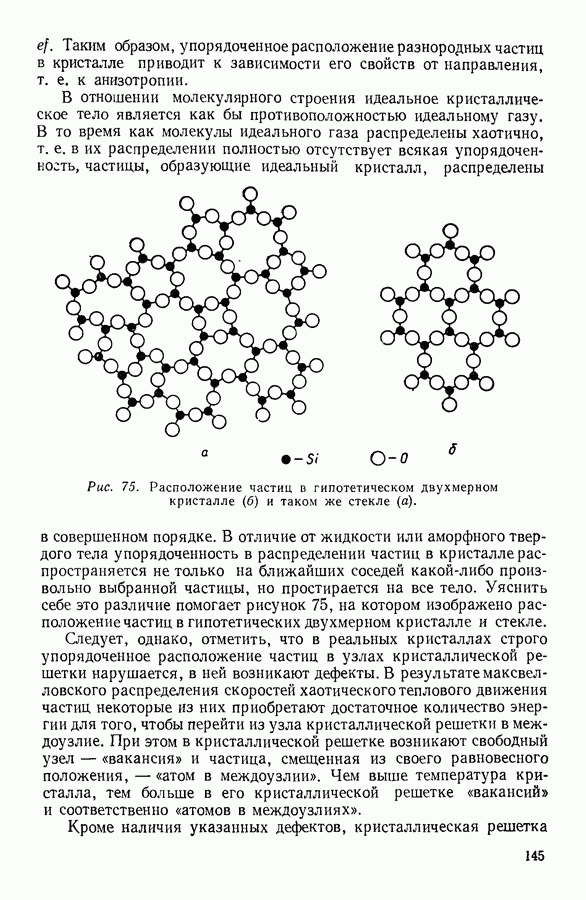
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
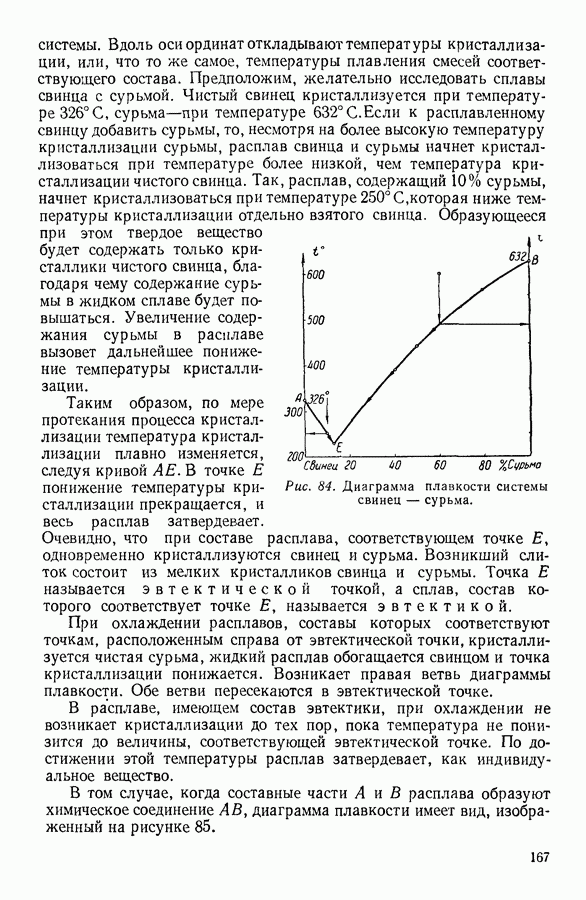
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
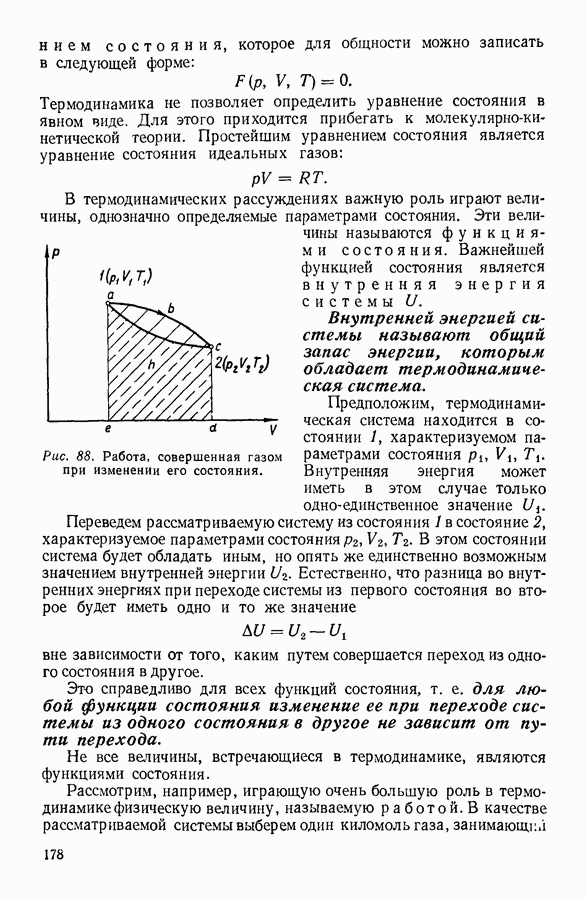
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
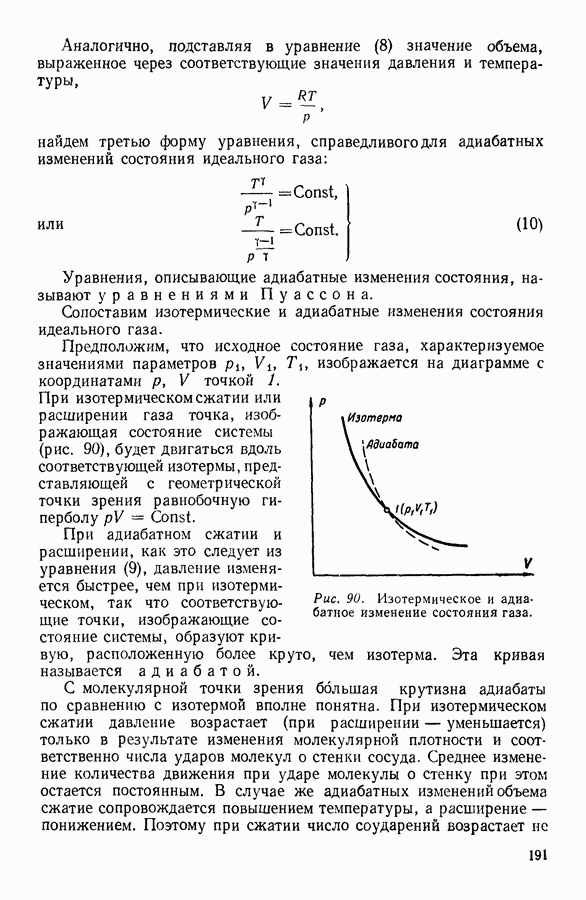
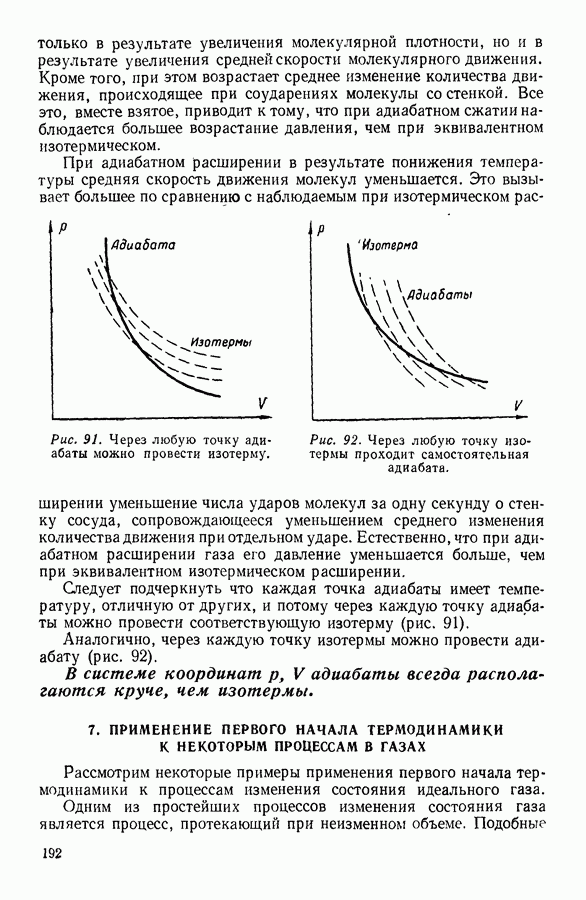
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
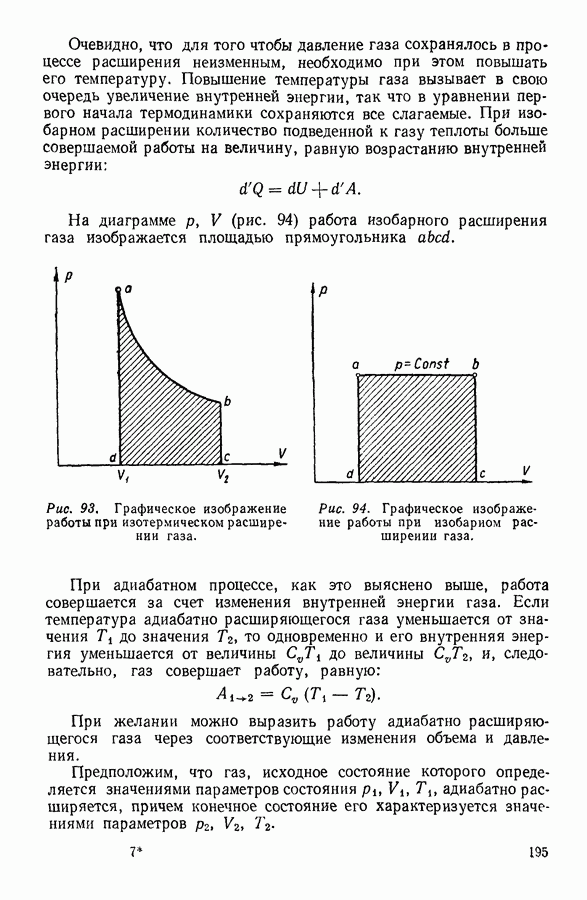
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
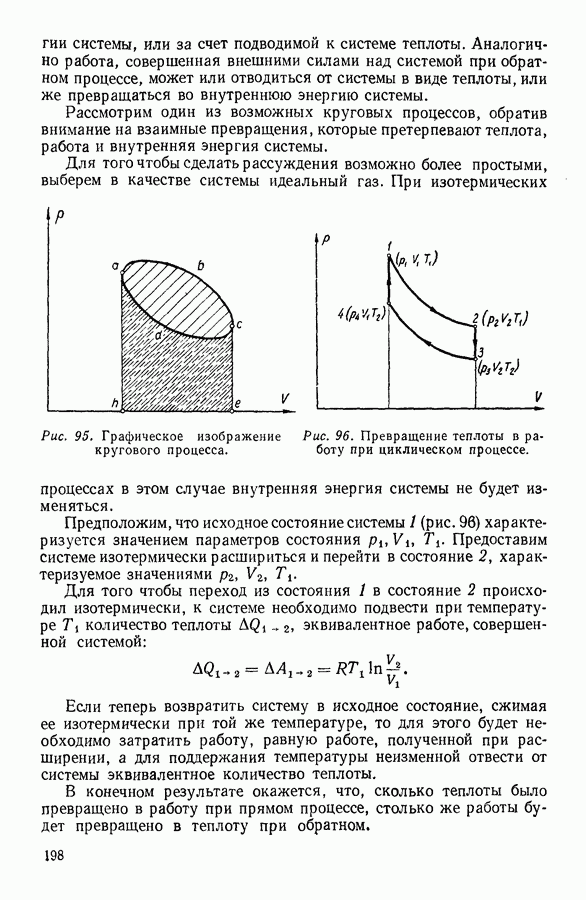
- 8. КРУГОВЫЕ ПРОЦЕССЫ
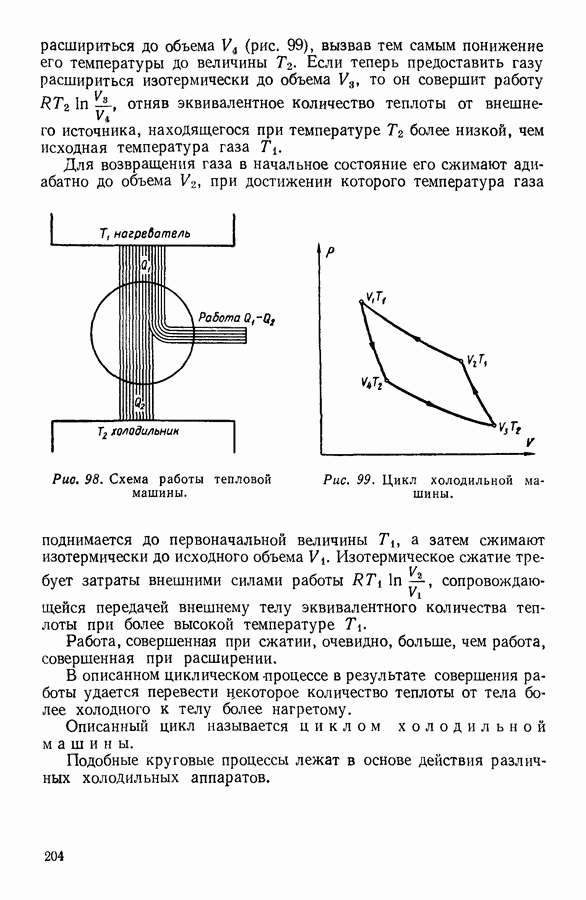
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»