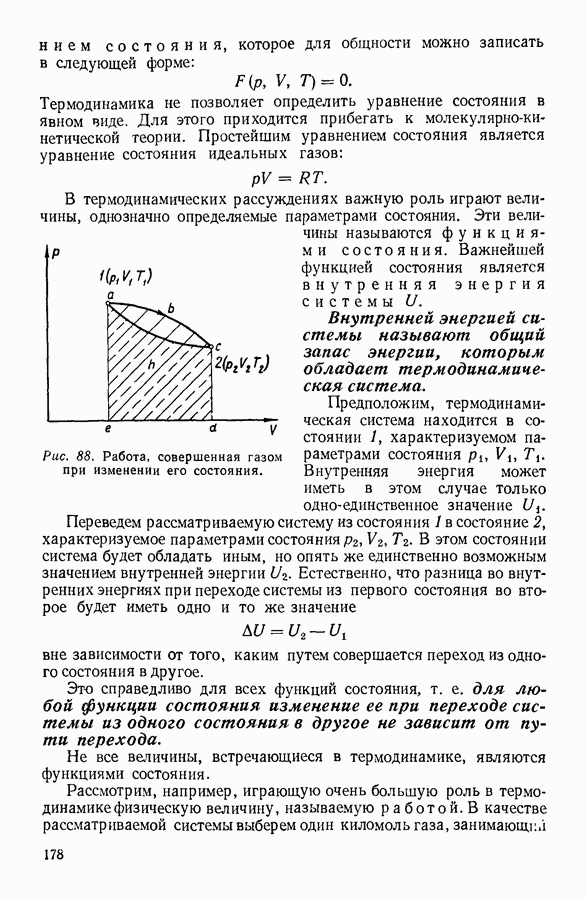
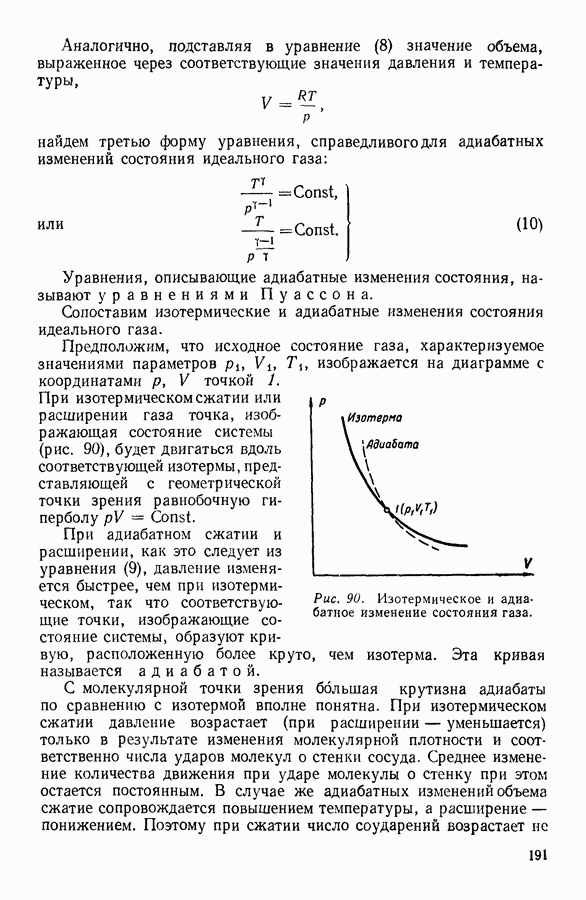
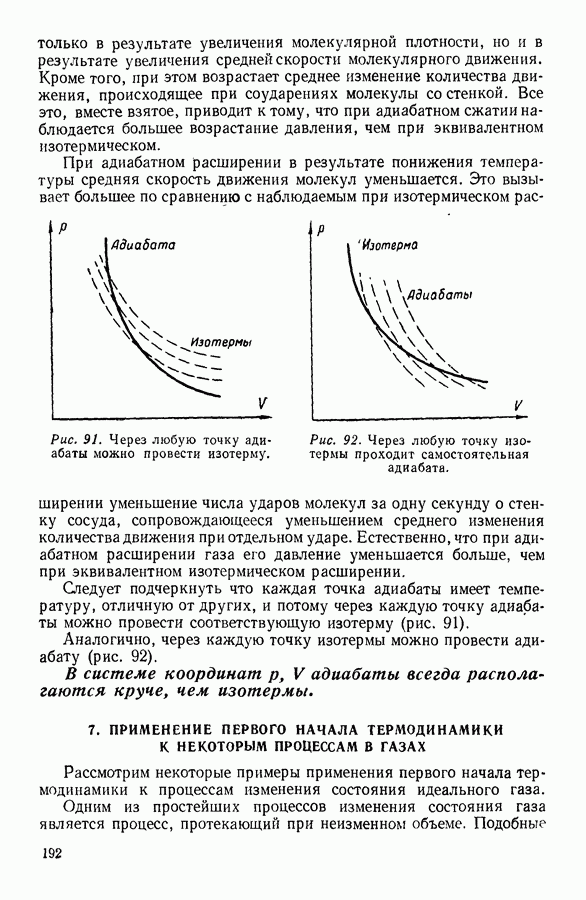
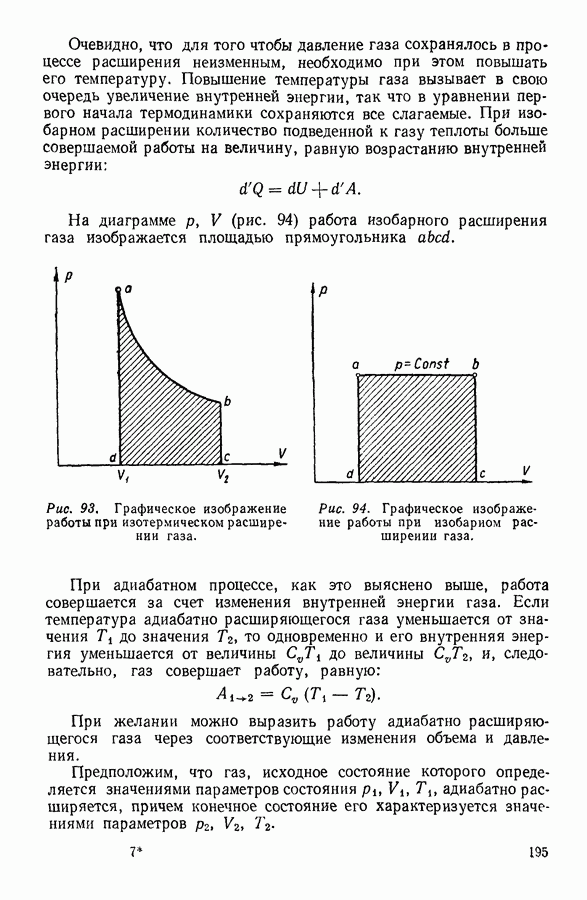
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
Основное уравнение кинетической теории газов можно получить различными способами, отличающимися большей или меньшей строгостью рассуждений. Поскольку окончательный результат во всех случаях оказывается одним и тем же, ниже приводится возможно более простой вывод этого важного уравнения. Предположим, что имеется сосуд в форме куба с ребром а, содержащий один киломоль
газа. Далее допустим, что все молекулы—шарики, имеющие одну и ту же массу  а число их
а число их  очень велико. Малость размеров молекул позволяет пренебречь соударениями их между собой и учитывать лишь соударения их со стенками сосуда. Конечно, последнее предположение справедливо только в том случае, если газ занимает достаточно большой объем, или, что то же самое, если давление газа невелико.
очень велико. Малость размеров молекул позволяет пренебречь соударениями их между собой и учитывать лишь соударения их со стенками сосуда. Конечно, последнее предположение справедливо только в том случае, если газ занимает достаточно большой объем, или, что то же самое, если давление газа невелико.
Влияние, которое оказывают молекулярные соударения, позднее будет рассмотрено специально. Будем считать дальше, что в отношении молекулярных скоростей  справедливы предположения, сделанные в предыдущем параграфе.
справедливы предположения, сделанные в предыдущем параграфе.

Рис. 10.
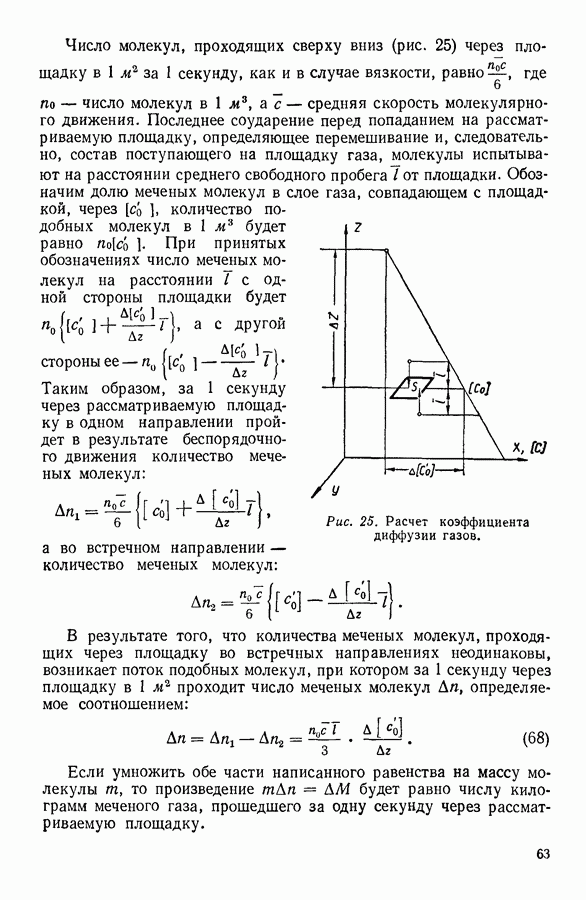
При своем движении молекулы будут непрерывно ударяться о стенки сосуда. Следующие очень быстро один за другим молекулярные удары будут усредняться и, как указал в 1738 г. академик Санкт-Петербургской Академии наук Д. Бернулли, создавать постоянную силу, действующую на стенки сосуда. Для того чтобы определить величину этой силы, рассмотрим соударение со стенкой какой-либо произвольно выбранной молекулы. Разложим скорость движения этой молекулы  на три взаимно перпендикулярные составляющие:
на три взаимно перпендикулярные составляющие:  которые направим вдоль трех ребер куба, пересекающихся в одной из его вершин. Если считать, что стенки содержащего газ сосуда абсолютно гладкие, то при упругом ударе молекулы-шарика об одну из стенок будет изменяться, как это доказывается в механике, только нормальная к данной стенке составляющая скорости. Две другие составляющие скорости будут при ударе оставаться без изменения. Допустим, что в некоторый момент времени рассматриваемая молекула ударилась о правую грань куба, соответствующую (см. рис. 10) в выбранной системе координат плоскости
которые направим вдоль трех ребер куба, пересекающихся в одной из его вершин. Если считать, что стенки содержащего газ сосуда абсолютно гладкие, то при упругом ударе молекулы-шарика об одну из стенок будет изменяться, как это доказывается в механике, только нормальная к данной стенке составляющая скорости. Две другие составляющие скорости будут при ударе оставаться без изменения. Допустим, что в некоторый момент времени рассматриваемая молекула ударилась о правую грань куба, соответствующую (см. рис. 10) в выбранной системе координат плоскости  При ударе нормальная составляющая скорости
При ударе нормальная составляющая скорости  сохранив неизменной свою величину, изменит направление на обратное, т. е. после удара эта составляющая скорости движения молекулы будет равна
сохранив неизменной свою величину, изменит направление на обратное, т. е. после удара эта составляющая скорости движения молекулы будет равна  С изменением скорости молекулы неразрывно связано изменение присущего ей количества движения, составляющее в данном случае
С изменением скорости молекулы неразрывно связано изменение присущего ей количества движения, составляющее в данном случае

Отразившись от стенки, рассматриваемая молекула после большего или меньшего числа соударений с различными гранями куба ударится о левую грань, противоположную первой. До этого момента составляющая скорости  изменяться не будет, поскольку предполагается, что между собой молекулы не соударяются, а из граней куба нормальны к этой составляющей скорости только правая и левая грани и поэтому только при соударении с ними она может измениться.
изменяться не будет, поскольку предполагается, что между собой молекулы не соударяются, а из граней куба нормальны к этой составляющей скорости только правая и левая грани и поэтому только при соударении с ними она может измениться.
После соударения с левой гранью куба составляющая скорости  изменит свое направление на обратное, т. е. сделается равной
изменит свое направление на обратное, т. е. сделается равной  Спустя некоторый промежуток времени рассматриваемая молекула вновь ударится о правую грань куба. Время
Спустя некоторый промежуток времени рассматриваемая молекула вновь ударится о правую грань куба. Время  разделяющее два последующих удара молекулы об одну и ту же грань, легко определить. Для этого необходимо разделить путь, пройденный молекулой между этими соударениями и измеренный вдоль данной оси координат, на соответствующую составляющую скорости движения молекулы. В рассматриваемом случае путь молекулы равен 2а, так что время между двумя последующими ударами найдется из соотношения
разделяющее два последующих удара молекулы об одну и ту же грань, легко определить. Для этого необходимо разделить путь, пройденный молекулой между этими соударениями и измеренный вдоль данной оси координат, на соответствующую составляющую скорости движения молекулы. В рассматриваемом случае путь молекулы равен 2а, так что время между двумя последующими ударами найдется из соотношения

Зная время, разделяющее два последующих удара молекулы об одну и ту же грань, можно определить, сколько раз за 1 секунду ударится данная молекула о рассматриваемую грань куба. Это число ударов  будет равно:
будет равно:

Поскольку при каждом ударе данной молекулы изменение количества движения составляет  общее изменение количества движения за 1 секунду будет:
общее изменение количества движения за 1 секунду будет:

Приведенные выше рассуждения можно повторить применительно к любой из  молекул, заключенных в рассматриваемом кубе.
молекул, заключенных в рассматриваемом кубе.
Общее изменение количества движения за 1 секунду, происходящее в результате соударения с данной гранью всех заполняющих куб молекул, найдется суммированием изменений количеств движений, обусловленных соударениями отдельных молекул, т. е.

Для дальнейших выводов следует учесть, что при разложении векторов молекулярных скоростей на составляющие вдоль трех
произвольно выбранных осей координат должны выполняться следующие условия:

Суммируя написанные уравнения, получим:

Условие хаотичности молекулярного движения требует, чтобы при любом расположении координатных осей выполнялось равенство:

или

Это дает возможность преобразовать уравнение (17), выражающее изменение количества движения, следующим образом:

Из механики известно, что изменение количества движения численно равно импульсу силы

Поскольку в приведенных выше рассуждениях подсчитано изменение количества движения, происходящее за промежуток времени  равный одной секунде, то очевидно, что в данном случае изменения количества движения, происходящие при ударе молекул о грань куба, численно равны силе
равный одной секунде, то очевидно, что в данном случае изменения количества движения, происходящие при ударе молекул о грань куба, численно равны силе  действующей со стороны газа на эту грань, т. е.
действующей со стороны газа на эту грань, т. е.

При характеристике свойств газов обычно говорят не о силе, действующей на стенки сосуда, а о давлении газа  Сила
Сила  действующая на грань куба площадью
действующая на грань куба площадью  связана с давлением газа простым соотношением:
связана с давлением газа простым соотношением: 
В рассматриваемом примере  следовательно,
следовательно,

Но  т. е. объему, занимаемому газом, так что окончательно для расчета получаем соотношение:
т. е. объему, занимаемому газом, так что окончательно для расчета получаем соотношение:

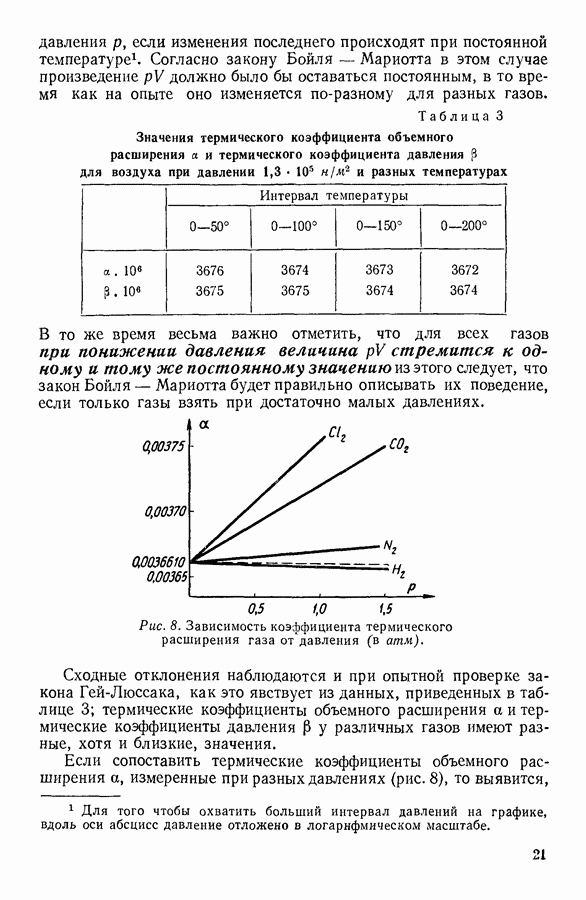
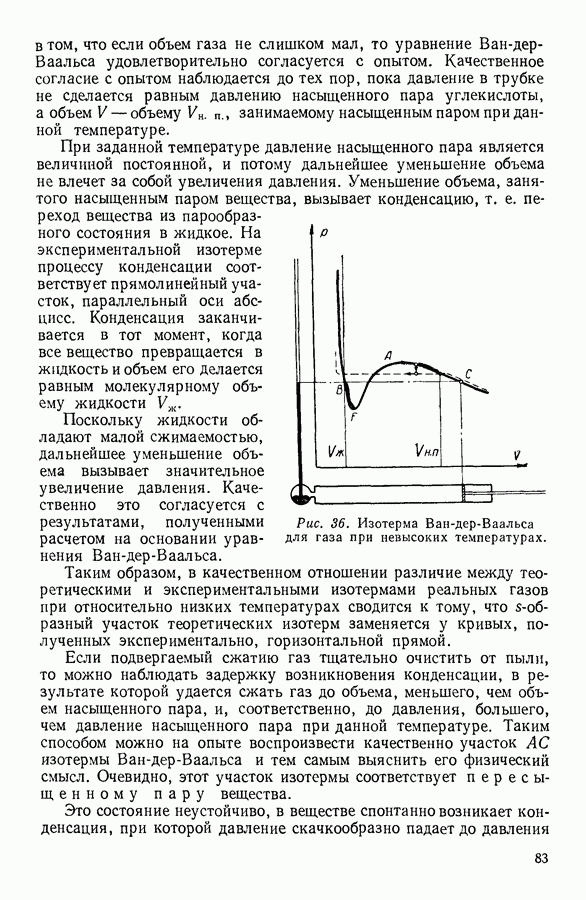
Приведенные выше рассуждения показывают, каким образом в результате рассмотрения поведения отдельных молекул можно сделать заключение о физической сущности макроскопического свойства газа — его давлении.
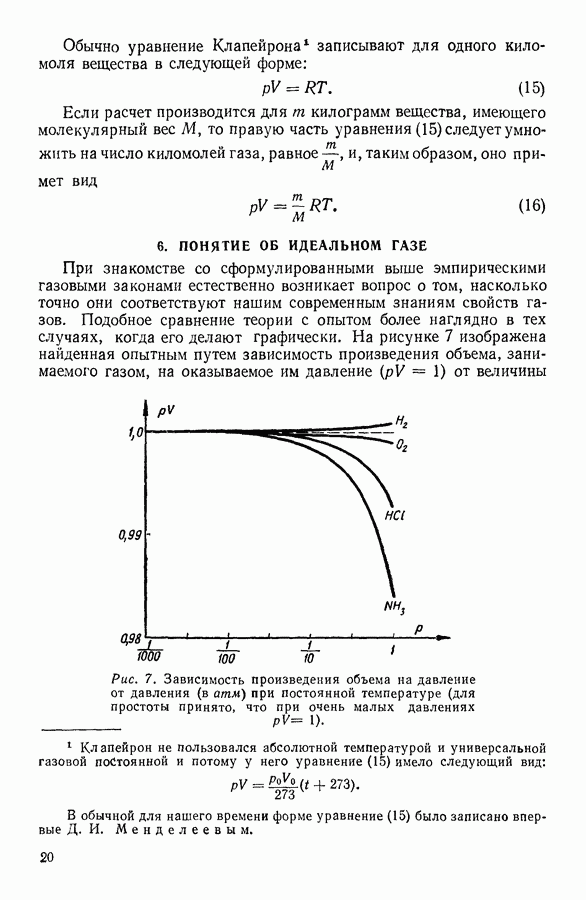
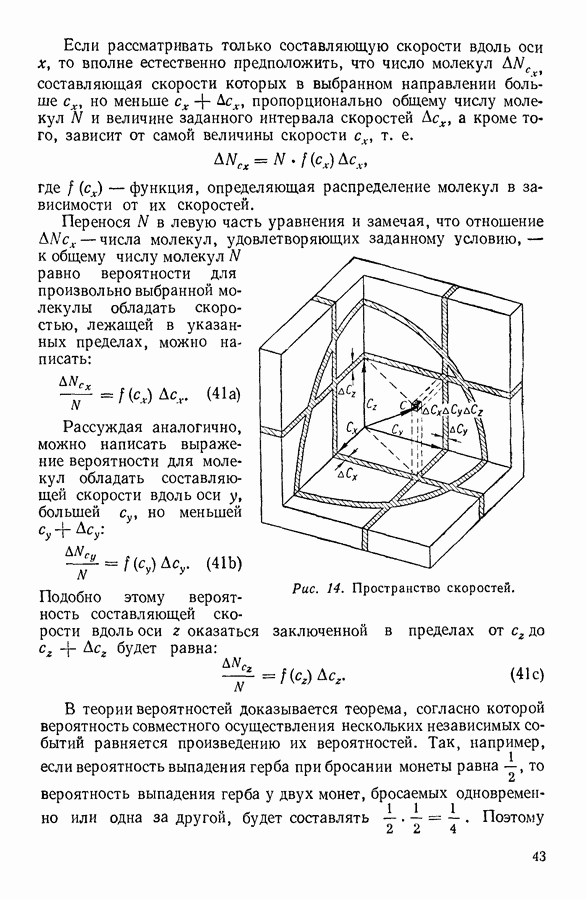
Проанализируем более внимательно полученное выражение для давления газа. Легко заметить, что стоящая в правой части уравнения (19) в числителе сумма представляет собой общую кинетическую энергию молекул газа

Поскольку в знаменателе стоит объем, занимаемый газом, то очевидно, что вся дробь будет представлять кинетическую энергию молекул, заключенных в единице объема газа, т. е. плотность кинетической энергии молекул.
Таким образом, мы приходим к важному выводу о том, что давление газа измеряется плотностью кинетической энергии движущихся молекул.
Все молекулы газа имеют одинаковую массу  значение которой можно вынести в выражении для кинетической энергии за знак суммирования. В этом случае общая кинетическая энергия молекул запишется в виде
значение которой можно вынести в выражении для кинетической энергии за знак суммирования. В этом случае общая кинетическая энергия молекул запишется в виде

Разделив и умножив правую часть выражения (20) на число молекул газа  получим:
получим:

Дробь

представляет собой средний квадрат скорости движения молекул  Корень квадратный из этой величины называют средней квадратичной скоростью движения молекул:
Корень квадратный из этой величины называют средней квадратичной скоростью движения молекул:

Пользуясь величиной средней квадратичной скорости, можно выразить кинетическую энергию молекул газа следующим соотношением:

Выражение для давления газа теперь будет:

Замечая, что дробь представляет число  молекул в единице объема газа, можно записать выражение для давления газа в следующем виде:
молекул в единице объема газа, можно записать выражение для давления газа в следующем виде:

Это уравнение обычно называют основным уравнением кинетической теории газов.
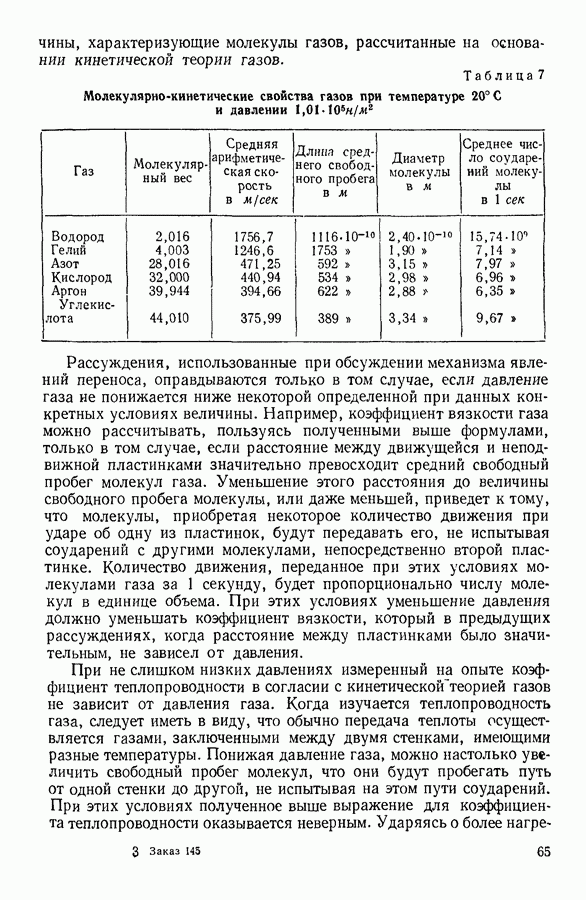
Заметим, что число молекул  находящихся при нормальных условиях в одном кубическом метре газа, равно
находящихся при нормальных условиях в одном кубическом метре газа, равно 
В дальнейшем наряду со средней квадратичной скоростью нам придется пользоваться и средней арифметической скоростью, определяемой соотношением:

Следует обратить внимание на то, что квадрат средней квадратичной скорости  отличается от квадрата средней арифметической скорости
отличается от квадрата средней арифметической скорости  Для того чтобы убедиться в этом, решим
Для того чтобы убедиться в этом, решим
следующую задачу: имеется 10 молекул, две из которых движутся со скоростью  четыре — со скоростью
четыре — со скоростью  три — со скоростью
три — со скоростью  и одна — со скоростью
и одна — со скоростью  Требуется определить квадрат средней арифметической скорости
Требуется определить квадрат средней арифметической скорости  и квадрат средней квадратичной скорости
и квадрат средней квадратичной скорости 
Согласно определению

Мы видим, таким образом, что величины  существенно различаются.
существенно различаются.
Если требуется на основании среднего значения молекулярной скорости найти величину кинетической энергии какой-то совокупности молекул, то для получения правильного ответа необходимо пользоваться средней квадратичной скоростью, а не средней арифметической.
Если в уравнении (23) перенести объем газа У в левую часть, то оно приобретет следующий вид:

Сопоставив написанное выражение с уравнением Клапейрона

и замечая, что левые части этих равенств одинаковы, можно написать

Перенеся  в правую часть уравнения, получим:
в правую часть уравнения, получим:

По своему физическому смыслу отношение  представляет собой универсальную газовую постоянную, отнесенную к одной молекуле. Эта величина называется постоянной Больцмана k. В системе СИ постоянная Больцмана
представляет собой универсальную газовую постоянную, отнесенную к одной молекуле. Эта величина называется постоянной Больцмана k. В системе СИ постоянная Больцмана  равна
равна 
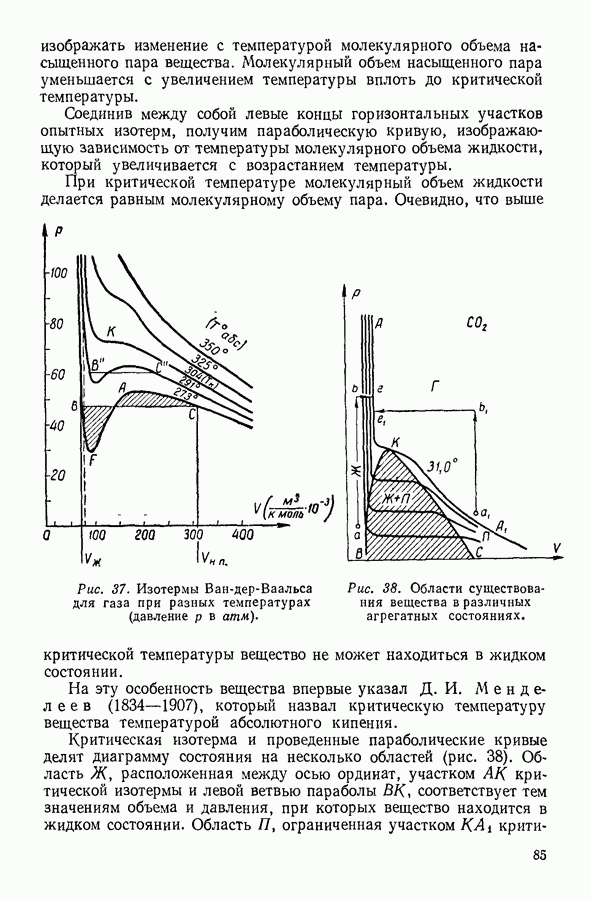
Полученное уравнение позволяет сделать чрезвычайно важный вывод о том, что средняя кинетическая энергия молекул газа зависит только от температуры газа.

Этот вывод раскрывает физический смысл абсолютной температуры.
Из уравнения (28) следует, что абсолютная температура является мерой средней кинетической энергии молекулярного движения. По мере приближения к абсолютному нулю средняя кинетическая энергия теплового движения молекул уменьшается
Следует также обратить внимание на то, что согласно уравнению (28) при одинаковой абсолютной температуре кинетические энергии, обусловленные перемещением молекул, будут одинаковыми даже у молекул, сильно различающихся своей массой. Процесс выравнивания температуры, который имеет место при соприкосновении или смешении холодного газа с газом нагретым, представляет по существу процесс выравнивания средних кинетических энергий поступательного движения молекул.
Уравнение (27) позволяет рассчитать среднюю квадратичную скорость движения молекул любого газа при разных температурах. Заметив, что произведение массы молекулы  на число Авогадро
на число Авогадро  равняется массе одного киломоля газа, т. е. молекулярному весу вещества
равняется массе одного киломоля газа, т. е. молекулярному весу вещества  можно записать выражение для вычисления средней квадратичной скорости газа в следующем виде:
можно записать выражение для вычисления средней квадратичной скорости газа в следующем виде:

или, подставляя численное значение универсальной газовой постоянной,

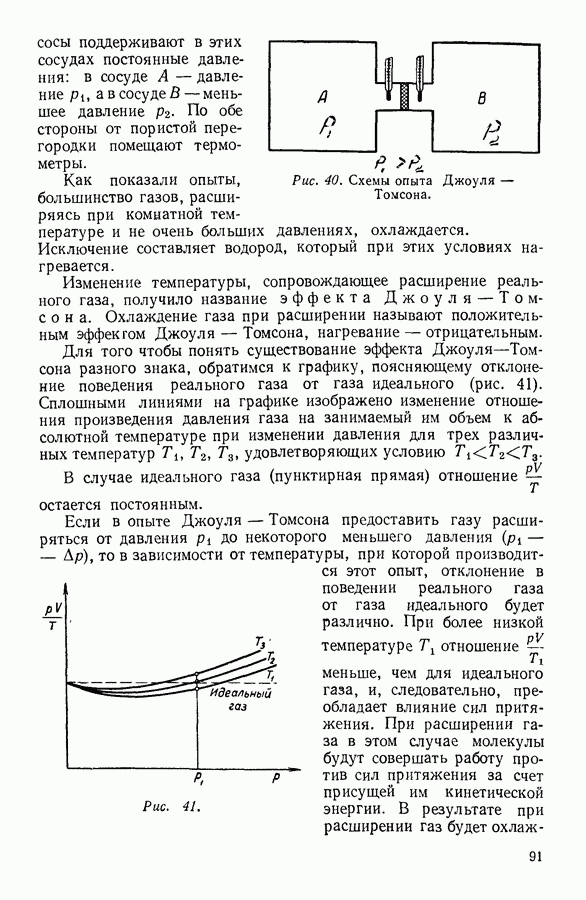
Таким образом, средняя квадратичная скорость поступательного движения молекул прямо пропорциональна квадратному корню из отношения абсолютной температуры к молекулярному весу.
Сходная зависимость существует и для средней
арифметической скорости движения молекул с. В этом случае справедливо соотношение:

или

Пример 1. Вычислить среднюю квадратичную и среднюю арифметическую скорости движения молекул водорода и атомов парообразной ртути при температуре 300° по абсолютной шкале. Молекулярный вес водорода 2, атомный вес ртути 200.
Решение.

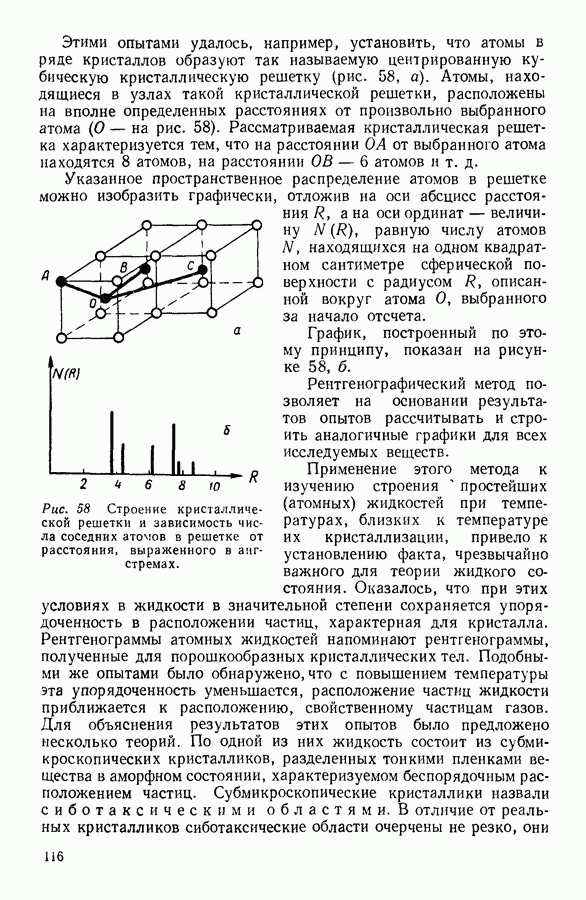
Пример 2. Какой вывод придется сделать, если при вычислении давления газа (стр. 25) предположить, что грань куба, о которую ударяются молекулы, удаляется от приближающихся молекул со скоростью и, измеренной по отношению к той же неподвижной системе координат, по отношению к которой измерена скорость молекулы.
Решение. При расчете скорости движения молекулы при соударении со стенкой следует принимать во внимание не абсолютное значение скорости движения молекулы, а относительное ее значение, измеренное с учетом движения стенки. Таким образом, поскольку и молекула и стенка движутся в одном направлении, относительная скорость движения молекулы до удара будет  . После удара скорость движения молекулы по отношению стенки должна сохранить свою величину, но изменить знак на обратный. Поскольку же после удара стенка и рассматриваемая молекула движутся в противоположных направлениях, то в системе координат, в которой измерены скорости
. После удара скорость движения молекулы по отношению стенки должна сохранить свою величину, но изменить знак на обратный. Поскольку же после удара стенка и рассматриваемая молекула движутся в противоположных направлениях, то в системе координат, в которой измерены скорости  это означает добавочное уменьшение скорости движения молекулы на величину, равную скорости движения стенки и.
это означает добавочное уменьшение скорости движения молекулы на величину, равную скорости движения стенки и.
Таким образом, в той системе координат, в которой до соударения со стенкой скорость движения молекулы была равна  после соударения она составит только
после соударения она составит только  следовательно, кинетическая энергия молекулы при ударе о движущуюся стенку будет изменяться, в рассмотренном случае — уменьшаться. Уменьшение кинетической энергии в условиях данной задачи равно:
следовательно, кинетическая энергия молекулы при ударе о движущуюся стенку будет изменяться, в рассмотренном случае — уменьшаться. Уменьшение кинетической энергии в условиях данной задачи равно:

Очевидно, что если энергия молекулярного движения не пополняется извне, то в результате соударений с движущейся стенкой величина средней кинетической энергии молекул газа уменьшается, т. е. газ охлаждается.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
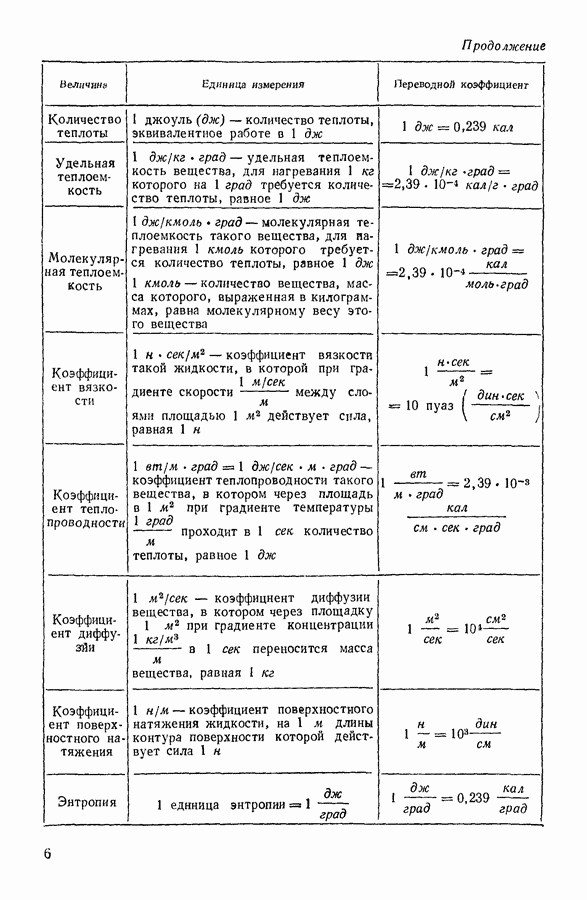
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
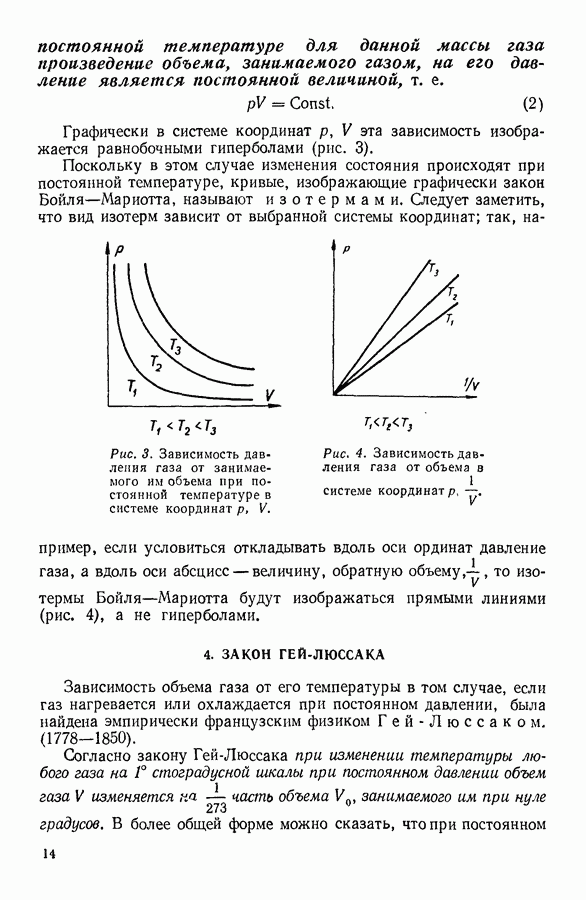
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
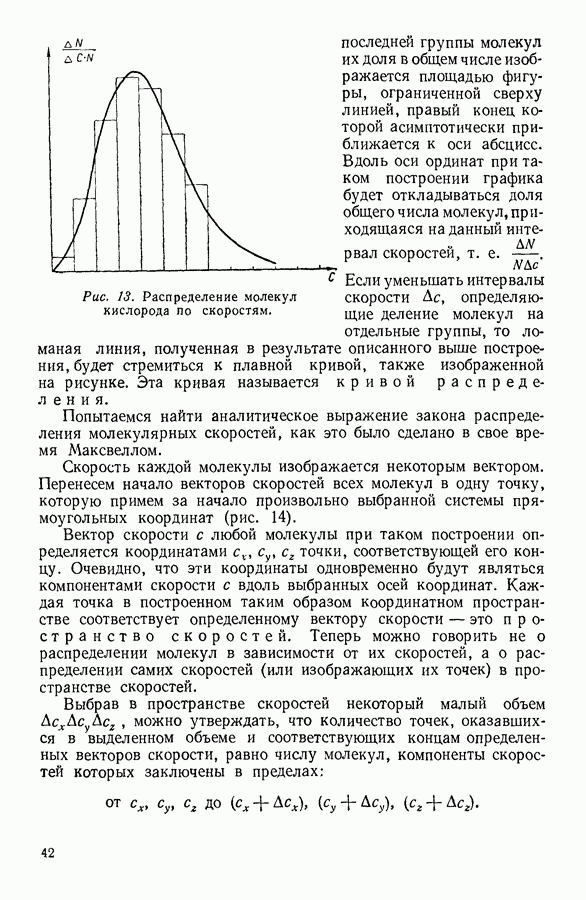
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
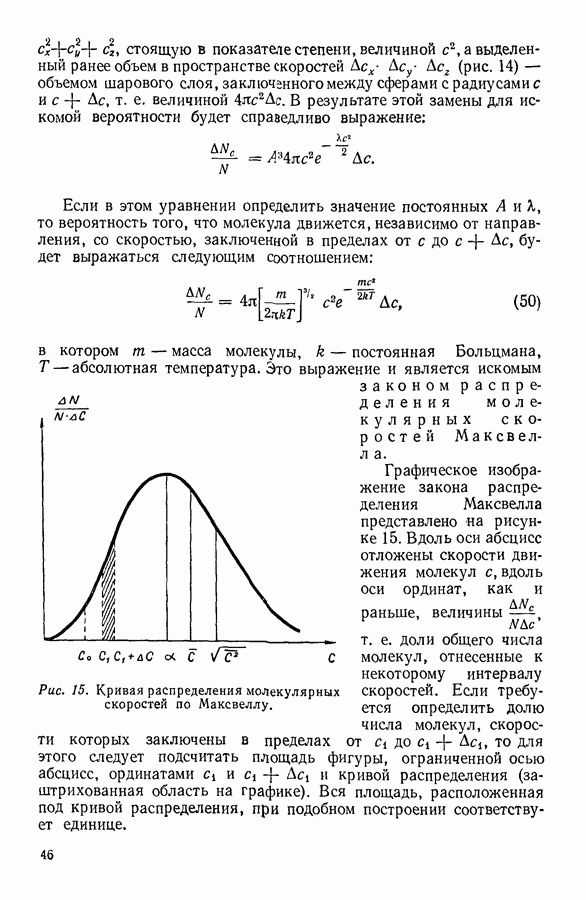
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
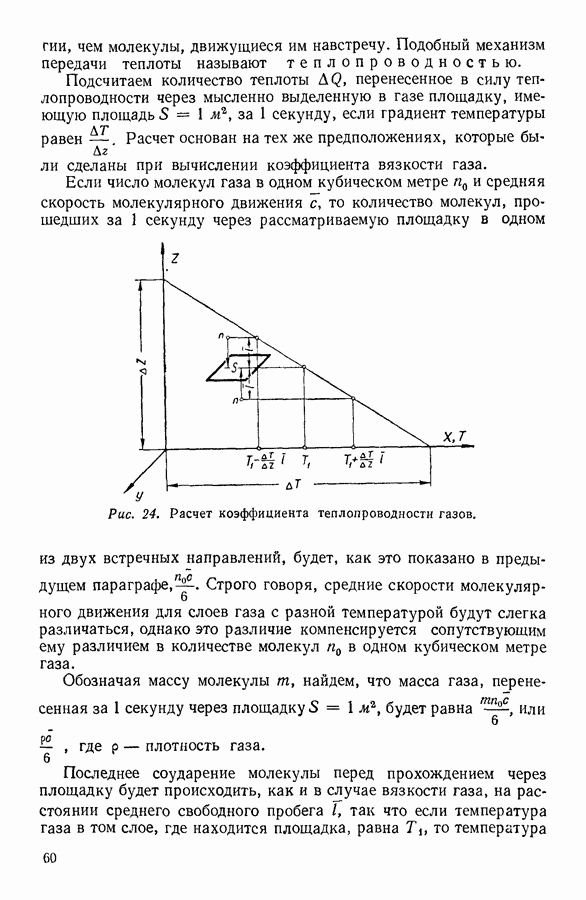
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
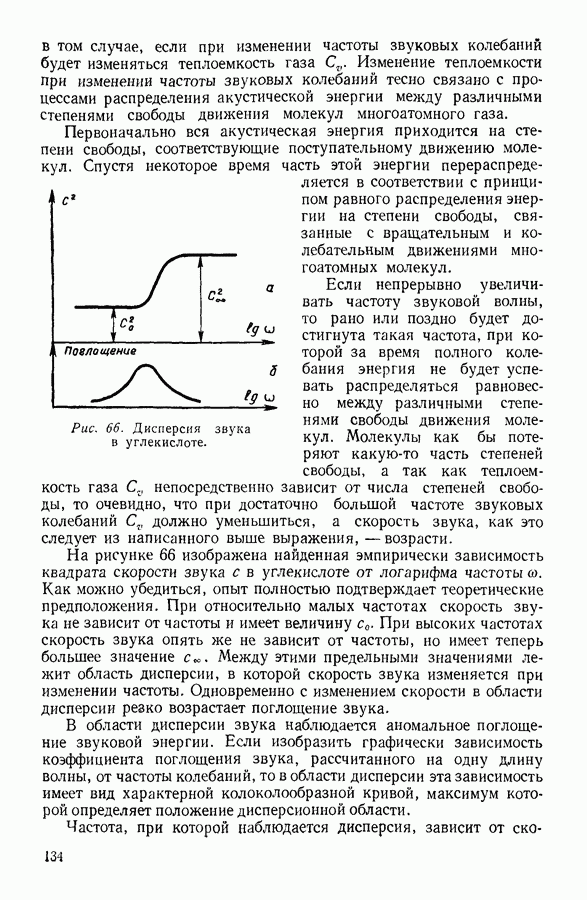
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
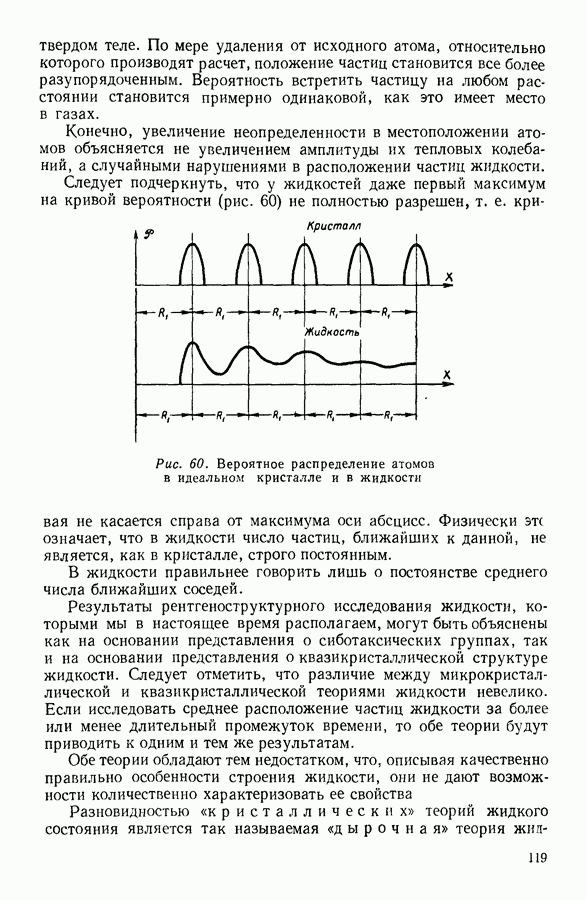
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
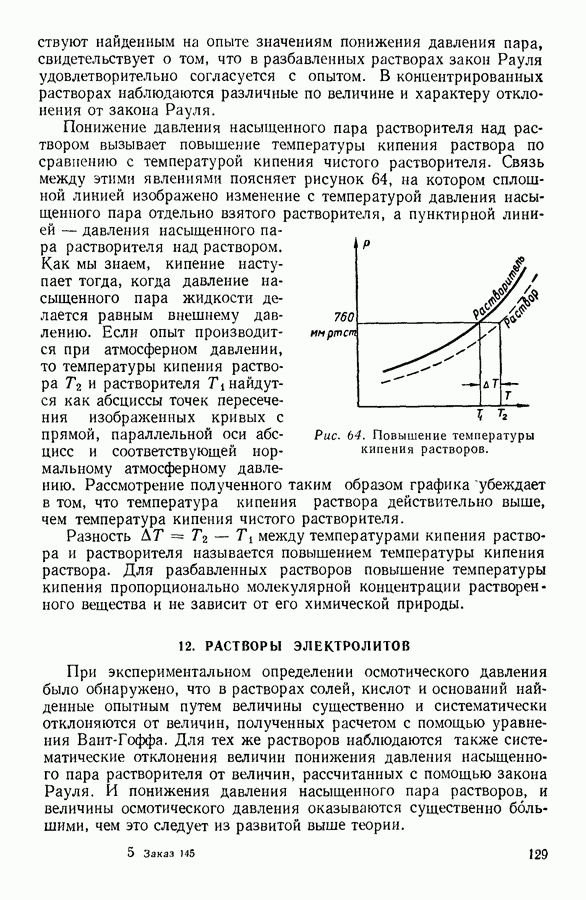
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
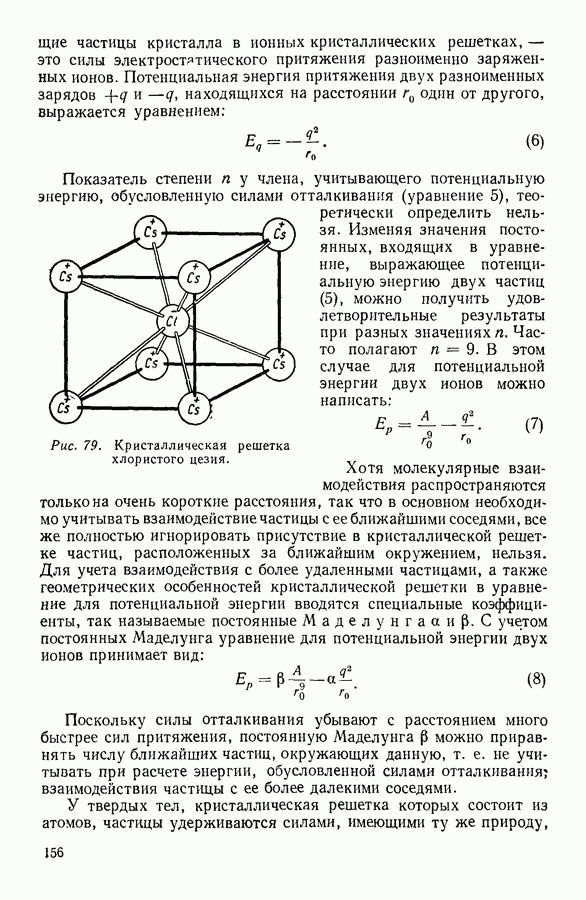
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
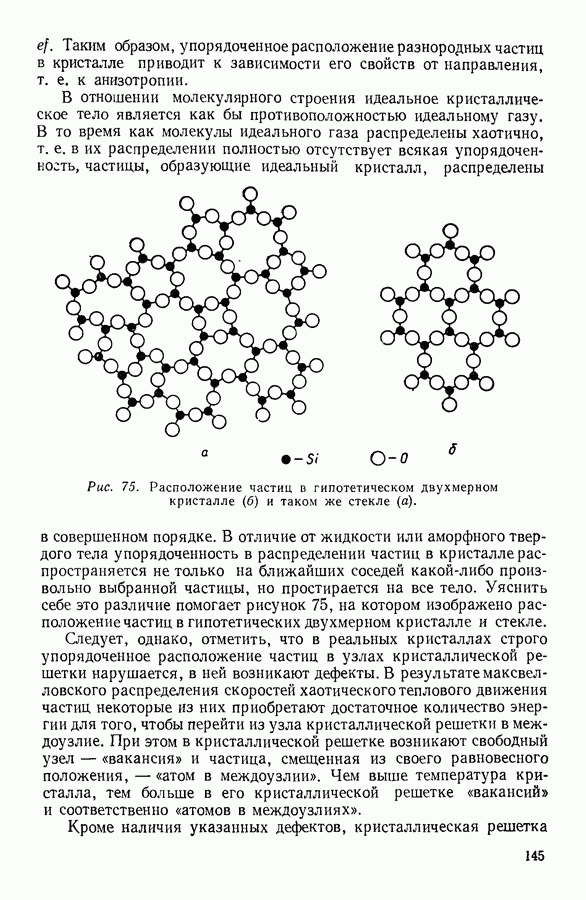
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
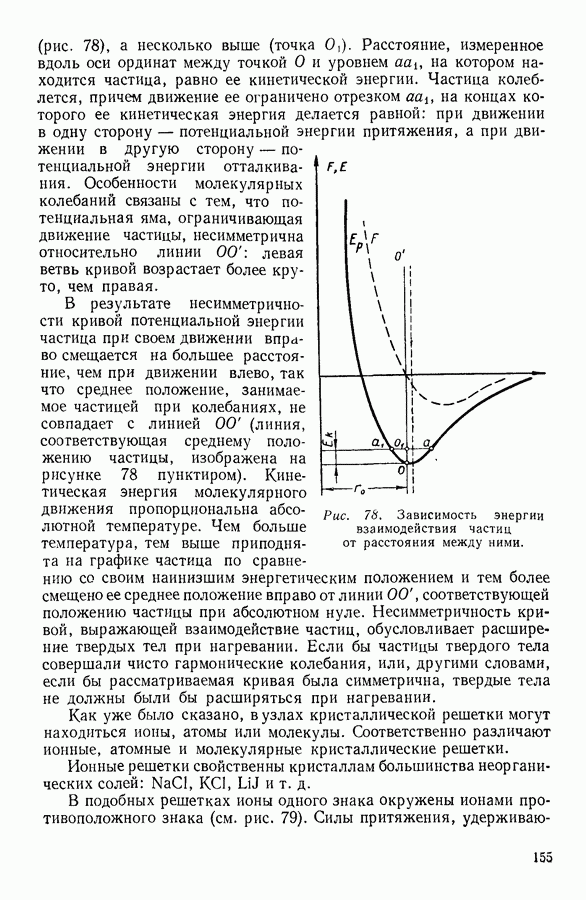
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
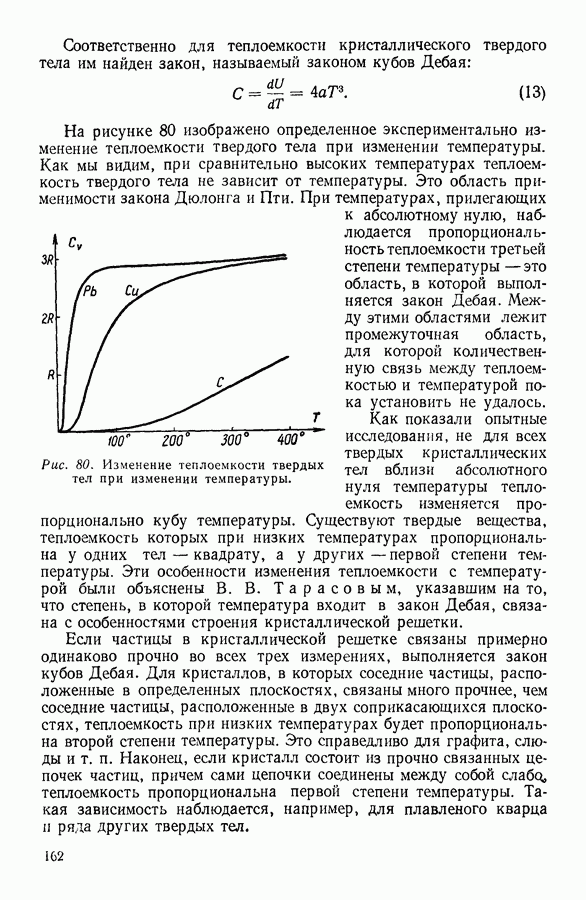
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
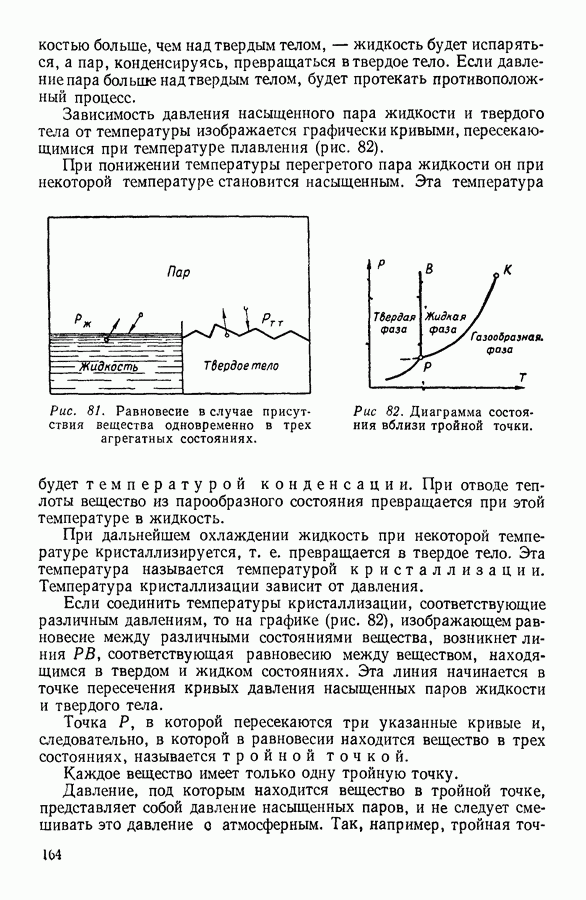
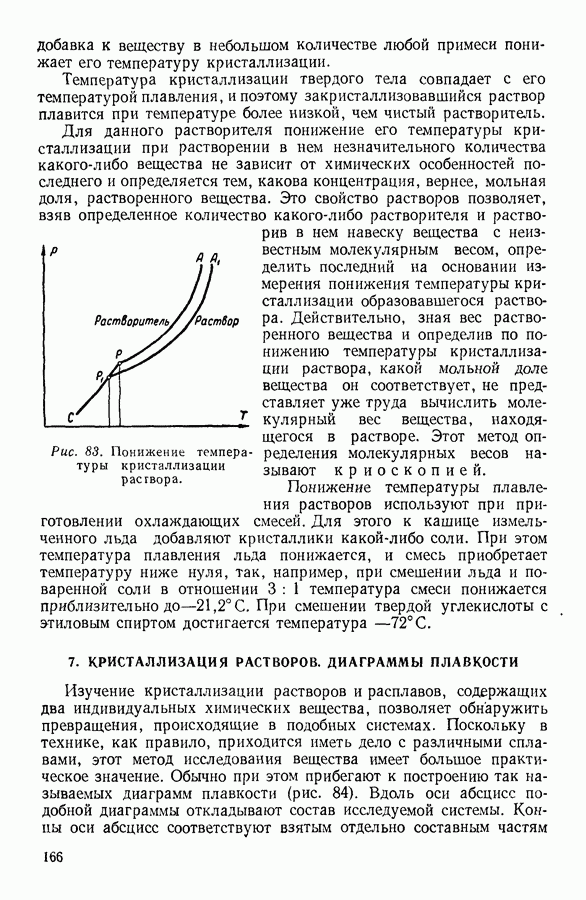
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
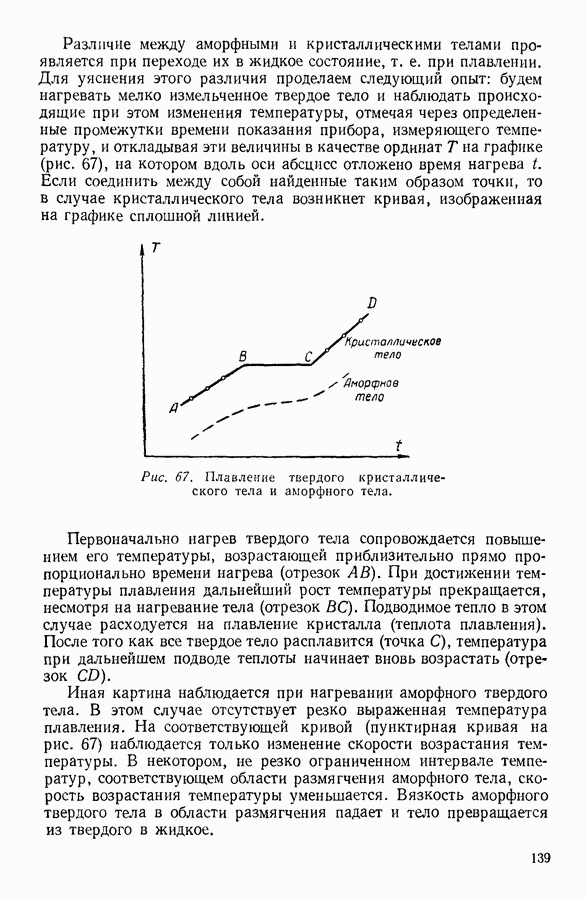
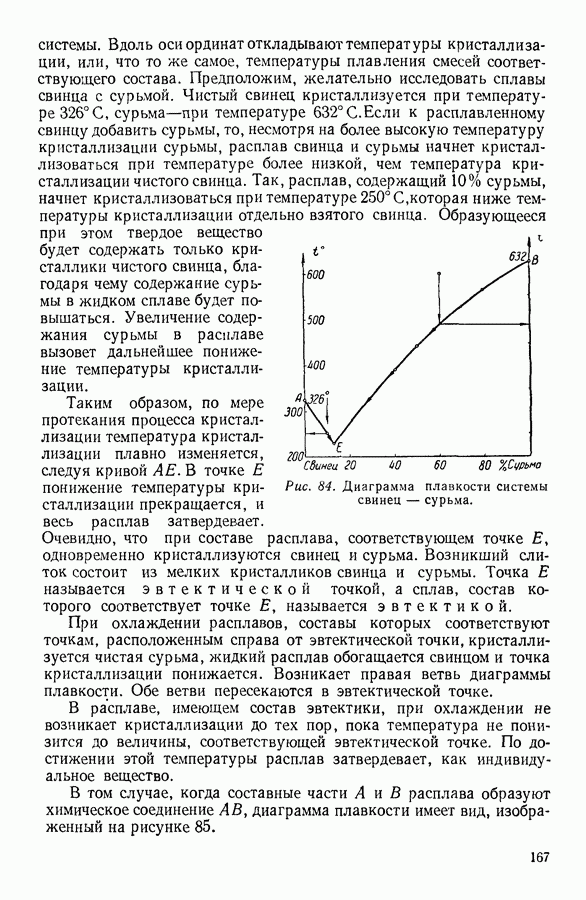
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
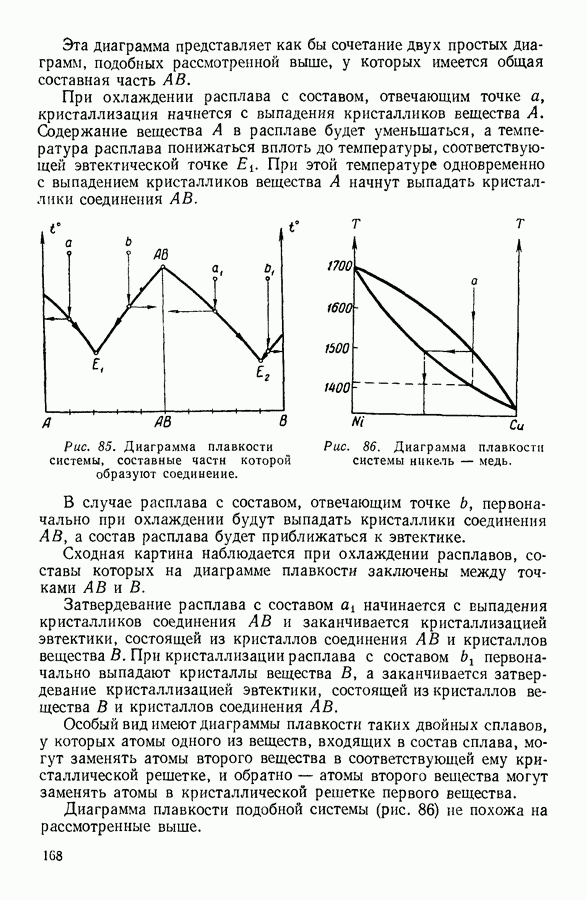
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
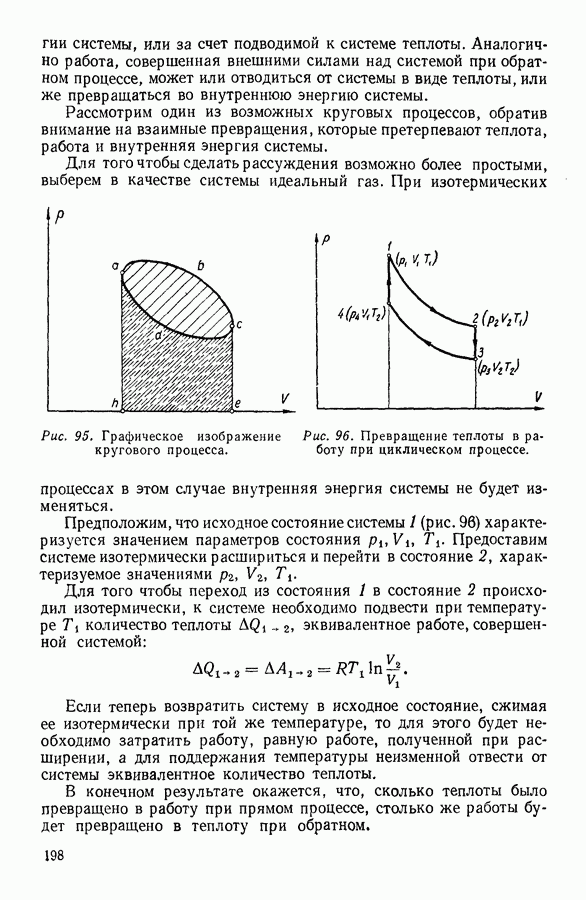
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
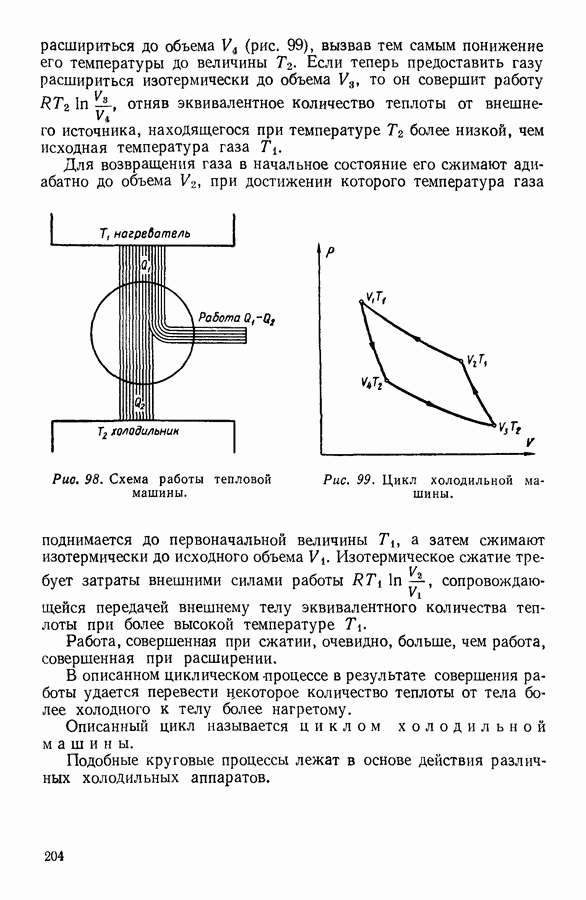
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
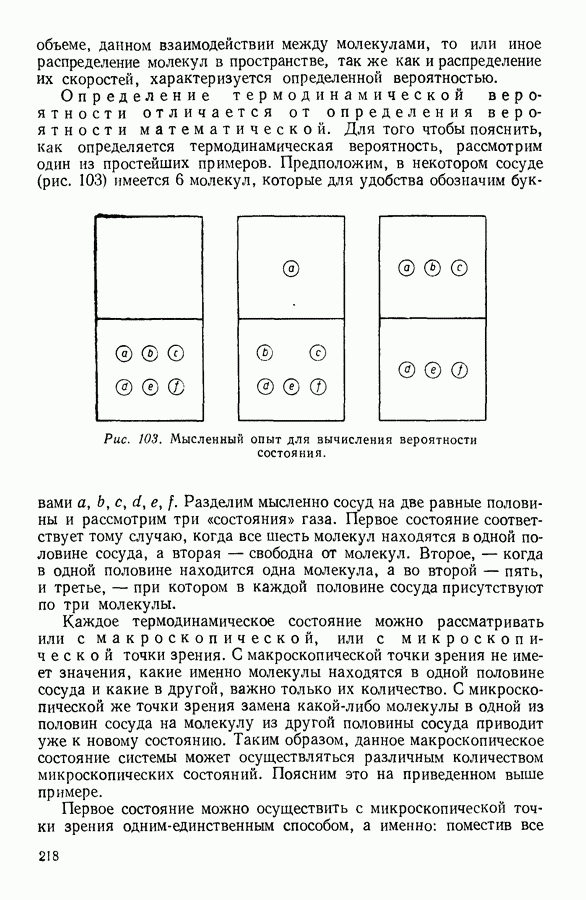
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»