20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА

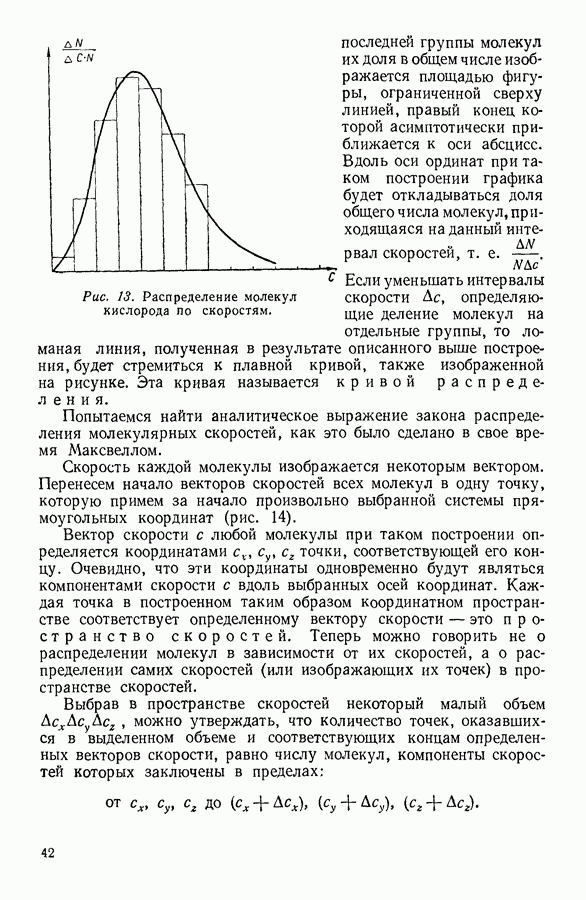
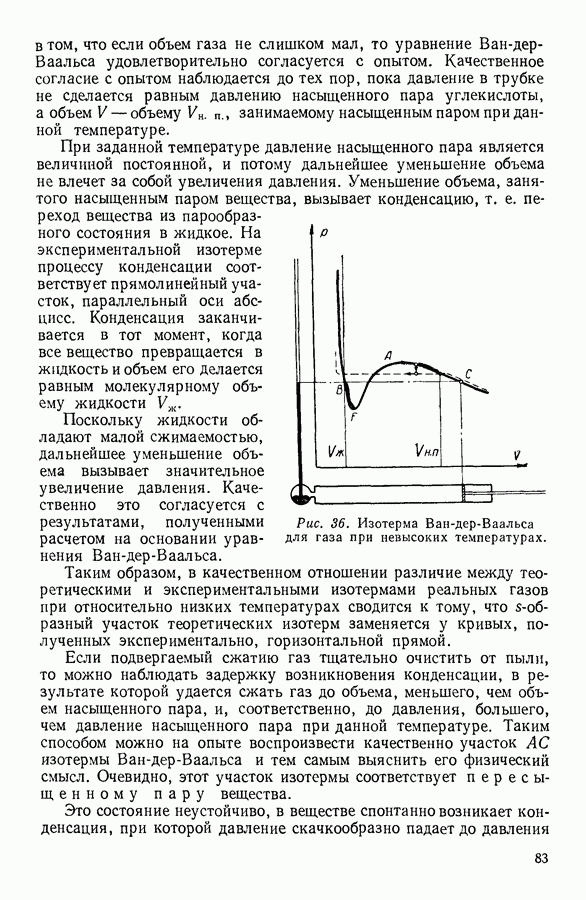
Газ состоит из движущихся с различными скоростями молекул, обладающих вследствие движения определенной кинетической энергией. Полная энергия, которой обладают в совокупности все молекулы газа, называется внутренней энергией газа.

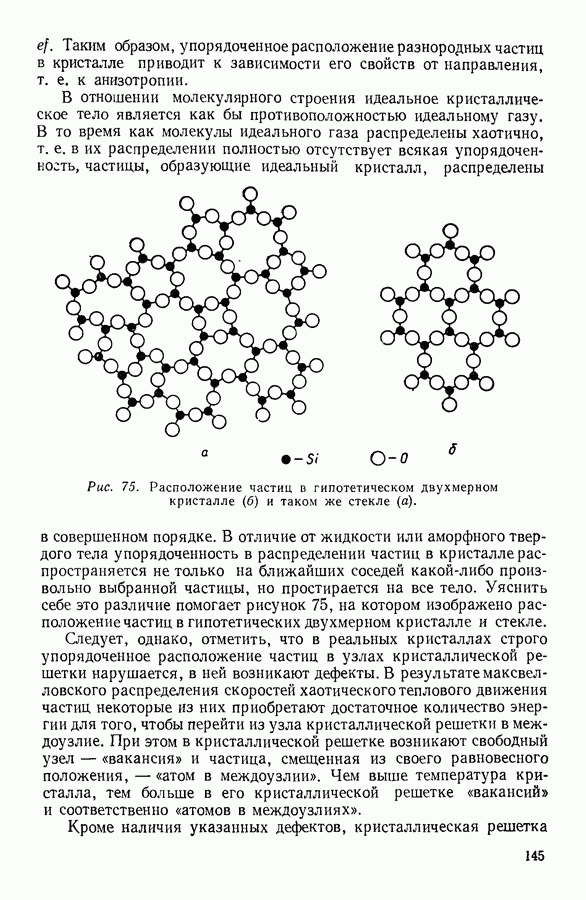
В общем случае внутренняя энергия газа представляет сумму всех видов энергии, которыми обладают молекулы, включая сюда и потенциальную энергию молекулярных взаимодействий, если таковые имеют место. В идеальном газе молекулярные взаимодействия отсутствуют, и поэтому внутренняя энергия его равна суммарной кинетической энергии молекул.

Выше (§ 8) было получено выражение для кинетической энергии молекул, обусловленной их перемещением в пространстве. В случае Молекул конечных размеров это движение соответствует поступательному движению. Поступательное движение твердого тела может быть разложено на три независимых движения, происходящих вдоль трех независимых осей координат. По предложению Максвелла эти независимые движения называют степенями свободы движения молекул. Заметим, что число степеней свободы совпадает с числом независимых координат, которые необходимо ввести для того, чтобы определить положение тела, в данном случае молекулы, в пространстве.

Любая молекула обладает тремя степенями свободы поступательного движения.

В классической кинетической теории молекулы, состоящие из одного атома, принимались за идеально гладкие твердые шарики, у которых при соударениях вращательного движения возникнуть не может. На этом основании предполагалось, что одноатомные молекулы не обладают степенями свободы вращательного движения. Хотя в настоящее время представление об атомах сильно отличается от этой простой модели, однако заключение о том, что при соударениях атомов не возникает вращательного движения, сохраняет свою силу.

Одноатомные молекулы обладают только тремя степенями свободы поступательного движения.

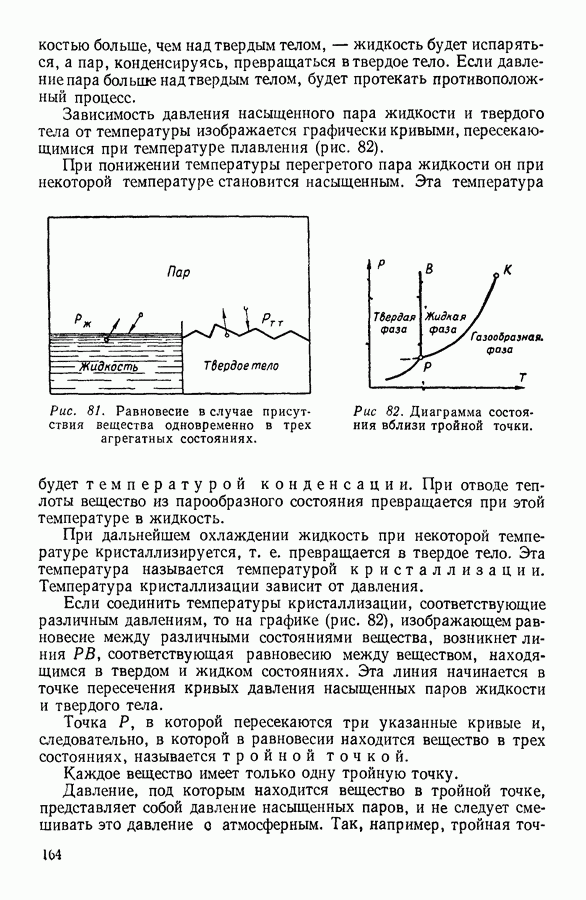
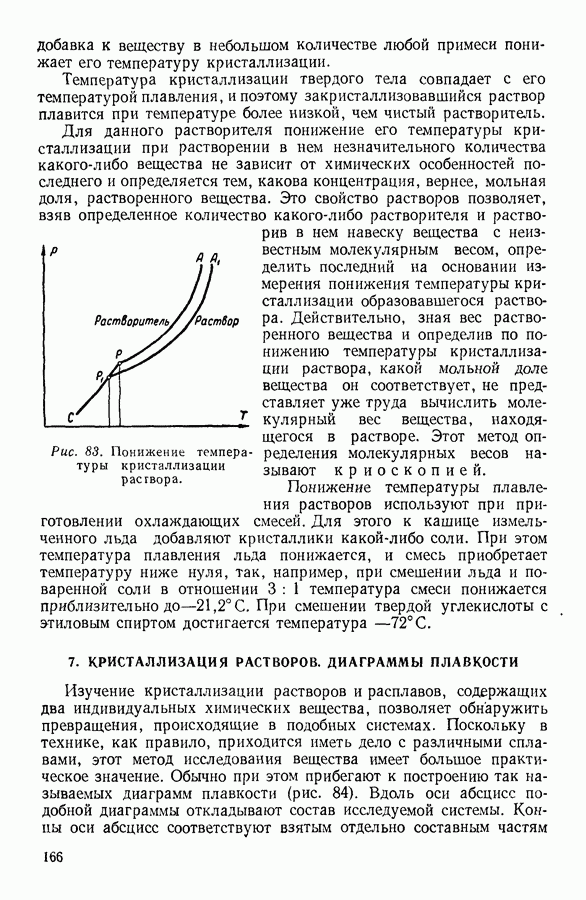
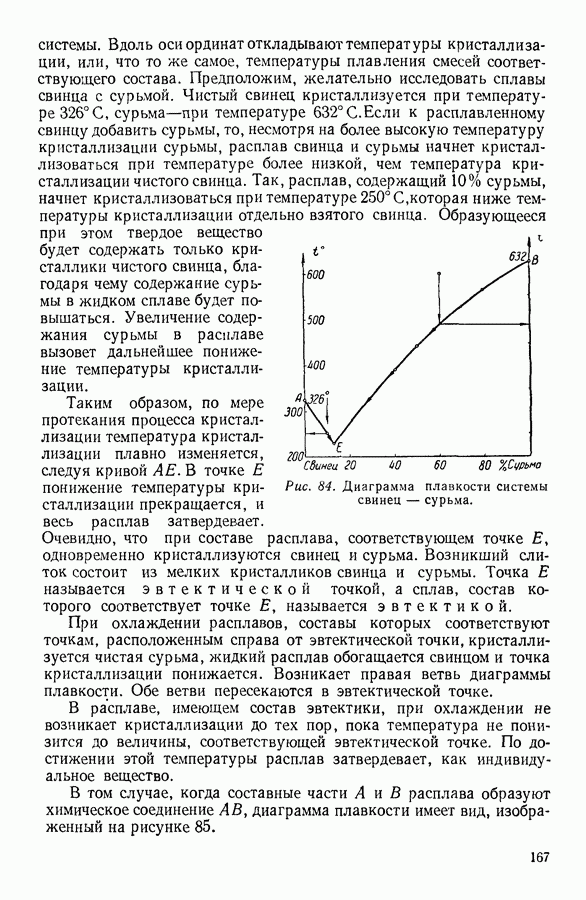
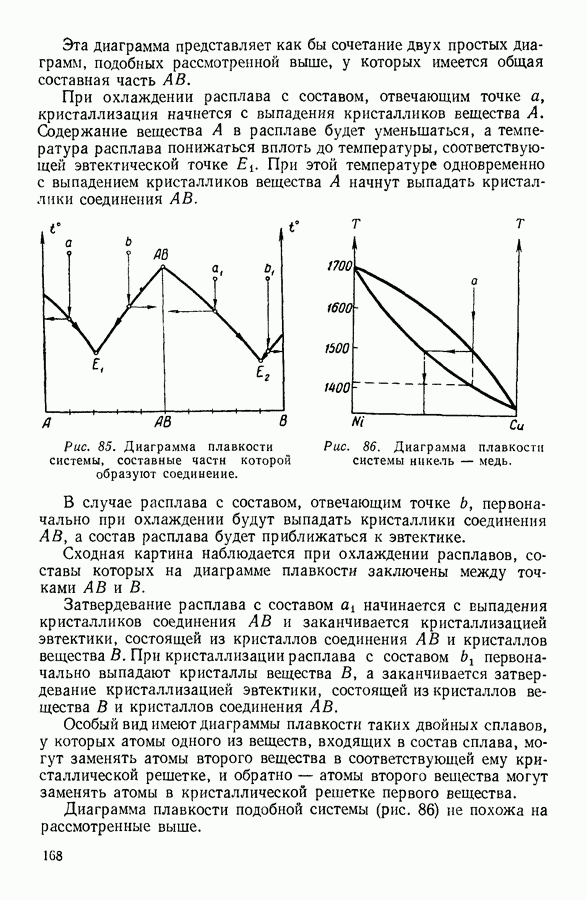
У двухатомной молекулы к трем степеням свободы поступательного движения следовало бы добавить три степени свободы вращательного движения (соответствующие трем взаимно перпендикулярным осям вращения). Однако одну из осей вращения всегда можно совместить с осью молекулы. Вращение вокруг этой оси равносильно вращению отдельных атомов, поэтому его не учитывают. Таким образом, всем двухатомным молекулам, а также тем многоатомным молекулам, атомы которых расположены вдоль прямой, следует приписать две степени свободы вращательного движения.

Общее число степеней свободы двухатомной молекулы равно пяти.

Это число совпадает с числом независимых координат, необходимых для определения положения двухатомной молекулы в пространстве. Действительно, для определения положения двухатомной молекулы в пространстве необходимо и достаточно указать координаты ее центра тяжести и два угла

Для многоатомной молекулы с нелинейным расположением атомов сохраняются все три степени свободы вращательного движения, и поэтому общее число степеней свободы, обусловленных поступательным и вращательным движением молекулы, равно шести.

В приведенном подсчете числа степеней свободы принималось, что атомы в молекулах закреплены неподвижно и не могут колебаться друг относительно друга. Опыт показывает, что при комнатной температуре для двухатомных газов это предположение оправдывается.

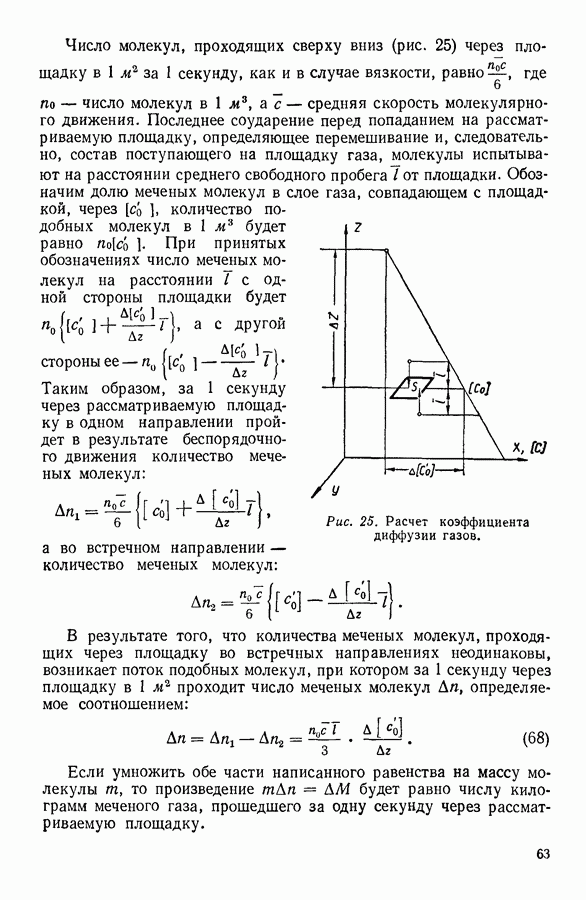
Рис. 31. Число степеней свободы двухатомной молекулы.

Средняя кинетическая энергия поступательного движения любой молекулы (уравнение 28) согласно молекулярно-кинетической теории является линейной функцией абсолютной температуры:

Эту величину можно разложить на три составляющие соответственно трем произвольно выбранным координатным осям, или, как можно теперь сказать, соответственно трем степеням свободы поступательного движения.

Хаотичность молекулярного движения требует, чтобы ни одно из направлений не было бы преимущественным в отношении движения, а это равносильно требованию равного распределения кинетической энергии, связанной с перемещением молекул, между тремя степенями свободы поступательного движения. Максвелл обобщил эту закономерность в знаменитом принципе равного распределения энергии, согласно которому в системе, состоящей из большого числа частиц, кинетическая энергия распределяется в среднем поровну между различными степенями свободы движения частиц.

На три степени свободы поступательного движения молекулы приходится в среднем кинетическая энергия, равная следовательно, на одну степень свободы будет приходиться:

Такое же количество кинетической энергии будет приходиться при температуре на любую другую степень свободы движения молекулы.

Таким образом, если молекула газа обладает степенями свободы, то средняя кинетическая энергия ее будет равна:

Умножив среднюю кинетическую энергию молекулы на число Авогадро получим кинетическую энергию одного киломоля газа, которая в случае идеального газа будет равна его внутренней энергии Замечая, что можно написать: