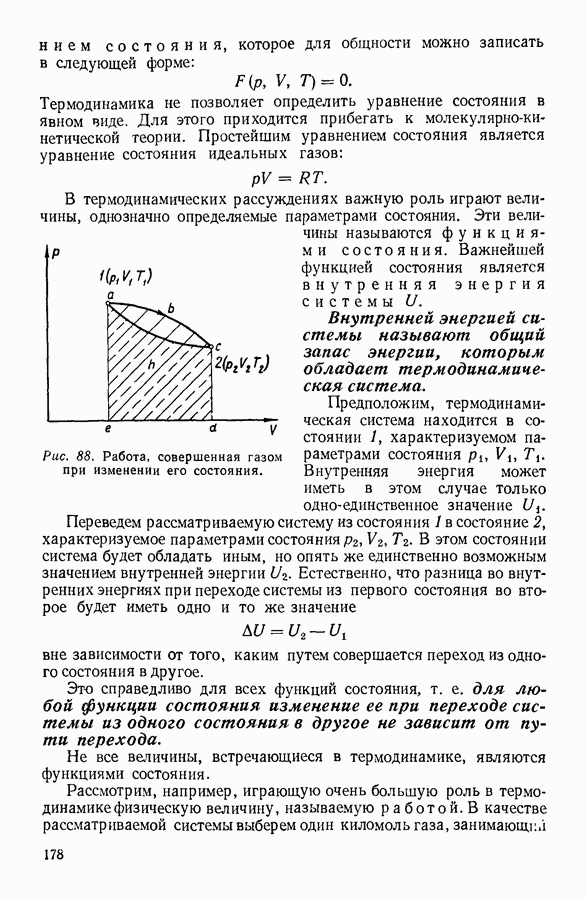
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
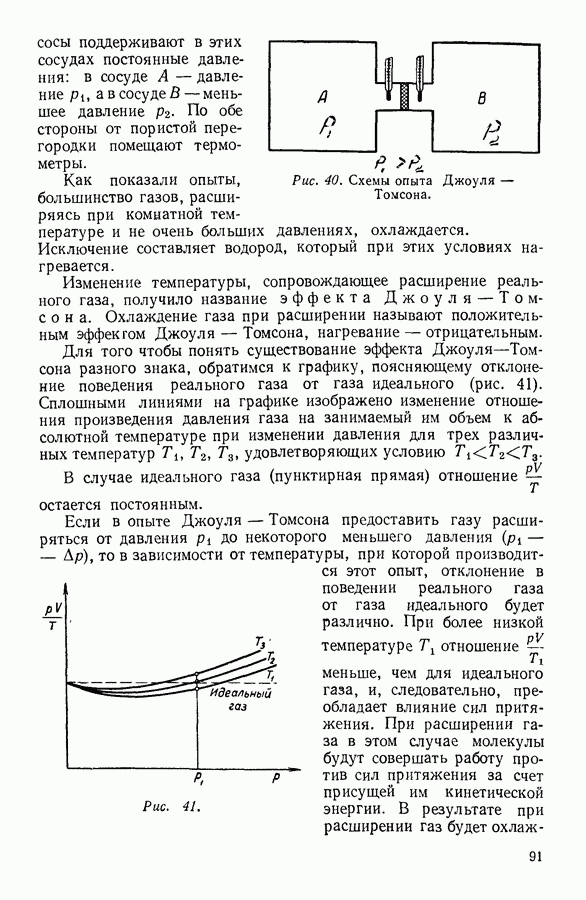
Одной из важных физических характеристик жидкости является ее вязкость. Вязкость жидкости очень сильно зависит от температуры. При изменениях температуры, которые сравнительно нетрудно осуществить на опыте, вязкость жидкости может изменяться в миллионы раз. При понижении температуры вязкость некоторых жидкостей настолько возрастает, что жидкости теряют характеризующую их способность течь, превращаясь в аморфные твердые тела. В настоящее время существует несколько теорий вязкости жидкостей. Наличие нескольких теорий указывает на то, что ни одна из них не свободна от недостатков.
Одним из наиболее удачных выражений, связывающих вязкость жидкостей с другими их свойствами, следует признать уравнение Бачинского (1877—1944).
Бачинским было найдено, что для очень большого количества жидкостей коэффициент вязкости  связан простой зависимостью с удельным объемом жидкости V:
связан простой зависимостью с удельным объемом жидкости V:

Входящие в это уравнение постоянные Сию имеют физический смысл, который легко расшифровать. Постоянная со — это
предельный объем, обусловленный несжимаемостью молекул вещества. В знаменателе в правой части уравнения Бачинского стоит, таким образом, свободный объем жидкости. Постоянная С учитывает силы молекулярного взаимодействия частиц жидкости. Она связана простой зависимостью с постоянной а в уравнении Ван-дер-Ваальса. Следует подчеркнуть, что для идеальных газов коэффициент вязкости рассчитывается без учета действия межмолекулярных сил, поскольку вязкость идеальных газов обусловлена только хаотическим движением молекул. В противоположность этому для жидкостей на первый план выступает учет силового взаимодействия молекул.
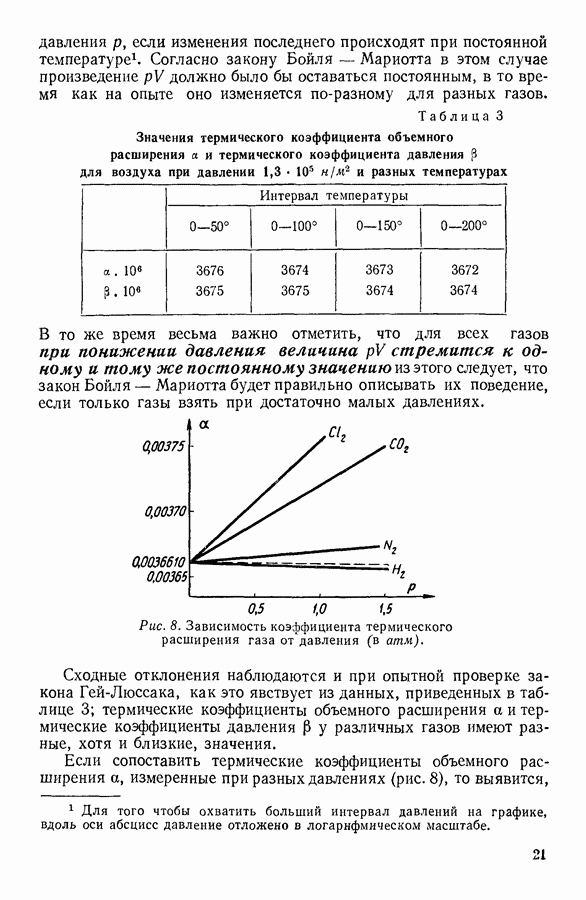
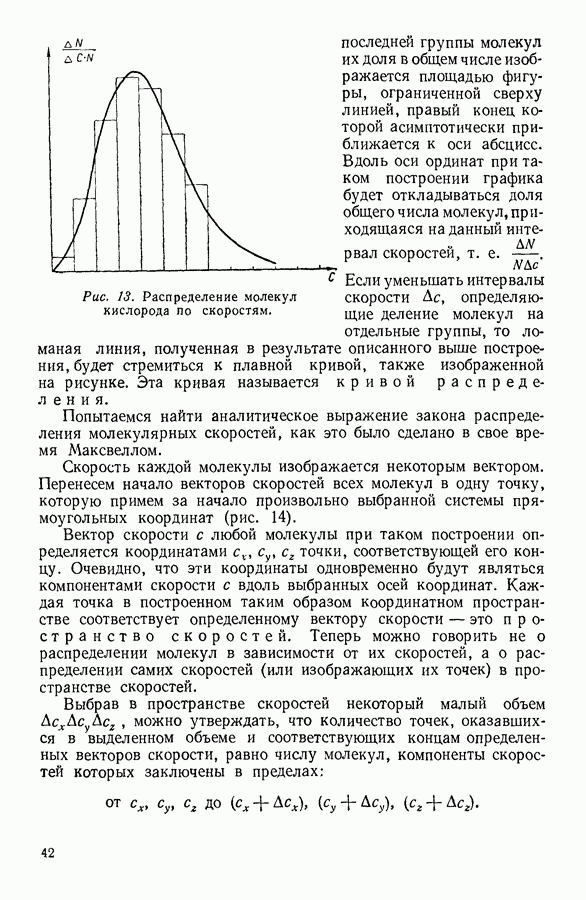
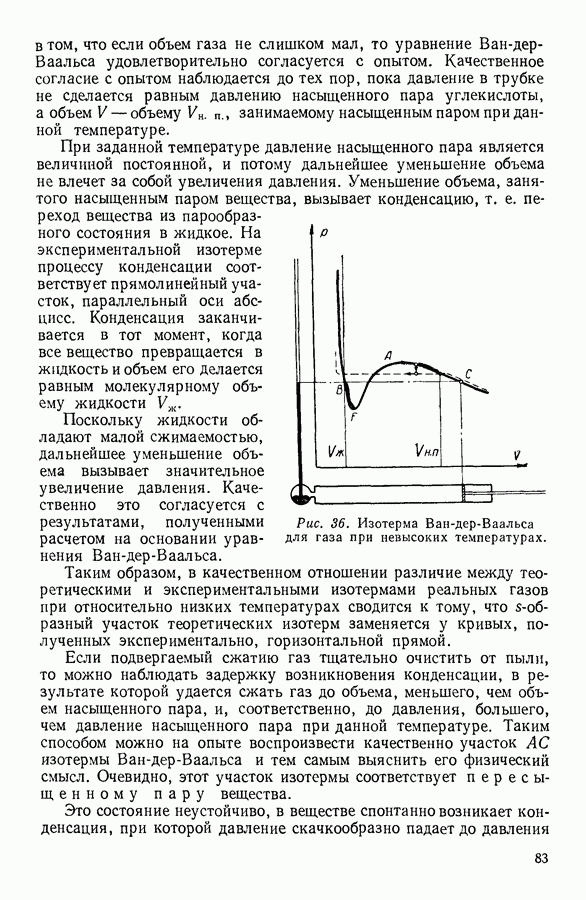
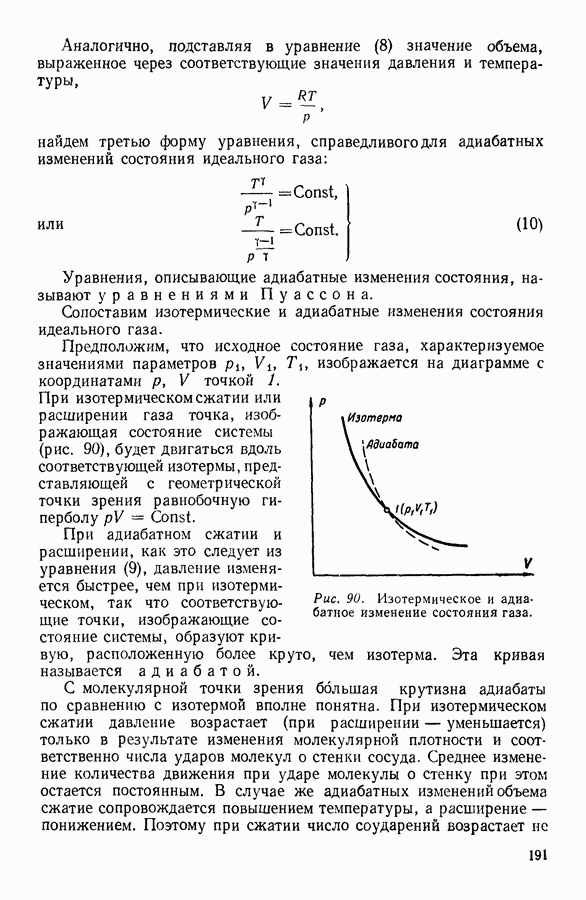
Для многих жидкостей уравнение Бачинского хорошо согласуется с опытом (см. рис. 61).

Рис. 61. Связь между текучестью жидкости  отложенной вдоль оси абсцисс, и ее удельным объемом
отложенной вдоль оси абсцисс, и ее удельным объемом  Сплошная линия рассчитана по уравнению Бачинского, точки нанесены на основании опытных данных.
Сплошная линия рассчитана по уравнению Бачинского, точки нанесены на основании опытных данных.
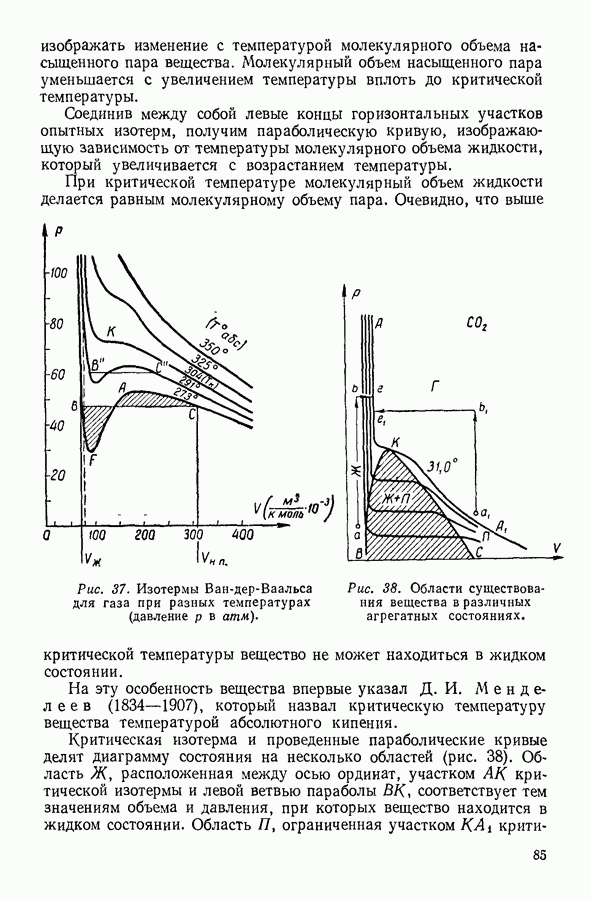
В уравнении Бачинского зависимость вязкости от температуры выражена в неявной форме: из величин, стоящих в правой части уравнения, от температуры зависит удельный объем жидкости 
В настоящее время для расчета коэффициента вязкости жидкости предложено большое количество уравнений, различающихся в деталях, но в то же время имеющих много общего. Обычно коэффициент вязкости представляют произведением:

в котором сомножитель А в одних уравнениях — постоянная величина, а в других — более или менее сложная функция абсолютной температуры  универсальная газовая постоянная и, наконец,
универсальная газовая постоянная и, наконец,  величина, определяемая силами межмолекулярного взаимодействия.
величина, определяемая силами межмолекулярного взаимодействия.
Присутствие температуры в показателе степени в уравнении (16) объясняет большое влияние ее на величину коэффициента вязкости.
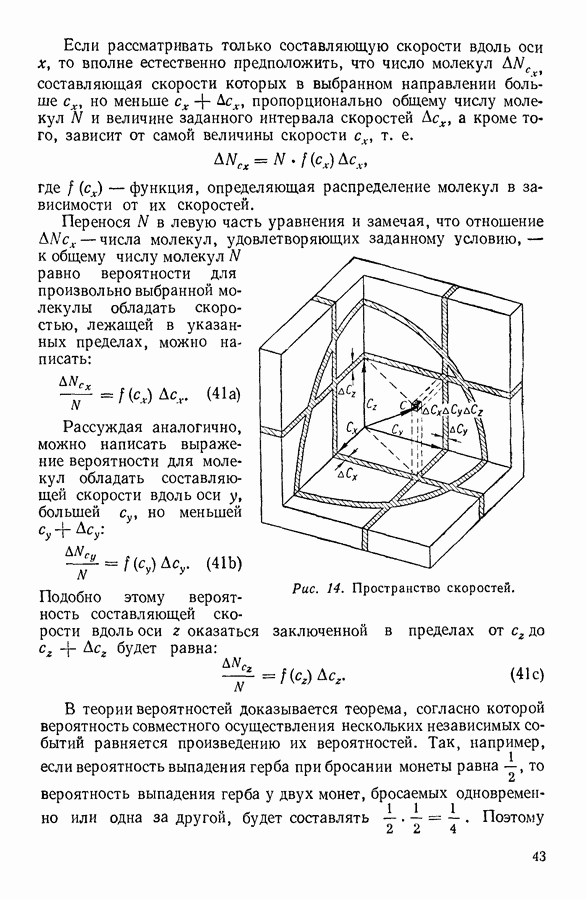
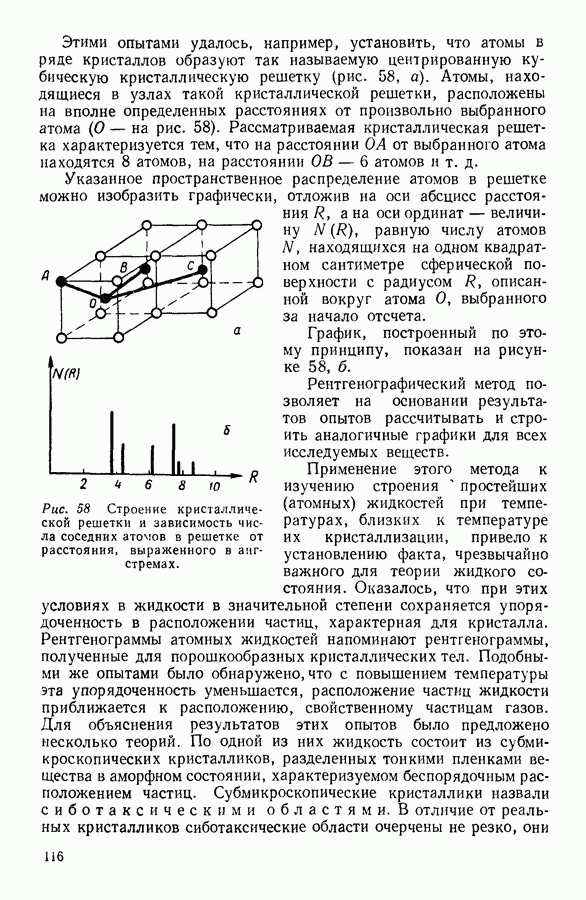
С молекулярно-кинетической точки зрения процесс течения жидкости представляет последовательный переход молекул жидкости из одного равновесного положения в соседнее. Эти положения разделены энергетическими барьерами, которые молекула должна преодолеть при своем движении. Согласно одной из распространенных теорий вязкости возникновение силы вязкости в жидкости связано с указанным преодолением потенциального барьера.
Сходная картина наблюдается при диффузии различных веществ в жидком состоянии.
Различие в механизме возникновения вязкости в газах и жидкостях приводит к тому, что связь между коэффициентами вязкости и диффузии в этих состояниях вещества различна.
В газах коэффициент вязкости и коэффициент диффузии увеличиваются при возрастании температуры, в жидкостях же при увеличении температуры коэффициент диффузии увеличивается, а коэффициент вязкости уменьшается. Соотношение между коэффициентом вязкости жидкости 1] и коэффициентом диффузии  часто выражают уравнением Стокса — Эйнштейна:
часто выражают уравнением Стокса — Эйнштейна:

в котором  абсолютная температура,
абсолютная температура,  постоянная Больцмана и
постоянная Больцмана и  радиус диффундирующей молекулы, принимаемой за шарик небольших размеров.
радиус диффундирующей молекулы, принимаемой за шарик небольших размеров.
Пользуясь современными представлениями о природе жидкости, можно показать, что из написанного соотношения следует близость коэффициентов диффузии у жидкостей, молекулы которых не очень сильно различаются своими размерами.
Опыт показывает, однако, что коэффициенты диффузии в растворах близки по величине и у таких веществ, молекулы которых очень сильно различаются. Так, например, в водных растворах при 18° коэффициенты диффузии радиоактивного газа радона, кислорода, соляной кислоты и сахара соответственно равны: 2,33; 1,61; 1,39 и  Мало зависят обычно коэффициенты диффузии и от природы растворителя. Молекулярно-кинетическая теория материи в настоящее время не может объяснить всех особенностей процесса диффузии в жидкостях.
Мало зависят обычно коэффициенты диффузии и от природы растворителя. Молекулярно-кинетическая теория материи в настоящее время не может объяснить всех особенностей процесса диффузии в жидкостях.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
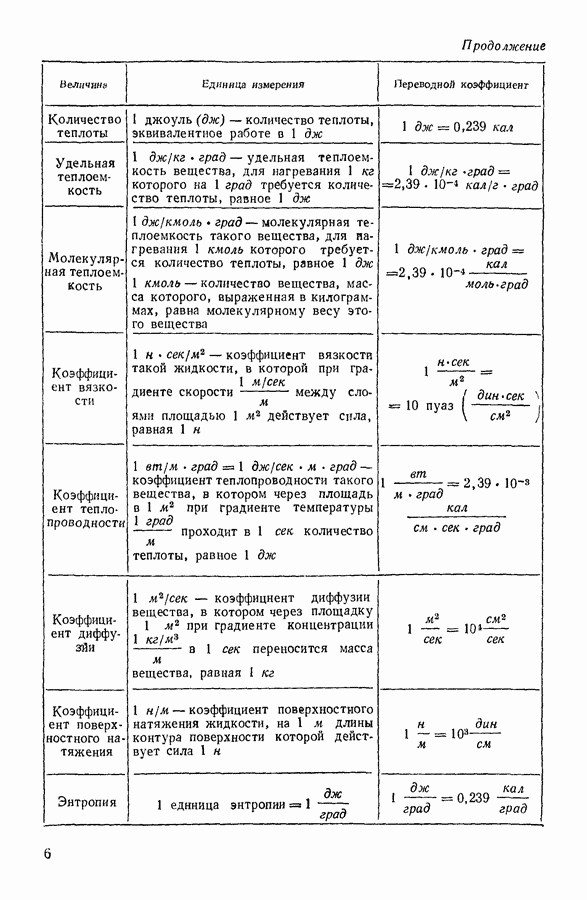
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
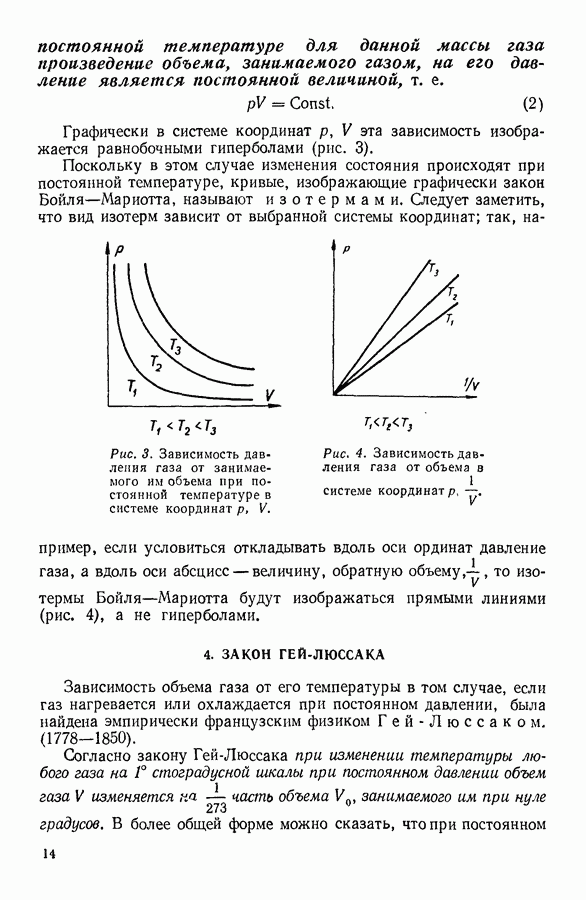
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
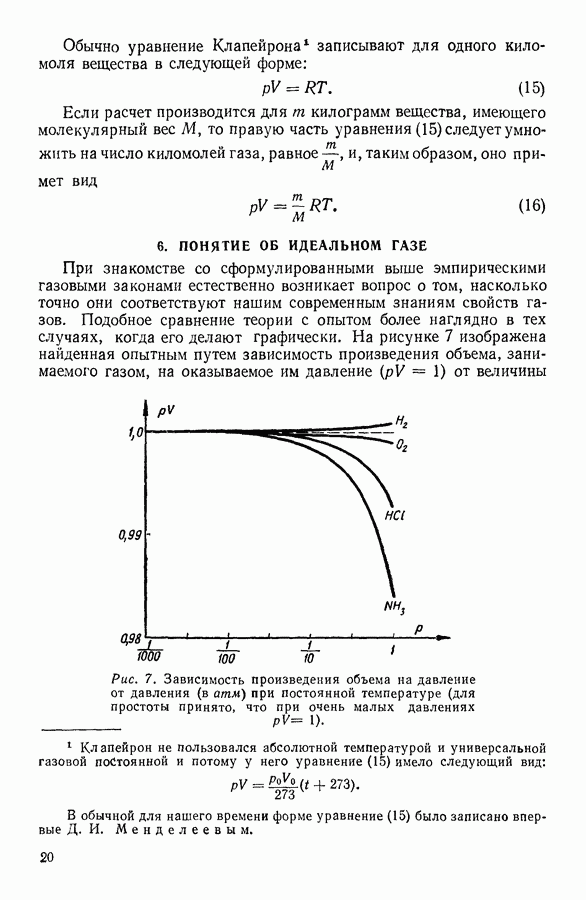
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
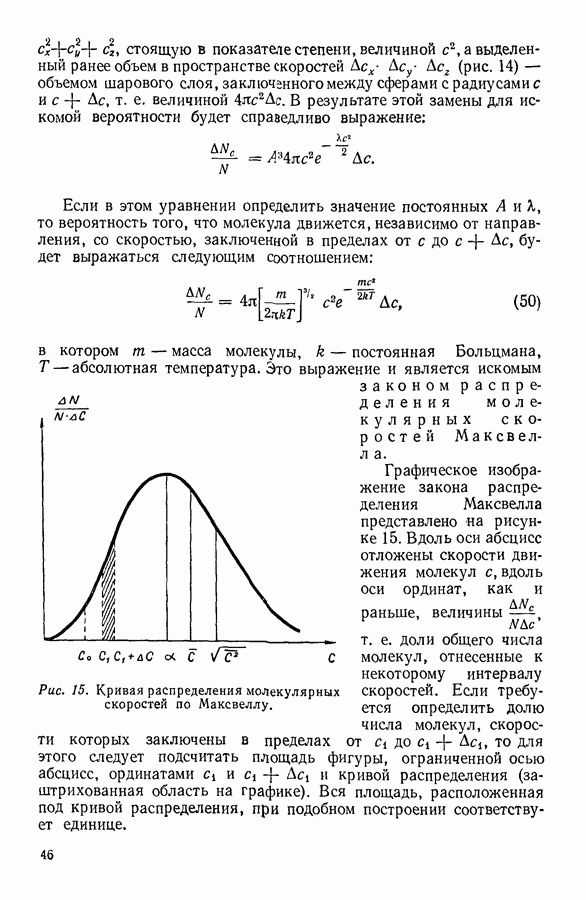
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
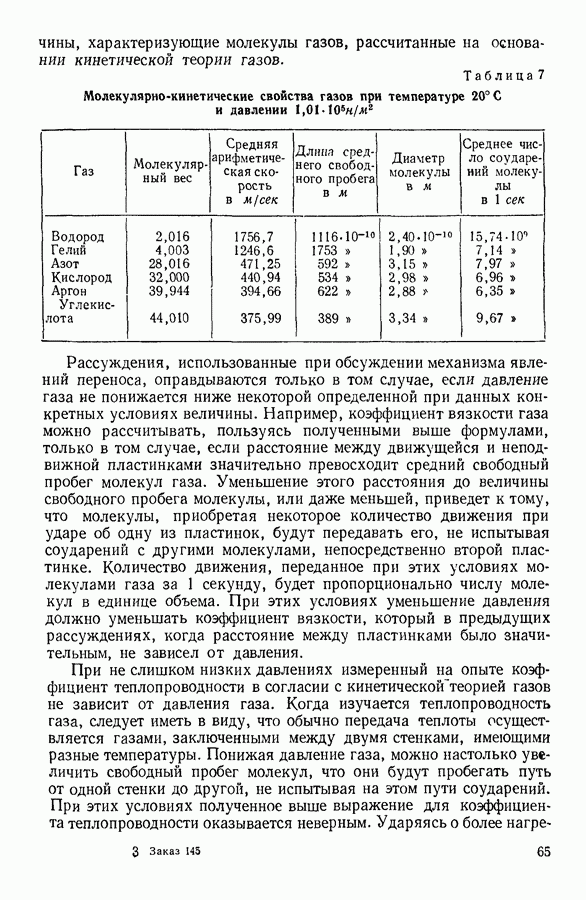
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
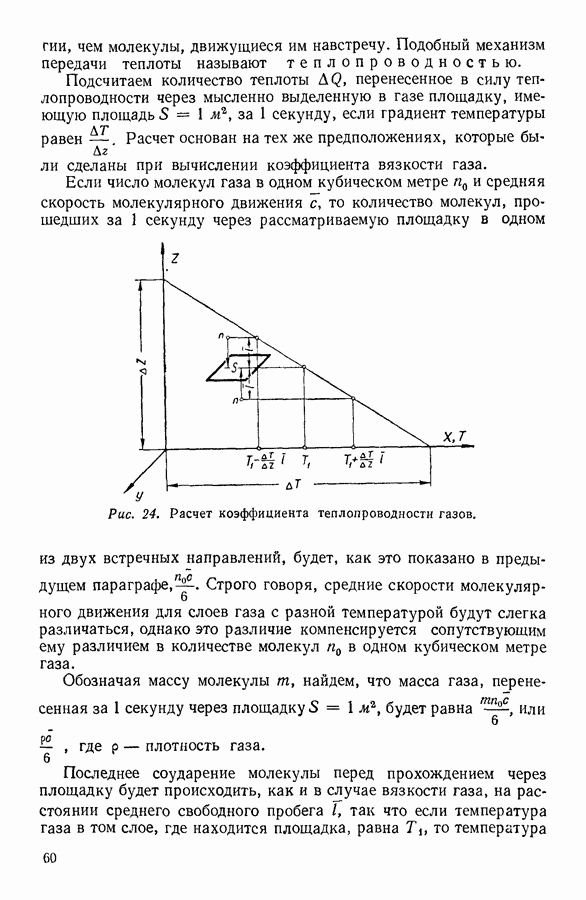
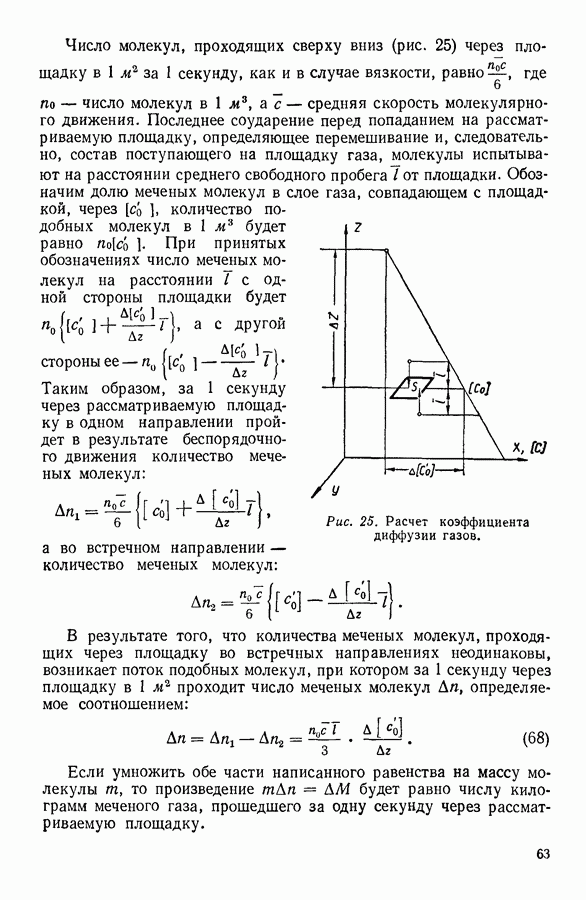
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
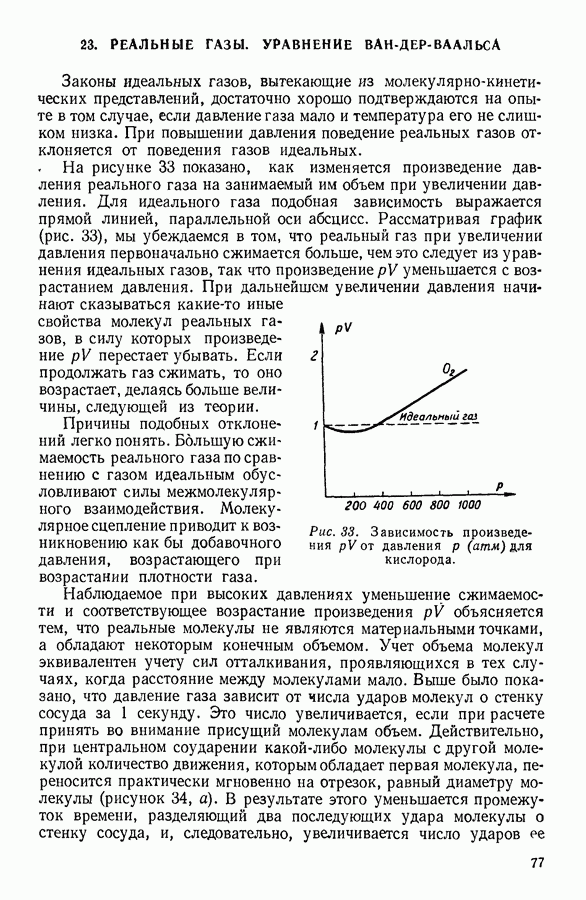
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
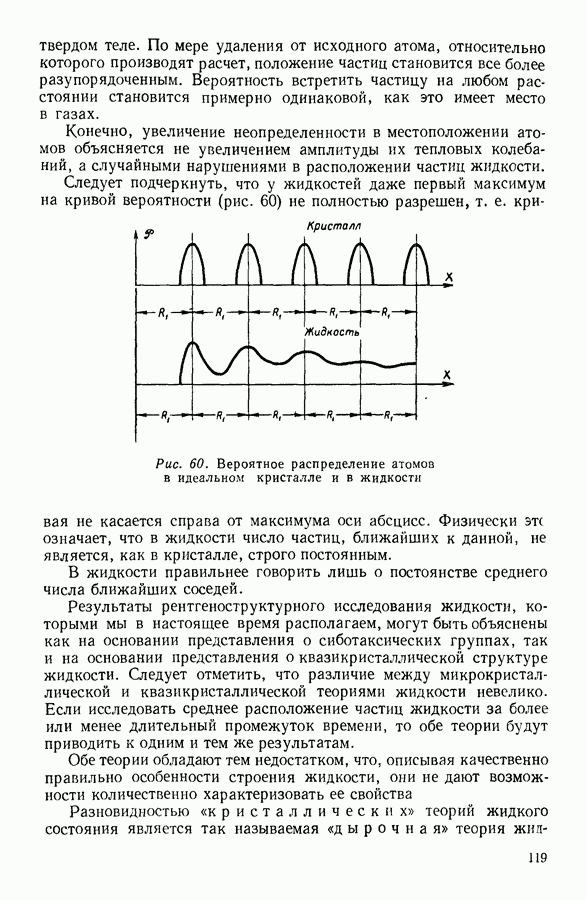
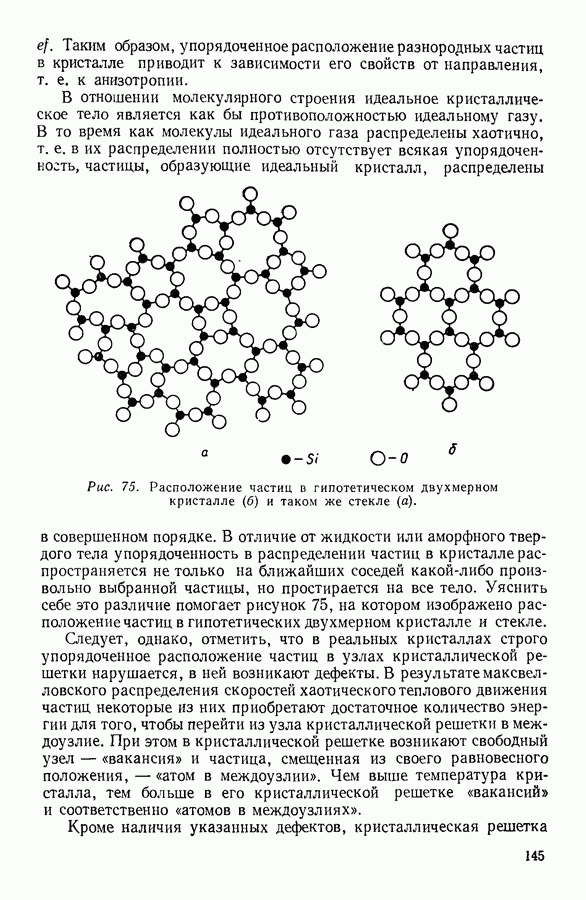
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
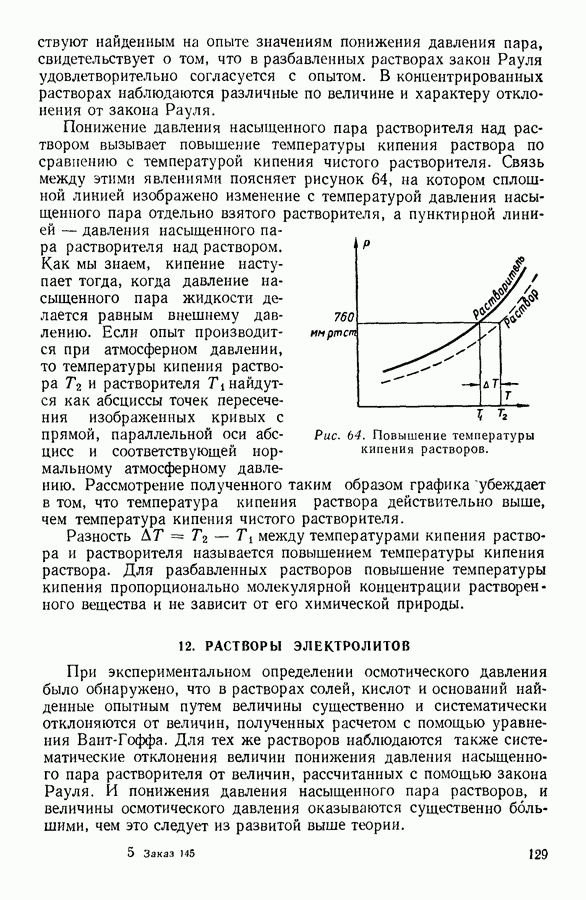
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
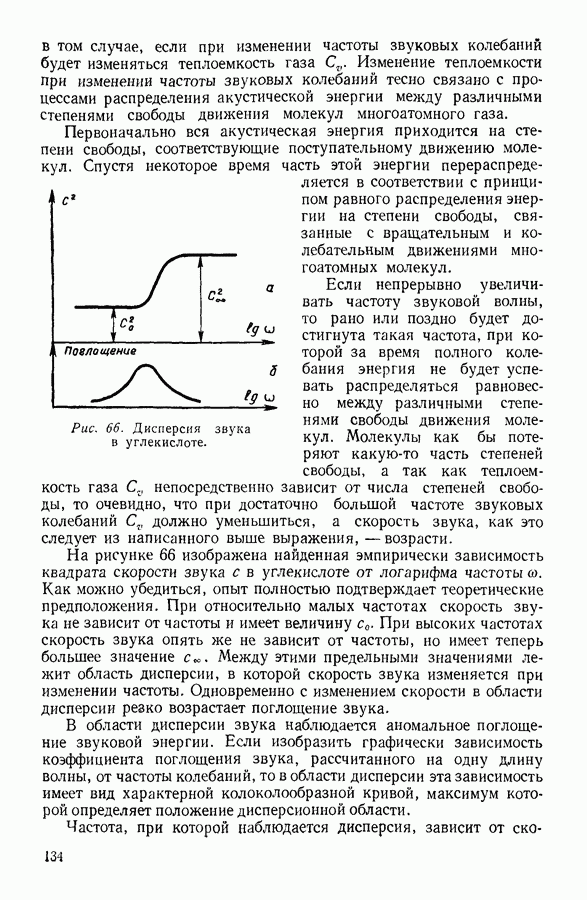
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
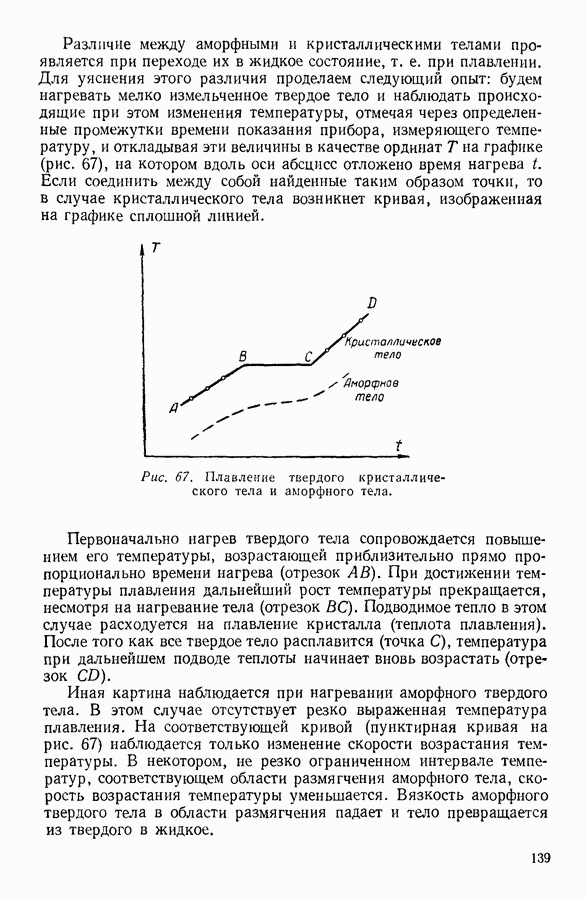
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
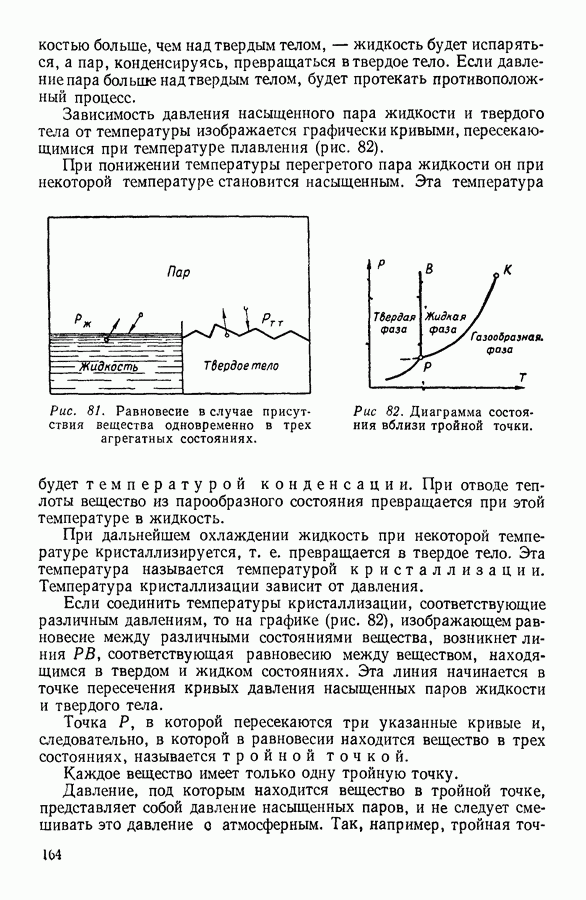
- 3. ПОЛИМЕРЫ
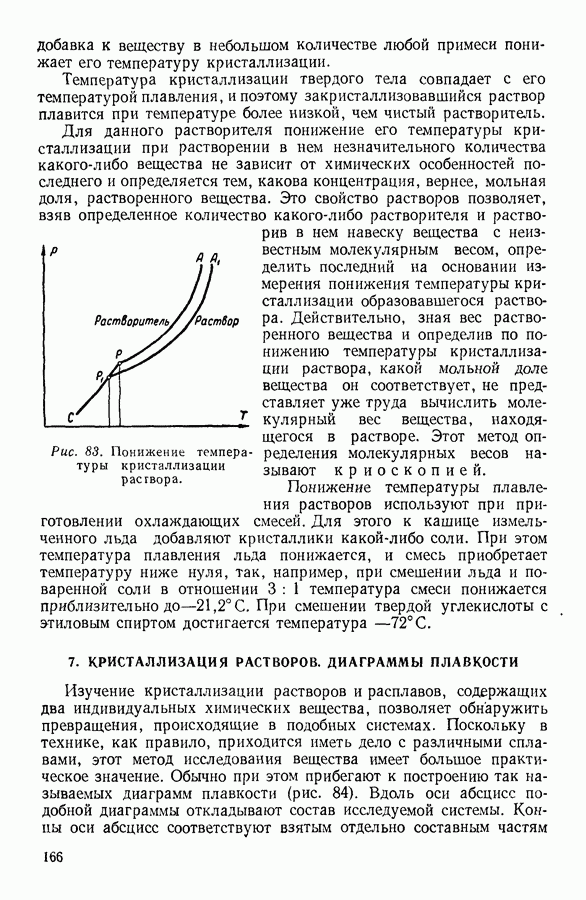
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
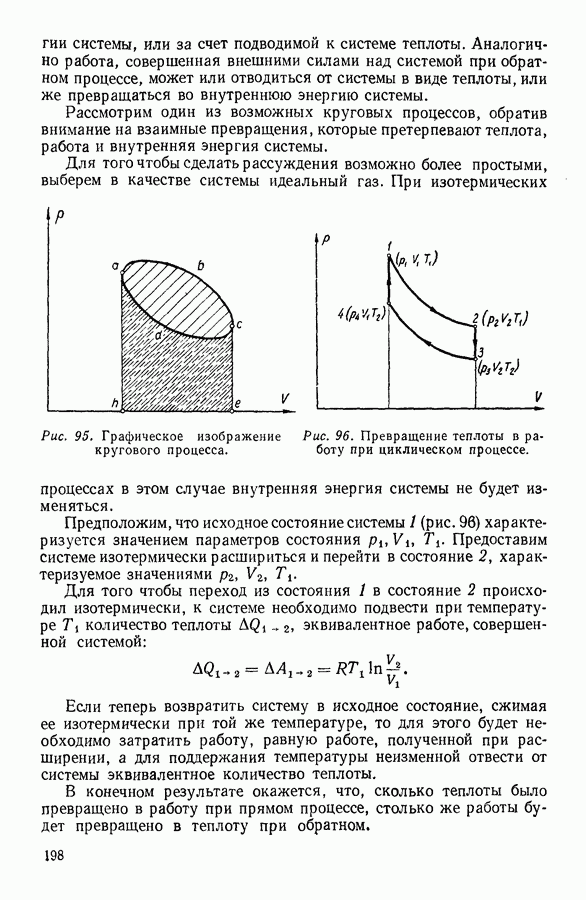
- 8. КРУГОВЫЕ ПРОЦЕССЫ
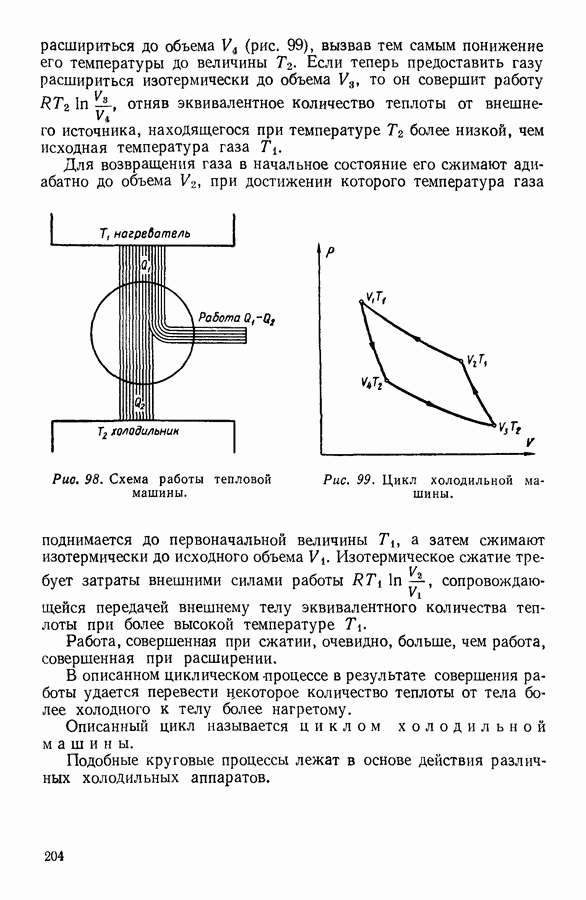
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
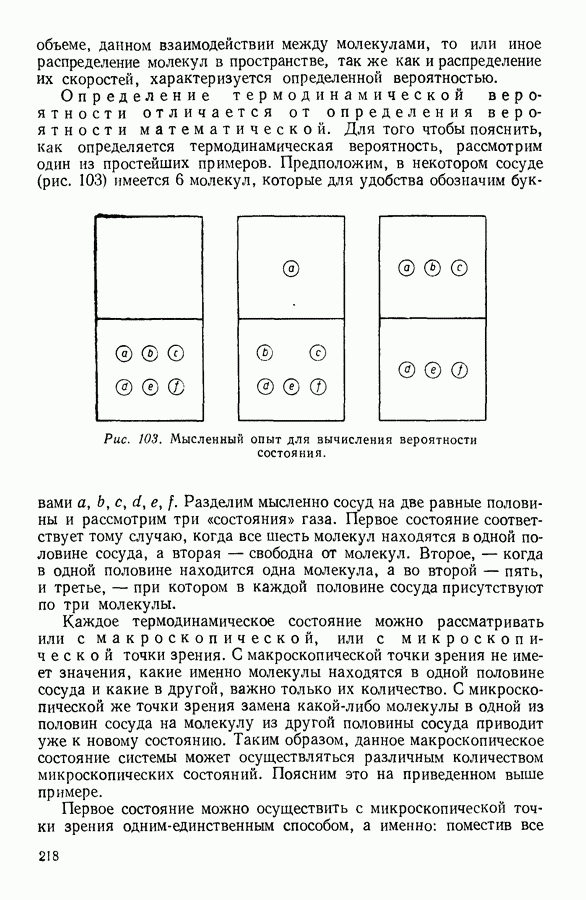
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»