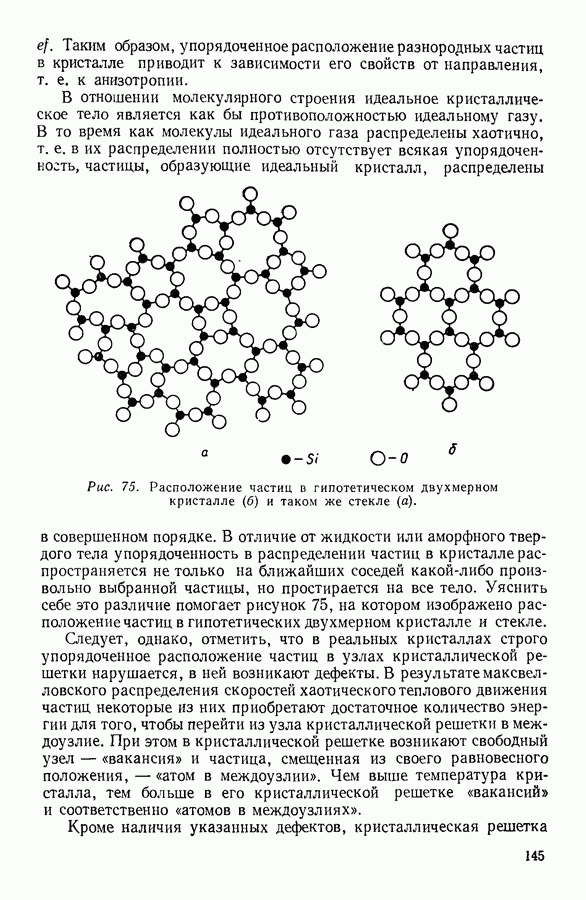
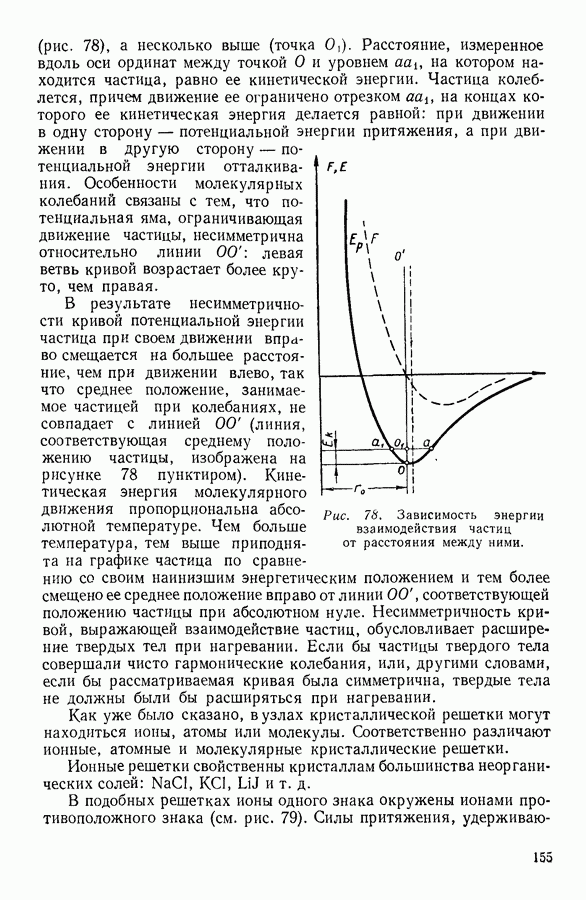
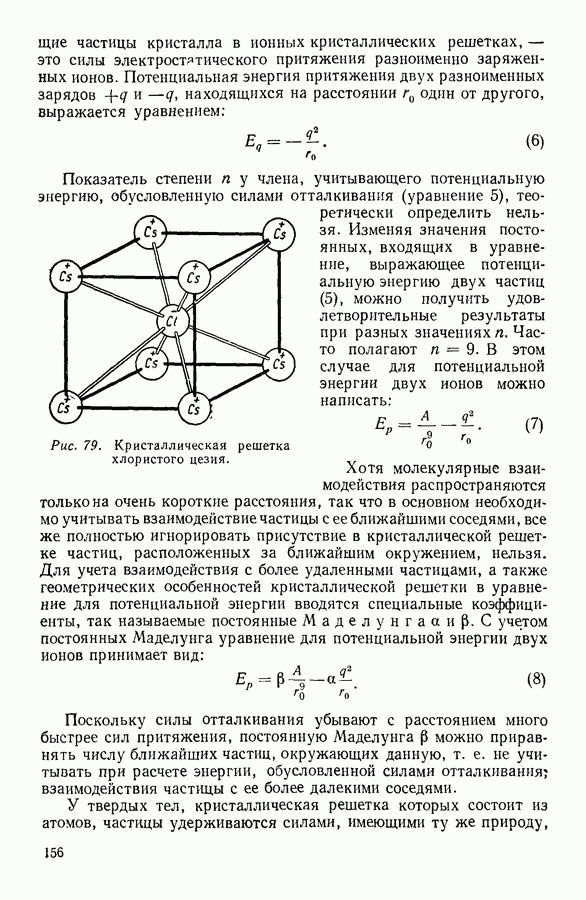
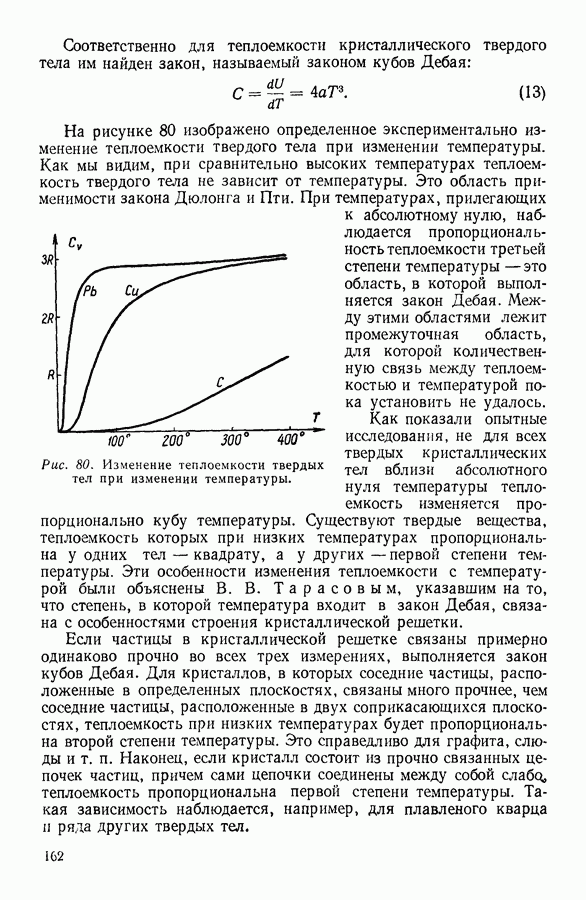
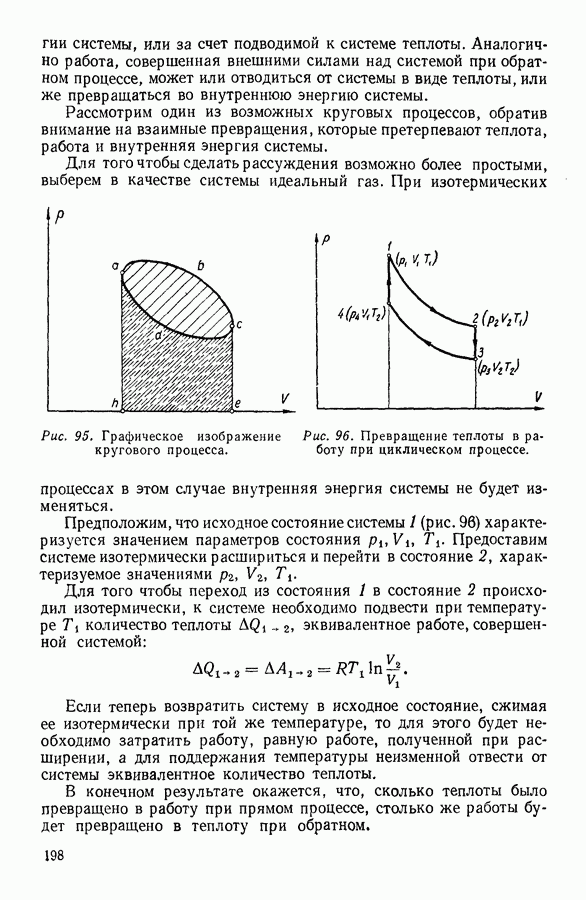
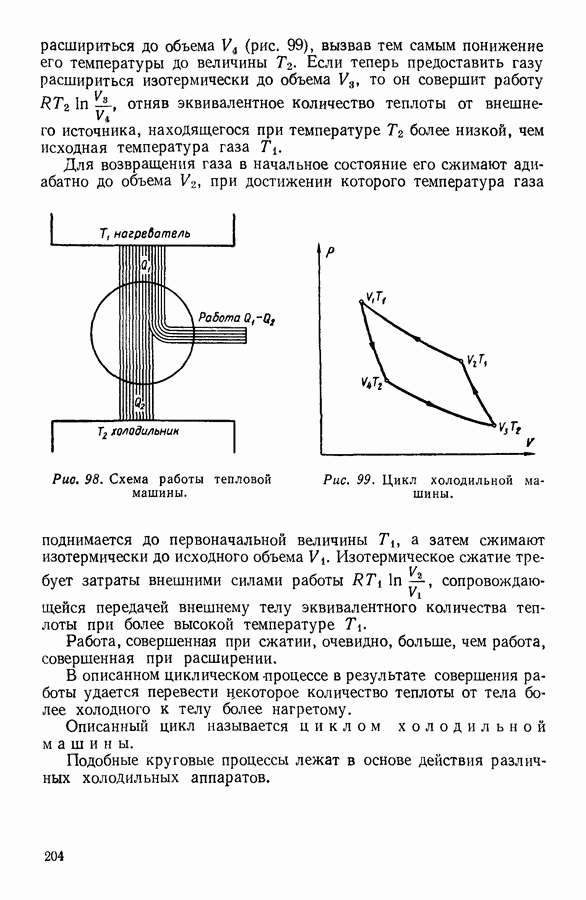
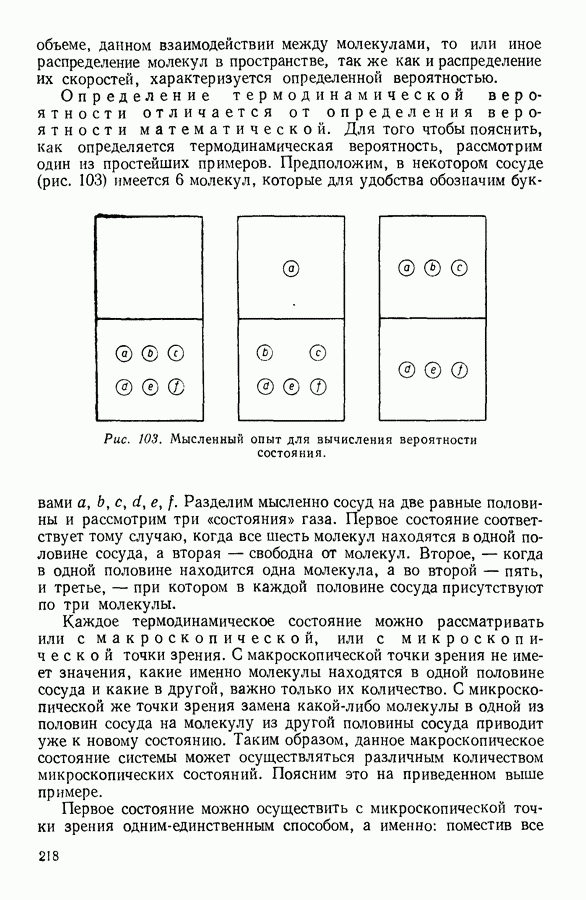
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
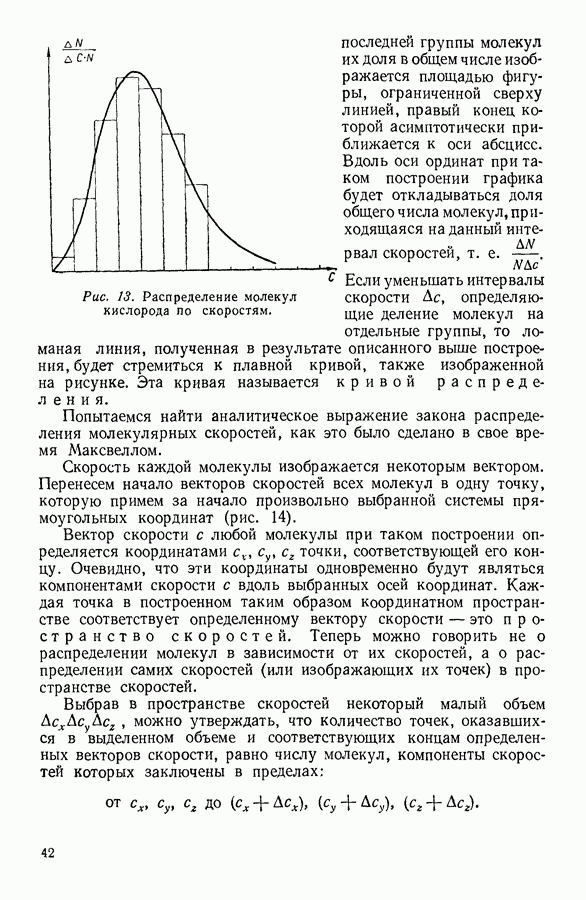
18. ДИФФУЗИЯ ГАЗОВ
Одним из наиболее наглядных примеров явлений переноса служит диффузия газов. Диффузией газов называют процесс взаимного проникновения двух соприкасающихся газов, обусловленный тепловым движением молекул.
Если процесс диффузии происходит достаточно длительное время, то устанавливается стационарное состояние, при котором концентрация  т. е. количество одного из диффундирующих газов в единице объема, плавно изменяется вдоль направления, в котором происходит диффузия. В газе возникает постоянный градиент концентрации, равный
т. е. количество одного из диффундирующих газов в единице объема, плавно изменяется вдоль направления, в котором происходит диффузия. В газе возникает постоянный градиент концентрации, равный  (рис. 25) и аналогичный градиенту скорости упорядоченного движения — или градиенту температуры
(рис. 25) и аналогичный градиенту скорости упорядоченного движения — или градиенту температуры  которые приходилось учитывать при рассмотрении вязкости и теплопроводности газов.
которые приходилось учитывать при рассмотрении вязкости и теплопроводности газов.
Может показаться, что для объяснения особенностей процесса диффузии газов достаточно механически повторить рассуждения, использованные при рассмотрении вязкости и теплопроводности. Однако это неверно. В явлении вязкости и теплопроводности приходилось иметь дело с градиентом какого-либо свойства молекул, в то время как сами молекулы оставались идентичными. В случае же диффузии двух различных газов молекулы их различаются массой, скоростью движения, размерами, свободным пробегом и т. д. Эти особенности диффузии не позволяют в этом случае перенести без изменений схему рассуждений, использованных в предыдущих параграфах.
Можно рассмотреть, однако, частный случай диффузии, при котором эти возражения отпадают, это случай самодиффузии, т.е. диффузионного распространения газа в самом себе. На практике самодиффузию можно реализовать, воспользовавшись радиоактивными изотопами какого-либо элемента и превратив с их помощью часть молекул соответствующего газа в меченые молекулы. Все физические свойства меченых и немеченых молекул, за исключением способности первых к радиоактивному распаду, будут одинаковы. Это сильно облегчит рассмотрение диффузии.
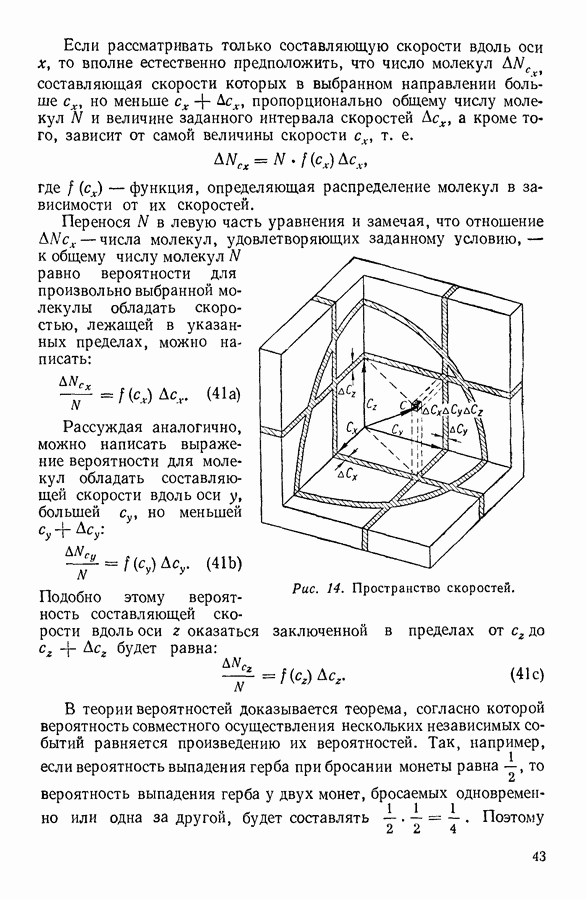
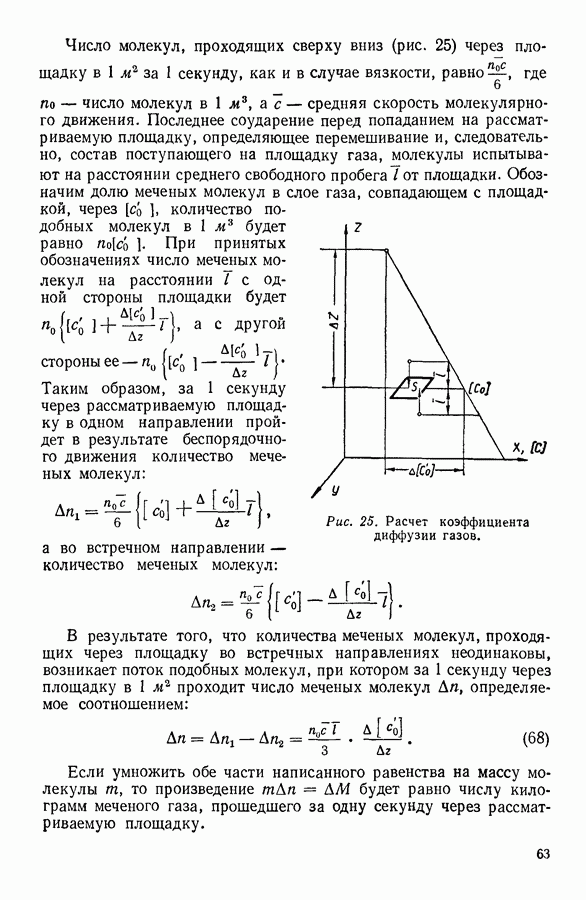
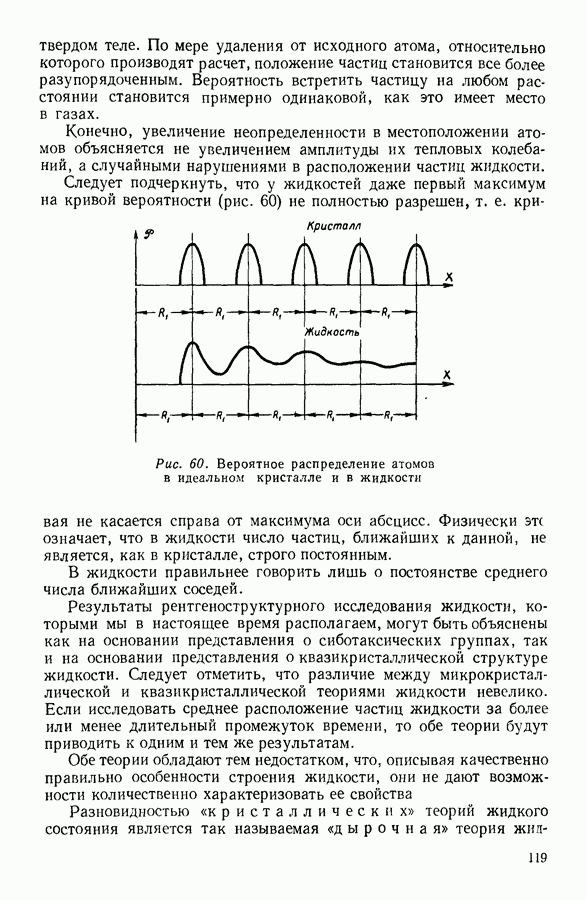
Число молекул, проходящих сверху вниз (рис. 25) через площадку в  за 1 секунду, как и в случае вязкости, равно
за 1 секунду, как и в случае вязкости, равно  , где
, где  число молекул в
число молекул в  а с — средняя скорость молекулярного движения. Последнее соударение перед попаданием на рассматриваемую площадку, определяющее перемешивание и, следовательно, состав поступающего на площадку газа, молекулы испытывают на расстоянии среднего свободного пробега
а с — средняя скорость молекулярного движения. Последнее соударение перед попаданием на рассматриваемую площадку, определяющее перемешивание и, следовательно, состав поступающего на площадку газа, молекулы испытывают на расстоянии среднего свободного пробега  от площадки. Обозначим долю меченых молекул в слое газа, совпадающем с площадкой, через
от площадки. Обозначим долю меченых молекул в слое газа, совпадающем с площадкой, через  количество подобных молекул в
количество подобных молекул в  будет равно
будет равно  При принятых обозначениях число меченых молекул на расстоянии
При принятых обозначениях число меченых молекул на расстоянии  с одной стороны площадки будет
с одной стороны площадки будет  а с другой стороны ее
а с другой стороны ее  Таким образом, за 1 секунду через рассматриваемую площадку в одном направлении пройдет в результате беспорядочного движения количество меченых молекул:
Таким образом, за 1 секунду через рассматриваемую площадку в одном направлении пройдет в результате беспорядочного движения количество меченых молекул:

а во встречном направлении — количество меченых молекул:


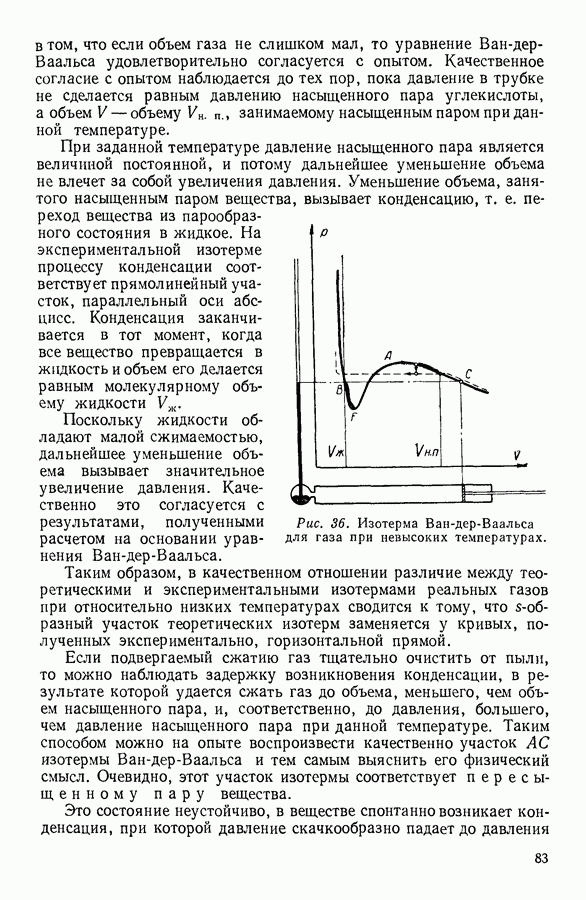
Рис. 25. Расчет коэффициента диффузии газов.
В результате того, что количества меченых молекул, проходящих через площадку во встречных направлениях неодинаковы, возникает поток подобных молекул, при котором за 1 секунду через площадку в  проходит число меченых молекул
проходит число меченых молекул  определяемое соотношением:
определяемое соотношением:

Если умножить обе части написанного равенства на массу молекулы  то произведение
то произведение  будет равно числу килограмм меченого газа, прошедшего за одну секунду через рассматриваемую площадку.
будет равно числу килограмм меченого газа, прошедшего за одну секунду через рассматриваемую площадку.
Стоящее в правой части уравнения выражение  можно тогда записать, перенося знак А, так:
можно тогда записать, перенося знак А, так:  Произведение
Произведение  равно числу меченых молекул в
равно числу меченых молекул в  умножение этого числа на массу молекулы,
умножение этого числа на массу молекулы,  дает концентрацию радиоактивного газа
дает концентрацию радиоактивного газа  Таким образом, мы приходим к заключению, что выражение
Таким образом, мы приходим к заключению, что выражение  оавно градиенту концентрации радиоактивного газа
оавно градиенту концентрации радиоактивного газа  Вводя эти обозначения, можно переписать уравнение (68) в следующем виде:
Вводя эти обозначения, можно переписать уравнение (68) в следующем виде:

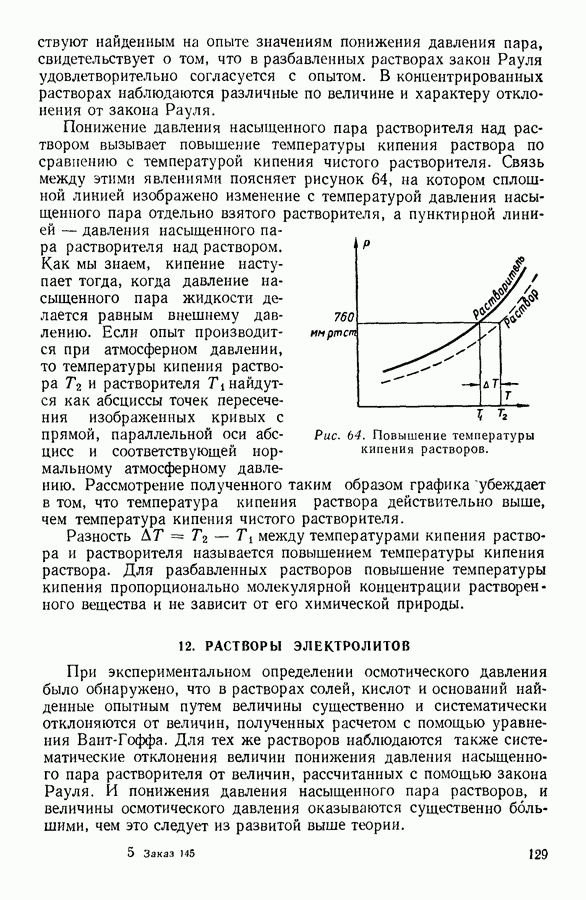
Согласно найденному эмпирически закону (закон Фика) количество вещества  диффундирующего за 1 секунду через площадку в
диффундирующего за 1 секунду через площадку в  пропорционально градиенту концентрации, т. е.
пропорционально градиенту концентрации, т. е.

Входящий в это уравнение коэффициент  называют коэффициентом диффузии. В случае самодиффузии коэффициент
называют коэффициентом диффузии. В случае самодиффузии коэффициент  определяется уравнением:
определяется уравнением:

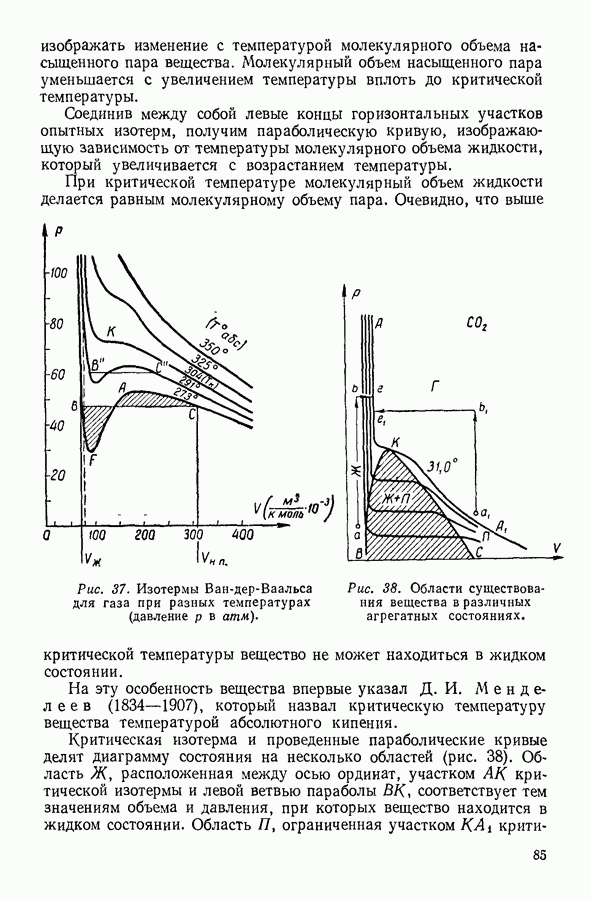
При постоянной плотности газа средний свободный пробег I молекул не зависит от температуры, а средняя скорость движения молекул с пропорциональна корню квадратному из абсолютной температуры. Поэтому коэффициент диффузии, а следовательно, и скорость диффузии при постоянной плотности возрастают пропорционально  При постоянной температуре, но изменяющемся давлении средняя скорость молекулярного движения остается постоянной, в то время как средний свободный пробег изменяется обратно пропорционально давлению. В силу этого коэффициент диффузии при постоянной температуре изменяется обратно пропорционально давлению.
При постоянной температуре, но изменяющемся давлении средняя скорость молекулярного движения остается постоянной, в то время как средний свободный пробег изменяется обратно пропорционально давлению. В силу этого коэффициент диффузии при постоянной температуре изменяется обратно пропорционально давлению.
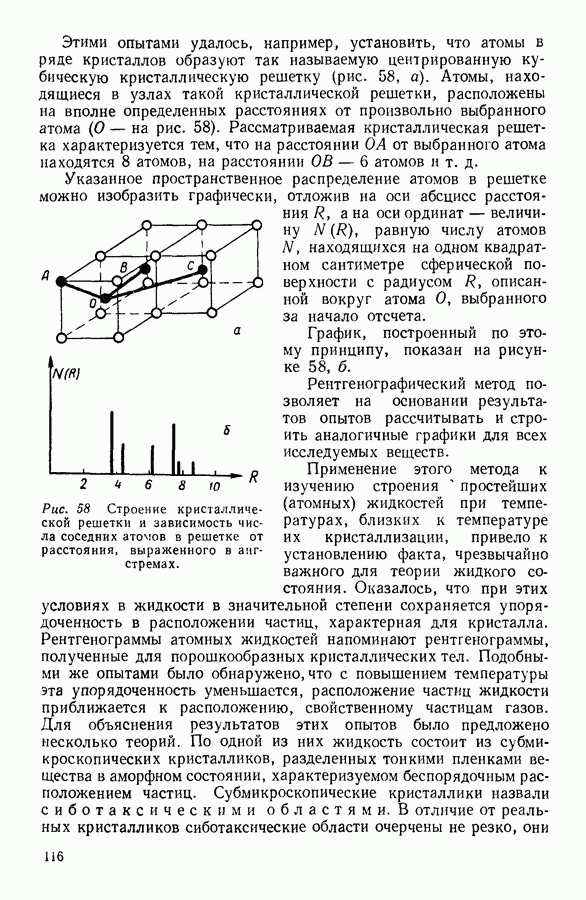
Все три коэффициента: вязкости, теплопроводности и диффузии (уравнения 64, 67 и 71) — зависят от величины среднего свободного пробега молекул. Поэтому, определив экспериментально какой-либо из этих коэффициентов, можно рассчитать величину среднего свободного пробега молекулы. Зная же средний свободный пробег молекулы и соответствующее значение плотности газа, можно, воспользовавшись уравнением (57), вычислить диаметр молекулы газа. Этим методом были определены диаметры многих молекул.
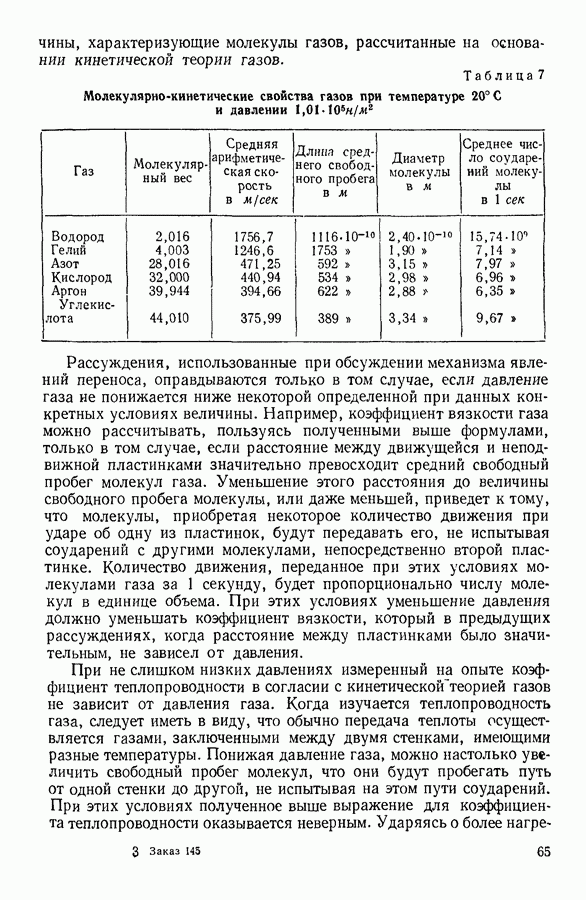
Найденные этим методом величины называют газокинетическими диаметрами молекул. В таблице 7 сопоставлены некоторые
величины, характеризующие молекулы газов, рассчитанные на основании кинетической теории газов.
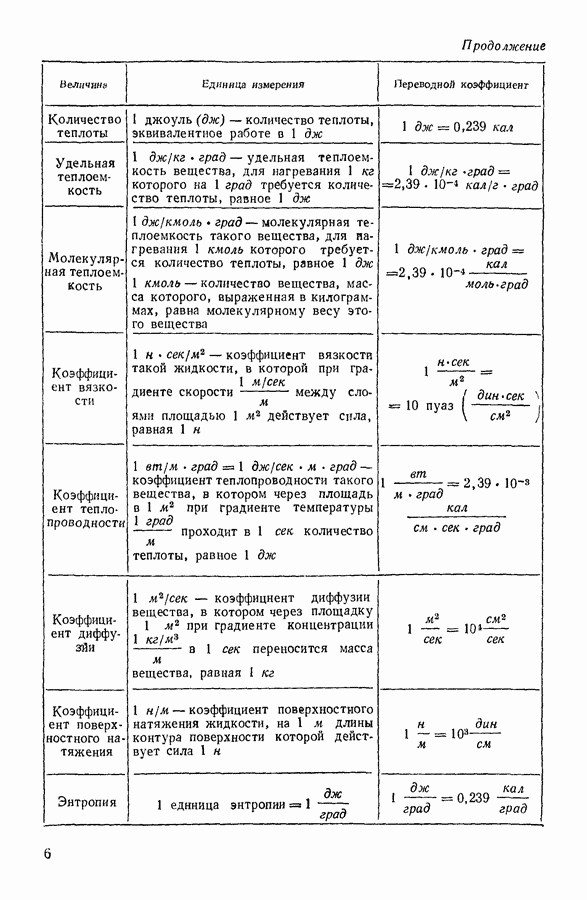
Таблица 7 (см. скан) Молекулярно-кинетические свойства газов при температуре 20° С и давлении 
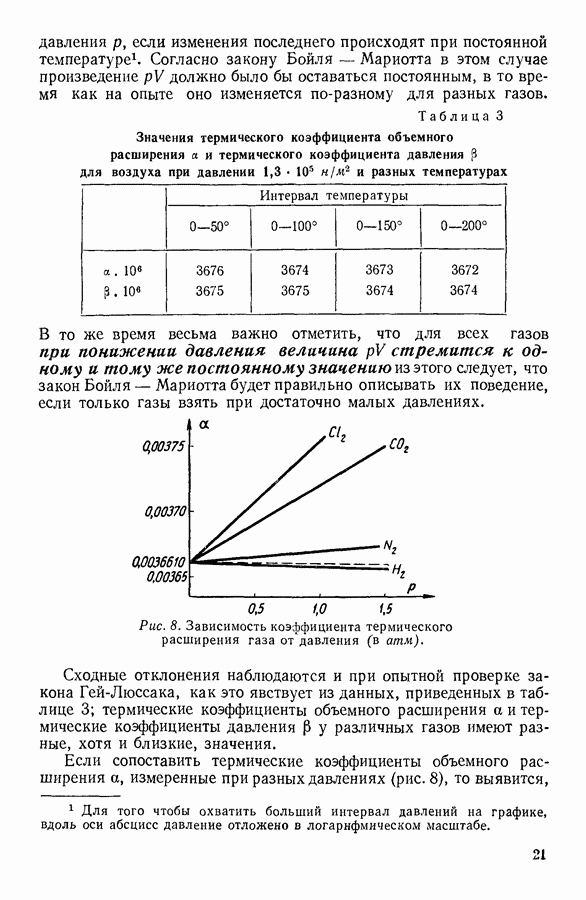
Рассуждения, использованные при обсуждении механизма явлений переноса, оправдываются только в том случае, если давление газа не понижается ниже некоторой определенной при данных конкретных условиях величины. Например, коэффициент вязкости газа можно рассчитывать, пользуясь полученными выше формулами, только в том случае, если расстояние между движущейся и неподвижной пластинками значительно превосходит средний свободный пробег молекул газа. Уменьшение этого расстояния до величины свободного пробега молекулы, или даже меньшей, приведет к тому, что молекулы, приобретая некоторое количество движения при ударе об одну из пластинок, будут передавать его, не испытывая соударений с другими молекулами, непосредственно второй пластинке. Количество движения, переданное при этих условиях молекулами газа за 1 секунду, будет пропорционально числу молекул в единице объема. При этих условиях уменьшение давления должно уменьшать коэффициент вязкости, который в предыдущих рассуждениях, когда расстояние между пластинками было значительным, не зависел от давления.
При не слишком низких давлениях измеренный на опыте коэффициент теплопроводности в согласии с кинетическои "теорией газов не зависит от давления газа. Когда изучается теплопроводность газа, следует иметь в виду, что обычно передача теплоты осуществляется газами, заключенными между двумя стенками, имеющими разные температуры. Понижая давление газа, можно настолько увеличить свободный пробег молекул, что они будут пробегать путь от одной стенки до другой, не испытывая на этом пути соударений. При этих условиях полученное выше выражение для коэффициента теплопроводности оказывается неверным. Ударяясь о более
нагретую стенку, молекулы приобретают большую по сравнению со средней кинетическую энергию, которую и передают непосредственно более холодной стенке. Дальнейшее понижение давления приводит к уменьшению числа молекул, осуществляющих этот процесс, и, следовательно, к уменьшению коэффициента теплопроводности.

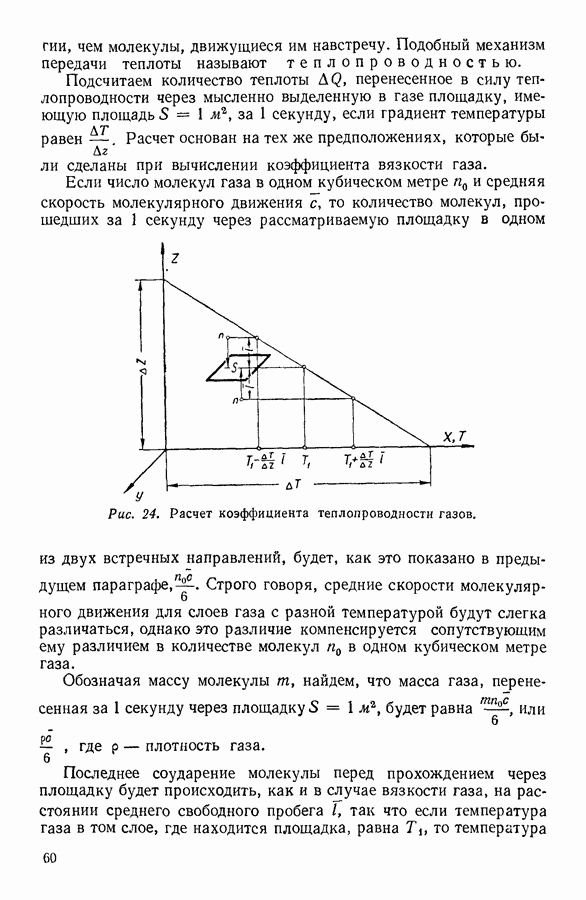
Рис. 26. Сосуд Дьюара.
Это обстоятельство используется при устройстве так называемых сосудов Дьюара, предназначенных для хранения сжиженных газов.
Сосуды Дьюара (рис. 26) имеют двойные стенки, в промежутке между которыми создан высокий вакуум. Благодаря этому теплопроводность сосудов Дьюара ничтожно мала, передача теплоты в них осуществляется в основном путем теплоизлучения, для уменьшения которого стеклянные стенки сосудов покрывают тонким зеркальным слоем серебра. Сосуды Дьюара небольших размеров используются при устройстве термосов, предназначенных для сохранения жидких пищевых продуктов в нагретом или охлажденном состоянии.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
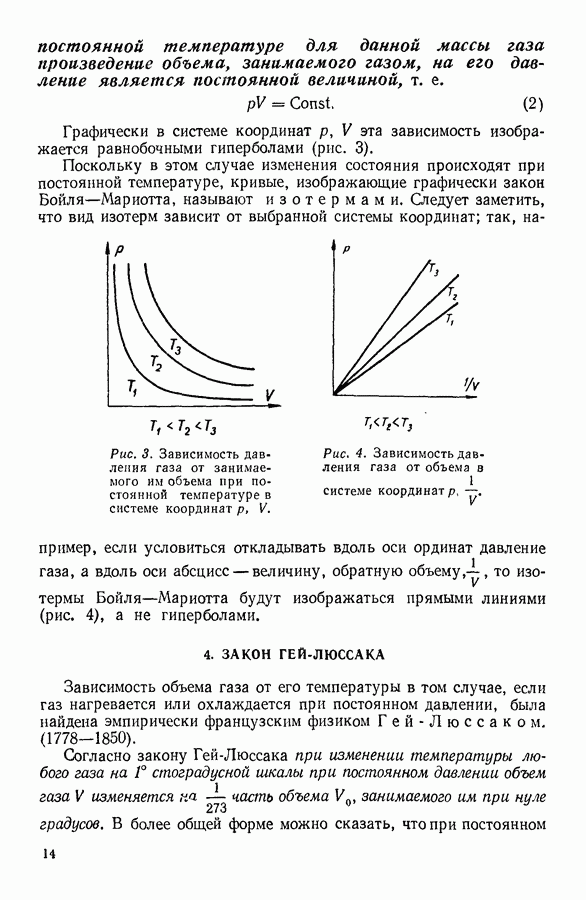
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
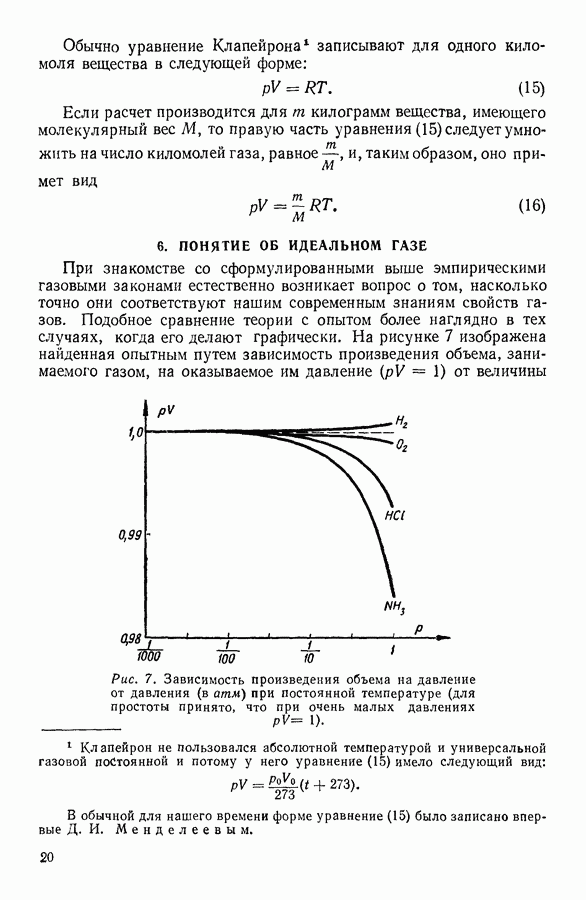
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
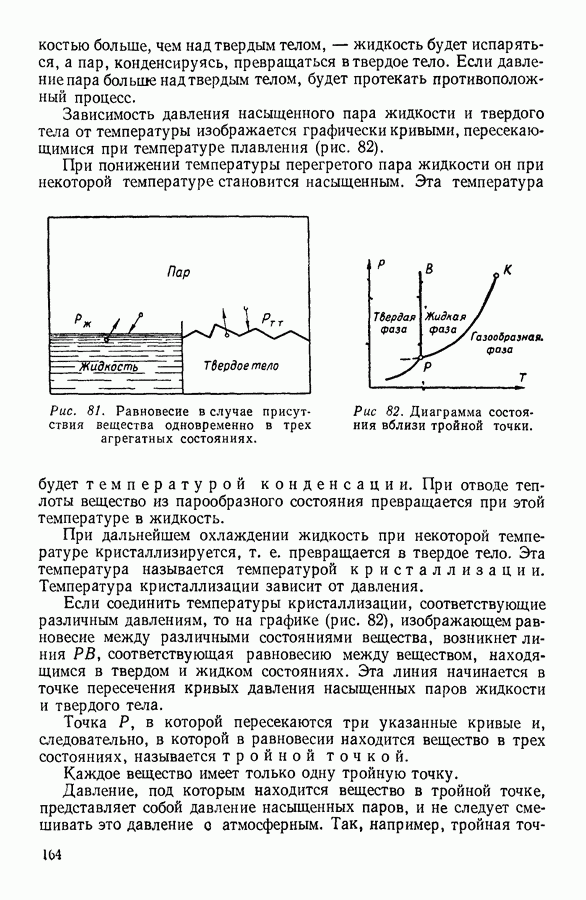
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
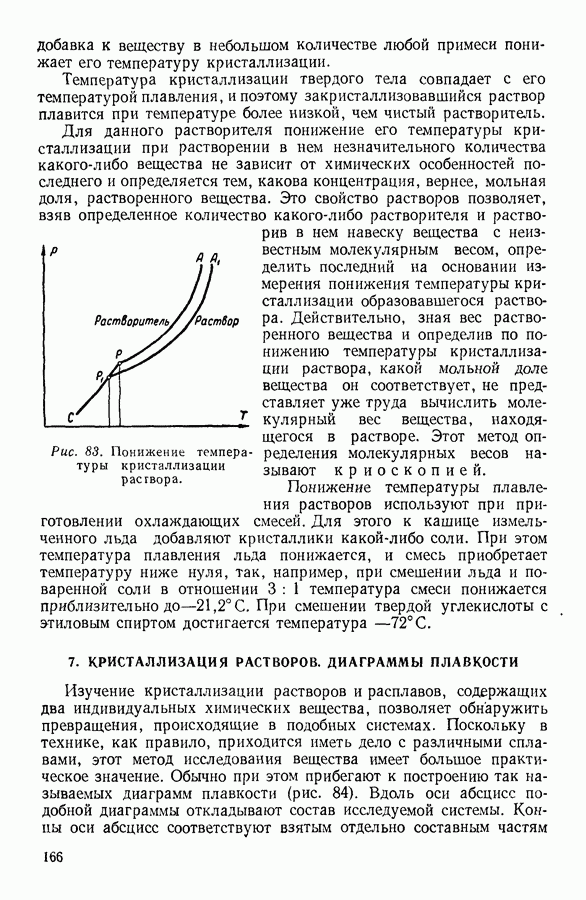
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»