| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
Рассмотрим некоторые примеры применения первого начала термодинамики к процессам изменения состояния идеального газа.
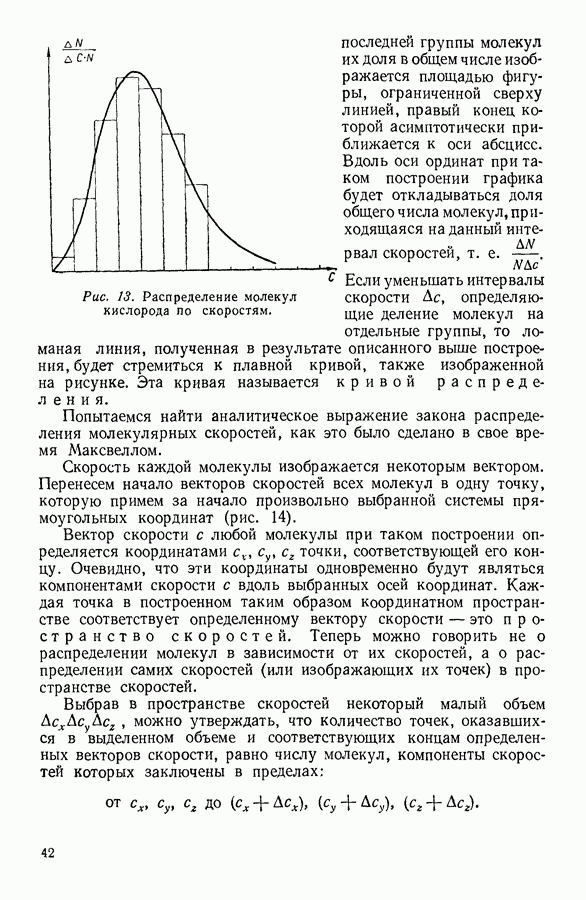
Одним из простейших процессов изменения состояния газа является процесс, протекающий при неизменном объеме. Подобные
процессы называют изохорными. Поскольку при изохорном процессе объем достается постоянным, то  следовательно, работа
следовательно, работа  равна нулю. Первое начало термодинамики запишется в этом случае в виде соотношения:
равна нулю. Первое начало термодинамики запишется в этом случае в виде соотношения:

Количество теплоты, которое необходимо сообщить системе для того, чтобы при постоянном объеме повысить ее температуру на величину  можно выразить, если известна теплоемкость вещества при постоянном объеме
можно выразить, если известна теплоемкость вещества при постоянном объеме  уравнением:
уравнением:

и, следовательно,

или

Теплоемкость  идеального одноатомного газа не зависит от температуры, и потому для внутренней энергии идеального одноатомного газа будет справедливо выражение:
идеального одноатомного газа не зависит от температуры, и потому для внутренней энергии идеального одноатомного газа будет справедливо выражение:

совпадающее с полученным ранее в молекулярно-кинетической теории.
Таким образом, при изохорном изменении состояния газа вся подведенная к системе теплота идет на увеличение внутренней энергии системы.
Иное положение наблюдается при изотермических изменениях состояния. В этом случае внутренняя энергия идеального газа остается неизменной:

и

Уравнение первого начала при изотермическом изменении состояния газа запишется в следующей форме:

или

Из этого выражения следует, что при изотермическом процессе все подведенное к системе количество теплоты превращается в работу.
Для того чтобы подсчитать работу, совершаемую газом, расширяющимся изотермически от объема  до объема
до объема  необходимо проинтегрировать в этих пределах выражение для элементарной работы, учтя при этом связь, существующую между объемом идеального газа и давлением:
необходимо проинтегрировать в этих пределах выражение для элементарной работы, учтя при этом связь, существующую между объемом идеального газа и давлением:

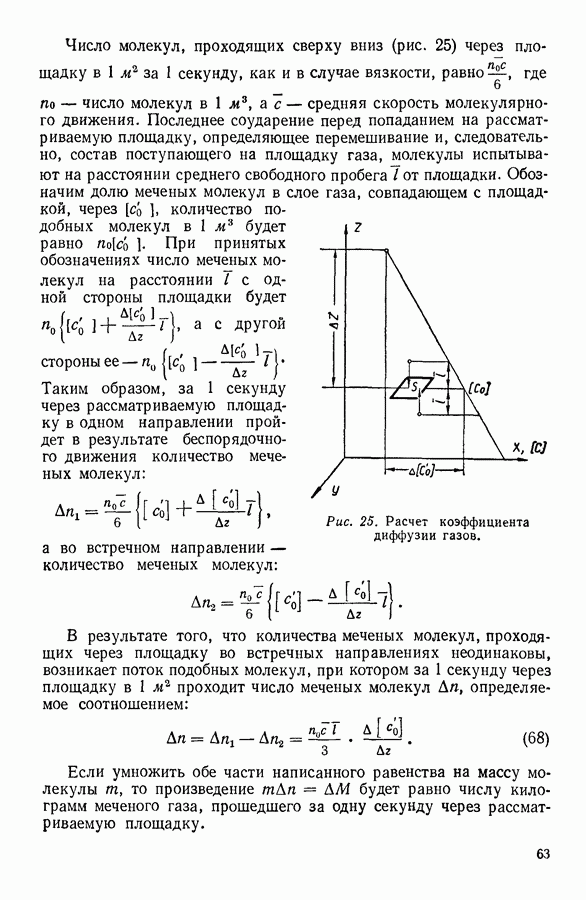
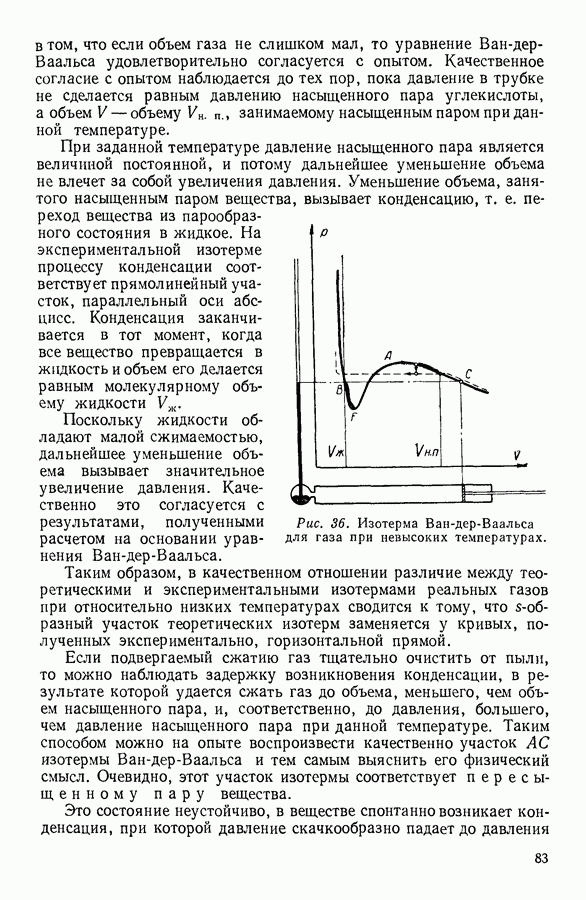
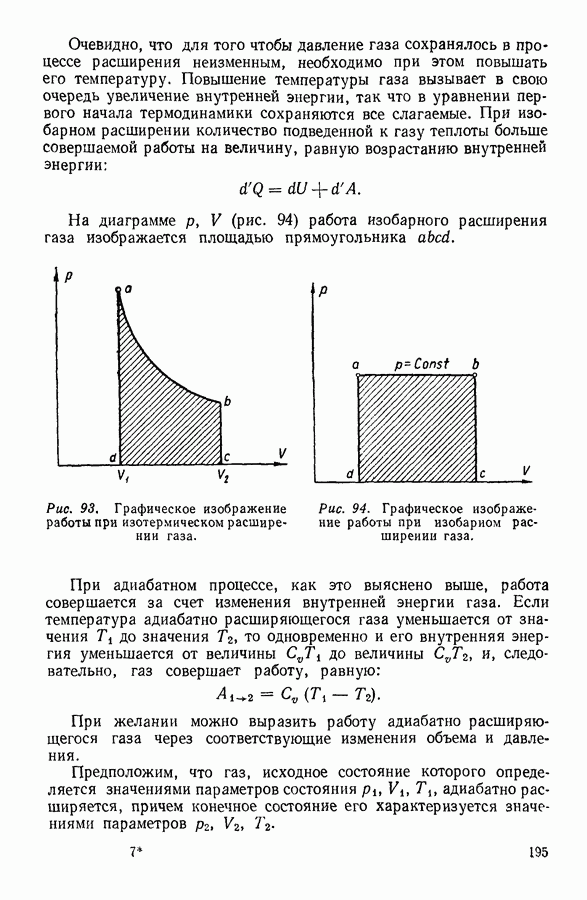
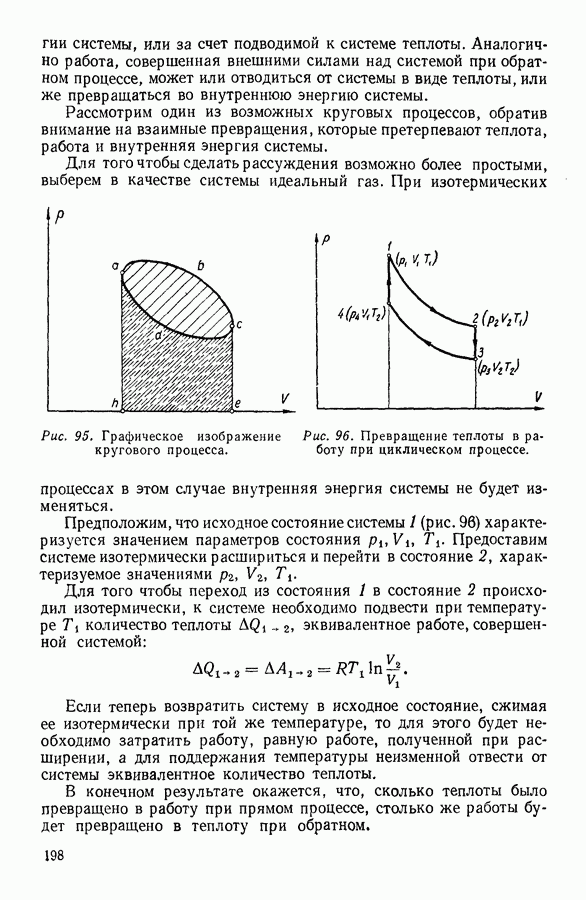
Графически вычисленная работа выражается на диаграмме с координатами  (рис. 93) площадью
(рис. 93) площадью  заштрихованной на графике.
заштрихованной на графике.
Из полученного уравнения следует, что работа, совершаемая при изотермическом расширении, зависит только от соотношения начального и конечного объемов газа, но не от их абсолютных величин. Следует иметь в виду, что написанное уравнение позволяет рассчитать работу изотермического расширения одного моля идеального газа.
Работа, совершаемая при расширении  молей газа, будет в
молей газа, будет в  раз больше, т. е.
раз больше, т. е.

Вместо отношения объемов  можно воспользоваться равным ему обратным отношением давлений:
можно воспользоваться равным ему обратным отношением давлений:

Расширение газа может происходить при таких условиях, что неизменным будет оставаться давление газа. Процессы, протекающие при неизменном давлении, называют изобарными. Выражение для работы при изобарном расширении особенно просто. Поскольку давление при этом остается постоянным, при интегрировании выражения для элементарной работы оно выносится за знак интеграла:

Очевидно, что для того чтобы давление газа сохранялось в процессе расширения неизменным, необходимо при этом повышать его температуру. Повышение температуры газа вызывает в свою очередь увеличение внутренней энергии, так что в уравнении первого начала термодинамики сохраняются все слагаемые. При изобарном расширении количество подведенной к газу теплоты больше совершаемой работы на величину, равную возрастанию внутренней энергии:

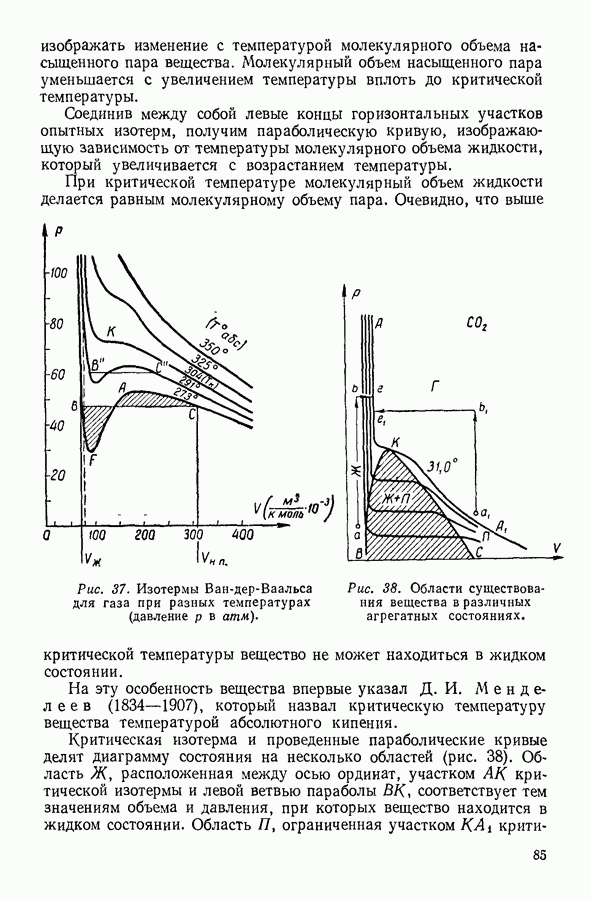
На диаграмме  (рис. 94) работа изобарного расширения газа изображается площадью прямоугольника
(рис. 94) работа изобарного расширения газа изображается площадью прямоугольника 

Рис. 93. Графическое изображение работы при изотермическом расширении газа.

Рис. 94. Графическое изображение работы при изобарном расширении газа.
При адиабатном процессе, как это выяснено выше, работа совершается за счет изменения внутренней энергии газа. Если температура адиабатно расширяющегося газа уменьшается от значения до значения  то одновременно и его внутренняя энергия уменьшается от величины
то одновременно и его внутренняя энергия уменьшается от величины  до величины
до величины  следовательно, газ совершает работу, равную:
следовательно, газ совершает работу, равную:

При желании можно выразить работу адиабатно расширяющегося газа через соответствующие изменения объема и давления.
Предположим, что газ, исходное состояние которого определяется значениями параметров состояния  адиабатно расширяется, причем конечное состояние его характеризуется значениями параметров
адиабатно расширяется, причем конечное состояние его характеризуется значениями параметров 
Совершенная при этом работа, как и раньше, будет выражаться интегралом:

Однако в этом случае объем и давление газа связаны уравнением Пуассона:

откуда

Подставляя это значение  в уравнение, выражающее работу, и интегрируя, найдем:
в уравнение, выражающее работу, и интегрируя, найдем:

но

Заменяя постоянную С в выражении для работы, совершаемой адиабатно расширяющимся газом, получим:

Рассмотренные выше закономерности справедливы применительно к идеальным газам. В случае реальных газов соответствующие закономерности усложняются.
Внутренняя энергия ван-дер-ваальсового газа зависит не только от температуры, но и от объема. Для того чтобы найти эту зависимость, рассмотрим процесс изотермического изменения объема реального газа. При изотермическом изменении состояния газа та часть внутренней энергии, которая обусловлена молекулярным движением, остается неизменной, поскольку не изменяется средняя скорость движения молекул.
Как показано выше, для этого к системе необходимо подвести в случае расширения или от системы отвести в случае сжатия количество теплоты, эквивалентное совершенной работе.
Если газ подчиняется уравнению Ван-дер-Ваальса, работа  обусловленная элементарным изменением объема, запишется в виде следующего соотношения:
обусловленная элементарным изменением объема, запишется в виде следующего соотношения:

или

Первый член в правой части написанного выражения  соответствует работе против внешнего давления — это внешняя работа. Второй член в правой части уравнения
соответствует работе против внешнего давления — это внешняя работа. Второй член в правой части уравнения  представляет собой работу, совершенную против сил молекулярного притяжения, и ее эквивалентом является изменение энергии взаимодействия молекул. Этот член соответствует потенциальной составляющей внутренней энергии реального газа.
представляет собой работу, совершенную против сил молекулярного притяжения, и ее эквивалентом является изменение энергии взаимодействия молекул. Этот член соответствует потенциальной составляющей внутренней энергии реального газа.
Изменение внутренней энергии реального газа при неизотермическом процессе складывается, таким образом, из изменения кинетической энергии теплового движения молекул и изменения потенциальной энергии их взаимодействия:

или

В различных термодинамических соотношениях, определяющих свойства реальных газов, необходимо учитывать наличие потенциальной энергии молекулярного взаимодействия.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ОСНОВНЫЕ ЕДИНИЦЫ СИ
- I. ГАЗООБРАЗНОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. РАЗВИТИЕ АТОМНЫХ ПРЕДСТАВЛЕНИЙ В НАУКЕ
- 2. ПОНЯТИЕ О СОСТОЯНИИ ВЕЩЕСТВА
- 3. ЗАКОН БОЙЛЯ — МАРИОТТА
- 4. ЗАКОН ГЕЙ-ЛЮССАКА
- 5. ОБЪЕДИНЕННЫЙ ГАЗОВЫЙ ЗАКОН
- 6. ПОНЯТИЕ ОБ ИДЕАЛЬНОМ ГАЗЕ
- 7. ОСНОВНЫЕ ПОЛОЖЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 9. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ОСНОВНОГО УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
- 10. РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ГАЗА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ
- 11. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО
- 12. ЗАКОН РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
- 13. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЗАКОНА РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 14. ЧИСЛО СОУДАРЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛЫ
- 15. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ СРЕДНЕГО СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- 16. ЯВЛЕНИЯ ПЕРЕНОСА. ВЯЗКОСТЬ ГАЗОВ
- 17. ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
- 18. ДИФФУЗИЯ ГАЗОВ
- 19. ВАКУУМ. ПОЛУЧЕНИЕ И ИЗМЕРЕНИЕ ВАКУУМА
- 20. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 21. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
- 22. СООТНОШЕНИЕ МЕЖДУ ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ОБЪЕМЕ И ТЕПЛОЕМКОСТЬЮ ГАЗА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- 23. РЕАЛЬНЫЕ ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 24. ИССЛЕДОВАНИЕ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- 25. ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ПАРАМЕТРОВ ВЕЩЕСТВА
- 26. ПРИРОДА СИЛ МОЛЕКУЛЯРНОГО ПРИТЯЖЕНИЯ
- 27. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- 28. СЖИЖЕНИЕ ГАЗОВ
- II. ЖИДКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. СРАВНЕНИЕ СВОЙСТВ ЖИДКОСТЕЙ СО СВОЙСТВАМИ ГАЗОВ И ТВЕРДЫХ ТЕЛ
- 2. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ
- 3. ПОВЕРХНОСТНЫЕ СВОЙСТВА ЖИДКОСТЕЙ
- 4. ЯВЛЕНИЯ НА ГРАНИЦЕ ЖИДКОСТИ С ТВЕРДЫМ ТЕЛОМ
- 5. ДАВЛЕНИЕ ПОД ИЗОГНУТОЙ ПОВЕРХНОСТЬЮ ЖИДКОСТИ
- 6. ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА
- 7. ИСПАРЕНИЕ ЖИДКОСТЕЙ. НАСЫЩЕННЫЙ ПАР И ЕГО СВОЙСТВА
- 8. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ ЖИДКОСТЕЙ
- 9. ВЯЗКОСТЬ ЖИДКОСТЕЙ
- 10. РАСТВОРЫ. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ
- 11. ПОНИЖЕНИЕ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА РАСТВОРИТЕЛЯ НАД РАСТВОРОМ
- 12. РАСТВОРЫ ЭЛЕКТРОЛИТОВ
- 13. ПРИМЕНЕНИЕ УЛЬТРААКУСТИЧЕСКИХ МЕТОДОВ К ИССЛЕДОВАНИЮ ГАЗОВ И ЖИДКОСТЕЙ
- III. ТВЕРДОЕ СОСТОЯНИЕ ВЕЩЕСТВА
- 1. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА
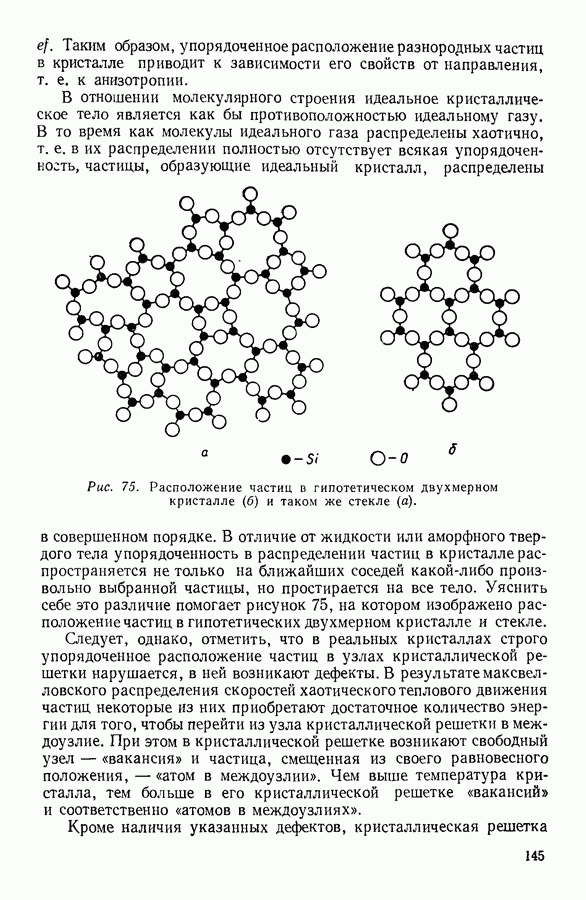
- 2. МОЛЕКУЛЯРНОЕ СТРОЕНИЕ КРИСТАЛЛОВ
- 3. ПОЛИМЕРЫ
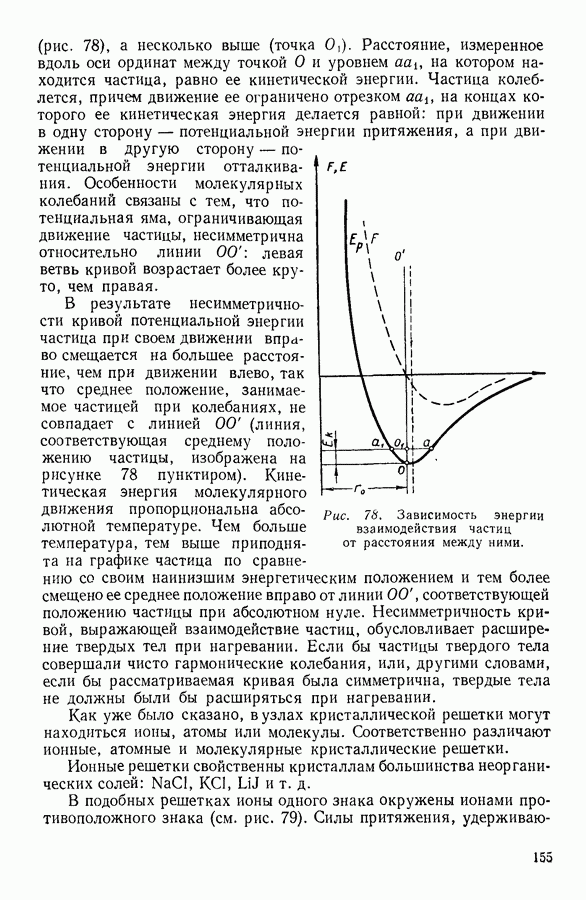
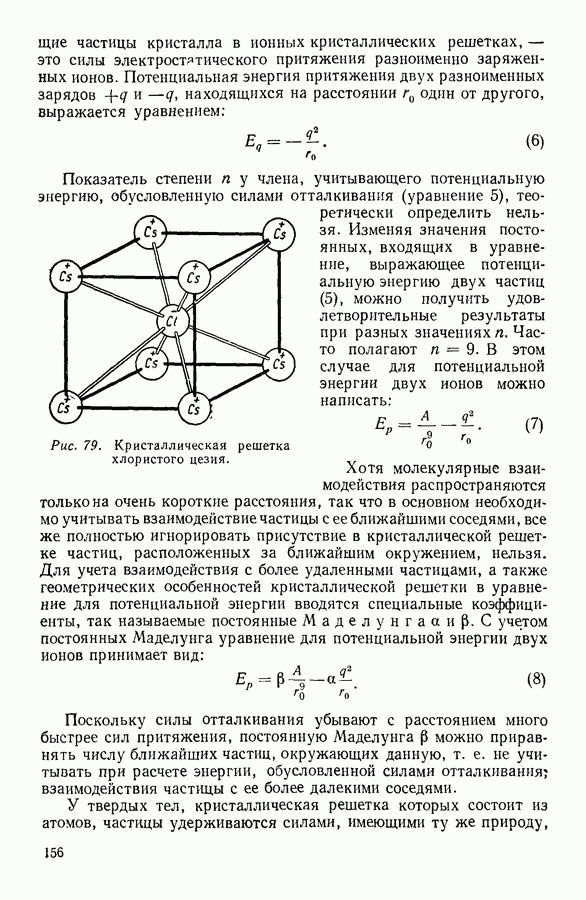
- 4. СИЛЫ, ДЕЙСТВУЮЩИЕ МЕЖДУ ЧАСТИЦАМИ В ТВЕРДЫХ ТЕЛАХ
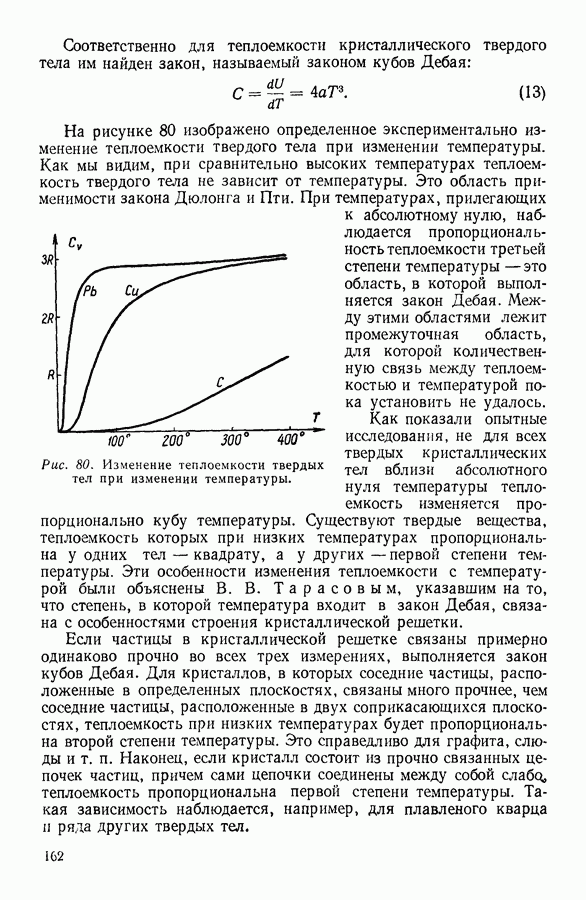
- 5. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ
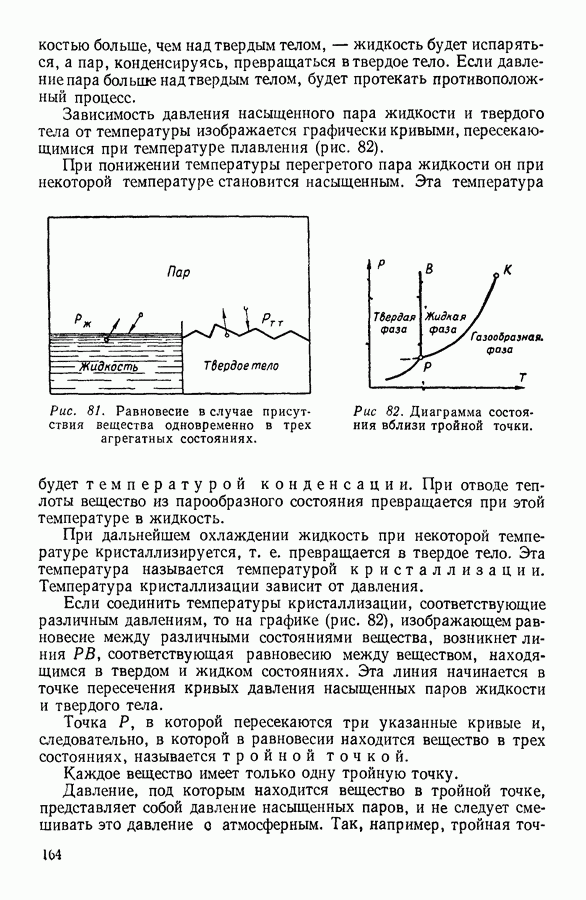
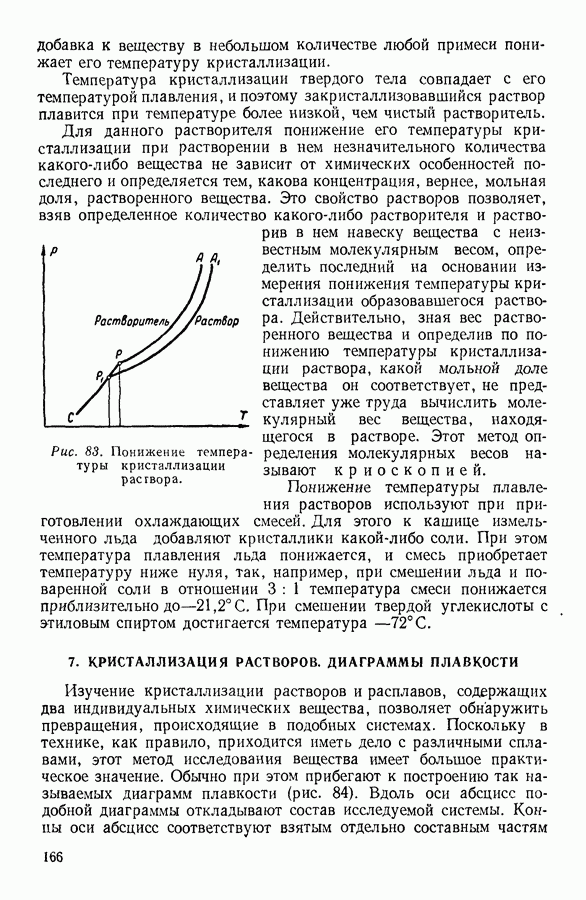
- 6. СУБЛИМАЦИЯ, ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ ТВЕРДЫХ ТЕЛ
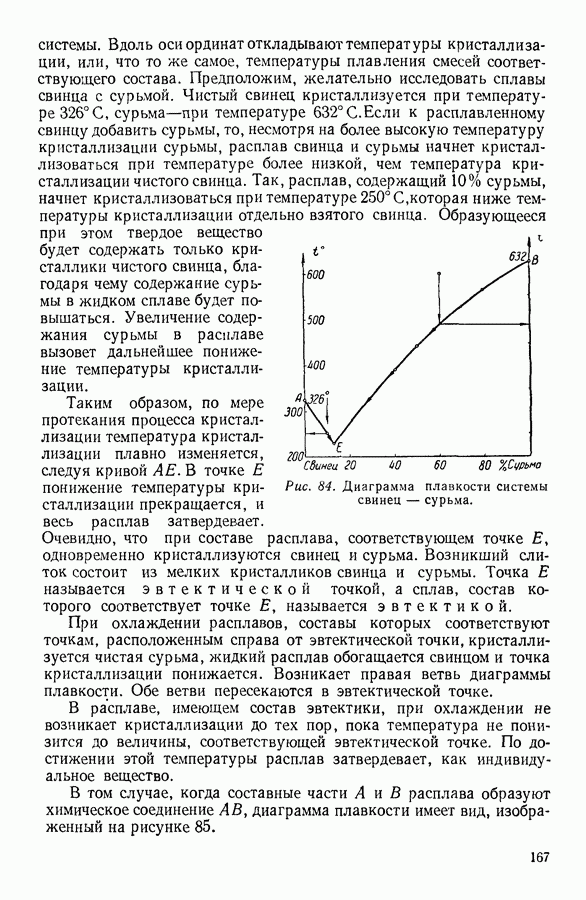
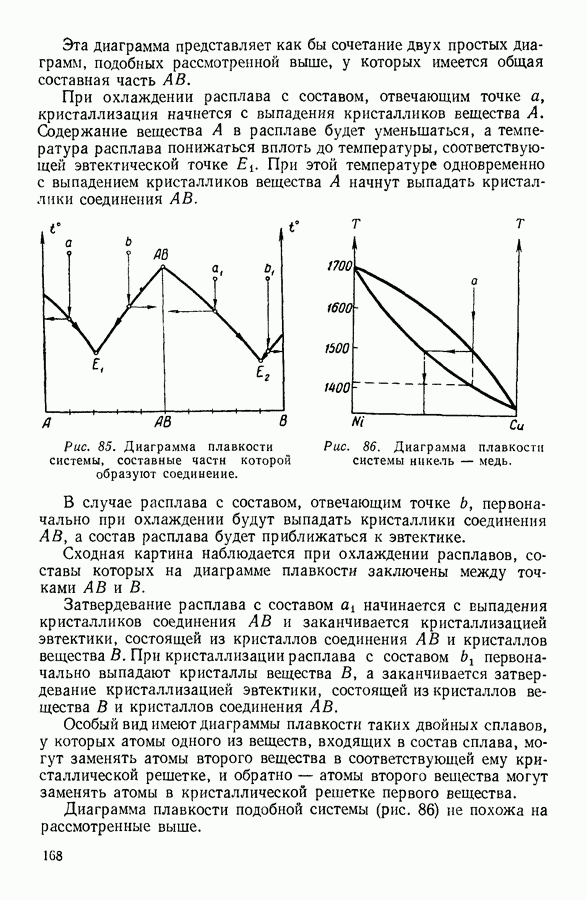
- 7. КРИСТАЛЛИЗАЦИЯ РАСТВОРОВ. ДИАГРАММЫ ПЛАВКОСТИ
- 8. АДСОРБЦИЯ
- IV. ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЙ МЕТОД, МЕТОД СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- 2. ПРЕДМЕТ ТЕРМОДИНАМИКИ. ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ.
- 3. ФИЗИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ «ТЕПЛОТА»
- 4. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 5. МЕТОДЫ НАХОЖДЕНИЯ ТЕРМОДИНАМИЧЕСКИХ СООТНОШЕНИЙ
- 6. АДИАБАТНЫЕ ПРОЦЕССЫ. УРАВНЕНИЕ ПУАССОНА
- 7. ПРИМЕНЕНИЕ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ К НЕКОТОРЫМ ПРОЦЕССАМ В ГАЗАХ
- 8. КРУГОВЫЕ ПРОЦЕССЫ
- 9. ЦИКЛ КАРНО
- 10. ИСПОЛЬЗОВАНИЕ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ В ТЕРМОДИНАМИЧЕСКИХ РАССУЖДЕНИЯХ
- 11. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- 12. СТАТИСТИЧЕСКИЙ СМЫСЛ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- 13. КРИТИКА ТАК НАЗЫВАЕМОЙ «ТЕОРИИ ТЕПЛОВОЙ СМЕРТИ ВСЕЛЕННОЙ»