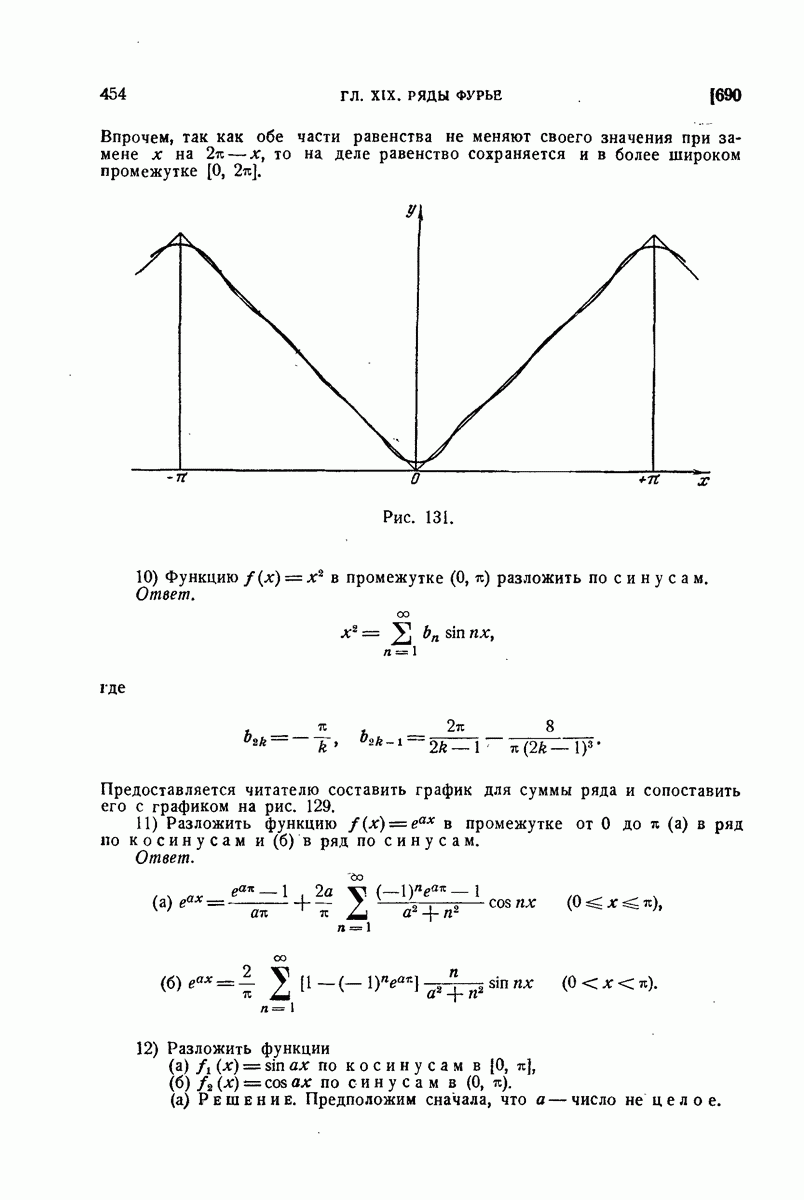
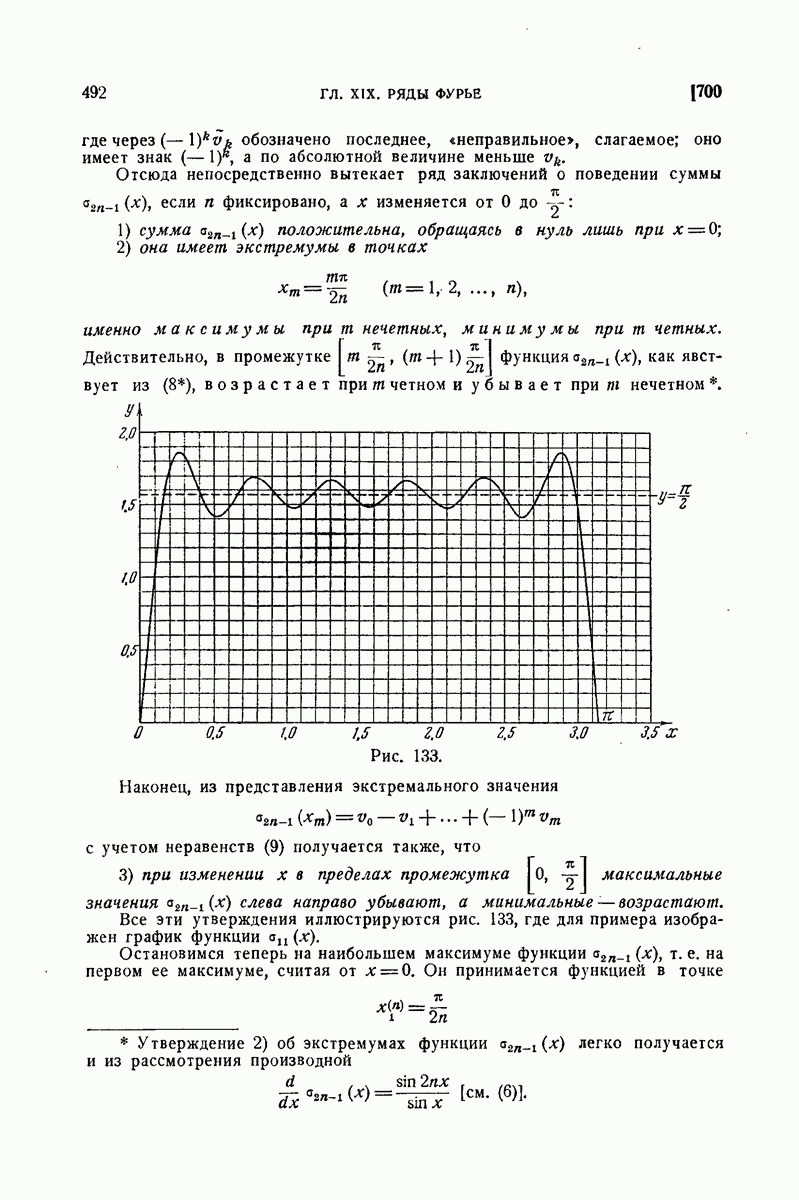
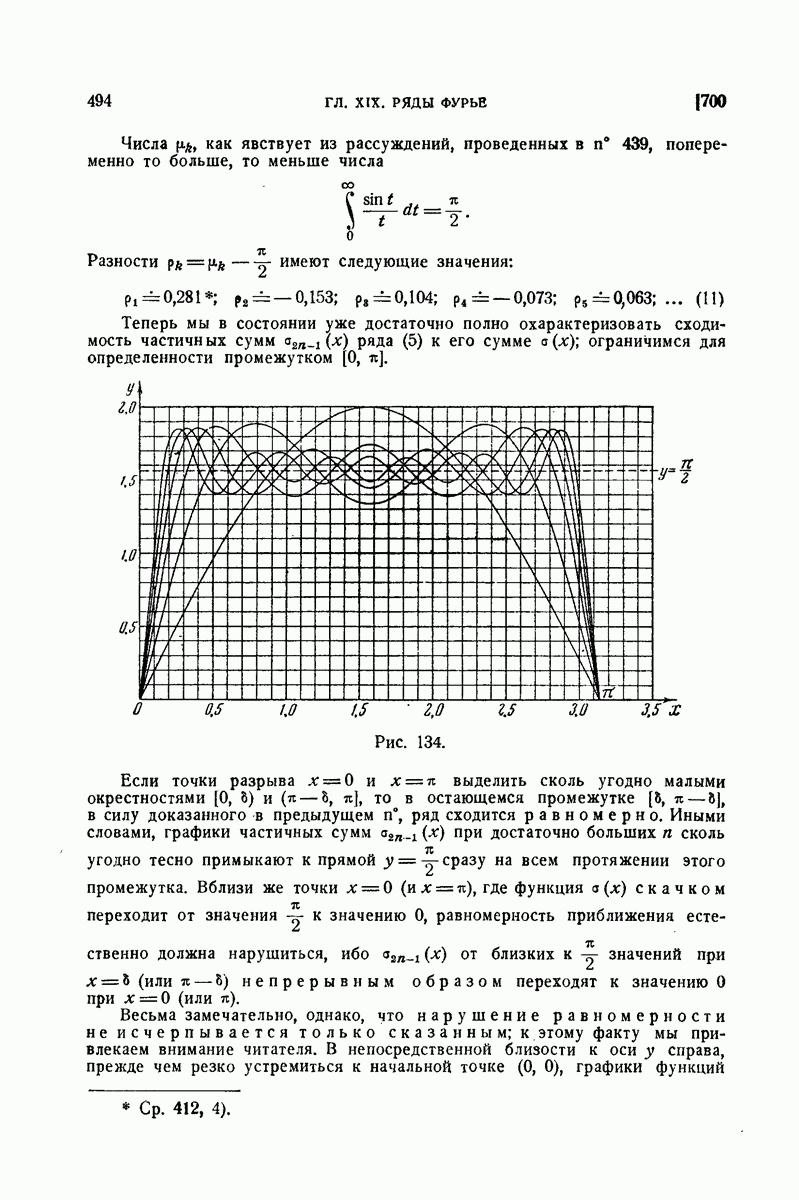
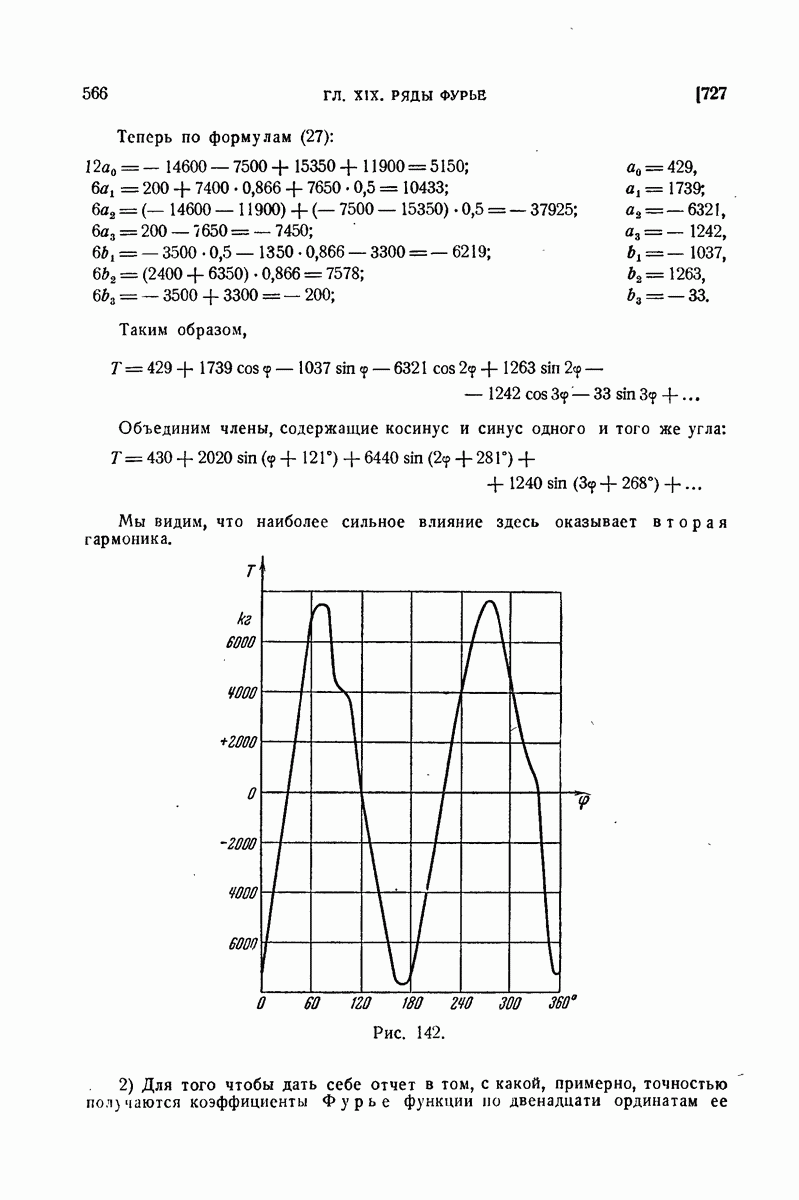
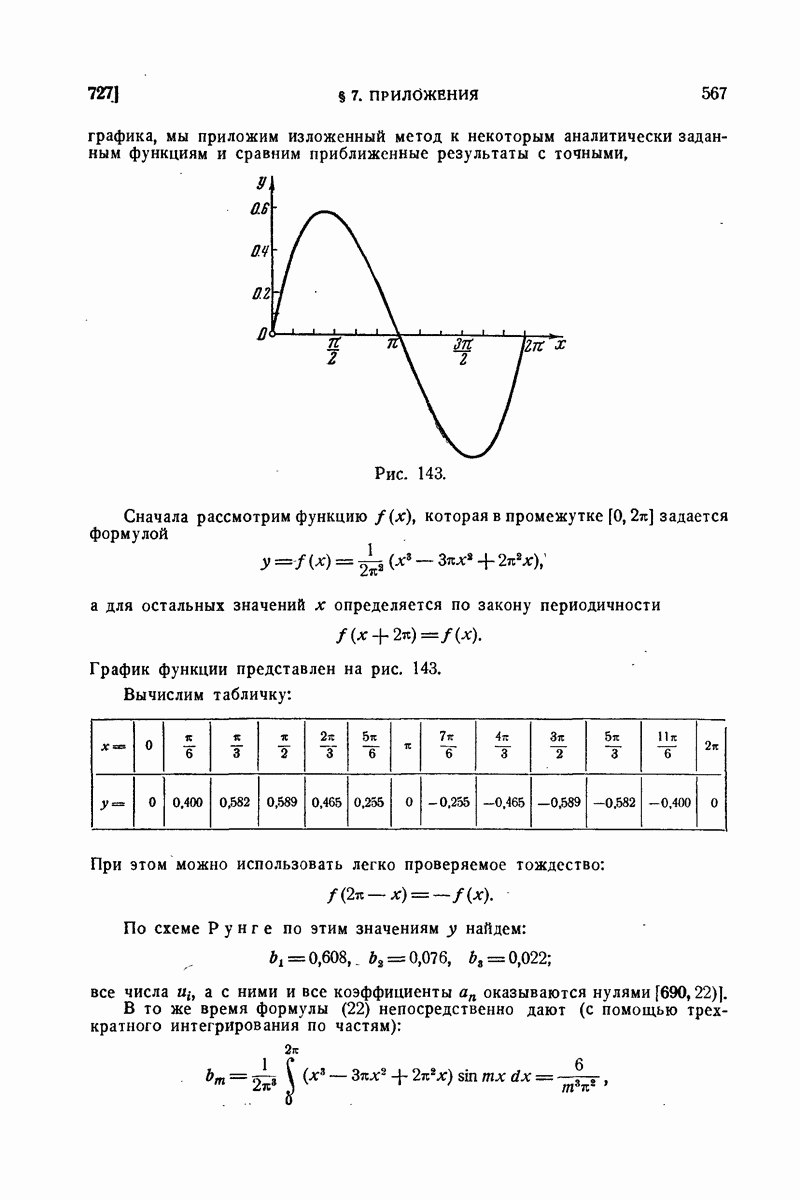
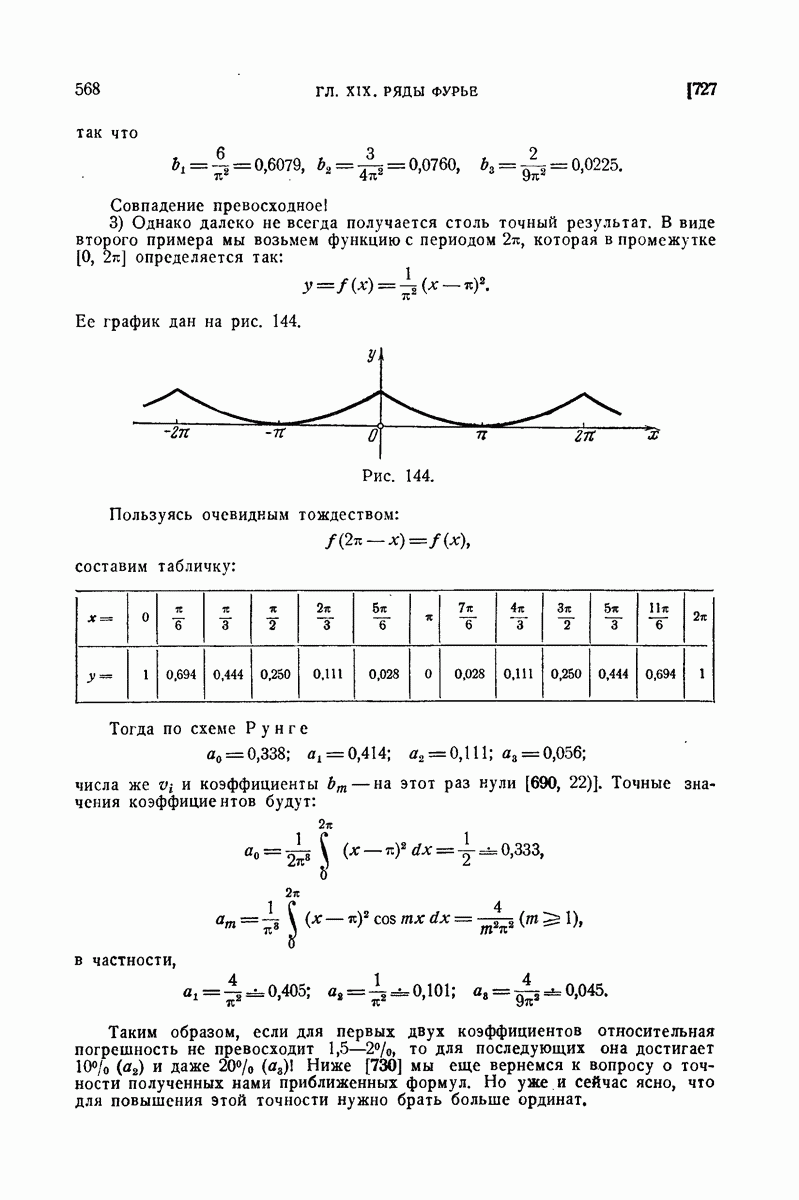
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
734. Равномерная аппроксимация функций.
Теоремы Вейерштрасса. Если какую-либо функцию  в промежутке
в промежутке  «аппроксимируют» с помощью другой,
«аппроксимируют» с помощью другой,  то качество этой аппроксимации можно, в зависимости от обстоятельств, оценивать по-разному. Но, естественно, в основу во всех случаях кладется рассмотрение разности
то качество этой аппроксимации можно, в зависимости от обстоятельств, оценивать по-разному. Но, естественно, в основу во всех случаях кладется рассмотрение разности

Если мы одинаково заинтересованы в малом отклонении одной из функций от другой во всех отдельно взятых точках, то за меру приближения принимают их максимальное отклонение в промежутке, т. е. число

В этом случае говорят о равномерной аппроксимации функции  с помощью функции
с помощью функции 
Мы приведем две фундаментальные теоремы Вейерштрасса, относящиеся к равномерной аппроксимации непрерывных функций, во-первых, с помощью тригонометрических многочленов и, во-вторых, с помощью обыкновенных (алгебраических) многочленов.
Теорема 1. Если функция  непрерывна в промежутке
непрерывна в промежутке  и удовлетворяет условию
и удовлетворяет условию

то, каково бы ни было число  найдется такой тригонометрический многочлен
найдется такой тригонометрический многочлен

что равномерно для всех значений х в упомянутом промежутке будет

Построим прежде всего такую кусочно-линейную функцию  , чтобы повсюду в
, чтобы повсюду в  выполнялось неравенство
выполнялось неравенство

Для этого разобьем промежуток  точками
точками

на столь малые части, чтобы в каждой из них колебание функции 
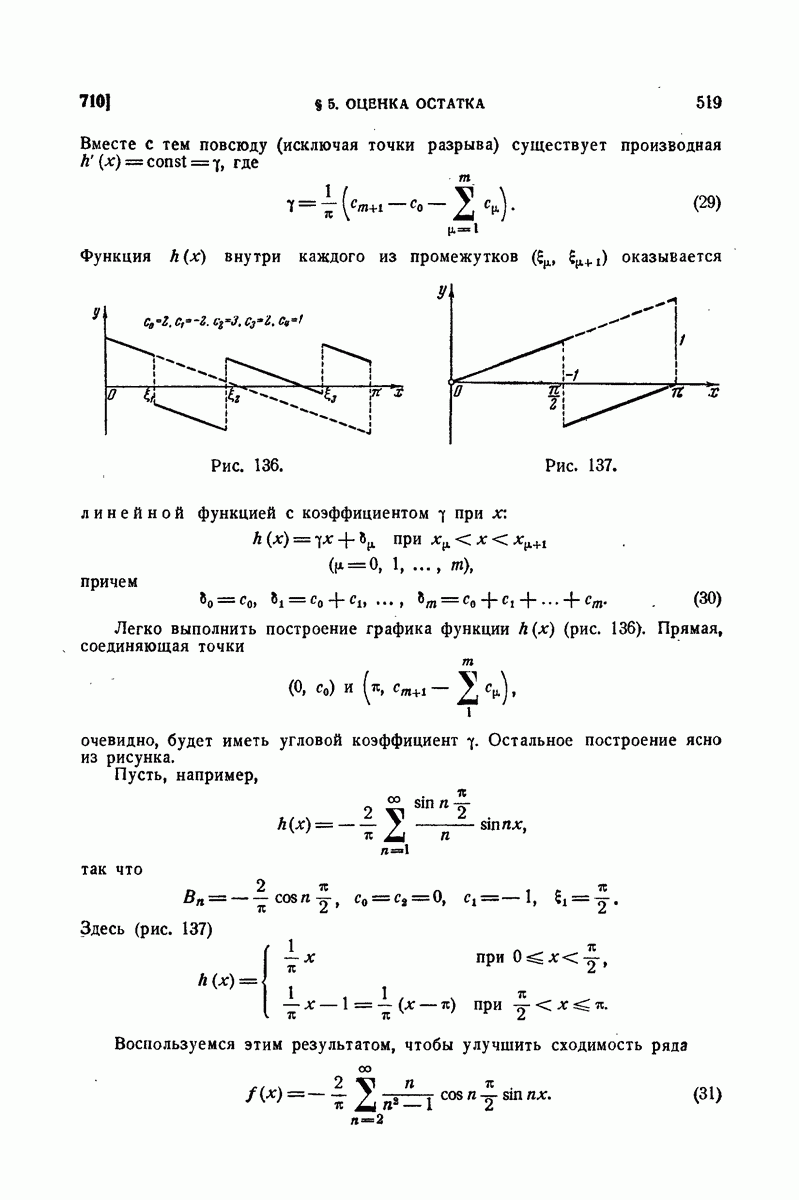
было  Функцию
Функцию  определим в промежутке
определим в промежутке  полагая ее в каждом отдельном промежутке
полагая ее в каждом отдельном промежутке  равной линейной функции
равной линейной функции

которая на концах промежутка совпадает с  По сути дела речь идет о вписывании ломаной линии в кривую, выражаемую уравнением
По сути дела речь идет о вписывании ломаной линии в кривую, выражаемую уравнением  Если через
Если через  и обозначить наименьшее и наибольшее значения функции
и обозначить наименьшее и наибольшее значения функции  промежутке, то по условию
промежутке, то по условию  и так как в этом промежутке значения обеих функций
и так как в этом промежутке значения обеих функций  содержатся между
содержатся между  и то выполнение неравенства (11) во всем промежутке
и то выполнение неравенства (11) во всем промежутке  удостоверено.
удостоверено.
Функция  подобно
подобно  непрерывна в промежутке
непрерывна в промежутке  и удовлетворяет условию
и удовлетворяет условию

но, сверх того, она, как кусочно-монотонная функция, имеет в этом промежутке ограниченное изменение  При этих условиях, согласно признаку Дирихле—Жордана [690],
При этих условиях, согласно признаку Дирихле—Жордана [690],  разлагается в равномерно сходящийся ряд Фурье:
разлагается в равномерно сходящийся ряд Фурье:

Следовательно, если в качестве многочлена  взять
взять  частичную сумму этого ряда при достаточно большом
частичную сумму этого ряда при достаточно большом  то он будет отличаться от
то он будет отличаться от  меньше, чем на
меньше, чем на 

сразу для всех рассматриваемых значений х.
Из (11) и (12) вытекает (10).
Возьмем теперь последовательность  убывающих до нуля положительных чисел и для каждого числа
убывающих до нуля положительных чисел и для каждого числа  построим многочлен
построим многочлен  о котором была речь в доказанной теореме; тогда получится последовательность
о котором была речь в доказанной теореме; тогда получится последовательность  тригонометрических многочленов, которая сходится к функции
тригонометрических многочленов, которая сходится к функции  равномерно в промежутке
равномерно в промежутке  Переходя обычным образом [427] от последовательности к бесконечному ряду, получим другую формулировку теоремы, очевидно, равносильную прежней; при указанных в теореме 1 условиях функция
Переходя обычным образом [427] от последовательности к бесконечному ряду, получим другую формулировку теоремы, очевидно, равносильную прежней; при указанных в теореме 1 условиях функция  разлагается в равномерно сходящийся ряд, членами которого являются тригонометрические многочлены.
разлагается в равномерно сходящийся ряд, членами которого являются тригонометрические многочлены.
Из теоремы 1 уже легко выводится
Теорема 2. Если функция  непрерывна в промежутке
непрерывна в промежутке  то, каково бы ни было число
то, каково бы ни было число  найдется такой целый алгебраический многочлен
найдется такой целый алгебраический многочлен

что равномерно для всех значений  будет
будет

Простой подстановкой

можно свести дело к рассмотрению промежутка  , ибо многочлен, целый относительно х, очевидно, будет целым и относительно х.
, ибо многочлен, целый относительно х, очевидно, будет целым и относительно х.
Чтобы не усложнять обозначений, будем считать, что первоначально данный промежуток и есть  .
.
Распространим теперь функцию  на весь промежуток
на весь промежуток  , полагая
, полагая 

Функция сохранит непрерывность и, очевидно, будет удовлетворять условию  . В таком случае по теореме 1 найдется такой тригонометрический многочлен
. В таком случае по теореме 1 найдется такой тригонометрический многочлен  что для всех значений х между
что для всех значений х между  будет
будет

Если заменить каждую из тригонометрических функций, входящих в состав Т, ее разложением по степеням  то и функция Т представится в виде суммы повсюду сходящегося степенного ряда:
то и функция Т представится в виде суммы повсюду сходящегося степенного ряда:

В промежутке  этот ряд сходится равномерно; поэтому, если отождествить многочлен
этот ряд сходится равномерно; поэтому, если отождествить многочлен  частичной суммой этого ряда, при достаточно большом
частичной суммой этого ряда, при достаточно большом  , то для всех х в промежутке
, то для всех х в промежутке  будет
будет

Остается сопоставить (14) и (15).
Как и выше, доказанной теореме можно дать другую формулировку: функция  непрерывная в промежутке
непрерывная в промежутке  разлагается в этом промежутке в равномерно сходящийся ряд, членами которого являются целые алгебраические многочлены.
разлагается в этом промежутке в равномерно сходящийся ряд, членами которого являются целые алгебраические многочлены.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- ГЛАВА ПЯТНАДЦАТАЯ. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. ИНТЕГРАЛ СТИЛТЬЕСА
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
- 544. Сведение к обыкновенному определенному интегралу.
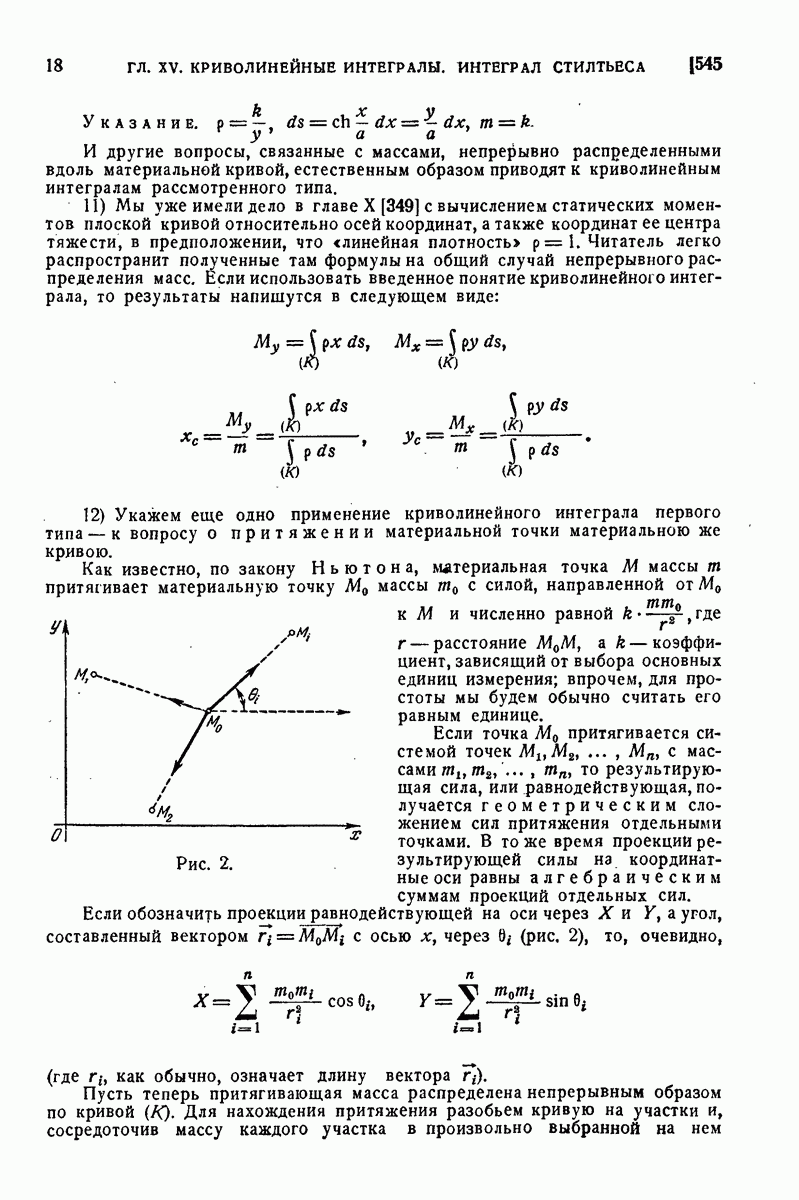
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- 545. Примеры.
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- § 2. Криволинейные интегралы второго типа
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
- 547. Существование и вычисление криволинейного интеграла второго типа.
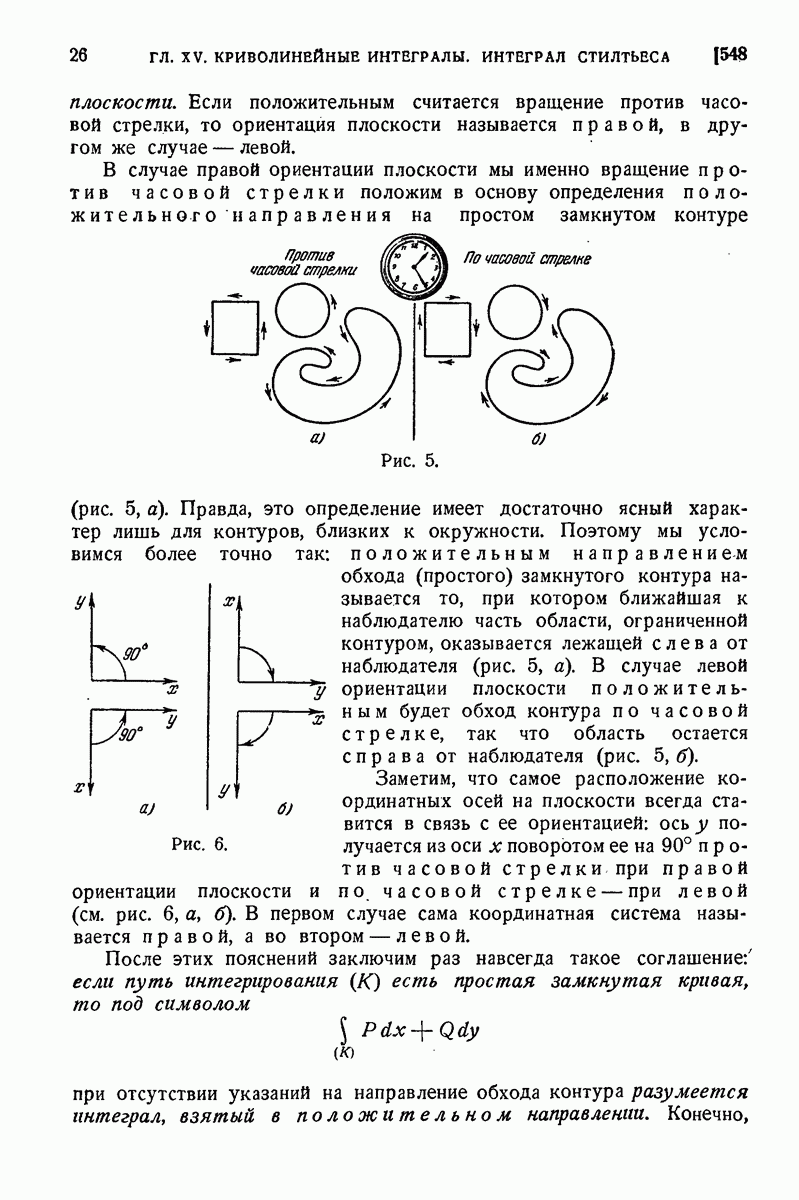
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 548. Случай замкнутого контура. Ориентация плоскости.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 549. Примеры.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
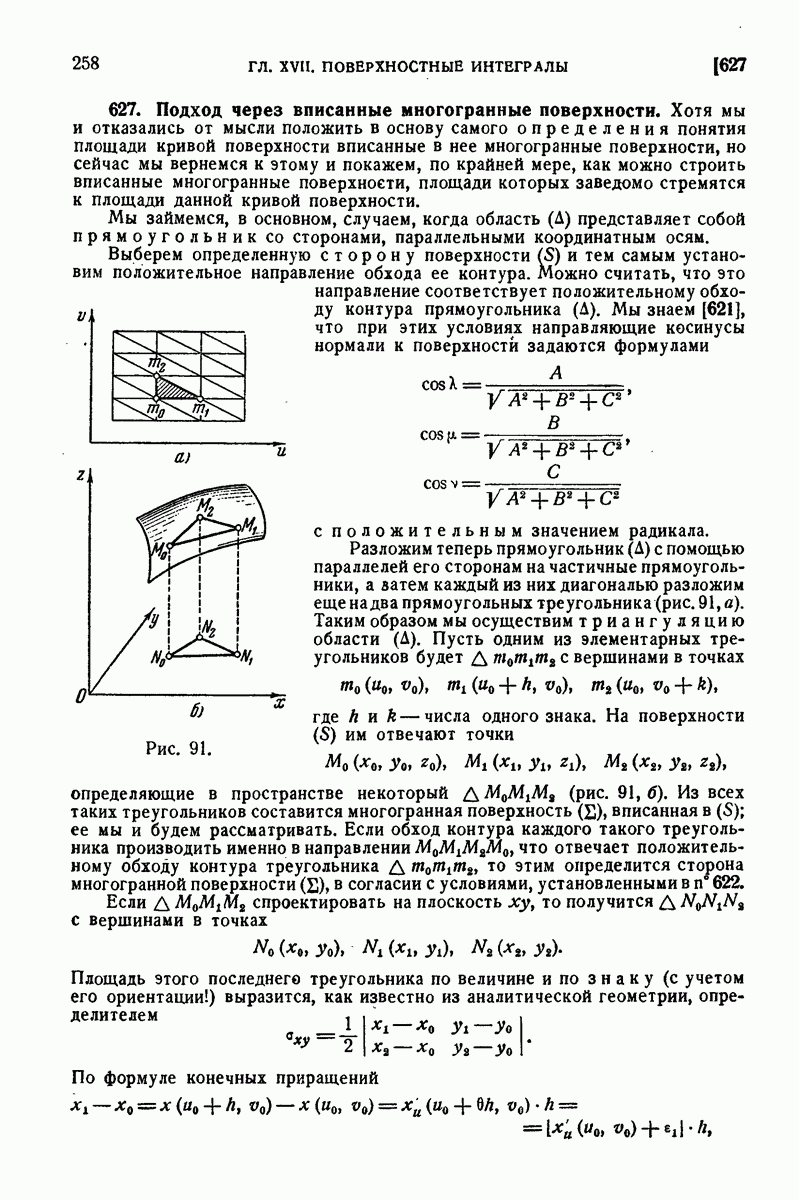
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
- 550. Приближение с помощью интеграла, взятого по ломаной.
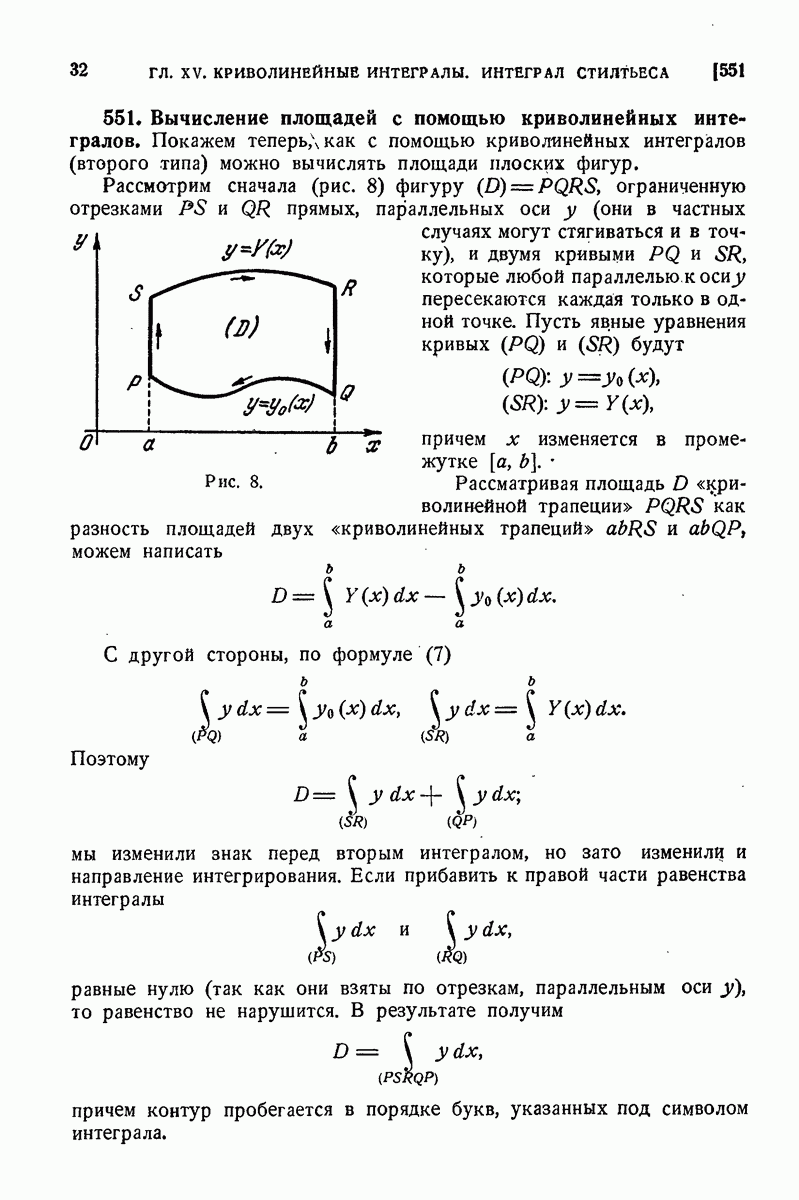
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
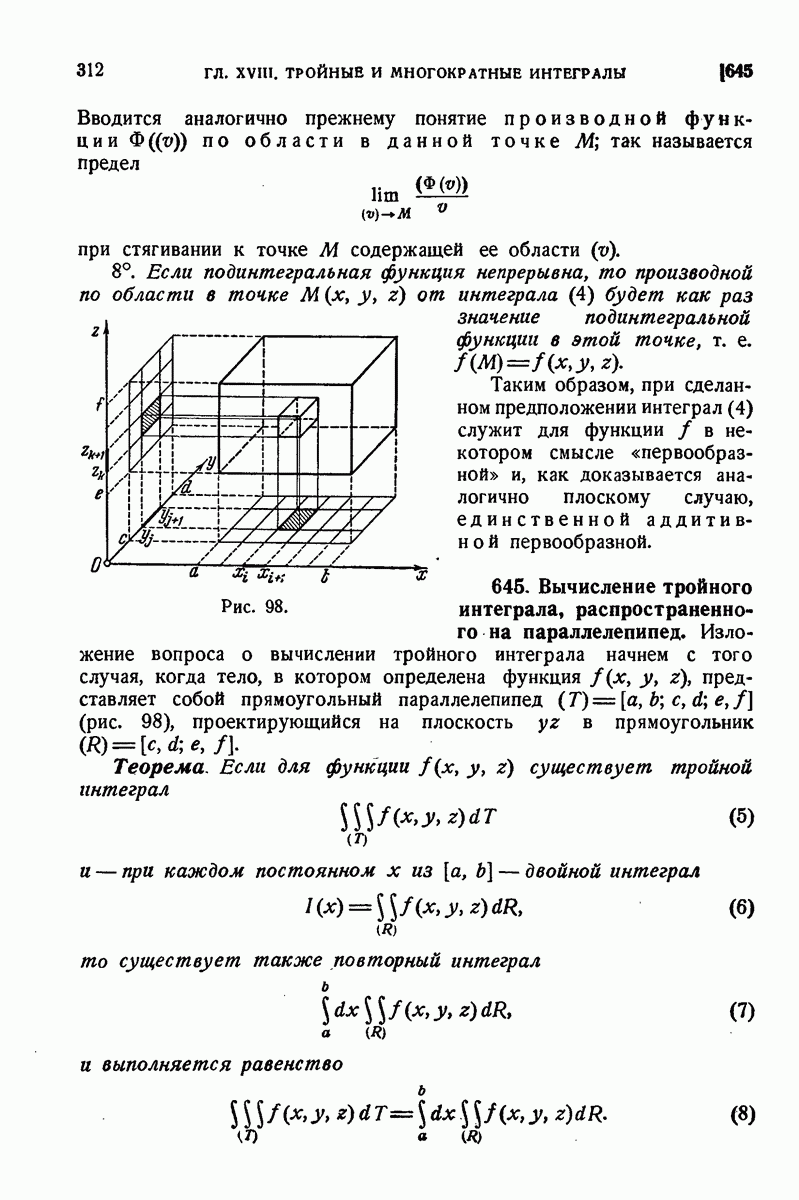
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
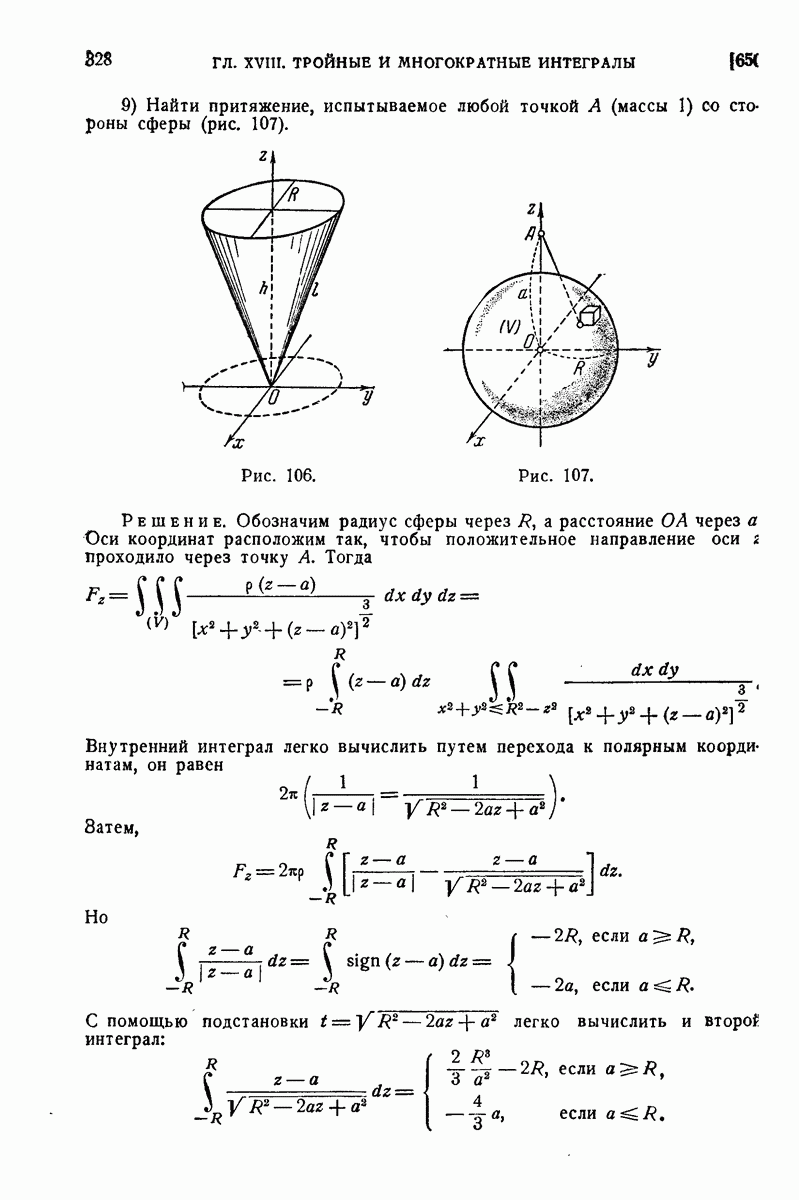
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
- 551. Вычисление площадей с помощью криволинейных интегралов.
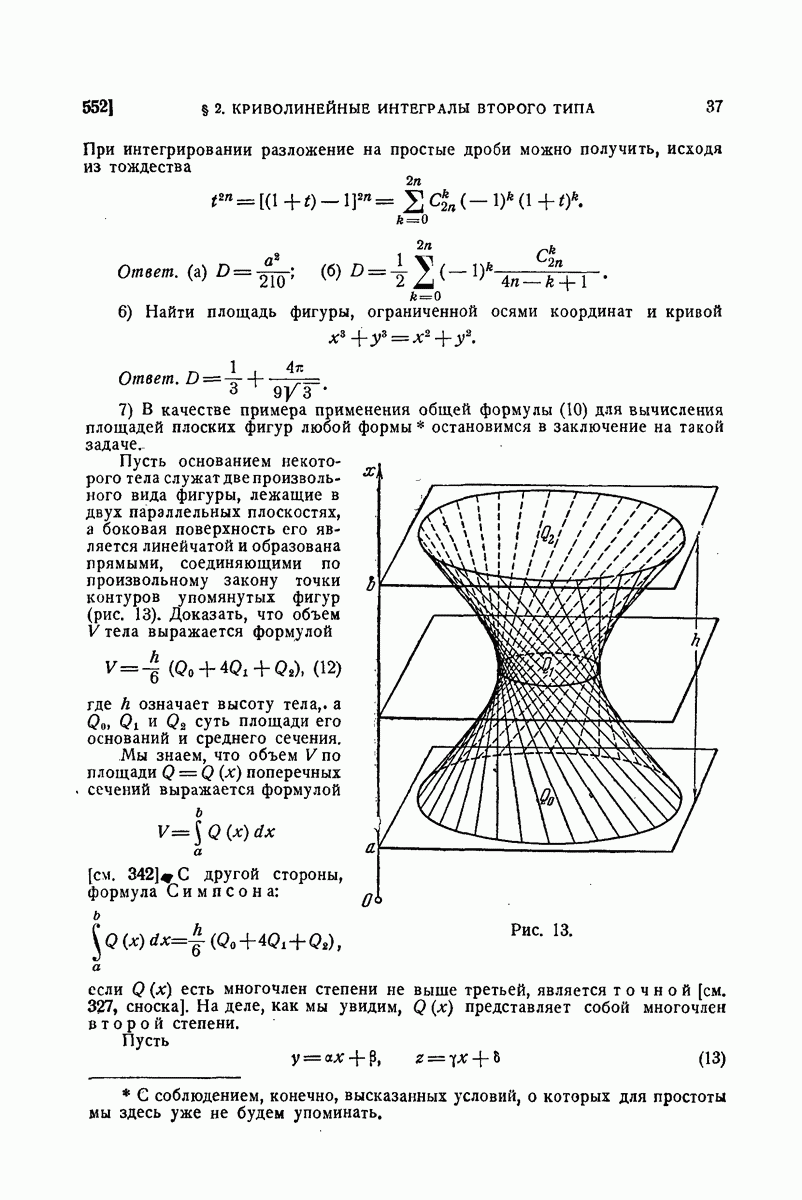
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
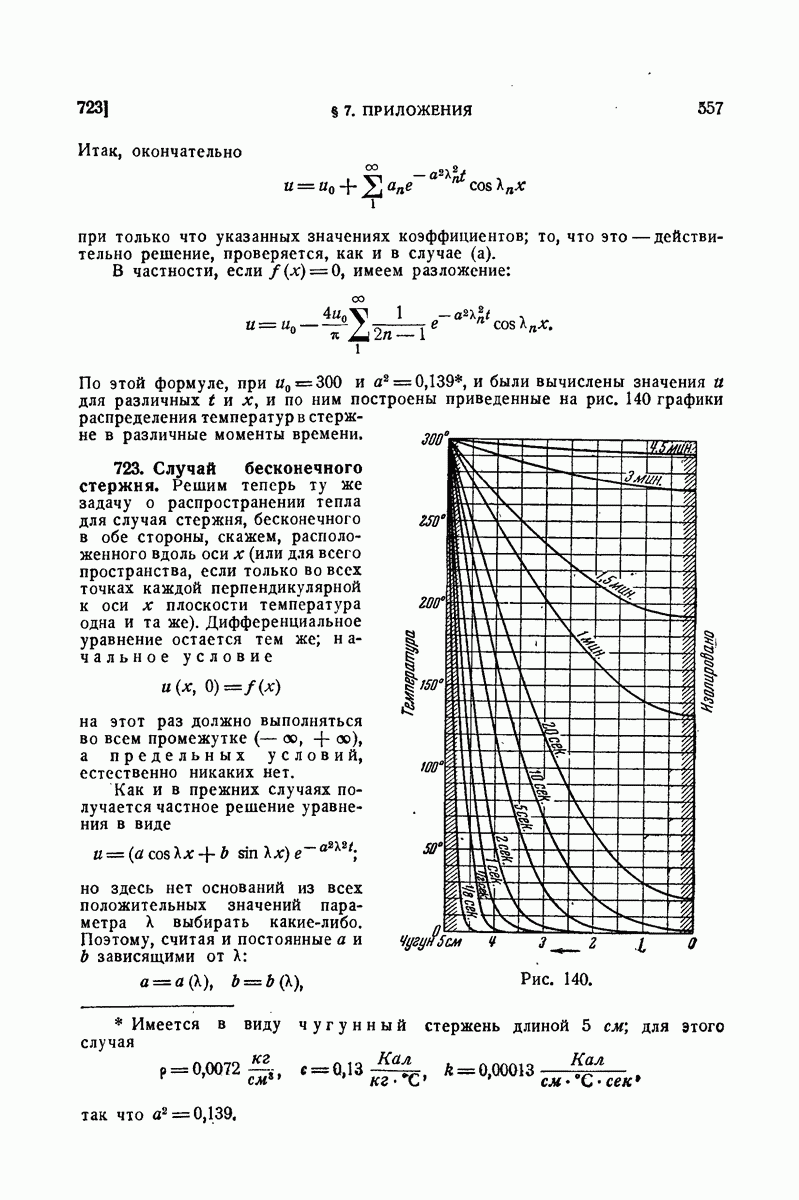
- 552. Примеры.
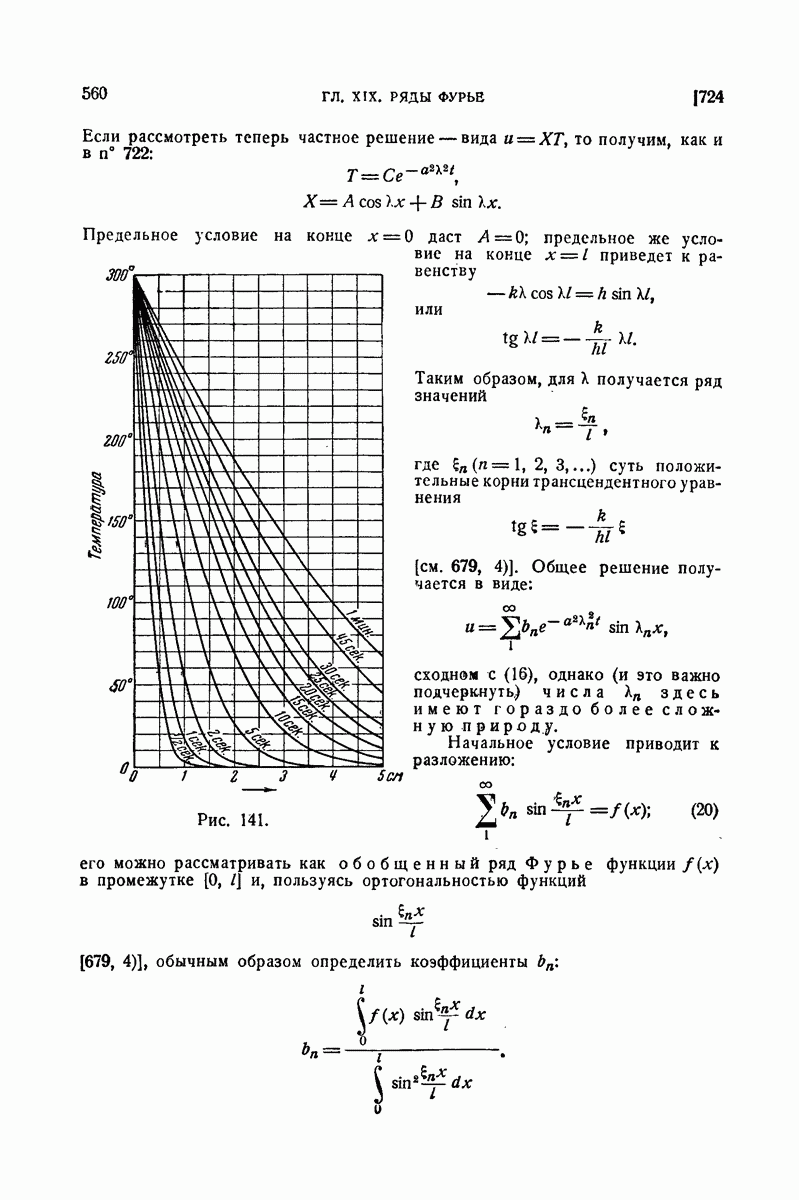
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
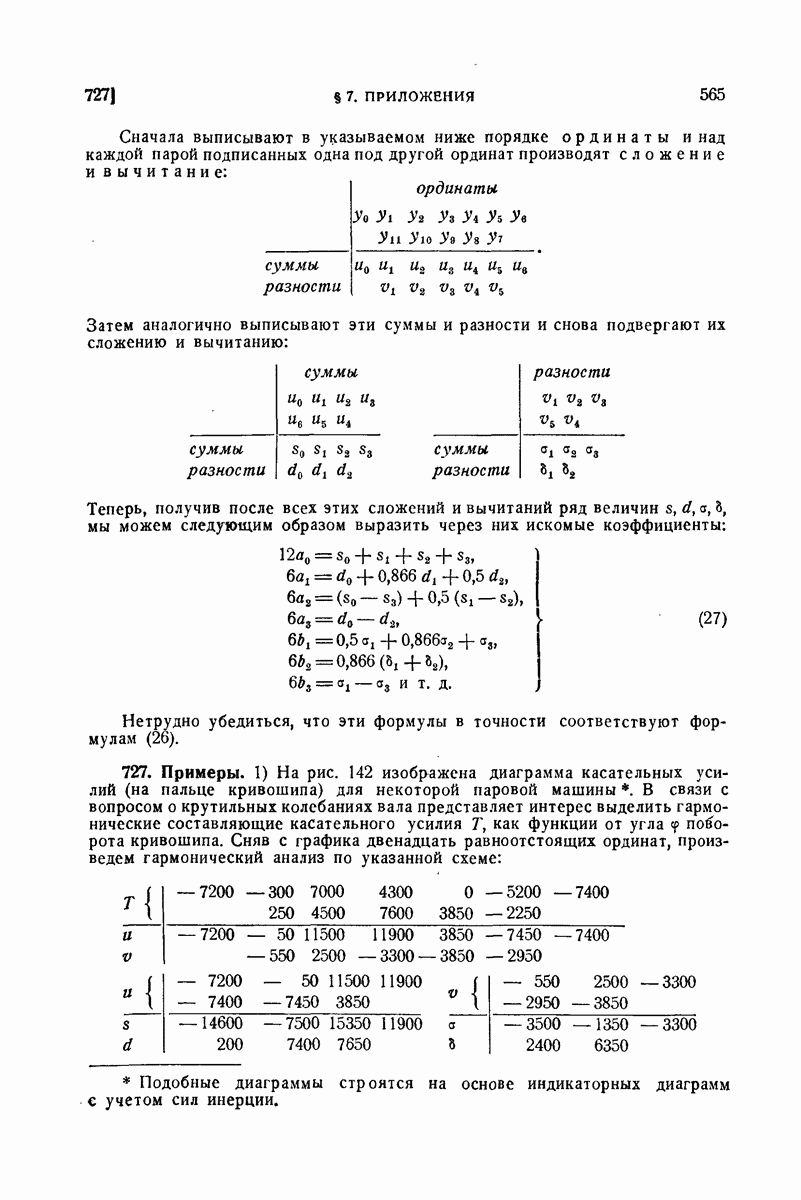
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 552. Примеры.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
- 553. Связь между криволинейными интегралами обоих типов.
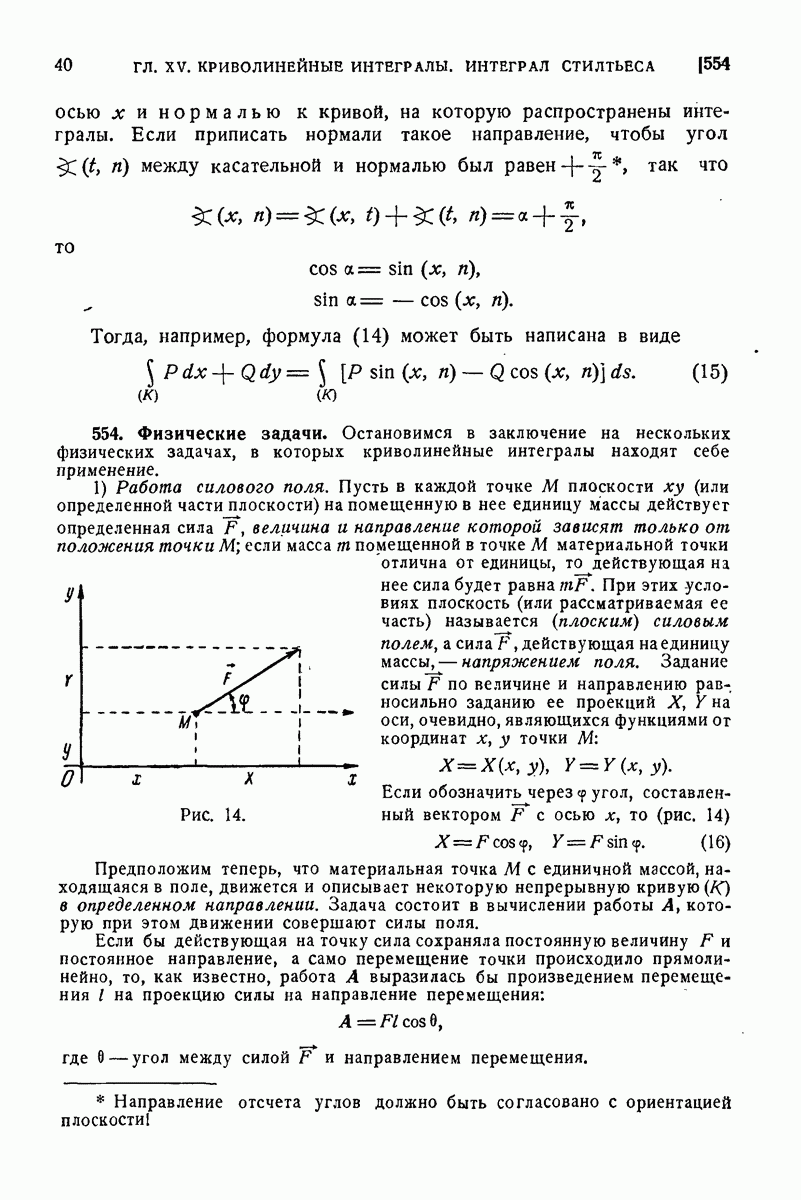
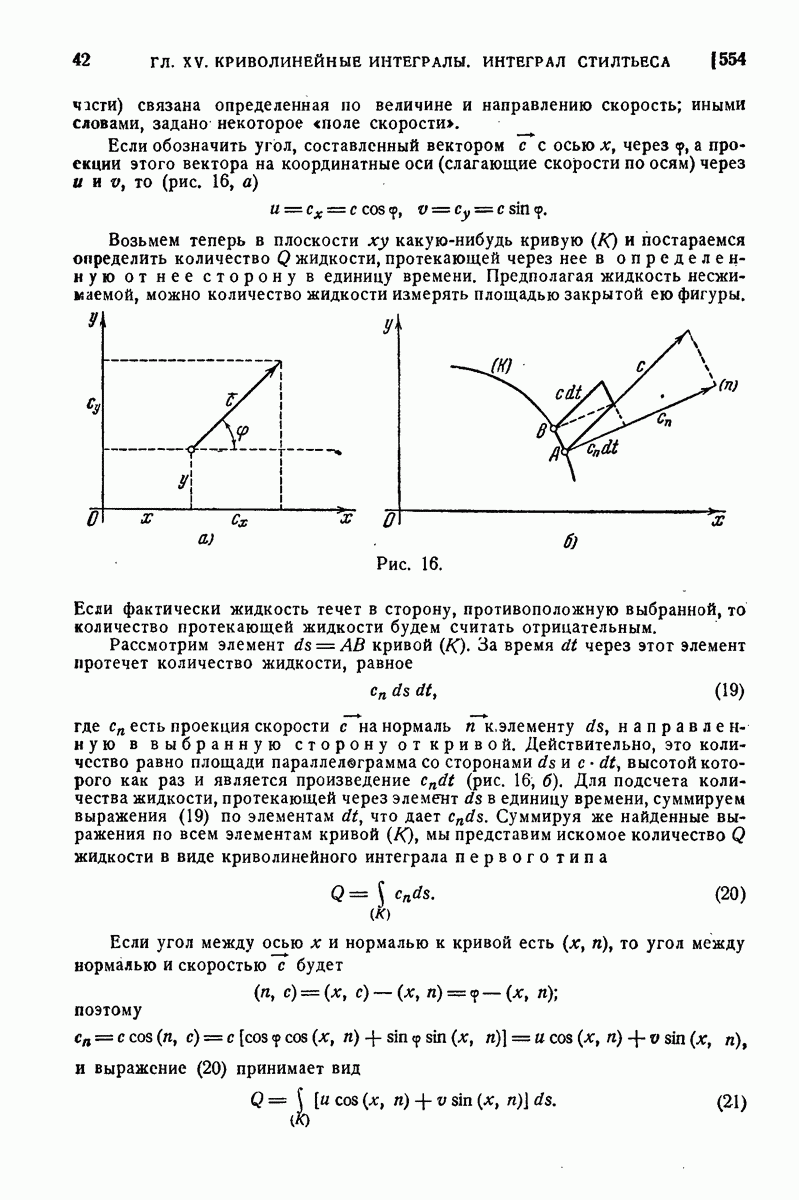
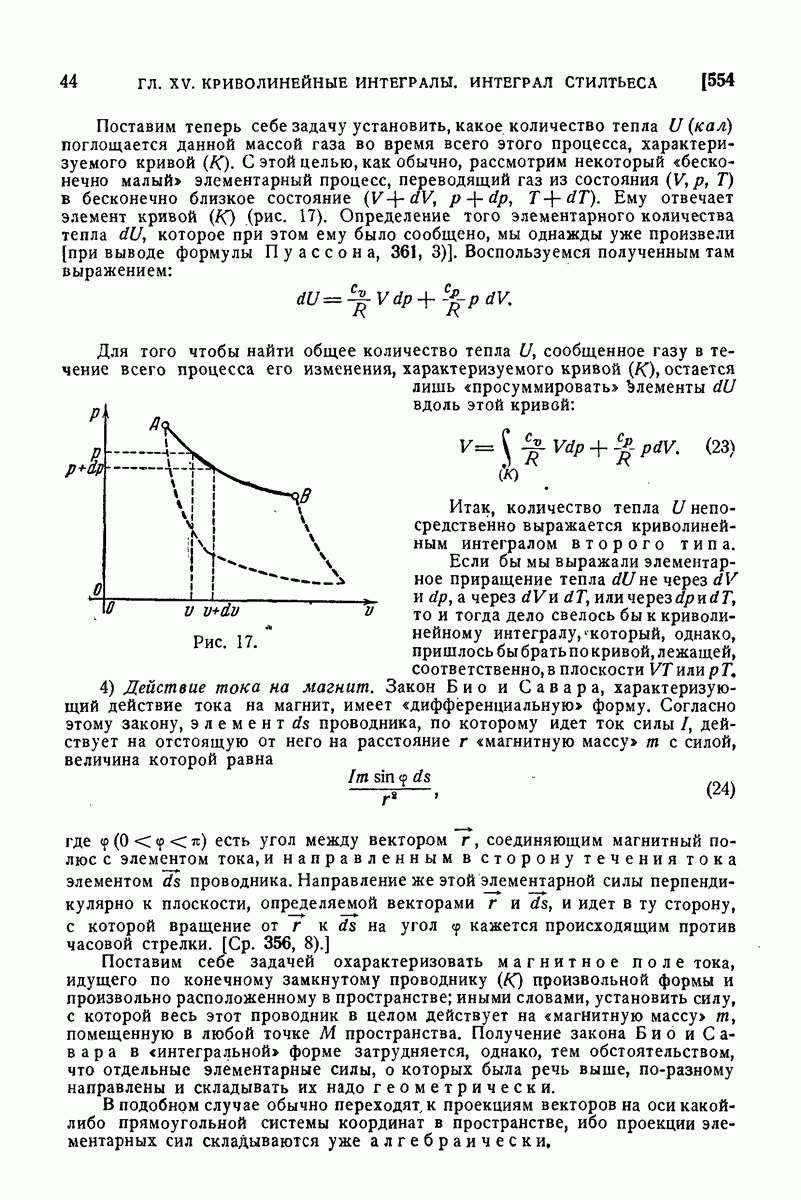
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
- 554. Физические задачи.
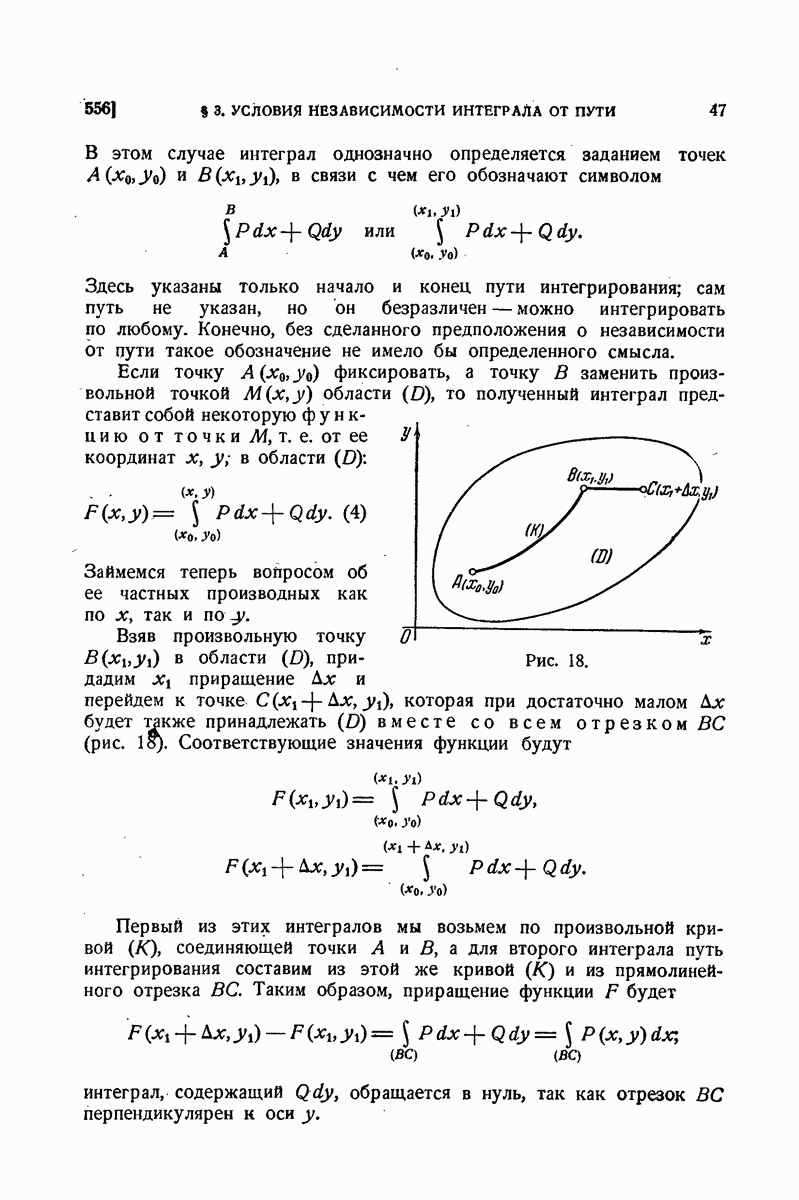
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- § 3. Условия независимости криволинейного интеграла от пути
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 556. Дифференцирование интеграла, не зависящего от пути.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 557. Вычисление криволинейного интеграла через первообразную.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 558. Признак точного дифференциала и нахождение первообразной в случае прямоугольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 559. Обобщение на случай произвольной области.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 560. Окончательные результаты.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 561. Интегралы по замкнутому контуру.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 562. Случай неодносвязной области или наличия особых точек.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 563. Интеграл Гаусса.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 564. Трехмерный случай.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 565. Примеры.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- 566. Приложение к физическим задачам.
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- § 4. Функции с ограниченным изменением
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 568. Классы функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 569. Свойства функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 570. Критерии для функций с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 571. Непрерывные функции с ограниченным изменением.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- 572. Спрямляемые кривые.
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- § 5. Интеграл Стилтьеса
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 574. Общие условия существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 575. Классы случаев существования интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 576. Свойства интеграла Стилтьеса.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 577. Интегрирование по частям.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 578. Приведение интеграла Стилтьеса к интегралу Римана.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 579. Вычисление интегралов Стилтьеса.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 580. Примеры.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 581. Геометрическая иллюстрация интеграла Стилтьеса.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 582. Теорема о среднем, оценки.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 583. Предельный переход под знаком интеграла Стилтьеса.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 584. Примеры и дополнения.
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- 585. Сведение криволинейного интеграла второго типа к интегралу Стилтьеса.
- ГЛАВА ШЕСТНАДЦАТАЯ. ДВОЙНЫЕ ИНТЕГРАЛЫ
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- § 1. Определение и простейшие свойства двойного интеграла
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 587. Сведение двойного интеграла к повторному.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 588. Определение двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 589. Условия существования двойного интеграла.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 590. Классы интегрируемых функций.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 591. Нижний и верхний интегралы, как пределы.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 592. Свойства интегрируемых функций и двойных интегралов.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- 593. Интеграл как аддитивная функция области; дифференцирование по области.
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- § 2. Вычисление двойного интеграла
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 595. Примеры.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 596. Приведение двойного интеграла к повторному в случае криволинейной области.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 597. Примеры.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 598. Механические приложения.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- 599. Примеры.
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- § 3. Формула Грина
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 601. Приложение формулы Грина к исследованию криволинейных интегралов.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- 602. Примеры и дополнения.
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- § 4. Замена переменных в двойном интеграле
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 604. Примеры.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 605. Выражение площади в криволинейных координатах.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 606. Дополнительные замечания.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 607. Геометрический вывод.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 608. Примеры.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 609. Замена переменных в двойных интегралах.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 610. Аналогия с простым интегралом. Интеграл по ориентированной области.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- 611. Примеры.
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- § 5. Несобственные двойные интегралы
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 613. Теорема об абсолютной сходимости несобственного двойного интеграла.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 614. Приведение двойного интеграла к повторному.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 615. Интегралы от неограниченных функций.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 616. Замена переменных в несобственных интегралах.
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 617. Примеры.
- ГЛАВА СЕМНАДЦАТАЯ. ПЛОЩАДЬ ПОВЕРХНОСТИ. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- § 1. Двусторонние поверхности
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 619. Примеры.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 620. Ориентация поверхностей и пространства.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 621. Выбор знака в формулах для направляющих косинусов нормали.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- 622. Случай кусочно-гладкой поверхности.
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- § 2. Площадь кривой поверхности
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 624. Определение площади кривой поверхности.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 625. Замечание.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 626. Существование площади поверхности и ее вычисление.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 627. Подход через вписанные многогранные поверхности.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 628. Особые случаи определения площади.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- 629. Примеры.
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- § 3. Поверхностные интегралы первого типа
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 631. Сведение к обыкновенному двойному интегралу.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 632. Механические приложения поверхностных интегралов первого типа.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- 633. Примеры.
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- § 4. Поверхностные интегралы второго типа
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 635. Простейшие частные случаи.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 636. Общий случай.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 637. Деталь доказательства.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 638. Выражение объема тела поверхностным интегралом.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 639. Формула Стокса.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 640. Примеры.
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- 641. Приложение формулы Стокса к исследованию криволинейных интегралов в пространстве.
- ГЛАВА ВОСЕМНАДЦАТАЯ. ТРОЙНЫЕ И МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- § 1. Тройной интеграл и его вычисление
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 643. Тройной интеграл и условия его существования.
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 644. Свойства интегрируемых функций и тройных интегралов
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 645. Вычисление тройного интеграла, распространенного на параллелепипед.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 646. Вычисление тройного интеграла по любой области.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 647. Несобственные тройные интегралы.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 648. Примеры.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 649. Механические приложения.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- 650. Примеры.
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- § 2. Формула Гаусса — Остроградского
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 652. Приложение формулы Остроградского к исследованию поверхностных интегралов.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 653. Интеграл Гаусса.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- 654. Примеры.
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- § 3. Замена переменных в тройных интегралах
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 656. Примеры.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 657. Выражение объема в криволинейных координатах.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 658. Дополнительные замечания.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 659. Геометрический вывод.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 660. Примеры.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 661. Замена переменных в тройных интегралах.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 662. Примеры.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- 663. Притяжение со стороны тела и потенциал на внутреннюю точку.
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- § 4. Элементы векторного анализа
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 665. Скалярное и векторное поля.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 666. Градиент.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 667. Поток вектора через поверхность.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 668. Формула Остроградского. Дивергенция.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 670. Специальные поля.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 671. Обратная задача векторного анализа.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- 672. Приложения.
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- § 5. Многократные интегралы
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 674. Объем n-мерного тела, n-кратный интеграл.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 675. Замена переменных в n-кратном интеграле.
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 676. Примеры.
- ГЛАВА ДЕВЯТНАДЦАТАЯ. РЯДЫ ФУРЬЕ
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 677. Периодические величины и гармонический анализ.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 678. Определение коэффициентов по методу Эйлера — Фурье.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 679. Ортогональные системы функций.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- 680. Тригонометрическое интерполирование.
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- § 2. Разложение функций в ряд Фурье
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 682. Первая основная лемма.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 683. Принцип локализации.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 684. Признаки Дин и и Липшица сходимости рядов Фурье.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 685. Вторая основная лемма.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 686. Признак Дирихле — Жордана.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 687. Случай непериодической функции.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 688. Случай произвольного промежутка.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 689. Разложения только по косинусам или только по синусам.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 690. Примеры.
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- 691. Разложение ln Г(x).
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- § 3. Дополнения
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 693. Суммирование тригонометрических рядов с помощью аналитических функций комплексной переменной.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 694. Примеры.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 695. Комплексная форма рядов Фурье.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 696. Сопряженный ряд.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- 697. Кратные ряды Фурье.
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- § 4. Характер сходимости рядов Фурье
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 699. Признаки равномерной сходимости рядов Фурье.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 700. Поведение ряда Фурье вблизи точки разрыва; частный случай.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 701. Случай произвольной функции.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 702. Особенности рядов Фурье; предварительные замечания.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- 703. Построение особенностей.
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- § 5. Оценка остатка в зависимости от дифференциальных свойств функции
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 705. Оценка частичной суммы в случае ограниченной функции.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 706. Оценка остатка в случае функции с ограниченной k-й производной.
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 707. Случай функции, имеющей k-ю производную с ограниченным изменением
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 708. Влияние разрывов функции и ее производных на порядок малости коэффициентов Фурье.
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 709. Случай функции, заданной в промежутке
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- 710. Метод выделения особенностей.
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- § 6. Интеграл Фурье
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 712. Предварительные замечания.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 713. Достаточные признаки.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 714. Видоизменение основного предположения.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 715. Различные виды формулы Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 716. Преобразование Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 717. Некоторые свойства преобразований Фурье.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 718. Примеры и дополнения.
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 719. Случай функции двух переменных.
- § 7. Приложения
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 720. Выражение эксцентрической аномалии планеты через ее среднюю аномалию.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 721. Задача о колебании струны.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 722. Задача о распространении тепла в конечном стержне.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 723. Случай бесконечного стержня.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 724. Видоизменение предельных условий.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 725. Распространение тепла в круглой пластине.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 726. Практический гармонический анализ.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 727. Примеры.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 728. Схема для двадцати четырех ординат.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 729. Примеры.
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- 730. Сопоставление приближенных и точных значений коэффициентов Фурье.
- ГЛАВА ДВАДЦАТАЯ. РЯДЫ ФУРЬЕ (продолжение)
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- § 1. Операции над рядами Фурье. Полнота и замкнутость
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 732. Почленное дифференцирование ряда Фурье.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 733. Полнота тригонометрической системы.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 734. Равномерная аппроксимация функций.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 735. Аппроксимация функций в среднем. Экстремальные свойства отрезков ряда Фурье.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 736. Замкнутость тригонометрической системы. Теорема Ляпунова.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 737. Обобщенное уравнение замкнутости.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 738. Умножение рядов Фурье.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- 739. Некоторые приложения уравнения замкнутости.
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- § 2. Применение методов обобщенного суммирования к рядам Фурье
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 741. Суммирование рядов Фурье по методу Пуассона—Абеля.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 742. Решение задачи Дирихле для круга.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 743. Суммирование рядов Фурье по методу Чезаро — Фейера.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 744. Некоторые приложения обобщенного суммирования рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- 745. Почленное дифференцирование рядов Фурье.
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- § 3. Единственность тригонометрического разложения функции
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 747. Риманов метод суммирования тригонометрических рядов.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 748. Лемма о коэффициентах сходящегося ряда.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 749. Единственность тригонометрического разложения.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 750. Заключительные теоремы о рядах Фурье.
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 751. Обобщение.
- ДОПОЛНЕНИЕ. ОБЩАЯ ТОЧКА ЗРЕНИЯ НА ПРЕДЕЛ
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 752. Различные виды пределов, встречающиеся в анализе.
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 753. Упорядоченные множества (в собственном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 754. Упорядоченные множества (в обобщенном смысле).
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 755. Упорядоченная переменная и ее предел.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 756. Примеры.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 757. Замечание о пределе функции.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 758. Распространение теории пределов.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 759. Одинаково упорядоченные переменные.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 760. Упорядочение с помощью числового параметра.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 761. Сведение к варианте.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.
- 762. Наибольший и наименьший пределы упорядоченной переменной.