| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава V. ЛАГРАНЖЕВЫ КООРДИНАТЫ
§ 5.1. Выбор лагранжевых координат.
До сих пор мы пользовались декартовыми координатами. В дальнейшем мы не будем себя связывать ограничениями в выборе системы координат и перейдем к координатам более общего типа. Введение таких координат может быть сопряжено с известными трудностями, однако это — трудности скорее алгебраического характера, чем динамического. Нужно отличать трудности, присущие самому изучаемому явлению, от трудностей, связанных с выбранной системой координат.
Выбор лагранжевых координат производится следующим образом. Выбираются  параметров
параметров  значения которых определяют конфигурацию системы в момент времени t. Декартовы координаты
значения которых определяют конфигурацию системы в момент времени t. Декартовы координаты  точек системы будут некоторыми функциями от
точек системы будут некоторыми функциями от  (В большей части случаев координаты х являются функциями только от
(В большей части случаев координаты х являются функциями только от  и не зависят от t.) Выбор координат
и не зависят от t.) Выбор координат  должен быть произведен таким образом, чтобы их значения представляли все возможные конфигурации системы, а не некоторую совокупность возможных конфигураций.
должен быть произведен таким образом, чтобы их значения представляли все возможные конфигурации системы, а не некоторую совокупность возможных конфигураций.
Как мы увидим, для голономной системы число  можно взять равным числу степеней свободы k. Для неголономной системы наименьшее значение
можно взять равным числу степеней свободы k. Для неголономной системы наименьшее значение  равно к
равно к  где I есть инвариант системы, определяемый уравнениями связи.
где I есть инвариант системы, определяемый уравнениями связи.
В дальнейшем (§§ 5.7 и 5.8) будет указана формальная процедура перехода от декартовых координат к лагранжевым. Однако в ряде задач выбор лагранжевых координат напрашивается сам, и потому нет необходимости обращаться к формальным методам, развитым для общей механической системы.
Ниже приводятся несколько примеров.
1) Простой маятник. Тяжелая точка движется без трения по окружности в вертикальной плоскости. Такое движение можно осуществить, например, заставив бусинку скользить по гладкой проволоке, изогнутой в форме окружности радиуса а. Или же можно частицу соединить с концом невесомого стержня длины а, другой конец которого шарнирно закреплен в точке О, так что стержень может свободно качаться в вертикальной плоскости около этой точки. Положение частицы на окружности будет определяться углом  отсчитываемым от наинизшей точки окружности. Декартовы координаты частицы х, у будут связаны с лагранжевой координатой
отсчитываемым от наинизшей точки окружности. Декартовы координаты частицы х, у будут связаны с лагранжевой координатой  формулами
формулами

Ось  здесь горизонтальна, а ось
здесь горизонтальна, а ось  направлена вертикально вниз.
направлена вертикально вниз.
2) Центральная орбита. Частица совершает плоское движение под действием силы, все время направленной в начало координат О. В качестве лагранжевых координат возьмем полярные координаты  Декартовы координаты х, у будут связаны с лагранжевыми координатами формулами
Декартовы координаты х, у будут связаны с лагранжевыми координатами формулами

3) Сферический маятник. Материальная точка  скользит под действием силы тяжести по гладкой поверхности сферы радиуса а с центром в точке О. В качестве лагранжевых координат выберем полярные углы
скользит под действием силы тяжести по гладкой поверхности сферы радиуса а с центром в точке О. В качестве лагранжевых координат выберем полярные углы  где
где  угол между вектором
угол между вектором  и направленной вверх вертикальной осью
и направленной вверх вертикальной осью  азимутальный угол между плоскостью
азимутальный угол между плоскостью  и координатной плоскостью
и координатной плоскостью  . В данном случае
. В данном случае

4) Твердая пластинка, движущаяся в своей плоскости. В качестве лагранжевых координат возьмем координаты
1] центра тяжести (центра масс)  пластинки относительно неподвижной системы отсчета и угол 6, образуемый прямой
пластинки относительно неподвижной системы отсчета и угол 6, образуемый прямой  проведенной на пластинке, с неподвижной осью
проведенной на пластинке, с неподвижной осью  Если
Если  координаты некоторой точки пластинки в системе
координаты некоторой точки пластинки в системе  связанной с самой пластинкой, то будем иметь
связанной с самой пластинкой, то будем иметь

5) Твердое тело, движущееся в пространстве. Система является голономной с шестью степенями свободы. В качестве лагранжевых координат можно выбрать координаты  центра тяжести
центра тяжести  относительно неподвижной системы
относительно неподвижной системы  и три угла
и три угла  , определяющие ориентацию тела.
, определяющие ориентацию тела.
Возьмем прямоугольный триэдр  связанный с телом (обычно в качестве осей
связанный с телом (обычно в качестве осей  выбирают главные оси инерции тела в точке
выбирают главные оси инерции тела в точке  и матрицу направляющих косинусов I
и матрицу направляющих косинусов I

Элементами первой строки этой матрицы служат направляющие косинусы оси  по отношению к осям системы
по отношению к осям системы  элементами второй строки — направляющие косинусы оси
элементами второй строки — направляющие косинусы оси  и элементами третьей строки — направляющие косинусы оси
и элементами третьей строки — направляющие косинусы оси  Элементы матрицы I являются известными функциями от углов
Элементы матрицы I являются известными функциями от углов  явные выражения для этих функций будут приведены позже (§ 7.11) для двух способов выбора углов
явные выражения для этих функций будут приведены позже (§ 7.11) для двух способов выбора углов  Для точки с координатами
Для точки с координатами  с в системе
с в системе  справедливы формулы
справедливы формулы

Их можно записать в матричной форме;

Здесь  вектор
вектор  -вектор
-вектор  а — вектор
а — вектор  матрица, полученная из I транспонированием.
матрица, полученная из I транспонированием.
В ряде случаев триэдр  связанный с телом, удобней обозначать через
связанный с телом, удобней обозначать через  а матрицу I записывать в виде
а матрицу I записывать в виде

6) В предыдущих примерах мы имели голономные системы и число  лаграижевых координат равнялось числу к степеней свободы механической системы. В заключение приведем простой пример неголономной системы.
лаграижевых координат равнялось числу к степеней свободы механической системы. В заключение приведем простой пример неголономной системы.
Стержень совершает плоское движение. Наложенная идеальная связь такова, что точка  может двигаться только вдоль направления
может двигаться только вдоль направления  (см. § 2.1). В качестве лагранжевых координат выберем координаты
(см. § 2.1). В качестве лагранжевых координат выберем координаты  точки
точки  по отношению к неподвижным осям
по отношению к неподвижным осям  и угол 9 наклона отрезка
и угол 9 наклона отрезка  к оси
к оси  Возможные перемещения удовлетворяют уравнению (см.
Возможные перемещения удовлетворяют уравнению (см. 

Это уравнение не допускает интегрирующего множителя. Система имеет две степени свободы  но число лагранжевых координат равно трем
но число лагранжевых координат равно трем  Декартовы координаты точки, находящейся на стержне на расстоянии а от точки
Декартовы координаты точки, находящейся на стержне на расстоянии а от точки  выражаются формулами
выражаются формулами

Несмотря на то, что система имеет лишь две степени свободы, множество достижимых конфигураций является трехпараметрическим. В самом деле, систему из любого начального положения можно перевести в любое конечное. Это было доказано уже в § 2.1.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1.1. Свободная материальная точка.
- § 1.2. Прямолинейное движение материальной точки в силовом поле.
- § 1.3. Либрационное движение.
- § 1.4. Заданная сила не может быть функцией от ускорения.
- § 1.5. Несвободная материальная точка (случай I).
- § 1.6. Несвободная материальная точка (случай II).
- § 1.7. Несвободная материальная точка (случай III).
- § 1.8. Голономные и неголономные системы.
- Глава II. МЕХАНИЧЕСКИЕ СИСТЕМЫ
- § 2.1. Система двух материальных точек.
- § 2.2. Система материальных точек.
- § 2.3. Катастатическая система.
- § 2.4. Реакции связей.
- § 2.5. К понятию о механической системе.
- Глава III. ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
- § 3.2. Сохранение импульса.
- § 3.3. Катастатическая система и первая форма уравнения энергии.
- § 3.4. Консервативные силы и вторая форма уравнения энергии.
- § 3.5. Третья форма уравнения энергии.
- § 3.6. Сохранение энергии.
- § 3.7. Принцип Гамильтона.
- § 3.8. Варьированный путь.
- § 3.9. Распределенные системы.
- Глава IV. ВТОРАЯ И ТРЕТЬЯ ФОРМЫ ОСНОВНОГО УРАВНЕНИЯ
- § 4.1. Вторая форма основного уравнения.
- § 4.2. Третья форма основного уравнения.
- § 4.3. Принцип Гаусса наименьшего принуждения.
- § 4.4. Приложения принципа Гаусса.
- § 4.5. Физический смысл принципа Гаусса.
- Глава V. ЛАГРАНЖЕВЫ КООРДИНАТЫ
- § 5.2. Некоторые классические задачи.
- § 5.3. Сферический маятник.
- § 5.4. Задача двух тел.
- § 5.5. Уравнение Кеплера.
- § 5.6. Столкновение.
- § 5.7. Лагранжевы координаты для голономной системы.
- § 5.8. Лагранжевы координаты для неголономной системы.
- § 5.9. Качение тела.
- § 5.10. Достижимость.
- § 5.11. Варьированный путь в принципе Гамильтона.
- § 5.12. Обзор полученных результатов.
- Глава VI. УРАВНЕНИЯ ЛАГРАНЖА
- § 6.1. Четвертая форма основного уравнения. Лагранжевы координаты.
- § 6.2. Уравнения Лагранжа.
- § 6.3. Вывод уравнений Лагранжа из принципа Гамильтона.
- § 6.4. Форма уравнений Лагранжа.
- § 6.5. Консервативные системы и другие системы, обладающие потенциальной функцией.
- § 6.6. Функция Лагранжа.
- § 6.7. Интеграл Якоби.
- § 6.8. Явная форма интеграла Якоби.
- § 6.9. Об одной ошибке.
- § 6.11. Циклические координаты.
- § 6.12. Инвариантность уравнений Лагранжа.
- Глава VII. ТЕОРИЯ ПОВОРОТОВ
- § 7.2. Теорема Эйлера.
- § 7.3. Матрица l и вектор Т.
- § 7.4. Обобщение теоремы Эйлера.
- § 7.5. Теорема Шаля.
- § 7.6. Формула поворота.
- § 7.7. Полуобороты и отражения.
- § 7.8. Кватернионная форма записи формулы поворота.
- § 7.9. Сложение вращений.
- § 7.10. Угловая скорость.
- § 7.11. Ориентация твердого тела в пространстве. Углы Эйлера.
- § 7.12. Ориентация твердого тела в пространстве. Углы …
- § 7.13. Повороты около движущихся осей.
- § 7.14. Повороты около неподвижных осей.
- § 7.15. Определение угловой скорости с помощью матриц
- § 7.16. Составляющие вектора угловой скорости.
- Глава VIII. ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
- § 8.1. Дифференциальные уравнения.
- § 8.2. Формулы ускорения в ортогональных координатах.
- § 8.3. Обезьяна и противовес.
- § 8.4. Кинетическая энергия твердого тела.
- § 8.5. Задача о движении в двух измерениях.
- § 8.6. Вращающийся волчок; основные уравнения.
- § 8.7. Вращающийся волчок; другое решение.
- § 8.8. Гироскопические силы.
- § 8.9. Вращающийся волчок; исследование движения.
- § 8.10. Численный пример.
- § 8.11. Стержень во вращающейся плоскости.
- § 8.12. Качение диска.
- Глава IX. ТЕОРИЯ КОЛЕБАНИЙ
- § 9.1. Колебания около положения равновесия.
- § 9.2. Теория преобразования к главным координатам.
- § 9.3. Приложение теории.
- § 9.4. Наложение связи.
- § 9.5. Принцип Релея.
- § 9.6. Устойчивость установившегося движения.
- § 9.7. Колебания в окрестности установившегося движения.
- § 9.8. Гироскоп Фуко.
- § 9.9. Спящий волчок.
- § 9.10. Вынужденные колебания.
- Глава X. ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
- § 10.2. Исключение одной координаты.
- § 10.3. Гироскопическая устойчивость.
- § 10.4. Явное выражение для R в общем случае.
- § 10.5. Вращающийся волчок.
- § 10.6. Линейные члены в функции L.
- § 10.7. Движение относительно подвижной системы отсчета.
- § 10.8. Движение частицы вблизи заданной точки на поверхности Земли.
- § 10.9. Маятник Фуко.
- § 10.10. Движение снаряда.
- § 10.11. Диссипативная функция Релея.
- § 10.12. Гироскопическая система с диссипацией.
- § 10.13. Уравнения Гамильтона.
- § 10.14. Уравнение энергии и явное выражение для Н.
- § 10.15. Главный триэдр.
- Глава XI. ПЕРЕМЕННАЯ МАССА
- § 11.1. Частица переменной массы. Функция Лагранжа.
- § 11.2. Кинетическая энергия.
- § 11.3. Функция Гамильтона.
- § 11.4. Движущийся электрон.
- § 11.2. Кинетическая энергия.
- § 11.5. Электрон в электромагнитном поле.
- Глава XII. УРАВНЕНИЯ ГИББСА-АППЕЛЯ
- § 12.3. Пятая форма основного уравнения.
- § 12.5. Уравнения Гиббса — Аппеля.
- Глава XIII. ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА-АППЕЛЯ
- § 13.2. Аналог теоремы Кёнига.
- § 13.3. Плоское движение.
- § 13.4. Движение твердого тела.
- § 13.5. Шар на вращающейся плоскости.
- § 13.6. Шар на вращающейся наклонной плоскости.
- § 13.7. Качение шара по неподвижной поверхности.
- § 13.8. Вращающийся волчок.
- § 13.9. Качение монеты (тонкого диска).
- § 13.10. Уравнения Эйлера.
- § 13.11. Свободное тело; случай осевой симметрии.
- § 13.12. Свободное тело; общий случай.
- § 13.13. Ориентация свободного тела.
- § 13.14. Теоремы Пуансо и Сильвестра.
- § 13.15. Качение эллипсоида по шероховатой горизонтальной плоскости.
- § 13.16. Устойчивость вращающегося эллипсоида.
- Глава XIV. ТЕОРИЯ УДАРА
- § 14.1. Ударный импульс.
- § 14.2. Импульсные связи.
- § 14.3. Движение системы, на которую действуют ударные импульсы. Основное уравнение теории удара.
- § 14.4. Катастатическая система.
- § 14.5. Принцип наименьшего принуждения в теории удара.
- § 14.6. Катастатическая система. Теорема о суперпозиции.
- § 14.7. Катастатическая система. Шесть теорем об энергии.
- § 14.8. Лагранжевы координаты и квазикоординаты.
- § 14.9. Лагранжева форма уравнений движения в теории удара.
- § 14.10. Другие доказательства теорем об энергии.
- § 14.11. Приложения теории удара.
- § 14.12. Импульсивное движение непрерывных систем.
- Глава XV. ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
- § 15.1. Шестая форма основного уравнения.
- § 15.2. Непосредственные выводы.
- § 15.3. Функция Рауса.
- § 15.4. Теорема …
- § 15.5. Главная функция.
- § 15.6. Примеры использования главной функции.
- § 15.7. Доказательство равенства …
- § 15.8. Свойства главной функции.
- § 15.9. Примеры непосредственного вычисления главной функции.
- Глава XVI. ТЕОРЕМА ГАМИЛЬТОНА—ЯКОБИ
- § 16.1. Уравнение Гамильтона в частных производных.
- § 16.2. Теорема Гамильтона — Якоби (доказательство первое).
- § 16.3. Теорема об эквивалентности.
- § 16.4. Теорема Гамильтона — Якоби (доказательство второе).
- § 16.5. Замечания по теореме Гамильтона — Якоби.
- § 16.6. Однородное поле.
- § 16.7. Гармонический осциллятор.
- § 16.8 Частица в переменном поле At.
- § 16.9. Центральная орбита.
- § 16.10. Сферический маятник.
- § 16.11. Вращающийся волчок.
- § 16.12. Стержень на вращающейся плоскости.
- § 16.13. Электрон в центральном поле.
- § 16.14. Пфаффова форма
- Глава XVII. СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ, ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
- § 17.2. Условия разделимости переменных в системах с двумя степенями свободы.
- § 17.3. Изучение движения системы.
- § 17.4. Классификация траекторий.
- § 17.5. Устойчивость.
- § 17.6. Приложения теории.
- § 17.7. Притяжение к центру по закону …
- § 17.8. Притяжение к центру по закону …
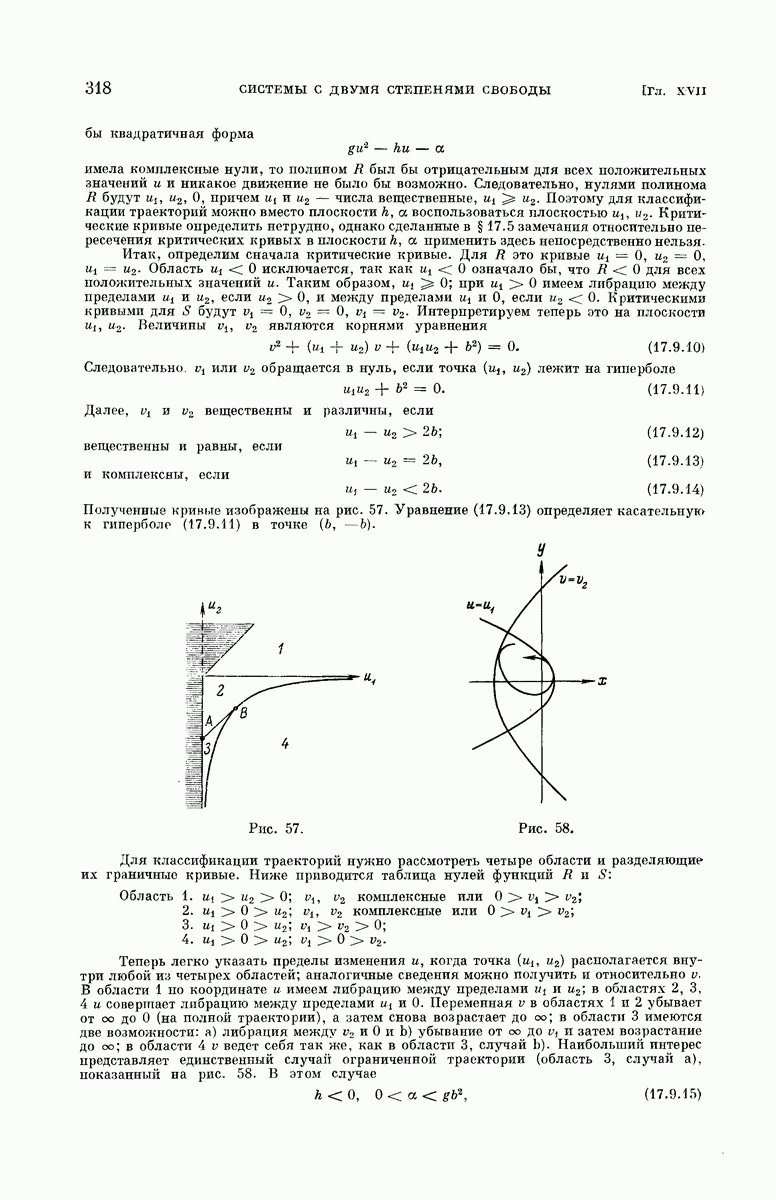
- § 17.9. Ньютоновское притяжение и однородное поле.
- § 17.10. Два неподвижных притягивающих центра
- § 17.11. Ограниченные траектории.
- § 17.12. Уравнения орбит.
- § 17.13. Неограниченные орбиты.
- § 17.14. Системы, допускающие разделение переменных более чем одним способом.
- Глава XVIII. СИСТЕМЫ С n СТЕПЕНЯМИ СВОБОДЫ, ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
- § 18.1. Система Лиувилля
- § 18.2. Теорема Штеккеля.
- § 18.3. Исследование интегралов.
- § 18.4. Дополнительные замечания к теореме Штеккеля.
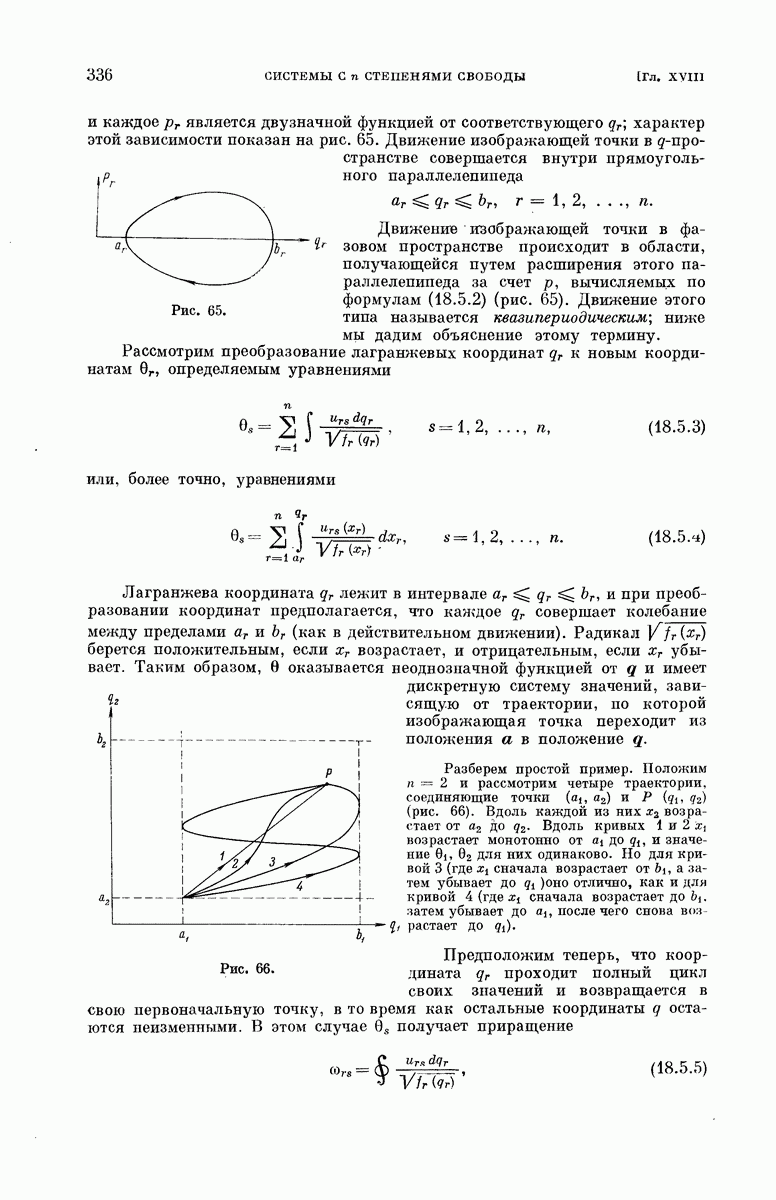
- § 18.5. Квазипериодические движения.
- § 18.6. Угловые переменные.
- § 18.7. Стандартный куб.
- § 18.8. Постоянные …
- § 18.9. Соотношения между q и v.
- § 18.10. Малые колебания.
- § 18.11. Сферический маятник.
- § 18.12. Задача двух тел.
- § 18.13. Интерпретация параметров a и b.
- § 18.14. Выражение r как функции от t.
- § 18.15. Угловые переменные.
- § 18.16. Постоянные …
- § 18.17. Возмущения.
- § 18.18. Неортогональные и ненатуральные разделимые системы.
- Глава XIX. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ, ДВИЖЕНИЕ В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ
- § 19.2. Движение частицы по прямой.
- § 19.3. Система с одной степенью свободы.
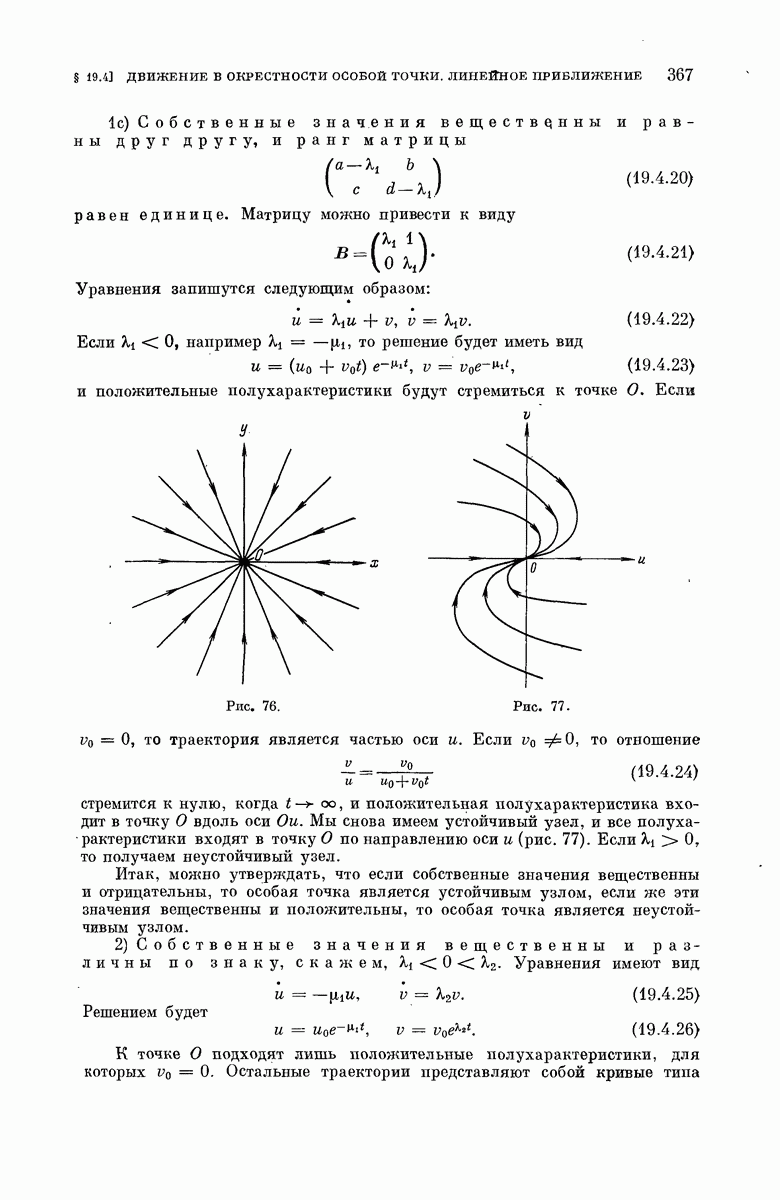
- § 19.4. Движение в окрестности особой точки. Линейное приближение.
- § 19.5. Устойчивость равновесия. Асимптотическая устойчивость и неустойчивость.
- § 19.6. Движение в окрестности особой точки. Общая теория.
- § 19.7. Движение в окрестности узла.
- § 19.8. Движение в окрестности седловой точки.
- § 19.9. Движение в окрестности фокуса.
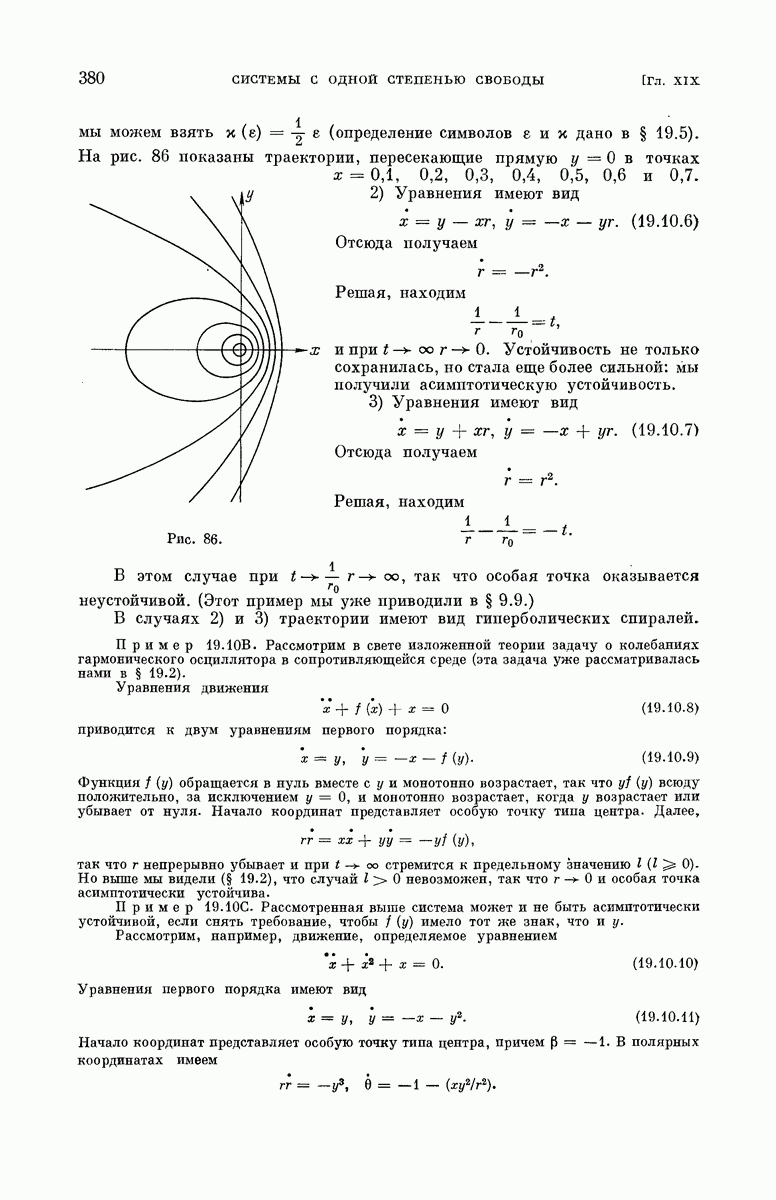
- § 19.10. Движение в окрестности центра.
- § 19.11. Связь линейного приближения с общей теорией.
- Глава XX. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ. ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- § 20.2. Положительное предельное множество.
- § 20.3. Отрезок без контакта.
- § 20.4. Отрезок без контакта, проходящий через точку множества A.
- § 20.5. Структура множества A.
- § 20.6. Теорема Пуанкаре — Бендиксона.
- § 20.7. Приложение к системе частного вида.
- § 20.8. Существование предельного цикла.
- § 20.9. Уравнение Ван-дер-Поля.
- Глава XXI. СИСТЕМЫ С n СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК
- § 21.2. Преобразование к новым координатам.
- § 21.3. Оператор Tt
- § 21.4. Решение в форме степенных рядов.
- § 21.5. Формула для X(x)-X(a)
- § 21.6. Интегральные инварианты.
- § 21.7. Интегральные инварианты порядка m.
- § 21.8. Свойства множителей.
- § 21.9. Последний множитель Якоби.
- § 21.10. Линейная система.
- § 21.11. Устойчивость равновесия.
- § 21.12. Дискретная устойчивость.
- § 21.13. Устойчивость преобразований.
- § 21.14. Приложение к дифференциальным уравнениям.
- § 21.15. Теорема Пуанкаре — Ляпунова.
- § 21.16. Критический случай.
- Глава XXII. УРАВНЕНИЯ ГАМИЛЬТОНА
- § 22.1. Уравнения Гамильтона.
- § 22.2. Скобки Пуассона.
- § 22.3. Теорема Пуассона.
- § 22.4. Использование известного интеграла.
- § 22.5. Линейный интегральный инвариант Пуанкаре.
- § 22.6. Теорема Лиувилля.
- § 22.7. Теорема возвращения (теорема Пуанкаре).
- § 22.8. Примеры инвариантных областей.
- § 22.9. Эргодические теоремы.
- § 22.10. Конкретные примеры.
- § 22.11. Множество …
- § 22.12. Собственные отрезки.
- § 22.13. Доказательство эргодической теоремы; первый этап.
- § 22.14. Доказательство эргодической теоремы; второй этап.
- § 22.15. Метрическая неразложимость.
- § 22.16. Интегралы уравнений движения.
- § 22.17. Следствие теоремы Лиувилля.
- § 22.18. Последний множитель.
- Глава XXIII. ДВИЖЕНИЕ В ОКРЕСТНОСТИ ЗАДАННОГО ДВИЖЕНИЯ. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- § 23.2. Решение уравнений в вариациях.
- § 23.3. Случай постоянных коэффициентов.
- § 23.4. Случай периодических коэффициентов.
- § 23.5. Нулевые показатели.
- § 23.6. Уравнения в вариациях для системы Гамильтона.
- § 23.7. Устойчивость траекторий (1).
- § 23.8. Устойчивость траекторий (2).
- § 23.9. Устойчивость периодических орбит.
- § 23.10. Вынужденные колебания.
- Глава XXIV. КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ
- § 24.1. Контактные преобразования.
- § 24.2. Формулы контактного преобразования.
- § 24.3. Другие формулы.
- § 24.4. Обобщенное точечное преобразование и другие однородные контактные преобразования.
- § 24.5. Специальная форма уравнений преобразований. Бесконечно малые контактные преобразования.
- § 24.6. Обобщение теоремы Лиувилля.
- § 24.7. Условия контактности преобразования, скобки Лагранжа.
- § 24.8. Соотношения между двумя системами производных.
- § 24.9. Условия контактности преобразования, выраженные с помощью скобок Пуассона.
- § 24.10. Соотношения между скобками Лагранжа и скобками Пуассона.
- § 24.11. Приложение к контактному преобразованию.
- § 24.12. Инвариантность скобки Пуассона.
- § 24.13. Другая форма условий контактности преобразования.
- § 24.14. Функции, находящиеся в инволюции.
- § 24.15. Некоторые примеры.
- Глава XXV. ТЕОРИЯ ПРЕОБРАЗОВАНИЙ
- § 25.1. Уравнения движения после контактных преобразований.
- § 25.2. Вариация элементов траектории.
- § 25.3. Вариация эллиптических элементов.
- § 25.4. Другие доказательства теоремы Якоби.
- § 25.5. Постоянство скобок Лагранжа.
- § 25.6. Бесконечно малые контактные преобразования.
- § 25.7. Интегралы в инволюции.
- § 25.8. Теорема Ли о системах в инволюции.
- § 25.9. Интегралы, линейные относительно импульсов.
- § 25.10. Случай, когда функция Гамильтона является однородной квадратичной формой
- Глава XXVI. ВАРИАЦИОННЫЕ ПРИНЦИПЫ
- § 26.2. Теорема Ливенса.
- § 26.3. Точки минимума и седловые точки.
- § 26.4. Асинхронное варьирование. Принцип Гёльдера.
- § 26.5. Принцип Фосса.
- § 26.6. Обобщение принципа Гамильтона.
- § 26.7. Замена независимой переменной.
- § 26.8. Нормальная форма системы с двумя степенями свободы.
- § 26.9. Система Лиувилля.
- § 26.10. Конформные преобразования.
- Глава XXVII. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
- § 27.3. Принцип наименьшего действия в форме Якоби.
- § 27.4. Теорема Уиттекера.
- § 27.5. Исключение координат.
- § 27.6. Характеристическая функция.
- § 27.7. Пространство конфигураций.
- § 27.8. Система с двумя степенями свободы.
- § 27.9. Теорема Кельвина.
- § 27.10. Однородное поле.
- § 27.11. Задача Тэта. Непосредственное решение.
- § 27.12. Задача Тэта. Теория огибающих.
- Глава XXVIII. ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 28.2. Ограниченная задача. Уравнения движения.
- § 28.3. Положения равновесия.
- § 28.4. Положения равновесия на прямой АВ.
- § 28.5. Положения равновесия, не лежащие на прямой АВ
- § 28.6. Поверхность z=U.
- § 28.7. Движение вблизи положения равновесия.
- § 28.8. Теория движения Луны.
- Глава XXIX. ЗАДАЧА ТРЕХ ТЕЛ
- § 29.2. Случай, когда вектор момента количеств движения равен нулю.
- § 29.3. Три точки Лагранжа.
- § 29.4. Решения, для которых треугольник Лагранжа сохраняет свою форму.
- § 29.5. Случай плоского движения.
- § 29.6. Координаты относительно частицы Az
- § 29.7. Движение в окрестности равновесного решения.
- § 29.8. Сведение к системе шести уравнений.
- § 29.9. Устойчивость трех точек Лагранжа.
- § 29.10. Преобразованная форма уравнений движения.
- § 29.11. Другой подход к задаче трех точек Лагранжа.
- § 29.12. Сведение к системе восьми уравнений.
- § 29.13. Невозможность тройных столкновений.
- § 29.14. Плоское движение. Другой способ приведения к системе шестого порядка.
- § 29.15. Равновесные решения.
- Глава XXX. ПЕРИОДИЧЕСКИЕ ОРБИТЫ
- § 30.1. Периодические орбиты.
- § 30.3. Условия вещественности.
- § 30.4. Уравнения Гамильтона.
- § 30.5. Сходимость.
- § 30.6. Три точки Лагранжа.
- § 30.7. Системы, содержащие параметр.
- § 30.8. Приложение к ограниченной задаче трех тел.
- § 30.9. Метод неподвижной точки.
- § 30.11. Периодические орбиты и теорема о кольце.
- § 30.12. Доказательство теоремы Пуанкаре о кольце.