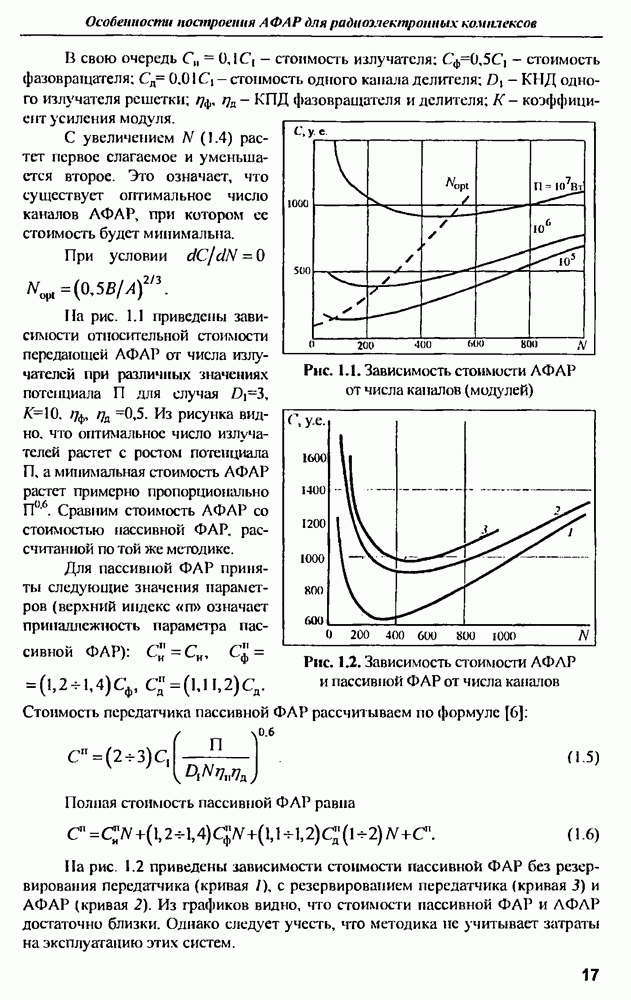
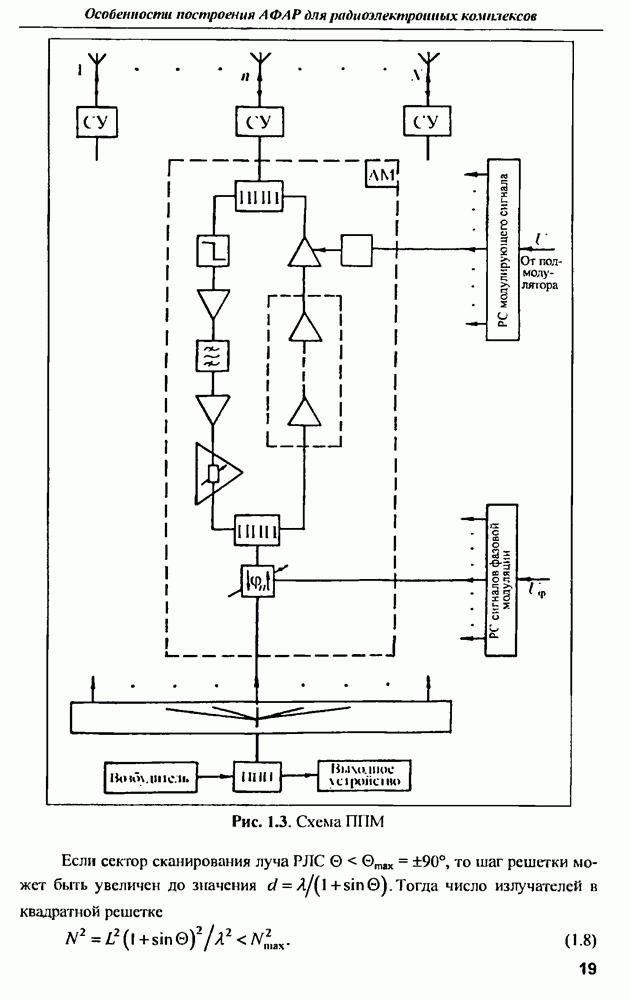
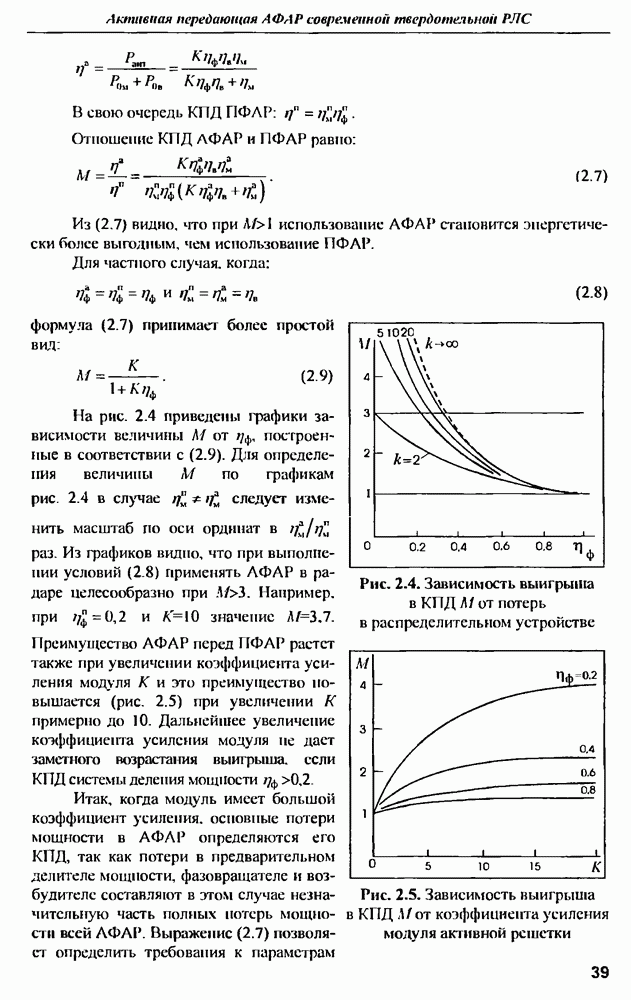
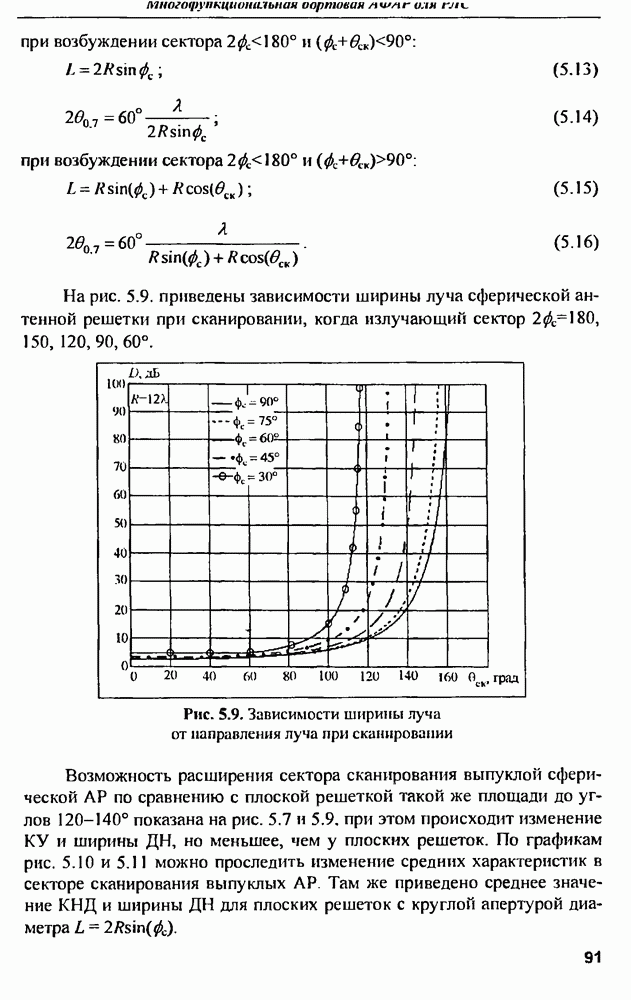
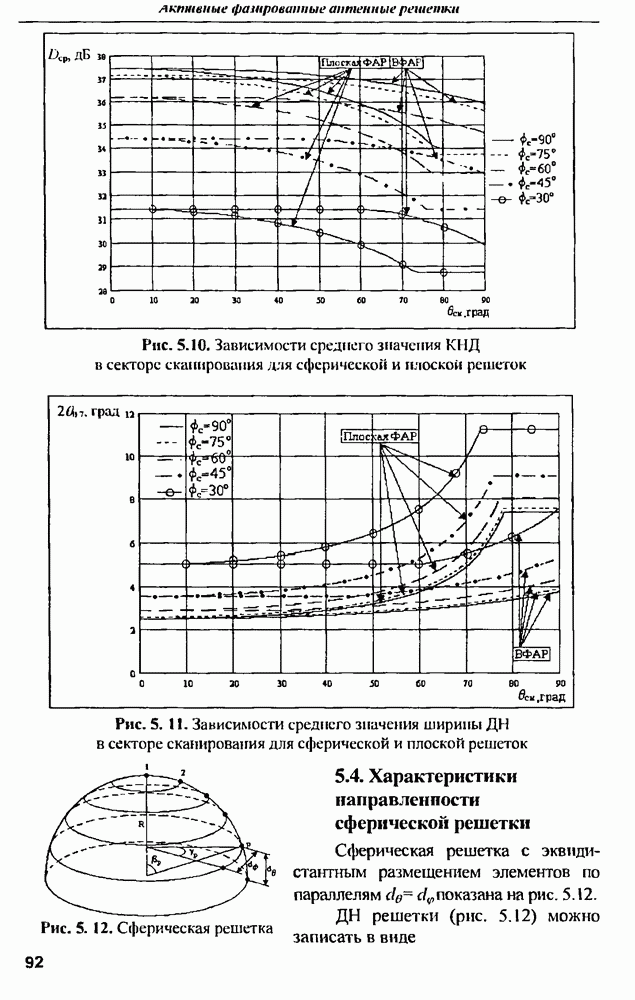
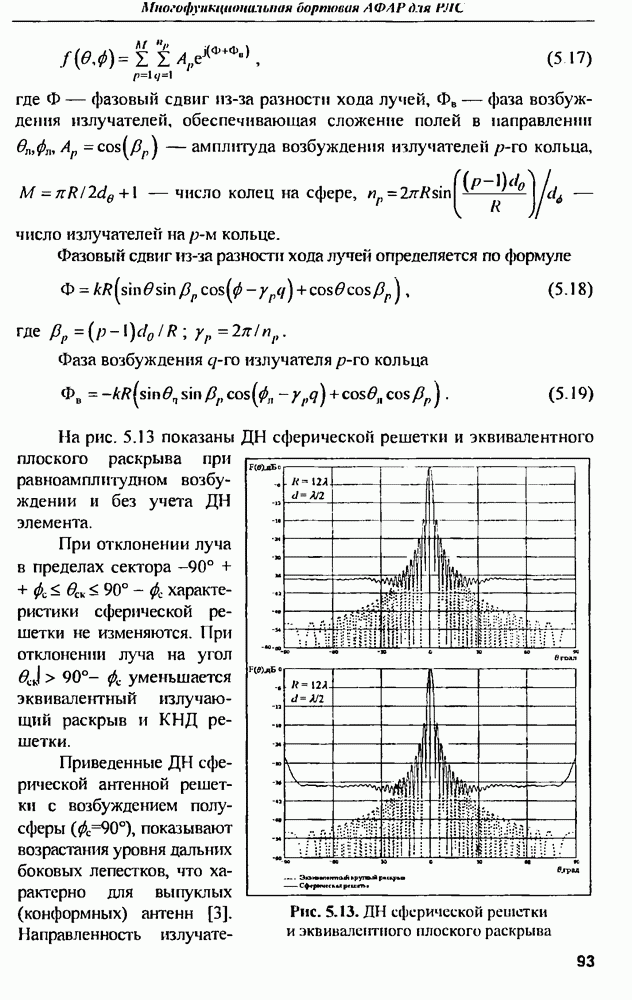
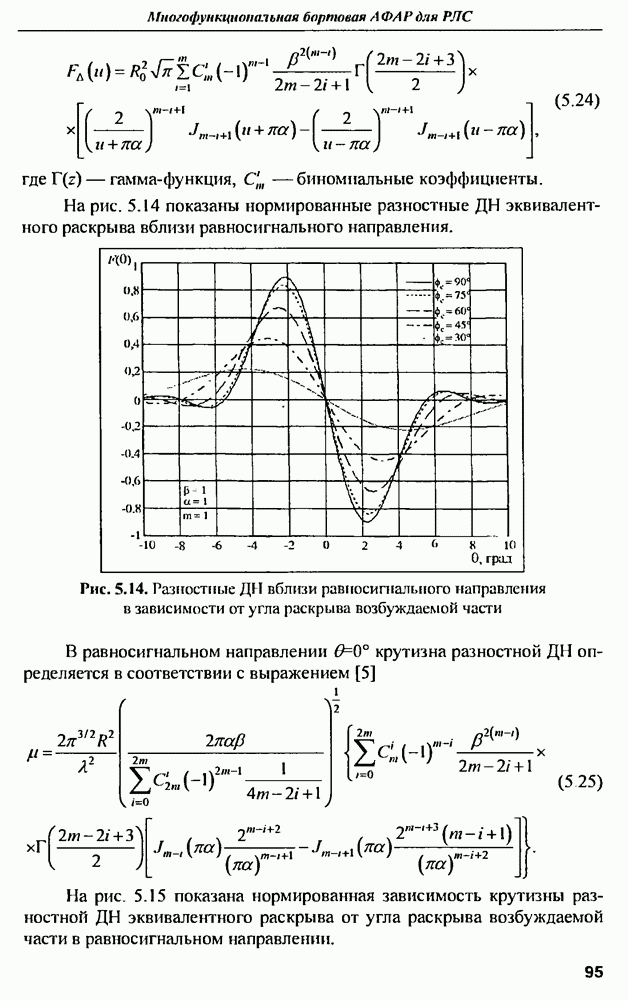
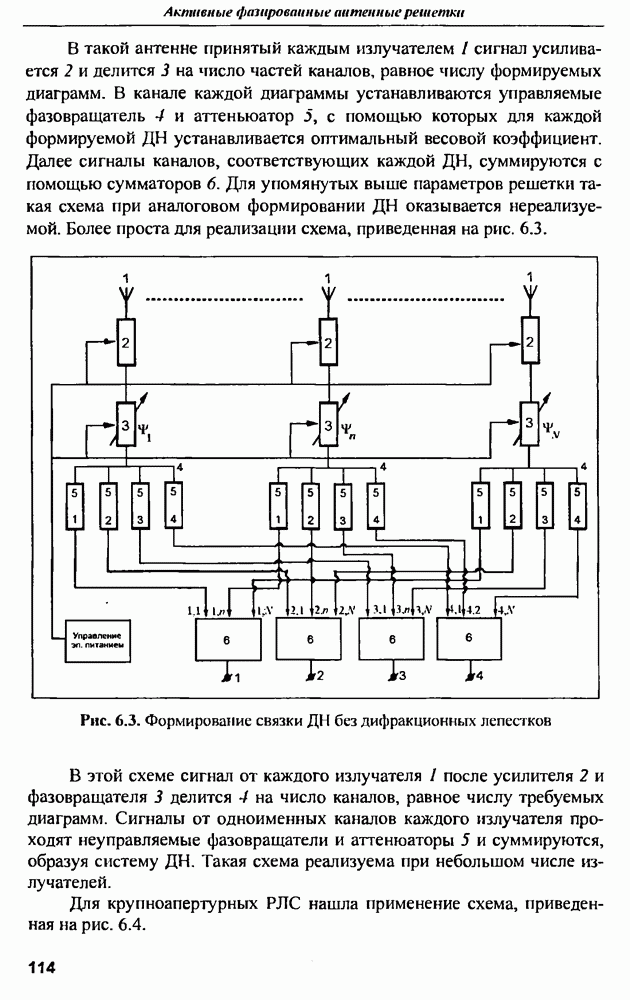
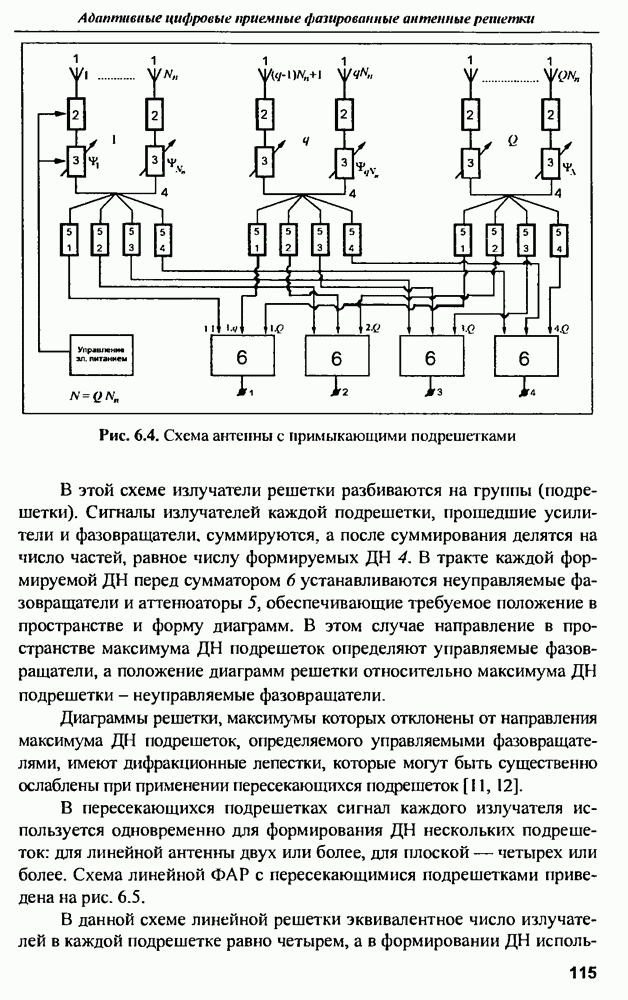
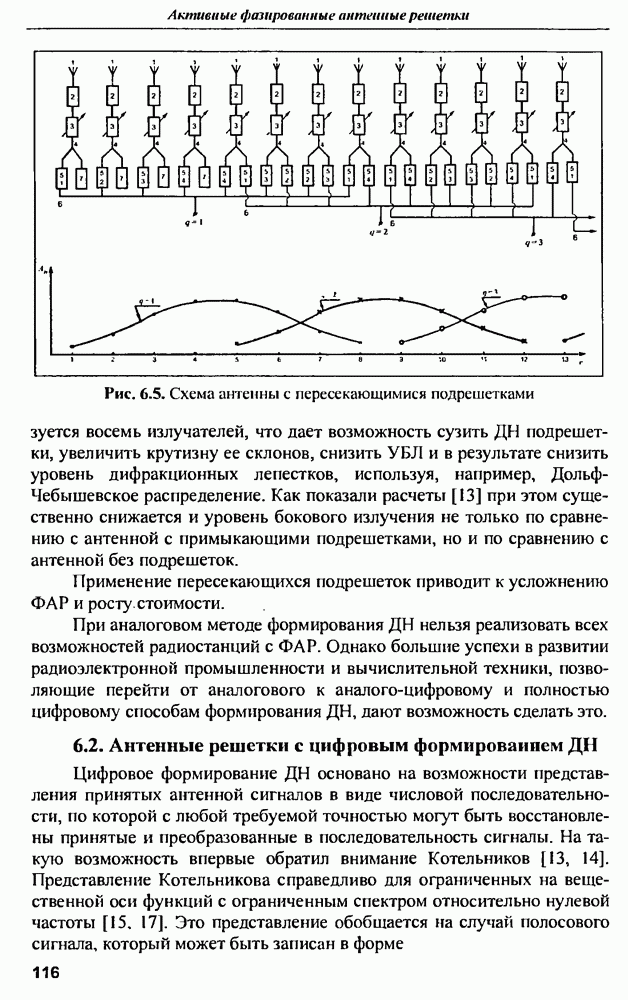
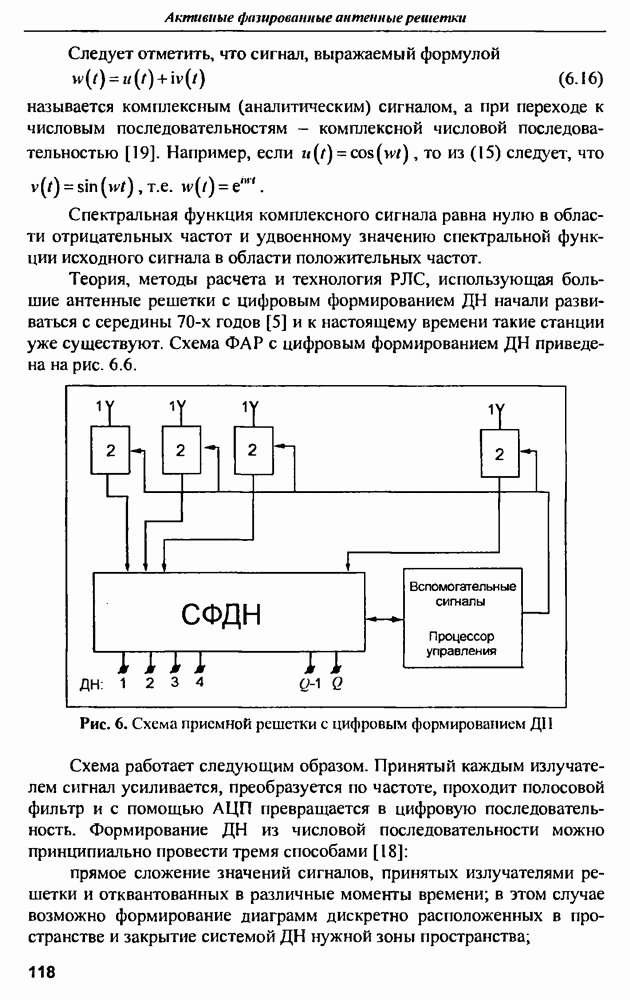
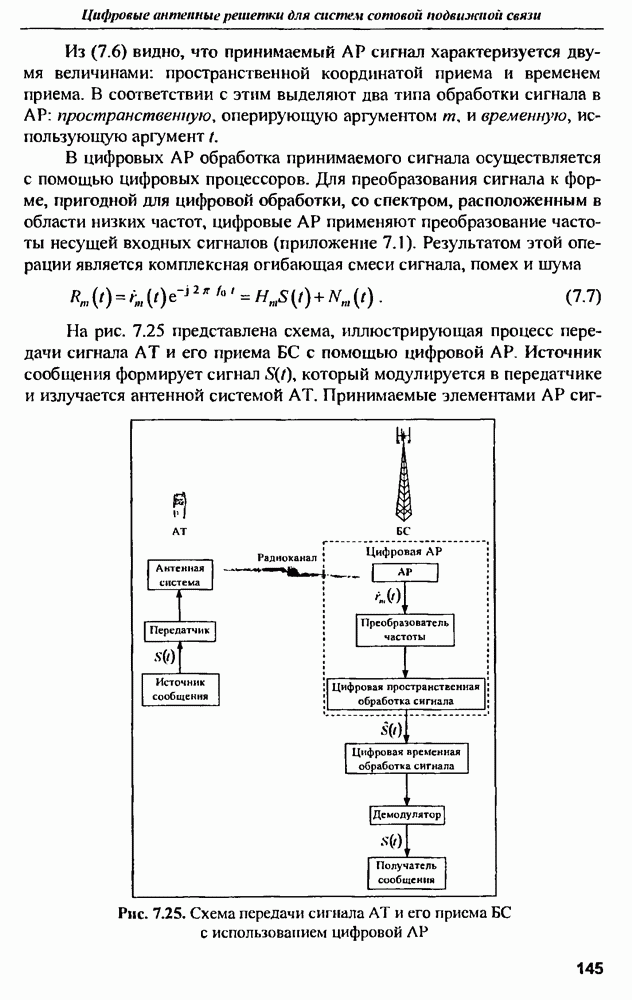
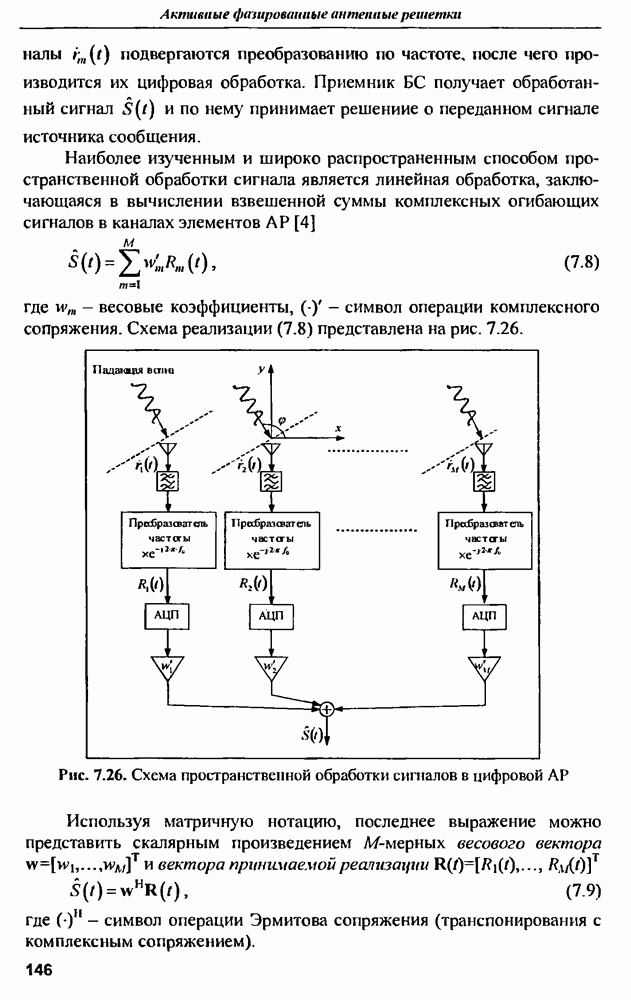
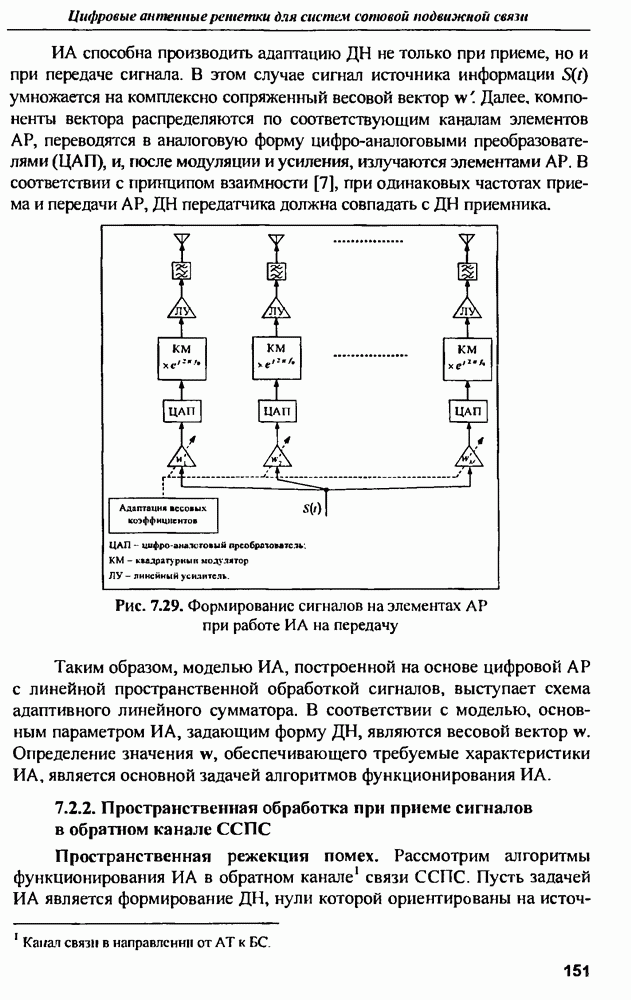
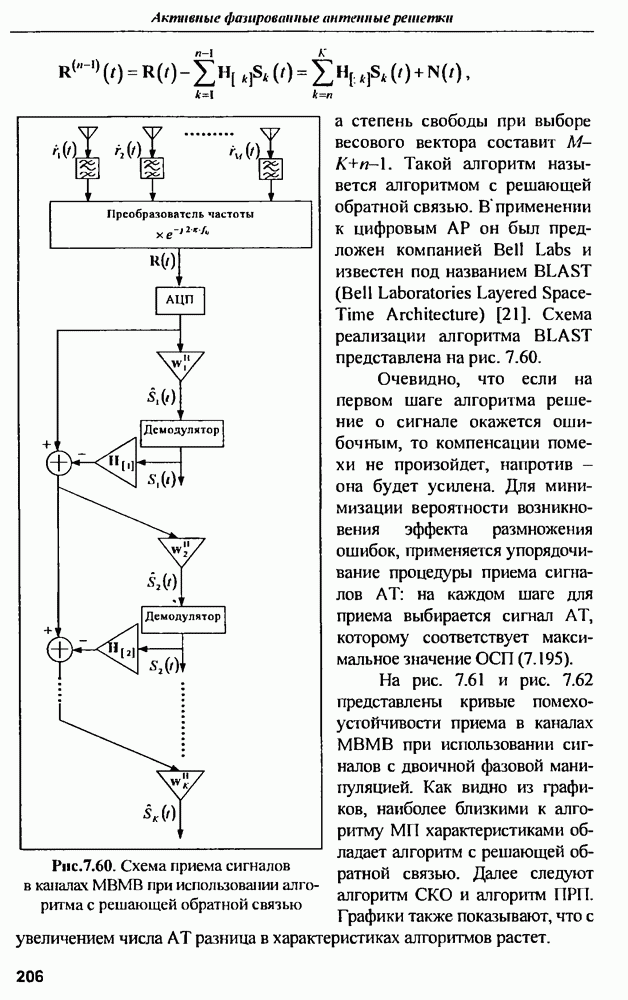
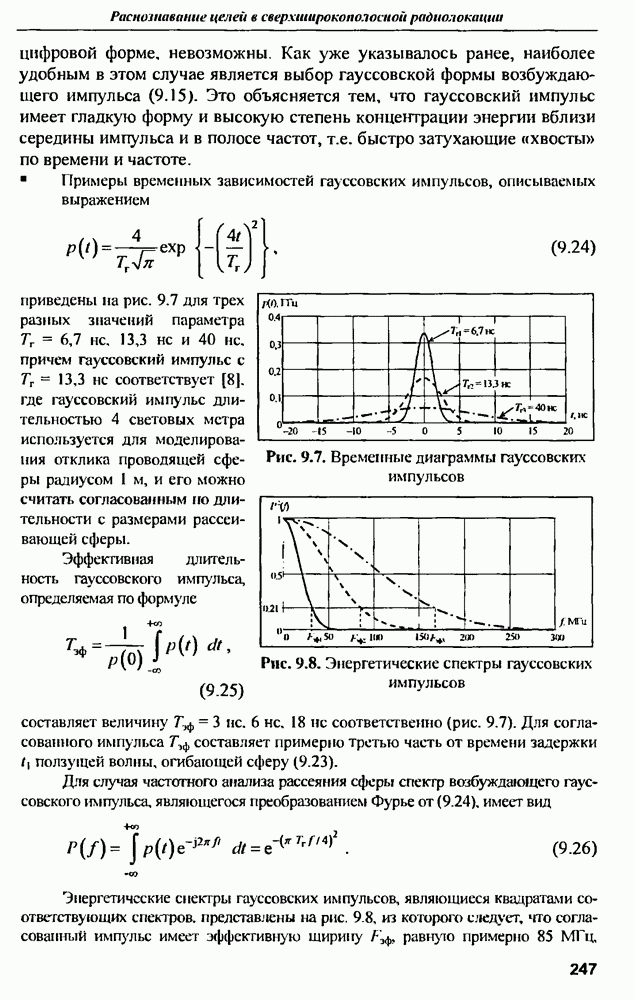
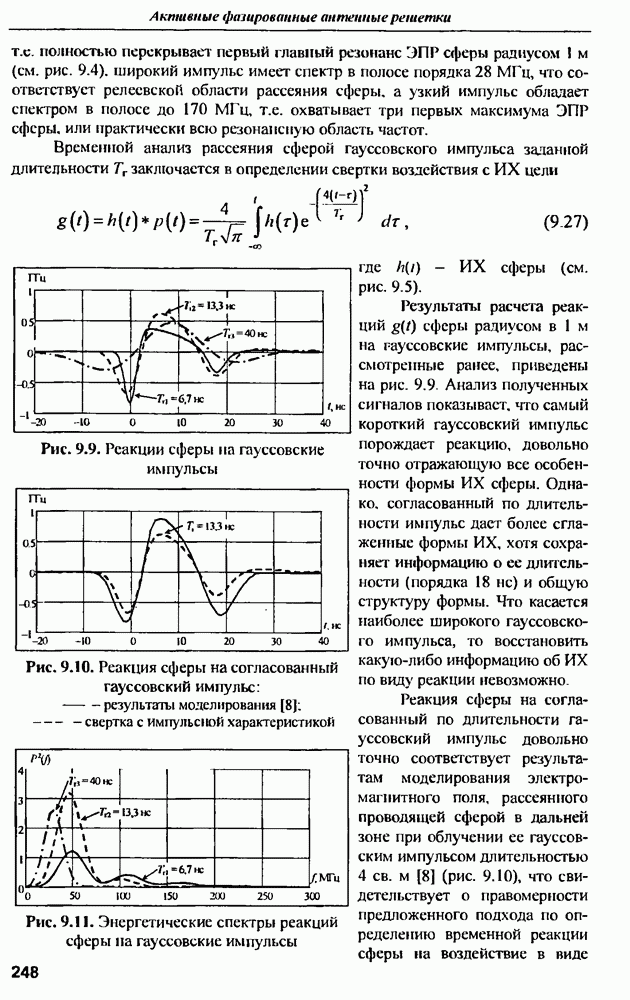
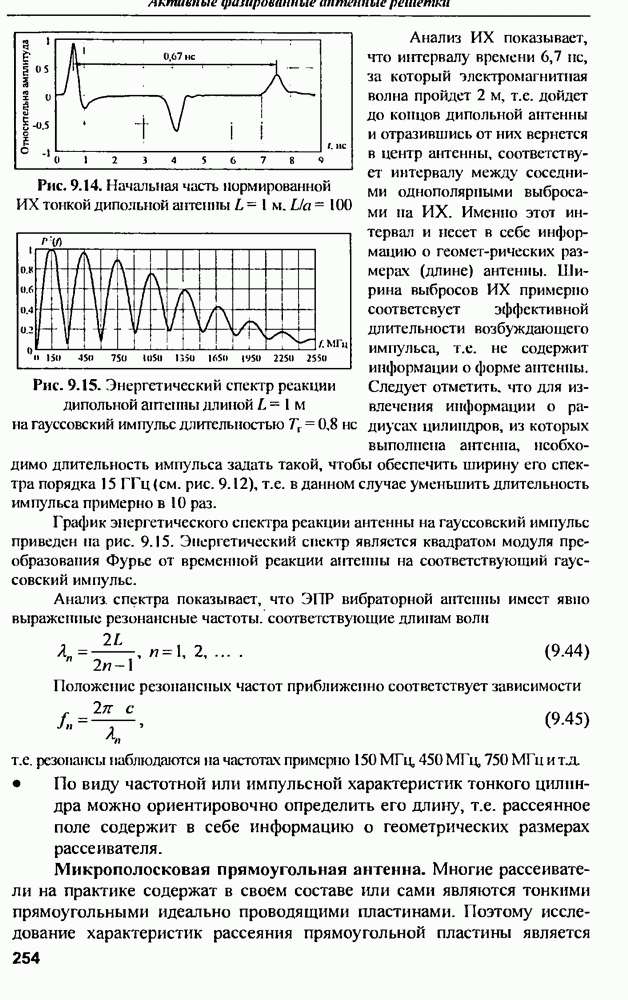
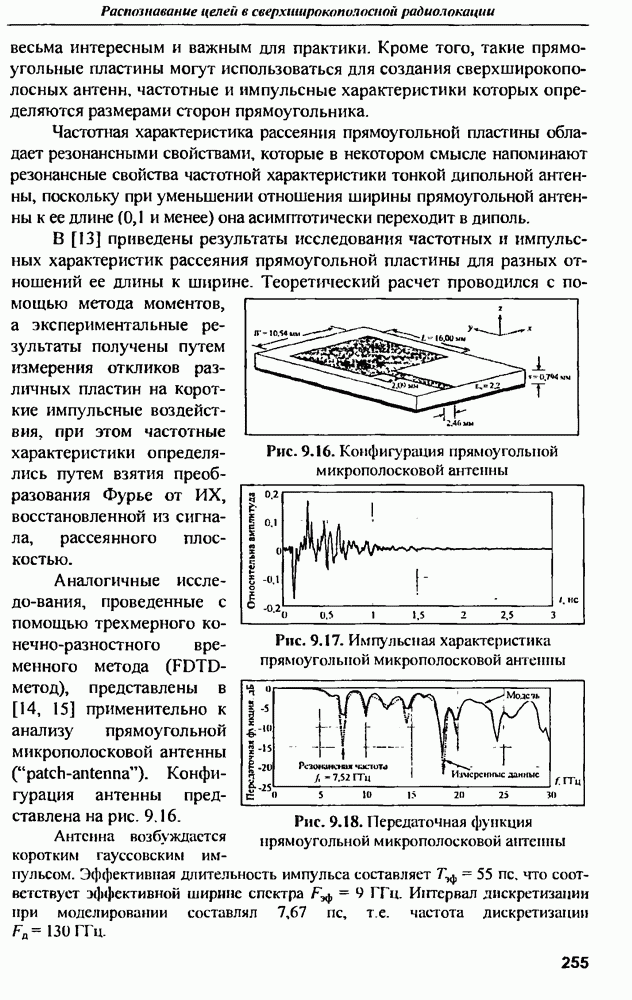
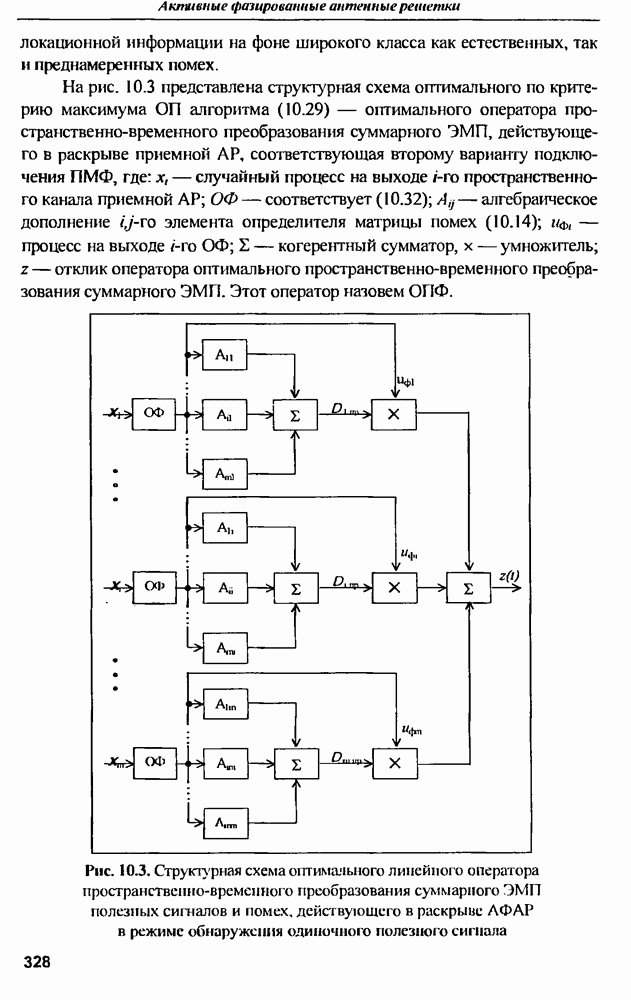
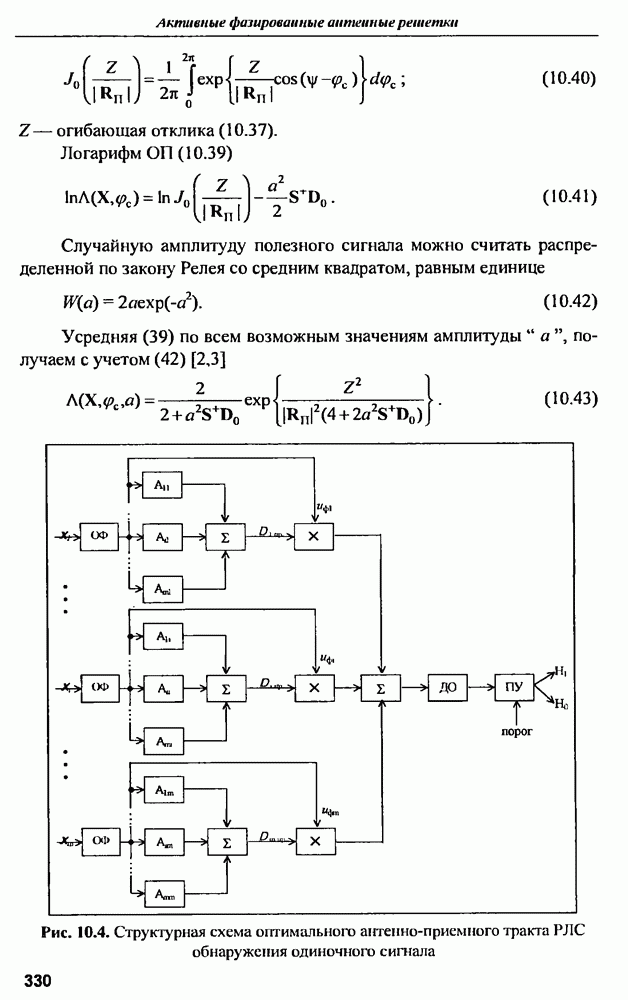
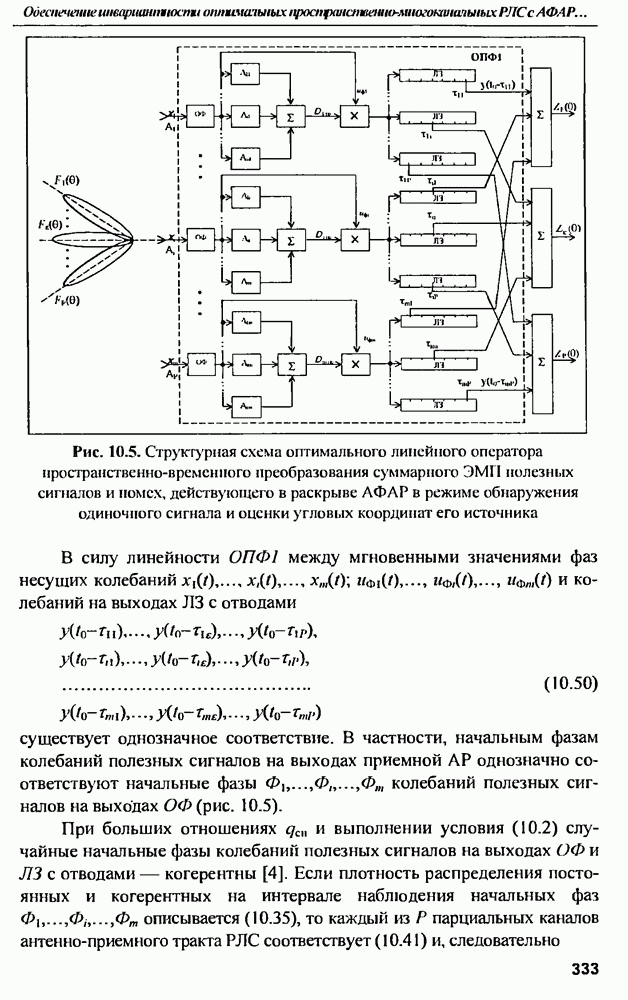
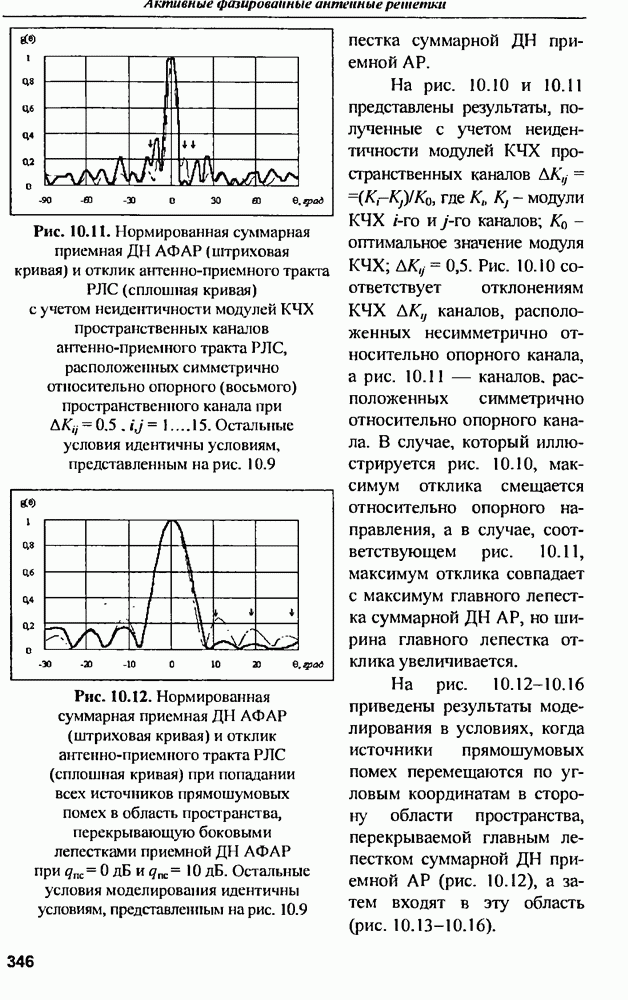
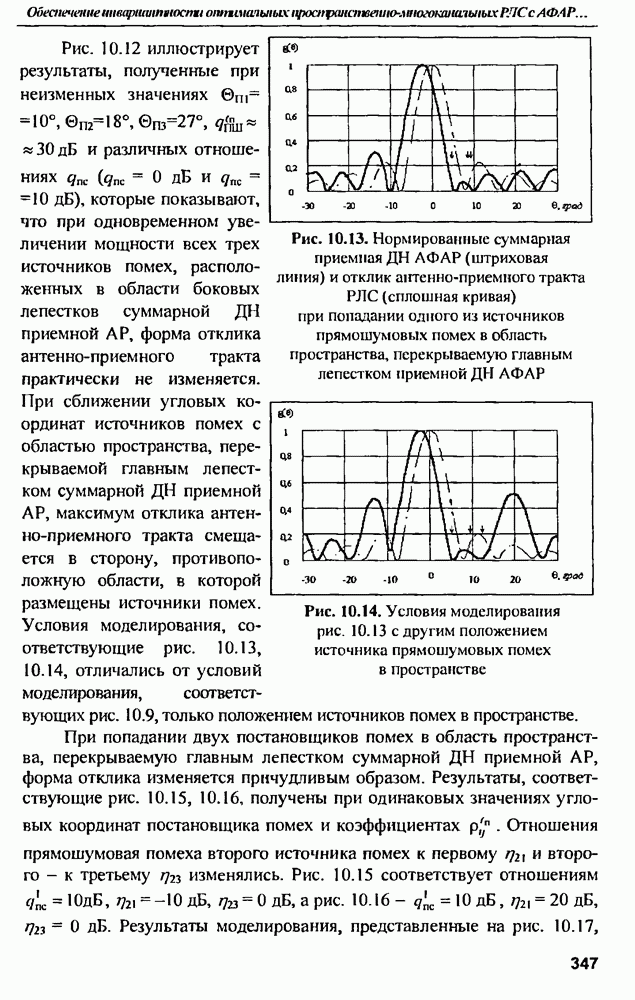
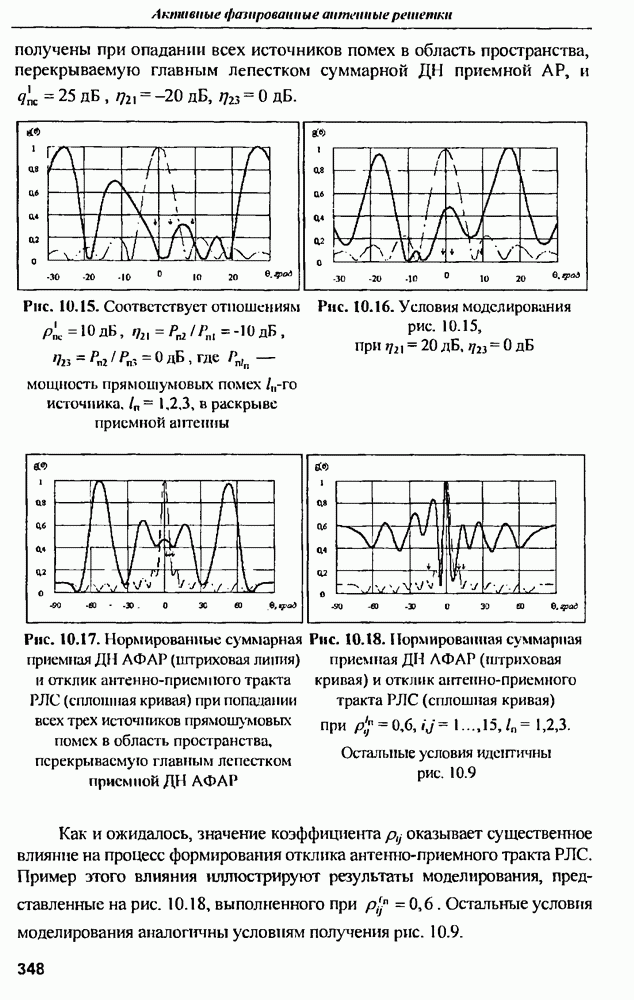
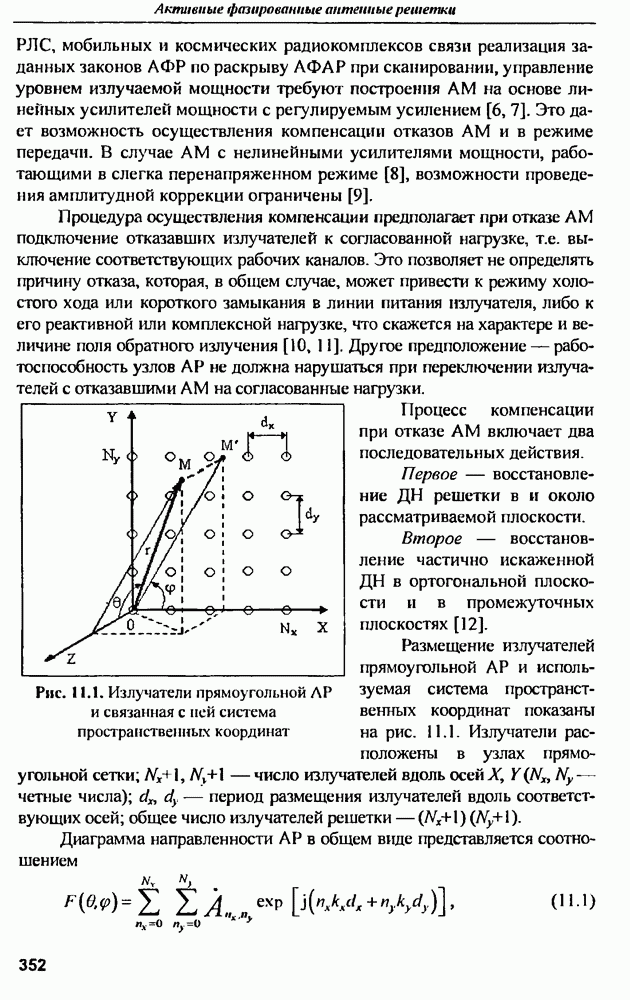
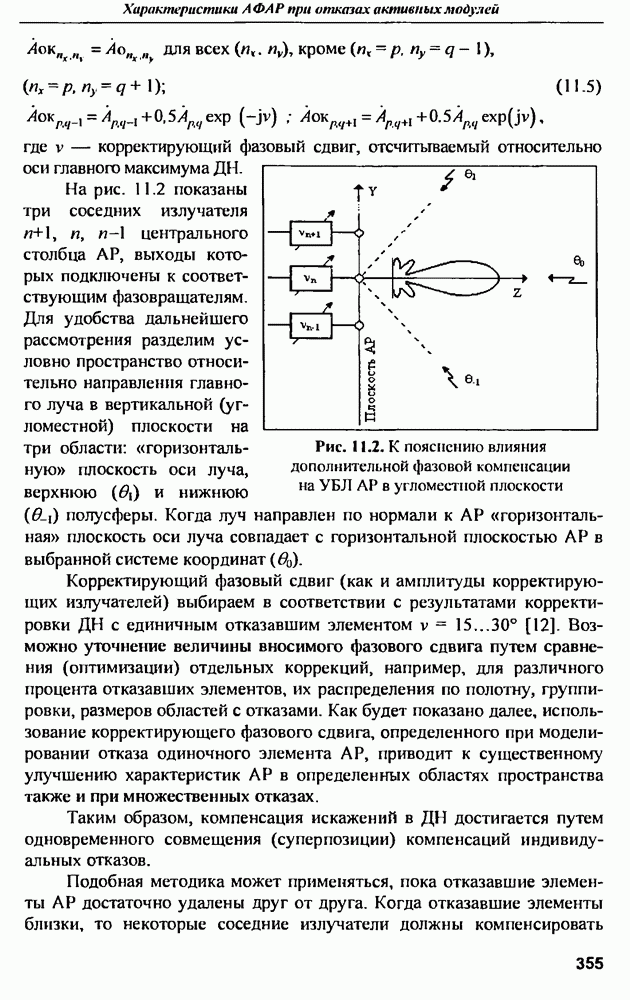
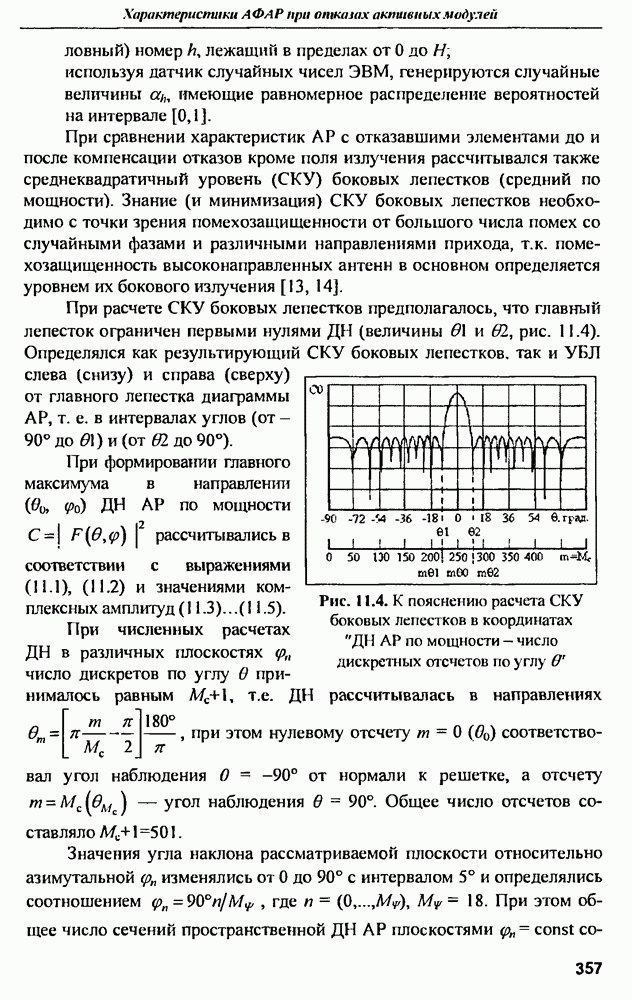
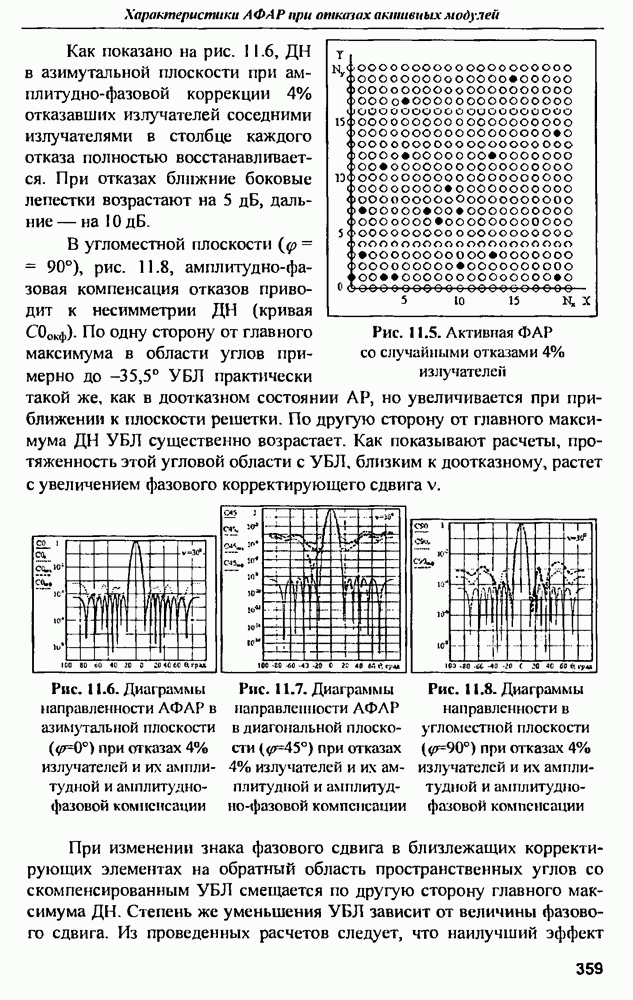
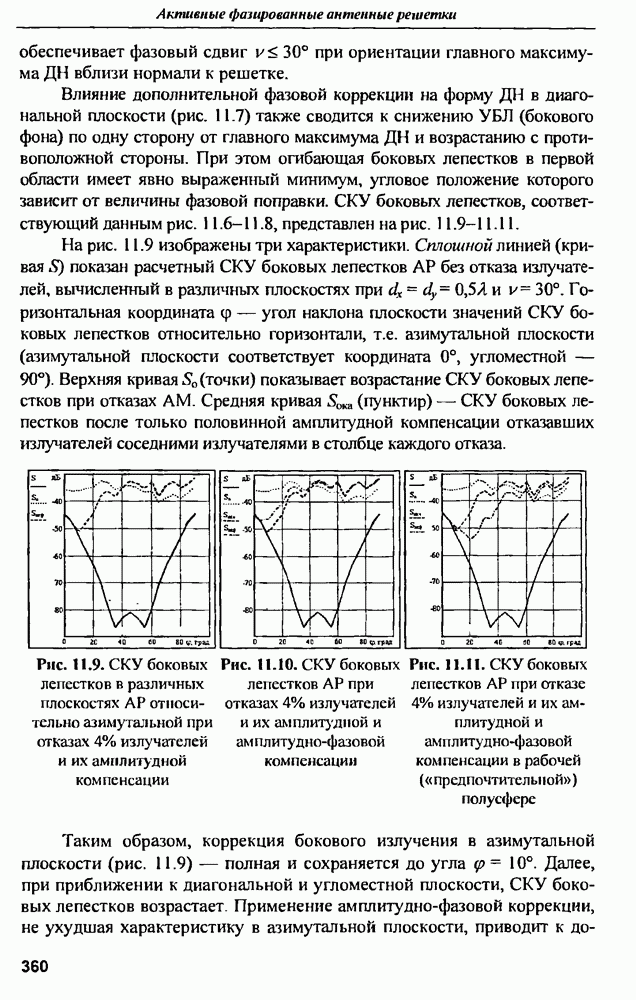
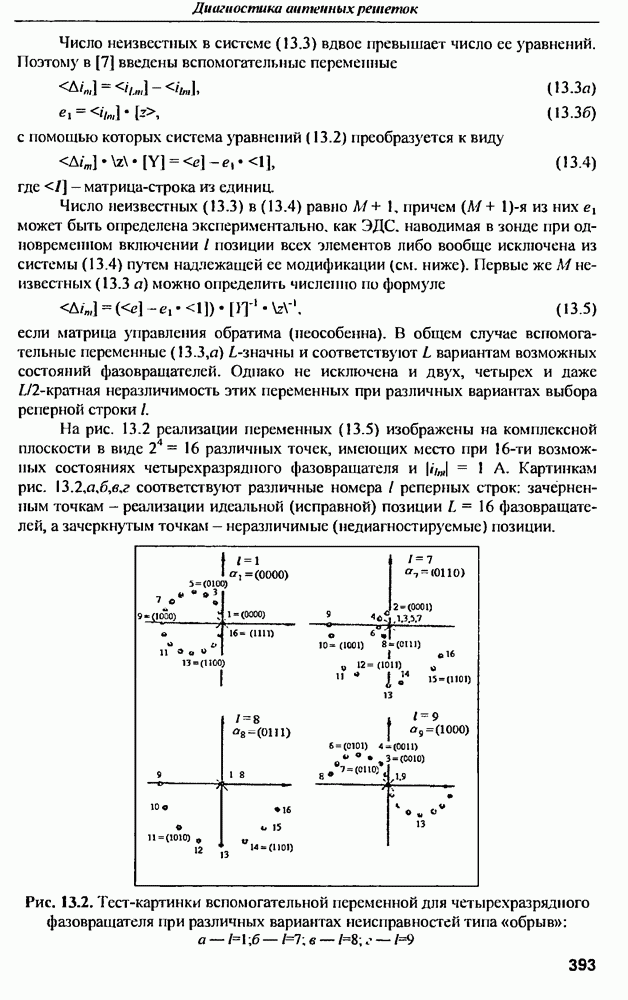
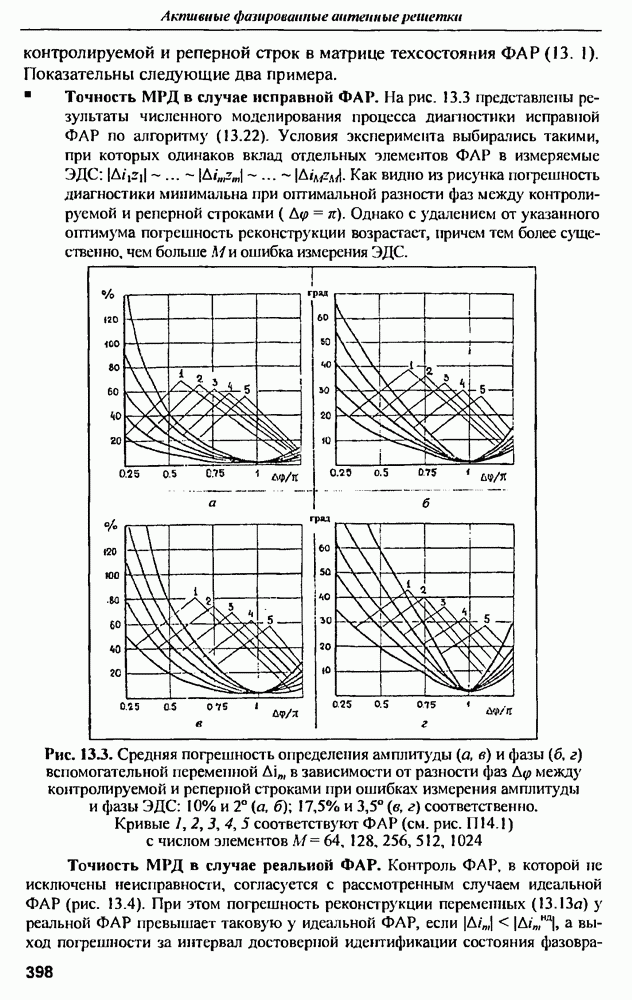
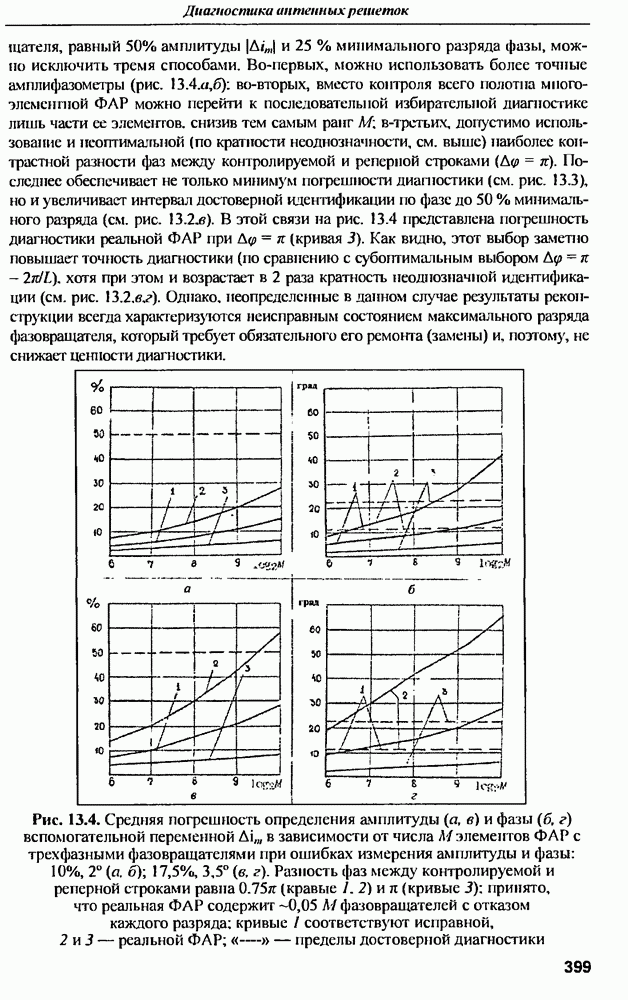
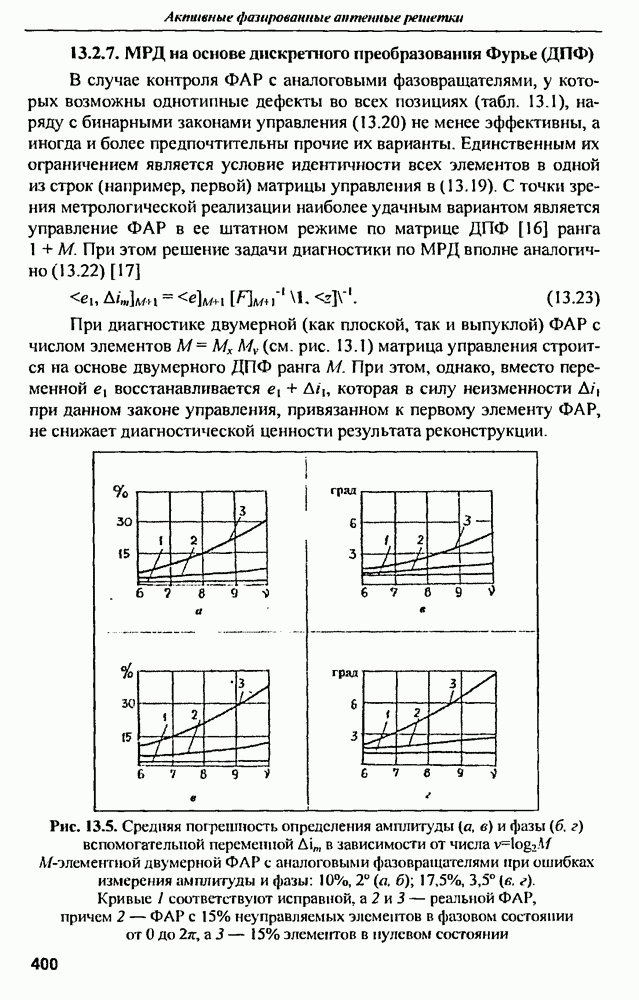
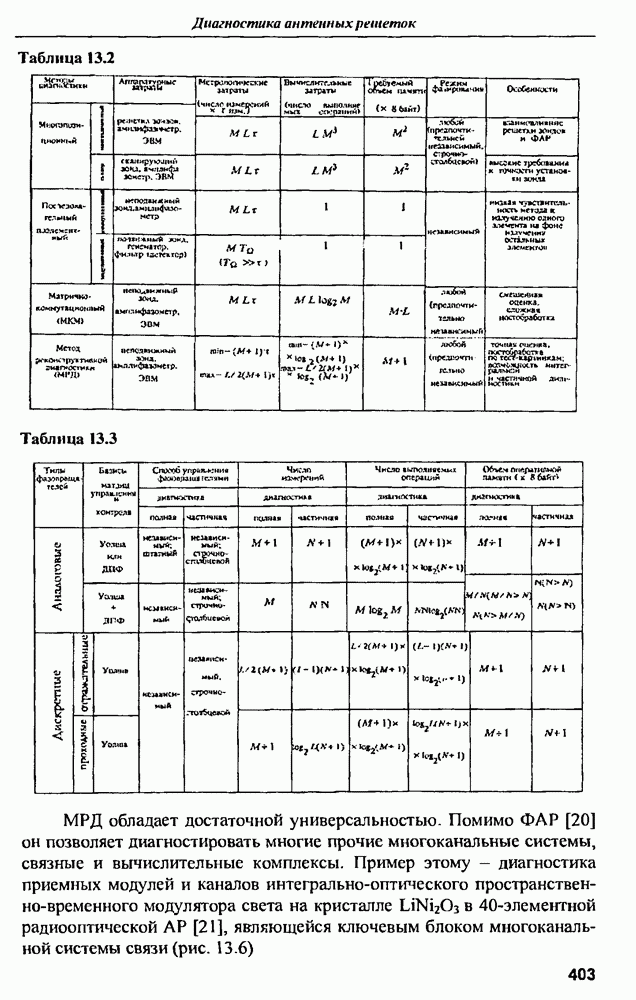
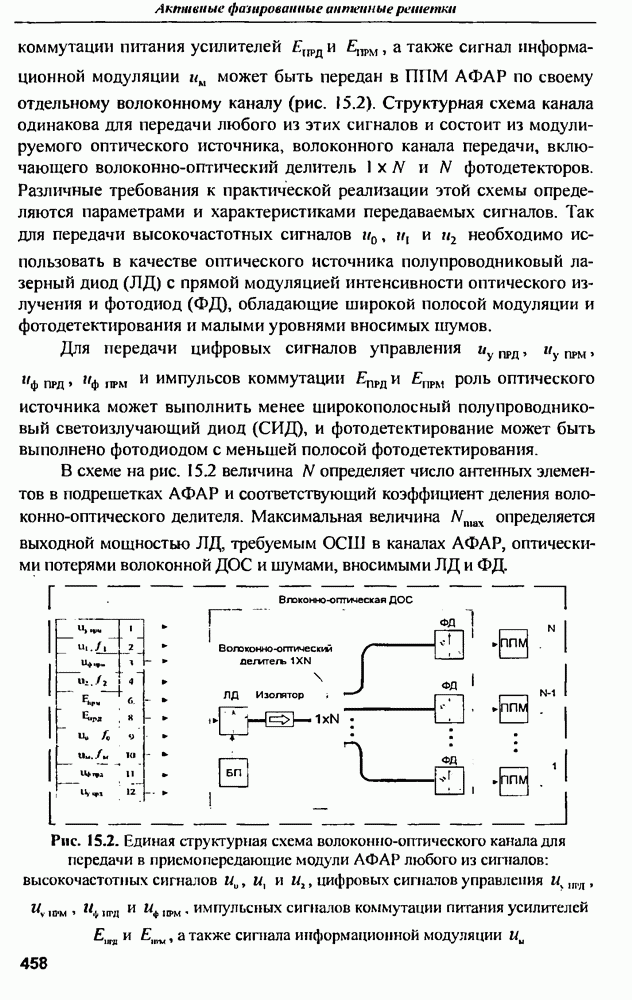
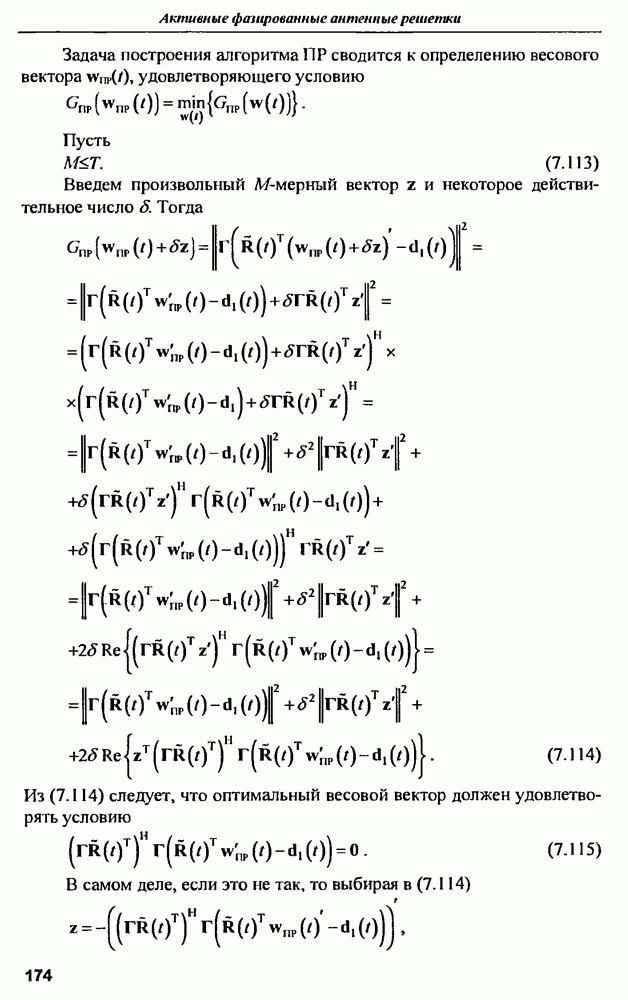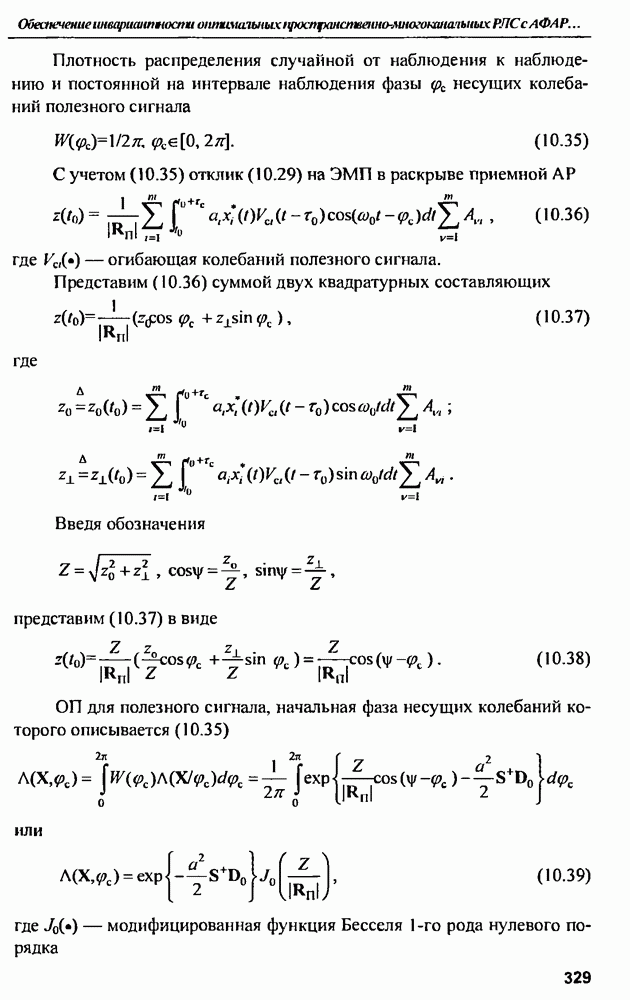| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
Как было указано выше, уменьшение КНД антенны определяется величиной  связь которой с ошибками распределения известна [3]. Если отклонения параметров элементов многоканального звена от номинального значения (и, соответственно, амплитудные и фазовые ошибки сигнала в каналах
связь которой с ошибками распределения известна [3]. Если отклонения параметров элементов многоканального звена от номинального значения (и, соответственно, амплитудные и фазовые ошибки сигнала в каналах  независимы, стационарны вдоль апертуры антенны и распределены по нормальному закону, то:
независимы, стационарны вдоль апертуры антенны и распределены по нормальному закону, то:

где  дисперсия относительных амплитудных ошибок по раскрыву антенны;
дисперсия относительных амплитудных ошибок по раскрыву антенны;  дисперсия фазовых ошибок по раскрыву антенны.
дисперсия фазовых ошибок по раскрыву антенны.
С точностью до членов второго порядка малости  из (2 10) может быть представлена в виде:
из (2 10) может быть представлена в виде:

Формулы (2 10) и (2.11) пригодны для линейной и плоской антенн при числе излучателей  и расстоянии между излучателями
и расстоянии между излучателями  Величина
Величина  является произведением
является произведением  которые могут быть определены по формуле (2.11), если известны дисперсии амплитудных <тамп, и фазовых
которые могут быть определены по формуле (2.11), если известны дисперсии амплитудных <тамп, и фазовых  ошибок распределения, которые создает
ошибок распределения, которые создает  звено АФАР на апертуре антенны (см. рис. 2.3). Однако, определение дисперсий этих ошибок вызывает определенные трудности, так как отклонение какого-нибудь параметра элементов данного звена от номинального значения, полученное, например, по результатам измерения этого параметра в большой партии элементов, позволяет
звено АФАР на апертуре антенны (см. рис. 2.3). Однако, определение дисперсий этих ошибок вызывает определенные трудности, так как отклонение какого-нибудь параметра элементов данного звена от номинального значения, полученное, например, по результатам измерения этого параметра в большой партии элементов, позволяет
этого параметра в большой партии элементов, позволяет определить дисперсию ошибок распределения этого параметра только на выходе звена, а не на апертуре антенны.
Для того чтобы определить величину  необходимо пересчитать дисперсию ошибки распределения рассматриваемого параметра с выхода
необходимо пересчитать дисперсию ошибки распределения рассматриваемого параметра с выхода  звена на апертуру антенны. Очевидно, что при этом пересчете все последующие звенья АФАР, через которые сигнал проходит до апертуры антенны, будут изменять величину дисперсии ошибок распределения этого параметра
звена на апертуру антенны. Очевидно, что при этом пересчете все последующие звенья АФАР, через которые сигнал проходит до апертуры антенны, будут изменять величину дисперсии ошибок распределения этого параметра  звена.
звена.
Известно, что в одноканальной системе любой параметр сигнала на выходе системы определяется перемножением этого параметра входного сигнала на коэффициент передачи системы по данному параметру. В многоканальной системе параметры выходного сигнала находятся аналогично, однако параметры входного сигнала и коэффициенты передачи звеньев системы в этом случае носят статистический характер. Одно и то же звено АФАР может быть источником нескольких независимых причин появления ошибок распределения. Так, например, фазовые ошибки на выходе многоканального звена ферритовых фазовращателей появляются как в результате нестабильности управляющего напряжения, так и из-за изменений внешней температуры.
С учетом изложенного расчет потерь полного КПД АФАР за счет ошибок распределения производится следующим образом. Сначала на основании анализа функциональной схемы конкретной АФАР строится «схема влияний», на которой указывается каждая причина  вызывающая
вызывающая  ошибку распределения на выходе
ошибку распределения на выходе  многоканального звена. Такими причинами могут быть изменения питающих напряжений, входной мощности,
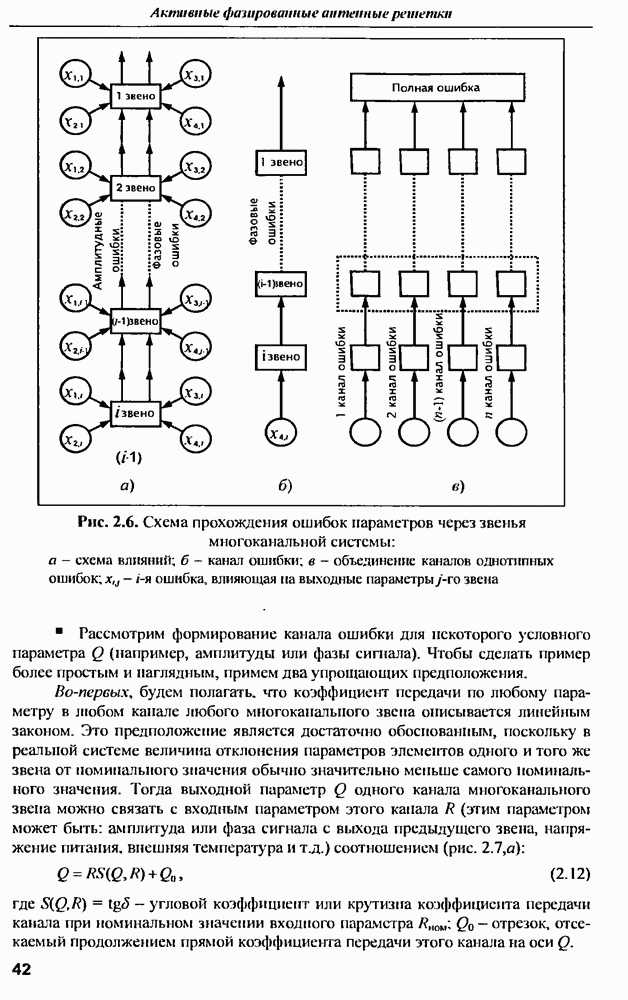
многоканального звена. Такими причинами могут быть изменения питающих напряжений, входной мощности,  нагрузки, температуры и других факторов. Пример схемы влияний в общем виде приведен на рис. 2.6,а. Затем выполняется инженерный анализ схемы влияний, который позволяет исключить из дальнейшего рассмотрения причины, вызывающие ошибки распределения, незначительные для данного многоканального звена. Далее для каждой из оставшихся причин составляется схема, называемая «каналом ошибки» (рис. 2.6,б). Канал ошибки показывает путь прохождения дисперсии ошибки распределения конкретного параметра (амплитуды или фазы) с выхода звена, где образуется эта ошибка, через последующие звенья АФАР до апертуры антенны. Эта схема позволяет преобразовать дисперсию ошибки распределения параметра с выхода звена в дисперсию ошибки распределения этого параметра на апертуре антенны. Для удобства и общей наглядности все каналы ошибок одного и того же параметра (например, фазы) могут быть объединены в один канал (рис. 2.6,в). При независимости причин ошибок общая дисперсия ошибки распределения в общем канале будет равна сумме дисперсий ошибок распределения всех каналов.
нагрузки, температуры и других факторов. Пример схемы влияний в общем виде приведен на рис. 2.6,а. Затем выполняется инженерный анализ схемы влияний, который позволяет исключить из дальнейшего рассмотрения причины, вызывающие ошибки распределения, незначительные для данного многоканального звена. Далее для каждой из оставшихся причин составляется схема, называемая «каналом ошибки» (рис. 2.6,б). Канал ошибки показывает путь прохождения дисперсии ошибки распределения конкретного параметра (амплитуды или фазы) с выхода звена, где образуется эта ошибка, через последующие звенья АФАР до апертуры антенны. Эта схема позволяет преобразовать дисперсию ошибки распределения параметра с выхода звена в дисперсию ошибки распределения этого параметра на апертуре антенны. Для удобства и общей наглядности все каналы ошибок одного и того же параметра (например, фазы) могут быть объединены в один канал (рис. 2.6,в). При независимости причин ошибок общая дисперсия ошибки распределения в общем канале будет равна сумме дисперсий ошибок распределения всех каналов.
Рис. 2.6. (см. скан) Схема прохождения ошибок параметров через звенья многоканальной системы: а - схема влнянмй;  канал ошибки; в - объединение каналов однотмпных ошибок;
канал ошибки; в - объединение каналов однотмпных ошибок;  ошибка, влияющая на выходные параметры j-го звена
ошибка, влияющая на выходные параметры j-го звена
Рассмотрим формирование канала ошибки для некоторого условного параметра  (например, амплитуды или фазы сигнала). Чтобы сделать пример более простым и наглядным, примем два упрощающих предположения.
(например, амплитуды или фазы сигнала). Чтобы сделать пример более простым и наглядным, примем два упрощающих предположения.
Во-первых, будем полагать, что коэффициент передачи по любому параметру в любом канале любого многоканального звена описывается линейным законом. Это предположение является достаточно обоснованным, поскольку в реальной системе величина отклонения параметров элементов одного и того же звена от номинального значения обычно значительно меньше самого поминального значения. Тогда выходной параметр  одного канала многоканального звена можно связать с входным параметром этого канала
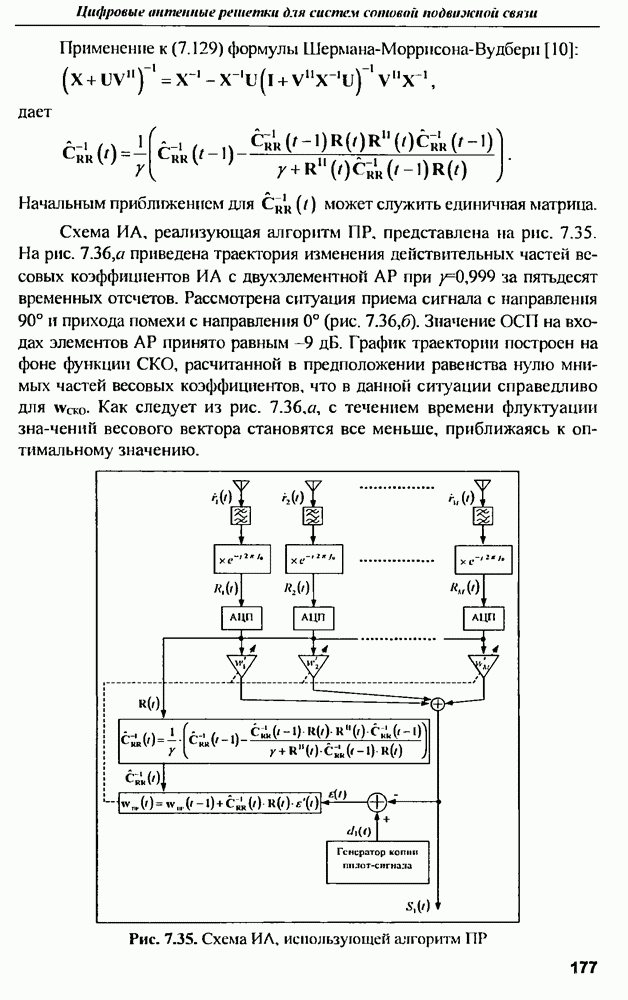
одного канала многоканального звена можно связать с входным параметром этого канала  (этим параметром может быть: амплитуда или фаза сигнала с выхода предыдущего звена, напряжение питания, внешняя температура и т.д.) соотношением (рис. 2.1,а):
(этим параметром может быть: амплитуда или фаза сигнала с выхода предыдущего звена, напряжение питания, внешняя температура и т.д.) соотношением (рис. 2.1,а):

где  угловой коэффициент или крутизна коэффициента передачи канала при номинальном значении входного параметра
угловой коэффициент или крутизна коэффициента передачи канала при номинальном значении входного параметра  отрезок, отсекаемый продолжением прямой коэффициента передачи этого канала на оси Q.
отрезок, отсекаемый продолжением прямой коэффициента передачи этого канала на оси Q.

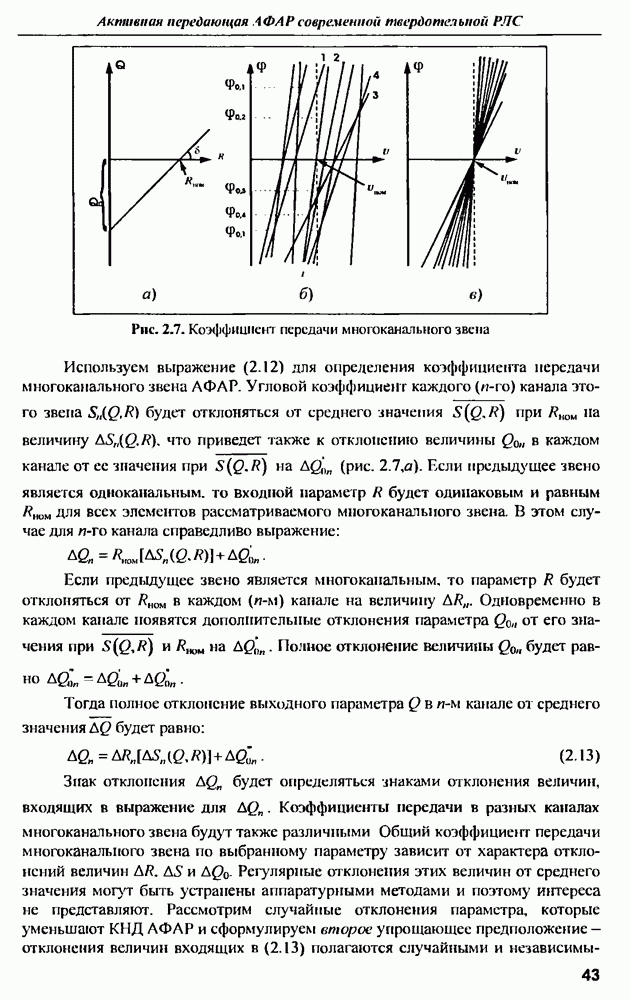
Рис. 2.7. Коэффициент передачи многоканального звена
Используем выражение (2.12) для определения коэффициента передачи многоканального звена АФАР. Угловой коэффициент каждого  канала этого звена
канала этого звена  будет отклоняться от среднего значения
будет отклоняться от среднего значения  при
при  на величину
на величину  что приведет также к отклонению величины
что приведет также к отклонению величины  в каждом канале от ее значения при
в каждом канале от ее значения при  на
на  (рис. 2.1, а). Если предыдущее звено является одноканальным, то входной параметр
(рис. 2.1, а). Если предыдущее звено является одноканальным, то входной параметр  будет одинаковым и равным
будет одинаковым и равным  для всех элементов рассматриваемого многоканального звена. В этом случае для
для всех элементов рассматриваемого многоканального звена. В этом случае для  канала справедливо выражение:
канала справедливо выражение:

Если предыдущее звено является многоканальным, то параметр  будет отклоняться от
будет отклоняться от  в каждом
в каждом  канале на величину
канале на величину  Одновременно в каждом канале появятся дополнительные отклонения параметра
Одновременно в каждом канале появятся дополнительные отклонения параметра  от его значения при
от его значения при  на
на  Полное отклонение величины
Полное отклонение величины  будет равно
будет равно 
Тогда полное отклонение выходного параметра  канале от среднего значения
канале от среднего значения  будет равно
будет равно

Знак отклонения  будет определяться знаками отклонения величин, входящих в выражение для
будет определяться знаками отклонения величин, входящих в выражение для  Коэффициенты передачи в разных каналах многоканального звена будут также различными Общий коэффициент передачи многоканального звена по выбранному параметру зависит от характера отклонений величин
Коэффициенты передачи в разных каналах многоканального звена будут также различными Общий коэффициент передачи многоканального звена по выбранному параметру зависит от характера отклонений величин  Регулярные отклонения этих величин от среднего значения могут быть устранены аппаратурными методами и поэтому интереса не представляют. Рассмотрим случайные отклонения параметра, которые уменьшают КНД АФАР и сформулируем второе упрощающее предположение — отклонения величин входящих в (2.13) полагаются случайными и независимыми.
Регулярные отклонения этих величин от среднего значения могут быть устранены аппаратурными методами и поэтому интереса не представляют. Рассмотрим случайные отклонения параметра, которые уменьшают КНД АФАР и сформулируем второе упрощающее предположение — отклонения величин входящих в (2.13) полагаются случайными и независимыми.
Тогда эти отклонения можно считать некоррелированными случайными величинами, распределенными но нормальному закону. На рис. 2.7,б приведен конкретный пример зависимости фазы выходного сигнала  группы усилителей мощности от напряжения питания
группы усилителей мощности от напряжения питания  Формула (2.13) для такой группы будет выглядеть следующим образом:
Формула (2.13) для такой группы будет выглядеть следующим образом:

Все три величины, входящие в это выражение, могут быть случайными.  будет случайной величиной, если звено источников питания усилителей многоканальное (т. е. каждый усилитель получает напряжение от отдельного источника питания).
будет случайной величиной, если звено источников питания усилителей многоканальное (т. е. каждый усилитель получает напряжение от отдельного источника питания).  если это звено одноканальное (все усилители АФАР запитываются от одного источника питания). Величины
если это звено одноканальное (все усилители АФАР запитываются от одного источника питания). Величины  и будут случайными, потому что в АФАР звено усилителей мощности всегда является многоканальным.
и будут случайными, потому что в АФАР звено усилителей мощности всегда является многоканальным.
Поскольку выходной сигнал предыдущего  звена в канале ошибки является входным для последующего
звена в канале ошибки является входным для последующего  звена, то в дальнейшем будем обозначать
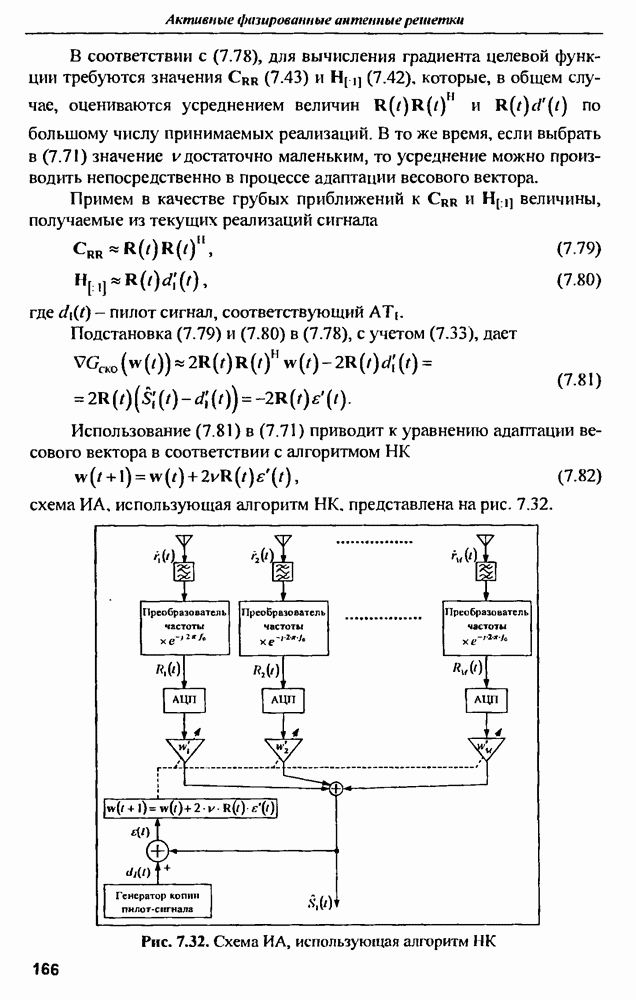
звена, то в дальнейшем будем обозначать  Для определения дисперсии параметра О в канале ошибки необходимо знать средние значения и дисперсии нормальных случайных величин
Для определения дисперсии параметра О в канале ошибки необходимо знать средние значения и дисперсии нормальных случайных величин  входящих в (2.13) [или
входящих в (2.13) [или  для (2.13.а)(см. рис. 2.7,б)].
для (2.13.а)(см. рис. 2.7,б)].
Средние значения и дисперсии этих случайных величин могут быть получены экспериментально путем измерения большой партии одинаковых элементов, входящих в состав многоканального звена. Если эти элементы к моменту проектирования АФАР не изготовлены, можно воспользоваться их ближайшими аналогами. Если аналоги также отсутствуют, выполняем расчет на основе допусков, заданных для изготовления данных элементов. Опыт проектирования показывает, что последний способ имеет большие погрешности.
Когда средние значения и дисперсии случайных величин, входящих в (2.13), определены, можно найти дисперсии параметра  на выходе
на выходе  звеньев многоканальной системы в рассматриваемом канале ошибки (см. рис. 2.3), пользуясь правилами определения дисперсии для произведения и суммы случайных некоррелированных величин
звеньев многоканальной системы в рассматриваемом канале ошибки (см. рис. 2.3), пользуясь правилами определения дисперсии для произведения и суммы случайных некоррелированных величин

где  дисперсия параметра
дисперсия параметра  на выходе
на выходе  звена;
звена;  дисперсия крутизны коэффициента передачи
дисперсия крутизны коэффициента передачи  звена по параметру
звена по параметру  среднее значение параметра
среднее значение параметра  на выходе
на выходе  звена;
звена;  среднее значение крутизны коэффициента передачи
среднее значение крутизны коэффициента передачи  звена по параметру
звена по параметру  дисперсия отклонения
дисперсия отклонения
параметра  на выходе
на выходе  звена от поминального значения при поминальном значении входного параметра.
звена от поминального значения при поминальном значении входного параметра.
Если в (2 14) ввести дисперсию каждого предыдущего звена в выражение для дисперсии последующего, мы получим значение дисперсии  параметра
параметра  которую создает данный канал ошибки на апертуре антенны:
которую создает данный канал ошибки на апертуре антенны:

Пользуясь (2.15) определяем дисперсию условного параметра  создаваемую каждым звеном данного канала ошибки на апертуре антенны
создаваемую каждым звеном данного канала ошибки на апертуре антенны
Так, для последнего звена (см. рис 2.3):

Для любого другого  звена:
звена:

Для определения истинной ошибки распределения, создаваемой данным каналом ошибки на апертуре антенны, необходимо в формулы (2.14) - (2.17) ввести статистические параметры  амплитуды или фазы реальных элементов многоканальных звеньев АФАР
амплитуды или фазы реальных элементов многоканальных звеньев АФАР
Аналогичные выражения могут быть получены и для всех остальных каналов ошибки в системе (см. рис. 2.6,в). Общая дисперсия ошибки распределения амплитуды пли фазы на раскрыве антенны находится как сумма дисперсий (2.15) всех каналов ошибки. Для определения снижения  суммарные дисперсии вводятся в (2.10) или (2.11). Полный КПД АФАР определяется по формуле (2.5) с учетом величины
суммарные дисперсии вводятся в (2.10) или (2.11). Полный КПД АФАР определяется по формуле (2.5) с учетом величины 
Дисперсия амплитуды или фазы, создаваемая одним звеном, необходимая для оценки его полного КПД по формуле (2.6), находится также как сумма дисперсшт (2.16) или (2.17) во всех каналах ошибки в пределах пунктирного прямоугольника (см. рис. 2.6,в). Для определения величины  полученные значения дисперсий следует подставить в (2.10) или (2.11).
полученные значения дисперсий следует подставить в (2.10) или (2.11).
Если в многоканальной системе имеются одноканальные звенья, то для этих звеньев в (2.16) и (2.17) вместо средних значений параметров подставляются их детерминированные значения, а дисперсии приравниваются к нулю.
Можно частично уменьшить дисперсию амплитуды и фазы на выходе системы с помощью подстройки параметров элементов каждого
звена. Для этого все элементы одного звена регулируются при одинаковом (номинальном) значении сигнала на входе и одинаковом (номинальном) напряжении питания. При регулировке у всех элементов устанавливается одинаковое (номинальное) значение выходного параметра, например амплитуды или фазы (электрической длины). После регулировки семейство характеристик, изображенное на рис. 2.7,б, принимает вид, показанный на рис. 2.7,в, а в (2.17) пропадает второе слагаемое. Дальнейшее уменьшение дисперсий параметров элементов АФАР возможно за счет выбора элементов с меньшей крутизной коэффициента передачи и с ее минимальным разбросом относительно среднего значения.
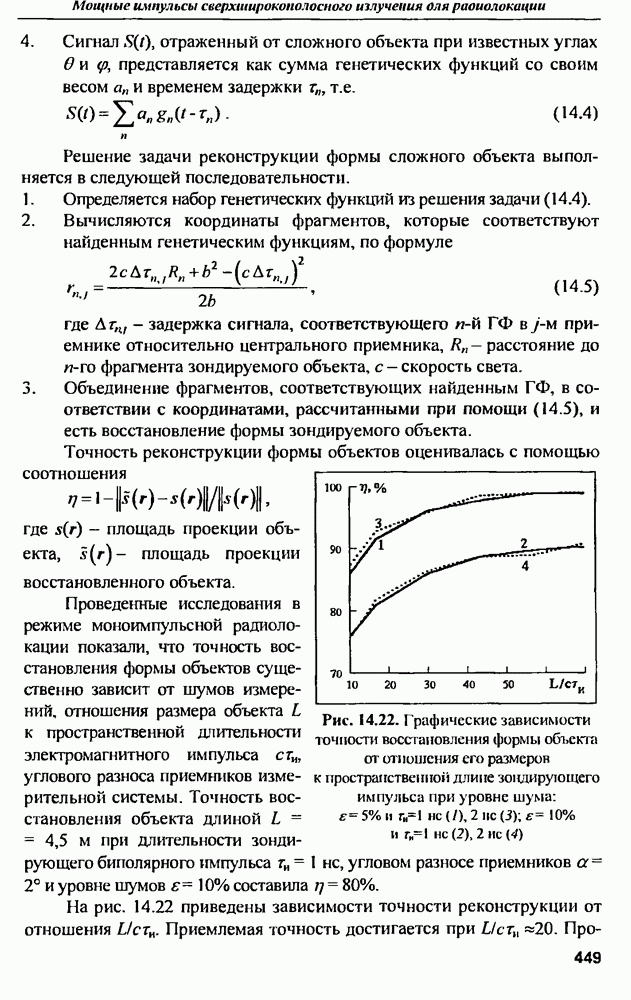
На рис. 2.8 приведен порядок примерного расчета энергетики многоканальной АФАР, построенной по схеме рис. 2.3
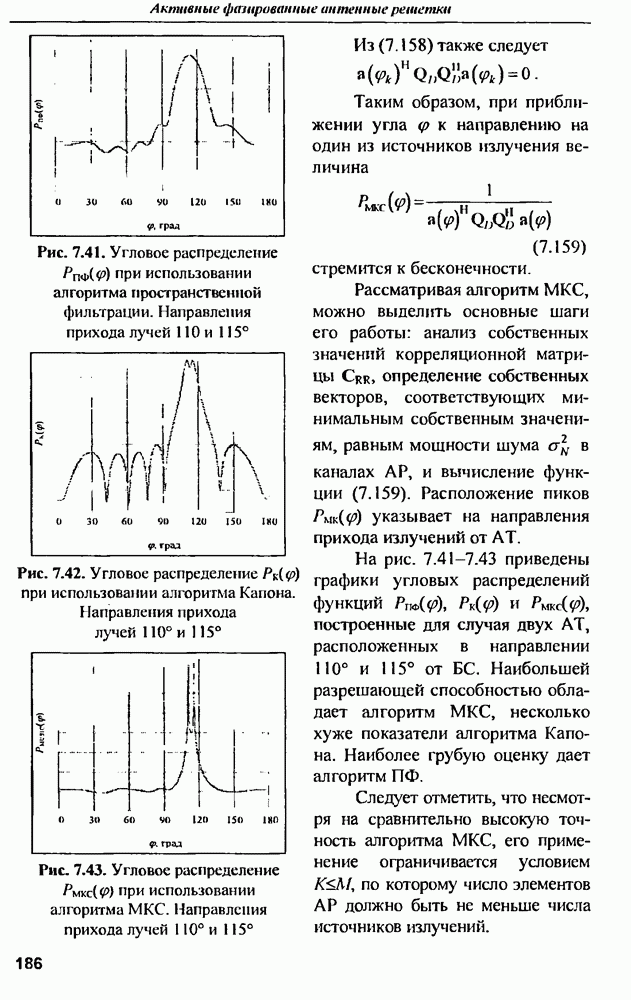
Рассмотрены только фазовые ошибки, поскольку эти ошибки оказывают наибольшее влияние на снижение КНД.
На рис. 2.8,а изображена упрощенная схема влияний рассматриваемой системы, а на рис.  каналы фазовых ошибок. Ниже в таблице приведены экспериментальные статистические характеристики звеньев АФАР и результаты расчета полного КПД, выполненного с использованием этих характеристик.
каналы фазовых ошибок. Ниже в таблице приведены экспериментальные статистические характеристики звеньев АФАР и результаты расчета полного КПД, выполненного с использованием этих характеристик.
Рис. 2.8. (см. скан) Схема влияний  и каналы фазовых ошибок (б)
и каналы фазовых ошибок (б)
Таблица (см. скан)
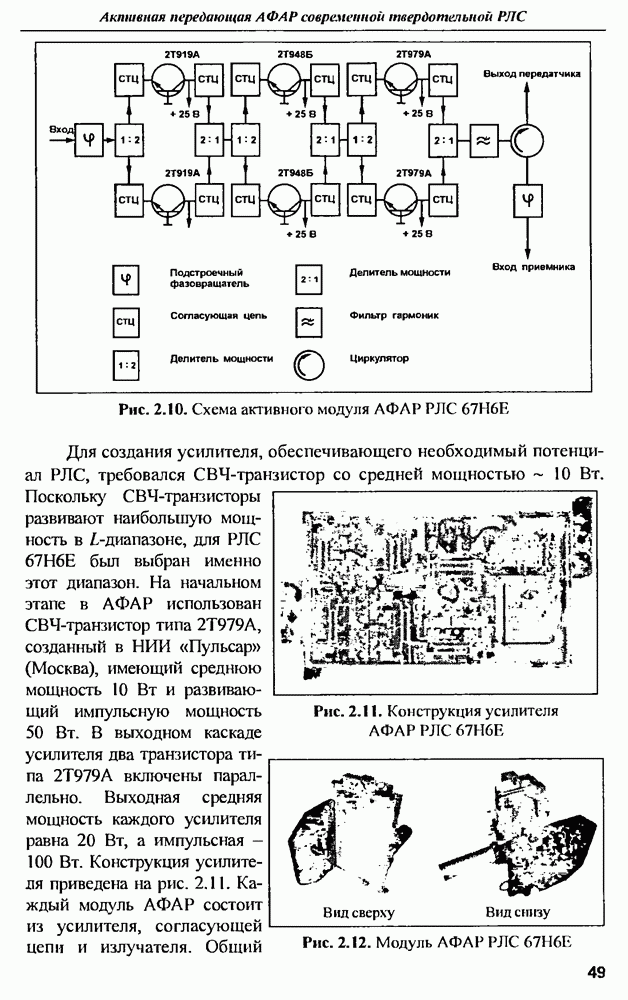
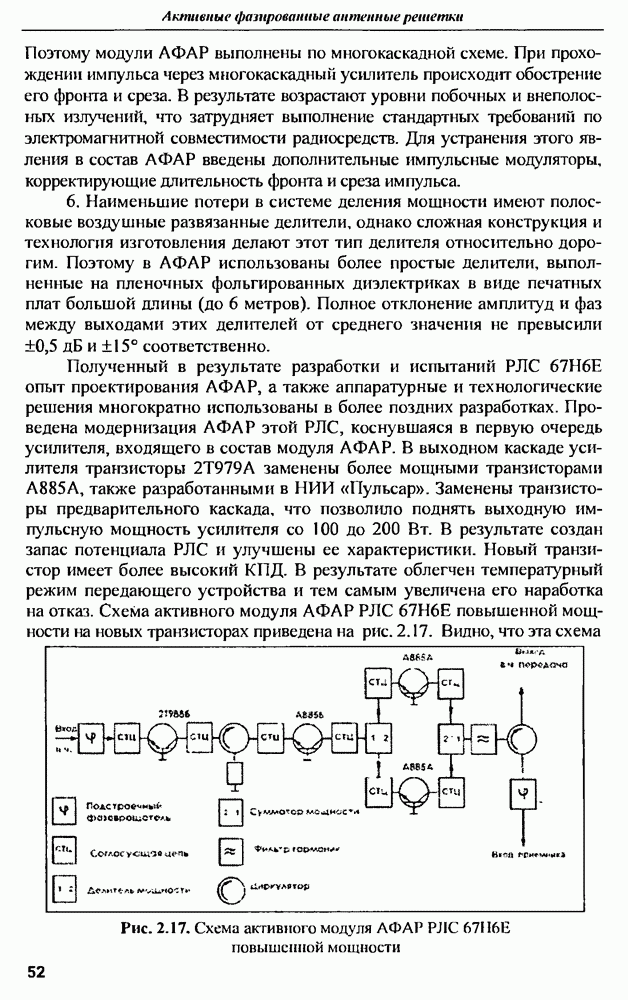
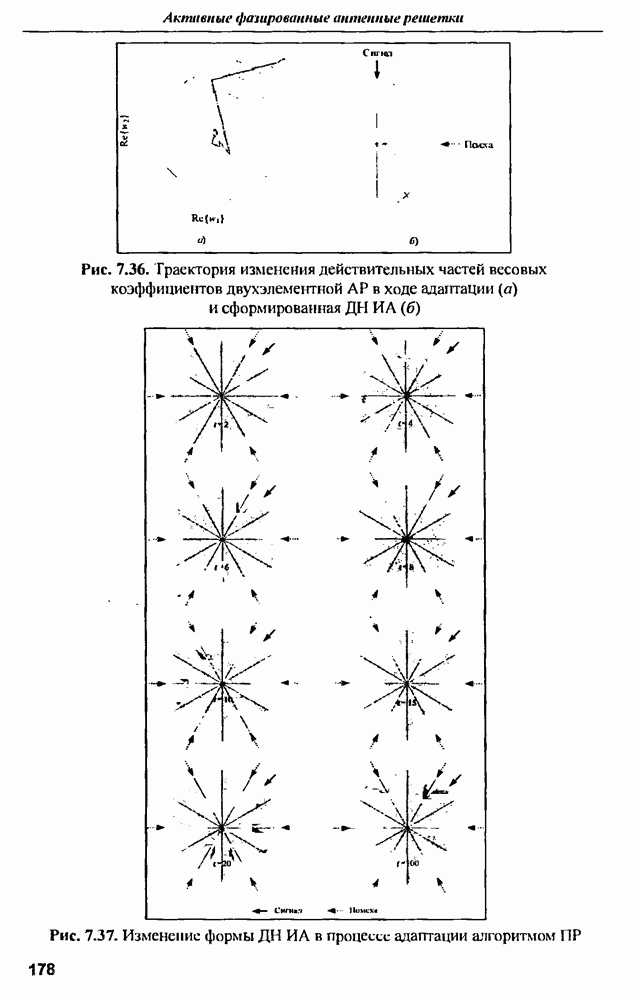
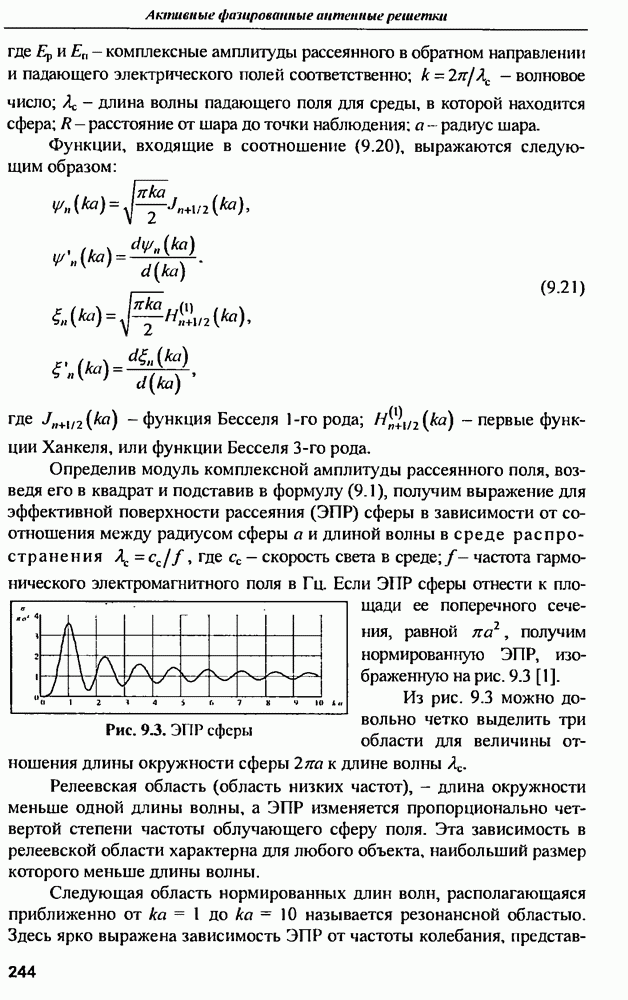
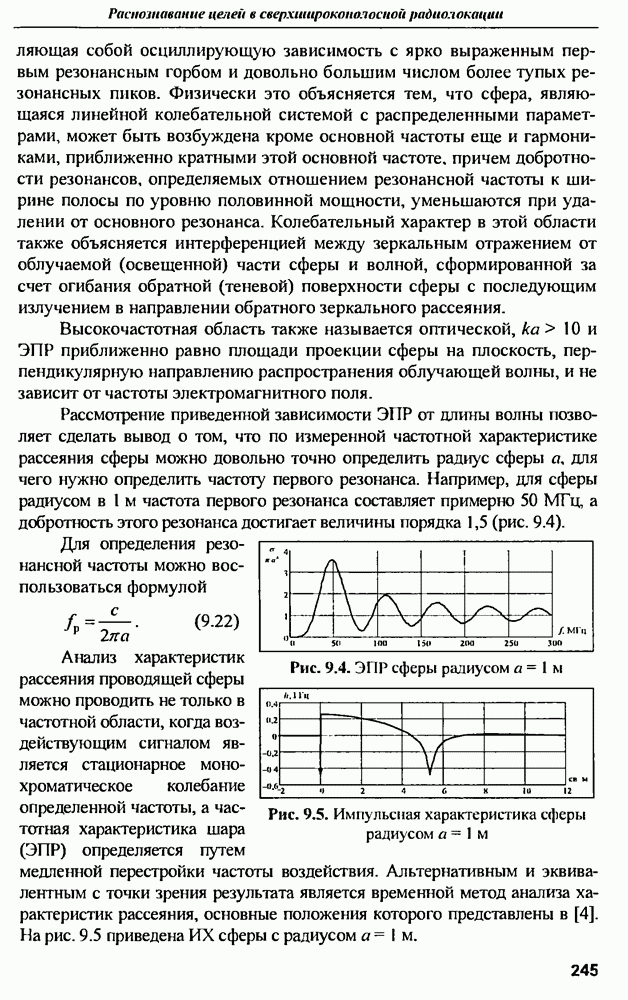
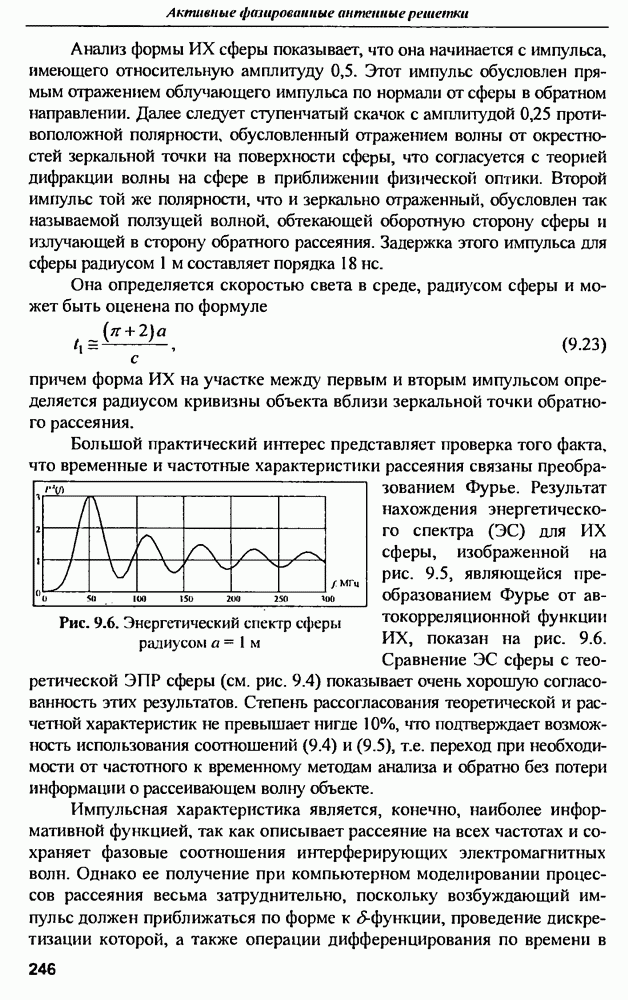
Для наглядности примера в качестве усилителя АФАР использована лампа бегущей волны (ЛБВ), (раза выходного сигнала которой имеет большую зависимость от напряжения питания (см. рис. 2.7,б.в). Как видно из таблицы, многоканальное звено усилителей существенно снижает полный КПД всех последующих звеньев Так, например, звено модуляторов имеет на выходе среднеквадратичное отклонение фазы выходного напряжения от номинала - всего 1,5%, но полный КПД этого звена падает почти вдвое (с 80 до 41%) за счет увеличения отклонений фазы в звене усилителей. КПД рассматриваемой  За счет фазовых ошибок в многоканальных звеньях ее полный КПД снижается до 3,3%. Таким образом, неидентичность параметров элементов в многоканальных звеньях может приводить к значительному ухудшению энергетики АФАР.
За счет фазовых ошибок в многоканальных звеньях ее полный КПД снижается до 3,3%. Таким образом, неидентичность параметров элементов в многоканальных звеньях может приводить к значительному ухудшению энергетики АФАР.
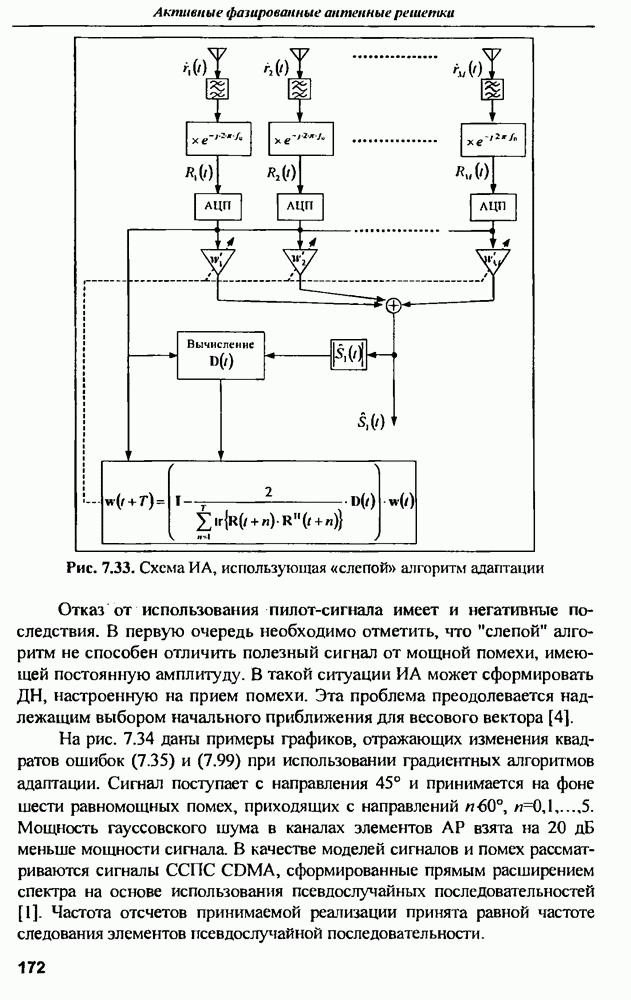
В современных АФАР используются транзисторные усилители мощности, имеющие значительно меньшую зависимость фазы выходного сигнала от напряжения питания, чем ЛБВ. Поэтому при замене ЛБВ транзисторными усилителями полный КПД АФАР повышается с 3.3 до 9.2% Однако и в этом случае вклад ошибок фазового распределения в уменьшение полного КПД составляет почти 6%. Причина заключается в низком коэффициенте усиления одного каскада транзисторного усилителя. Чтобы получить такой же высокий коэффициент усиления, как у ЛБВ необходим транзисторный усилитель состоящий из 6-7 каскадов. В результате КПД многокаскадного усилителя уменьшается, а зависимость фазы выходного сигнала от напряжения питания (по сравнению с одним каскадом) увеличивается. Снижается и надежность усилителя Поэтому в некоторых случаях (например, на космических платформах) оказывается целесообразнее использовать в АФАР не транзисторы, а дешевые ЛБВ, выполненные методом печатной технологии, и стабильный источник питания.
Полученные выше формулы позволяют получить статистические характеристики амплитудного и фазового распределения на апертуре, а на следующем этапе проектирования АФАР определить не только КНД, но и ширину луча, УБЛ и другие характеристики излучения этой антенны.
Расчет основных энергетических характеристик АФАР (п.п. 2.3 и 2.4) выполнен с рядом приближений. Есть также и другие характеристики, которые необходимо учитывать при проектировании АФАР - это степень согласования усилителя и излучателя, величина корреляции амплитудных и фазовых ошибок по раскрыву антенны и другие. Для полной оценки характеристик АФАР создана ее математическая модель, позволяющая сформировать структуру системы и выбрать ее основные элементы.
Основной задачей моделирования является оптимизация структуры АФАР, которая заключается в сравнении различных вариантов этой структуры по принятому критерию и выбору варианта, наилучшим образом соответствующего этому критерию Для этого созданы программы. позволяющие выделить параметры оптимизации, составить целевую функцию (показатель качества) и численными методами решить задачу оптимизации АФАР по выбранному критерию.
Если АФАР характеризуется несколькими показателями качества, то задача оптимизации становится многокритериальной. Для ее решения создана процедура формирования единой целевой функции. При оптимизации АФАР, в зависимости от ее назначения, в качестве критерия чаще всего выбираются энергетический потенциал, потребляемая мощность, полная масса, стоимость. Описание полной модели АФАР и процесса ее оптимизации выходят за рамки настоящей главы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
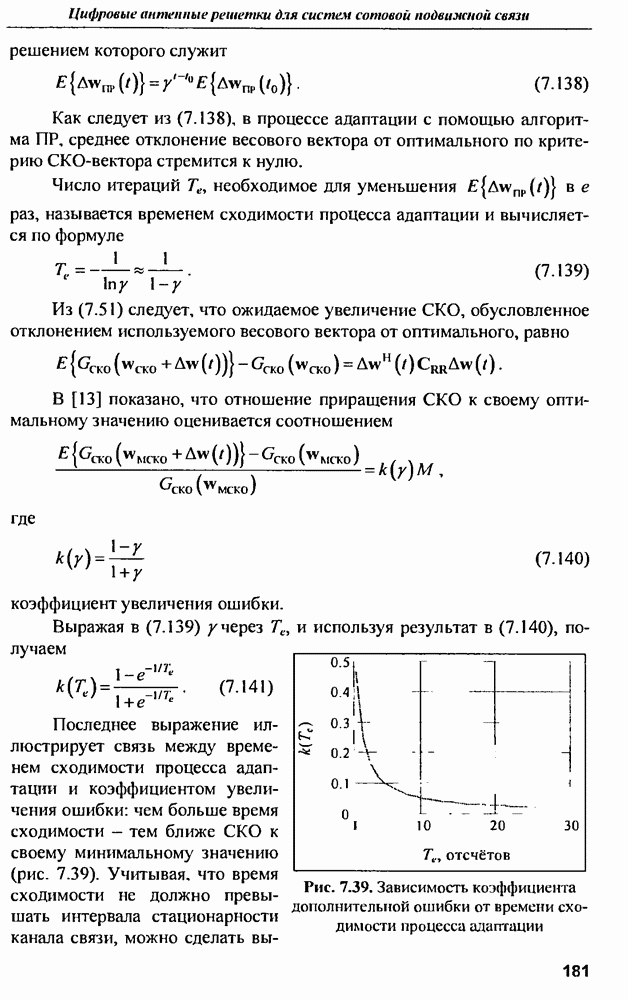
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
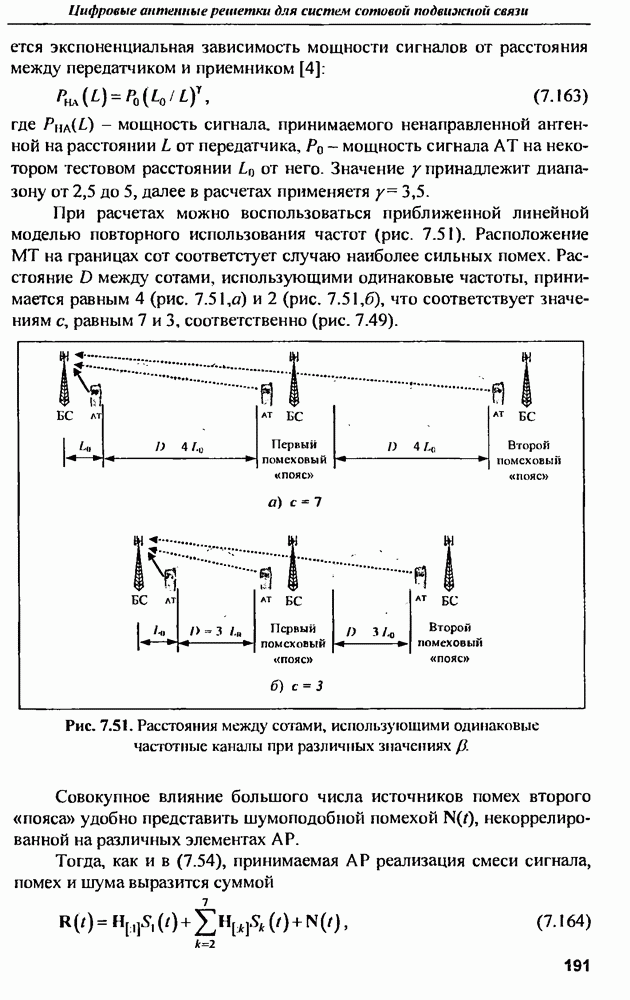
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
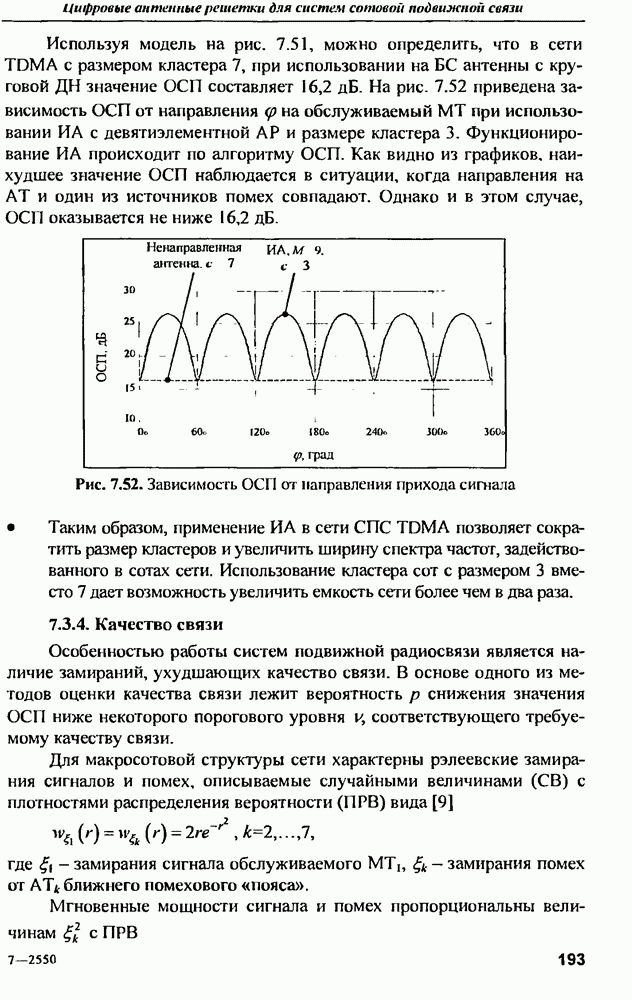
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
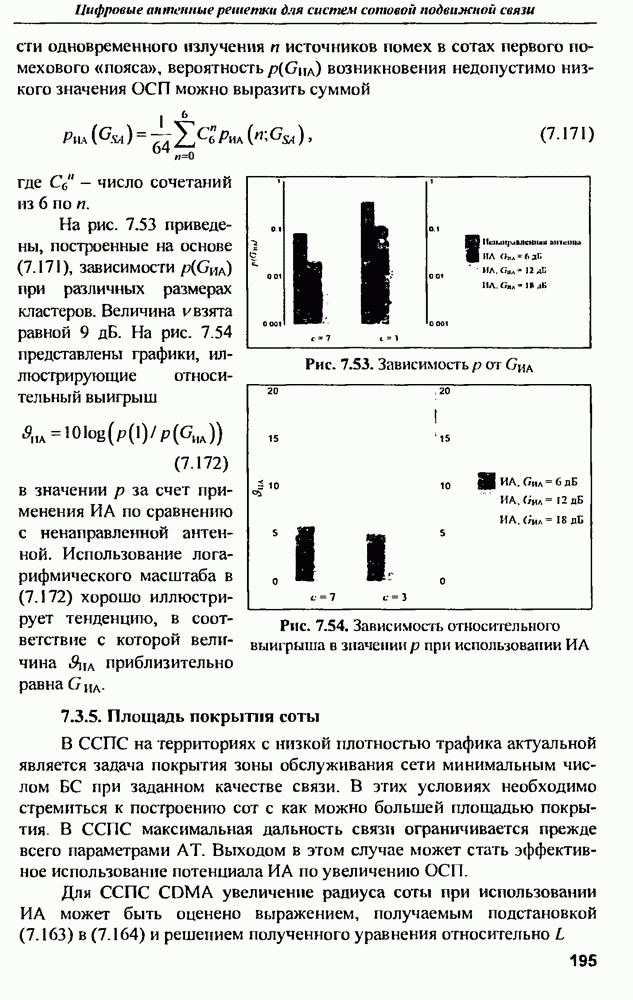
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
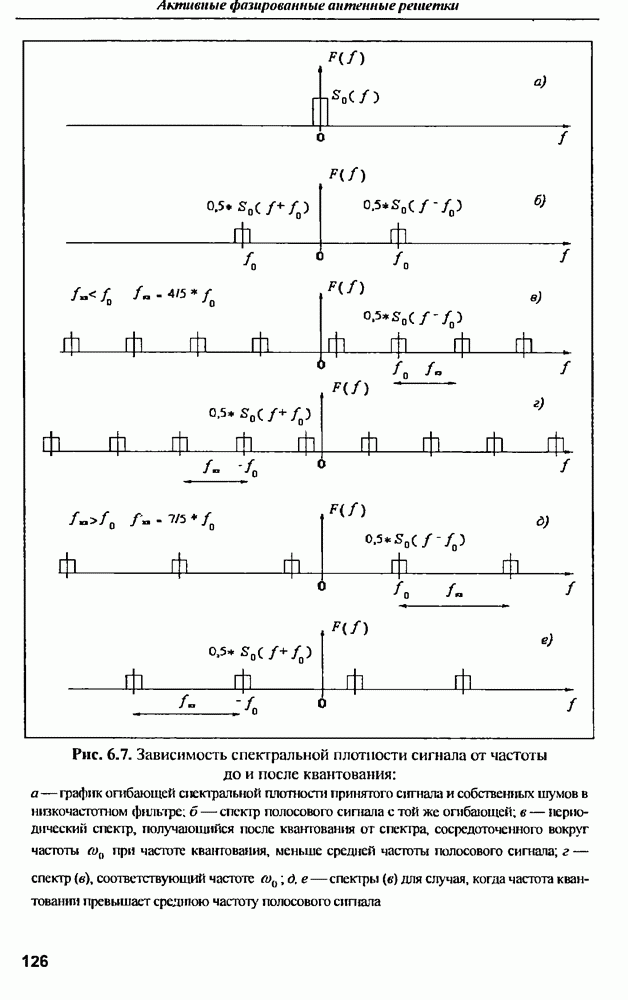
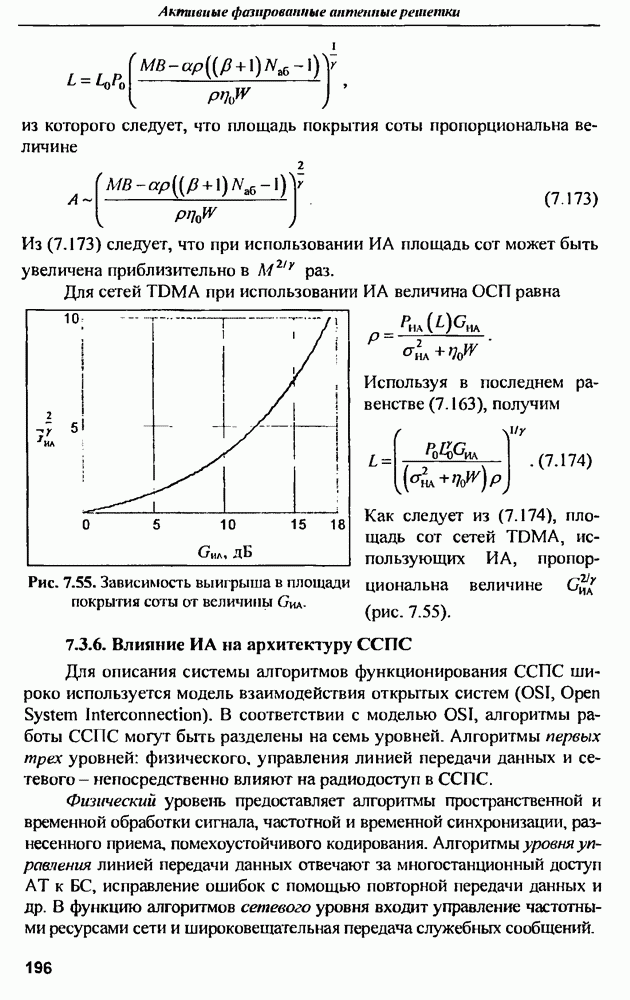
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
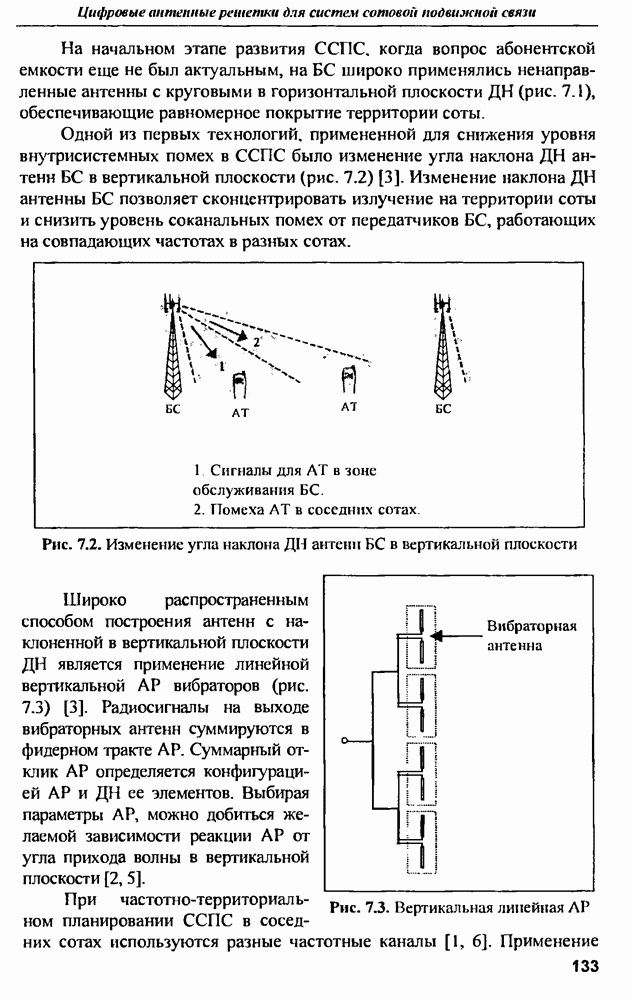
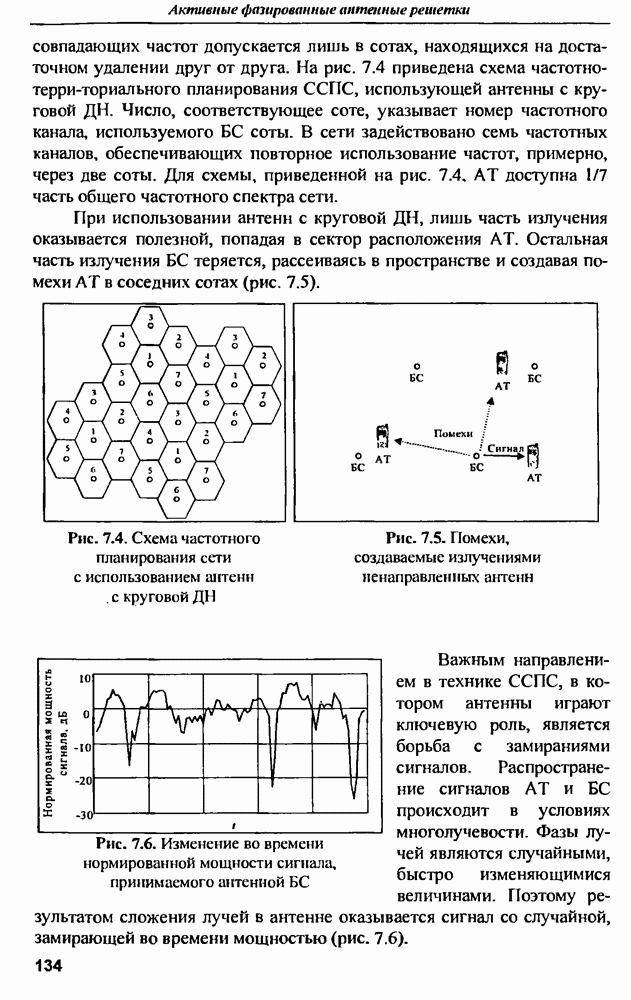
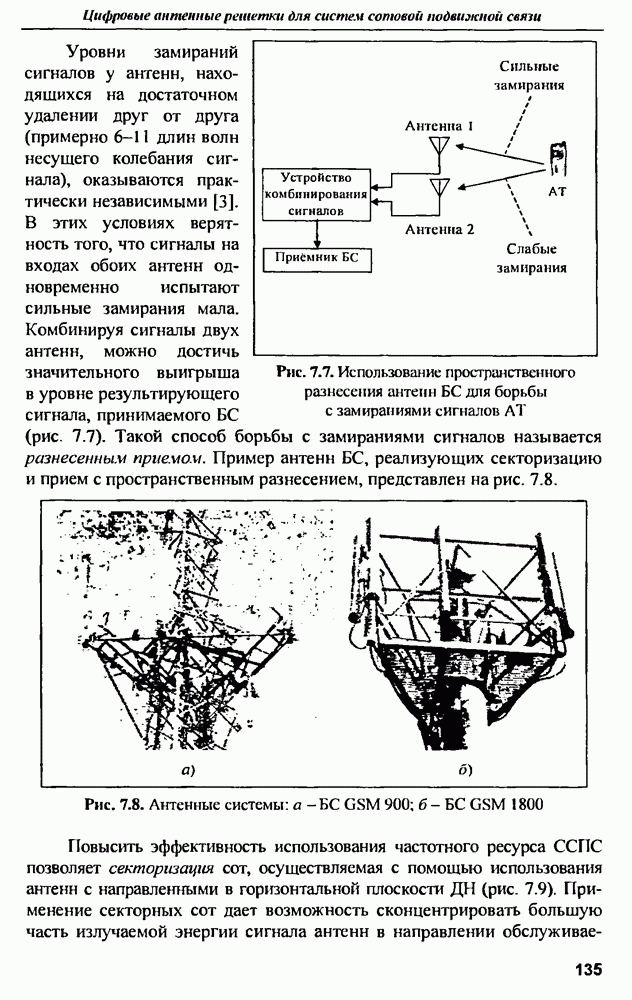
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
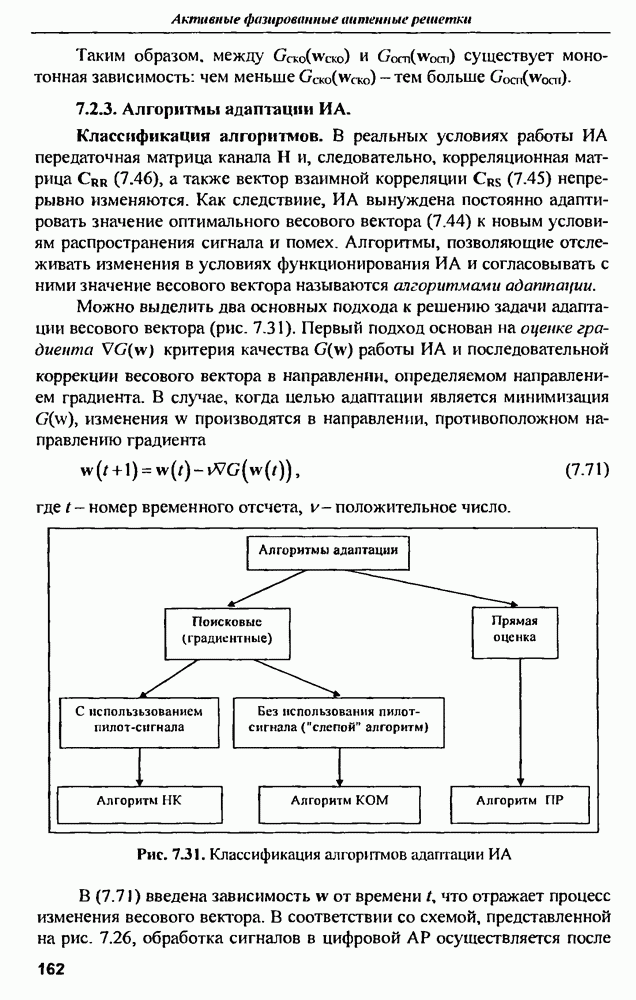
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
- 7.3.4. Качество связи
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
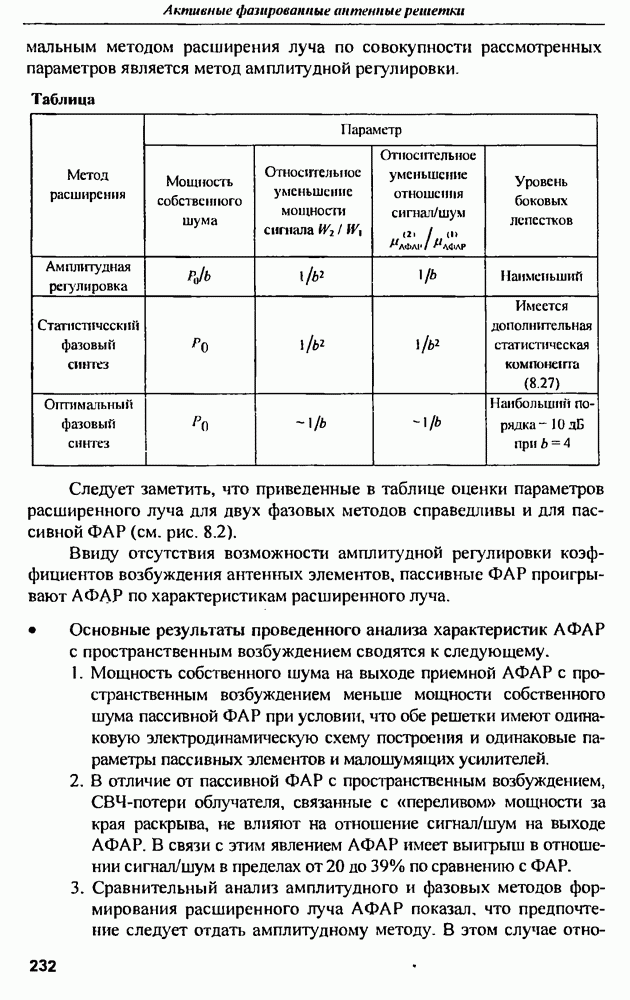
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
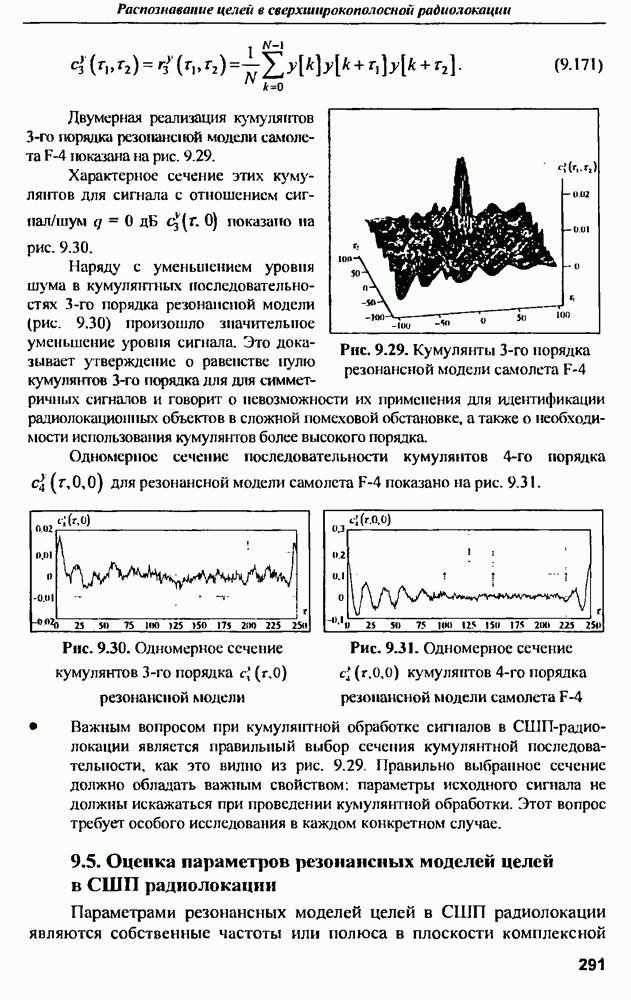
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
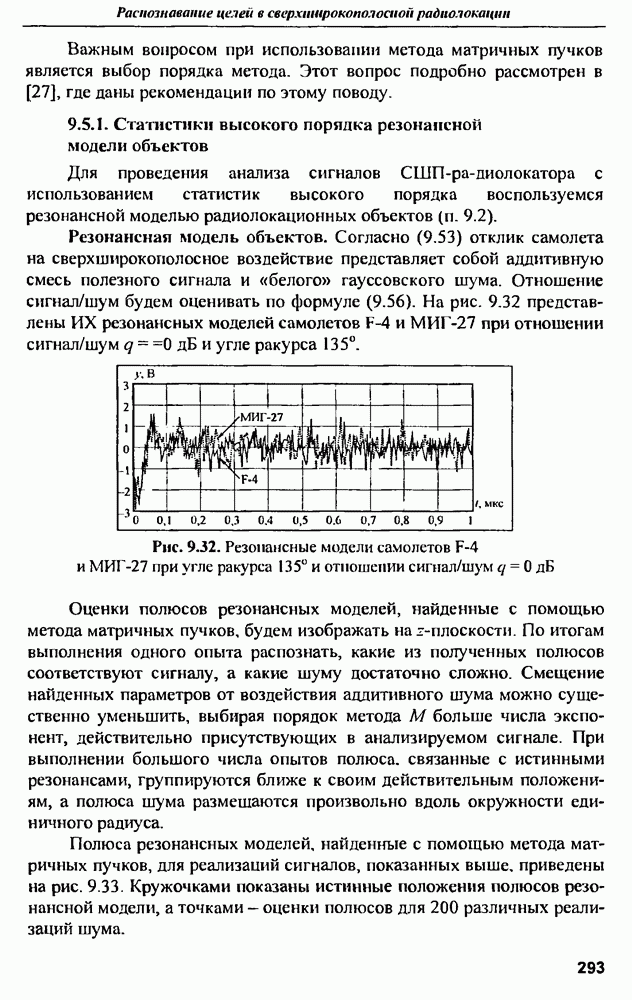
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
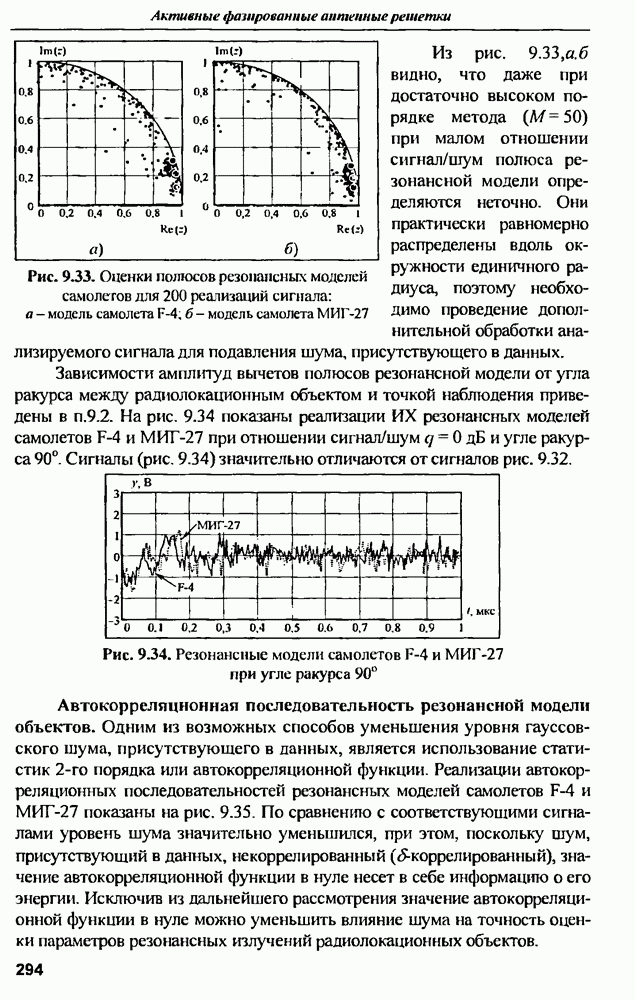
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
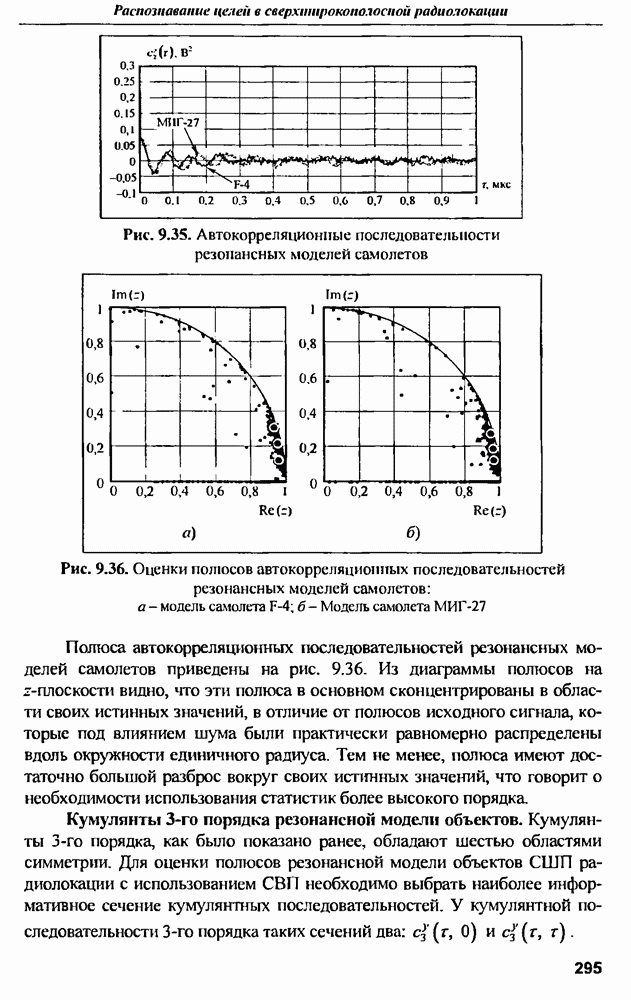
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
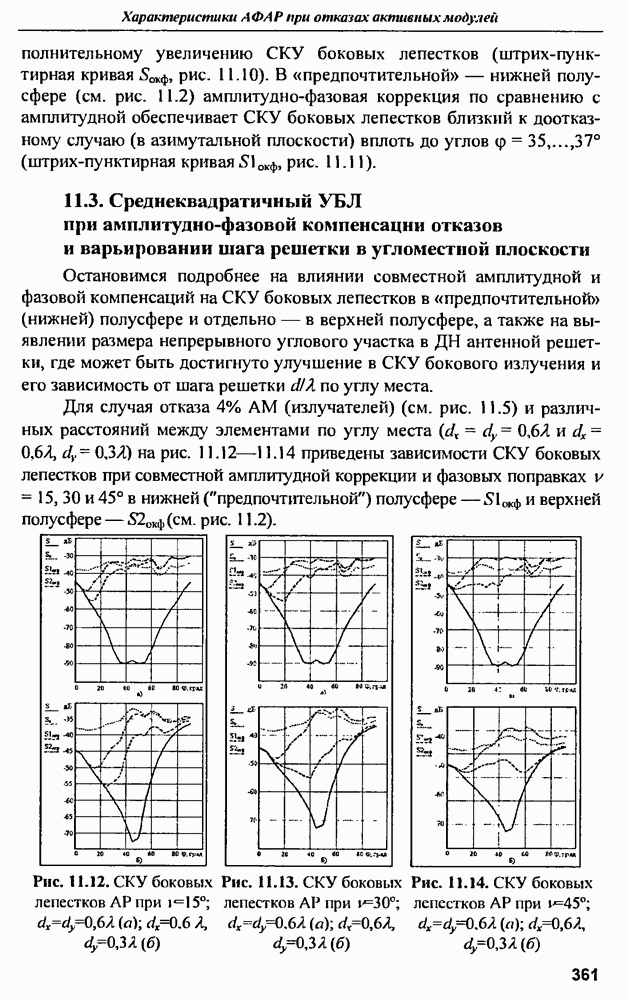
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
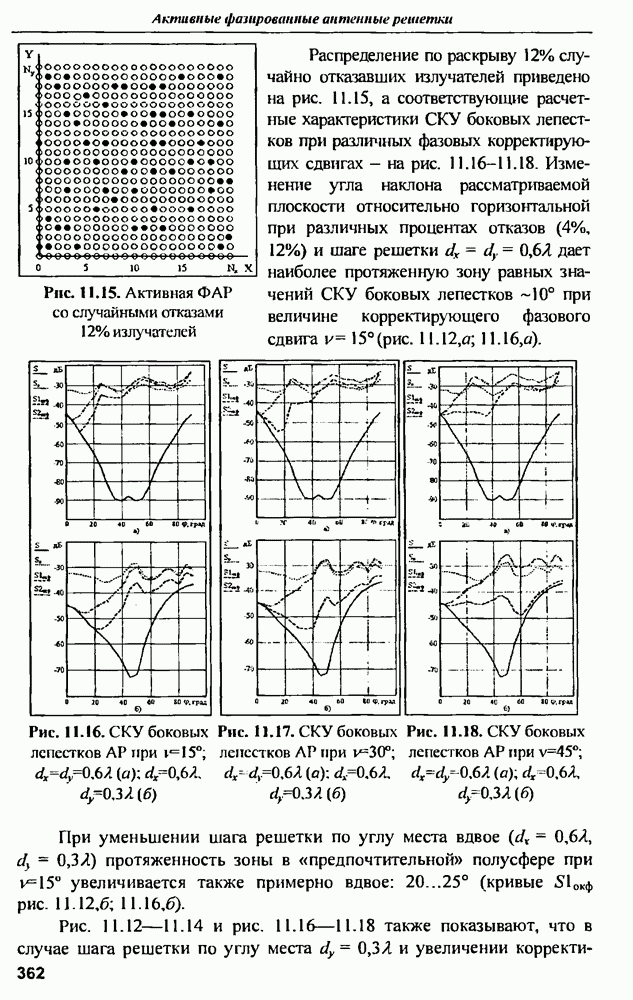
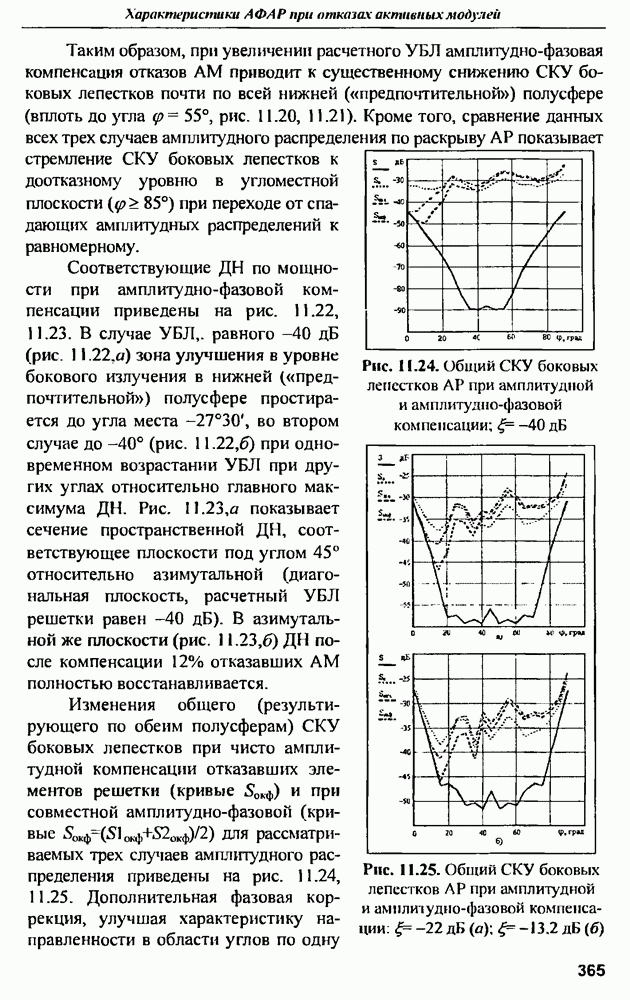
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
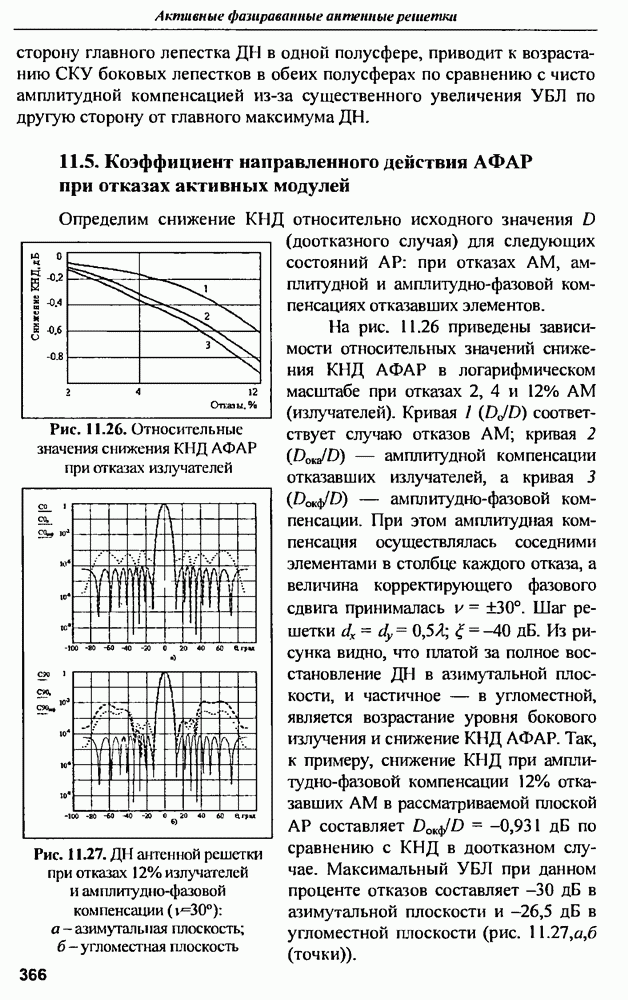
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
- 14.3. Комбинированные антенны
- 14.4. Антенные решетки
- 14.5. Приемные антенны
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
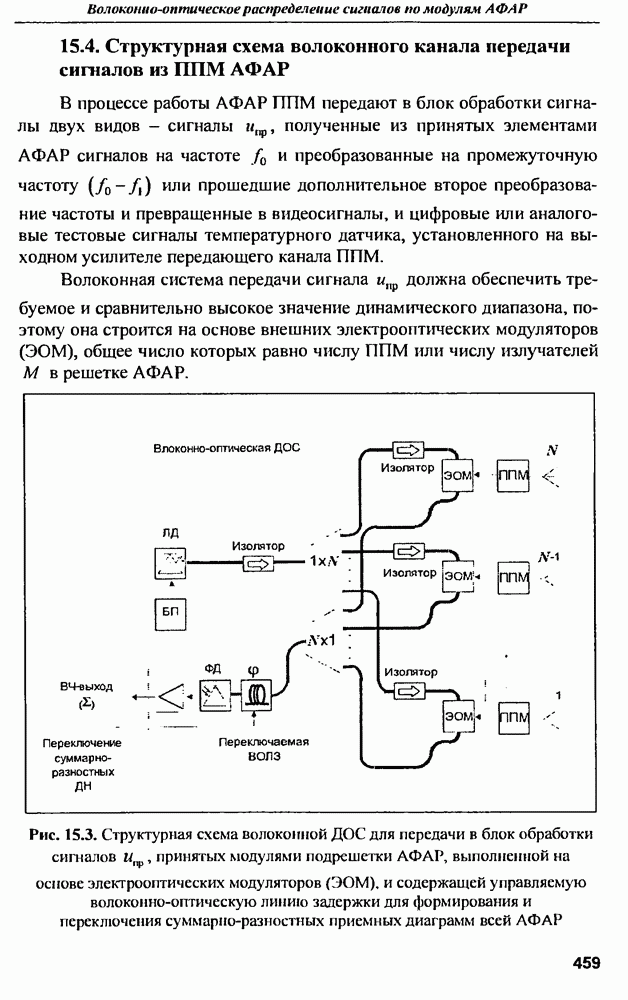
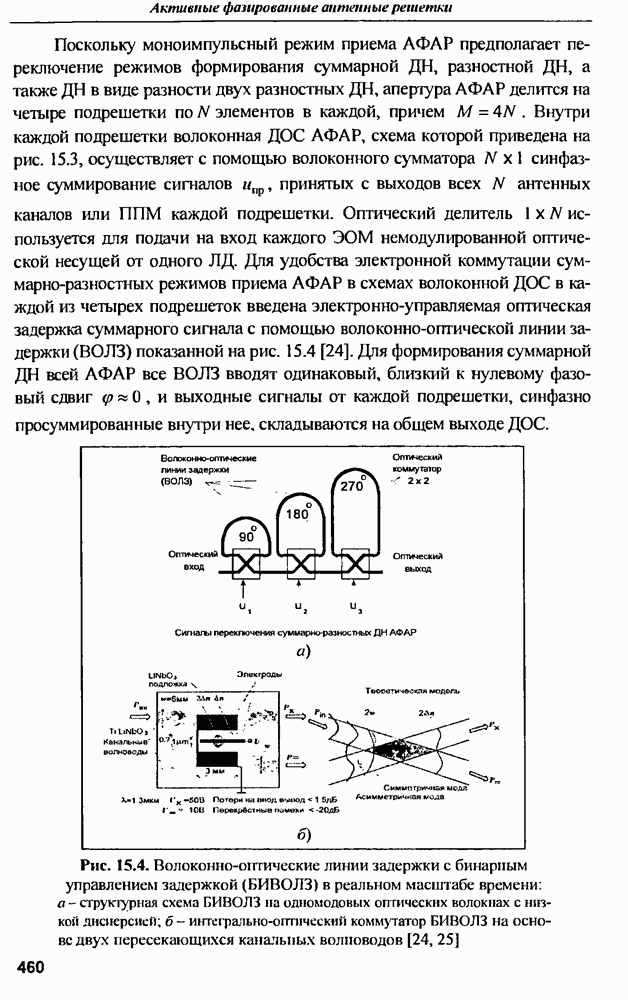
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
- 15.8.4. Оптические делители
- 15.8.5. Внешние модуляторы
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР