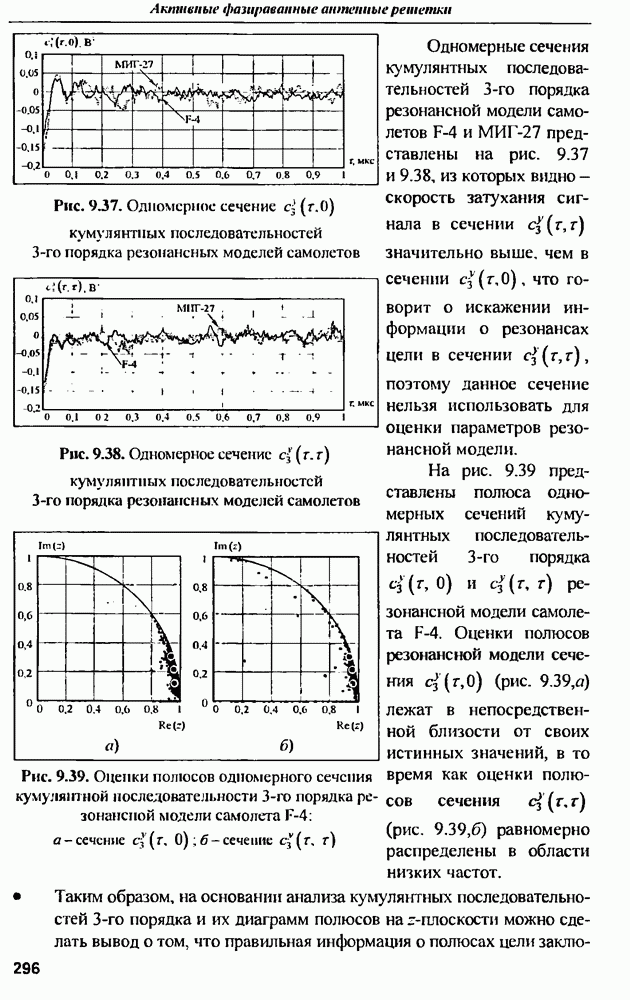
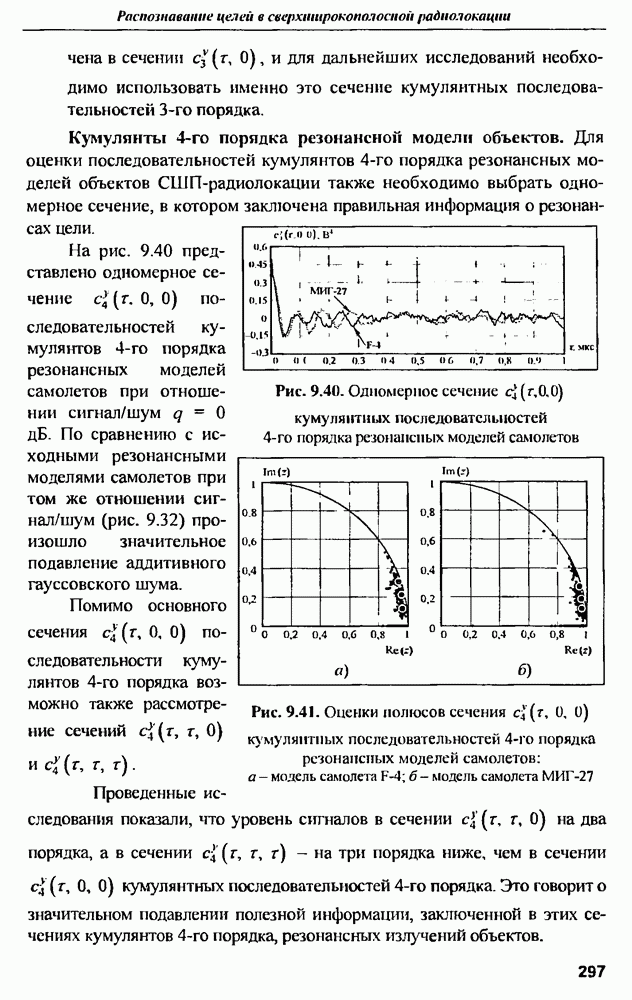
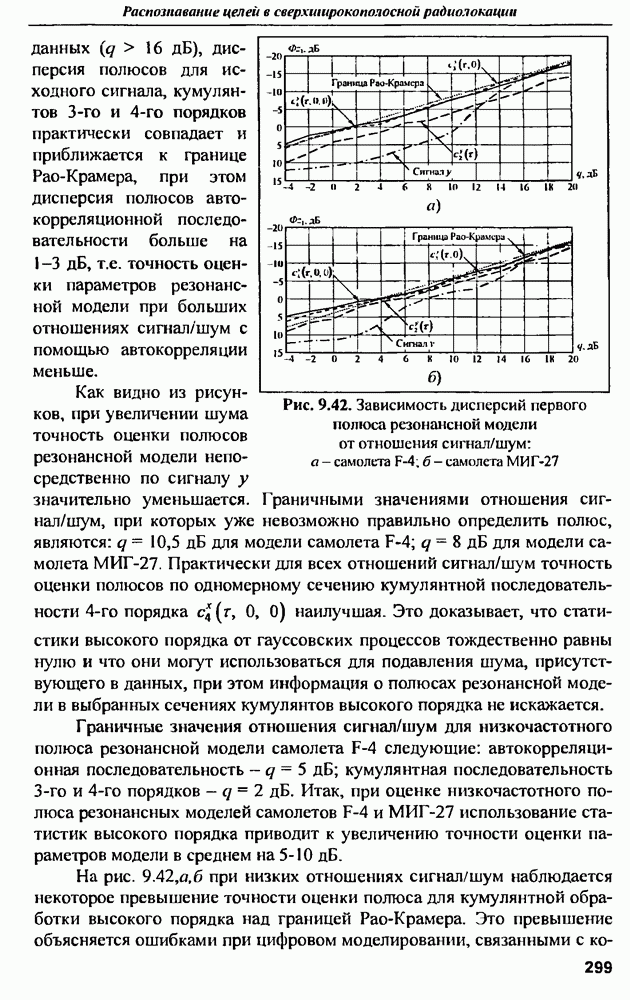
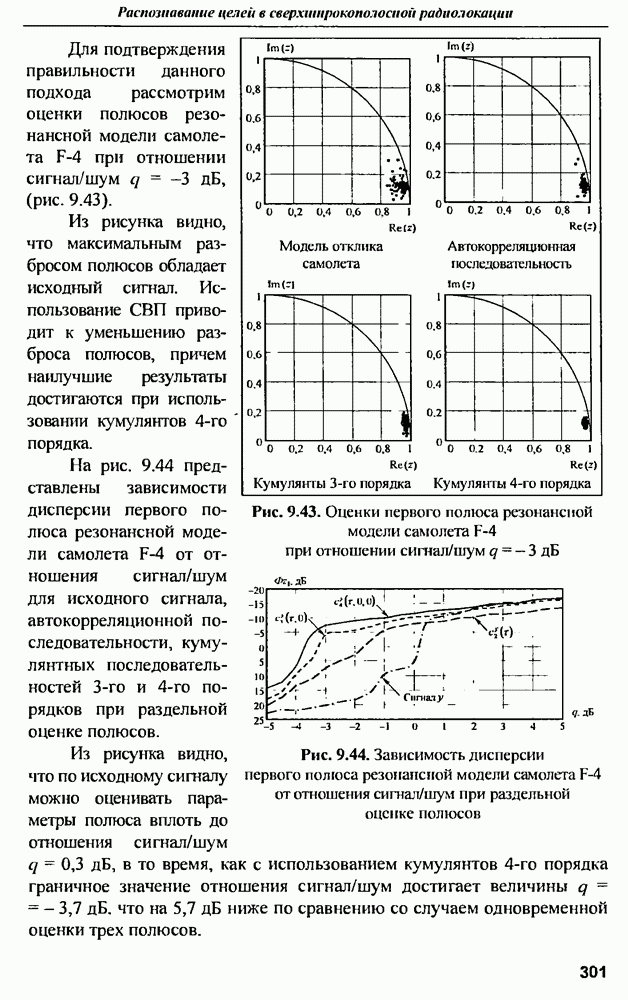
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.2. Антенные решетки с цифровым формированием ДН
Цифровое формирование ДН основано на возможности представления принятых антенной сигналов в виде числовой последовательности, по которой с любой требуемой точностью могут быть восстановлены принятые и преобразованные в последовательность сигналы. На такую возможность впервые обратил внимание Котельников [13, 14]. Представление Котельникова справедливо для ограниченных на вещественной оси функций с ограниченным спектром относительно нулевой частоты [15, 17]. Это представление обобщается на случай полосового сигнала, который может быть записан в форме

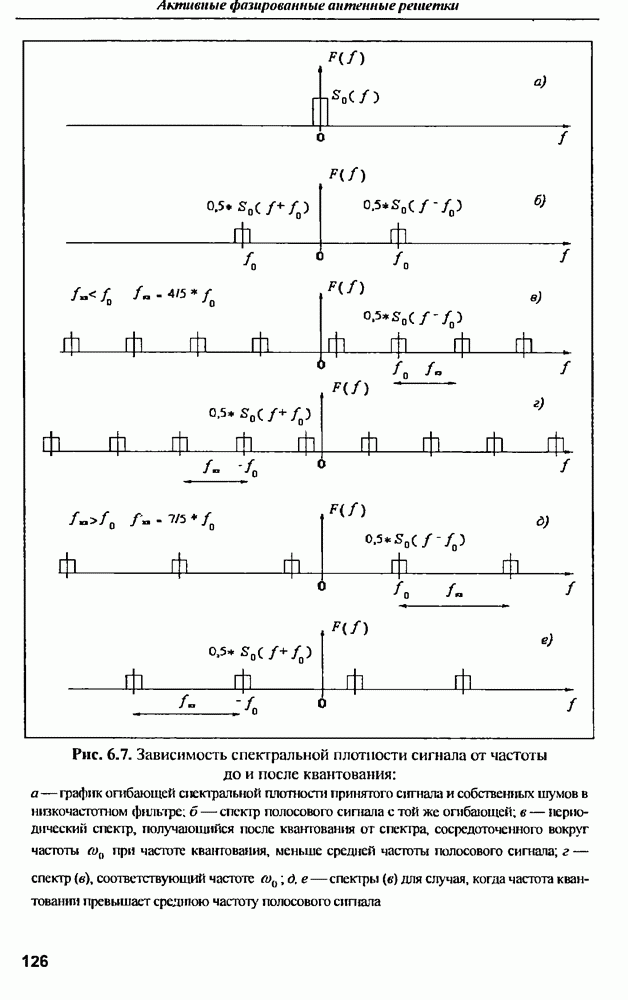
Форма спектра такого сигнала определяется его огибающей  , а положение — частотой
, а положение — частотой  . Если спектр огибающей (сигнала с нулевой средней частотой)
. Если спектр огибающей (сигнала с нулевой средней частотой)  то спектр сигнала (12) расщепляется [17], располагаясь в токчах
то спектр сигнала (12) расщепляется [17], располагаясь в токчах  на частотной оси. В этих точках он соответственно равен:
на частотной оси. В этих точках он соответственно равен:  Так как используется комплексная форма спектрального разложения вещественного сигнала, то модуль спектра — симметричная функция относительно средней частоты
Так как используется комплексная форма спектрального разложения вещественного сигнала, то модуль спектра — симметричная функция относительно средней частоты  , фаза — антисимметричная.
, фаза — антисимметричная.
Последовательность должна быть образована путем измерения значений сигнала в последовательные моменты времени  обычно с постоянным шагом
обычно с постоянным шагом  При этом должно соблюдаться неравенство
При этом должно соблюдаться неравенство

где  ширина спектра огибающей принятого сигнала по уровню, принятому за нулевой.
ширина спектра огибающей принятого сигнала по уровню, принятому за нулевой.
Сигнал может быть восстановлен с помощью формулы

При  получаем формулу Котельникова. В соответствии с неравенством (6.13) частота квантования может превышать ширину спектра сигнала, поэтому в (6 14) используется
получаем формулу Котельникова. В соответствии с неравенством (6.13) частота квантования может превышать ширину спектра сигнала, поэтому в (6 14) используется 
Следует отметить, что в случае радиолокации восстановление сигнала не требуется, так как характеристики целей вычисляются с помощью числовых последовательностей Для цифровой обработки принятых излучателями сигналов обычно используют их комплексную форму. Сопряженный сигнал  может быть получен из принятого сигнала
может быть получен из принятого сигнала  с помощью преобразования Гильберта [17]
с помощью преобразования Гильберта [17]

или путем введения запаздывания по фазе на величину  всех спектральных составляющих принятого сигнала, применением квадратурного смесителя и двух аналогоцифровых преобразователей (АЦП), а также цифровым способом, например цифровым преобразованием частоты, из числовой последовательности принятого сигнала.
всех спектральных составляющих принятого сигнала, применением квадратурного смесителя и двух аналогоцифровых преобразователей (АЦП), а также цифровым способом, например цифровым преобразованием частоты, из числовой последовательности принятого сигнала.
Следует отметить, что сигнал, выражаемый формулой

называется комплексным (аналитическим) сигналом, а при переходе к числовым последовательностям - комплексной числовой последовательностью [19]. Например, если  то из (15) следует, что
то из (15) следует, что

Спектральная функция комплексного сигнала равна нулю в области отрицательных частот и удвоенному значению спектральной функции исходного сигнала в области положительных частот
Теория, методы расчета и технология  использующая большие антенные решетки с цифровым формированием
использующая большие антенные решетки с цифровым формированием  начали развиваться с середины 70-х годов [5] и к настоящему времени такие станции уже существуют. Схема ФАР с цифровым формированием
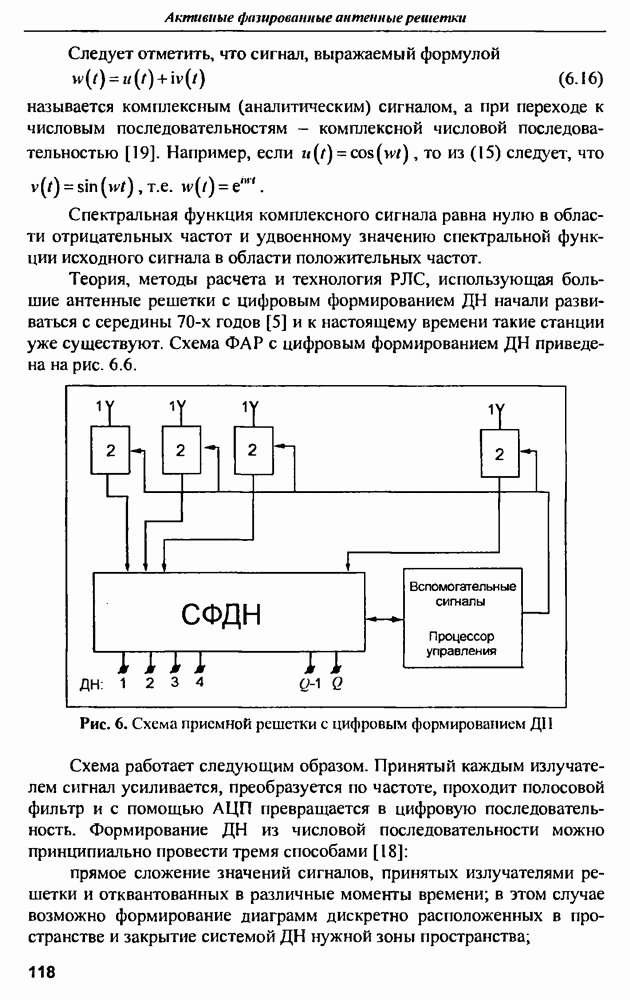
начали развиваться с середины 70-х годов [5] и к настоящему времени такие станции уже существуют. Схема ФАР с цифровым формированием  приведена на рис. 6.6.
приведена на рис. 6.6.

Рис. 6. Схема приемной решетки с цифровым формированием ДН
Схема работает следующим образом. Принятый каждым излучателем сигнал усиливается, преобразуется по частоте, проходит полосовой фильтр и с помощью АЦП превращается в цифровую последовательность. Формирование  из числовой последовательности можно принципиально провести тремя способами [18]:
из числовой последовательности можно принципиально провести тремя способами [18]:
прямое сложение значений сигналов, принятых излучателями решетки и отквантованных в различные моменты времени, в этом случае возможно формирование диаграмм дискретно расположенных в пространстве и закрытие системой  нужной зоны пространства;
нужной зоны пространства;
сложение вычисленных, например, с помощью выражения (6.15), значений сигналов от излучателей в моменты времени, обеспечивающие квазинепрерывное перемещение  в пространстве (между двумя последовательными моментами квантования);
в пространстве (между двумя последовательными моментами квантования);
введение в числовые последовательности излучателей фазовых сдвигов с последующим сложением получаемых значений, соответствующих одним и тем же моментам квантования.
Во всех случаях возможно управление амплитудным распределением путем умножения значений сигналов излучателей на амплитудные коэффициенты перед сложением. Рассмотрим эти способы более подробно.
Прямое сложение значений сигналов. В этом случае алгоритм формирования диаграммы для случая расположения излучателей в узлах прямоугольной сетки может быть выражен формулой

где  — номер формируемой
— номер формируемой  номер излучателей по отношению к центральному;
номер излучателей по отношению к центральному;  — числовая последовательность на выходе излучателя
— числовая последовательность на выходе излучателя  . В (17) формирование
. В (17) формирование  произведено относительно момента квантования
произведено относительно момента квантования  Принятый излучателем
Принятый излучателем  сигнал может быть записан в форме
сигнал может быть записан в форме

где

 направление максимума формируемой диаграммы,
направление максимума формируемой диаграммы,  функция округления аргумента до целого числа;
функция округления аргумента до целого числа;  шаг аналого-цифрового преобразования.
шаг аналого-цифрового преобразования.
Положение максимумов формируемых  через период квантования
через период квантования  определяется соотношениями
определяется соотношениями

где  целые числа, которые могут быть отождествлены с номером
целые числа, которые могут быть отождествлены с номером  Если положить
Если положить  то
то  и требуемая частота квантования определится выражением
и требуемая частота квантования определится выражением  где
где  расстановка диаграмм.
расстановка диаграмм.
Обычно ширина  больших
больших  бывает
бывает  При этом оптимальная расстановка
При этом оптимальная расстановка  в системе пересекающихся диаграмм составляет
в системе пересекающихся диаграмм составляет
примерно половину ширины  по уровню
по уровню  . Возьмем
. Возьмем  рад, тогда расстановка
рад, тогда расстановка  равна 0,02, для чего требуется частота квантования
равна 0,02, для чего требуется частота квантования  Такая частота дискретизации сигнала даже при работе в дециметровом диапазоне волн к настоящему времени неосуществима Этот метод реализуется в акустических станциях, так как скорость распространения звуковых волн на несколько порядков меньше чем электромагнитных.
Такая частота дискретизации сигнала даже при работе в дециметровом диапазоне волн к настоящему времени неосуществима Этот метод реализуется в акустических станциях, так как скорость распространения звуковых волн на несколько порядков меньше чем электромагнитных.
Сложение вычисленных значений сигналов. Из проведенного выше рассмотрения следует, что для реализации метода временных задержек нужно знать значения принятых излучателями сигналов в более частые промежутки времени, чем это нужно для их представления в виде числовых последовательностей по занимаемой сигналами полосе частот в соответствии с теоремой Котелъникова. Кроме того, для возможности ориентации формируемых  в произвольном направлении в пространстве нужно иметь значения сигналов в любые значения времени между моментами квантования. Такая возможность позволяет также производить адаптивное формирование
в произвольном направлении в пространстве нужно иметь значения сигналов в любые значения времени между моментами квантования. Такая возможность позволяет также производить адаптивное формирование 
Значение сигнала в любой момент времени может быть определено с помощью выражения (6 15) или других формул. Этот способ формирования  недостаточно изучен, хотя требуемая для его реализации производительность вычислительных средств по результатам оценки частного случая [18] лишь в несколько раз превосходит производительность средств, для получившего распространение способа непосредственного ввода фазового сдвига, рассмотренного ниже. Внедрение способа формирования
недостаточно изучен, хотя требуемая для его реализации производительность вычислительных средств по результатам оценки частного случая [18] лишь в несколько раз превосходит производительность средств, для получившего распространение способа непосредственного ввода фазового сдвига, рассмотренного ниже. Внедрение способа формирования  путем сложения вычисленных значений сигнала весьма перспективно для РЛС с высоким разрешением по дальности.
путем сложения вычисленных значений сигнала весьма перспективно для РЛС с высоким разрешением по дальности.
Метод введения фазового сдвига в числовые последовательности. Практическое применение для ФАР РЛС к настоящему времени получил способ формирования  основанный на введении фазового сдвига в числовые последовательности. Это возможно при узкополосном сигнале, т.е. когда он представим в виде произведения медленно меняющейся огибающей на синусоидальный временной множитель При использовании этого способа принятый каждым излучателем сигнал представляется в аналитической форме (6.16): в последовательность каждого излучателя в сигнал, соответствующий моменту квантования
основанный на введении фазового сдвига в числовые последовательности. Это возможно при узкополосном сигнале, т.е. когда он представим в виде произведения медленно меняющейся огибающей на синусоидальный временной множитель При использовании этого способа принятый каждым излучателем сигнал представляется в аналитической форме (6.16): в последовательность каждого излучателя в сигнал, соответствующий моменту квантования  вводится фазовый сдвиг, который умножается на амплитудный коэффициент. Эти множители обеспечивают адаптивное формирование
вводится фазовый сдвиг, который умножается на амплитудный коэффициент. Эти множители обеспечивают адаптивное формирование  с заданным расположением в пространстве.
с заданным расположением в пространстве.
В множестве вещественных чисел введение фазового сдвига  в колебание
в колебание  (сопряженное колебание
(сопряженное колебание  ) заключается в умножении исходного колебания на
) заключается в умножении исходного колебания на  , а сопряженного колебания на
, а сопряженного колебания на
 и их последующего сложения. В результате получим
и их последующего сложения. В результате получим  т.е. принятый сигнал с введенным фазовым сдвигом. В случае использования метода комплексных амплитуд введение фазового сдвига заключается в умножении отквантованного сигнала в аналитической форме на
т.е. принятый сигнал с введенным фазовым сдвигом. В случае использования метода комплексных амплитуд введение фазового сдвига заключается в умножении отквантованного сигнала в аналитической форме на 
В результате алгоритм цифрового формирования  выражается формулой
выражается формулой

При адаптивном формировании  вектор весовых коэффициентов
вектор весовых коэффициентов  определяется, исходя из выбранного критерия эффективности [7, 8]. Наиболее часто применяется критерий, обеспечивающий максимум отношения мощности сигнала к суммарной мощности сигнала и шумоподобной помехи. В этом случае вектор весовых коэффициентов определяется выражением
определяется, исходя из выбранного критерия эффективности [7, 8]. Наиболее часто применяется критерий, обеспечивающий максимум отношения мощности сигнала к суммарной мощности сигнала и шумоподобной помехи. В этом случае вектор весовых коэффициентов определяется выражением

где  произвольная постоянная;
произвольная постоянная;  ковариационная матрица собственных шумов и принимаемых шумовых сигналов на выходе каналов излучателей;
ковариационная матрица собственных шумов и принимаемых шумовых сигналов на выходе каналов излучателей;  вектор огибающих компонентов полезного сигнала, принимаемого с направления
вектор огибающих компонентов полезного сигнала, принимаемого с направления  в виде плоской волны.
в виде плоской волны.
Ковариационная матрица вычисляется путем обработки системы замеров (матриц) сигналов, принятых излучателями решетки перед зондированием пространства в заданном направлении. Для плоской решетки с излучателями в узлах прямоугольной сетки

При отсутствии внешних шумов матрица  становится диагональной и
становится диагональной и

что соответствует формированию  с постоянным амплитудным и линейным фазовым распределением в раскрыве.
с постоянным амплитудным и линейным фазовым распределением в раскрыве.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
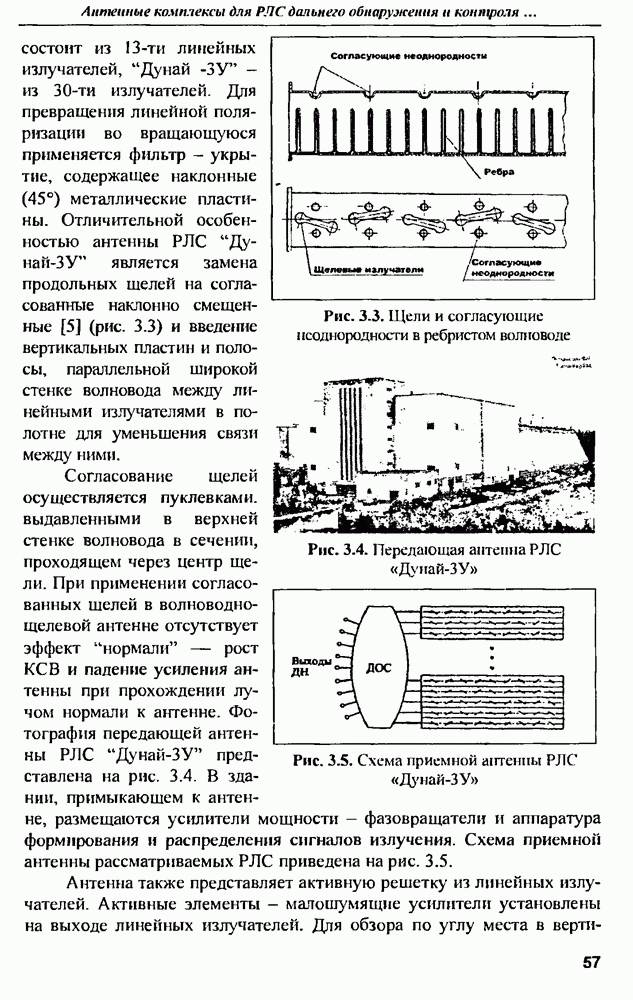
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
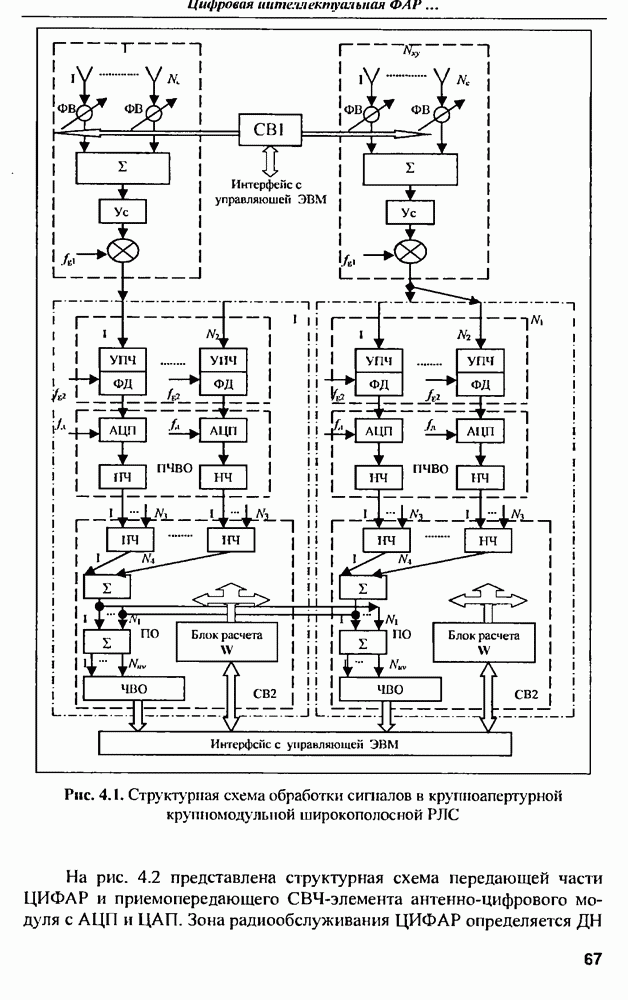
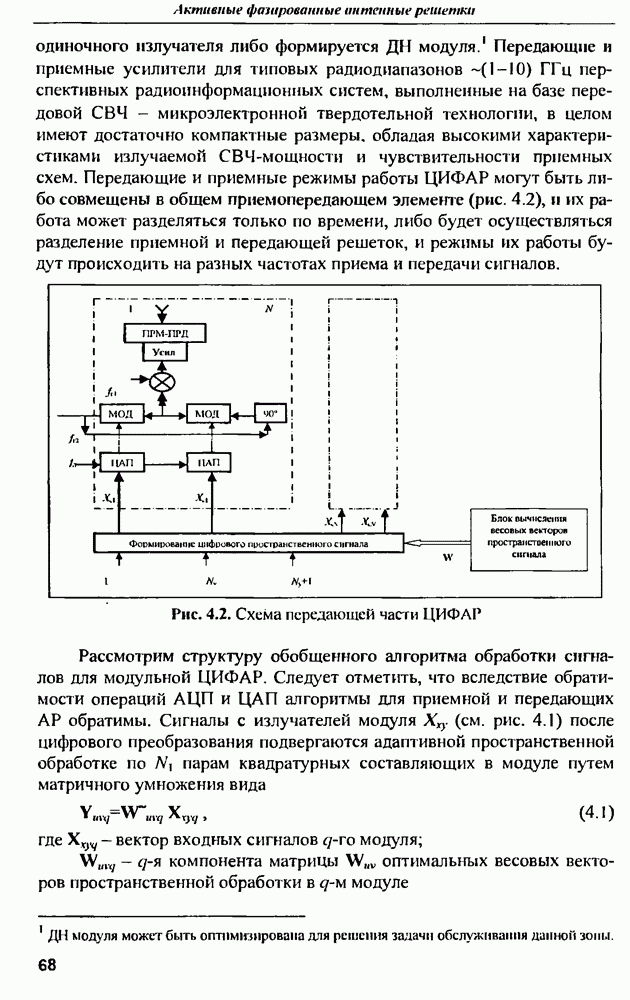
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
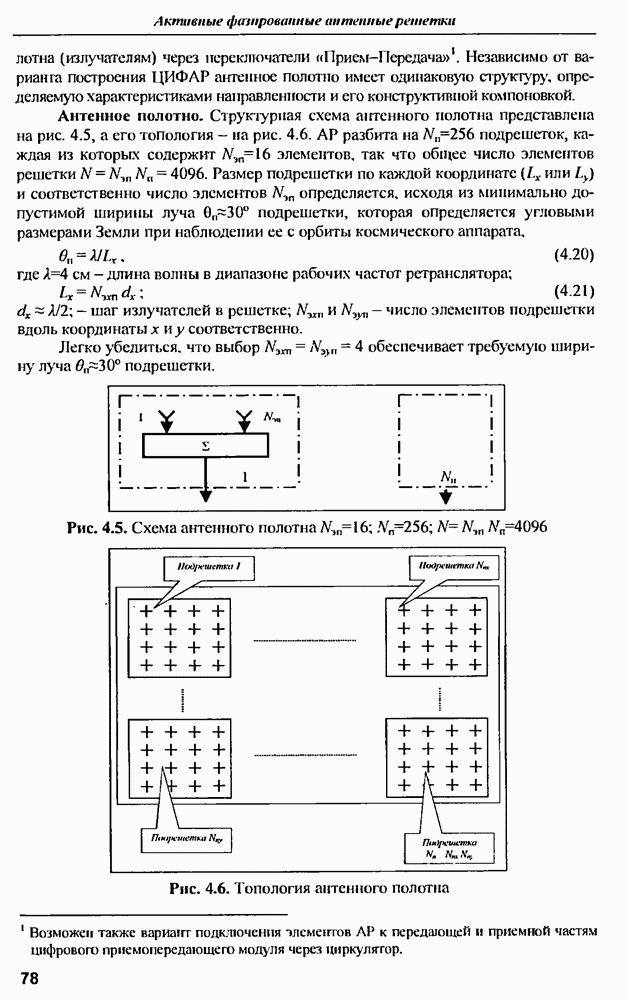
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
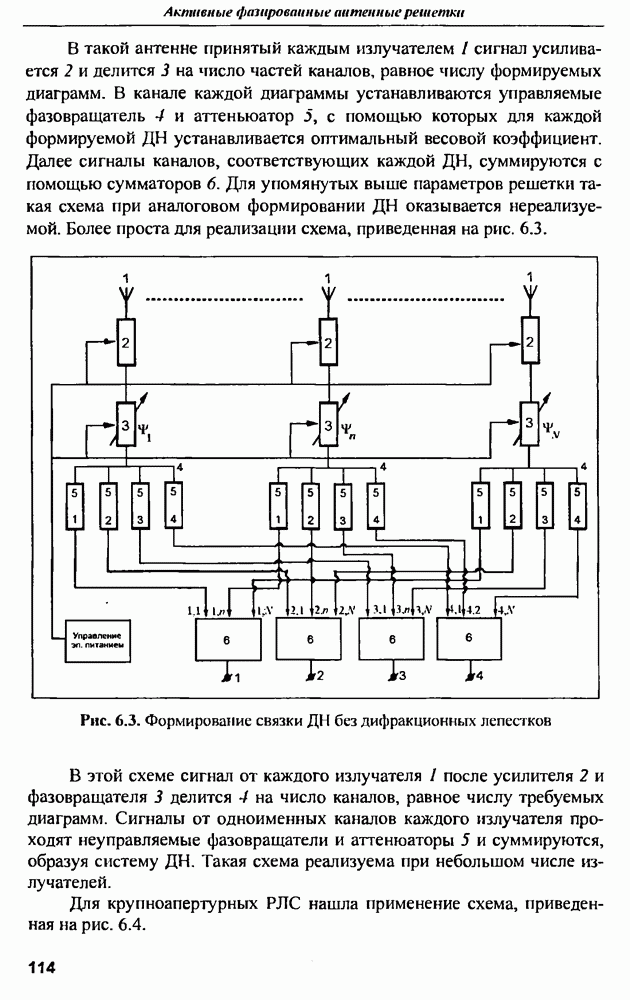
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
- 7.3.4. Качество связи
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
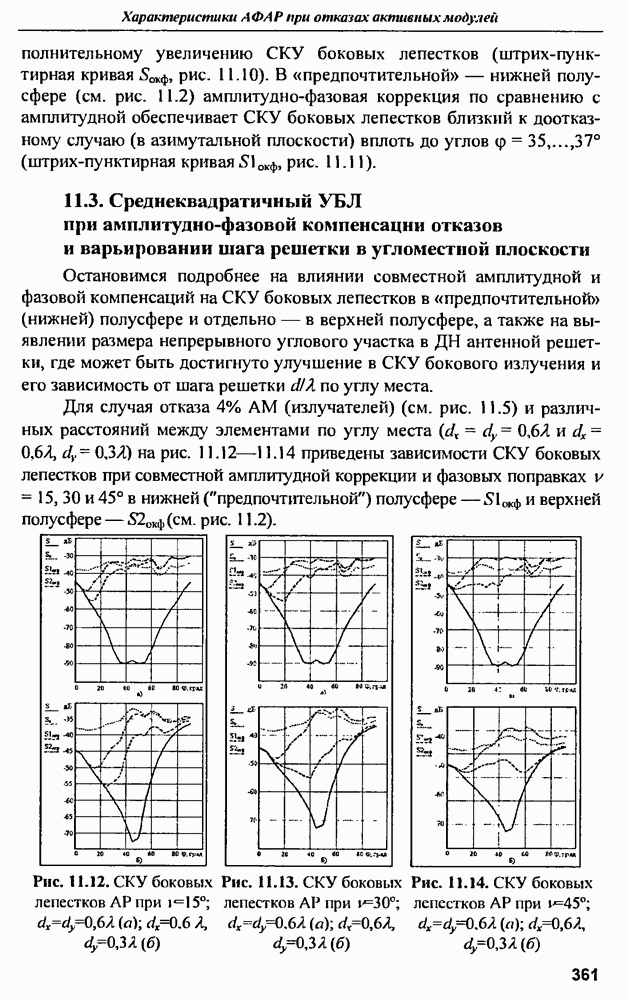
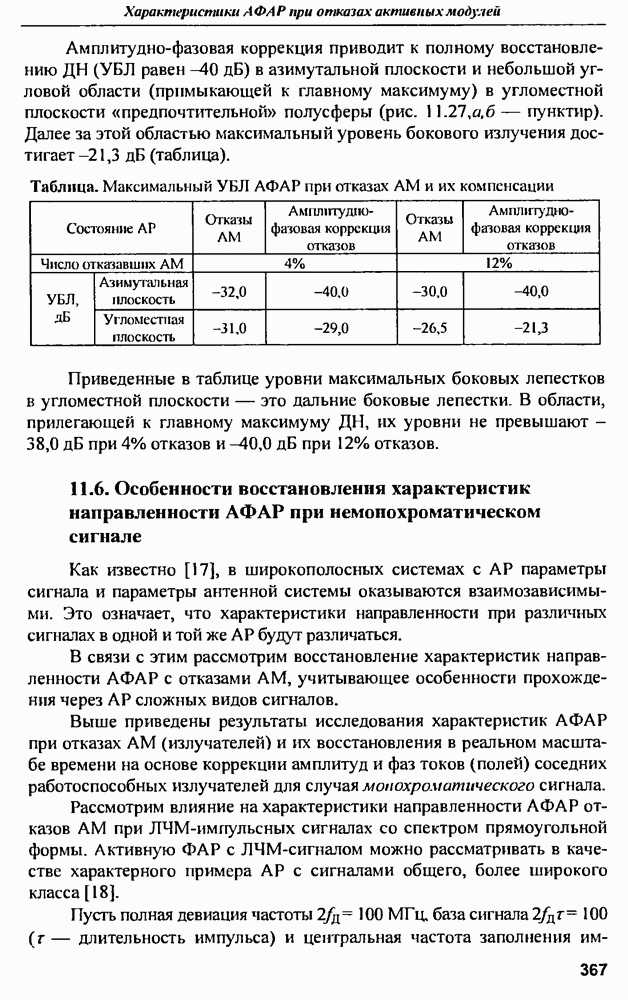
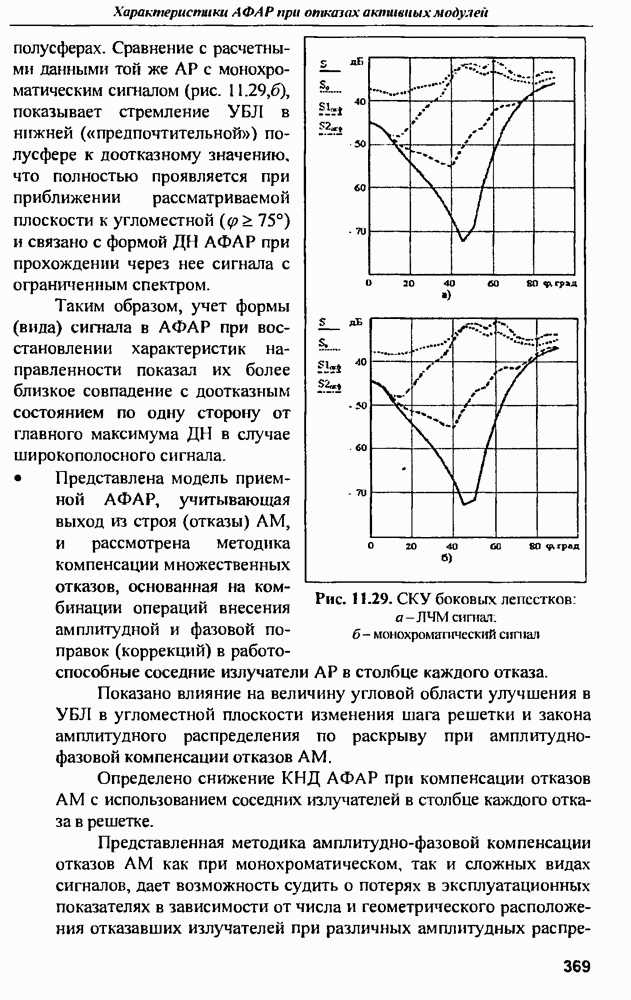
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
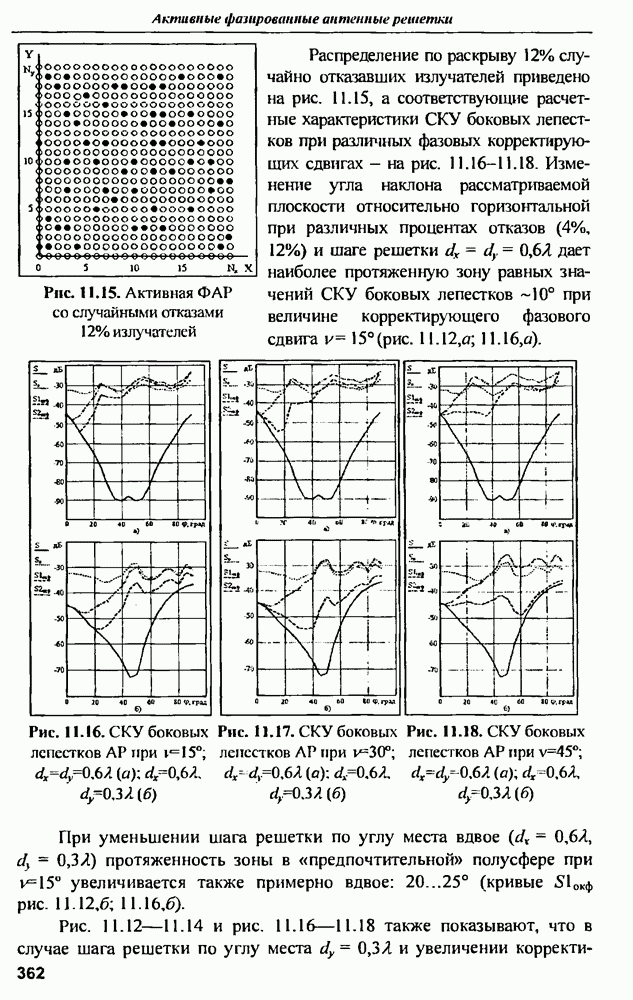
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
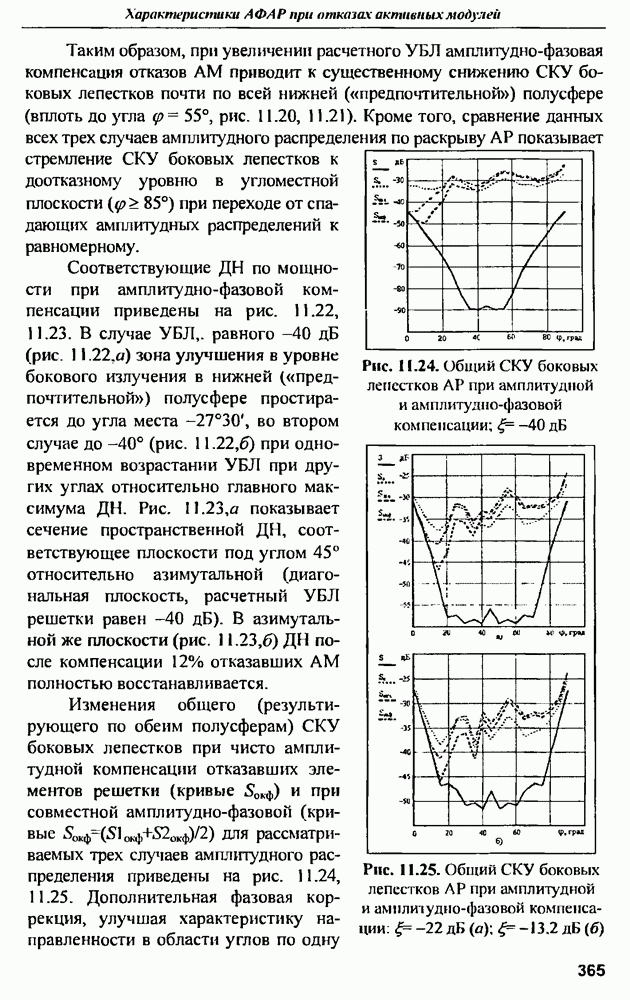
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
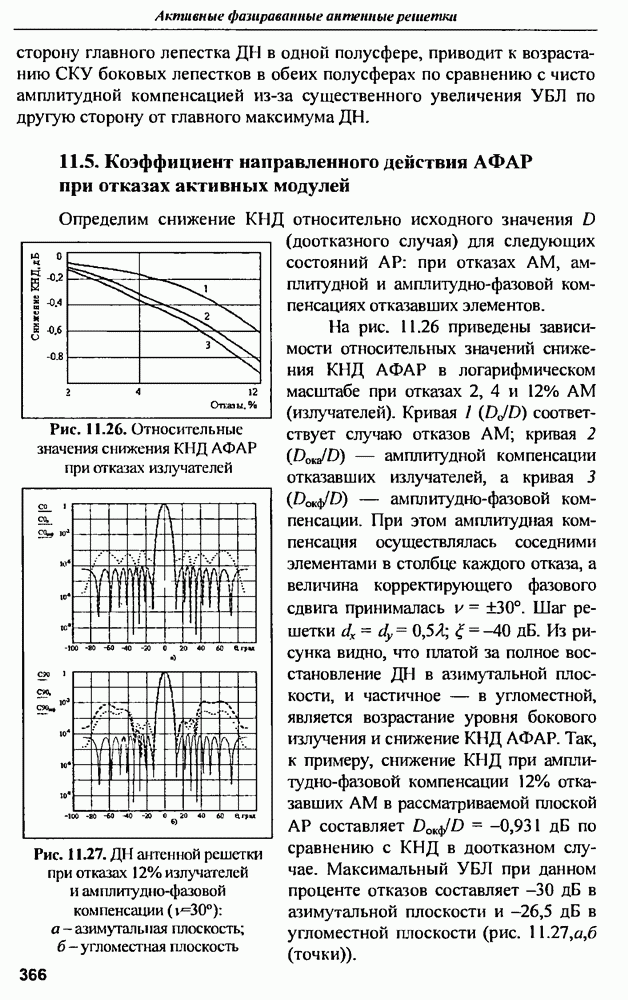
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
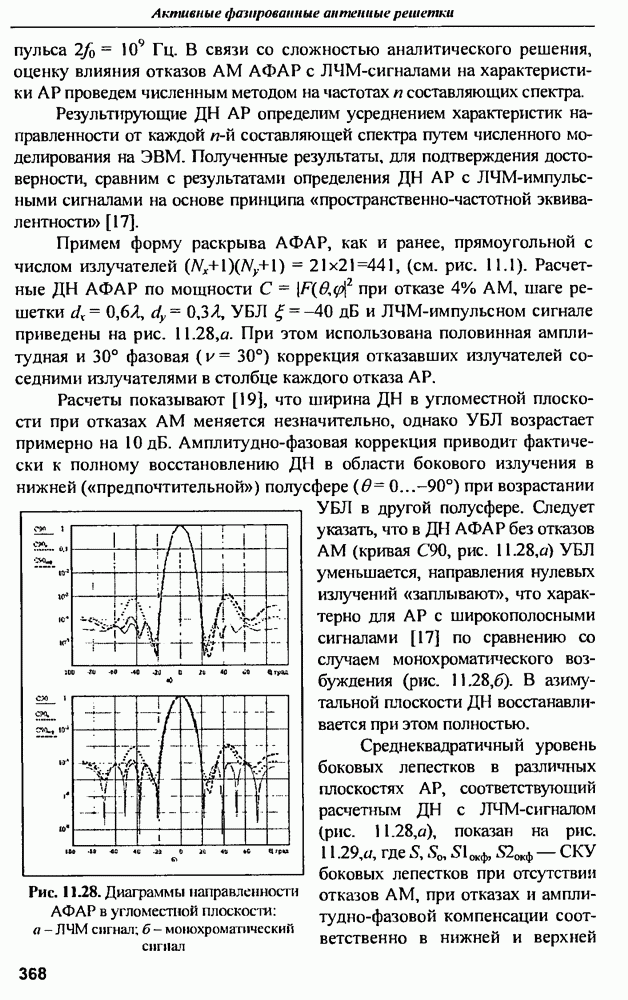
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
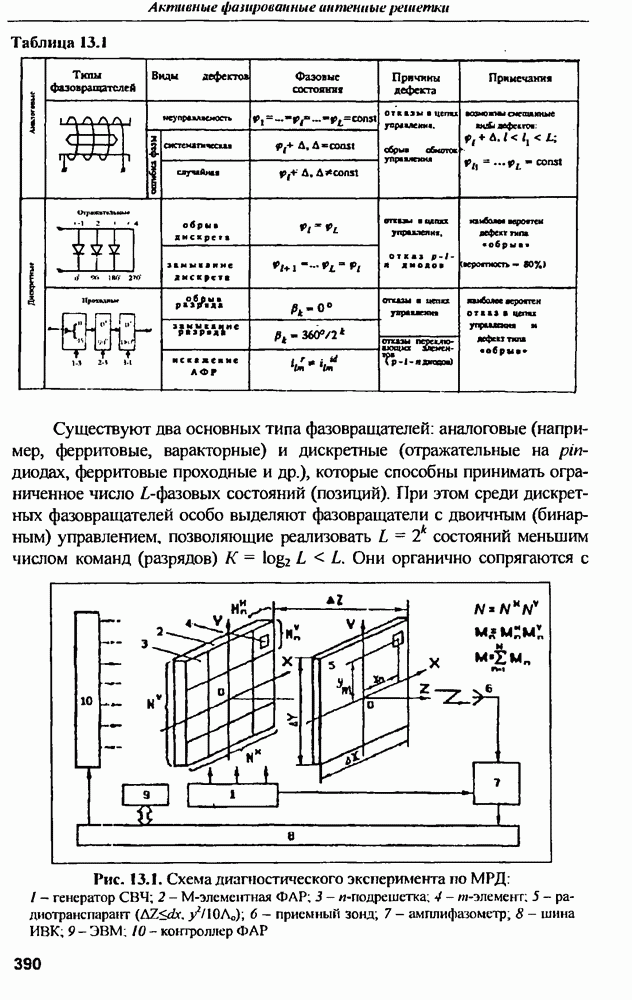
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
- 14.3. Комбинированные антенны
- 14.4. Антенные решетки
- 14.5. Приемные антенны
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
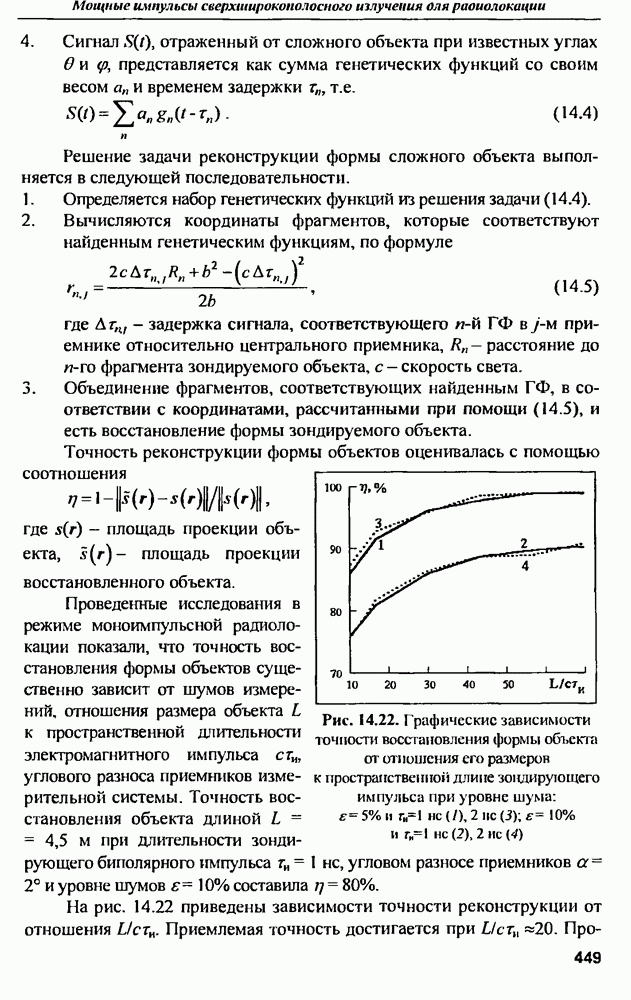
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
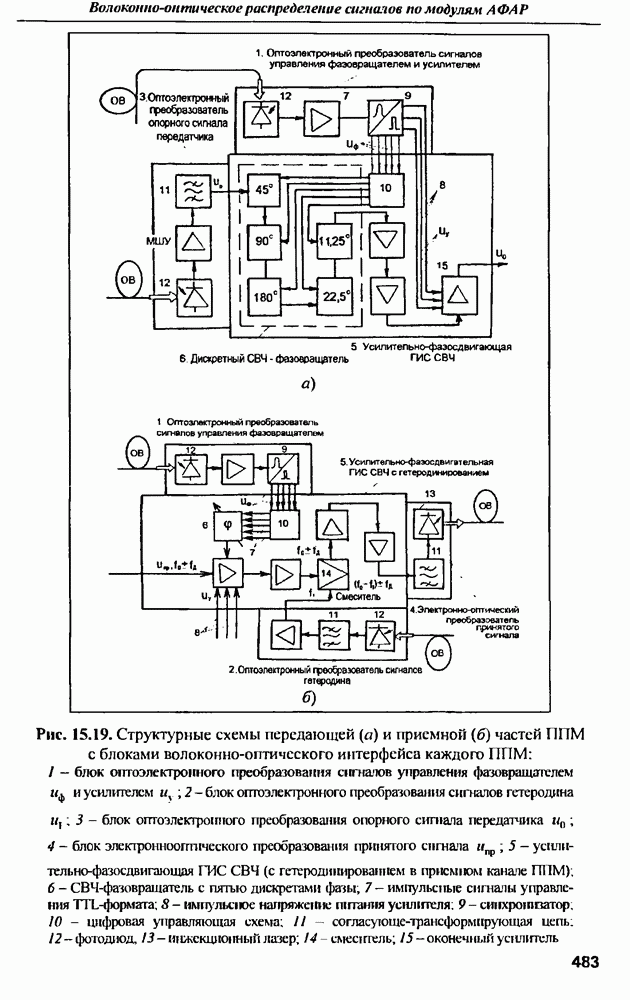
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
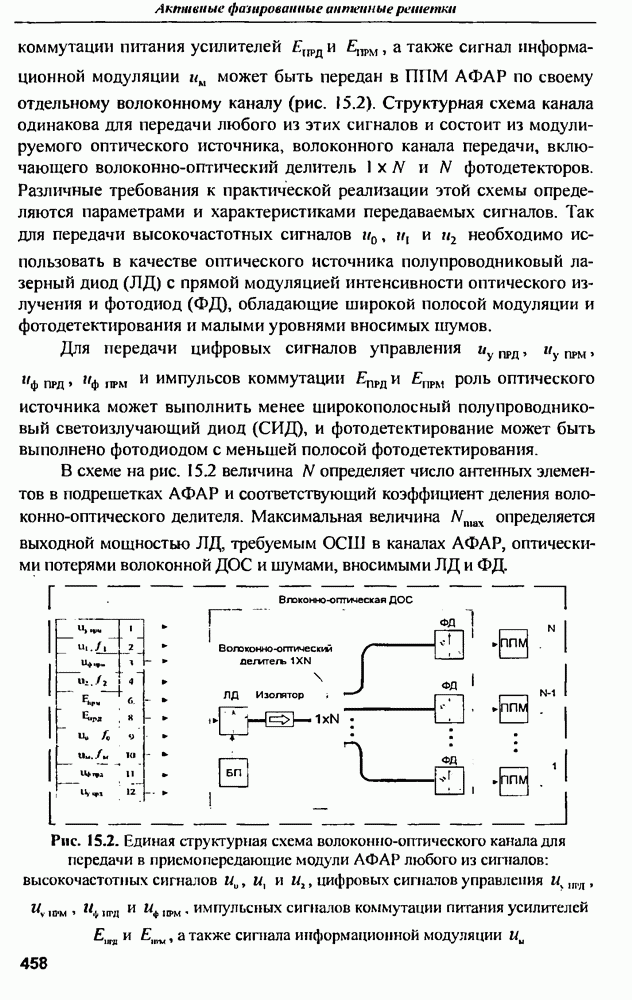
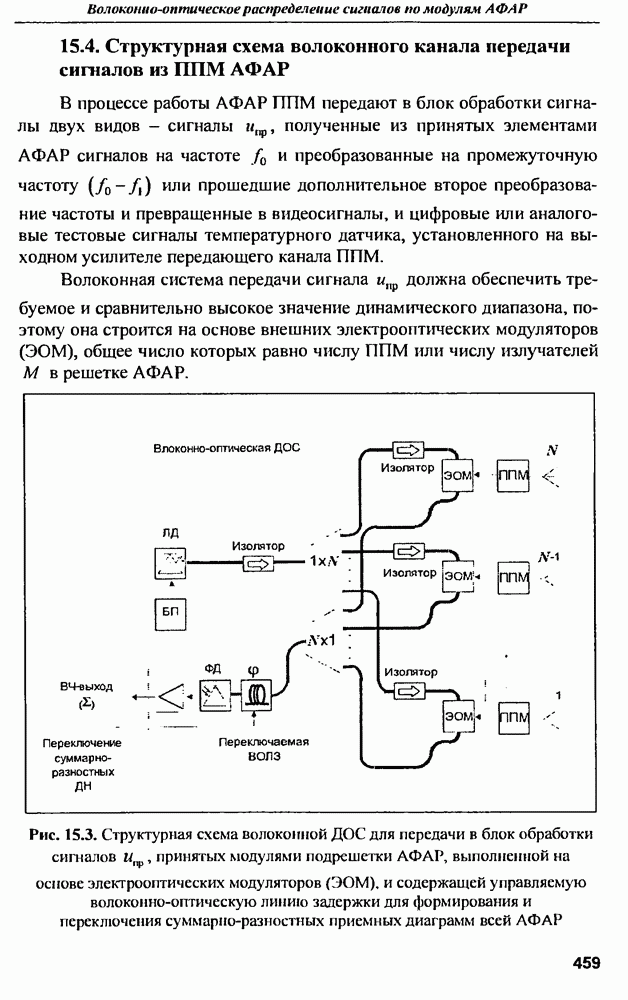
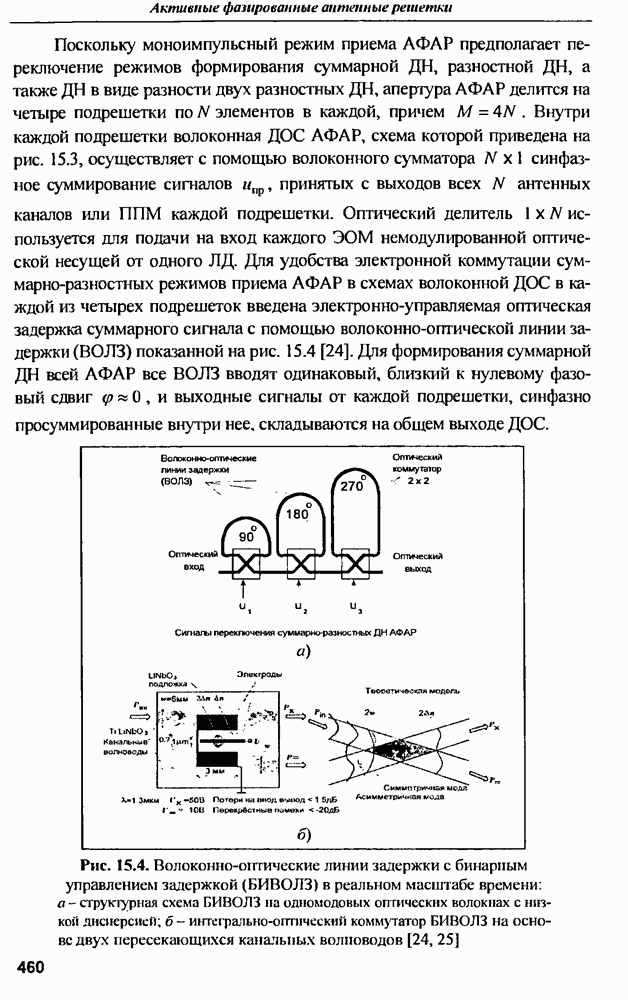
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
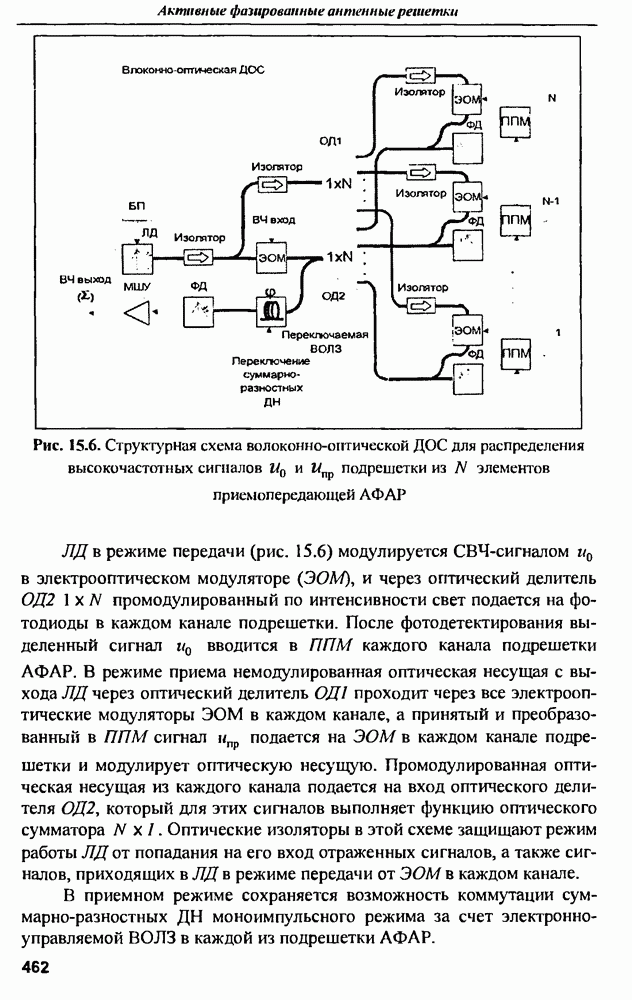
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
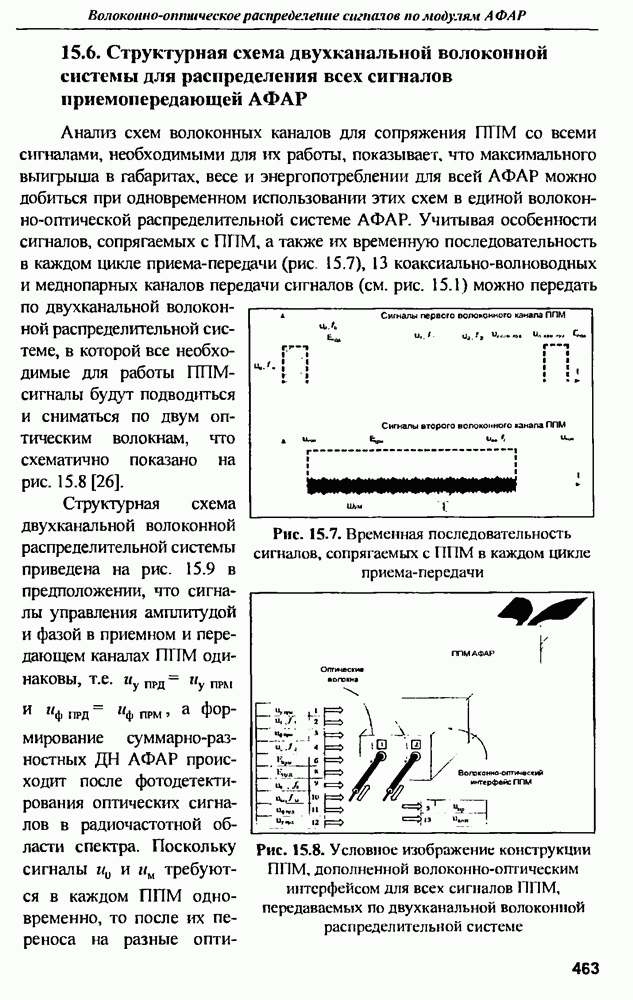
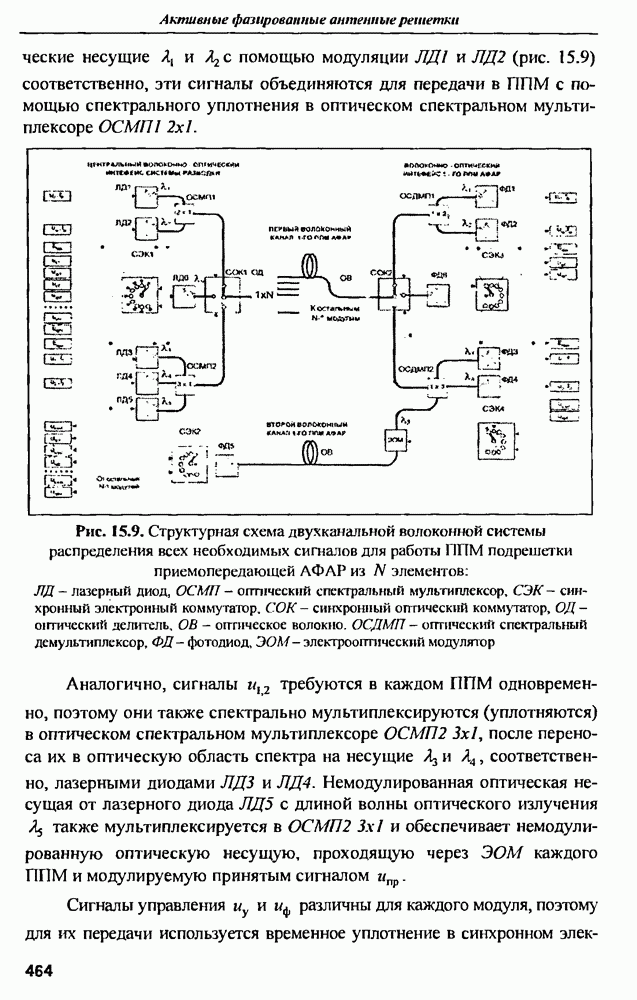
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
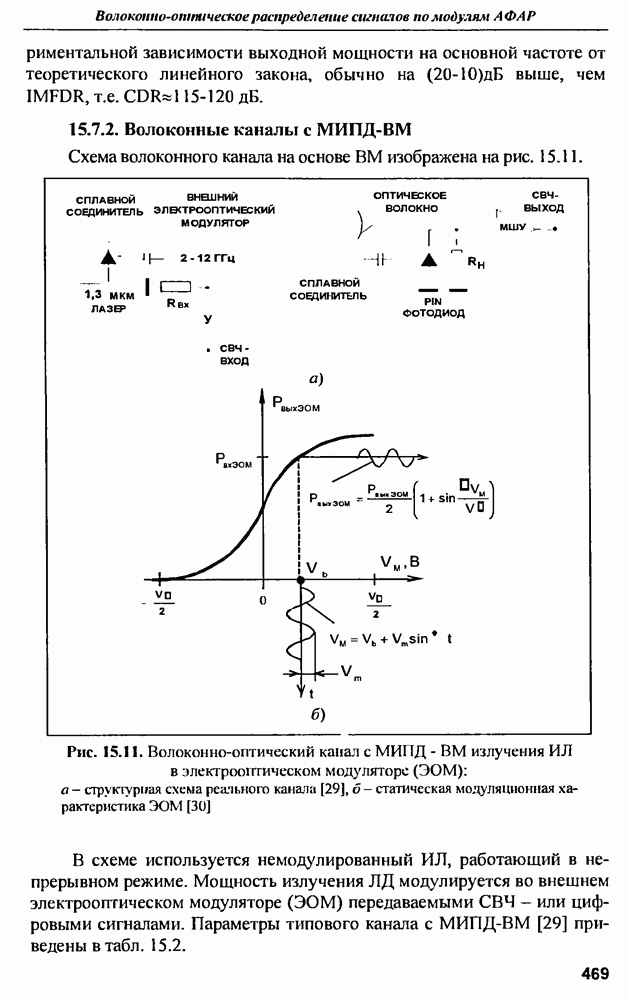
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
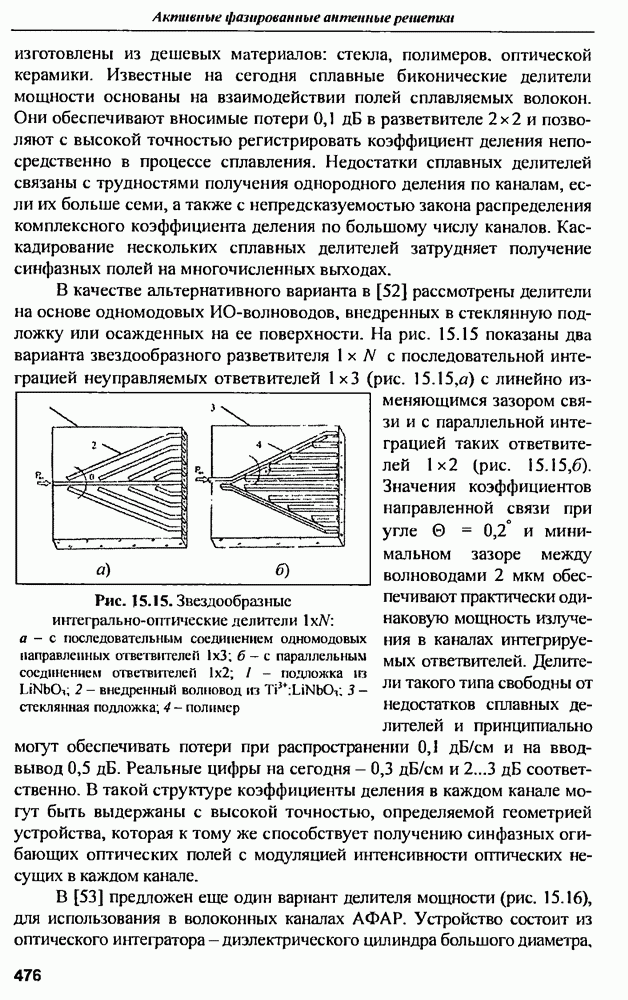
- 15.8.4. Оптические делители
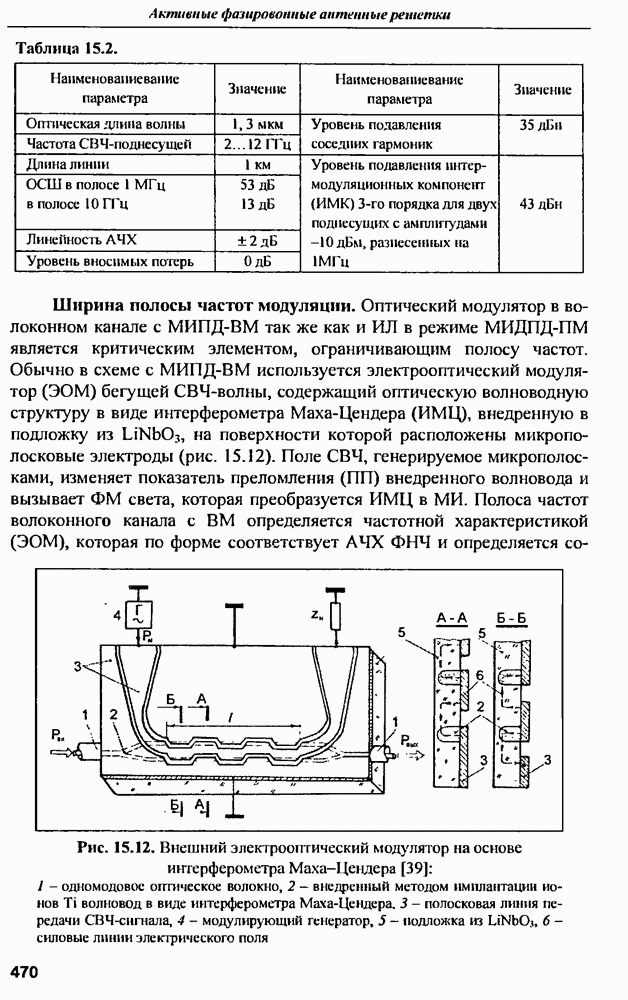
- 15.8.5. Внешние модуляторы
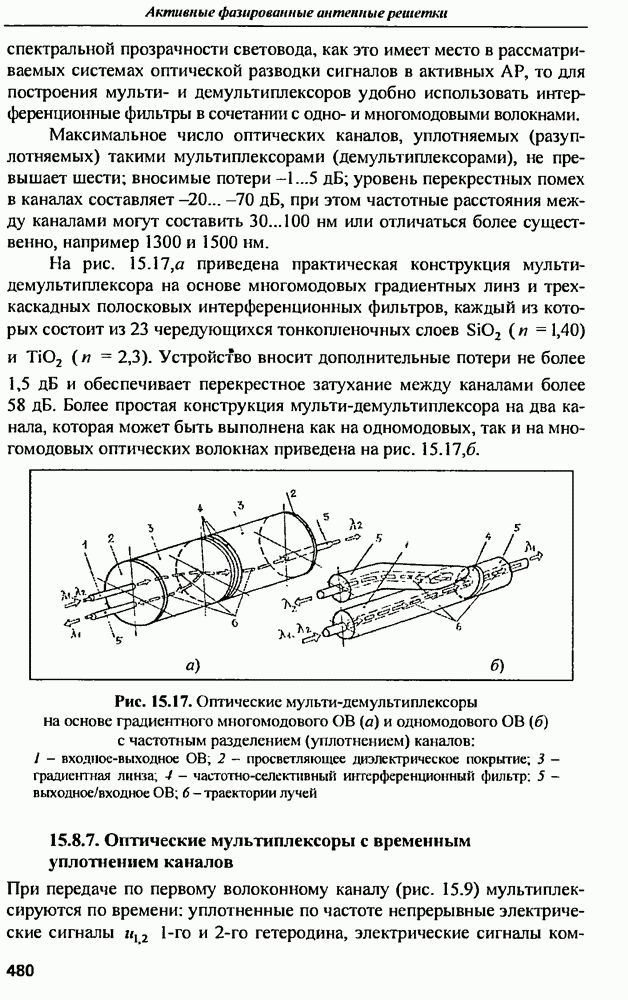
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР