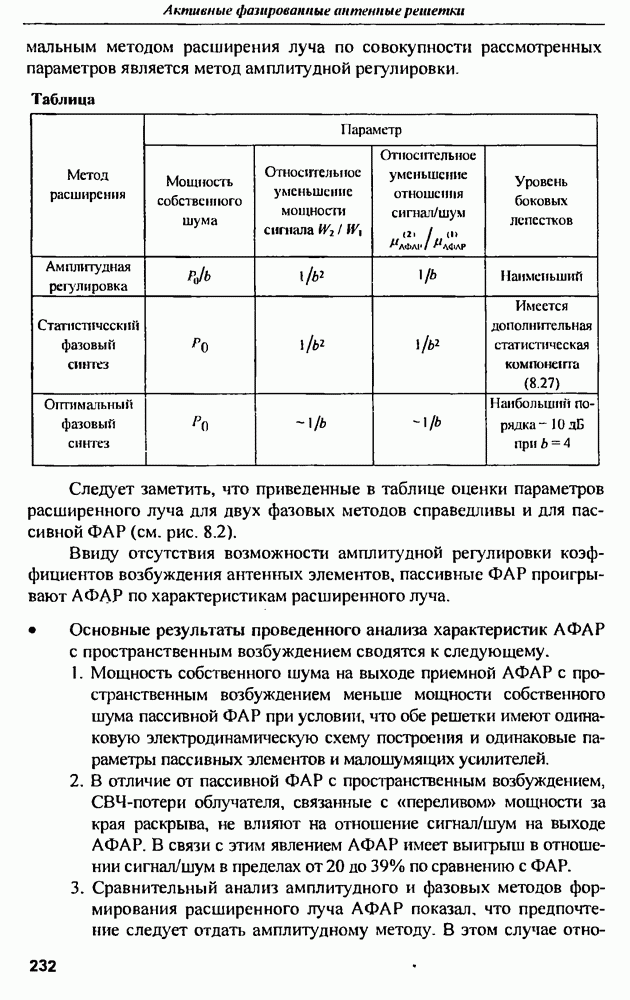
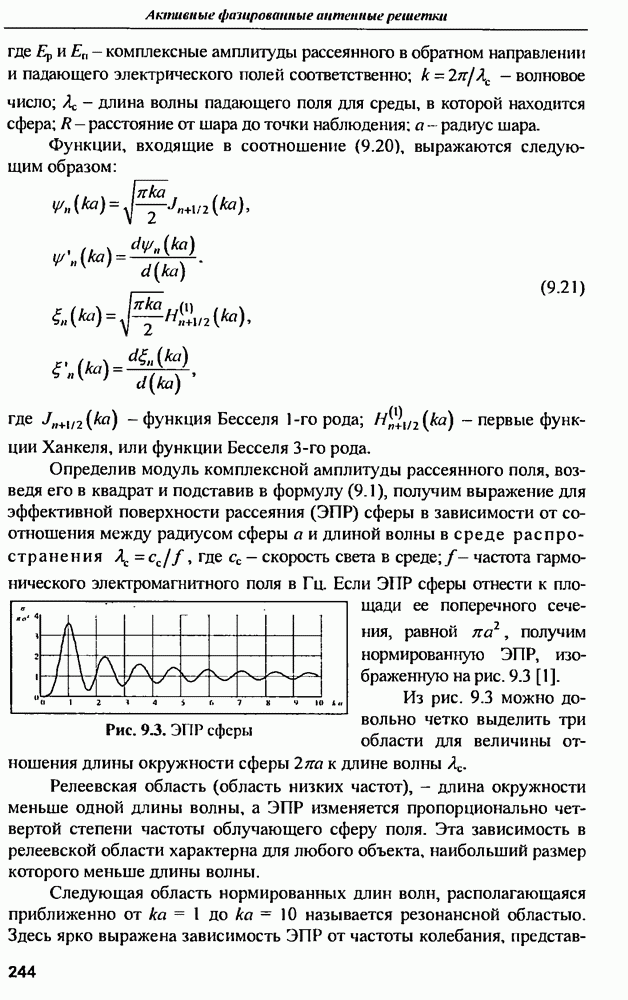
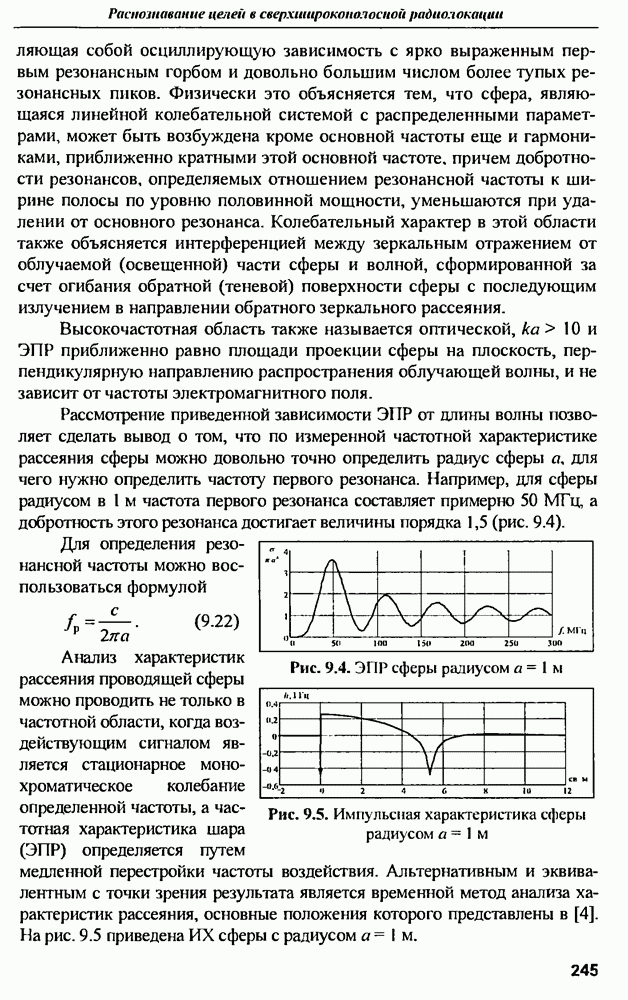
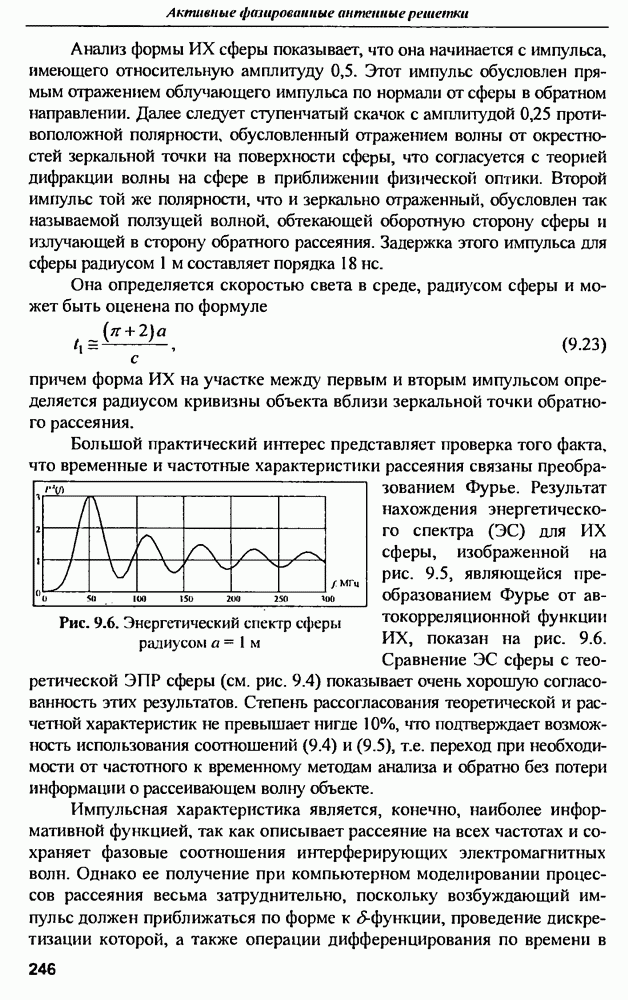
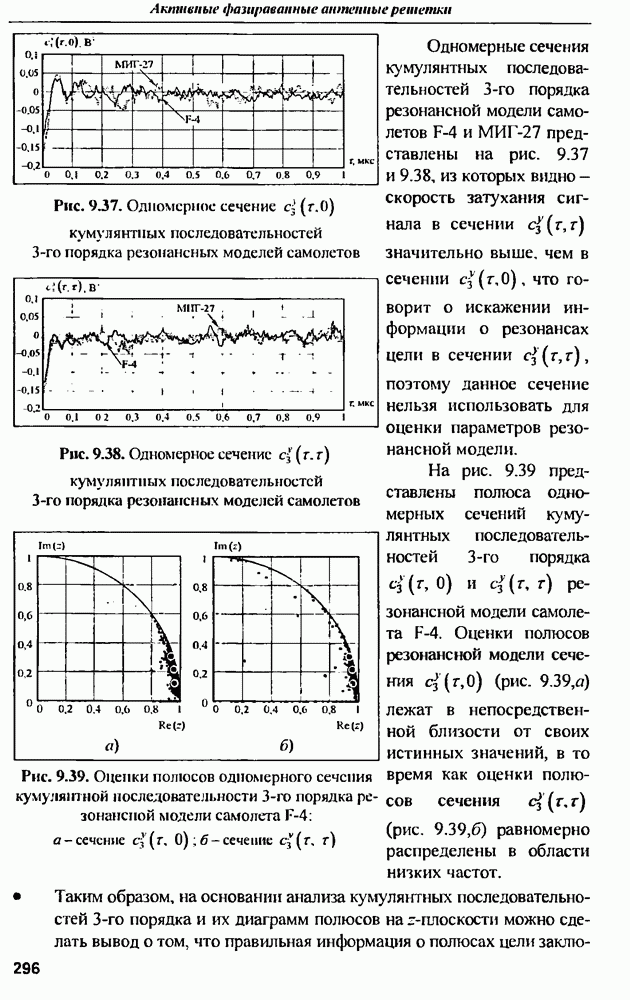
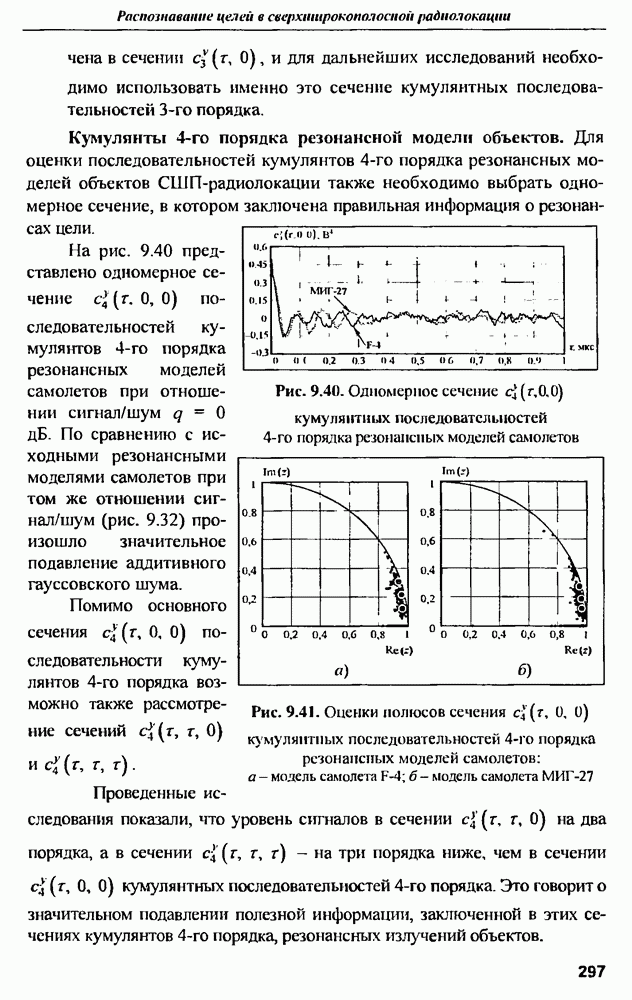
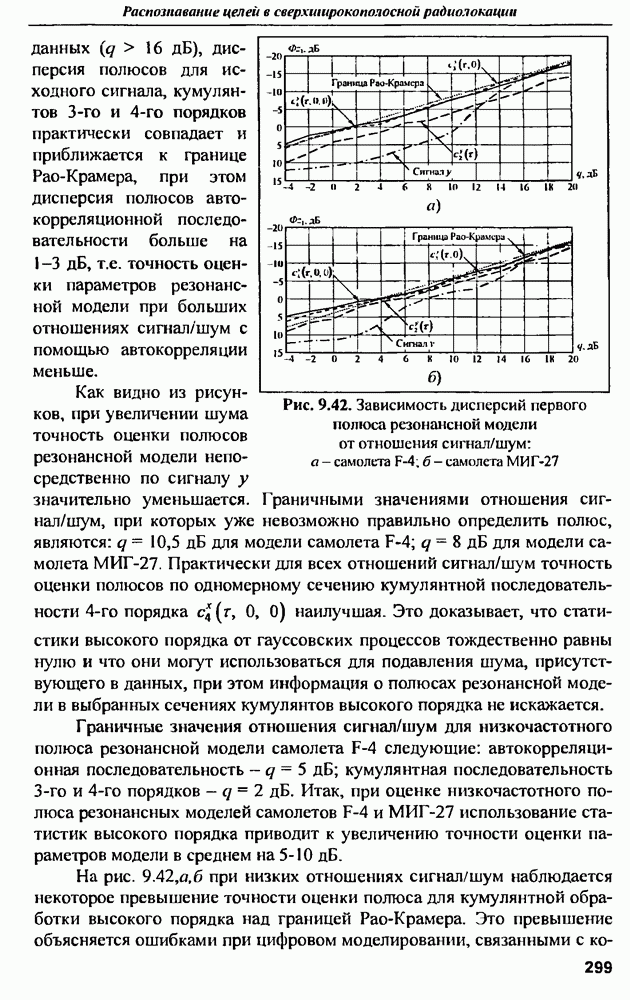
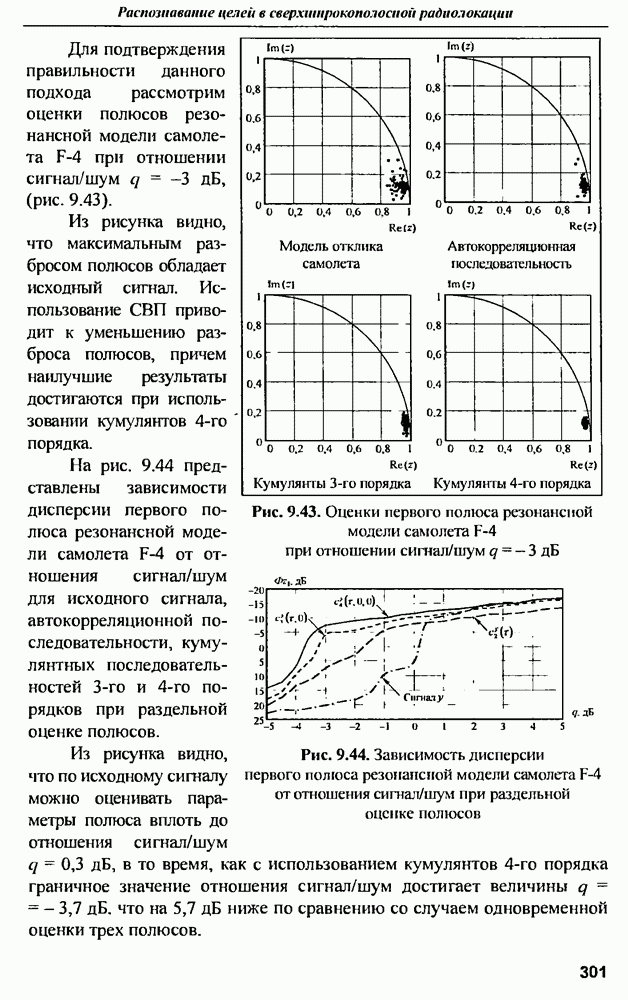
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
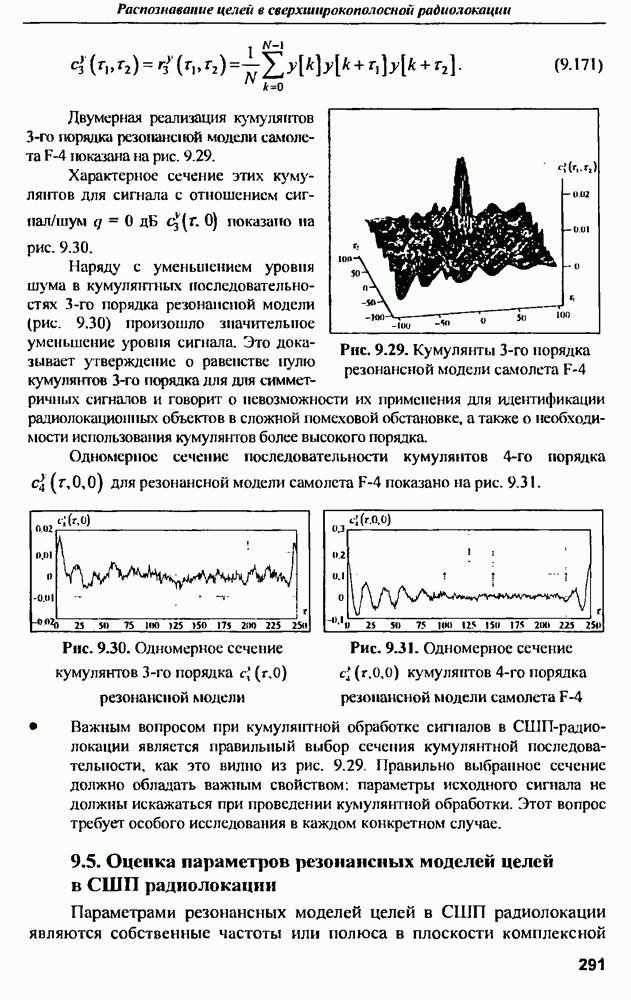
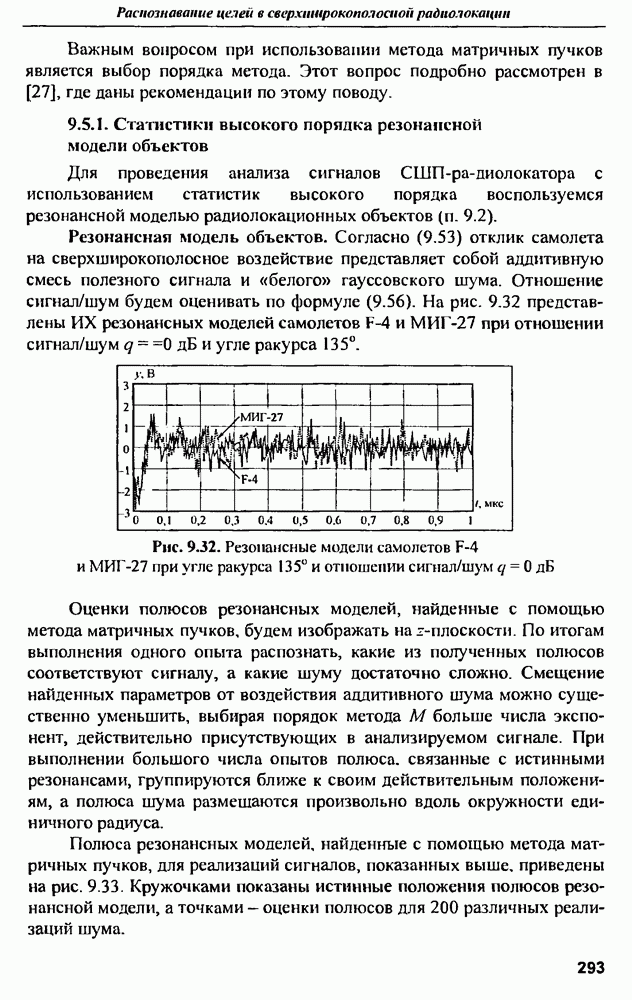
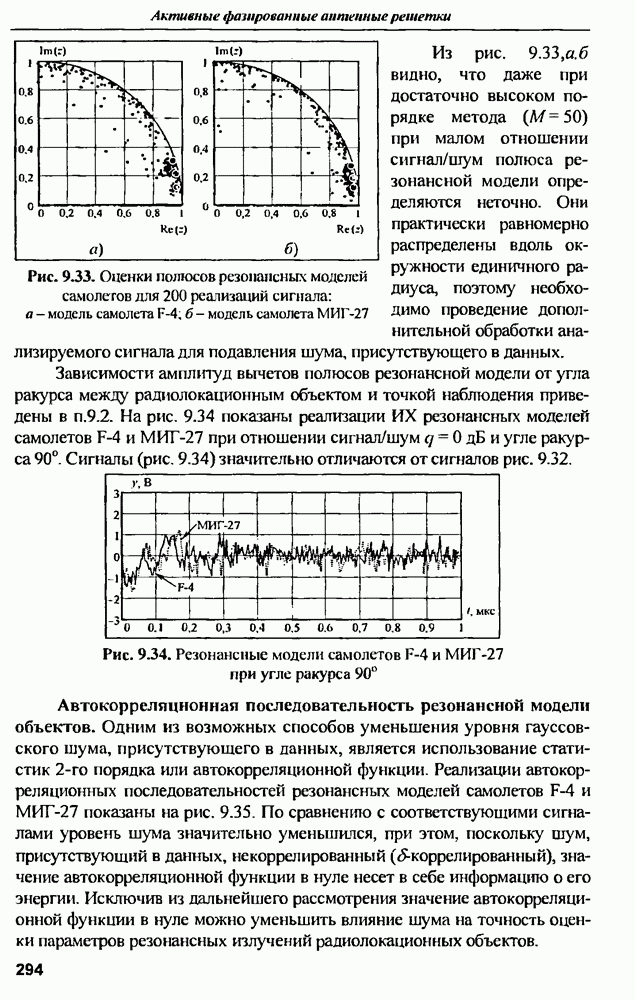
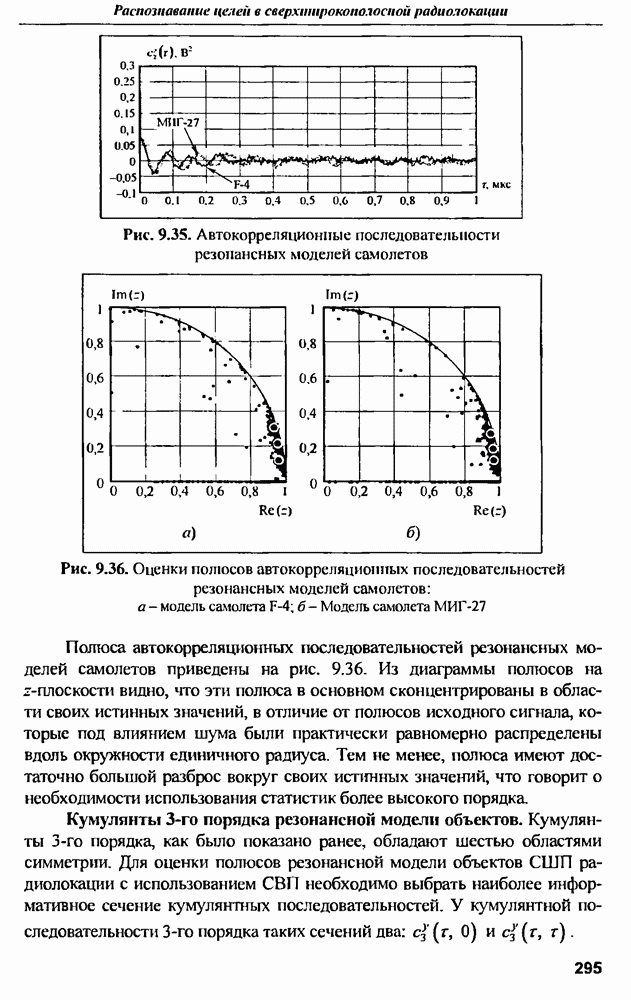
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
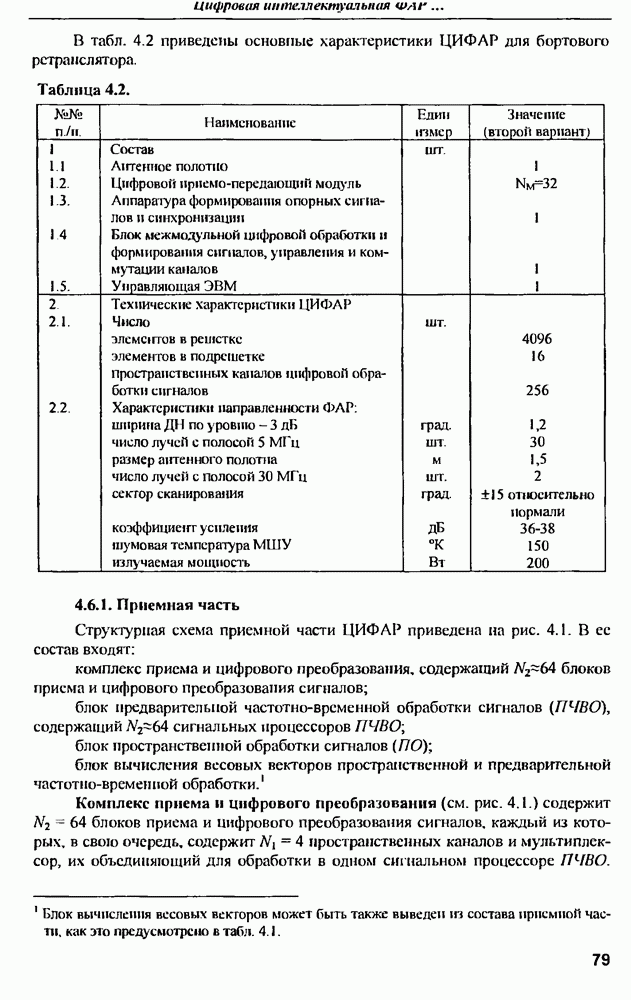
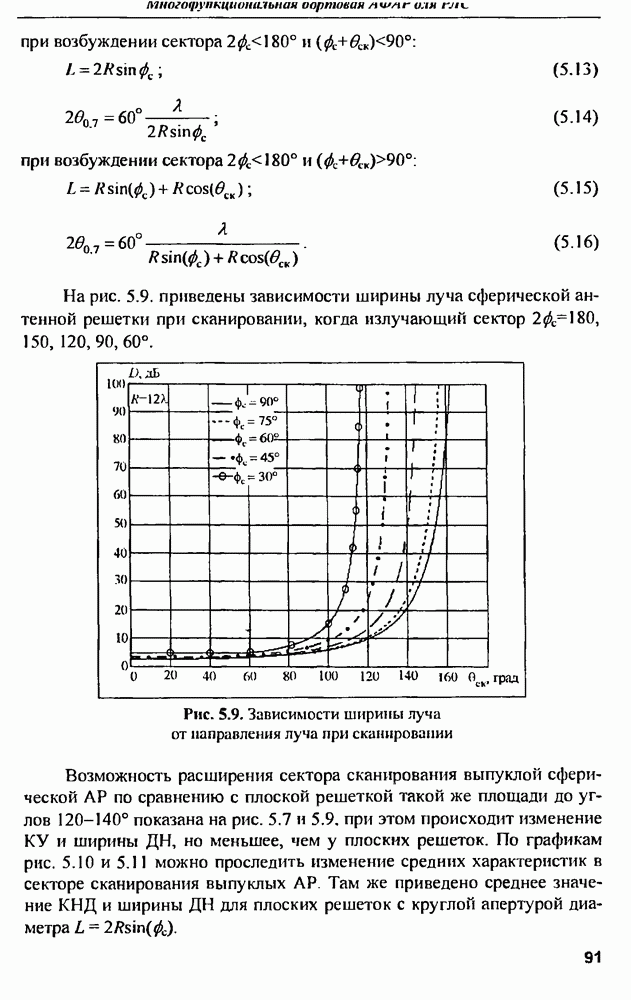
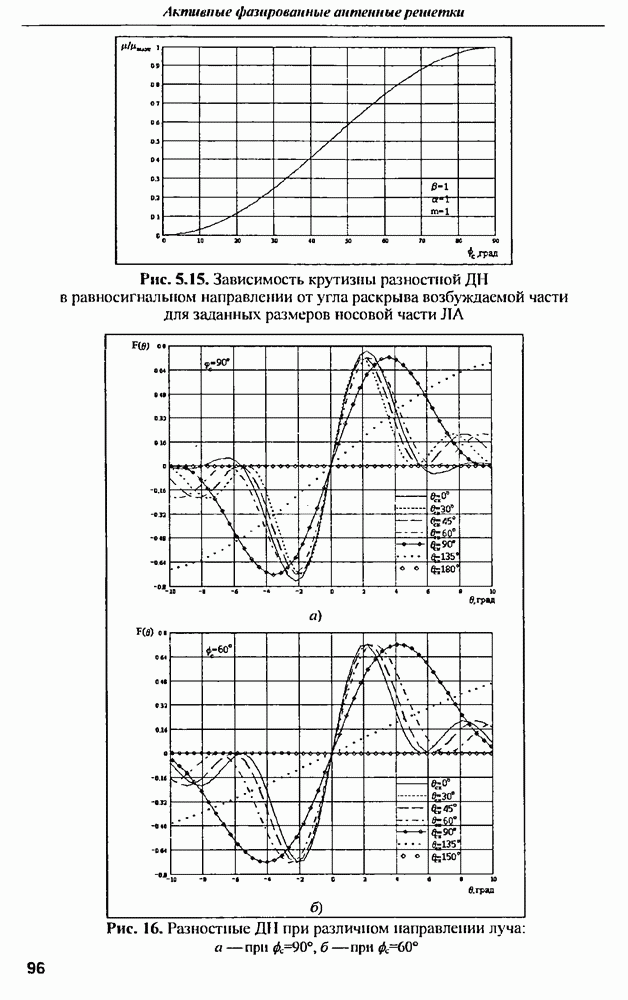
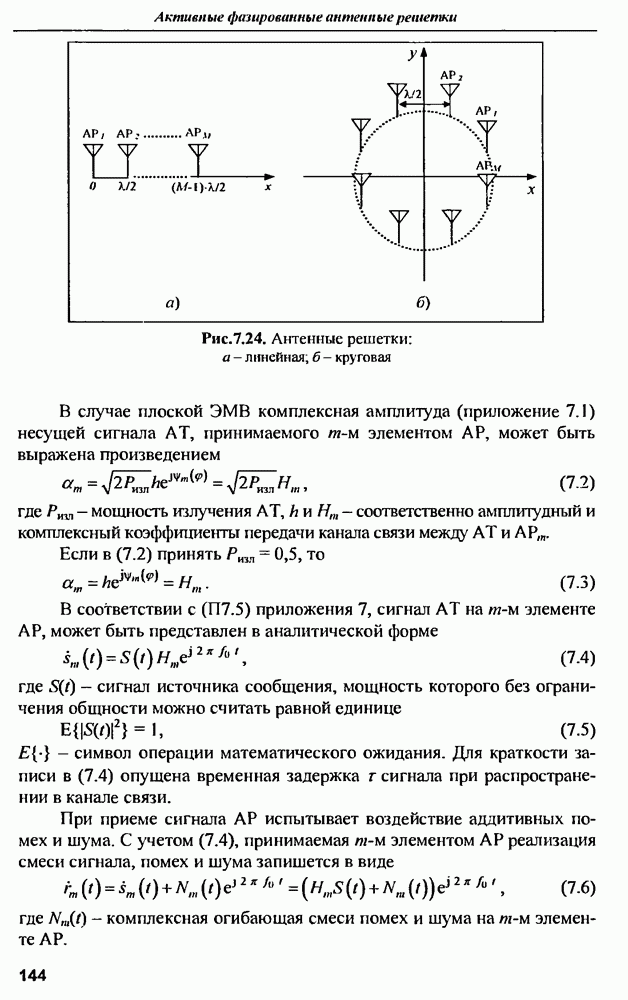
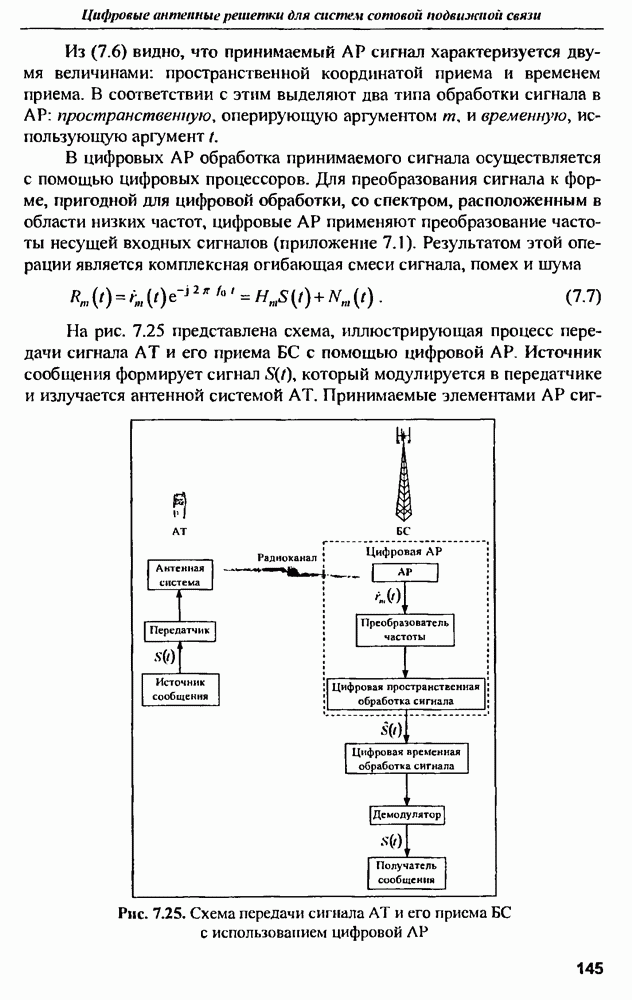
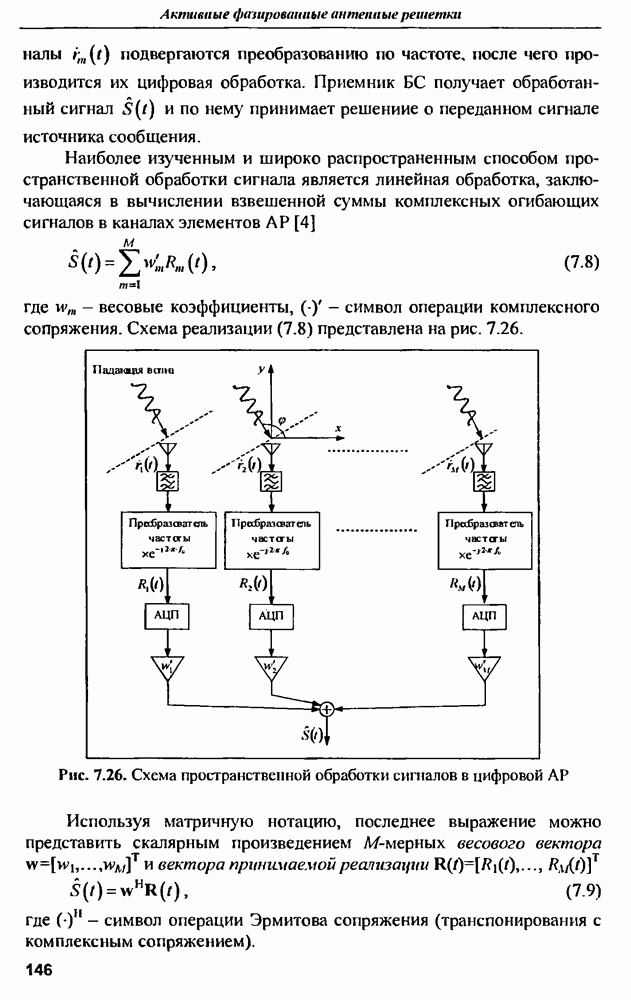
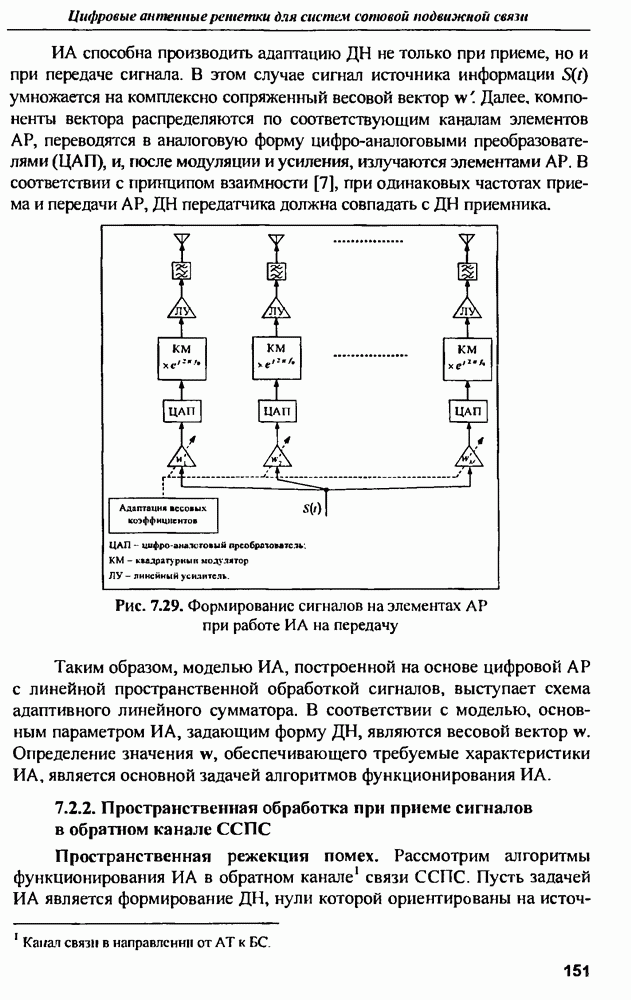
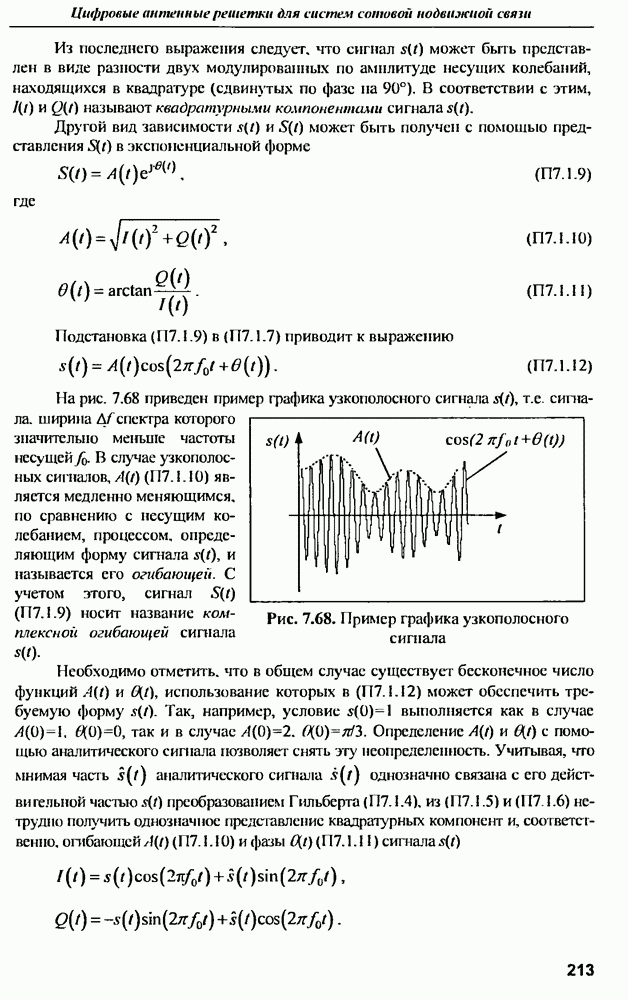
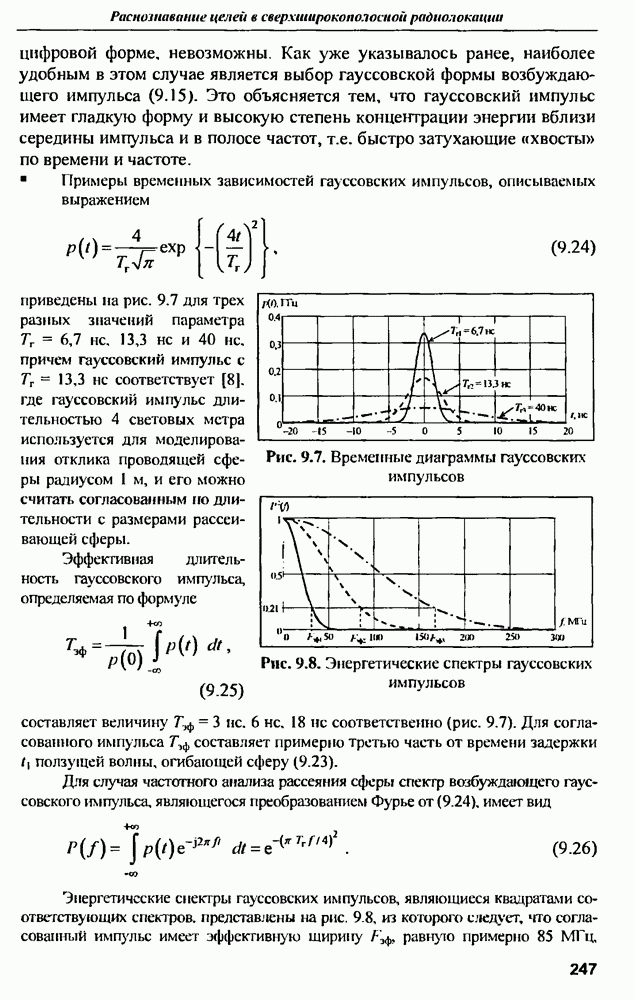
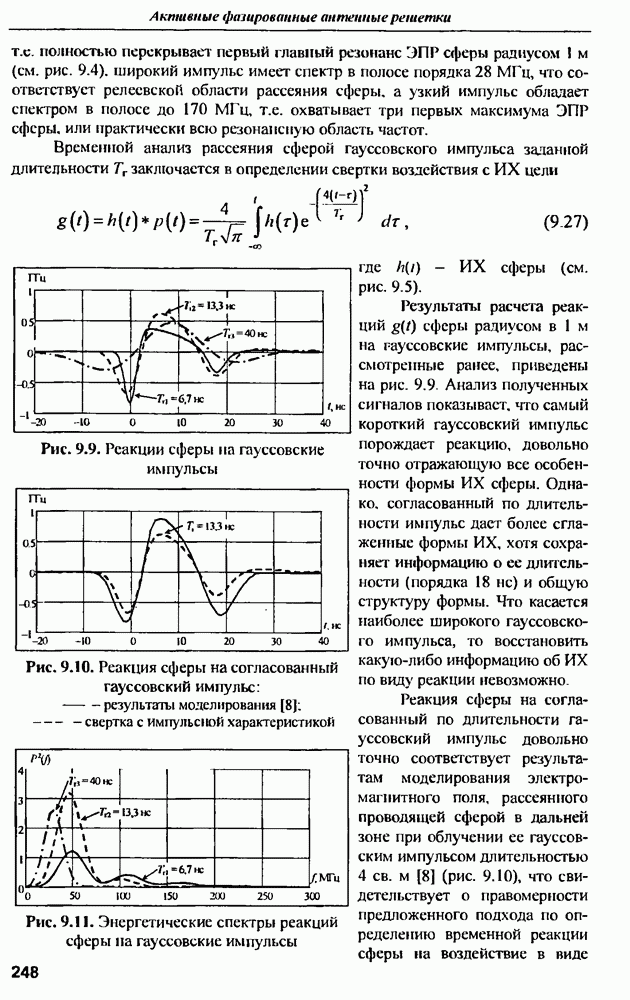
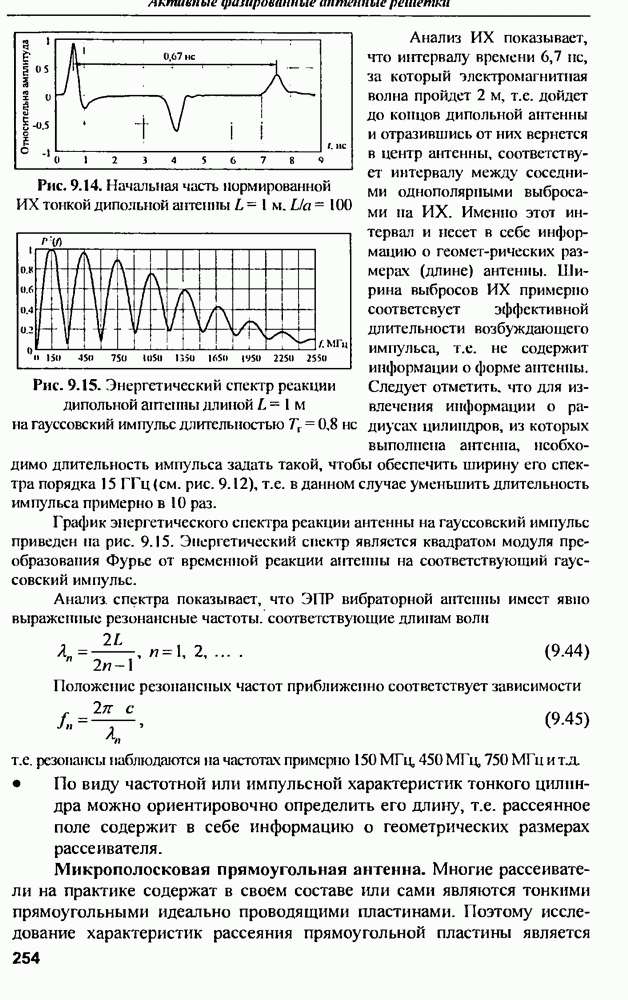
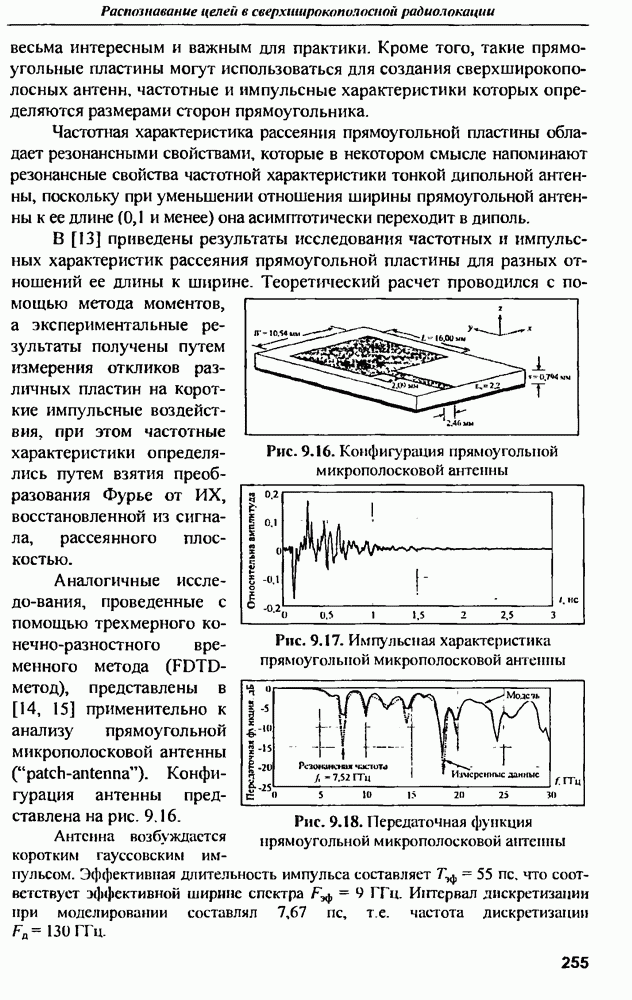
7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
Принципы формирования ДН. Работа ССПС требует сбалансированности характеристик обратного и прямого каналов связи, поэтому применение  не должно ограничиваться приемом сигналов в обратном канале связи.
не должно ограничиваться приемом сигналов в обратном канале связи.
Следует различать случаи временного и частотного разделения обратного и прямого каналов связи. При временном разделении коэффициенты передачи обратного и прямого каналов совпадают. В этой ситуации применим принцип взаимности [7], из которого следует, что  оптимальная при приеме сигнала в обратном канале, будет также оптимальной и в случае передачи сигнала в прямом канале, имея в виду отношение мощности сигнала, приходящего на
оптимальная при приеме сигнала в обратном канале, будет также оптимальной и в случае передачи сигнала в прямом канале, имея в виду отношение мощности сигнала, приходящего на  адресата, к суммарной мощности помех другим
адресата, к суммарной мощности помех другим  (рис. 7.40). Очевидно, что временной промежуток между приемом и передачей сигналов
(рис. 7.40). Очевидно, что временной промежуток между приемом и передачей сигналов  не должен превышать
не должен превышать
интервал стационарности канала связи.
Напротив, в системах с частотным разделением прямого и обратного каналов несущие принимаемых и передаваемых сигналов имеют значительный частотный разнос. По этой причине параметры прямого и обратного каналов оказываются различными и использование одного и того же весового вектора при приеме и передаче приведет к различным ДН ИА. В этих условиях при передаче сигналов в прямом канале наилучшей стратегией является формирование  с главным лепестком, ориентированным на обслуживаемый AT, и «нулями», сформированными в направлениях остальных
с главным лепестком, ориентированным на обслуживаемый AT, и «нулями», сформированными в направлениях остальных 
Таким образом, для выбора весового вектора при передаче сигналов в прямом канале необходимо знать направления с  на обслуживаемый
на обслуживаемый  и другие, расположенные поблизости. Эти сведения позволяют построить направляющие векторы
и другие, расположенные поблизости. Эти сведения позволяют построить направляющие векторы  сигналов рассматриваемых
сигналов рассматриваемых  для диапазона частот прямого канала и вычислить оптимальный весовой вектор, пользуясь алгоритмом
для диапазона частот прямого канала и вычислить оптимальный весовой вектор, пользуясь алгоритмом  (если общее число AT не превышает М), или алгоритмом СКО.
(если общее число AT не превышает М), или алгоритмом СКО.

Рис. 7.40. Использование принципа взаимности при приеме и передаче сигналов  в обратном и прямом каналах связи
в обратном и прямом каналах связи
Методы оценки направлений прихода сигналов и помех. Метод пространственной фильтрации. Суммарная мощность сигнала и помех на выходе  определяется квадратичной функцией весового вектора
определяется квадратичной функцией весового вектора 
Используя в качестве весового вектора направляющий вектор, согласованный с направлением  получим
получим 
Можно ожидать, что если с направления  приходит сигнал или помеха, то функция
приходит сигнал или помеха, то функция  будет иметь в точке локальный максимум [4]. Алгоритм пространственной фильтрации
будет иметь в точке локальный максимум [4]. Алгоритм пространственной фильтрации  анализирует положения максимумов и выносит решения о направлениях прихода излучений.
анализирует положения максимумов и выносит решения о направлениях прихода излучений.
Алгоритм Канона. Алгоритм Капона (Capon) [4] основан на получении с помощью  максимально правдоподобной оценки мощности излучений, приходящих с заданного направления [4]. Оценка мощности находится из решения вариационной задачи
максимально правдоподобной оценки мощности излучений, приходящих с заданного направления [4]. Оценка мощности находится из решения вариационной задачи

означающей, что используемый для измерения весовой вектор должен формировать  при которой снгнал, приходящий с направления
при которой снгнал, приходящий с направления  усиливается в фиксированное число раз, тогда как мощности излучений с других направлений минимизируются.
усиливается в фиксированное число раз, тогда как мощности излучений с других направлений минимизируются.
Для решения задачи (7.145) можно воспользоваться методом множителей Лагранжа. Функция Лагранжа имеет следующий вид:

Оптимальный вектор  должен удовлетворять условию
должен удовлетворять условию

где  градиент
градиент  как функции
как функции  .
.
С учетом (7.76), (7.146) преобразуется к виду

Решением (7.147) является вектор

Подстановка (7.148) в (7.145) окончательно дает

Алгоритм множественной классификации сигналов. Алгоритм множественной классификации сигналов  предложенный Шмидтом (Schmidt) [15], основан на анализе собственных векторов и значений автокорреляционной матрицы
предложенный Шмидтом (Schmidt) [15], основан на анализе собственных векторов и значений автокорреляционной матрицы  принимаемой реализации. В соответствии с (7.46)
принимаемой реализации. В соответствии с (7.46)

где  передаточпая матрица канала, столбцами которой являются направляющие векторы сигналов
передаточпая матрица канала, столбцами которой являются направляющие векторы сигналов 

 - мощность шума в каналах АР.
- мощность шума в каналах АР.
По определению, собственные значения матрицы  выражаются из уравнения
выражаются из уравнения

где  — детерминант матрицы,
— детерминант матрицы,  собственное значение. Подстановка (7.149) в (7.150) дает
собственное значение. Подстановка (7.149) в (7.150) дает

Из (7.151) следует, что собственными значениями матрицы  являются числа
являются числа

При  в случае линейно независимых направляющих векторов, ранг матрицы
в случае линейно независимых направляющих векторов, ранг матрицы  равен К. Это означает, что
равен К. Это означает, что  ее собственных значений равны нулю.
ее собственных значений равны нулю.
Учитывая, что матрица  эрмитово сопряженная, остальные ее собственные значения действительные положительные числа, т.е.
эрмитово сопряженная, остальные ее собственные значения действительные положительные числа, т.е.

Из (7.153) и (7.152) следует, что

Из (7.154) видно, что анализ собственных значении матрицы  при известной мощности шума в каналах элементов
при известной мощности шума в каналах элементов  позволяет оценить число излучающих
позволяет оценить число излучающих 
В соответствии с определением собственных векторов

Подставляя в (7.155) выражение для корреляционной матрицы (7.149), и, учитывая (7.154), для первых  собственных векторов получаем
собственных векторов получаем

Поскольку при  матрица
матрица  имеет полный столбцовый ранг, а
имеет полный столбцовый ранг, а  несингулярная матрица, то условием выполнения (7.156) служит тождество
несингулярная матрица, то условием выполнения (7.156) служит тождество

Равенство (7.157) показывает, что направляющие вектора  сигнала и помех ортогональны всем собственным векторам корреляционной матрицы
сигнала и помех ортогональны всем собственным векторам корреляционной матрицы  соответствующим собственным значениям
соответствующим собственным значениям  равным
равным 
Условие (7.157) может также быть записано в виде

где

Из (7.158) также следует

Таким образом, при приближении угла  к направлению на один из источников излучения величина
к направлению на один из источников излучения величина

стремится к бесконечности.
Рассматривая алгоритм МКС, можно выделить основные шаги его работы: анализ собственных значений корреляционной матрицы  определение собственных векторов, соответствующих минимальным собственным значениям, равным мощности шума
определение собственных векторов, соответствующих минимальным собственным значениям, равным мощности шума  в каналах
в каналах  и вычисление функции (7.159). Расположение пиков
и вычисление функции (7.159). Расположение пиков  указывает на направления прихода излучений от
указывает на направления прихода излучений от 
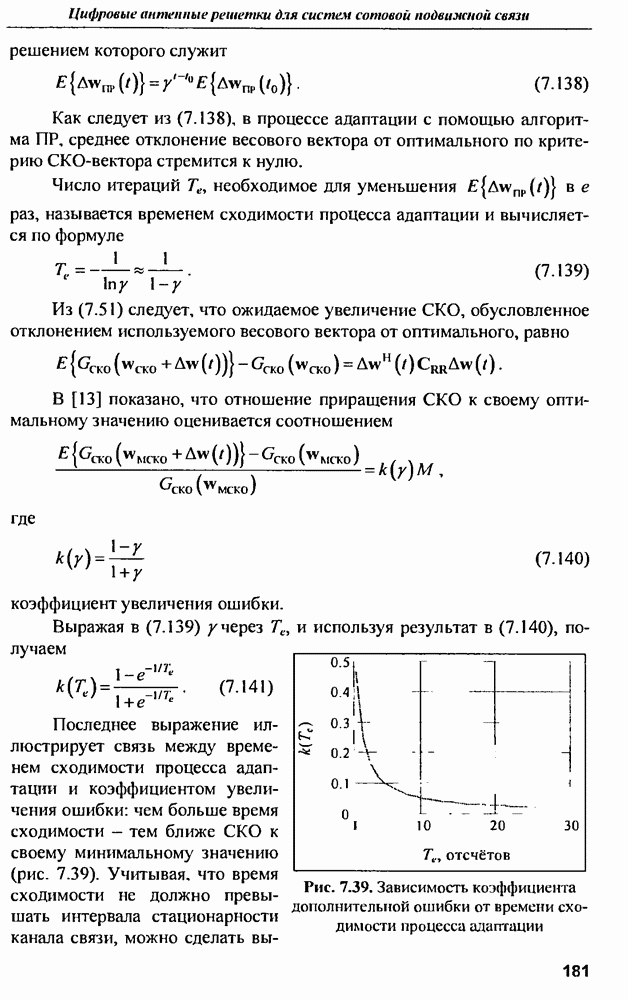
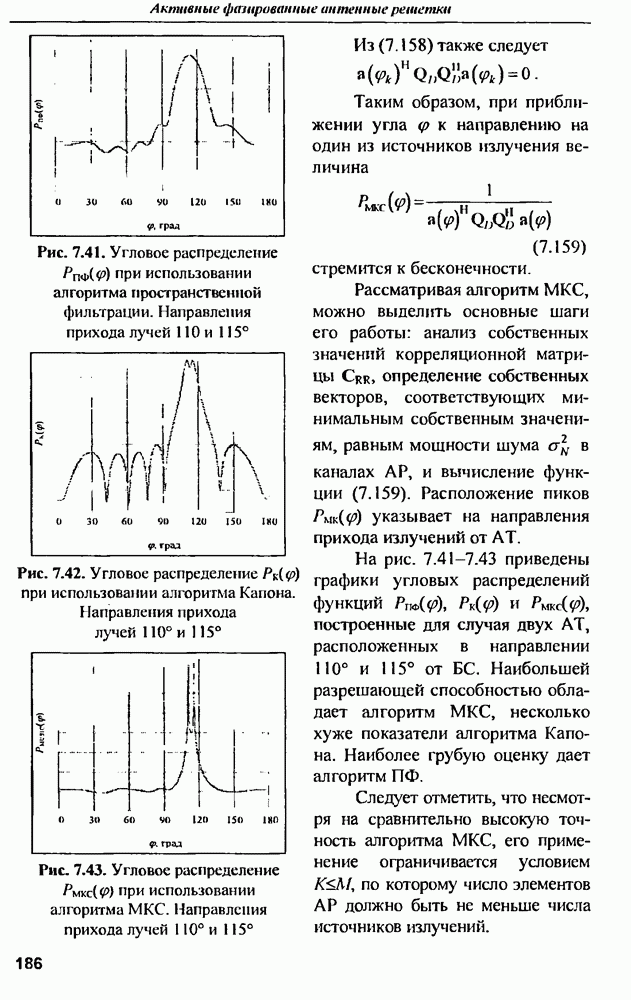
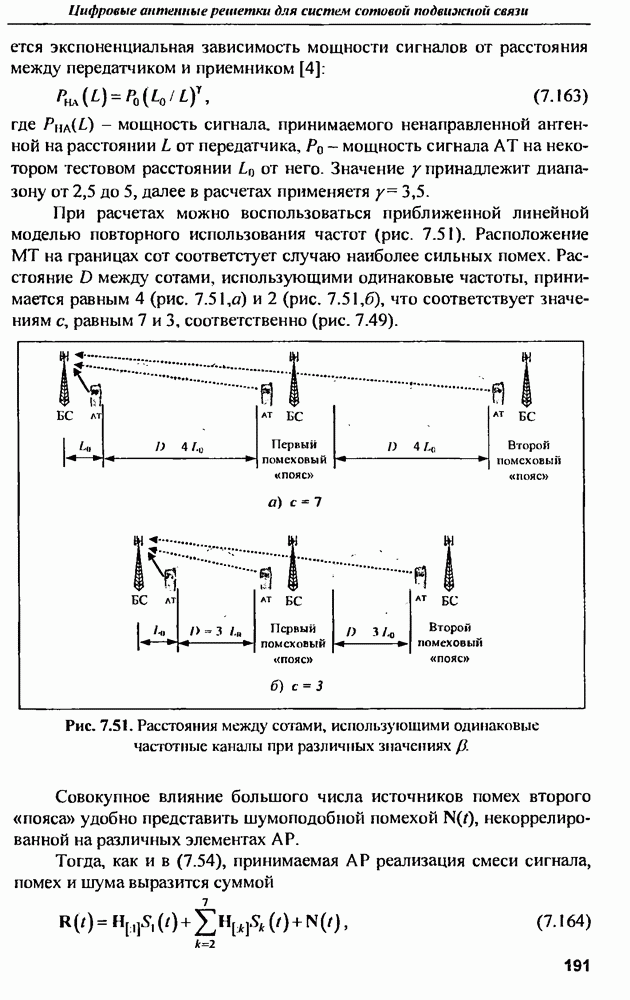
На рис. 7.41-7.43 приведены графики угловых распределений функций  построенные для случая двух
построенные для случая двух  расположенных в направлении 110° и 115° от
расположенных в направлении 110° и 115° от  Наибольшей разрешающей способностью обладает алгоритм МКС, несколько хуже показатели алгоритма Капона Наиболее грубую оценку дает алгоритм
Наибольшей разрешающей способностью обладает алгоритм МКС, несколько хуже показатели алгоритма Капона Наиболее грубую оценку дает алгоритм 
Следует отметить, что несмотря на сравнительно высокую точность алгоритма МКС, его применение ограничивается условием  по которому число элементов
по которому число элементов  должно быть не меньше числа источников излучений.
должно быть не меньше числа источников излучений.

Рис. 7.41. Угловое распределение  при использовании алгоритма пространственной фильтрации. Направления прихода лучей 110 и 115°
при использовании алгоритма пространственной фильтрации. Направления прихода лучей 110 и 115°

Рис. 7.42. Угловое распределение  при использовании алгоритма Капона. Направления прихода лучей 110°и 115°
при использовании алгоритма Капона. Направления прихода лучей 110°и 115°

Рис. 7.43. Угловое распределение  при использовании алгоритма МКС. Направления прихода лучей 110° и 115°
при использовании алгоритма МКС. Направления прихода лучей 110° и 115°
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
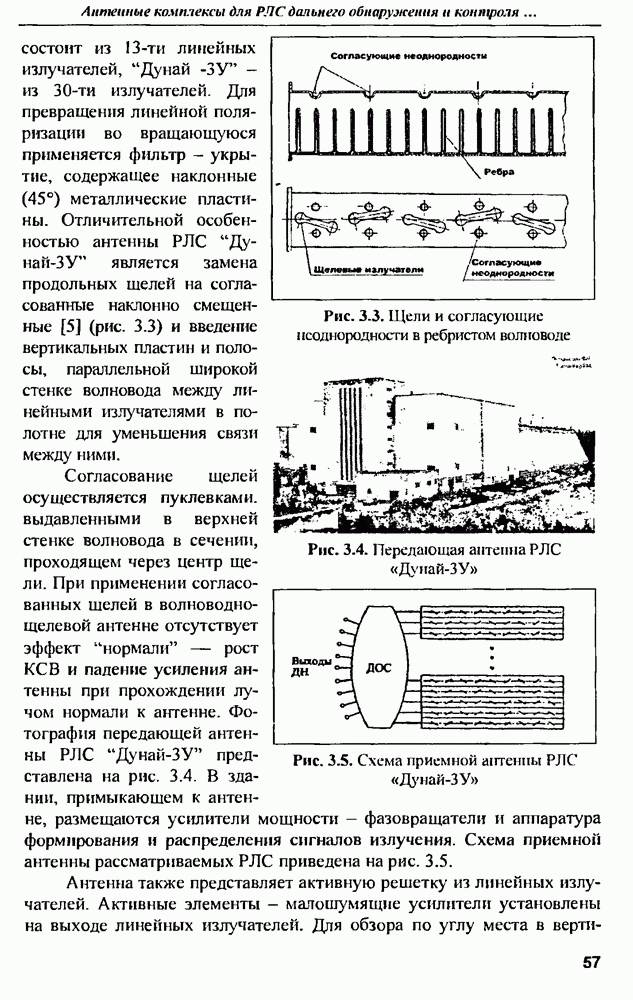
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
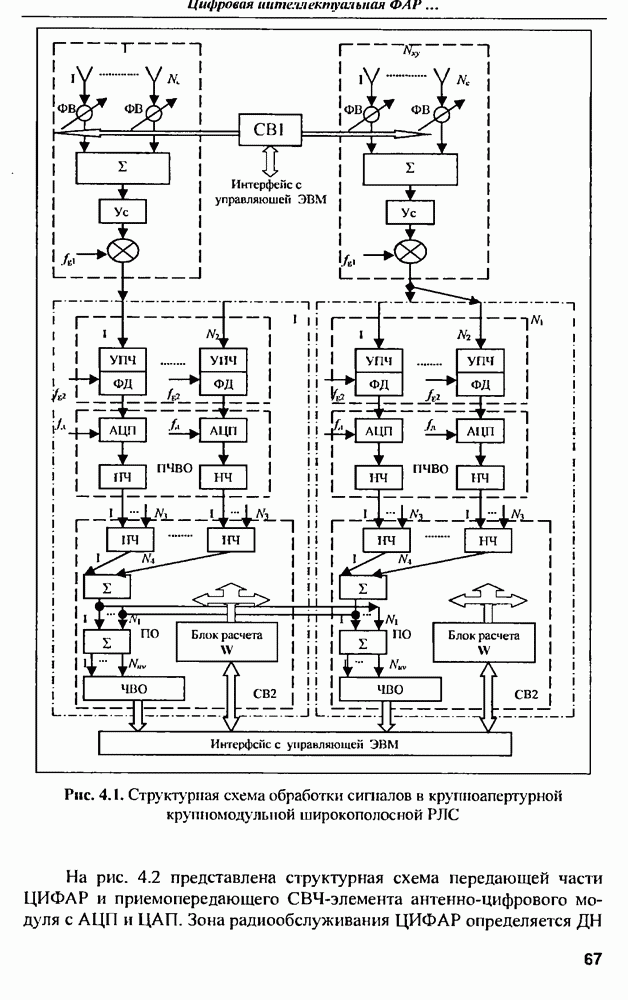
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
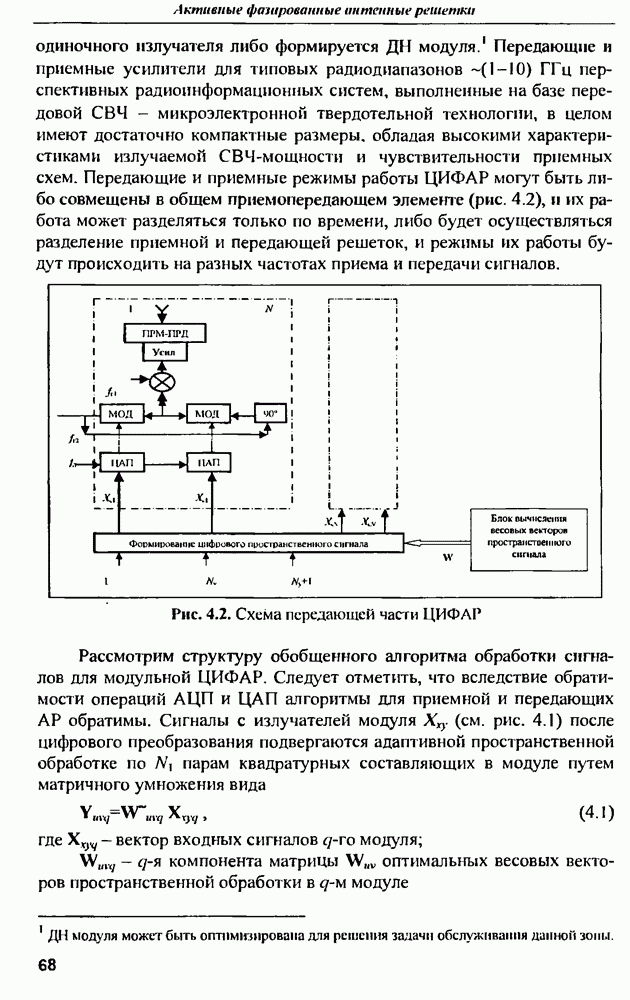
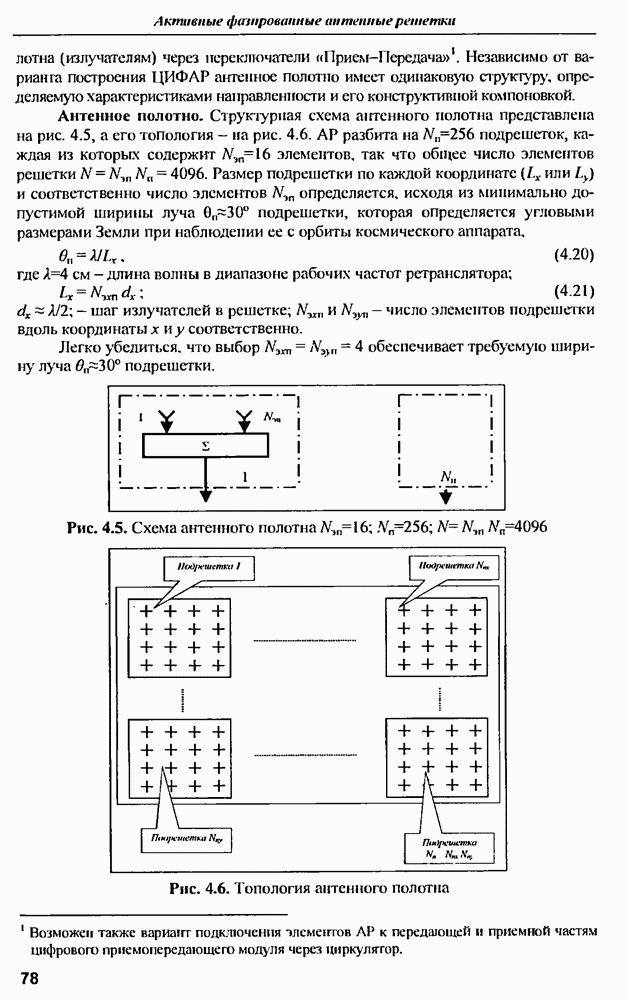
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
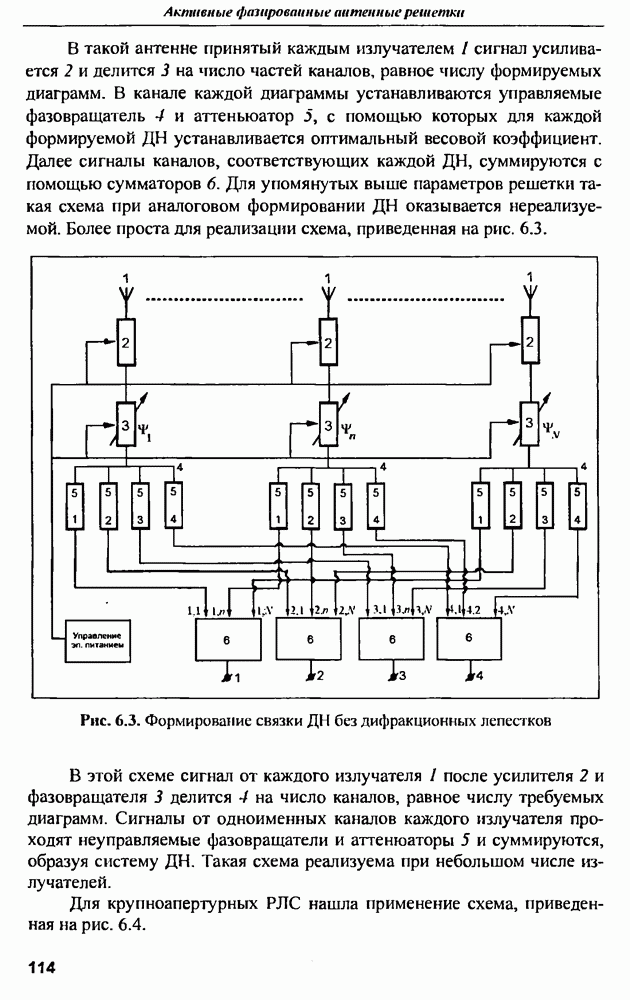
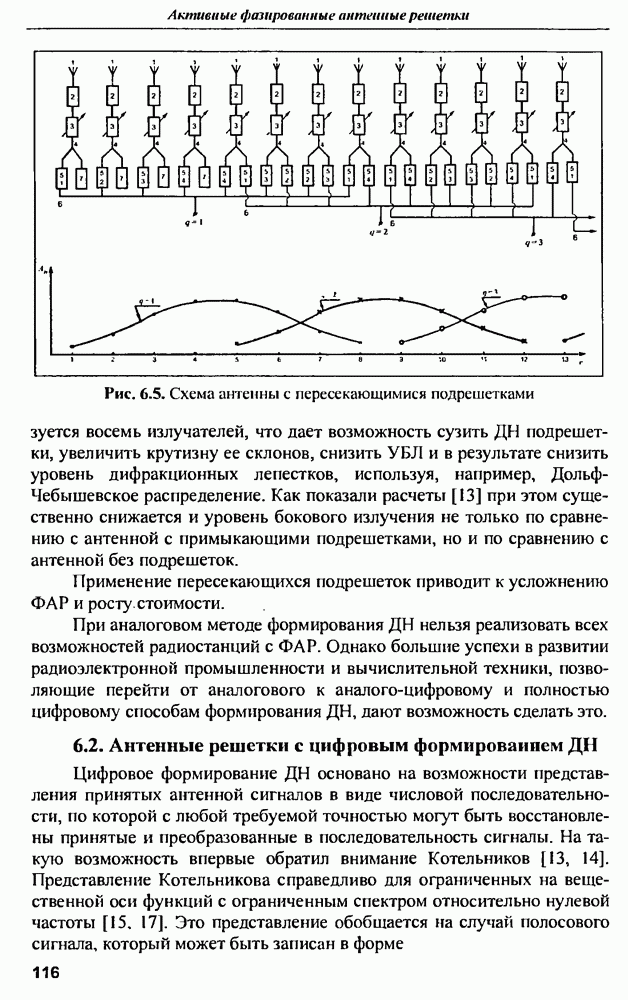
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
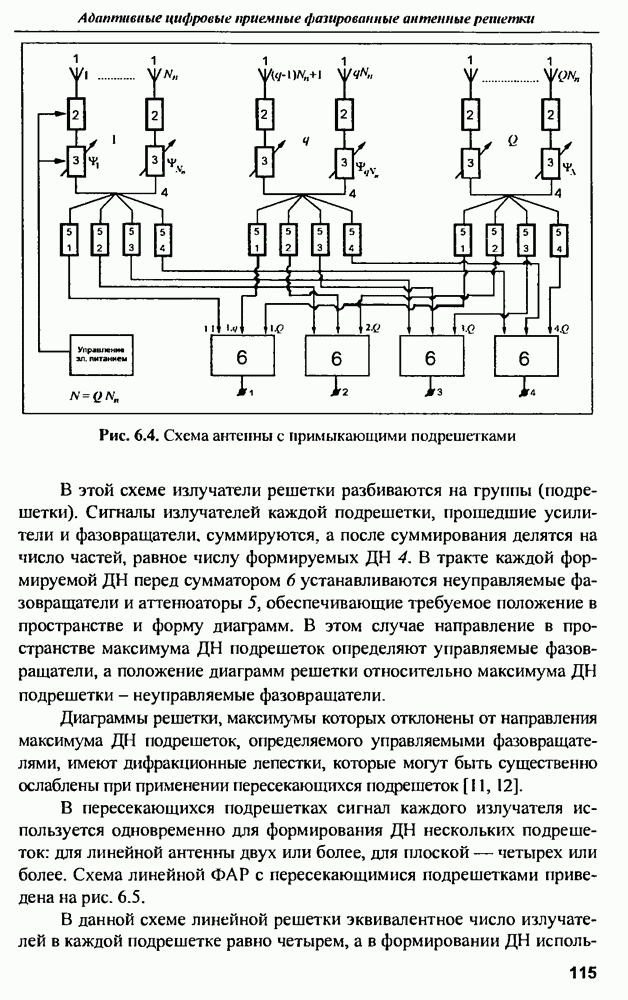
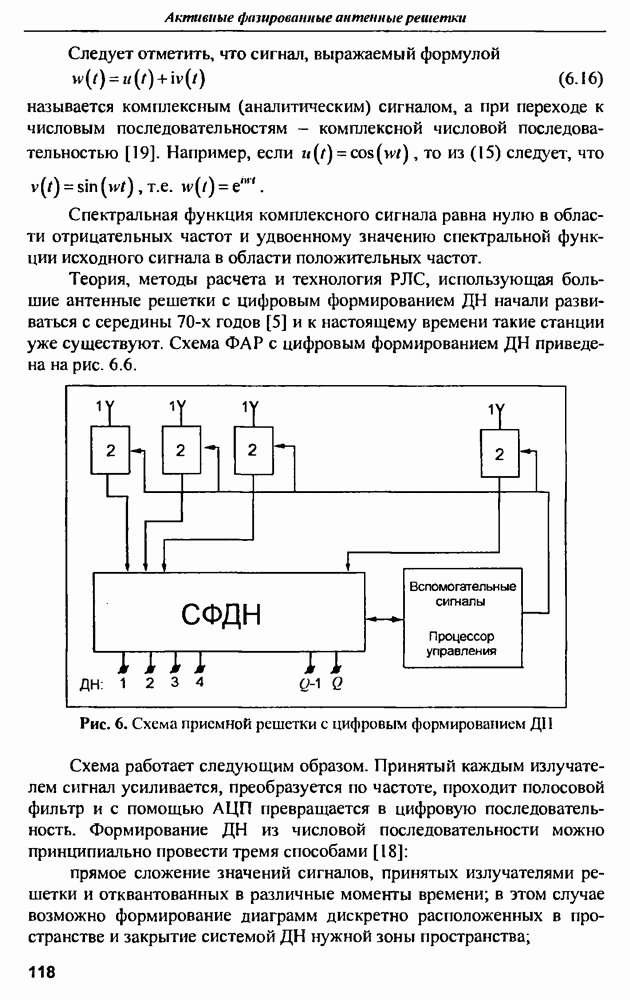
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
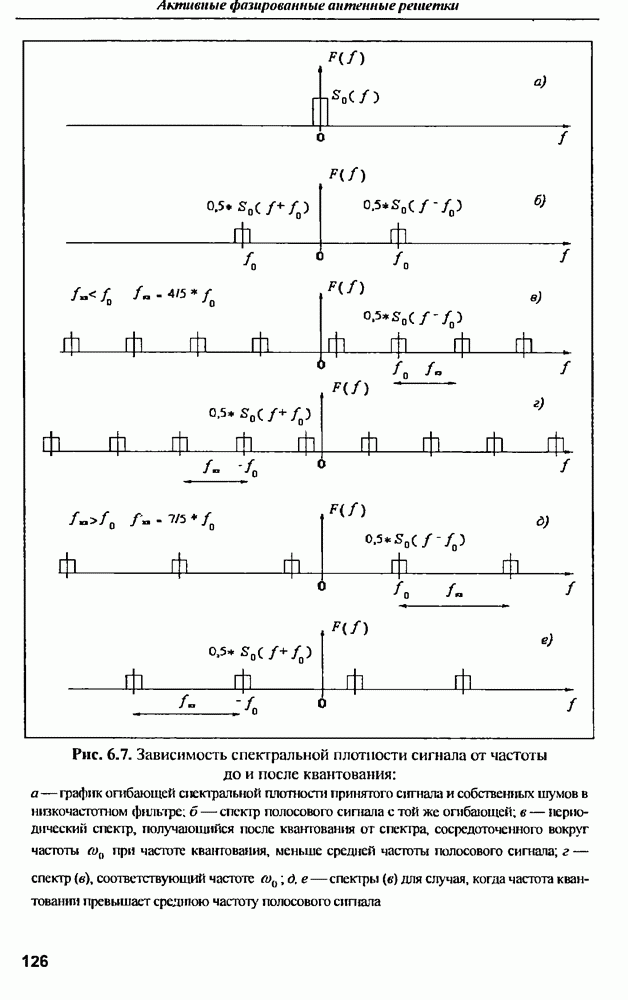
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
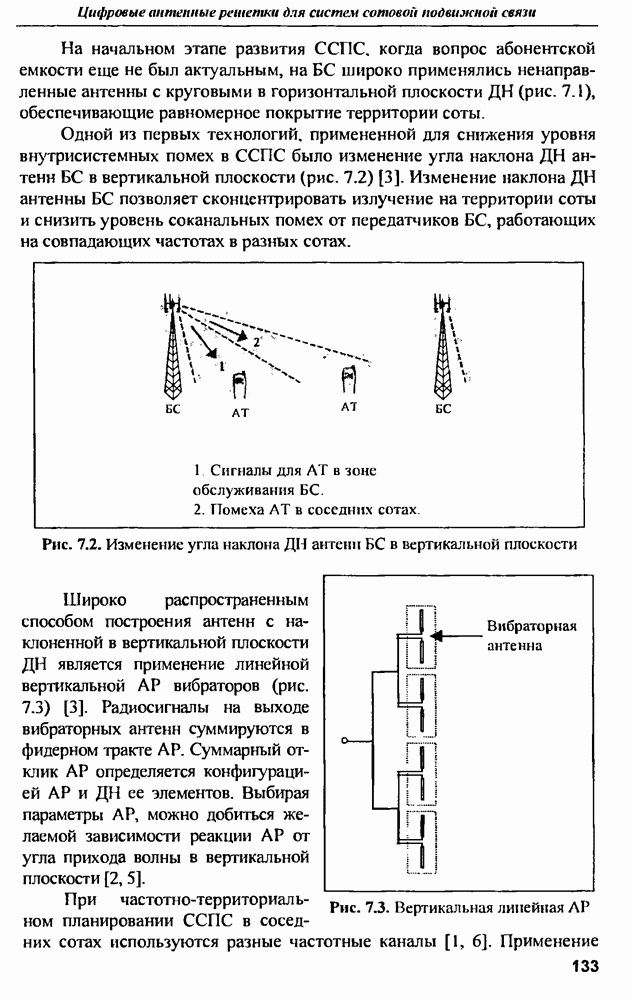
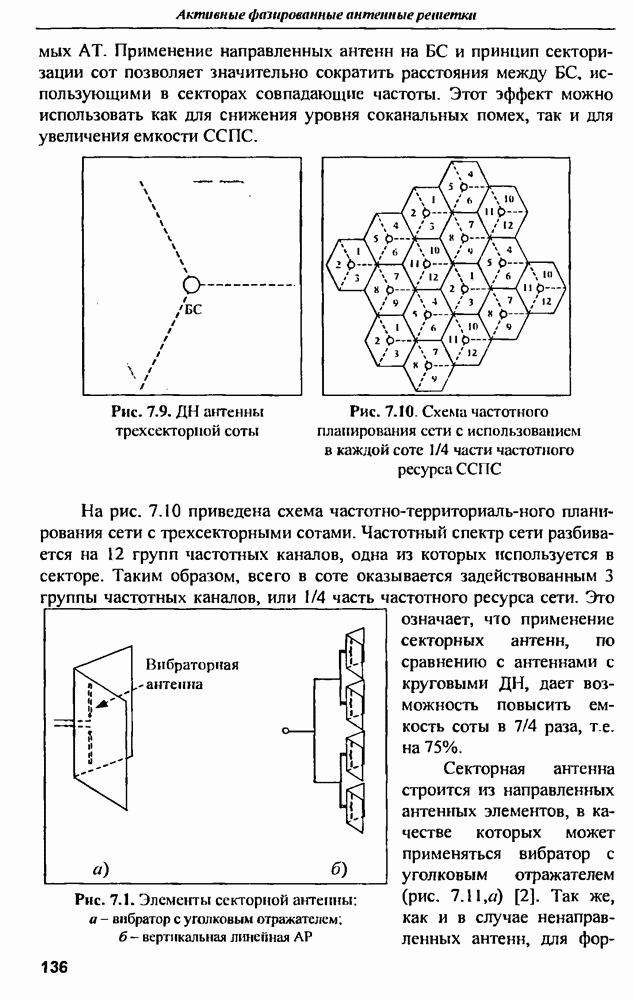
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
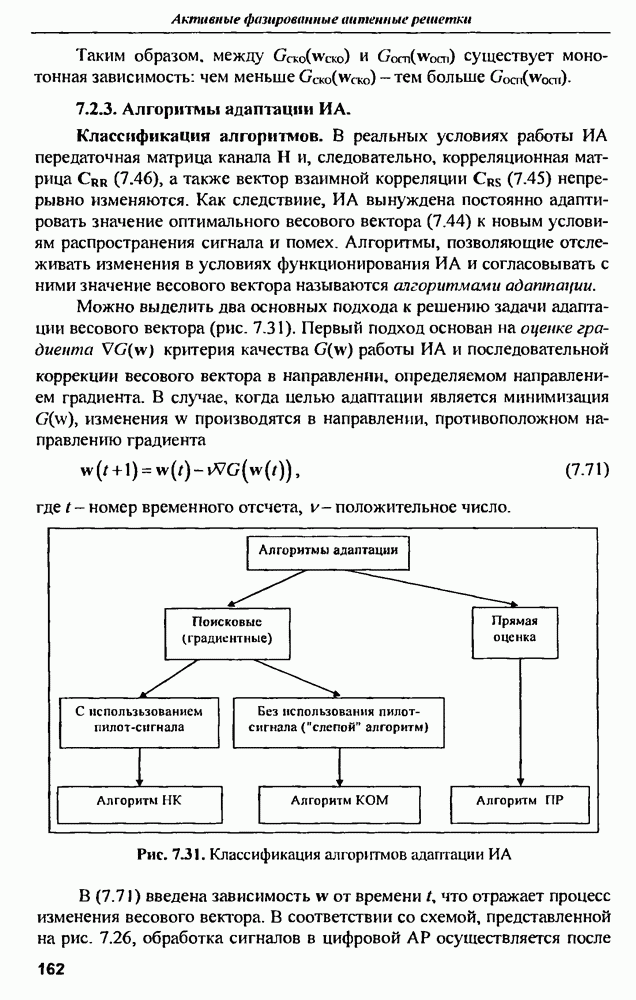
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
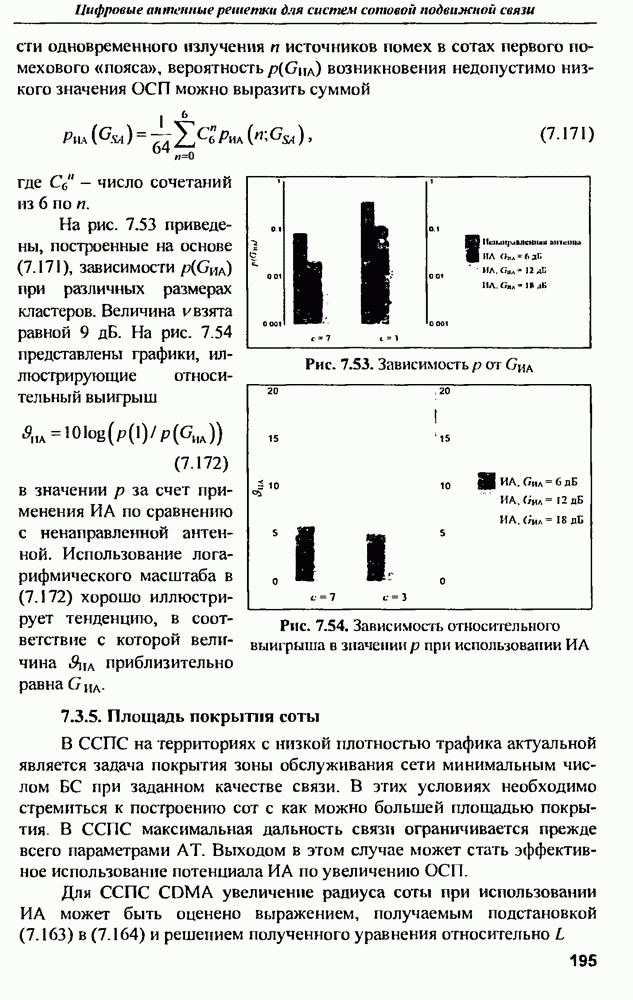
- 7.3.4. Качество связи
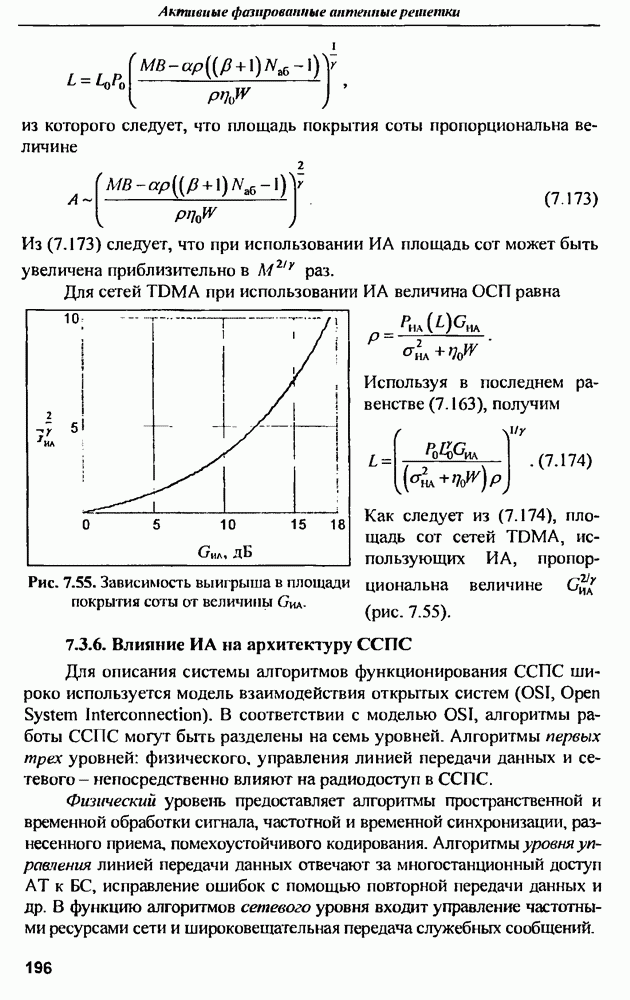
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
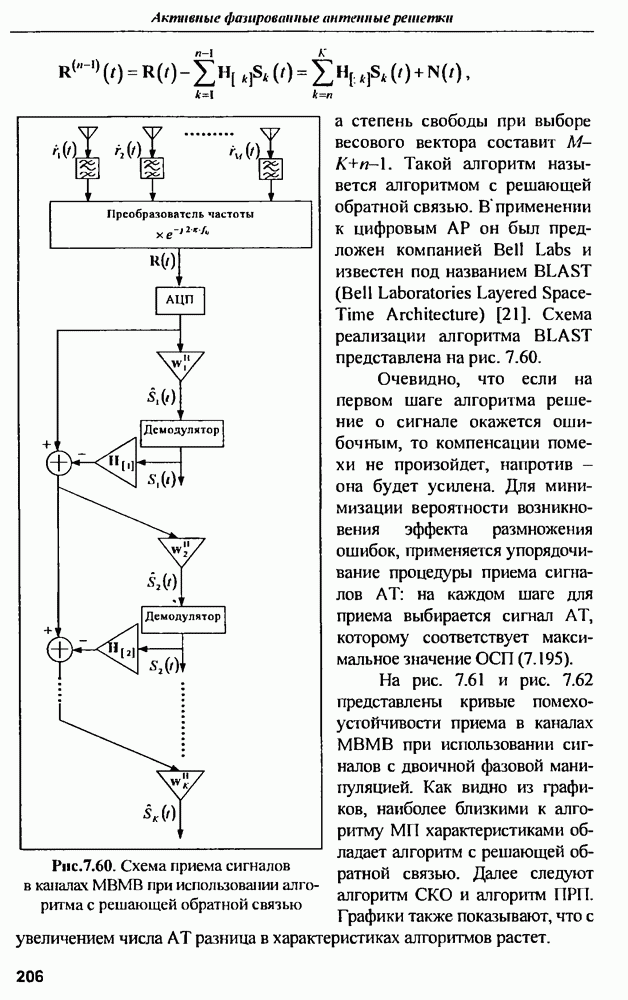
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
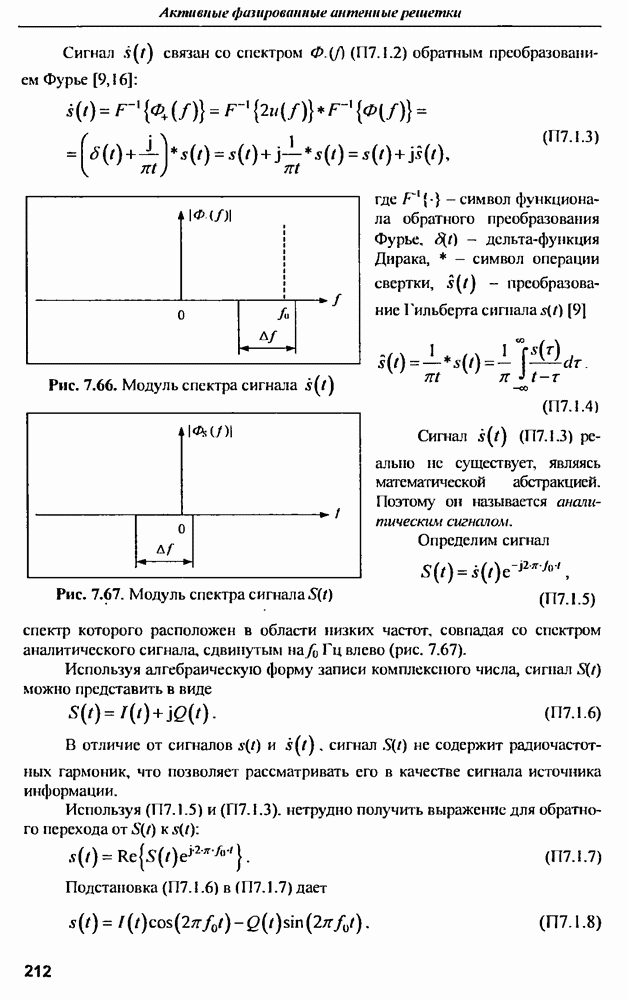
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
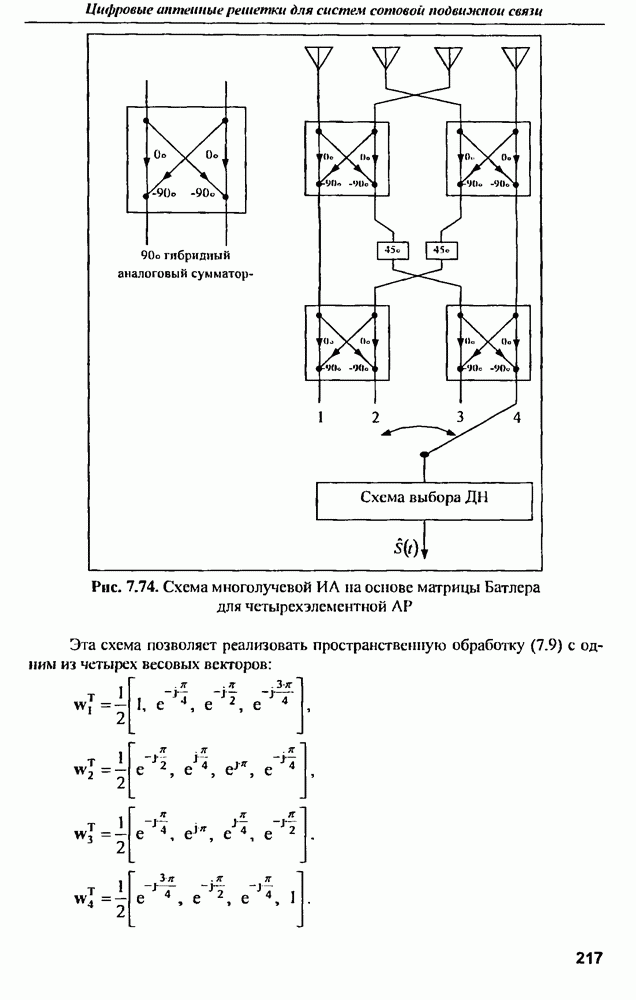
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
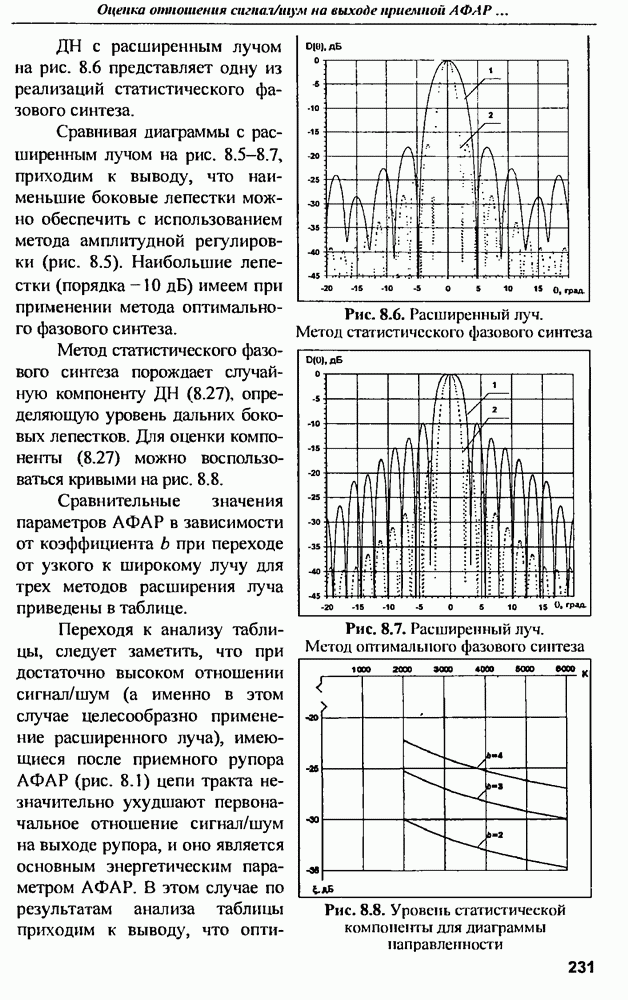
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
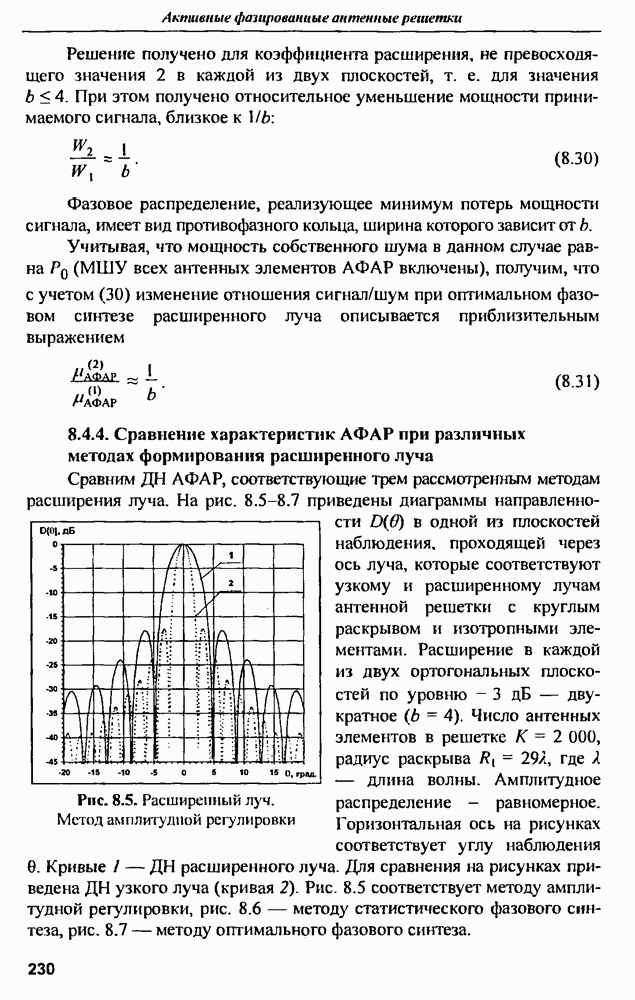
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
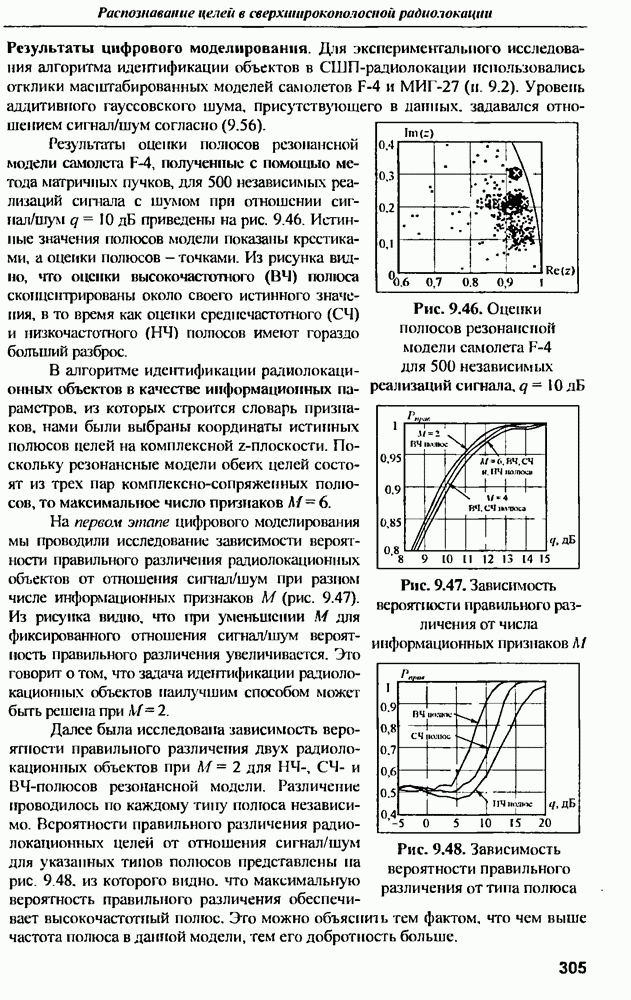
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
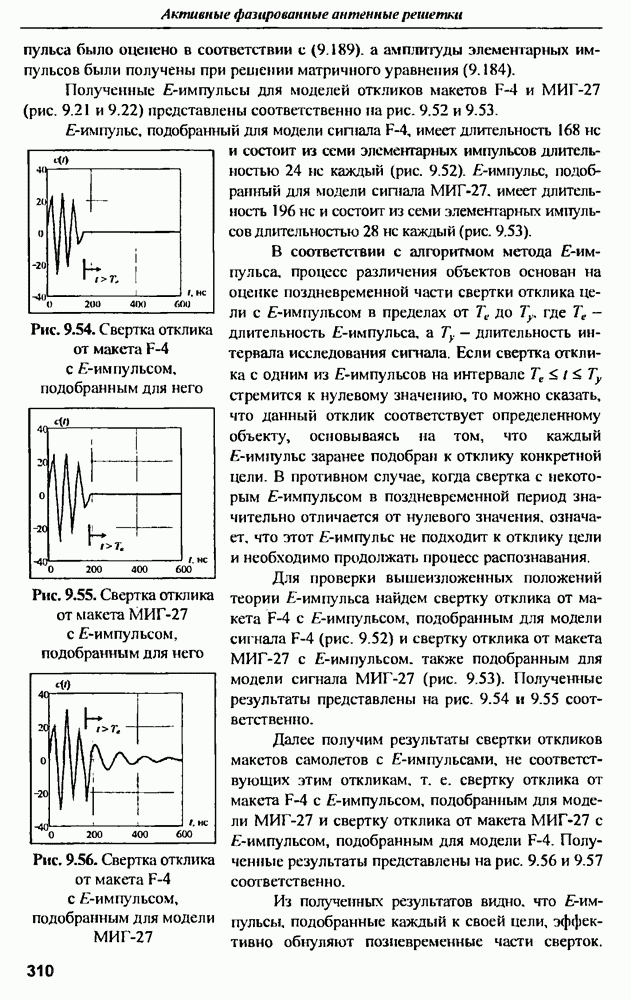
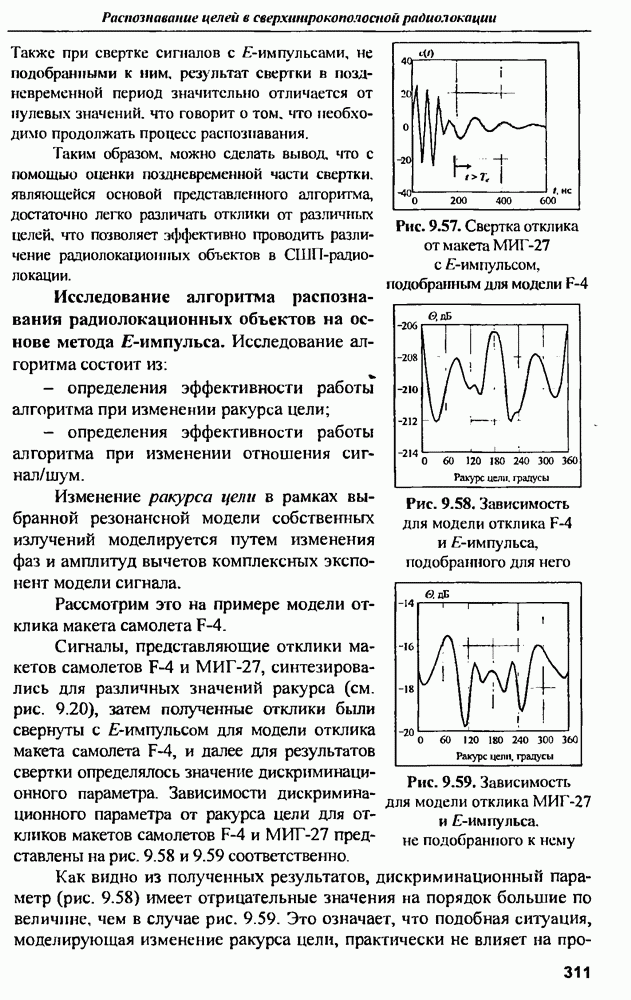
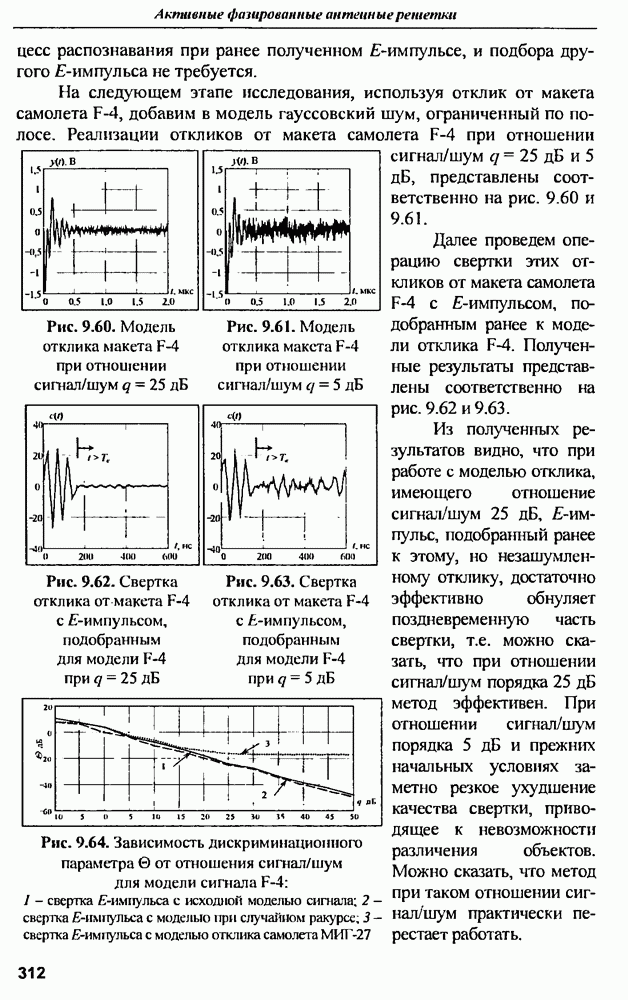
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
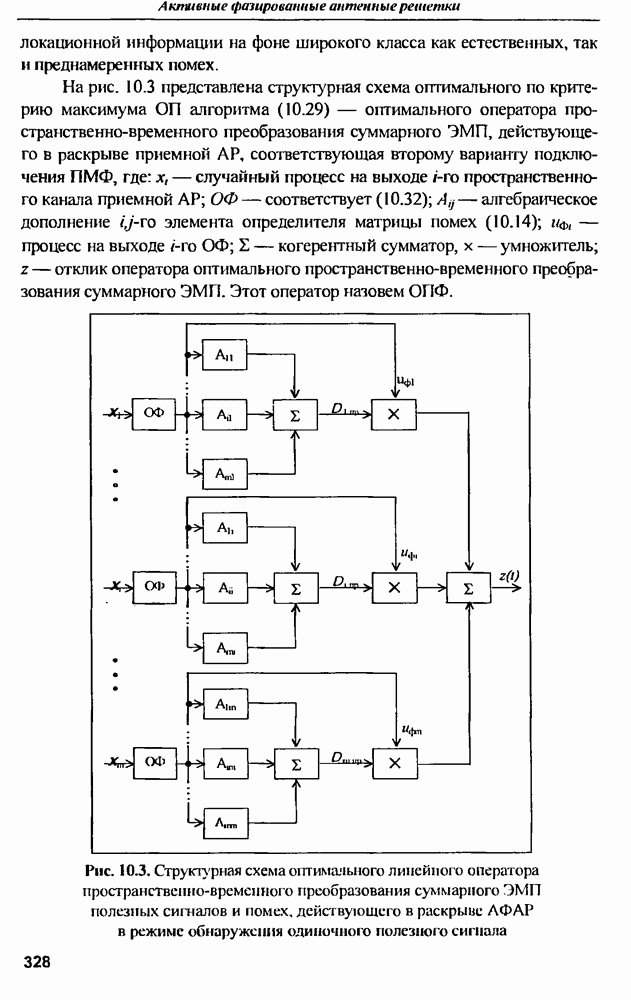
- 10.3. Обнаружение цели и определение ее угловых координат
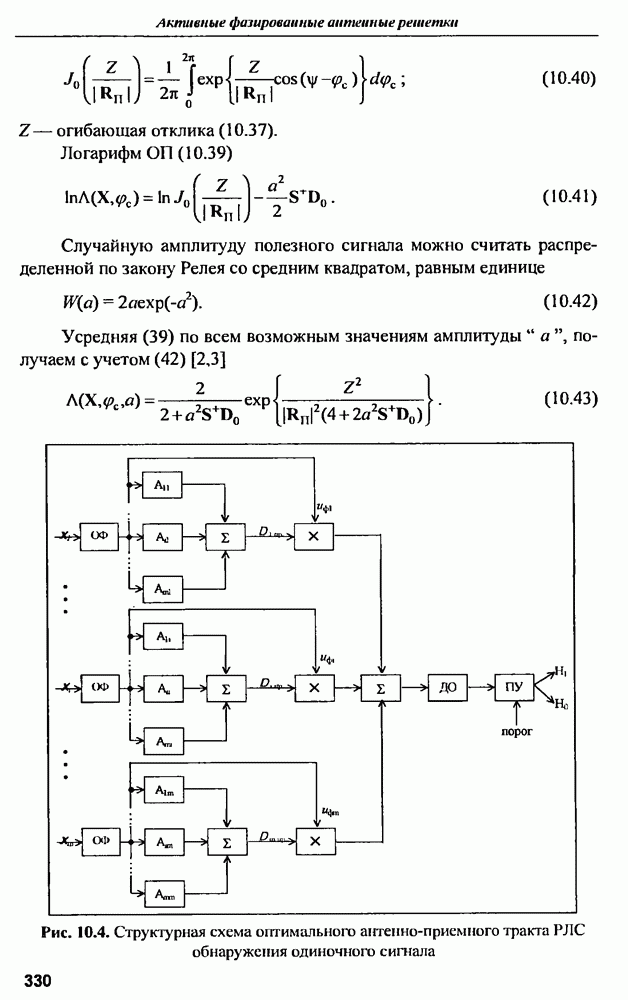
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
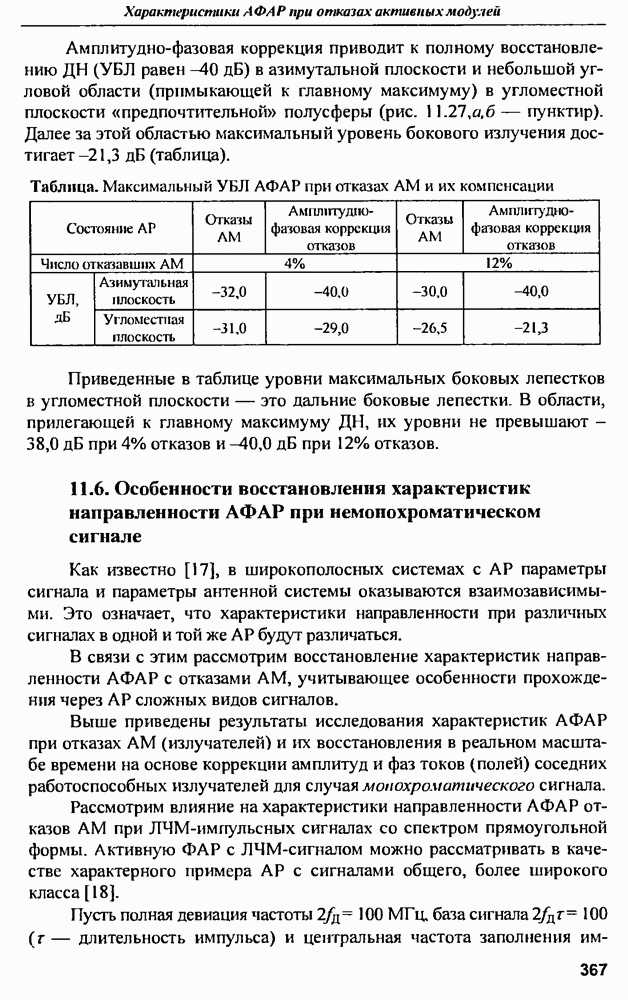
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
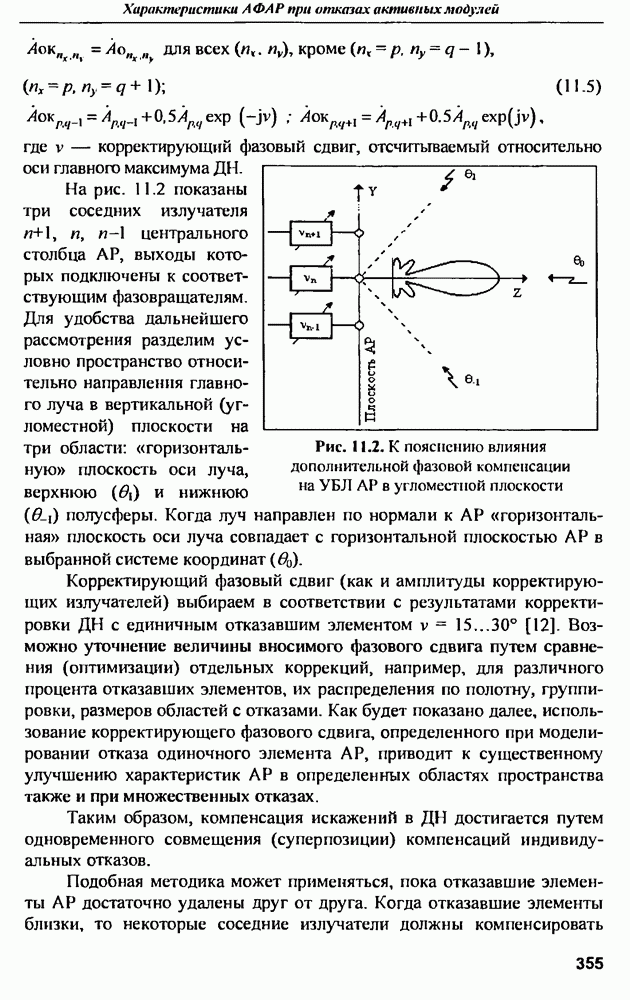
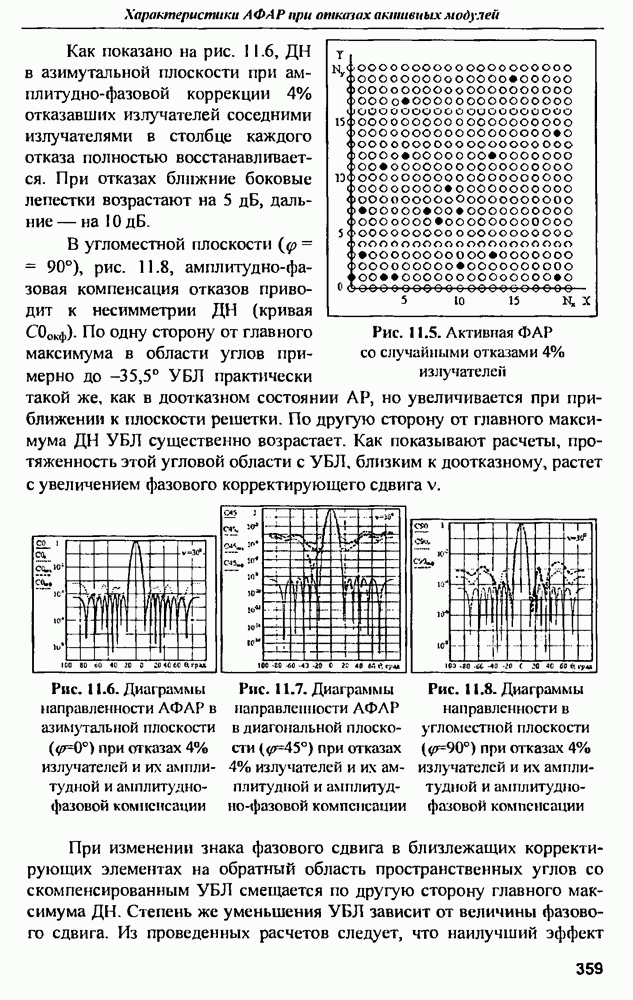
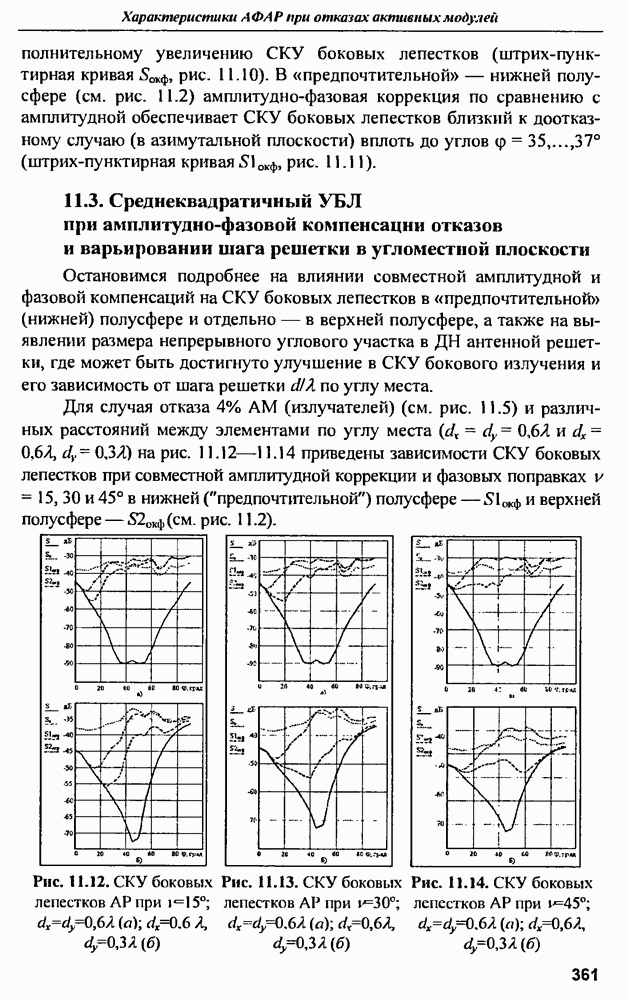
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
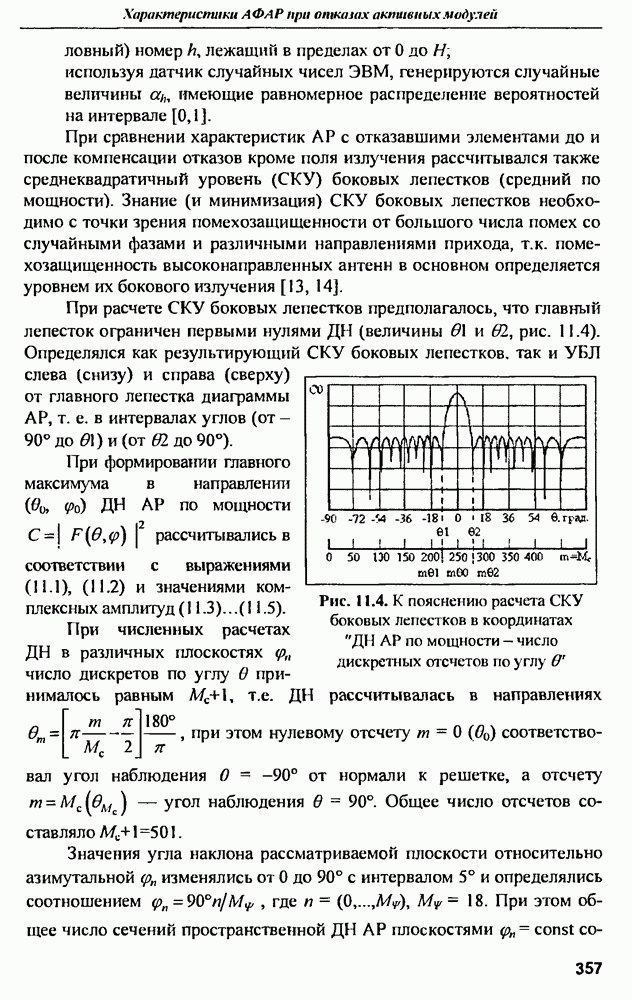
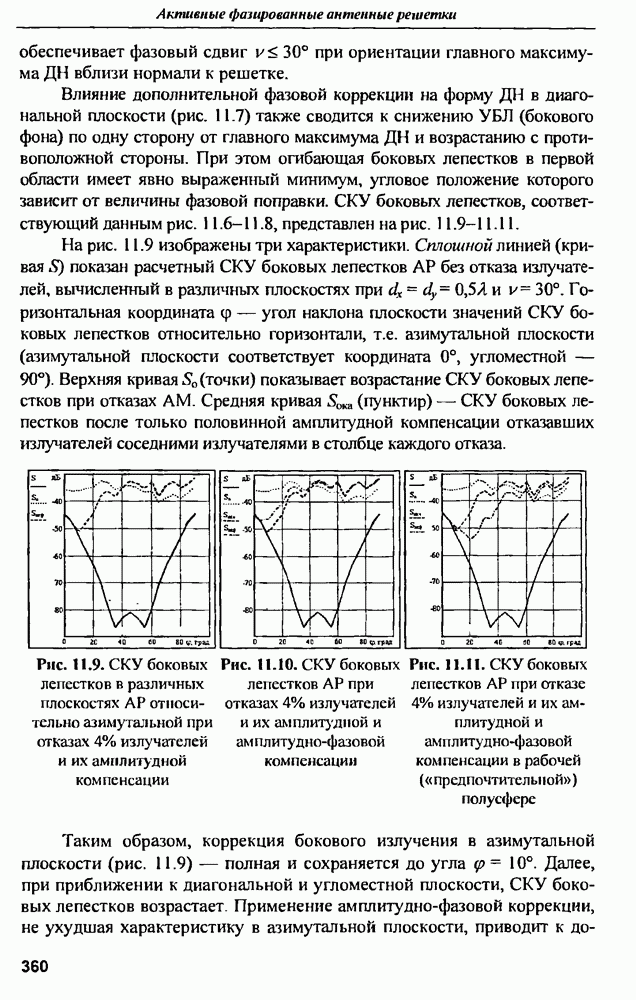
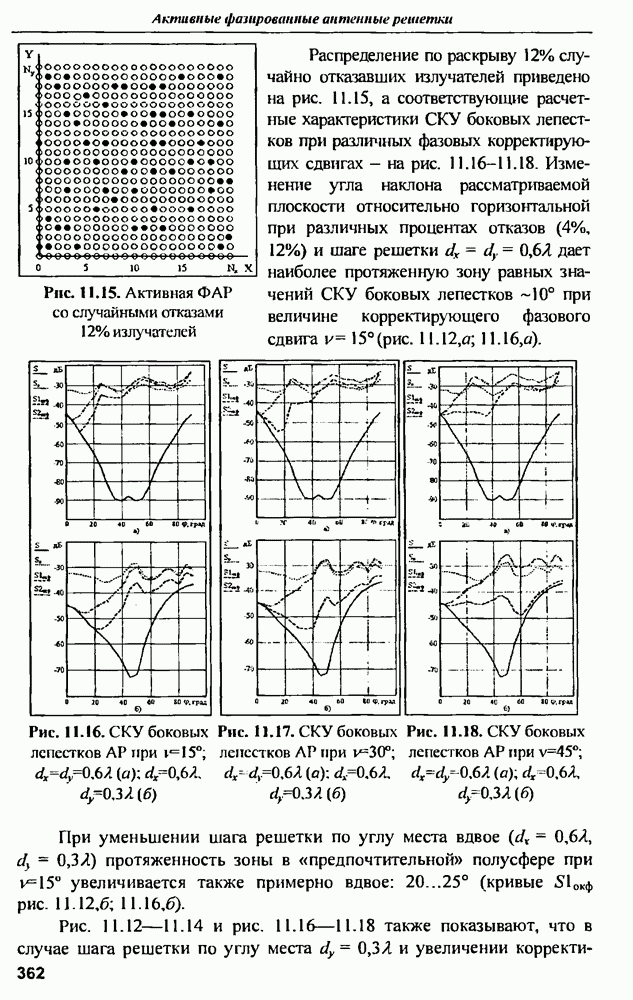
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
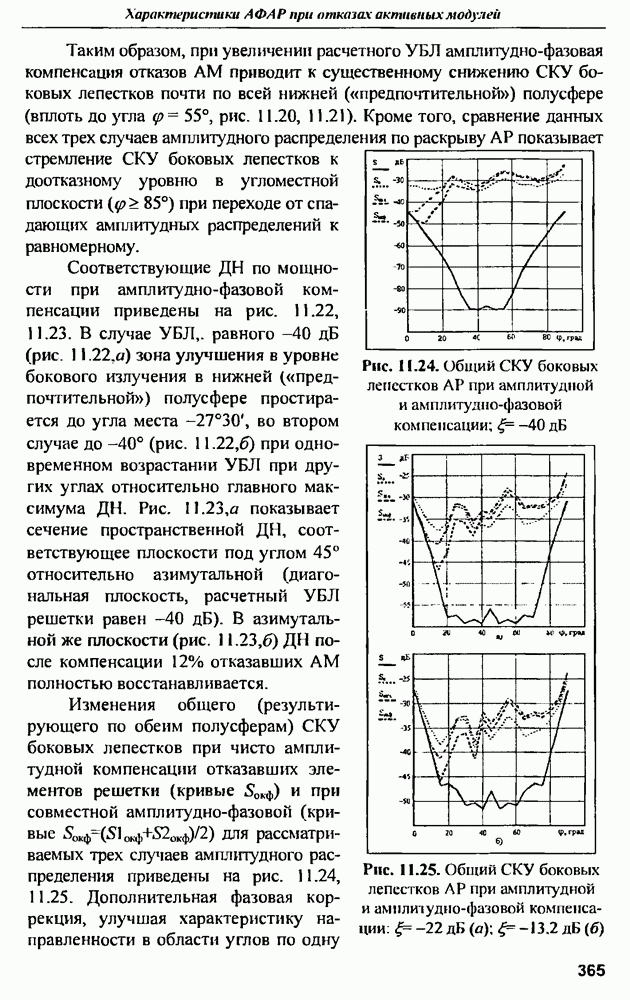
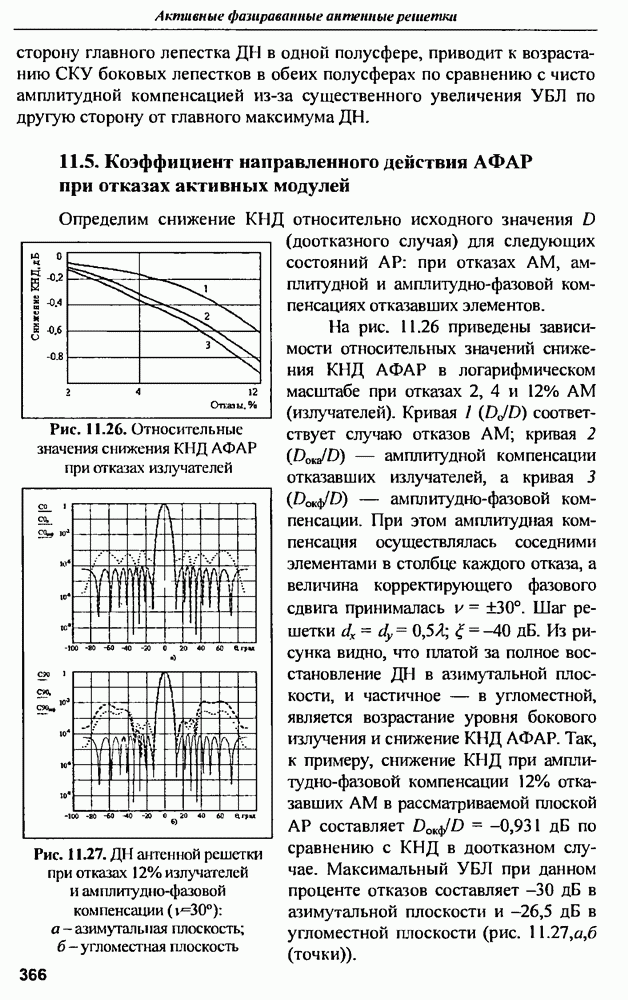
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
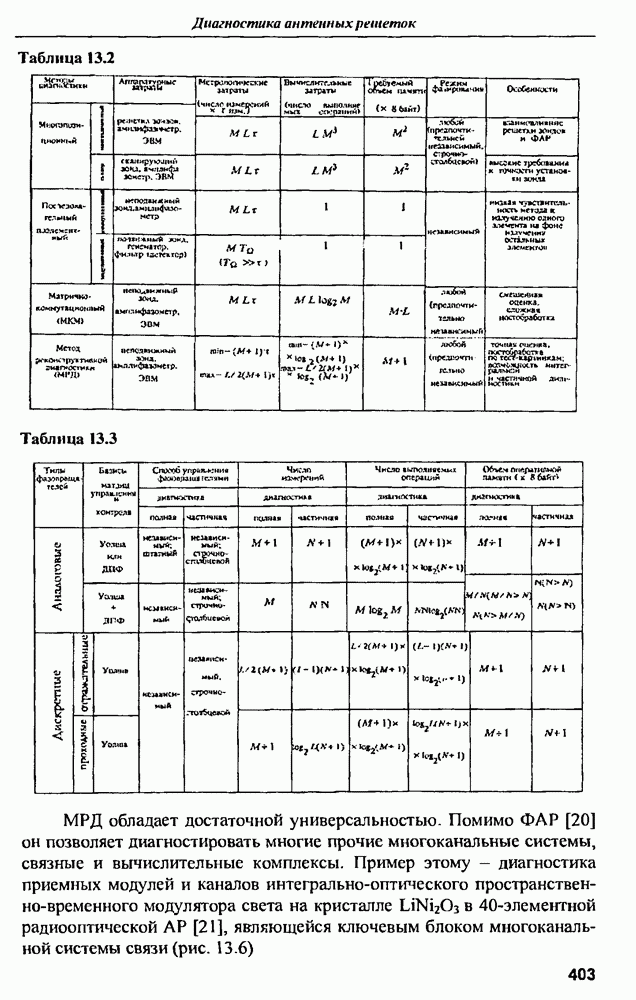
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
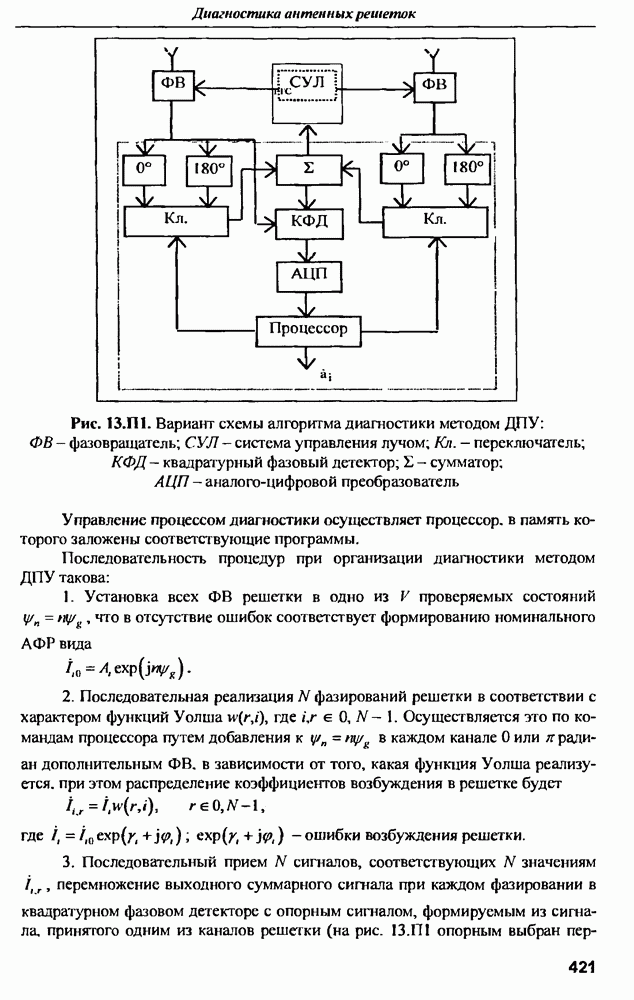
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
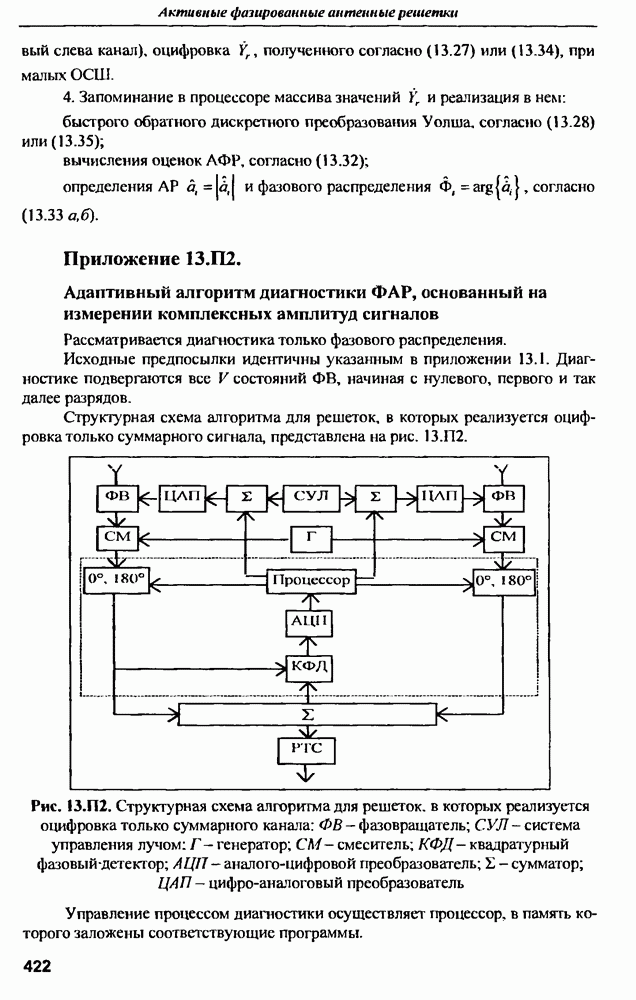
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
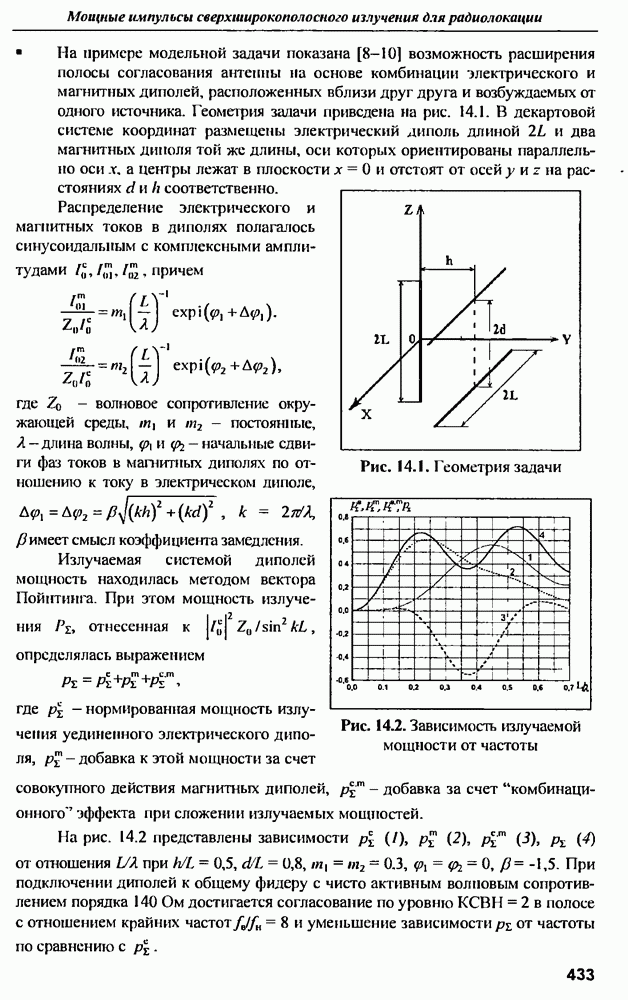
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
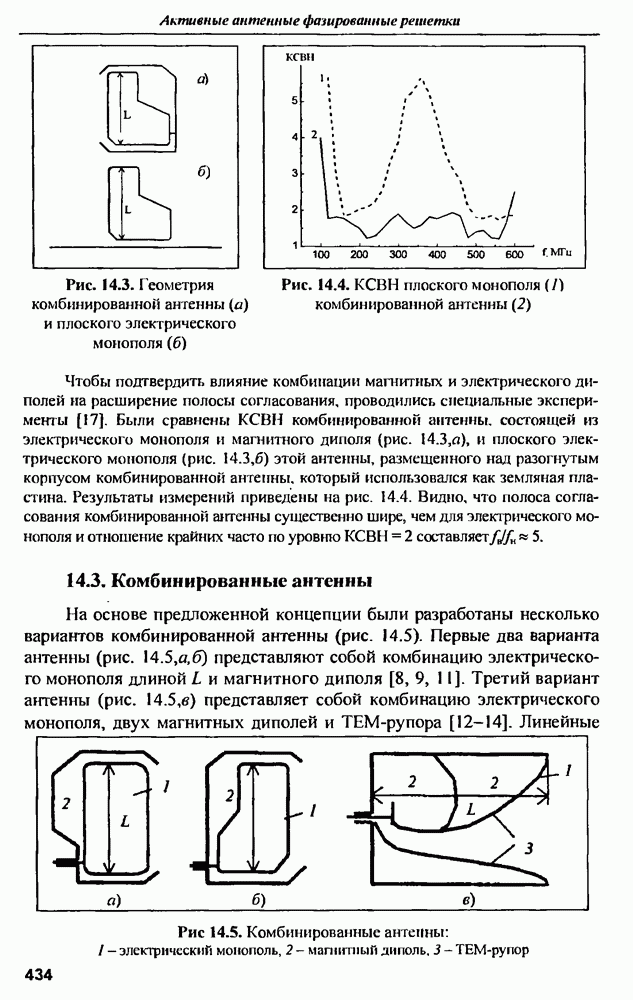
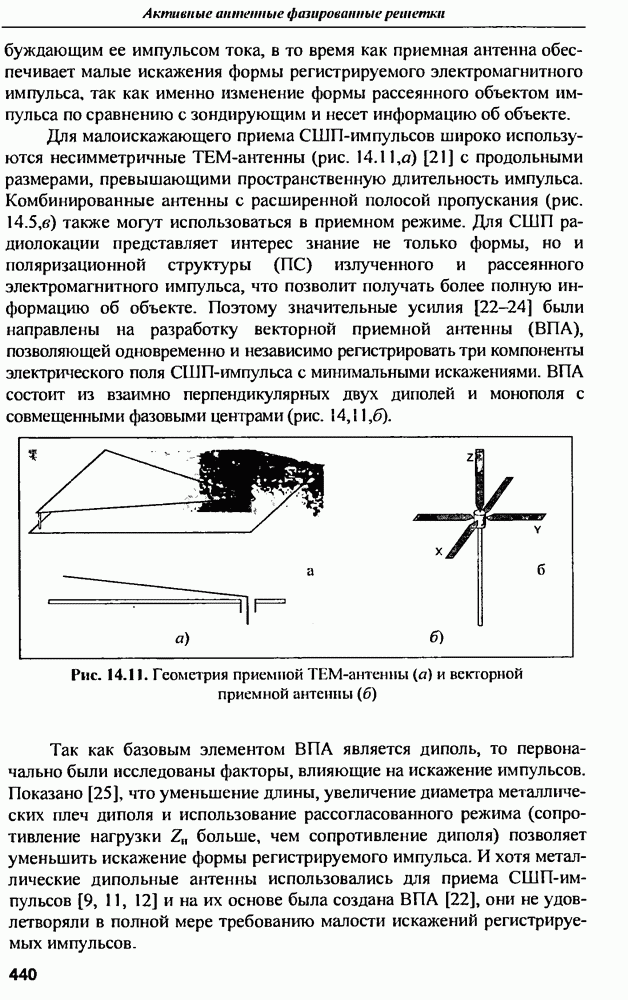
- 14.3. Комбинированные антенны
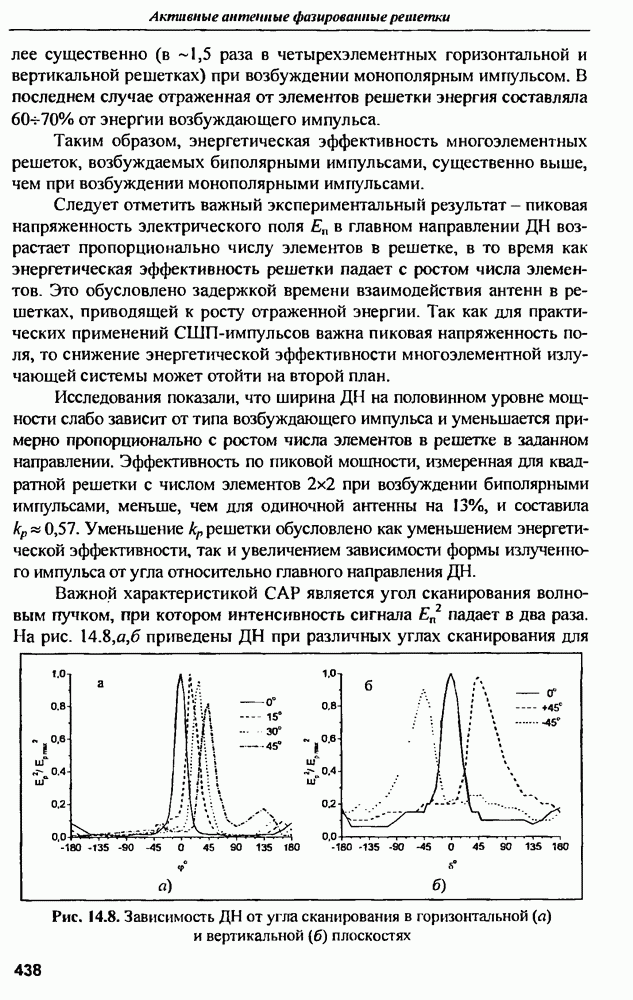
- 14.4. Антенные решетки
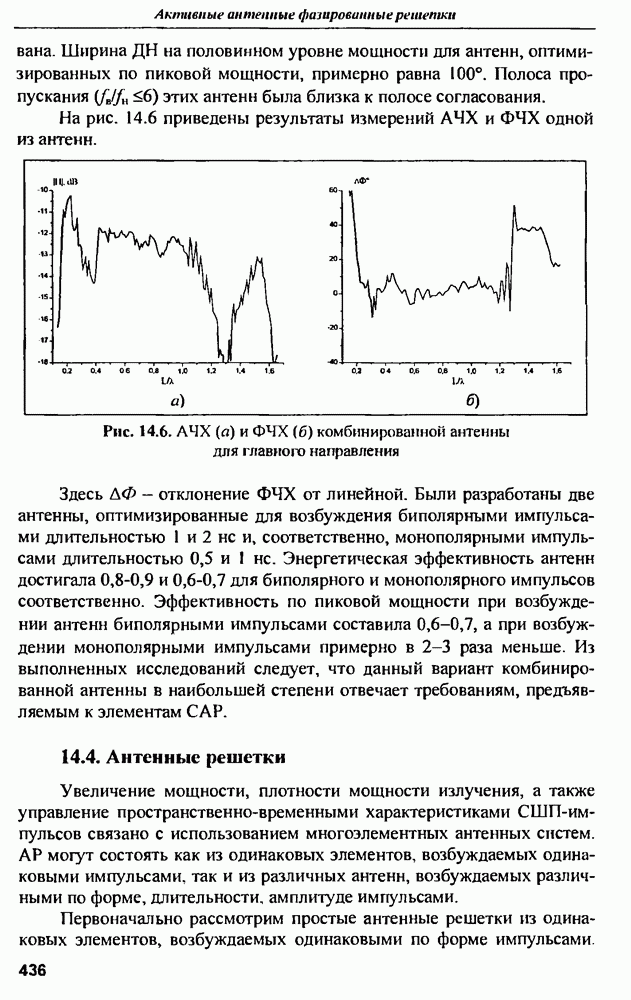
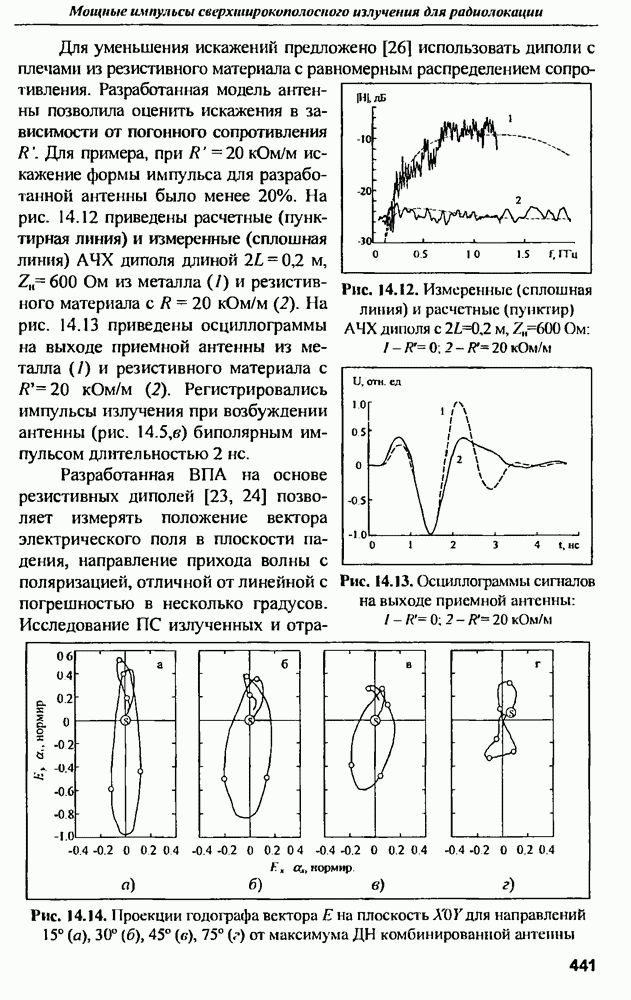
- 14.5. Приемные антенны
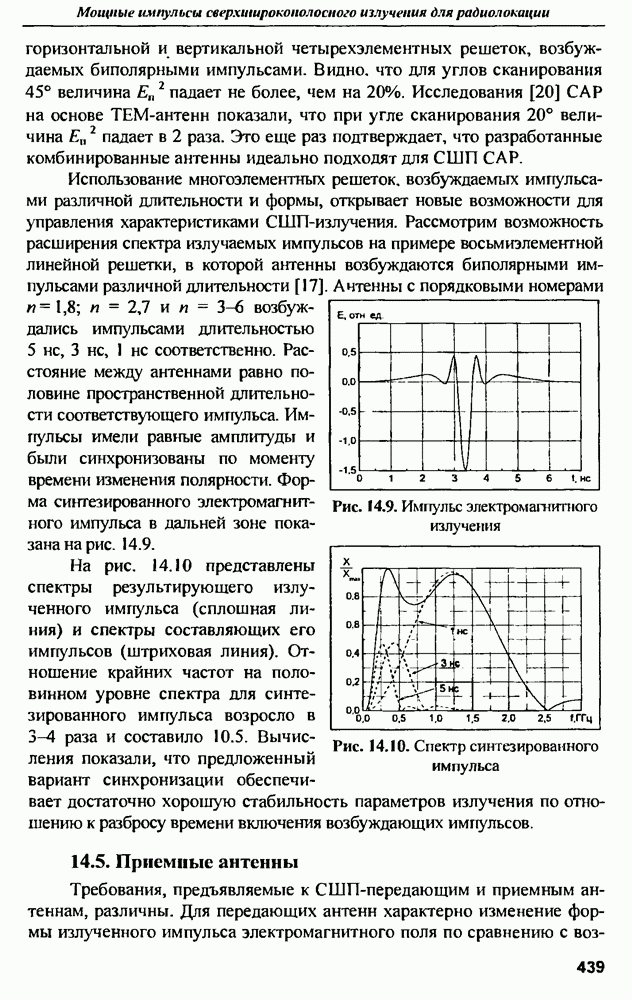
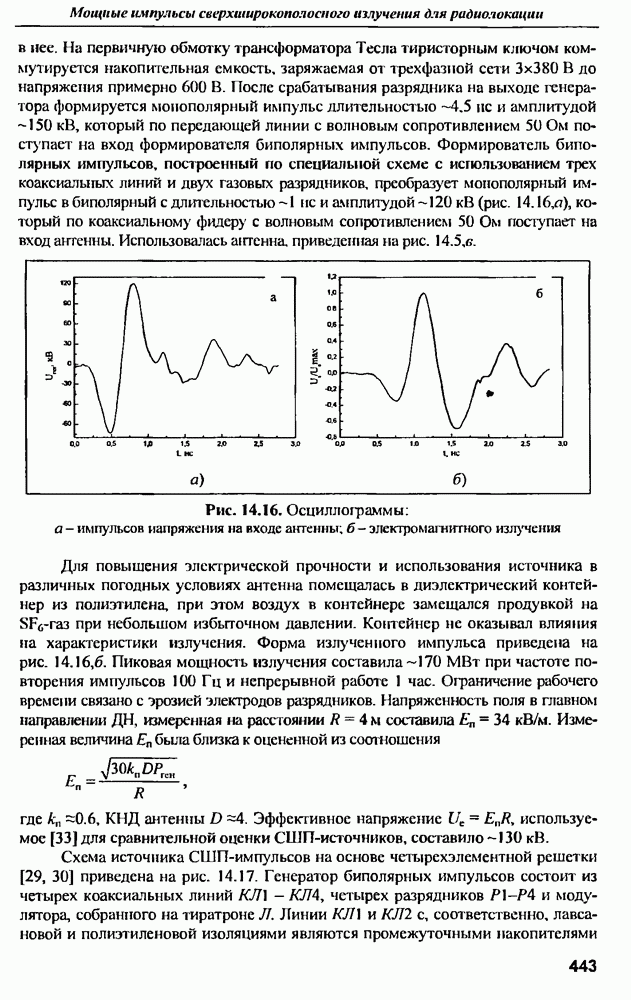
- 14.6. Мощные источники СШП-излучения
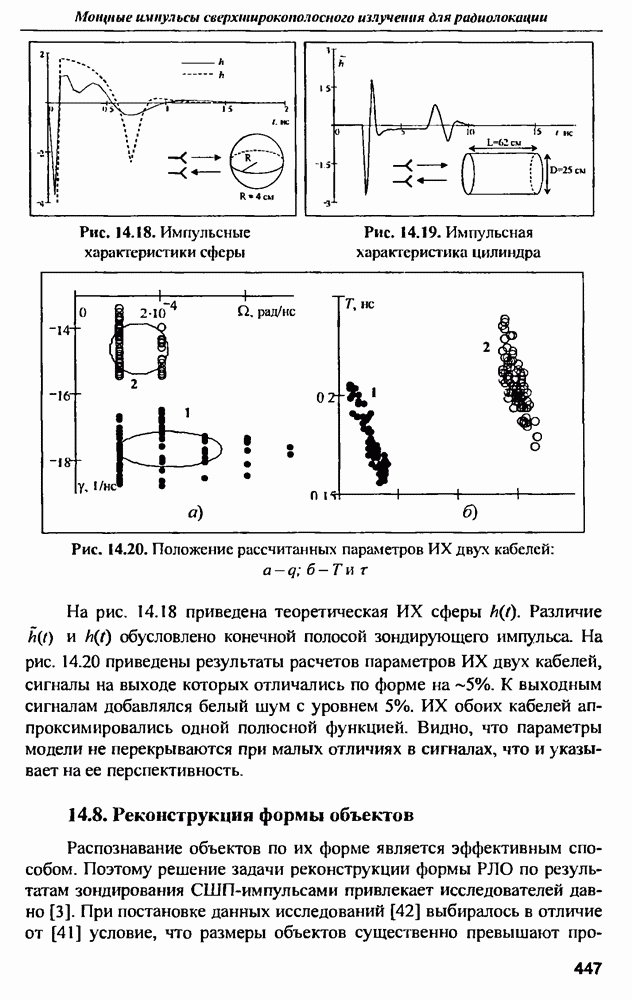
- 14.7. Методы оценивания импульсных характеристик
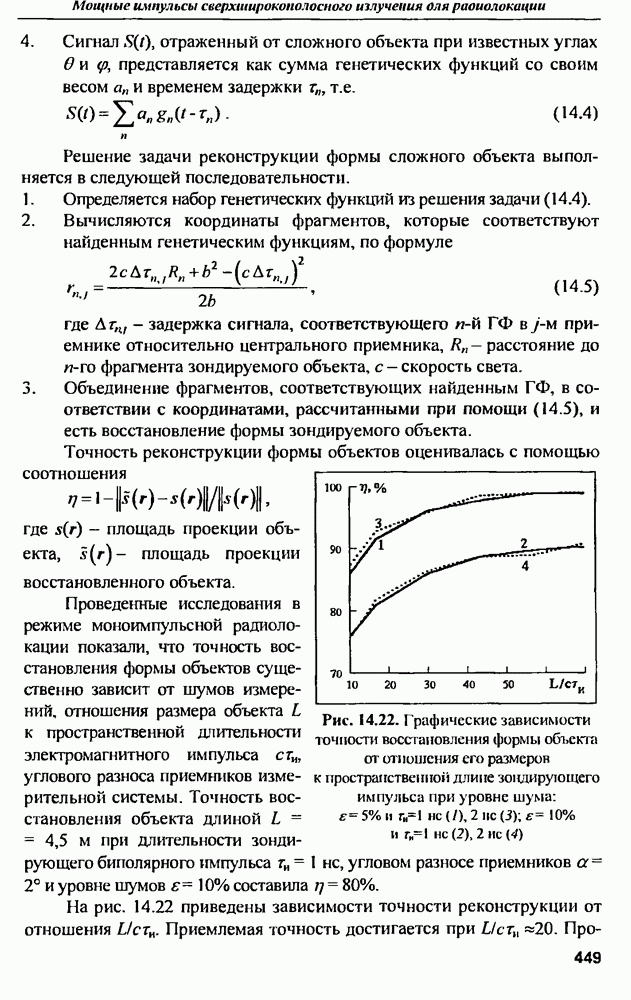
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
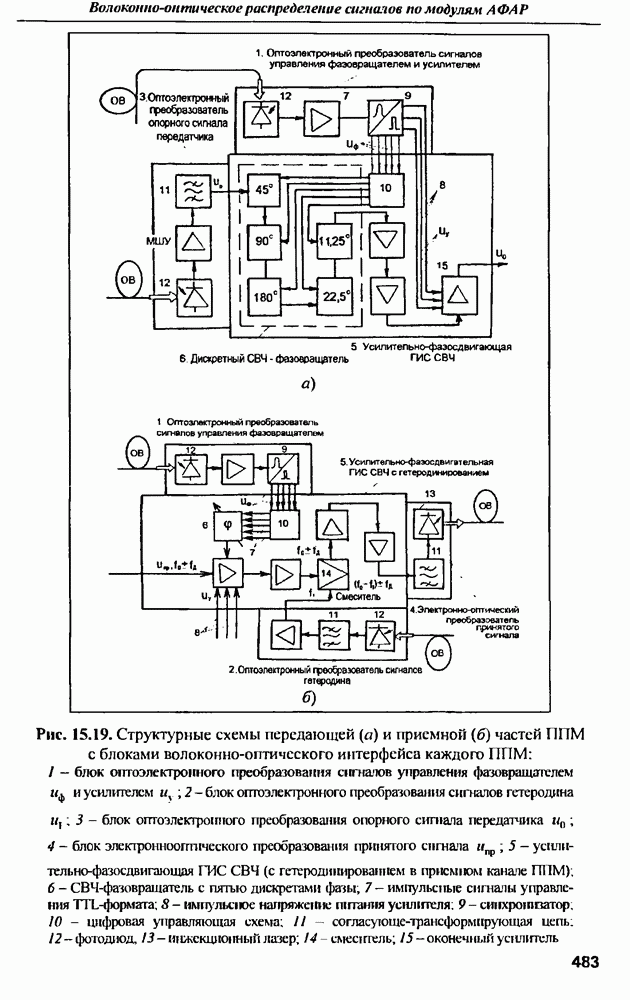
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
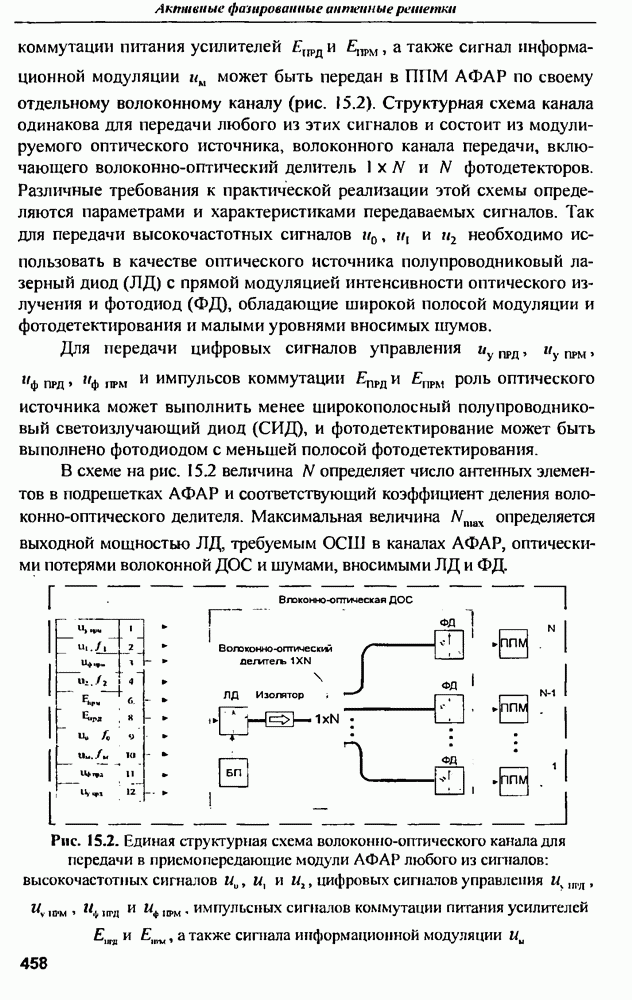
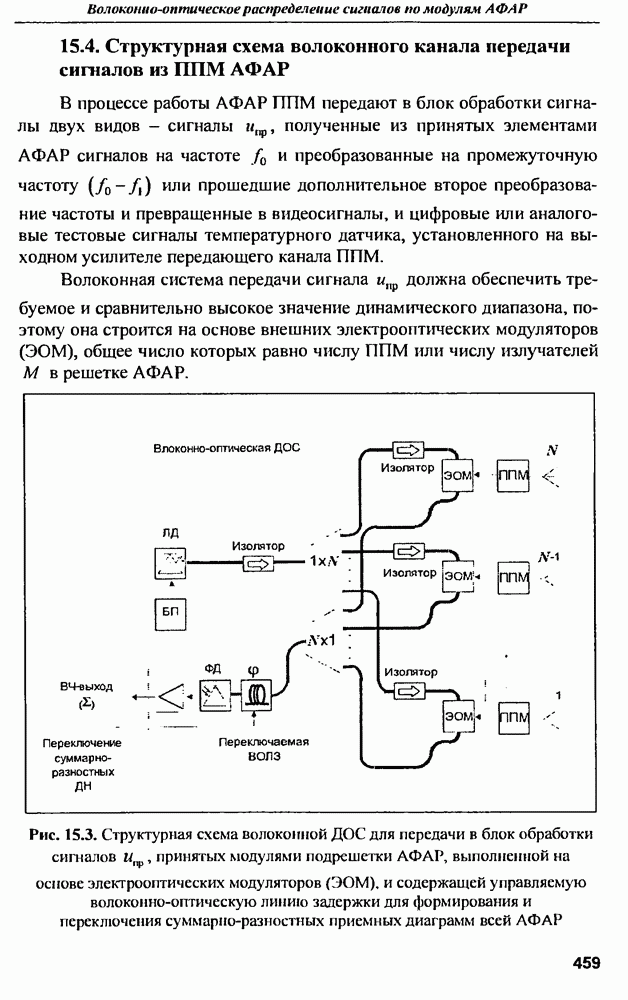
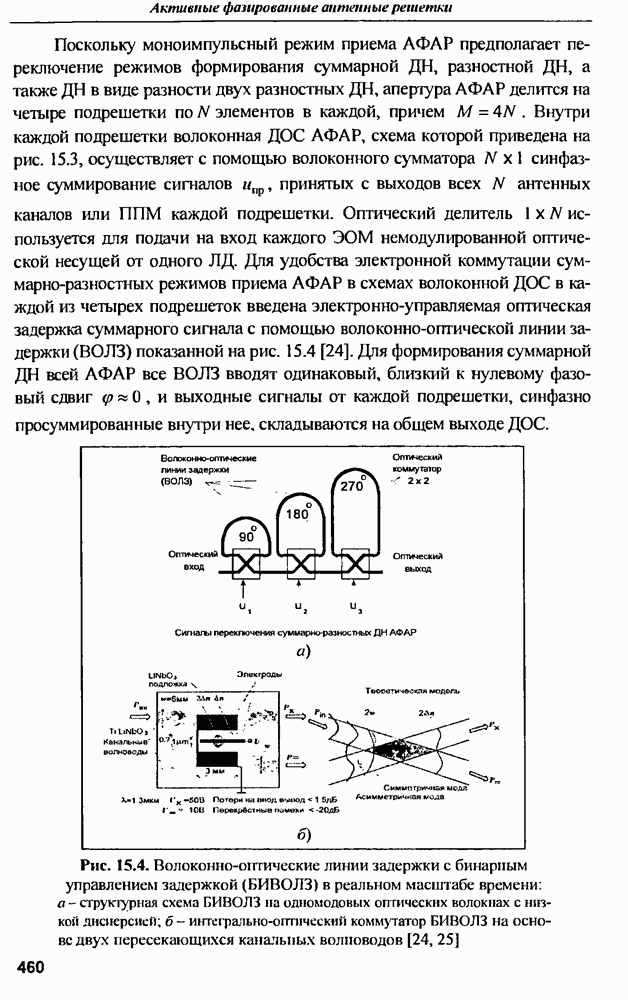
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
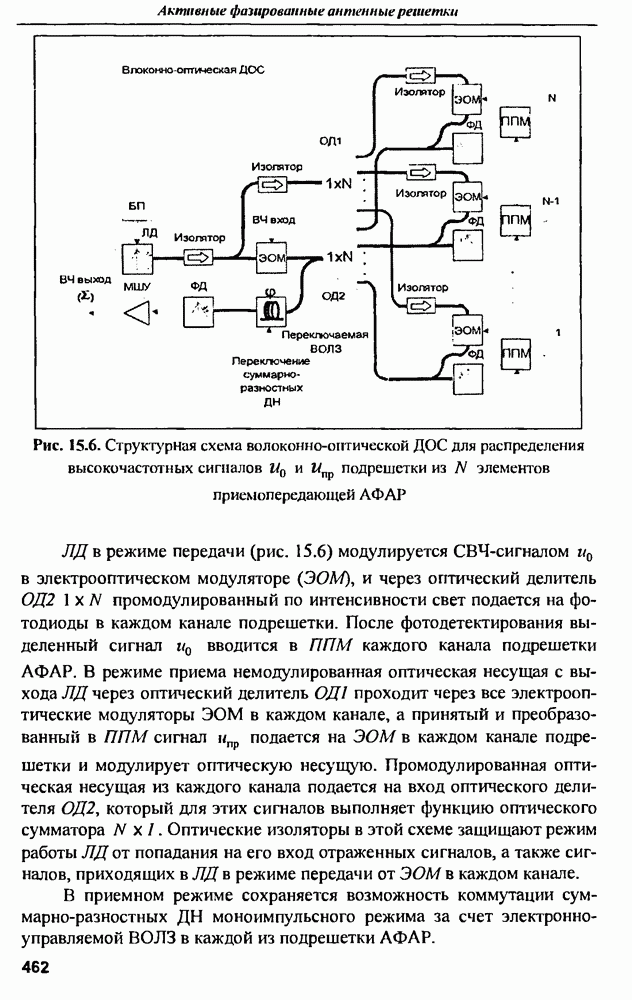
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
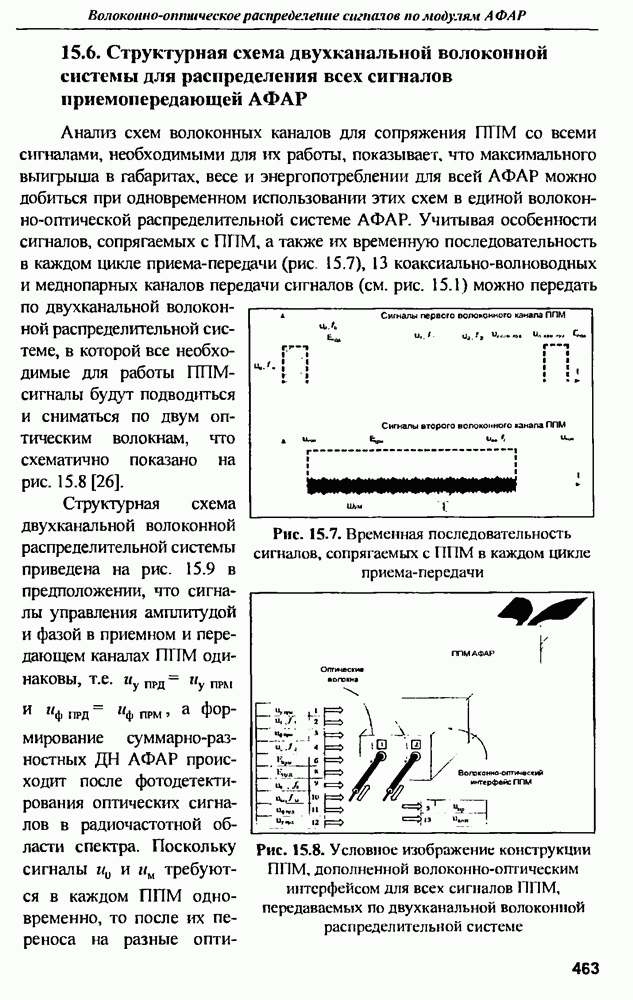
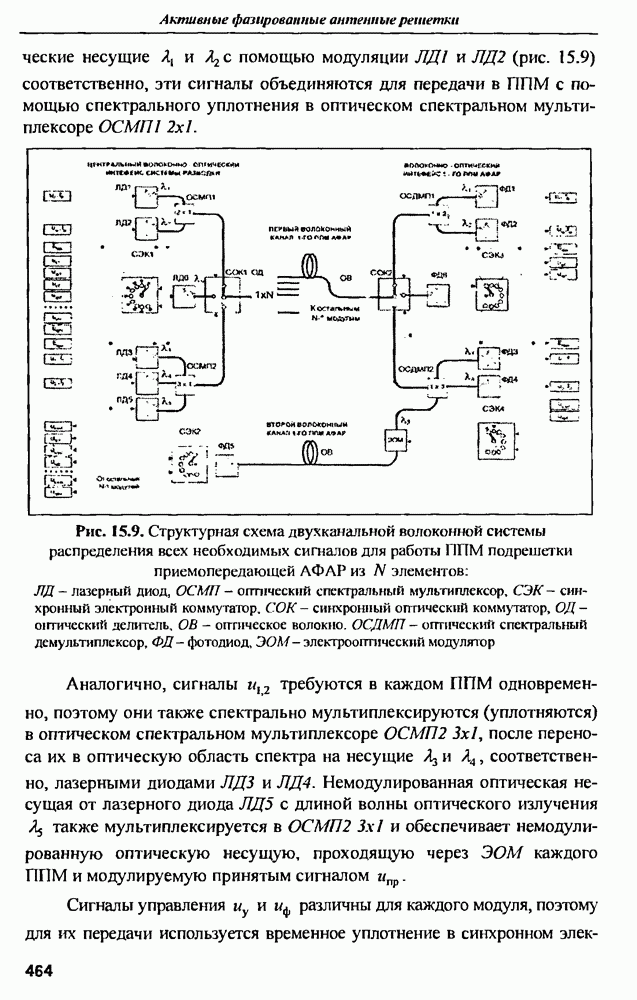
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
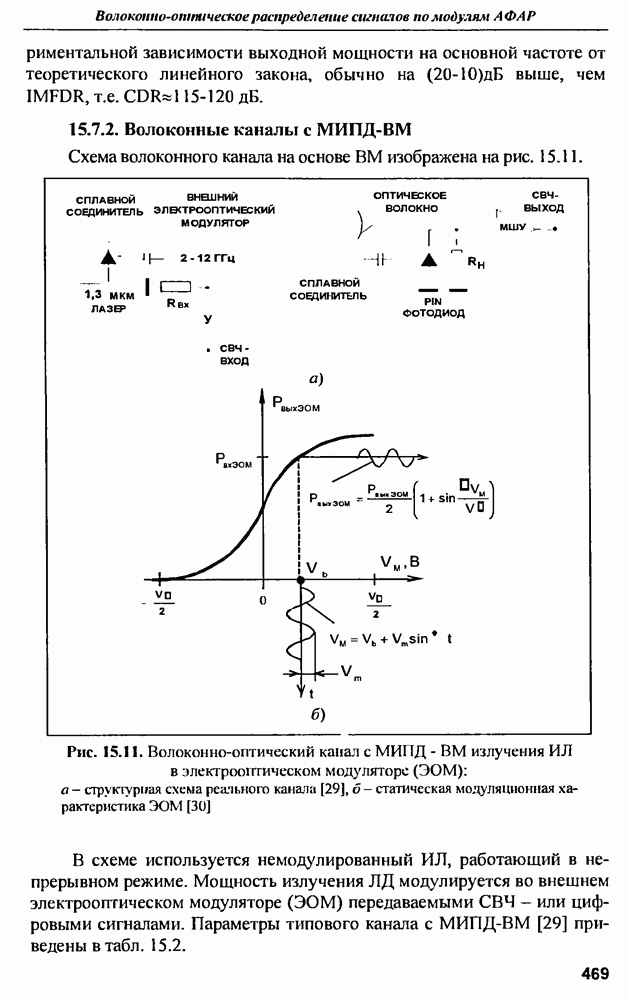
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
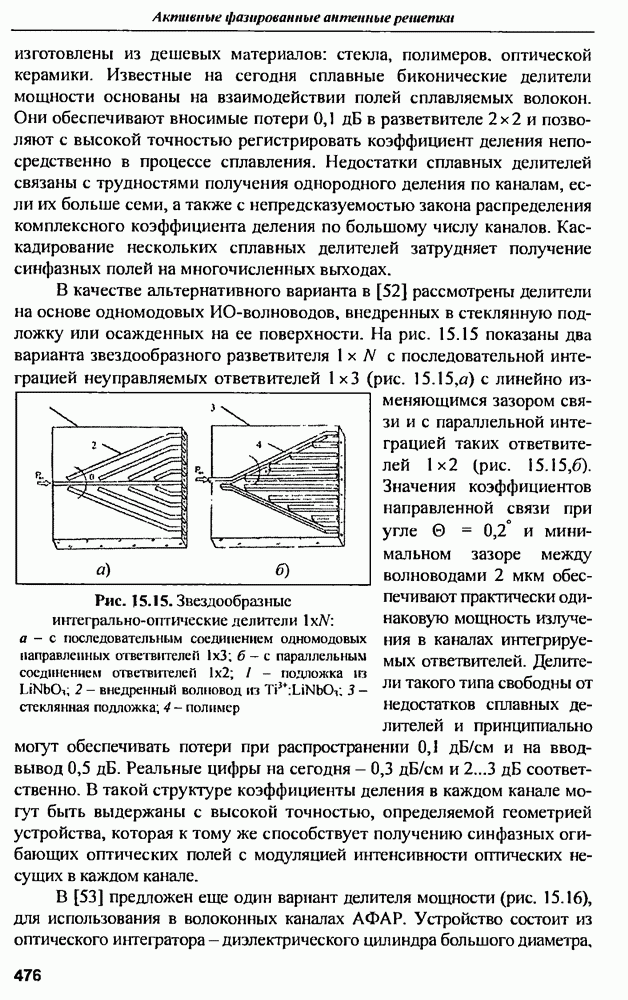
- 15.8.4. Оптические делители
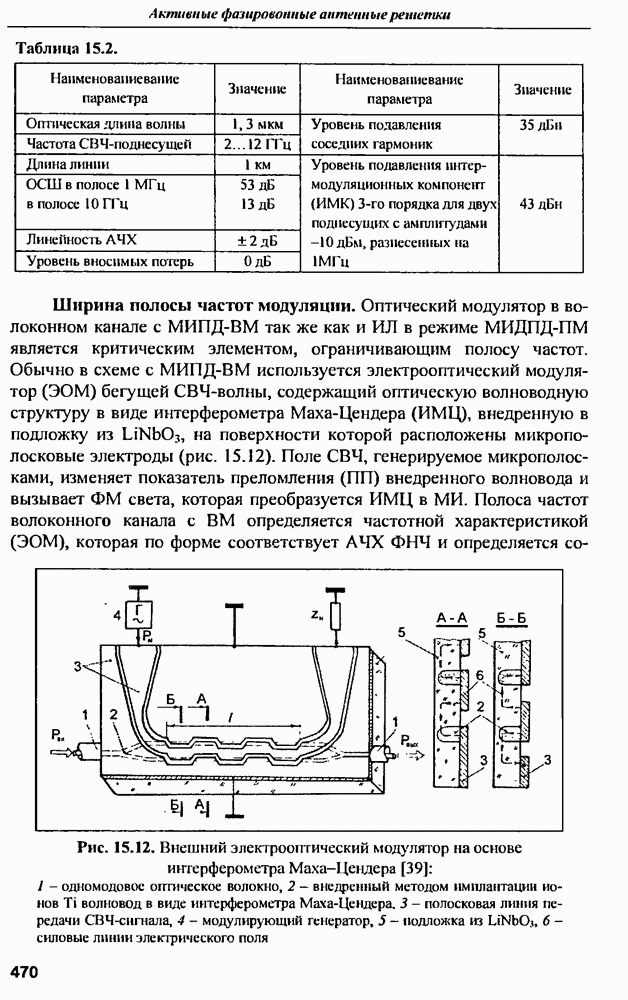
- 15.8.5. Внешние модуляторы
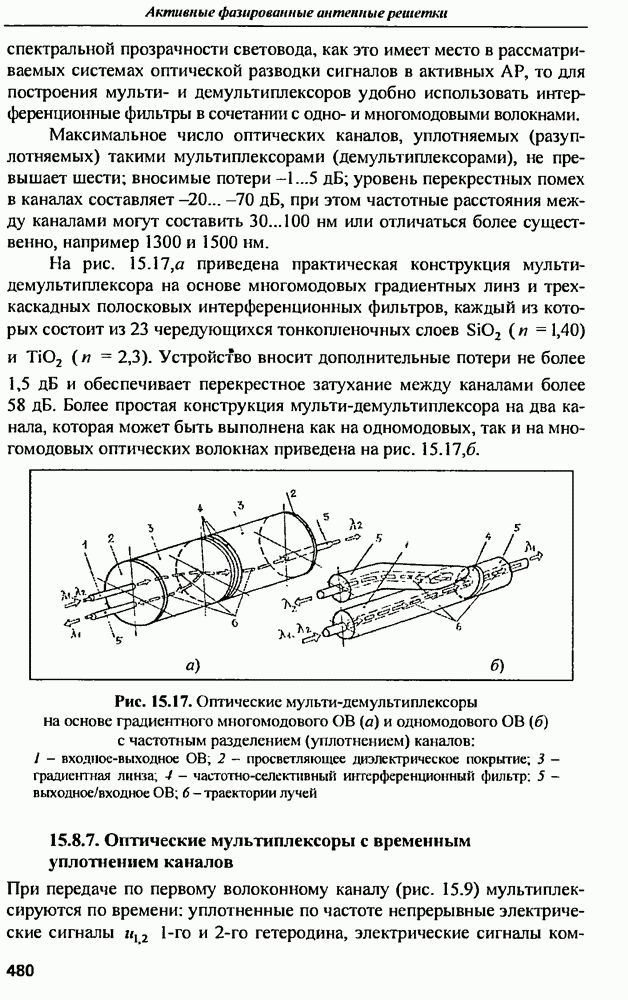
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР