| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
9.2.1. Метод сингулярных разложений
Метод сингулярных разложений  имеет исключительное значение в теории и практике сверхширокополосных радиолокационных систем. Впервые он был сформулирован Карлом Баумом (С.Е. Baum) в 1971 г. и явился результатом электродинамического анализа процессов рассеяния электромагнитных волн объектами произвольной формы и выявления основных особенностей этого рассеяния во временной и частотной областях [17].
имеет исключительное значение в теории и практике сверхширокополосных радиолокационных систем. Впервые он был сформулирован Карлом Баумом (С.Е. Baum) в 1971 г. и явился результатом электродинамического анализа процессов рассеяния электромагнитных волн объектами произвольной формы и выявления основных особенностей этого рассеяния во временной и частотной областях [17].
Согласно МСР структура рассеянного электромагнитного поля имеет довольно сложный характер, зависящий от временной формы, поляризации и направления прихода возбуждающего импульса, а также геометрической формы и ракурса наблюдения рассеивающего объекта. При этом на поверхности объекта формируются токи, вызванные разными физическими эффектами. Собственно, эти токи и формируют рассеянное поле во всех направлениях и на всех частотах, существующих в возбуждающем сигнале.
Главным свойством, присущим взаимодействию электромагнитной волны и объекта, является линейность процесса рассеяния, т.е. уравнения, описывающие взаимодействие падающей волны с объектом, не содержат коэффициентов и функций, зависящих от амплитуды возбуждающей
волны. В МСР сформулированы основные свойства преобразования Лапласа от временных функций поверхностных токов, зависящих также от поляризации и ориентации объекта относительно источника возбуждения. Поверхностный ток формируется в результате проявления большого числа разных явлений, наиболее важными из которых являются:
— составляющие, определяемые принципом геометрической оптики;
— составляющие, описывающие «ползущие» волны по поверхности объекта, возбужденные источниками на его поверхности;
— составляющие, описывающие режим «стоячих» волн или собственных резонансов на поверхности объекта.
Именно третья составляющая и есть источник косвенной информации о геометрической форме объекта. Важной особенностью этой составляющей поверхностных токов является независимость их некоторых свойств от ракурса объекта и даже от поляризации возбуждающего импульса. Эта особенность лежит в основе популярности МСР, в связи с появлением возможности проводить идентификацию целей независимо от их ракурса относительно точки наблюдения.
МСР породил также целое направление в электродинамике, связанное с упрощением моделей сложных электромагнитных структур за счет сверхширокополосного описания их методами теории радиотехнических цепей и сигналов [16].
Из теории цепей известно, что ИХ линейной цепи может быть найдена по известным полюсам передаточной функции на комплексной плоскости частоты и соответствующих вычетов. Она определяется как сумма экспоненциально затухающих синусоид с весовыми коэффициентами, равными соответствующим вычетам. Аналогичный подход используется для описания откликов радиолокационных объектов на возбуждающее сверхширокополосное электромагнитное воздействие [18, 19].
В МСР переходная характеристика записывается как сумма экспоненциально затухающих синусоид, для правильной записи которой необходимо сначала определить расположение комплексных собственных частот или диаграмму нулей и полюсов изучаемой структуры. Обычный подход для определения полюсов системы основан на итерационной процедуре поиска — она ищет нули системной передаточной функции в области комплексных частот. Этот подход успешно использовался и дал положительные результаты.
Поскольку итерационный поиск - медленная процедура, обычно удавалось извлечь только несколько полюсов. В обычных методах полюса не могут быть извлечены из временной реализации отклика объекта.
В настоящее время для оценки собственных резонансных частот широко применяется метод Прони, осуществляющий аппроксимацию данных с использованием детерминированной экспоненциальной модели [20, 25-26].
Известна связь этого метода с другими известными процедурами обработки: методом линейного предсказания, теорией фильтрации, методами ковариации, автокорреляции и многими другими методами.
К классу нелинейных методов обработки данных относятся методы оценивания комплексных полюсов, основанные на анализе собственных значений автокорреляционной матрицы или матрицы данных. Ключевой операцией в этих методах является разделение информации на два векторных подпространства - подпространство сигнала и подпространство шума. Основные представители этого класса: метод классификации множественных сигналов (MUSIC, DMUSIC) [20], метод матричных пучков [21-23, 27] и другие.
Согласно методу сингулярных разложений, нормированная передаточная функция в  -плоскости для объекта конечной длительности в свободном пространстве может быть записана [18, 19, 24] как
-плоскости для объекта конечной длительности в свободном пространстве может быть записана [18, 19, 24] как

где  собственная частота, собственный резонанс, это комплексная частота, присутствующая на выходе системы при отсутствии возбуждающего сигнала (полюса существуют комплексно-сопряженными парами, поскольку соответствуют действительным сигналам, кроме того они не должны лежать в положительной половине
собственная частота, собственный резонанс, это комплексная частота, присутствующая на выходе системы при отсутствии возбуждающего сигнала (полюса существуют комплексно-сопряженными парами, поскольку соответствуют действительным сигналам, кроме того они не должны лежать в положительной половине  -плоскости);
-плоскости);  собственная гармоника, - отклик системы на частоте
собственная гармоника, - отклик системы на частоте  который зависит только от положения
который зависит только от положения  на структуре и параметров объекта;
на структуре и параметров объекта;  коэффициент связи, - интенсивность собственных колебаний
коэффициент связи, - интенсивность собственных колебаний  в терминах параметров системы и возбуждающего воздействия, он не зависит от положения;
в терминах параметров системы и возбуждающего воздействия, он не зависит от положения;  поляризация фронта возбуждающей волны;
поляризация фронта возбуждающей волны;  вектор положения - положение на структуре, в которой наблюдается или измеряется передаточная функция;
вектор положения - положение на структуре, в которой наблюдается или измеряется передаточная функция;  кратность
кратность  полюса. Слагаемое
полюса. Слагаемое  является целой функцией
является целой функцией  и зависит от формы коэффициента связи возбуждающей волны. Коэффициент связи
и зависит от формы коэффициента связи возбуждающей волны. Коэффициент связи  по-существу является вычетом передаточной функции (9.48) в точке
по-существу является вычетом передаточной функции (9.48) в точке 
Если эти коэффициенты являются константами для каждого полюса

тогда они относятся к коэффициентам связи 1-го рода, когда эти коэффициенты задаются как функции частоты, они относятся к коэффициентам 2-го рода.
Обратное преобразование Лапласа от выражения (9.48) задает отклик цели во временной области, т.е. его 

Если используются коэффициенты связи 2-го рода, то коэффициенты функции в выражении (9.50) зависят от времени, а для коэффициентов связи  рода они являются константами.
рода они являются константами.
В практических задачах, таких как формирование базы данных для идентификации радиолокационных объектов с использованием резонансных частот, необходимо получить параметры сингулярных разложений из измеренных данных. Реальные объекты не могут быть эффективно и, в большинстве случаев, точно смоделированы в цифровой форме. Как говорилось выше, для извлечения параметров резонансных частот из измеренных данных используют алгоритмы цифровой обработки.
Для извлечения комплексных полюсов и вычетов необходимо, чтобы они были константами, поэтому выражение (9.50) обычно записывают в форме

где  и
и  включены в вычеты
включены в вычеты  не зависящие от времени.
не зависящие от времени.
Таким образом, модель поздневременной компоненты отклика объектов СШП радиолокации можно представить в следующем виде [20]:

или в дискретном времени:

где  номера отсчетов сигнала
номера отсчетов сигнала  число отсчетов данных; К — число гармонических составляющих сигнала;
число отсчетов данных; К — число гармонических составляющих сигнала;  отсчеты шума;
отсчеты шума;  значения амплитуд, коэффициентов затухания, частот и начальных фаз компонент сигнала соответственно;
значения амплитуд, коэффициентов затухания, частот и начальных фаз компонент сигнала соответственно;  период дискретизации.
период дискретизации.
Как упоминалось выше, полюса  и вычеты
и вычеты 

существуют комплексно-сопряженными парами, поскольку значения отсчетов сигнала — действительные числа.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
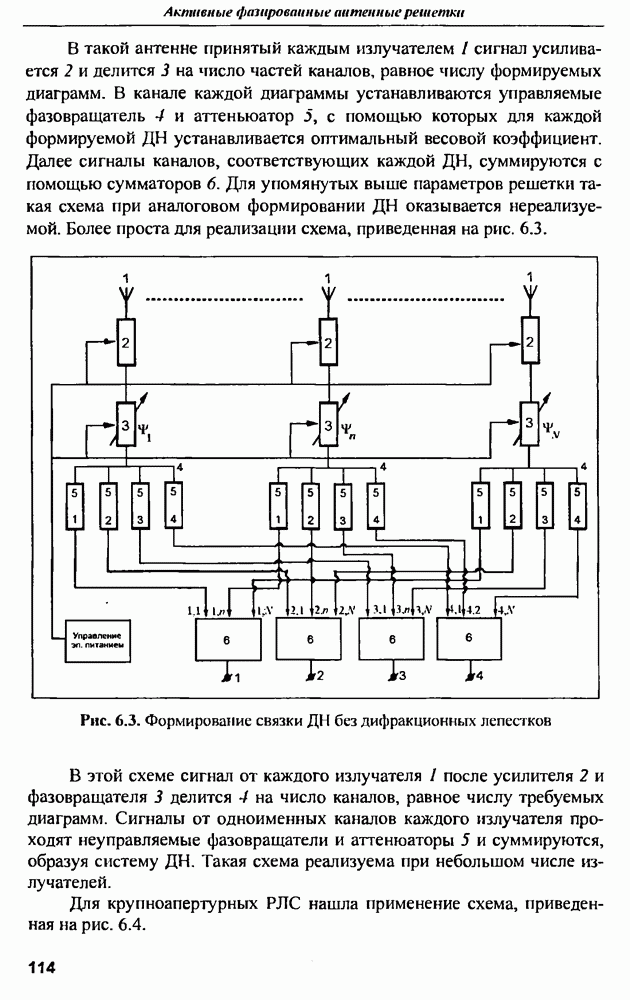
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
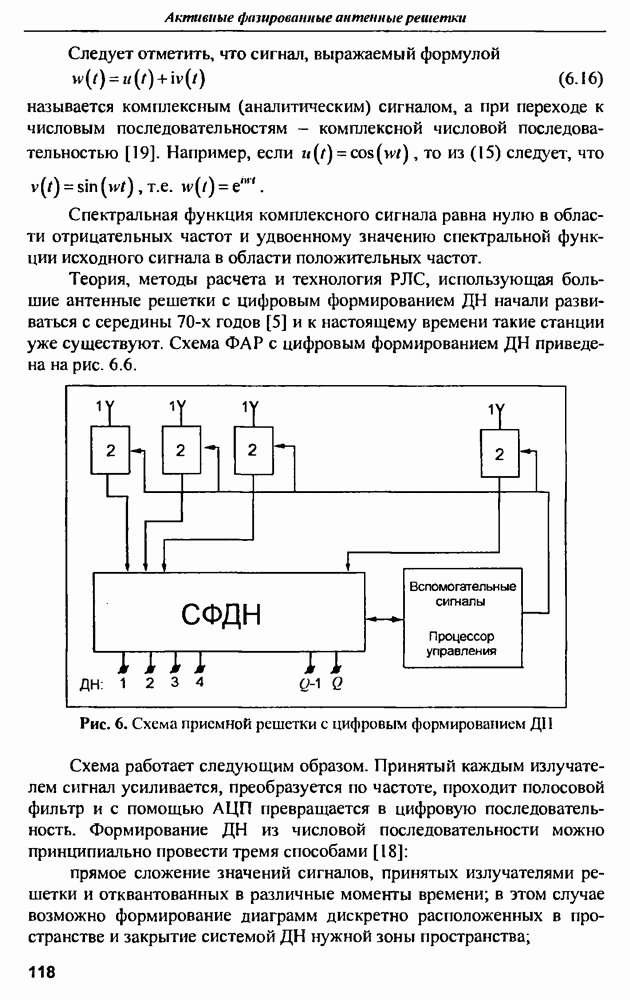
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
- 7.3.4. Качество связи
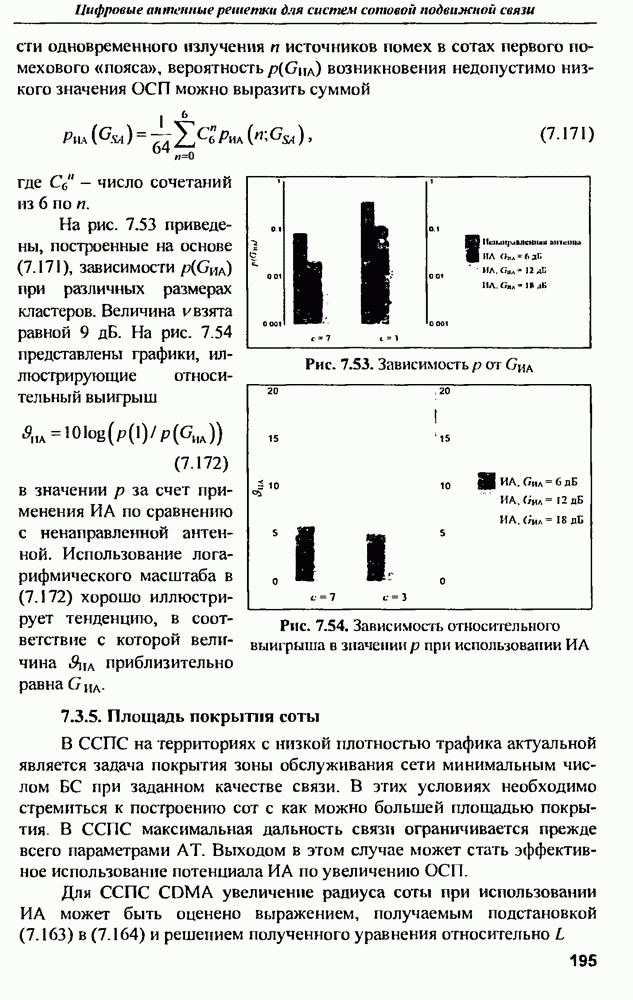
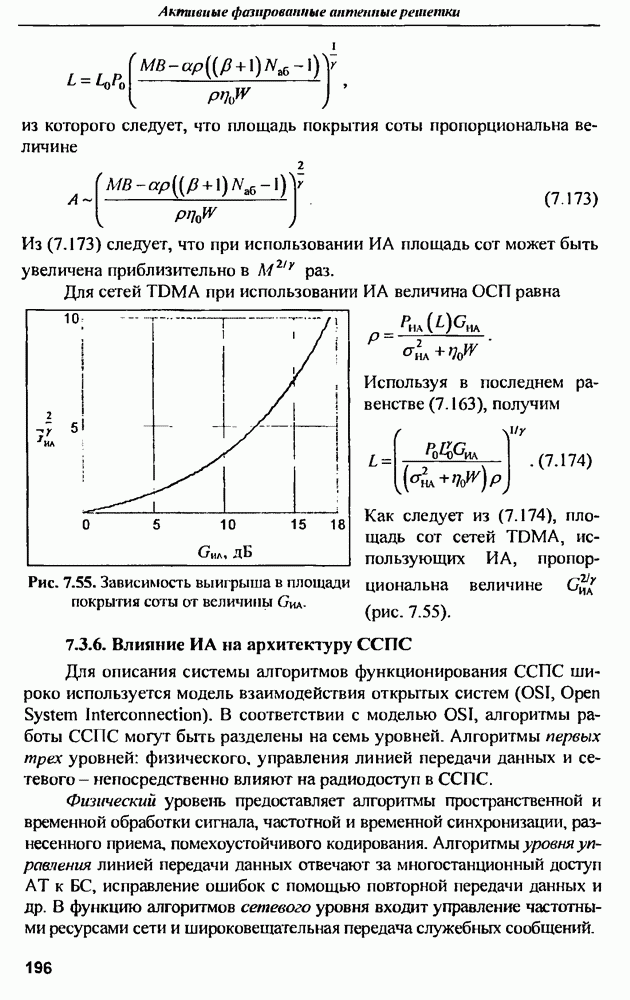
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
- 14.3. Комбинированные антенны
- 14.4. Антенные решетки
- 14.5. Приемные антенны
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
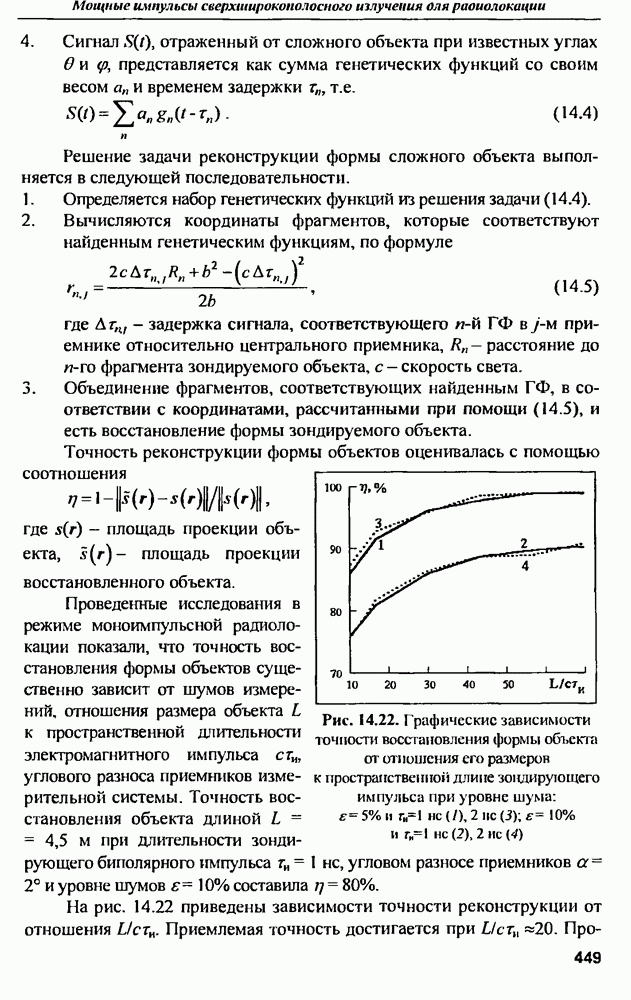
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
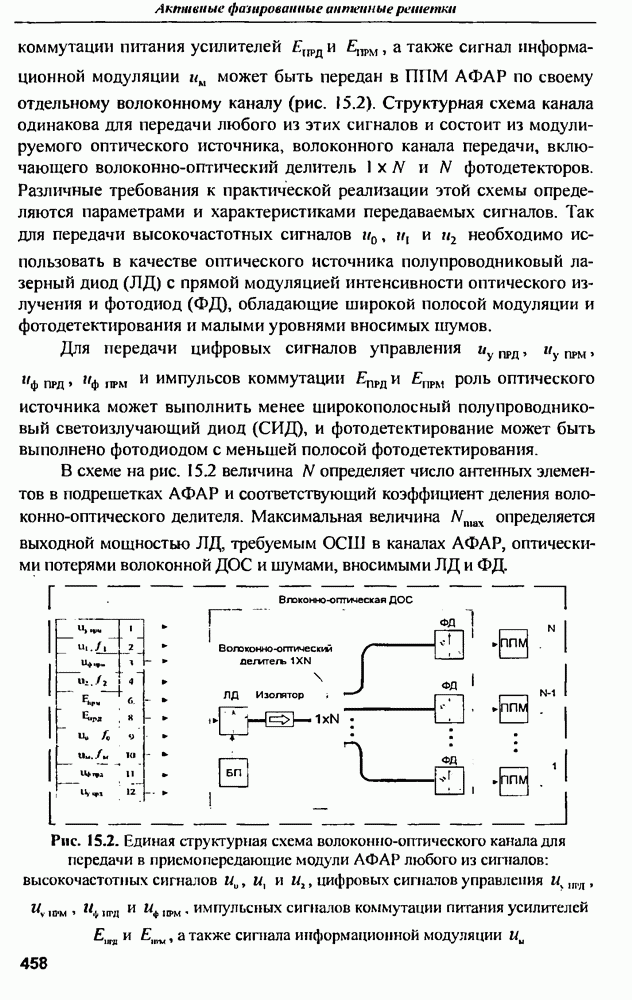
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
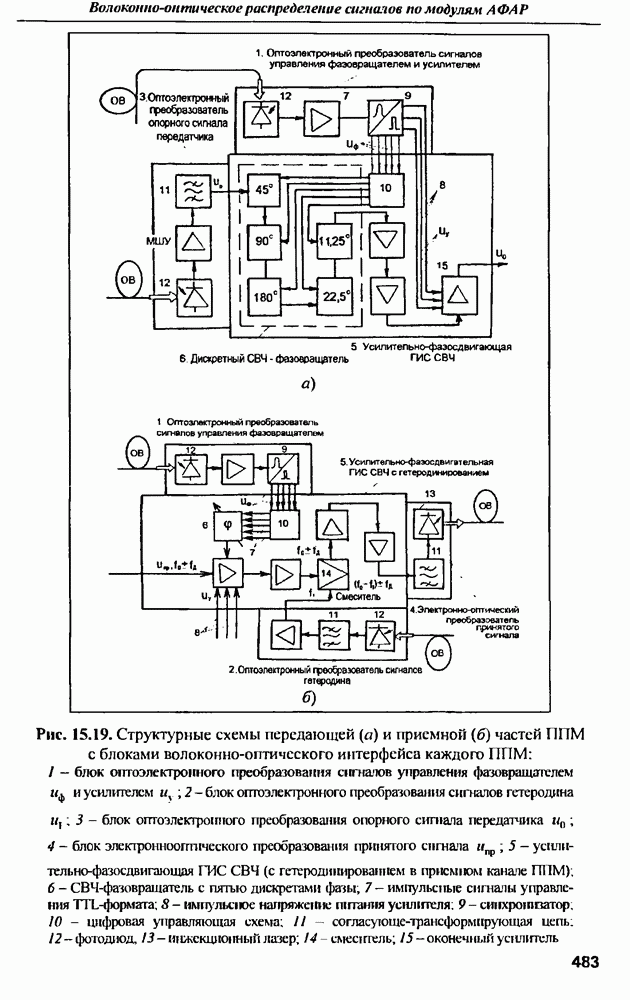
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
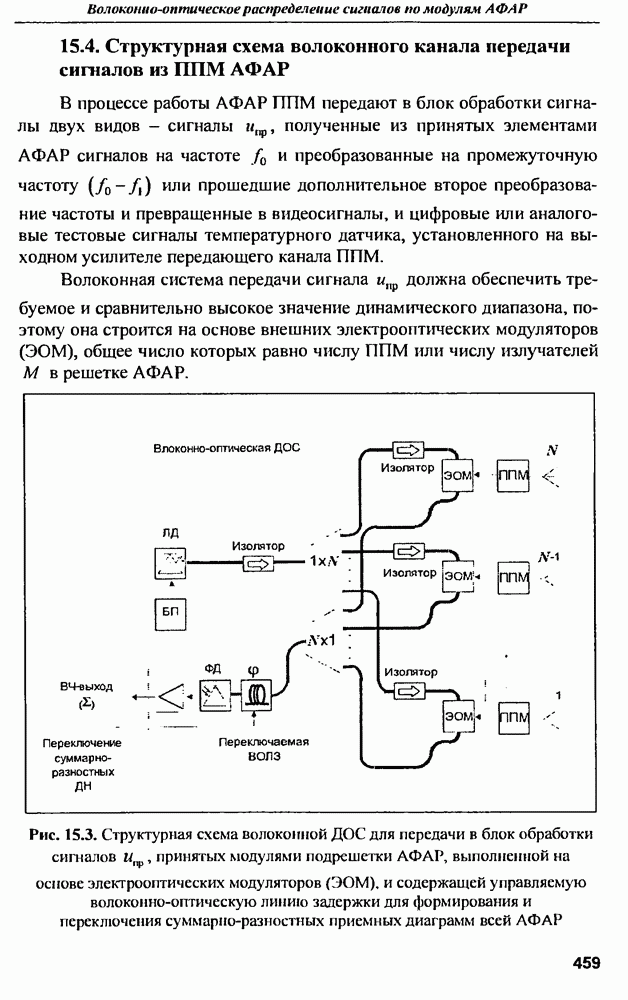
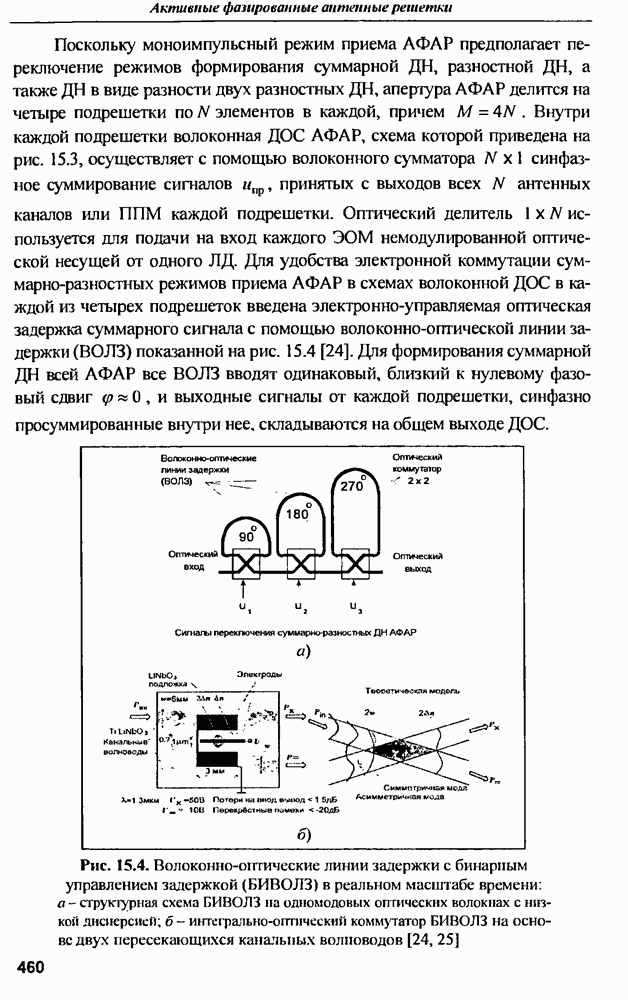
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
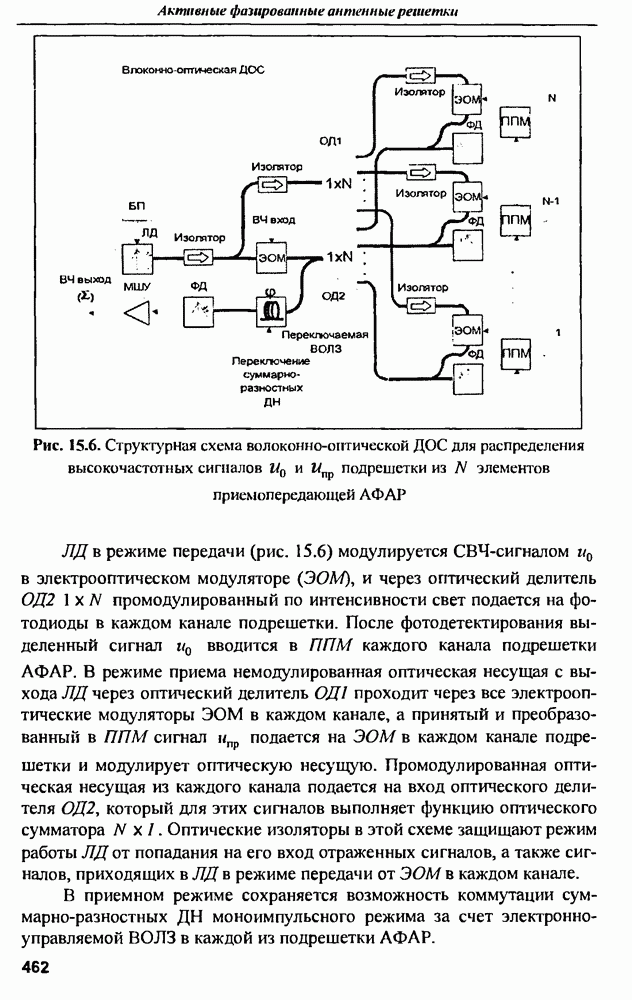
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
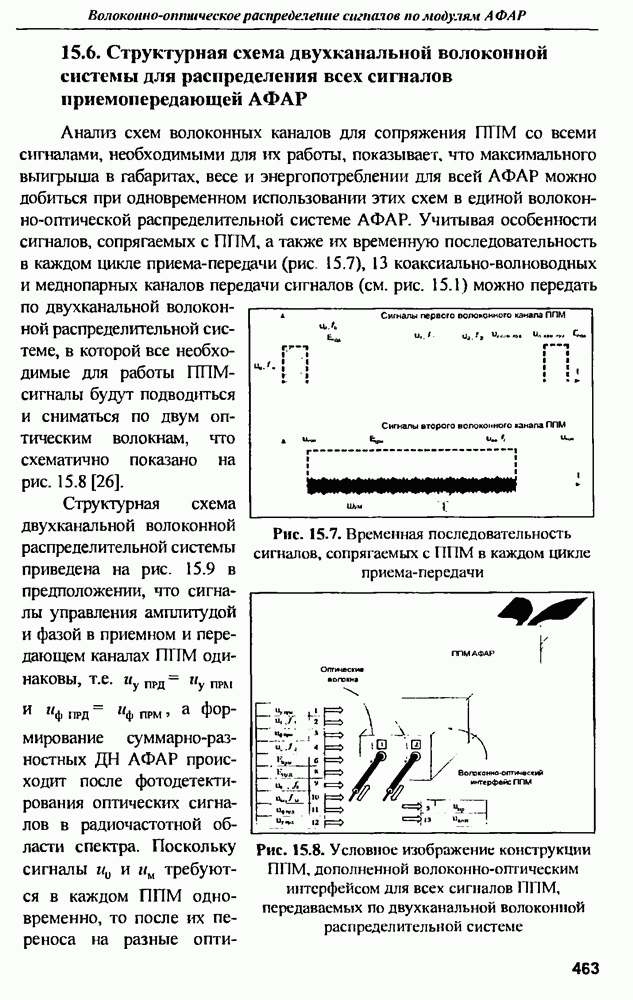
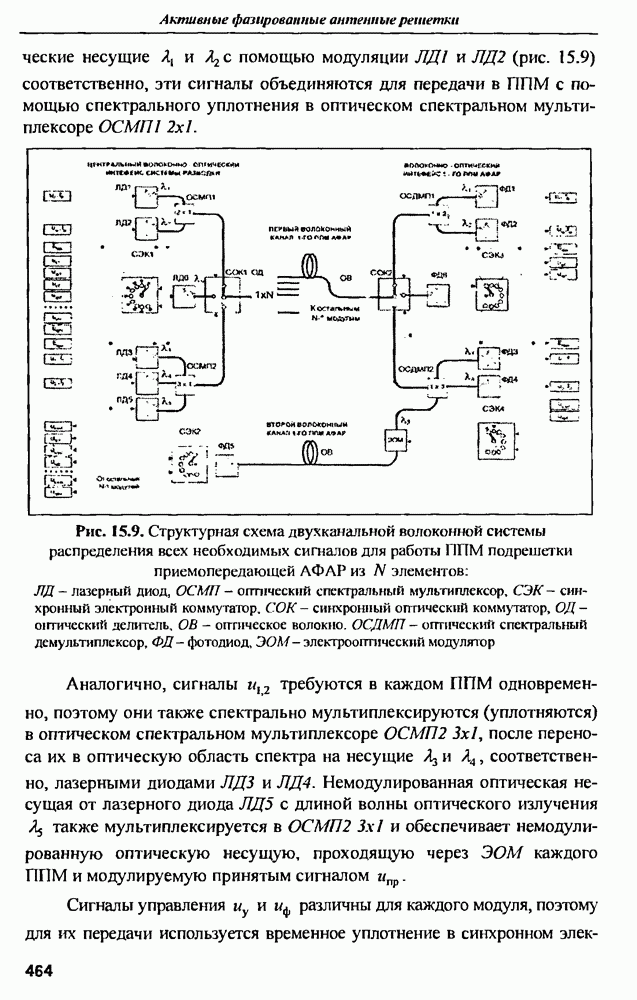
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
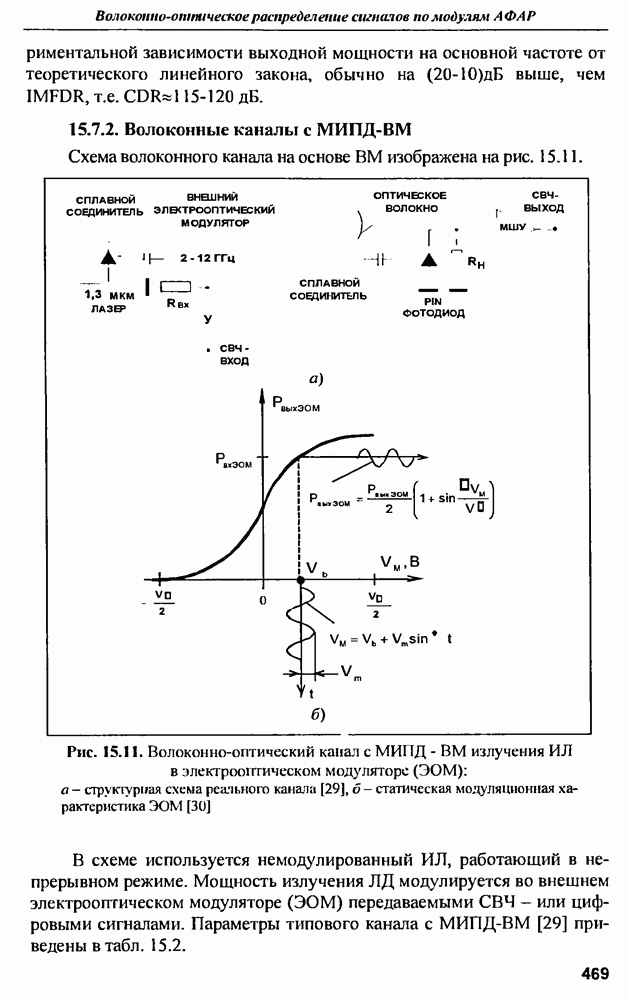
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
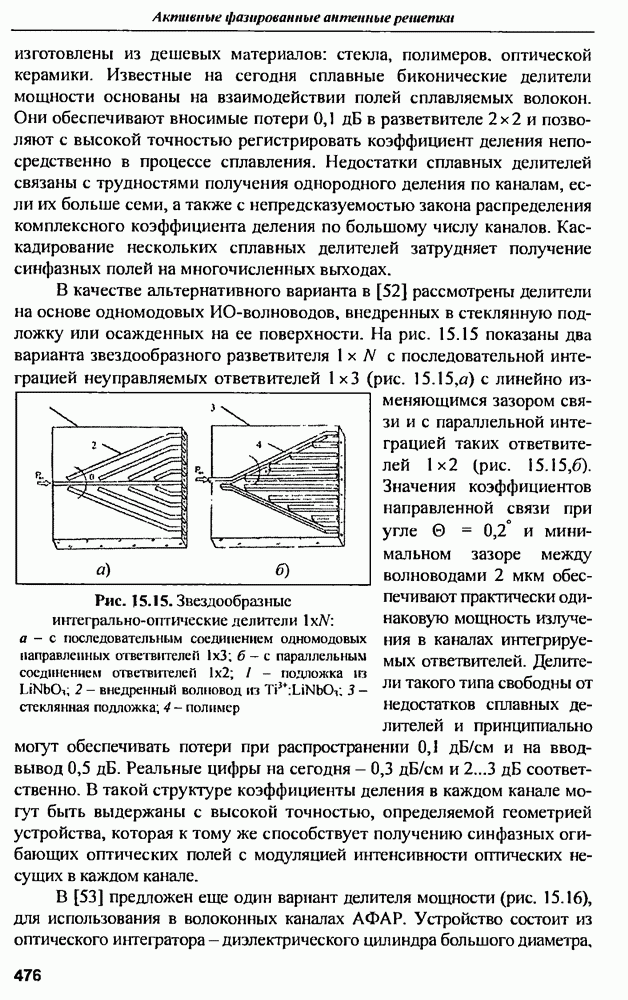
- 15.8.4. Оптические делители
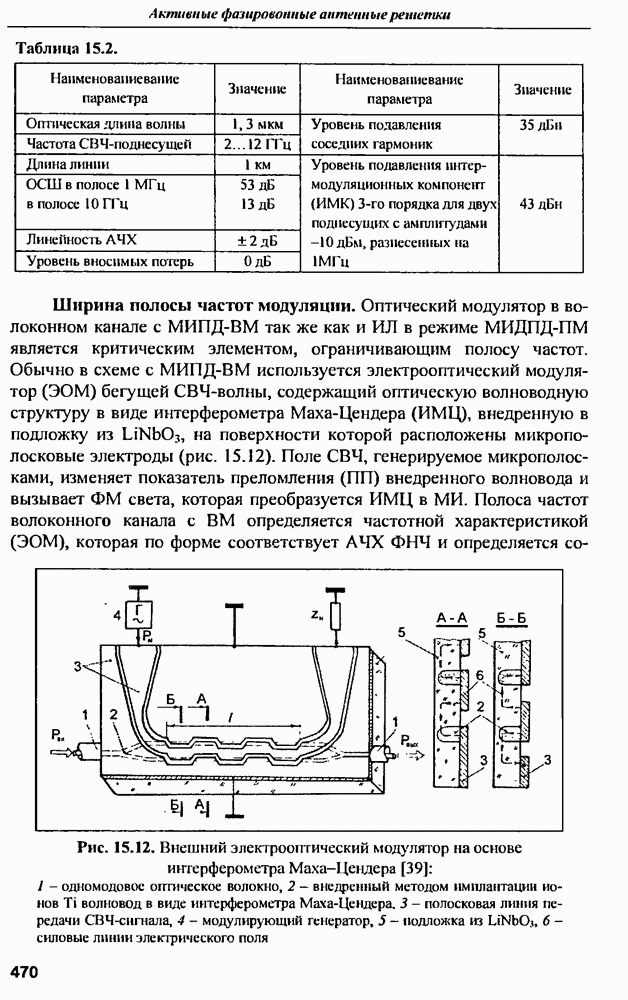
- 15.8.5. Внешние модуляторы
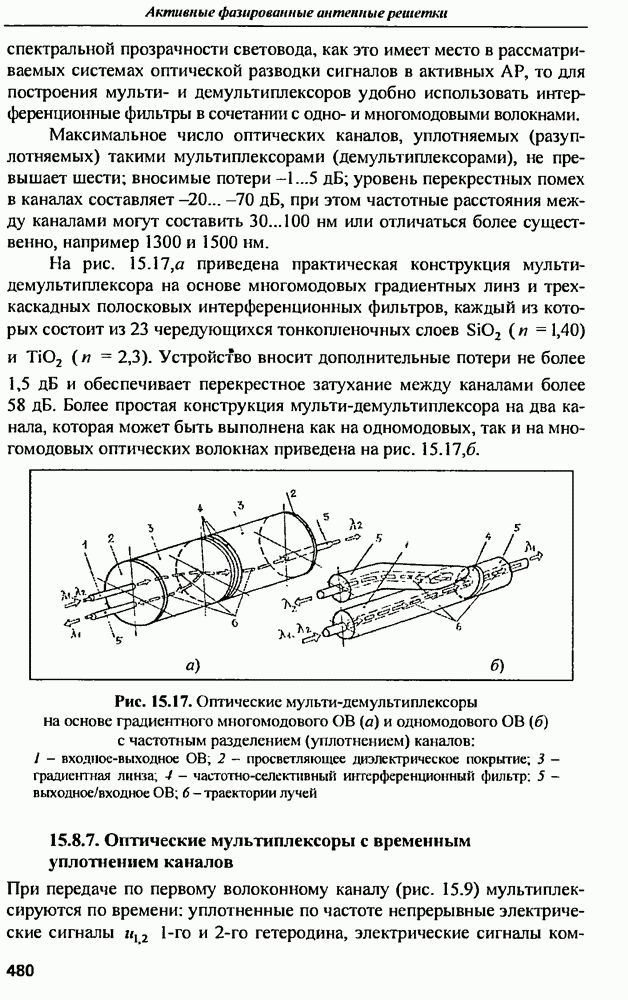
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР