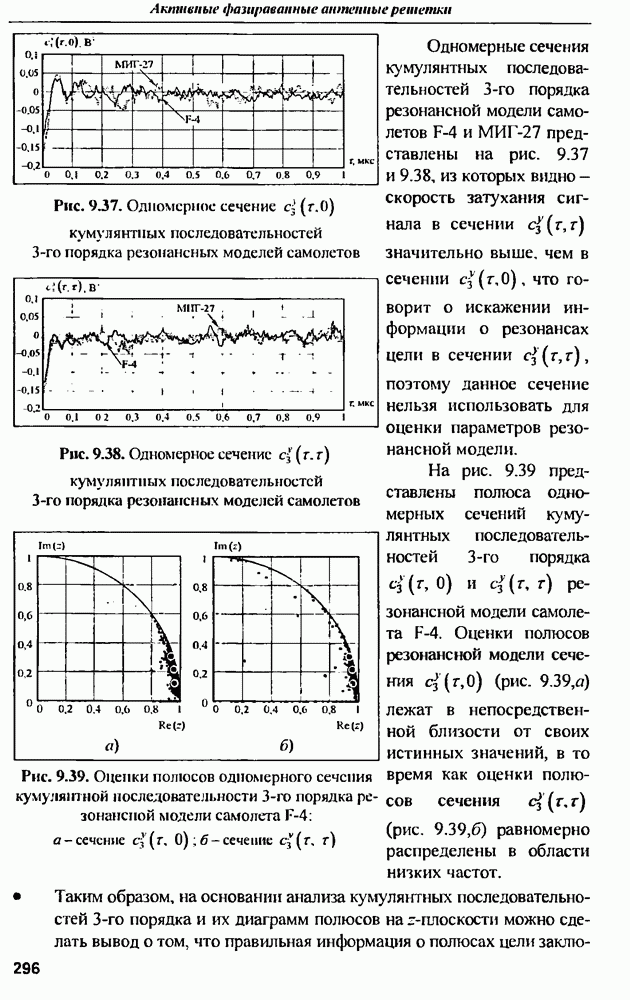
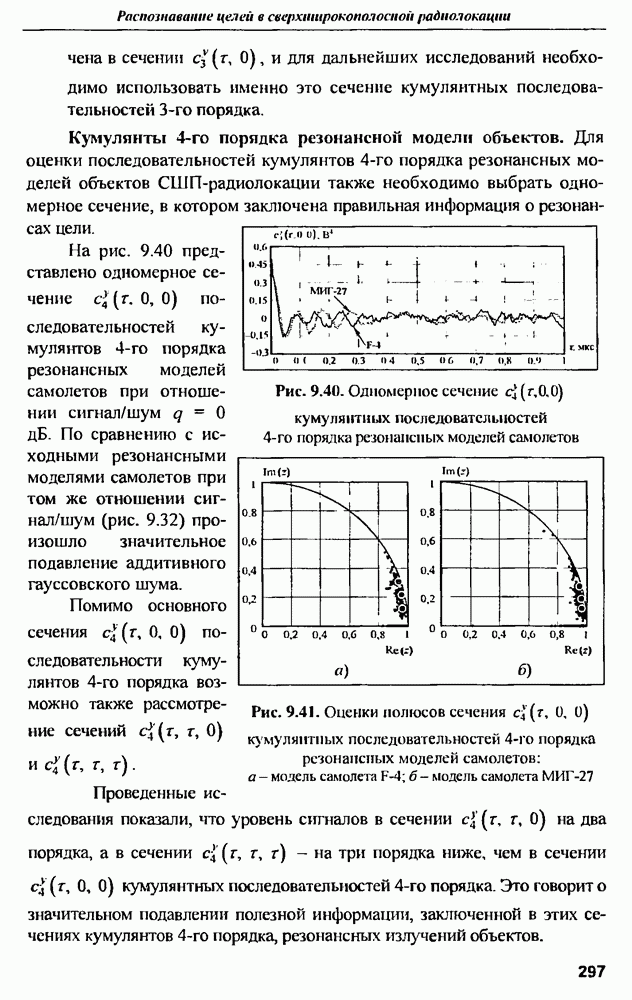
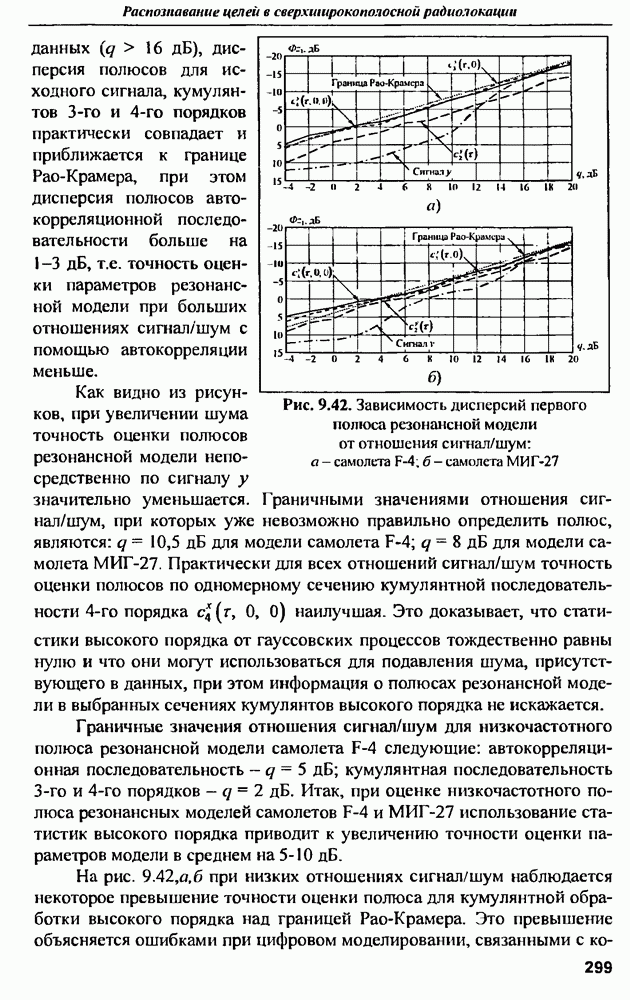
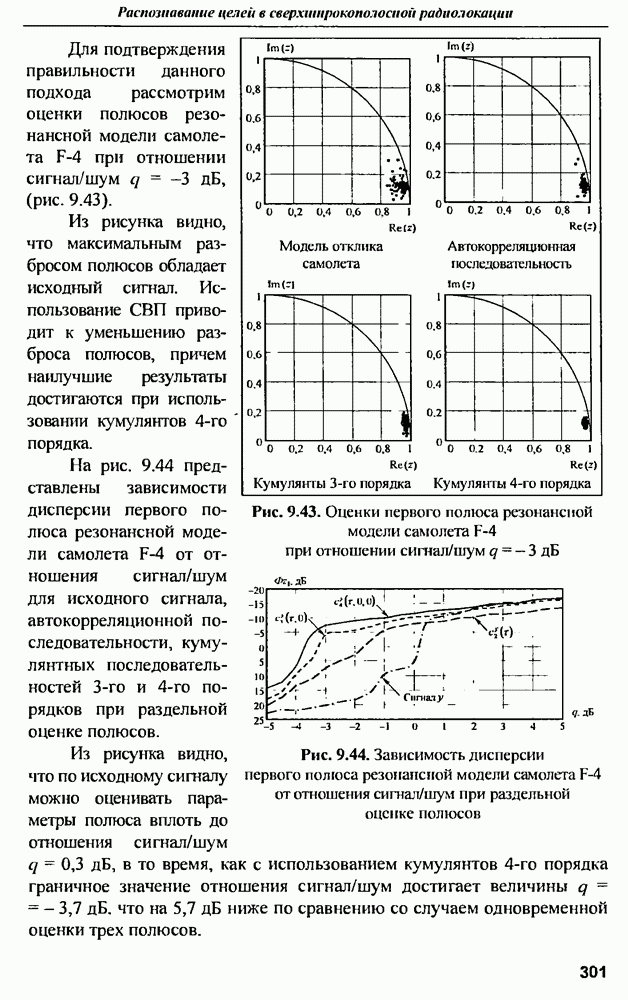
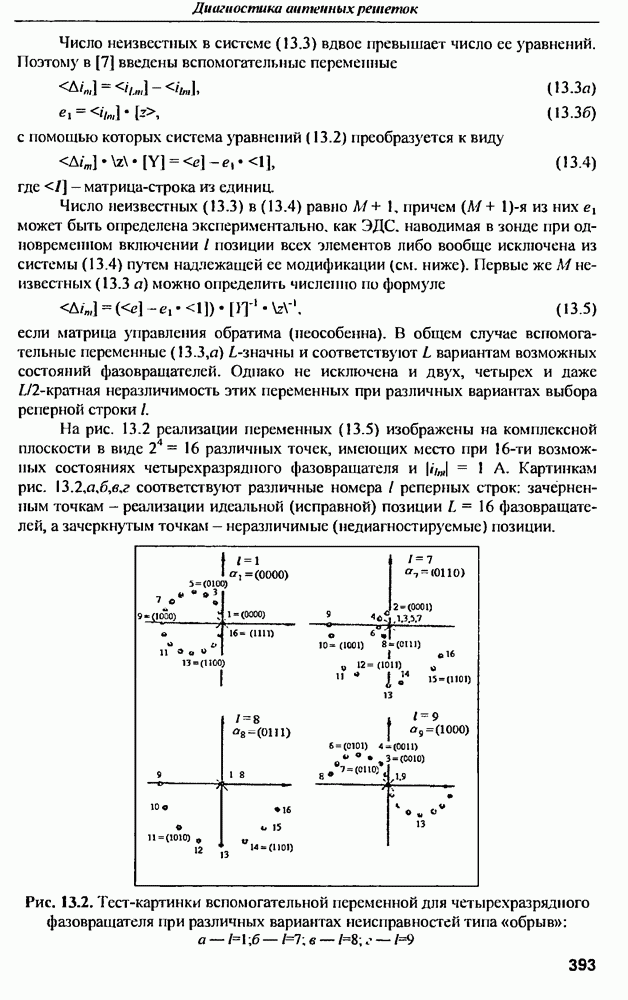
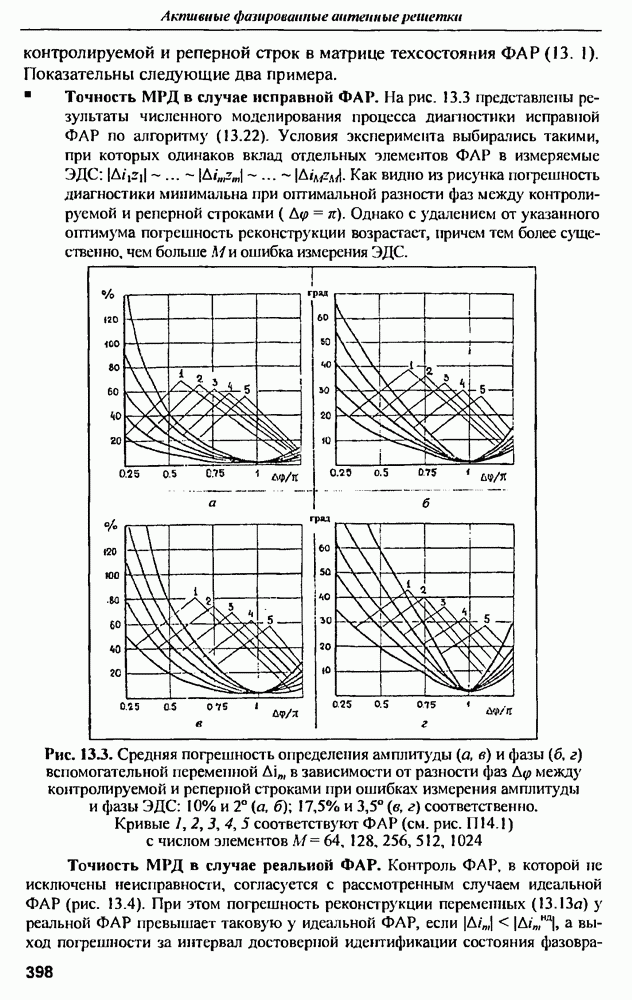
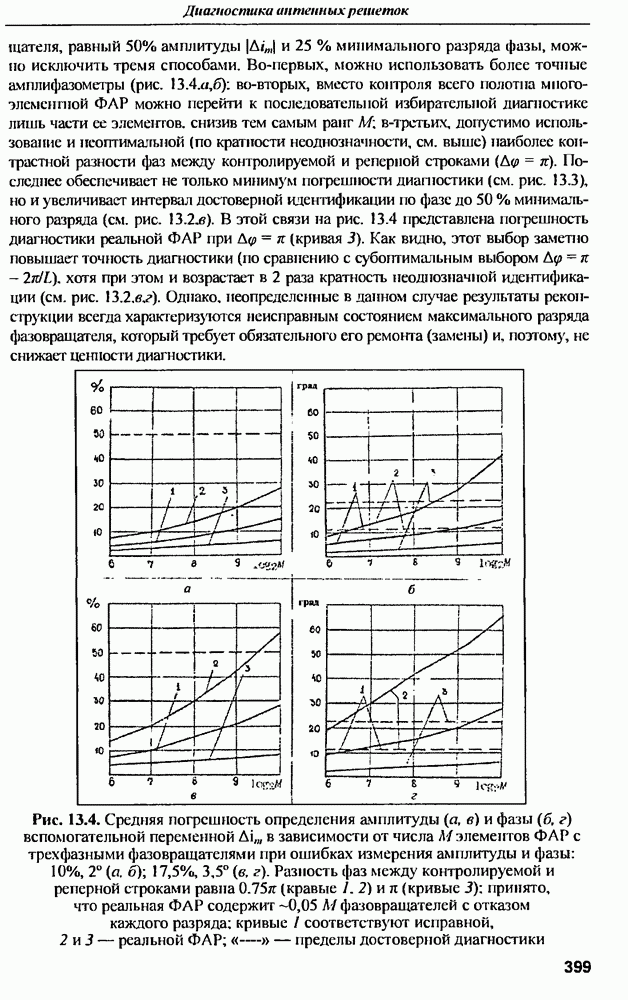
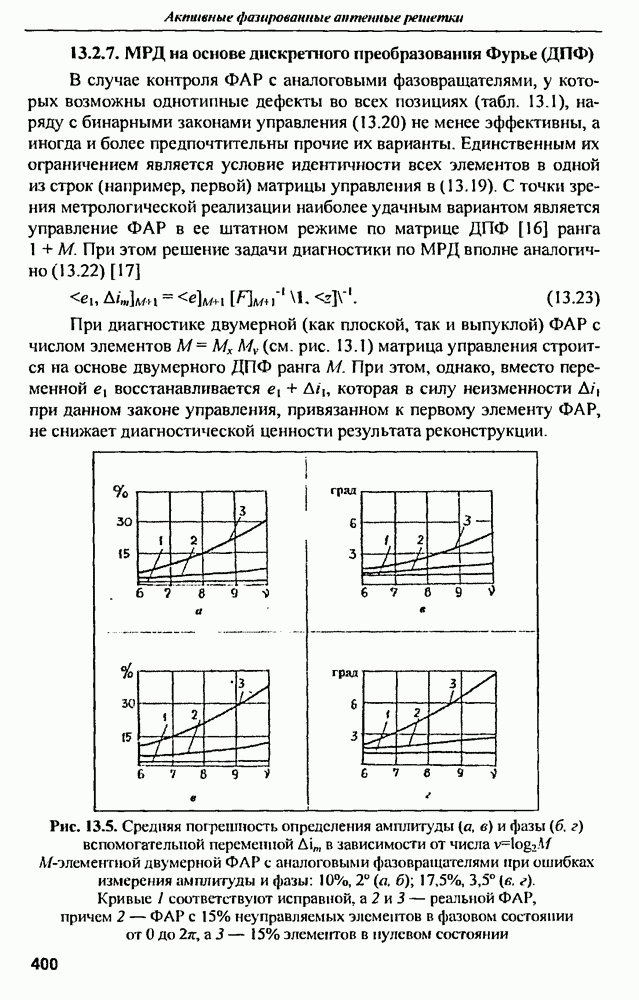
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
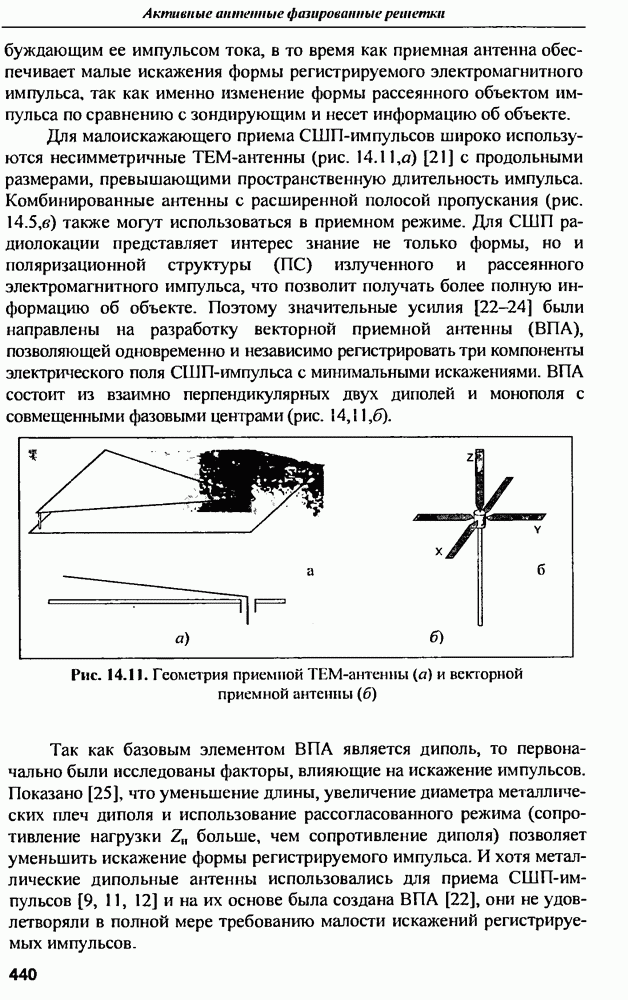
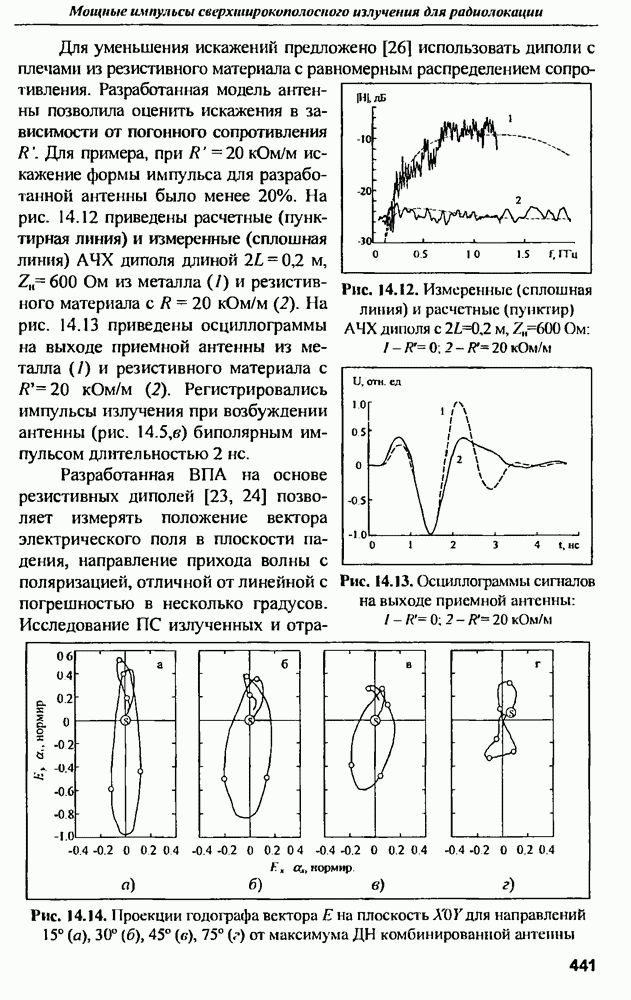
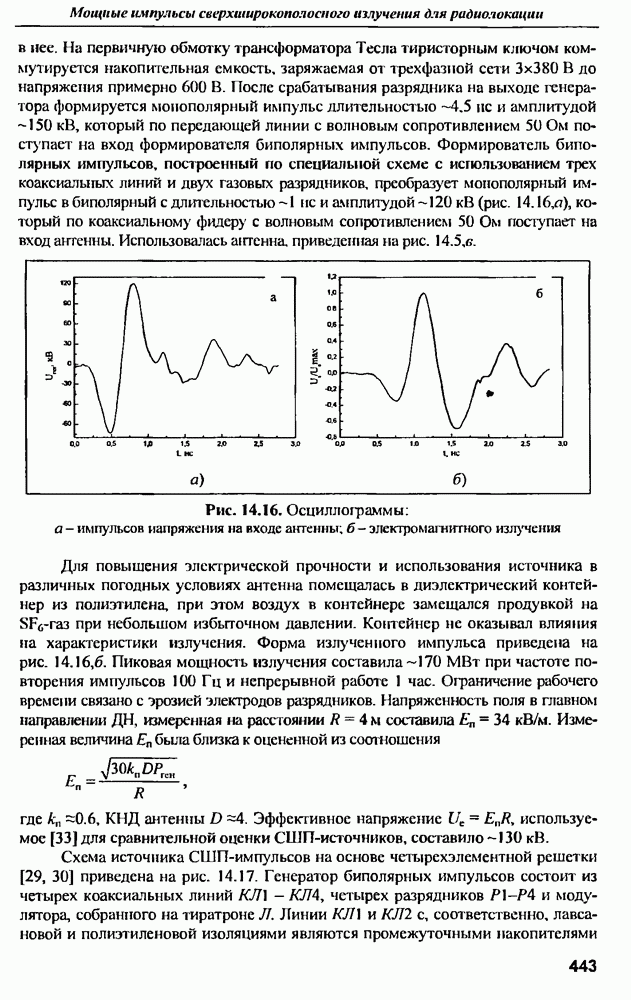
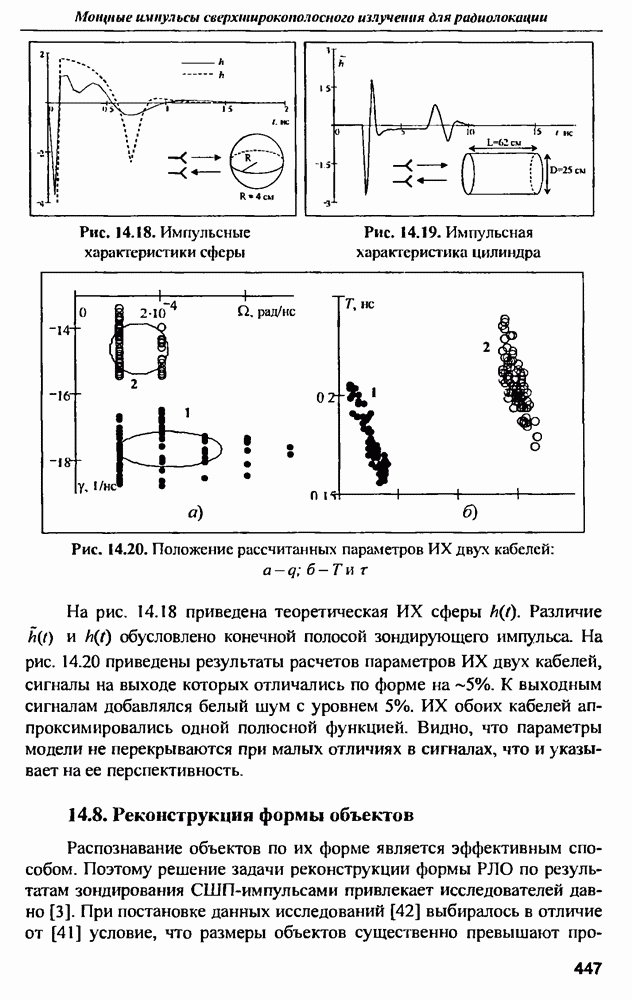
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
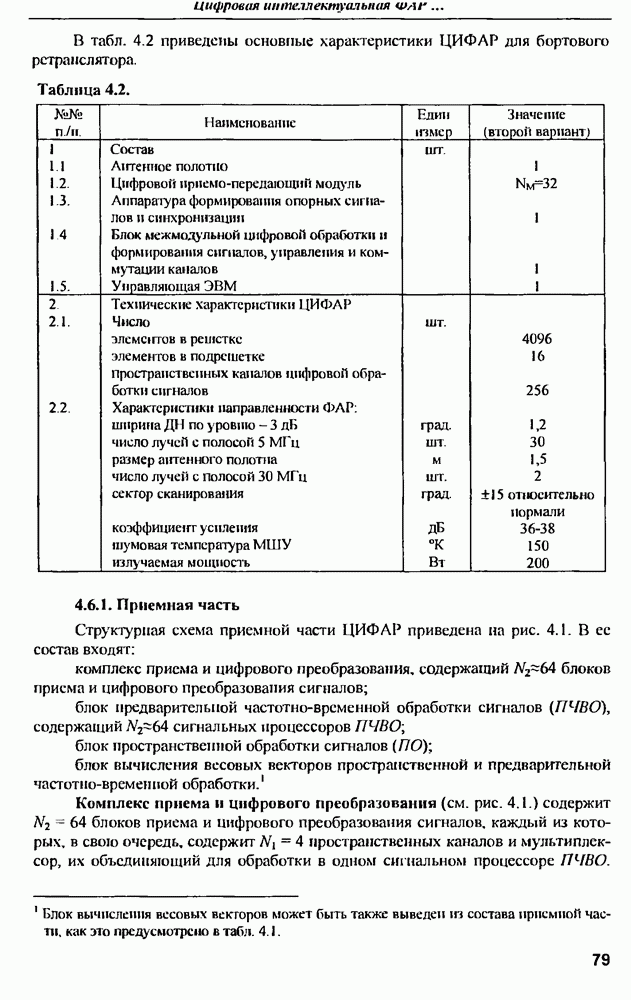
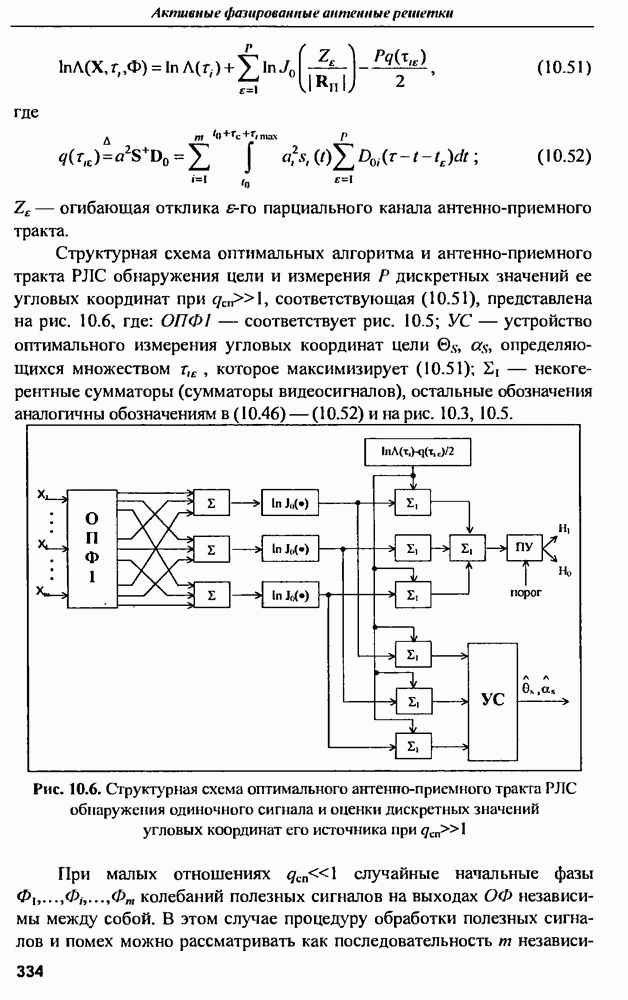
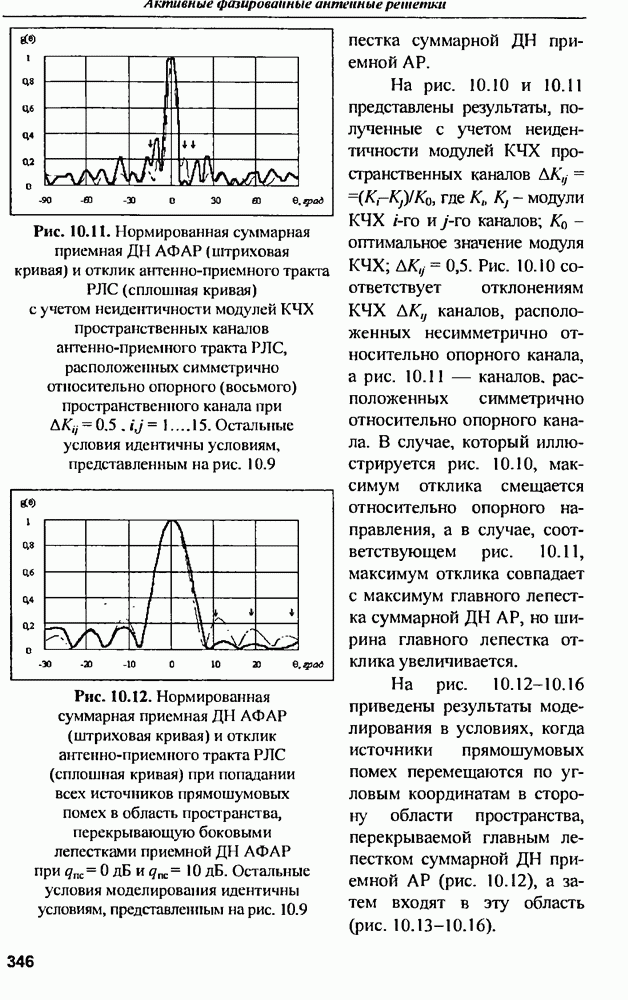
ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
10.1. Постановка задачи
Пусть в области пространства  (рис. 10.1), отведенной под обработку, действует суммарное электромагнитное поле
(рис. 10.1), отведенной под обработку, действует суммарное электромагнитное поле  точечных, независимых друг от друга, источников излучения полезных сигналов (точечных целей) со случайными от наблюдения к наблюдению и постоянными на интервале наблюдения релеевскими амплитудами и равновероятными начальными фазами несущих колебаний,
точечных, независимых друг от друга, источников излучения полезных сигналов (точечных целей) со случайными от наблюдения к наблюдению и постоянными на интервале наблюдения релеевскими амплитудами и равновероятными начальными фазами несущих колебаний,  точечных независимых друг от друга и от полезных сигналов, источников случайных гауссовских стационарных флюктуаций (пря-мошумовых помех) с математическими ожиданиями, равными нулю и дельта-коррелированного по пространству и времени шума окружающего пространства.
точечных независимых друг от друга и от полезных сигналов, источников случайных гауссовских стационарных флюктуаций (пря-мошумовых помех) с математическими ожиданиями, равными нулю и дельта-коррелированного по пространству и времени шума окружающего пространства.

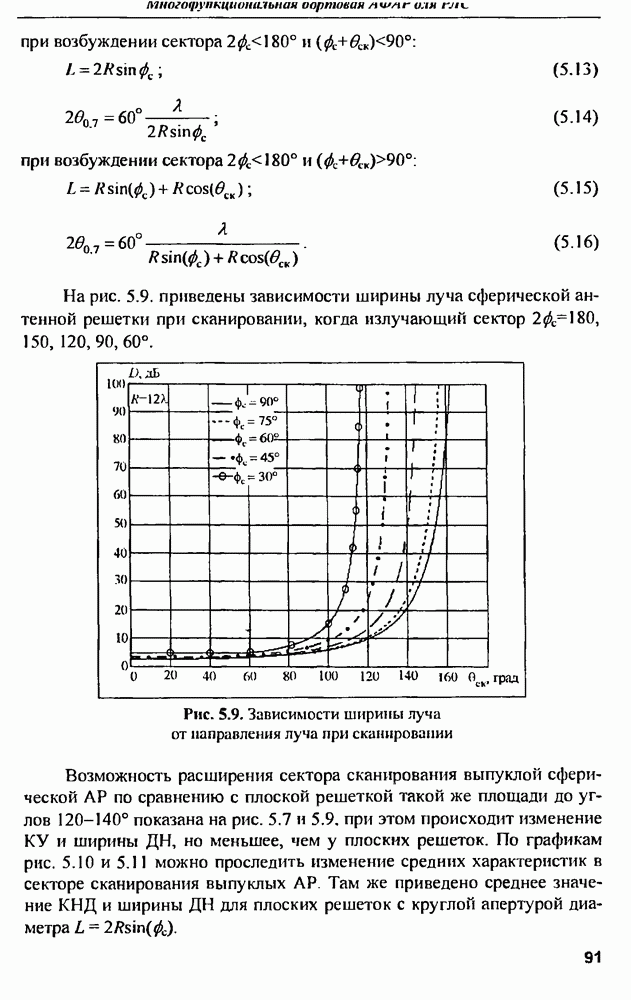
Рис. 10.1. Область пространства  отведенная под обработку ЭМП полезных сигналов и помех
отведенная под обработку ЭМП полезных сигналов и помех
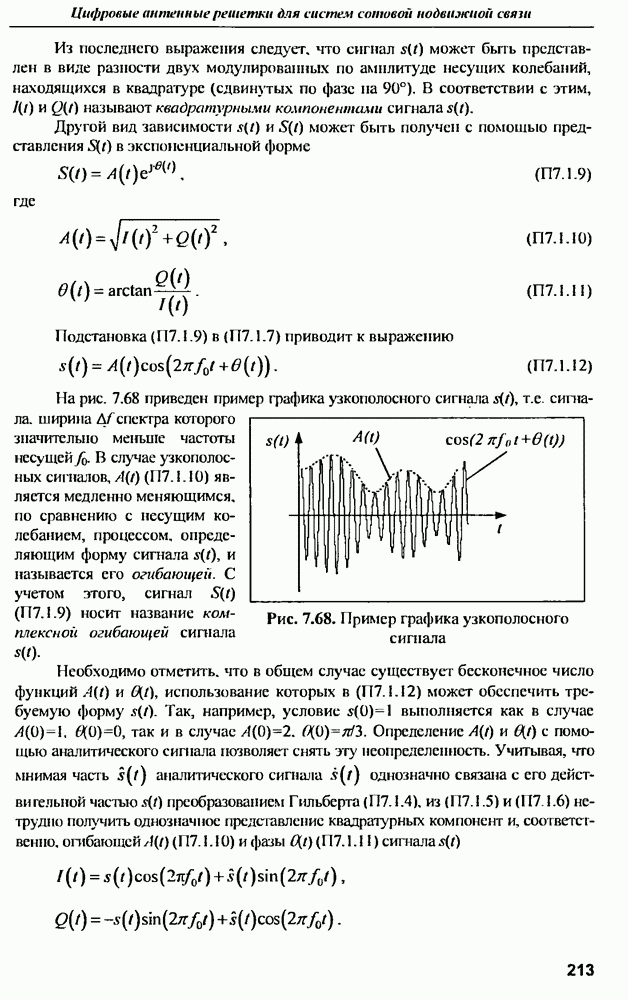
Временная структура полезных сигналов определяется выражением

где  средняя мощность и угловая несущая частота;
средняя мощность и угловая несущая частота;  — законы амплитудной и фазовой модуляции, причем
— законы амплитудной и фазовой модуляции, причем  — период модуляции.
— период модуляции.
Поместим в область пространства  независимых, линейных (в смысле применимости принципа суперпозиции) элементарных антенн или
независимых, линейных (в смысле применимости принципа суперпозиции) элементарных антенн или  групп элементарных антенн, образующих приемную
групп элементарных антенн, образующих приемную  расположение
расположение

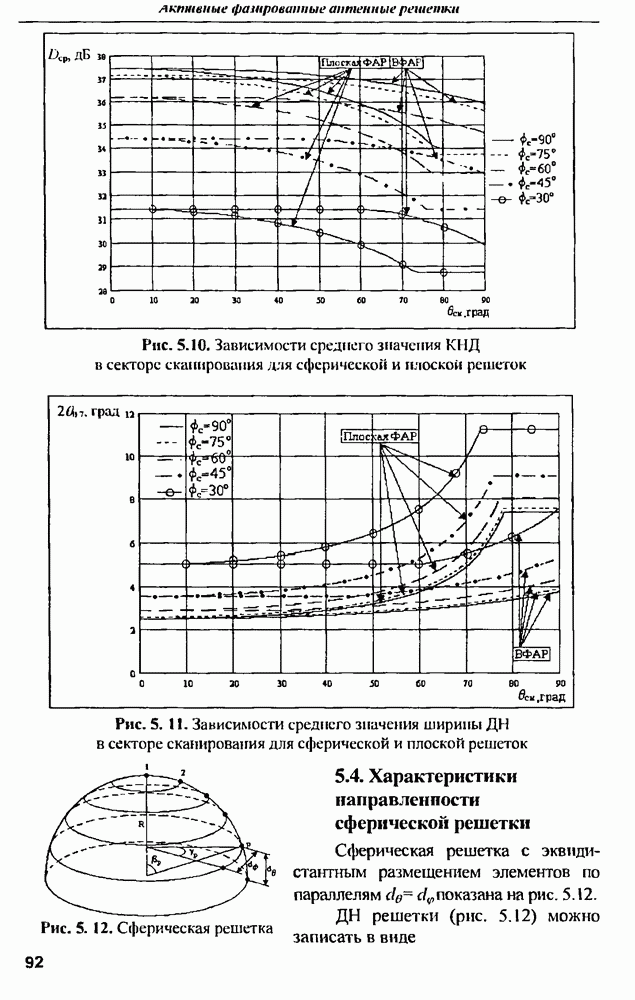
Рис. 10.2. Простраиственно-m-канальная эквидистантная АФАР в режиме «прием»
которых по раскрыву  удовлетворяет условиям пространственной дискретизации по Котельникову (рис. 10.2). Для современных РЛС, как правило, выполняется следующее условие:
удовлетворяет условиям пространственной дискретизации по Котельникову (рис. 10.2). Для современных РЛС, как правило, выполняется следующее условие:

где  рабочая частота и ширина спектра полезного сигнала;
рабочая частота и ширина спектра полезного сигнала;  максимальное значение линейного размера раскрыва приемной
максимальное значение линейного размера раскрыва приемной  длина волны, соответствующая несущей частоте
длина волны, соответствующая несущей частоте 
 целей и
целей и  источников помех считаем расположенными в дальней зоне приемной
источников помех считаем расположенными в дальней зоне приемной  поэтому расстояние между одной из целей (точкой
поэтому расстояние между одной из целей (точкой  на рис. 10.2) и точкой приема, определяемой концом вектора
на рис. 10.2) и точкой приема, определяемой концом вектора  при
при 

где  — угол между векторами
— угол между векторами  индекс
индекс  означает транспонирование.
означает транспонирование.
Время распространения плоского фронта волны электромагнитных колебаний  от точки
от точки  до точки
до точки  раскрыва приемной
раскрыва приемной  где
где  время распространения фронта волны
время распространения фронта волны  от точки
от точки  до фазового центра приемной
до фазового центра приемной  — время задержки фронта
— время задержки фронта  в произвольной точке раскрыва
в произвольной точке раскрыва  относительно фазового центра приемной
относительно фазового центра приемной 
При выполнении (10.2) огибающая  сигнала при движении фронта волны вдоль раскрыва приемной
сигнала при движении фронта волны вдоль раскрыва приемной  практически не изменяется за время
практически не изменяется за время  т.е.
т.е.

Если поляризация приемной  соответствует вертикальной или горизонтальной составляющей вектора напряженности электрического поля, действующего в раскрыве
соответствует вертикальной или горизонтальной составляющей вектора напряженности электрического поля, действующего в раскрыве  то связь между реализацией поля
то связь между реализацией поля  и откликами
и откликами  пространственных каналов
пространственных каналов  может быть задана системой базисных функций
может быть задана системой базисных функций  представляющих АФР токов по раскрыву антенны
представляющих АФР токов по раскрыву антенны

В большинстве практических случаев

где  постоянный коэффициент, имеющий размерность длины;
постоянный коэффициент, имеющий размерность длины;  вектор, конец которого определяет положение фазового центра
вектор, конец которого определяет положение фазового центра  пространственного канала приемной
пространственного канала приемной  дельта-функция Дирака.
дельта-функция Дирака.
При выполнении (10.6) и  реализации ЭМП в раскрыве приемной
реализации ЭМП в раскрыве приемной 

где  составляющие полезных сигналов и помех;
составляющие полезных сигналов и помех;  момент прихода и временной интервал, в течение которого ожидается приход полезного сигнала, соответствуют следующие отклики ее пространственных каналов
момент прихода и временной интервал, в течение которого ожидается приход полезного сигнала, соответствуют следующие отклики ее пространственных каналов

Соотношения (10.8) представим вектором

где

В случае, когда  пространственных каналов приемной
пространственных каналов приемной  неизотропны
неизотропны 

где  пространственного канала приемной
пространственного канала приемной  — угловые координаты
— угловые координаты  цели и
цели и  источника прямошумовых помех, соответственно.
источника прямошумовых помех, соответственно.
В соответствии с выбранной моделью полезных сигналов и помех случайный процесс (10.9) является гауссовским стационарным, матрица взаимных корреляционных функций которого

может принимать одно из двух значений

или

где

 — матрица корреляционных функций случайных гауссовских стационарных на интервале наблюдения помех, зависящая только от разности аргументов;
— матрица корреляционных функций случайных гауссовских стационарных на интервале наблюдения помех, зависящая только от разности аргументов;  матрица дельта-коррелированного шума;
матрица дельта-коррелированного шума;  матрица независимых полезных сигналов со случайными от наблюдения к наблюдению релеевскими амплитудами и равновероятными начальными фазами несущих колебаний; индекс
матрица независимых полезных сигналов со случайными от наблюдения к наблюдению релеевскими амплитудами и равновероятными начальными фазами несущих колебаний; индекс  означает операцию статистического усреднения
означает операцию статистического усреднения 

 векторы комплексных законов модуляции
векторы комплексных законов модуляции  прямошумовой помехи и
прямошумовой помехи и  полезного сигнала
полезного сигнала  индекс
индекс  означает эрмитово сопряжение.
означает эрмитово сопряжение.
Из теории статистических решений [3] известно, что минимальной достаточной статистикой при решении рассматриваемой задачи является корреляционный интеграл

где  вектор
вектор  оптимальных опорных сигналов, определяемый из следующего уравнения
оптимальных опорных сигналов, определяемый из следующего уравнения

 момент прихода и длительность полезного сигнала соответственно;
момент прихода и длительность полезного сигнала соответственно;  вектор ожидаемых комплексных законов модуляции полезных сигналов.
вектор ожидаемых комплексных законов модуляции полезных сигналов.
Подставляя значение  из (10.14) в (10.17), получаем
из (10.14) в (10.17), получаем

где I — единичная матрица, или

интегральное уравнение Фредгольма 2-го рода с вырожденным ядром. Полученное в [2] решение (10.18) выглядит следующим образом:

где  — постоянные коэффициенты (числа), определяемые как
— постоянные коэффициенты (числа), определяемые как

 вектор оптимальных опорных сигналов, рассчитанных на обнаружение
вектор оптимальных опорных сигналов, рассчитанных на обнаружение  полезного сигнала на фоне помех;
полезного сигнала на фоне помех;

Из (10.18) и (10.19) видно, что оптимальная обработка принимаемых колебаний (10.9) распадается на операции, связанные с воздействием только сигналов со случайными от наблюдения к наблюдению и постоянными на интервале наблюдения релеевскими амплитудами и равновероятными фазами несущих колебаний или только независимых друг от друга случайных гауссовских стационарных флюктуаций.
В реальных условиях в зоне обзора обычно действует одна или несколько разнесенных в пространстве одиночных (точечных) целей или целей, образующих плотные группы. Поэтому ниже достаточно строго решаются следующие бинарные задачи:
обнаружения точечной цели с известными координатами;
обнаружения точечной цели и измерения ее угловых координат;
обнаружения цели и измерения скорости ее сближения с РЛС;
оценки потенциальных возможностей синтезированных алгоритмов и соответствующих им антенно-приемных трактов РЛС в различной помеховой обстановке;
определения необходимых и достаточных условий инвариантности оптимальных пространственно-многоканальных РЛС к помехам.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
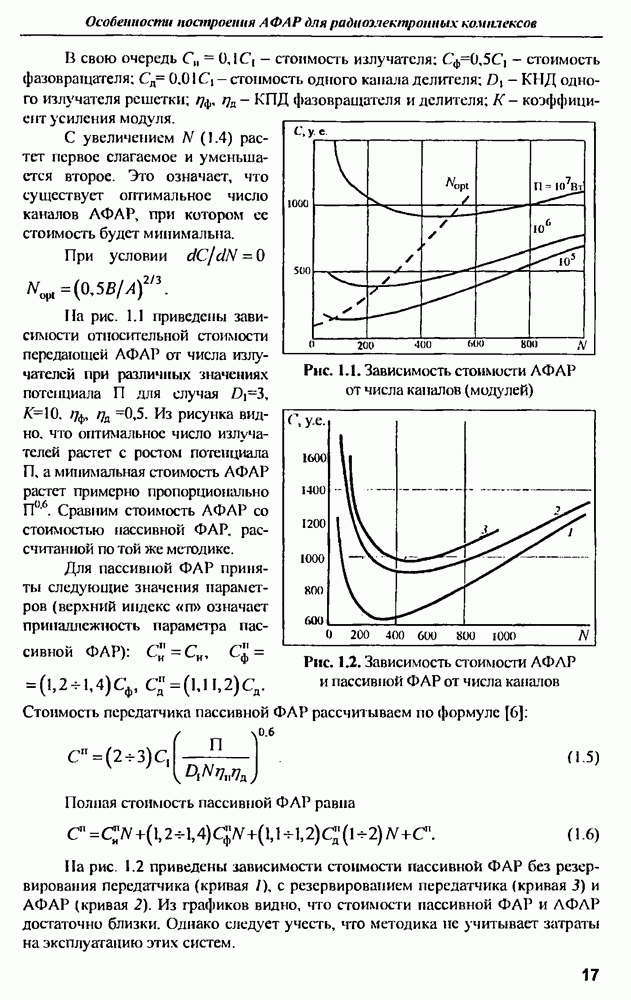
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
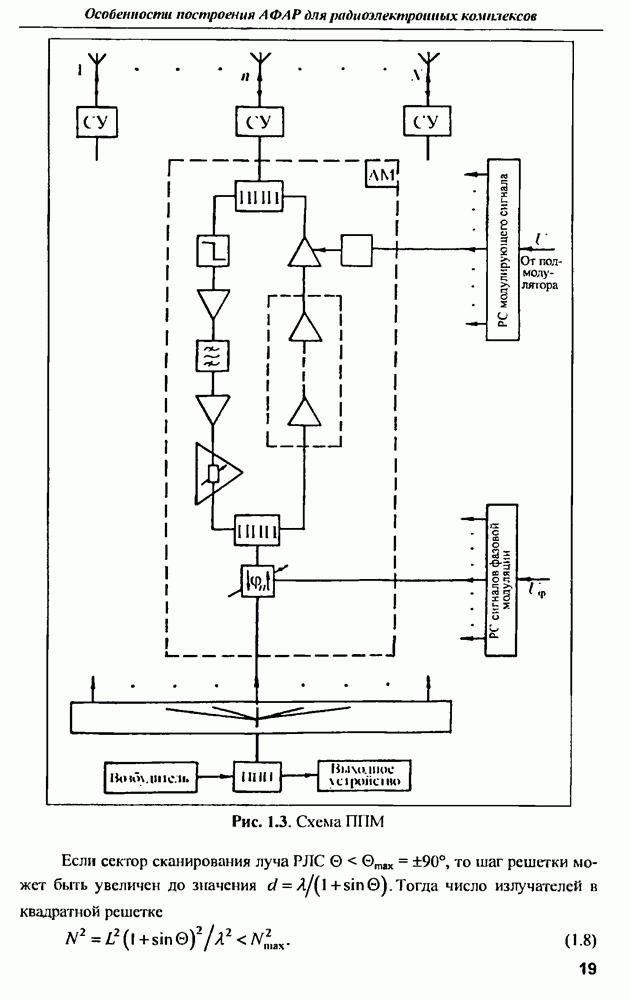
- 1.3. Приемопередающий модуль АФАР
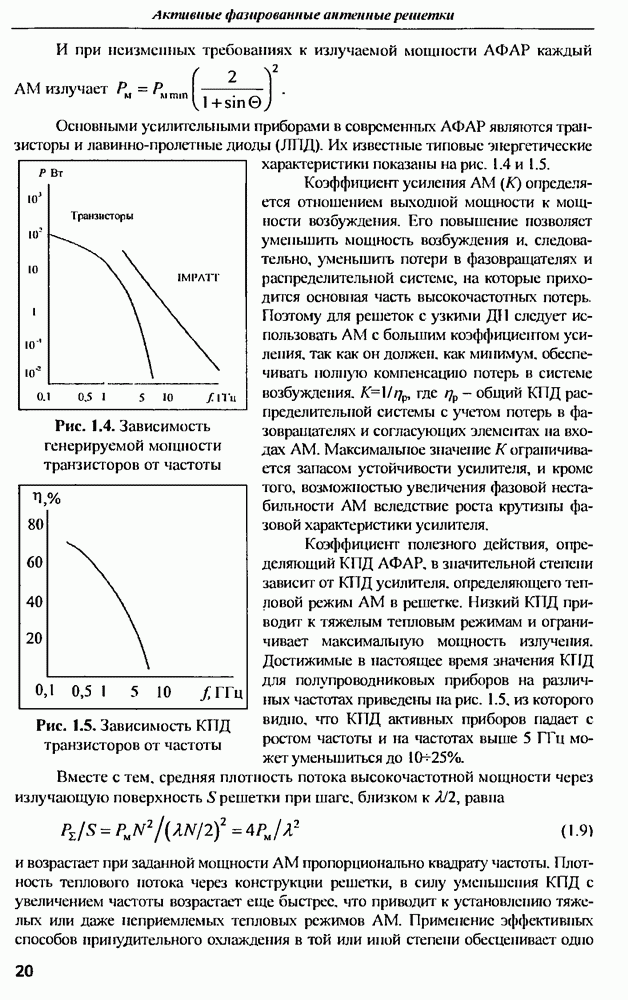
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
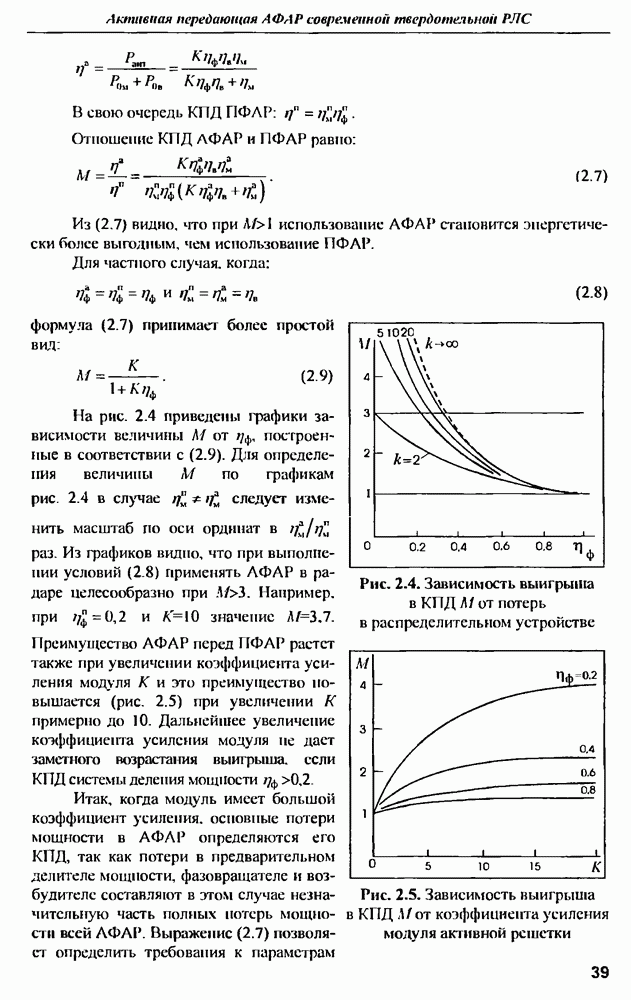
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
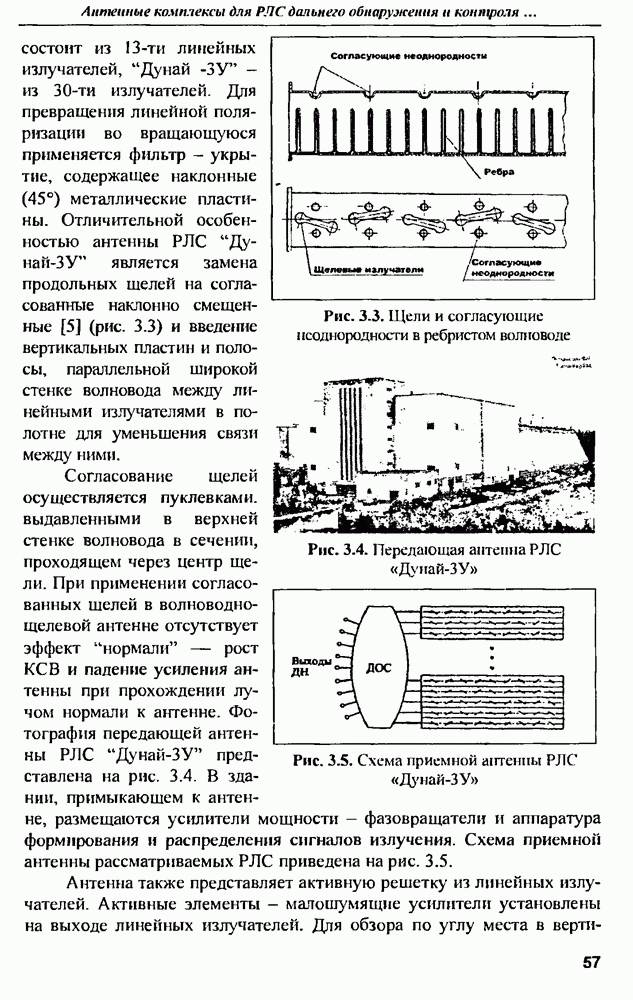
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
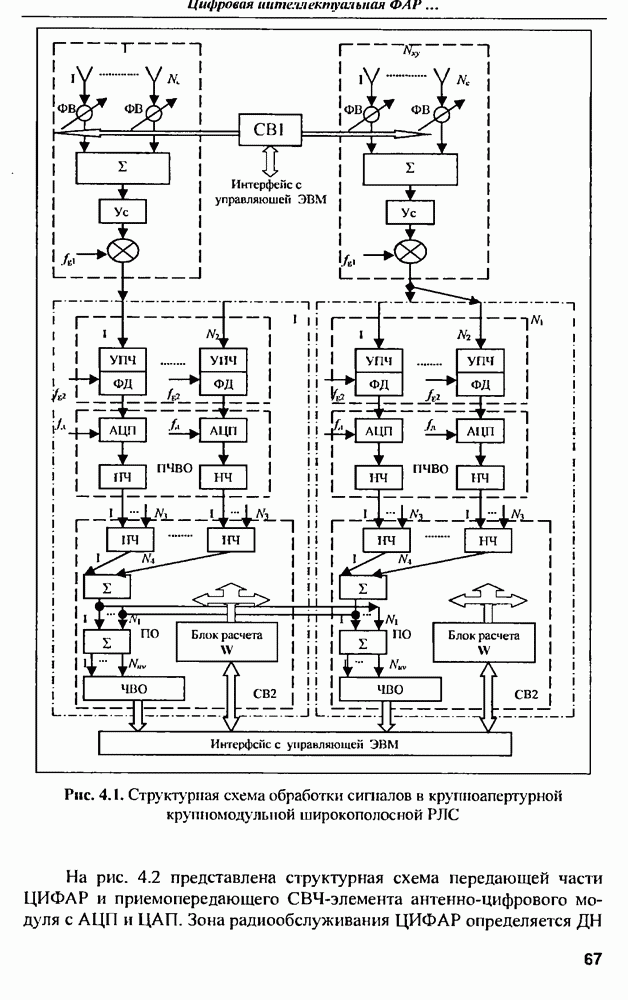
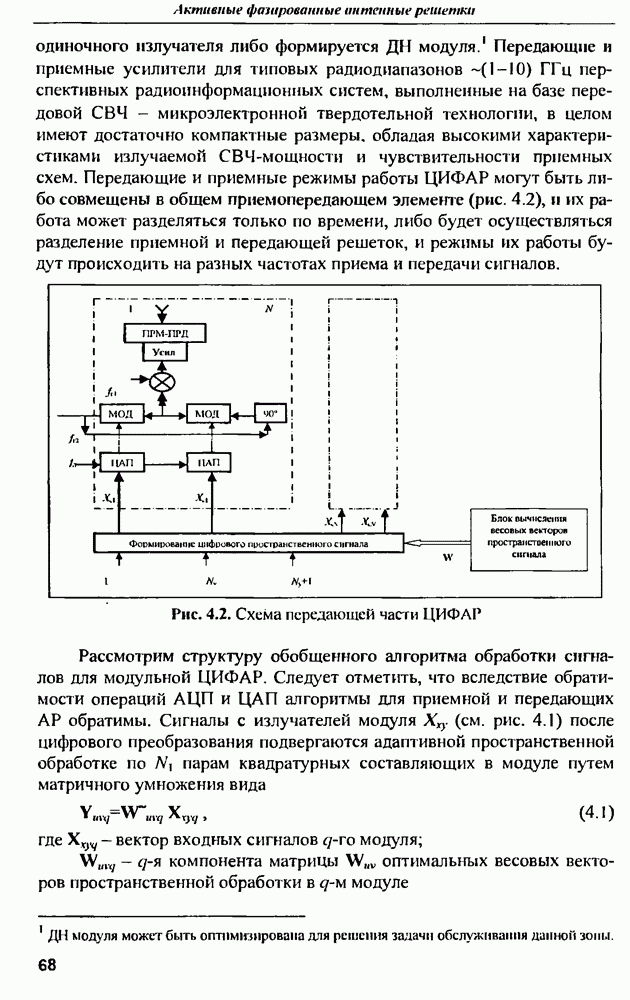
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
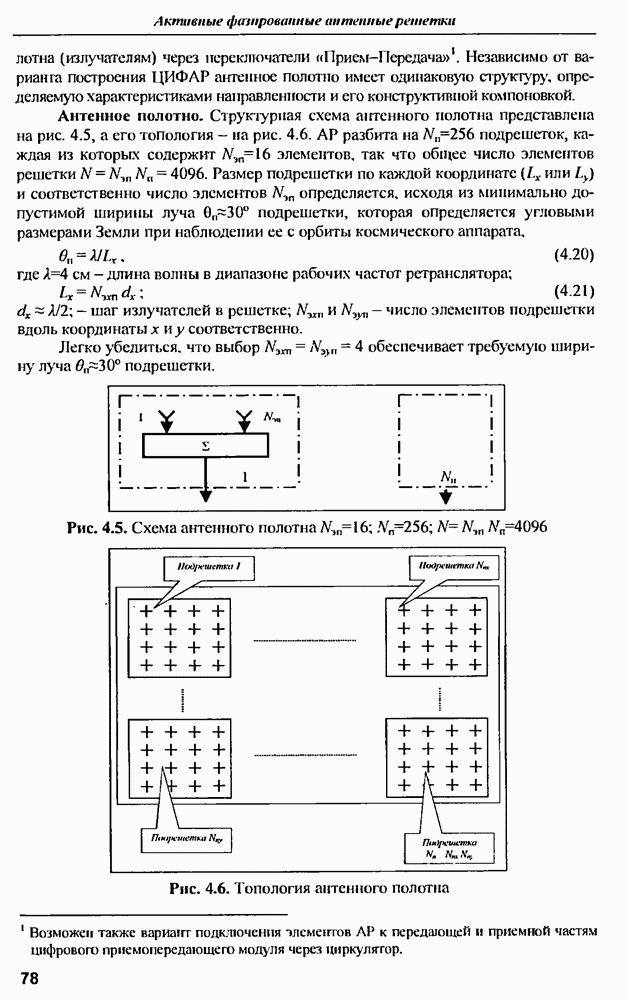
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
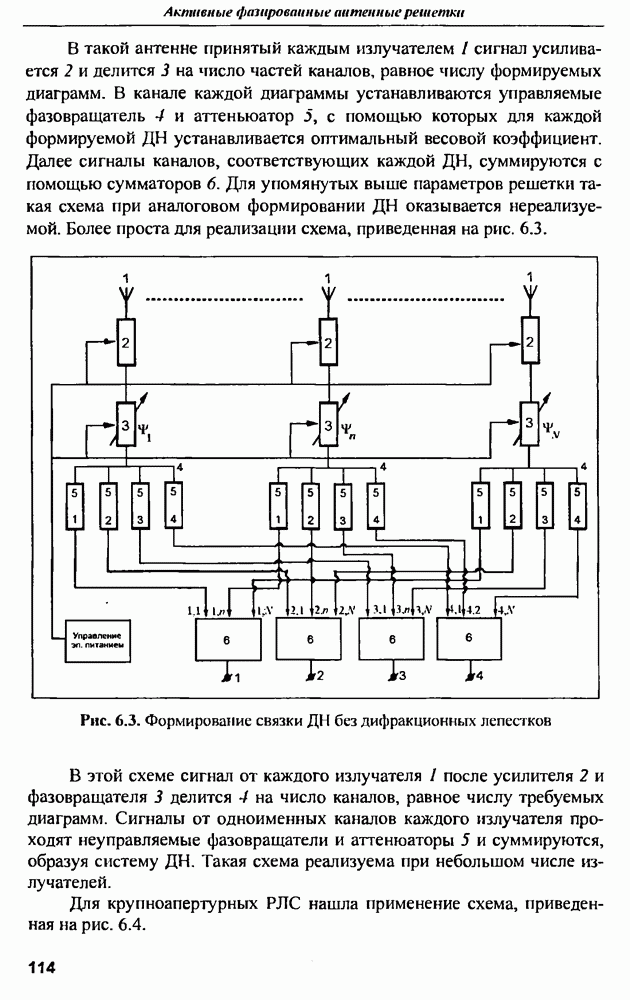
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
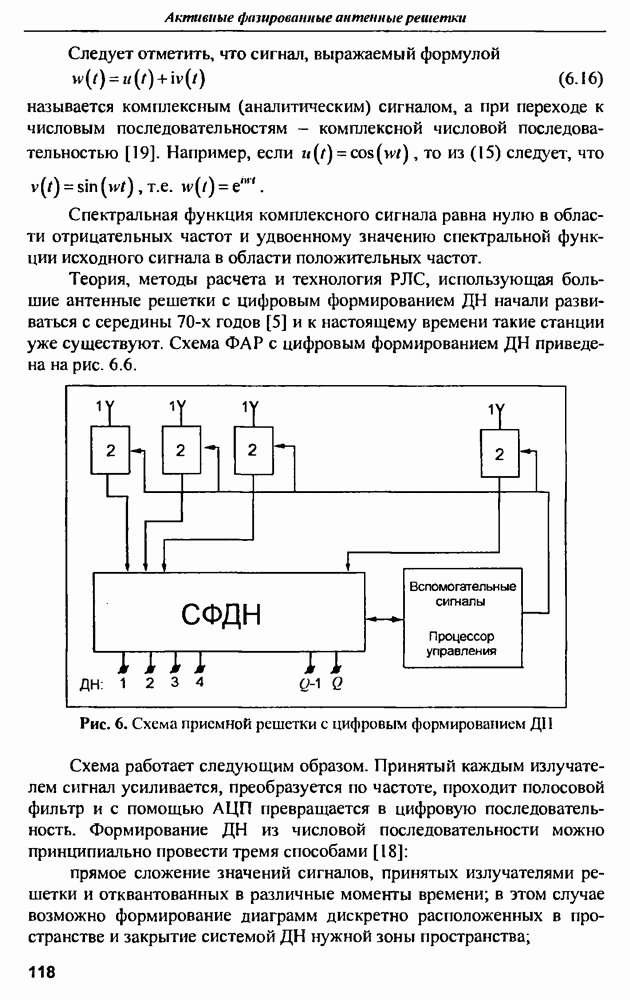
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
- 7.3.4. Качество связи
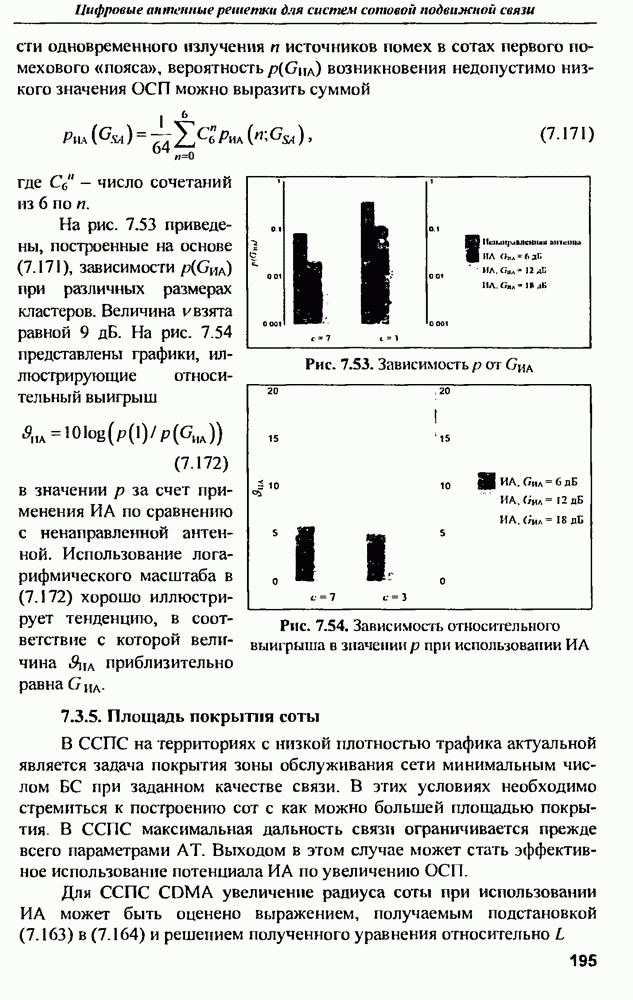
- 7.3.5. Площадь покрытия соты
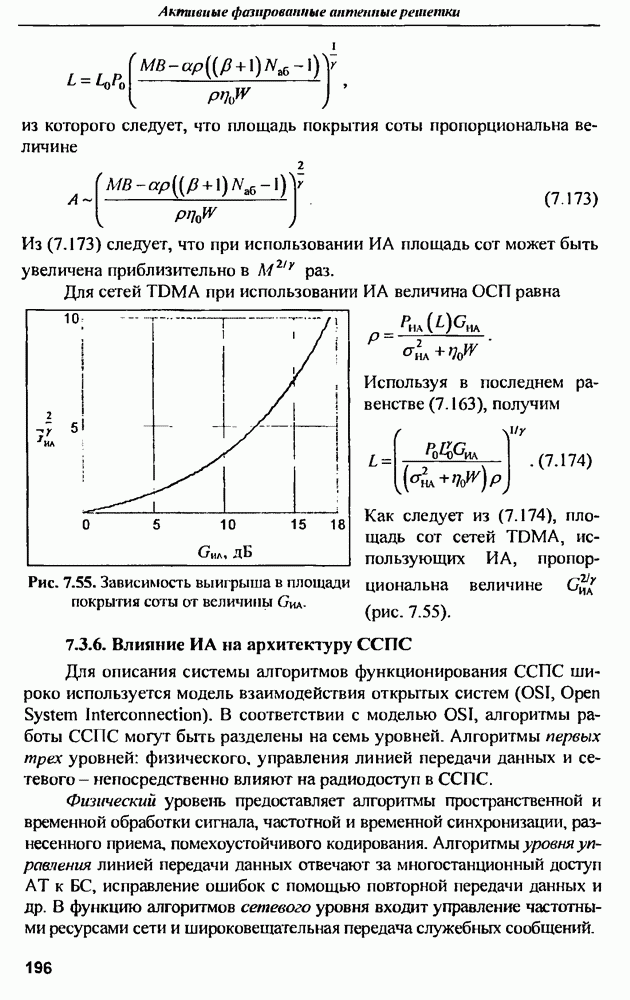
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
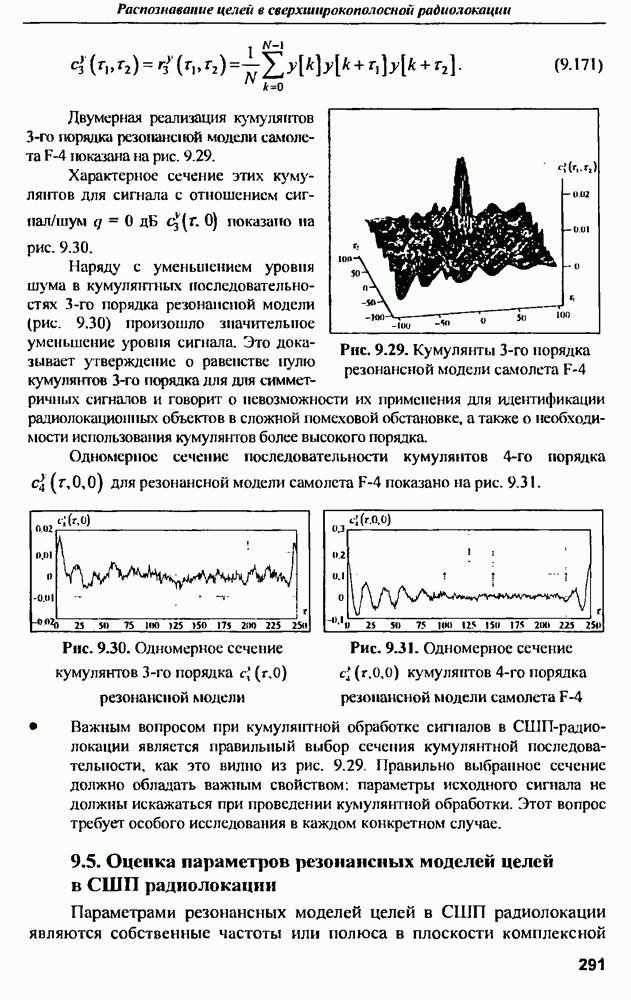
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
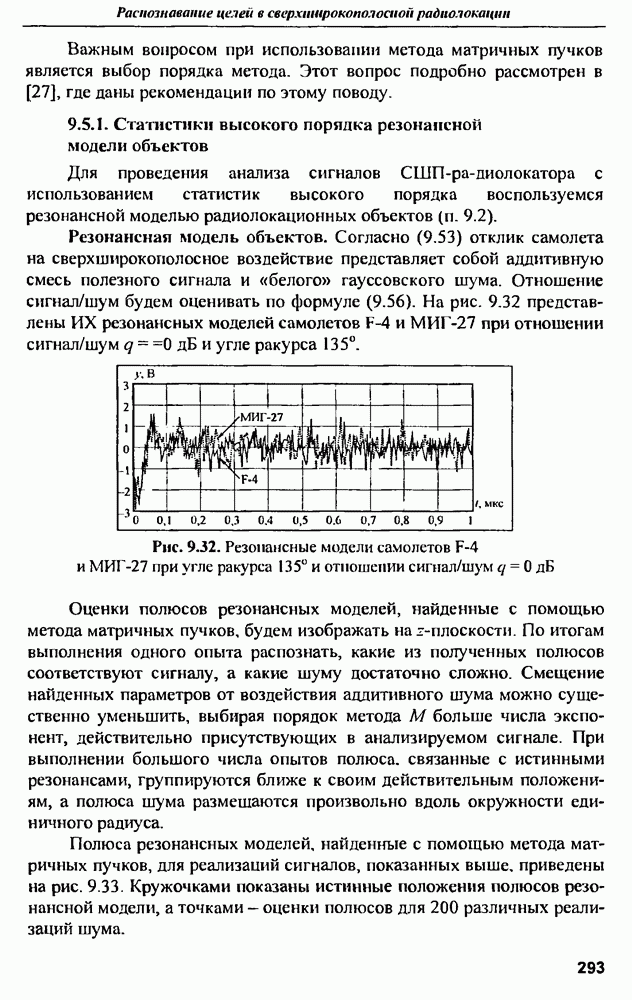
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
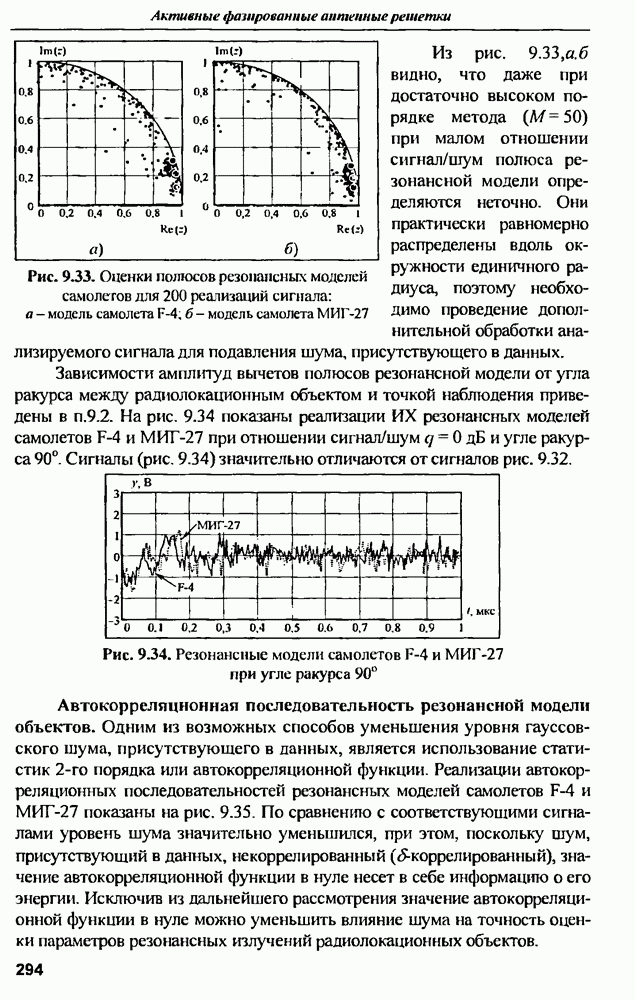
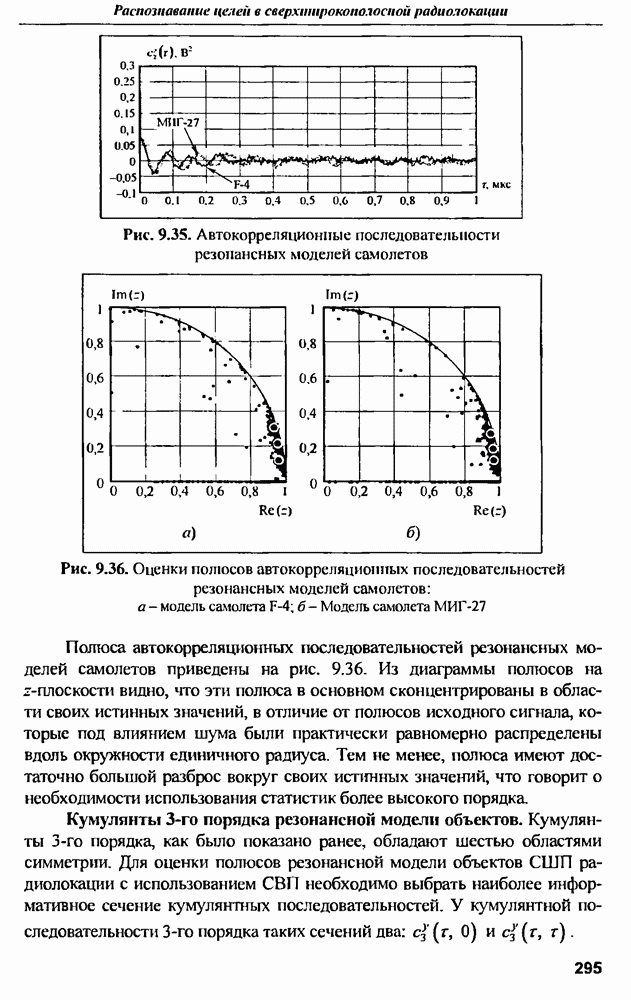
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
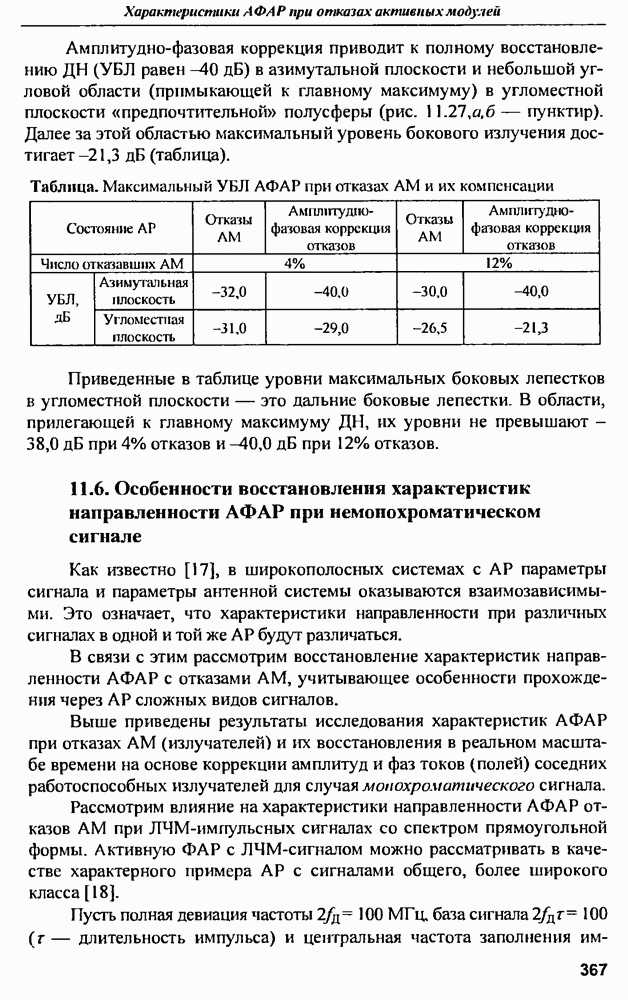
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
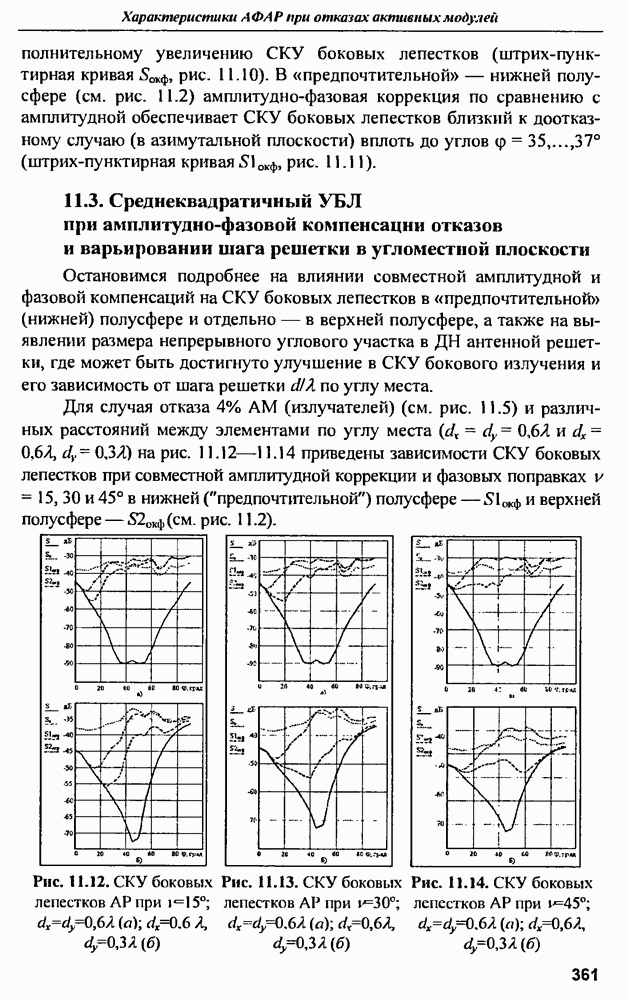
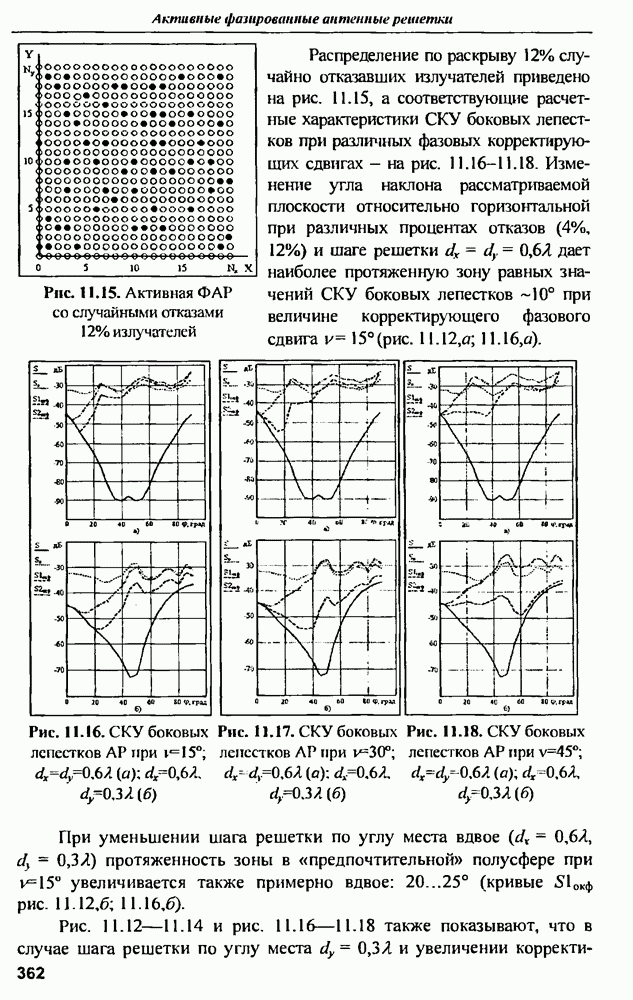
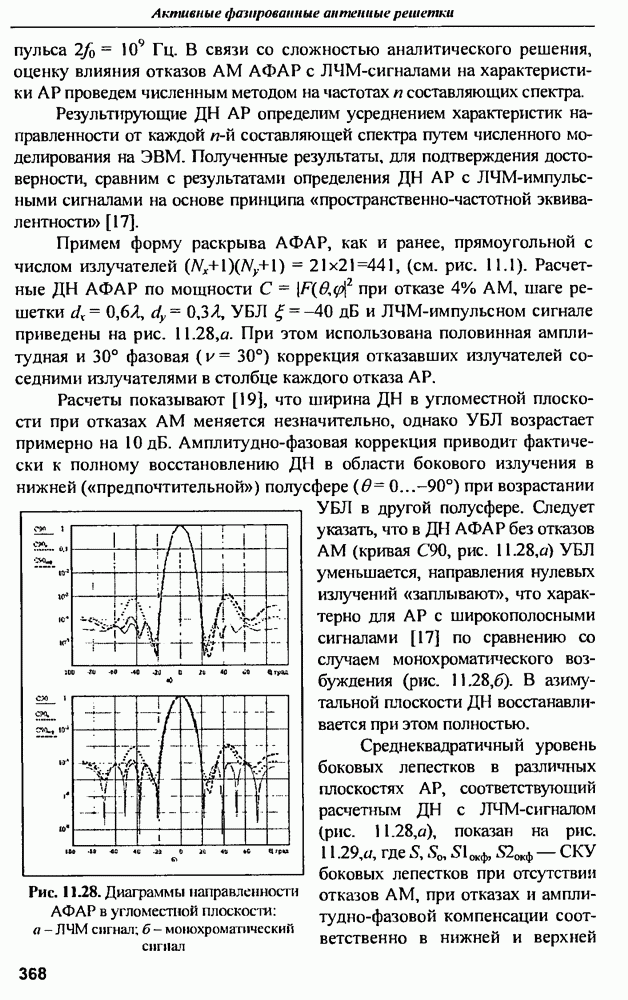
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
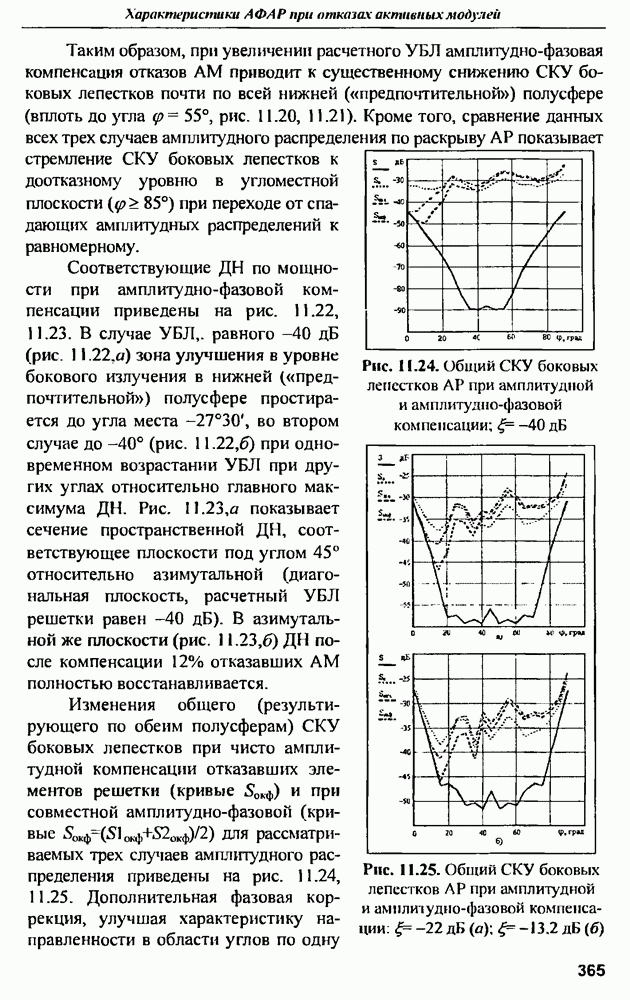
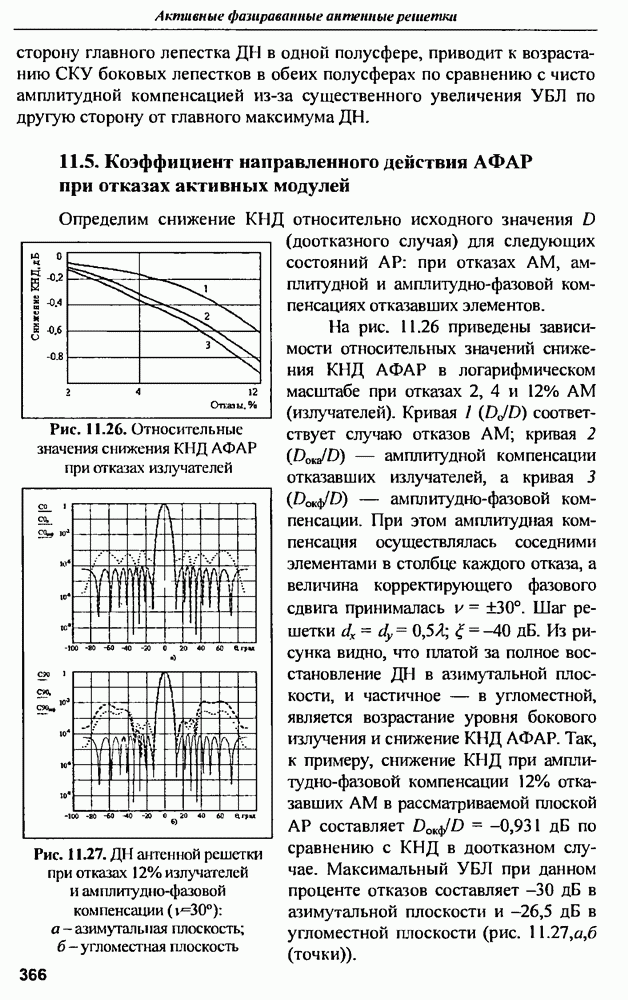
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
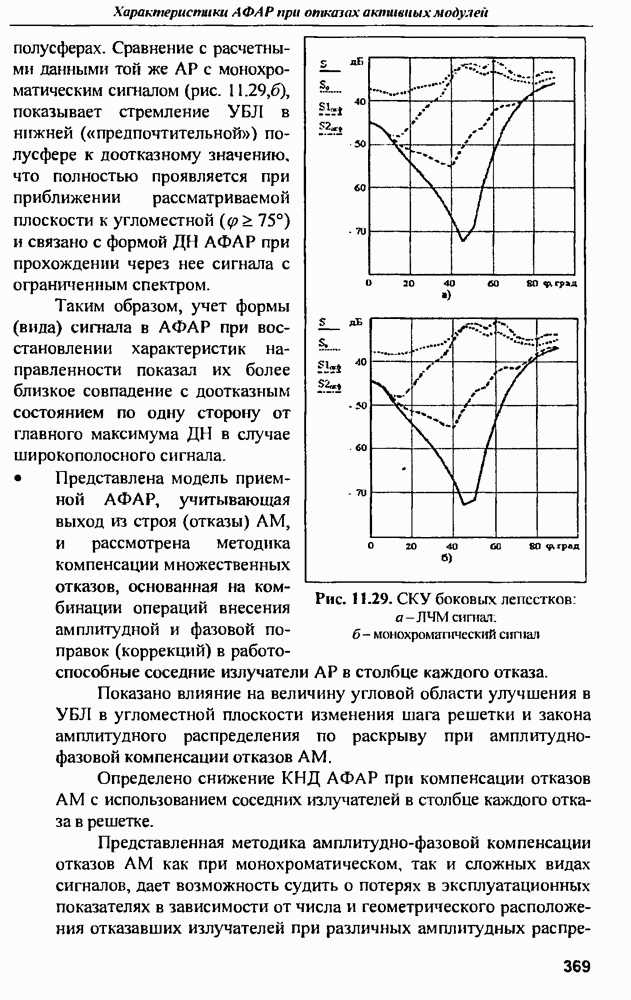
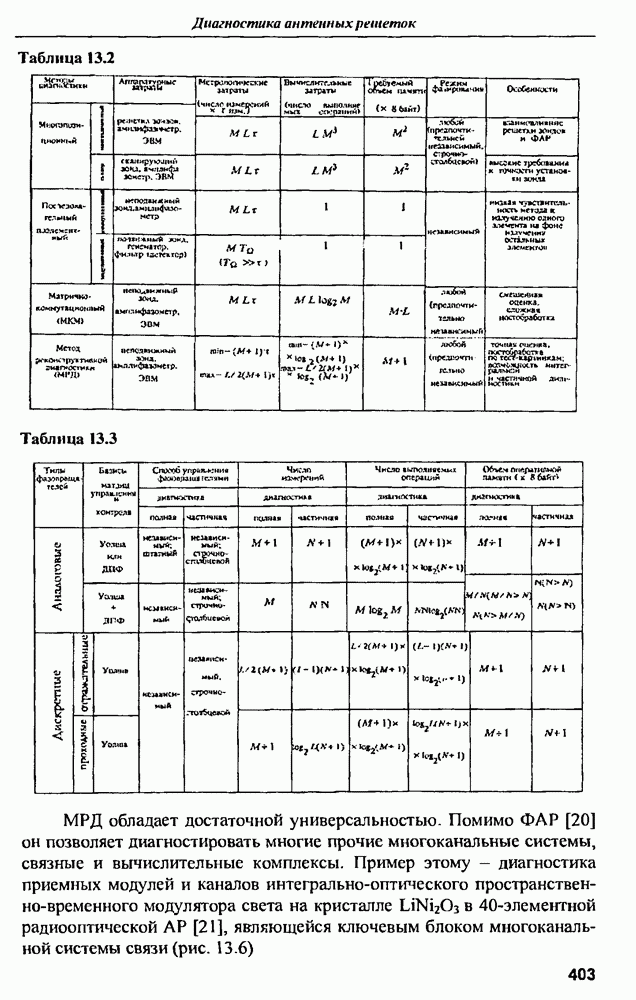
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
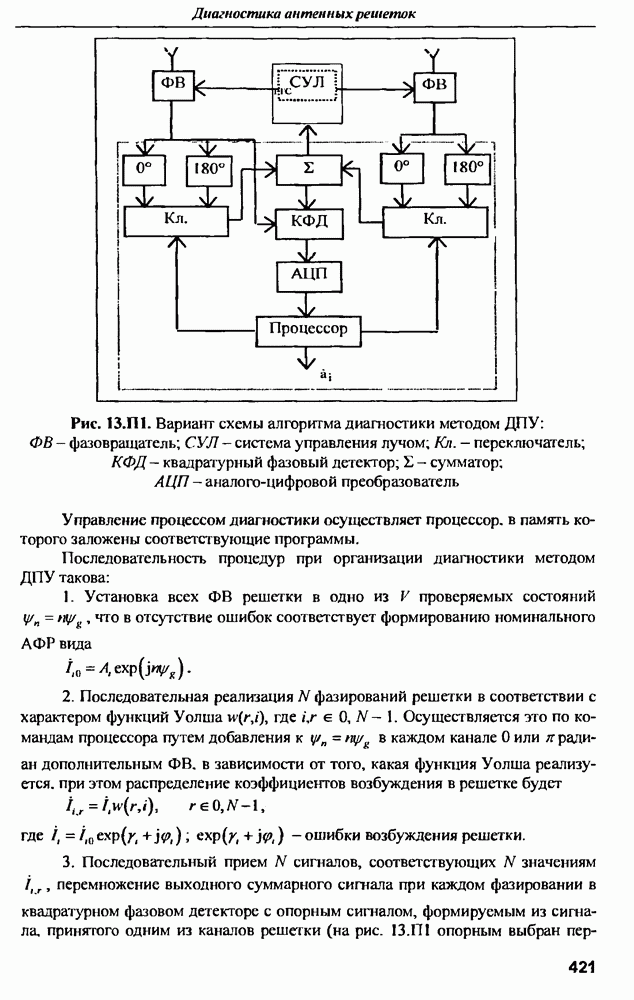
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
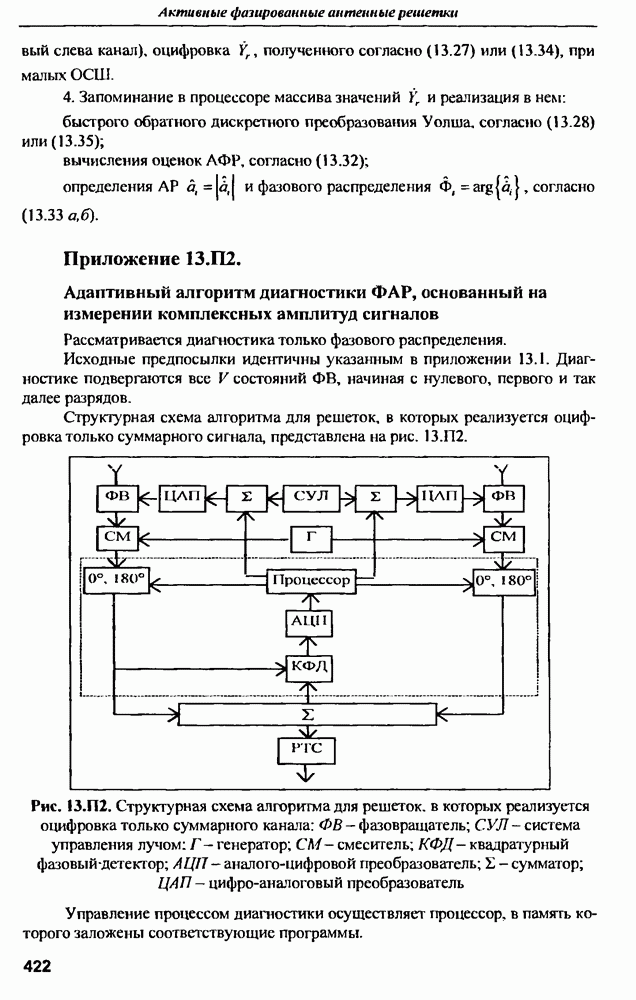
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
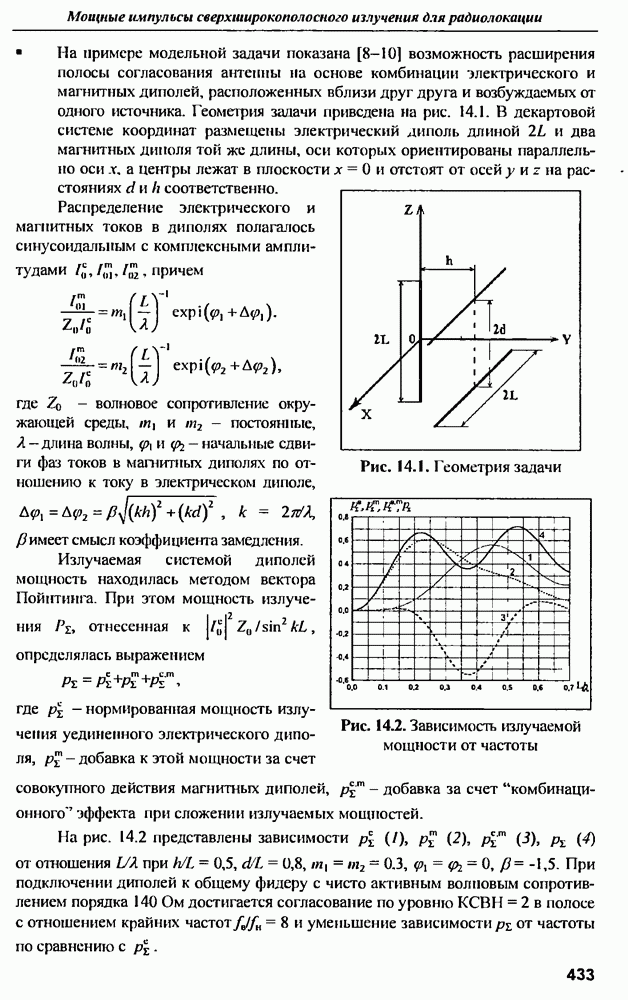
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
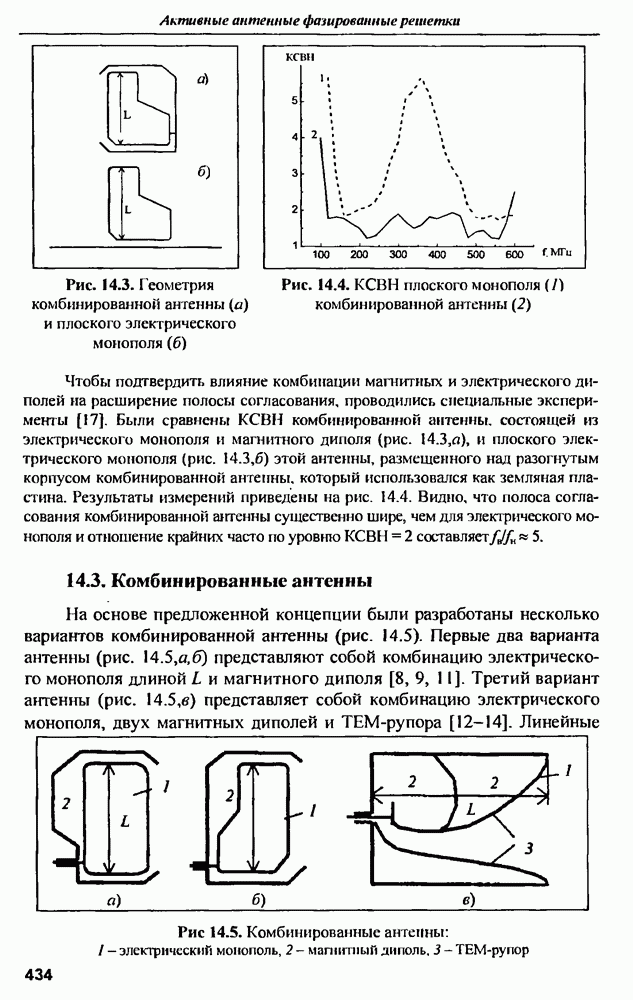
- 14.3. Комбинированные антенны
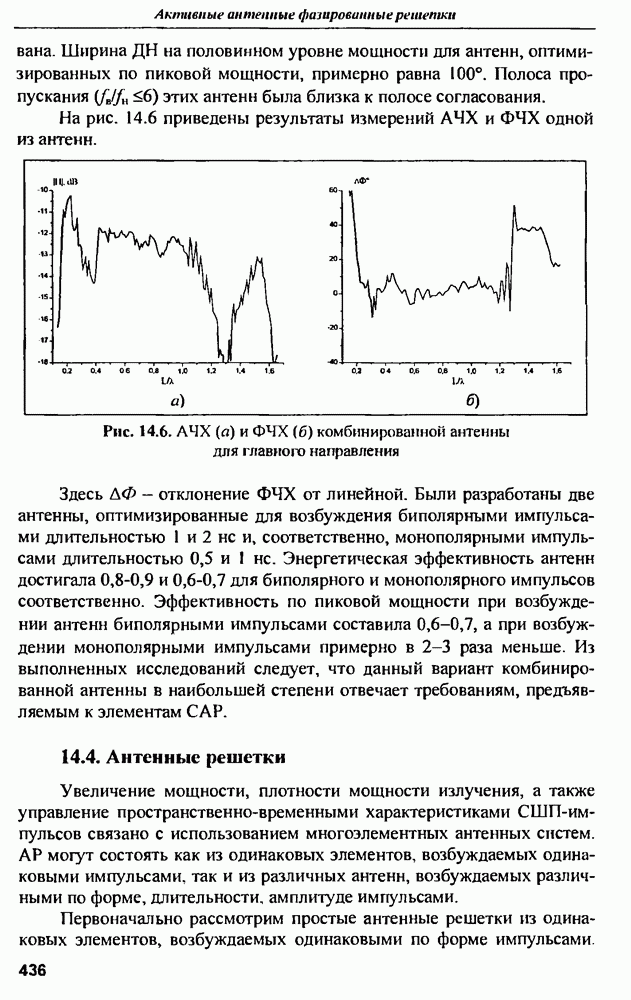
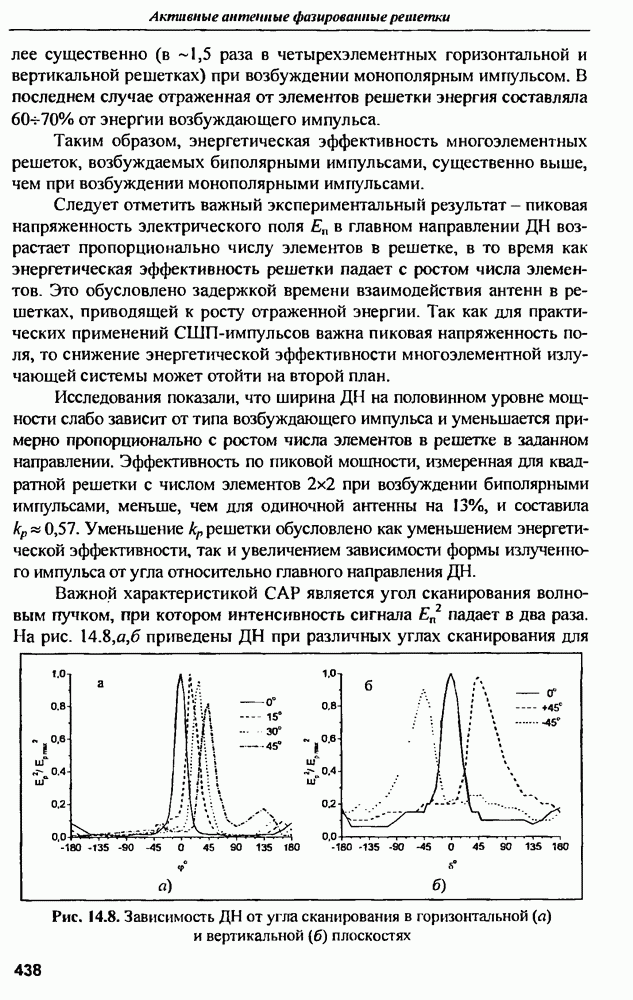
- 14.4. Антенные решетки
- 14.5. Приемные антенны
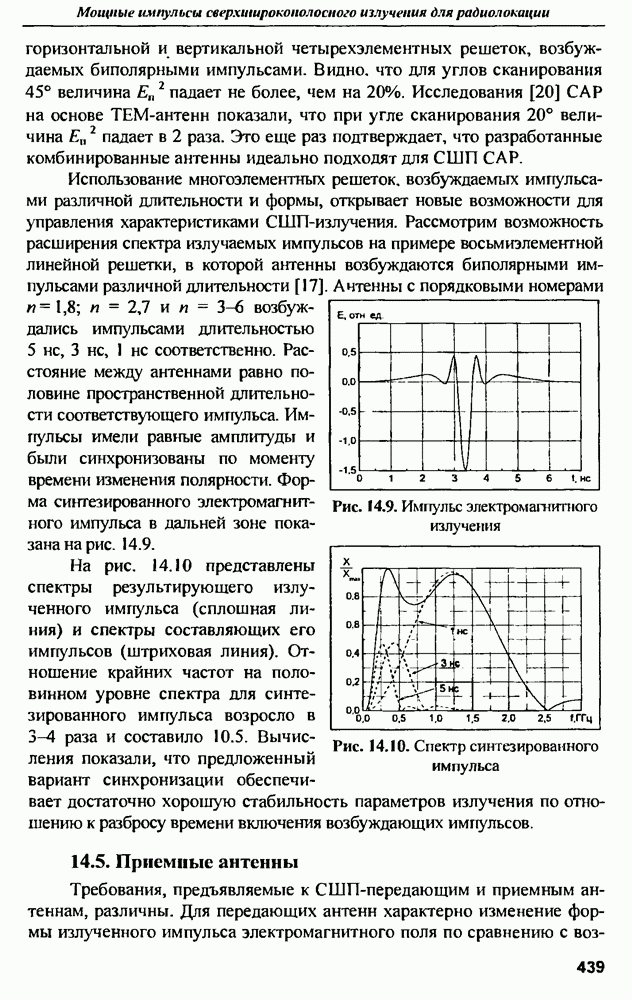
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
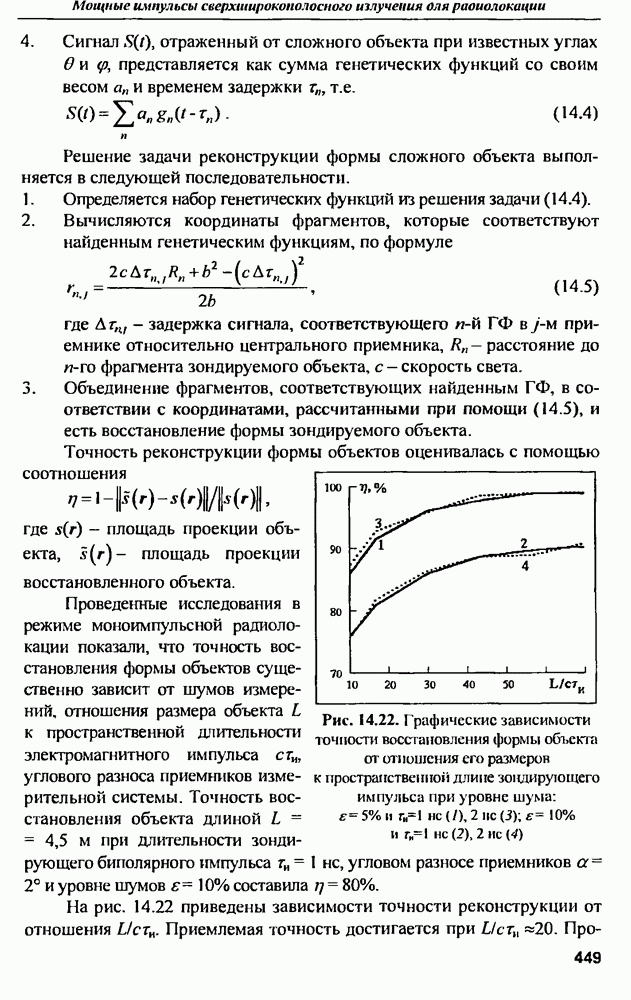
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
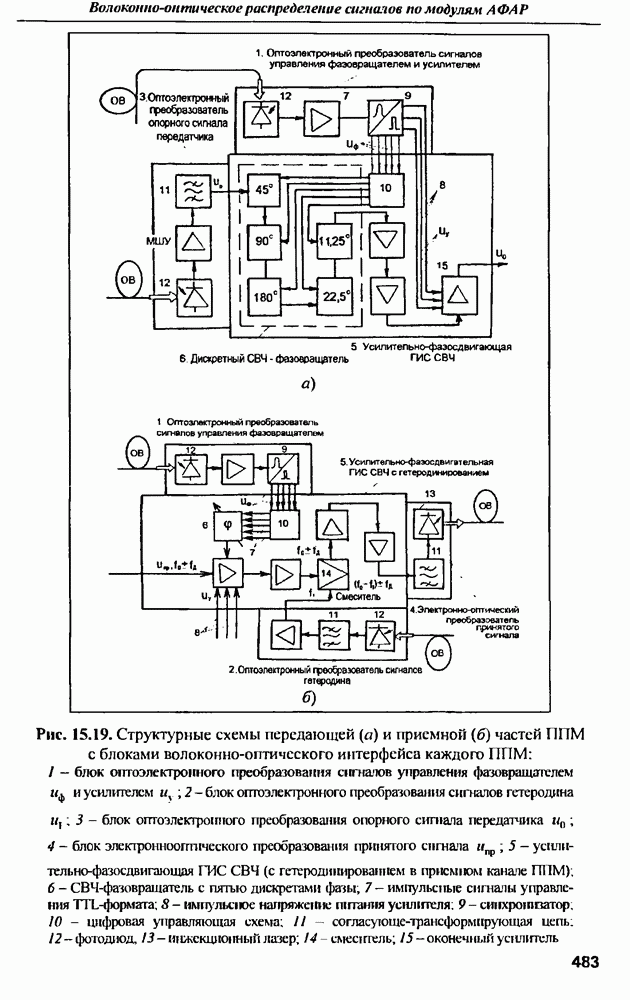
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
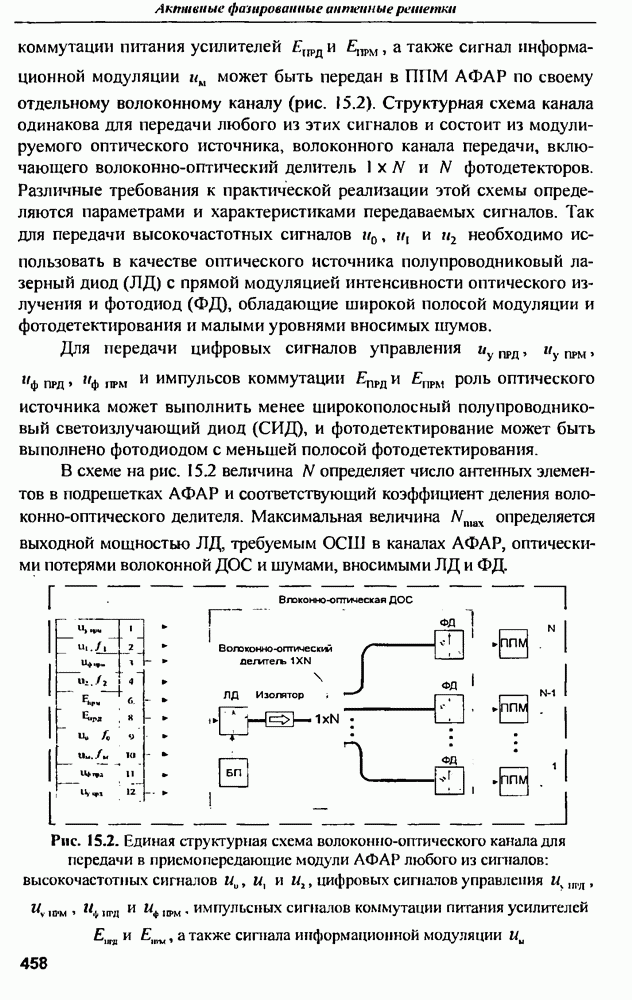
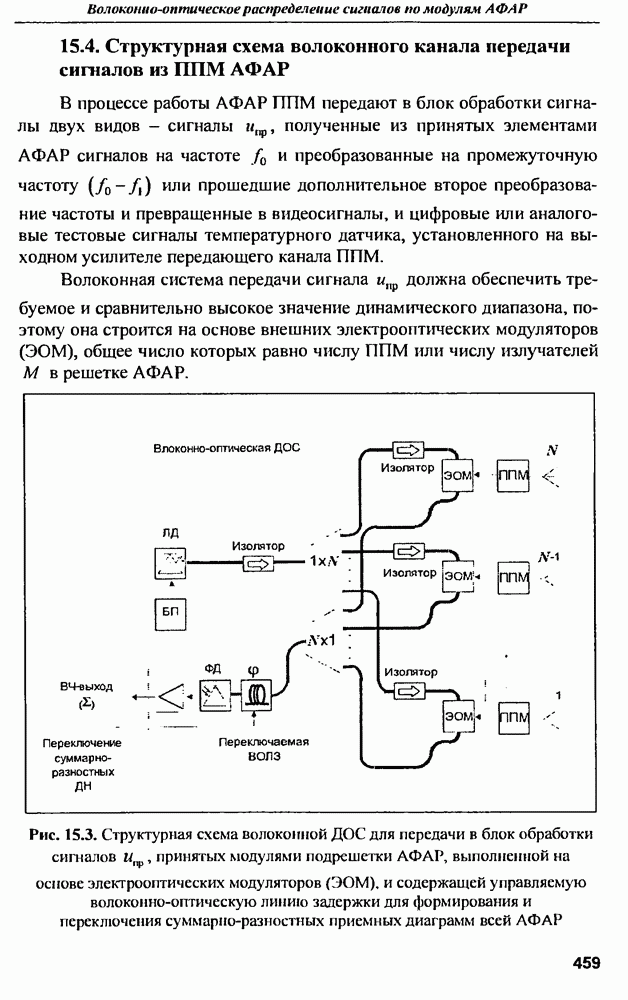
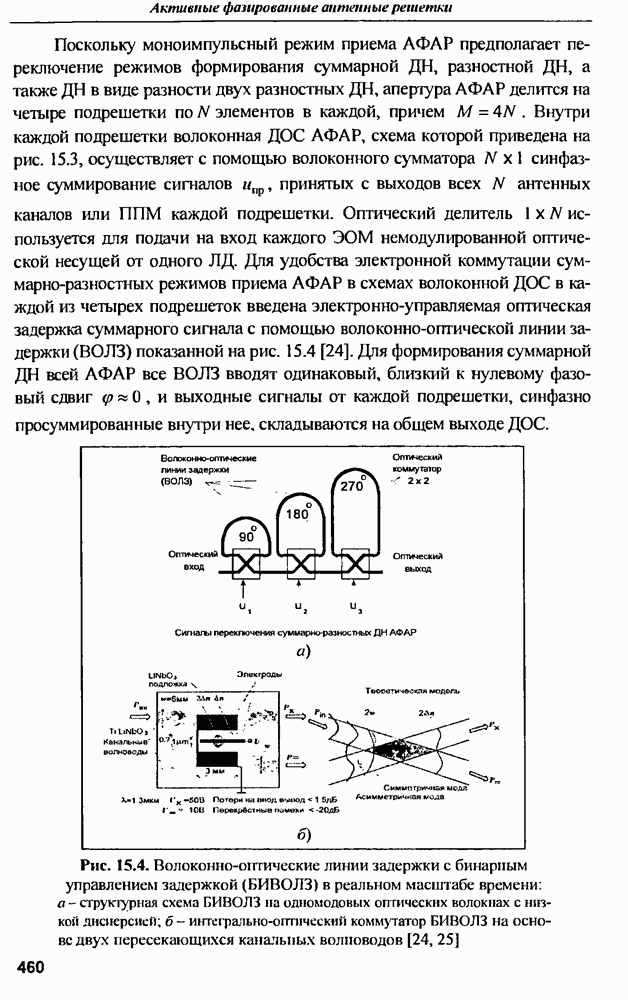
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
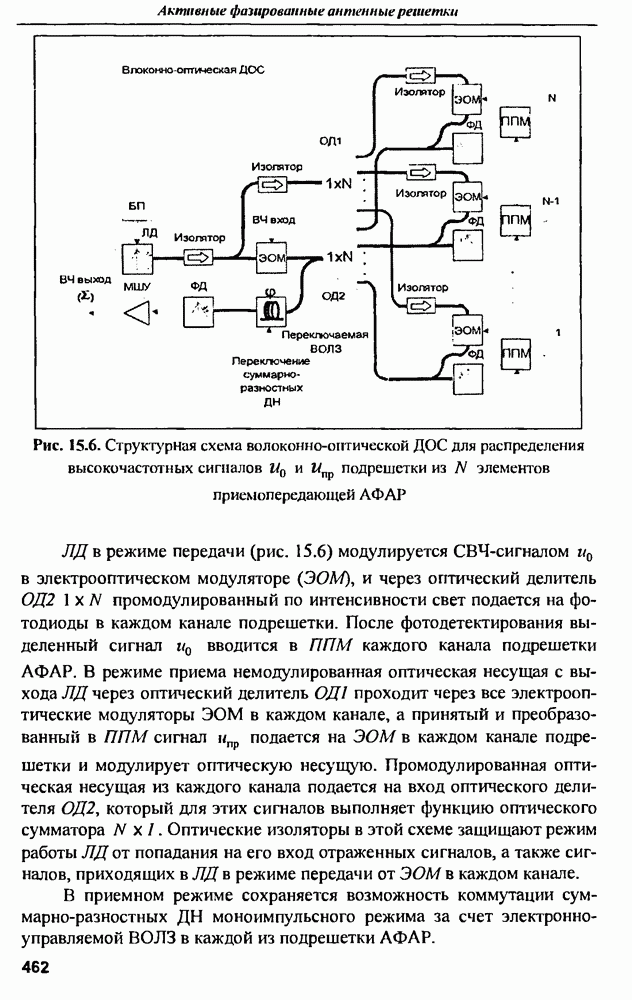
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
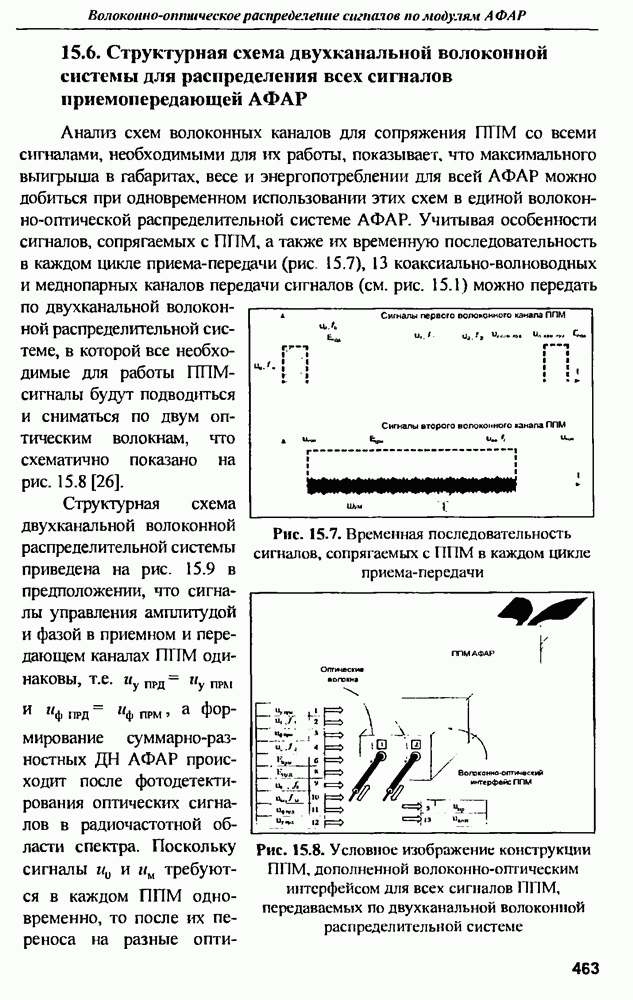
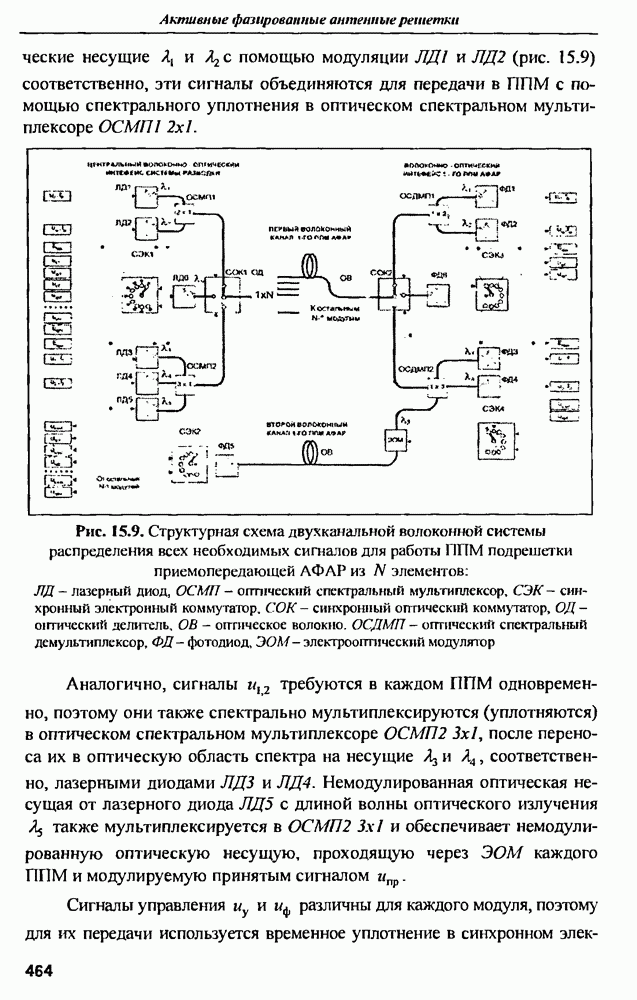
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
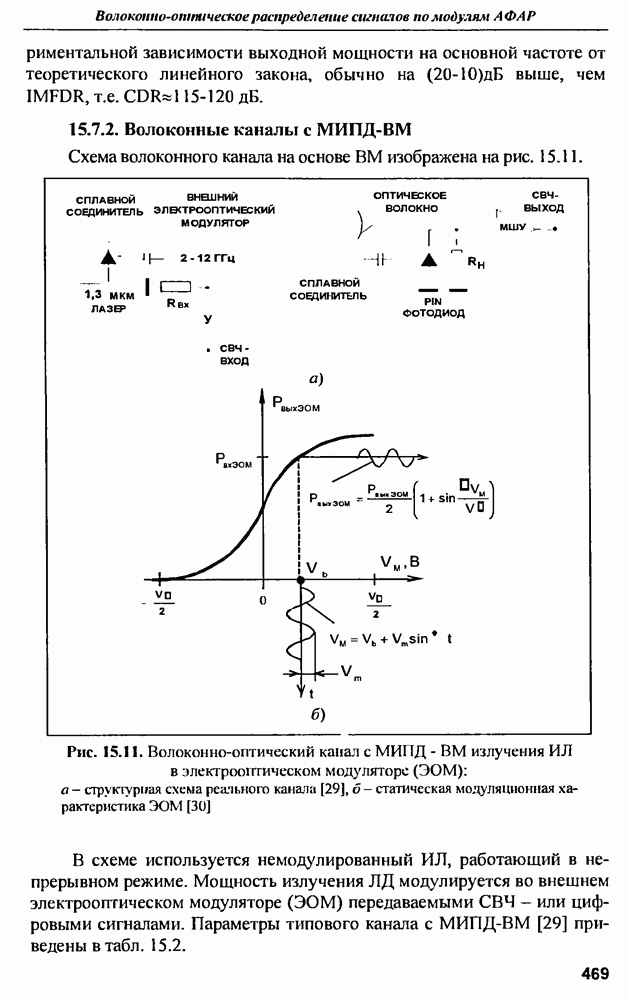
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
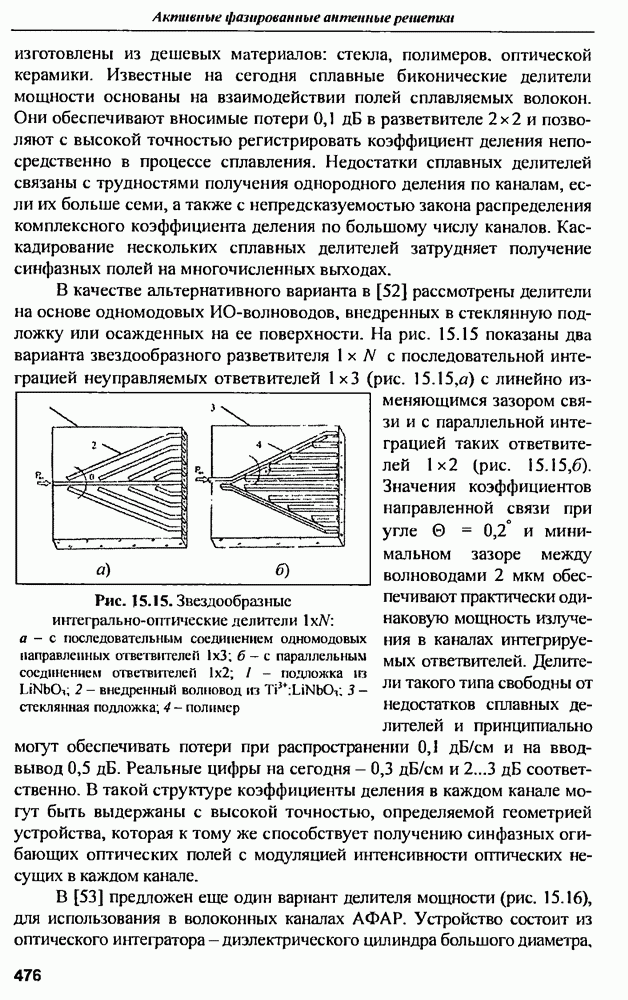
- 15.8.4. Оптические делители
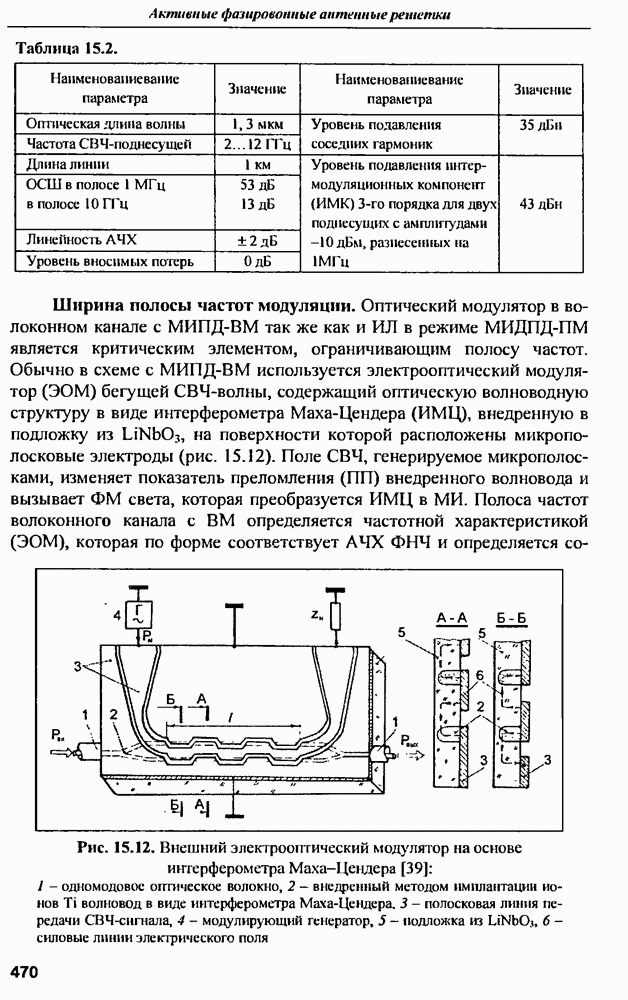
- 15.8.5. Внешние модуляторы
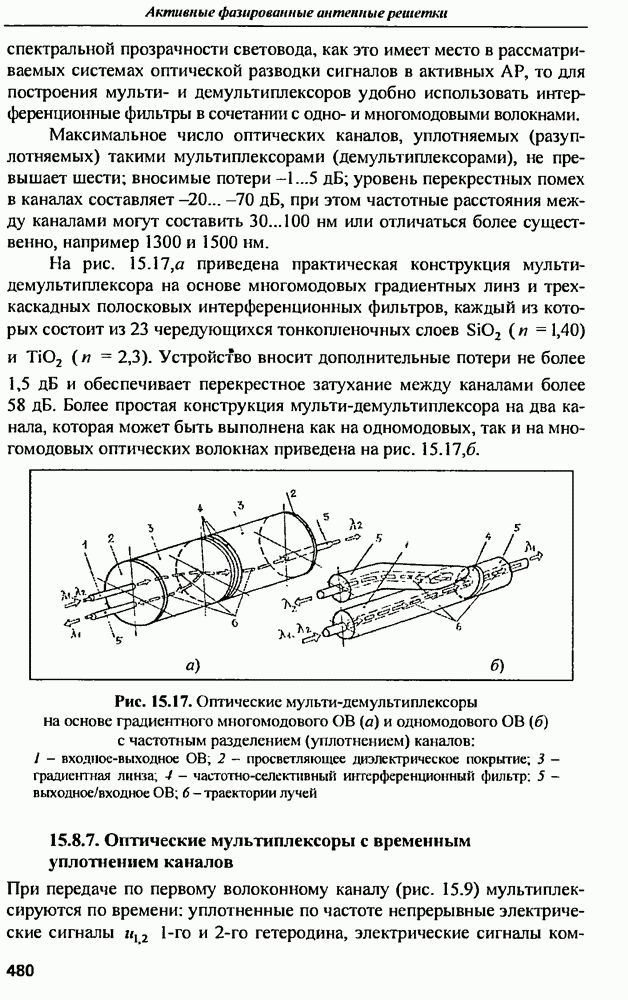
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР