| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
При обработке сигналов на практике часто возникают ситуации, при которых кроме шумового сигнала в анализируемой последовательности присутствует детерминированный сигнал. К числу таких сигналов можно отнести, например, сигналы конечной длительности (импульсные сигналы), значения которых принимаются нулевыми вне интервала времени, равного длительности сигнала. Такие сигналы называют детерминированными в противовес стохастическим сигналам (случайным
процессам), значения которых точно не известны в каждый момент времени. Основные определения и свойства моментов, кумулянтов и кумулянтных спектров стохастических процессов обсуждались выше. Далее мы рассмотрим определения и свойства статистик высокого порядка детерминированных сигналов. В частности будут рассмотрены кумулянты и кумулянтные спектры периодических сигналов на примере модели резонансных излучений радиолокационных объектов, рассмотренных в п. 9.2.
Сопоставление импульсных и периодических сигналов. Если  действительный дискретный детерминированный сигнал, его мгновенная мощность равна
действительный дискретный детерминированный сигнал, его мгновенная мощность равна  , а полная энергия определяется выражением
, а полная энергия определяется выражением

Соответственно средняя мощность 

где  является оператором усреднения по времени.
является оператором усреднения по времени.
Детерминированные импульсы имеют конечную общую энергию и нулевую среднюю мощность  назовем их энергетическими. Периодические сигналы имеют среднюю мощность больше нуля и бесконечную полную энергию
назовем их энергетическими. Периодические сигналы имеют среднюю мощность больше нуля и бесконечную полную энергию  их называют мощностными. Например, все периодические сигналы
их называют мощностными. Например, все периодические сигналы  и стационарные случайные процессы являются мощностными, а сигналы конечной длительности, затухающие экспоненты и синусоиды - энергетическими сигналами.
и стационарные случайные процессы являются мощностными, а сигналы конечной длительности, затухающие экспоненты и синусоиды - энергетическими сигналами.
Фурье-анализ импульсных сигналов Пусть  - детерминированный дискретный сигнал с конечной энергией, т.е.
- детерминированный дискретный сигнал с конечной энергией, т.е. 
Дискретное по времени преобразование Фурье (ДВПФ) от сигнала  определяется выражением
определяется выражением

а обратное дискретное по времени преобразование Фурье

Здесь и далее частота дискретизации принимается за единицу Поскольку имеет конечную энергию, представление сигнала в частотной области всегда существует, а сумма сходится так, что среднеквадратическая ошибка равна нулю.  является периодической функцией частоты
является периодической функцией частоты  и в общем случае комплексной функцией.
и в общем случае комплексной функцией.
Соотношение Парсеваля для импульсного сигнала  имеет вид
имеет вид

Отсюда следует альтернативное выражение для полной энергии  сигнала по его ДВПФ.
сигнала по его ДВПФ.
Фурье-анапиз периодических сигналов. Рассмотрим периодическую последовательность с периодом  т.е.
т.е.  для любого целого значения k. Она имеет конечную среднюю мощность
для любого целого значения k. Она имеет конечную среднюю мощность  бесконечную полную энергию
бесконечную полную энергию  и может быть представлена в виде взвешенной суммы комплексных экспонент с частотами, кратными основной частоте
и может быть представлена в виде взвешенной суммы комплексных экспонент с частотами, кратными основной частоте  однако число таких разных комплексных экспонент в точности равно
однако число таких разных комплексных экспонент в точности равно 
В этом случае пара дискретного преобразования Фурье  для периодической дискретной последовательности имеет вид
для периодической дискретной последовательности имеет вид

Очевидно, что последовательность в спектральной области  является в общем случае комплексной и периодической с периодом
является в общем случае комплексной и периодической с периодом  т.е.
т.е.  для любого целого значения
для любого целого значения  Аналогично можно описывать и конечные сигналы длительностью
Аналогично можно описывать и конечные сигналы длительностью  отсчетов в предположении об их периодическом повторении за пределами интервала
отсчетов в предположении об их периодическом повторении за пределами интервала 
Средняя мощность периодического сигнала

где  начальное произвольное число суммирования,
начальное произвольное число суммирования,  оператор усреднения по времени периодической последовательности. Оператор
оператор усреднения по времени периодической последовательности. Оператор  усреднения по времени эквивалентен
усреднения по времени эквивалентен  если сигнал периодический с периодом
если сигнал периодический с периодом  . С учетом этого обратное дискретное преобразование Фурье
. С учетом этого обратное дискретное преобразование Фурье  может быть записано в виде
может быть записано в виде

Из дискретного преобразования Фурье  видно, что для действительной последовательности значение
видно, что для действительной последовательности значение  действительно,
действительно,  обладает сопряженной симметрией.
обладает сопряженной симметрией.
Соотношение Парсеваля для периодической последовательности с периодом  имеет вид
имеет вид

или с использованием оператора усреднения

Анализ конечных по длительности сигналов. Выше приведен Фурье-анализ импульсных сигналов (детерминированных импульсов) и специального подкласса периодических сигналов, называемых периодическими последовательностями. Важным подклассом импульсных сигналов являются последовательности конечной длительности, для которых значения вне этого конечного шггервала равны нулю Далее будет рассмотрено соотношение между представлением Фурье последовательностей конечной длительности и периодическими последовательностями и установлено, при каких условиях это соотношение выполняется.
При обработке сигналов довольно часто мы имеем дело с сигналом  чьи значения известны в ограниченном интервале времени
чьи значения известны в ограниченном интервале времени  Значение сигнала вне этого интервала, т.е. для
Значение сигнала вне этого интервала, т.е. для  неизвестны. Поэтому мы не можем отнести сигнал ни к импульсному, ни к периодическому, пока не сделаем определенных предположений относительно неизвестных отсчетов сигнала.
неизвестны. Поэтому мы не можем отнести сигнал ни к импульсному, ни к периодическому, пока не сделаем определенных предположений относительно неизвестных отсчетов сигнала.
Можно предположить, что эти отсчеты равны нулю, либо являются периодическим повторением сигнала, заданного на конечном интервале в  значений. Ясно, что эти предположения не являются единственно возможными.
значений. Ясно, что эти предположения не являются единственно возможными.
Рассмотрим два вида сигналов:
- сигнал конечной длительности  с
с  ;
;
- периодический сигнал 
Очевидно, что  детерминированный импульсный сигнал с преобразованием Фурье
детерминированный импульсный сигнал с преобразованием Фурье

При этом мы имеем

С другой стороны, сигнал - периодический сигнал с периодом  Тогда коэффициенты ряда Фурье
Тогда коэффициенты ряда Фурье

Уравнение Парсеваля определяется как

Для получения связи между и  учтем, что
учтем, что

Дискретное по времени преобразование Фурье  от функции имеет
от функции имеет 

при условии, что  нечетное число.
нечетное число.
Определим спектр сигнала 

где  означает операцию свертки.
означает операцию свертки.
После преобразований получим

Поскольку  найдем
найдем

Из сопоставления  и видно, что
и видно, что

Таким образом, если мы примем, что  для
для  является одним периодом последовательности
является одним периодом последовательности  то преобразование Фурье последовательности с конечной длительностью
то преобразование Фурье последовательности с конечной длительностью  можно получить из коэффициентов ряда Фурье
можно получить из коэффициентов ряда Фурье  с помощью формулы интерполяции (9.131).
с помощью формулы интерполяции (9.131).
С другой стороны, если принять, что является последовательностью конечной длительности  с нулевыми отсчетами вне интервала
с нулевыми отсчетами вне интервала  коэффициенты ряда Фурье эквивалентной периодической последовательности
коэффициенты ряда Фурье эквивалентной периодической последовательности  являются результатом дискретизации
являются результатом дискретизации  в каждой из точек
в каждой из точек 

Моменты импульсных сигналов. Далее рассмотрим определения и свойства моментов высокого порядка детерминированных сигналов с конечной энергией.
Если  действительный сигнал с конечной энергией и его моменты существуют, тогда моментом
действительный сигнал с конечной энергией и его моменты существуют, тогда моментом  порядка импульсного сигнала является
порядка импульсного сигнала является  -мерная функция
-мерная функция

где  для всех значений
для всех значений 
Эти моменты представляют собой численную меру степени похожести сигнала и произведения задержанных или опережающих копий этого же сигнала. Например, значение функции момента  порядка в начале координат, т.е.
порядка в начале координат, т.е.  является внутренним произведением или взаимной энергией и
является внутренним произведением или взаимной энергией и 
Рассмотрим частные случаи определения моментов высокого порядка. Момент 1-го порядка (среднее значение) определяется как

Момент 2-го порядка (автокорреляционная последовательность) определяется как

Очевидно, что от,  - это энергия
- это энергия  для действительного сигнала
для действительного сигнала  Автокорреляционная последовательность всегда четная, т.е.
Автокорреляционная последовательность всегда четная, т.е.  для всех целых значений
для всех целых значений  можно также рассматривать как линейную свертку между
можно также рассматривать как линейную свертку между 
Момент 3-го порядка (тройная корреляция) находится как

Тройная корреляционная функция обладает свойствами симметрии относительно своих аргументов, как и у кумулянтов 3-го порядка стационарного случайного процесса. Отметим, что  это мера асимметрии сигнала, а
это мера асимметрии сигнала, а  являются взаимной корреляцией и
являются взаимной корреляцией и 
Момент 4-го порядка определяется как

Сечения  моментов 4-го порядка представляют собой взаимную корреляцию между
моментов 4-го порядка представляют собой взаимную корреляцию между 
Моментные спектры импульсных сигналов. Моментный спектр  порядка от импульсного сигнала
порядка от импульсного сигнала  определяется как
определяется как  мерное дискретное по времени преобразование Фурье от момента
мерное дискретное по времени преобразование Фурье от момента  порядка
порядка 

где  .
.
Моментный спектр является непрерывной функцией частот  кроме того, это в общем случае комплексная для
кроме того, это в общем случае комплексная для  и периодическая, с периодом
и периодическая, с периодом  функция.
функция.
В амплитудно-фазовой форме моментный спектр записывается как

Моментный спектр также можно определить с помощью дискретного по времени преобразования Фурье сигнала 

В амплитудно-фазовой форме моментный спектр определяется как 

Соотношение между моментным спектром  порядка и моментным спектром
порядка и моментным спектром  порядка вытекает из формулы (9.142)
порядка вытекает из формулы (9.142)

Особый интерес для дальнейшего использования представляют частные случаи моментных спектров для n = 2,3 и 4.
Энергетический спектр определяется соотношением

Энергетический спектр — это действительная неотрицательная четная функция, т.е. в ней подавлена фазовая информация. С ее помощью можно полностью восстанавливать (включая знак и задержку) только минимально-фазовые или максимально-фазовые сигналы.
Моментный спектр 3-го порядка (биспектр) определяется соотношением

 это комплексная функция, обладающая такими же свойствами симметрии, что и введенный ранее биспектр Главное отличие биспектра от энергетического спектра состоит в том, что в нем сохраняется фазовая информация.
это комплексная функция, обладающая такими же свойствами симметрии, что и введенный ранее биспектр Главное отличие биспектра от энергетического спектра состоит в том, что в нем сохраняется фазовая информация.
Триспектр определяется соотношением

По спектрам высокого порядка можно восстановить спектры более низкого порядка

Моменты периодических сигналов. В общем случае к периодическим сигналам относят также детерминированные и случайные сигналы заданные на конечном интервале отсчетов в предположении о их периодическом продолжении за пределами этого интервала.
Пусть  действительный периодический сигнал, для которого существуют моменты высокого порядка, определяемые следующим выражением
действительный периодический сигнал, для которого существуют моменты высокого порядка, определяемые следующим выражением

где  оператор усреднения по времени
оператор усреднения по времени 
Если сигнал периодический с периодом  , то определение моментов высокого порядка несколько изменяется
, то определение моментов высокого порядка несколько изменяется

где  задан выражением (9.120).
задан выражением (9.120).
Дополнительное свойство периодических сигналов заключается в периодичности моментов

Рассмотрим специальные случаи моментов высокого порядка периодических сигналов.
Момент 1-го порядка (среднее значение)

Момент 2-го порядка (автокорреляция)

При  средняя мощность сигнала,
средняя мощность сигнала,  четная функция, удовлетворяющая условию
четная функция, удовлетворяющая условию 
Автокорреляцию можно определить через операцию круговой свертки

Очевидно, что  для любого целого
для любого целого 
Моменты 3-го порядка

Значение  является мерой несимметрии последовательности в пределах периода.
является мерой несимметрии последовательности в пределах периода.
Одномерные сечения моментов 3-го порядка определяются следующими выражениями:

Моменты 4-го порядка:

Одномерные сечения моментов 4-го порядка определяются следующими выражениями:

Очевидно, что, зная моменты высокого порядка периодических и импульсных сигналов, с помощью (9.98) можно найти их кумулянтные последовательности, но на практике ими пользуются очень редко.
Моментные спектры периодических сигналов. Пусть  действительный периодический сигнал с периодом
действительный периодический сигнал с периодом  имеющий моменты высокого порядка
имеющий моменты высокого порядка  .
.
В этом случае моментный спектр  порядка определяется как
порядка определяется как

где  — дискретные значения частот,
— дискретные значения частот,  в общем случае комплексная для
в общем случае комплексная для  и многомерная периодическая функция с периодом
и многомерная периодическая функция с периодом  .
.
Моментные спектры высокого порядка от периодических сигналов являются дискретными функциями с частотами  .
.
Как и в случае моментных спектров импульсных сигналов с конечной энергией, моментные спектры периодических сигналов могут быть выражены через их представления дискретным преобразованием Фурье

Моментный спектр  порядка получается из моментного спектра
порядка получается из моментного спектра  порядка соотношением
порядка соотношением

Наиболее часто на практике используется спектр мощности и моментные спектры 3-го и 4-го порядков Они являются частными случаями общего выражения для моментных спектров. Спектр мощности

Спектр мощности представляет собой периодическую последовательность действительных неотрицательных чисел и является четной функцией на дискретных частотах - Средняя мощность сигнала равна 

Моментный спектр 3-го порядка, или биспектр, имеет модуль и фазу, поскольку является комплексной функцией

Скалярная мера симметрии  периодического сигнала определяется для моментов 3-го порядка при
периодического сигнала определяется для моментов 3-го порядка при 

Моментный спектр 4-го порядка, или триспектр, имеет вид

Отсюда следуют выражения для сечений триспектра

Следовательно, триспектр включает в себя спектр мощности и биспектр сигнала. Мера «эксцентриситета» (0, 0, 0) периодического сигнала определяется выражением

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
- 7.3.4. Качество связи
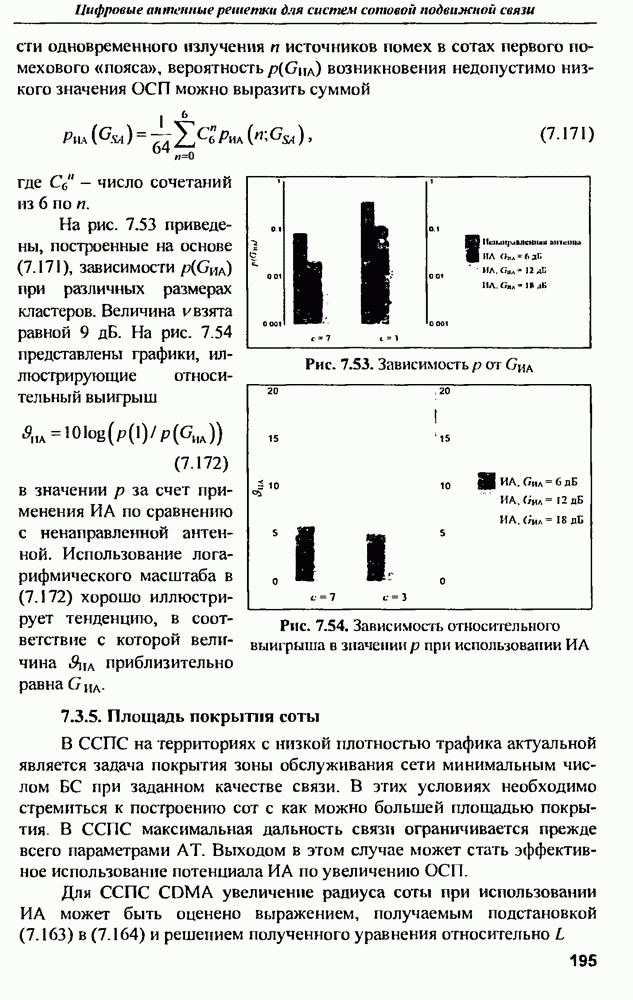
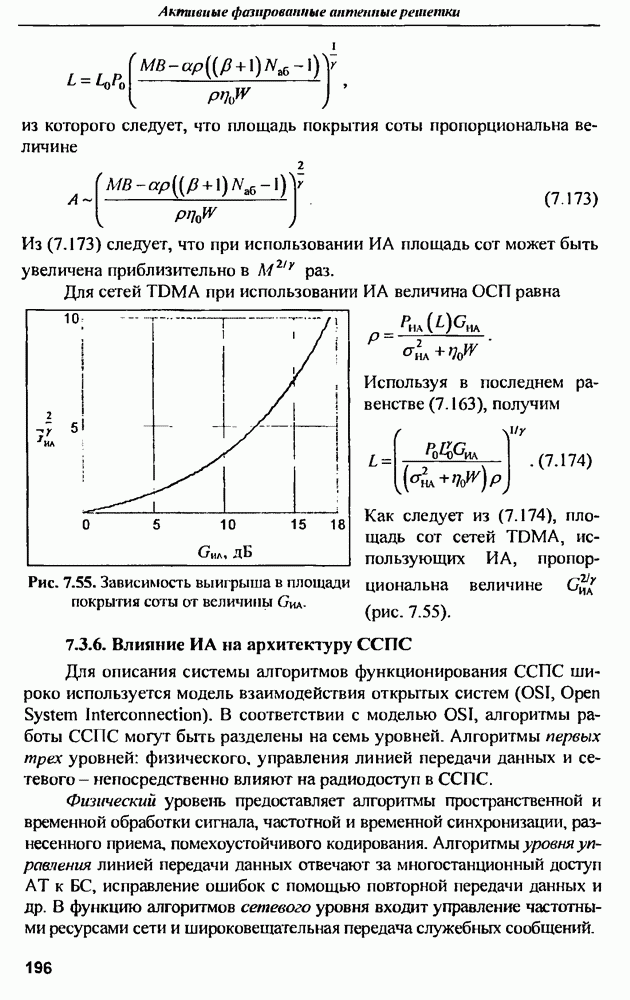
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
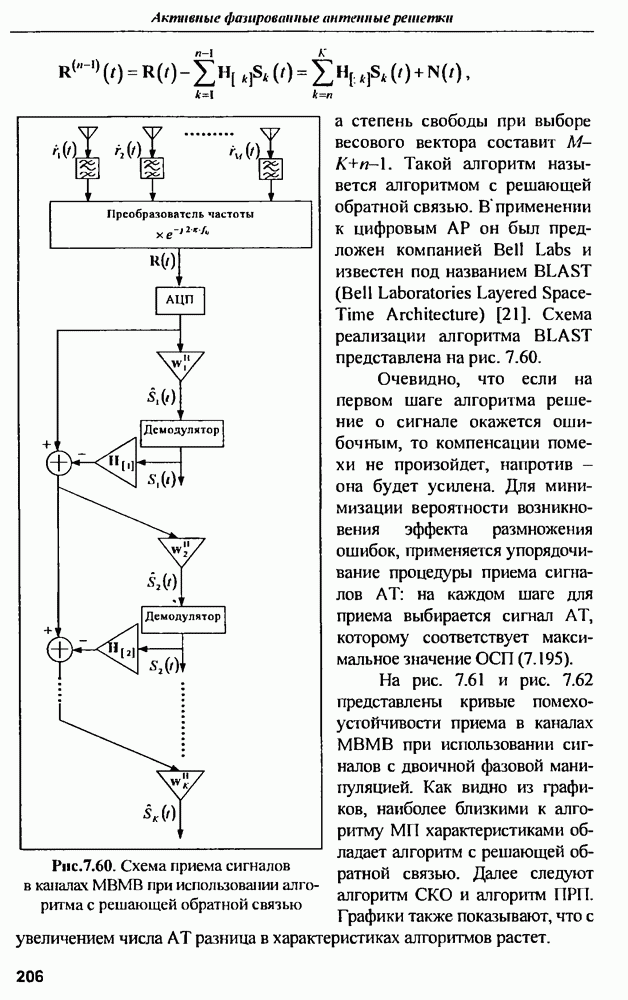
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
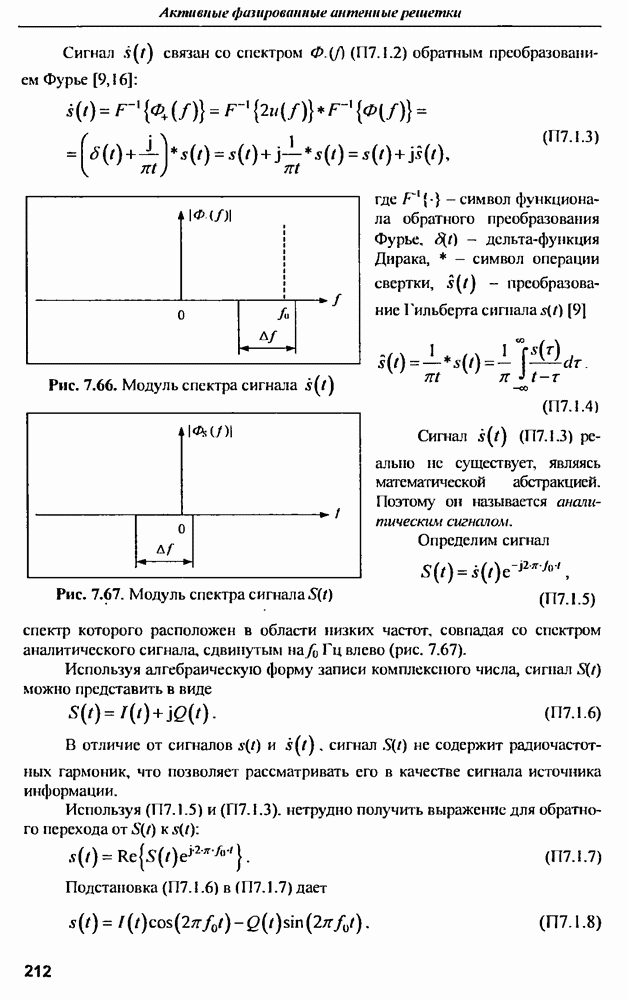
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
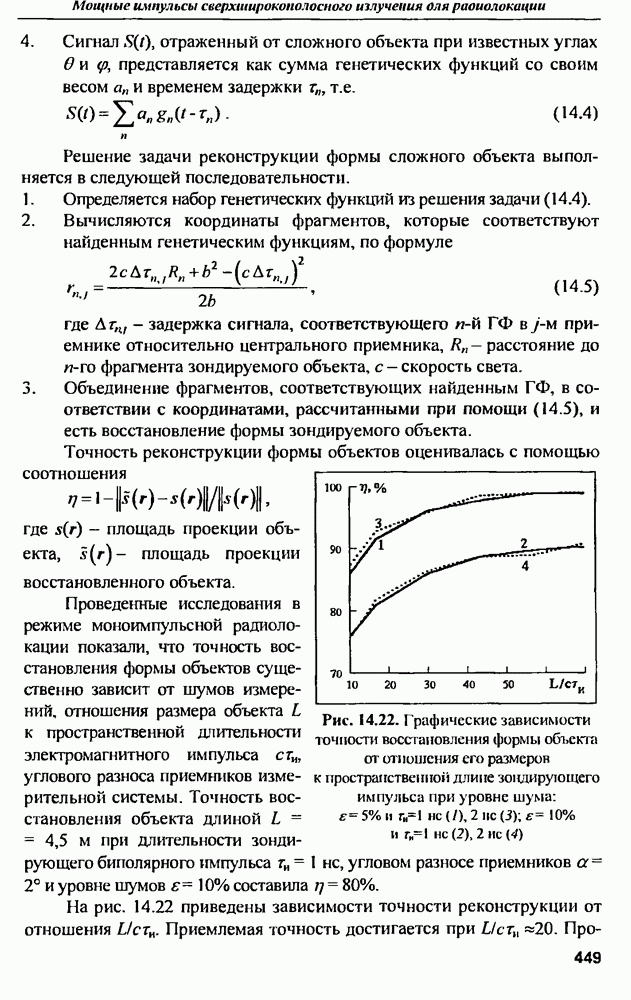
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
- 14.3. Комбинированные антенны
- 14.4. Антенные решетки
- 14.5. Приемные антенны
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
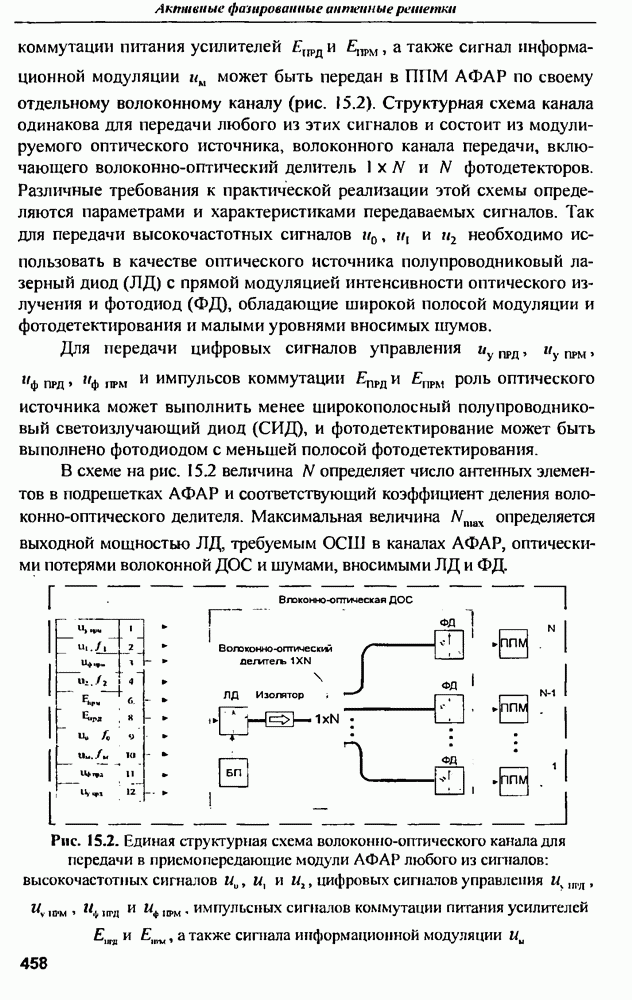
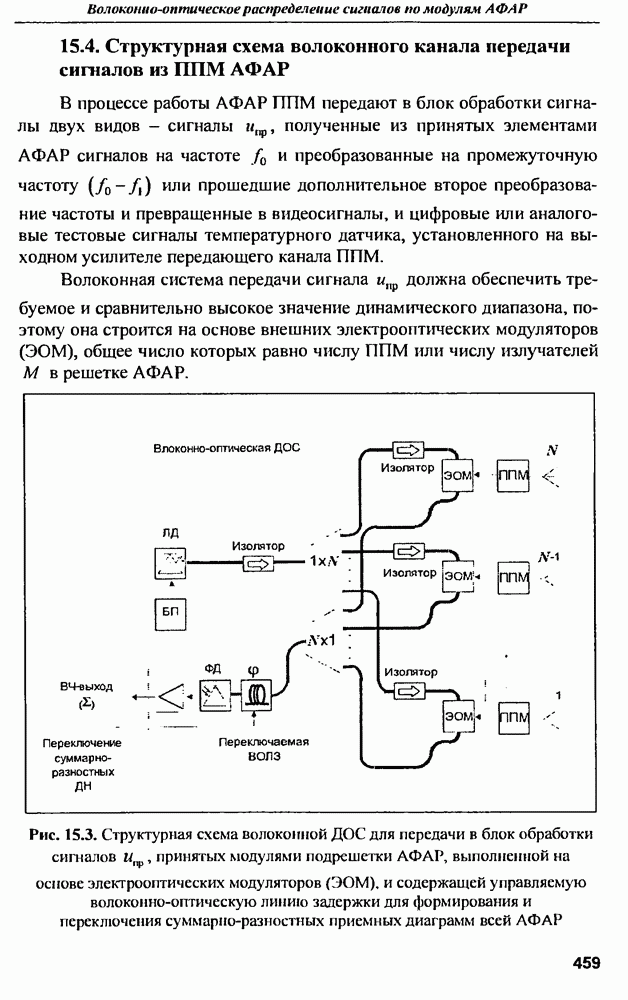
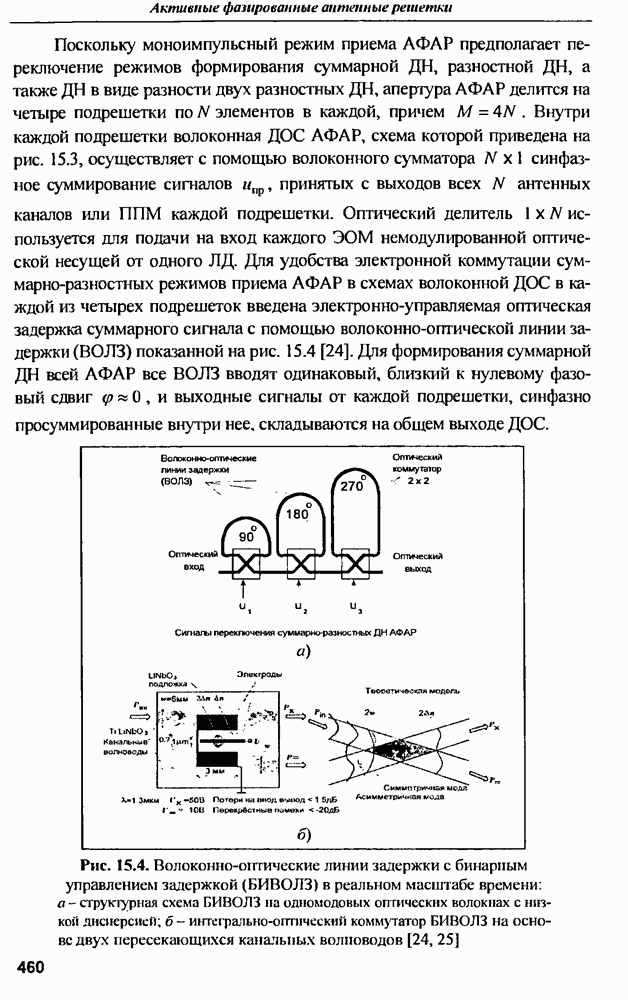
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
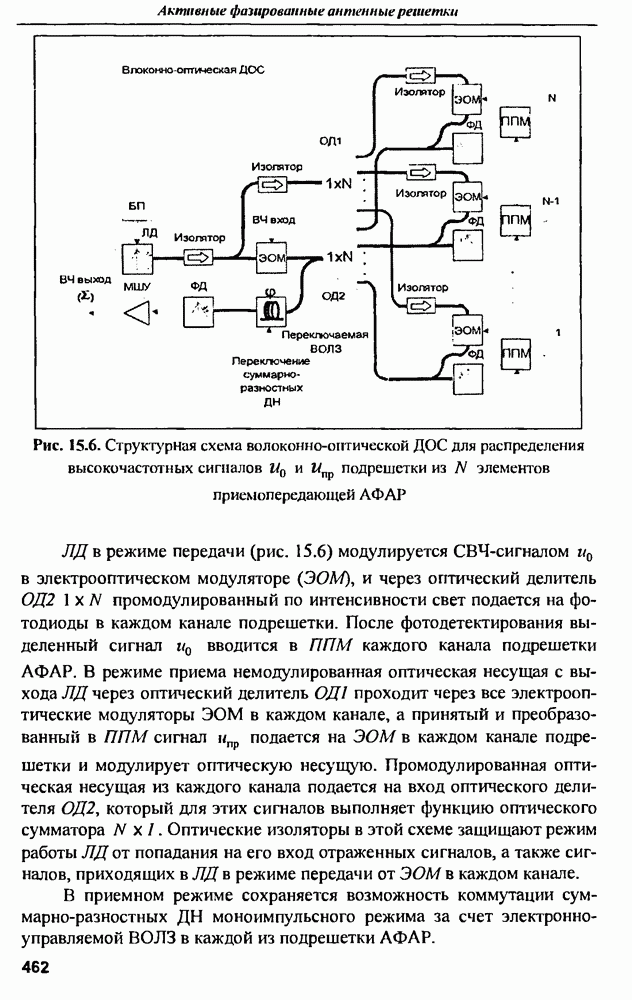
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
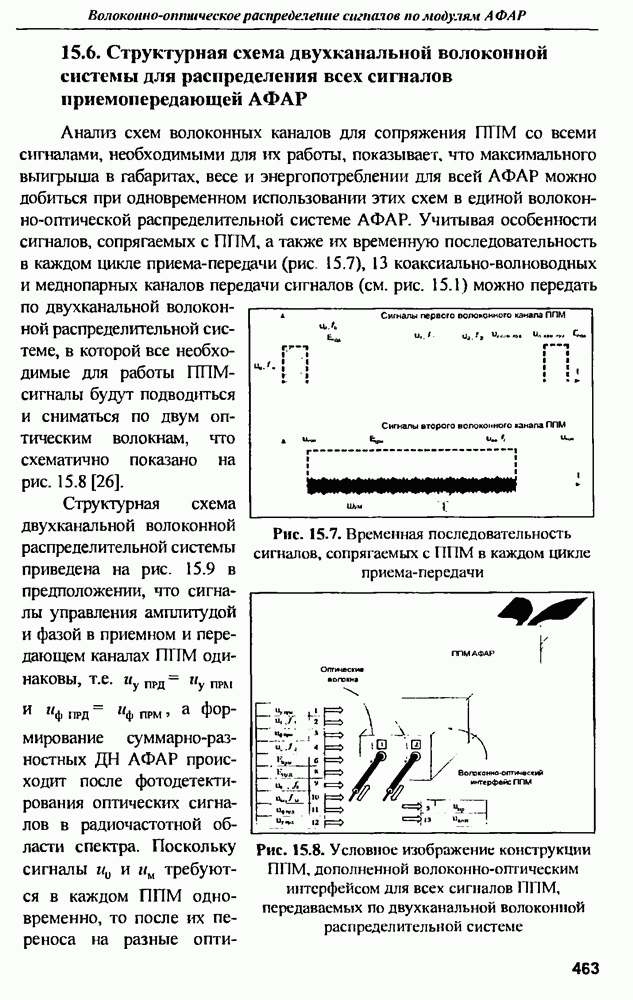
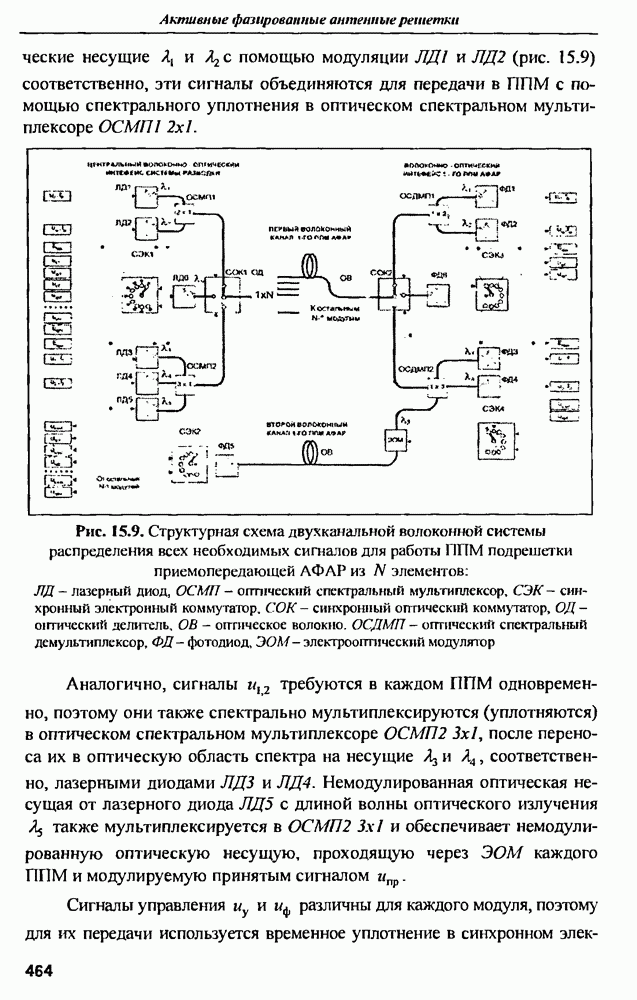
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
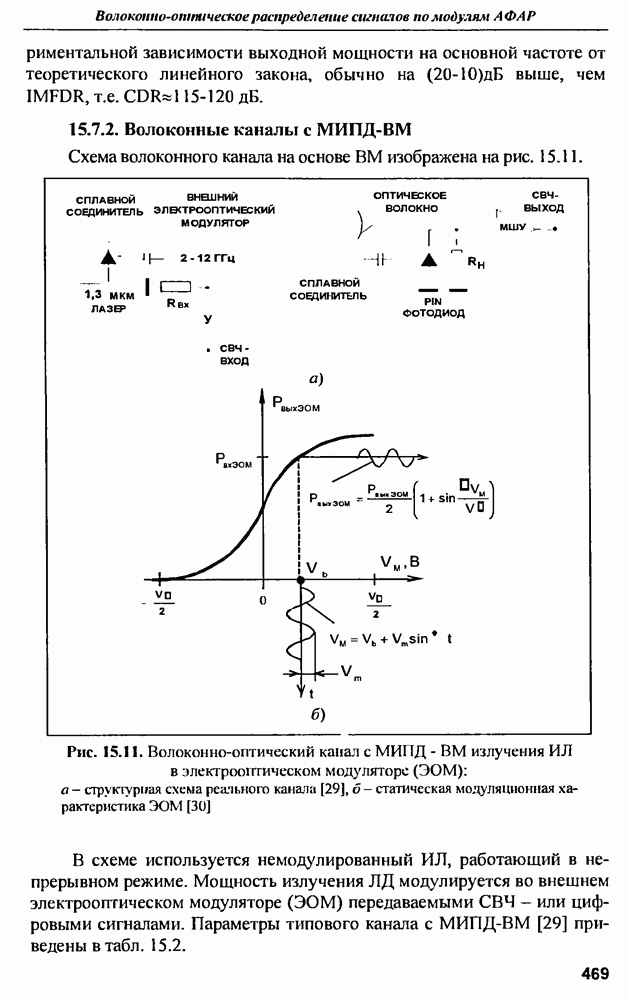
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
- 15.8.4. Оптические делители
- 15.8.5. Внешние модуляторы
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР