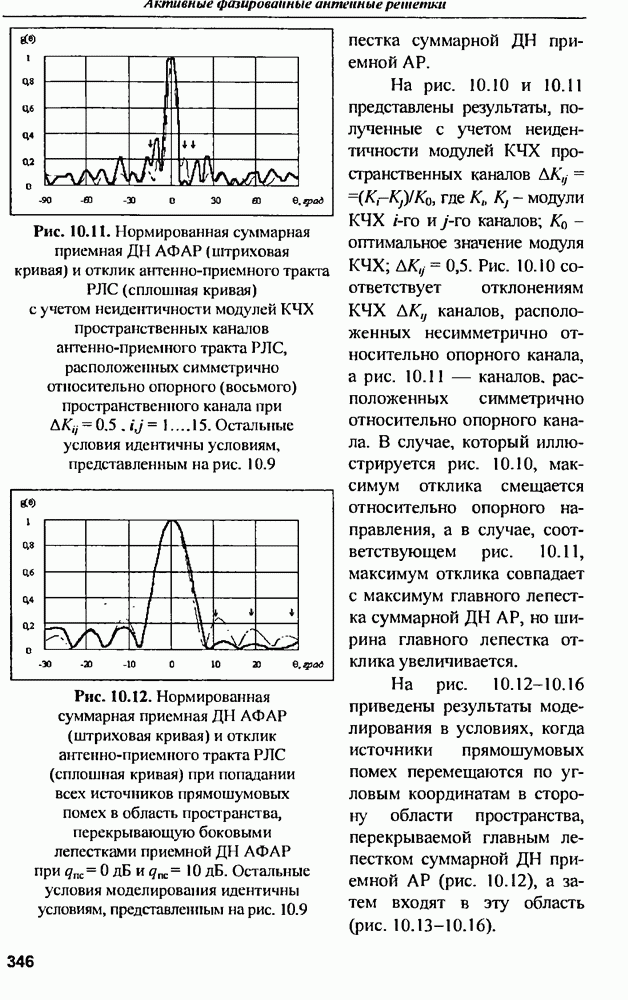
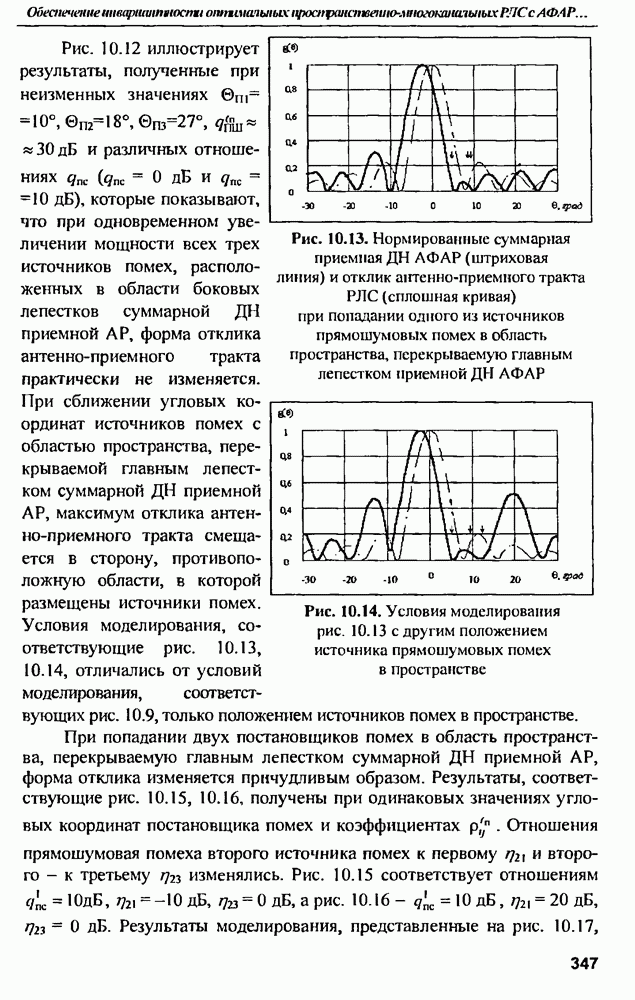
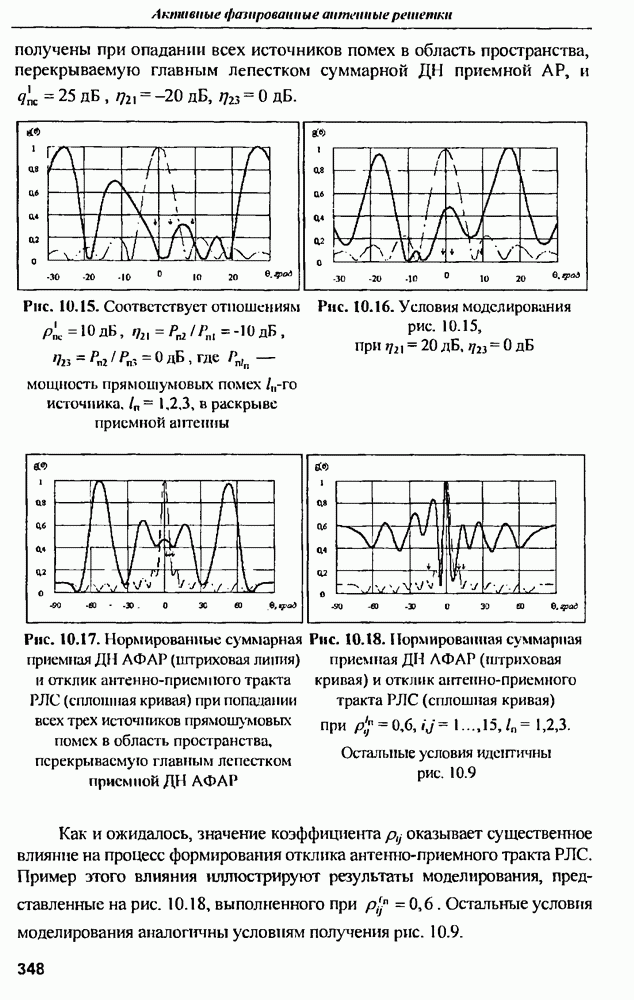
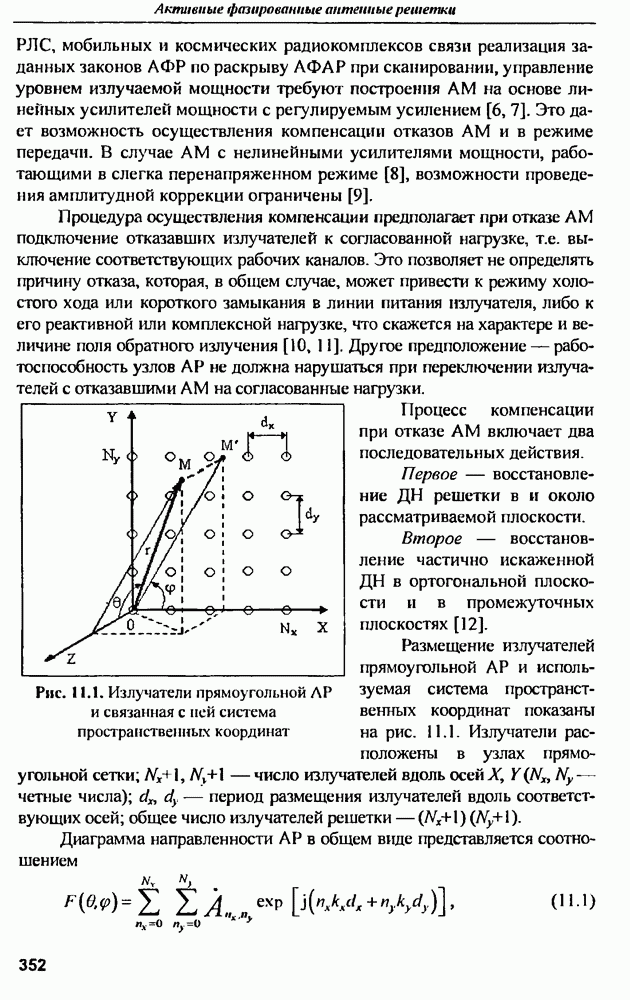
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.1.1. Методы теоретического расчета ЭПР
Значение теоретических расчетов ЭПР различных объектов заключается в возможности интерпретации результатов измерений близких по форме, но имеющих более сложную конфигурацию радиолокационных целей, и предсказании наиболее важных свойств ЭПР, используемых при обнаружении и идентификации целей.
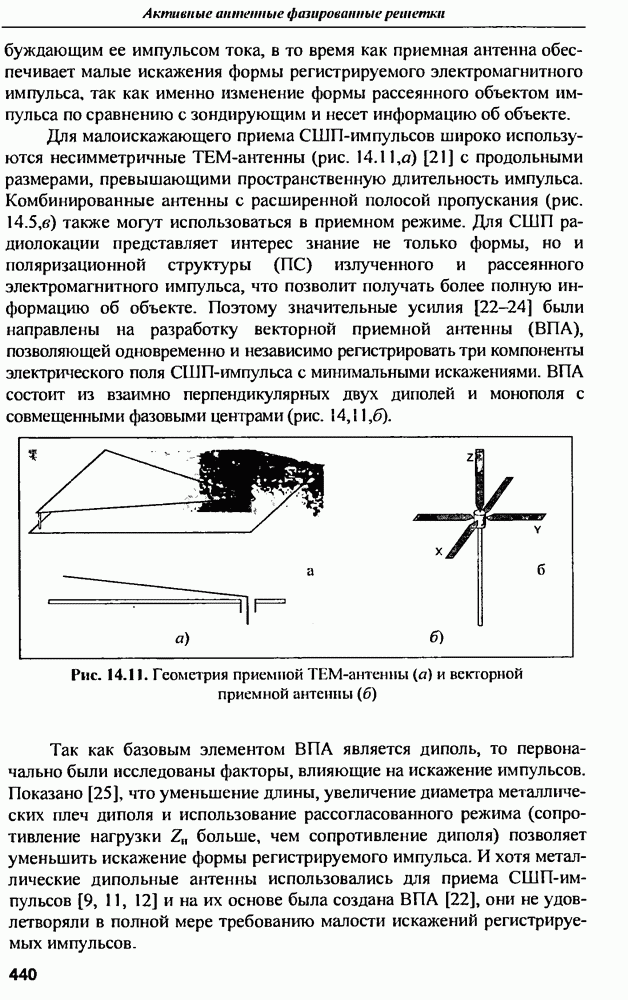
Особый интерес представляют ЭПР объектов правильной геометрической формы: сфера, цилиндр, конус, эллипсоид и т.д. С одной стороны, теоретические исследования ЭПР таких объектов позволяют более глубоко понять особенности рассеяния электромагнитных волн радиолокационными целями, имеющими сложную геометрическую конфигурацию, а с другой - реальные цели очень часто имеют форму, достаточно хорошо аппроксимируемую правильными геометрическими фигурами. Наибольший интерес в дальнейшем будет представлять не зависимость ЭПР от ракурса объекта относительно точки наблюдения, а ее изменение при использовании разных частот или длин волн электромагнитных колебаний. В дальнейшем зависимость ЭПР от частоты будем называть энергетической частотной характеристикой, или энергетическим спектром радиолокационной цели 
Обратное преобразование Фурье от энергетического спектра, как известно, дает автокорреляционную функцию (АКФ) импульсной характеристики цели

Что касается самой  цели
цели  то однозначно определить ее по энергетическому спектру или автокорреляционной функции удается не всегда, поскольку процедура факторизации
то однозначно определить ее по энергетическому спектру или автокорреляционной функции удается не всегда, поскольку процедура факторизации  требует введения некоторых предположений о характере поведения и свойствах
требует введения некоторых предположений о характере поведения и свойствах 
Тем не менее, поскольку выполняется равенство 

где  означает операцию свертки, в АКФ содержится много полезной информации об ИХ цели: эффективная длительность, скорость затухания огибающей, доминирующие частоты колебаний и т.д.
означает операцию свертки, в АКФ содержится много полезной информации об ИХ цели: эффективная длительность, скорость затухания огибающей, доминирующие частоты колебаний и т.д.
Возможны два пути теоретического расчета ЭПР цели: временной и частотный Оба эти метода должны дать одинаковый результат, а выбор конкретного метода зависит от решаемой задачи и геометрической формы объекта.
Временной метод расчета ЭПР требует нахождения численного решения интегро-дифференциального пространственно-временного уравнения, удовлетворяющего граничным условиям на поверхности объекта для электрической или магнитной компоненты поля, при этом возбуждающий сигнал должен представлять собой достаточно короткий импульс без несущей частоты [4].
Традиционный частотный метод расчета ЭПР [6, 7] заключается в определении рассеянной волны при облучении объекта стационарным гармоническим полем определенной частоты. Проводя этот расчет для разных частот во всем диапазоне частотного изменения ЭПР, получаем интересующий нас энергетический спектр цели. Теоретическое определение ЭПР в частотной области также возможно путем решения уравнений Максвелла для граничных условий применительно к соответствующему телу в случае стационарного гармонического колебания электромагнитного поля. Здесь можно отметить фундаментальный математический метод точного решения, заключающийся в разделении переменных и составлении интегрального уравнения, однако разделение переменных возможно лишь в нескольких особых случаях, когда переменные в волновом уравнении удается разделить за счет использования системы координат, одна из координатных плоскостей которой совпадает с поверхностью тела. К этим случаям относятся такие геометрические формы, как сфера, сфероид, тор, а также полубесконечные поверхности: полуплоскость, коническая поверхность, параболоид и т.д.
Численное решение задачи рассеяния в частотной области основано на представлении поля интегралом Чу-Стреттона [3]. Однако основной сложностью метода является определение в общем виде поверхностных токов на теле, имеющем достаточно сложную форму и большие
габариты по сравнению с длиной волны. На практике чаще используют приближенные теории геометрической оптики, физической оптики и геометрической теории дифракции [6]
Энергетические спектры радиолокационных целей, рассчитанные частотными методами, не позволяют однозначно определять импульсную характеристику цели, так как не содержат фазо-частотной характеристики, т.е. в них отсутствует информация о взаимном расположении во времени гармоник образующих короткий импульсный отклик цели на нестационарное возбуждение. Тем не менее автокорреляционная функция цели, являющаяся обратным преобразованием Фурье от энергетического спектра цели, несет довольно много информации о геометрической форме рассеивающего тела Таким образом, временные методы расчета ЭПР цели являются более информативными с точки зрения распознавания целей в сверхширокополосной радиолокации.
Временной метод расчета ЭПР заключается в решении уравнений Максвелла дня граничных условий, определяемых материалом и геометрической формой объекта. В частности предположим, что объект имеет абсолютно проводящую поверхность  и облучается нестационарным электромагнитным импульсом (рис. 9.2), электрическое поле которого на поверхности объекта описывается выражением
и облучается нестационарным электромагнитным импульсом (рис. 9.2), электрическое поле которого на поверхности объекта описывается выражением

где  вектор, определяющий поляризацию падающей волны; k - вектор единичной длины, определяющий направление распространения волны;
вектор, определяющий поляризацию падающей волны; k - вектор единичной длины, определяющий направление распространения волны;  - вектор, определяющий положение точки на объекте в системе координат, связанной с объектом; с - скорость распространения электромагнитной волны в вакууме;
- вектор, определяющий положение точки на объекте в системе координат, связанной с объектом; с - скорость распространения электромагнитной волны в вакууме;  временная функция падающего электромагнитного импульса. Облучающий импульс не имеет несущей частоты и обладает достаточно короткой длительностью, те является нестационарным сверхширокополосным сигналом.
временная функция падающего электромагнитного импульса. Облучающий импульс не имеет несущей частоты и обладает достаточно короткой длительностью, те является нестационарным сверхширокополосным сигналом.

Рис. 9.2. Рассеяние электромагнитной волны объектом
Падающее электромагнитное поле возбудит ток, плотность которого на поверхности объекта  в свою очередь формирует рассеянное электромагнитное поле, электрическая компонента которого в точке наблюдения
в свою очередь формирует рассеянное электромагнитное поле, электрическая компонента которого в точке наблюдения  (рис. 9.2)
(рис. 9.2)  определяется производной по времени векторного потенциала поля и градиентом скалярного потенциала
определяется производной по времени векторного потенциала поля и градиентом скалярного потенциала

где векторный потенциал

 расстояние от объекта до точки наблюдения; скалярный потенциал
расстояние от объекта до точки наблюдения; скалярный потенциал

плотность поверхностного заряда

В случае рассеивателя с абсолютно проводящей поверхностью  граничными условиями, выполнение которых позволит определить пространственно-временное распределение плотности тока
граничными условиями, выполнение которых позволит определить пространственно-временное распределение плотности тока  на поверхности объекта, является равенство нулю тангенциальной (касательной) составляющей производной по времени суммарной электрической компоненты электромагнитного поля в любой точке на поверхности объекта в любой момент времени
на поверхности объекта, является равенство нулю тангенциальной (касательной) составляющей производной по времени суммарной электрической компоненты электромагнитного поля в любой точке на поверхности объекта в любой момент времени

Электрическая компонента рассеянного поля  на поверхности объекта определяется предельным переходом выражения для рассеянного поля в любой точке пространства на расстоянии
на поверхности объекта определяется предельным переходом выражения для рассеянного поля в любой точке пространства на расстоянии  от объекта путем устремления этой точки на поверхность объекта, т.е.
от объекта путем устремления этой точки на поверхность объекта, т.е.  . В результате получим пространственно-временное интегро-дифференциальное уравнение, неизвестной величиной в котором является пространственно-временное распределение плотности тока
. В результате получим пространственно-временное интегро-дифференциальное уравнение, неизвестной величиной в котором является пространственно-временное распределение плотности тока  на поверхности
на поверхности  объекта
объекта

причем из (9.9) и (9.10) следует, что производная по времени скалярного потенциала определяется как

Обозначая операции дивергенции и градиента через оператор набла, получим

Полученное уравнение является интегральным уравнением 1-го рода и может быть решено численным интегрированием с помощью компьютера путем дискретизации функций времени  и разбиения поверхности
и разбиения поверхности  на элементарные сегменты
на элементарные сегменты  Далее составляется разностное уравнение в явной форме, согласно которому плотность тока в центре каждого сегмента поверхности в данный момент времени определяется падающим полем в этой точке в данное время и найденными ранее плотностями тока в центрах остальных сегментов в предыдущие моменты времени [8].
Далее составляется разностное уравнение в явной форме, согласно которому плотность тока в центре каждого сегмента поверхности в данный момент времени определяется падающим полем в этой точке в данное время и найденными ранее плотностями тока в центрах остальных сегментов в предыдущие моменты времени [8].
Важным моментом является выбор интервала дискретизации  по времени и по пространству, поскольку это определяет точность численного решения и требования к объему памяти и быстродействию компьютера. Можно выбрать
по времени и по пространству, поскольку это определяет точность численного решения и требования к объему памяти и быстродействию компьютера. Можно выбрать  исходя из длительности падающего нестационарного импульса, например, 10% от эффективной длительности импульса. Тогда дискретизация поверхности объекта проводится так, чтобы за интервал дискретизации по времени волна в среде, окружающий объект, прошла путь между центрами соседних сегментов поверхности.
исходя из длительности падающего нестационарного импульса, например, 10% от эффективной длительности импульса. Тогда дискретизация поверхности объекта проводится так, чтобы за интервал дискретизации по времени волна в среде, окружающий объект, прошла путь между центрами соседних сегментов поверхности.
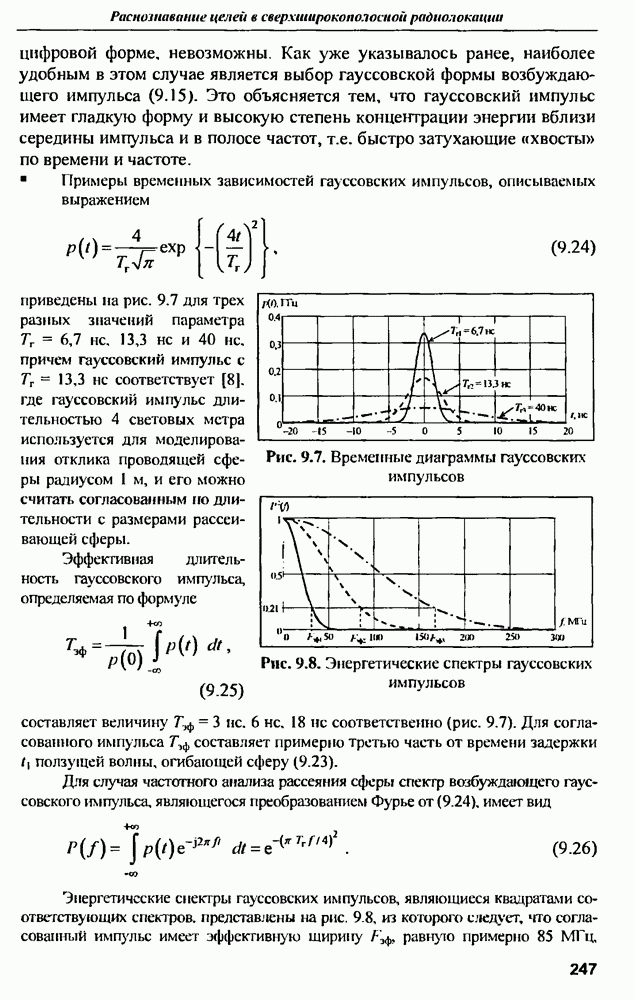
Для численного решения уравнения необходимо задаться импульсом  имеющим гладкую форму, поскольку требуется его дифференцирование. Наиболее удобной является гауссовская форма:
имеющим гладкую форму, поскольку требуется его дифференцирование. Наиболее удобной является гауссовская форма:

Если провести предельный переход  то приведенный гауссовский импульс приобретет свойства функции с площадью, равной
то приведенный гауссовский импульс приобретет свойства функции с площадью, равной  На практике
На практике  необходимо выбирать исходя из размеров рассеивающего объекта так, чтобы за время длительности импульса
необходимо выбирать исходя из размеров рассеивающего объекта так, чтобы за время длительности импульса  волна в среде обошла достаточно малую часть поверхности объекта. Присутствие операции производной по времени импульса падающего поля в выражении (9.14) накладывает существенные ограничения на форму этого импульса. В частности, не допустимо использование таких сигналов, которые имеют разрывы, например, импульсы или ступенчатые функции, которые непосредственно и определяют
волна в среде обошла достаточно малую часть поверхности объекта. Присутствие операции производной по времени импульса падающего поля в выражении (9.14) накладывает существенные ограничения на форму этого импульса. В частности, не допустимо использование таких сигналов, которые имеют разрывы, например, импульсы или ступенчатые функции, которые непосредственно и определяют  цели.
цели.
С другой стороны, для получения численного решения для  цели необходимо провести операцию обращения свертки, или деконволюции, решения для отклика цели на гауссовский импульс. Эта операция требует проведения деления спектров Фурье импульсов реакции и воздействия. что может сопровождаться появлением искажений, вызванных конечной точностью численных расчетов в компьютере. В связи с этим произведем модификацию алгоритма расчета поверхностных токов (9 14) путем интегрирования по времени правой и левой частей уравнения (9.14), что соответствует требованию равенства нулю тангенциальной составляющей суммарной электрической компоненты поля на идеально проводящей поверхности объекта
цели необходимо провести операцию обращения свертки, или деконволюции, решения для отклика цели на гауссовский импульс. Эта операция требует проведения деления спектров Фурье импульсов реакции и воздействия. что может сопровождаться появлением искажений, вызванных конечной точностью численных расчетов в компьютере. В связи с этим произведем модификацию алгоритма расчета поверхностных токов (9 14) путем интегрирования по времени правой и левой частей уравнения (9.14), что соответствует требованию равенства нулю тангенциальной составляющей суммарной электрической компоненты поля на идеально проводящей поверхности объекта 

Получив численное решение для пространственно-временного распределения плотности тока на поверхности объекта и подставив его в выражение (9.7) для электрической компоненты поля в точке наблюдения  получим реакцию радиолокационной цели на короткий импульс, т.е.
получим реакцию радиолокационной цели на короткий импульс, т.е.  объекта
объекта 
Полученное численное решение для плотности тока можно использовать и для расчета магнитной компоненты электромагнитного поля, рассеянного объектом, в точке наблюдения  (рис. 9.2)
(рис. 9.2)

Если точка наблюдения  находится в дальней зоне, выражение для магнитной компоненты поля можно упростить [8]
находится в дальней зоне, выражение для магнитной компоненты поля можно упростить [8]

где  единичный вектор в направлености точки наблюдения.
единичный вектор в направлености точки наблюдения.
Зная магнитную компоненту поля, определяем и электрическую компоненту поля в дальней зоне с помощью выражения

где  характеристическое сопротивление среды, окружающей рассеиватель.
характеристическое сопротивление среды, окружающей рассеиватель.
Далее с помощью (9.5) найдем автокорреляционную функцию объекта  преобразование Фурье от которой, т.е. спектр в частотной области, представляет зависимость эффективной поверхности цели от частоты
преобразование Фурье от которой, т.е. спектр в частотной области, представляет зависимость эффективной поверхности цели от частоты  Поскольку
Поскольку  является четной функцией с максимумом при
является четной функцией с максимумом при  то ЭПР цели представляет собой четную действительную функцию частоты.
то ЭПР цели представляет собой четную действительную функцию частоты.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
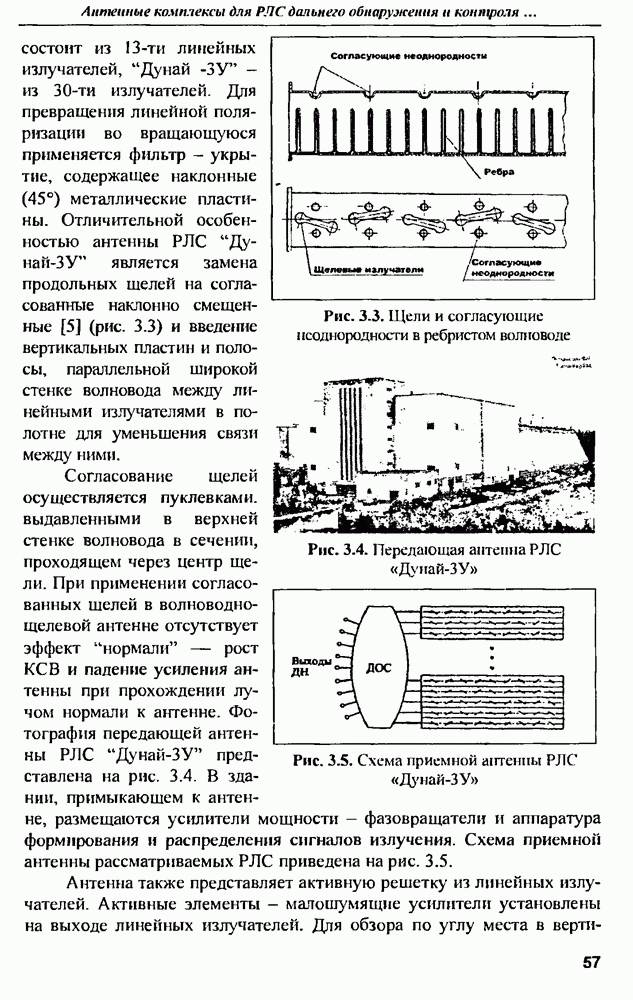
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
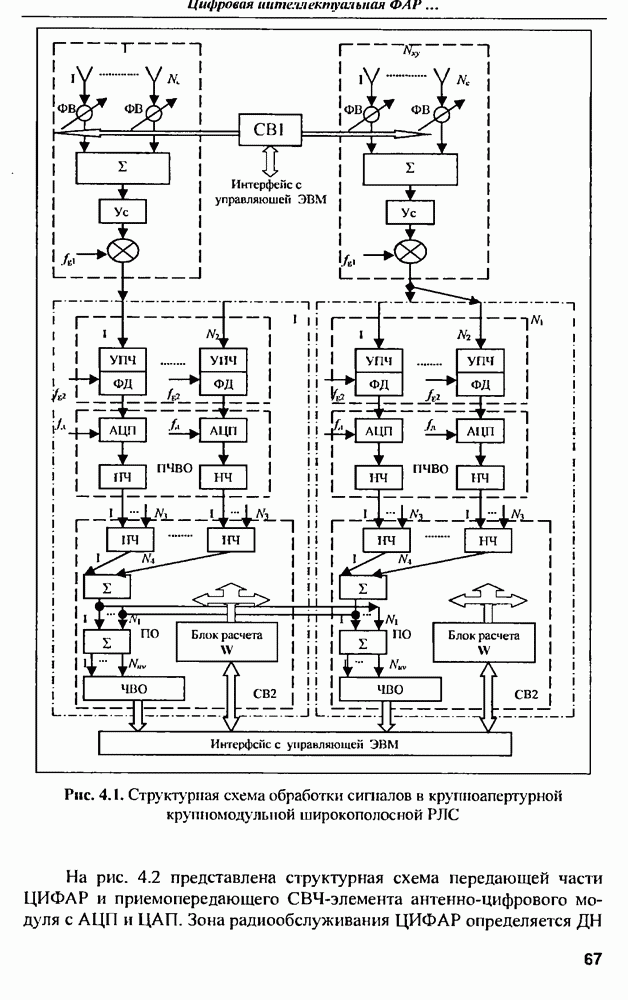
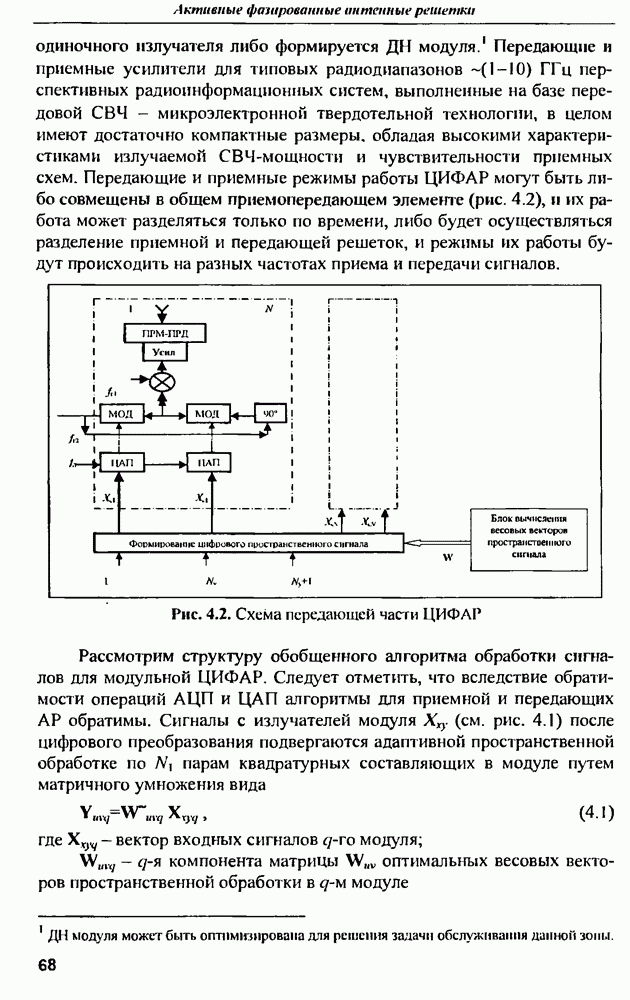
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
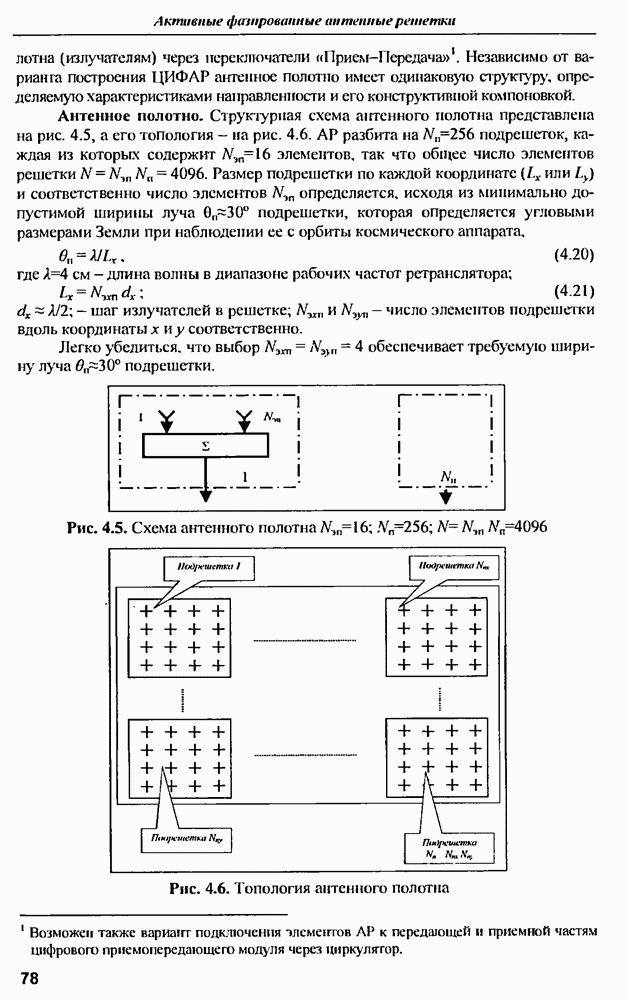
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
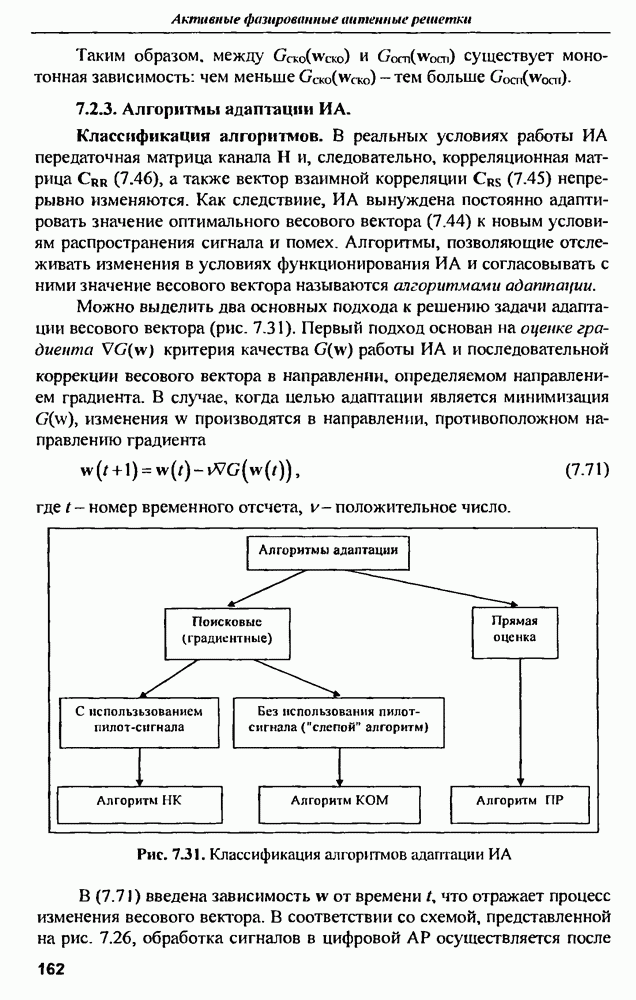
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
- 7.3.4. Качество связи
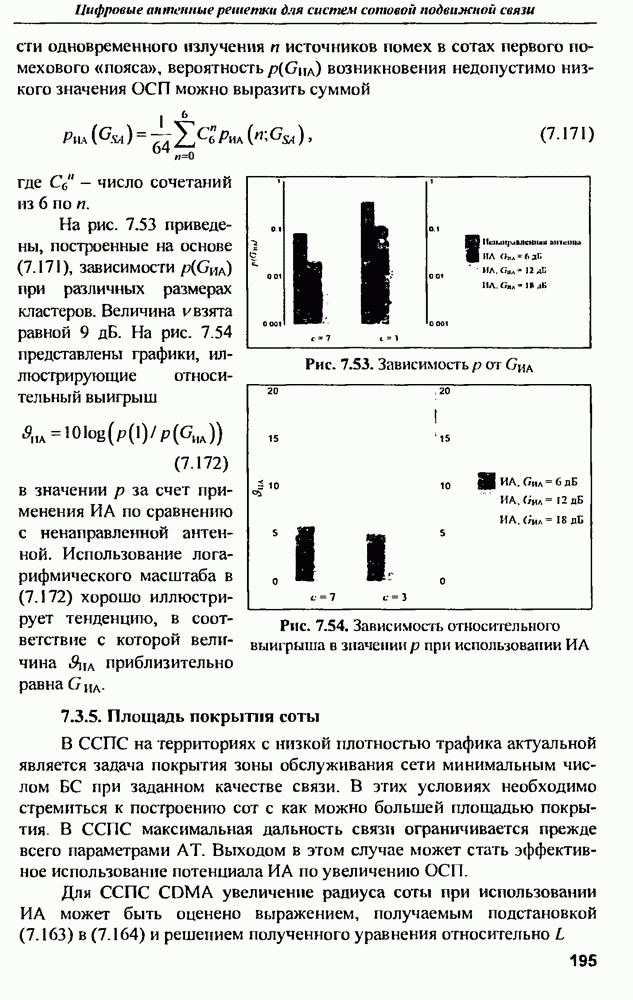
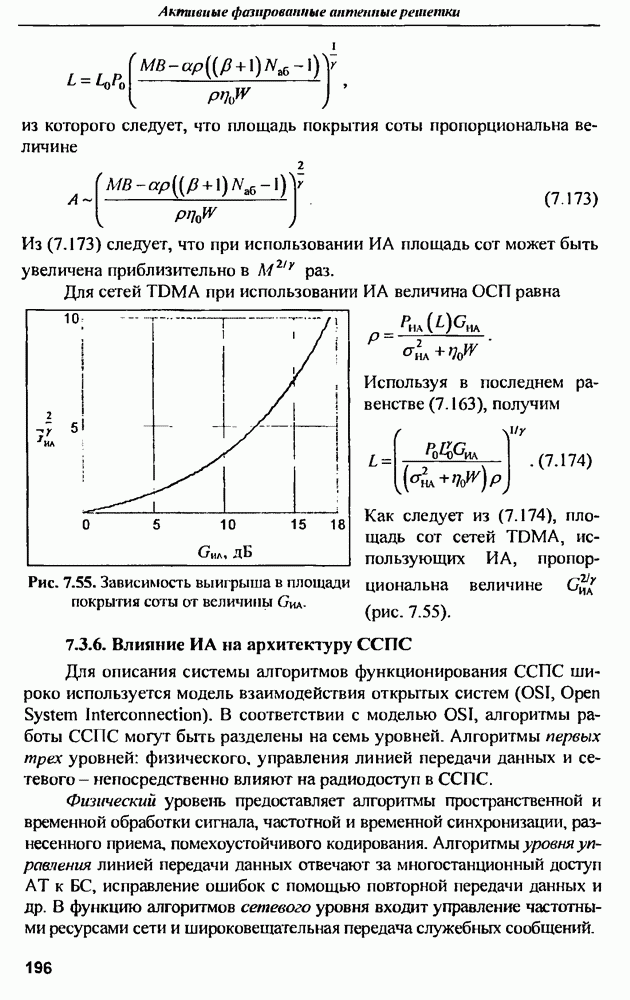
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
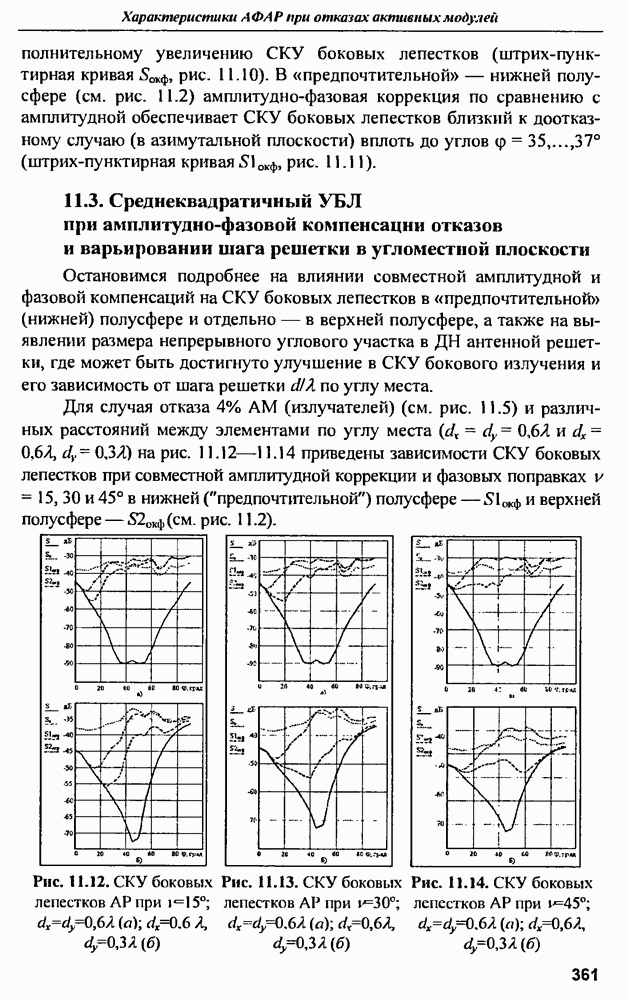
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
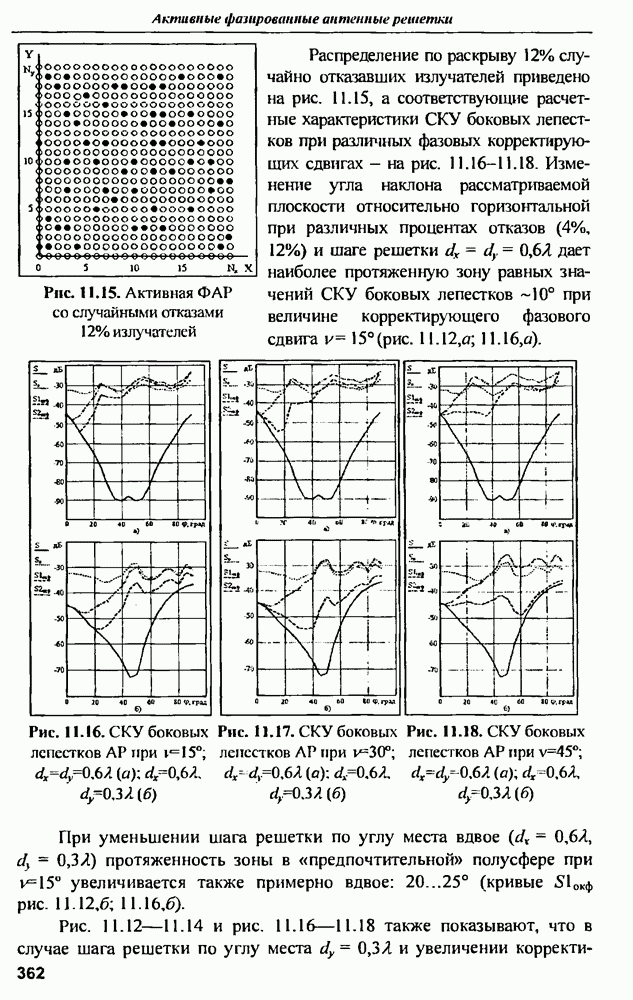
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
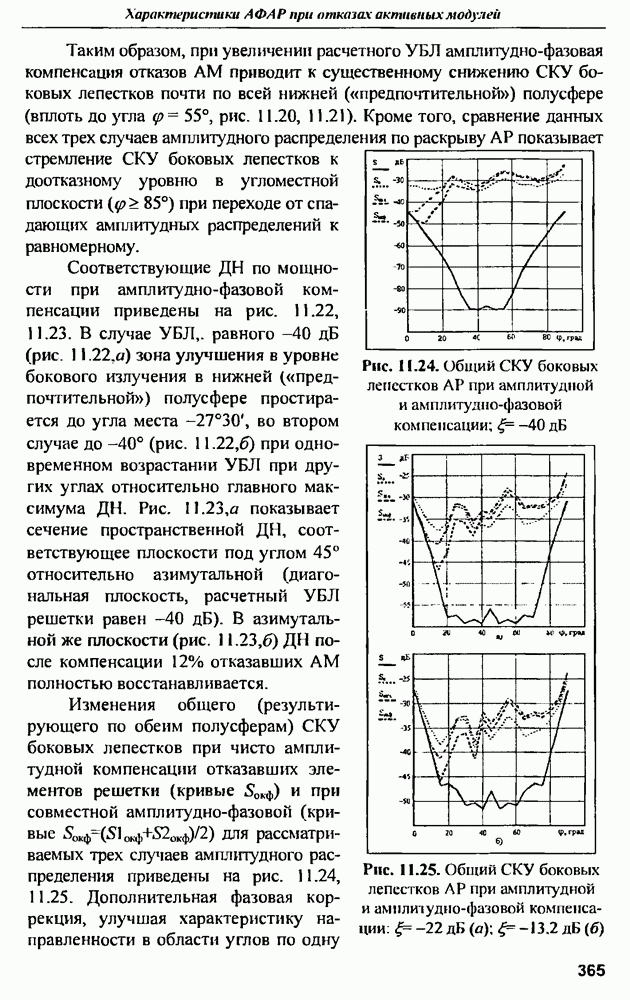
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
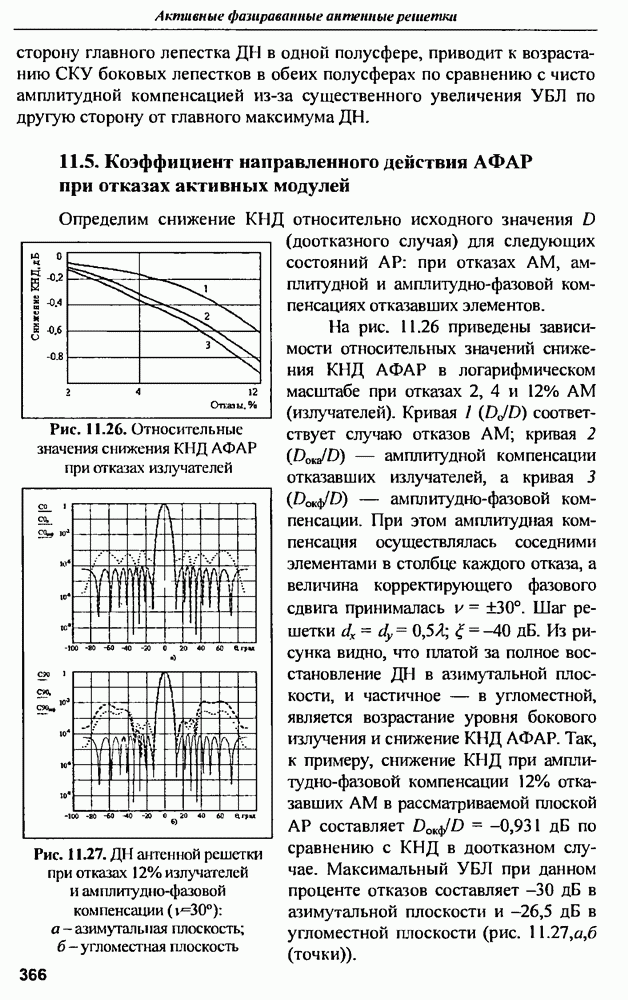
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
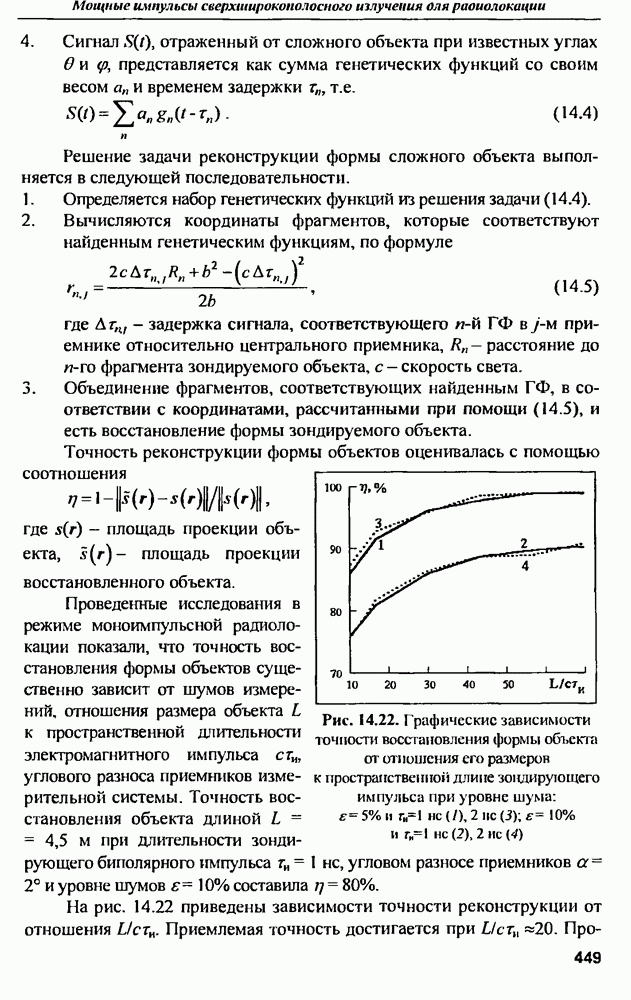
- 14.2. Синтез сверхширокополосных антенн
- 14.3. Комбинированные антенны
- 14.4. Антенные решетки
- 14.5. Приемные антенны
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
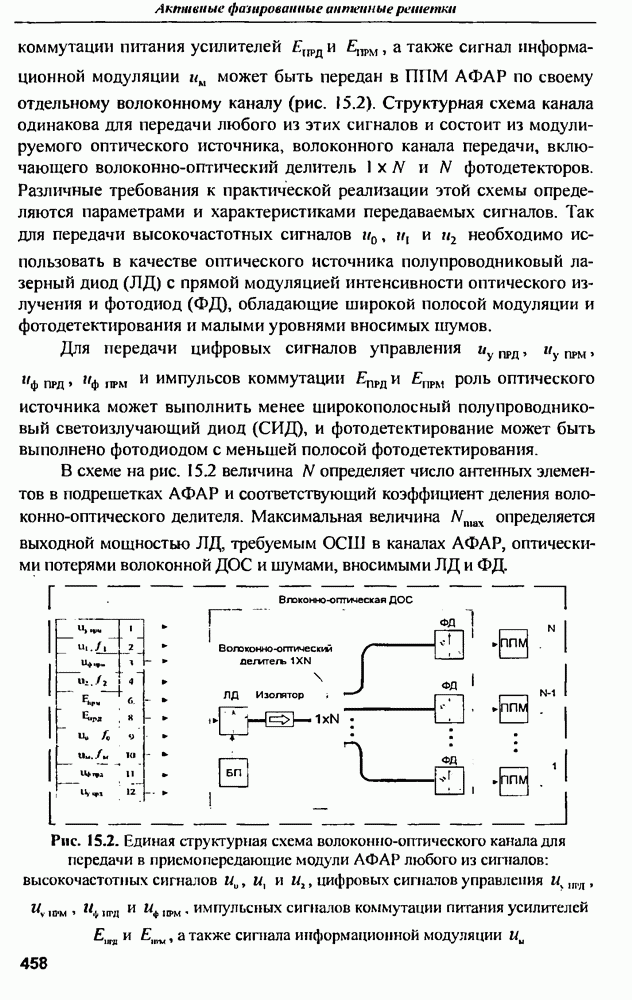
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
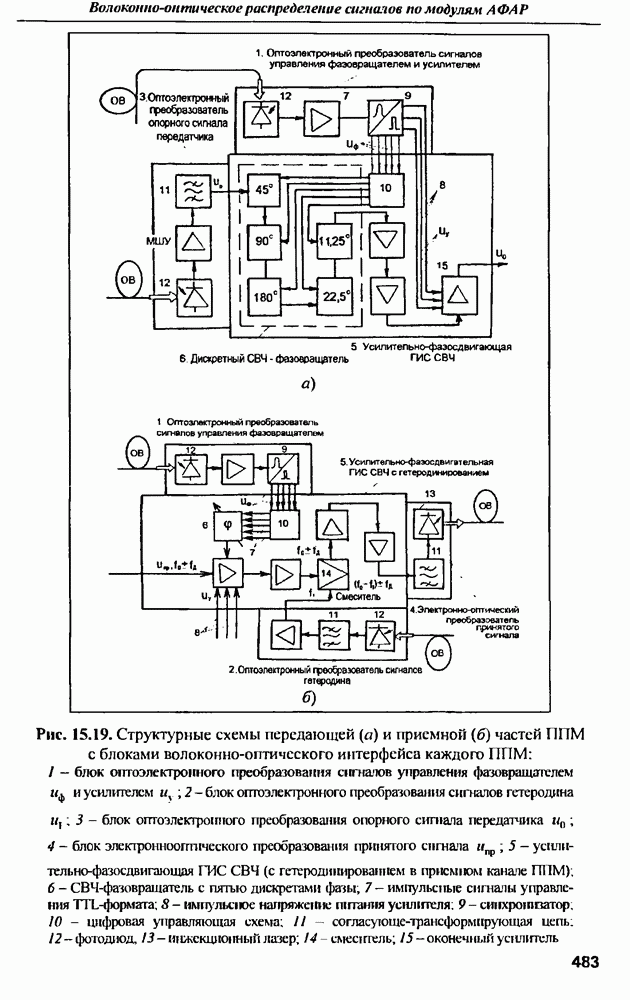
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
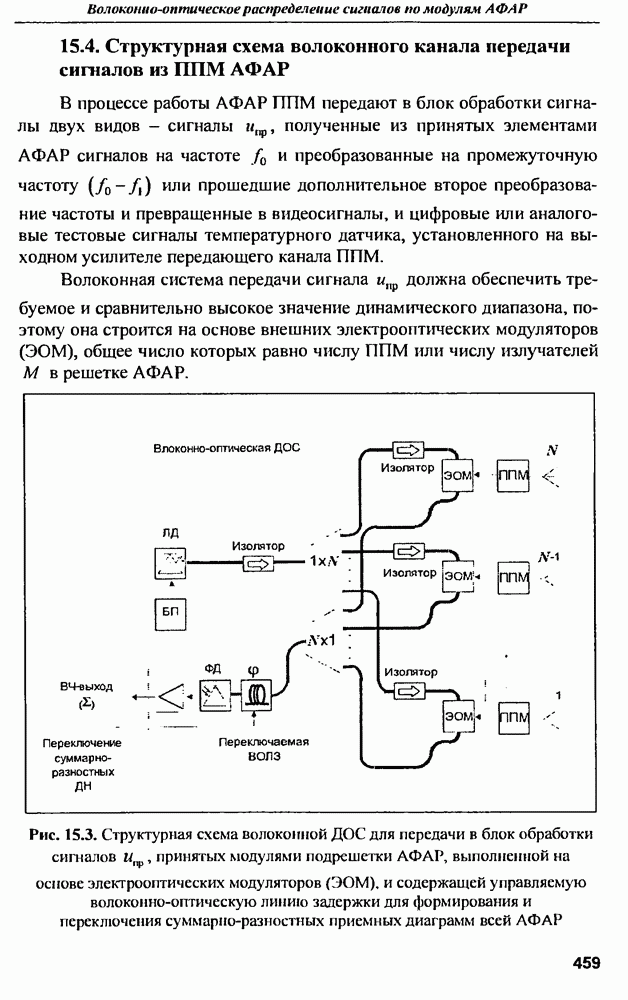
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
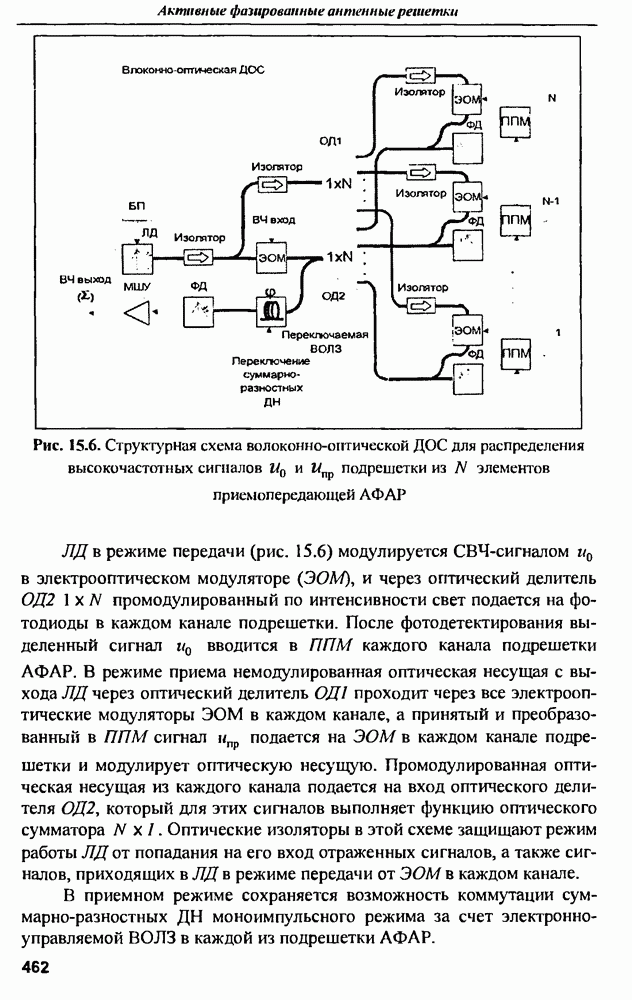
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
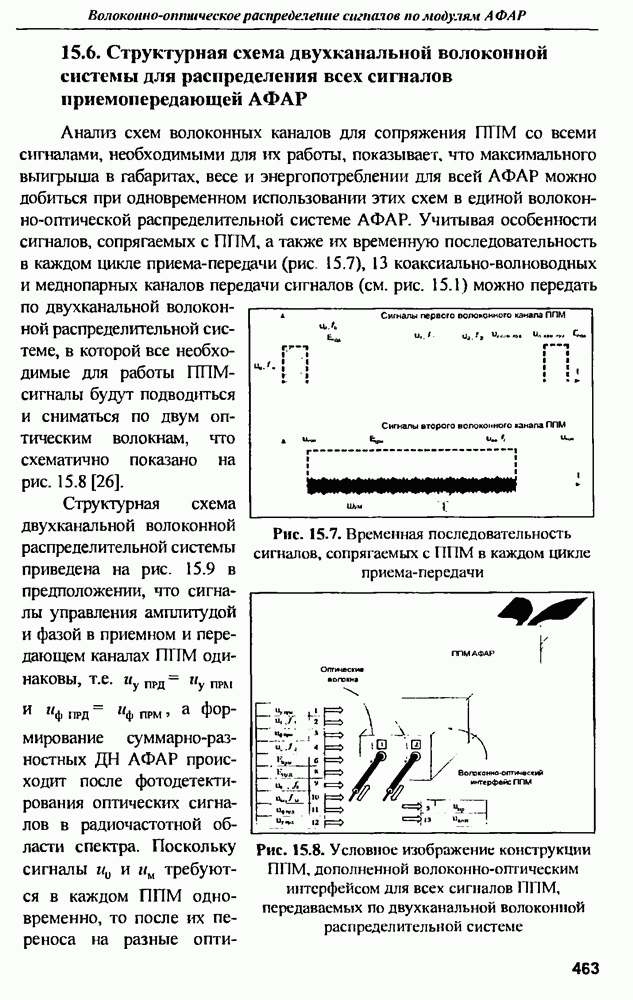
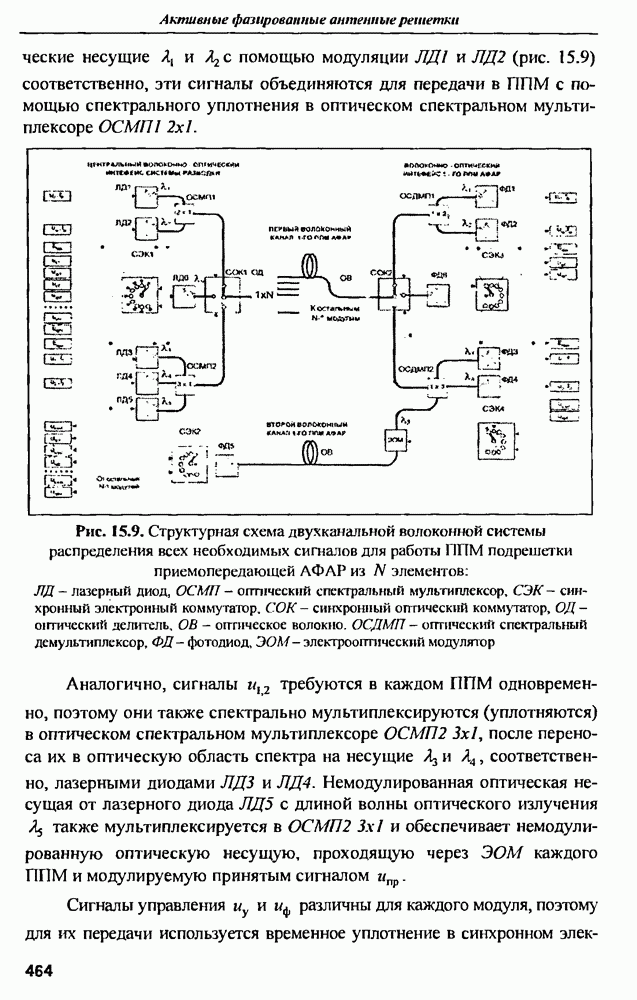
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
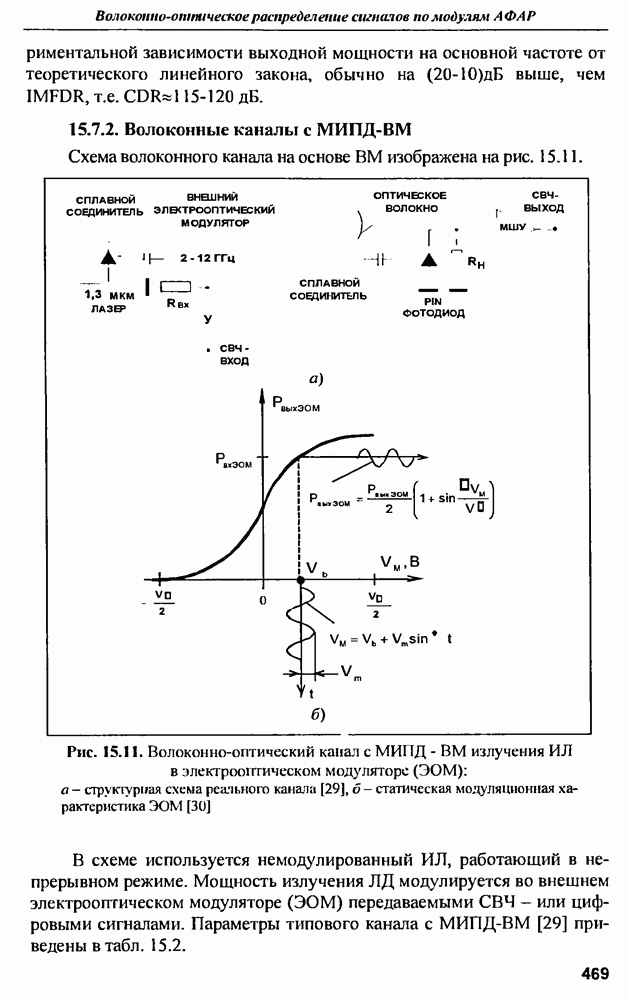
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
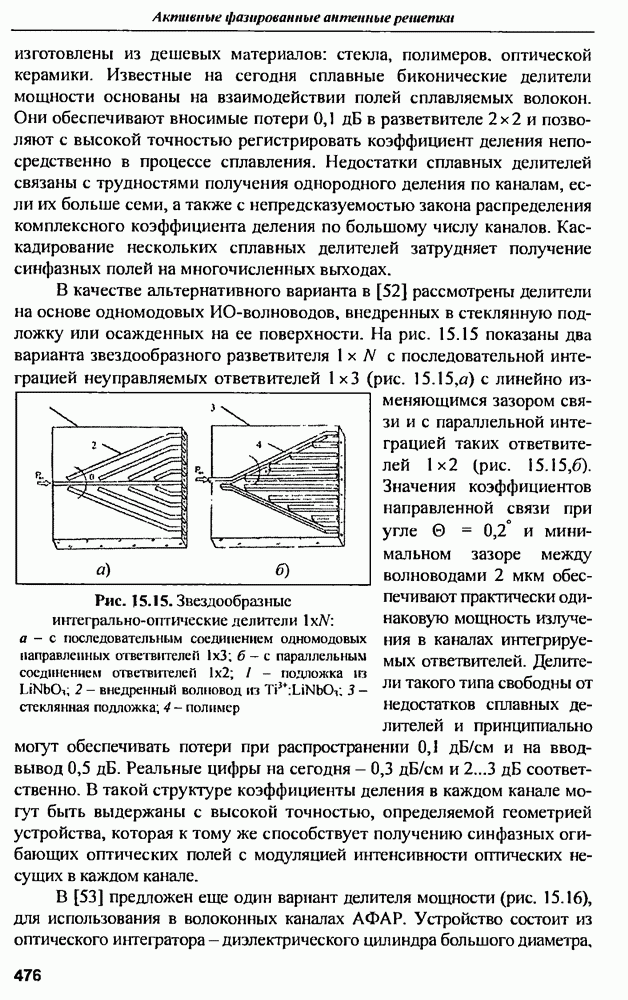
- 15.8.4. Оптические делители
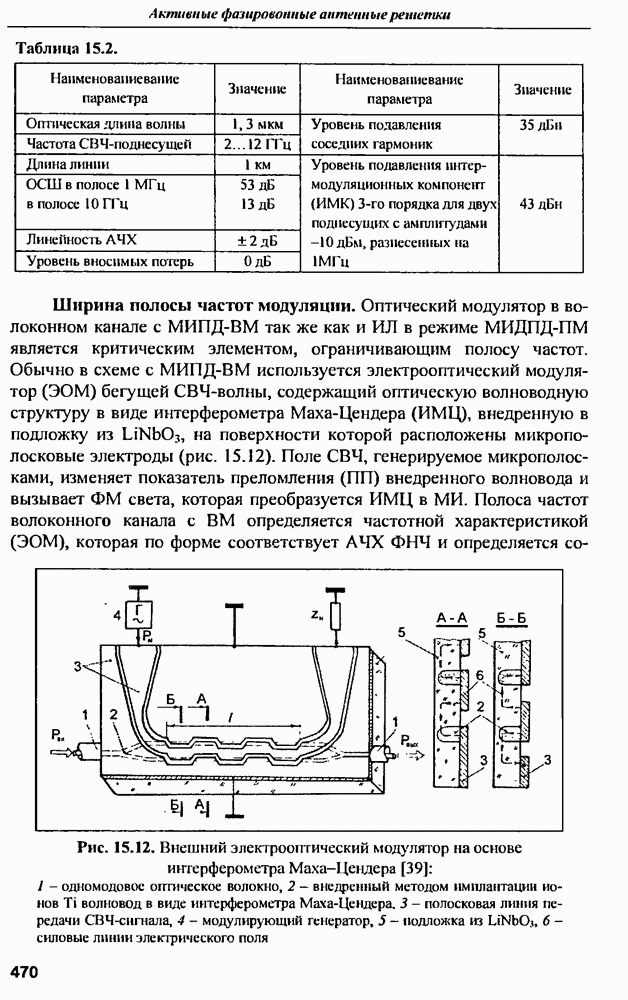
- 15.8.5. Внешние модуляторы
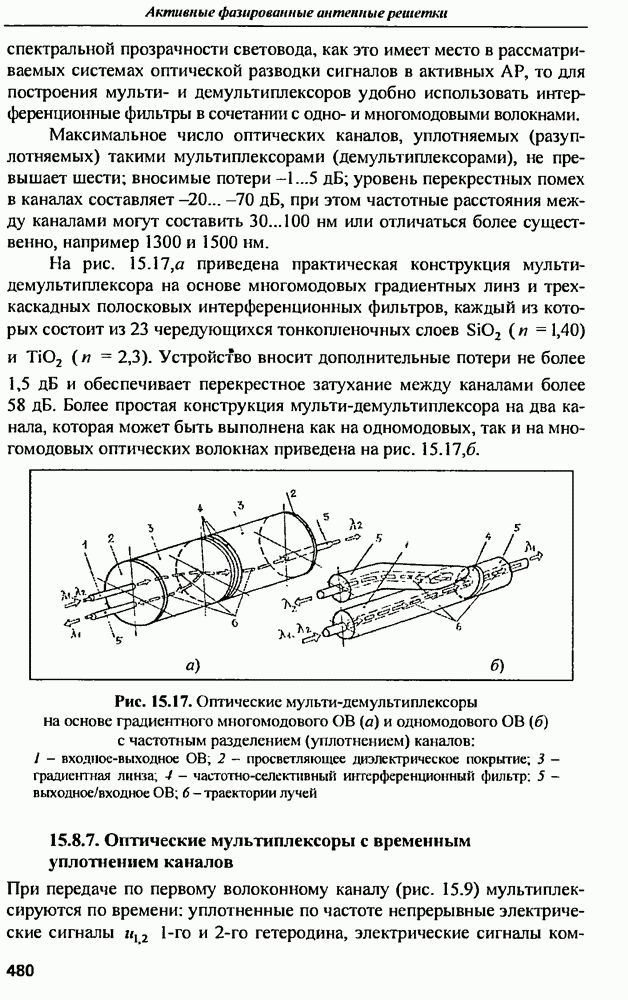
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР