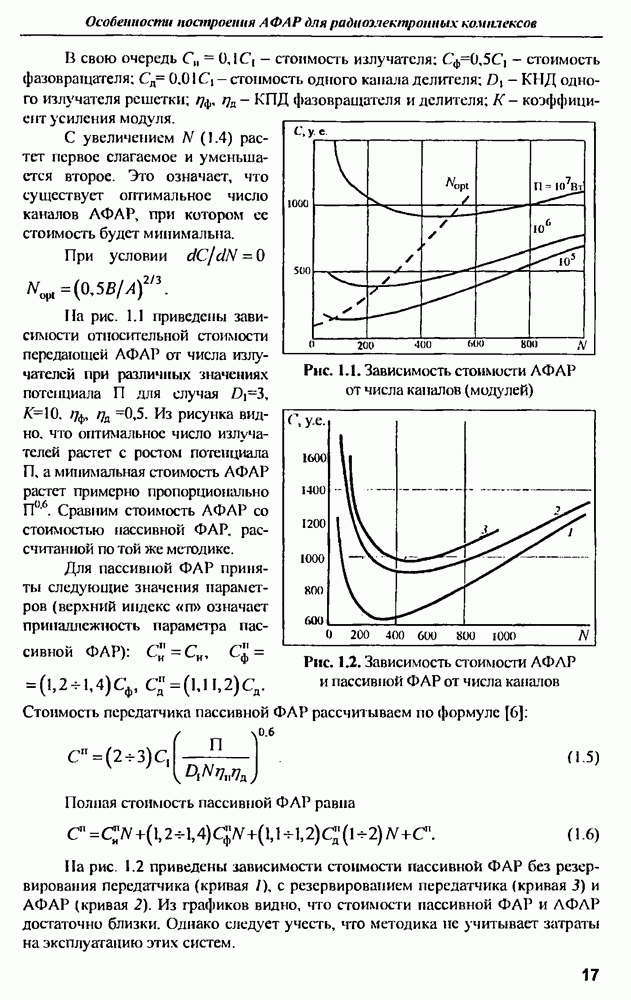
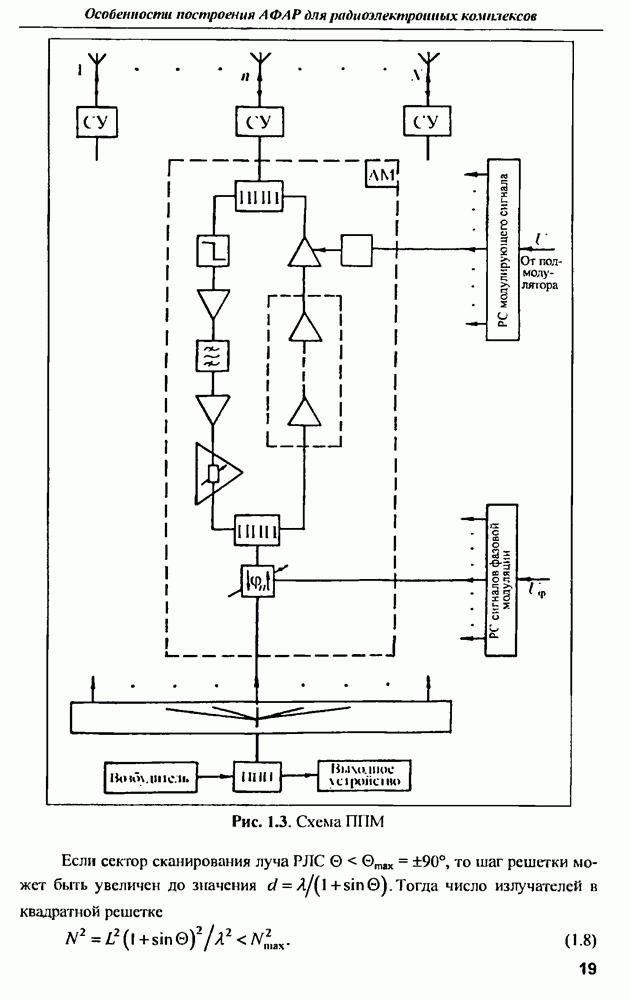
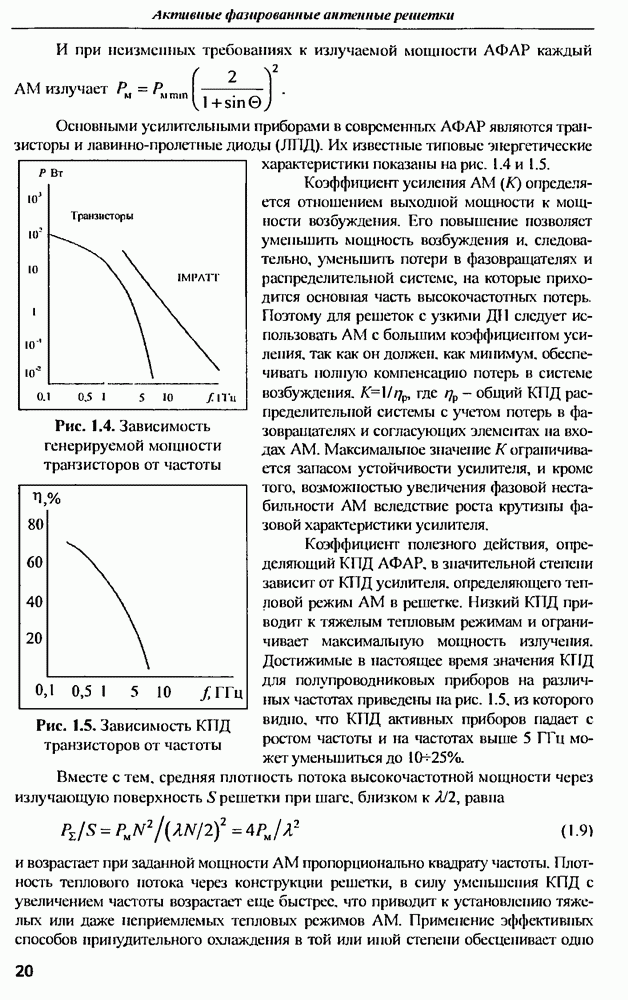
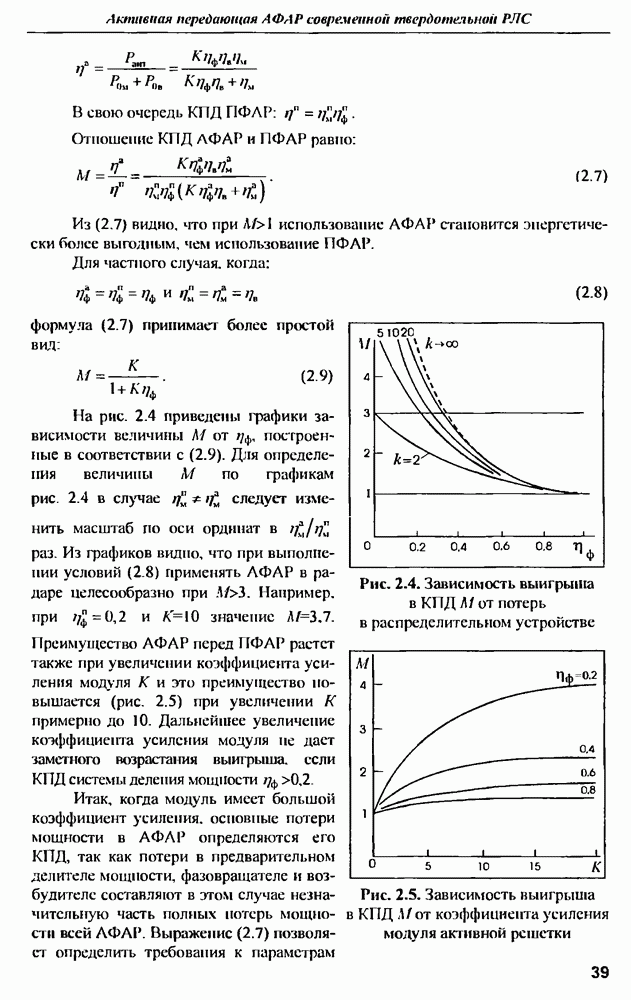
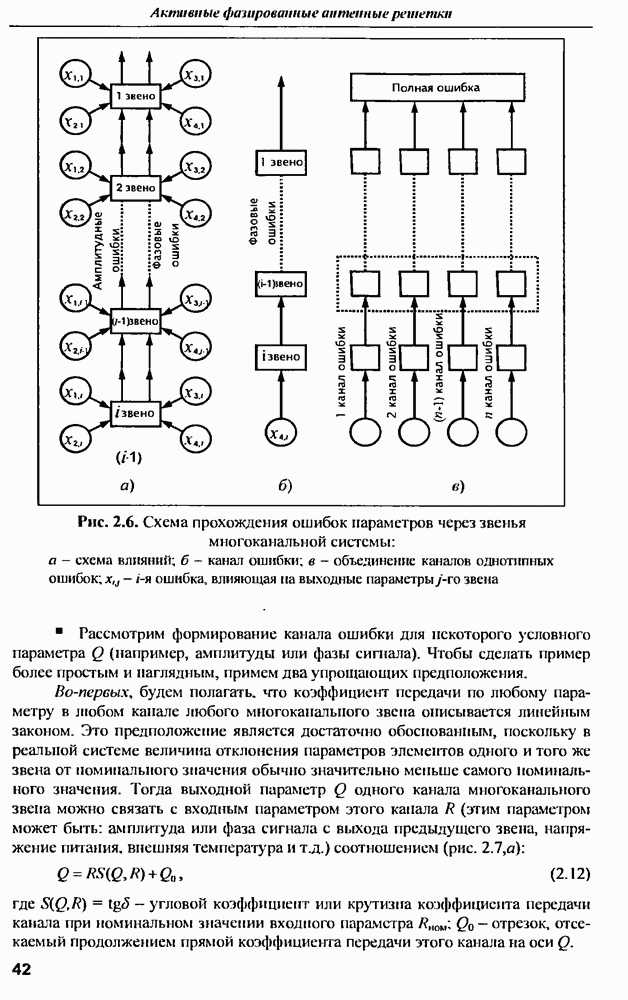
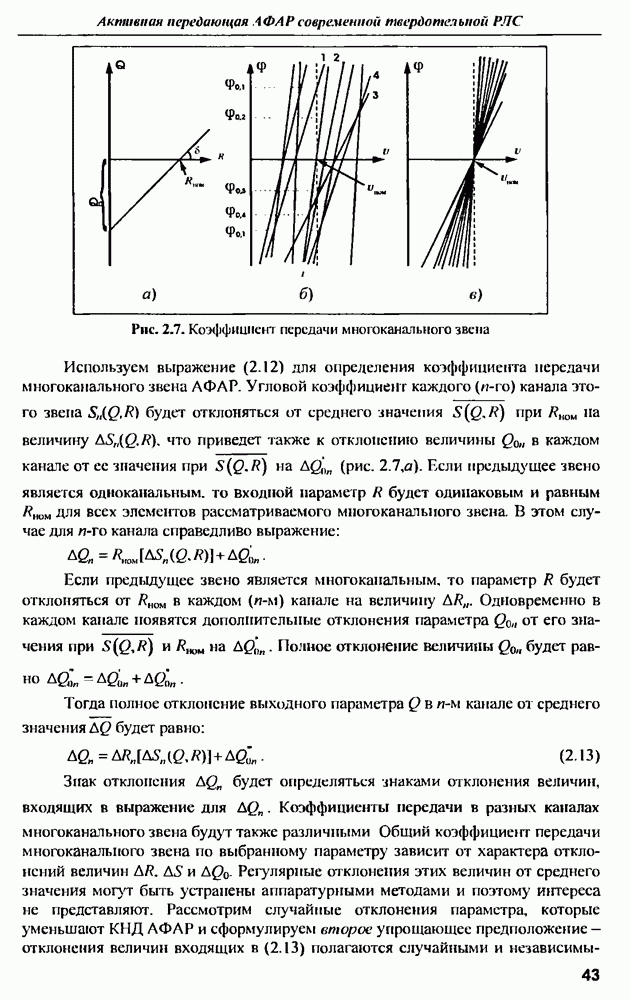
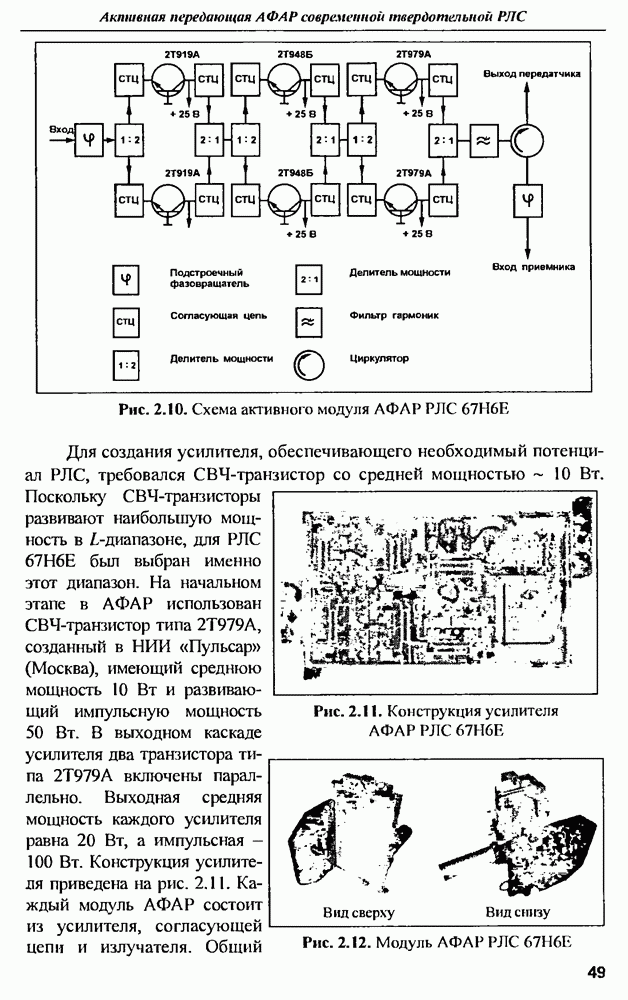
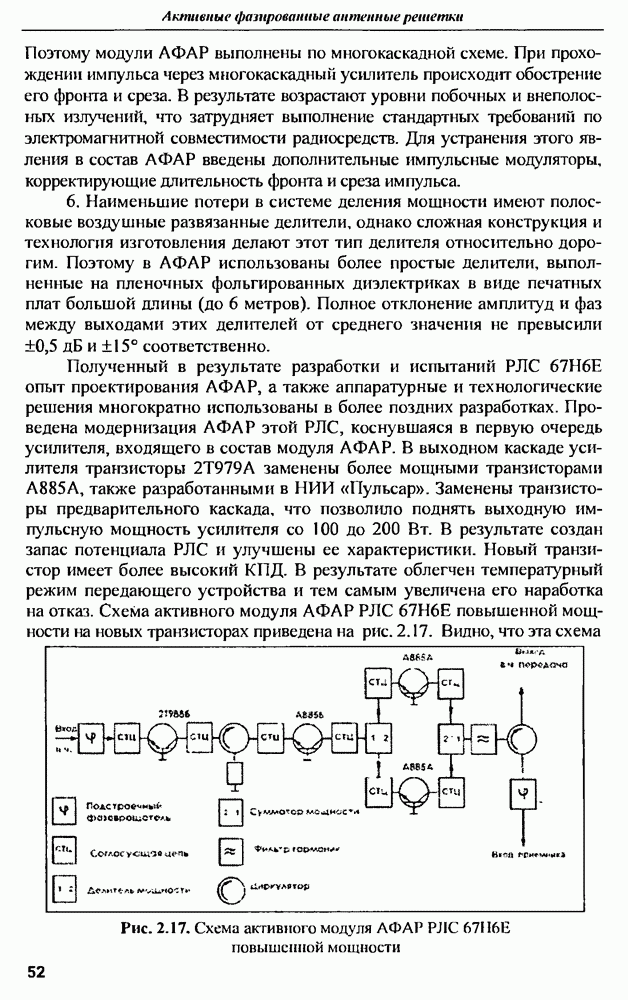
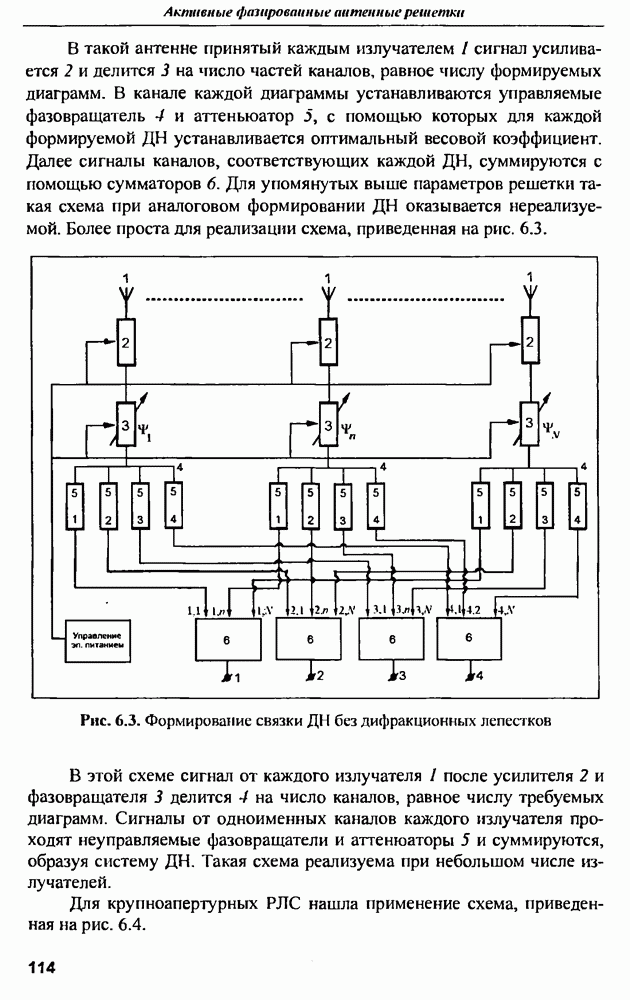
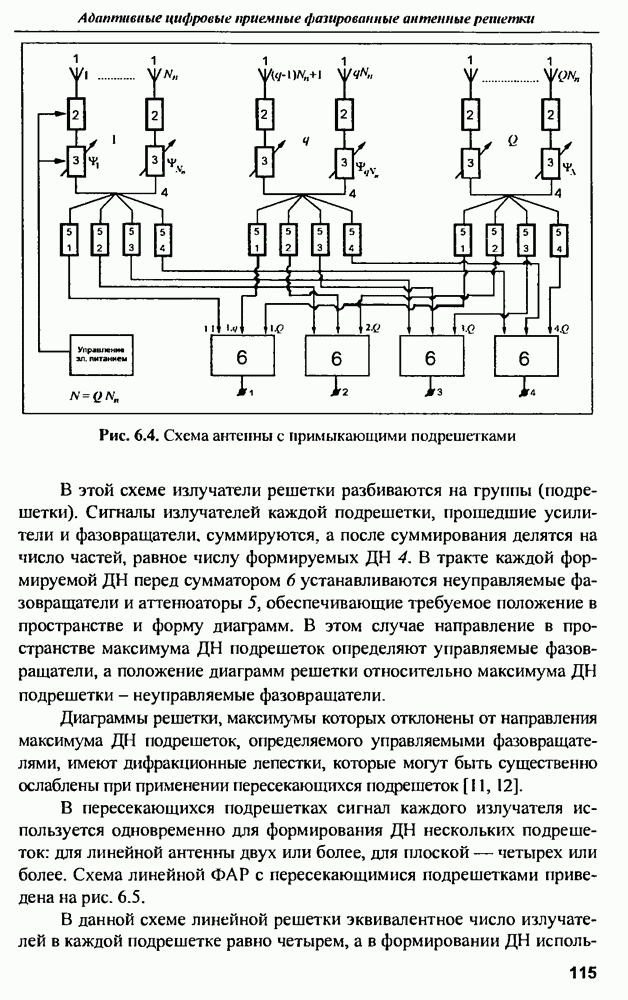
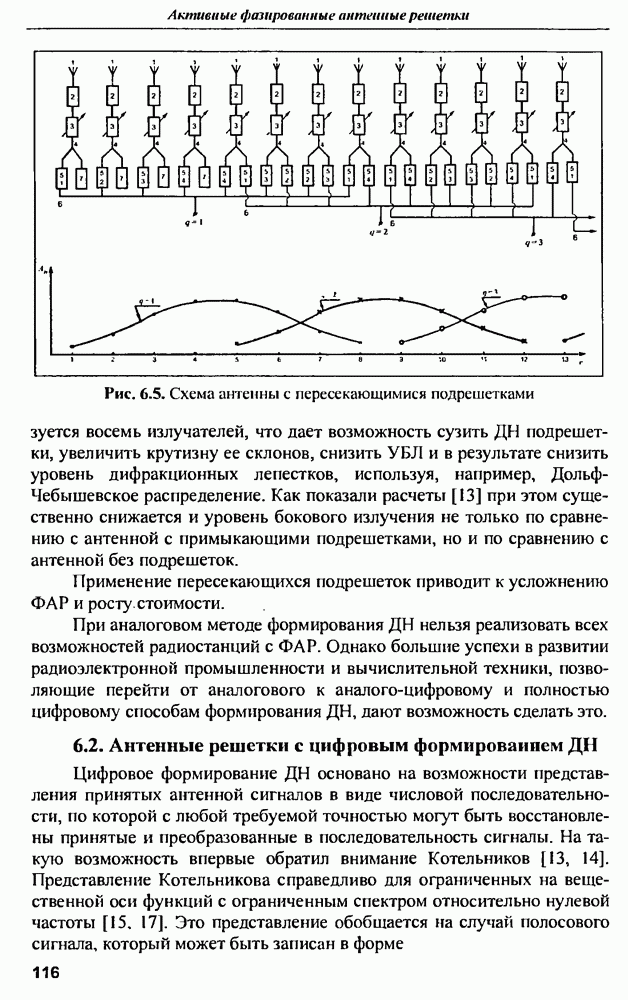
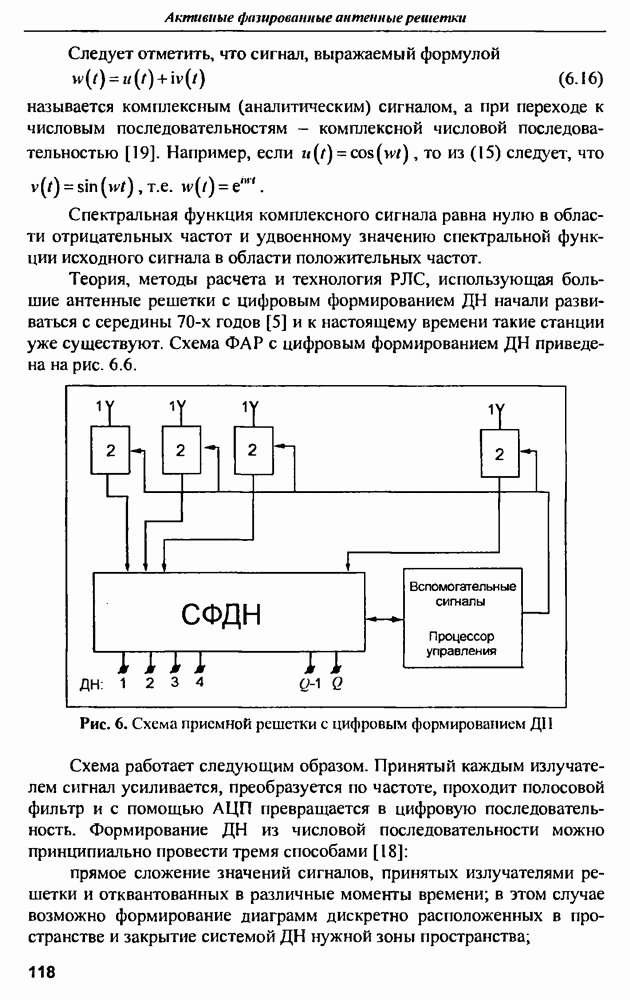
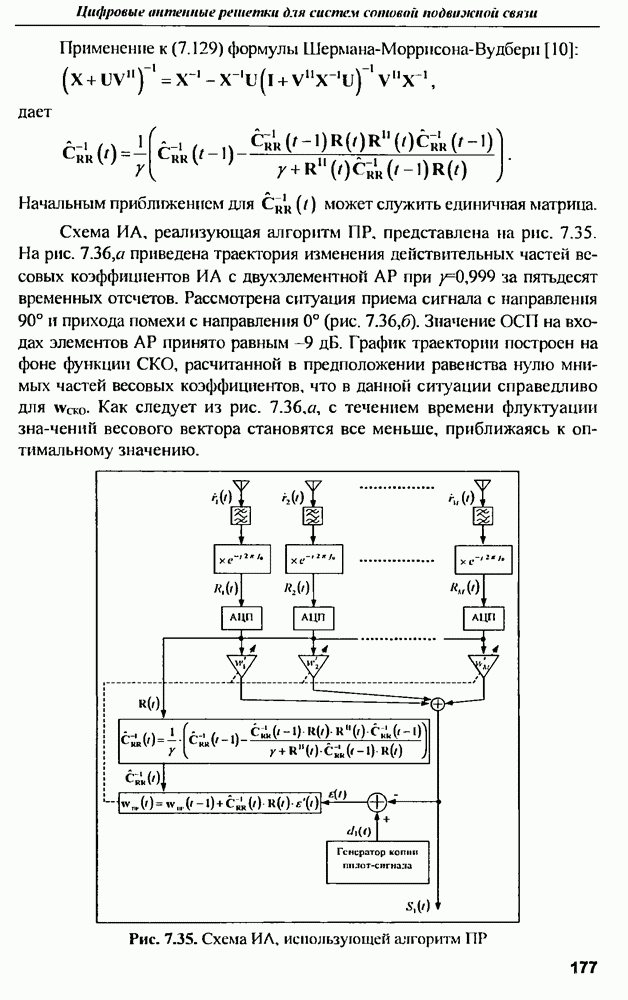
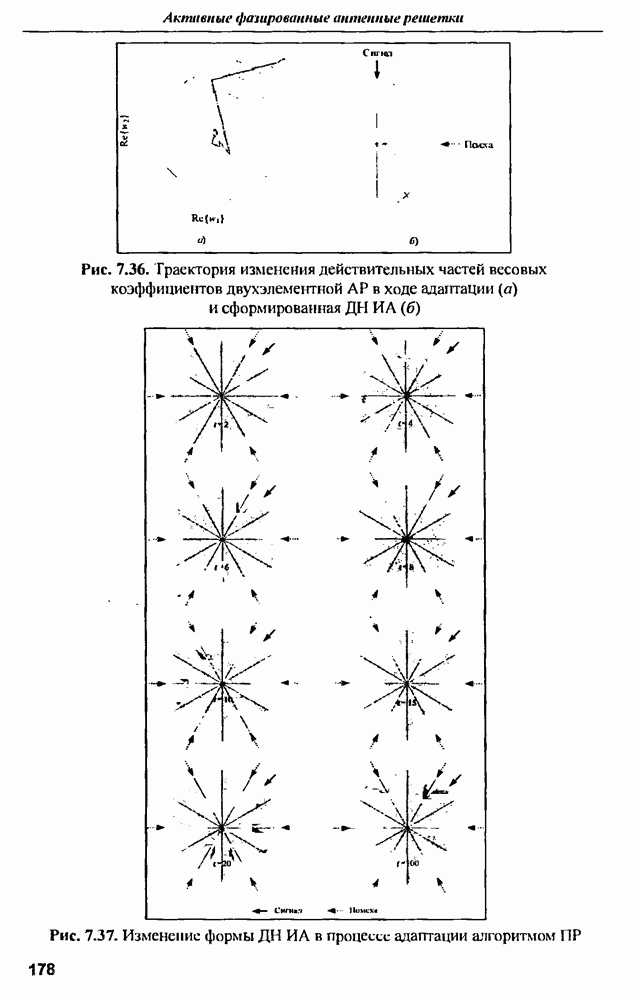
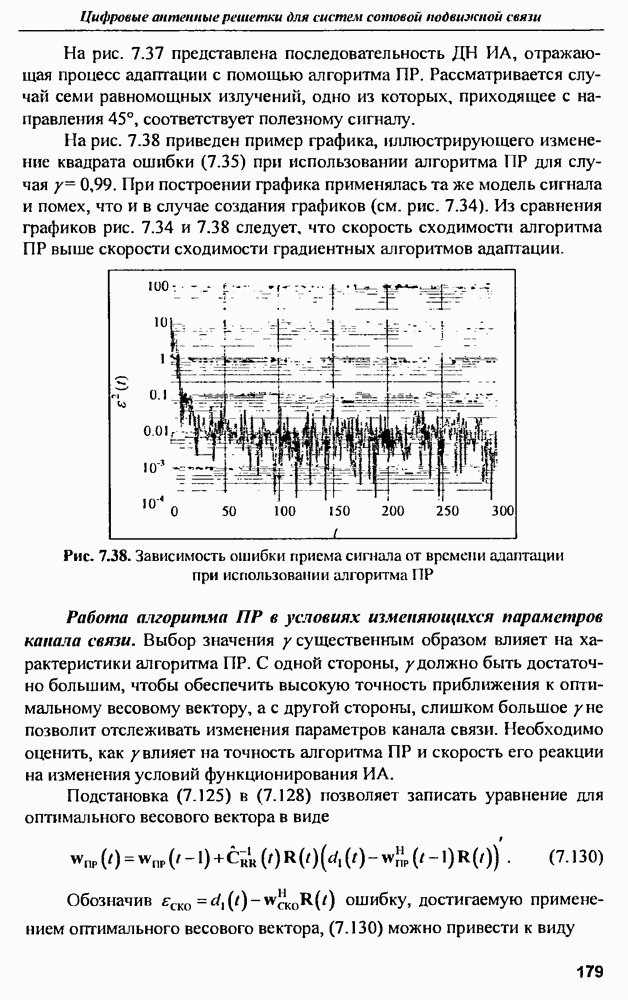
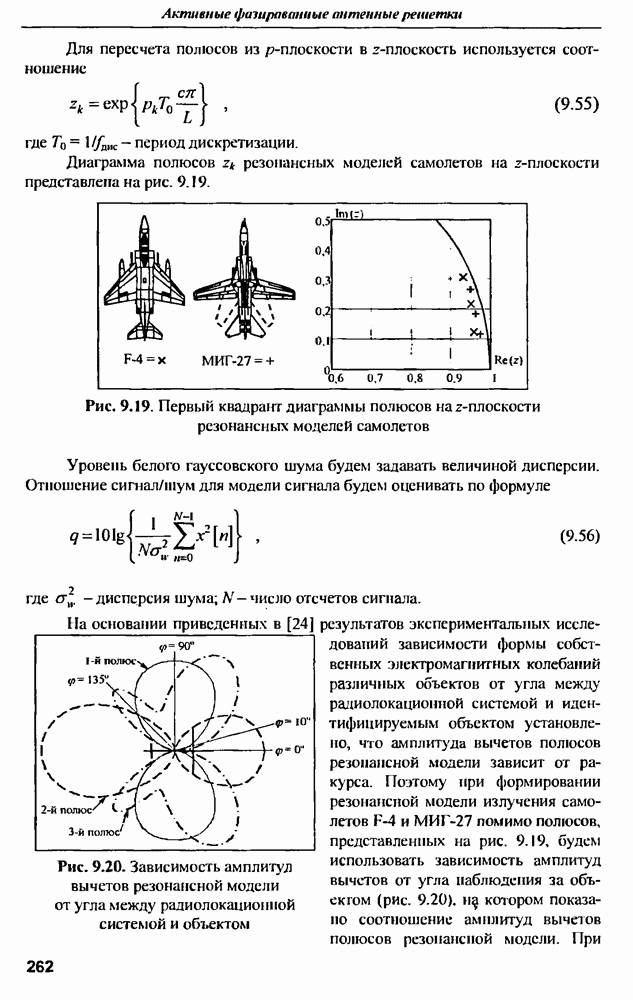
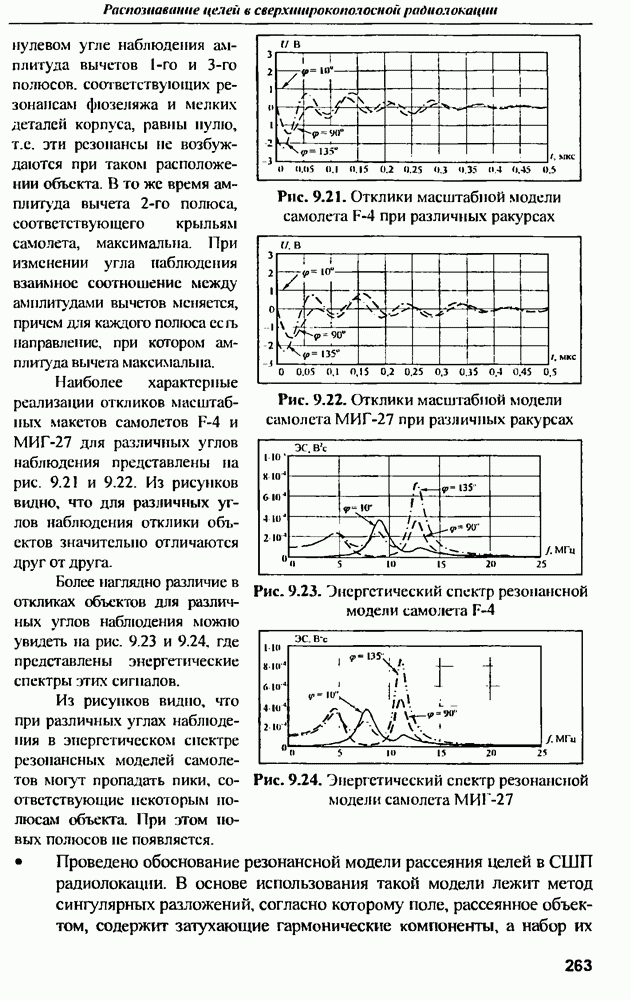
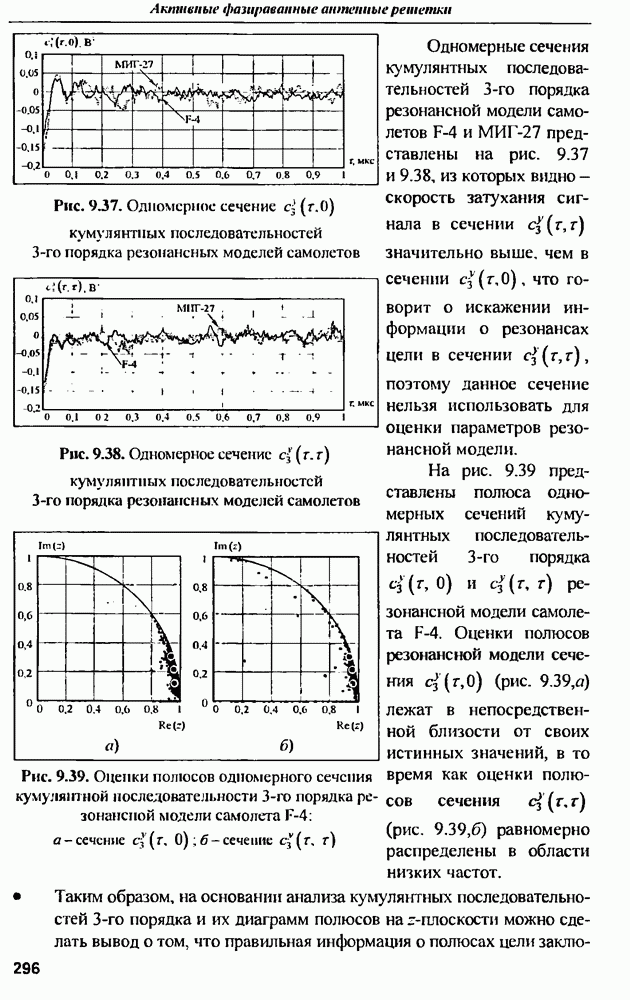
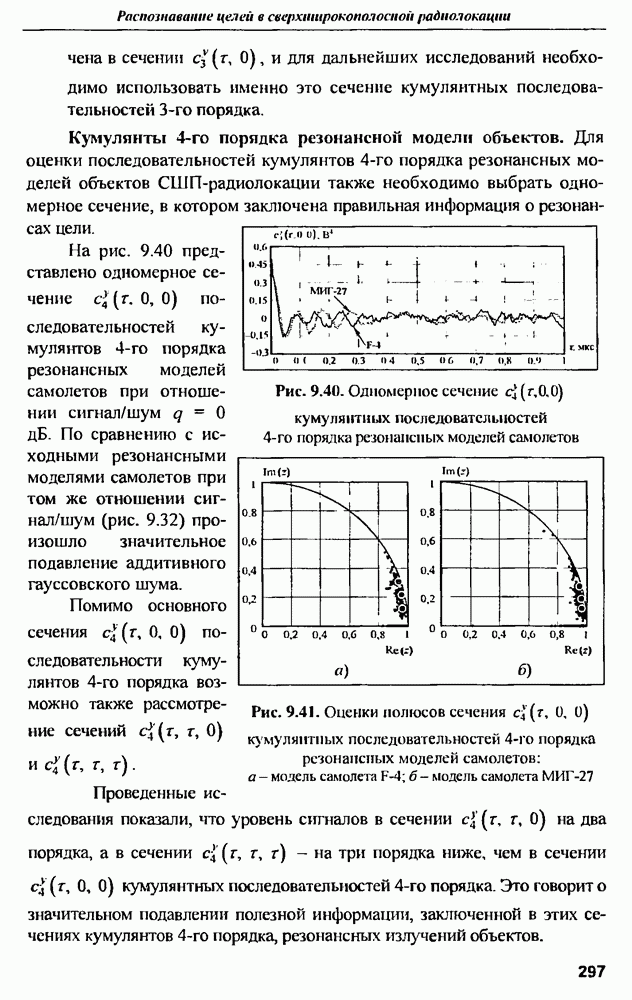
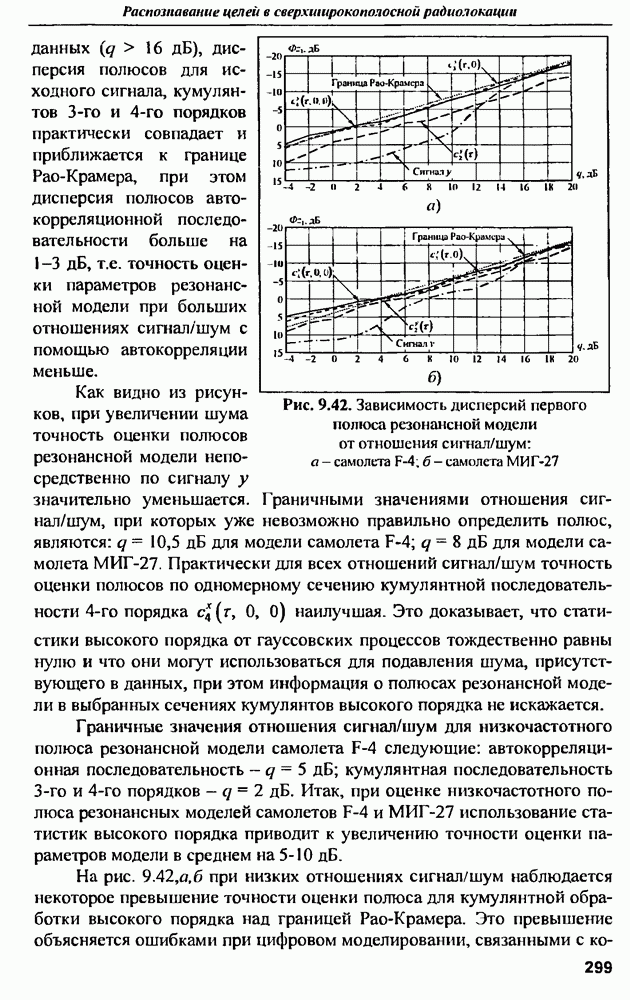
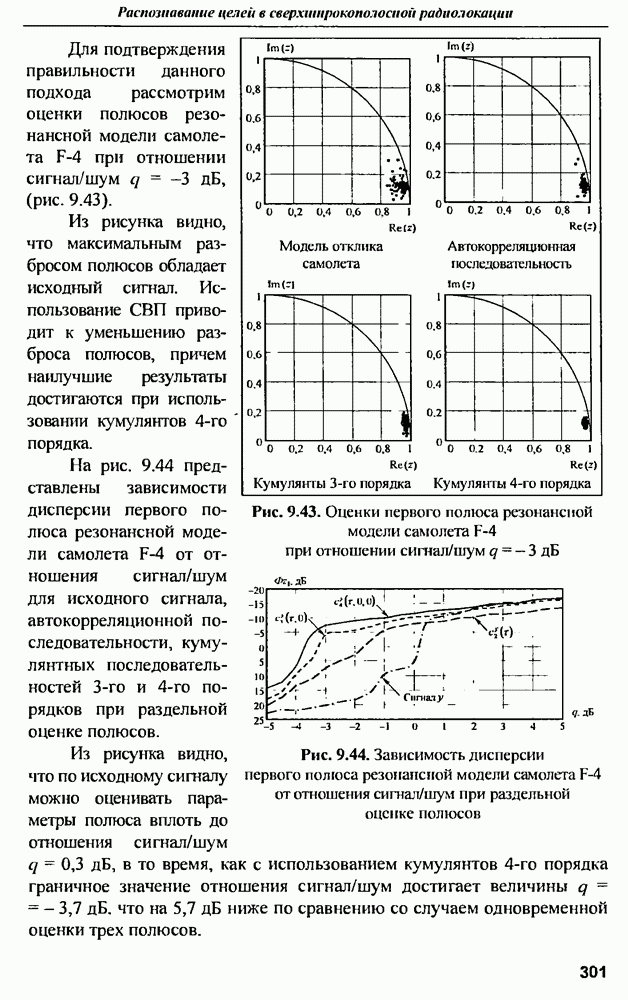
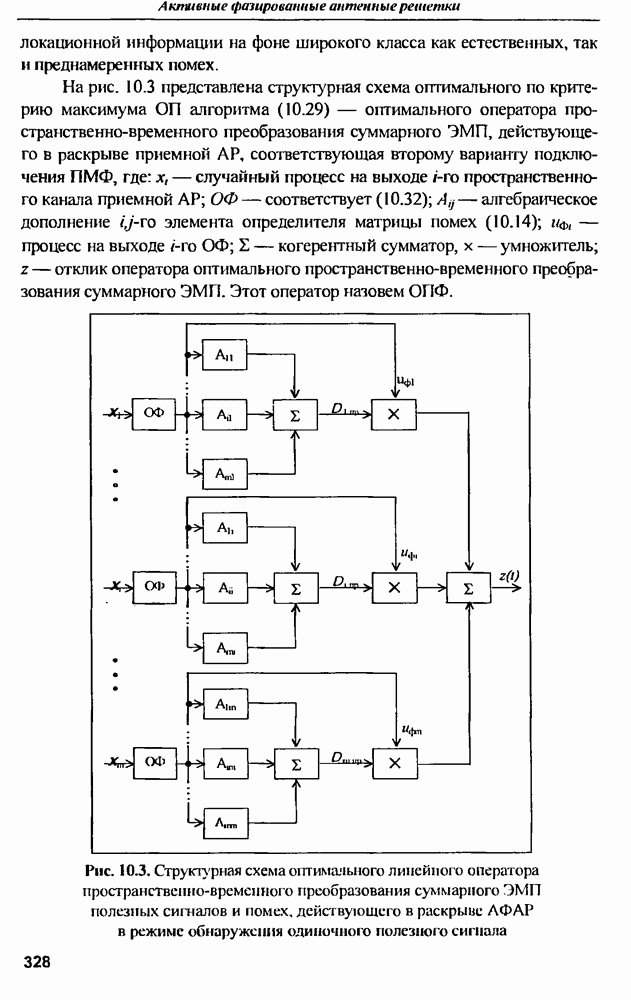
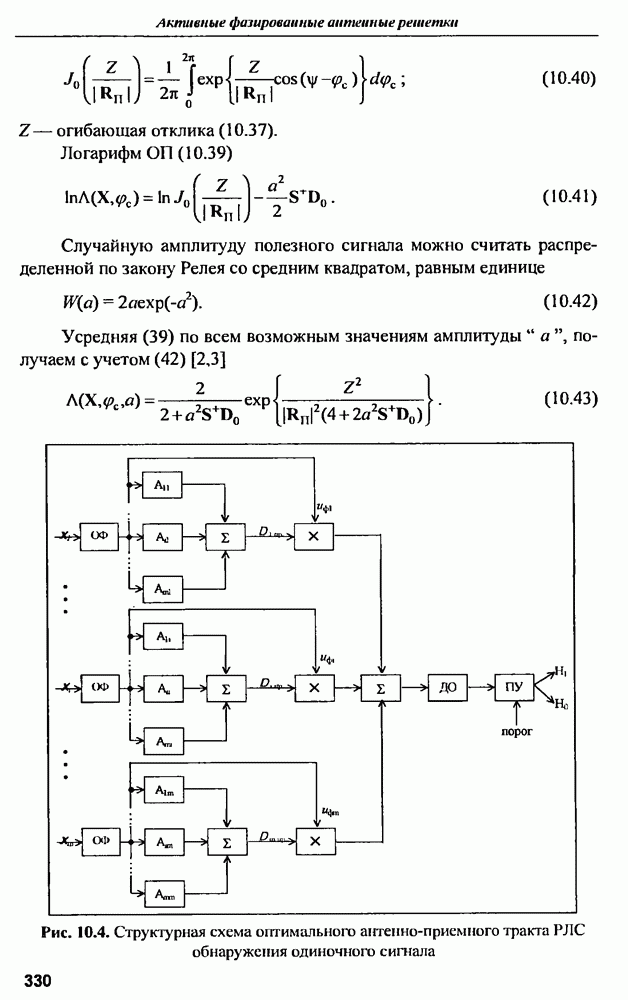
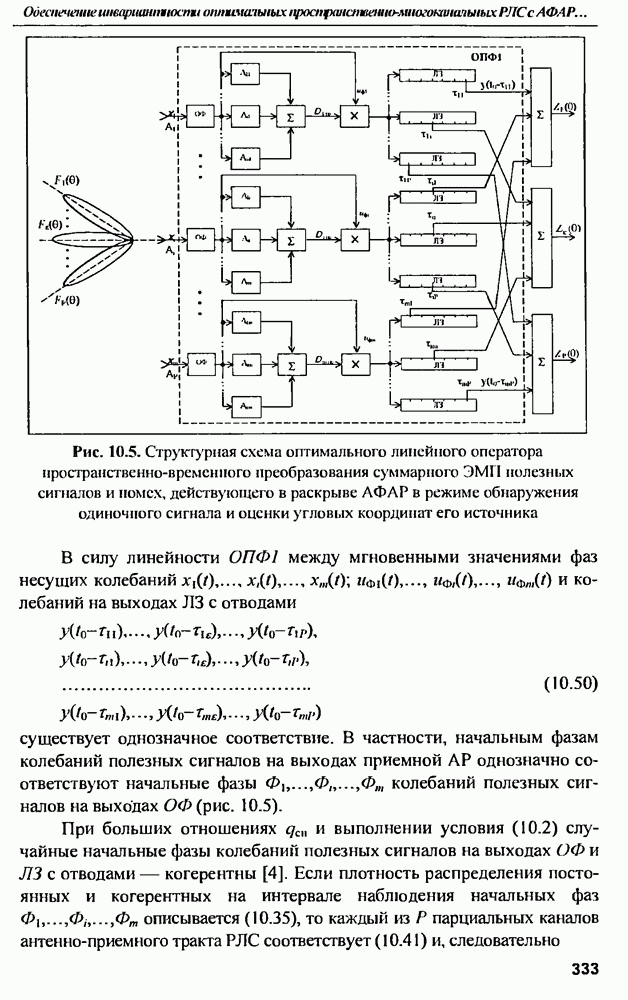
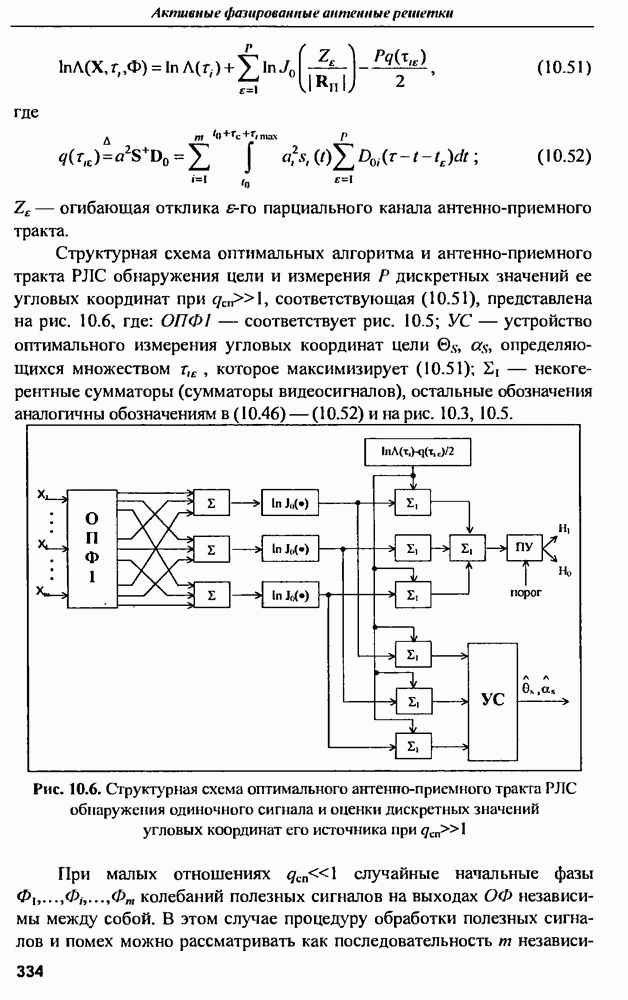
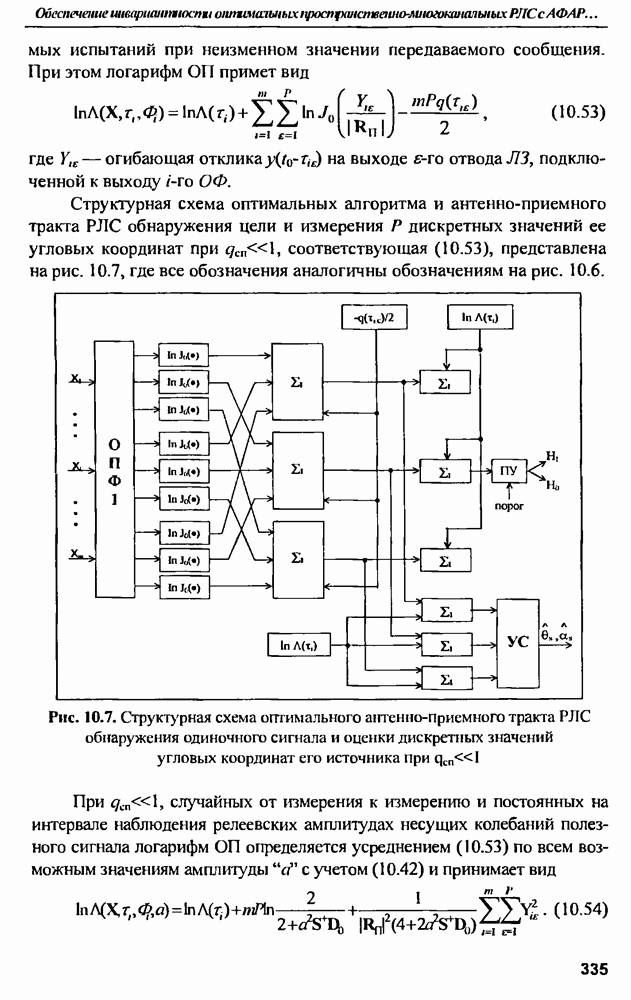
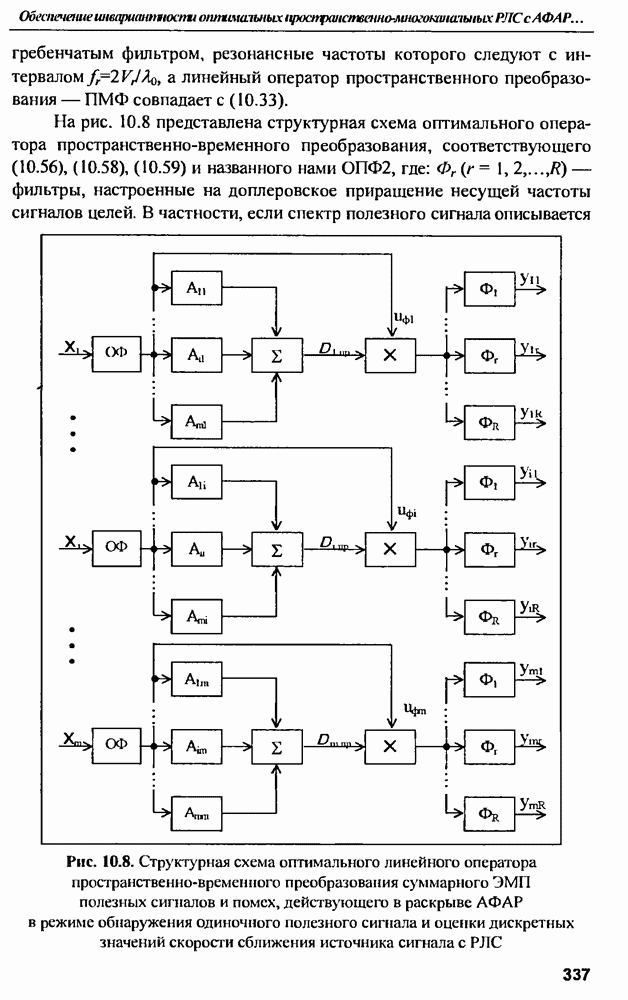
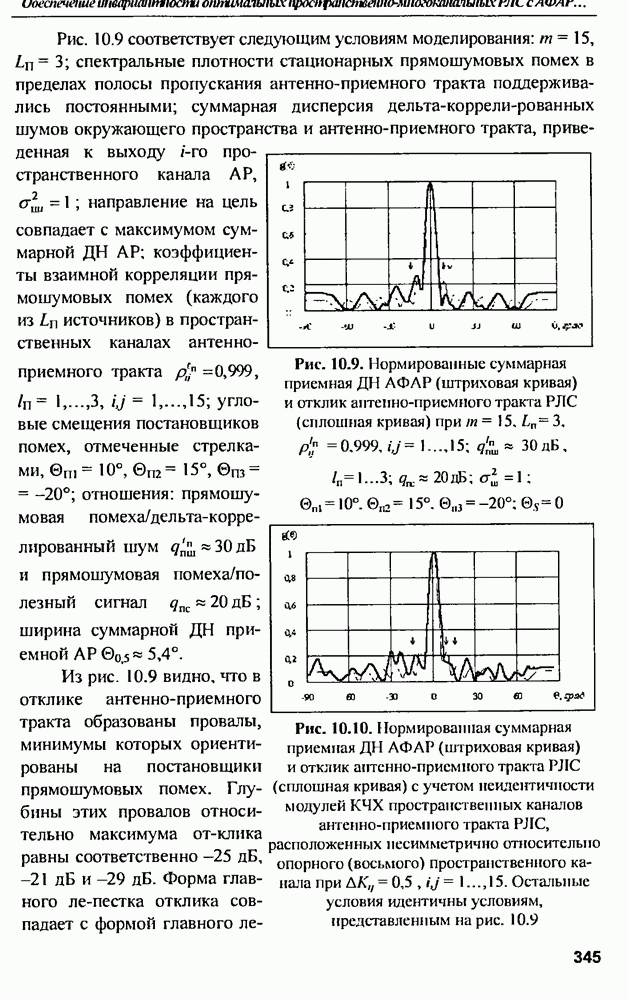
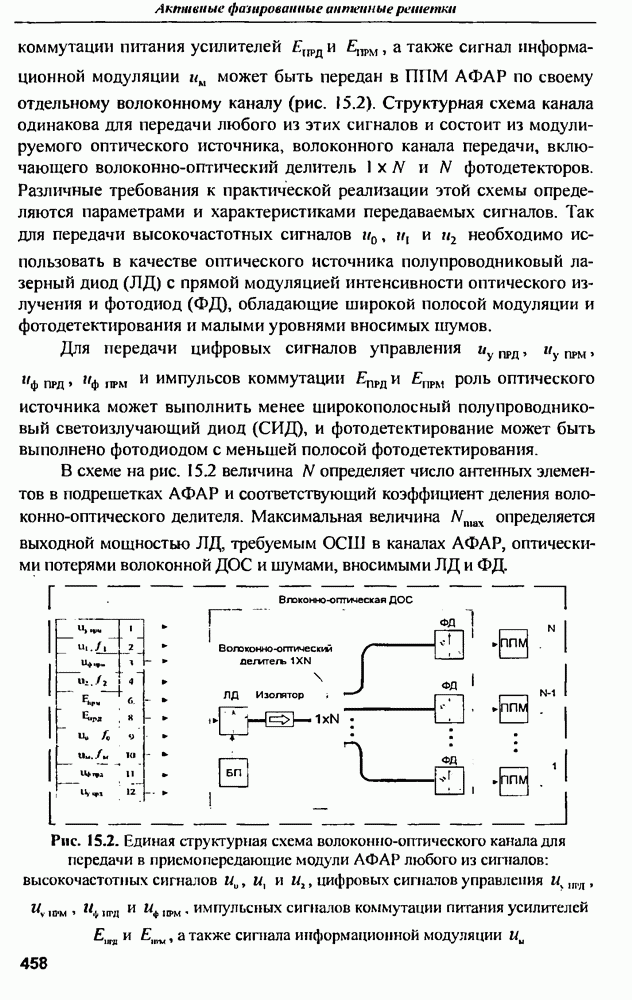
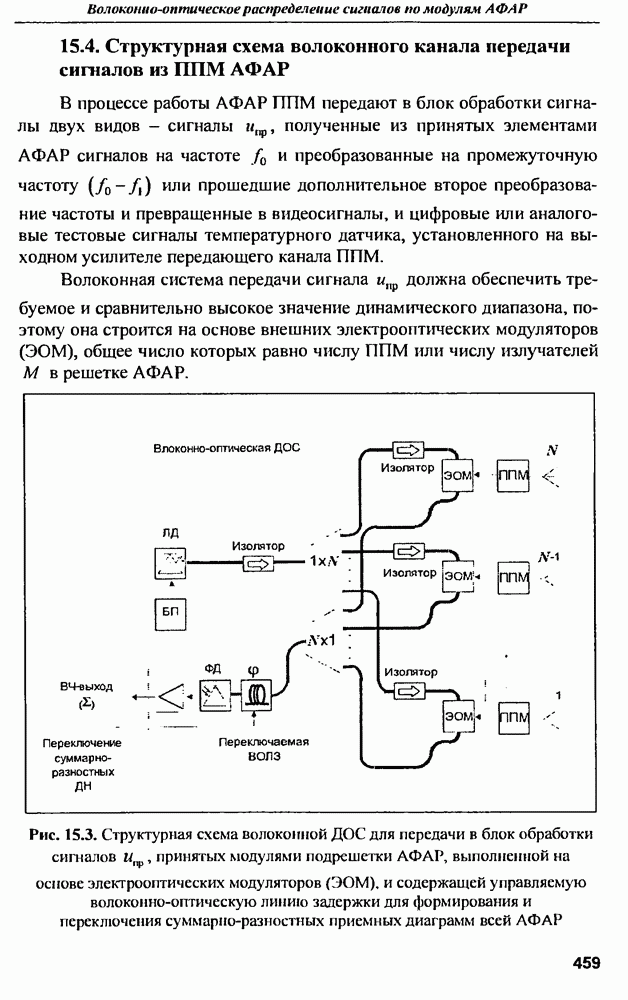
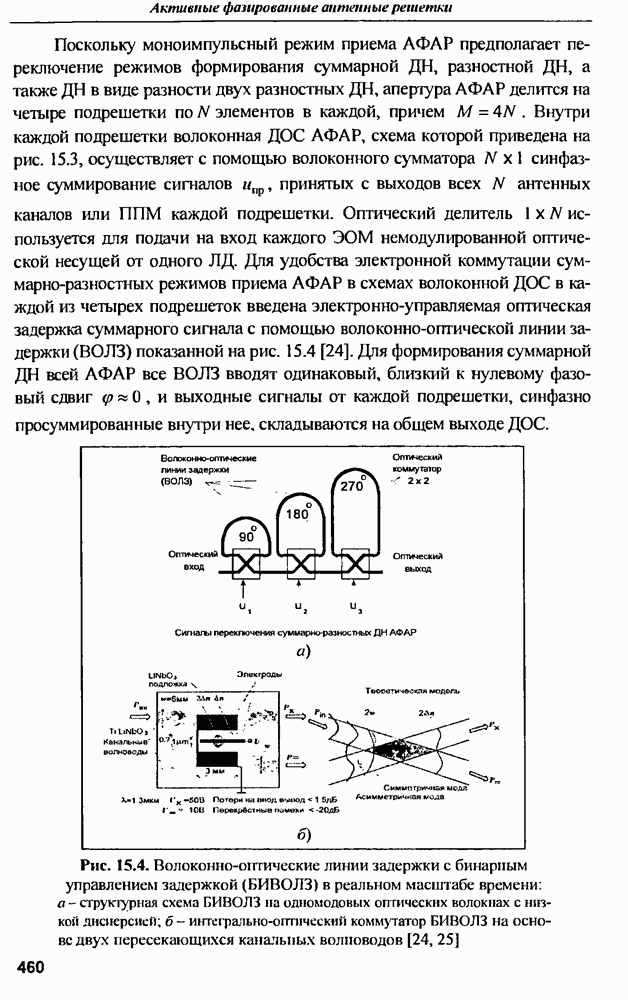
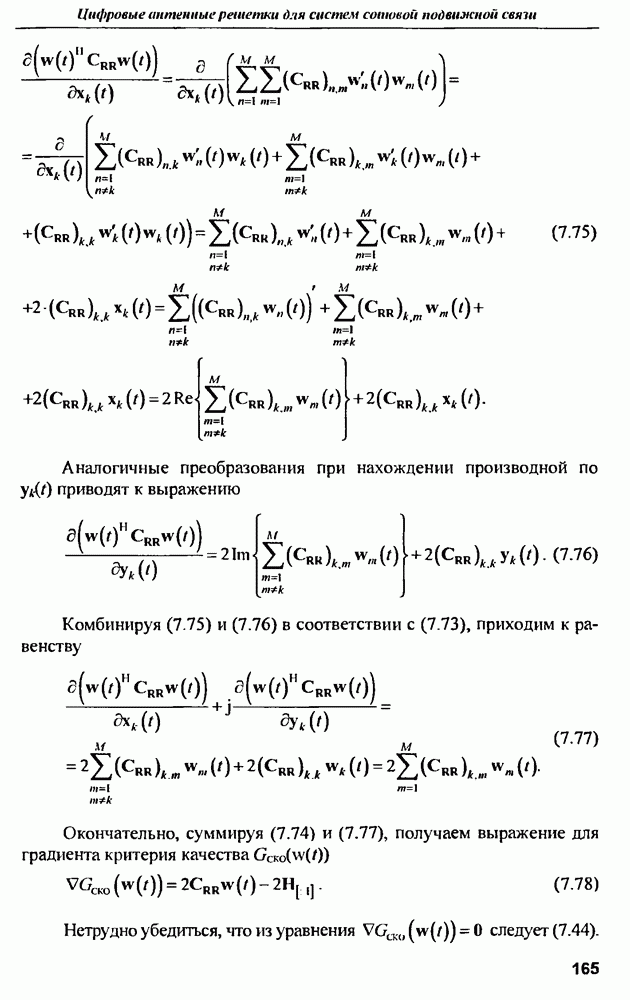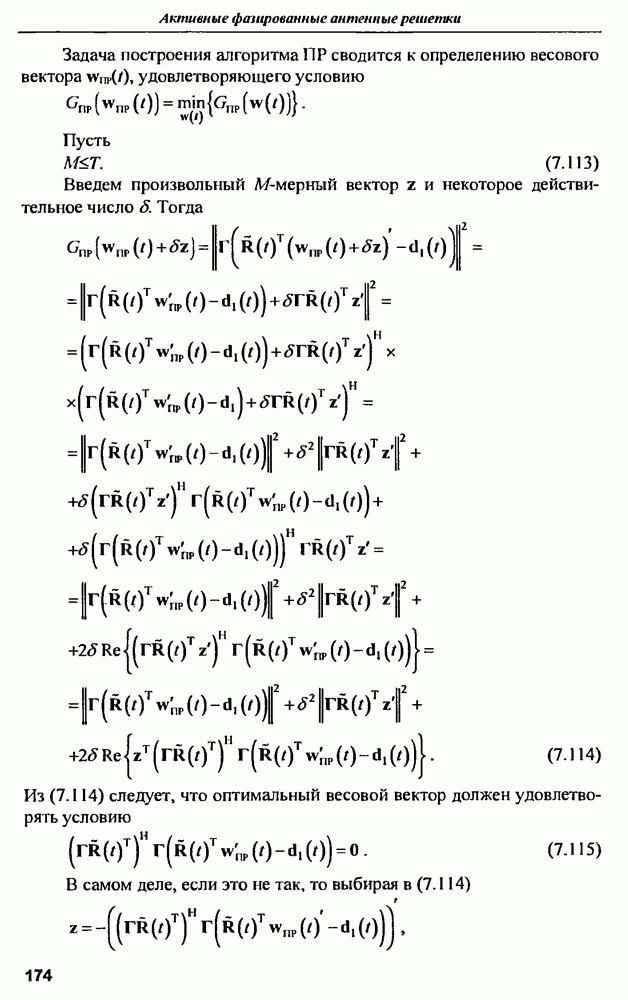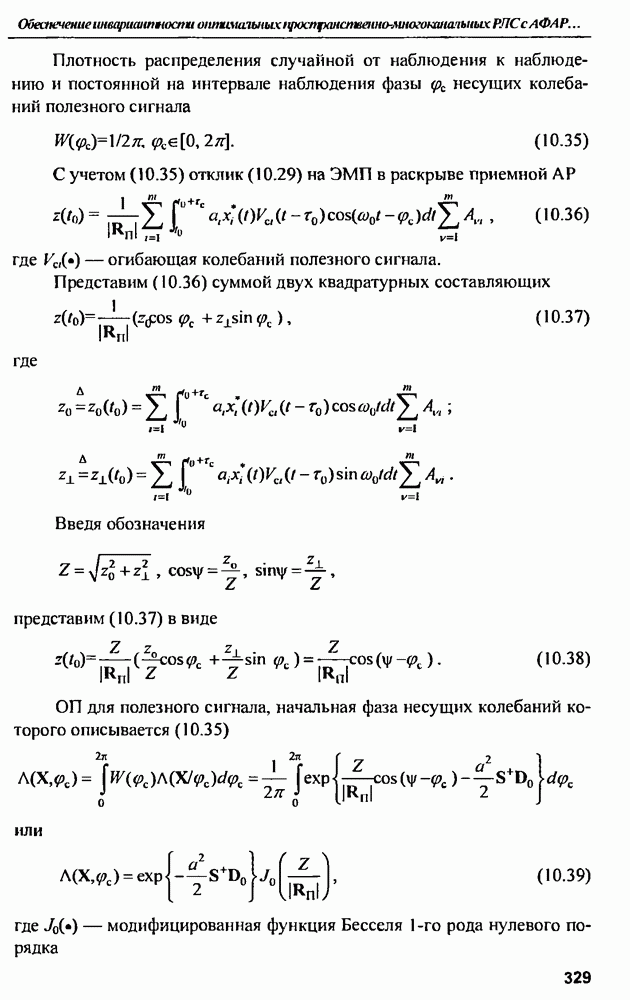| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
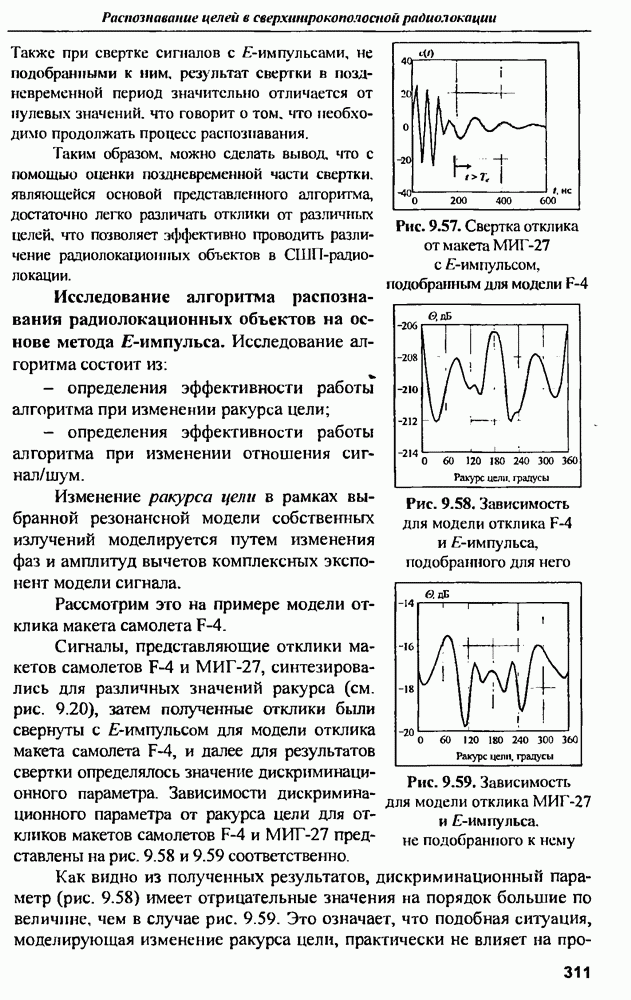
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
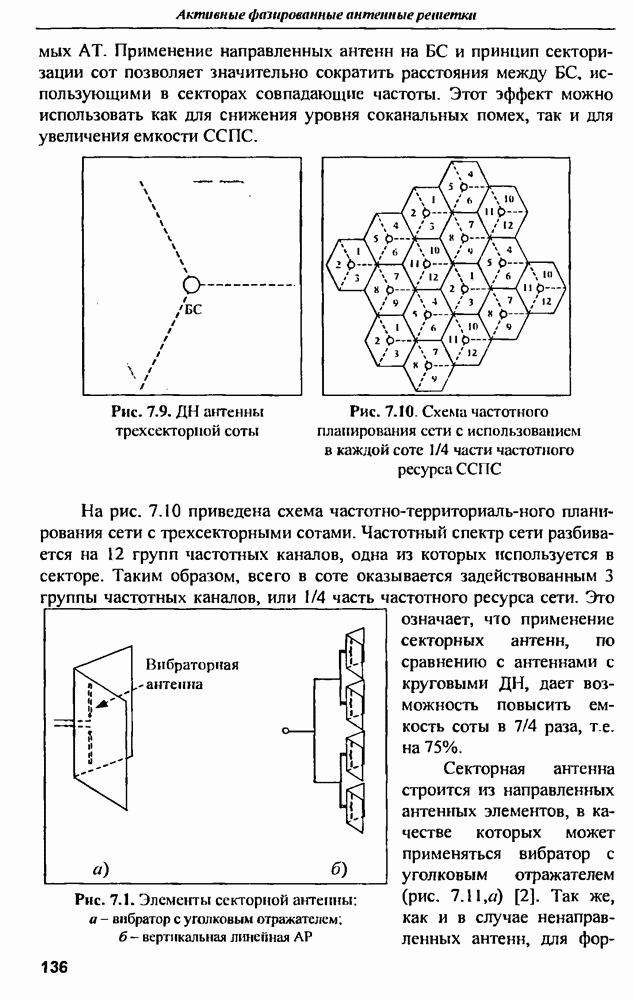
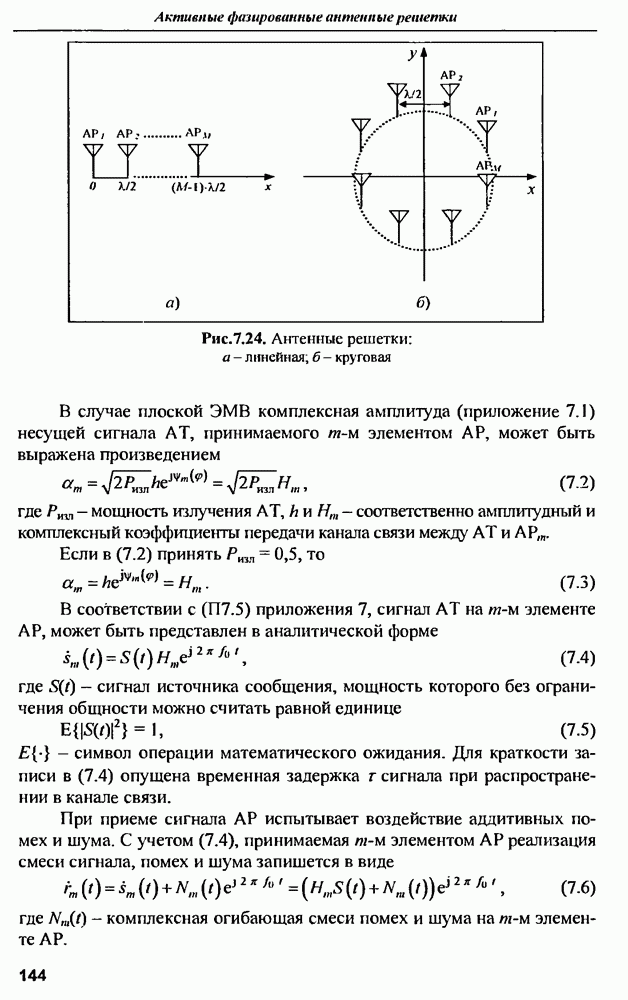
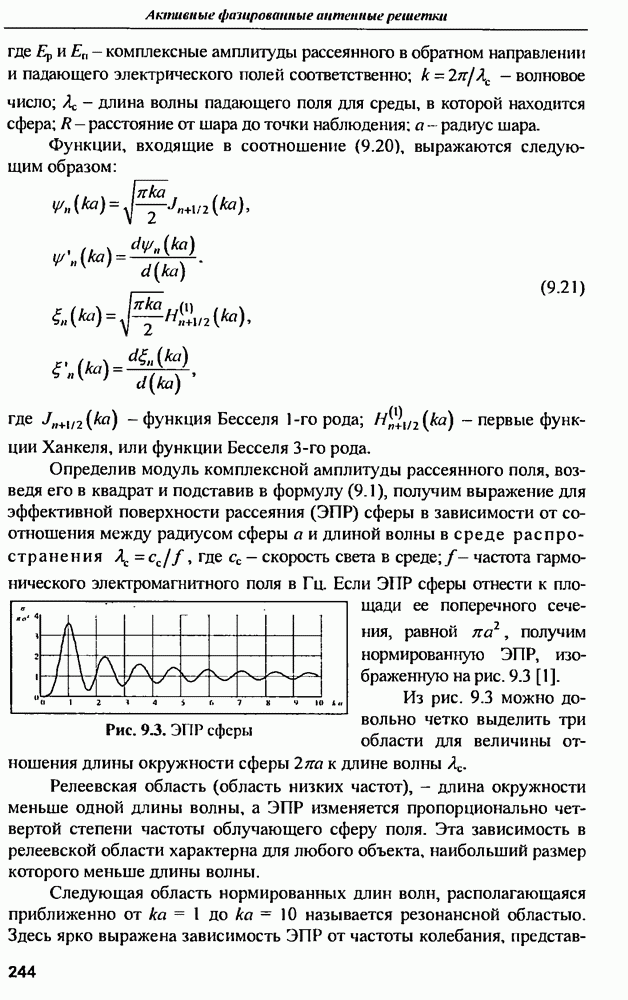
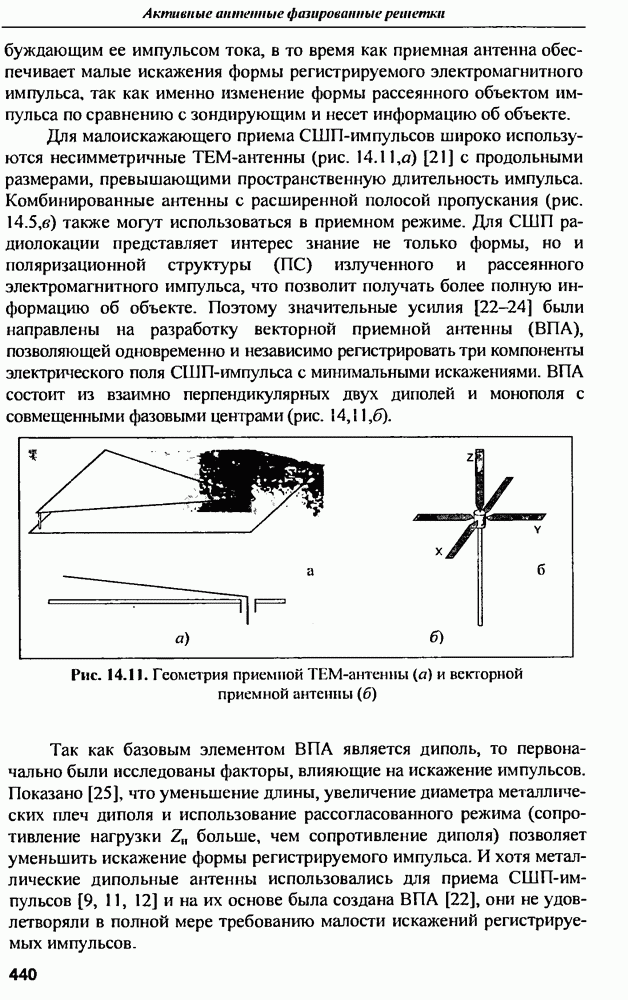
9.1.3. Характеристики рассеянна антенн
Хорошо известные в теории антенн вибраторы, прямоугольные микрополосковые и другие антенны обычно используются в узких частотных диапазонах вблизи резонансных частот Вместе с тем указанные антенны взаимодействуют с СШП возбуждающим сигналом в значительно большей полосе частот. По характеру этого взаимодействия можно косвенно судить о геометрической форме и размерах соответствующей антенны, для чего необходимо проанализировать частотную или импульсную характеристики, выявить особенности их поведения и сопоставить с известными свойствами антенны  Таким образом, можно сформулировать задачу распознавания антенн по их характеристикам рассеяния электромагнитных волн в широком диапазоне частот, охватывающим их резонансные частоты. В такой постановке задача распознавания практически соответствует проблеме распознавания радиолокационной цели, которую можно представить совокупностью рассеивателей относительно простой геометрической формы
Таким образом, можно сформулировать задачу распознавания антенн по их характеристикам рассеяния электромагнитных волн в широком диапазоне частот, охватывающим их резонансные частоты. В такой постановке задача распознавания практически соответствует проблеме распознавания радиолокационной цели, которую можно представить совокупностью рассеивателей относительно простой геометрической формы
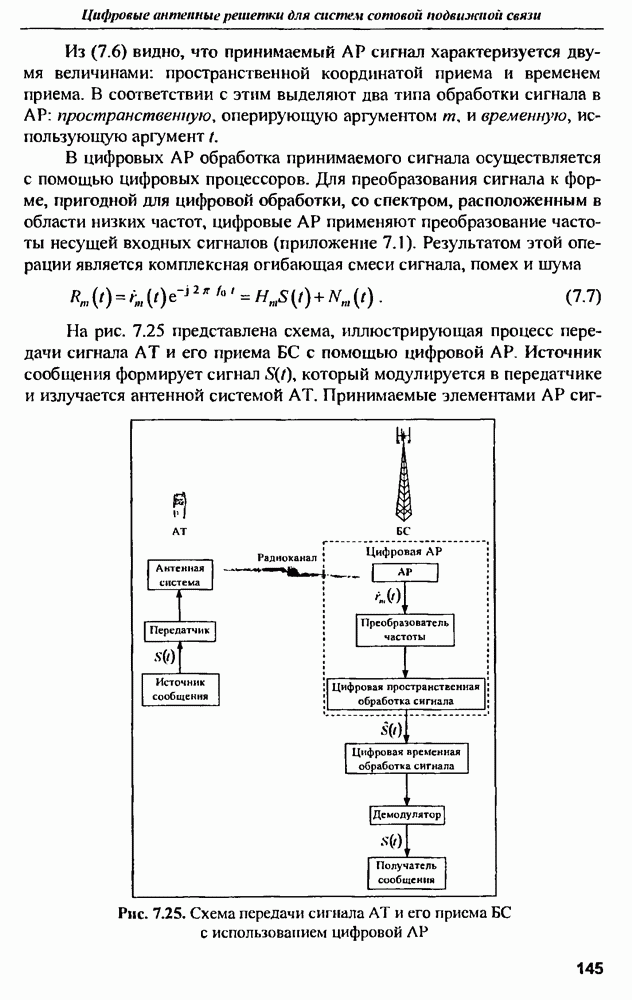
Тонкая днпольная антенна. Ярко выраженные резонансные свойства проявляет тонкий цилиндр конечной длины, облучаемый полем, электрическая компонента которого параллельна оси цилиндра. Такой цилиндр можно назвать проволокой. Хорошим примером такого типа рассеивателя является тонкая дипольная антенна, имеющая резонансы на частотах, соответствующих длинам волн  где
где  обозначает длину одного плеча вибратора антенны.
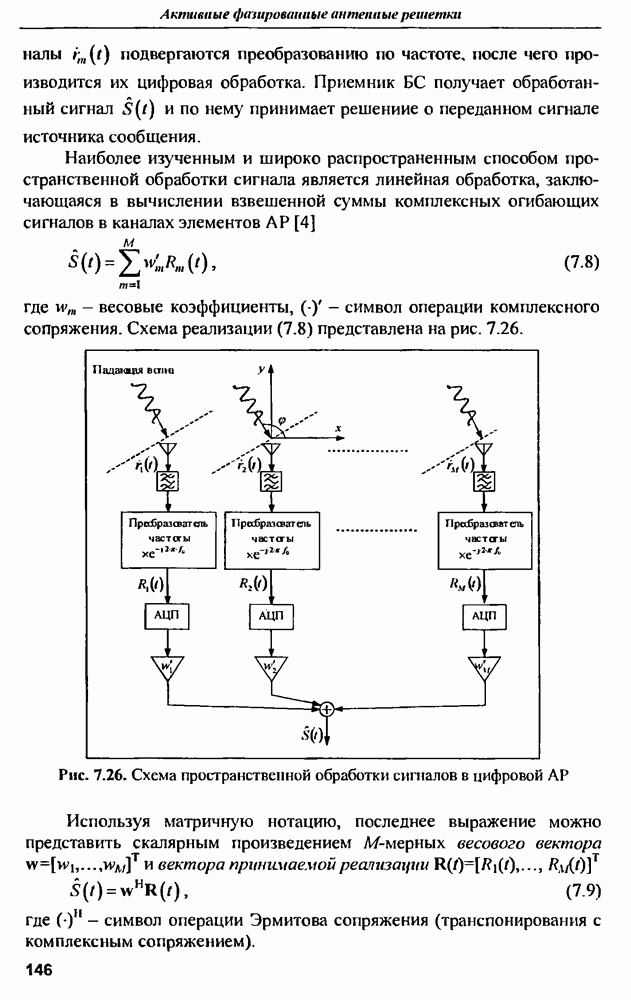
обозначает длину одного плеча вибратора антенны.
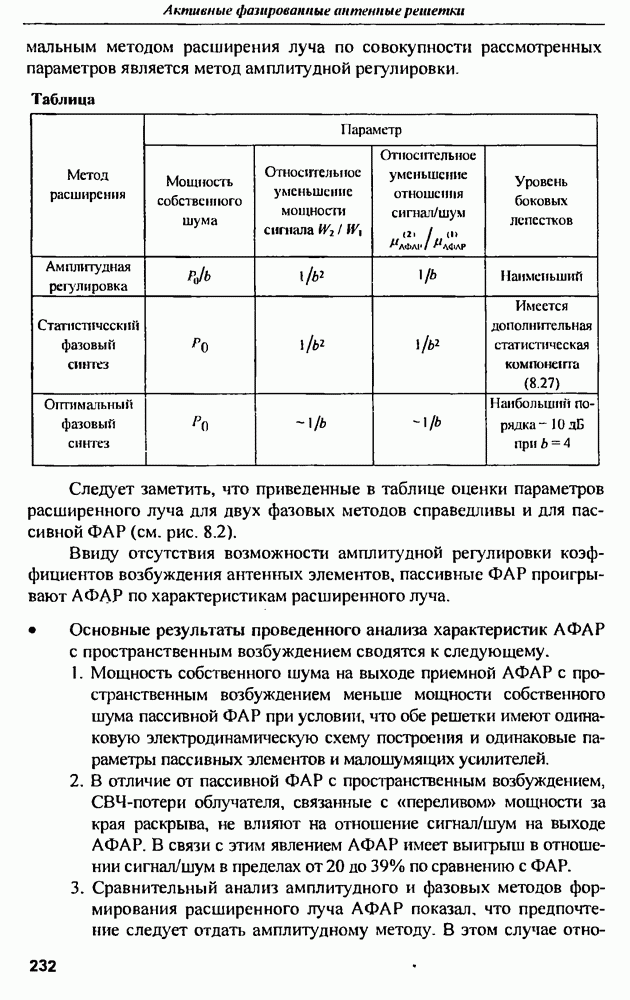
Импульсная характеристика проволочной дипольной антенны приближенно описывается временной функцией тока, возбуждаемого коротком импульсом электрического поля. Приближенность состоит в том, что  строго определяется как реакция на бесконечно узкий импульс в виде функции, а реальный импульс имеет конечную длительность, при этом эффективная длительность возбуждающего импульса определяет ширину спектра воздействующего электрического поля, а значит и спектральную границу колебаний, возбужденных в антенне.
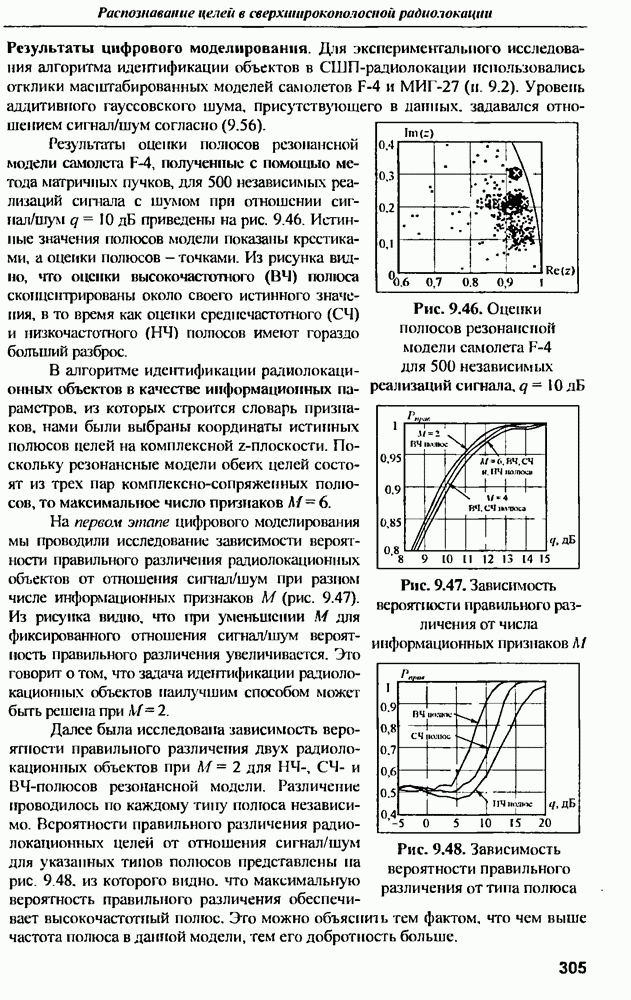
строго определяется как реакция на бесконечно узкий импульс в виде функции, а реальный импульс имеет конечную длительность, при этом эффективная длительность возбуждающего импульса определяет ширину спектра воздействующего электрического поля, а значит и спектральную границу колебаний, возбужденных в антенне.
Пример расчета такой  тонкой дипольной антенны
тонкой дипольной антенны  приведен в [12]. В качестве возбуждающего импульса использовался гауссовский импульс (9.24), имеющий параметр
приведен в [12]. В качестве возбуждающего импульса использовался гауссовский импульс (9.24), имеющий параметр  не и эффективную длительность
не и эффективную длительность  . Эффективная ширина спектра такого импульса составляет
. Эффективная ширина спектра такого импульса составляет  Интервал дискретизации при моделировании
Интервал дискретизации при моделировании  составлял
составлял  т.е. частота дискретизации
т.е. частота дискретизации  что значительно превосходит
что значительно превосходит 
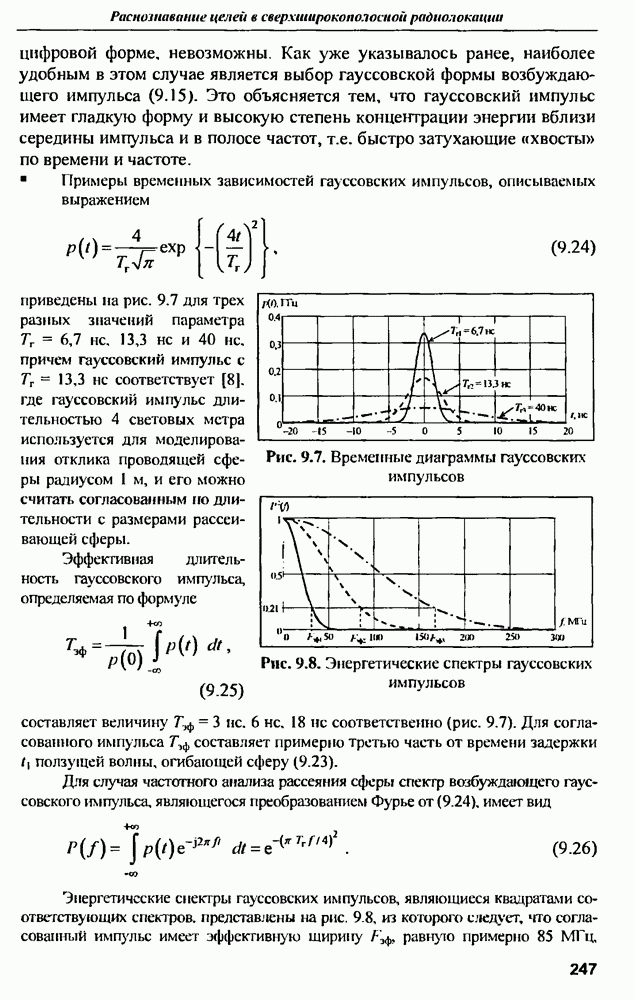
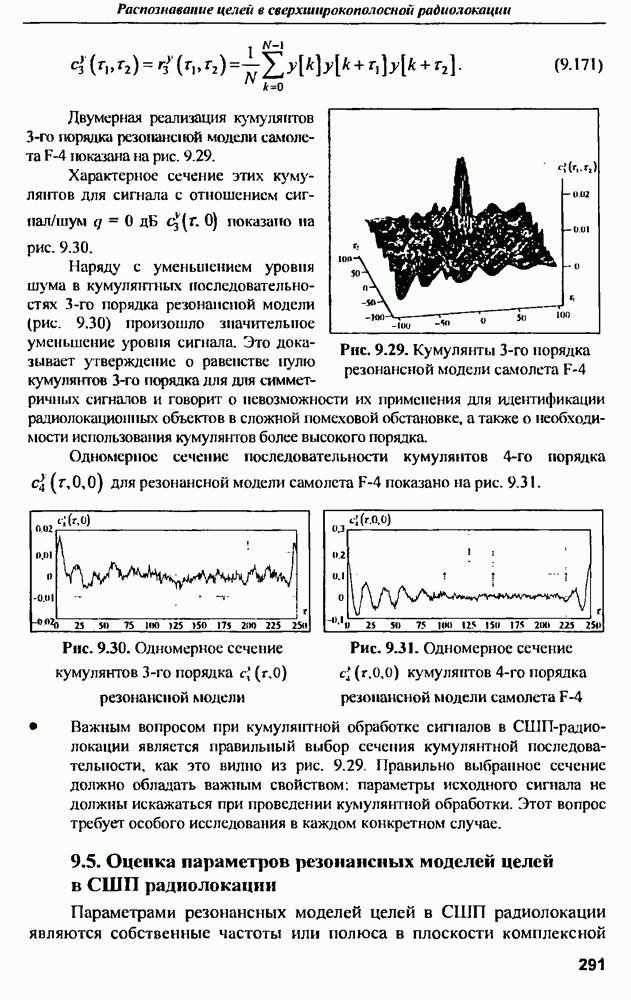
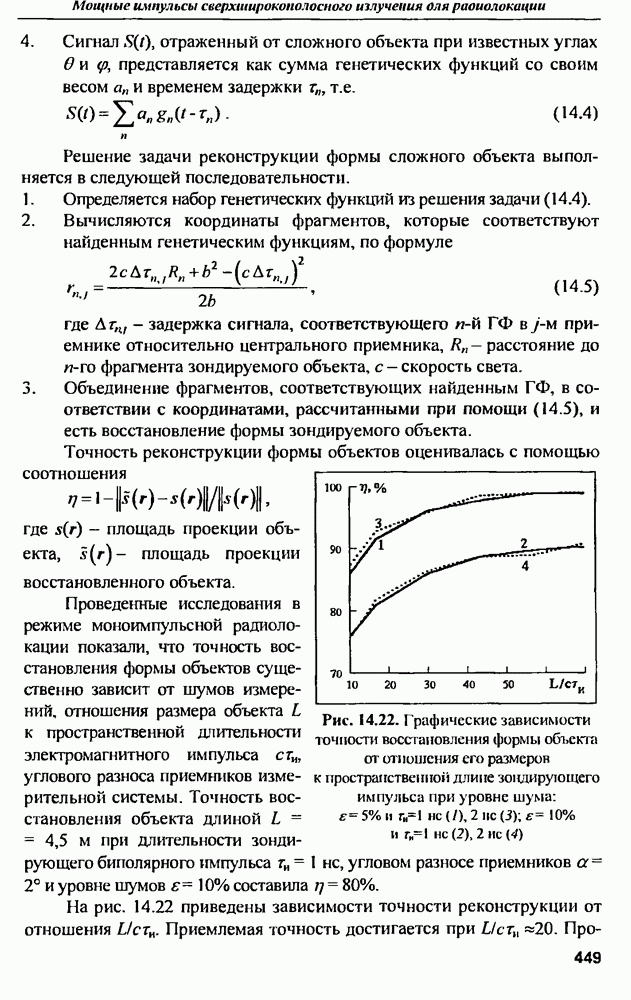
Результат расчета начальной части реакции дипольной антенны с указанными параметрами на воздействие в виде короткого гауссовского импульса приведена на рис. 9.14.
Анализ  показывает, что интервалу времени 6,7 нс, за который электромагнитная волна пройдет 2 м, т.е. дойдет до концов дипольной антенны и отразившись от них вернется в центр антенны, соответствует интервалу между соседними однополярпыми выбросами на
показывает, что интервалу времени 6,7 нс, за который электромагнитная волна пройдет 2 м, т.е. дойдет до концов дипольной антенны и отразившись от них вернется в центр антенны, соответствует интервалу между соседними однополярпыми выбросами на  Именно этот интервал и несет в себе информацию о геометрических размерах (длине) антенны. Ширина выбросов
Именно этот интервал и несет в себе информацию о геометрических размерах (длине) антенны. Ширина выбросов  примерно соответсвует эффективной длительности возбуждающего импульса, т.е. не содержит информации о форме антенны. Следует отметить, что для извлечения информации о радиусах цилиндров, из которых выполнена антенна, необходимо длительность импульса задать такой, чтобы обеспечить ширину его спектра порядка
примерно соответсвует эффективной длительности возбуждающего импульса, т.е. не содержит информации о форме антенны. Следует отметить, что для извлечения информации о радиусах цилиндров, из которых выполнена антенна, необходимо длительность импульса задать такой, чтобы обеспечить ширину его спектра порядка  рис. 9.12), т.е. в данном случае уменьшить длительность импульса примерно в 10 раз.
рис. 9.12), т.е. в данном случае уменьшить длительность импульса примерно в 10 раз.
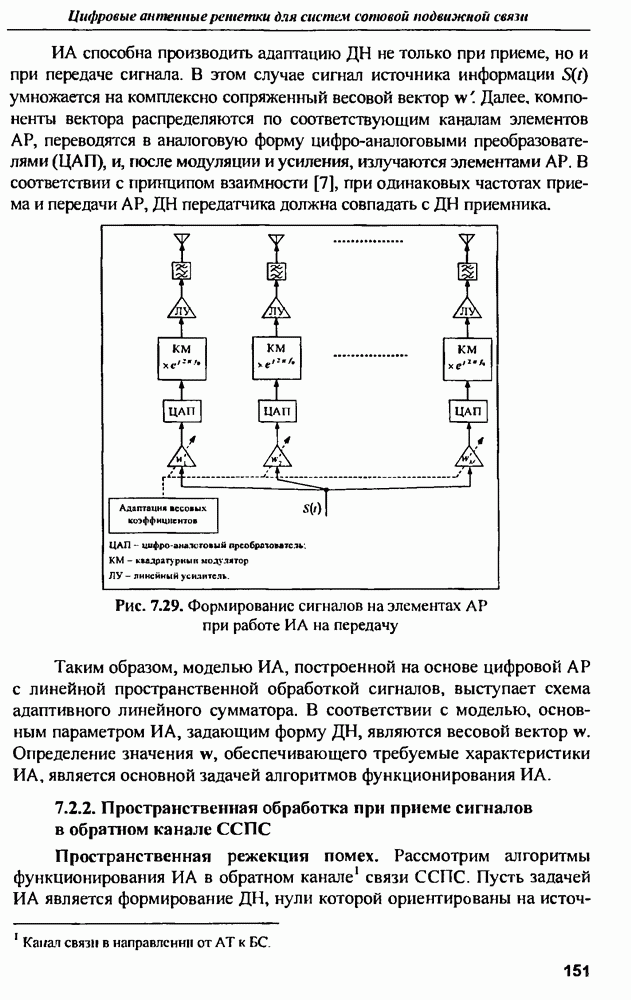
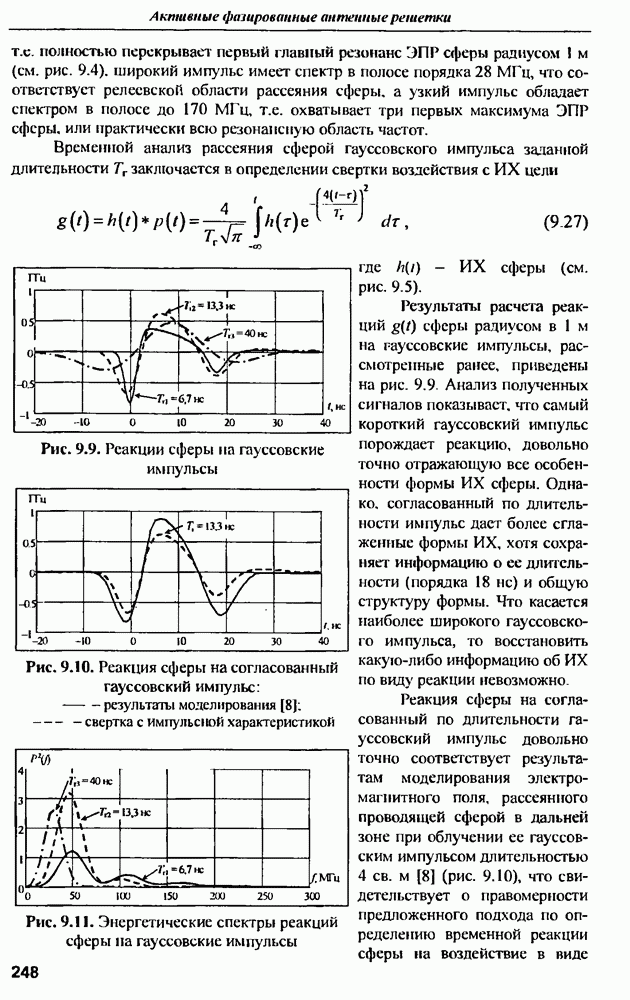
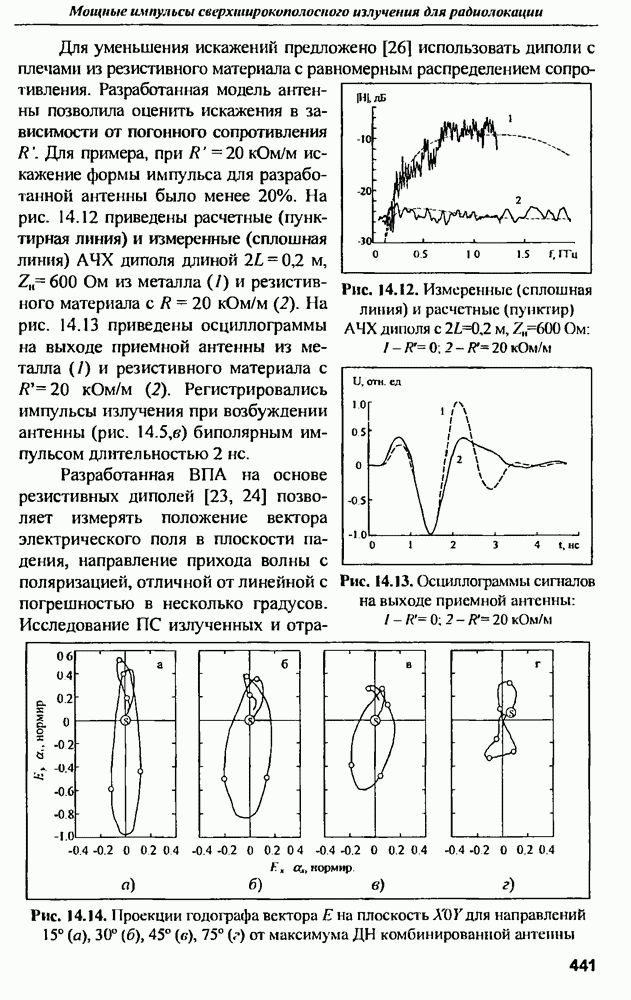
График энергетического спектра реакции антенны на гауссовский импульс приведен на рис. 9.15. Энергетический спектр является квадратом модуля преобразования Фурье от временной реакции антенны на соответствующий гауссовский импульс.
Анализ, спектра показывает, что ЭПР вибраторной антенны имеет явно выраженные резонансные частоты, соответствующие длинам волн


Рис. 9.14. Начальная часть нормированной  тонкой дипольной антенны
тонкой дипольной антенны 

Рис. 9.15. Энергетический спектр реакции дипольной антенны длиной  на гауссовский импульс длительностью
на гауссовский импульс длительностью  не
не
Положение резонансных частот приближенно соответствует зависимости

т.е. резонансы наблюдаются на частотах примерно  и т.д.
и т.д.  По виду частотной или импульсной характеристик тонкого цилиндра можно ориентировочно определить его длину, т.е. рассеянное поле содержит в себе информацию о геометрических размерах рассеивателя.
По виду частотной или импульсной характеристик тонкого цилиндра можно ориентировочно определить его длину, т.е. рассеянное поле содержит в себе информацию о геометрических размерах рассеивателя.
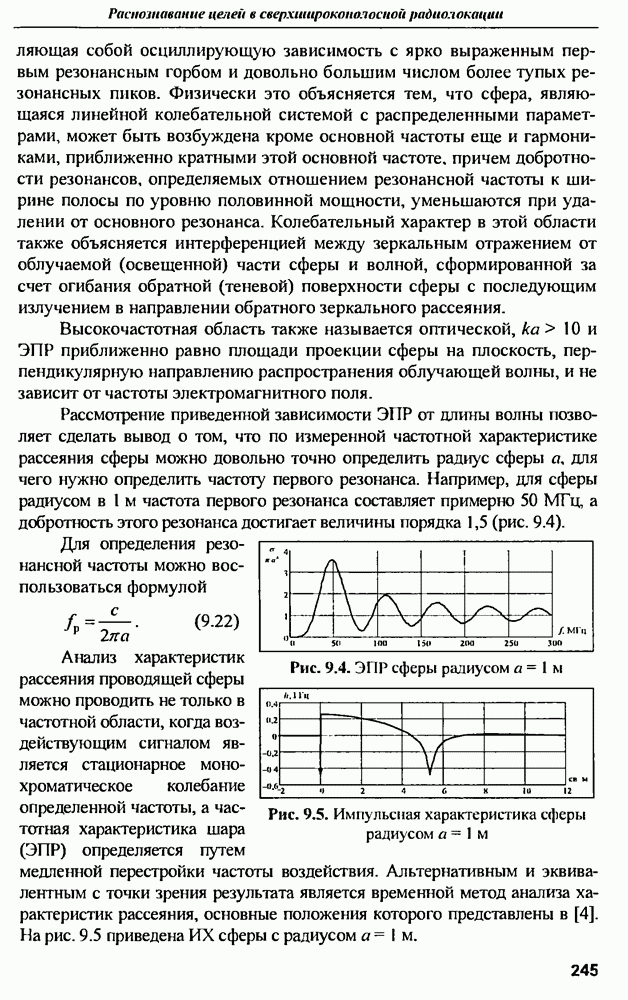
Микрополосковая прямоугольная антенна. Многие рассеиватели на практике содержат в своем составе или сами являются тонкими прямоугольными идеально проводящими пластинами. Поэтому исследование характеристик рассеяния прямоугольной пластины является
весьма интересным и важным для практики. Кроме того, такие прямоугольные пластины могут использоваться для создания сверхширокополосных антенн, частотные и импульсные характеристики которых определяются размерами сторон прямоугольника.
Частотная характеристика рассеяния прямоугольной пластины обладает резонансггьтми свойствами, которые в некотором смысле напоминают резонансные свойства частотной характеристики тонкой дипольной антенны, поскольку при уменьшении отношения ширины прямоугольной антенны к ее длине ( и менее) она асимптотически переходит в диполь.
и менее) она асимптотически переходит в диполь.
В [13] приведены результаты исследования частотных и импульсных характеристик рассеяния прямоугольной пластины для разных отношений ее длины к ширине. Теоретггческий расчет проводился с помощью метода моментов, а экспериментальные результаты получены путем измерения откликов различных пластин на короткие импульсные воздействия, при этом частотные характеристики определялись путем взятия преобразования Фурье от  восстановленной из сигнала, рассеянного плоскостью.
восстановленной из сигнала, рассеянного плоскостью.
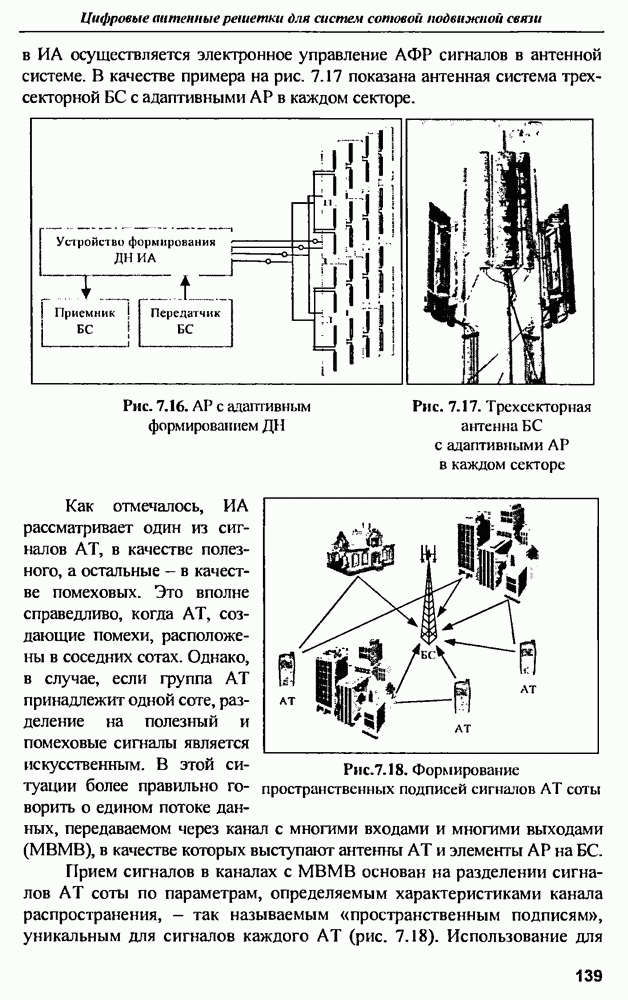
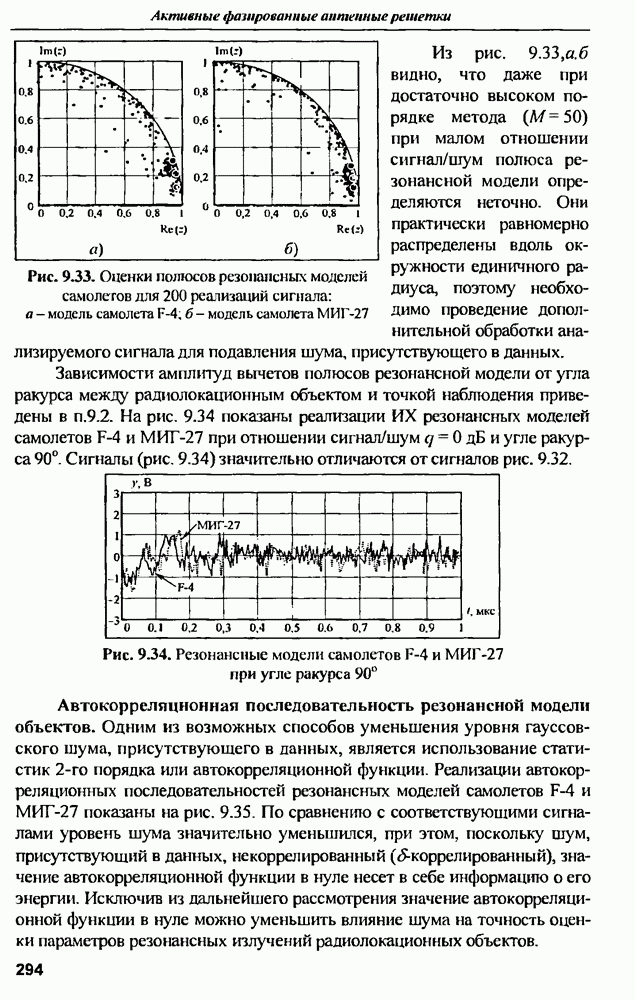
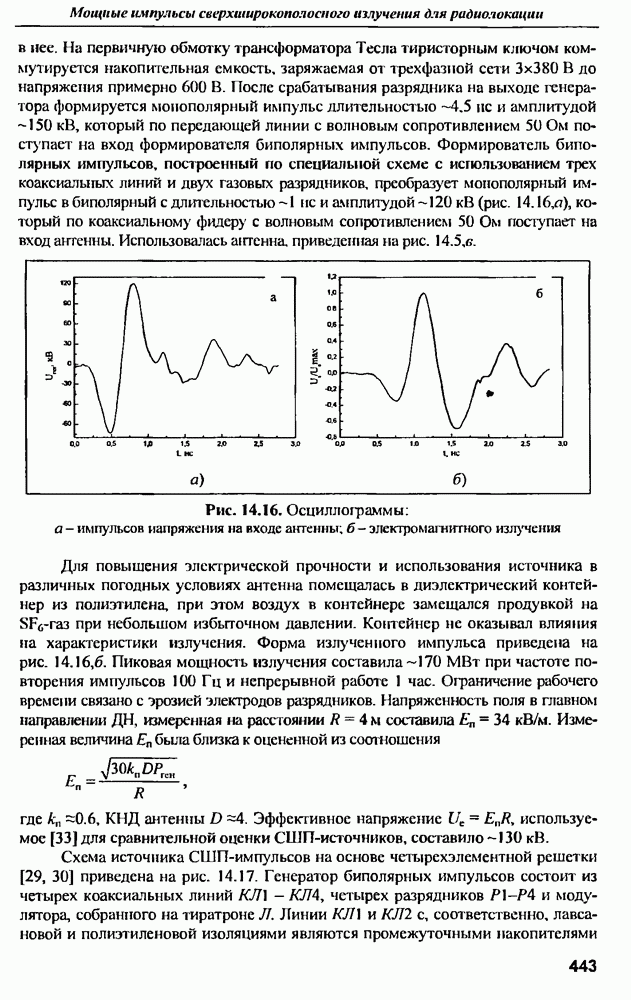
Аналогичные исследования, проведенные с помощью трехмерного конечно-разностного временного метода  -метод), представлены в [14, 15] применительно к анализу прямоугольной микрополосковой антенны ("patch-antenna"). Конфигурация антенны представлена на рис. 9.16.
-метод), представлены в [14, 15] применительно к анализу прямоугольной микрополосковой антенны ("patch-antenna"). Конфигурация антенны представлена на рис. 9.16.
Антенна возбуждается коротким гауссовским импульсом Эффективная длительность импульса составляет  что соответствует эффективной ширине спектра
что соответствует эффективной ширине спектра  Интервал дискретизации при моделировании составлял
Интервал дискретизации при моделировании составлял  т.е. частота дискретизации
т.е. частота дискретизации  .
.

Рис. 9.16. Конфигурация прямоугольной микрополосковой антенны

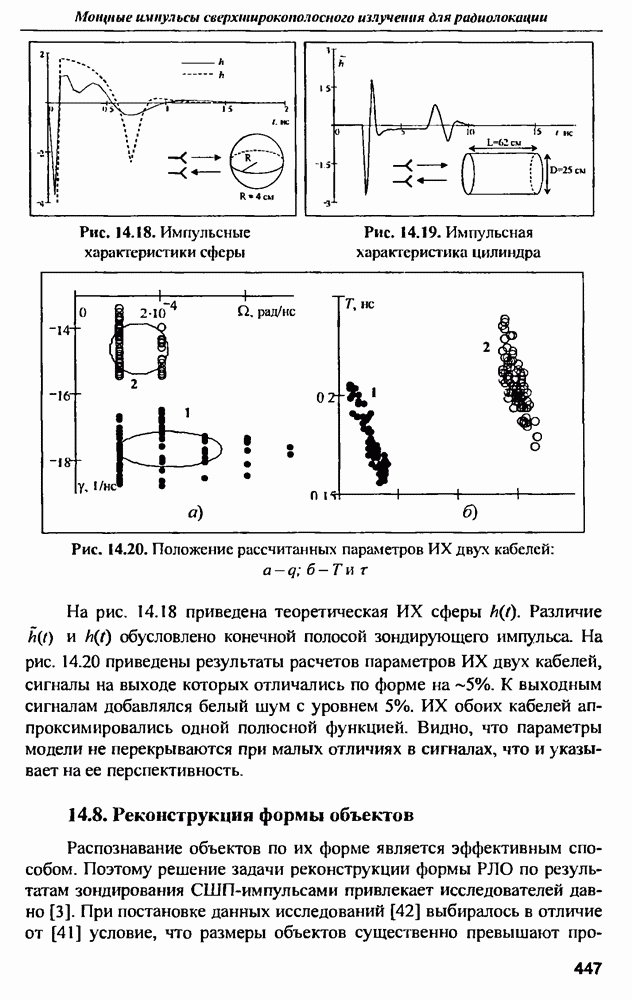
Рис. 9.17. Импульсная характеристика прямоугольной микрополосковой антенны

Рис. 9.18. Передаточная функция прямоугольной микрополосковой антенны
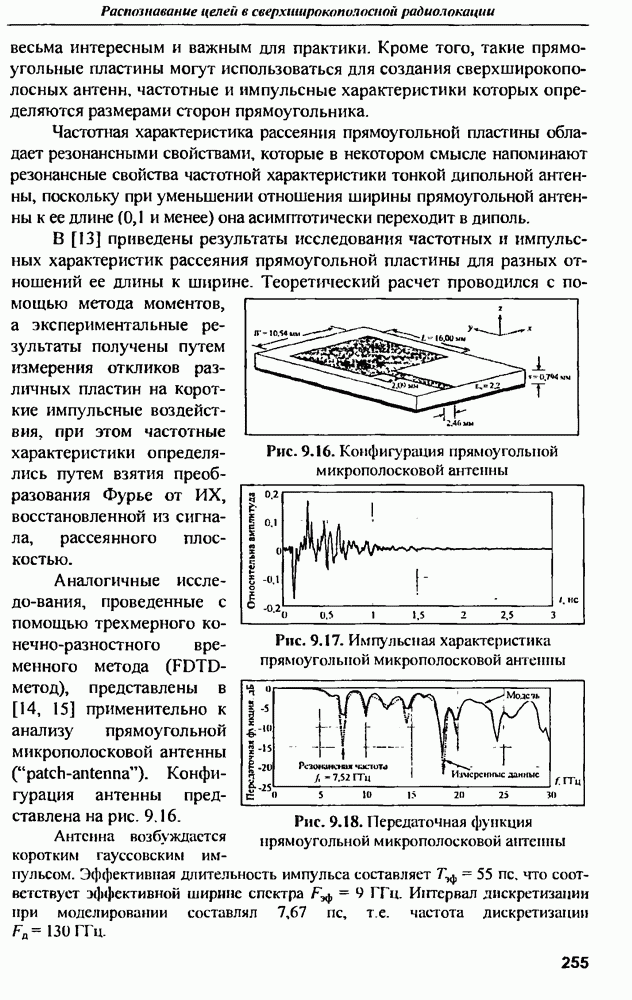
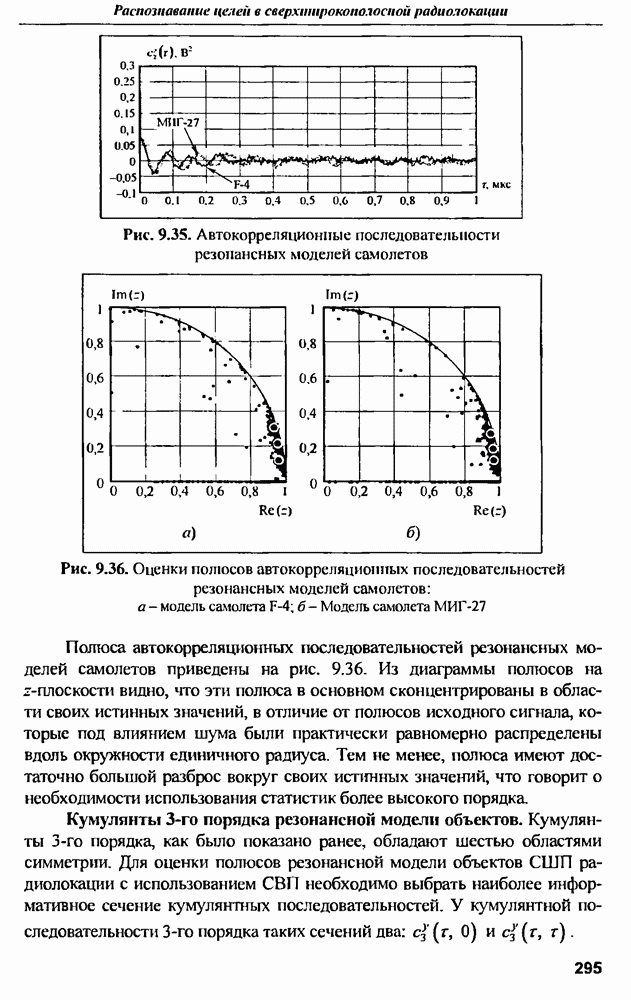
На рис. 9.17 представлены результаты моделирования  прямоугольной микрополосковой антенны 114].
прямоугольной микрополосковой антенны 114].
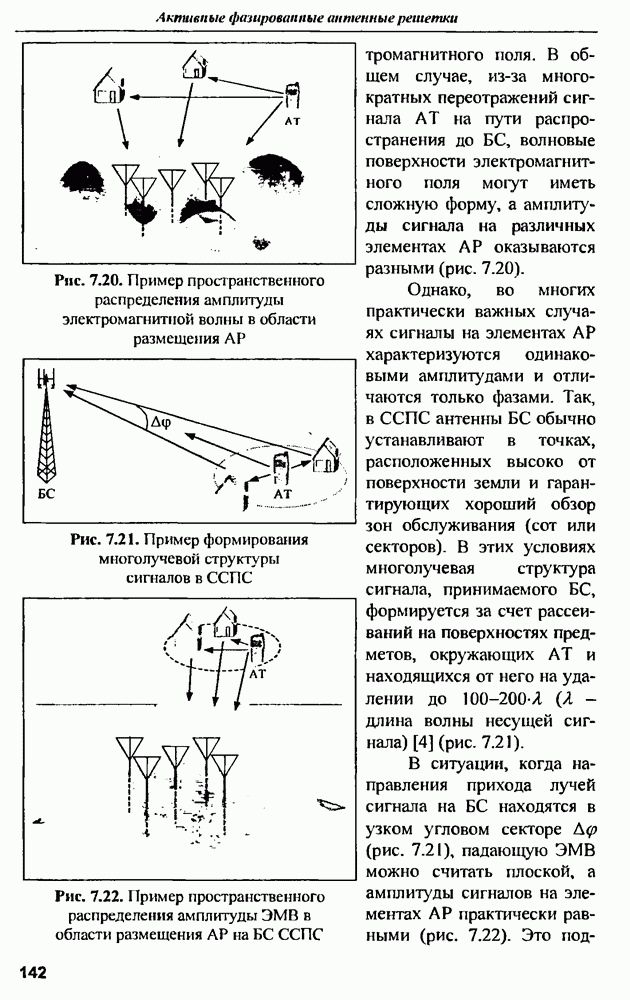
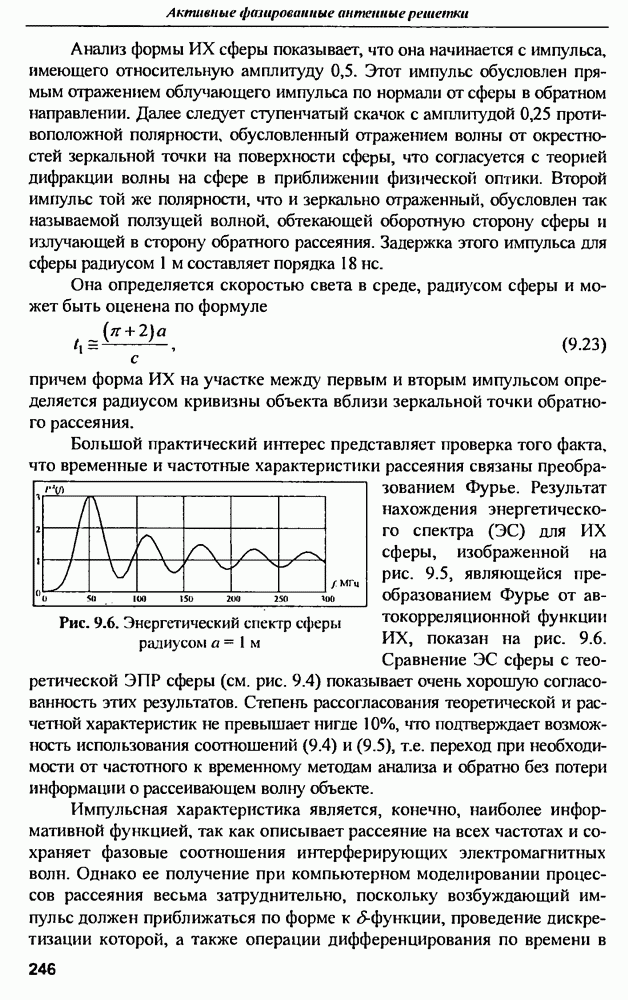
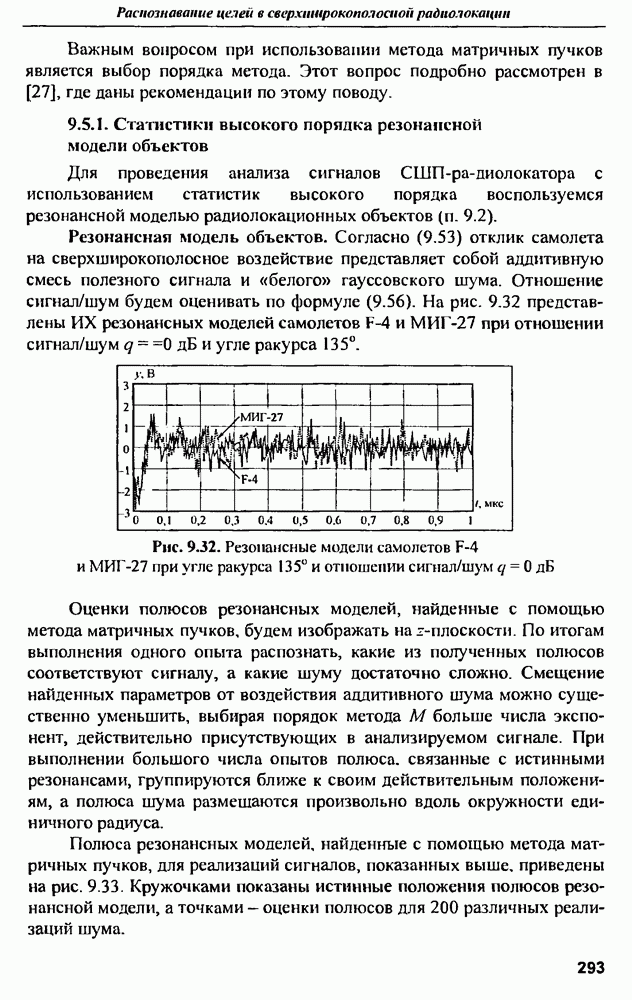
Преобразование Фурье от  прямоугольной антенны дает передаточную функцию (рис. 9.18), на рисунке для сравнения приведены результаты измерения передаточной функции (модуля комплексного входного сопротивления) реальной антенны в диапазоне частот от 0 до 30 ГГц. Сопоставление графиков показывает их высокую согласованность. Особенно важным параметром является резонансная частота антенны, которая по результатам измерений и моделирования составила примерно 7.52 ГГц.
прямоугольной антенны дает передаточную функцию (рис. 9.18), на рисунке для сравнения приведены результаты измерения передаточной функции (модуля комплексного входного сопротивления) реальной антенны в диапазоне частот от 0 до 30 ГГц. Сопоставление графиков показывает их высокую согласованность. Особенно важным параметром является резонансная частота антенны, которая по результатам измерений и моделирования составила примерно 7.52 ГГц.
Оцепим резонансную частоту по формуле [16]

где с - скорость света в вакууме:  относительная диэлектрическая проницаемость материала.
относительная диэлектрическая проницаемость материала.
Расчет, произведенный по формуле (9.46), подтверждает правильность нахождения резонансной частоты по результатам моделирования антенны.
В [15] приведена формула оценки частотного диапазона В. зависящего от размеров и материала антенны

где  ширина микрополосковой антенны;
ширина микрополосковой антенны;  длина микрополосковой антенны;
длина микрополосковой антенны;  - толщина микрополосковой антенны:
- толщина микрополосковой антенны:  рабочая длина волны.
рабочая длина волны.
Расчет по этой формуле дает полосу пропускания порядка 1%. что также соответствует результатам моделирования и измерений.
Прямоугольная микрополоековая антенна также проявляет свои резонансные свойства, а, следовательно, может быть идентифицирована по результатам сверхширокополосных измерений.
Проведен анализ временных и частотных характеристик рассеяния объектов относительно простых геометрических форм: сфера, цилиндр, прямоугольная пластина, также даны основные соотношения для теоретического анализа характеристик рассеяния объектов произвольной формы и определения передаточной частотной и импульсной характеристик рассеяния объектов.
В результате проведенного анализа можно сделать следующие выводы. 1. При рассмотрении частотной характеристики рассеяния любого объект а с конечными геометрическими размерами можно выделить три области частот:
низкочастотная область, — размеры объекта значительно меньше длины волны облучающего сигнала (область Рэлея);
резонансная область, - размеры объекта соизмеримы с длиной облучающей волны, в этой области возможно формирование резонансных токов на поверхности объекта, определяющих характеристики рассеянного поля;
высокочастотная область (оптическая область),  - длина волны значительно меньше размеров объекта и наблюдается рассеяние палающей волны на «блестящих» точках объекта.
- длина волны значительно меньше размеров объекта и наблюдается рассеяние палающей волны на «блестящих» точках объекта.
2. Значения резонансных частот тел простой геометрической формы известны заранее, так как они непосредственно связаны с геометрическими размерами объекта, при этом можно выделить основную резонансную частоту, на которой наблюдается наиболее мощное рассеяние, и частоты приблизительно кратные этой основной частоте, соответствующие рассеянию «стоячих» волн более высокого порядка.
3 Для возбуждения колебаний в резонансной области частот объекта необходимо использовать возбуждающий импульс с полосой частот спектра, соответствующий резонансной области частот. При моделировании процессов рассеяния наиболее удобно пользоваться гауссовским импульсом или его производными по времени, поскольку этот импульс имеет гладкую форму и ограниченный спектр.
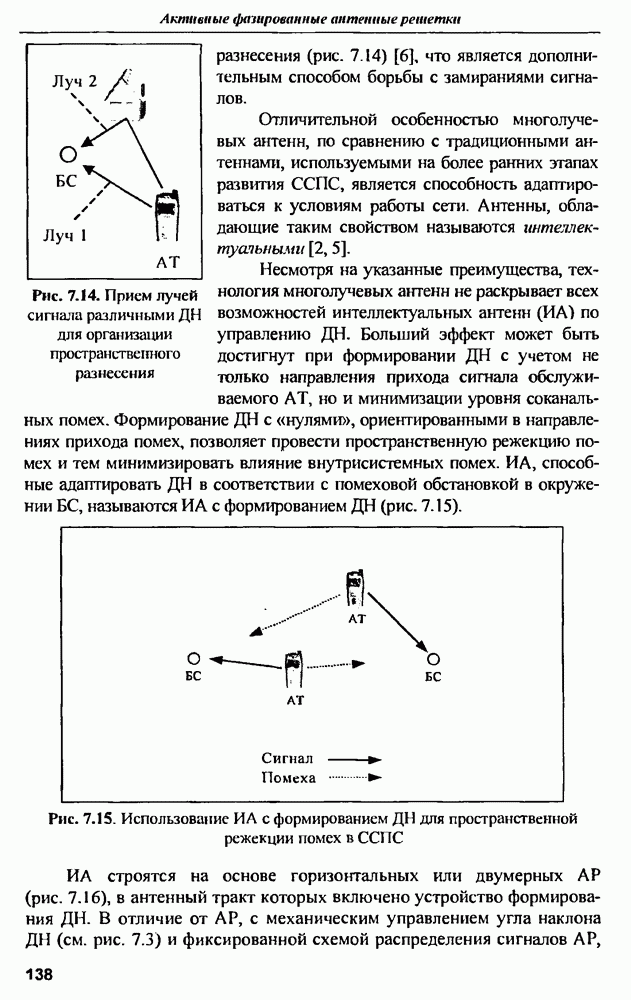
4. Импульсная характеристика рассеяния объекта является результатом преобразования Фурье от частотной характеристики, поэтому она не содержит никакой дополнительной информации о нем. Вместе с тем  является более удобной формой отображения спектральных свойств объекта в широкой полосе частот, поскольку несет в себе одновременно амплитудно-частотную и фазо-частотную информации об объекте, а ее измерение занимает значительно меньше времени, чем измерение частотной характеристики Поэтому определение спектральных параметров рассеяния объектов проводится во временной области по измеренной или восстановленной
является более удобной формой отображения спектральных свойств объекта в широкой полосе частот, поскольку несет в себе одновременно амплитудно-частотную и фазо-частотную информации об объекте, а ее измерение занимает значительно меньше времени, чем измерение частотной характеристики Поэтому определение спектральных параметров рассеяния объектов проводится во временной области по измеренной или восстановленной  объекта.
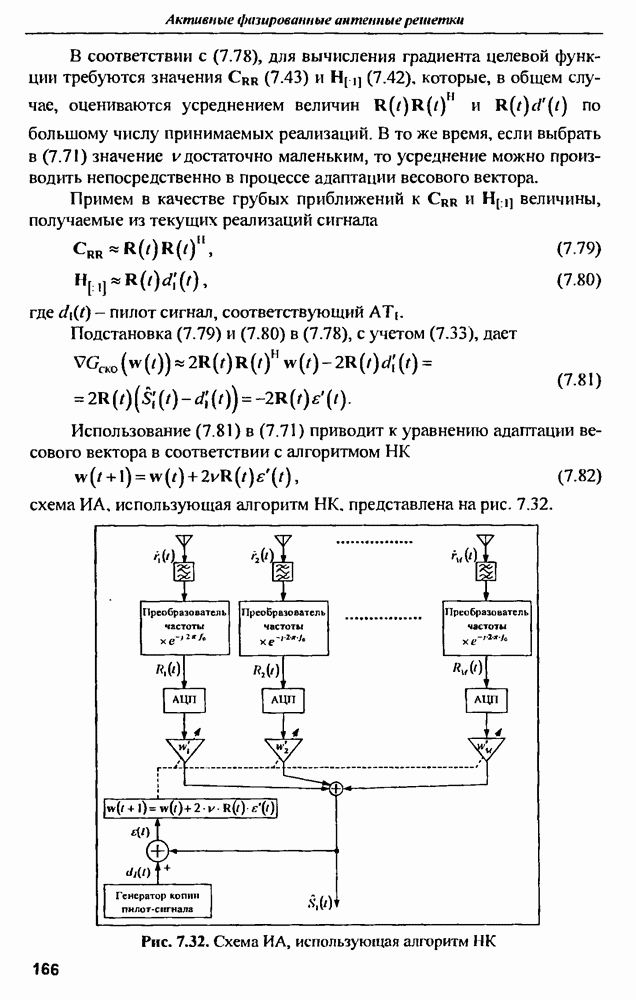
объекта.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
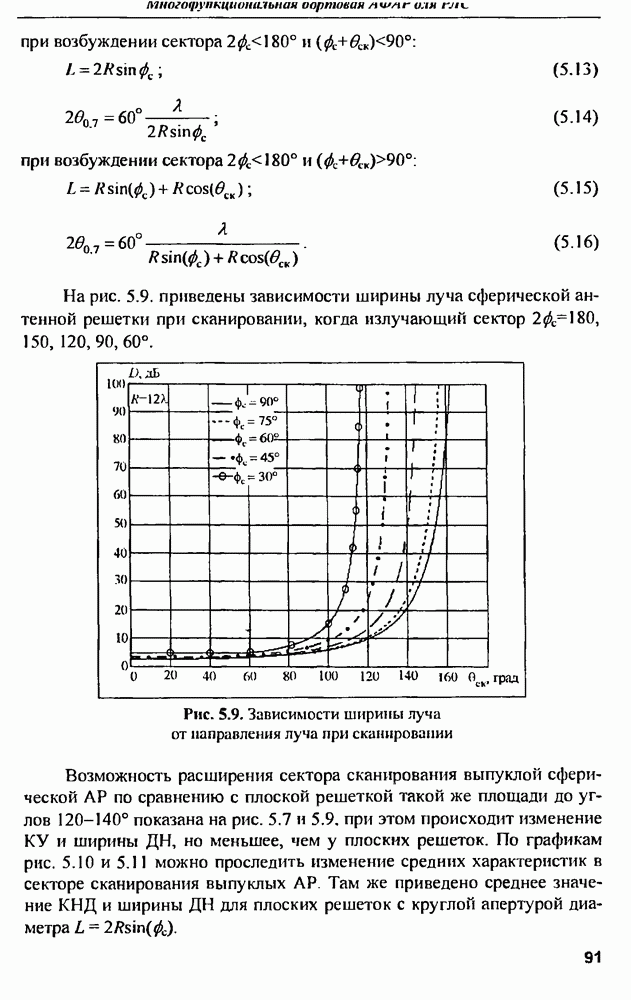
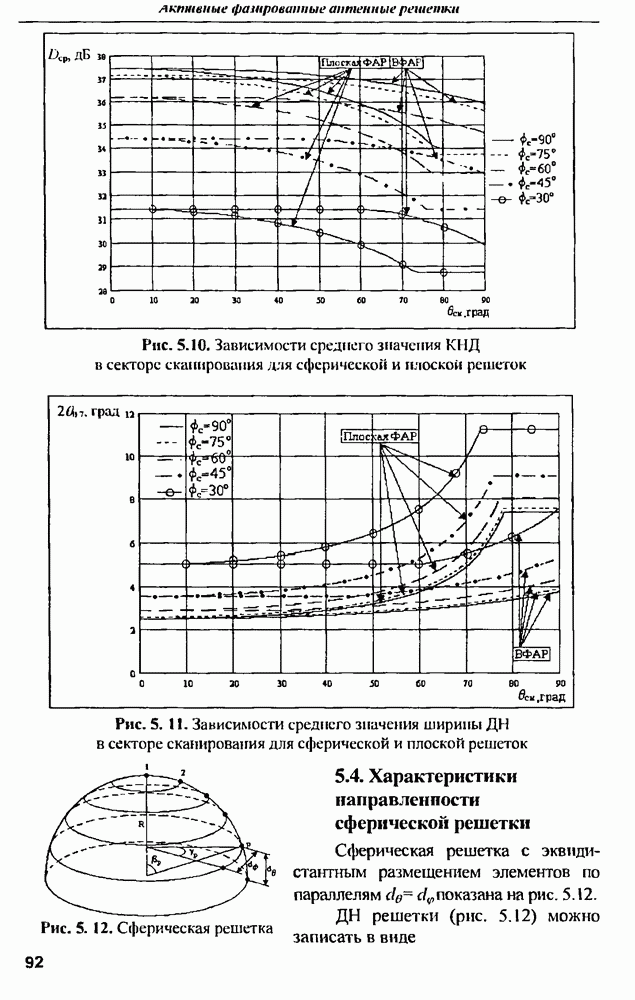
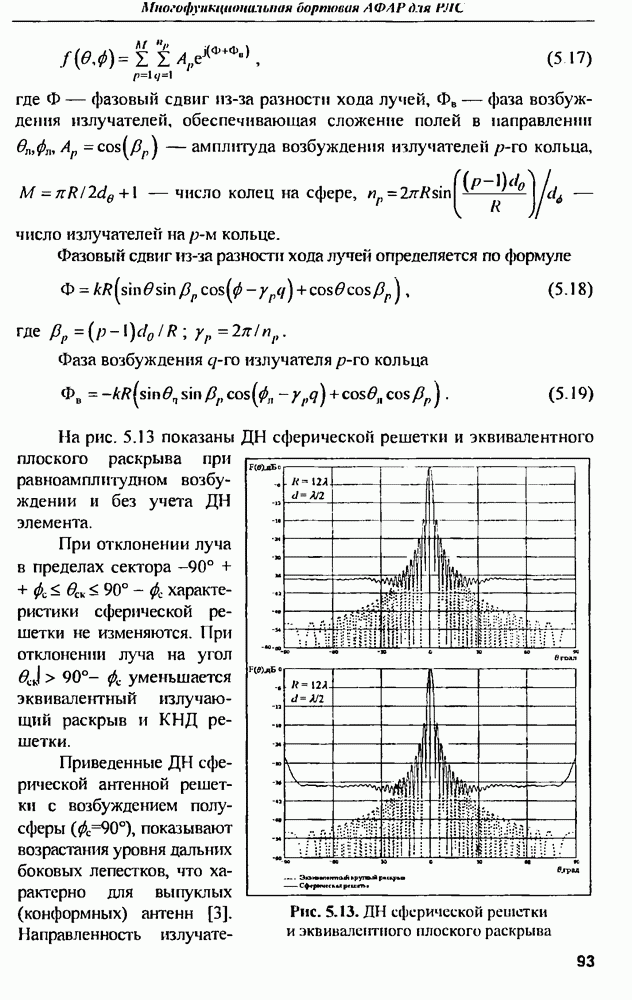
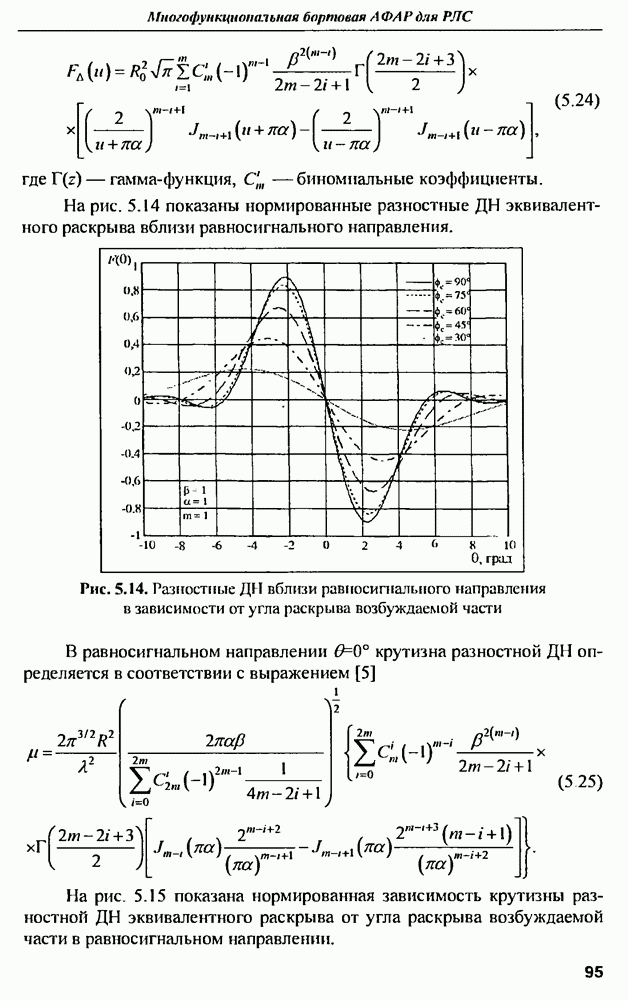
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
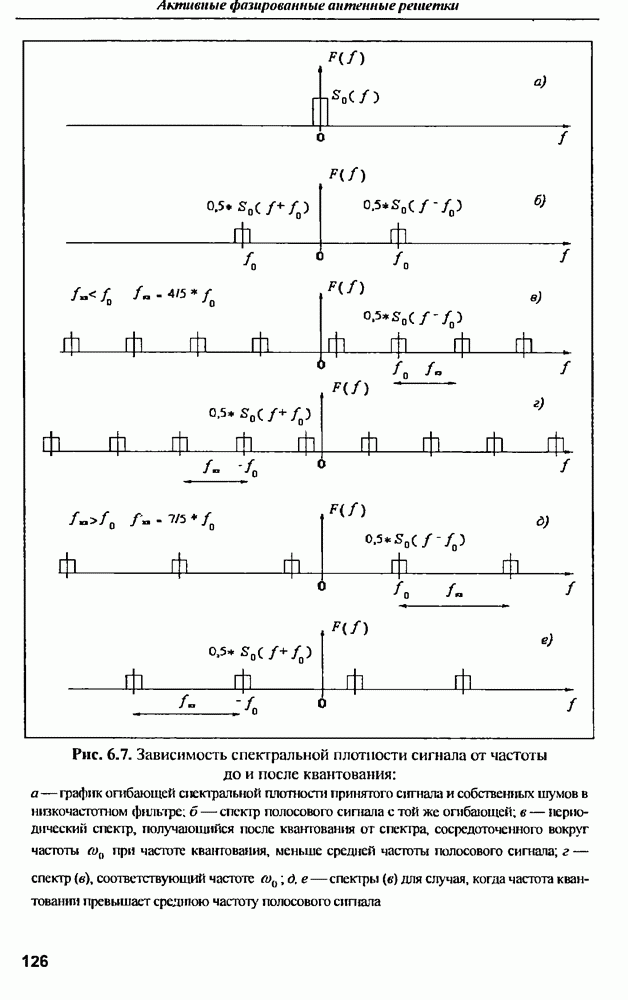
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
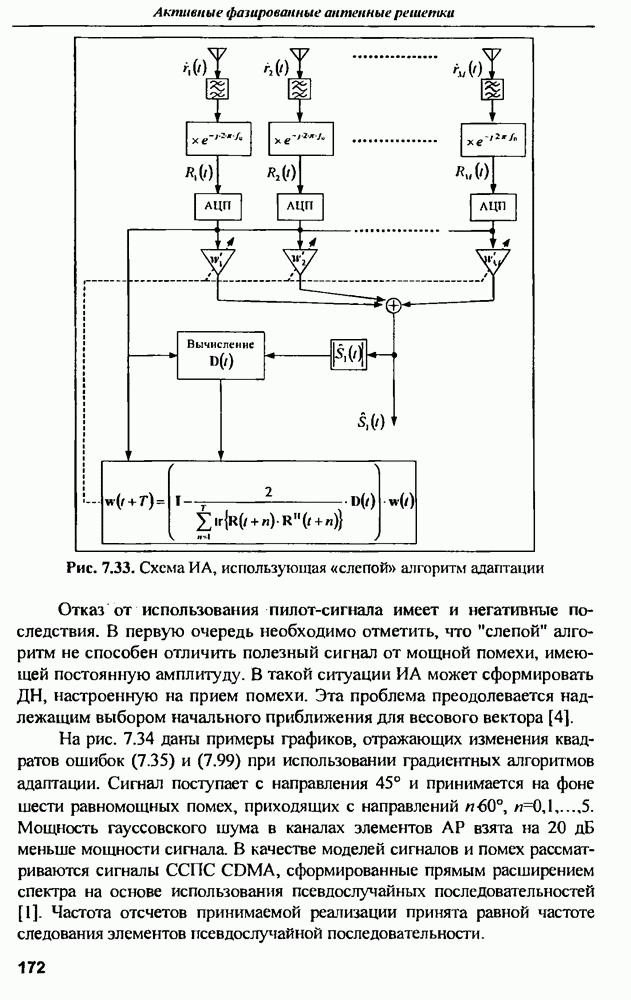
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
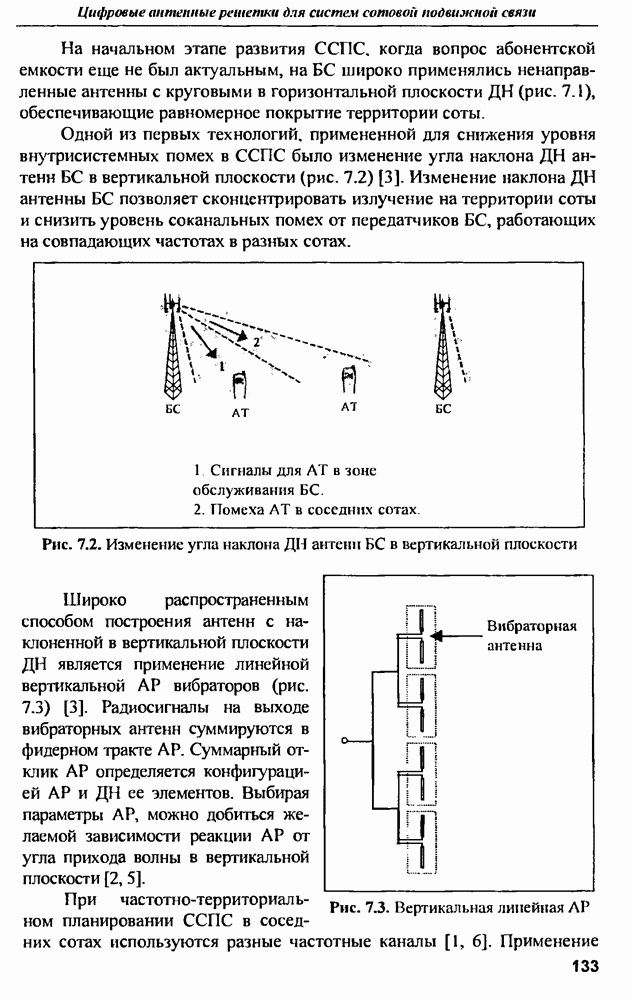
- 7.3.3. Абонентская емкость ССПС
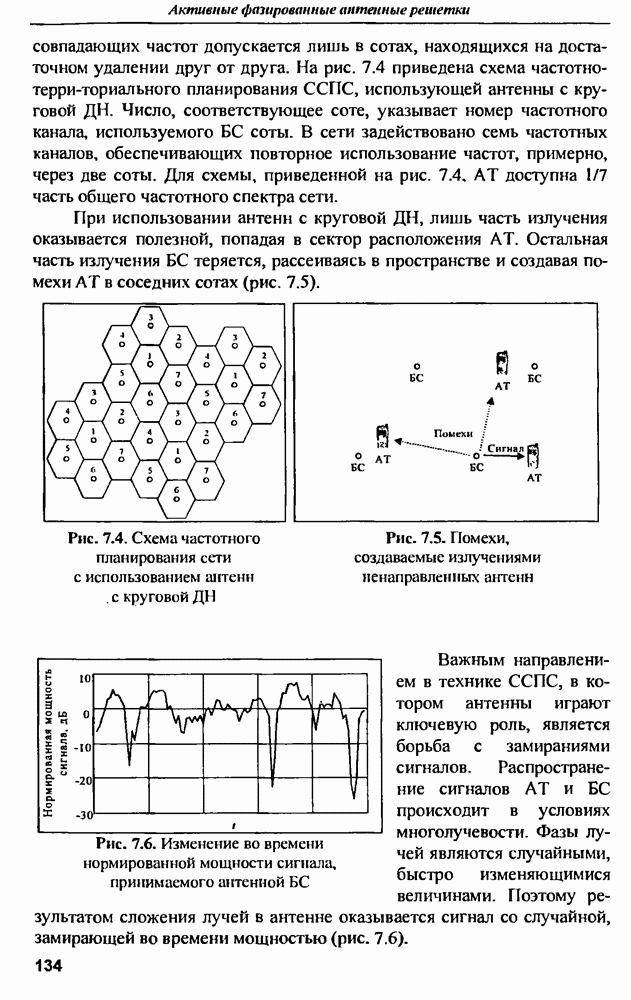
- 7.3.4. Качество связи
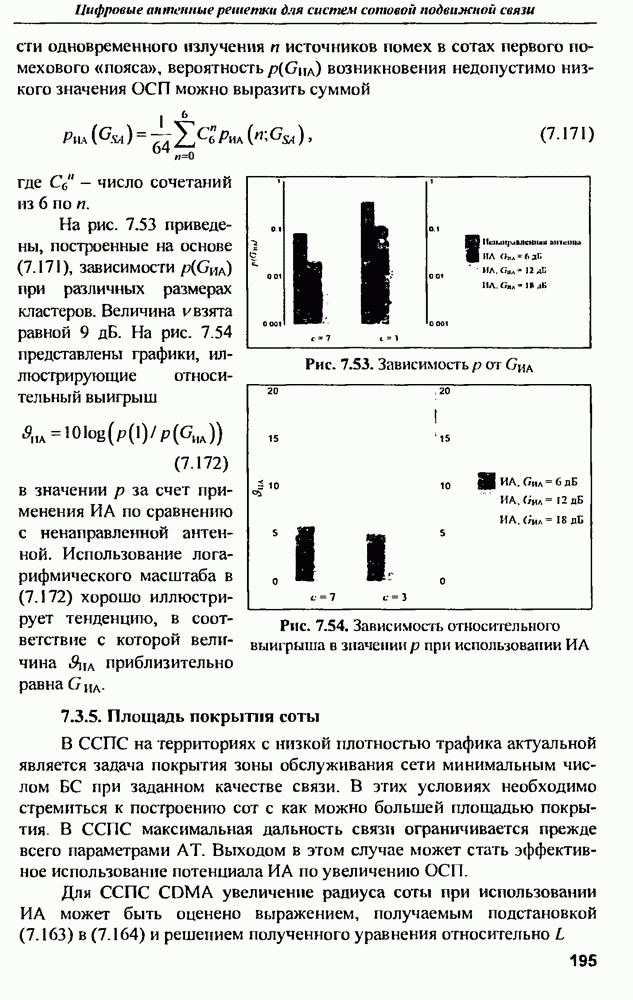
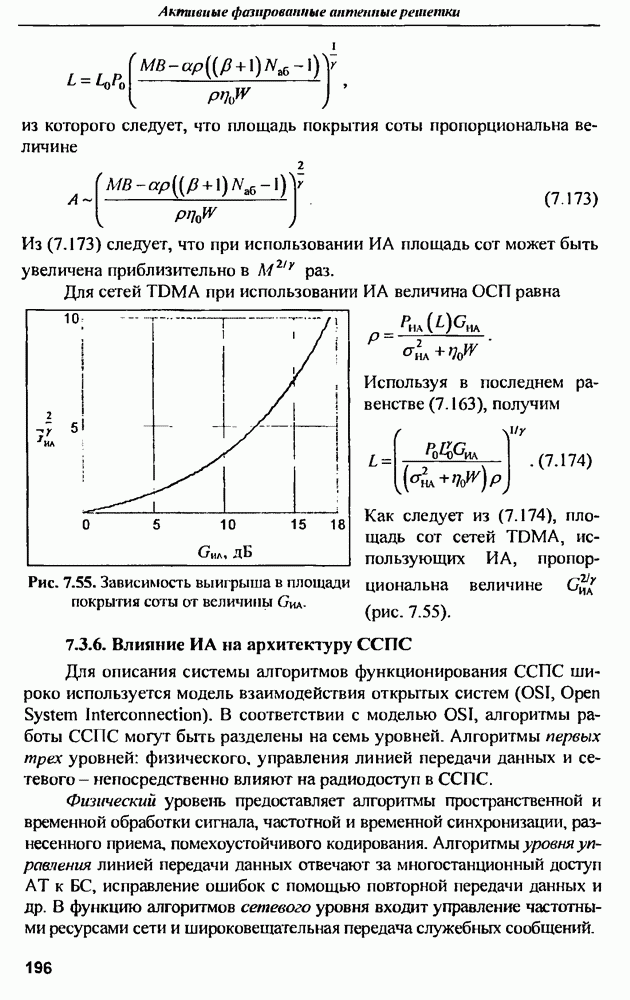
- 7.3.5. Площадь покрытия соты
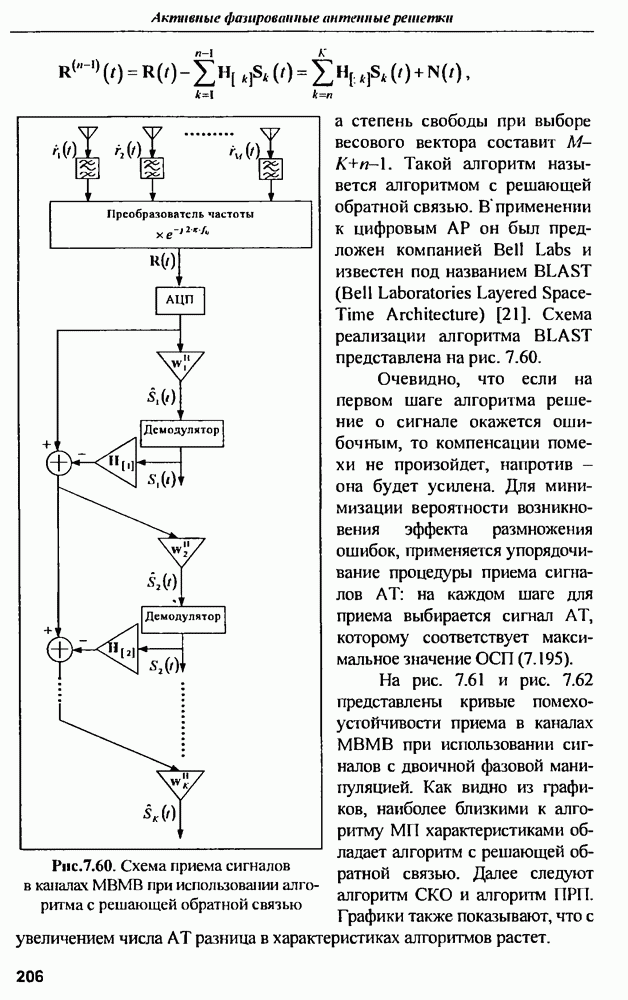
- 7.3.6. Влияние ИА на архитектуру ССПС
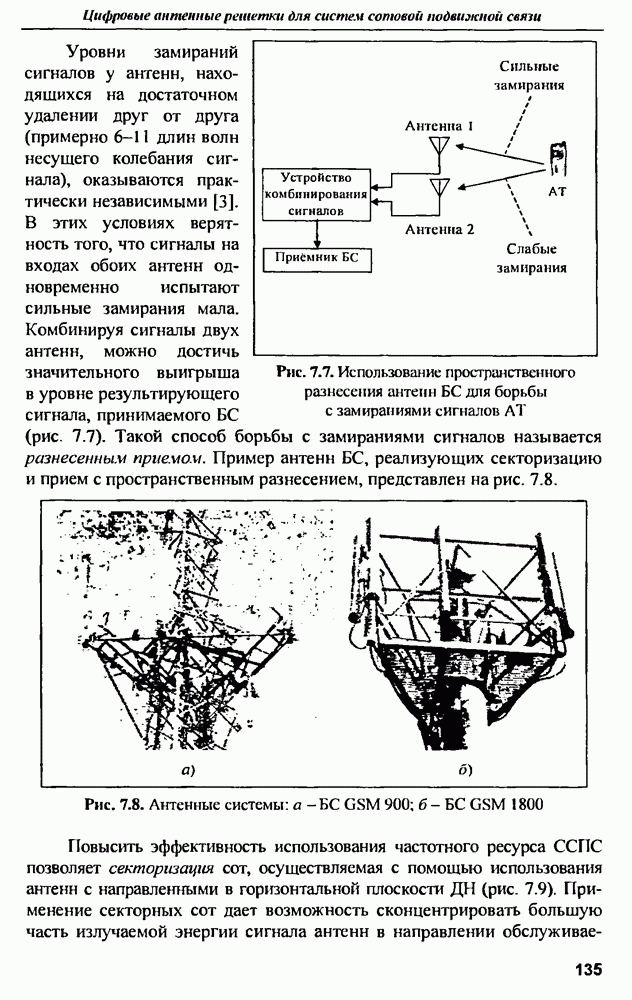
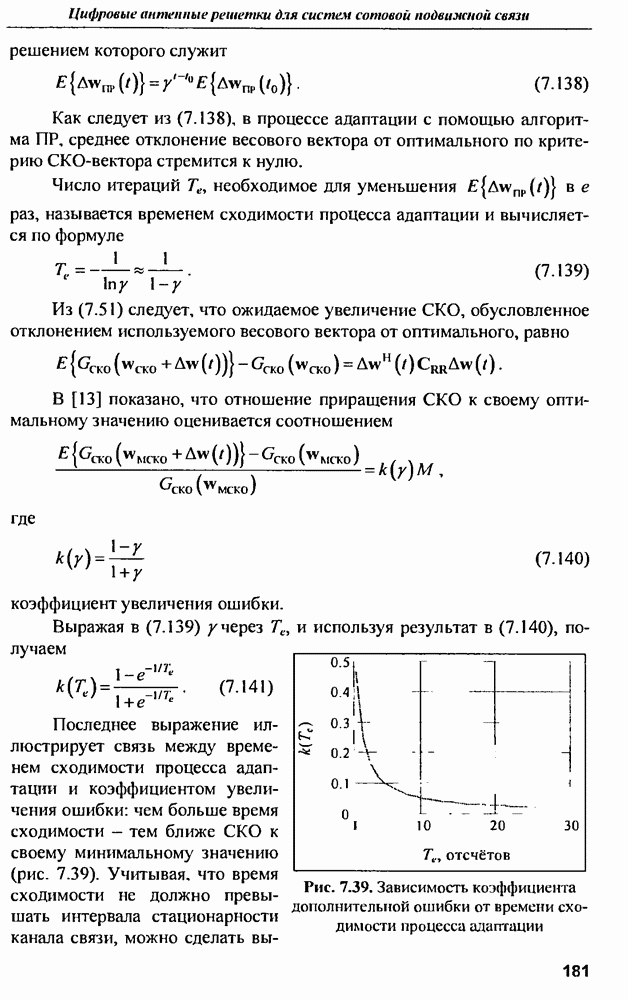
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
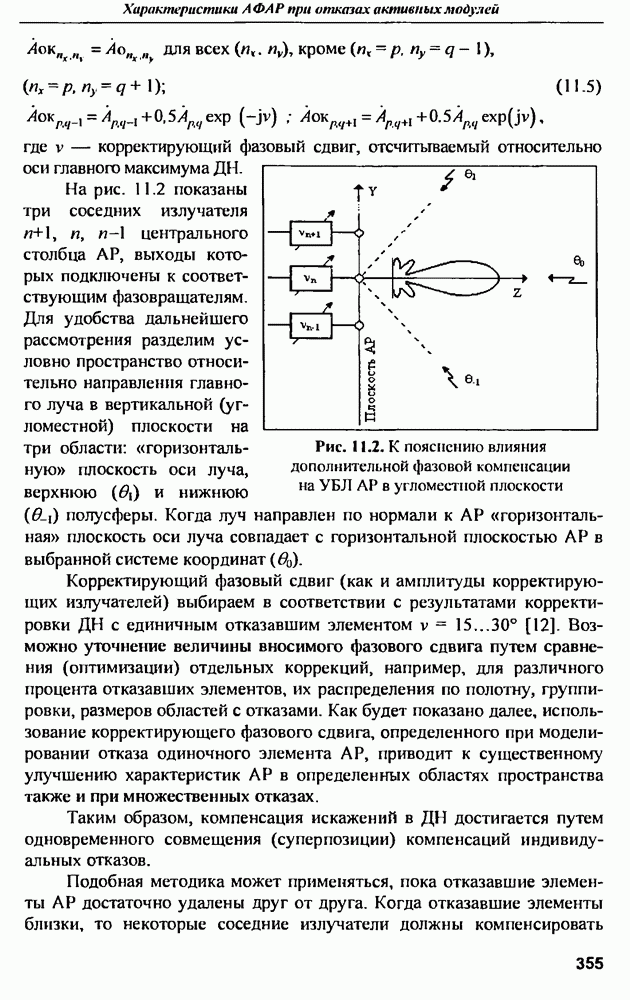
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
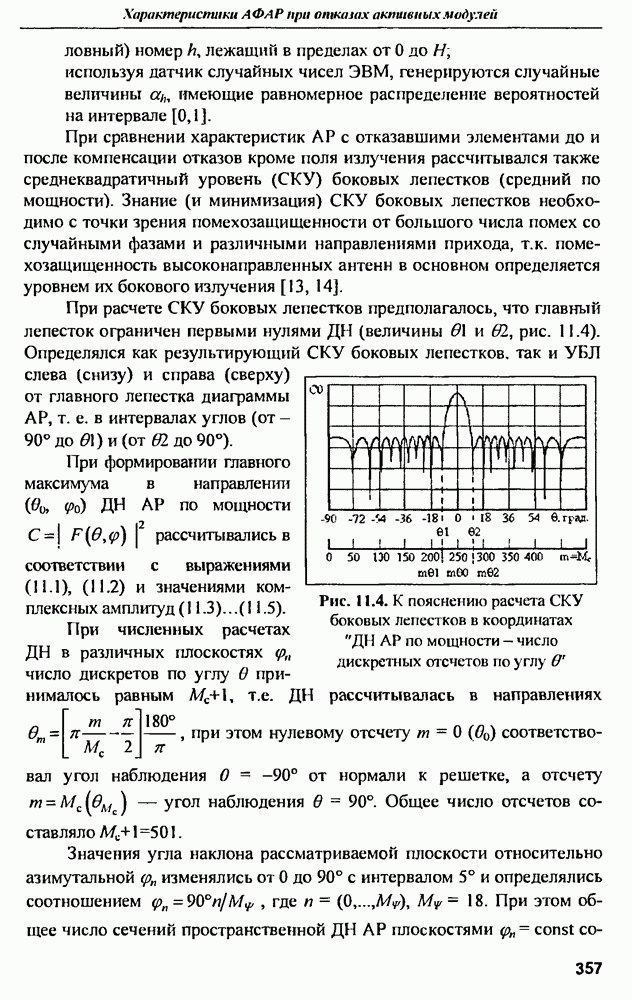
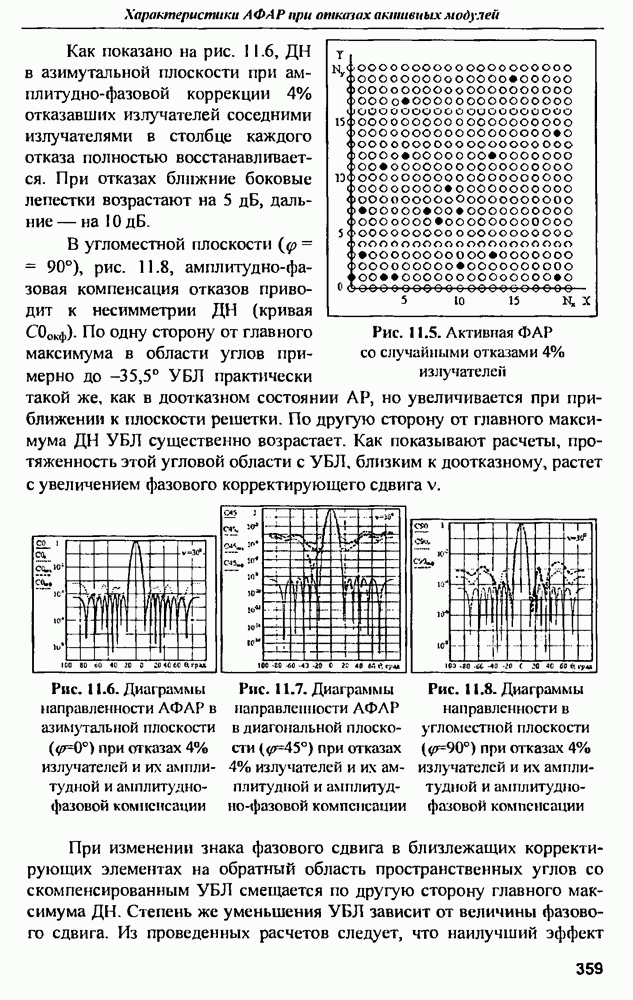
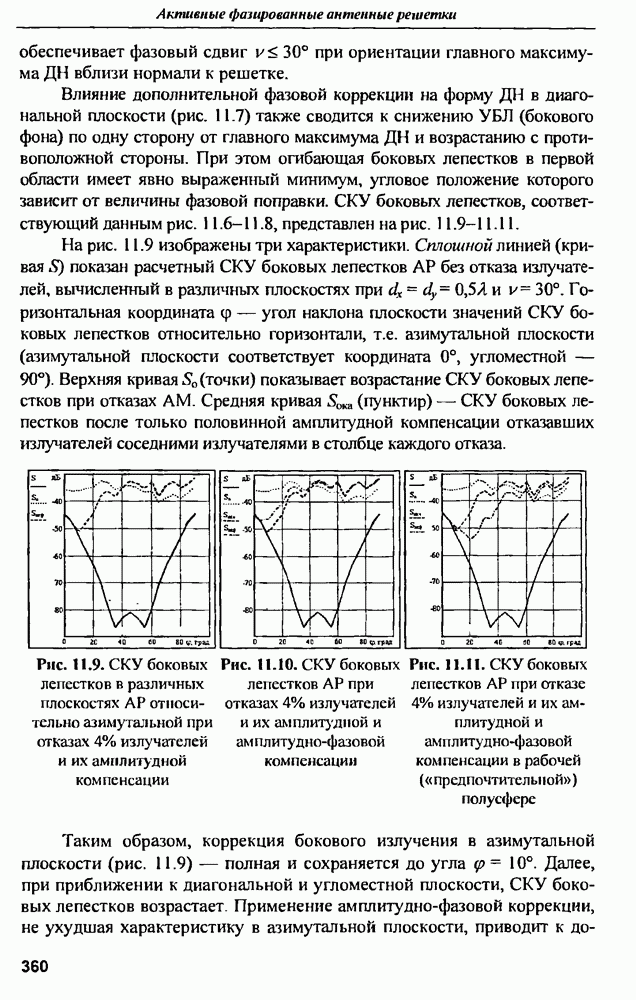
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
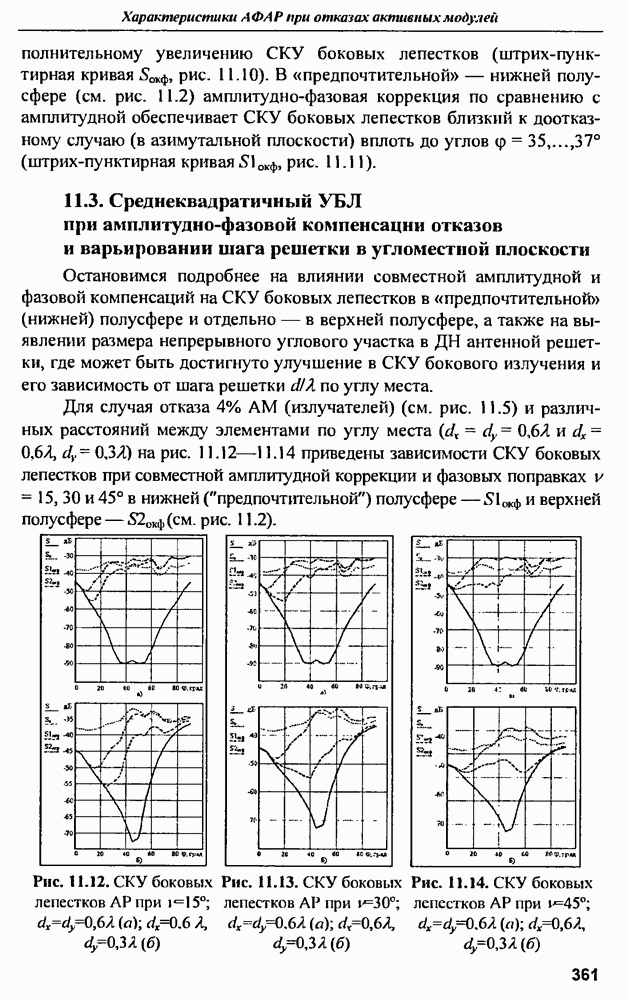
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
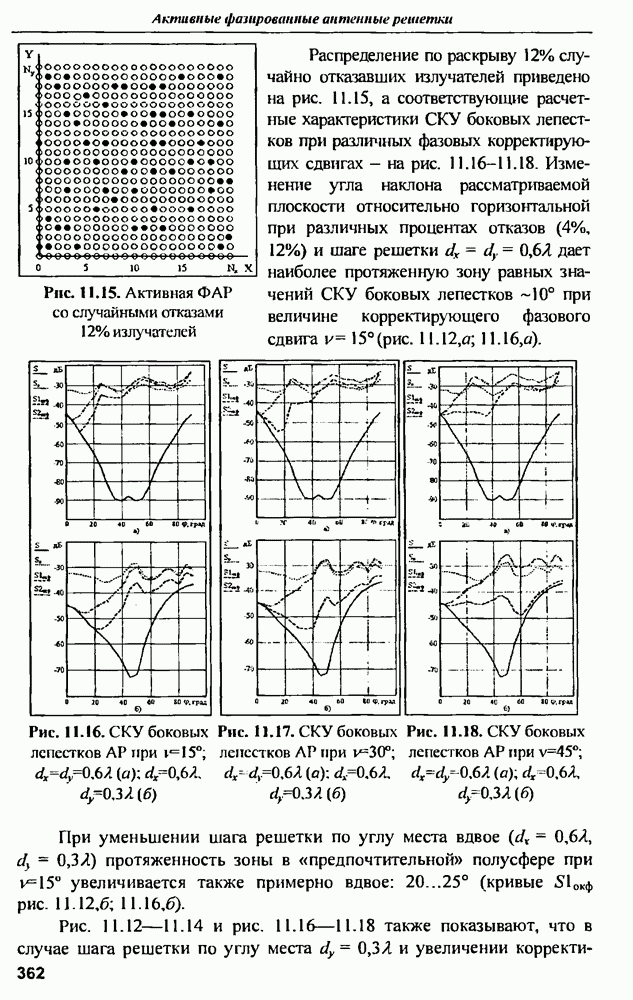
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
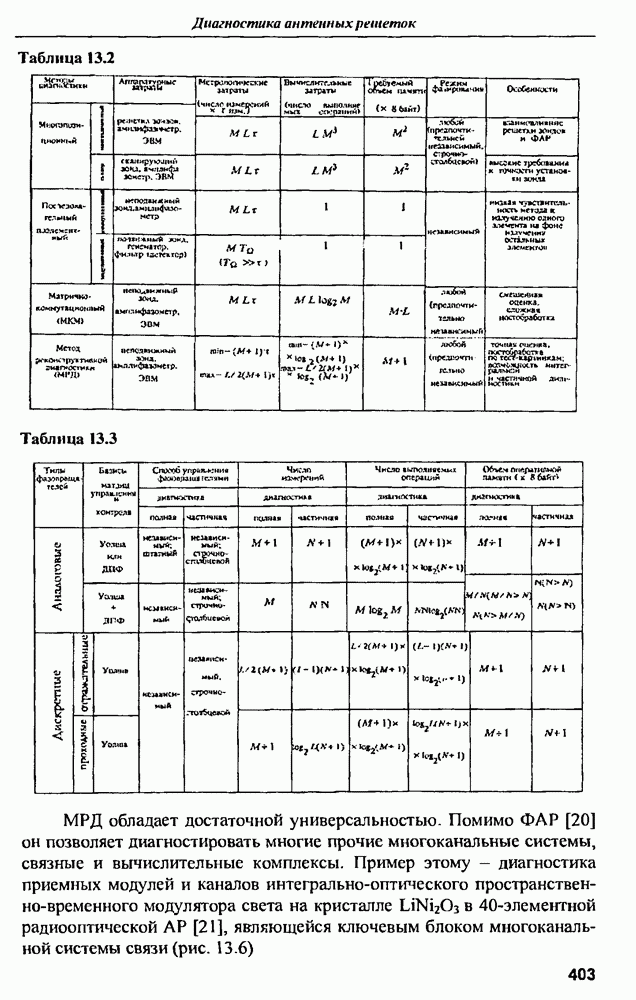
- ГЛАВА 13. Диагностика антенных решеток
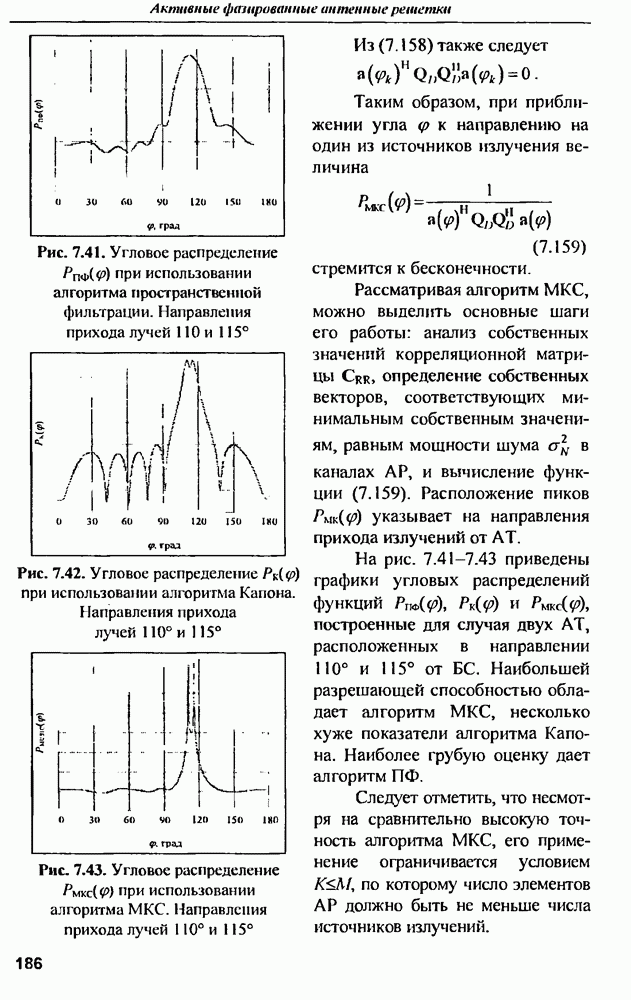
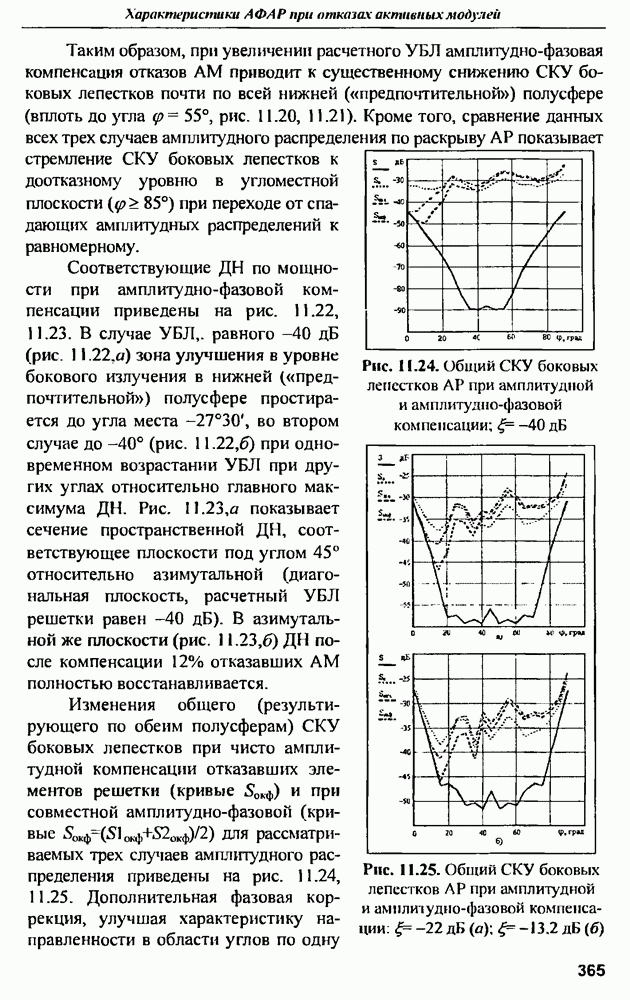
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
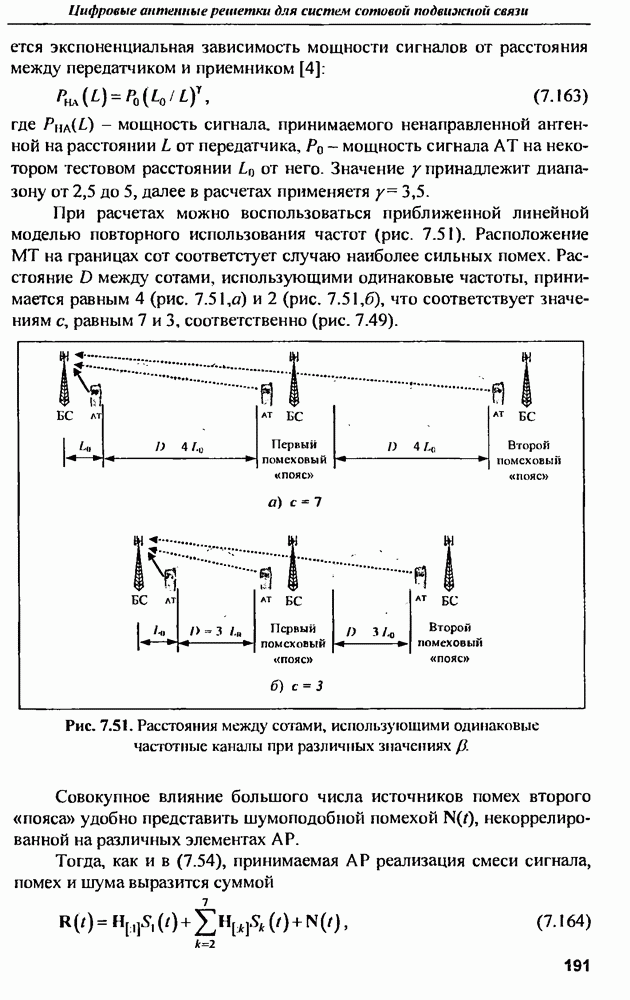
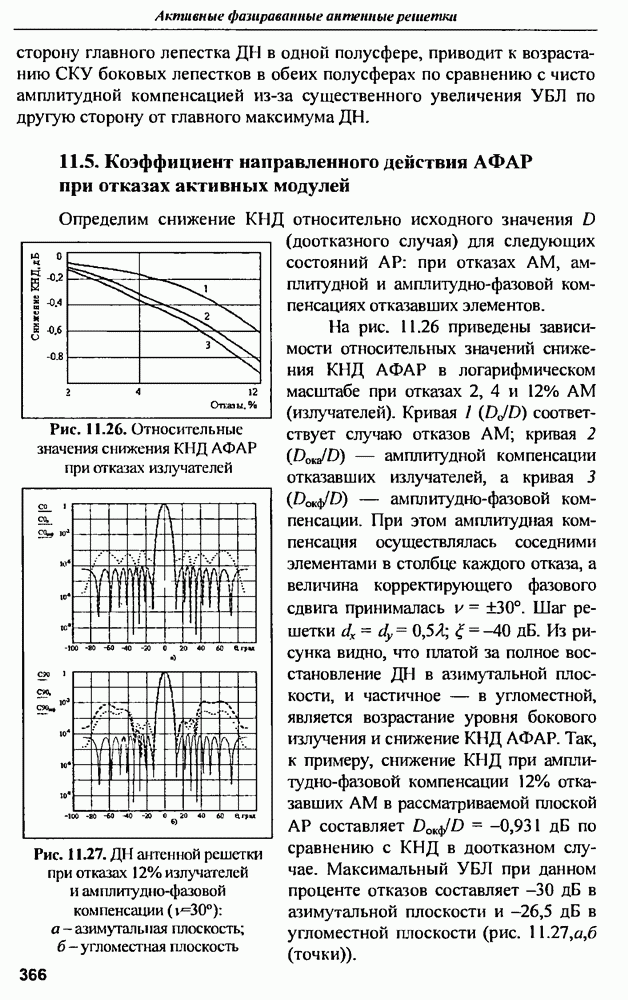
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
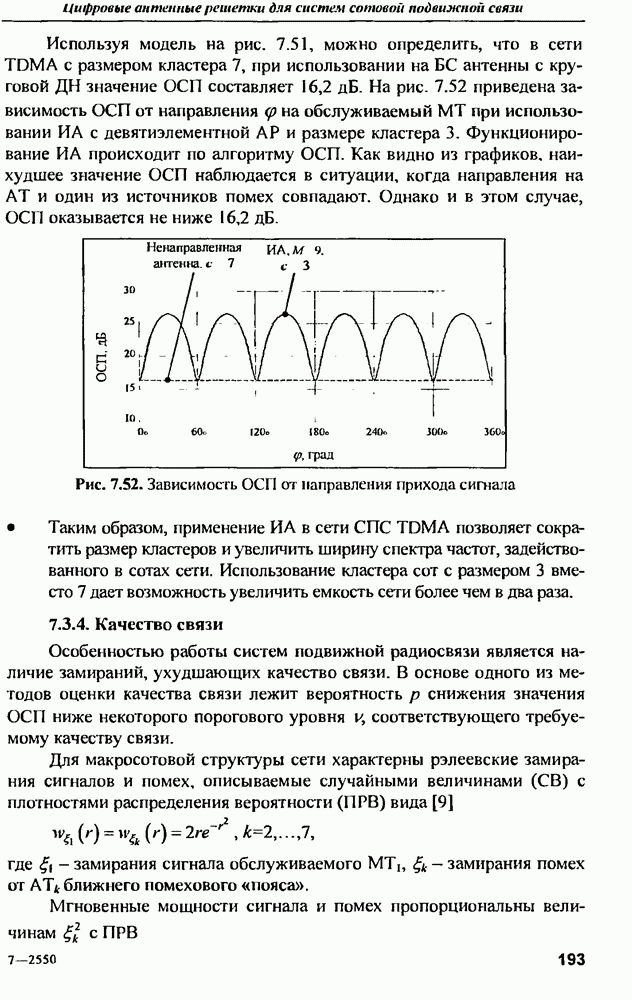
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
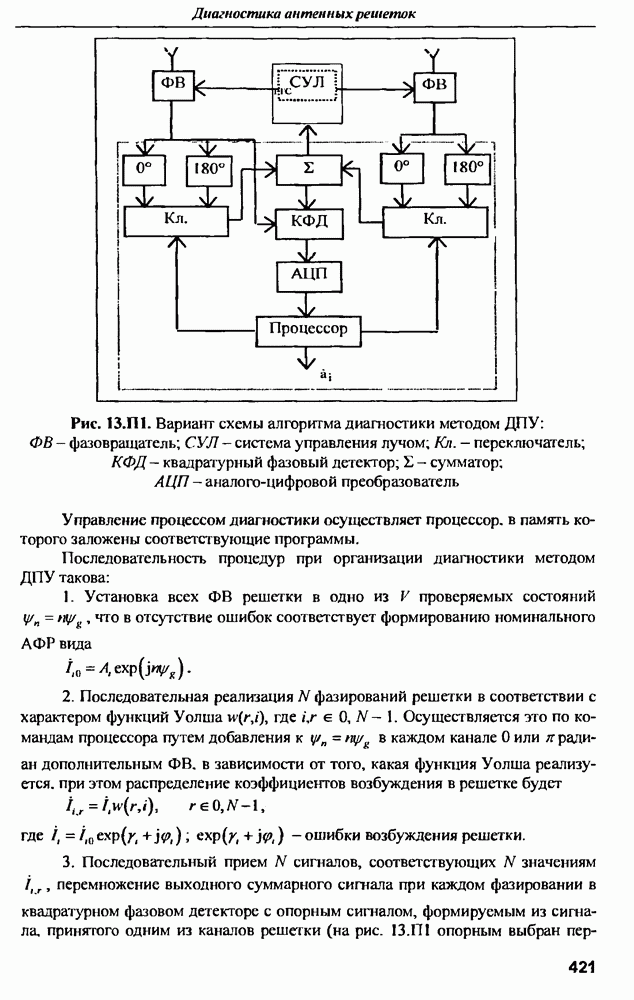
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
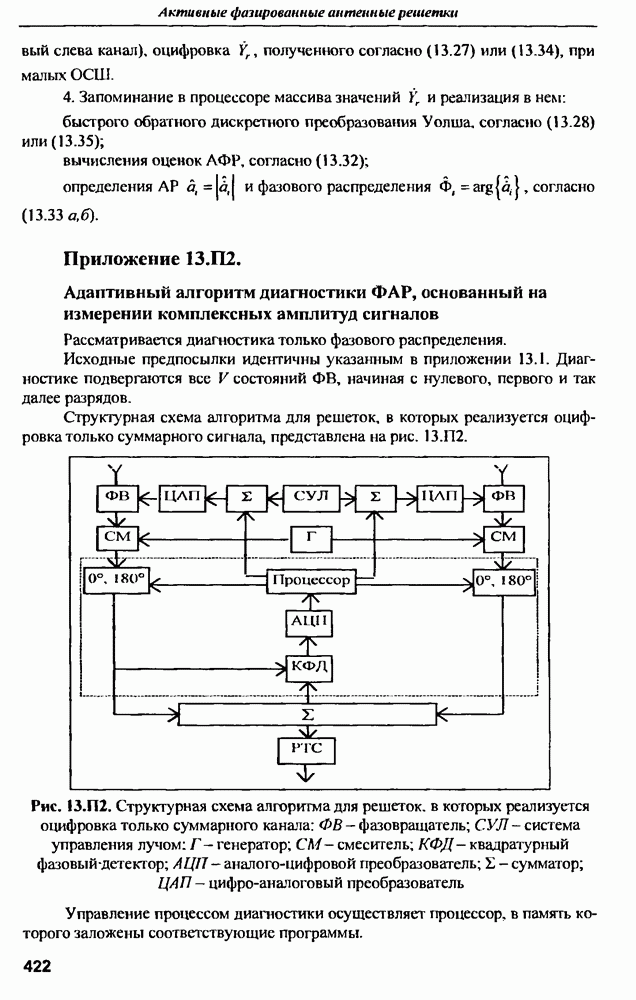
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
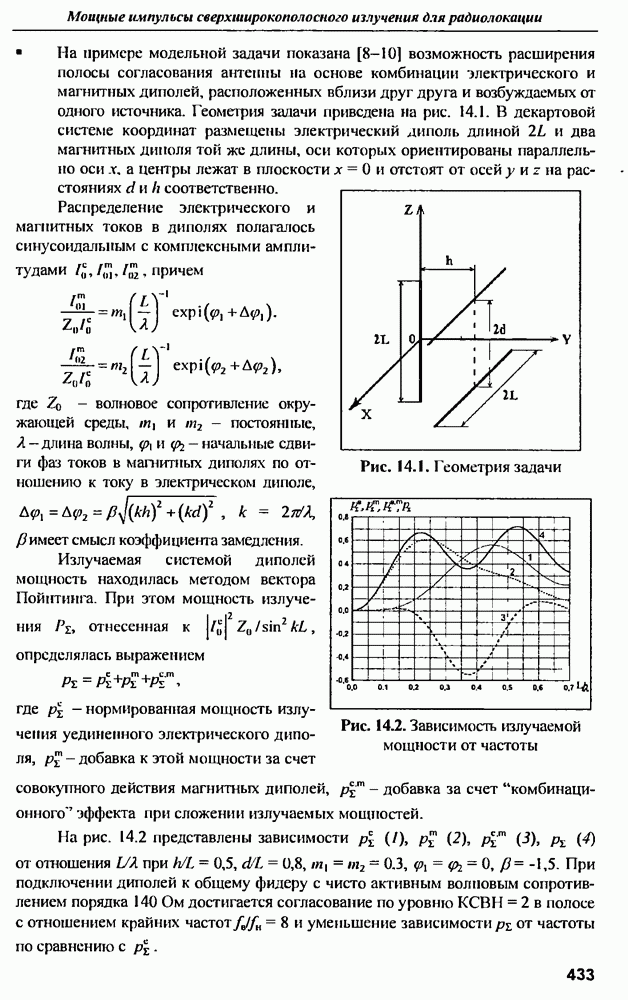
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
- 14.3. Комбинированные антенны
- 14.4. Антенные решетки
- 14.5. Приемные антенны
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
- 14.8. Реконструкция формы объектов
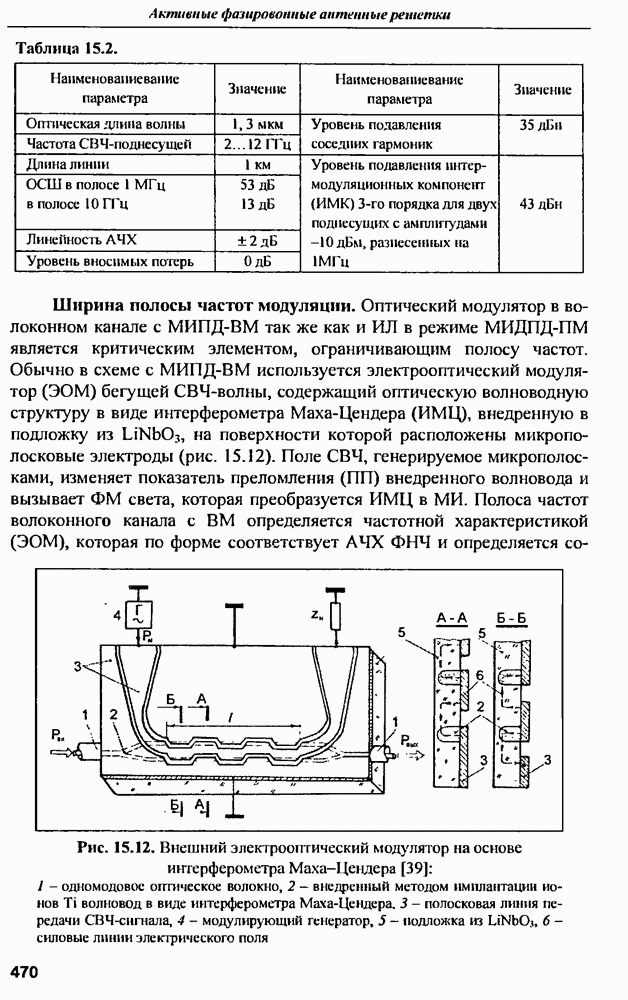
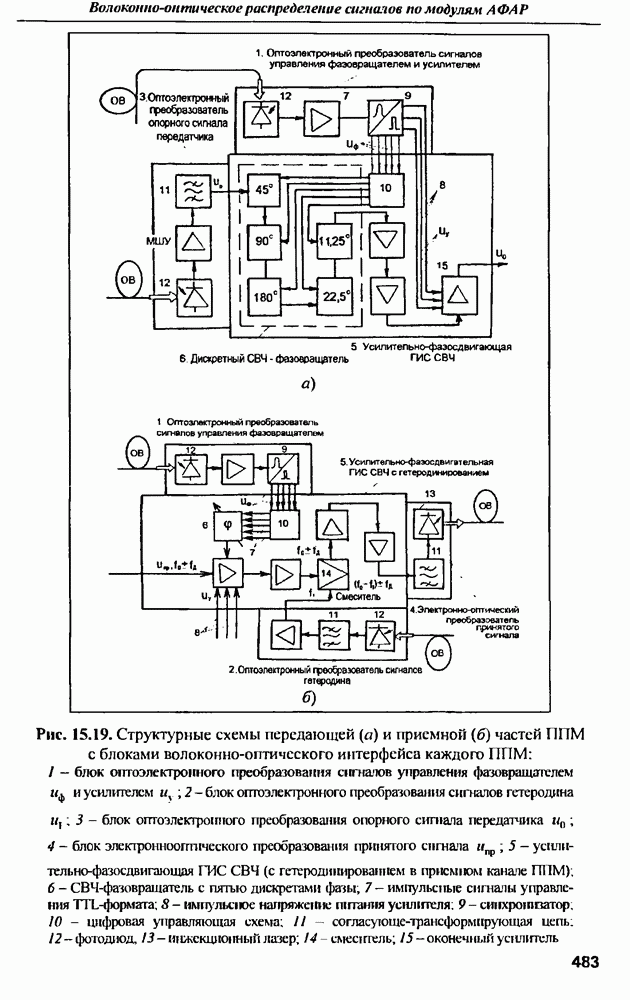
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
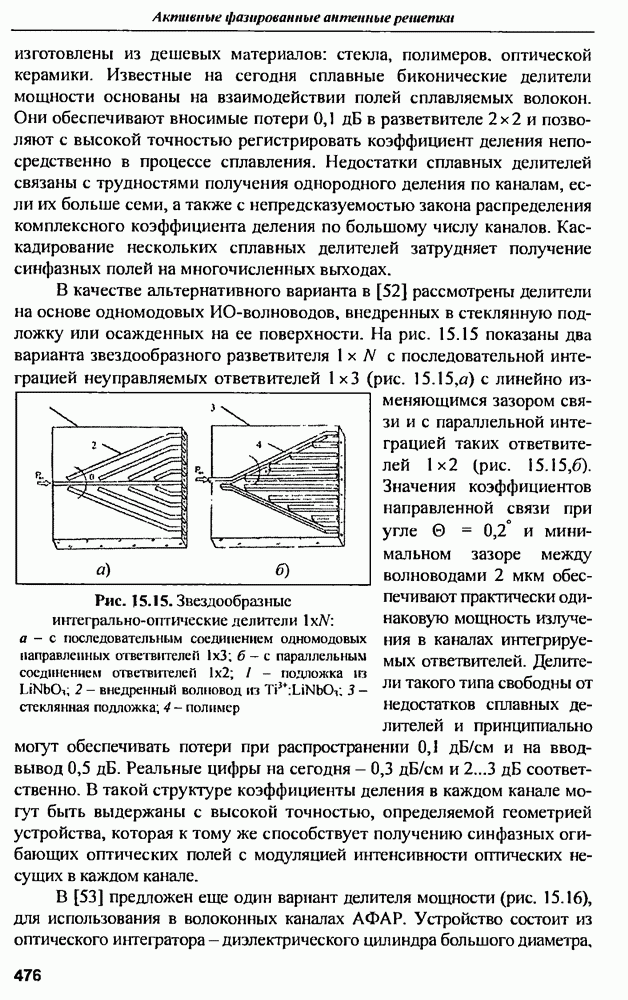
- 15.8.4. Оптические делители
- 15.8.5. Внешние модуляторы
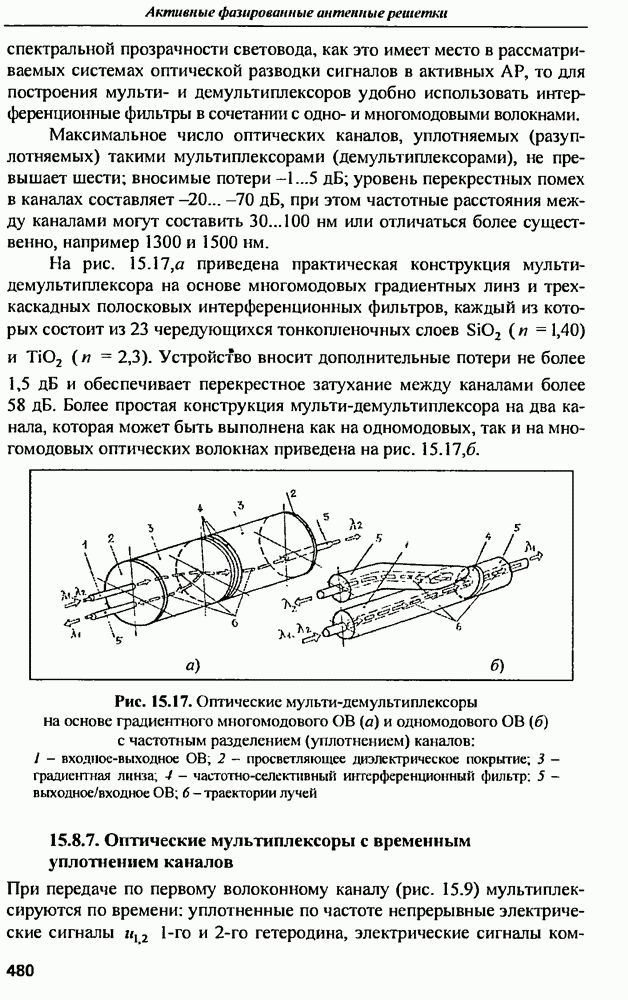
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР