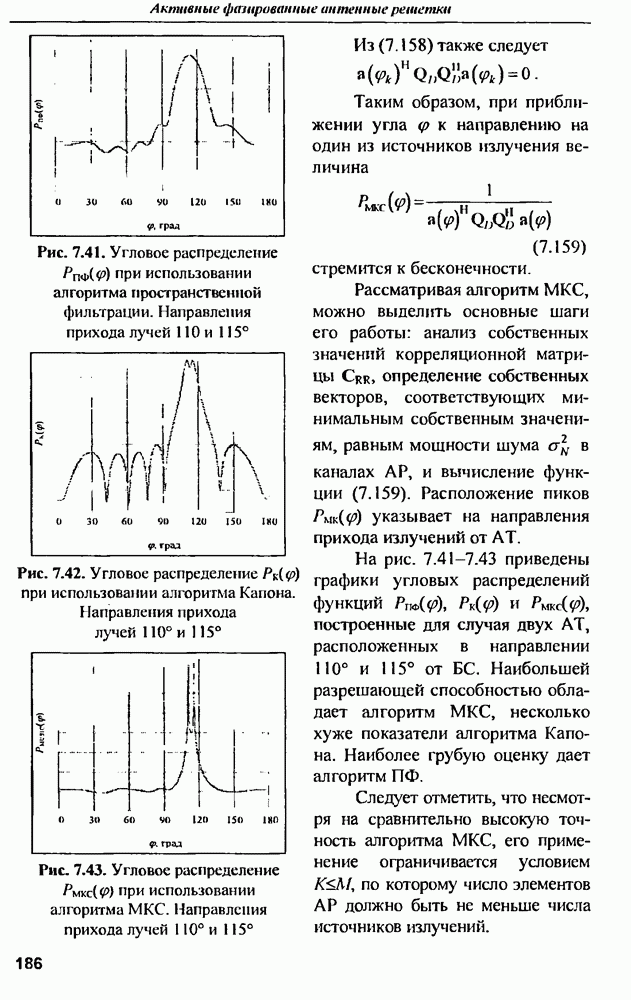
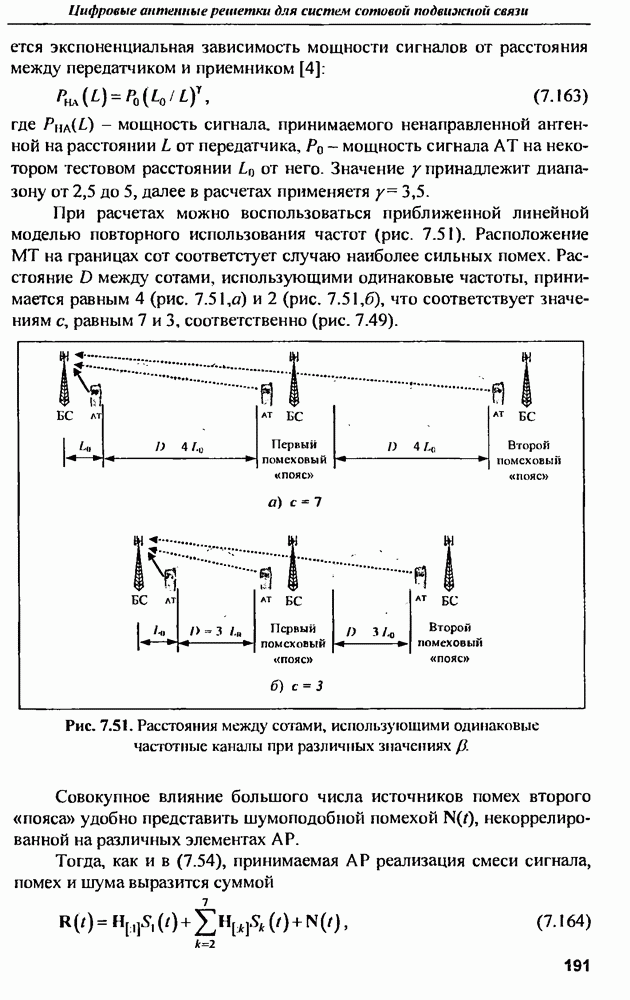
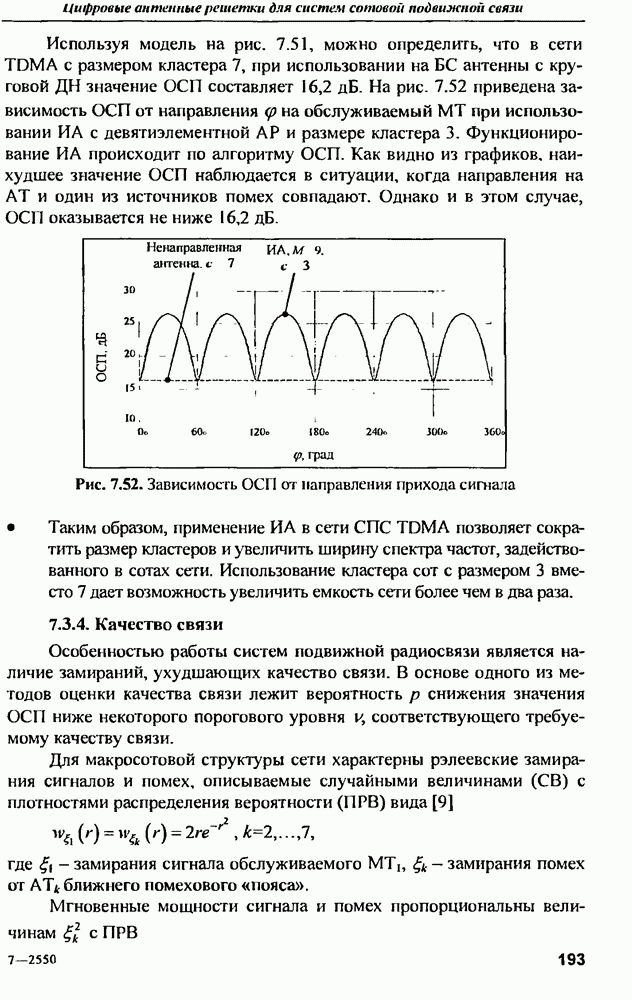
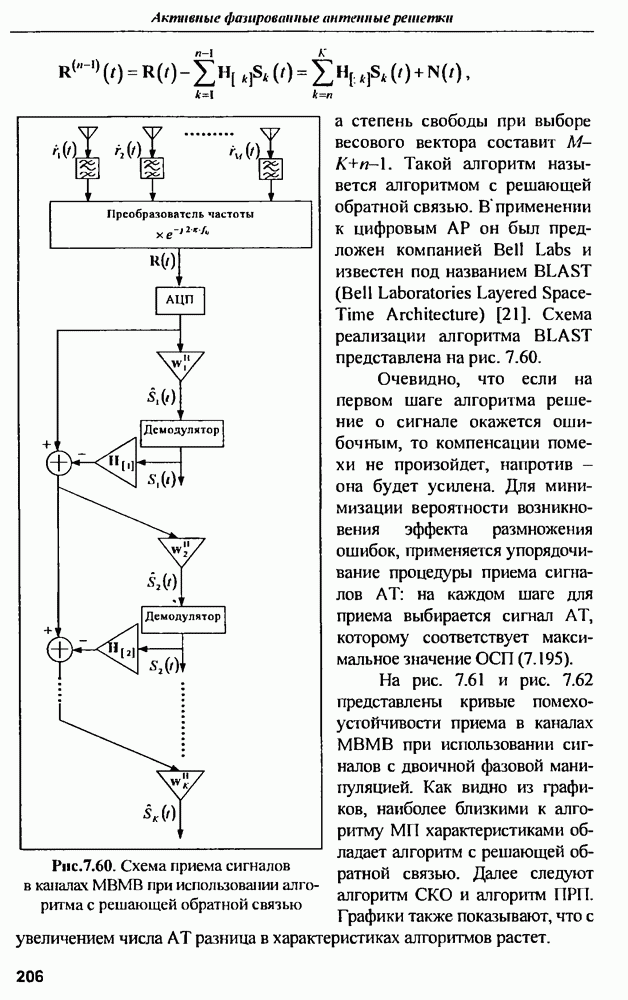
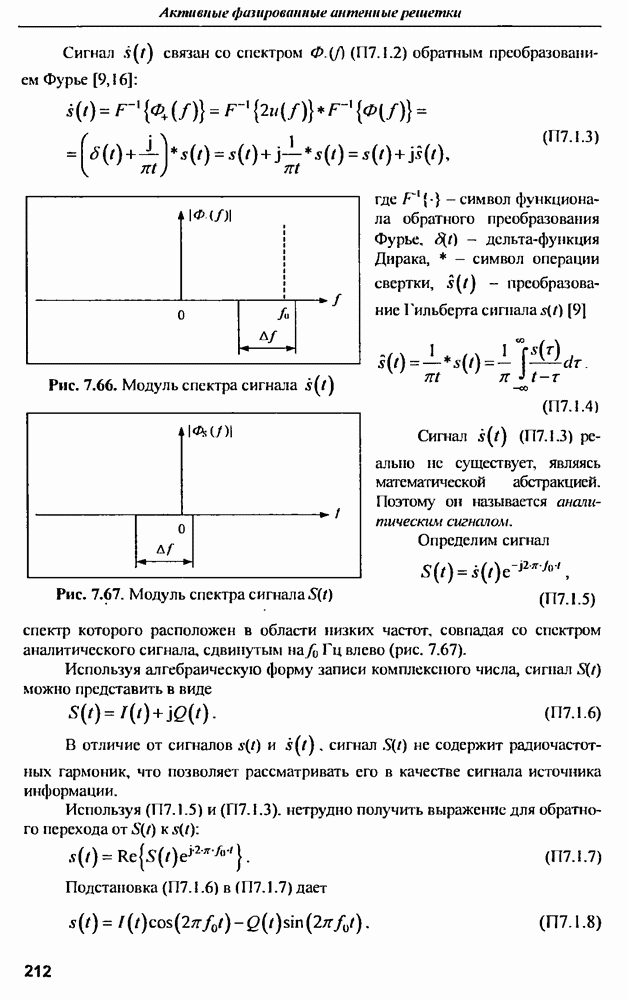
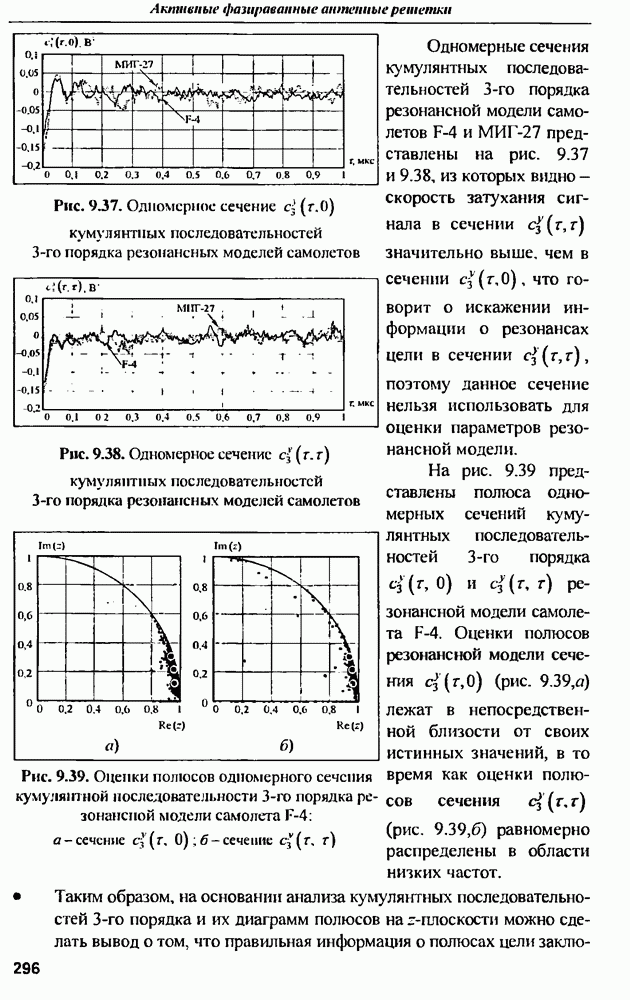
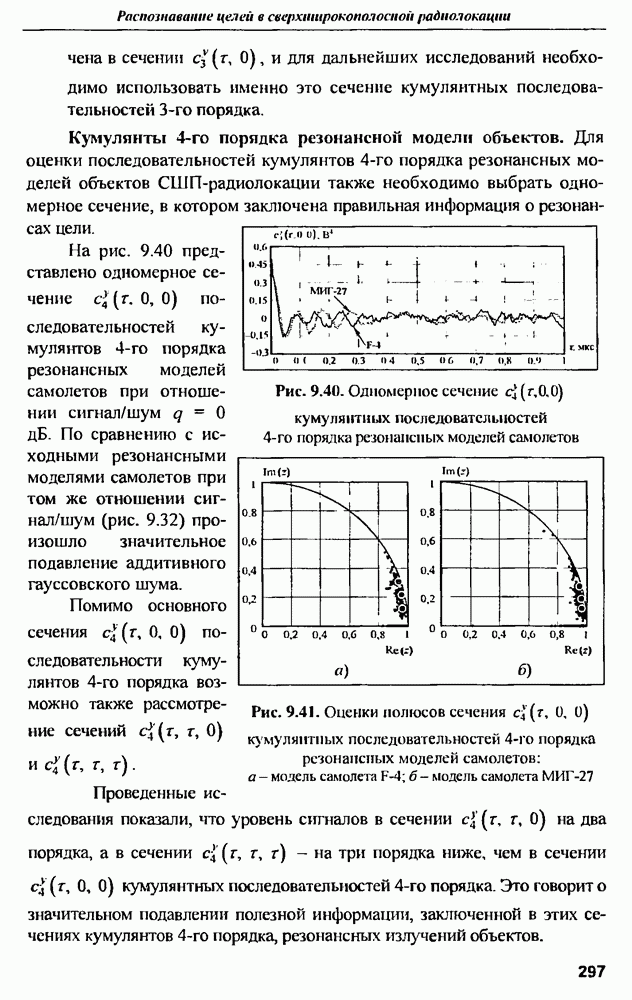
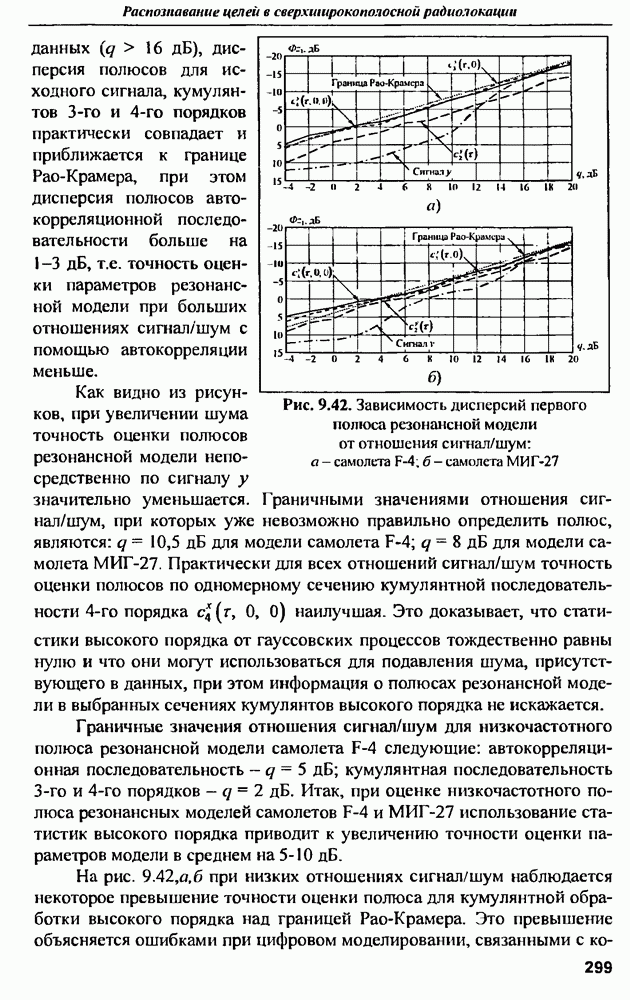
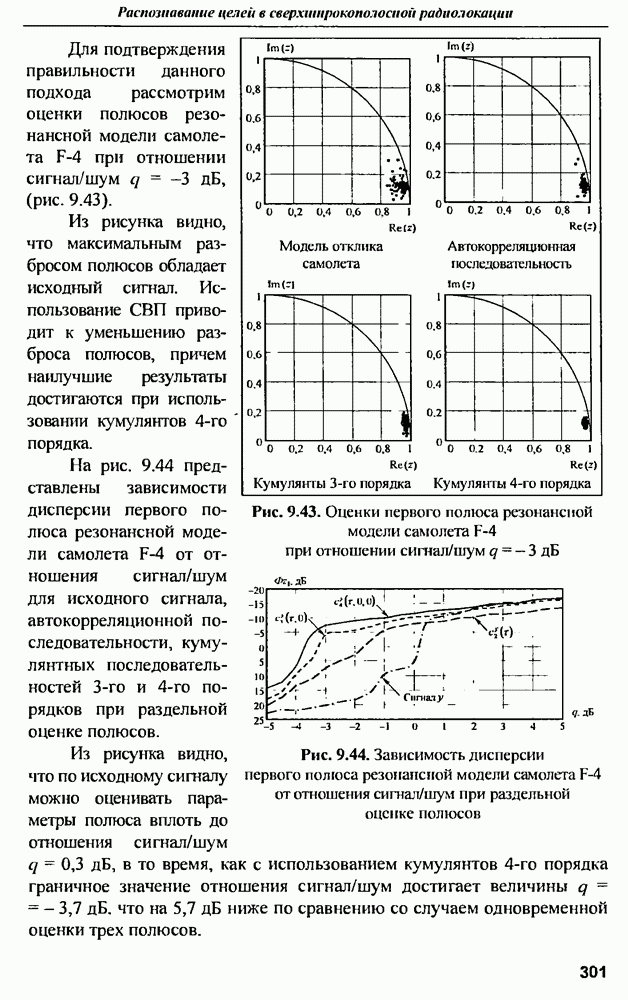
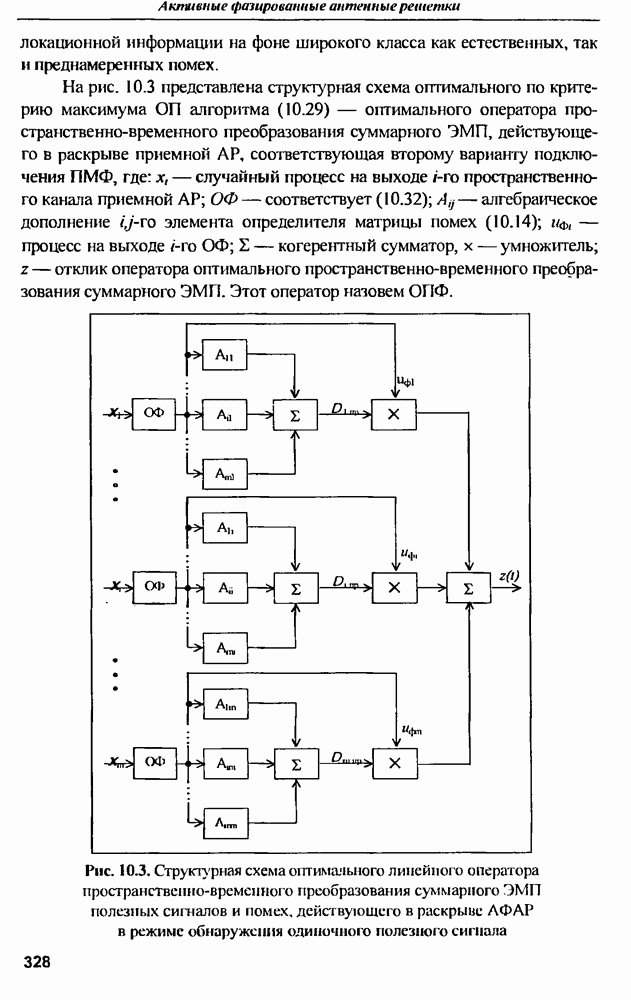
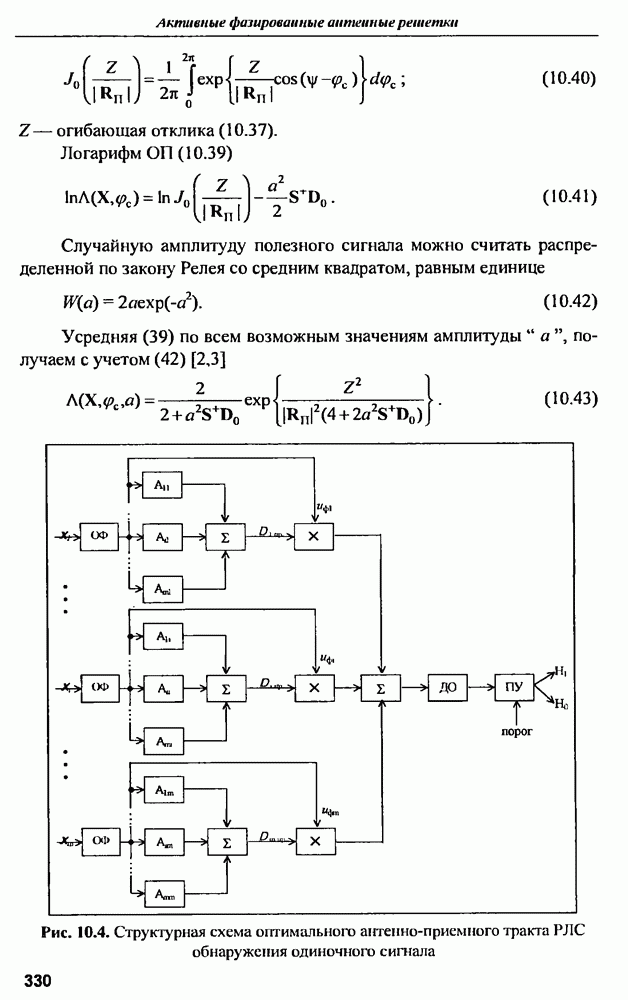
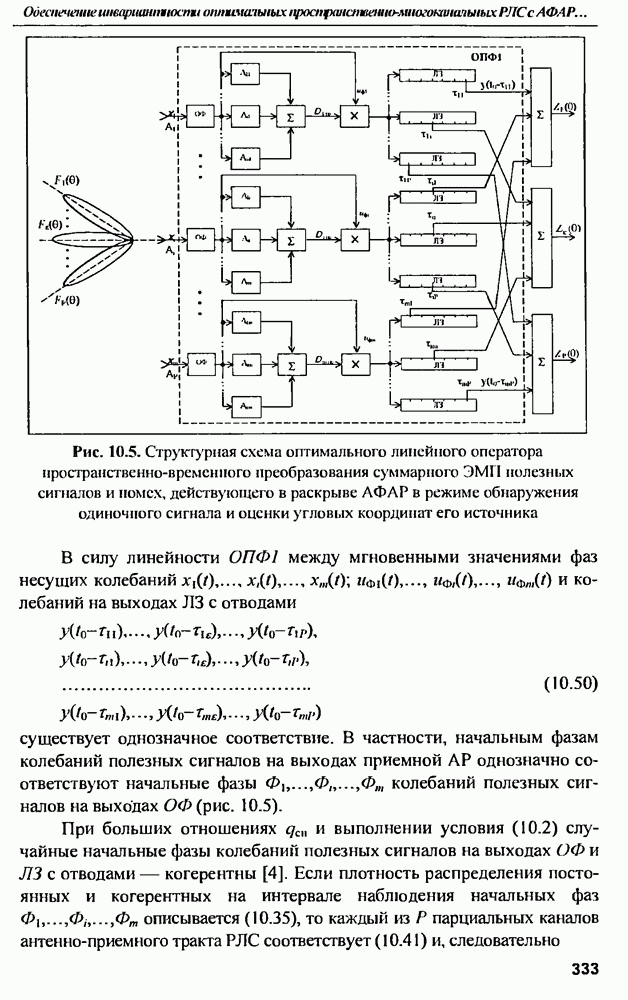
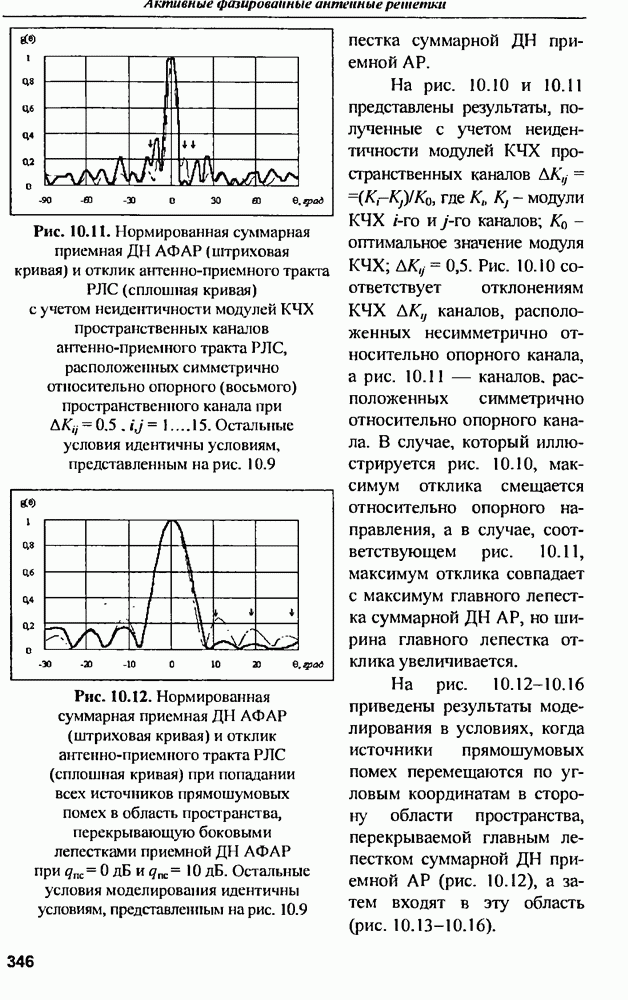
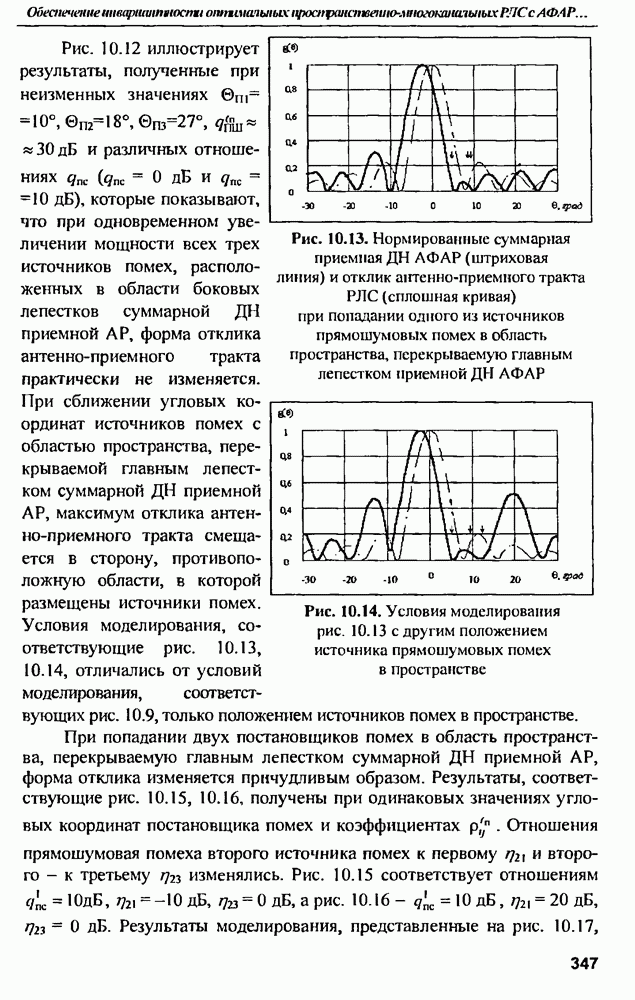
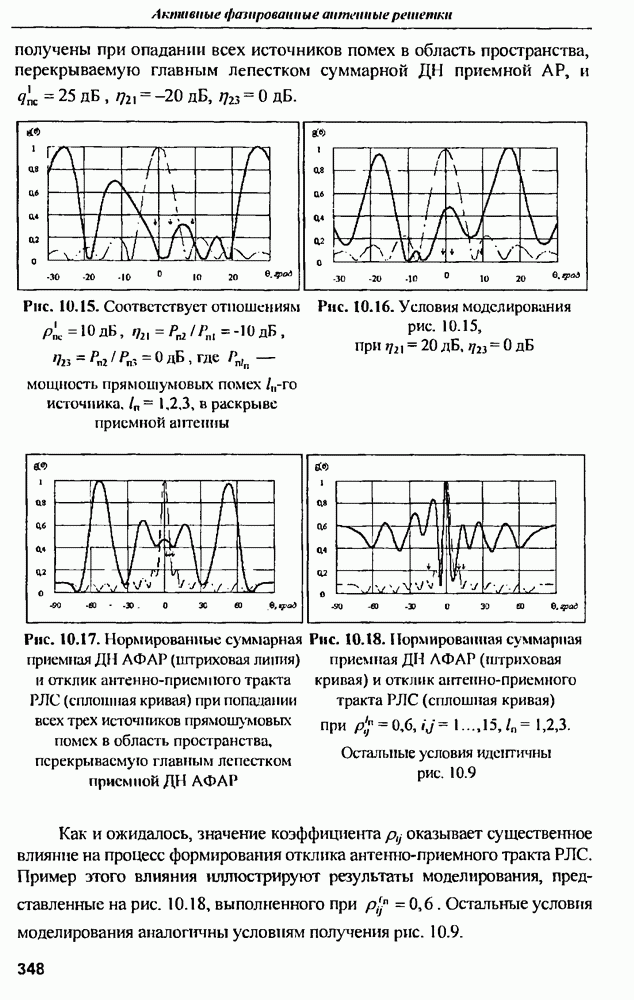
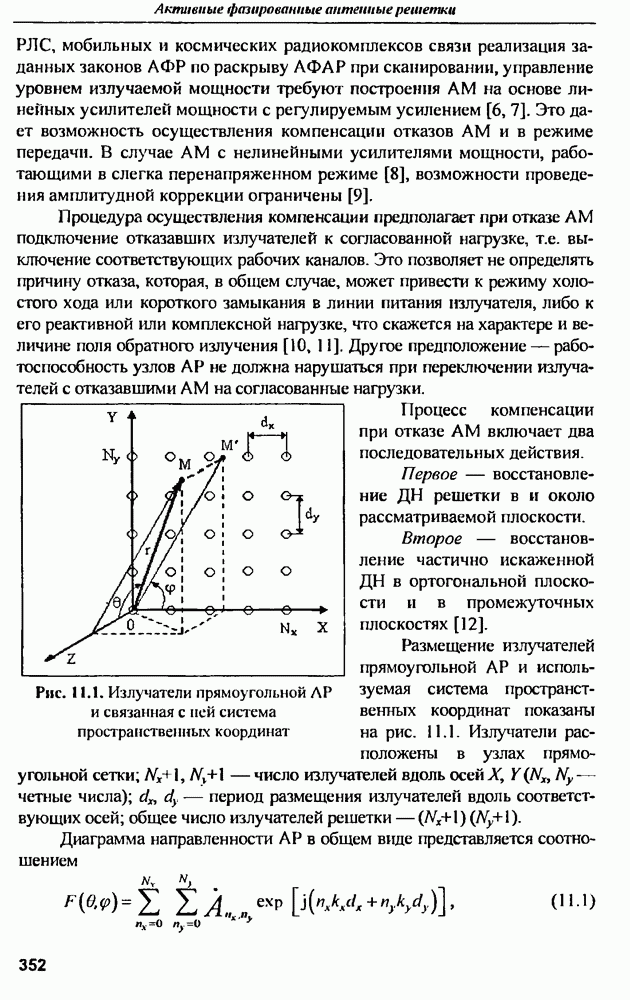
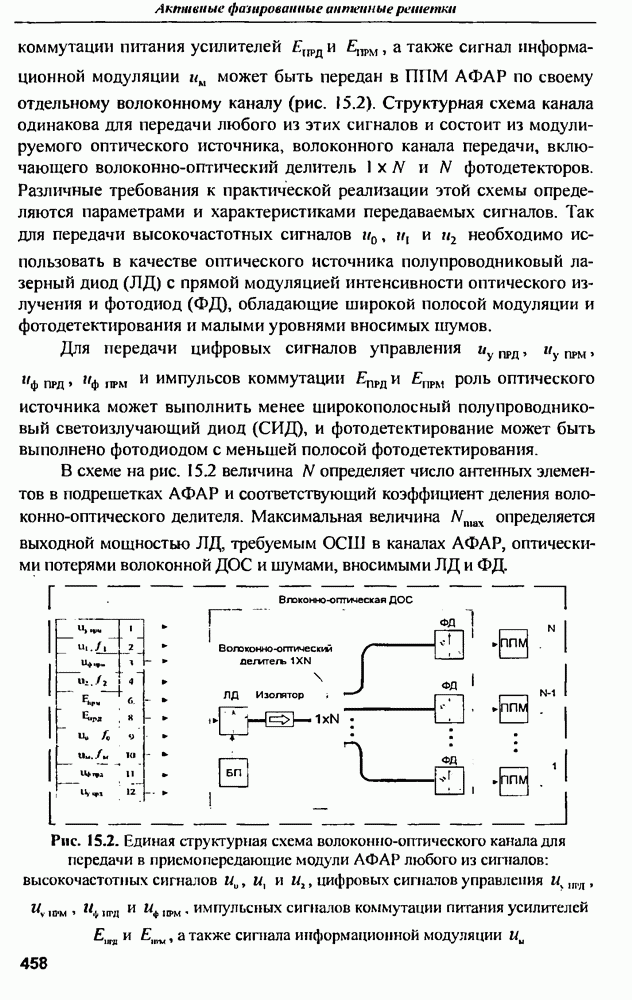
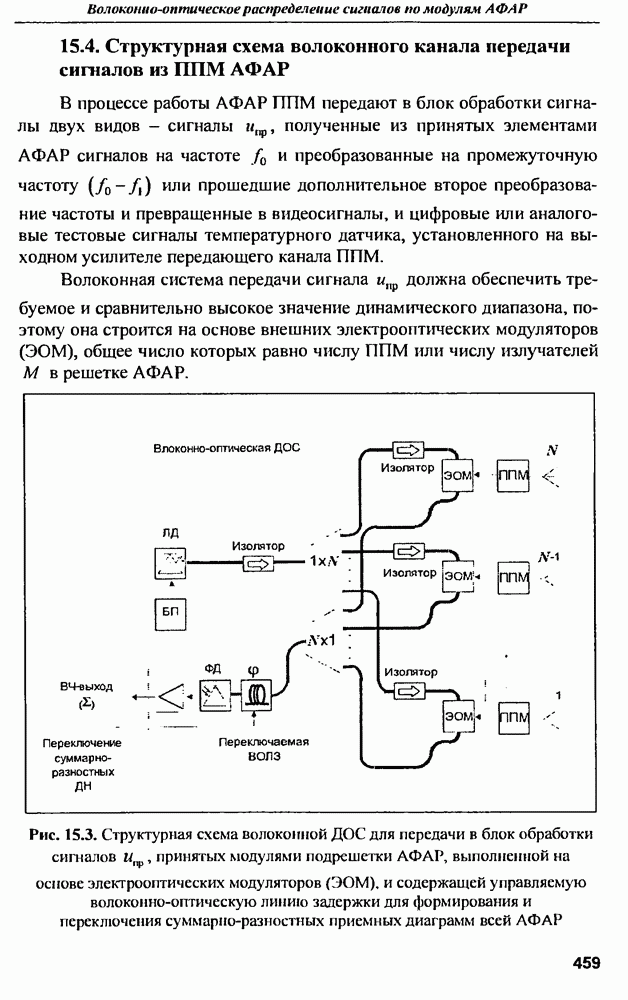
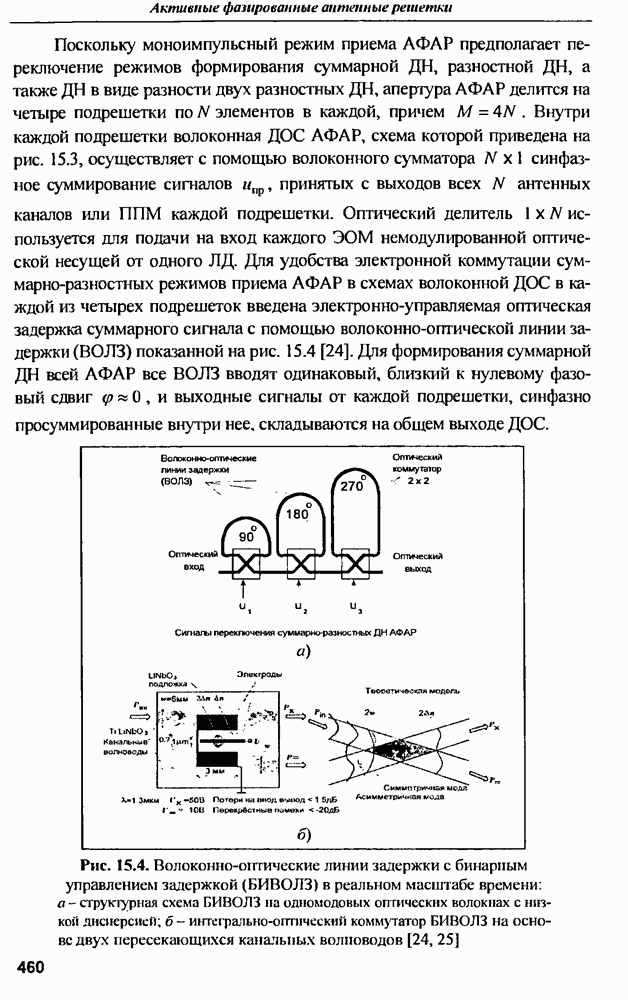
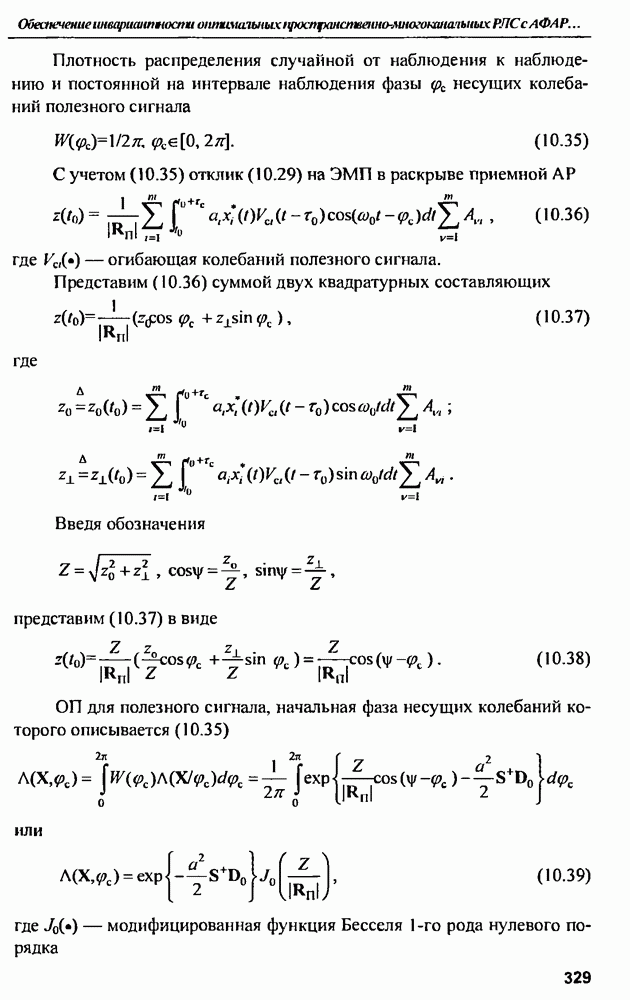| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
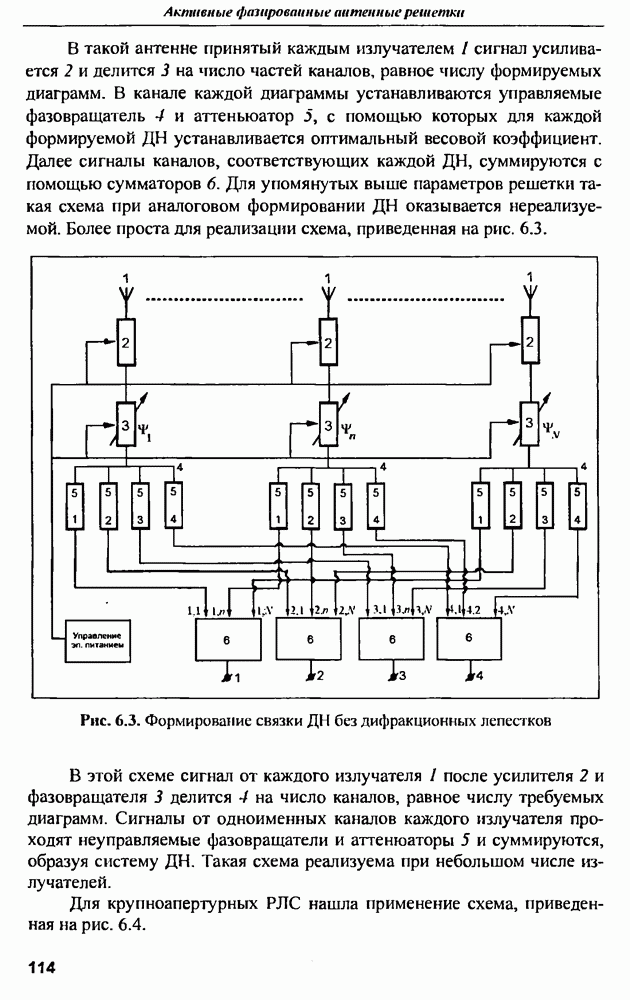
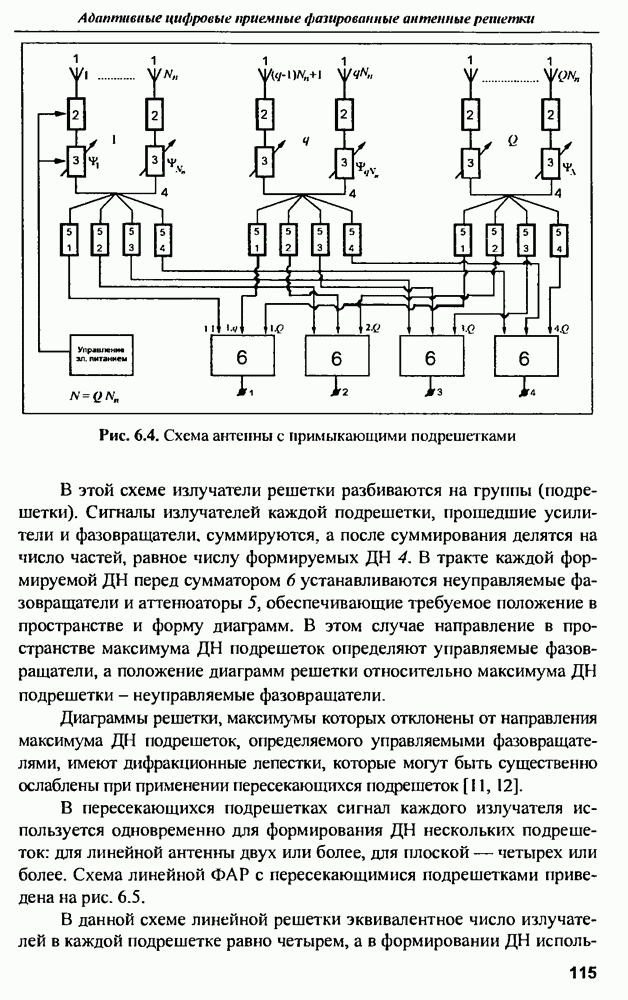
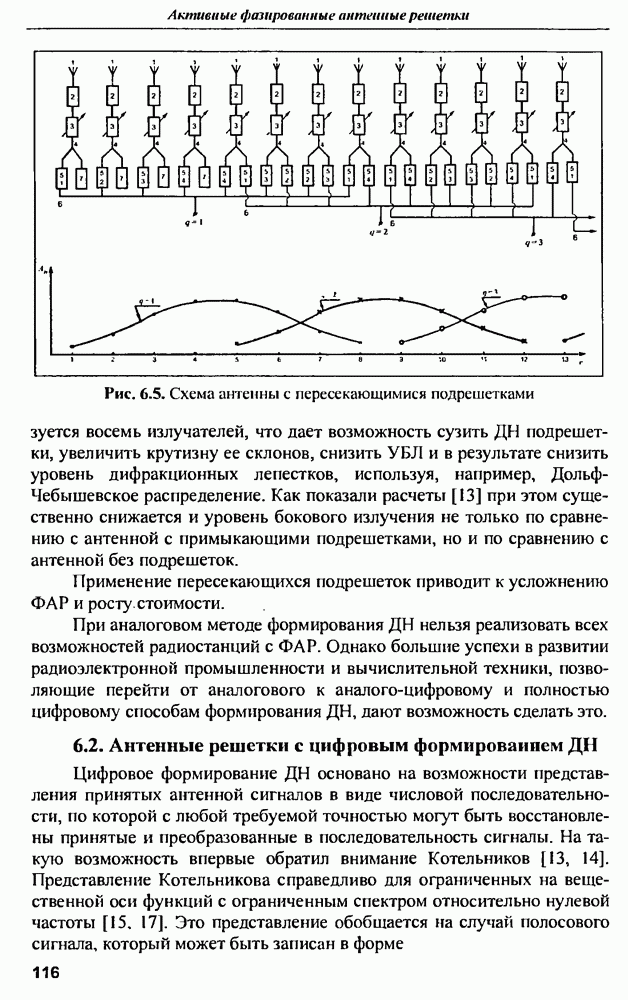
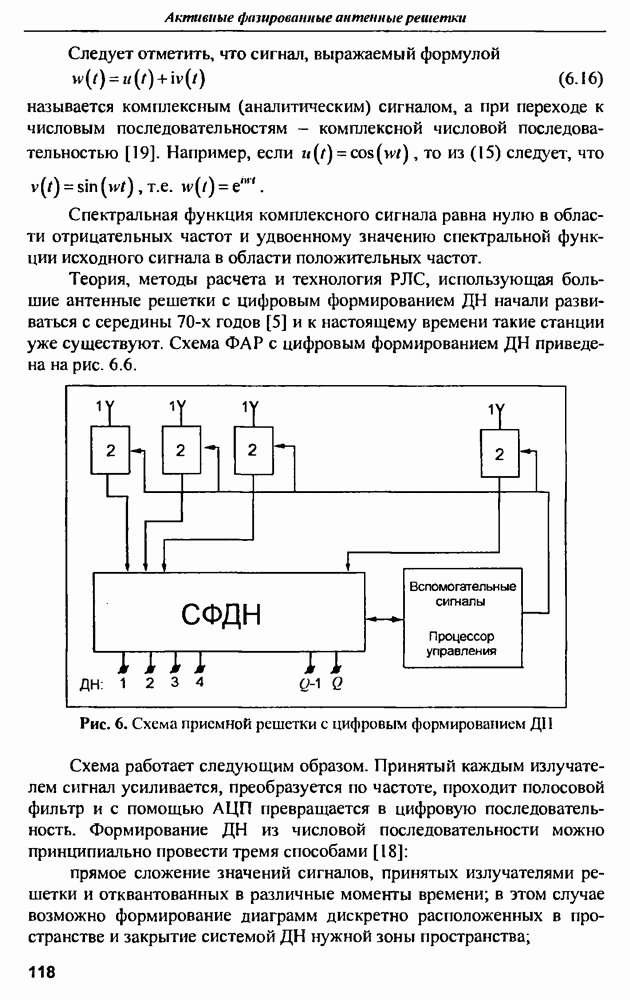
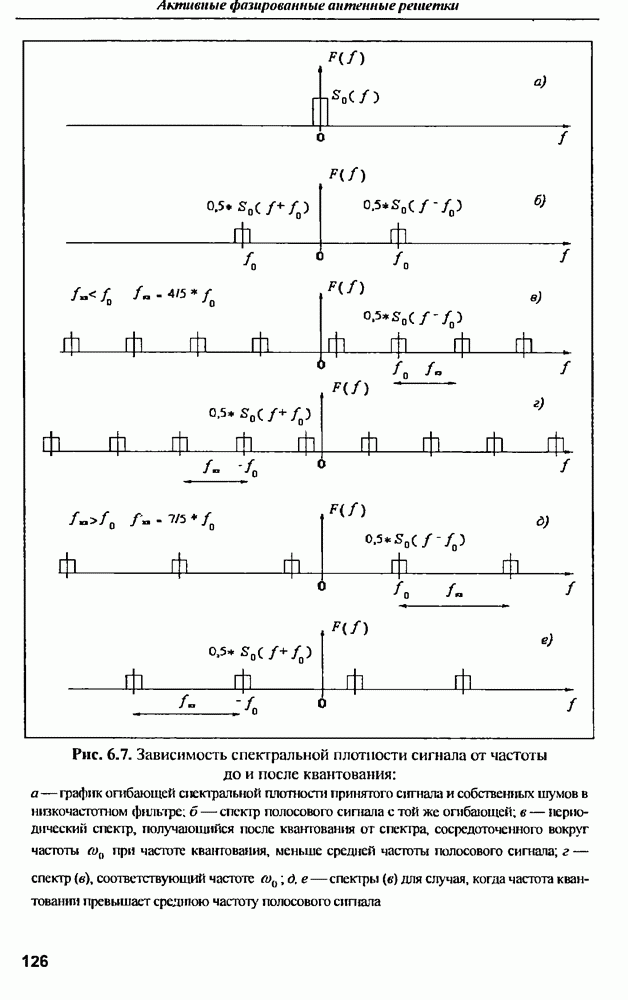
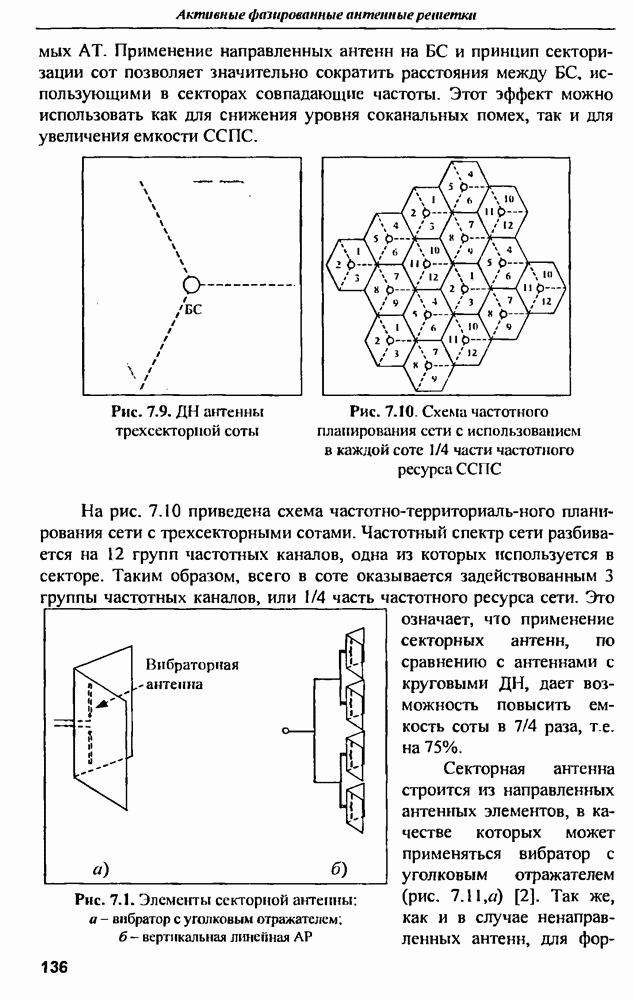
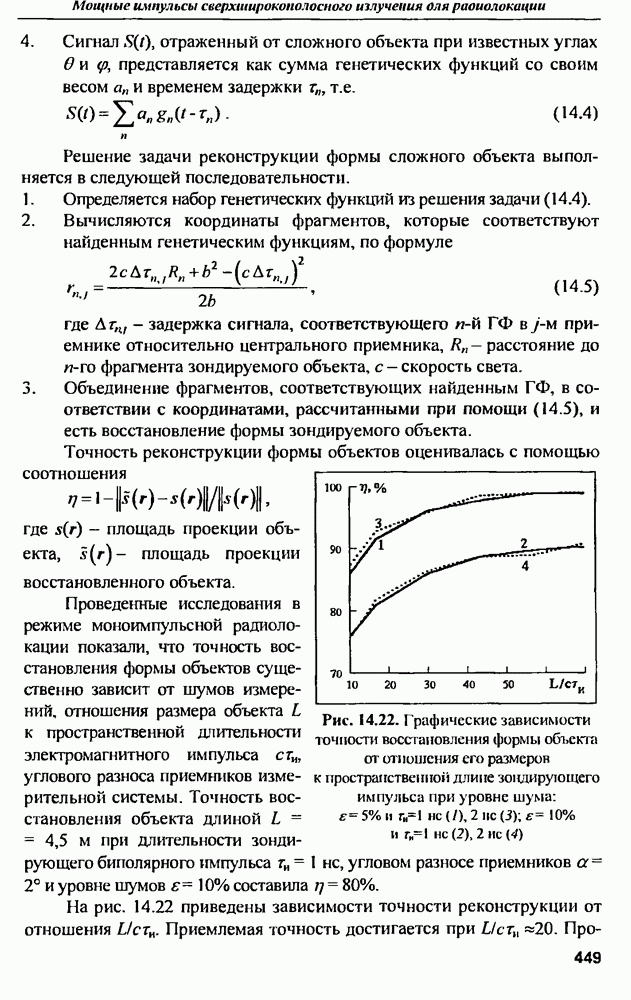
9.3. Методы оценки характеристик сигналов
9.3.1. Метод Прони
Рассмотрим один из методов определения значений параметров линейной комбинации экспоненциальных функций - метод Прони [20]. Ставится задача: при наличии  отсчетов данных одновременно минимизировать по параметрам
отсчетов данных одновременно минимизировать по параметрам  и числу экспонент
и числу экспонент  сумму квадратов следующих ошибок
сумму квадратов следующих ошибок

Решить такую задачу можно с использованием итеративных процедур, таких как метод градиентного спуска и метод Ньютона. Эти алгоритмы требуют больших вычислительных затрат и, кроме того, могут не сходиться к глобальному минимуму. Указанные трудности привели к разработке субоптимальных процедур минимизации  решающих поставленную задачу с помощью линейных уравнений.
решающих поставленную задачу с помощью линейных уравнений.
При равенстве числа отсчетов входной последовательности числу экспоненциальных параметров возможна точная подгонка экспонент под имеющиеся данные. Перепишем выражение (9.53) в виде

где  используется для подгонки к модели с
используется для подгонки к модели с  комплексными параметрами
комплексными параметрами  Входящие в (9.58) К уравнений, запишем в матричной форме:
Входящие в (9.58) К уравнений, запишем в матричной форме:

Матрица с временными индексами элементов  имеет структуру матрицы Вандермонда. Прони нашел метод для раздельного определения элементов
имеет структуру матрицы Вандермонда. Прони нашел метод для раздельного определения элементов  решив (9 59), определил неизвестный вектор комплексных амплитуд.
решив (9 59), определил неизвестный вектор комплексных амплитуд.
Принцип разделения основан на том факте, что уравнение (9.59) является решением некоторого однородного линейного разностного уравнения с постоянными коэффициентами. Для того чтобы определить вид этого уравнения, необходимо сначала определить полином  корнями которого являются экспоненты
корнями которого являются экспоненты 

Если произведения в (9.60) выразить в виде степенной последовательности, то полином можно представить в виде

с комплексными коэффициентами  уравнений для нахождения значений
уравнений для нахождения значений  запишем в виде рекуррентного разностного уравнения
запишем в виде рекуррентного разностного уравнения

или в матричном виде:

Итак, процедуру Прони для подгонки К экспонент к  отсчетам данных можно представить в виде следующих трех этапов. На первом этапе получается решение уравнения (9.62) для коэффициентов полинома. На втором этапе вычисляются корни полинома, определяемого уравнением (9.61).
отсчетам данных можно представить в виде следующих трех этапов. На первом этапе получается решение уравнения (9.62) для коэффициентов полинома. На втором этапе вычисляются корни полинома, определяемого уравнением (9.61).
Используя корень  можно определить коэффициент затухания
можно определить коэффициент затухания  и частоту синусоиды
и частоту синусоиды  с помощью соотношений
с помощью соотношений

Для завершения процедуры Прони корни полинома, вычисленные на втором этапе, используются далее для формирования элементов матрицы уравнения (9.59), которое затем решается относительно К комплексных параметров  Каждый параметр
Каждый параметр  используется далее для определения амплитуды
используется далее для определения амплитуды  и начальной фазы
и начальной фазы 
Если число отсчетов данных превышает число экспонент в сигнале, как и бывает на практике, то на первом этапе алгоритма Прони можно использовать ряд методов на основе критерия среднеквадратической ошибки. К этим методам относятся, например, метод линейного предсказания среднеквадратической оценки вперед и комбинация линейною предсказания вперед и назад.
Использовав (9.57) и (9.63), запишем уравнение, определенное при 

Уравнение (9.66) показывает, что альтернативной моделью суммы экспонент и аддитивного шума является модель на основе авторегрессии  и скользящего среднего
и скользящего среднего  возбуждаемого шумовым процессом
возбуждаемого шумовым процессом  Минимизируя величину квадрата ошибки
Минимизируя величину квадрата ошибки  первая часть метода Прони сводится к процедуре оценивания
первая часть метода Прони сводится к процедуре оценивания  параметров. Существуют различные способы их определения.
параметров. Существуют различные способы их определения.
Рассмотрим оценку  параметров с помощью метода линейного предсказания
параметров с помощью метода линейного предсказания  вперед
вперед

где  коэффициенты линейного предсказания вперед порядка К.
коэффициенты линейного предсказания вперед порядка К.
Предсказание «вперед» понимается в том смысле, что результат предсказания для текущего отсчета данных представляет собой взвешенную сумму из К предшествующих отсчетов. Ошибку  вперед
вперед  можно записать в виде матричного уравнения
можно записать в виде матричного уравнения

Используя при расчетах ту или иную часть матрицы данных, нормальные уравнения (9.68) носят названия ковариационных, автокорреляционных, предвзвешанных или поствзвешанных.
Рассмотрим, например, оценку  основанную на ковариационном методе. Соотношение между ошибками линейного предсказания вперед и коэффициентами
основанную на ковариационном методе. Соотношение между ошибками линейного предсказания вперед и коэффициентами  можно в краткой форме записать в следующем виде:
можно в краткой форме записать в следующем виде:

где Т - теплицева матрица данных размера  ; вектор ошибок
; вектор ошибок  - элементный вектор коэффициентов
- элементный вектор коэффициентов  определяются выражениями
определяются выражениями

 Нормальные уравнения, минимизирующие средний квадрат ошибки
Нормальные уравнения, минимизирующие средний квадрат ошибки  а и
а и

порядка К, будут иметь следующий вид:

где  означает эрмитово сопряжение.
означает эрмитово сопряжение.
Элементы эрмитовой  матрицы
матрицы  имеют вид корреляционных форм
имеют вид корреляционных форм

где  знак комплексного сопряжения.
знак комплексного сопряжения.
Рассмотренный выше метод, в случае гауссовских процессов, дает для  параметров оценку, приближающуюся в оценке максимального правдоподобия.
параметров оценку, приближающуюся в оценке максимального правдоподобия.
Рассмотрим ковариационный метод применительно к оценке линейного предсказания назад

где  коэффициенты
коэффициенты  назад порядка К. В этом случае результат предсказания для текущего отсчета данных является взвешенной суммой К последующих отсчетов. Для конечного набора отсчетов данных параметры
назад порядка К. В этом случае результат предсказания для текущего отсчета данных является взвешенной суммой К последующих отсчетов. Для конечного набора отсчетов данных параметры  назад, определяемые по методу наименьших квадратов, в общем случае не идентичны параметрам линейного предсказания вперед.
назад, определяемые по методу наименьших квадратов, в общем случае не идентичны параметрам линейного предсказания вперед.
Нормальное уравнение для линейного предсказания назад будет иметь следующую форму:

где  средний квадрат ошибки линейного предсказания назад.
средний квадрат ошибки линейного предсказания назад.
Если значения параметров  были определены с помощью линейного предсказания вперед или назад по методу наименьших квадратов и факторизацией полинома, то экспоненциальная аппроксимация становится линейной относительно оставшихся неизвестных параметров
были определены с помощью линейного предсказания вперед или назад по методу наименьших квадратов и факторизацией полинома, то экспоненциальная аппроксимация становится линейной относительно оставшихся неизвестных параметров 
После минимизации суммы квадратов ошибок по каждому параметру  получим следующее комплексное нормальное уравнение:
получим следующее комплексное нормальное уравнение:

где  матрица
матрица  - вектор
- вектор  вектор отсчетов данных у определяются выражениями:
вектор отсчетов данных у определяются выражениями:

Процедура, использующая на первом и втором этапе метода Прони соответствующие линейные процедуры наименьших квадратов, называется обобщенным методом Прони.
Использование других алгоритмов оценки  модели приводит к множеству модификаций метода Особого внимания заслуживает совместное использование
модели приводит к множеству модификаций метода Особого внимания заслуживает совместное использование  назад и вперед и сочетание линейного метода Прони с нелинейной операцией усечения матрицы данных с использованием сингулярного разложения.
назад и вперед и сочетание линейного метода Прони с нелинейной операцией усечения матрицы данных с использованием сингулярного разложения.
Максимальное значение порядка метода в любом случае ограничено величиной  а определение истинного числа К в реальных условиях является труднорешаемой задачей. При использовании
а определение истинного числа К в реальных условиях является труднорешаемой задачей. При использовании  модели разработаны различные критерии оптимизации К в зависимости от отношения сигнал/шум. Для определения оптимального критерия при решении задачи целесообразно проведение математического моделирования.
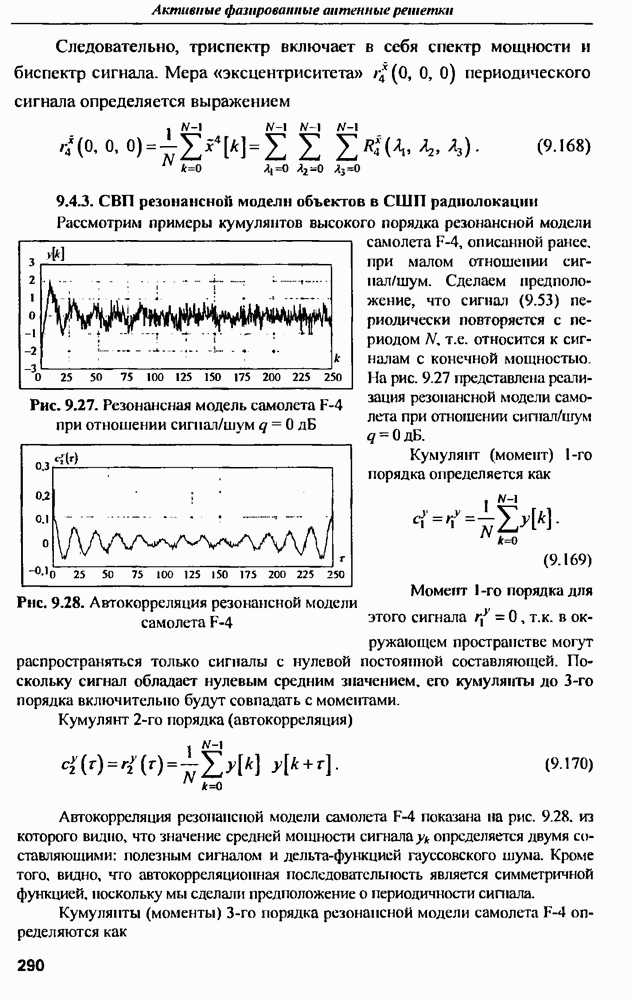
модели разработаны различные критерии оптимизации К в зависимости от отношения сигнал/шум. Для определения оптимального критерия при решении задачи целесообразно проведение математического моделирования.  Исходный метод Прони подгоняет экспоненты к любому аддитивному шуму, присутствующему в данных, поскольку экспоненциальная модель не позволяет получать раздельную оценку этого шумового процесса. Именно по этой причине исходный метод Прони часто не обеспечивает удовлетворительных результатов при значительном уровне аддитивного шума, поскольку не позволяет учесть наличие шума в анализируемом процессе. Использование, например, значения К, превышающего число действительно имеющихся полюсов, позволяет повысить точность оценки полюсов резонансной модели объектов в сверхширокополосной радиолокации.
Исходный метод Прони подгоняет экспоненты к любому аддитивному шуму, присутствующему в данных, поскольку экспоненциальная модель не позволяет получать раздельную оценку этого шумового процесса. Именно по этой причине исходный метод Прони часто не обеспечивает удовлетворительных результатов при значительном уровне аддитивного шума, поскольку не позволяет учесть наличие шума в анализируемом процессе. Использование, например, значения К, превышающего число действительно имеющихся полюсов, позволяет повысить точность оценки полюсов резонансной модели объектов в сверхширокополосной радиолокации.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
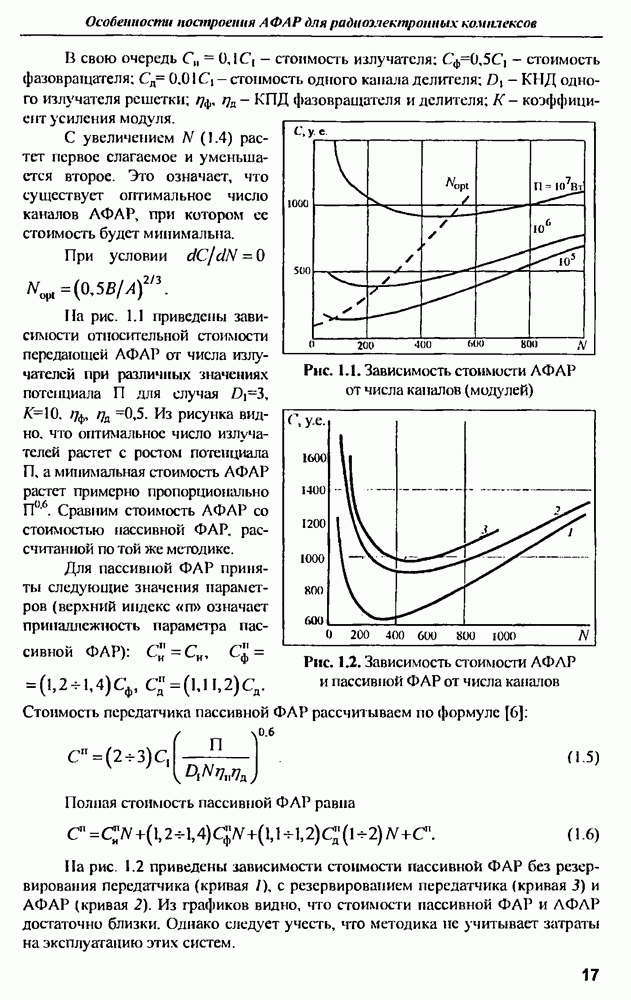
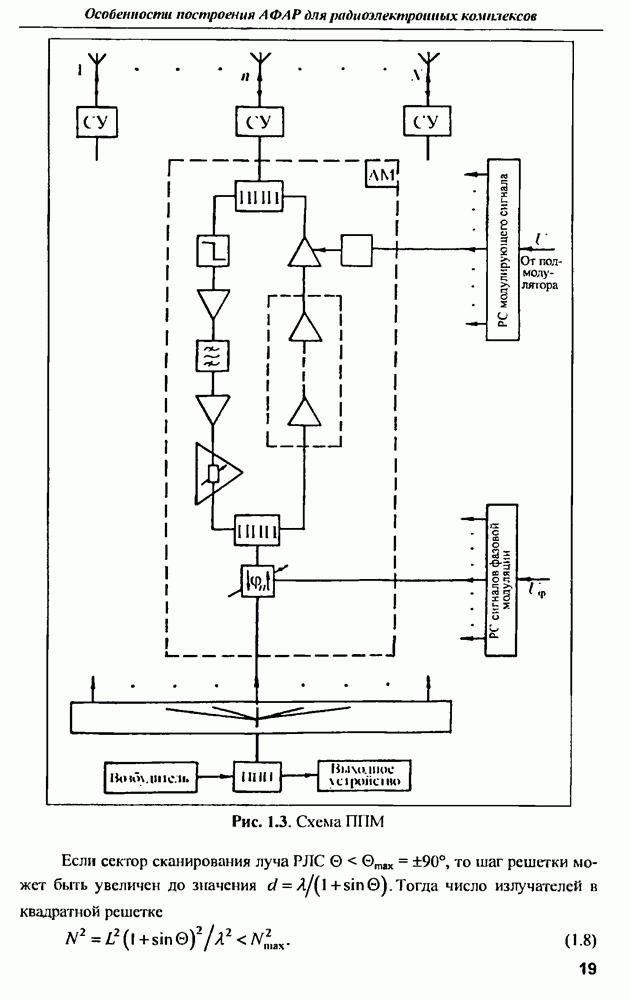
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
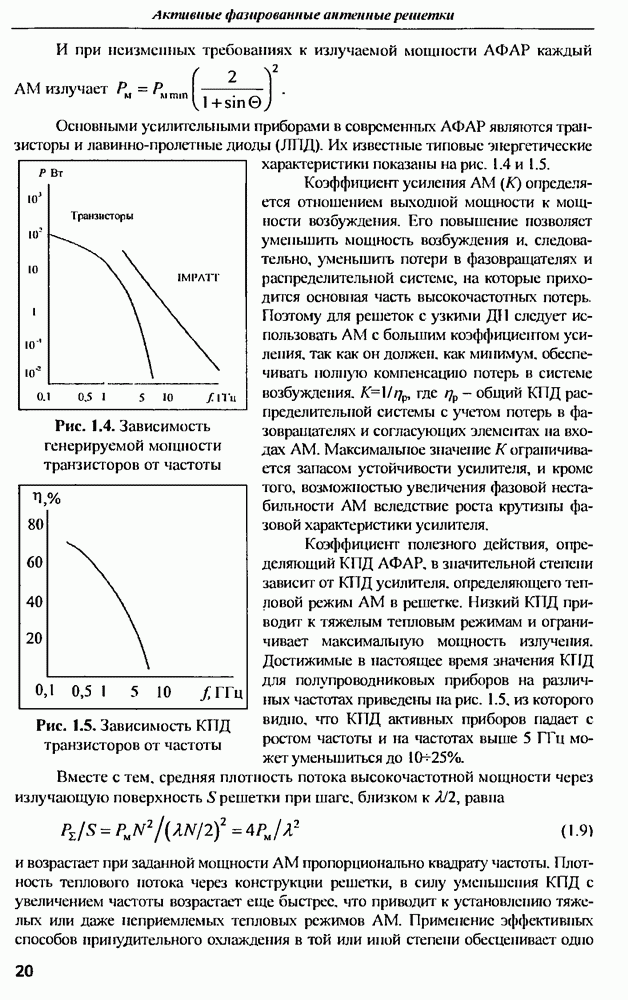
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
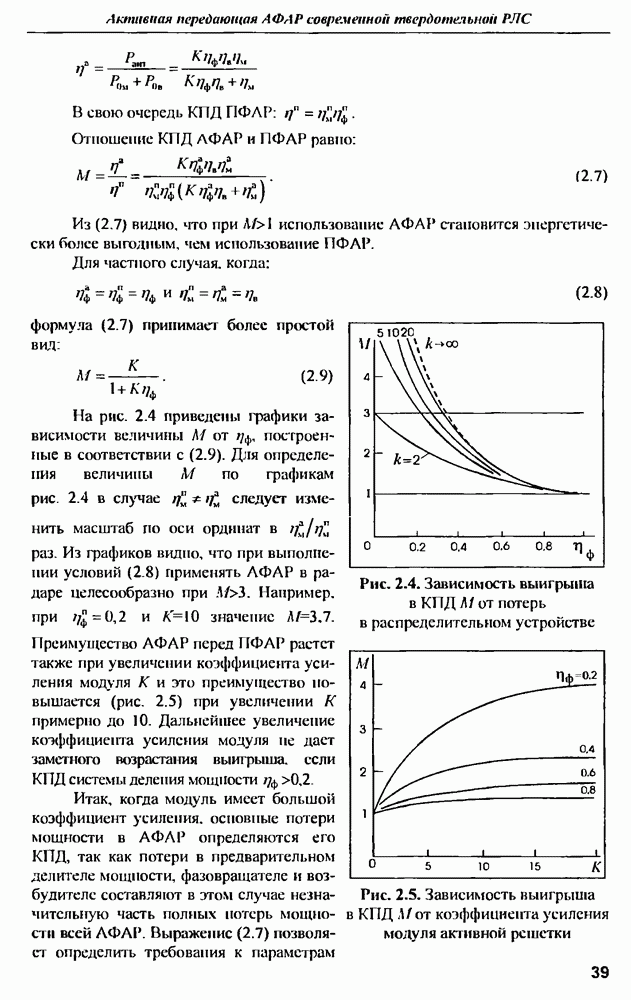
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
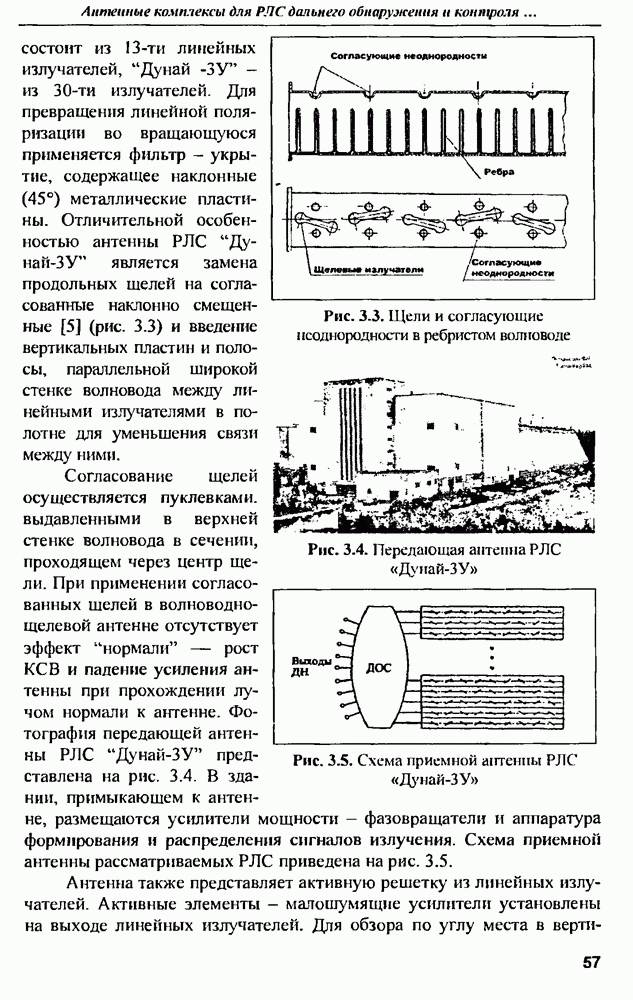
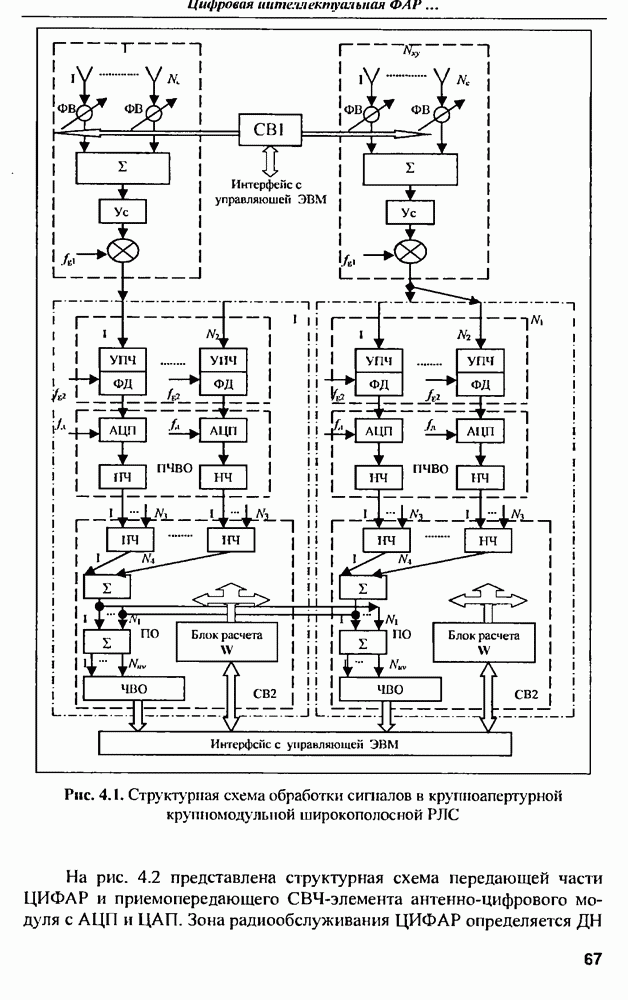
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
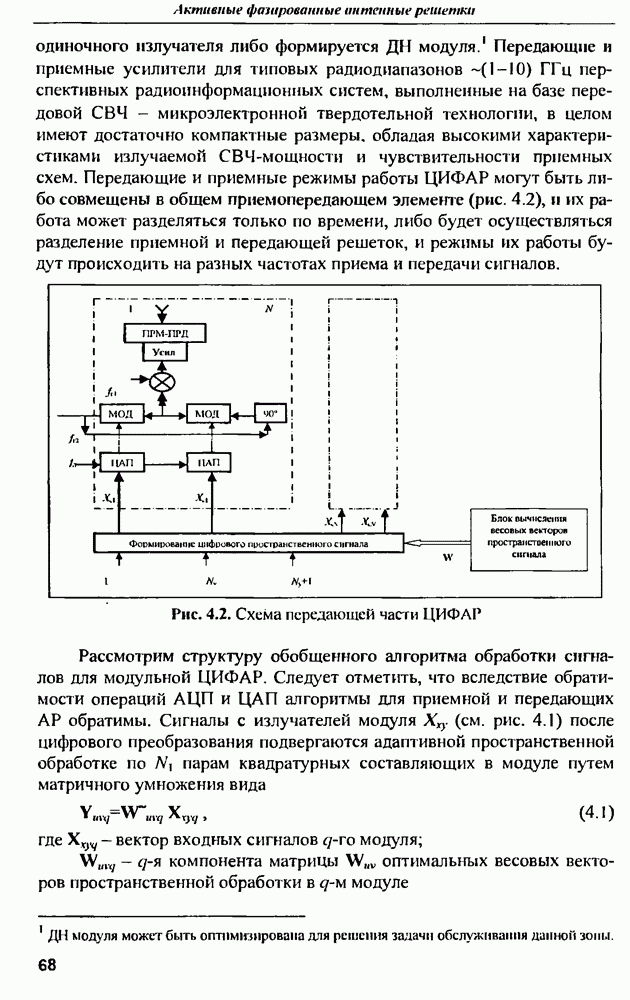
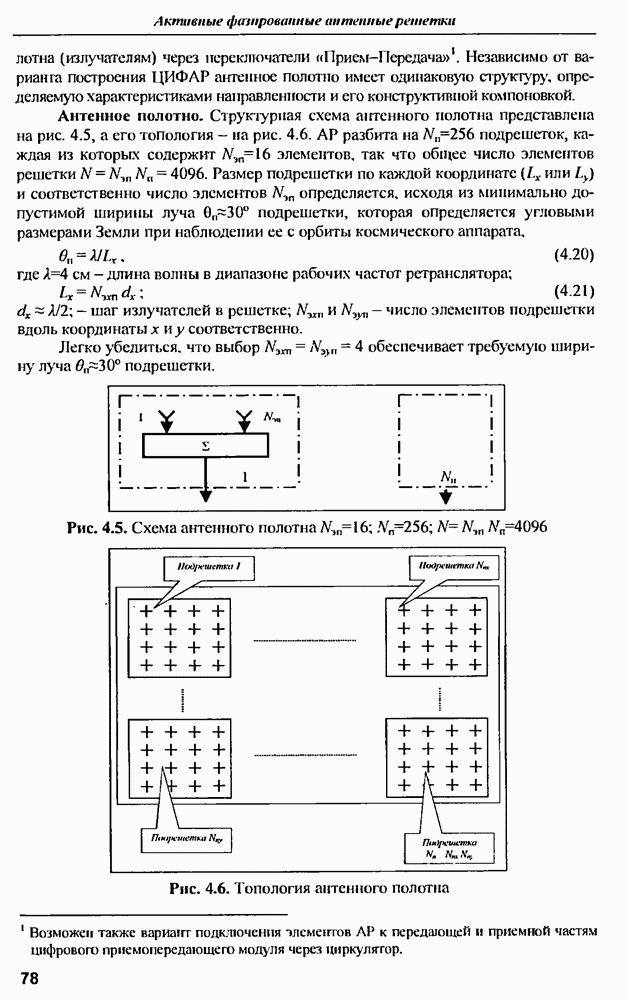
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
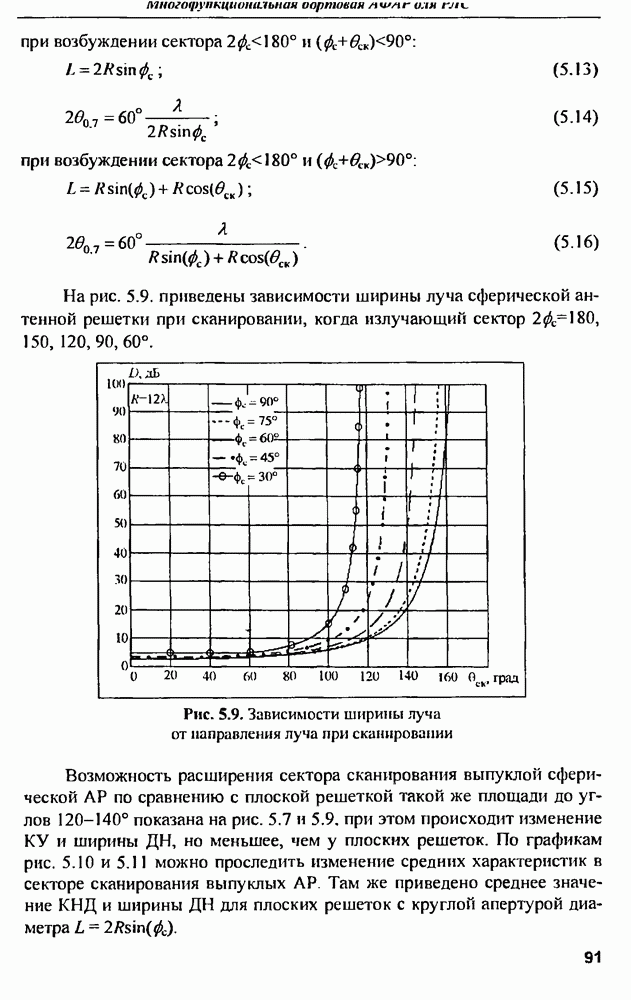
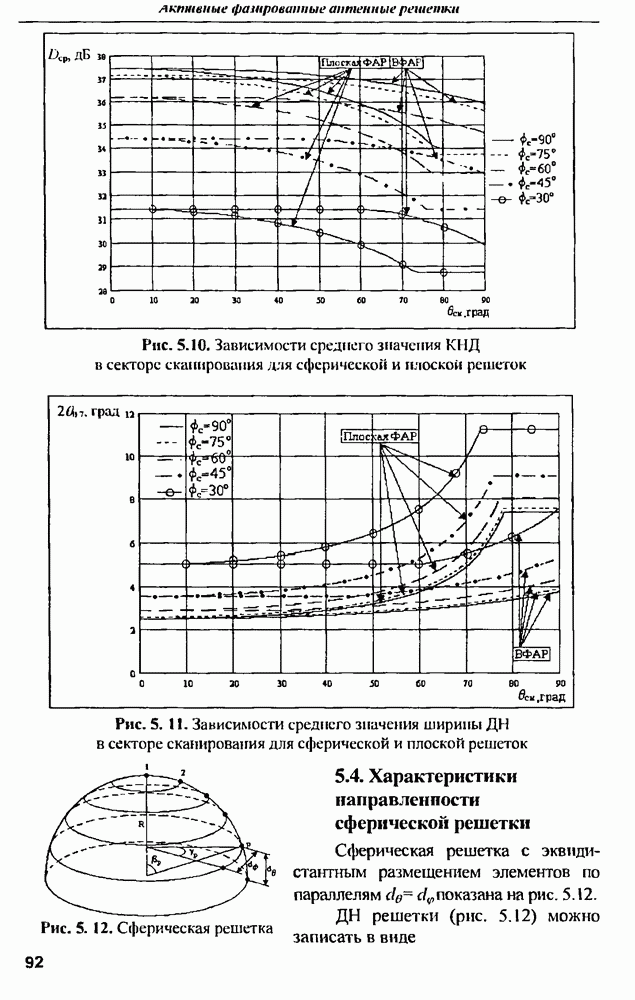
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
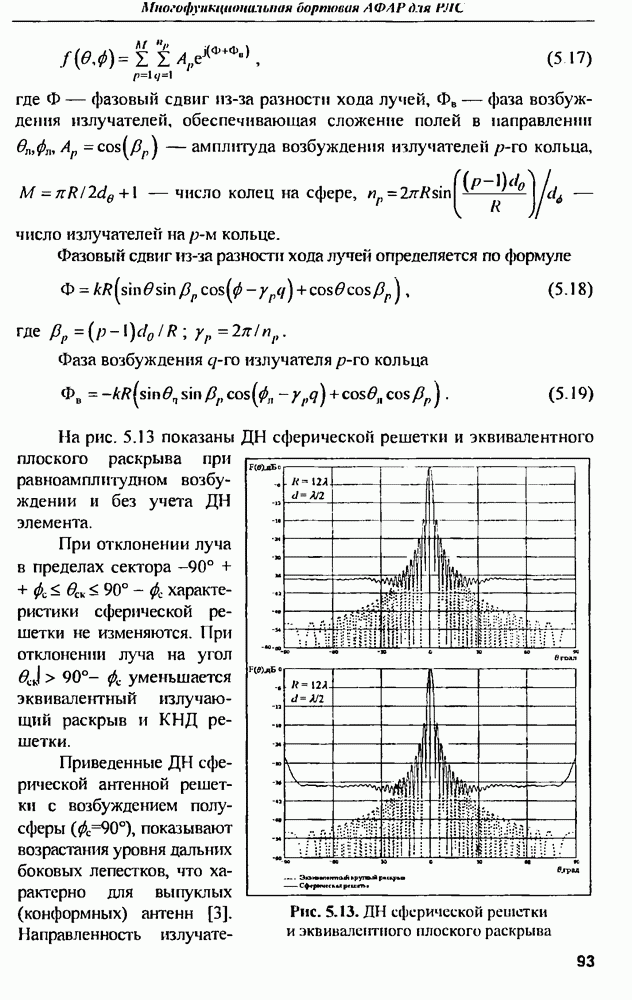
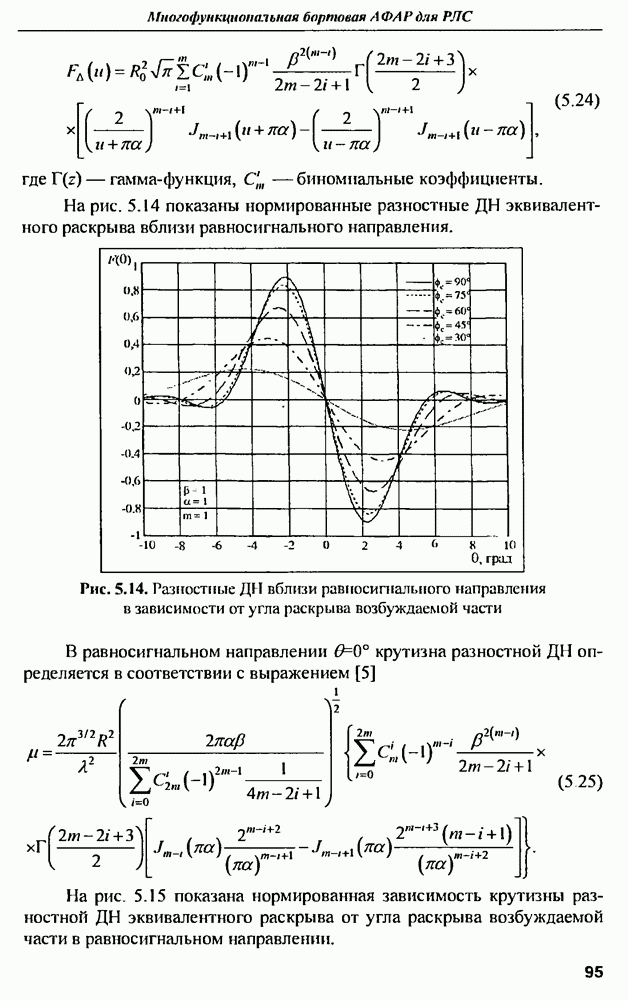
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
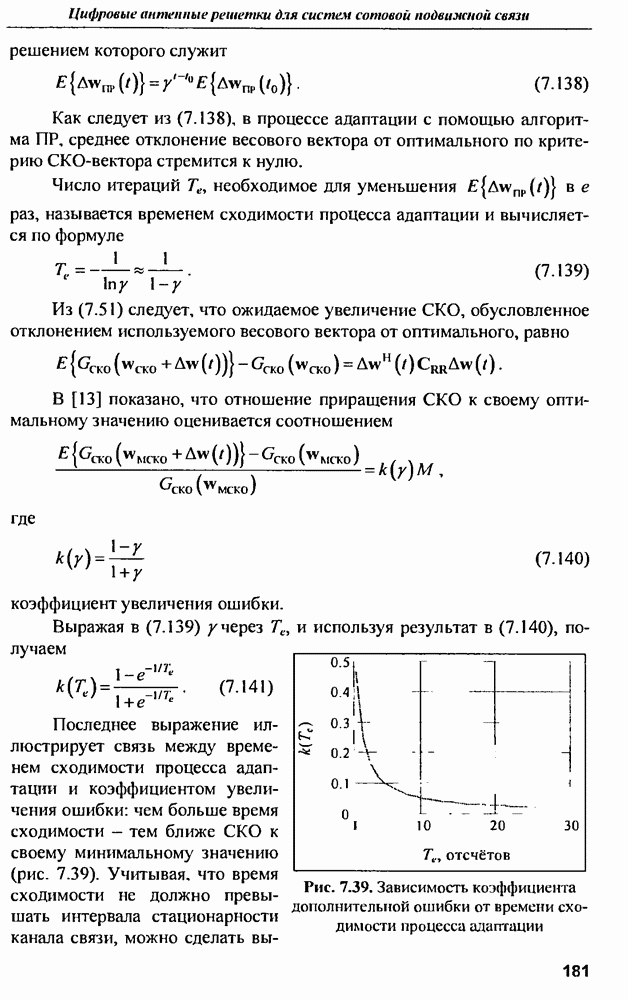
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
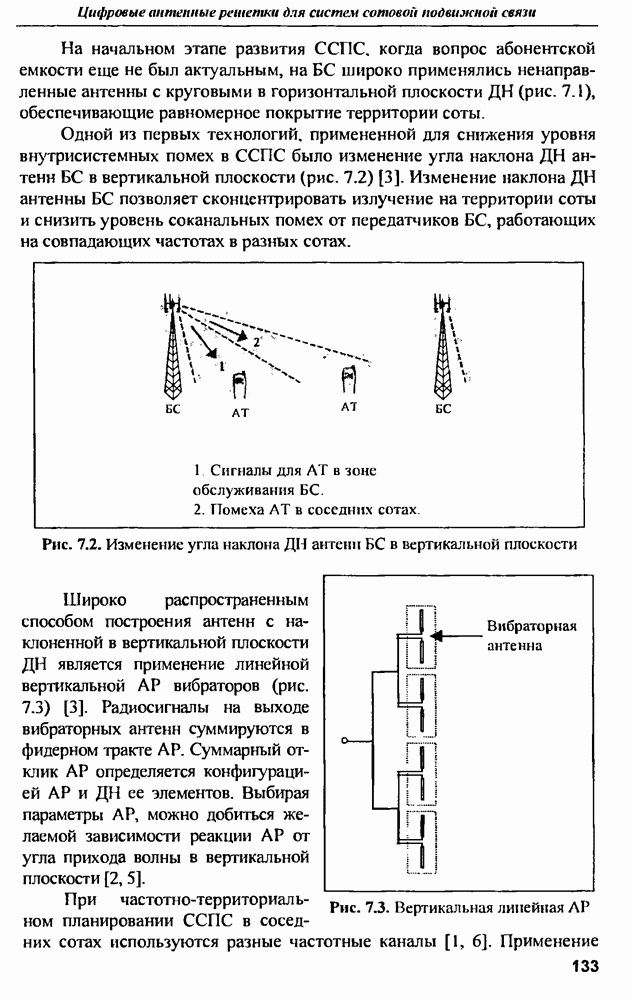
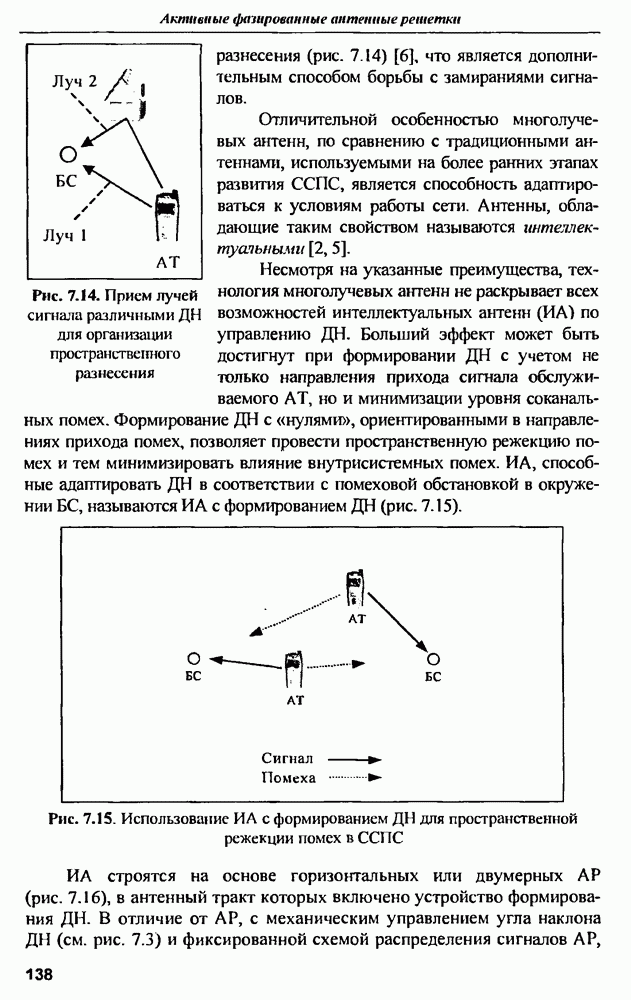
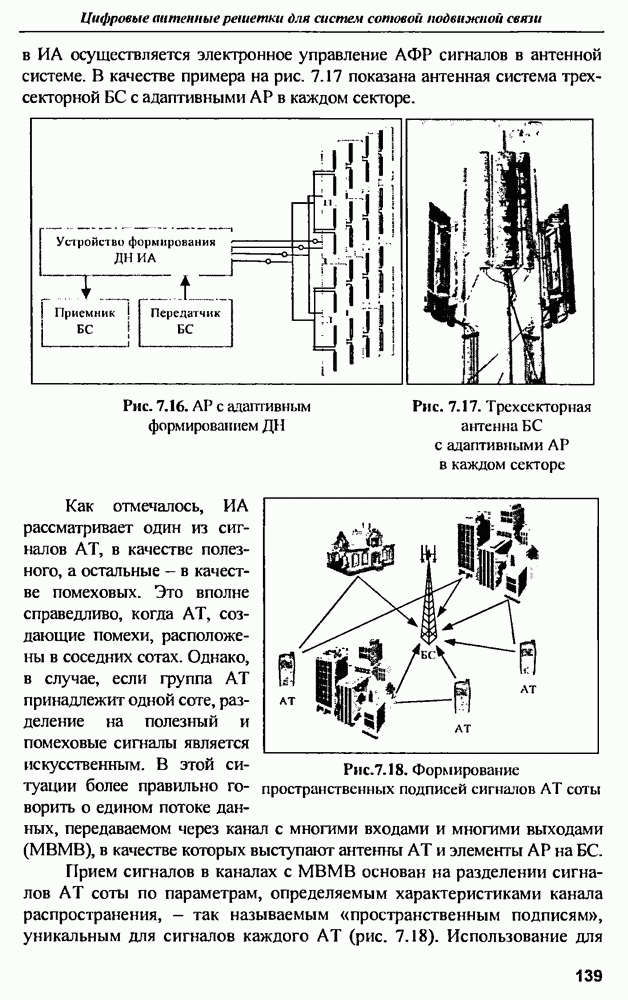
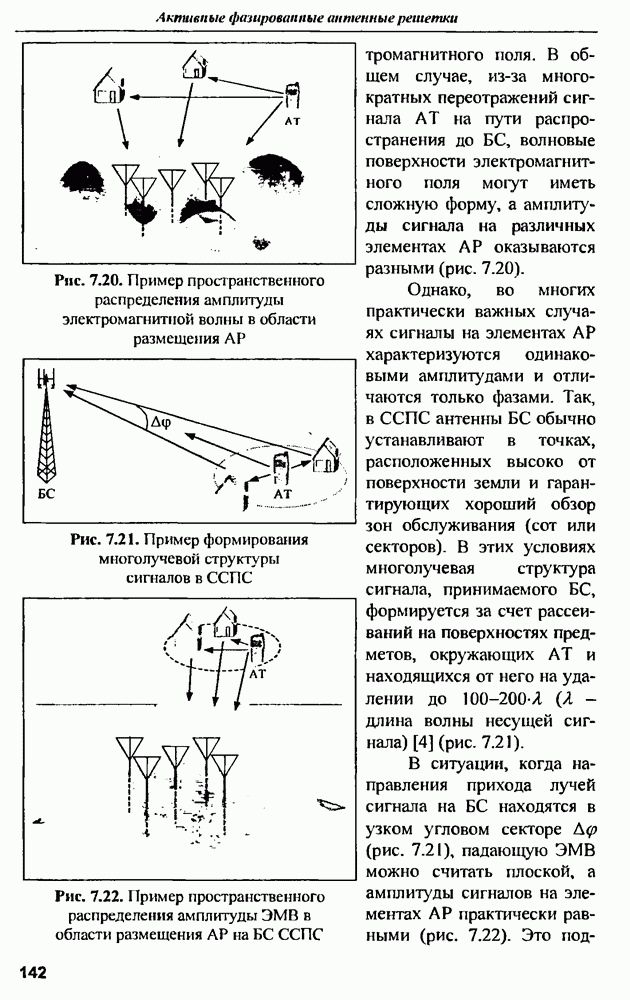
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
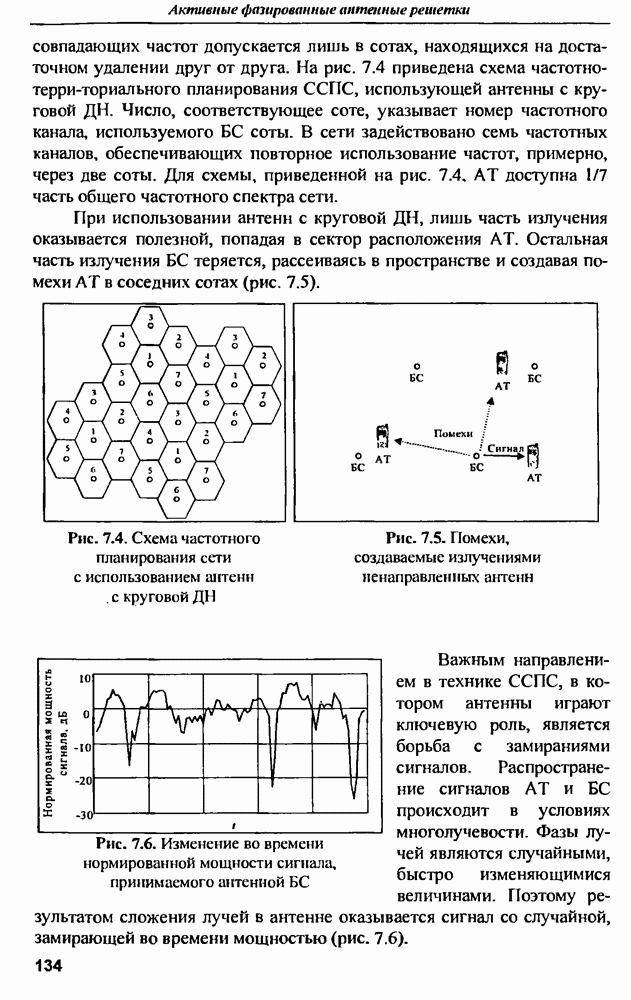
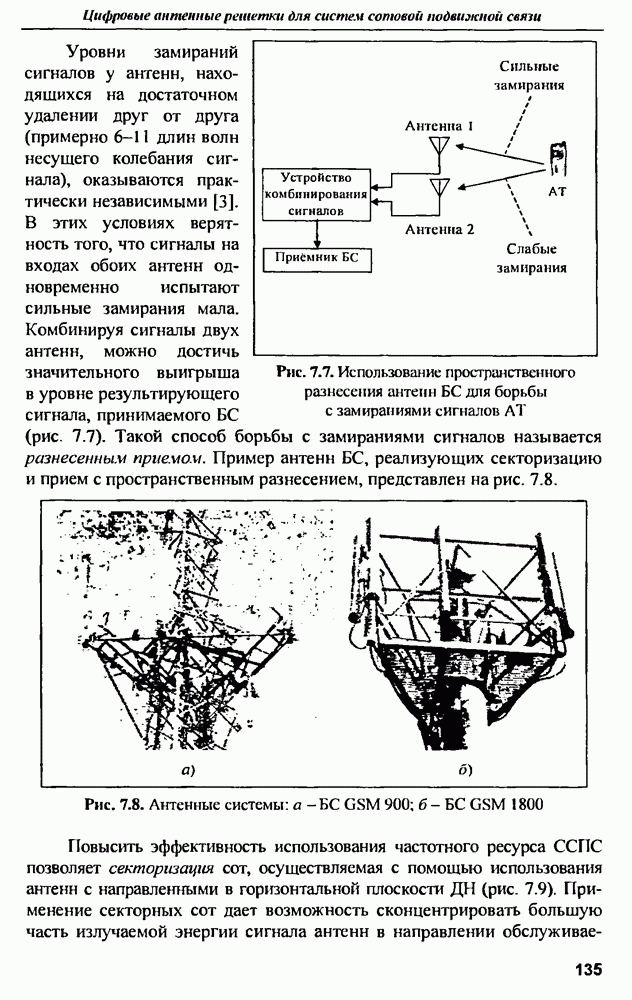
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
- 7.3.4. Качество связи
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
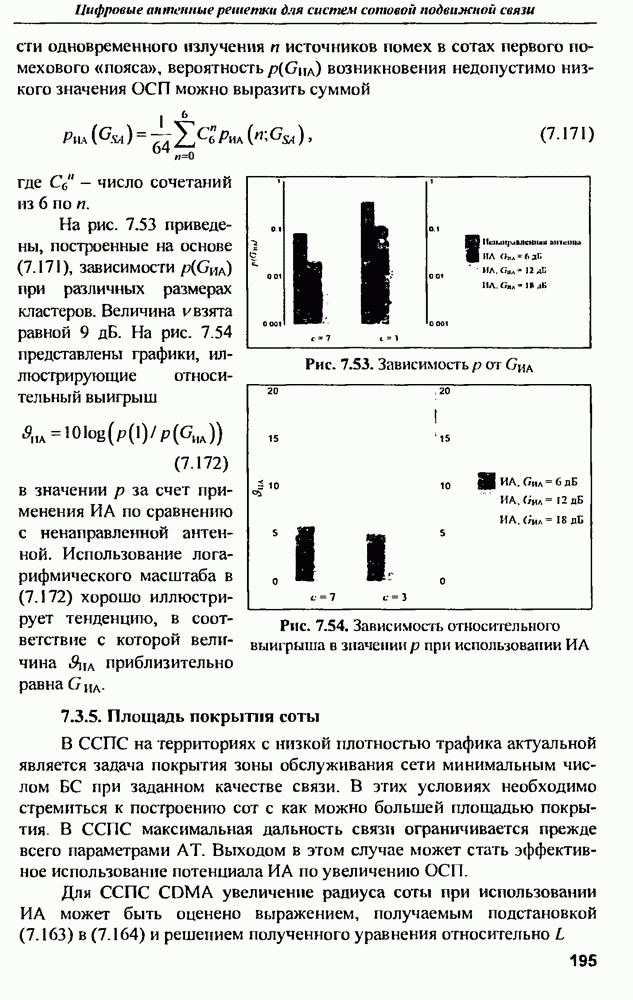
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
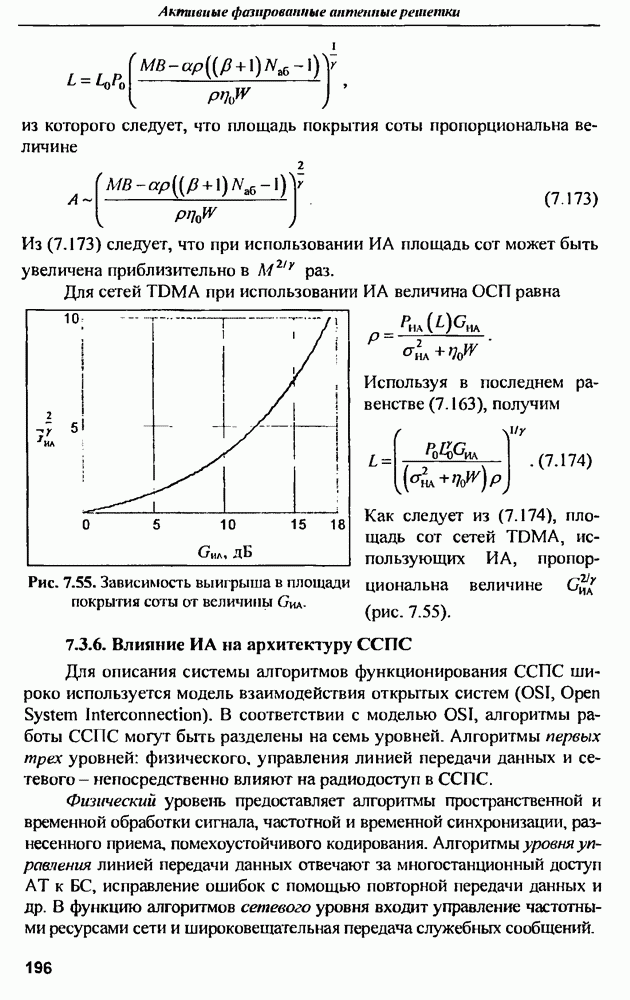
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
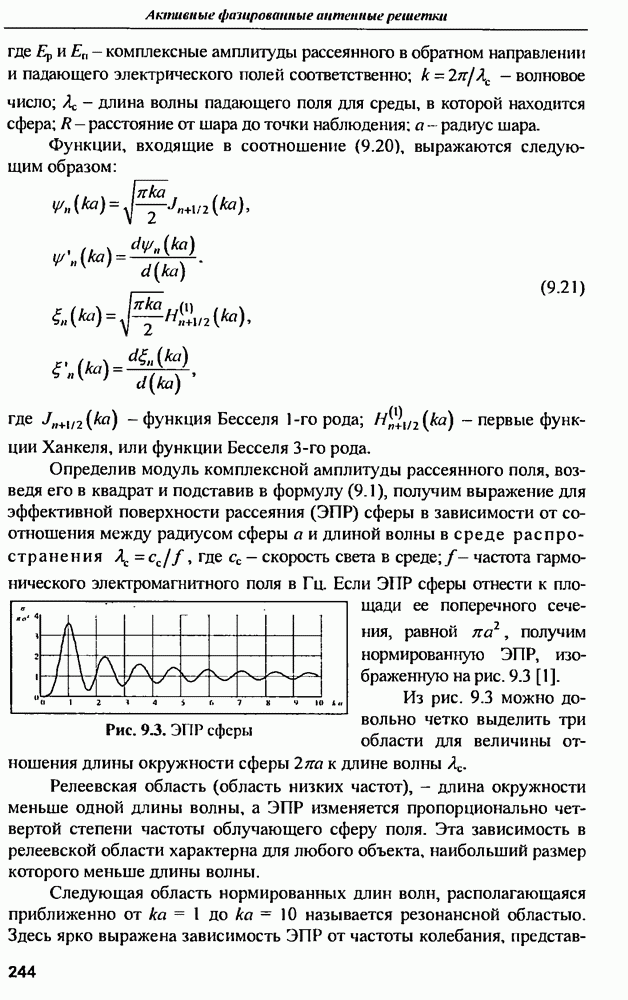
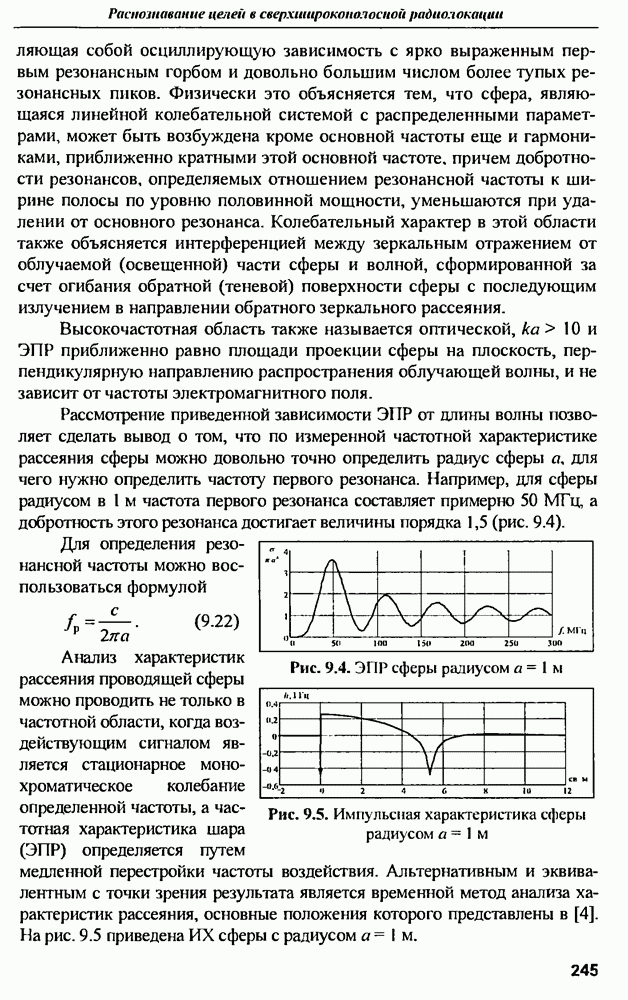
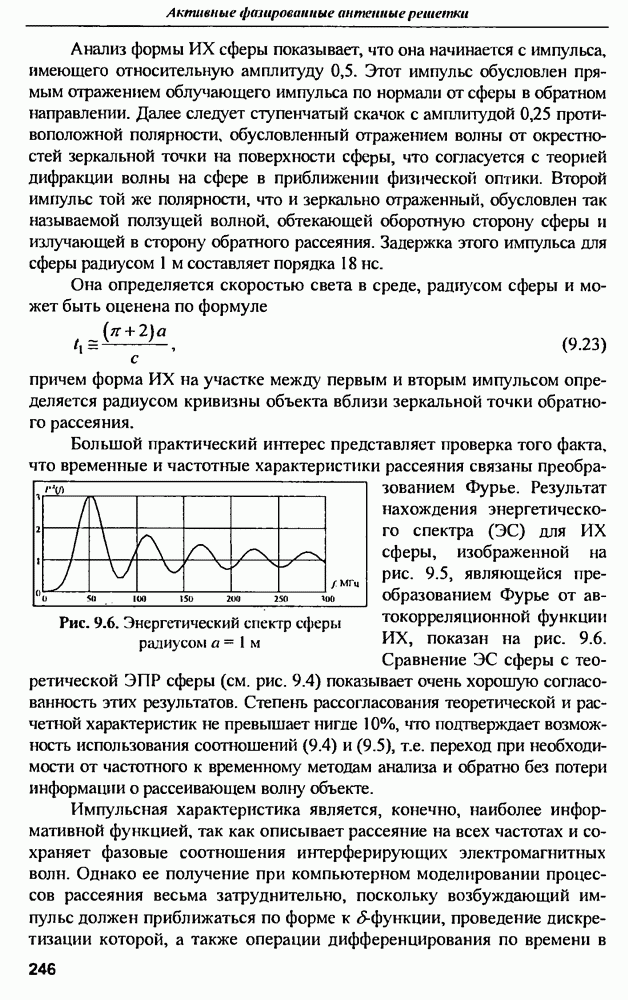
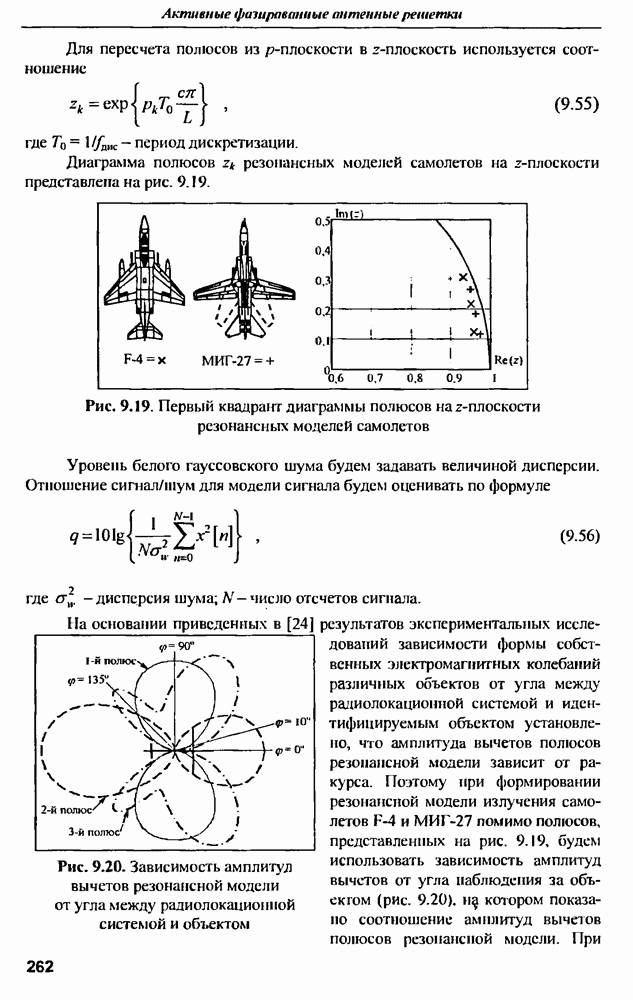
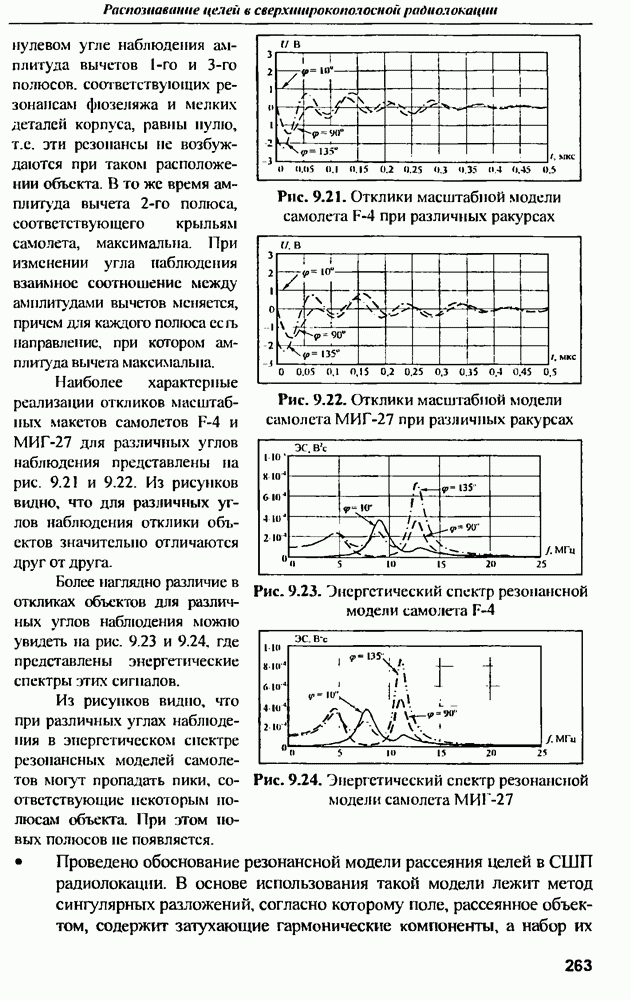
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
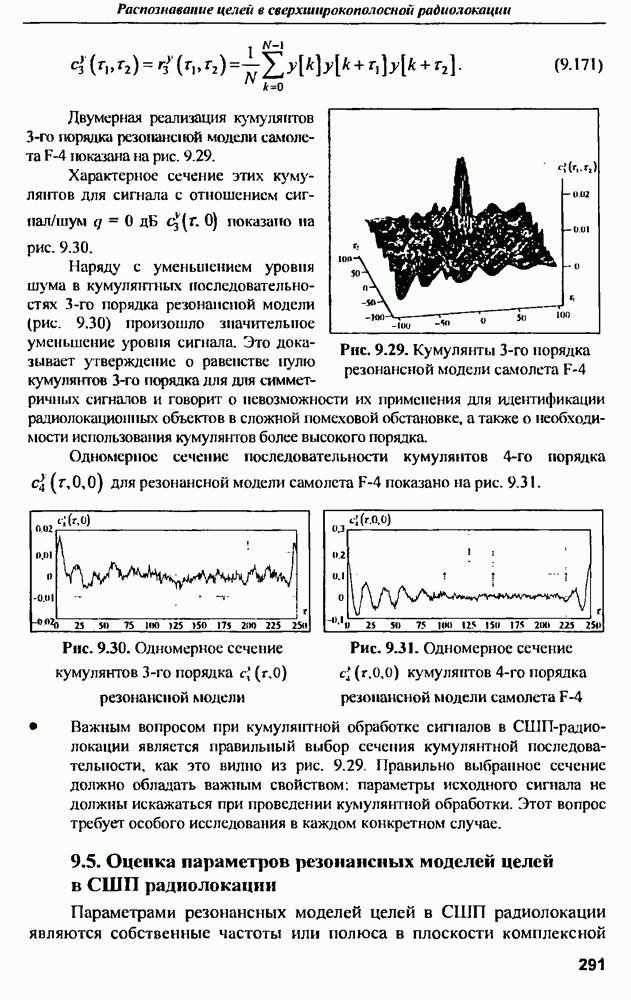
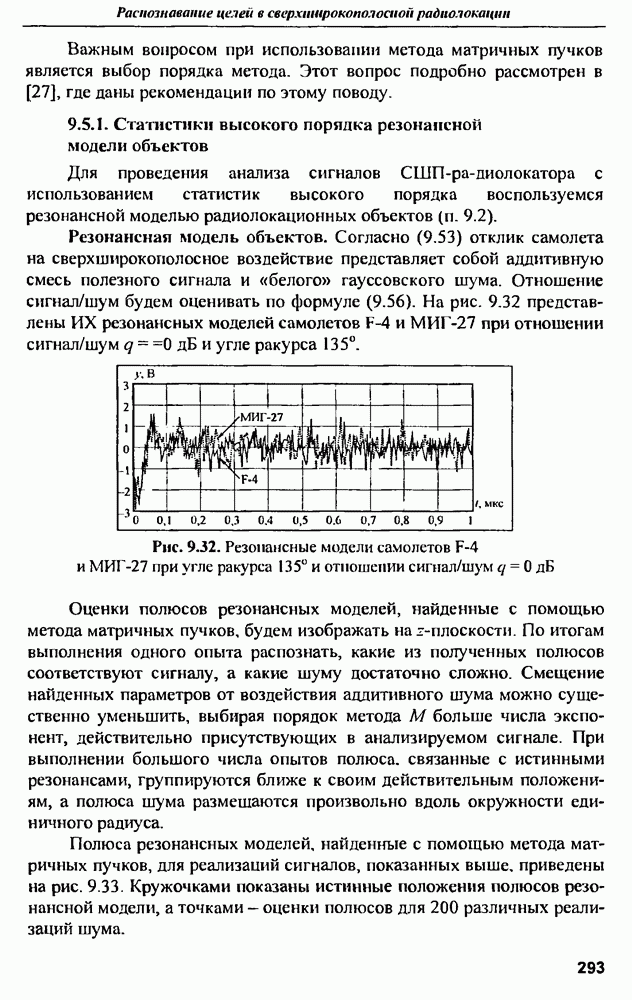
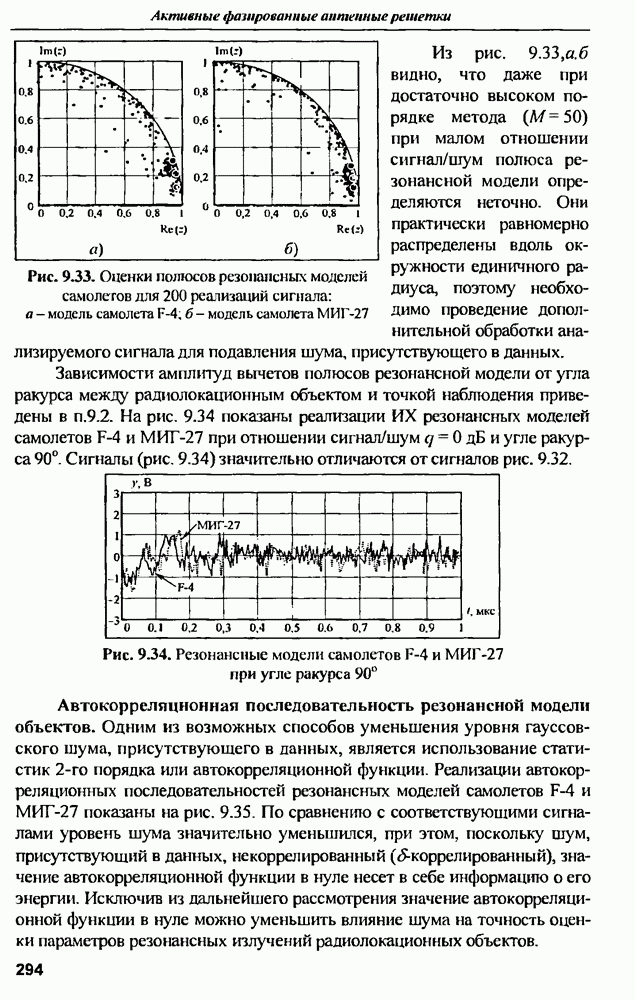
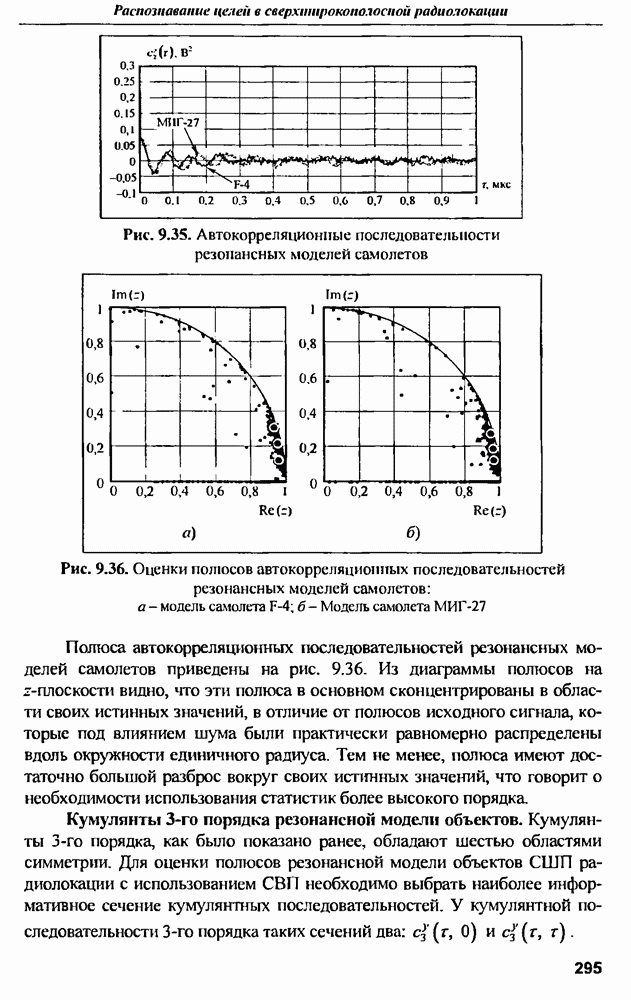
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
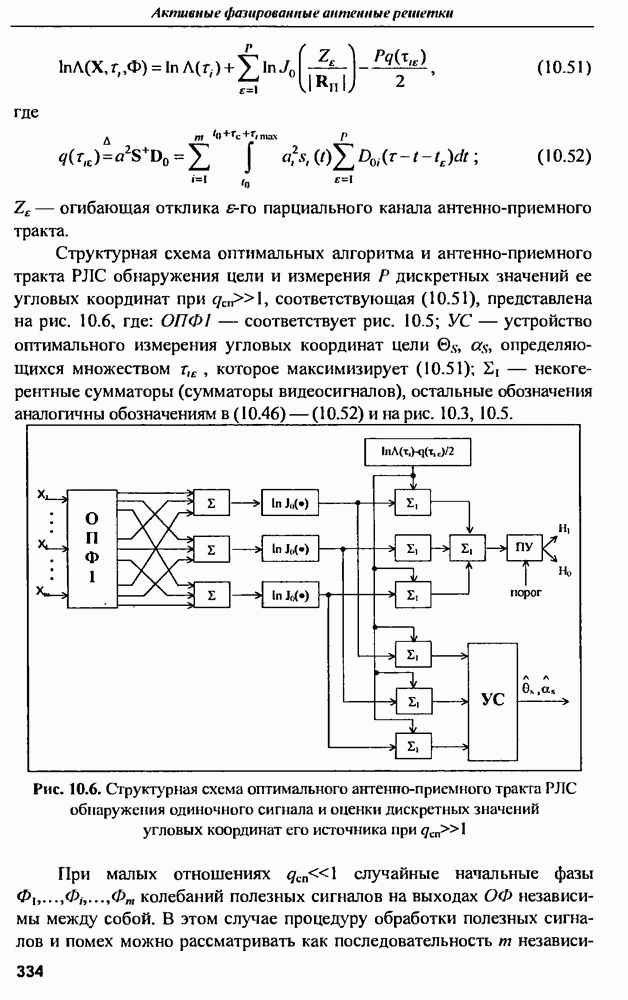
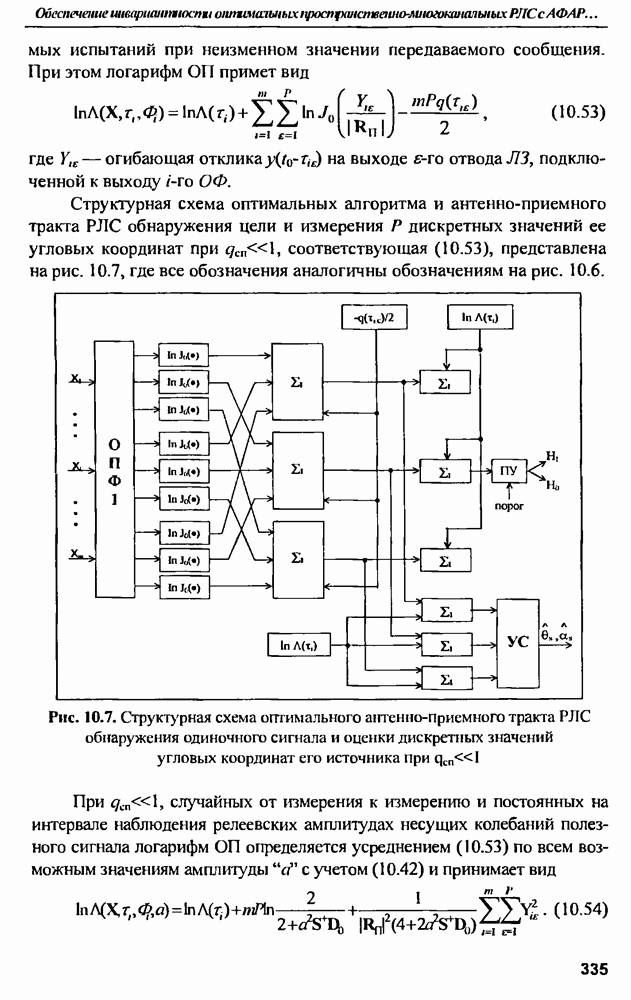
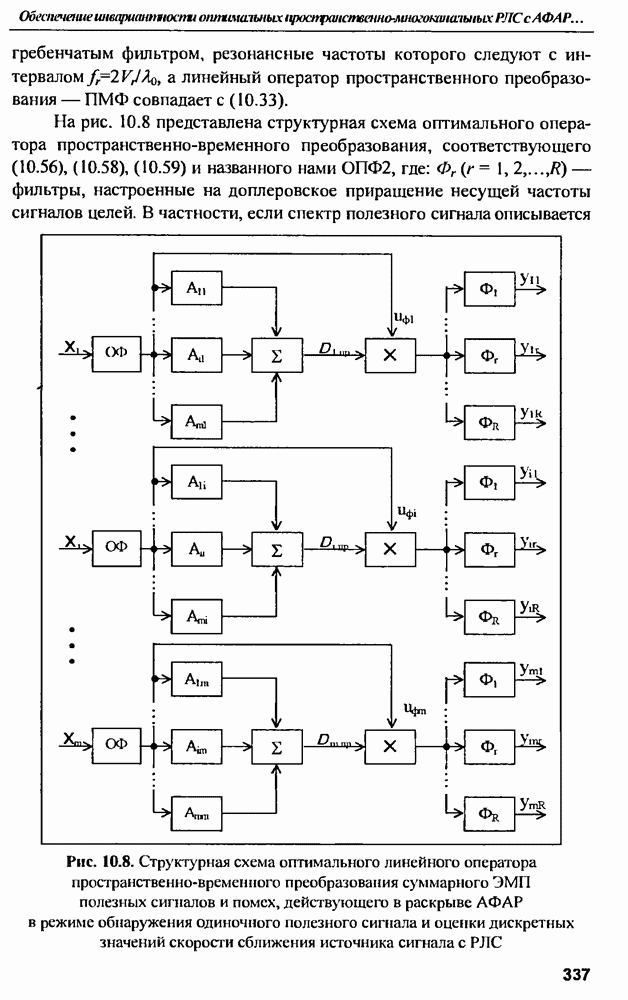
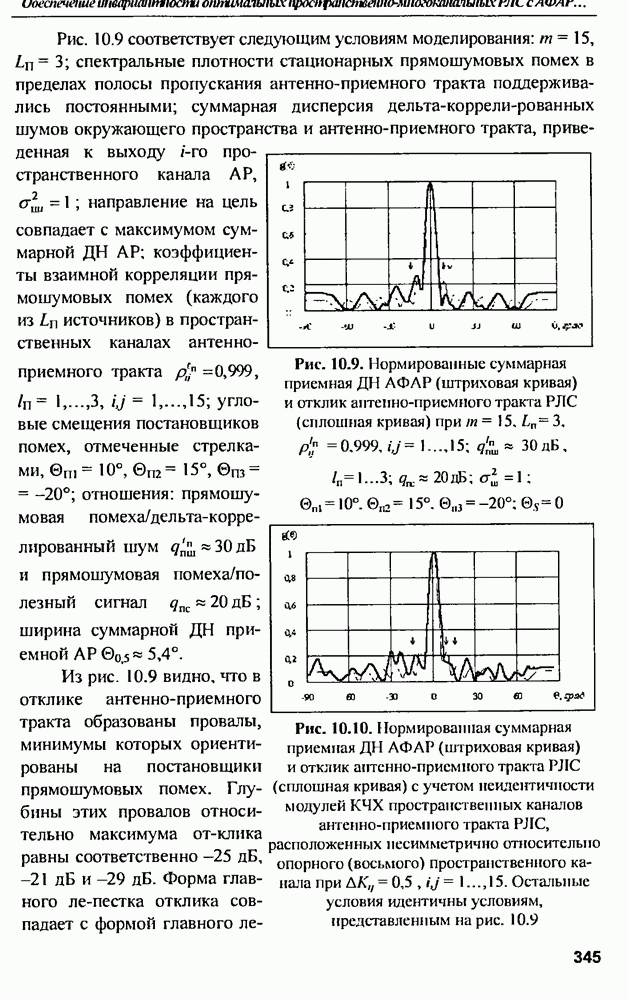
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
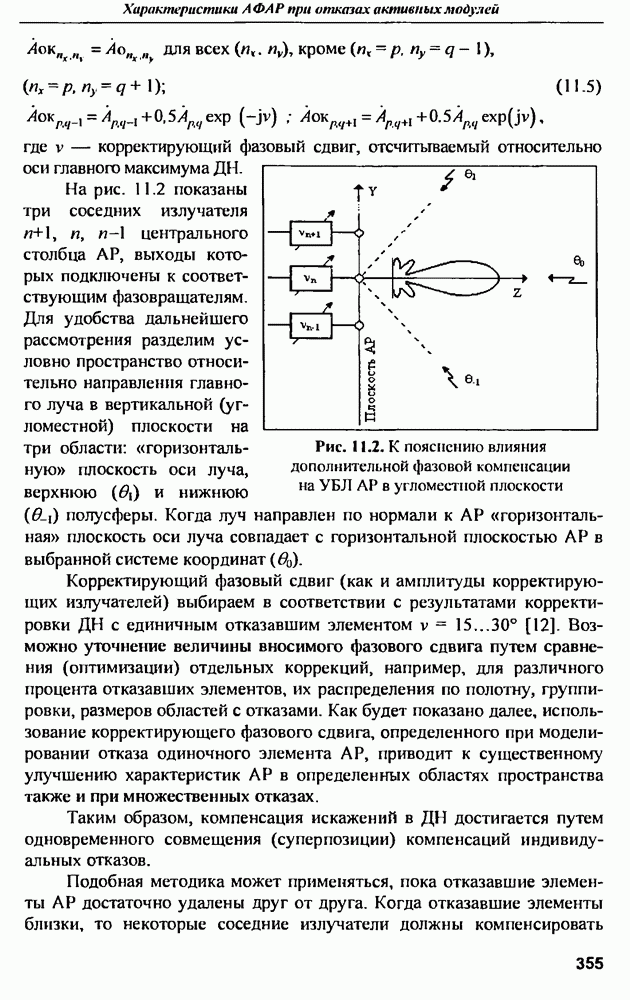
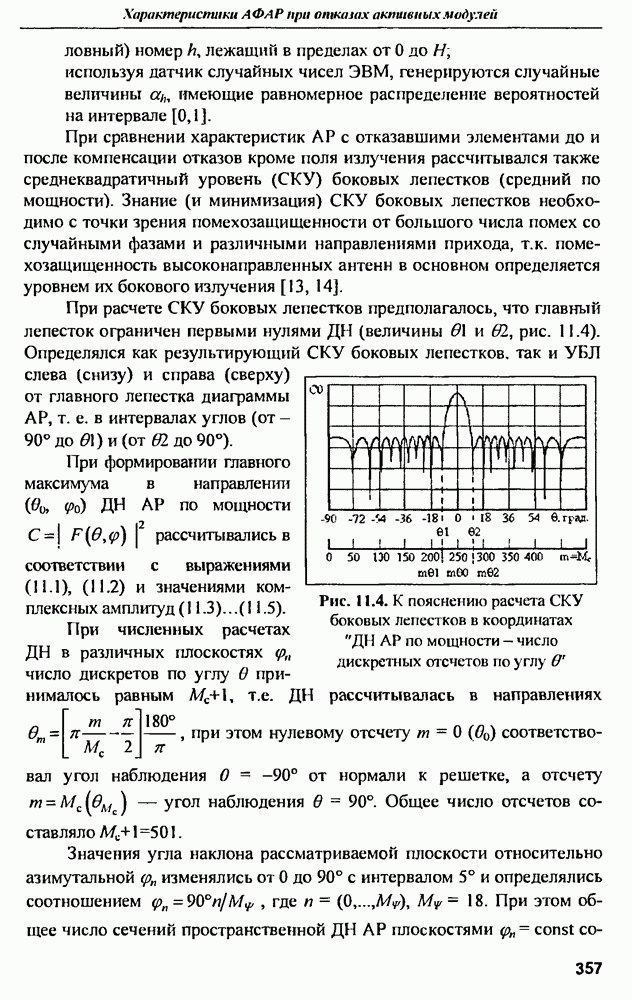
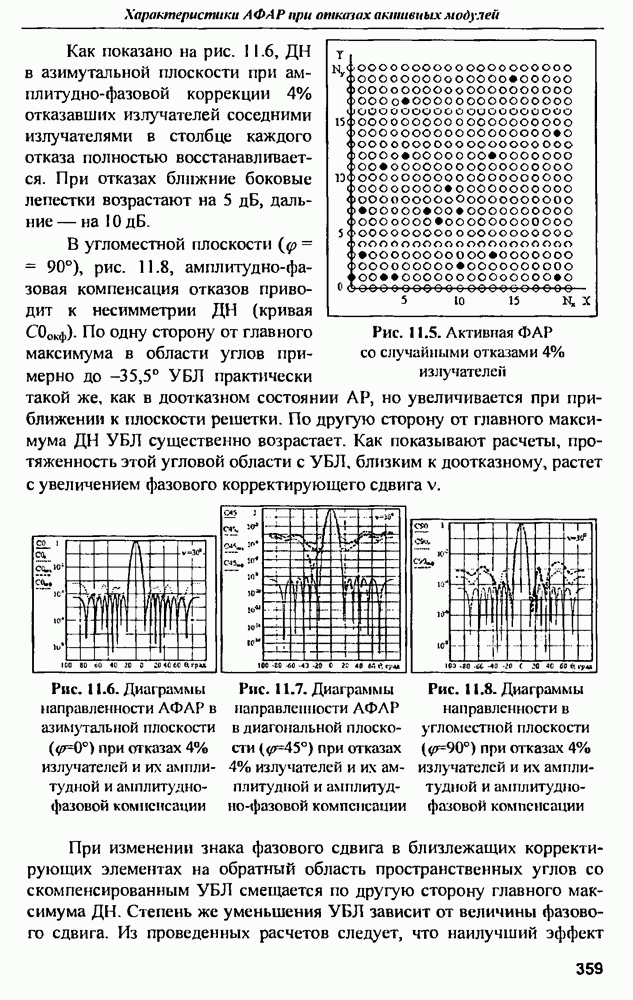
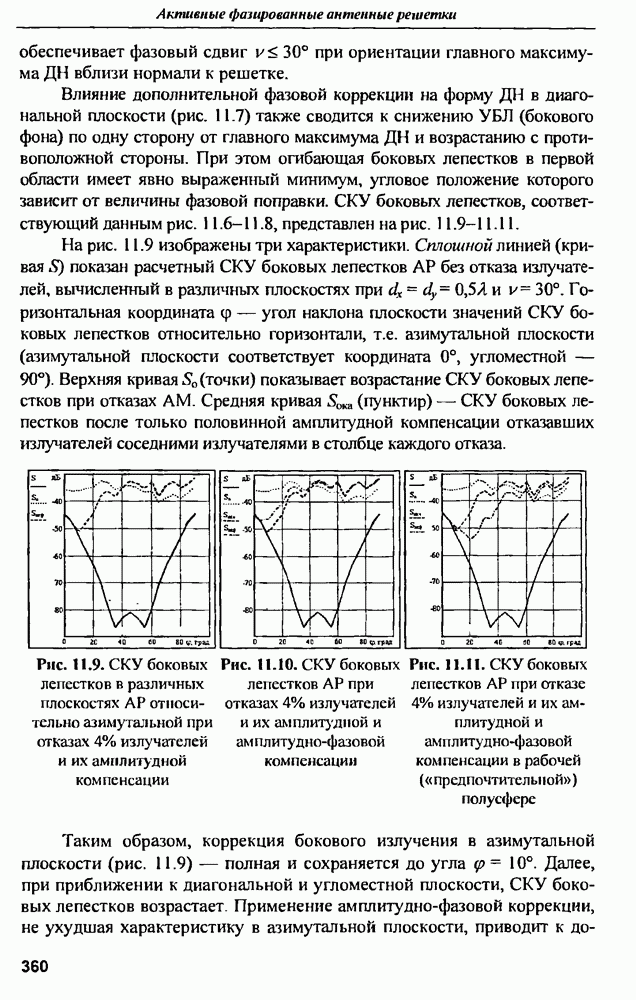
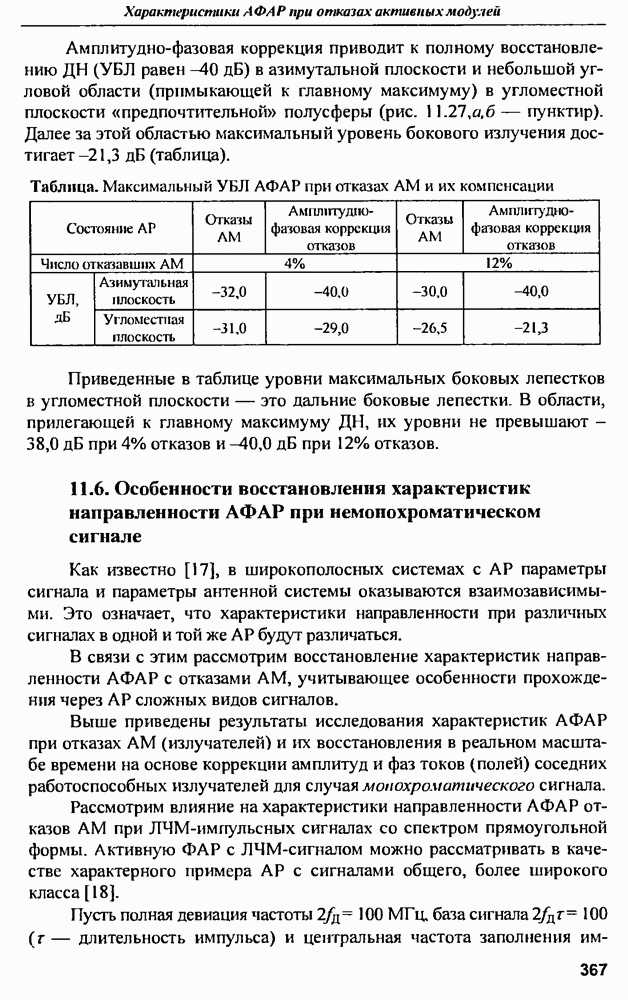
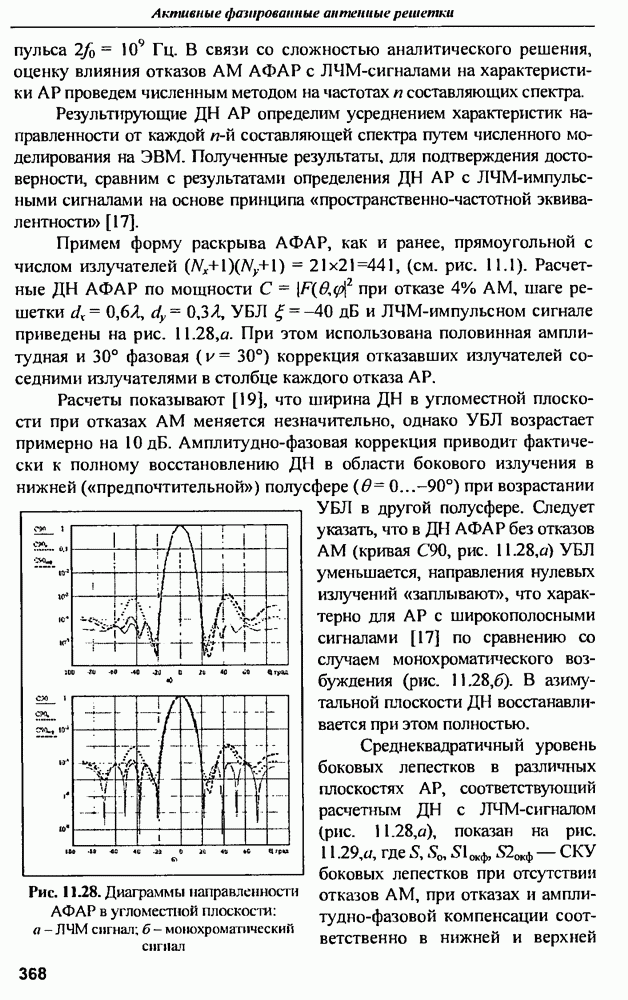
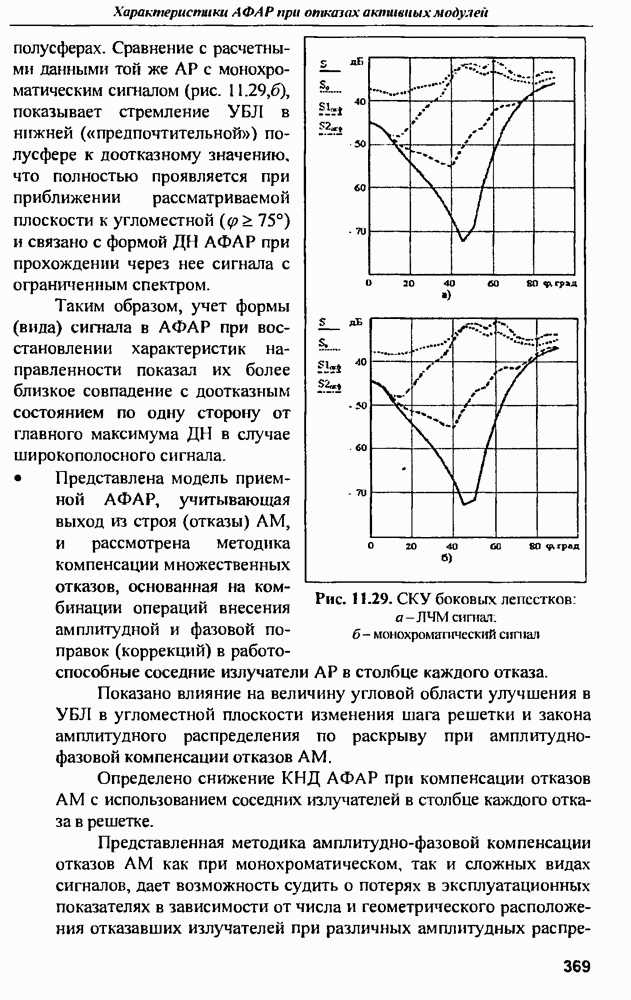
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
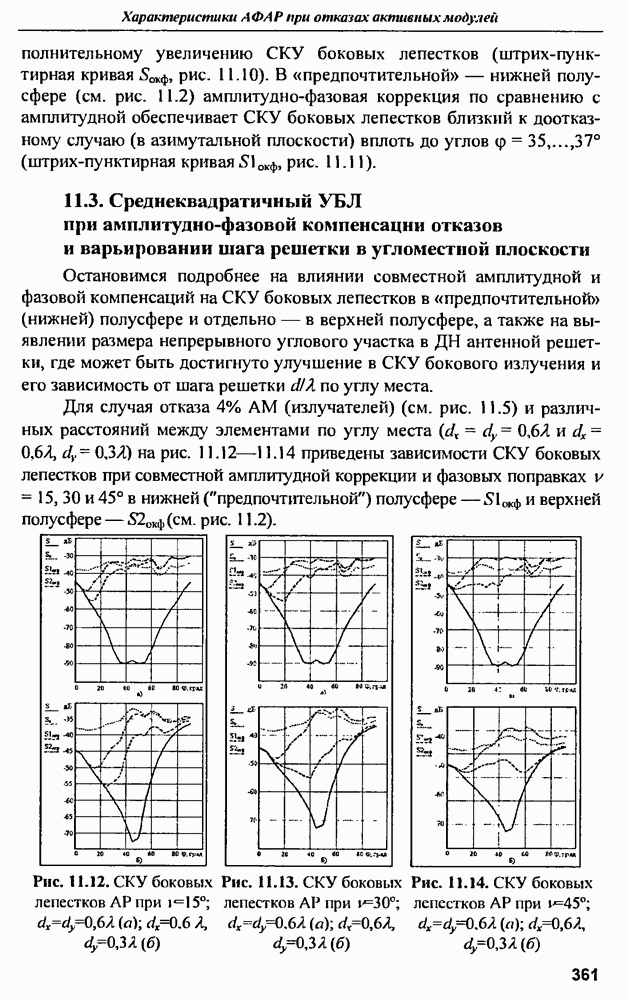
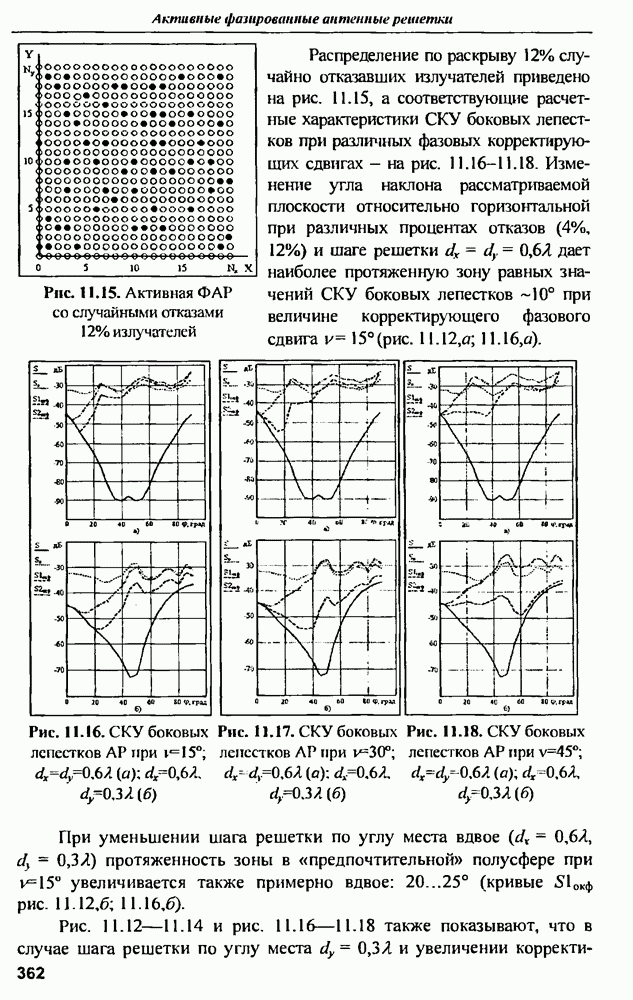
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
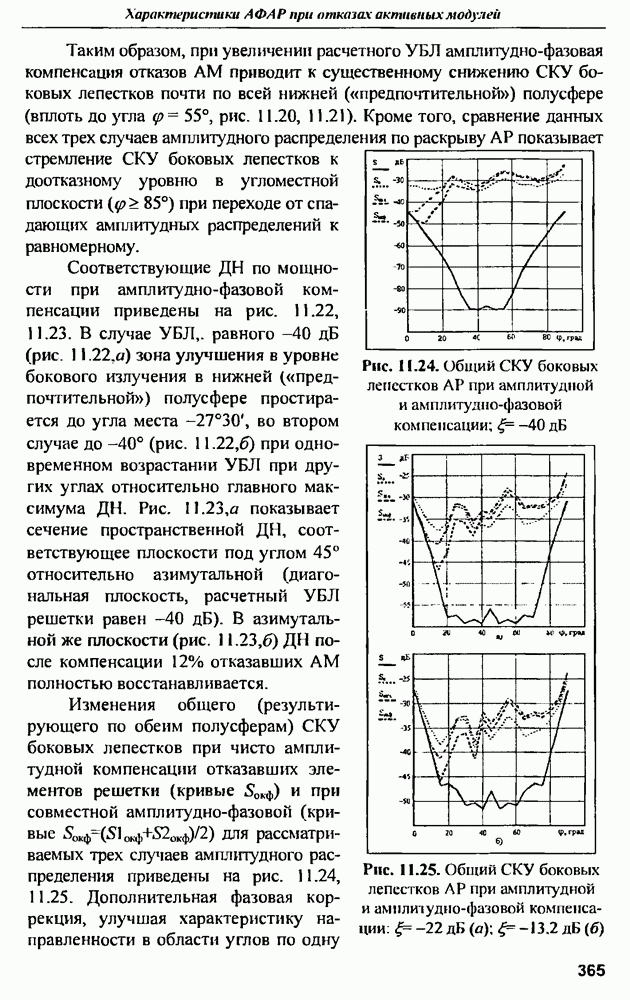
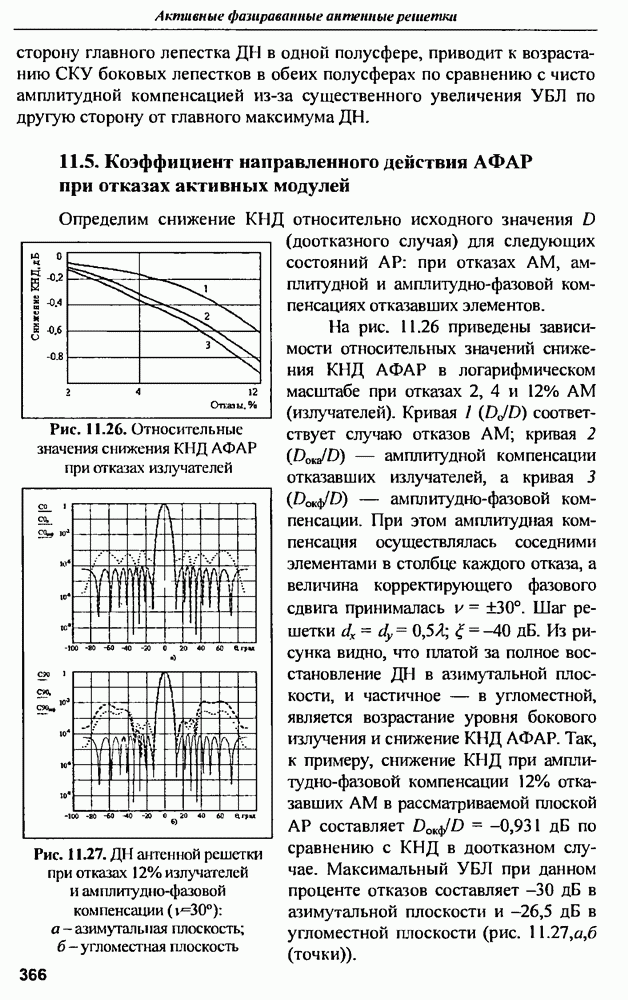
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
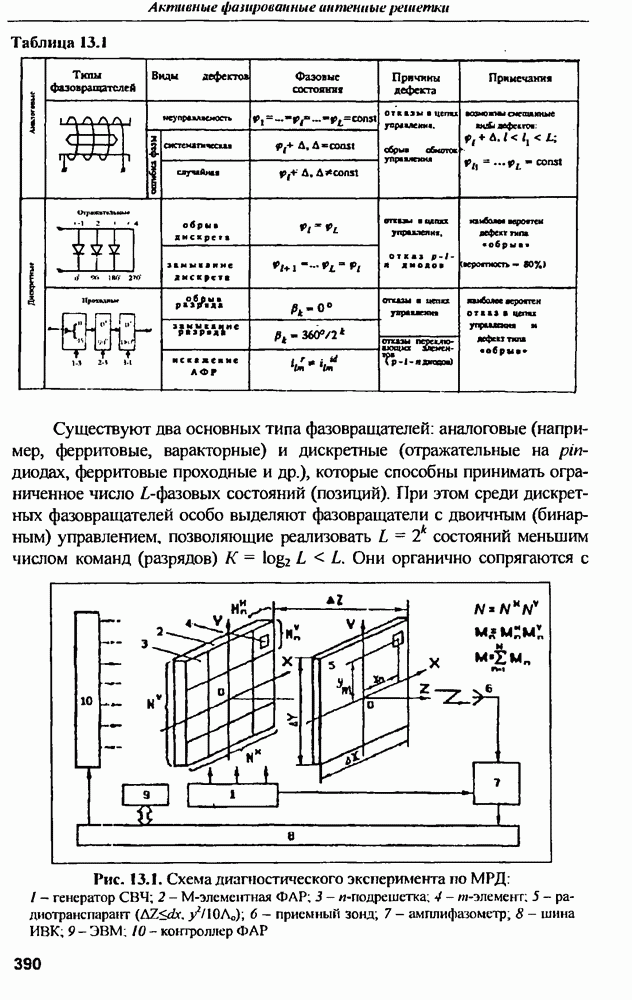
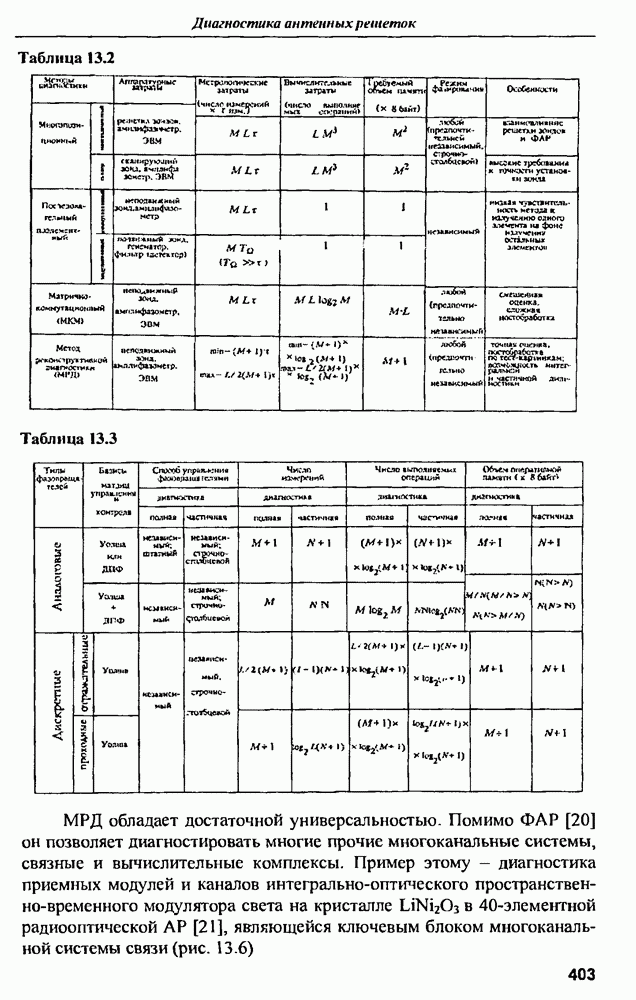
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
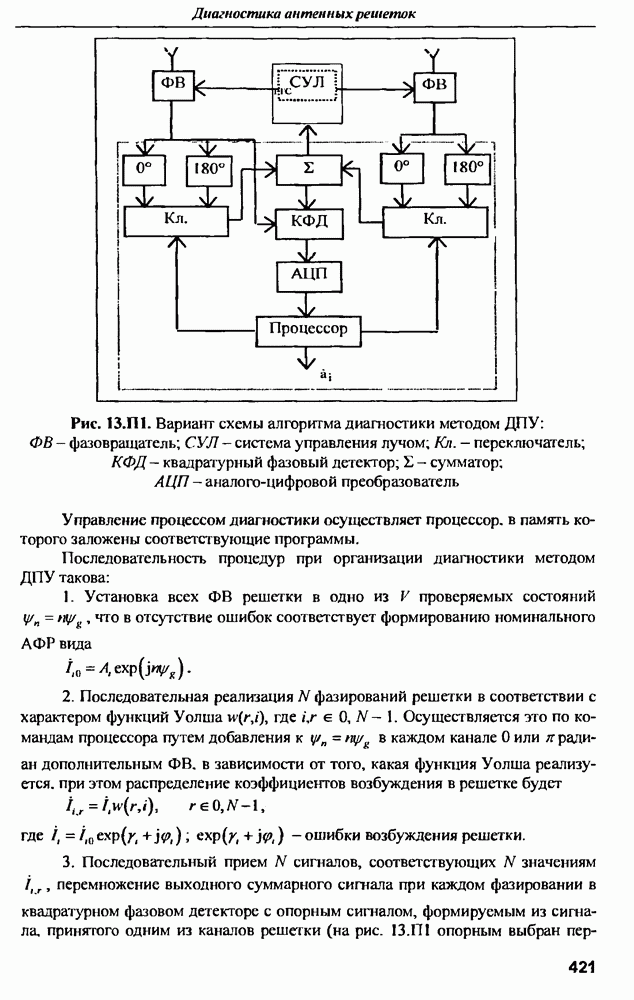
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
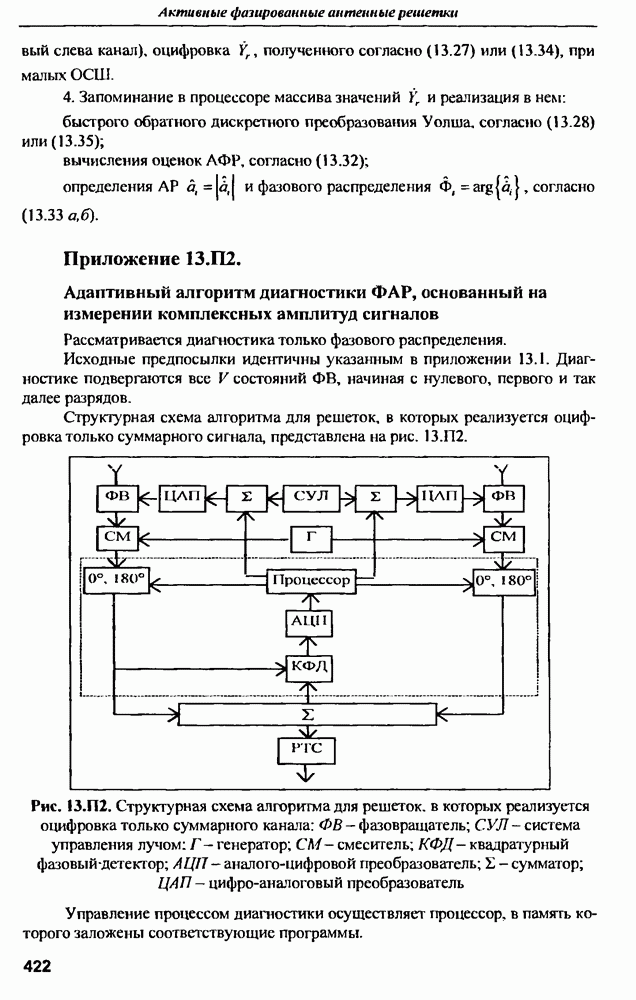
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
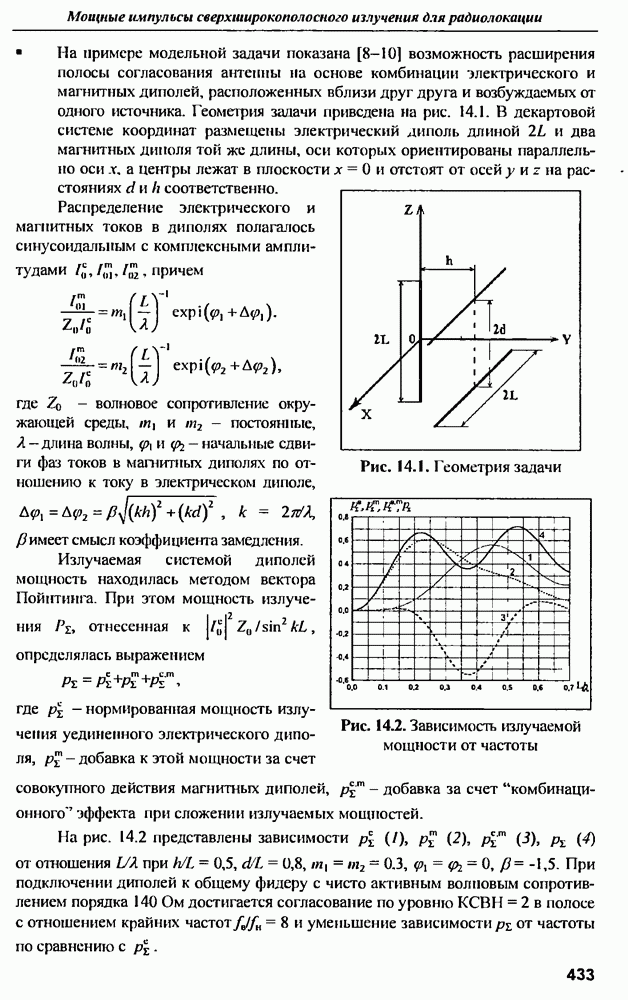
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
- 14.2. Синтез сверхширокополосных антенн
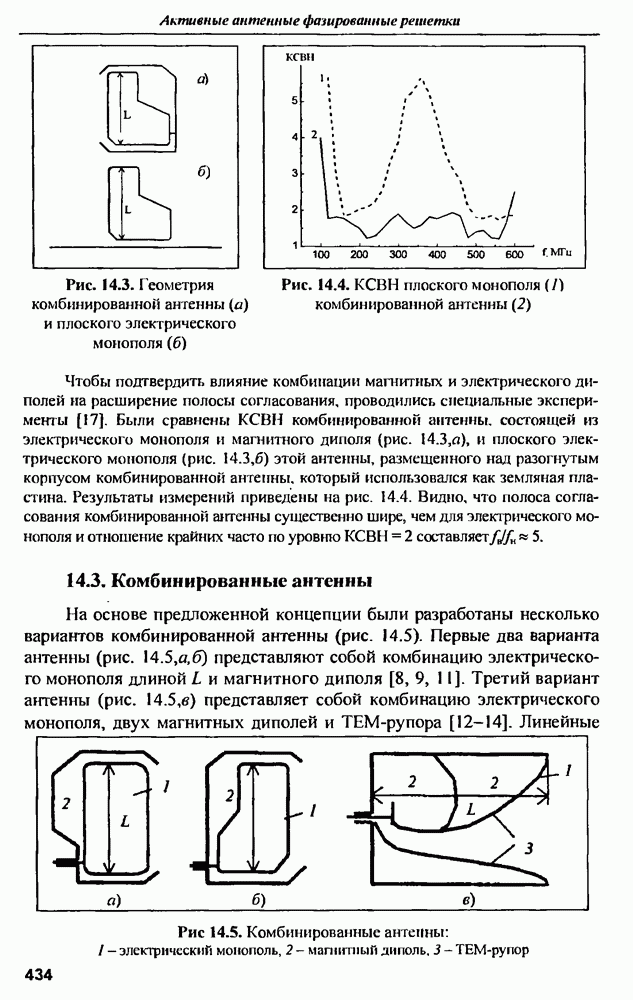
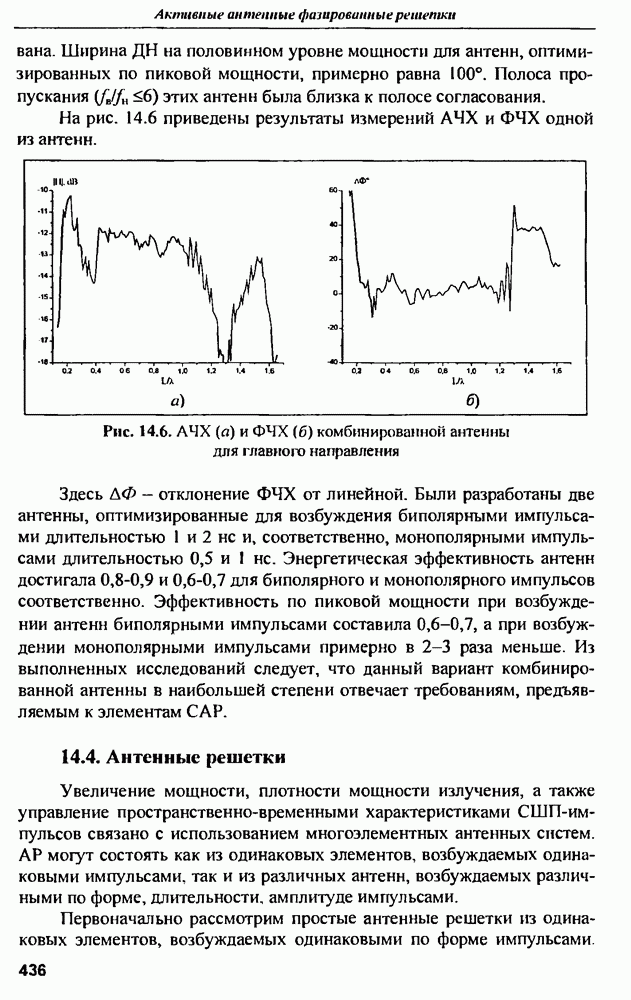
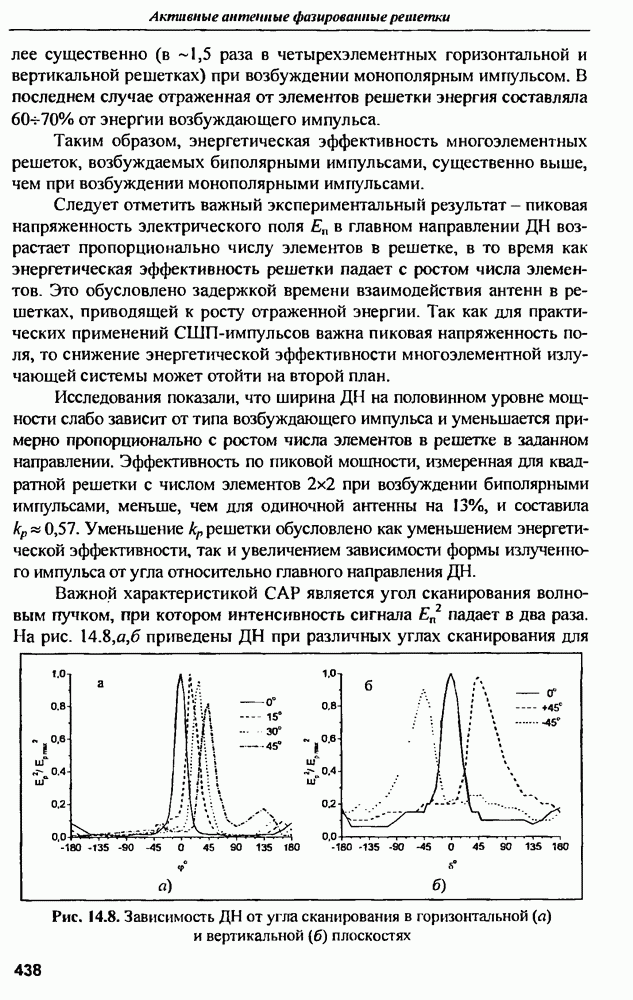
- 14.3. Комбинированные антенны
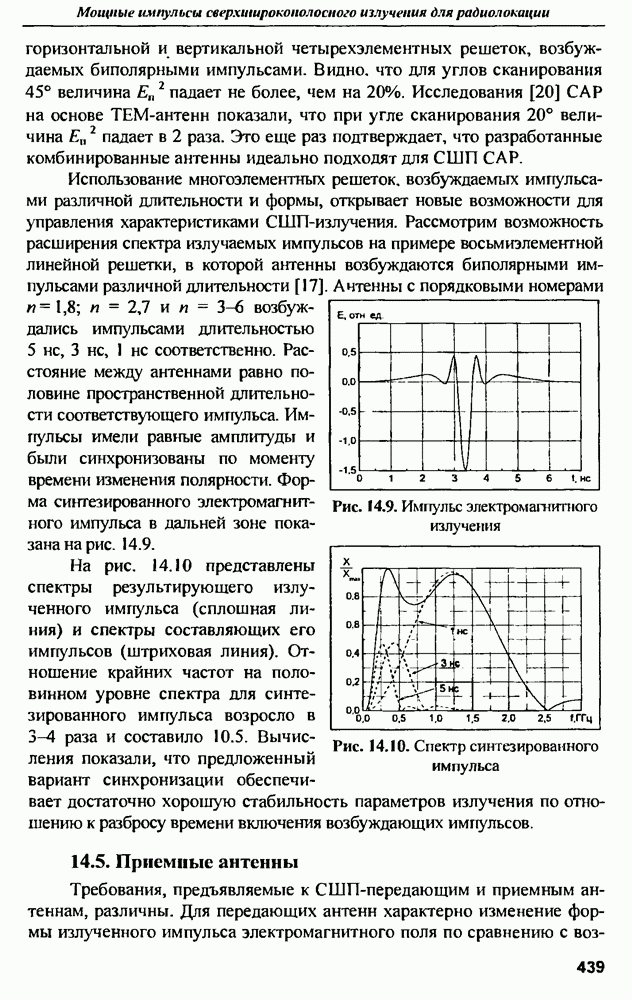
- 14.4. Антенные решетки
- 14.5. Приемные антенны
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
- 14.8. Реконструкция формы объектов
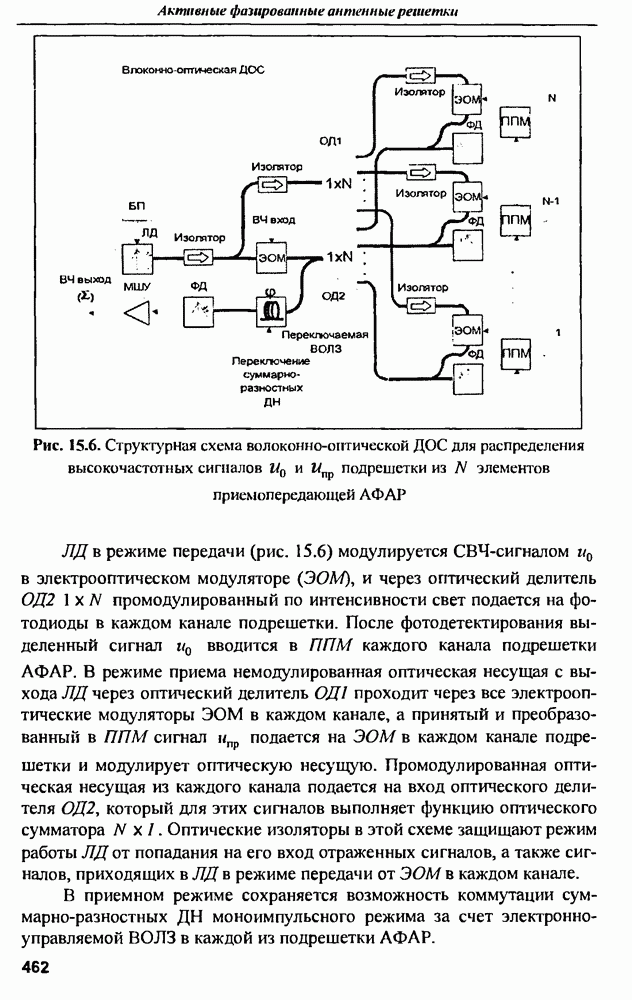
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
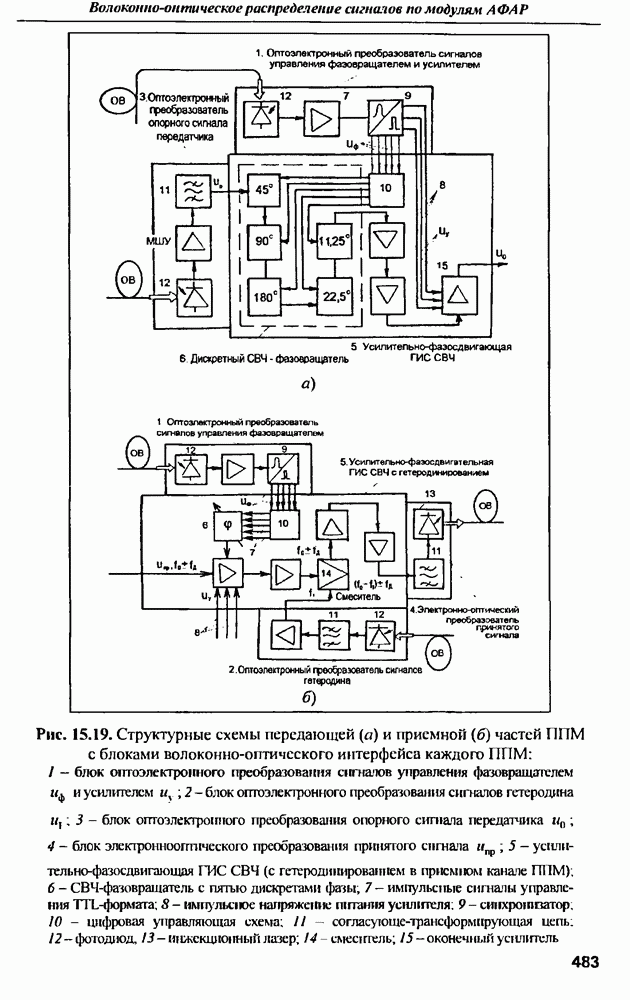
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
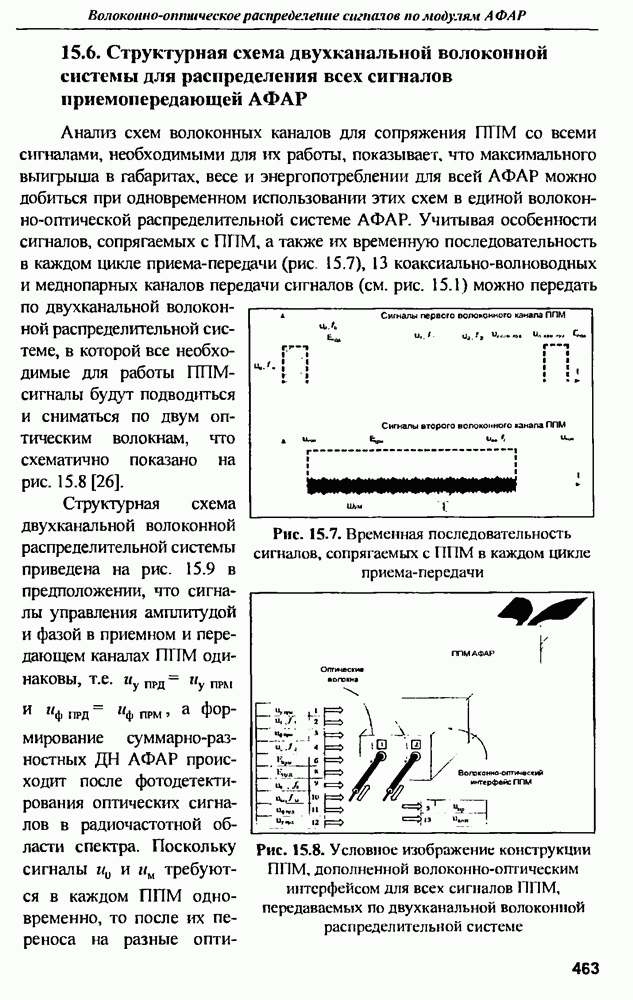
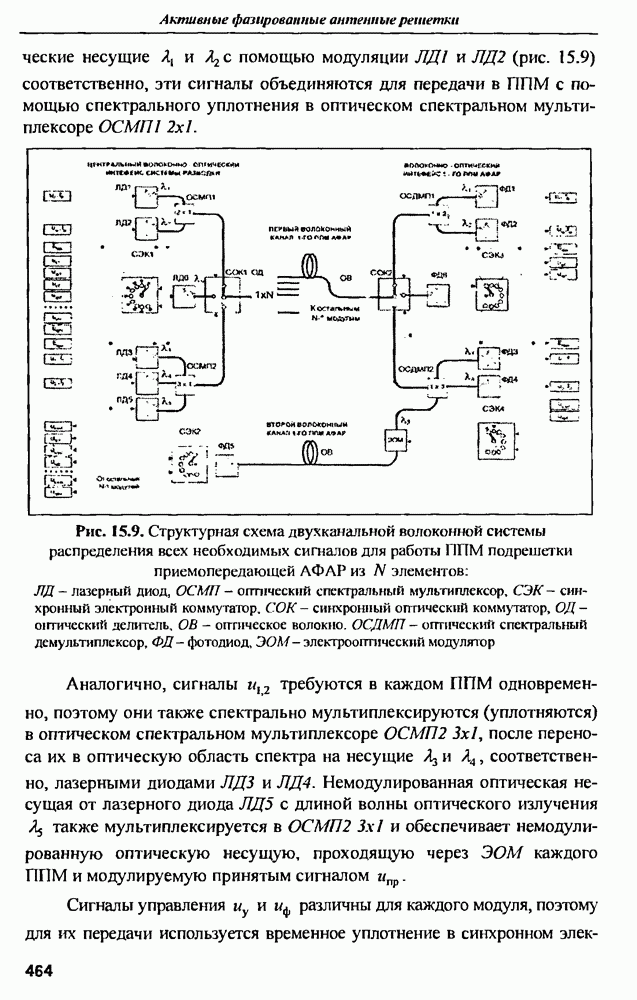
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
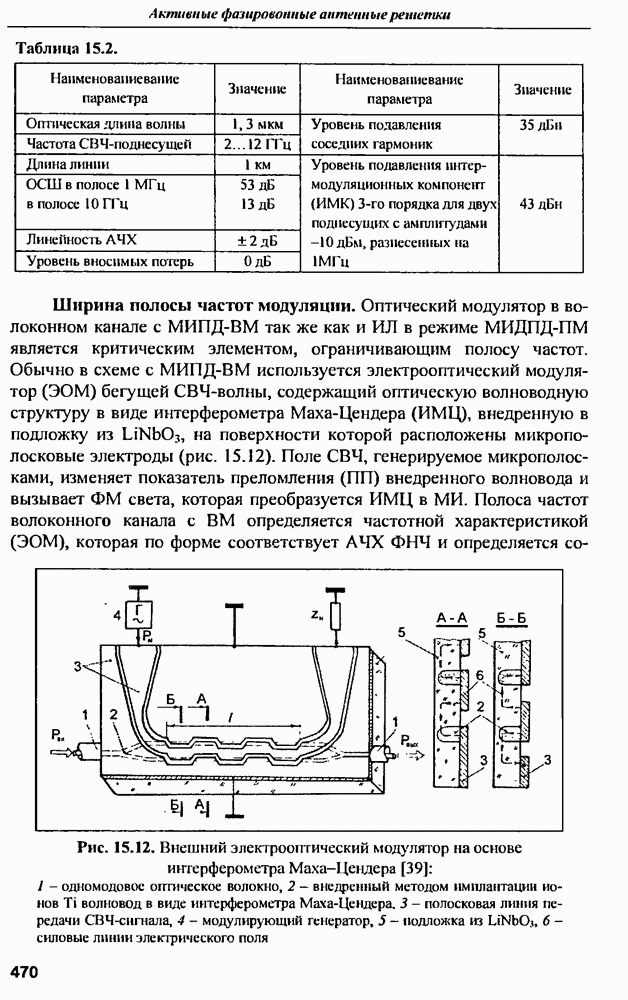
- 15.7.1. Волоконный канал с МИПД-ПМ
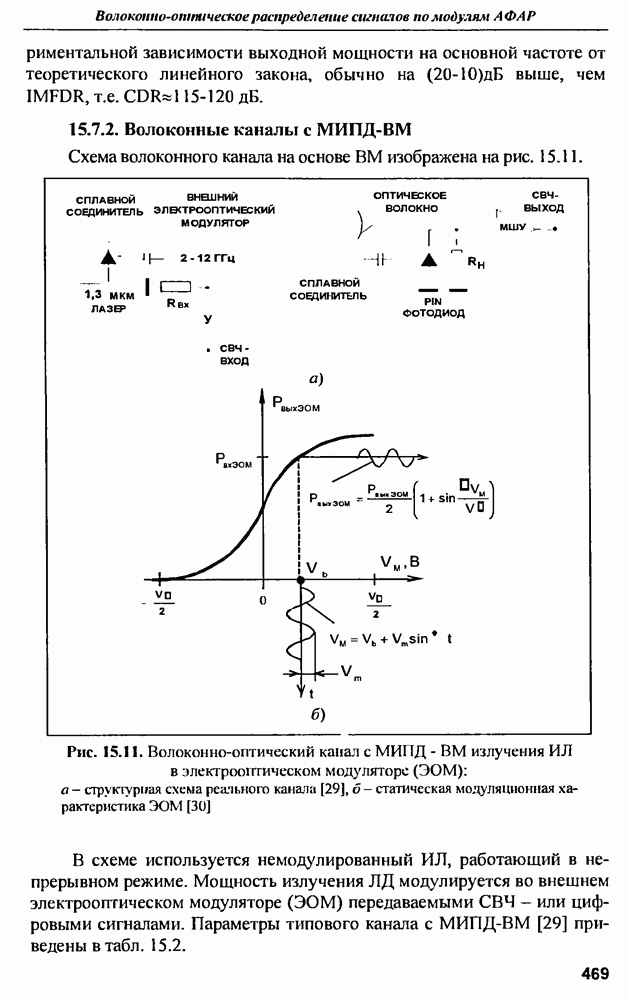
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
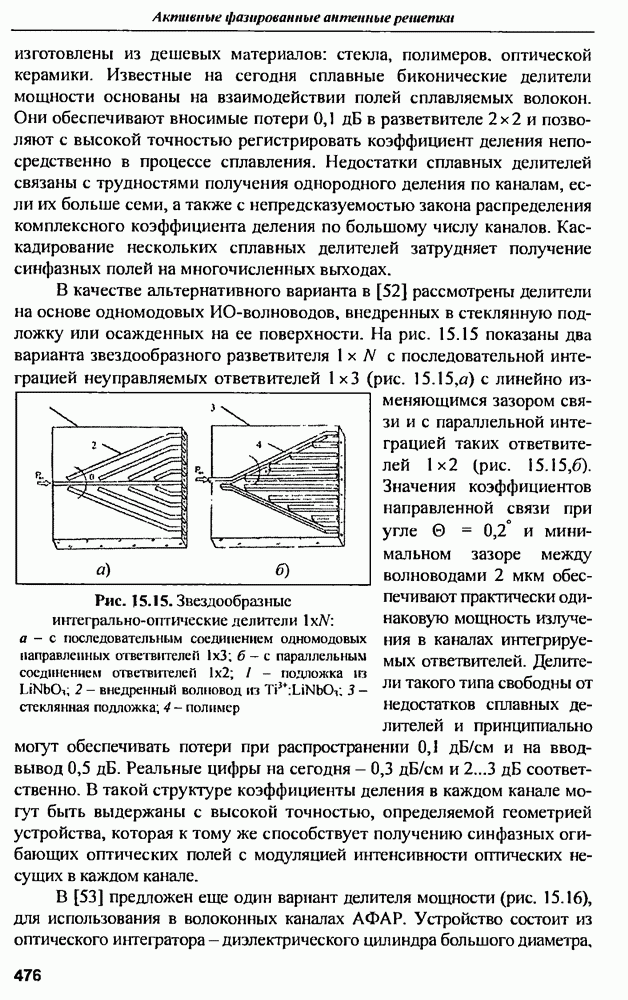
- 15.8.4. Оптические делители
- 15.8.5. Внешние модуляторы
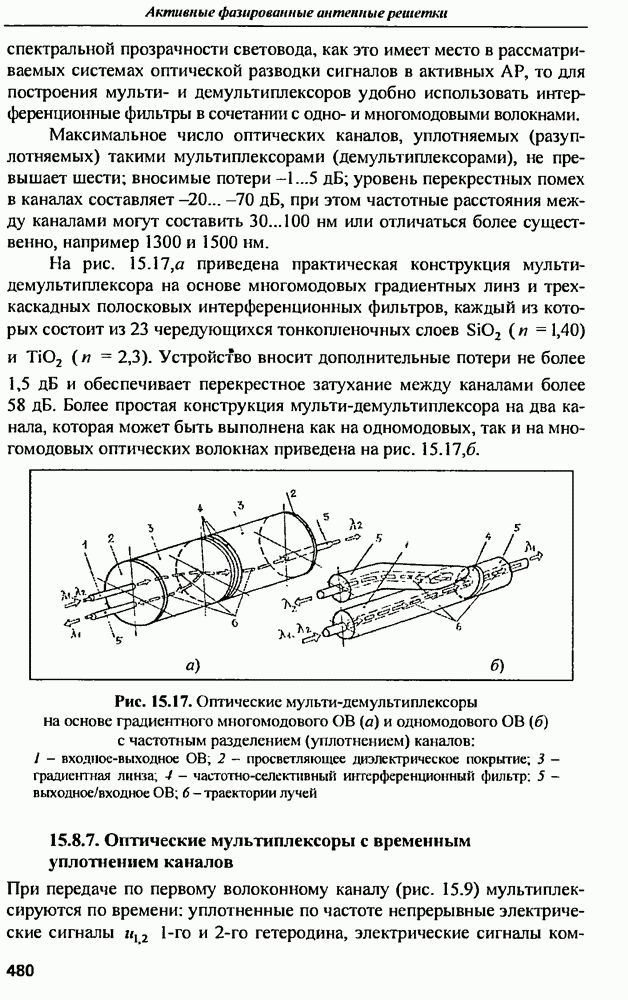
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР