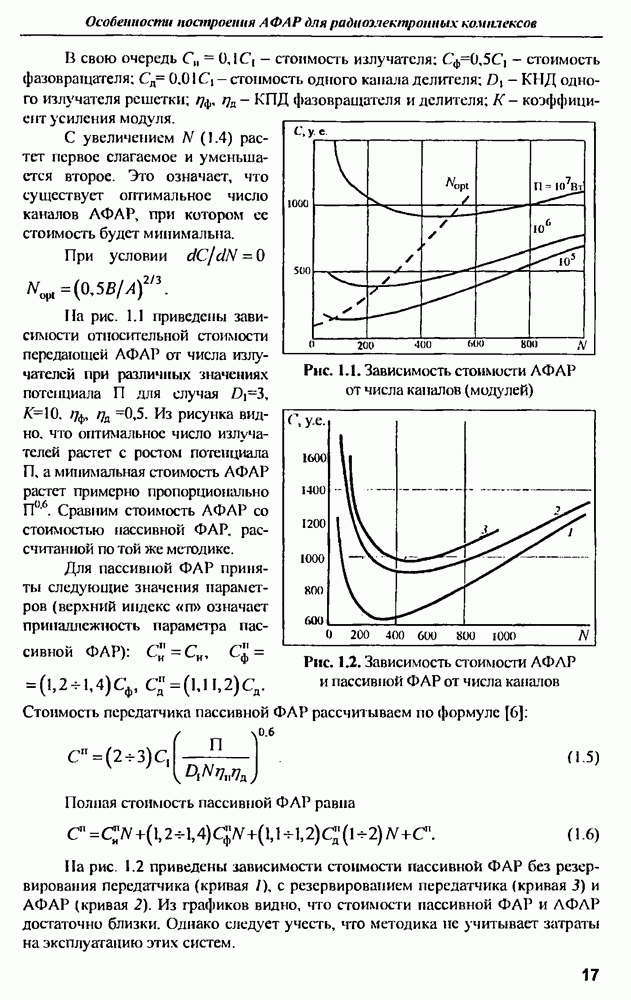
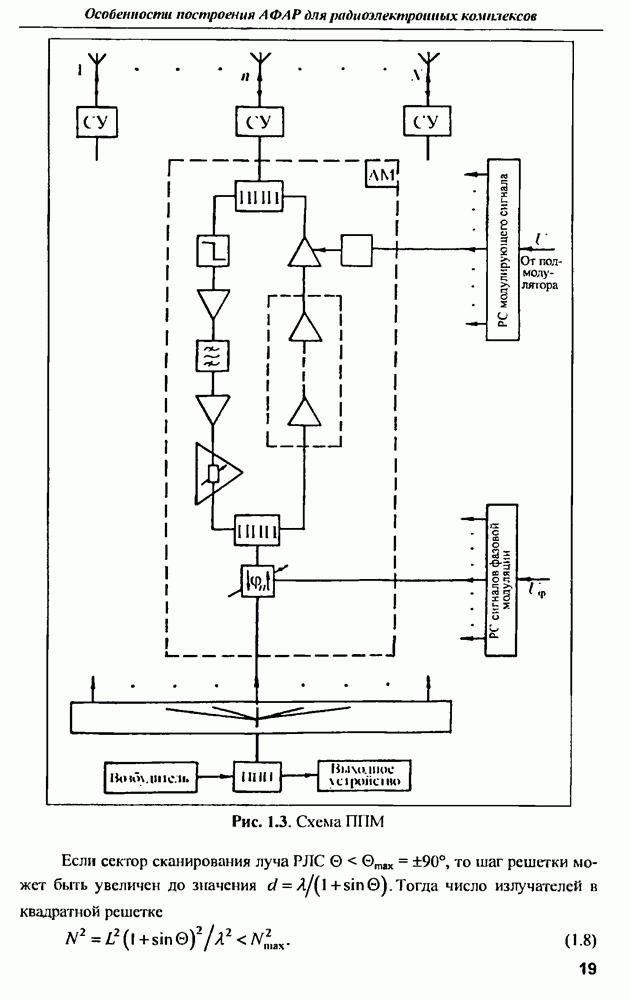
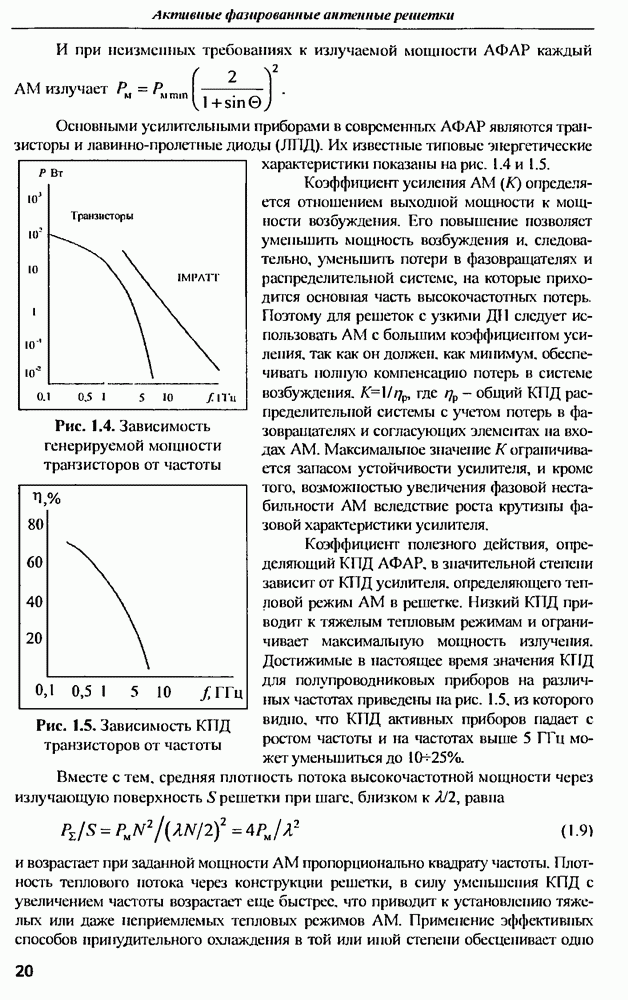
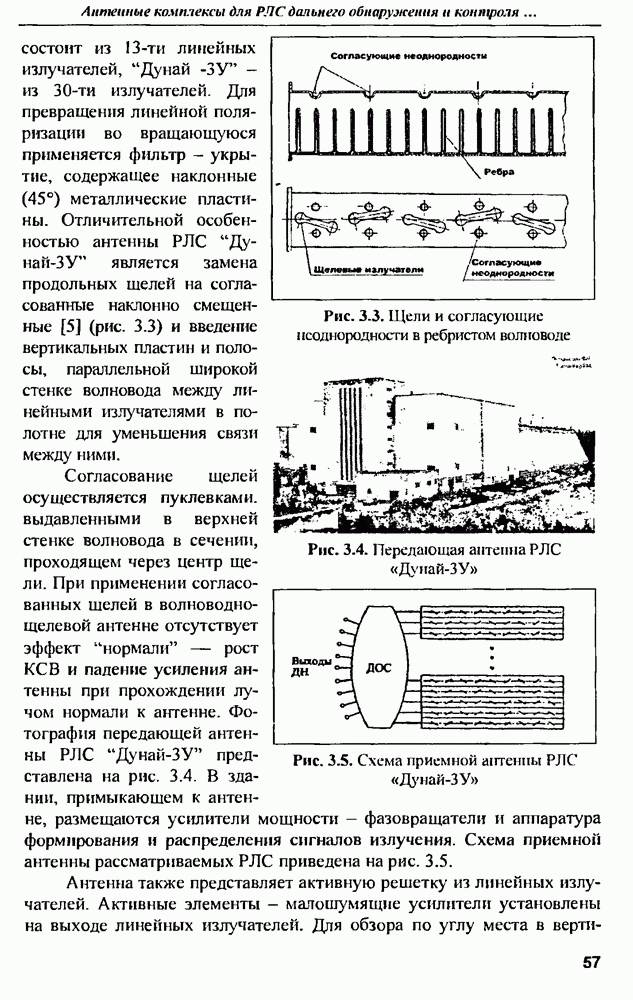
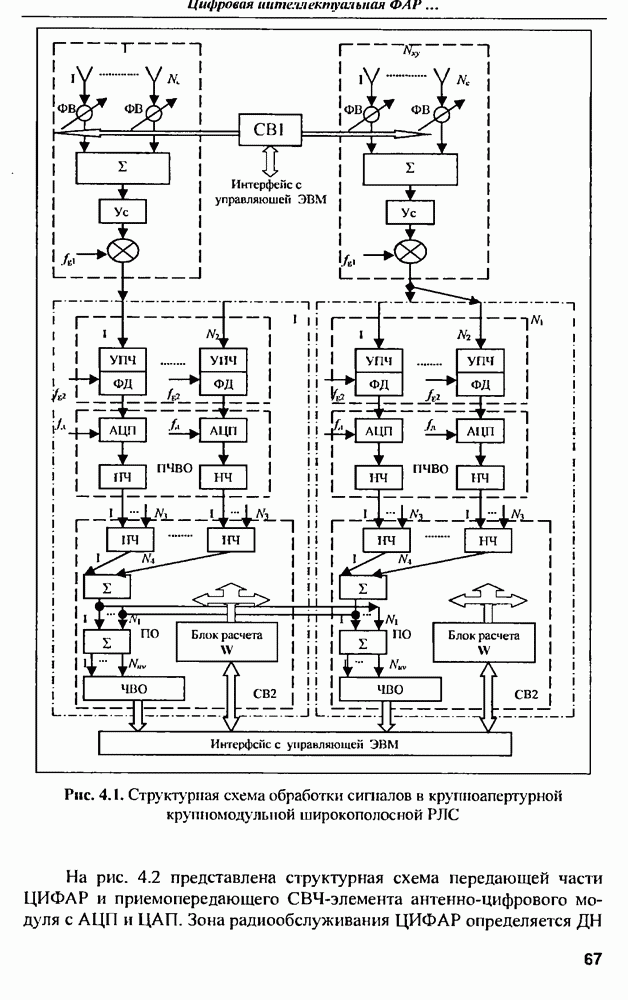
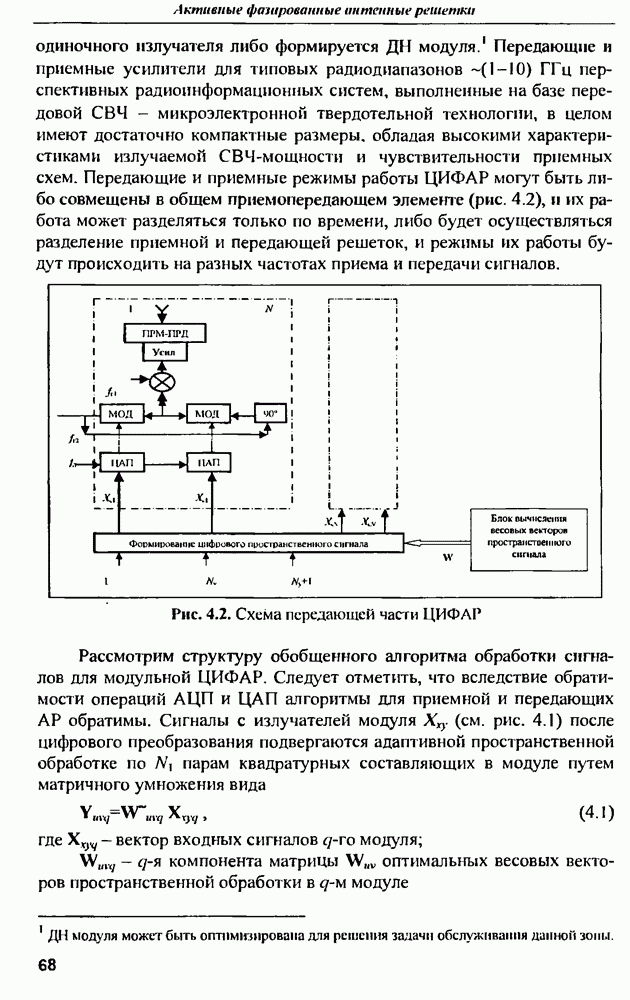
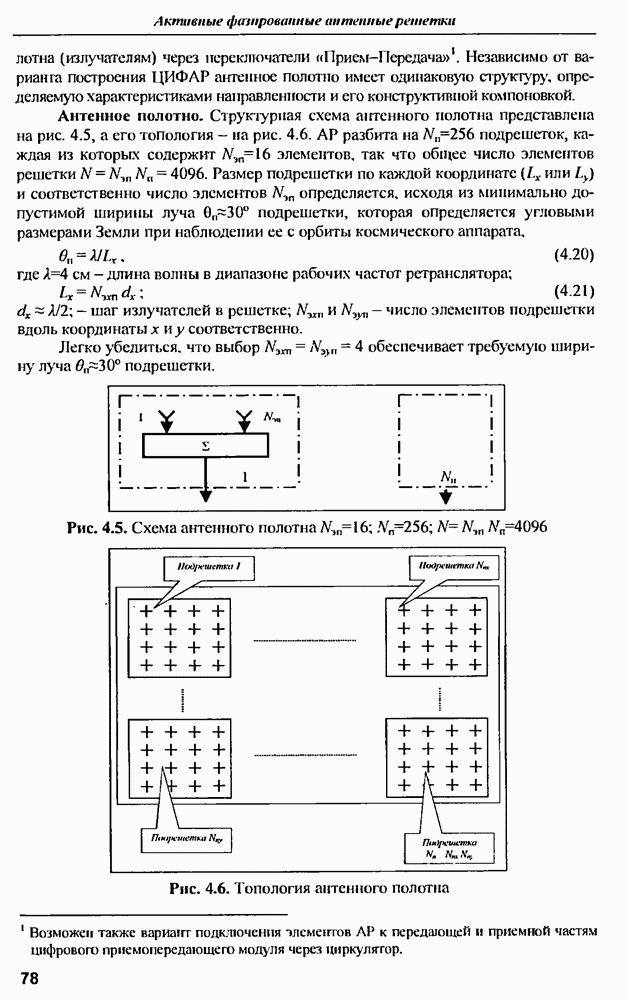
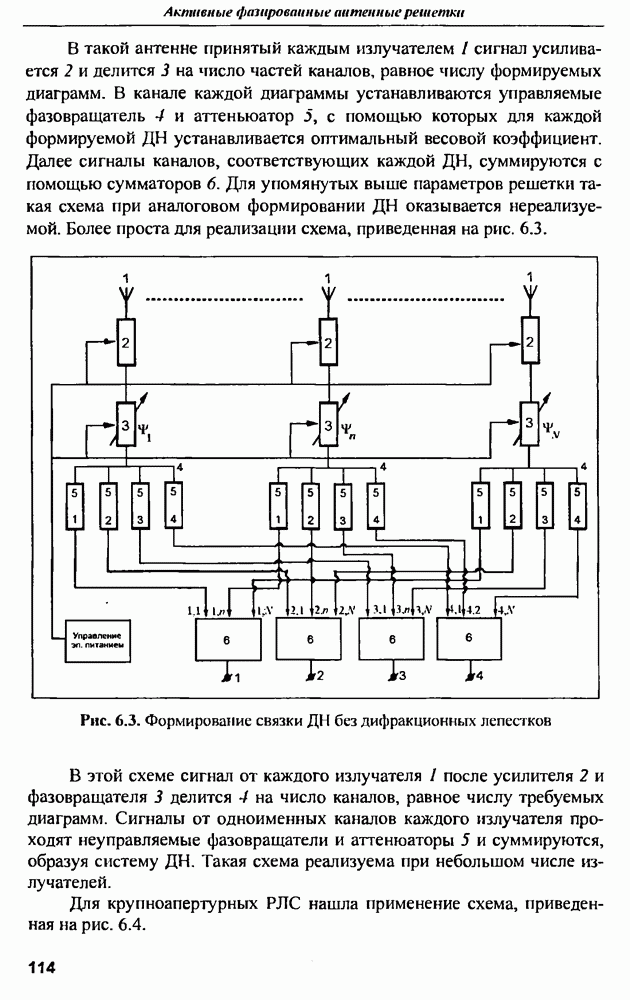
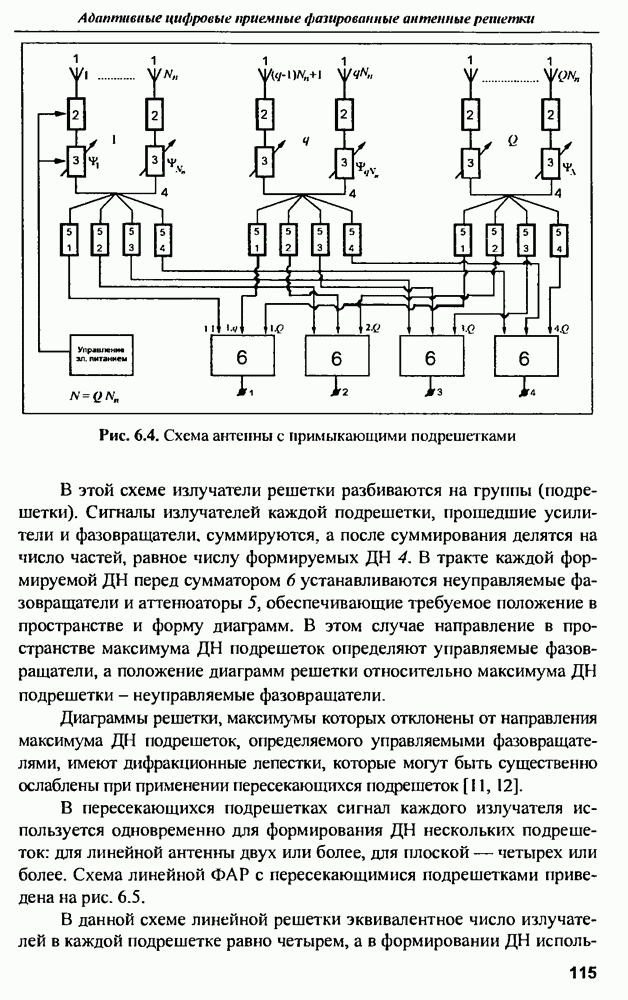
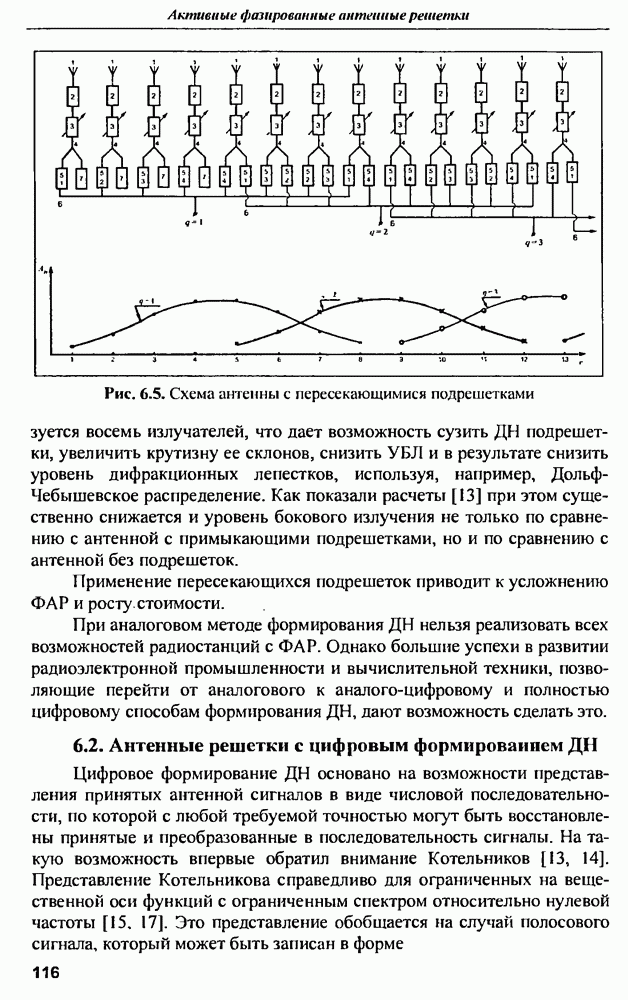
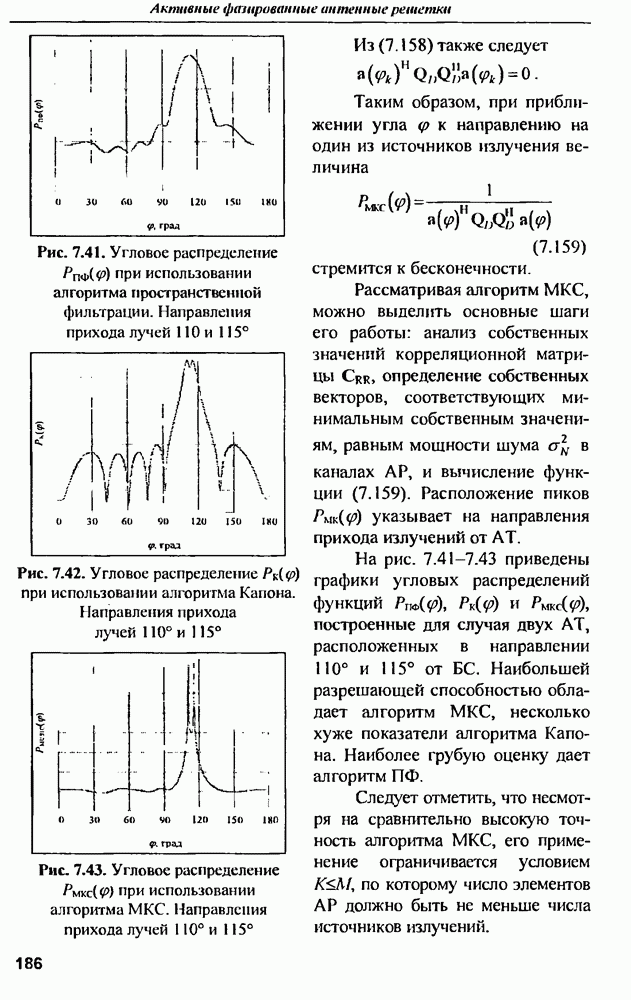
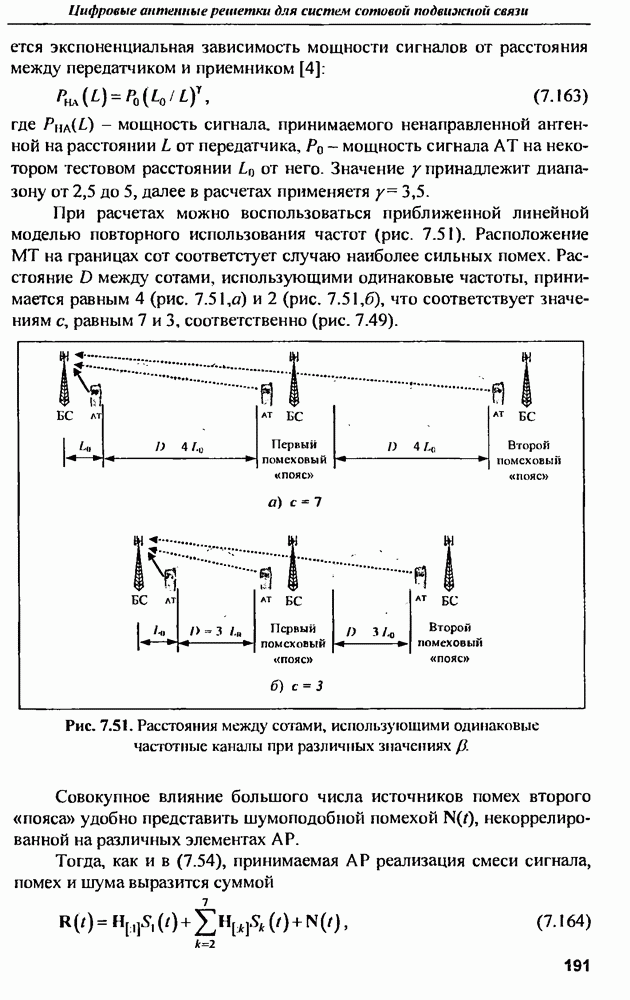
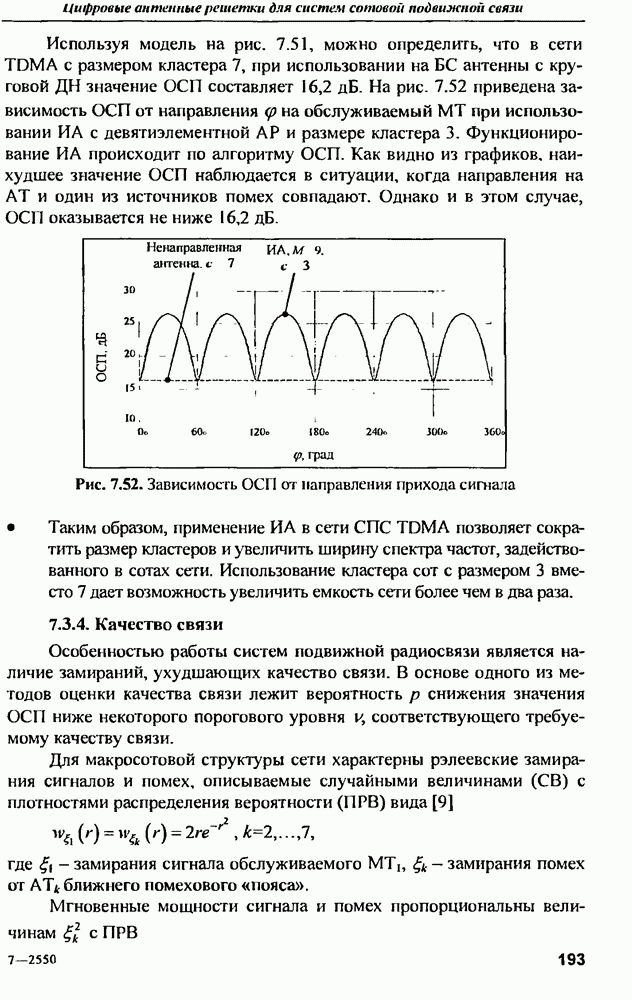
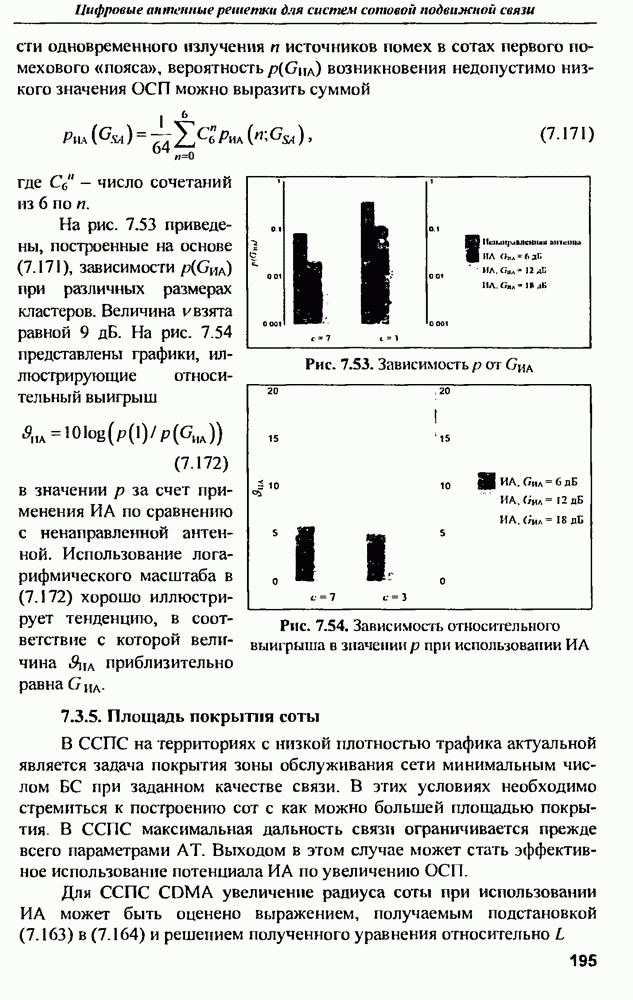
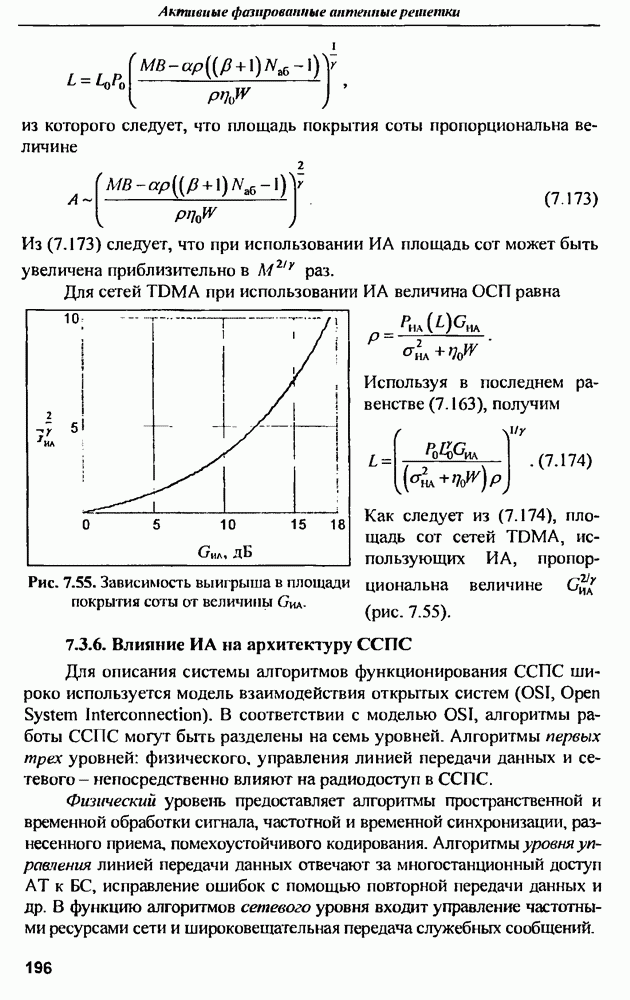
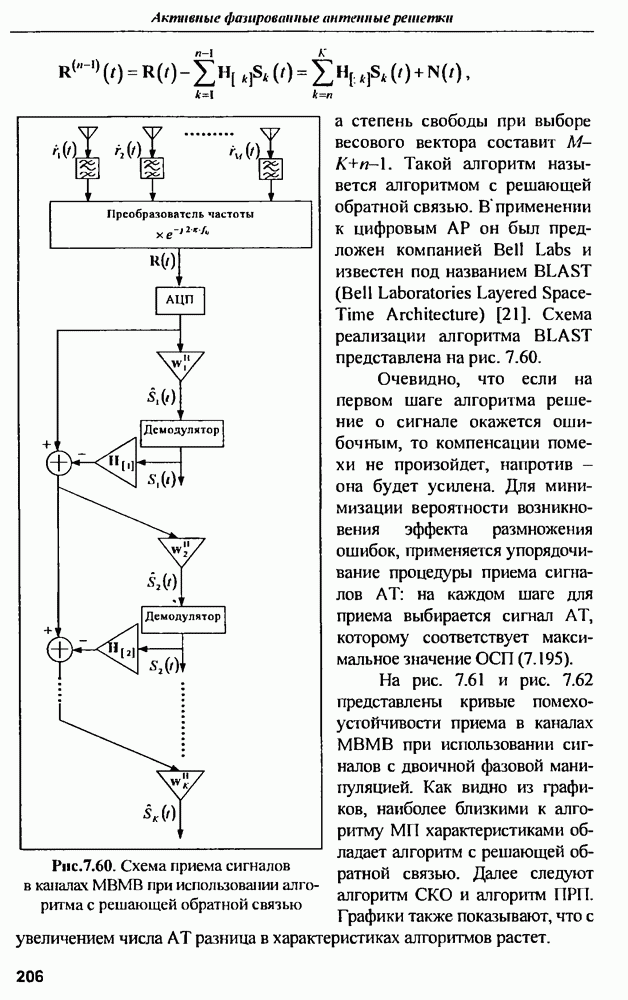
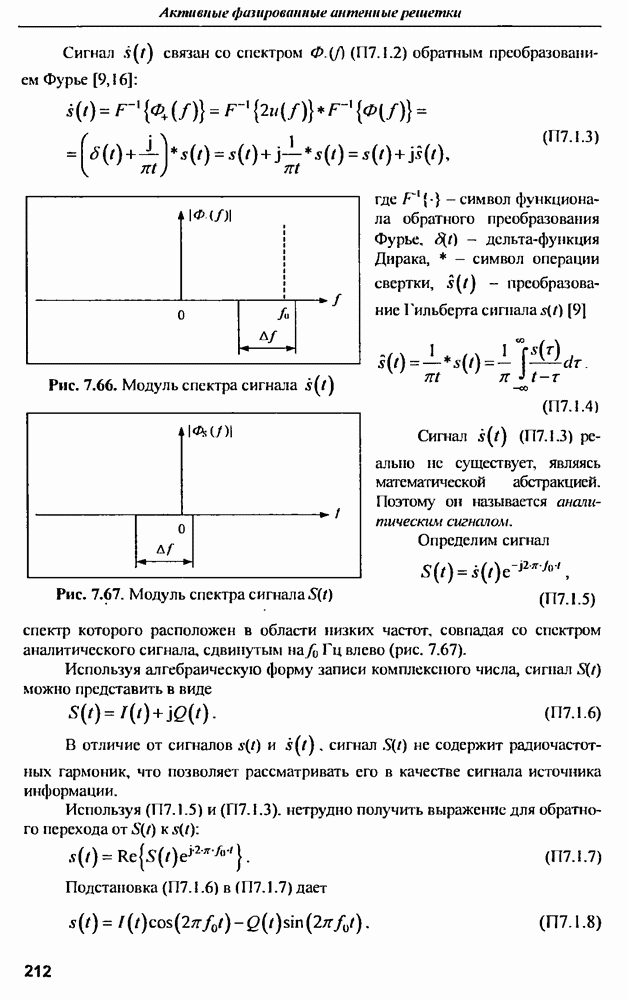
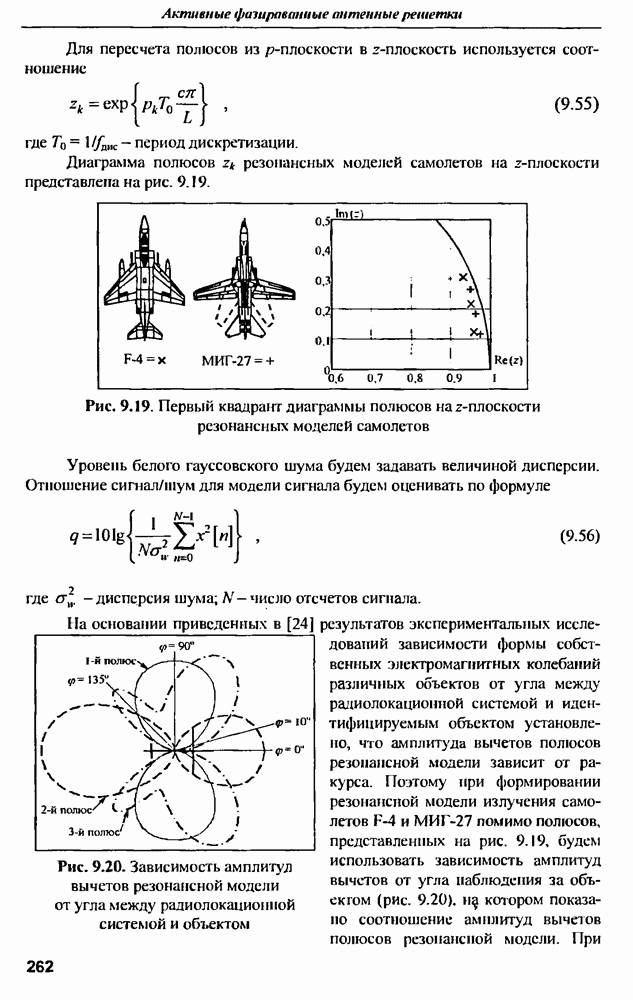
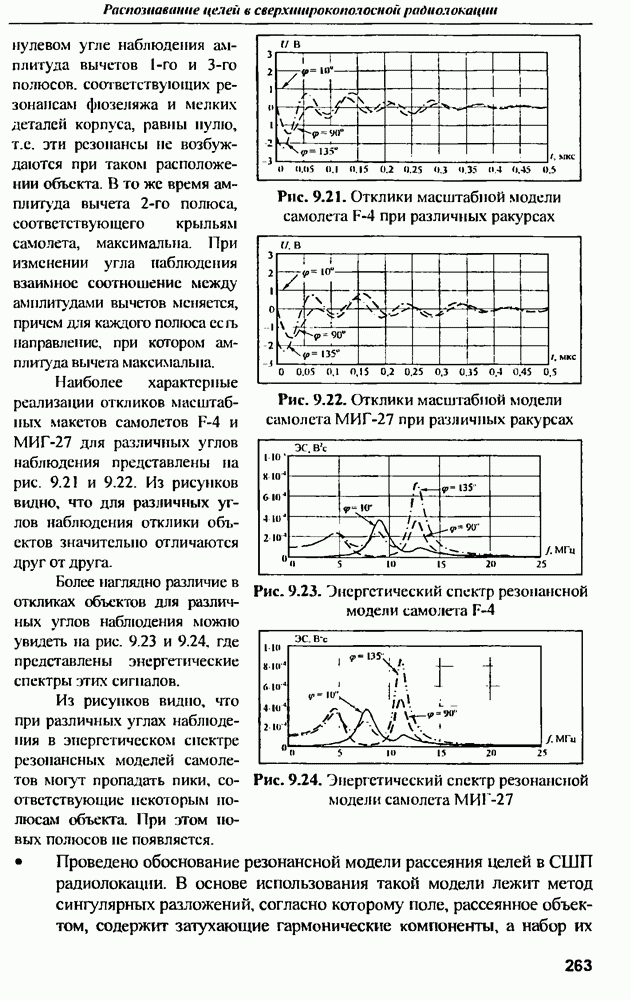
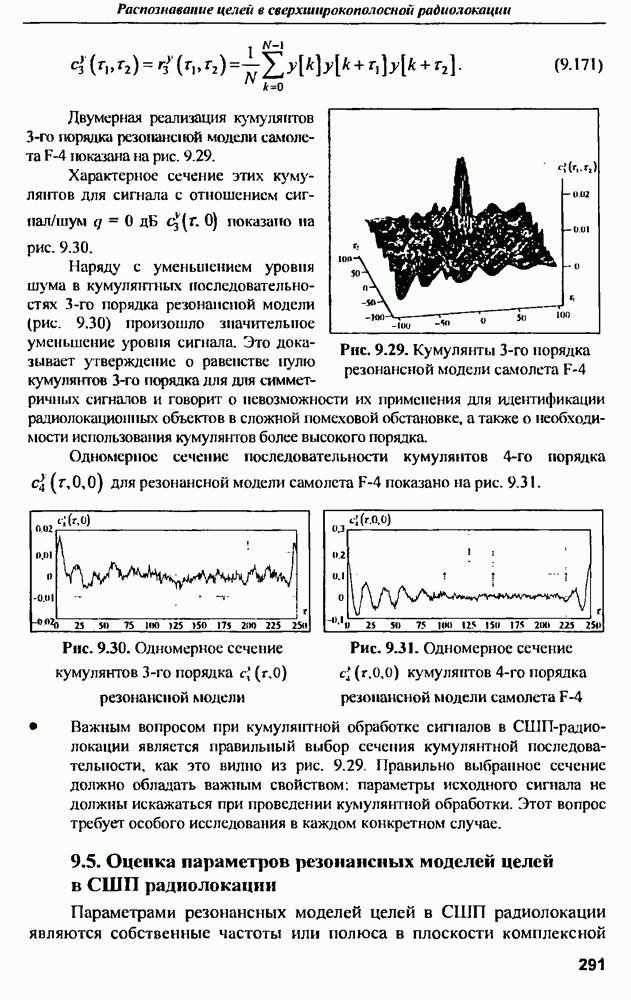
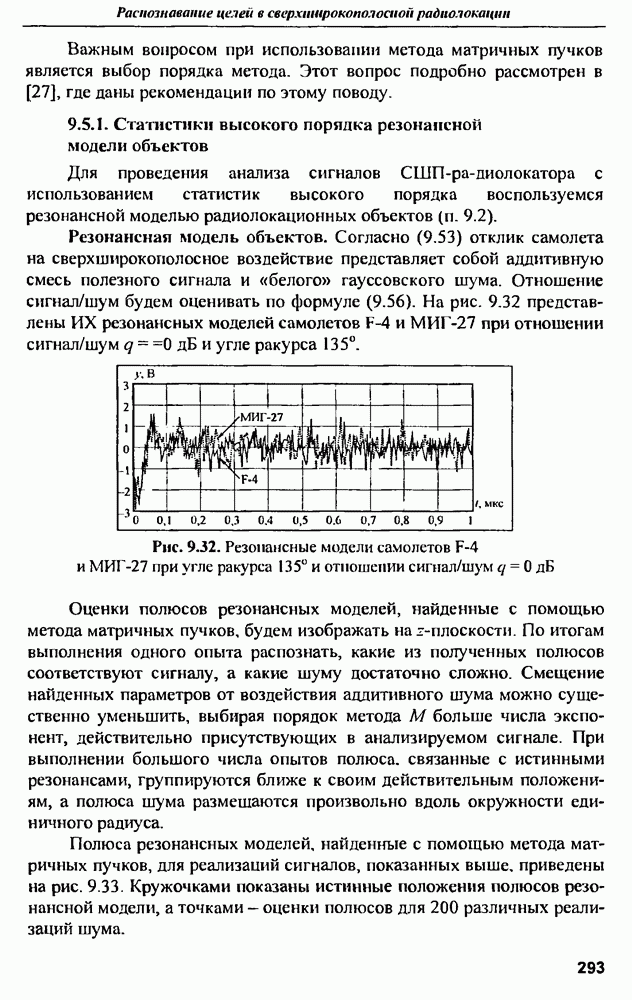
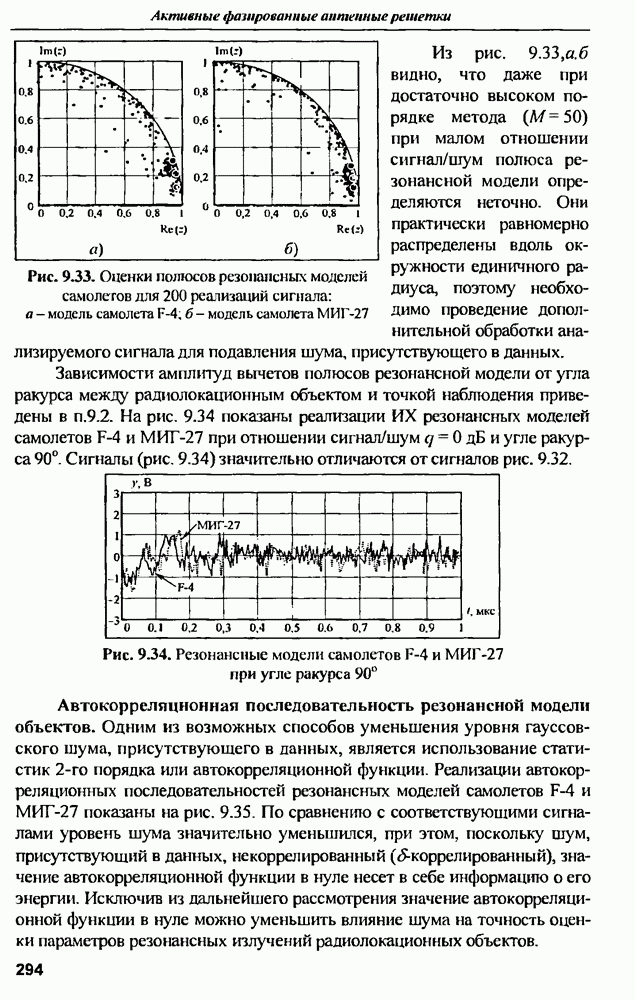
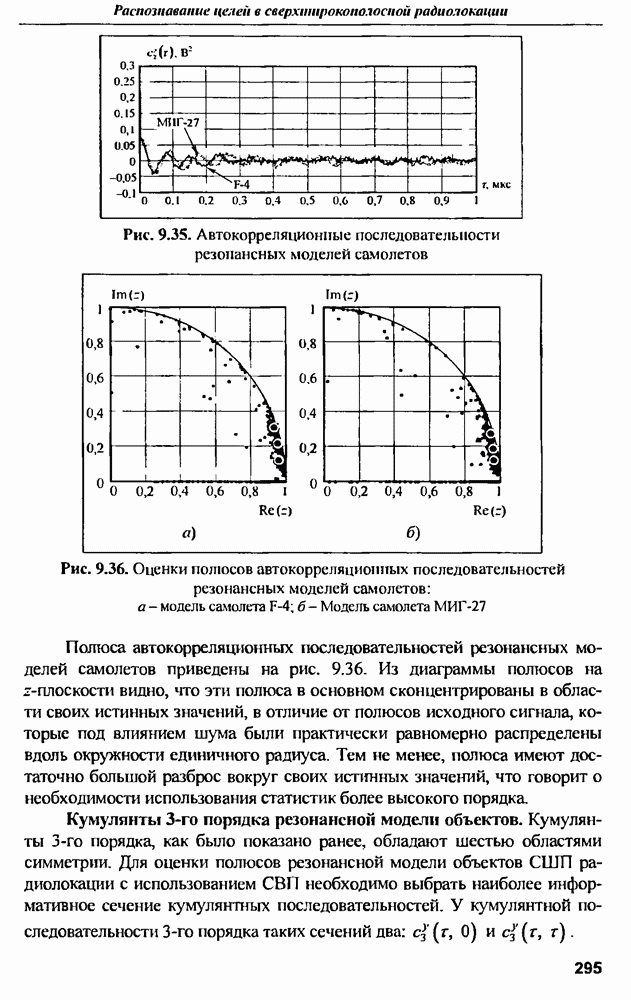
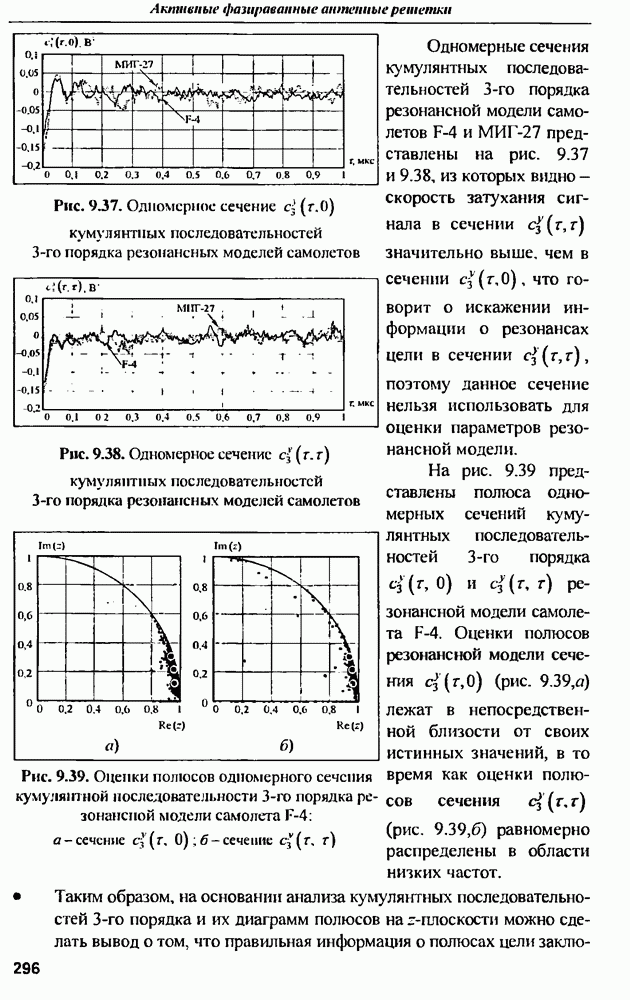
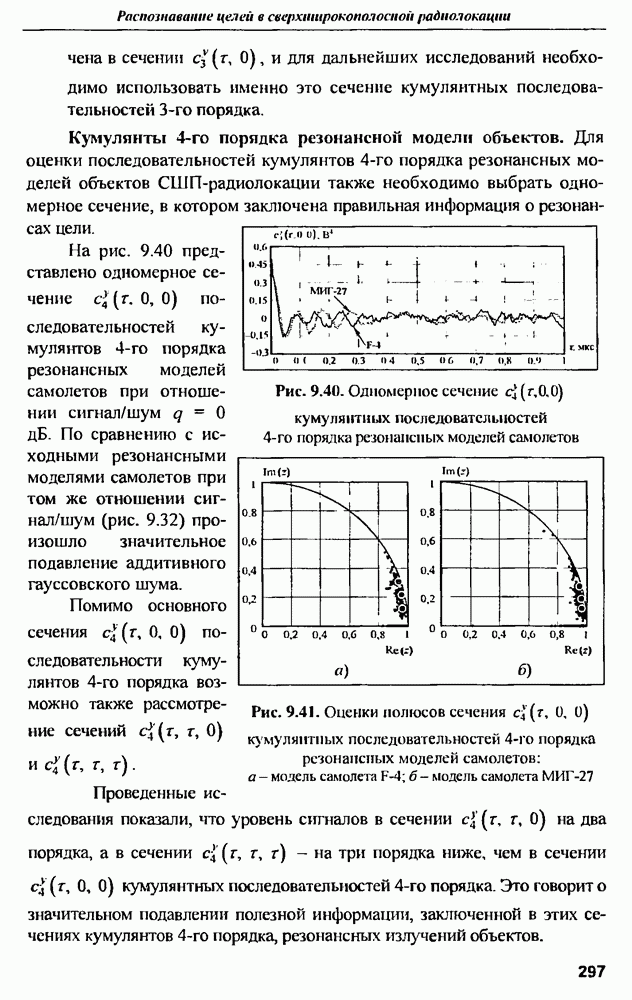
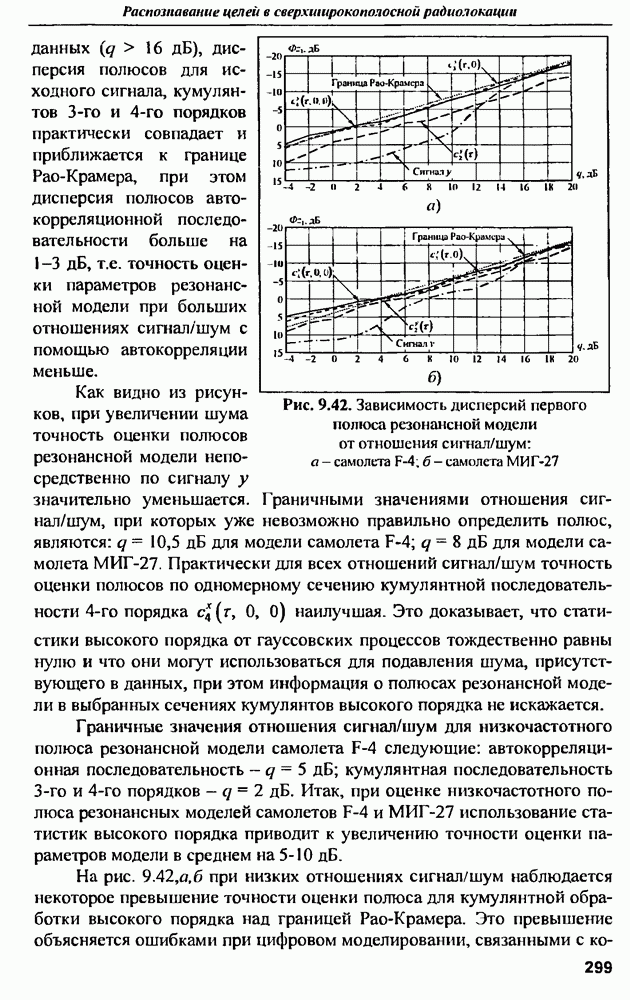
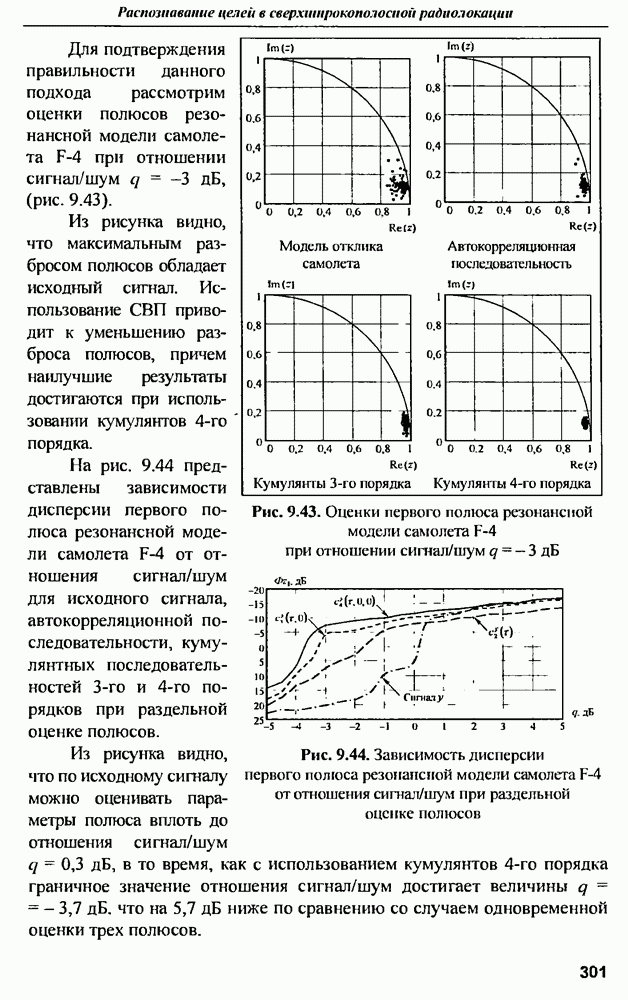
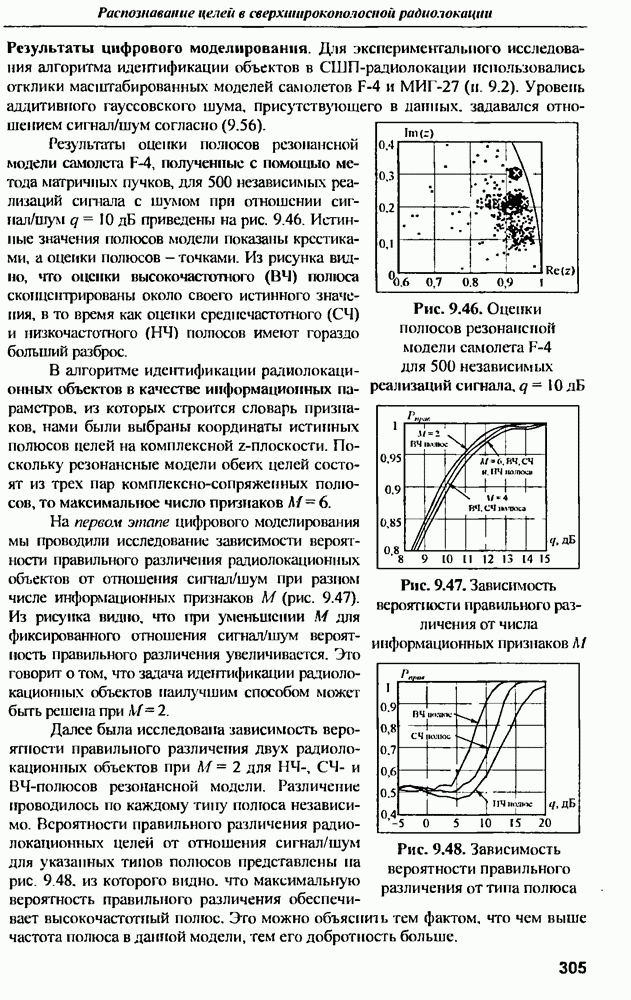
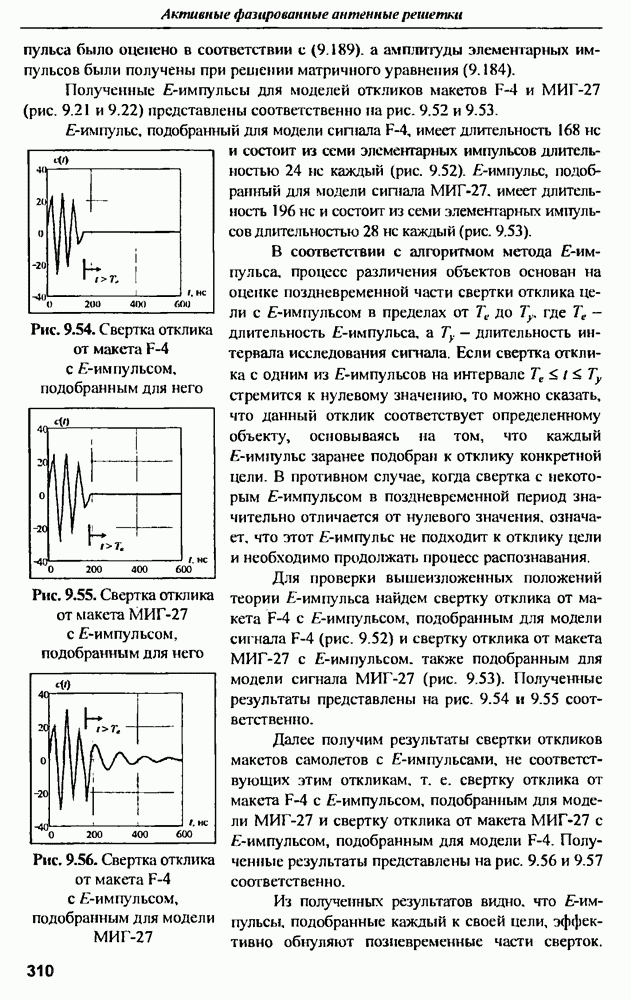
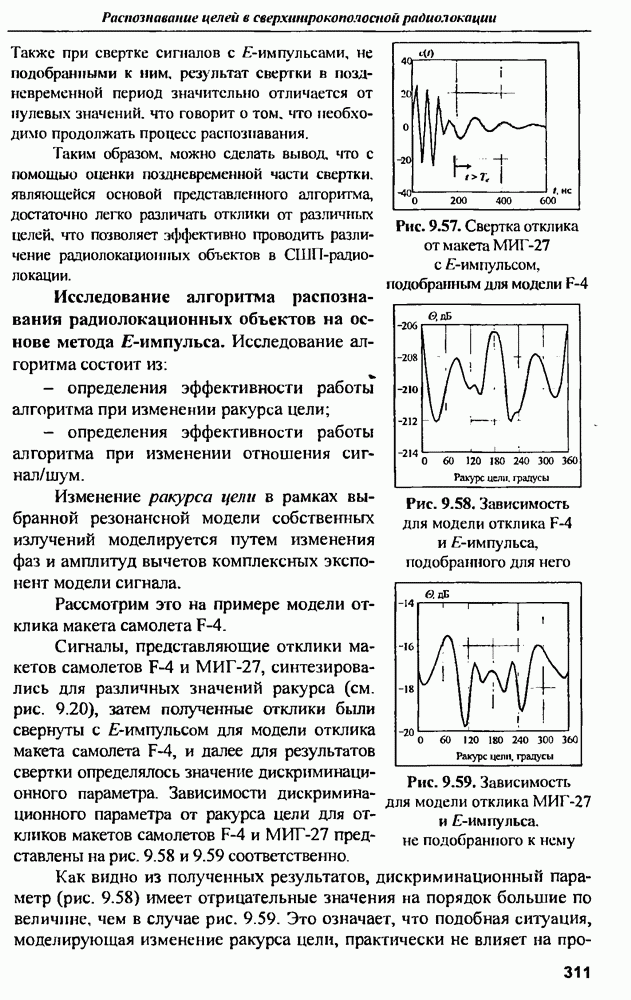
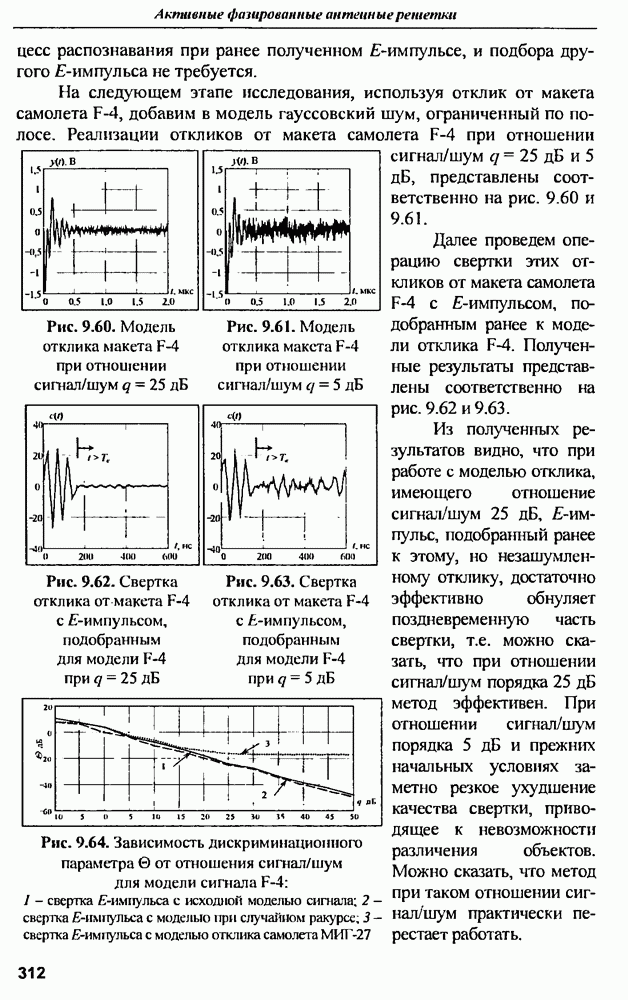
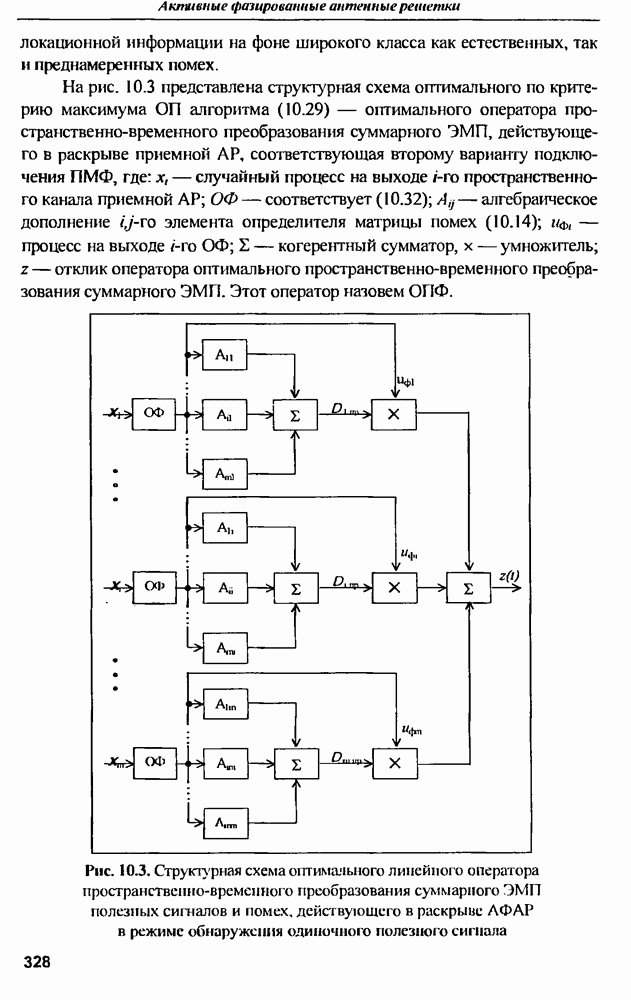
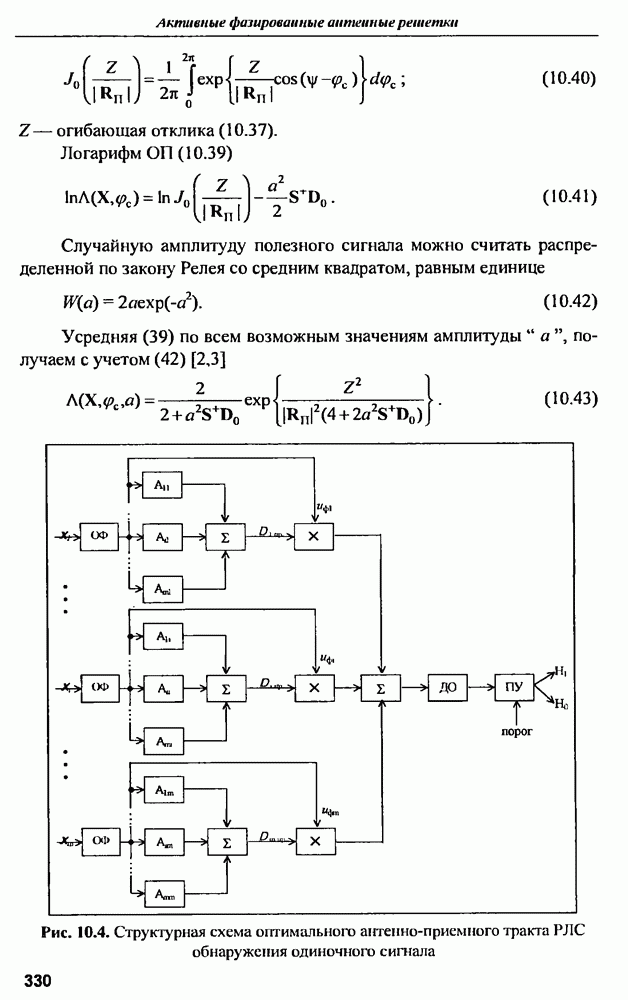
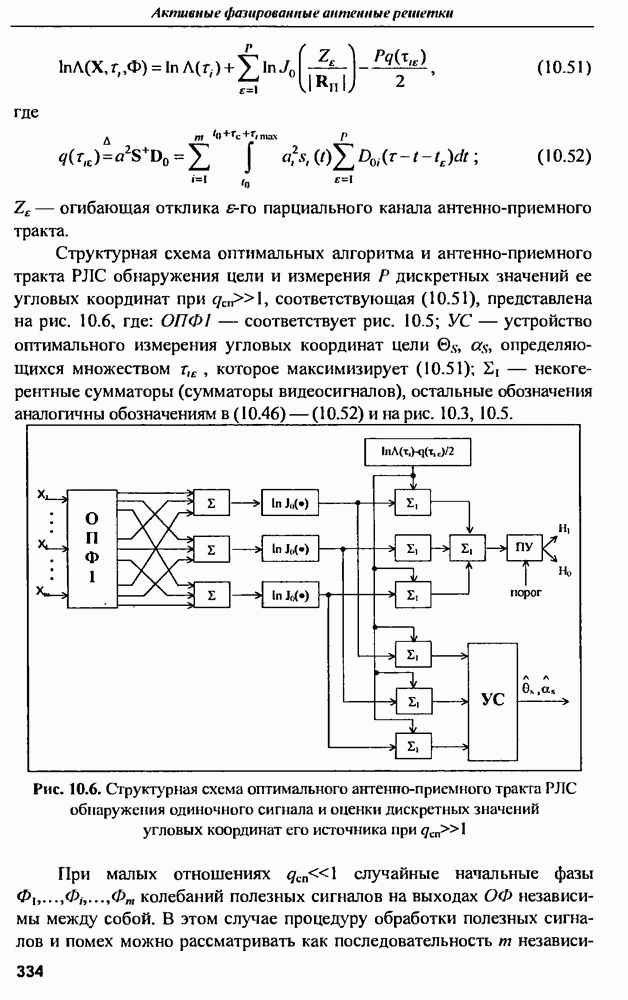
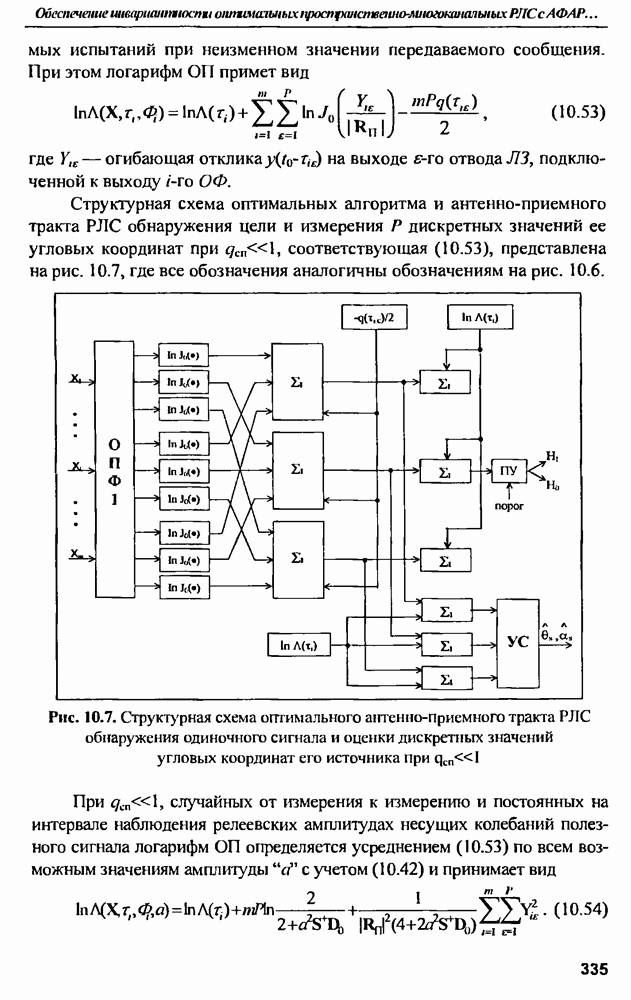
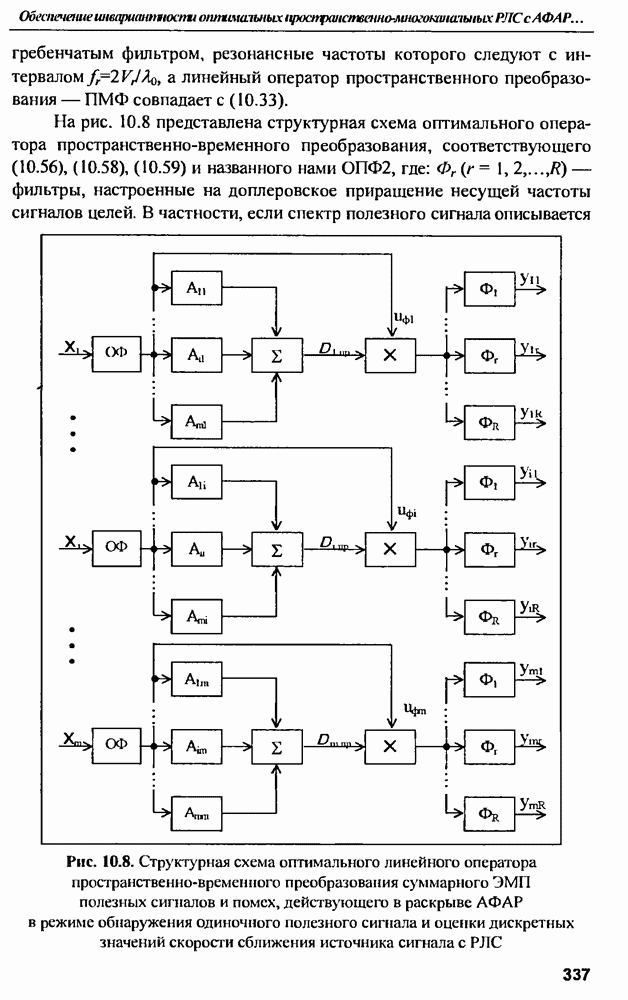
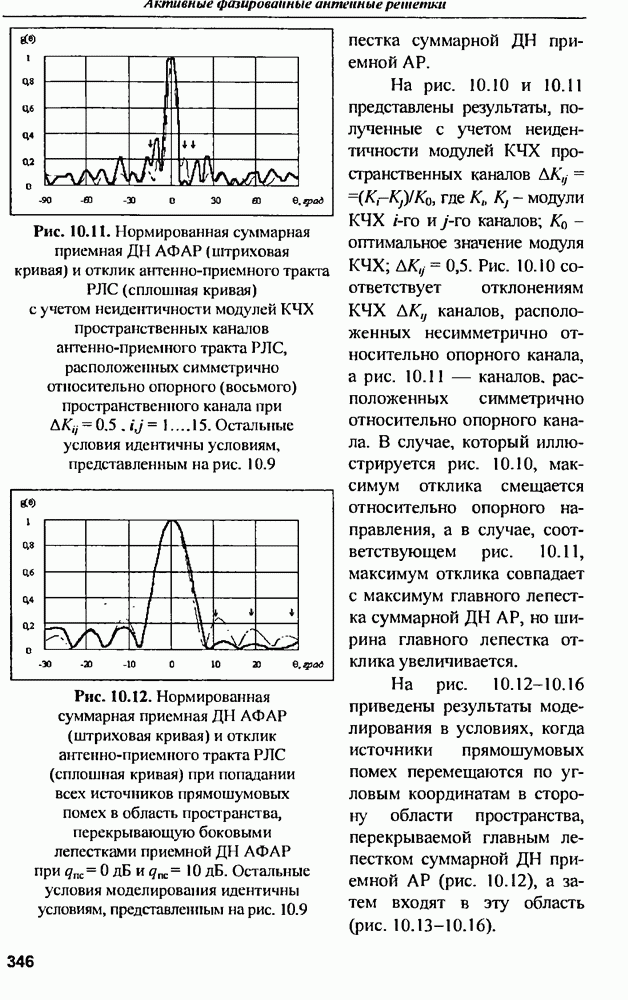
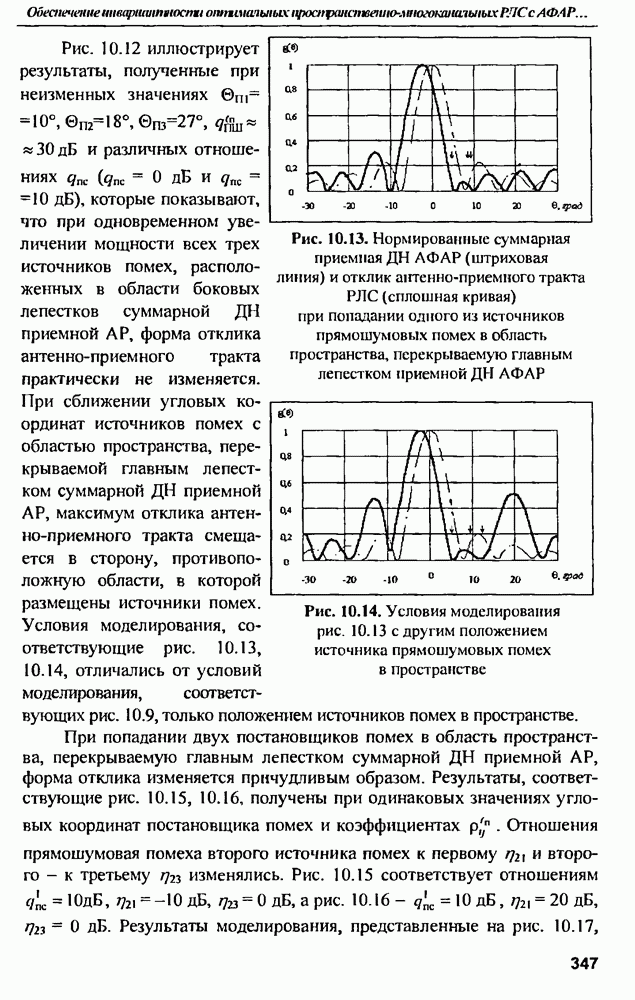
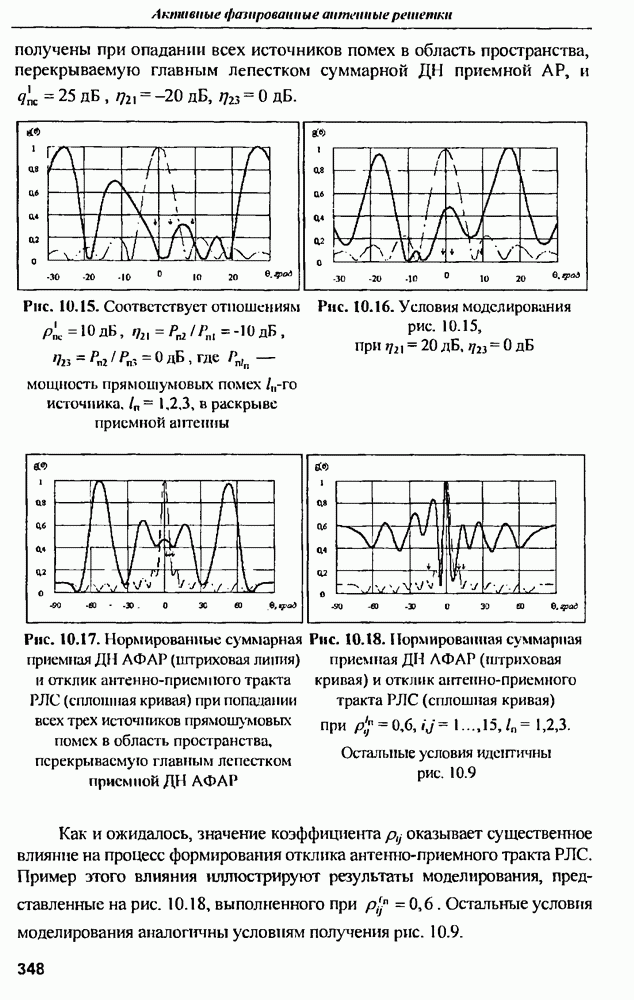
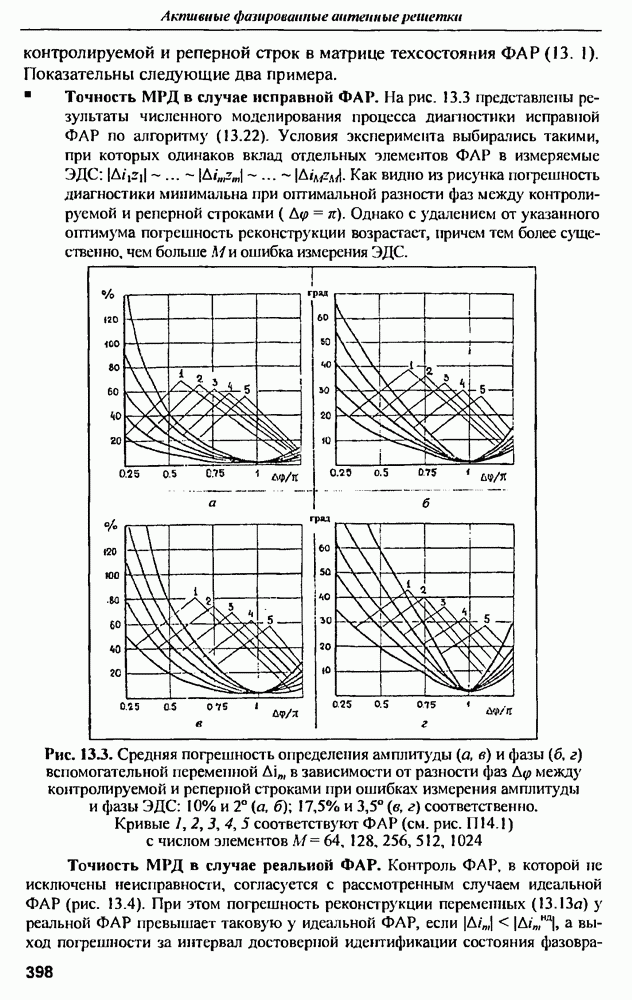
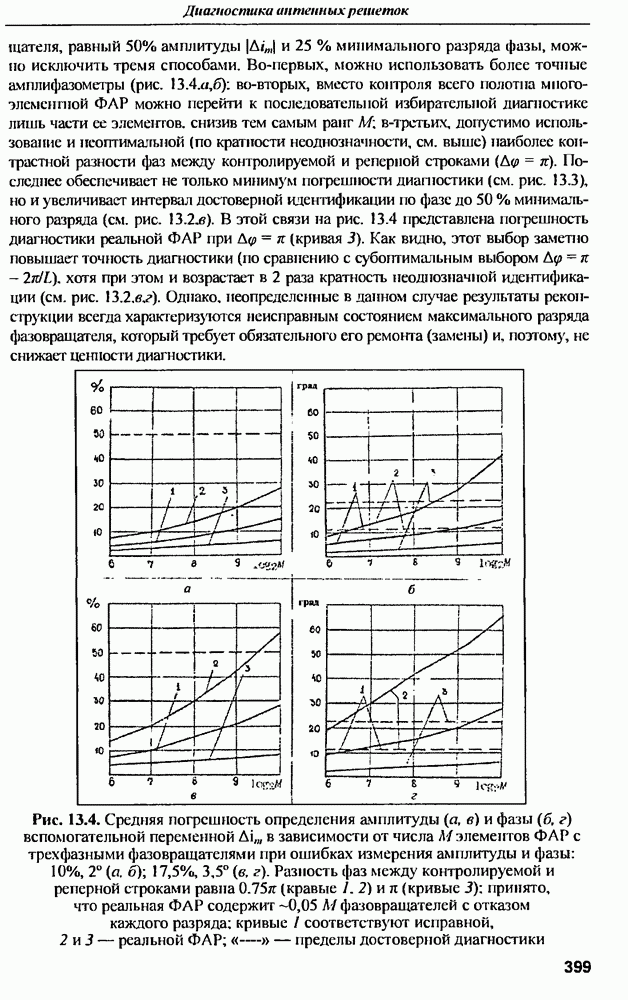
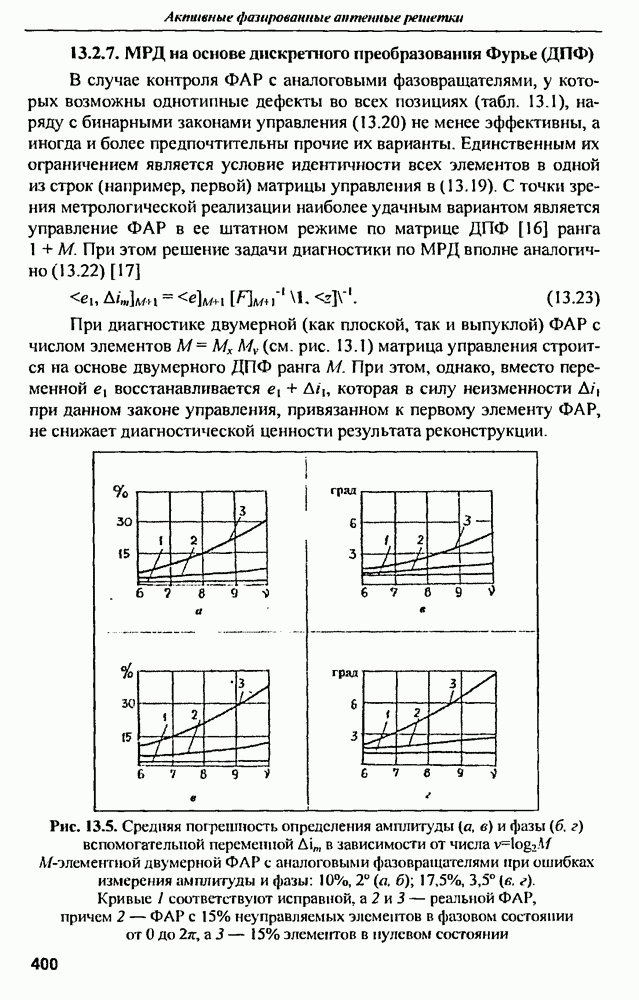
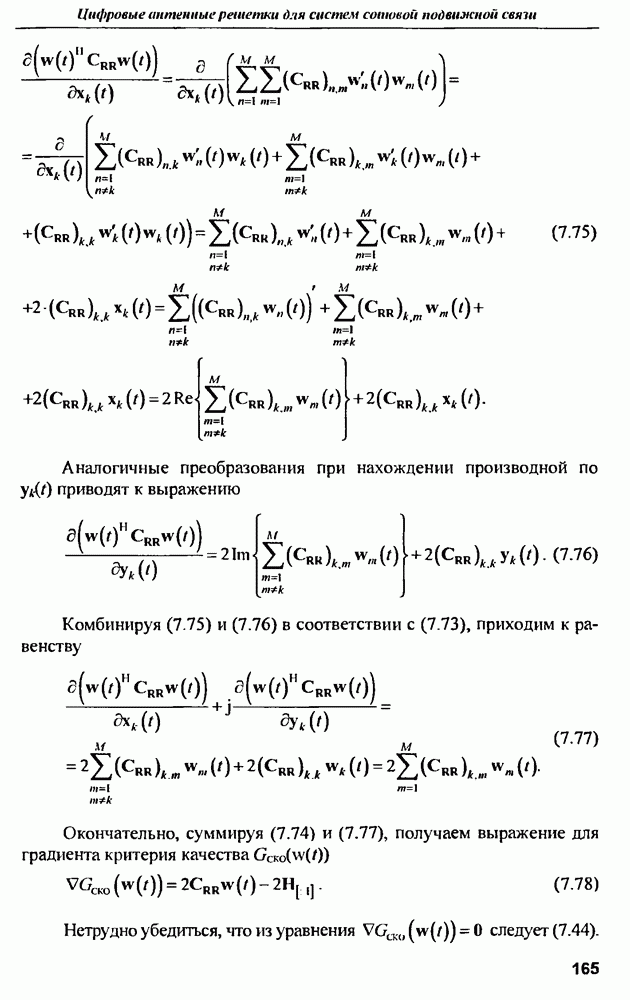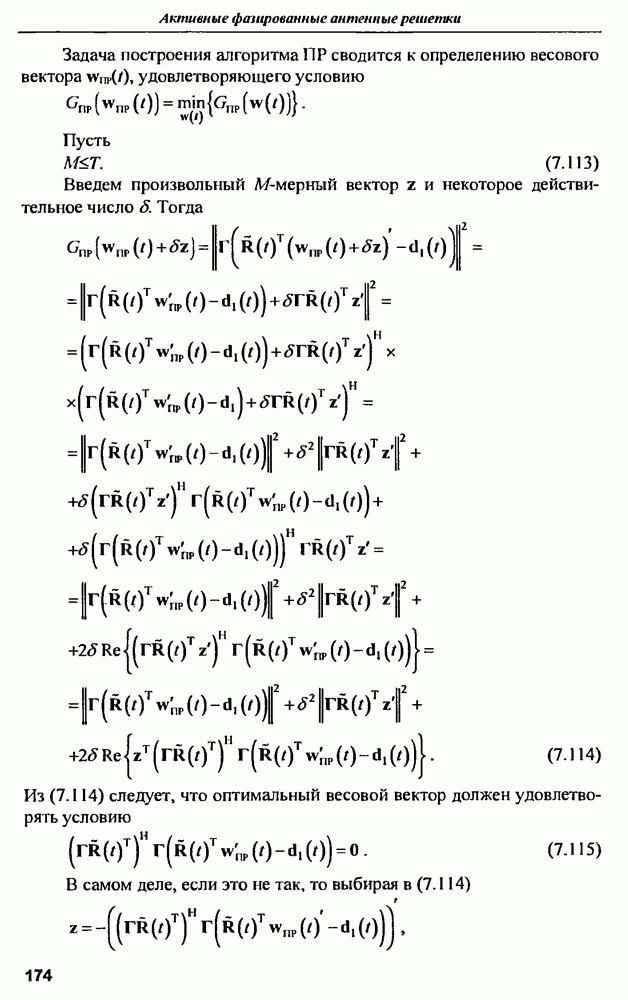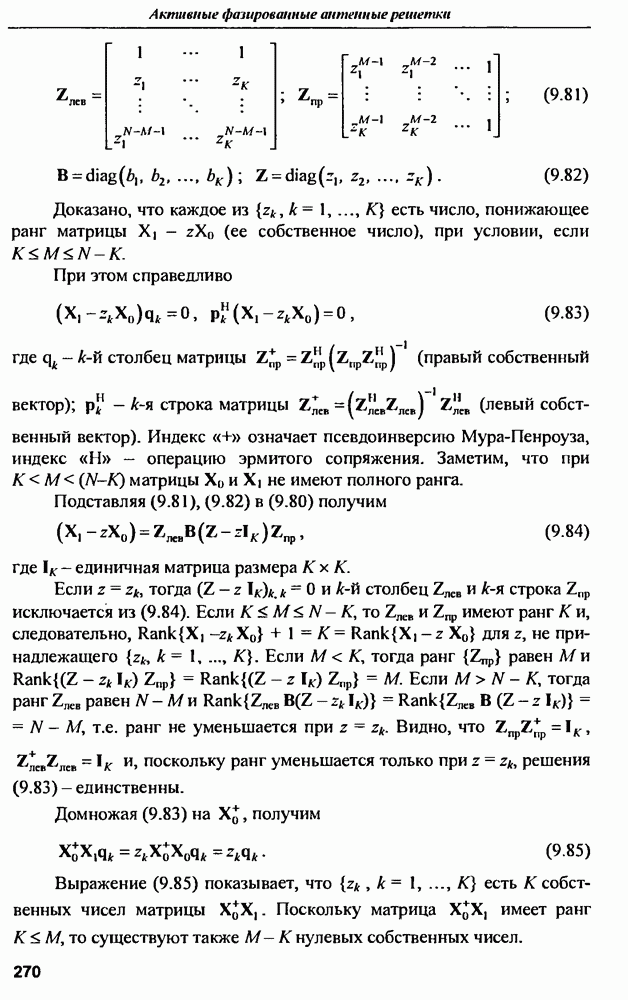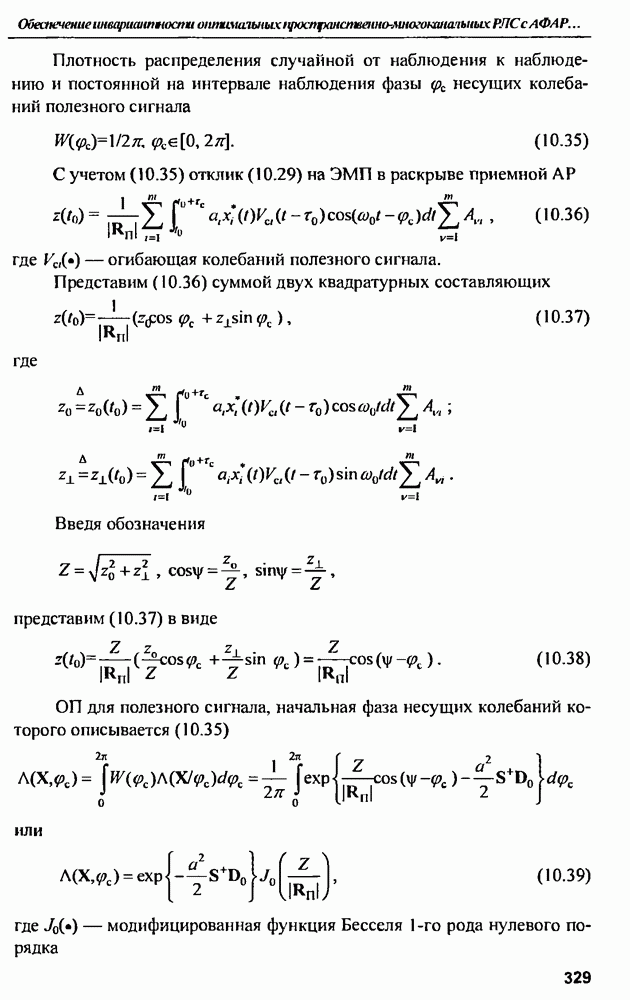| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
На практике получили распространение в основном антенны с щелевыми излучателями. Расчету линейных решеток бегущей волны на заданное амплитудное распределение посвящена обширная литература. В [12] предложен метод, учитывающий взаимодействие излучателей как по внешнему пространству так и по всем типам волн внутри волновода. Его реализация требует дополнительного решения весьма сложных задач, что затрудняет его практическое применение. Также отмечается, что основное значение имеет взаимодействие по распространяющимся типам волн внутри волновода. В [13] развит графоаналитический, а в [14] — аналитический метод расчета, учитывающий взаимодействие щелевых излучателей по основной, распространяющейся в волноводе волне.
Наиболее общими и распространенными являются энергетические методы расчета, различные варианты которых изложены в [15—19]. Широкое распространение на практике получил метод распределенных параметров. В этом методе дискретные излучатели заменяются непрерывным распределением, а интенсивность излучения вдоль антенны обычно характеризуется затуханием волны в волноводе, обусловленным излучением (затухание на излучение). В случае дискретных излучателей один излучатель должен вносить затухание, приходящееся на шаг излучателей.
Метод расчета антенны на заданное непрерывное амплитудное распределение. Характеризуя излучающую способность антенны затуханием на излучение  мощность в любом сечении волновода можно записать в форме
мощность в любом сечении волновода можно записать в форме

где  — затухание на омические потери на половине длины антенны; мощность на входе антенны принята равной единице; начало координат совпадает с началом раскрыва антенны.
— затухание на омические потери на половине длины антенны; мощность на входе антенны принята равной единице; начало координат совпадает с началом раскрыва антенны.
Если требуемое амплитудное распределение  то для каждого сечения необходимо потребовать
то для каждого сечения необходимо потребовать

где  нормирующий множитель, определяемый из равенства
нормирующий множитель, определяемый из равенства

 — КПД антенны; длина антенны прпнята равной двум.
— КПД антенны; длина антенны прпнята равной двум.
Из (12.24) после умножения на  интегрирования, логарифмирования и дифференцирования, получим
интегрирования, логарифмирования и дифференцирования, получим

Величина КПД при расчетах подбирается из условия реализуемости получающегося затухания на излучение, которое должно быть положительным и не превышать некоторого значения.
Расчет антенны на заданное дискретное амплитудное распределение. В случае антенн с большим числом излучателей для определения связи излучателей с волноводом может быть использована формула (12.26), причем величина затухания, вносимого излучателем, должна быть равна затуханию, рассчитанному по формуле и умноженному на шаг излучателей. При малом числе излучателей нужно пользоваться формулой для дискретного распределения. Приведем вывод формулы для этого случая.
Мощность, дошедшая до  излучателя,
излучателя,

Мощность, излученная  излучателем
излучателем

Для обеспечения амплитудного распределения  для каждого излучателя должно выполняться уравнение
для каждого излучателя должно выполняться уравнение

где  искомые величины вносимого затухания на излучение каждым излучателем.
искомые величины вносимого затухания на излучение каждым излучателем.
Суммируя левую и правую части (12 29), получим выражение

Заменяя в  на
на  решая новое уравнение совместно с предыдущим, найдем
решая новое уравнение совместно с предыдущим, найдем

где  величина затухания на излучение, которую должен вносить каждый
величина затухания на излучение, которую должен вносить каждый  излучатель для обеспечения заданного амплитудного распределения
излучатель для обеспечения заданного амплитудного распределения 
Нормирующий множитель  в этом выражении определяется из равенства
в этом выражении определяется из равенства

Величина КПД  выбирается из условия реализации получаемого максимального затухания на излучение.
выбирается из условия реализации получаемого максимального затухания на излучение.
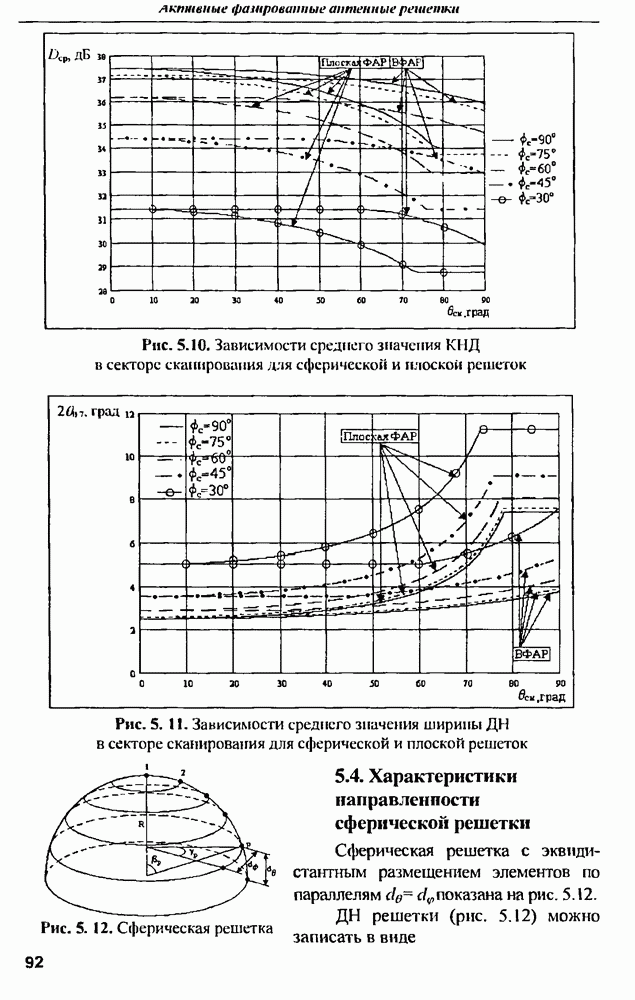
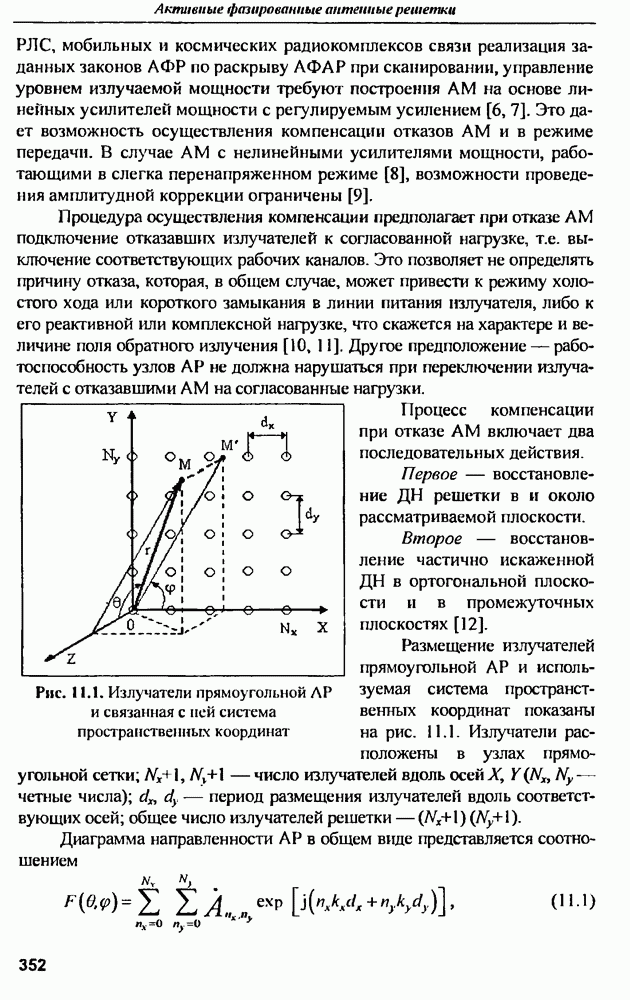
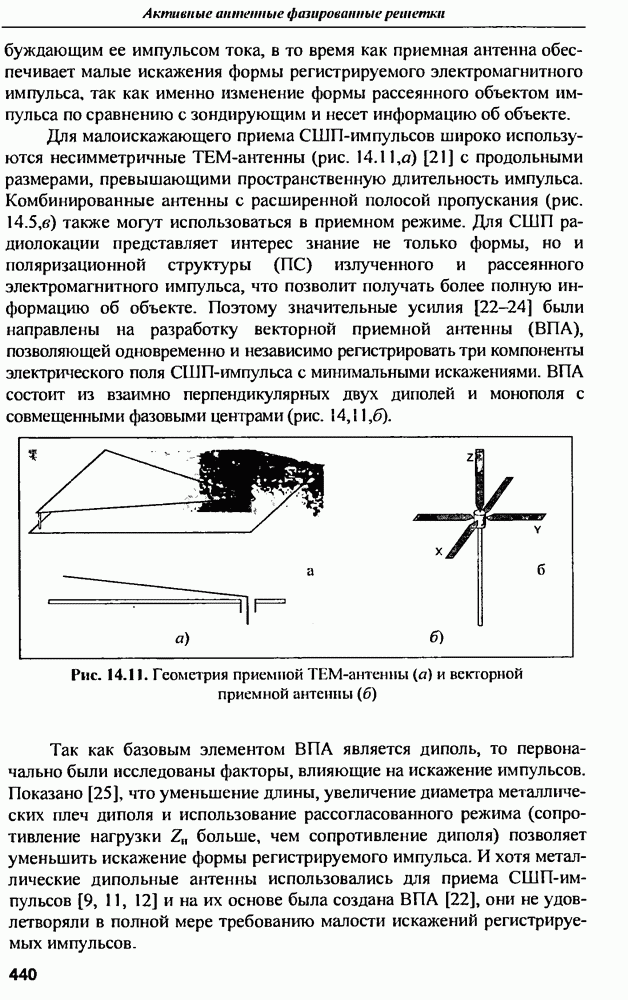
Случай симметричной антенны. Антенна бегущей волны имеет вход, к которому подсоединяется передатчик или приемник, и выход, куда подключается нагрузка. Под симметричными понимают антенны, которые при подключении передатчика или приемника к входу и выходу имеют одинаковые характеристики и лишь  изменяет свое положение зеркально относительно нормали к раскрыву антенны. Это свойство позволяет в два раза расширить сектор обзора в случае антенн с электрическим качанием луча.
изменяет свое положение зеркально относительно нормали к раскрыву антенны. Это свойство позволяет в два раза расширить сектор обзора в случае антенн с электрическим качанием луча.
Впервые расчет многолучевых антенных систем рассматривался в [20, 21], где решалась задача достижения максимального коэффициента усиления. В этих работах отмечалось, что характеристики симметричной антенны определяются четной составляющей амплитудного распределения, а нечетная — приводит лишь к незначительному повышению дальшгх боковых лепестков.
Для симметричных антенн амплитудное распределение  является четной функцией относительно середины антенны, затухание же на излучение
является четной функцией относительно середины антенны, затухание же на излучение  четная функция. В этих условиях (12.24), с учетом (12.23), может быть преобразовано (при переносе начала координат в центр антенны,
четная функция. В этих условиях (12.24), с учетом (12.23), может быть преобразовано (при переносе начала координат в центр антенны,  к виду
к виду


где введены обозначения

В работах [20, 21] решена задача об отыскании функции  , реализующей максимальный КПД в симметричных антеннах, причем получающаяся при этом диаграмма часто не удовлетворяет предъявленным к ней требованиям по УБЛ. Максимальный УБЛ обычно определяет четная составляющая амплитудного распределения, тогда возникает задача расчета
, реализующей максимальный КПД в симметричных антеннах, причем получающаяся при этом диаграмма часто не удовлетворяет предъявленным к ней требованиям по УБЛ. Максимальный УБЛ обычно определяет четная составляющая амплитудного распределения, тогда возникает задача расчета  по выбранной четной составляющей. Уравнение для
по выбранной четной составляющей. Уравнение для  получим из (12.33)
получим из (12.33)

Решение уравнения (12.37) дано в [18], где показано, что это уравнение имеет единственное решение, которое является пределом последовательных приближений при любом начальном приближении из множества положительных функций пространства 
Реализуемое амплитудное распределение и КПД рассчитываются по формулам

В случае дискретных излучателей


 параметры распределения, которые могут быть объединены в один параметр
параметры распределения, которые могут быть объединены в один параметр 

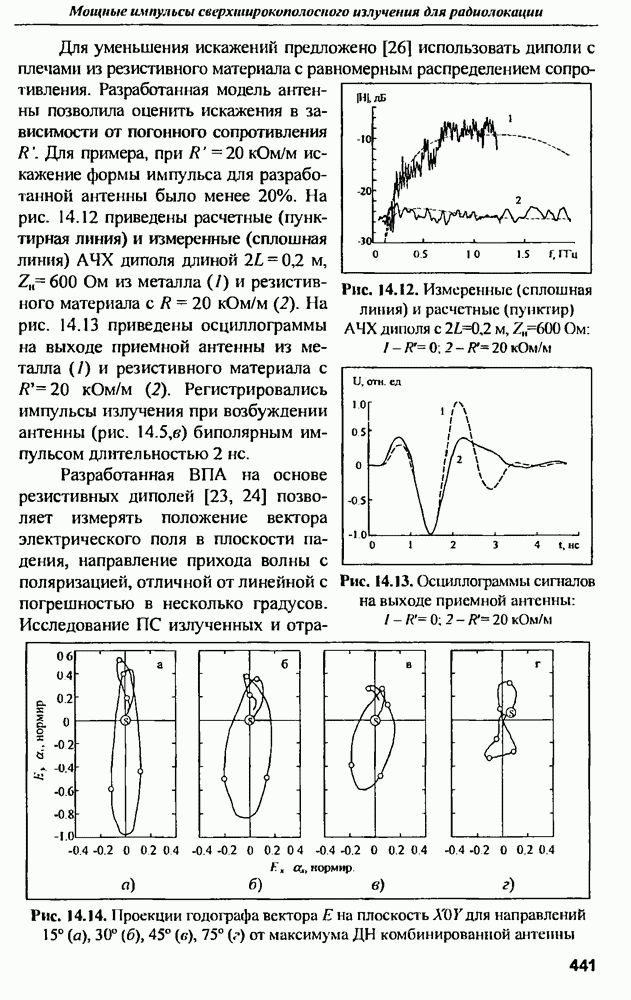
Определение КПД антенны бегущей волны по измеренным амплитудному распределению и мощности, идущей в нагрузку. Характеристики антенн бегущей волны (ДН и КПД) после изготовления можно определить по измеренному АФР мощности, идущей в нагрузку, и известным омическим потерям (затуханию) в волноводе Формулы для расчета диаграмм общеизвестны, формулы для КПД для случая непрерывного распределения имеем из (12.26).
Интегрируя правую часть этого выражения по длине антенны и прибавляя затухание на омические потери на всю длину антенны, получим формулу для суммарного затухания волны в волноводе

Решая полученное уравнение относительно КПД, входящего в  , найдем
, найдем

где  измеренное суммарное затухание в волноводе на излучение и омические потери, выраженное в неперах;
измеренное суммарное затухание в волноводе на излучение и омические потери, выраженное в неперах;  — затухание на омические потери в волноводе;
— затухание на омические потери в волноводе;  — измеренное амплитудное распределение антенны по мощности.
— измеренное амплитудное распределение антенны по мощности.
Для случая антенной решетки

Предельный и реализуемый КПД антенн бегущей волны. При заданном амплитудном распределении и затухании на омические потери КПД антенны растет с увеличением затухания на излучение. Предельное значение КПД получается из (12.26) для случая бесконечного суммарного затухания, что приводит к соотношению

из которого получаем

Для случая дискретных излучателей

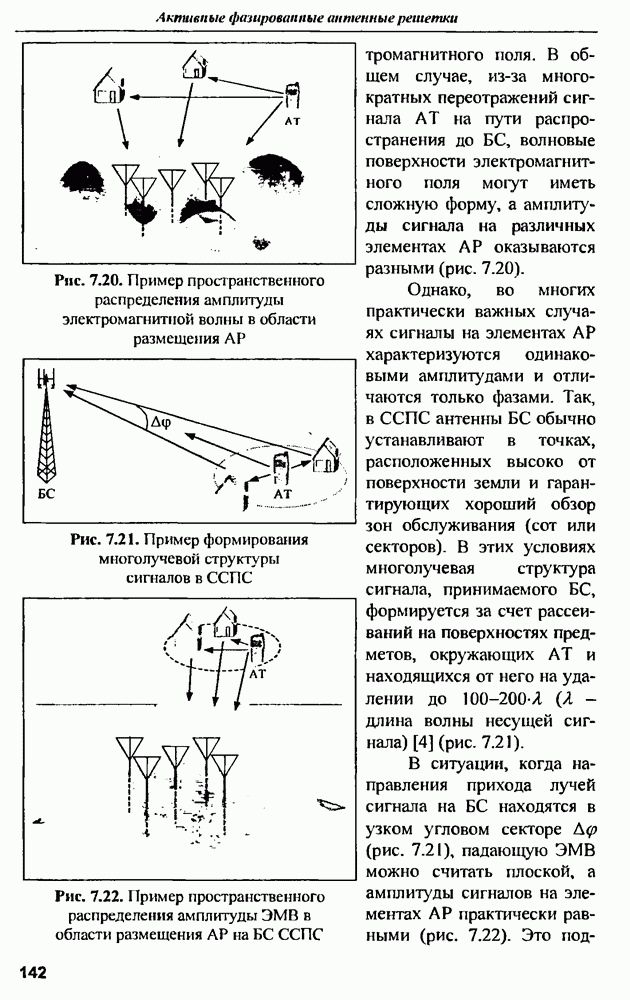
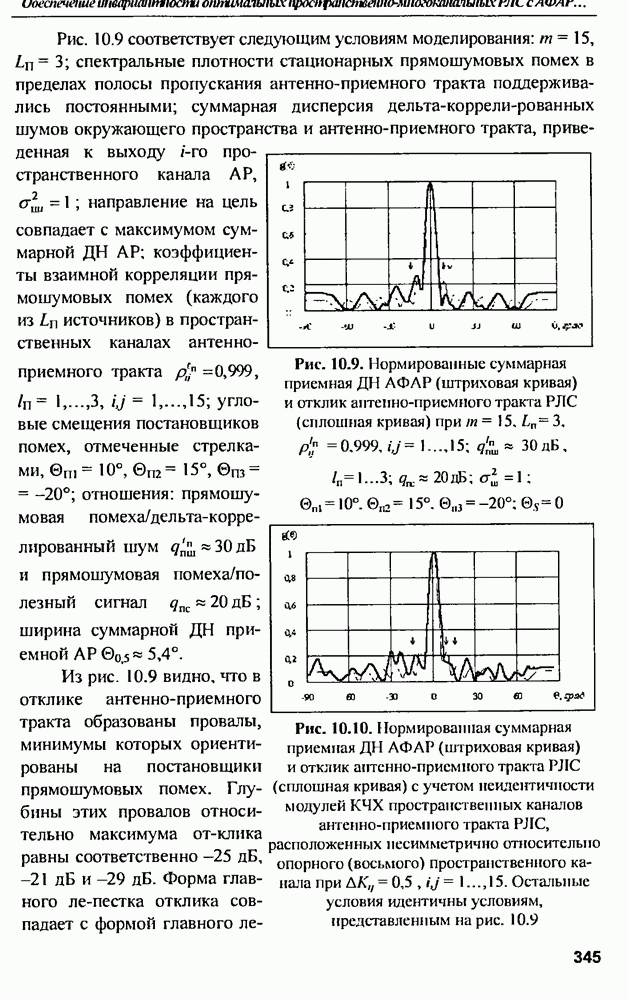
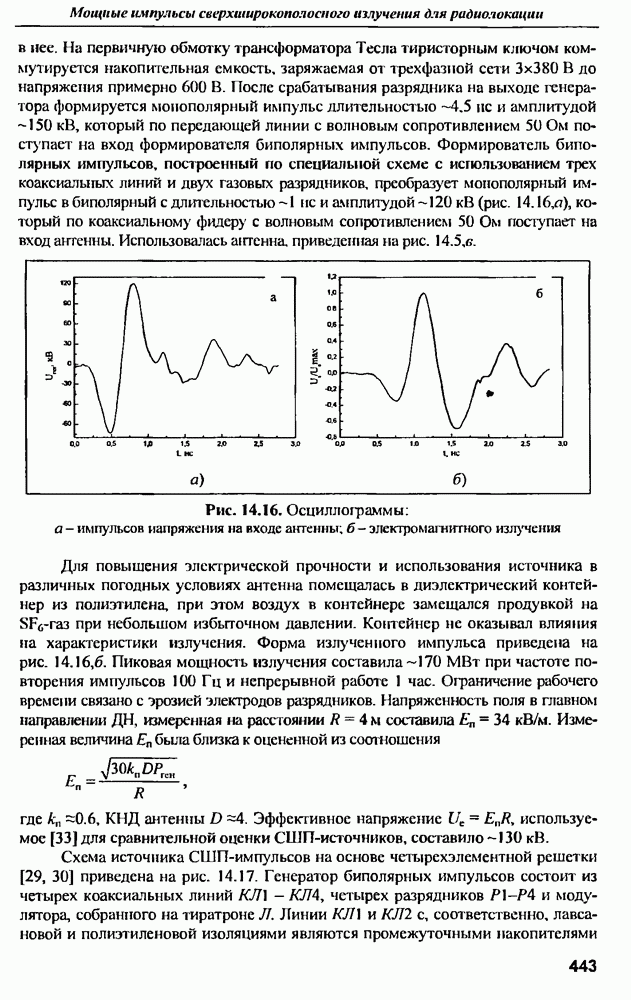
Оценим величину предельного КПД на примере широко известного распределения «косинус на подставке» [22]:  , обеспечивающего изменение максимального УБЛ от
, обеспечивающего изменение максимального УБЛ от  до
до  в зависимости от значения
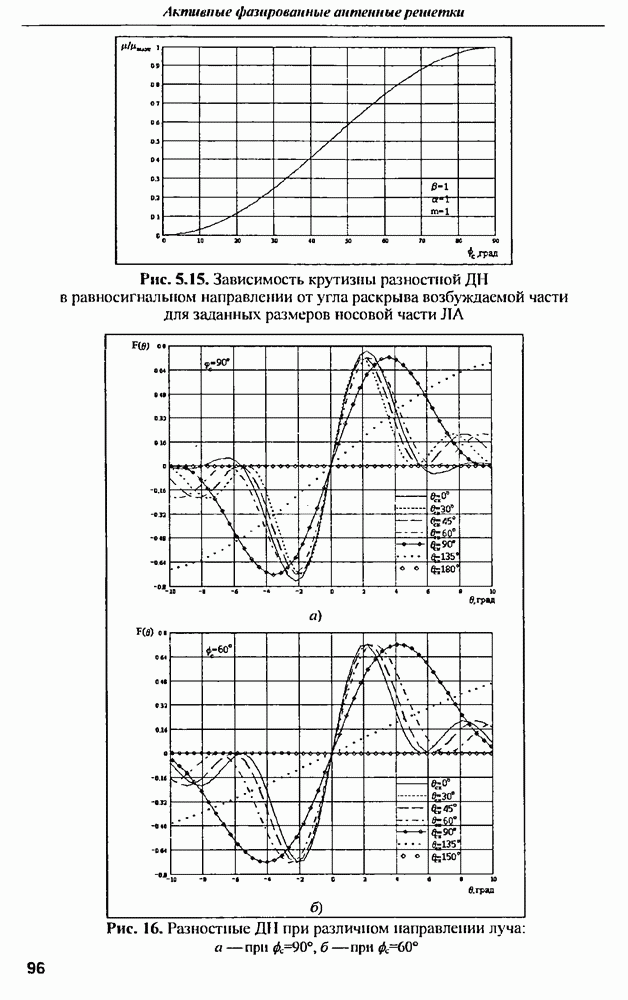
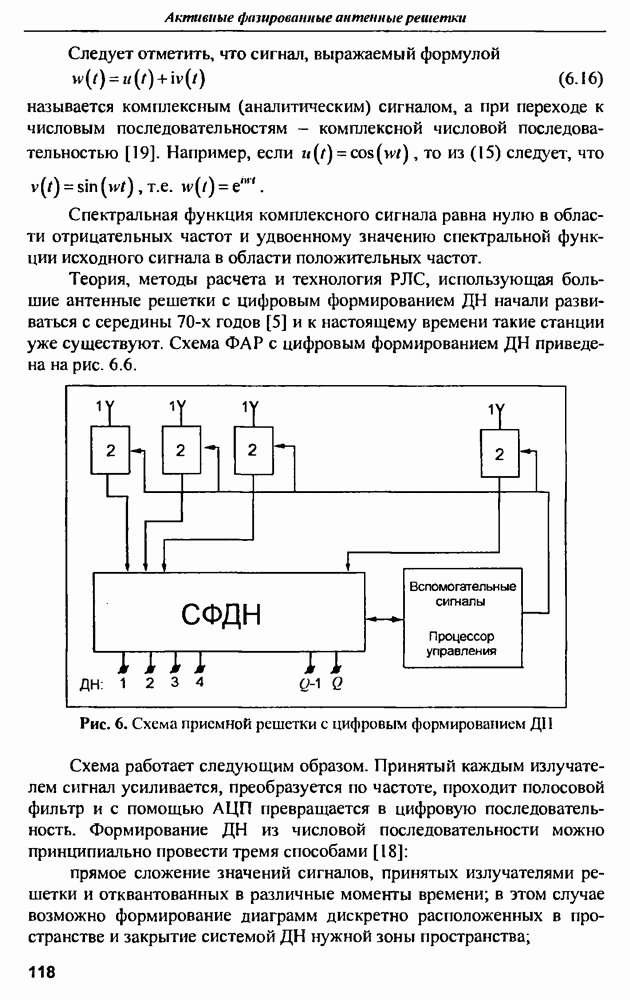
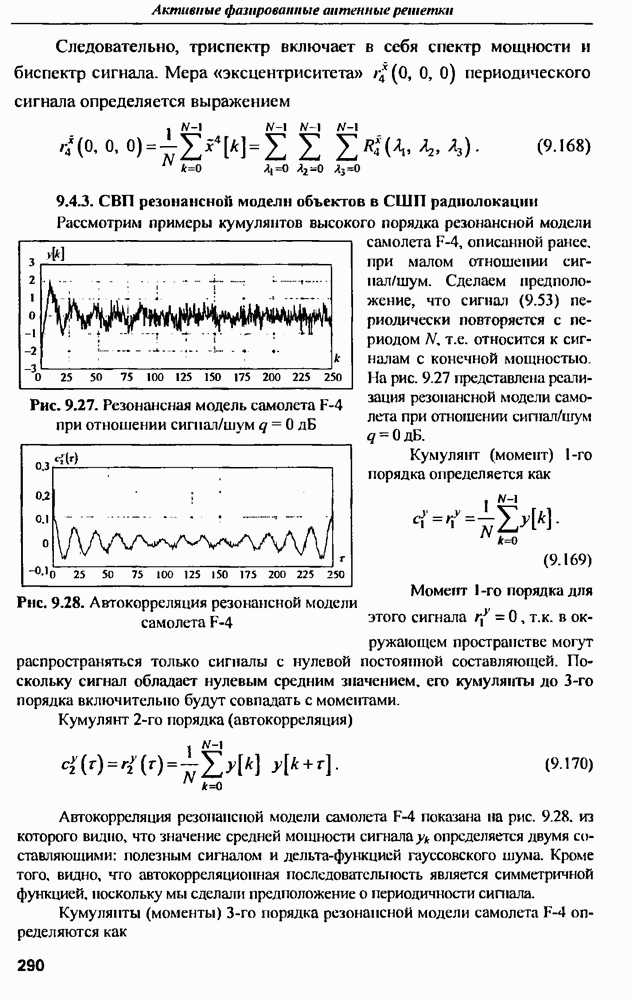
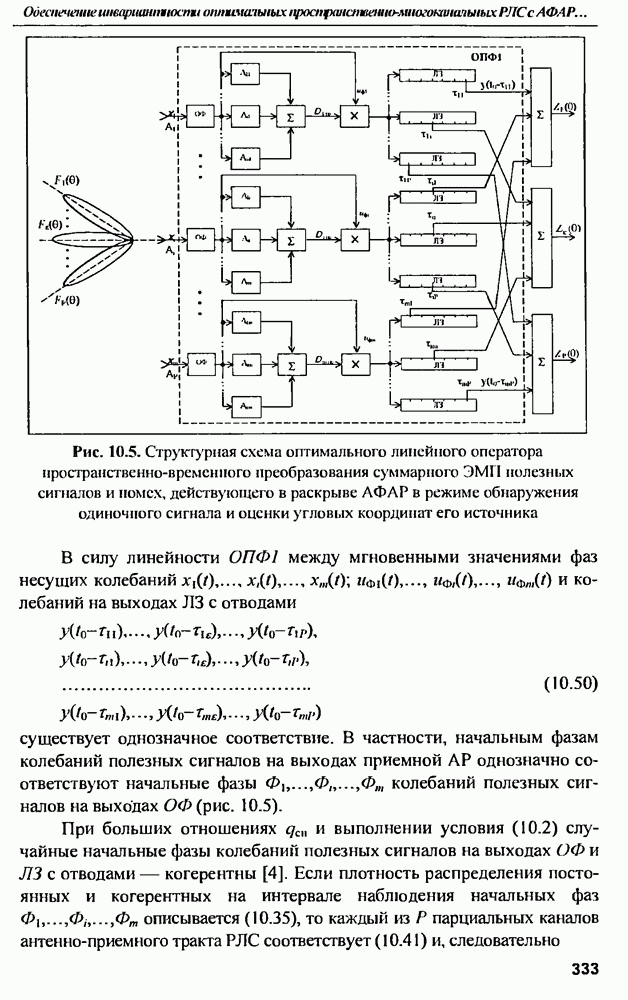
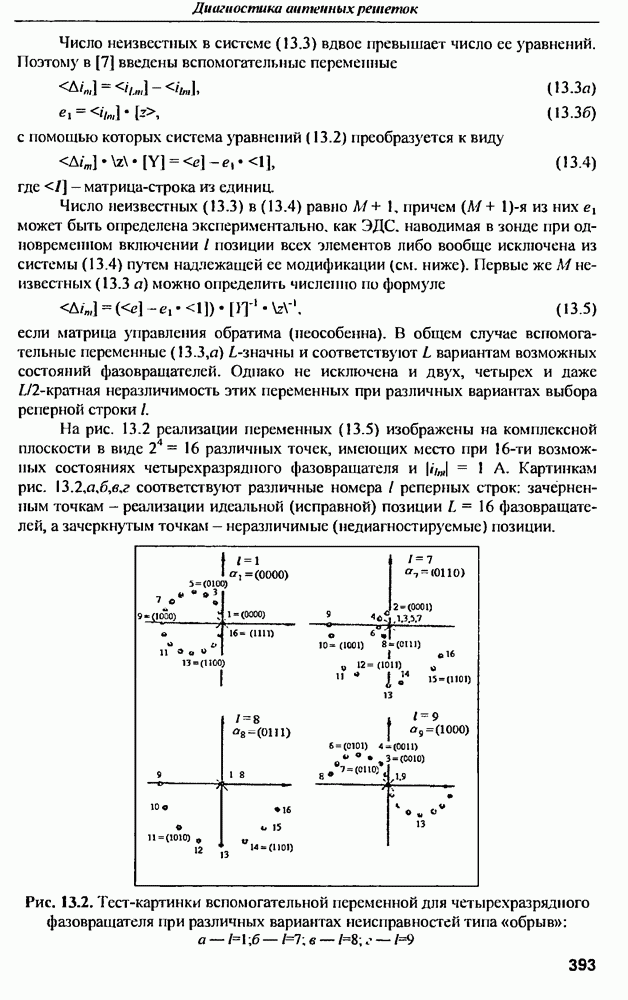
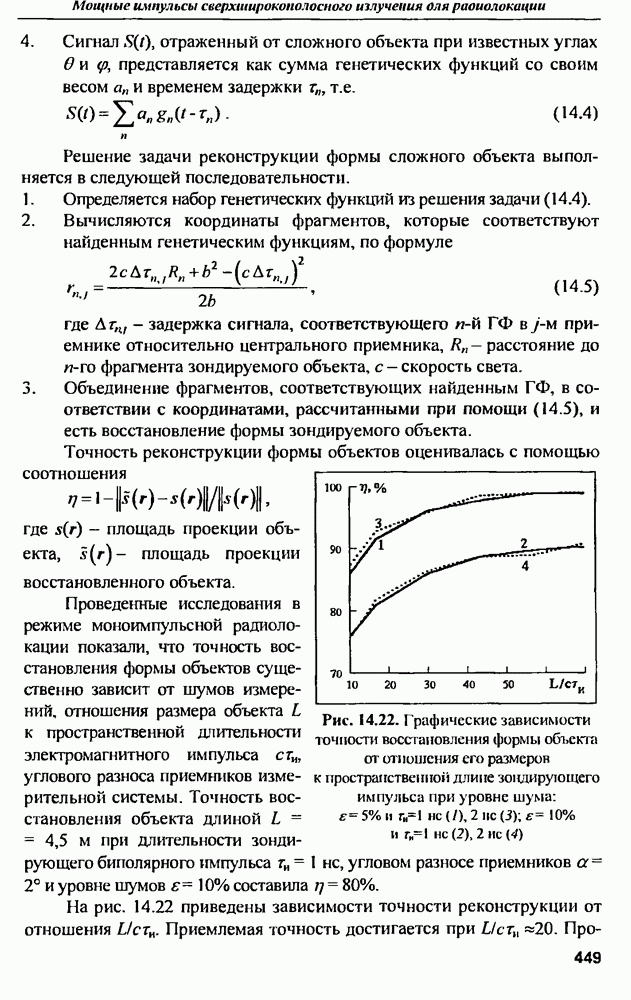
в зависимости от значения  параметра распределения. Результаты расчетов приведены на рис. 12.3.
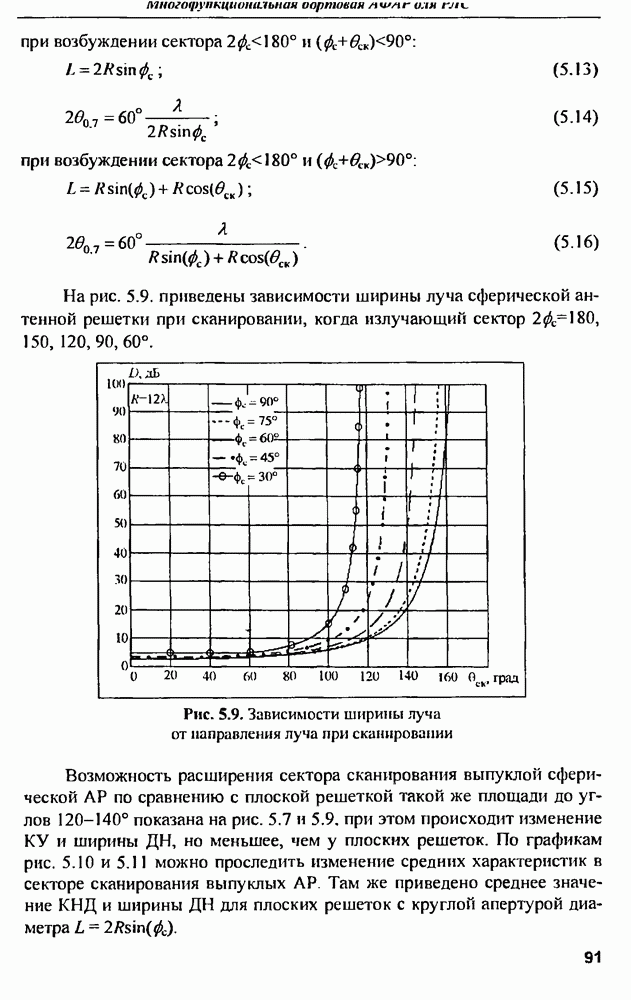
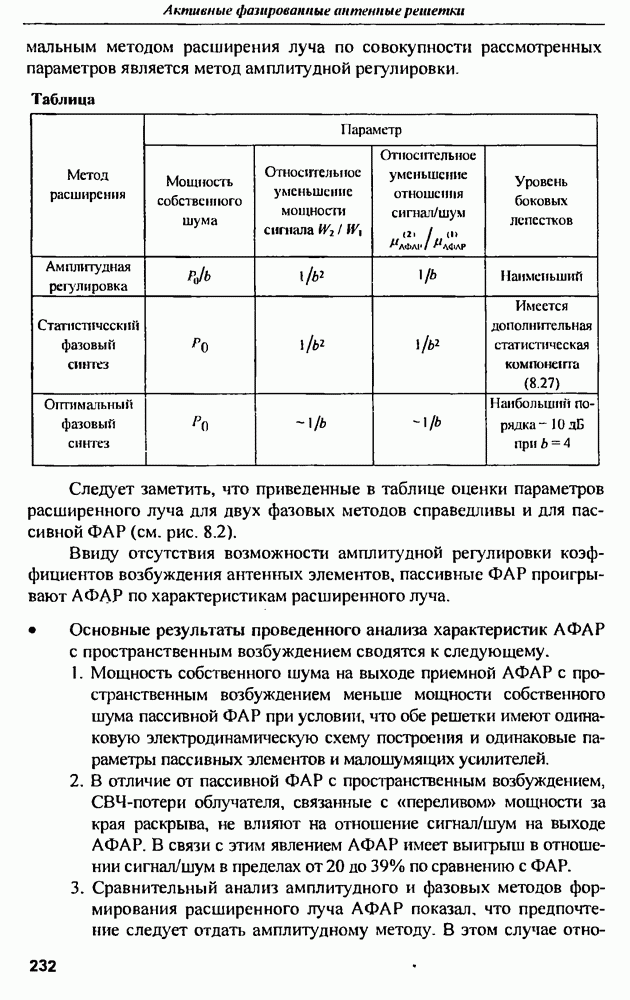
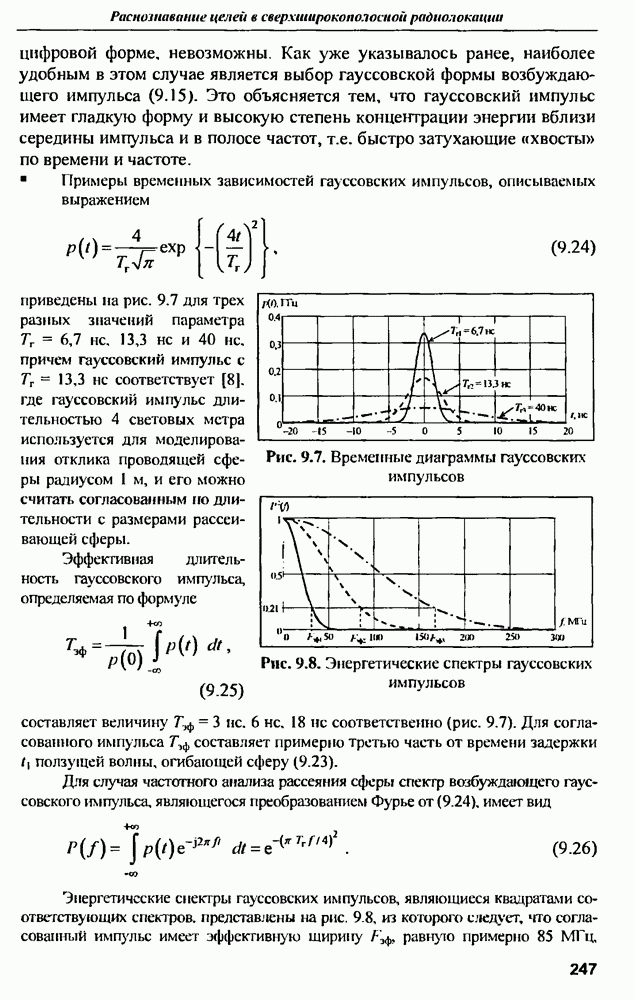
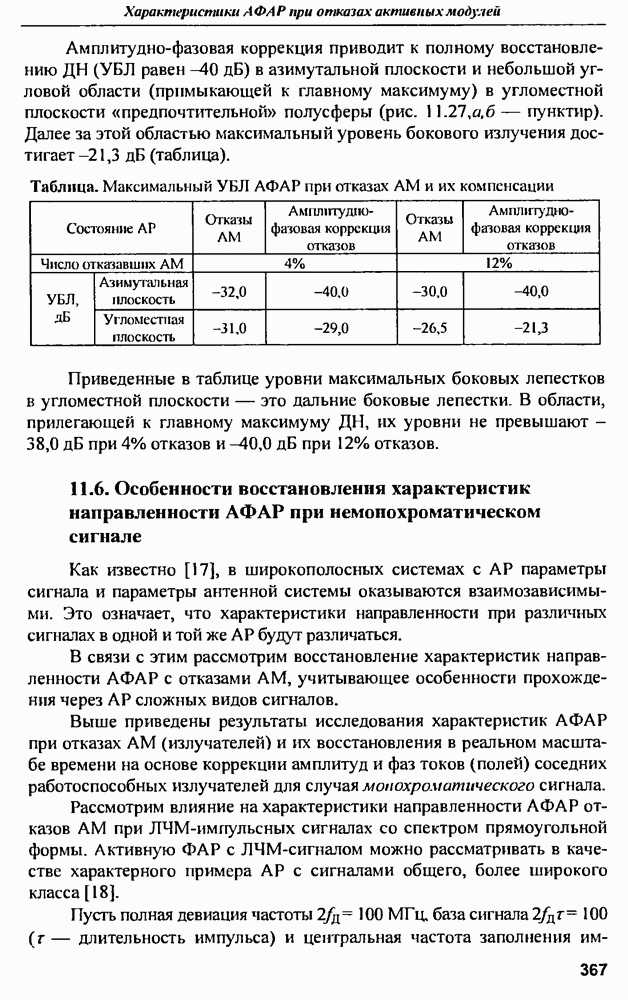
параметра распределения. Результаты расчетов приведены на рис. 12.3.

Рис. 12.3. Зависимость предельного КПД от параметра распределения  для величии затуханий на омические потери: 0, 1, 2, 3, 4 и 5 дБ
для величии затуханий на омические потери: 0, 1, 2, 3, 4 и 5 дБ
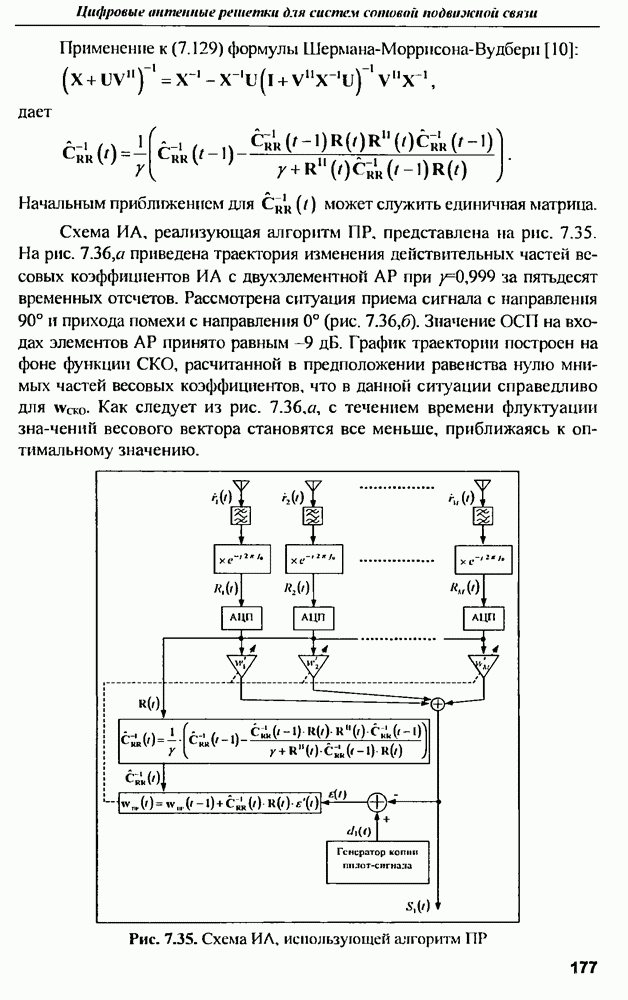
Из графиков следует, что, при разумных омических потерях  предельный КПД мало зависит от параметра распределения и близок к предельному КПД равномерного распределения
предельный КПД мало зависит от параметра распределения и близок к предельному КПД равномерного распределения 

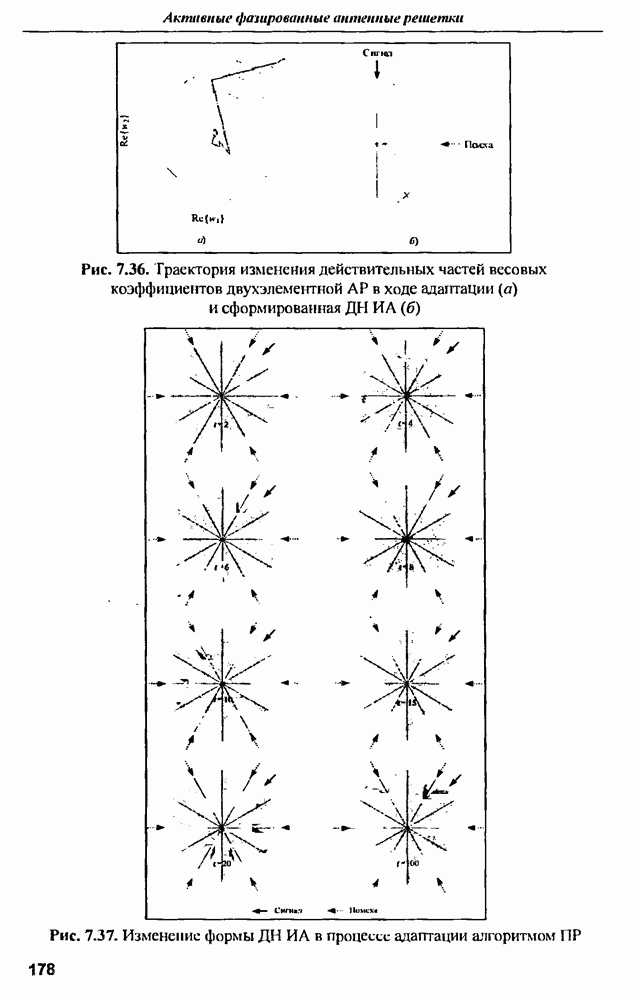
В реальной антенне затухание на излучение не может быть сделано бесконечным и обычно лежит в пределах  .
.
Формула для реального КПД получается из выражения

с учетом (12.25)

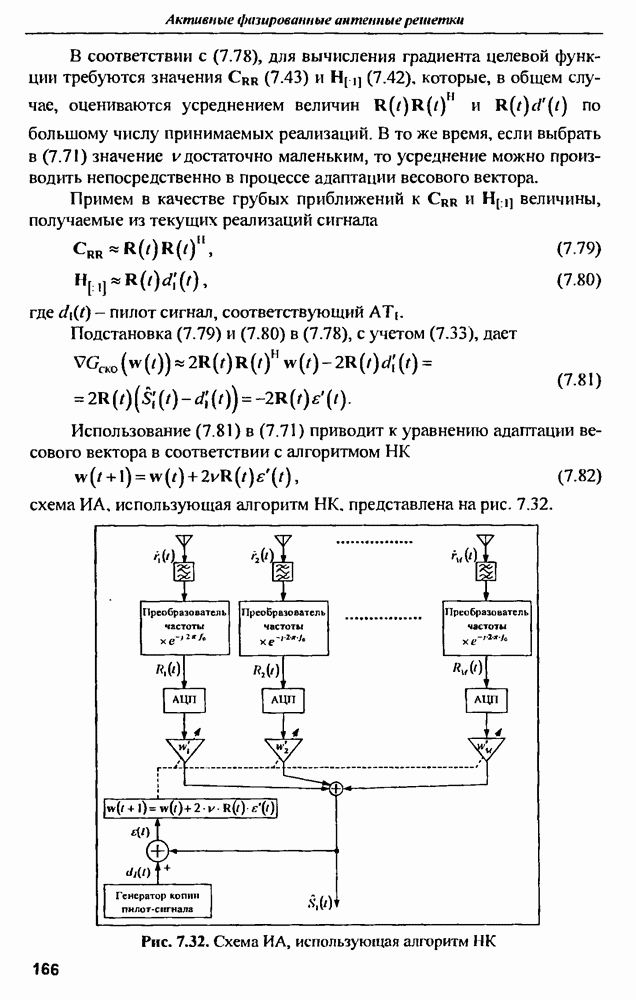
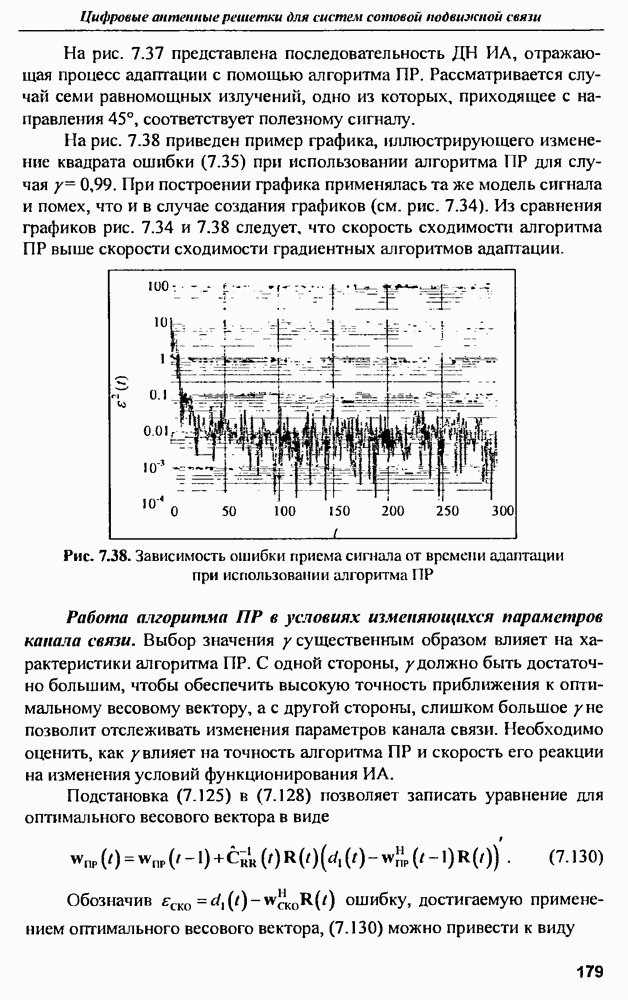
Расчеты показывают, что при затухании 1,5 непера реализуемое значение КПД отличается от предельного примерно на 5%, при 2-х неперах — на 2%. при 2,5 — на 1%. Большая величина затухания на излучение приводит к увеличенным амплитудным и фазовым ошибкам в раскрыве антенны, т. е. к ухудшению характеристик антенны, включая коэффициент усиления [14].
ЛИТЕРАТУРА
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. Особенности построения активной фазированной антенной решетки для радиоэлектронных комплексов
- 1.2. Особенности расчета характеристик АФАР
- 1.3. Приемопередающий модуль АФАР
- 1.4. Активные приборы, используемые в модулях современных АФАР
- 1.5. Состояние и перспективы развития ППМ
- 1.5.2. Параметры и конструкции типичных модулей АФАР
- ГЛАВА 2. Активная передающая ФАР современной твердотельной РЛС
- 2.2. Особенности энергетики АФАР
- 2.3. Расчет прямых потерь мощности в АФАР
- 2.4. Расчет потерь мощности в АФАР за счет ошибок распределения
- 2.5. АФАР твердотельной РЛС 67Н6Е
- ГЛАВА 3. Антенные комплексы для РЛС дальнего обнаружения и контроля космического пространства
- 3.2. Антенные комплексы РЛС «Дунай-3» и «Дунай-3У»
- 3.3. Приемопередающая ФАР для РЛС наблюдения за космическими объектами
- 3.4. Антенный комплекс РЛС дальнего обнаружения «Волга»
- 3.5. Приемопередающее антенно-фидерное устройство РЛС сантиметрового диапазона
- 3.6. Антенные комплексы для перспективных РЛС дальнего обнаружения «Воронеж-ДМ»
- ГЛАВА 4. Цифровая интеллектуальная ФАР — перспективная технология для радиолокационных и радиоинформационных комплексов XXI века
- 4.1. Преимущества адаптивной цифровой ФАР
- 4.2. Структура ЦИФАР и ее основные алгоритмы обработки сигналов
- 4.3. Требования к частоте дискретизации и уровням квантования сигналов в ЦИФАР
- 4.4. Требования к производительности цифровых вычислителен ЦИФАР
- 4.5. Пример реализации ЦИФАР для перспективной крупноапертурной крупномодульной широкополосной РЛС в диапазонах 10—20 см
- 4.6. Пример построения ЦИФАР для бортового ретранслятора в диапазоне частот 8 ГГц перспективной спутниковой телекоммуникационной системы высокоскоростной мобильной связи «Ростелесат»
- ГЛАВА 5. Многофункциональная бортовая активная фазированная антенная решетка для РЛС
- 5.2. Формулировка задач
- 5.3. Решение внешней задачи для сферической решетки
- 5.4. Характеристики направленности сферической решетки
- 5.5. Пеленгационные характеристики сферической решетки
- 5.6. Сектор обзора сферической решетки и других вариантов выпуклой ФАР
- 5.7. Решение внутренней задачи
- 5.8. Система возбуждения модулей
- ГЛАВА 6. Адаптивная цифровая приемная ФАР
- 6.1. Антенные решетки с аналоговым формированием диаграмм направленности
- 6.2. Антенные решетки с цифровым формированием ДН
- 6.3. Элементы и характеристики АЦПФАР
- 6.3.2. Полоса пропускания приемного канала и частота квантования
- 6.3.3. Аналого-цифровое преобразование
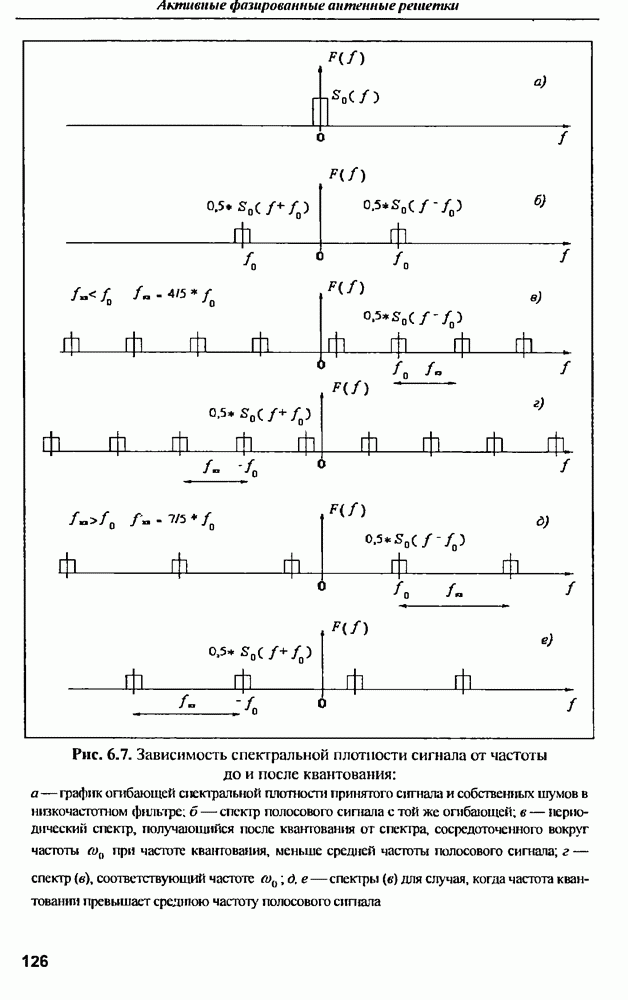
- 6.3.4. Спектры шумов и сигналов после квантования
- 6.3.5. Температура шумов приемного тракта
- 6.3.6. Динамическим диапазон
- 6.4. Применение, особенности и элементная база АЦПФАР
- ГЛАВА 7. Цифровые антенные решетки для систем сотовой подвижной связи
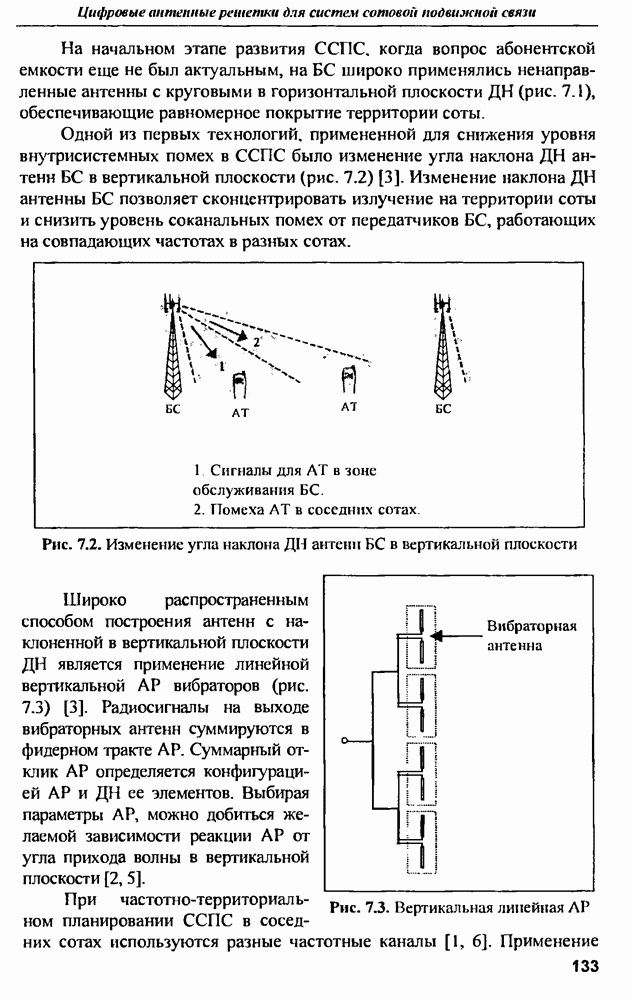
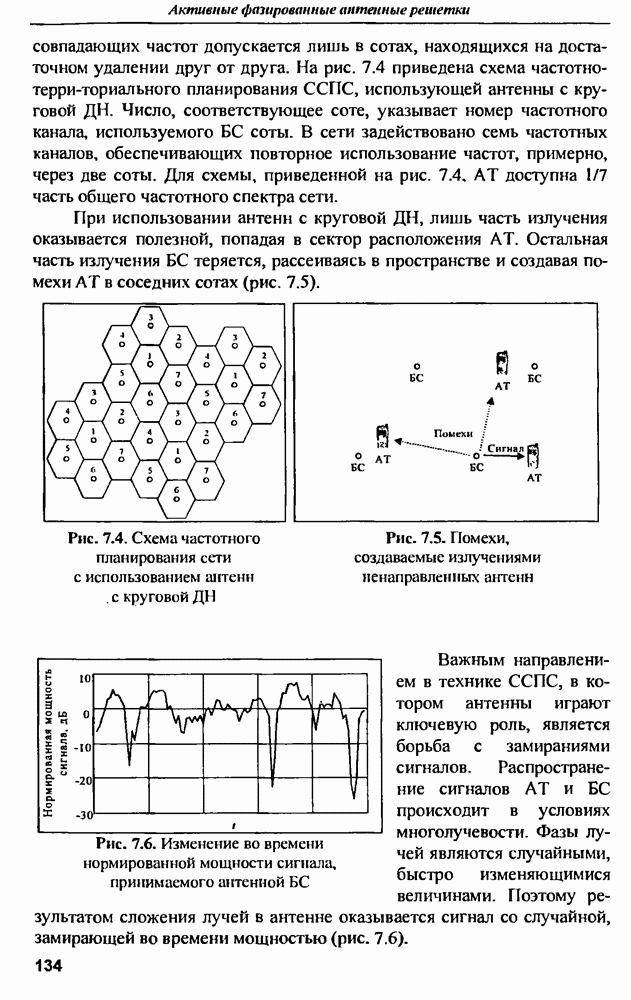
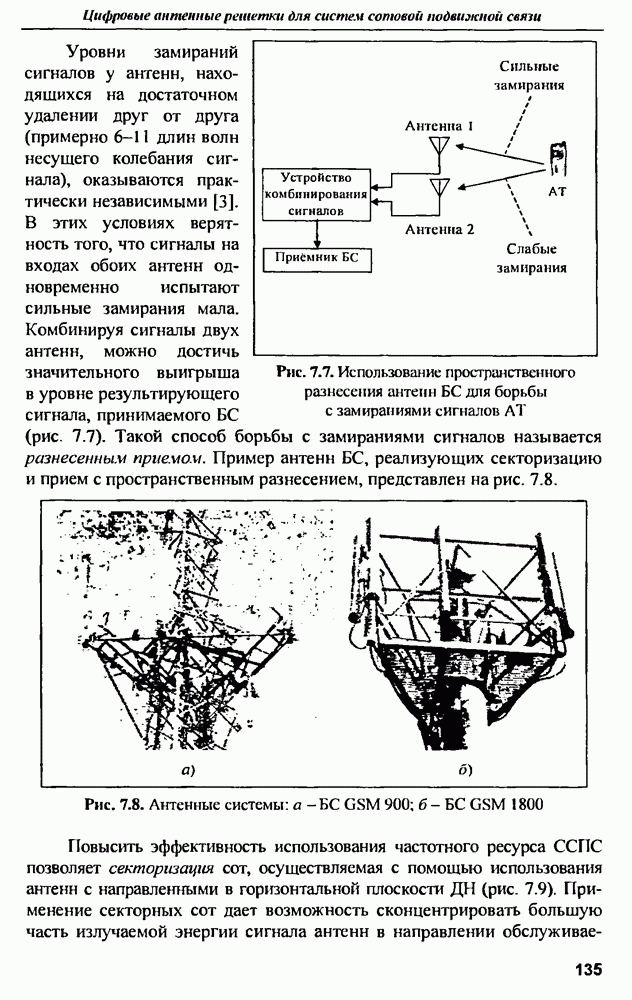
- 7.1. Влияние антенных технологий на развитие систем сотовой подвижной связи (ССПС)
- 7.2. Интеллектуальные антенны на основе цифровых АР
- 7.2.1. Принципы работы: модель адаптивного линейного сумматора
- 7.2.2. Пространственная обработка при приеме сигналов в обратном канале ССПС
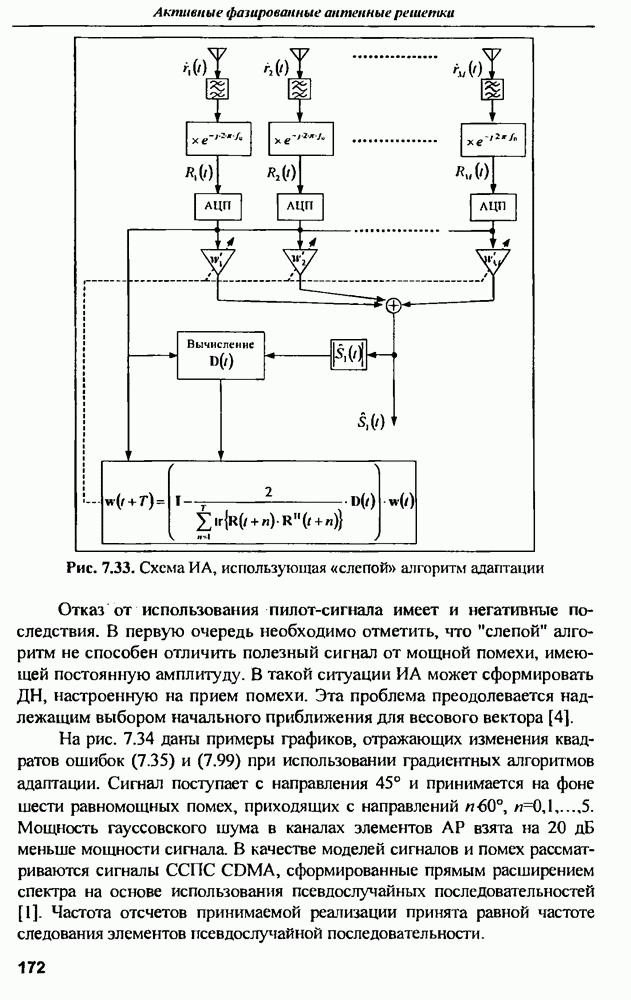
- 7.2.3. Алгоритмы адаптации ИА
- 7.2.4. Применение ИА для передачи сигналов в прямом канале ССПС
- 7.3. Влияние ИА на характеристики ССПС
- 7.3.2. Расчетные модели
- 7.3.3. Абонентская емкость ССПС
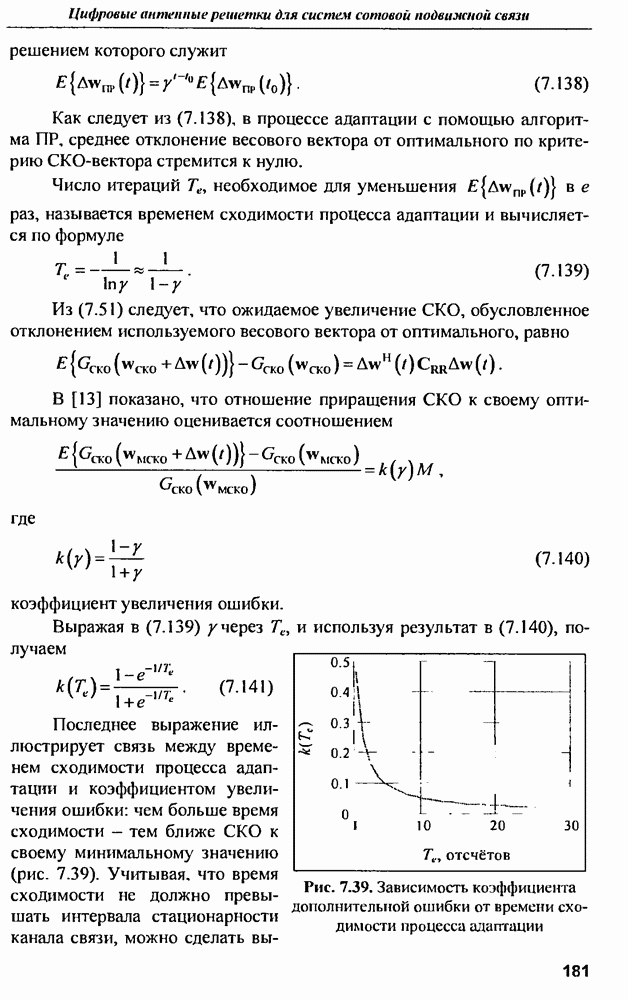
- 7.3.4. Качество связи
- 7.3.5. Площадь покрытия соты
- 7.3.6. Влияние ИА на архитектуру ССПС
- 7.4. Пространственные каналы с МВМВ на основе цифровых АР
- 7.4.1. Теоретико-информационные аспекты передачи данных в пространственных каналах МВМВ
- 7.4.2. Алгоритмы приема сигналов
- 7.4.3. Передача сигналов в каналах с МВМВ
- 7.4.4. Пространственно-временное кодирование и разнесенная передача
- Приложение 7.1. Комплексная огибающая сигнала и квадрату рная обработка в системах радиосвязи
- Приложение 7.2. Многолучевые ИА
- ГЛАВА 8. Оценка отношения сигнал/шум на выходе приемной АФАР с пространственным возбуждением
- 8.2. Определение мощности шума на выходе приемной АФАР
- 8.3. Отношение сигнал/шум на выходе приемной АФАР
- 8.4. Задача формирования расширенного луча АФАР
- 8.4.2. Использование метода статистического фазового синтеза для расширения луча
- 8.4.3. Оценка возможностей метода оптимального фазового синтеза расширенного луча, минимизирующего потери принимаемой мощности
- 8.4.4. Сравнение характеристик АФАР при различных методах формирования расширенного луча
- ГЛАВА 9. Распознавание целей в сверхширокополосной радиолокации
- 9.1.1. Методы теоретического расчета ЭПР
- 9.1.2. Тела простой геометрической формы
- 9.1.3. Характеристики рассеянна антенн
- 9.2. Резонансная модель рассеяния целей в сверхширокополосной радиолокации
- 9.2.2. Резонансная модель рассеяння электромагнитного поля радиолокационных объектов
- 9.3. Методы оценки характеристик сигналов
- 9.3.1. Метод Прони
- 9.3.2. Метод матричных пучков
- 9.4. Обработка сигналов с использованием статистик высокого порядка
- 9.4.2. Статистики высокого порядка детерминированных импульсных и периодических сигналов
- 9.4.3. СВП резонансной модели объектов в СШП радиолокации
- 9.5. Оценка параметров резонансных моделей целей в СШП радиолокации
- 9.5.1. Статистики высокого порядка резонансной модели объектов
- 9.5.2. Сравнительный анализ методов оценки параметров резонансных моделей с использованием статистик высокого порядка
- 9.6. Распознавание радиолокационных объектов
- 9.6.1. Сигнатурное распознавание целей по результатам оценки параметров резонансной модели
- 9.6.2. Распознавание радиолокационных объектов с помощью метода Е-импульса
- 9.7. Заключение
- ГЛАВА 10. Обеспечение инвариантности оптимальных пространственно-многоканальных РЛС с АФАР к коррелированным помехам
- 10.2. Обнаружение цели с известными координатами
- 10.3. Обнаружение цели и определение ее угловых координат
- 10.4. Обнаружение цели и измерение ее скорости сближения с РЛС
- 10.5. Условия инвариантности оптимальных РЛС к помехам
- 10.6. Потенциальные возможности оптимальных антенно-приемных трактов РЛС, соответствующих алгоритмам (10.39), (10.43)
- ГЛАВА 11. Характеристики активных ФАР при отказах активных модулей
- 11.2. Диаграммы направленности и СКУ боковых лепестков при амплитудной и амплитудно-фазовой компенсании множественных отказов
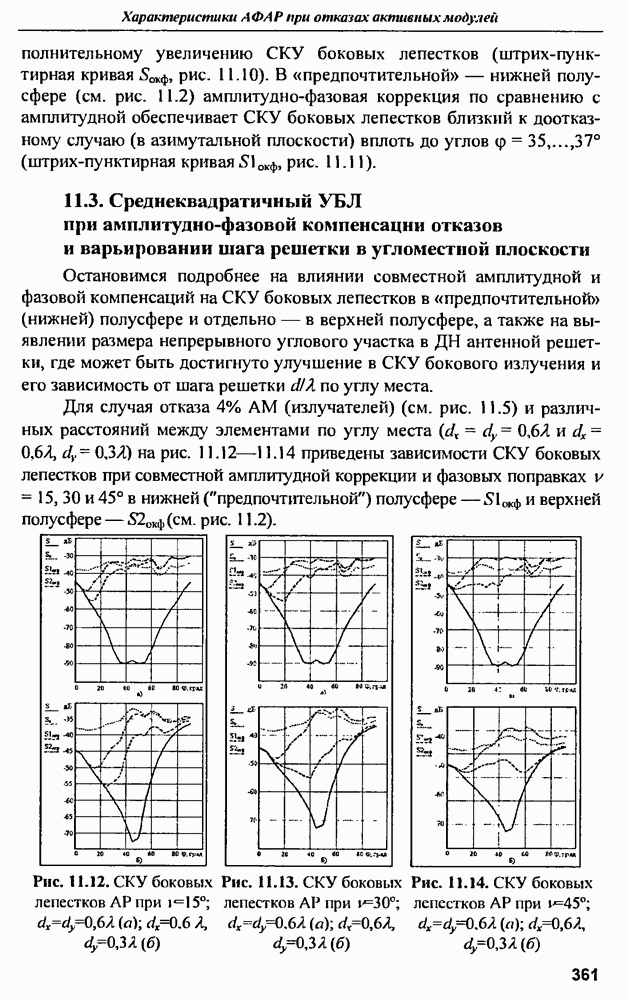
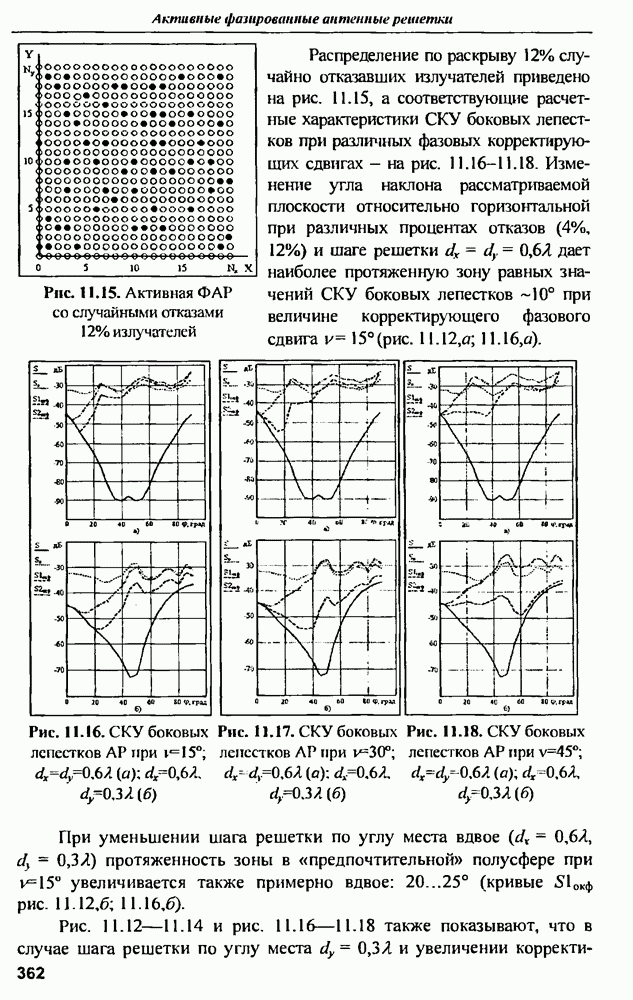
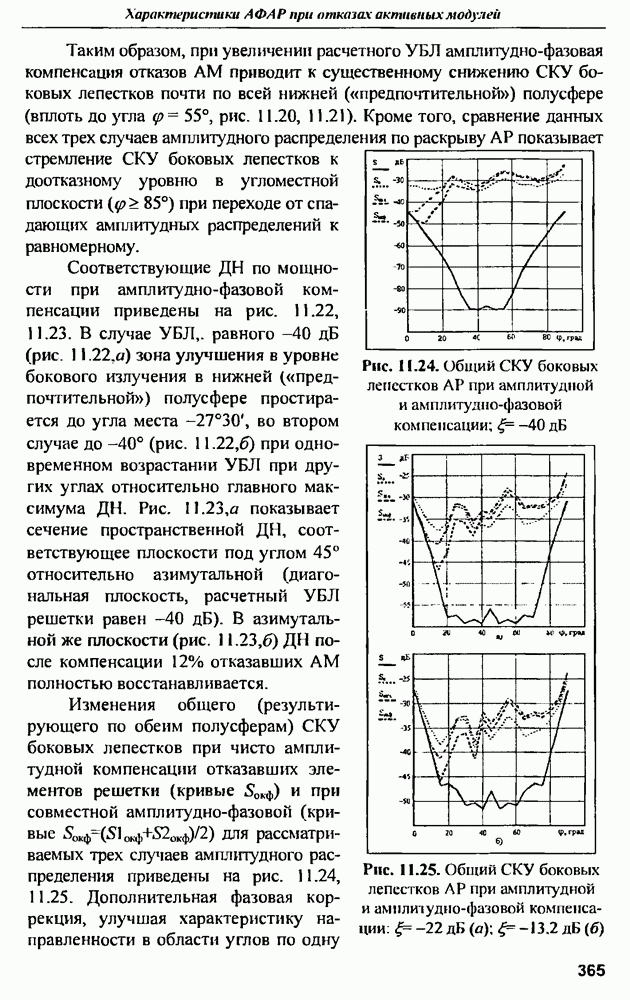
- 11.3. Среднеквадратичный УБЛ при амплитудно-фазовой компенсации отказов и варьировании шага решетки в угломестной плоскости
- 11.4. Влияние закона амплитудного распределения на характеристики АФАР при отказах АМ
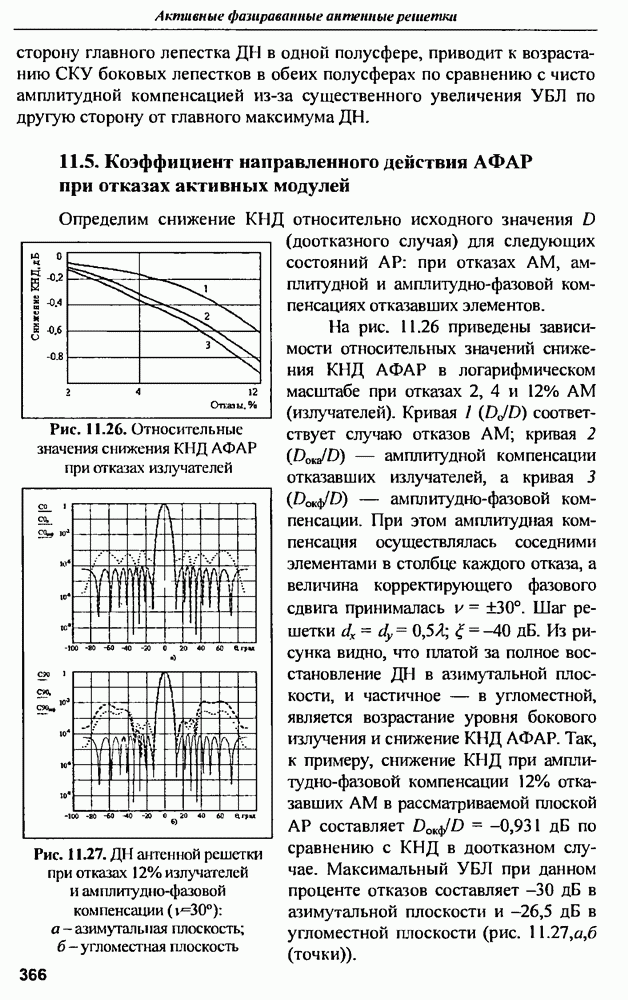
- 11.5. Коэффициент направленного действия АФАР при отказах активных модулей
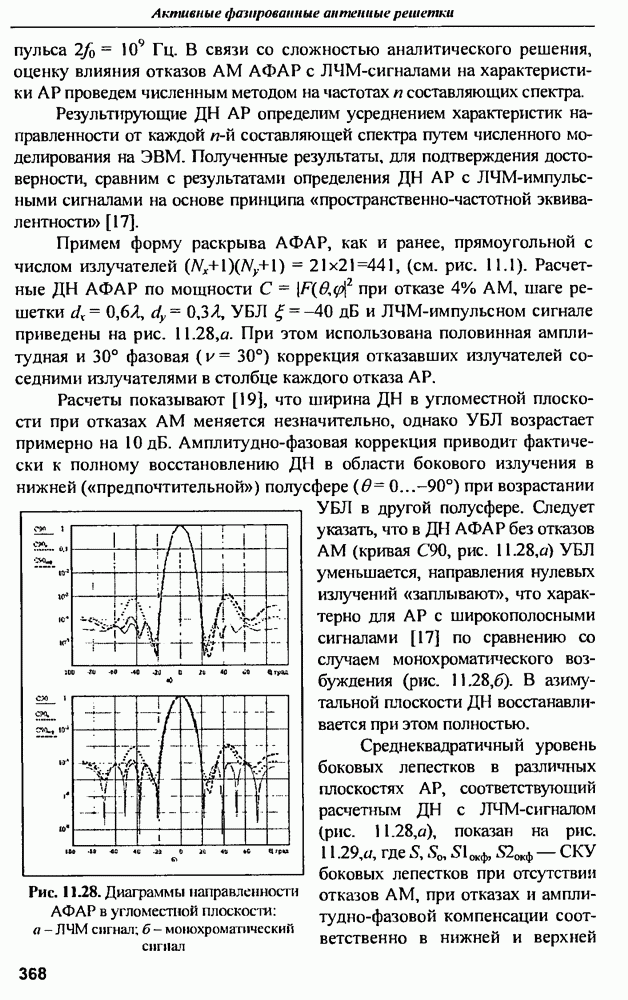
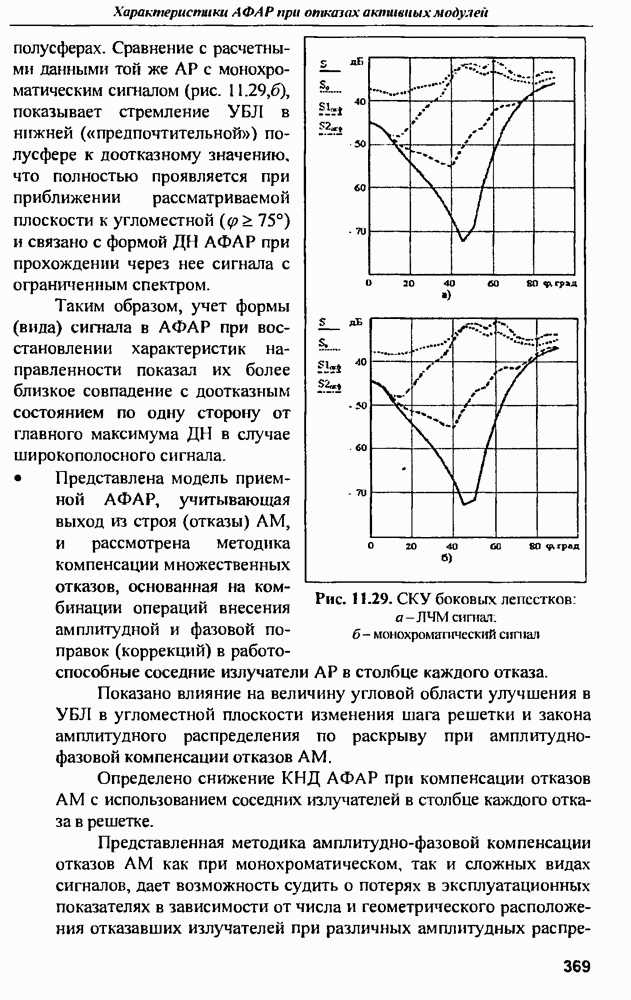
- 11.6. Особенности восстановления характеристик направленности АФАР при немонохроматическом сигнале
- ГЛАВА 12. Вопросы расчета линейных антенных решеток бегущей волны
- 12.1. Общие свойства линейных антенных решеток бегущей волны
- 12.2. Расчет на заданное амплитудное распределение и энергетические характеристики антенны
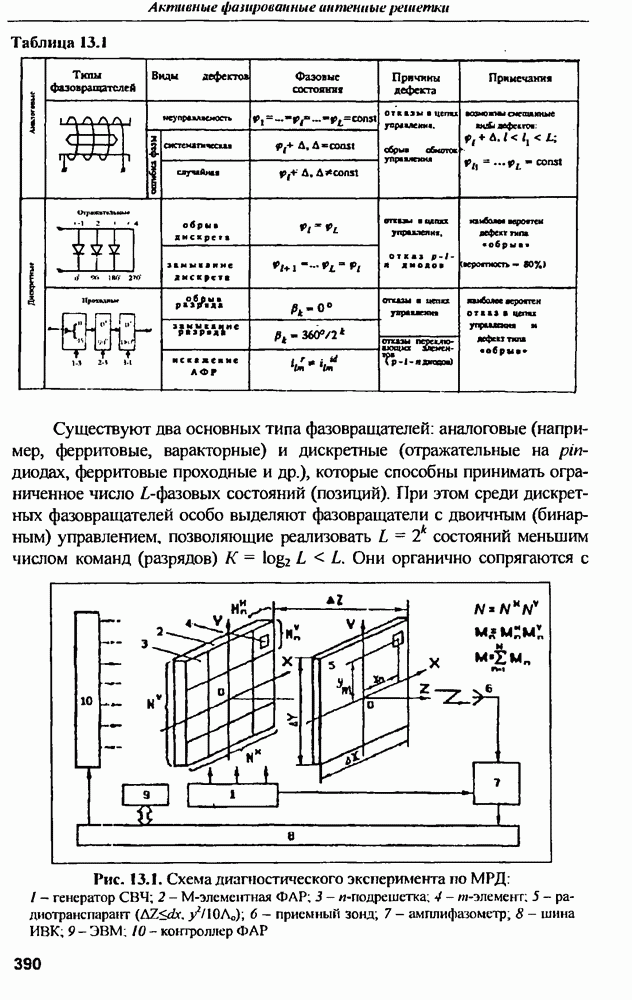
- ГЛАВА 13. Диагностика антенных решеток
- 13.2. Ближнезонные фазовые методы диагностики ФАР
- 13.2.2. Метод реконструктивной диагностики (МРД) ФАР
- 13.2.4. Селективная диагностика ФАР
- 13.2.5. Цифровая реализация МРД
- 13.2.6. Возможности МРД
- 13.2.7. МРД на основе дискретного преобразования Фурье (ДПФ)
- 13.2.8. Комбинированный МРД на основе БПУА и БПФ
- 13.2.9. Сопоставление МРД с другими методами
- 13.3. Бесфазовые методы диагностики ФАР
- 13.3.1. Метод, использующий ДПФ в базисе экспоненциальных функций
- 13.3.2 Метод, использующий ДПФ в базисе функций Уолша (метод ДПУ)
- 13.3.3. Адаптивный алгоритм диагностики ФАР
- 13.3.4. Сравнение метода ДПУ и адаптивного метода диагностики ФАР
- Приложение 13.П1. Алгоритм диагностики ФАР методом ДПФ в базисе функций Уолша (метод ДПУ)
- Приложение 13.П2. Адаптивный алгоритм диагностики ФАР, основанный на измерении комплексных амплитуд сигналов
- Приложение 13.П3. Адаптивный алгоритм диагностики ФАР, основанный на измерении мощности сигналов
- Дополнения к приложениям 13.П1, 13.П2,13.П3
- ГЛАВА 14. Мощные импульсы сверхширокополосного излучения для радиолокации
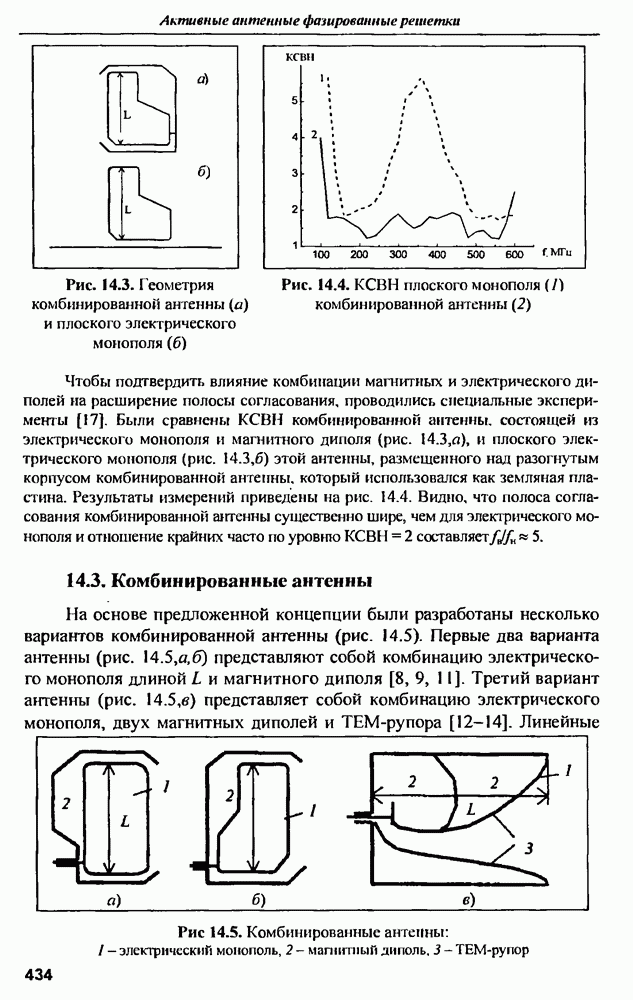
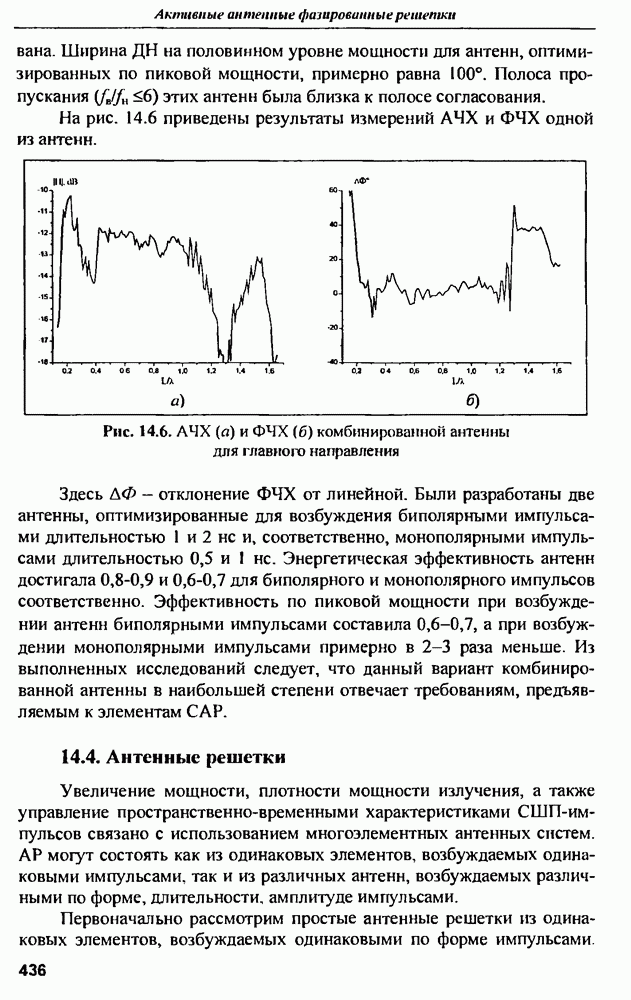
- 14.2. Синтез сверхширокополосных антенн
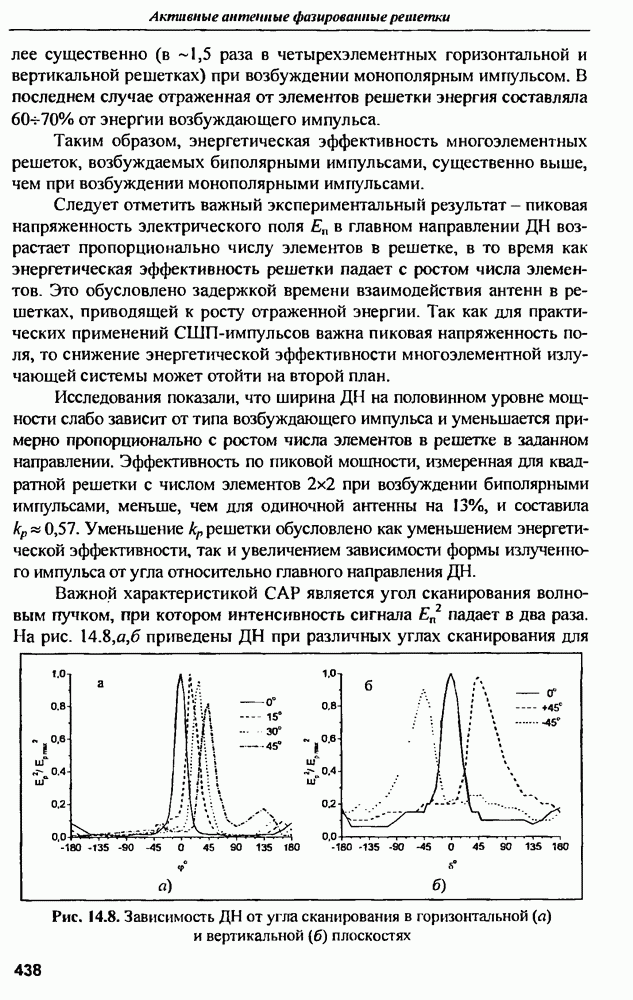
- 14.3. Комбинированные антенны
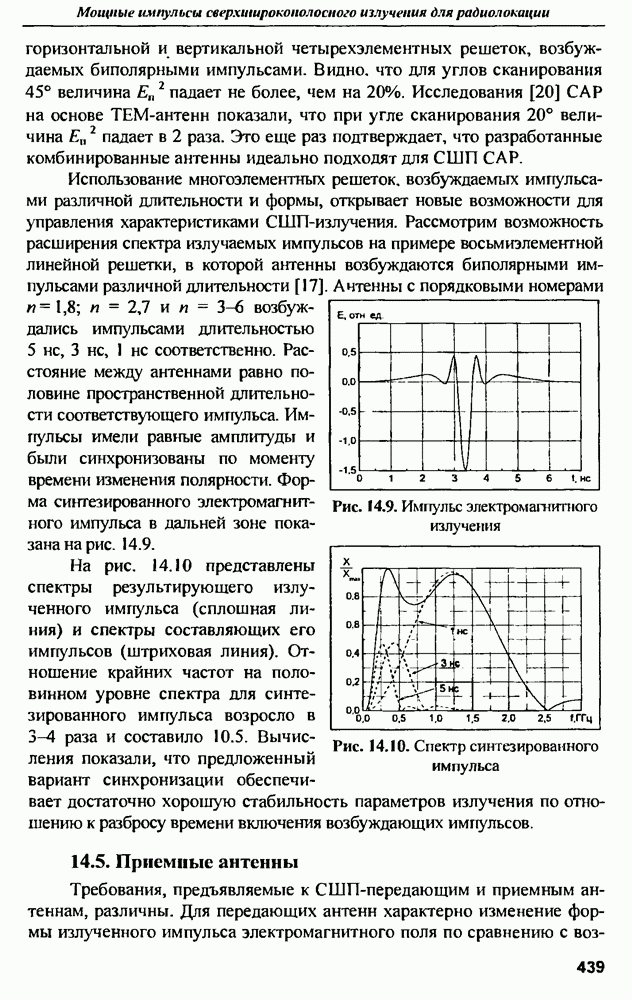
- 14.4. Антенные решетки
- 14.5. Приемные антенны
- 14.6. Мощные источники СШП-излучения
- 14.7. Методы оценивания импульсных характеристик
- 14.8. Реконструкция формы объектов
- ГЛАВА 15. Волоконно-оптическое распределение сигналов по модулям АФАР
- 15.1. Проблема распределения сигналов АФАР и основные подходы к ее решению с использовнием волоконных систем
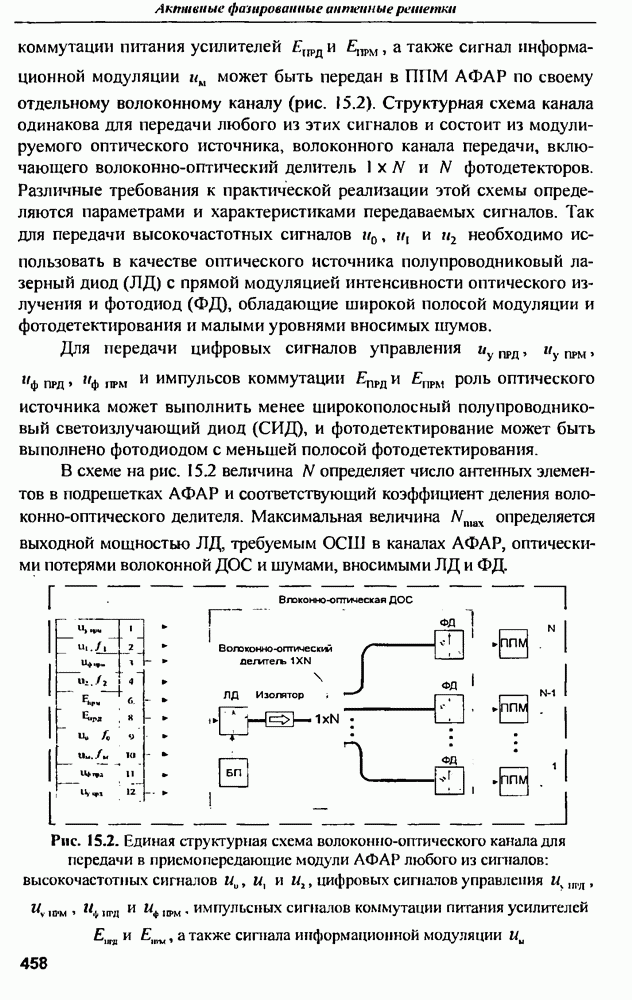
- 15.2. Краткий анализ и классификация сигналов активного модуля ФАР
- 15.3. Структурная схема волоконного канала передачи сигналов в ППМ АФАР
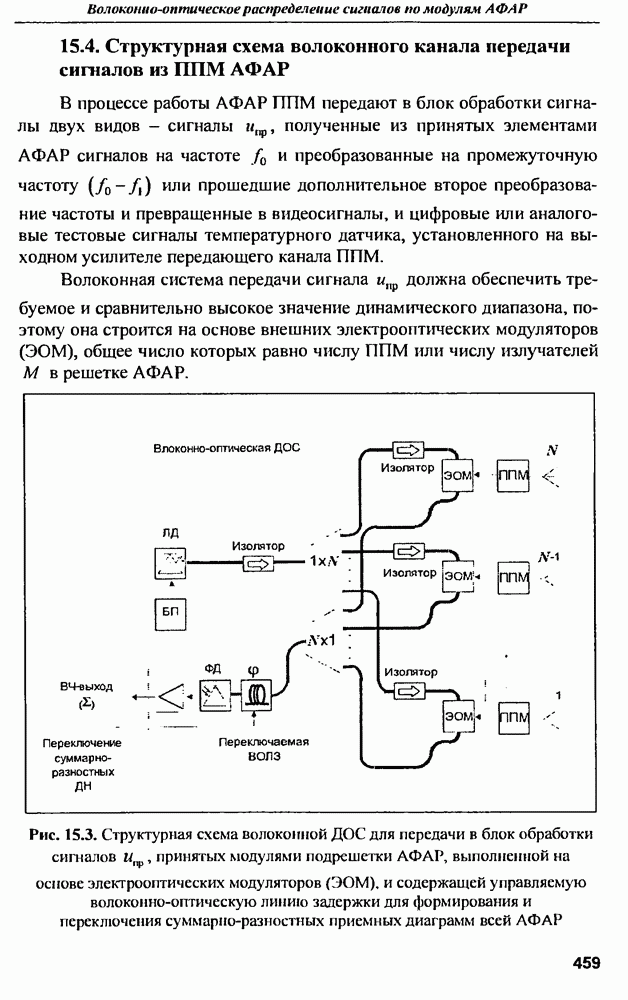
- 15.4. Структурная схема волоконного канала передачи сигналов из ППМ АФАР
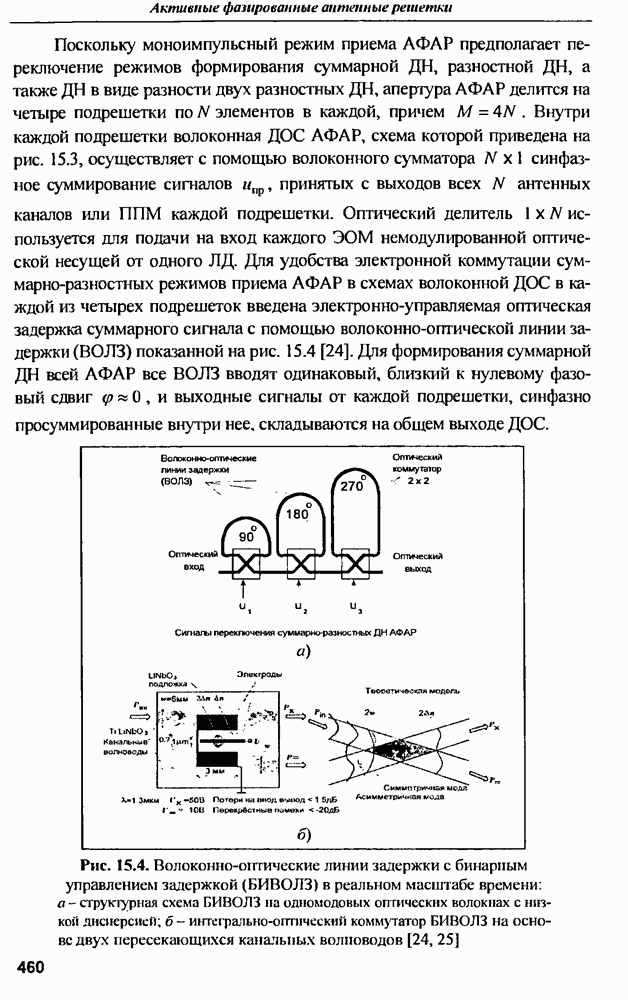
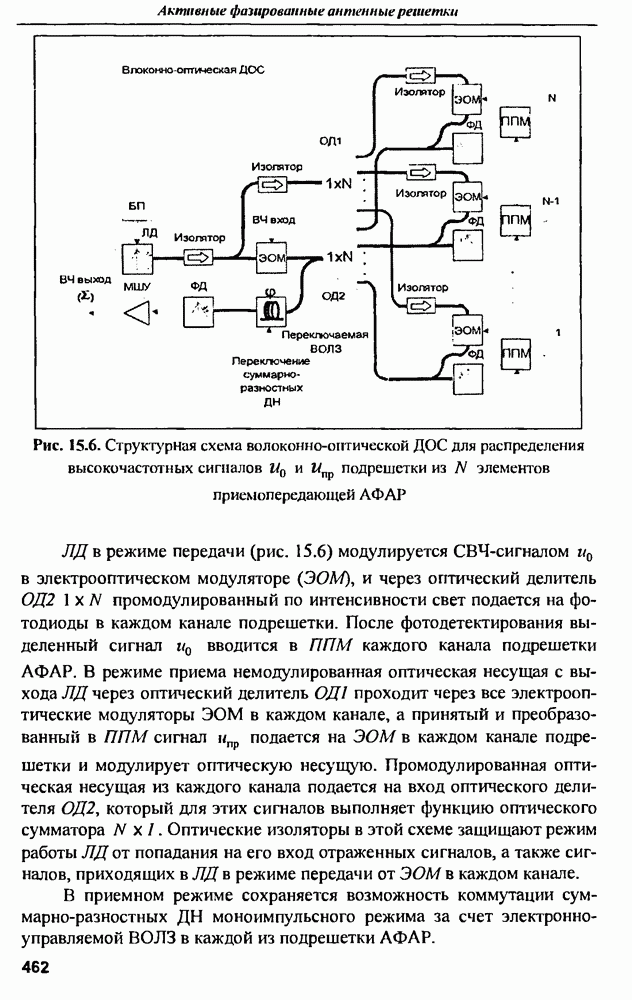
- 15.5. Структурные схемы волоконных систем распределения высокочастотных сигналов по модулям приемопередающей АФАР
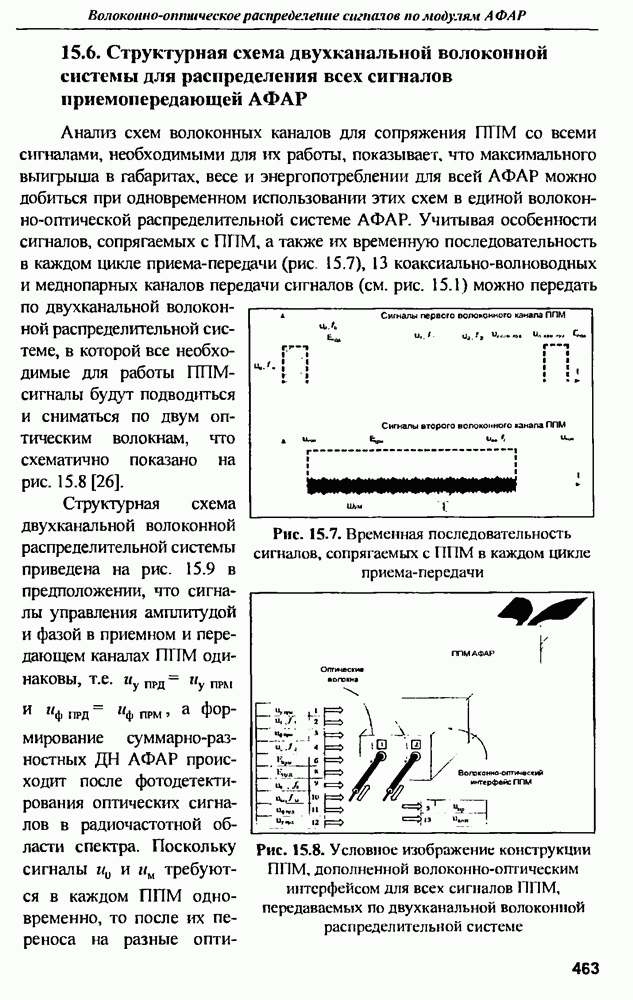
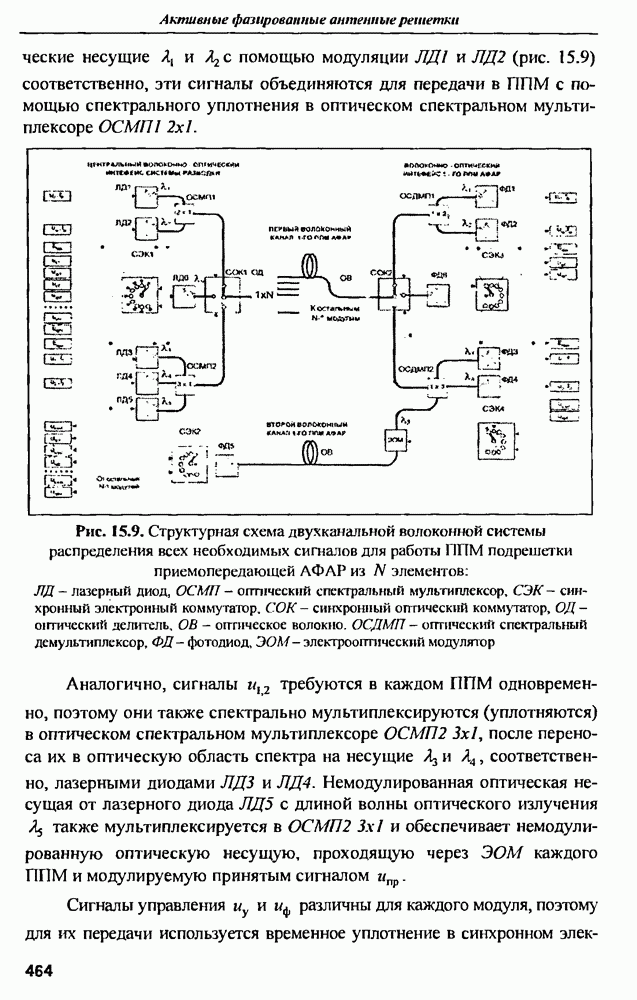
- 15.6. Структурная схема двухканальной волоконной системы для распределения всех сигналов приемопередающей АФАР
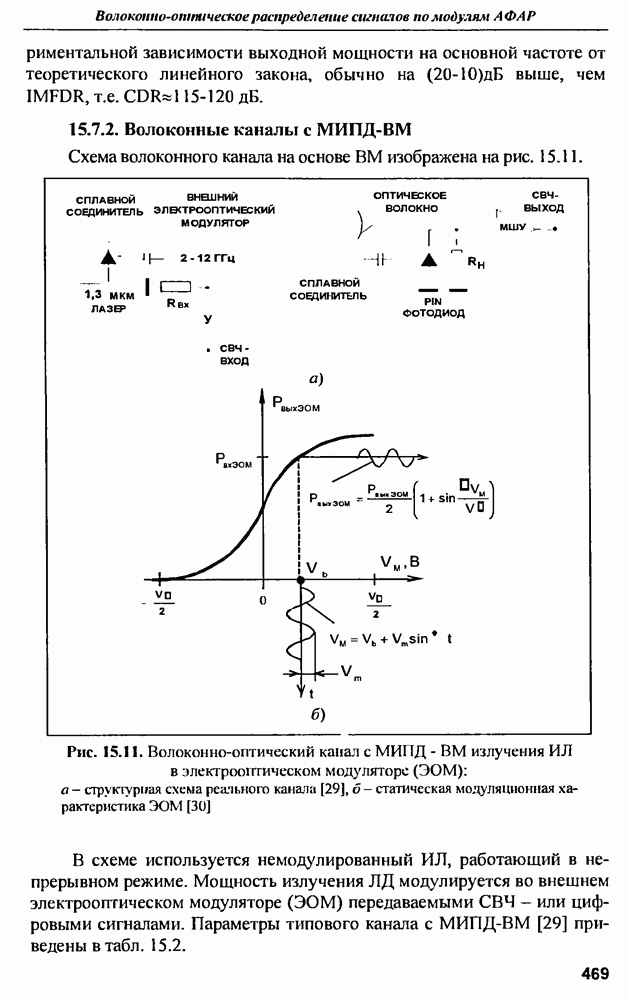
- 15.7. Основные типы волоконных каналов, используемых для построения волоконных распределительных систем.
- 15.7.1. Волоконный канал с МИПД-ПМ
- 15.7.2. Волоконные каналы с МИПД-ВМ
- 15.7.3. Сравнение характеристик волоконных каналов с прямой и внешней модуляцией оптической несущей
- 15.8. Элементная база волоконной распределительной системы АФАР
- 15.8.1. Источники оптического излучения
- 15.8.2. Фотодетекторы
- 15.8.3. Оптическое волокно
- 15.8.4. Оптические делители
- 15.8.5. Внешние модуляторы
- 15.8.6. Оптические мультиплексоры с частотным уплотнением каналов
- 15.8.7. Оптические мультиплексоры с временным уплотнением каналов
- 15.9. Примеры практической реализации волоконных каналов для передачи отдельных сигналов АФАР